Geum.ru

Примерный тест для полусеместровой аттестации

Вид материалаДокументы
Подобный материал:
Численные методы

Содержание текущего и промежуточного контроля

Примерный тест для полусеместровой аттестации

ВАРИАНТ 1
  1. Что не является этапом решения задач с использованием ЭВМ:
    1. этап моделирования
    2. этап алгоритмизации
    3. этап минимизации
    4. этап реализации
  2. а = 2,91385; а = 0,0097, тогда в числе а в широком смысле верны цифры:
    1. 2,9,1
    2. 9,1,3
    3. 1,3,8
    4. нет верных цифр
  3. Выберите два варианта ответа

Процесс нахождения корней разбивается на два этапа:
    1. отделение корней
    2. нахождение корней
    3. уточнение корней
    4. выбор корней
  1. Рисунком описан метод уточнения корней:


у



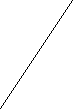
а


в

х

    1. метод касательных
    2. метод итераций
    3. метод хорд
    4. метод половинного деления
  1. В методе касательных для нахождения х n+1 при выполнении условия F(a)*F’’(a) >0 за х0 будет взято:
    1. а
    2. x1
    3. b
    4. задается в условии задачи
  2. Какой метод является самым точным из всех методов решения уравнений:
    1. метод итераций
    2. метод хорд
    3. метод интерполирования
    4. нет метода
  3. Выберите два варианта ответа

К точным методам решения систем линейных алгебраических уравнений относятся:
    1. метод итераций
    2. метод Гаусса
    3. метод Крамера
    4. метод Зейделя
  1. В
    x
    геометрической интерпретации точки х0, х1, х2, х3, …хn называются:











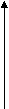
X0 X1 X2 X3 X4 … XN y

    1. узлы интерполирования
    2. узлы интерполяризации
    3. узлы интерполяции
    4. узлы итерации
  1. К интерполированию не относятся:
    1. многочлен Лагранжа
    2. первый многочлен Ньютона
    3. многочлен Ларанжа
    4. второй многочлен Ньютона
  2. Выберите два варианта ответа

При решении нелинейных уравнений методом итераций, итерационная

последовательность бывает:
    1. сходящаяся
    2. возрастающая
    3. убывающая
    4. расходящаяся



Примерный перечень вопросов к коллоквиуму
  1. Этапы решения прикладной задачи. Структура полной погрешности.
  2. Абсолютная и относительная погрешность. Верные значащие цифры в узком и широком смысле. Оценка погрешностей арифметических действий.
  3. Постановка задачи численного нахождения корней уравнения. Способы отделения корней: графический и аналитический.
  4. Методы уточнения корней: половинного деления, хорд, касательных, комбинированный (геометрическая интерпретация и вывод формул).
  5. Метод простой итерации. Теорема о сходимости итерационной последовательности. Оценка погрешности методов.
  6. Метод Ньютона решения системы нелинейных уравнений.
  7. Решение системы линейных уравнений методом Крамера.
  8. Решение системы линейных уравнений методом Гаусса.
  9. Решение системы линейных уравнений методом итераций.
  10. Методы наилучшего приближения.
  11. Дискретный вариант среднеквадратичных приближений.



Примерный перечень вопросов к зачету
  1. Этапы решения прикладной задачи. Структура полной погрешности.
  2. Абсолютная и относительная погрешность. Верные значащие цифры в узком и широком смысле. Оценка погрешностей арифметических действий.
  3. Постановка задачи численного нахождения корней уравнения. Способы отделения корней: графический и аналитический.
  4. Методы уточнения корней: половинного деления, хорд, касательных, комбинированный (геометрическая интерпретация и вывод формул).
  5. Метод простой итерации. Теорема о сходимости итерационной последовательности. Оценка погрешности методов.
  6. Метод Ньютона решения системы нелинейных уравнений.
  7. Решение системы линейных уравнений методом Крамера.
  8. Решение системы линейных уравнений методом Гаусса.
  9. Решение системы линейных уравнений методом итераций.
  10. Методы наилучшего приближения.
  11. Дискретный вариант среднеквадратичных приближений.
  12. Интерполирование и численная интерполяция.
  13. Алгебраический интерполяционный многочлен.
  14. Обратное интерполирование.
  15. Постановка задачи приближенного вычисления определенного интеграла, формула прямоугольников.
  16. Формулы Ньютона - Котеса.
  17. Формула трапеций.
  18. Практическая оценка погрешности квадратурных формул.
  19. Формула Симпсона.
  20. Вычислительная погрешность квадратурных формул.


Критерии оценивания ответа студентов на зачете

Зачет принимается при условии выполнения студентом предусмотренной программы работы: освоения теоретического уровня программы; выполнение всех практических заданий.

Оценка «зачтено» ставиться при условии, если студент: раскрывает содержание курса в объеме обязательного минимума содержания; раскрывает основные понятия курса; переносит знания на ситуации в жизни и быту.

Оценка «не зачтено» ставиться, если студент: 1) не раскрывает содержание курса в объеме обязательного минимума содержания; 2) не раскрывает основные понятия курса.


Работа при подготовке к зачету:
  • Внимательно прочитать вопрос.
  • Составить план и при необходимости конспект вопроса.
  • Вспомнить основные термины, понятия, закономерности и законы по теме.
  • Найти соответствующие наглядные пособия (таблицы, схемы и т.д.).
  • Подтвердить ответ схематическими рисунками и примерами.

Работа с литературными источниками.
  1. Ознакомиться с имеющимися в библиотеке систематическими, алфавитными, предметными каталогами.
  2. В первую очередь изучить научную, периодическую литературу содержащую теоретические основы проблемы. Затем познакомиться с литературными источниками, раскрывающими более узкие и частные вопросы.
  3. Детально проработать публикации (если таковые есть) преподавателей кафедры посвященной данной теме.
  4. Составить собственную библиографическую картотеку.