Geum.ru

Протягом багатьох сторіч математика є невід’ємним елементом системи освіти в усьому світі

Вид материалаДокументы

Содержание


Некоторые аспекты изложения курса «математика для экономистов»
Формирование математических
Математика в современном мире
Особенности математического стиля мышления
Подобный материал:
1   2   3

НЕКОТОРЫЕ АСПЕКТЫ ИЗЛОЖЕНИЯ КУРСА

«МАТЕМАТИКА ДЛЯ ЭКОНОМИСТОВ»



Образование является главным компонентом технологического общества, а подготовка специалистов – основное назначение системы образования. Для решения задач обеспечения экономического роста недостаточно подготовить высококвалифицированных, исполнительных работников. Современное информационное общество и его развивающаяся экономика нуждаются в энергичных и инициативных высококвалифицированных специалистах, умеющих принимать и грамотно реализовывать самостоятельные творческие решения, отвечать за их осуществление. Предъявляются новые требования к результатам освоения образовательных программ бакалавра, специалиста и магистра, а также отдельных разделов данных программ. Обязательным компонентом основной образовательной программы становится научно-исследовательская работа студента. От идеи передачи «готовых знаний» нужно перейти к идее формирования умений, навыков, компетенций. На смену парадигме пассивной передачи знаний приходит парадигма дееспособности.

В настоящее время усиливается математизация экономических курсов. Курс математики для экономистов имеет общеобразовательное значение, является одним из базисных для профессиональной подготовки.

Возник комплекс экономических и математических дисциплин, объединяющий экономико-статистические методы, эконометрию, исследование операций, экономическую кибернетику.

Возросла роль знаний в области смежных со специальностью наук и умений их комплексного применения при решении научных, производственных и социально-экономических задач.

Студенты должны уметь распространять полученные в курсе математики для экономистов знания на профильные предметы. Для этого необходимо пояснять изучаемый материал, основываясь на знании разделов экономических дисциплин, связанных с будущей специализацией студентов. На преподавателях математических кафедр лежит тяжелая и ответственная обязанность таким образом организовать процесс преподавания, что бы студент постоянно ощущал, что, изучая математику, он приближается к более глубокому пониманию своей специальности. Именно поэтому очень важно подобрать наиболее доступный и удобный метод преподавания, который принесёт максимальную пользу в виде знаний, которые останутся у будущих специалистов.

Качество математической подготовки студентов экономического профиля будет повышено, если:

выявить межпредметные связи математики с дисциплинами социально-экономического цикла, ориентированные на формирование системы профессионально значимых умений и математических понятий, создающих теоретическую базу для изучения профилирующих предметов;

разработать функциональную программу, методику изучения профессионально значимых тем курса математики, организации практических занятий, предусматривающих реализацию выявленных межпредметных связей.

Решая экономические задачи, можно одновременно формировать строгое математическое мышление. И наоборот, решая те или иные математические задачи, можно овладеть приемами, методами и аппаратом для решения экономических задач.


Вербецкая Л.В.

Донецкий учебно-воспитательный комплекс №1


ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКИХ

КОМПЕТЕНТНОСТЕЙ УЧАЩИХСЯ


Одним из приоритетов современной образовательной политики в Украине является разработка и внедрение компетентностного подхода в образовании, приближение нашей образовательной системы к международным и европейским стандартам. В связи с этим возникает необходимость формирования у учащихся математических компетентностей для воспитания гармонично развитой личности. Полноценное развитие мыслительных операций, искусство анализировать, классифицировать, выдвигать гипотезы, опровергать или доказывать их, пользоваться аналогиями и т.д. человек получает благодаря изучению математики. Лаконизм, точность, полнота, ясность – способы выражения мысли и навыки рационального мышления развиваются с опытом решения математических задач. Понимание научной картины мира, развитие ее эстетического и объективного восприятия человек приобретает на пути формирования математических компетентностей.

В научных исследованиях существуют разные подходы толкования терминов «компетенция», «компетентность», «математическая компетентность», определения уровней, структуры компетентности.

В педагогическом аспекте целесообразно использовать термин «компетентность» – как способность действовать на основе приобретенных знаний. Компетентность выступает результативно-деятельной характеристикой образования. Предметную компетентность предлагается мыслить как конкретизацию ключевых компетентностей. Ключевые компетентности учащихся, которые отслеживаются в системе регионального мониторинга качества образования: познавательная, личностная, самообразовательная, социальная, технологическая, компетентное отношение к своему здоровью изучались на школьных, районных семинарах, конференциях, поэтому остановимся на определении и классификации обще-предметных компетентностей.

Математическая компетентность – это не только умение работать с числовой информацией, владение математическими умениями, но и умения видеть и применять математику в реальной жизни, понимать содержание и метод математического моделирования, умения строить математическую модель и следовать ее методами математики, интерпретировать полученные результаты, оценивать погрешности вычислений. В работах современных педагогов указывается, что математическая компетентность характеризуется математической грамотностью и включает математические способности и умения, математический стиль мышления, письменную и устную аргументацию, применение современных технических средств и компьютерных технологий. Они выделяют три иерархических уровня математической компетентности:

1 уровень – воспроизведение математических фактов, методов выполнения вычислений;

2 уровень – установление связей и интеграция материала разных тем для решения поставленных задач;

3 уровень (высокий) – математические рассуждения, требующие обобщения и интуиции.

Составляющие математической компетентности представлены на рис.1.





Рисунок 1 – Составляющие математической компетентности


В тоже время, математическая компетентность – это сложная система, поэтому к ключевым и общим предметным компетентностям стоит добавить специальные предметные, опирающиеся на содержательные линии курса математики. Например, содержательные линии курса алгебры 9 класса: числа, выражения, уравнения, неравенства, функции. Математическая компетентность, связанная с понятием функции (МКФ) включает в себя применение компьютерной технологии как необходимый элемент МКФ ученика. Требования знать доказательства теорем не является привязанным ни к возрасту, ни к классу обучения учащихся. Сейчас осуществляется разработка системы измерения и анализ показателей специальных предметных компетентностей, потому что уровень учебных достижений и показателей компетентностей не являются тождественными, так как компетентность содержит намного больше информации (мотивацию, рефлексию, ценностные ориентиры личности, и т.д.).

Компонентами математической компетентности являются:

мотивационный;

содержательный;

деятельный.

Пути формирования математической компетентности представлены на рис. 2.





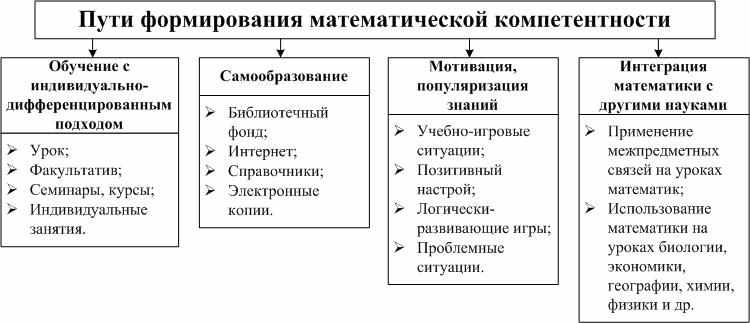
Рисунок 2 – Пути формирования математической компетентности


Таким образом, математика является неотъемлемым элементом системы общего образования всех стран мира. По результатам международного исследования учебных достижений 2007 г. лучшие математические знания показали школьники стран Восточной и Юго-Восточной Азии, низкий уровень знаний продемонстрировали украинские школьники. А стране нужны квалифицированные инженеры, математики, нанотехнологи.

Возникает вопрос, а какая технология обучения в состоянии дать возможность эффективного формирования практической математической компетентности, социально-личностной компетентности, общекультурной компетентности учащихся? Единого рецепта не существует. Наше методическое объединение учителей математики и информатики в своей работе продуктивно использует технологии: обобщение и систематизации учебного материала; реконструирования и усовершенствования учебного материала; информационно-коммуникативные технологии и др.


Возняк А.А., Сидоренко О.И.

Донецкий национальный университет экономики и торговли

имени Михаила Туган-Барановского


МАТЕМАТИКА В СОВРЕМЕННОМ МИРЕ


Математика – наука о количественных отношениях и пространственных формах действительного мира.

Академик А.Н. Колмогоров выделил четыре периода развития математики: зарождение математики, элементарная математика, математика переменных величин, современная математика.

Развитие математической науки неизбежно повлекло за собой специализацию и обособление; математика оказалась под угрозой потери единства и внутренней взаимосвязи. Благодаря молодым ученым, пользовавшихся решительной поддержкой общества, которое осознало возрастающую роль математики, были достигнуты значительные успехи, а растущий объём математических исследований повлёк за собой множество публикаций и многочисленные конференции математиков. В связи с этим появилась настоятельная потребность в чётком понимании существа математики, её проблем и целей, а также в отыскании идей, которые смогли бы объединить людей самых различных интересов.

Возросшая роль математики в современном мире, прежде всего, сказалась в резком увеличении числа математиков. Математика перестала быть предметом занятий только академической элиты; теперь профессия математика стала одной из наиболее распространённых, привлекая к себе всё большее число одарённых людей. Значительно расширились область математических исследований и программа математического образования.

Математический аппарат проник далеко за пределы математики: в физику, новые отрасли техники, биологию и даже в экономику и другие социальные науки. Счётные машины и вычислительная техника способствовали появлению новых областей научных исследований, имеющих важное (хотя и не полностью ещё осознанное) значение, как для самой математики, так и для всех наук, органически связанных с ней.

Одним из главных достижений последних 150 лет было введение понятия группы: в результате различные разделы математики обрели ясность и единообразие.

Много усилий направлялось на вспомогательный, «высший» участок «линии развития» — на анализ структуры абстрактных понятий. Это неизменно способствовало выяснению строения конкретных областей математики, таких, как теория чисел и алгебра.

Абстрактная теория групп нашла блестящее применение в решении ещё более конкретных проблем физики элементарных частиц. Здесь возможности теории групп обусловливаются наличием довольно запутанных групп явных и скрытых симметрий во взаиморасположениях и взаимодействиях ядерных частиц. Успех теории групп в систематизации массы экспериментальных данных, а также в предсказании существования новых элементарных частиц, очевидно, свидетельствует о пользе абстракций в поисках вполне реальных истин.

Обращение с реальностью, преобразованной в абстрактные математические модели, и оценка точности достигаемых при этом соответствий требуют интуитивных навыков, совершенствуемых опытом. Часто необходимо как-то преобразовать исходную математическую проблему, которая оказывается слишком сложной для решения современными методами.

Таким образом, для современной математики характерно закрепление достигнутых результатов в духе математической строгости. Такой подход приводит к более интенсивной разработке оснований математики, детальному выяснению структуры самой математики и смысла «существования» объектов математического мышления.


Возняк А.А., Калита М.А.

Донецкий национальный университет экономики и торговли

имени Михаила Туган-Барановского


ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО СТИЛЯ МЫШЛЕНИЯ


Взаимодействие конкретного и абстрактного привело математическое мышление к освоению новых и новых понятий и философских категорий. В античной математике (математике постоянных величин) таковыми были «число» и «пространство», которые первоначально нашли отражение в арифметике и евклидовой геометрии, а позже в алгебре и различных геометрических системах. Математика переменных величин базировалась на понятиях, в которых отражалось движение материи: «конечное», «бесконечное», «непрерывность», «дискретное», «бесконечно малая», «производная» и т.п.

Раскрывая сущность стиля математического мышления, можно выделить четыре общие для всех эпох черты, заметно отличающие этот стиль от стилей мышления в других науках.

Во-первых, это доминирование логической схемы рассуждения. Эта своеобразная черта стиля математического мышления имеет в себе много ценного. Очевидно, что она в максимальной степени позволяет следить за правильностью течения мысли; с другой стороны, она заставляет мыслящего при анализе иметь перед глазами всю совокупность имеющихся возможностей и обязывает его учесть каждую из них, не пропуская ни одной (такого рода пропуски вполне возможны и фактически часто наблюдаются при других стилях мышления).

Во-вторых, лаконизм, т.е. сознательное стремление всегда находить кратчайший ведущий к данной цели логический путь. Черта эта имеет большую ценность не только для математического, но и для любого другого серьезного рассуждения. Лаконизм, стремление не допускать ничего излишнего, помогает и самому мыслящему, и его читателю или слушателю полностью сосредоточиться на данном ходе мыслей, не отвлекаясь побочными представлениями и не теряя непосредственного контакта с основной линией рассуждения.

В-третьих, четкая расчлененность хода рассуждений. При всякого рода разветвленных перечислениях необходимо в каждый момент помнить о том, для какого родового понятия перечисляются составляющие его видовые понятия. В обыденном, не научном мышлении часто наблюдается смешения и перескоки, приводящие к путанице и ошибкам в рассуждении. Для того чтобы сделать такие смешения и перескоки невозможными, издавна широко используются простые внешние приемы нумерации понятий и суждений. Те возможные случаи или те родовые понятия, которые надлежит рассмотреть в данном рассуждении, заранее перенумеровываются; внутри каждого такого случая те подлежащие рассмотрению подслучаи, которые он содержит, также перенумеровываются (иногда, для различения, с помощью какой-либо другой системы нумерации). Перед каждым абзацем, где начинается рассмотрение нового подслучая, ставится принятое для этого подслучая обозначение (например, II 3, – это означает, что здесь начинается рассмотрение третьего подслучая второго случая, или описание третьего вида второго рода, если речь идет о классификации). Разумеется, что такая нумерация служит лишь внешним приемом, очень полезным, но не обязательным, и что суть состоит не в ней, а в той отчетливой расчлененности аргументации или классификации, которую она и стимулирует.

В-четвертых, скрупулезная точность символики, формул, уравнений. То есть каждый математический символ имеет строго определенное значение: замена его другим символом или перестановка на другое место, как правило, влечет за собою искажение, а подчас и полное уничтожение смысла данного высказывания.

Таким образом, выделив основные черты математического стиля мышления, можно сделать вывод, что математика (особенно математика переменных величин) по своей природе имеет диалектический характер, а следовательно, способствует развитию диалектического мышления. Действительно, в процессе математического мышления происходит взаимодействие наглядного (конкретного) и понятийного (абстрактного). «Мы не можем мыслить линии, – писал Кант, – не проведя её мысленно, не можем мыслить себе три измерения, не проведя из одной точки трех перпендикулярных друг к другу линий».