Совершенствование теории размерного анализа на основе кромочной модели деталей типа тел вращения 05. 02. 08 Технология машиностроения
| Вид материала | Автореферат |
- 1. Классификация деталей типа тел вращения (2 ч.), 72.62kb.
- 6М071200 – Машиностроение, 45.26kb.
- Программа вступительного экзамена в аспирантуру по специальной дисциплине 05. 02., 266.3kb.
- Экзаменационные вопросы по предмету «Технология машиностроения», 36.61kb.
- «Технология машиностроения» Специализация «Дизелестроение», 37.35kb.
- Рабочая программа и методические указания к выполнению контрольной работы для заочной, 305.14kb.
- Программа преддипломной практики студентов специальности 1-36 01 01 «Технология машиностроения», 336.91kb.
- Программа и контрольные задания для учащихся-заочников по специальности 2-36, 764.27kb.
- Временные ряды, 100.85kb.
- Примерная программа профессионального модуля разработка технологических процессов изготовления, 413.36kb.
На правах рукописи
МАСЯГИН ВАСИЛИЙ БОРИСОВИЧ
СОВЕРШЕНСТВОВАНИЕ ТЕОРИИ РАЗМЕРНОГО АНАЛИЗА НА ОСНОВЕ КРОМОЧНОЙ МОДЕЛИ ДЕТАЛЕЙ
ТИПА ТЕЛ ВРАЩЕНИЯ
05.02.08 – Технология машиностроения
Автореферат
диссертации на соискание ученой степени
доктора технических наук
Омск - 2010
Работа выполнена в ГОУ ВПО «Омский государственный технический университет».
Научный консультант – доктор технических наук, профессор
А.П. Моргунов
Официальные оппоненты: – доктор технических наук, профессор
А.А. Ситников
– доктор технических наук, профессор
А.А. Кошин
– доктор технических наук, доцент
В.И. Глухов
Ведущая организация: ПО «Полет», филиал ФГУП ГКНПЦ
им. М.В. Хруничева
Защита состоится “19” _ноября__2010 г. в ____ часов на заседании диссертационного совета Д 212.178.05 в Омском государственном техническом университете по адресу: 644050, г. Омск, проспект Мира, 11,
ауд. 6-340.
С диссертацией можно ознакомиться в библиотеке ОмГТУ.
Автореферат разослан “___”_____________2010 г.
И. о. ученого секретаря
диссертационного совета
доктор технических наук, профессор В.С. Калекин
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность проблемы. Требования к качеству, надежности, экономичности машиностроительной продукции и самого машиностроительного производства, его технологии постоянно повышаются. Вследствие этого повышаются требования к качеству конструкторско-технологической подготовки производства, которая включает в качестве своей основы размерный анализ. Размерный анализ – это большой комплекс расчетно-аналитических действий, осуществляемых при разработке и анализе конструкций и технологических процессов: построение специальных размерных схем конструкций и технологических процессов, выявление и фиксация взаимосвязей всех размерных параметров, выявление размерных цепей, проверка и установление рациональных способов простановки размеров в чертежах, назначение достаточного и необходимого числа технических требований, назначение обоснованных допусков, минимальных припусков, проверочный расчет возможности обеспечения чертежных размеров и технических требований, расчет средних припусков, определение номинальных значений и отклонений операционных размеров, определение толщины покрытий, глубины азотирования и других характеристик.
Среди изделий машиностроения значительную часть составляют узлы, агрегаты и машины осесимметричной формы: насосы, газотурбинные двигатели, турбодетандеры, и т.п. Основные детали подобных изделий имеют форму тел вращения, ограниченную цилиндрическими, плоскими, коническими, сферическими и другими (фасонными) поверхностями вращения. К таким деталям относятся детали классов валов, втулок, дисков. Размерный анализ конструкций из таких деталей и технологических процессов данных классов деталей предусматривает расчет трех типов параметров: 1) продольных размеров; 2) диаметральных размеров; 3) отклонений расположения (отклонений от параллельности торцов и осей, отклонений от перпендикулярности).
Практика размерного анализа конструкций из деталей типа тел вращения и технологических процессов данных классов деталей выявила следующие трудности:
- расчет линейных конструкторских и технологических размеров, диаметральных размеров, отклонений расположения выполняется раздельно, без учета взаимного влияния отклонений от перпендикулярности торцов и цилиндрических поверхностей, и отклонений от соосности цилиндрических поверхностей;
- расчет точности сборки изделия также выполняется раздельно для размеров и отклонений расположения, не учитывается влияние отклонений расположения отдельных деталей на точность сборки;
- проблемы самого расчета – неполная автоматизация, необходимость построения изображений размерных схем, неопределенность направлений звеньев размерной цепи при расчете технологических размеров.
Дальнейшее совершенствование размерного анализа связано с созданием более точных моделей и методов, проверкой их путем сопоставления с существующими моделями и методами, строгим теоретическим обоснованием существующих методов, заменой ручных методов подготовки, обработки информации и принятия решений на автоматизированные и автоматические, созданием предпосылок более полного использования результатов размерного анализа в инженерном анализе при конструировании и проектировании технологических процессов механической обработки и сборки.
Диссертационная работа связана с выполнением госбюджетной НИР по тематическому плану фундаментальных исследований Минобрнауки РФ «Исследование динамических процессов и прочности механических систем с учетом особенностей реальных связей»(2004-2005гг.), и с конструкторско-технологическим обеспечением реализации проекта по аналитической ведомственной целевой программе «Развитие научного потенциала высшей школы» (2006-2008гг.), проект «Рабочие процессы поршневых пневмодвигателей и пневмодвигатель-компрессорных агрегатов».
Целью работы является совершенствование теории размерного анализа технологических процессов и конструкций на основе синтеза наиболее совершенных существующих понятий и методов с их модернизацией путем разработки математических моделей, учитывающих взаимное влияние размерных параметров и отклонений от расположения поверхностей, и применения методов математического и компьютерного моделирования. Для решения поставленной цели были сформулированы следующие задачи:
- проанализировать существующие понятия, модели, методы размерного анализа с целью выявления системы допущений, лежащих в их основе;
- разработать математическую модель детали типа тел вращения, позволяющую объединить расчет линейных, диаметральных размеров, параметров отклонений от расположения поверхностей, более точно отразить погрешности изготовления;
- разработать теоретические схемы, позволяющих более полно отразить структуру размерных связей, а также обеспечить визуализацию объектов размерного анализа;
- разработать математическую модель детали, позволяющую теоретически решить задачу определения взаимного расположения деталей после их соединения при сборке с учетом точности соединяемых деталей;
- разработать метод расчета технологических размеров и отклонений расположения, позволяющий выполнить расчет линейных технологических размеров, диаметральных технологических размеров, отклонений расположения совместно, с учетом взаимного влияния отклонений от перпендикулярности и отклонений от соосности;
- разработать метод расчета технологических размеров и отклонений расположения, позволяющий полностью автоматизировать подготовку и обработку информации при размерном анализе;
- разработать программное обеспечение для размерного анализа технологических процессов и конструкций на основе усовершенствованных методов расчета.
Методы исследований. В качестве общей основы использованы положения технологии машиностроения, связанные с понятием точности и ее обеспечением.
Теоретические исследования проводились на базе основных положений и методов размерного анализа, теории размерных цепей. Для разработки математических моделей использовались: теория графов, аналитическая и вычислительная геометрия, методы формализации, алгоритмизации, математического и компьютерного моделирования.
Широко использовались возможности современных ПЭВМ.
Научная новизна выполненной диссертационной работы заключается в следующем.
1. Введение в число объектов размерного анализа новых элементов формы деталей – кромок.
2. Описание формы деталей типа тел вращения кромочной моделью, охватывающей большее число отклонений взаимного расположения поверхностей за счет описания отклонений расположения кромок.
3. Система взаимосвязанных теоретических и измеряемых параметров кромочной модели детали типа тела вращения.
4. Структурные изображения сборочной единицы и технологического процесса механической обработки на основе кромок.
5. Метод решения задач размерного анализа на основе применения кромочной модели детали с использованием матричного представления графа линейных размеров, позволяющий учесть взаимное влияние перекосов и радиальных смещений поверхностей детали при расчете отклонений расположения.
6. Метод информационной связи кромочной модели и модели на основе понятия – поверхность.
7. Метод расчета технологических размеров и отклонений расположения на основе матричного представления графа в случае наложения поверхностей на размерной схеме и в случае заранее неизвестных направлений звеньев размерных цепей.
Практическая ценность и реализация результатов работы. Результаты научных исследований вносят вклад в технологию машиностроения, дополняя расчетные методики учетом взаимосвязи размерных параметров и отклонений от расположения поверхностей и их взаимного влияния. Для руководства и использования в инженерной деятельности разработаны:
- рекомендации по применению усовершенствованных методик размерного анализа с использованием результатов в автоматизированных системах проектирования, технологической подготовки производства и инженерного анализа.
- методика применения комплекса программ размерного анализа технологических процессов и конструкций; осуществлена опытная эксплуатация программ на ФГУП «ОМО им. П.И. Баранова» и ОАО ОмПО «Радиозавод им. А.С. Попова» (РЕЛЕРО).
Результаты исследований используются в учебном процессе при преподавании дисциплин «Математическое моделирование процессов в машиностроении», «Основы выбора и принятия технологических решений», «Информационная технология», в курсовом и дипломном проектировании на кафедре «Технология машиностроения» Машиностроительного института ОмГТУ при подготовке дипломированных специалистов по специальности 151001 «Технология машиностроения» и по другим машиностроительным специальностям.
На защиту выносятся:
- математическая модель деталей типа тел вращения на основе понятия кромки с соответствующим аппаратом теоретических и измеряемых параметров и их преобразования и метод ее применения для решения технологических задач обеспечения точности деталей и сборочных единиц;
- структурные изображения сборочной единицы и технологического процесса механической обработки, являющиеся аналогами размерных схем, отражающих положение объектов – поверхностей – и связанных с ними кромок при размерном анализе, позволяющие связать между собой кромочную модель и модель на основе поверхностей, а также обеспечить визуализацию изображений деталей, сборочных единиц, операционных эскизов, схем обработки;
- методика определения размеров детали на основе матричного представления графа конструкторских размеров и её применение для расчета линейных, радиальных, диаметральных технологических размеров, отклонений расположения, ожидаемых погрешностей, координат кромок при визуализации;
- комплекс программного обеспечения, реализующий методы аппарата кромок, расчета конструкторских и технологических размеров, отклонений расположения, визуализации изображений деталей, операционных эскизов, схем обработки и сборочных единиц.
Апробация работы. Результаты выполненной работы докладывались и обсуждались на: науч.-практ. семинаре «Программные системы в автоматизации проектирования изделий машиностроения», Ижевск. мех. ин-т, Ижевск, 1988; Всесоюз. науч.-техн. конф «Конструктивно-технологические методы повышения надежности и их стандартизация», Тульск. политехн. ин-т, Тула, 1988; научно-техн. конф. «Проблемы машиностроения и металлообработки», Омск. политехн. ин-т., Омск, 1992; III, IV, V, VI VII междунар. науч.-техн. конф. «Динамика систем, механизмов и машин», ОмГТУ, Омск, 1999-2009; междунар. науч.-техн. конф. «Новые технологии – железнодорожному транспорту: подготовка специалистов, организация перевозочного процесса, эксплуатация технических средств», Омский гос. унив. путей сообщения, Омск, 2000; I Всеросс. науч. internet-конф. «Компьютерное и математическое моделирование в естественных и технических науках» ТГУ им. Г.Р. Державина, Тамбов, 2001; науч.-метод. конф. «Совершенствование форм и методов управления качеством учебного процесса», ОмГТУ, Омск, 2001; междунар. науч.-техн. конф., посвящ. памяти ген. конструктора аэрокосм. техники акад. Н.Д. Кузнецова. СГАУ им. С.П. Королева, Самара, 2001; науч.-техн. конф «Развитие оборонно-промышленного комплекса на современном этапе», Омск. гос. университет, Омск, 2003; 43-й межд. науч.-техн. конф. Ассоциации автомоб. инж. «Проблемы создания и эксплуатации автомобилей, специальных и технологических машин в условиях Сибири и Крайнего Севера», СибАДИ, Омск, 2004; I, II, III регион., IV всерос. науч. конф., посвящ. памяти главн. констр. ПО «Полет» А.С. Клинышкова «Проблемы разработки, изготовления и эксплуатации ракетно-космической и авиационной техники», ОмГТУ, Омск, 2004-2009; всеросс. науч.-техн. конф. «Новые материалы и технологии в машиностроении», Рубцовский индустриальный институт, Рубцовск, 2004; III междунар. технолог. конгр. «Военная техника, вооружение и технологии двойного применения», ОмГУ, Омск, 2005; III межд. науч.-техн. конф. «Новые материалы, неразрушающий контроль и наукоемкие технологии в машиностроении», ТюмГНГУ, Тюмень, 2005; междунар. науч.-техн. конф. «Новые материалы и технологии в машиностроении», Брянская гос. инж.-технолог. акад., Брянск, 2006; IV междунар. технолог. конгр. «Военная техника, вооружение и современные технологии при создании продукции военного и гражданского назначения», ОмГТУ, Омск, 2007; II съезде инженеров Сибири, г. Омск, 2008; I Всеросс. науч.-техн. конф «Россия молодая: передовые технологии – в промышленность», Омск, 2008; семинарах кафедры “Технология машиностроения” и научных конференциях ОмГТУ; расширенном заседании кафедры «Технология машиностроения» ОмГТУ; на научном семинаре кафедры «Общая технология машиностроения» Алтайского государственного технического университета им. И.И. Ползунова, г. Барнаул; на научном семинаре кафедры «Технология машиностроения» Южно-Уральского государственного университета, г. Челябинск.
Публикации. Основное содержание работы опубликовано в 54 печатных работах, в том числе в 13 статьях в журналах, рекомендованных ВАК РФ, зарегистрированы 5 программ для ЭВМ.
Структура и объем работы. Диссертация состоит из введения, 6 глав, основных выводов, списка литературы из 219 наименований, приложений.
Диссертация изложена на 350 страницах, содержит 52 таблицы, 136 рисунков.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность темы, сформулированы цель и задачи исследования, научная новизна и практическая значимость работы, положения, выносимые на защиту.
В первой главе выполнен обзор состояния проблемы совершенствования теории размерного анализа технологических процессов и конструкций.
Размерный анализ конструкций основывается на понятии точности деталей и машин, и на аппарате размерных цепей.
Понятие точности деталей и машин связано с параметрами точности поверхностей, осей, их размеров, формы, взаимного расположения, определяемыми в процессе измерений. Параметры точности разделяются на две группы – комплексные и аналитические. Комплексные параметры, характеризующие точность детали с помощью одного значения и допуска на это значение, рассмотрены в работах Балакшина Б.С., Корсакова В.С., Соколовского А.П. и других ученых. Аналитические параметры точности входят в аналитические уравнения поверхности детали или сечения. Аналитические параметры исследованы в работах Кравцова В.И., Ляндона Ю.Н. и других ученых.
Проблема построения математических моделей машины является одной из составных частей проблемы исследования точности машины. Данная проблема рассматривается в трудах Базрова Б.М., Балакшина Б.С.,
Безъязычного Б.Ф., Дальского А.М., Жигалова Б.К., Журавлева А.Н.,
Колесова И.М., Косова М.Г., Медаря А.В., Митрофанова В.Г.,
Мордвинова Б.С., Непомилуева В.В., Семенова А.И., Соломенцева Ю.М.,
Тимирязева В.А. и других ученых. Сформулированы принципы построения математических моделей машины: рассмотрение всех этапов изготовления машины; построение геометрических структур качественной модели по исходной информации, которой являются чертеж и технология; использование представления о координатных системах, связанных с деталями для количественной оценки положения соединенных между собой деталей.
Метод размерных цепей, являющийся теоретической основой размерного анализа, разрабатывали Балакшин Б.С., Пузанова В.П., Брук С.И., Лившиц Б.И., Базров Б.М., Дунаев П.Ф., Леликов О.П., Иващенко И.А. и другие ученые. Выявлены возможности, которые представляют метод размерных цепей при рассмотрении конструкции машин – размерные цепи позволяют: проверить взаимозаменяемость деталей, узлов и изделий в целом; проверить обеспеченность нормальных условий работы механизма; определить степень точности функционирования данного механизма; определить величины допусков и отклонений размеров при замене одной базовой поверхности другой; в некоторых случаях рационализировать конструкцию машины, обеспечить достижение требуемой точности. В отношении технологии изготовления размерные цепи позволяют: установить числовые данные сборочных размеров для технических условий контроля, сборки и приемки узлов и изделий; установить возможные причины дефектов при сборке и испытании объектов; произвести увязку межоперационных базовых поверхностей обрабатываемых деталей; установить оптимальные значения межоперационных припусков; установить допуски и согласовать их с технологией сборки и обработки машины; найти определяющие точность исходные данные для разработки технологии изготовления машины. Размерный анализ технологических процессов основывается на теории размерных цепей Балакшина Б.С. и оригинальных методах расчета технологических размеров, разработанных Матвеевым В.В., Тверским М.М., Бойковым Ф.И.,
Свиридовым Ю.Н., Блюменкранцем Д.Л., Иващенко И.А., Пакидовым П.А., Мордвиновым Б.С., Сметаниным Ю.М., Ситниковым А.А. и другими учеными.
В результате изучения известных методов размерного анализа выявлены следующие затруднения: 1) установление размерных связей осуществляется путем построения линейных размерных цепей и цепей относительных поворотов, оба подвида размерных связей строятся как независимые, без учета их взаимной связи, что в некоторых случаях приводит к значительным ошибкам;
2) для расчета допусков на несколько соответствующих звеньев размерной цепи имеется лишь одно уравнение и в дальнейшем производится корректировка допусков с учетом технологии изготовления, организационных условий и экономических соображений, причем эта корректировка допусков осуществляется в большинстве случаев без серьезного анализа и изучения особенностей конструкции деталей; 3) размерный анализ, расчет размерных цепей машины отличается высокой трудоемкостью из-за многочисленности размерных цепей.
Для решения проблемы большой трудоемкости размерного анализа конструкций и технологических процессов применяются автоматизированные методы размерного анализа конструкций, разработанные Аввакумовым В.Д., Скворцовым А.В. и другими учеными, и автоматизированные методы размерного анализа технологических процессов, разработанные Матвеевым В.В., Иващенко И.А., Мордвиновым Б.С., Сметаниным Ю.М., Калачевым О.Н.,
Рахимовым Э.Г. и другими учеными, модуль «Расчет размерных технологических цепей» в КОМПАС-АВТОПРОЕКТ.
В ходе анализа различных методов расчета технологических размеров был выявлены трудности: 1) большая трудоемкость предварительной подготовки исходных данных перед вводом в ЭВМ, обусловленная необходимостью учета и упорядочивания большого количества как цифровых, так и графических данных; 2) при подготовке данных технолог вынужден самостоятельно определять ориентировочные технологические размеры, назначать, используя справочную литературу квалитет, допуски на технологические размеры и припуски на обработку; 3) расчет диаметральных размеров проводится по отдельной методике, хотя его теоретической основой являются линейные размерные цепи, поэтому для расчета линейных размеров, диаметральных размеров и отклонений расположения созданы отдельные алгоритмы, хотя возможно применение единого алгоритма.
Мордвинов Б.С. в своей методике в центр расчета пространственных отклонений ставит уравнение прямой в пространстве и предлагает несколько способов расчета отклонений через графический метод (построение эпюр) и аналитический (расчетные формулы) с отображением на графе. Расчеты отклонений по данной методике затрудняет то, что необходимо вручную строить множество размерных эпюр даже для несложных деталей. При появлении нескольких общих осей, то есть при переустановке деталей, выполнять расчеты очень затруднительно, так как появляются последовательные, параллельные связи и их комбинации.
Таким образом, выполненный анализ существующих понятий, моделей, методов размерного анализа и связанного с ним понятия точности деталей и сборочных единиц позволил выявить дальнейшие направления исследований:
- уточнение и модернизация существующих понятий, моделей и методов размерного анализа технологических процессов деталей типа тел вращения и размерного анализа конструкций;
- разработка усовершенствованных методик теоретического исследования и практического решения задач размерного анализа;
- экспериментальная проверка разработанных моделей и методов размерного анализа;
- разработка рекомендаций по использованию результатов исследований в автоматизированных системах проектирования, технологической подготовки производства и инженерного анализа.
Вторая глава содержит разработку и теоретические исследования математического аппарата кромок.
Проанализирована информация чертежа детали, технологического процесса мехничексой обработки, сборочной единицы с точки зрения математического моделирования.
Выявлено, что наряду с поверхностями на детали типа тела вращения имеются еще другие элементы – кромки – линии пересечения торцов и цилиндрических поверхностей (рис. 1). Кромки – идеальные, абстрактные элементы, поскольку реально на детали в местах пересечения поверхностей имеются фаски или радиусы.
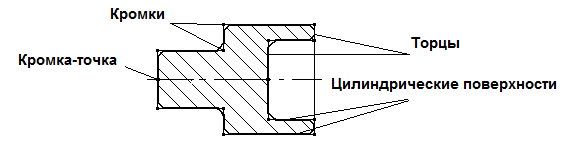
Рисунок 1 – Поверхности и кромки
Несмотря на идеальный характер кромок, они отражают свойства реальных объектов, так как все измерения поверхностей интерпретируются как измерения кромок. При измерении кромок измеряются одновременно торцы и цилиндрические поверхности (рис. 2), т. е. кромка – предельный случай, когда места измерений торцов и цилиндрических поверхностей совпадают.
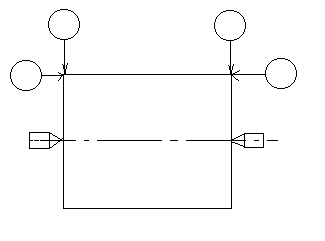
Рисунок 2 – Схема измерения кромок
Существует связь кромок с поверхностями – каждой поверхности можно поставить в соответствие одну и более кромок.
Важное свойство кромки в том, что кромка – теоретически применимый элемент с точки зрения обеспечения определенности положения детали в пространстве, то есть, с точки зрения лишения детали шести степеней свободы. При подходе, основывающемся на рассмотрении поверхностей, для этого необходимо сочетание, например, цилиндрической поверхности, которая лишает деталь четырех степеней свободы, и плоскости, которая лишает деталь одной степени свободы. Или сочетание двух шеек, которые лишают деталь каждая по две степени свободы, и торца, лишающего деталь одной степени свободы. Или сочетание торца, который лишает деталь трёх степеней свободы, и одной шейки, лишающей деталь двух степеней свободы. Вращательная степень лишается за счет трения или дополнительного крепления. При подходе, основывающемся на рассмотрении кромок, следует отметить, что кромка, с одной стороны, – часть цилиндрической поверхности, – с другой стороны – часть плоскости. Как элемент плоской поверхности кромка лишает деталь одной или трёх степеней свободы. Как элемент цилиндрической поверхности кромка лишает деталь двух или четырех степеней свободы; одна вращательная степень свободы лишается дополнительными средствами. Таким образом, кромка или сочетание кромок лишает деталь шести степеней свободы.
Отсюда следует, что если определить взаимное положение кромок детали математически строго точными соотношениями, то по известному положению в пространстве одной кромки детали однозначно определяется положение любой другой кромки. И не только кромки готовой детали, но и любой кромки заготовки на любой операции механической обработки или в сборочной единице, поскольку при установке базовая кромка лишает заготовку шести степеней свободы, то есть фиксирует положение кромок обрабатываемых поверхностей относительно кромок необрабатываемых поверхностей, или положение кромок присоединяемой детали относительно кромок деталей сборочной единицы.
В качестве объектов, у которых рассматриваются кромки, принимаются: а) собранная машина; б) узлы и детали машины в процессе сборки; в) отдельные готовые детали машины; г) заготовки и детали машины в процессе механической обработки.
Указанные объекты различаются с точки зрения рассматриваемых кромок. Для собранной машины – это кромки, посредством которых детали контактируют друг с другом и кромки, взаимное расположение которых задано конструктором и необходимо для нормальной работы машины. На сборочном чертеже рассматриваются все кромки и соприкосновения кромок, хотя это могут быть не явные кромки, а окружности на цилиндрической или плоской поверхности. Для технологического процесса сборки к кромкам собранной машины добавляются кромки базовые, те, которыми детали контактируют со сборочными приспособлениями. Для отдельных готовых деталей рассматриваются все кромки этих деталей. Для технологического процесса механической обработки к кромкам деталей добавляются кромки заготовки и кромки маршрута обработки, возникающие и исчезающие в процессе обработки, причем некоторые из них служат базовыми кромками в процессе механической обработки.
Для описания положения кромок друг относительно друга необходимо построить структурное изображение объектов, содержащих кромки. На этом изображении показываются кромки в виде точек на сечении, проходящем через ось машины, детали.
На схеме машины (рис. 3) проводятся линии, связанные с плоскими поверхностями (базовыми при сборке и входящими в сопряжения между деталями) – вертикальные; и горизонтальные линии, связанные с аналогичными цилиндрическими поверхностями.
Рисунок 3 – Схематичное изображение машины на основе кромок
Нумерация этих линий производится раздельно. Рядом с номерами линий ставится число, показывающее количество поверхностей, входящих в сопряжение в сечении, отмеченном линией.
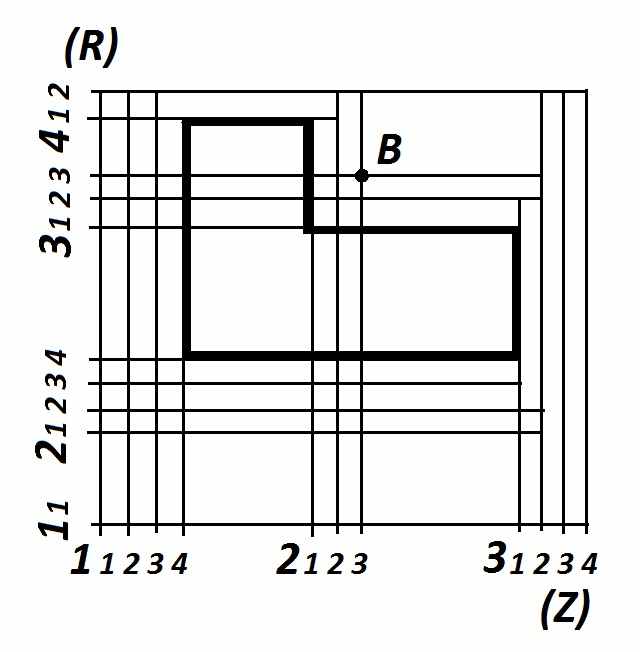
Строится структурное изображения машины (рис. 4). Проводятся вертикальные и горизонтальные линии так, чтобы они образовали координатную сетку или поле.
Рисунок 4 – Структурное изображение машины
Количество линий на схеме координатного поля определяется числом линий на схеме машины в соответствии с числами, проставленными рядом с номерами линий. На координатном поле отмечаются все кромки деталей маленькими кружками, и соединяются отрезками кромки, относящиеся к отдельным деталям и входящими в сопряжение, тем самым получается структурное изображение машины. Структурное изображение дополняется табличным описанием связей между кромками.
Описание технологического процесса в виде структурного изображения также осуществляется аналогично (рис. 5, 6).
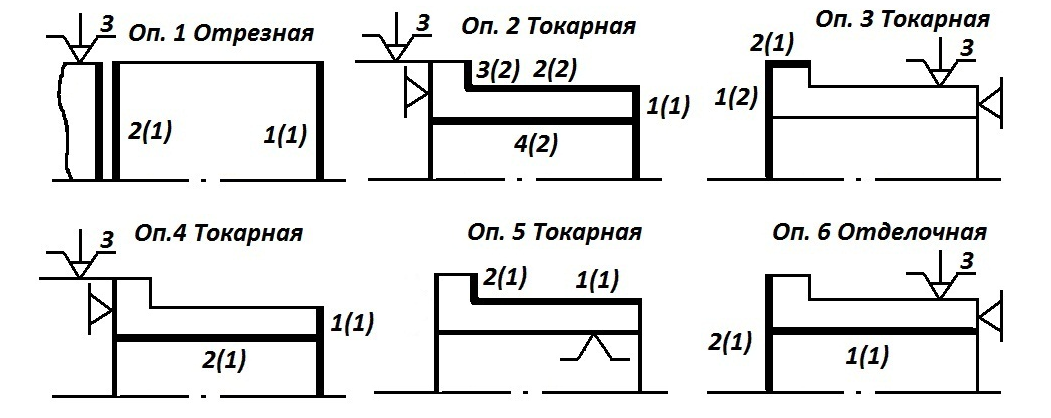
Рисунок 5 – Схематичное изображение операционных эскизов
а) б)
Рисунок 6 – Схематичное изображение схемы припусков (а) и структурное изображения технологического процесса механической обработки (б)
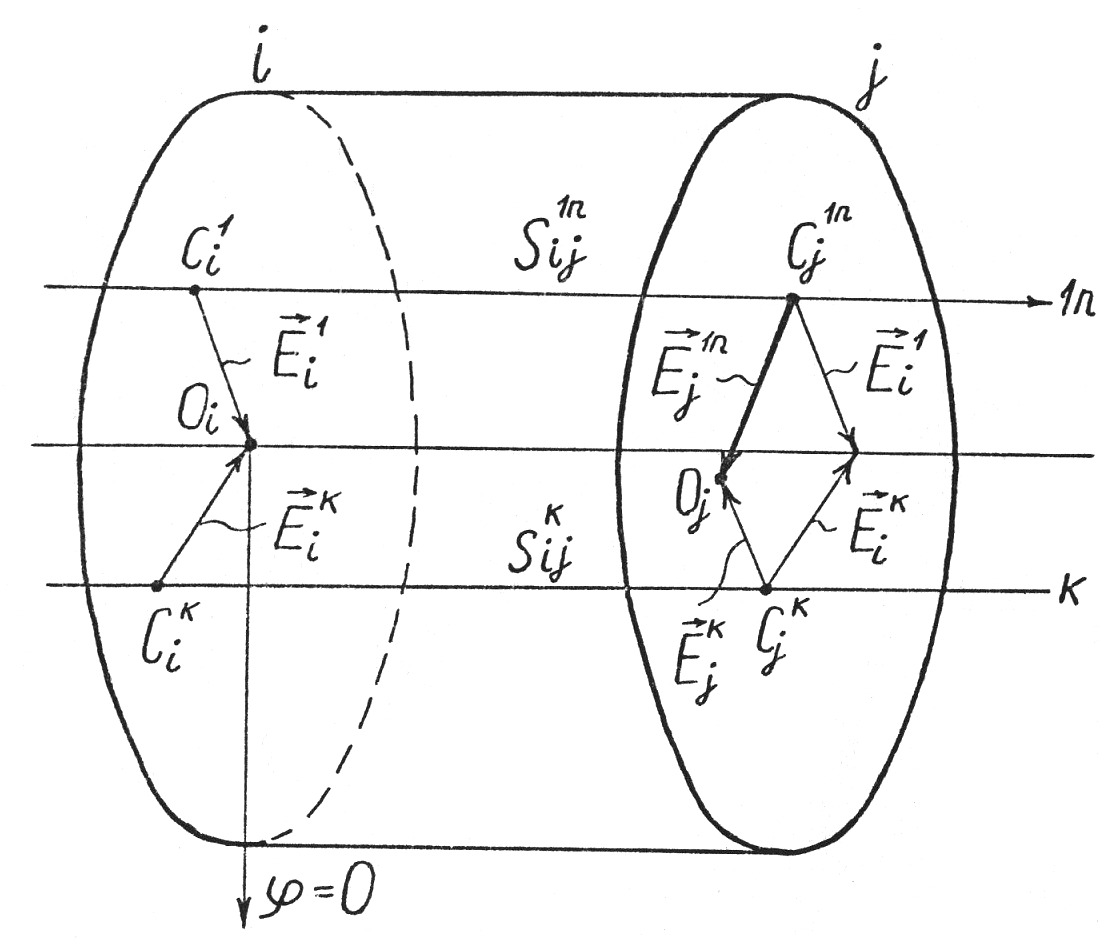
Кромку теоретически можно охарактеризовать радиусом Ri (рис. 7), расположение кромки i относительно данной оси вращения N – наклоном ФiN и эксцентриситетом EiN и углами их направления yiN и eiN. Взаимное расположение двух кромок i и j характеризуется расстоянием вдоль оси вращения SijN.
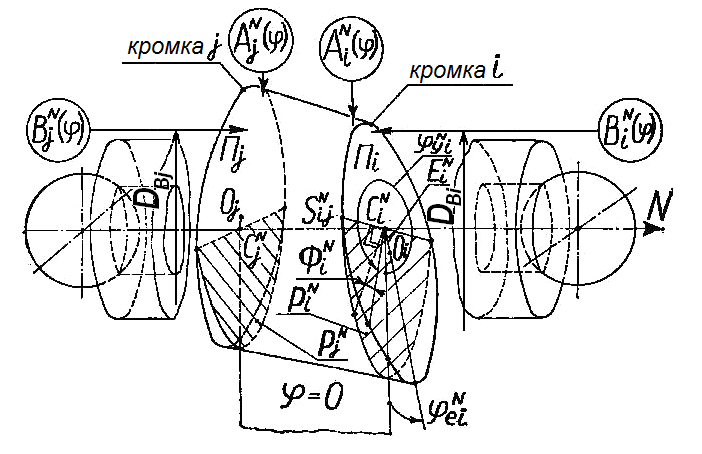
Рисунок 7 – Теоретические и измеряемые параметры кромок
На рисунке 7 показаны: Оi – центр кромки i; Сi – точка пересечения плоскости кромки Пi и оси N (индекс N означает номер оси вращения); EiN – эксцентриситет кромки i по отношению к оси вращения N (считается одинаковым по малости наклонов кромки); eiN – угловое положение отрезка, характеризующего эксцентриситет, отсчитываемое против часовой стрелки; ФiN – угол наклона плоскости кромки i к оси вращения N, определяется между прямыми, перпендикулярными линии пересечения плоскости кромки Пi и плоскости РiN, перпендикулярной оси вращения N и проходящей через точку пересечения плоскости кромки Пi и оси N, причем одна из прямых, между которыми определяется угол ФiN, принадлежит плоскости Пi, а другая – плоскости РiN; yiN – угловое положение прямых, между которыми определяется угол ФiN, отсчитываемое против часовой стрелки; SijN – расстояние между точками пересечения оси N и плоскостей Пi, Пj кромок i и j (считается одинаковым при любых осях вращения по малости эксцентриситетов и наклонов кромок).
Связь теоретических параметров кромок с результатами измерений кромок обеспечивается тем, что должны быть измерены все необходимые измеряемые параметры кромок, в общем случае, за несколько установок, например, для кромки i – радиальные смещения АiN() и торцовые ВiN() смещения на диаметре измерения DВi (рис. 7), и их максимальные и минимальные значения и соответствующие углы, измеренные относительно нулевой метки; диаметр Di и расстояние до кромки j вдоль оси Lij измеренное в сечении нулевой метки. Результаты измерений смещений записываются с индексом, обозначающим номер установки или оси. Установка с наибольшим количеством измеренных кромок считается главной. Для обеспечения связи измерений на разных установках хотя бы одна кромка должна измеряться на каждой из двух установок.
Взаимная связь теоретических и измеряемых параметров кромок определяется следующими зависимостями:
Ri= Di(0)2; (1)
EiN=(AiNmax–AiNmin)/2; (2)
eiN= (AiNmax); (3)
ФiN=(BiNmax–BiNmin)/DВi; (в радианах) (4)
yiN= (BiNmax); (5)
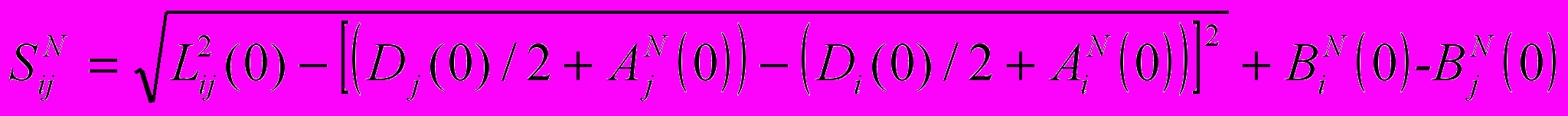 . (6)
. (6)На основе теоретических параметров кромок составляются уравнения кромок. С учетом формы деталей – тел вращения – вводится цилиндрическая система координат, в которой ось z совмещена с осью N, плоскость = 0 совмещена с плоскостью начала отсчета углов eiN и yiN отмеченной меткой на детали, плоскость z = 0 совмещена с плоскостью РjN, связанной с одной из кромок, принятой за базовую. Положение точек кромки i в данной системе координат определяется двумя уравнениями, в которые войдут теоретические параметры кромок:
ri = fi1(), (7)
zi = fi2(). (8)
В случае ФiN = 0, когда кромка i перпендикулярна оси z и имеются параметры EiN и eiN, а положение кромки i вдоль оси z определяется величиной SijN, где j – базовая кромка, уравнения кромки i будут:
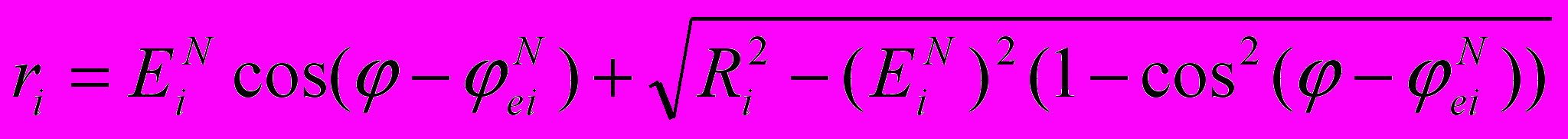 , (9)
, (9)z = SijN. (10)
В случае EiN = 0, когда кромка i не имеет эксцентриситета и имеются параметры наклона ФiN, yiN и параметр SijN, уравнения кромки i будут:
ri = Ri , (11)
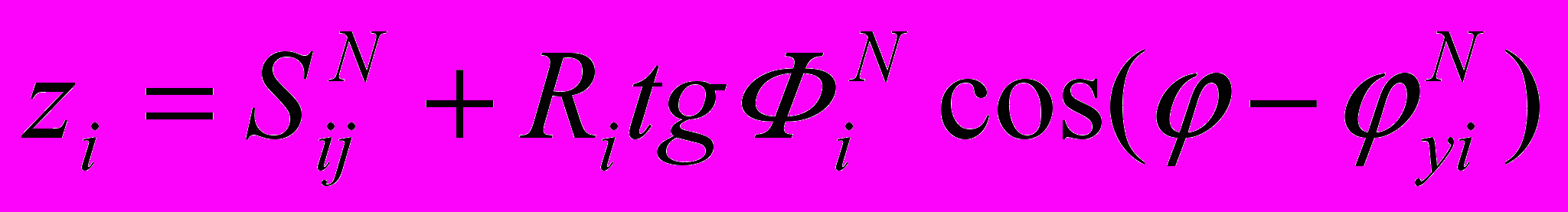 . (12)
. (12)Если все теоретические параметры кромки i имеют значения, отличные от нуля, то, по малости величин ФiN и EiN, можно записать общие уравнения кромки:
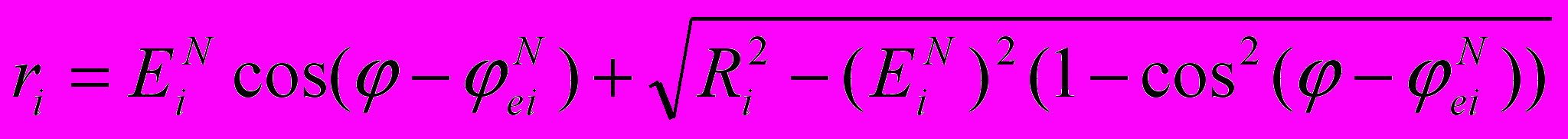 , (13)
, (13)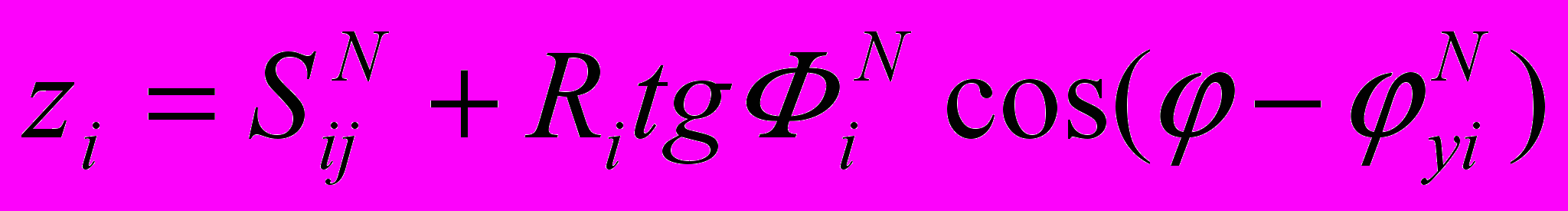 . (14)
. (14)Если известны уравнения двух кромок i и j, то уравнения размерных связей (расстояний) между кромками определяются как разности уравнений кромок
rij= rj – ri, (15)
zij= zj – zi. (16)
Уравнения расстояний между кромками содержат информацию о величинах зазоров, положении точек контакта кромок, если рассматриваются кромки различных деталей в собранной машине, или о припусках, если рассматриваются кромки обрабатываемых заготовок. Например, условие, означающее точку контакта кромок или нулевой припуск, имеет вид:
rij = 0, (17)
zij = 0. (18)
Основные задачи, связанные с размерным анализом конструкций и технологических процессов, и решаемые с помощью аппарата кромок, следующие.
1. Задача контроля деталей, исходной и обработанных заготовок, сборочных единиц.
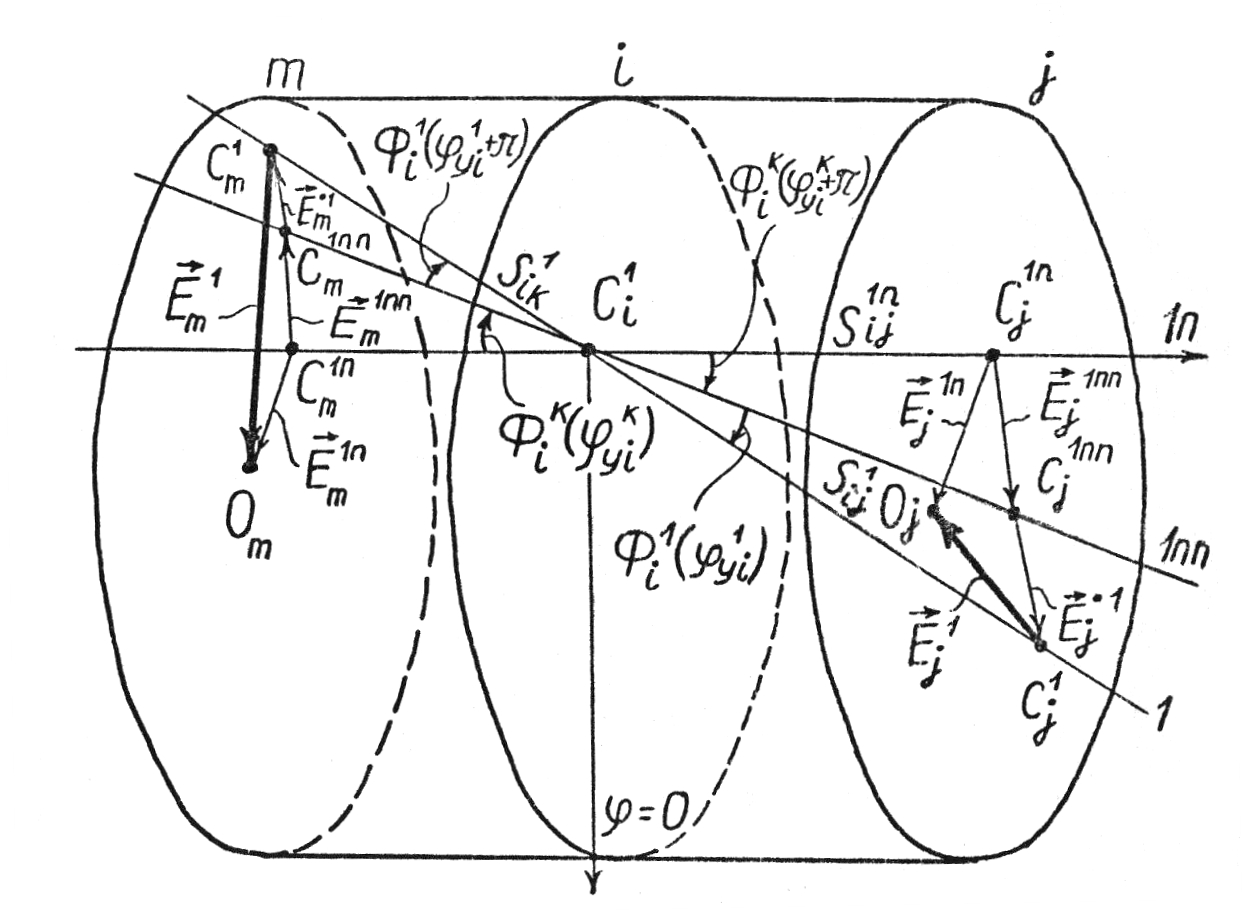
Задача контроля связана с тем, что невозможно определить параметры всех кромок детали за одну установку при измерениях, и для некоторых кромок теоретические параметры будут определены относительно одной оси, а для других – относительно другой или даже третьей оси. В то время как для оценки взаимного расположения всех кромок требуется, чтобы все их теоретические параметры были определены относительно одной оси.
Пусть ось, к которой будут приводиться теоретические параметры всех кромок, является осью при измерениях на 1 установке. Для кромки i определены параметры Ei1, ei1, i1, yi1. На k-ой установке были измерены параметры двух кромок i, j и определены параметры Eik, eik, ik, yik, Ejk, eik, jk, yjk, Sijk. Требуется найти параметры кромки j относительно оси на 1 установке – Ej1, ei1, j1, yj1, Sij1.
Общий подход к определению искомых величин следующий: нужно так мысленно двигать деталь в пространстве, чтобы сначала параметр Eik стал равным нулю, а затем равным Ei1 при ei1 и неизменных ik, yik (параллельный перенос детали, рис. 8а); затем, чтобы параметр ik стал равным нулю и, далее, стал равным i1 при yi1 и при неизменных Ei1, ei1 (поворот детали, рис. 8б и рис. 9). В процессе этих движений будут изменяться значения Ejk, ejk, jk, yjk, Sijk, в результате получаются Ej1, ej1, j1, yj1, Sij1.
а) б)
Рисунок 8 – Параллельный перенос (а) детали и поворот (б) детали
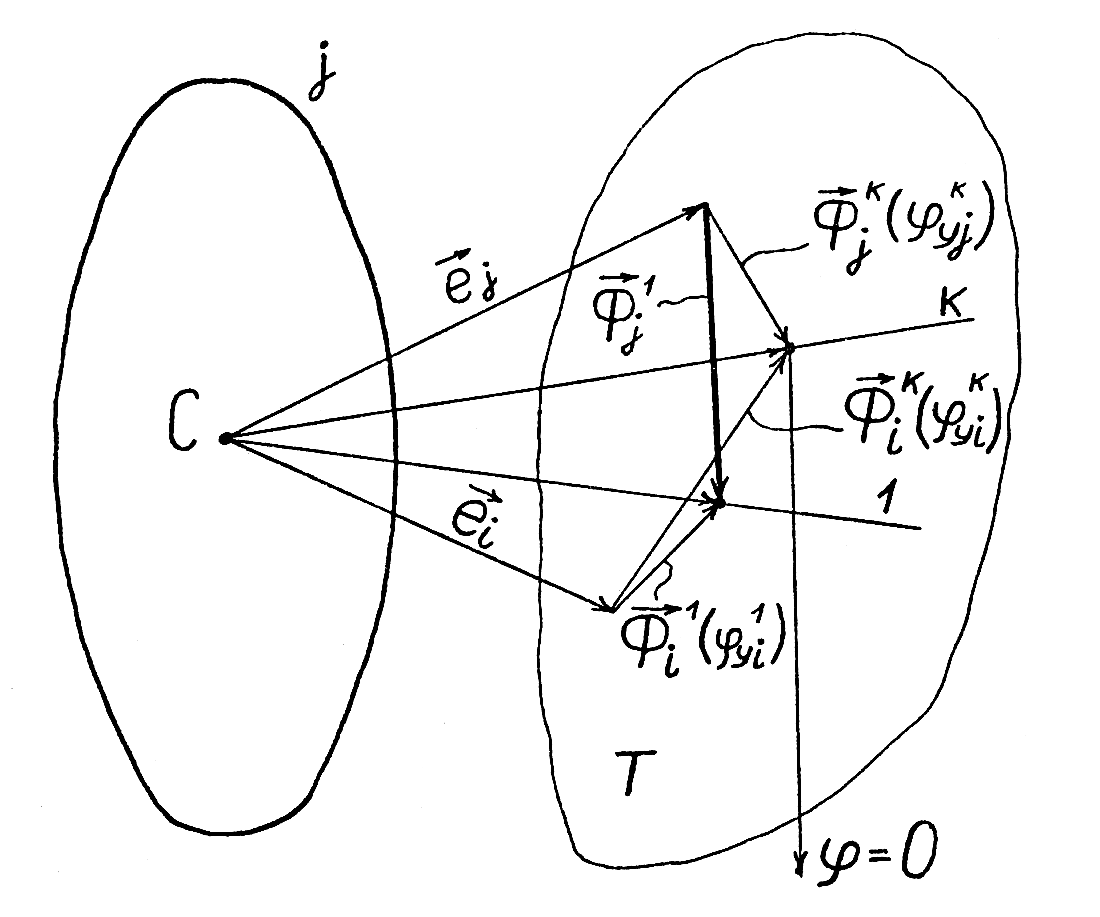
Рисунок 9 – Движение нормали к плоскости кромки при повороте детали
Предполагается совмещение начала отсчета углов = 0 для начального и конечного положений детали, то есть деталь не испытывает поворота вокруг оси при пересчете параметров. Предполагается также равенство расстояний между кромками i и j при преобразованиях – Sij1 = Sij1n= Sij1nn =Sijk вследствие малости величин Е и Ф.
Расчет параметров кромки j выполняется на основе векторных уравнений:
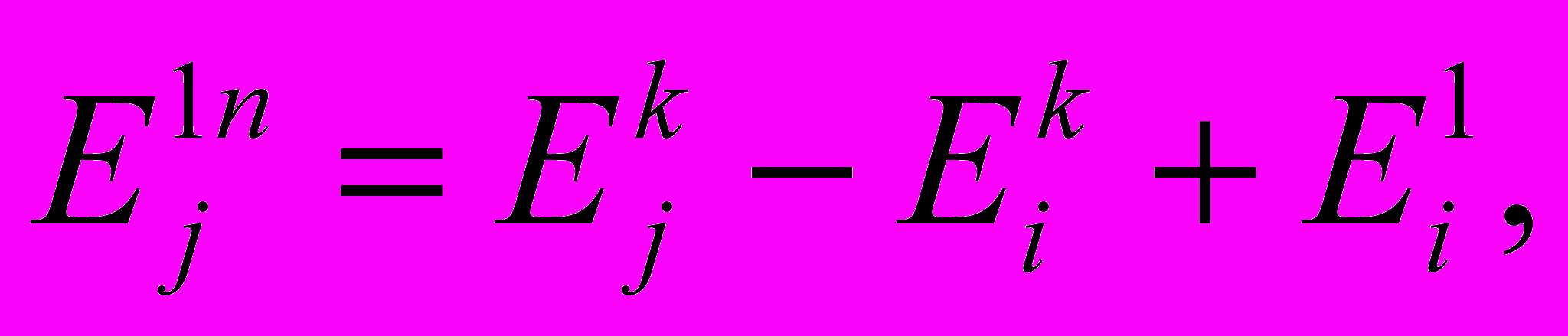 (19)
(19)Ej1nn = Sijk Фik, (20)
Ej1 = Sijk Фi1, (21)
 (22)
(22)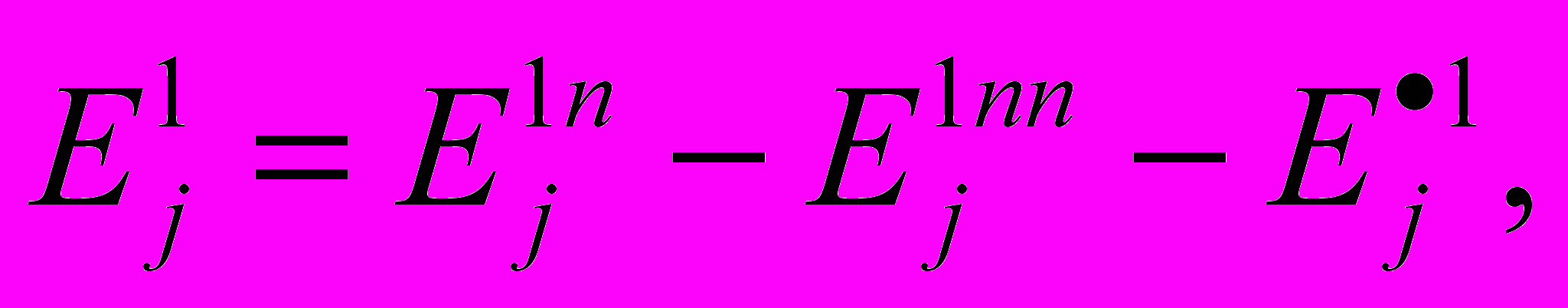 (23)
(23)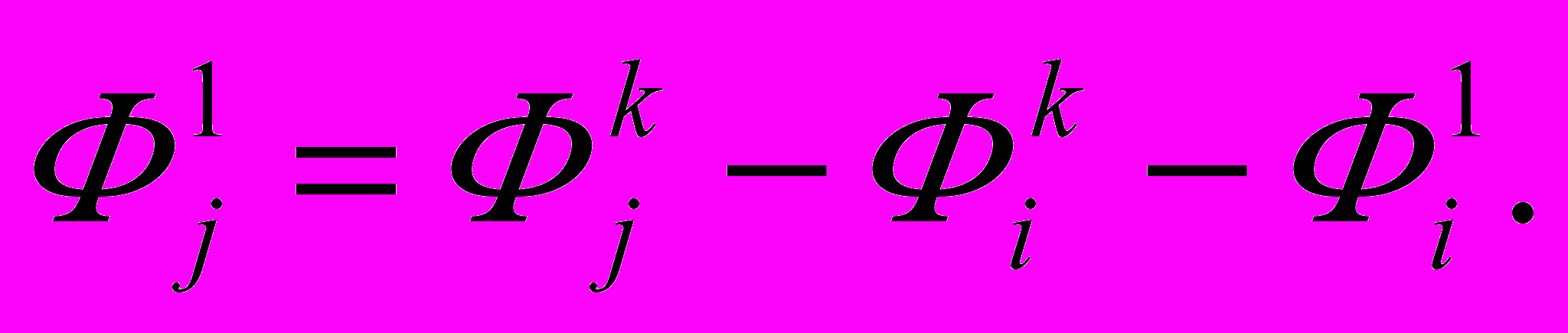 (24)
(24)2. Задача анализа точности сборки при соединении деталей. Известны теоретические параметры кромок деталей, которые соединяются. Необходимо найти новые теоретические параметры кромок после соединения и найти положения точек контакта между кромками.
При соединении 2-х деталей предполагается, что теоретические параметры кромок 2-х деталей известны. Одна из деталей принимается за базовую и считается неподвижной, закрепленной в таком положении, что реализуются теоретические параметры, известные ранее. Вторая деталь присоединяется к первой детали, при этом теоретические параметры второй детали изменяются.
Для упрощения решения, можно предварительно повернуть обе детали так, чтобы эксцентриситеты контактирующих кромок i и k этих деталей стали равны нулю. Тогда возможные смещения кромок j и k для второй детали будут ограничены величинами зазоров между кромками j и k деталей (рис. 10а).
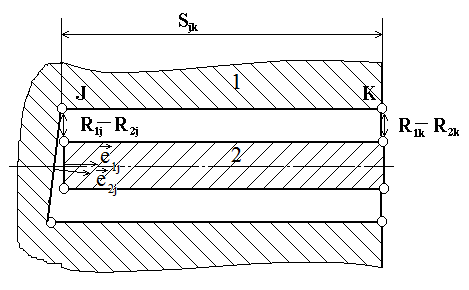
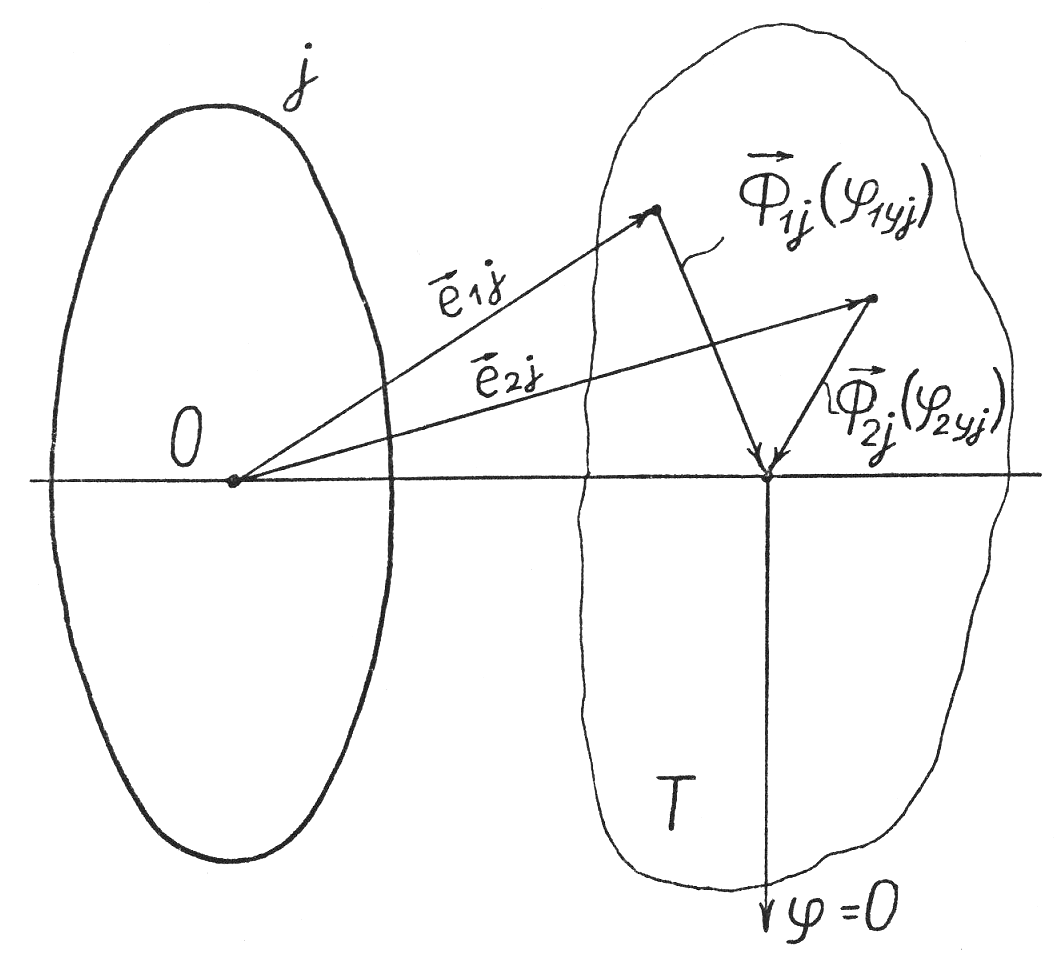
а) б)
Рисунок 10 – Схема зазора между кромками k и j в радиальном направлении (а), и схема, показывающая положение концов единичных векторов, перпендикулярных плоскостям кромок (б)
Деталь 2 может повернуться на угол Ф2 в любом направлении y.
Ф2= ((R1j –R2j) + (R1k – R2k)) / Sjk . (25)
Можно построить схему, показывающую положение концов единичных векторов, перпендикулярных плоскостям кромок j (рис 10б).
Для простоты можно показать координатную плоскость Т (рис. 11а), на которой лежат концы единичных векторов
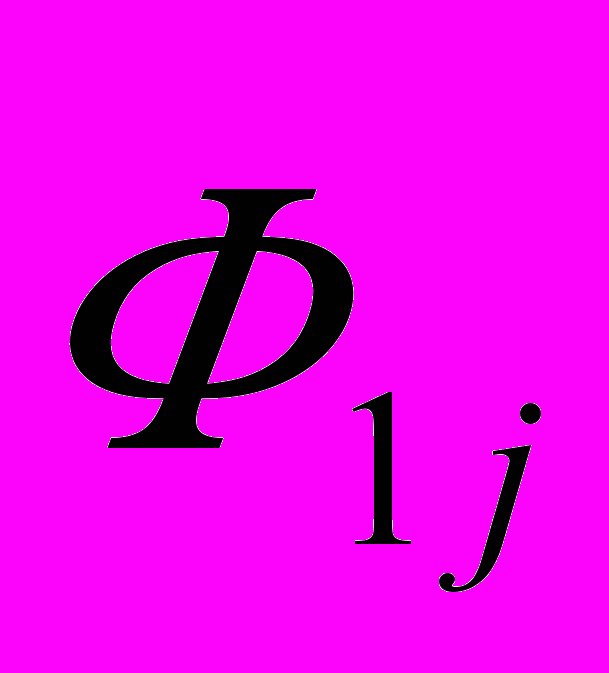 и
и 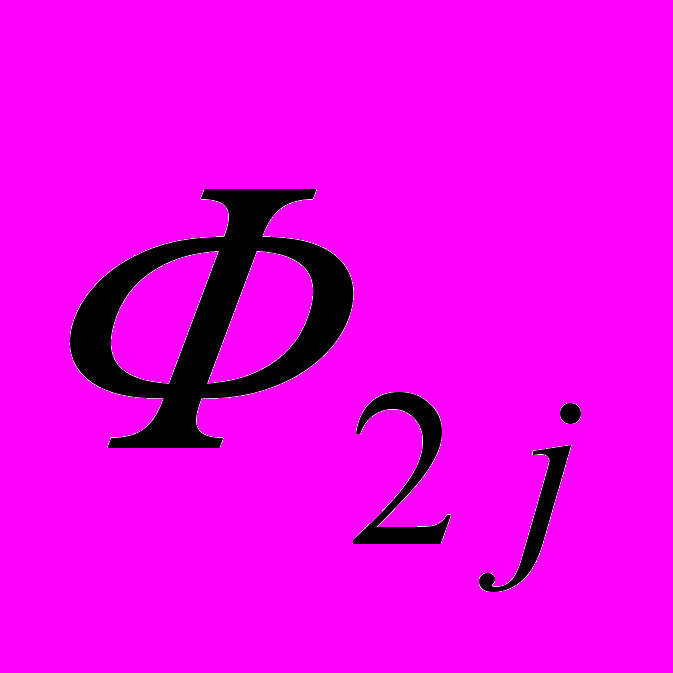 . Возможность наклона второй детали в любом направлении на угол Ф2 означает, что вершина вектора
. Возможность наклона второй детали в любом направлении на угол Ф2 означает, что вершина вектора 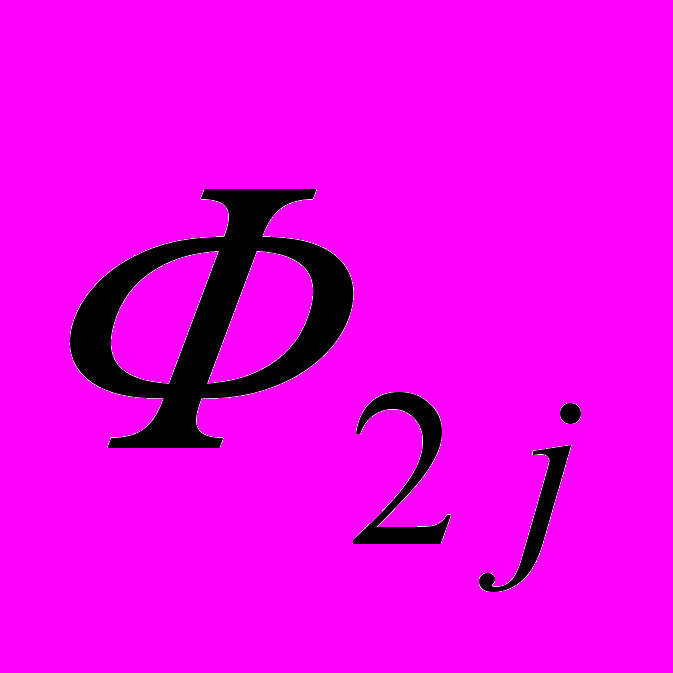 может дополнительно быть смещена в плоскости на расстояние Ф2, т.е. лежит в пределах круга радиуса Ф2 с вершиной V2j.
может дополнительно быть смещена в плоскости на расстояние Ф2, т.е. лежит в пределах круга радиуса Ф2 с вершиной V2j.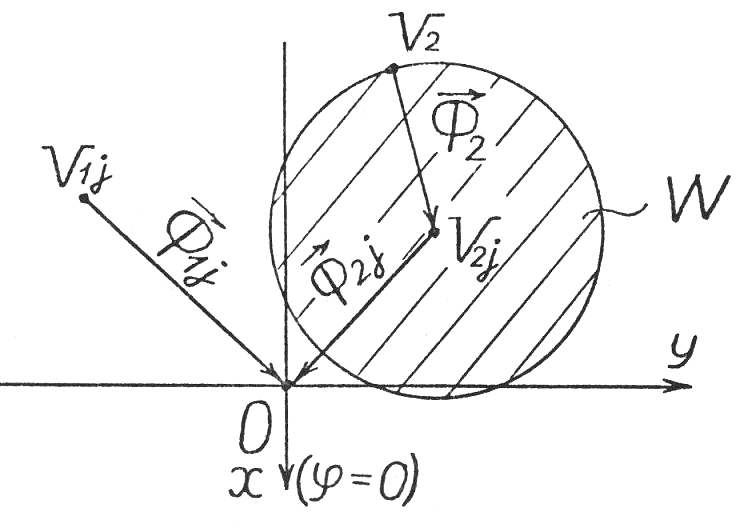
а) б)
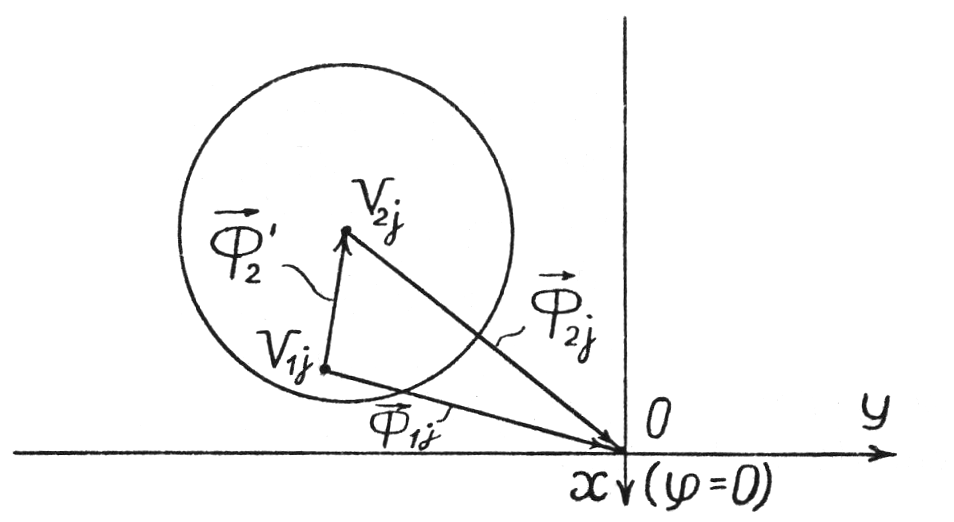
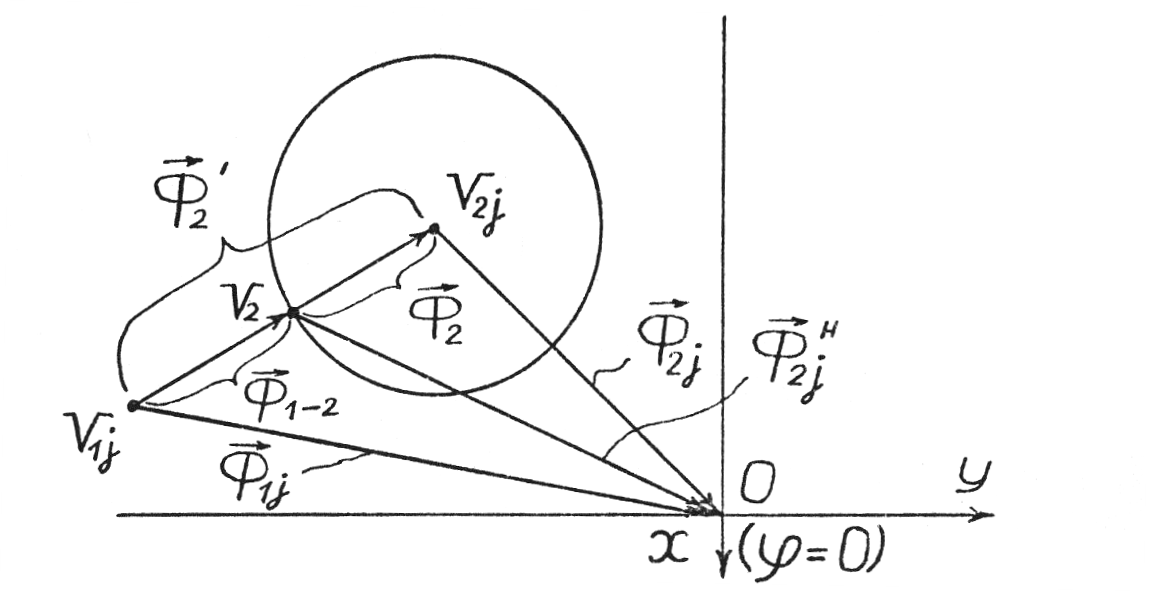
Рисунок 11 – Координатная плоскость с векторами наклона кромок двух деталей: а – при невозможности совпадения плоскостей кромок; б – при возможности совпадения плоскостей кромок
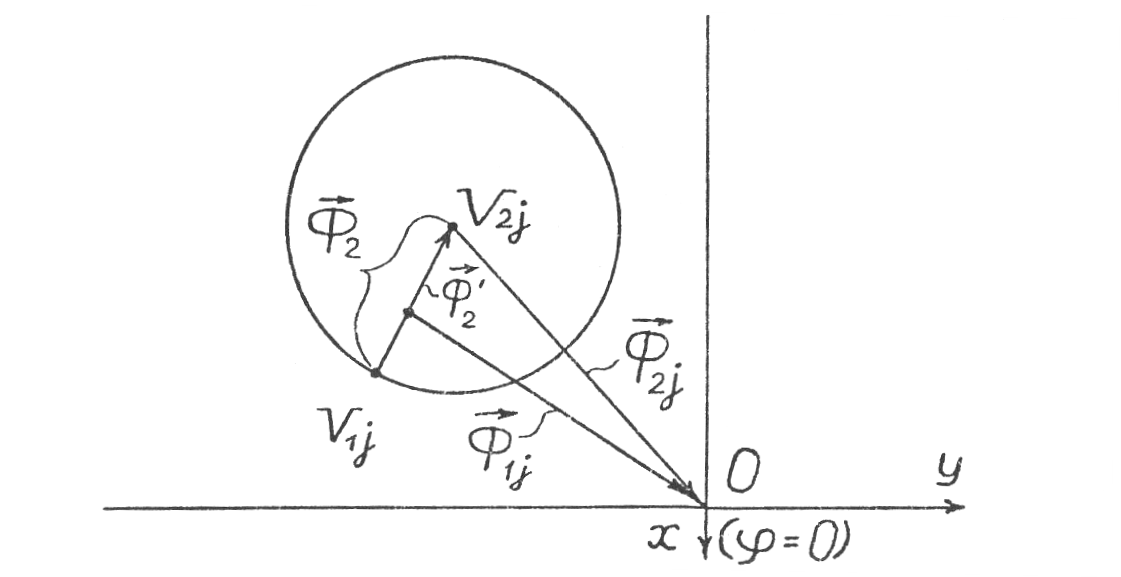
Плоскости кромок j 1-й и 2-й деталей могут совпасть (стать параллельными) только в том случае, если Ф1j = Ф2j и 1yj = 2yj, т.е. когда совпадут начала векторов
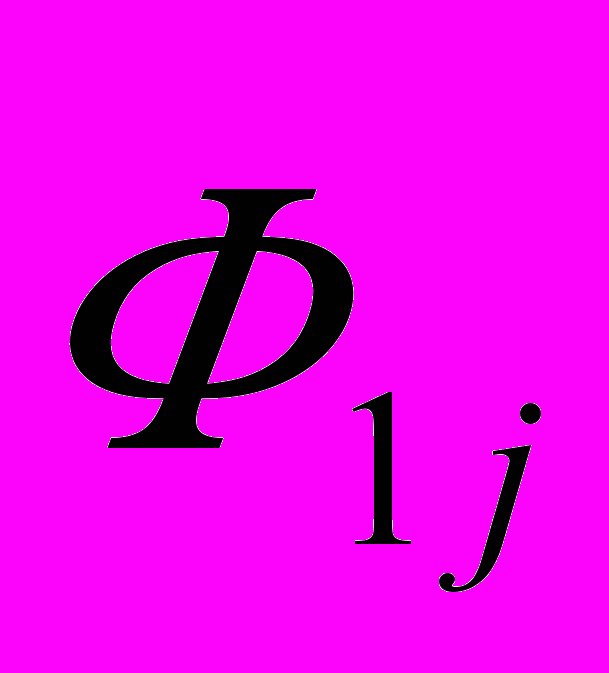 и
и 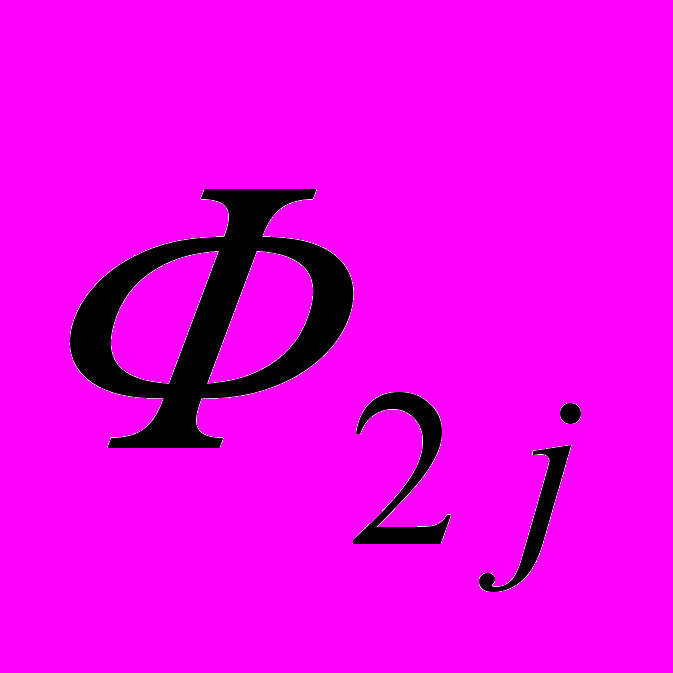 на координатной плоскости. Это может случиться, если начало вектора Ф1j – точка V1j – попадет в область круга W (рис. 11б). При этом деталь 2 испытает наклон на угол Ф2' под углом '2y. Проверка попадания в круг может состоять в определении разности векторов
на координатной плоскости. Это может случиться, если начало вектора Ф1j – точка V1j – попадет в область круга W (рис. 11б). При этом деталь 2 испытает наклон на угол Ф2' под углом '2y. Проверка попадания в круг может состоять в определении разности векторов 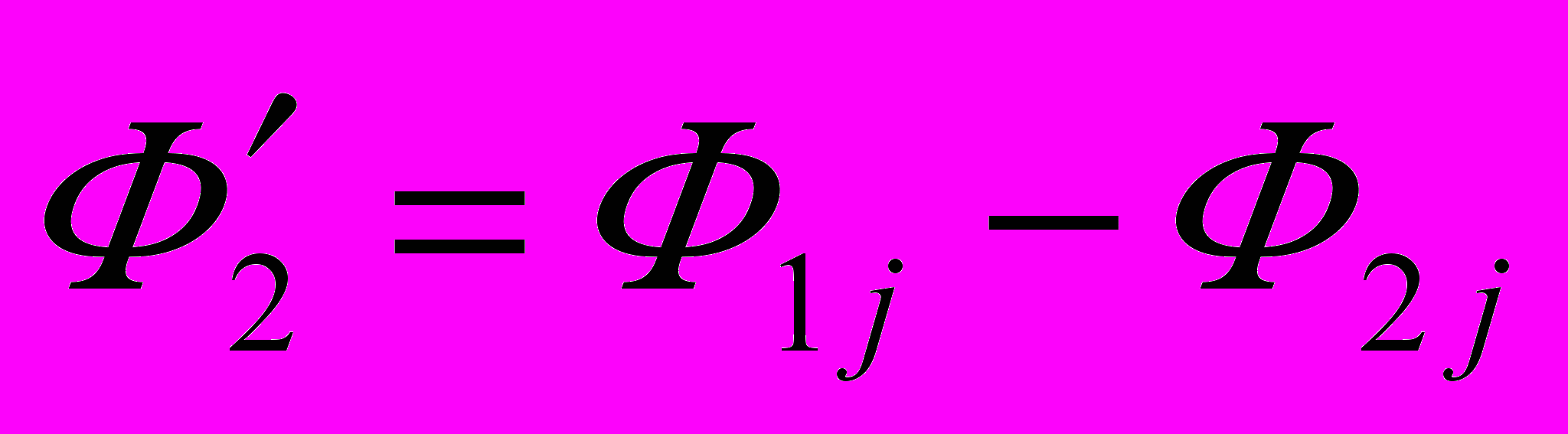 . Если
. Если 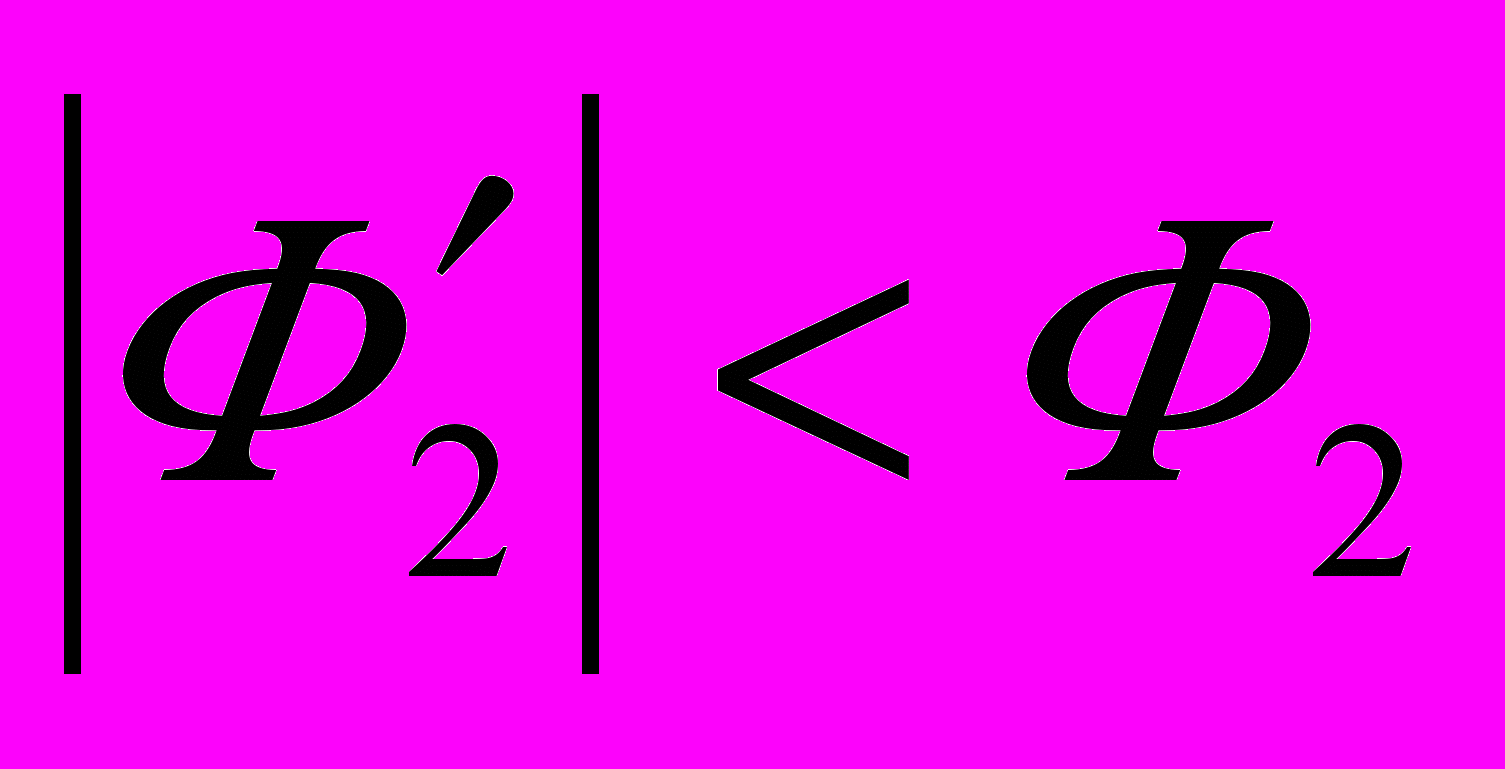 , то кромки j 1-й и 2-й деталей могут соприкоснуться по всей длине в осевом направлении и одна из кромок j или k по точке в радиальном направлении. Равенство
, то кромки j 1-й и 2-й деталей могут соприкоснуться по всей длине в осевом направлении и одна из кромок j или k по точке в радиальном направлении. Равенство 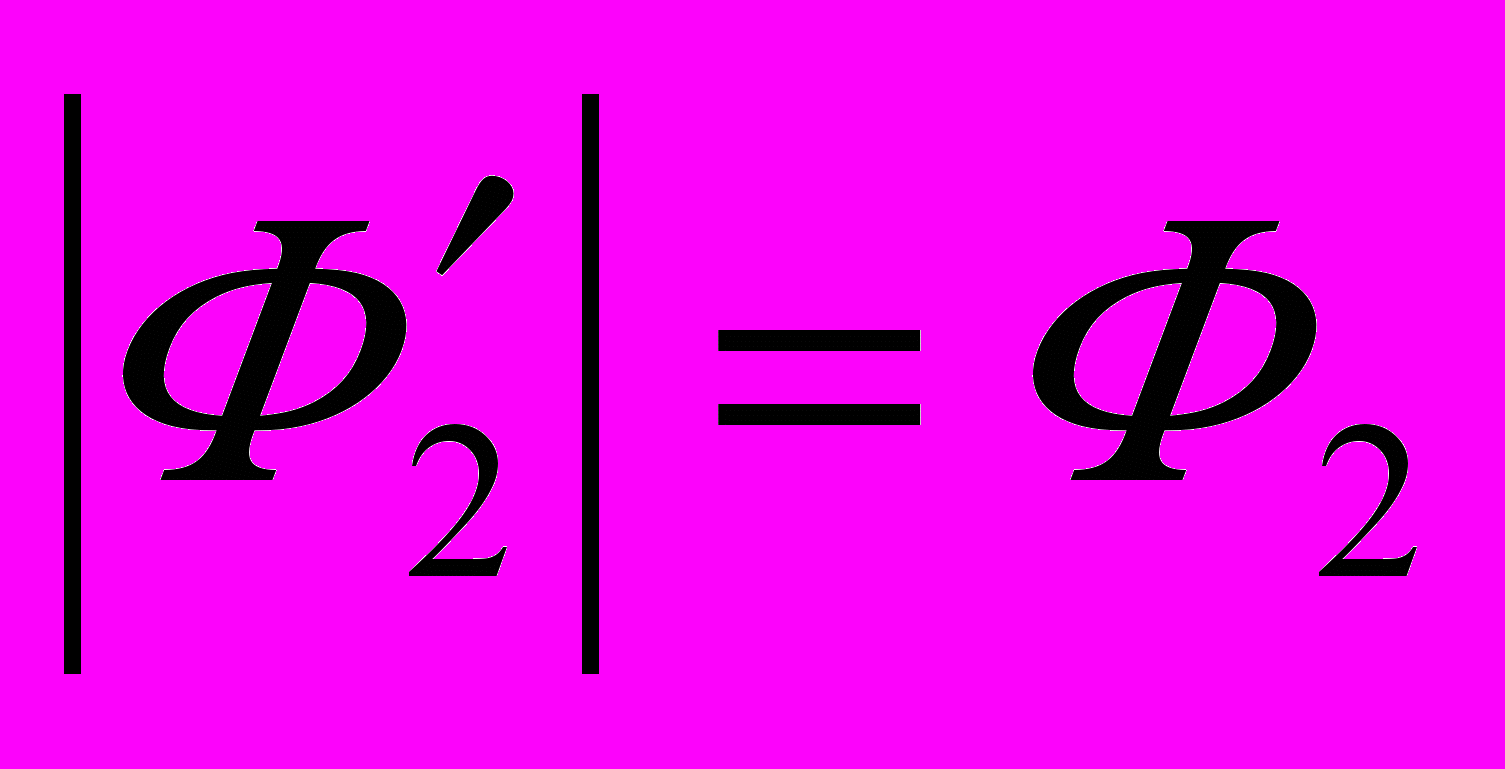 означает, что соприкасаются кромки j по всей длине (по оси), и одновременно кромки j и k по точкам в радиальном направлении.
означает, что соприкасаются кромки j по всей длине (по оси), и одновременно кромки j и k по точкам в радиальном направлении.После наклона и соприкосновения 2-я деталь может скользить кромкой j по 1-й детали в плоскости кромки j. Можно принять, что скольжение происходит в направлении поворота (рис. 12а). Причем то, с какой кромкой произойдет касание, зависит от того, какой из зазоров меньше. Будем предполагать, что устраняется наименьший из зазоров. Тогда параметры кромок 2-й детали примут следующие значения: для кромки, у которой зазор с кромкой 1-й детали наименьший в радиальном направлении, касание будет при 2ejH = 2y+π или 2ekH = 2y (новые параметры помечены индексом «Н»). Значение эксцентриситета E2jH (E2kH) будет равно зазору между кромками – для кромки, по которой будут происходить касание. Так как расстояние между кромками j деталей равно нулю, то S01j = S02j.
а) б)
Рисунок 12 – Положение векторов наклона при совпадении (а) и несовпадении (б) плоскостей кромок
Если
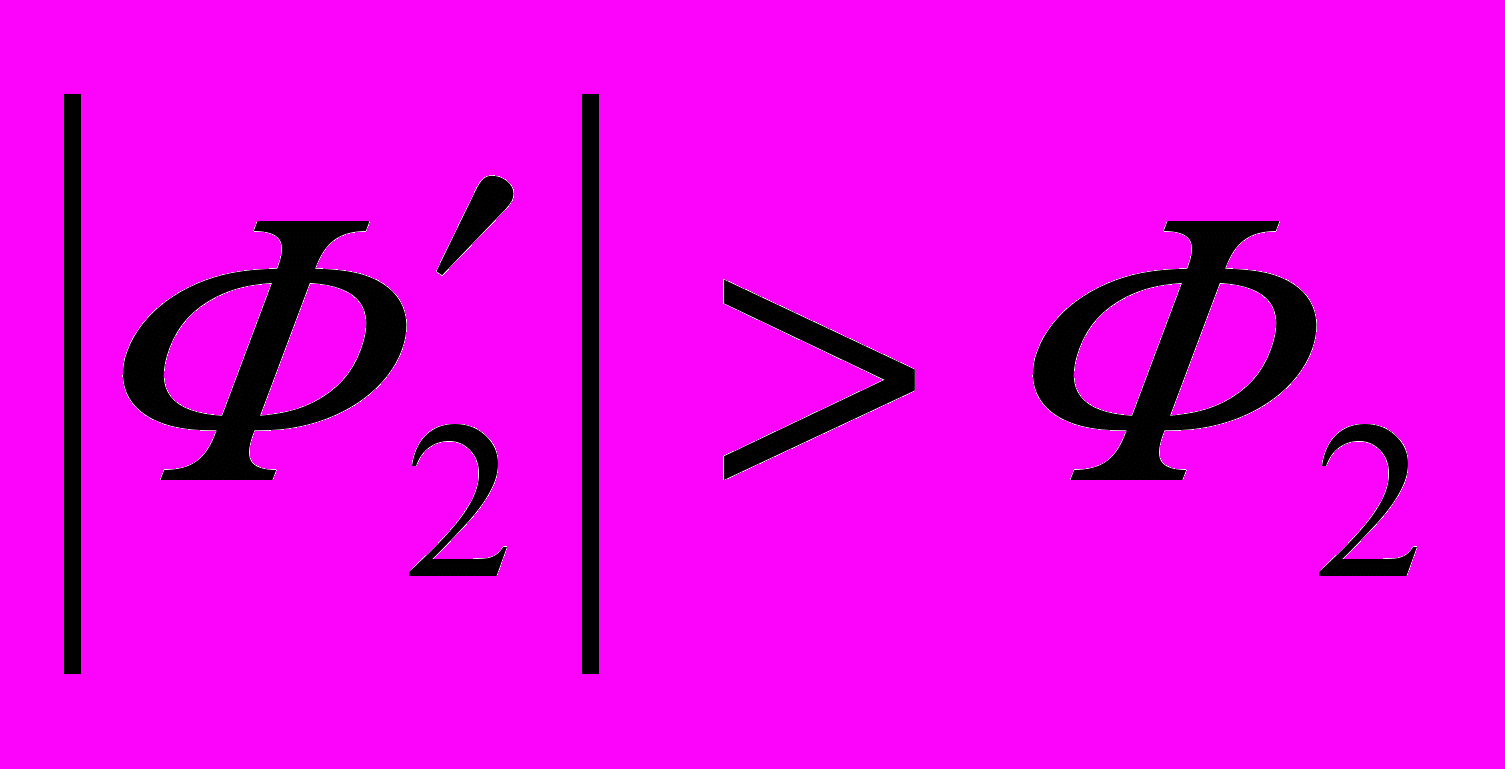 , то при любом положении 2-й детали, касание кромок j вдоль оси происходит в точке, при одновременном касании по точкам кромок j и k в радиальном направлении, т. е. плоскости кромок не совпадают. Можно принять, что угол между плоскостями кромок деталей принимает наименьшее из возможных значений (рис. 12б). Деталь поворачивается на угол Ф2, допускаемый кромками j и k в направлении '2y.
, то при любом положении 2-й детали, касание кромок j вдоль оси происходит в точке, при одновременном касании по точкам кромок j и k в радиальном направлении, т. е. плоскости кромок не совпадают. Можно принять, что угол между плоскостями кромок деталей принимает наименьшее из возможных значений (рис. 12б). Деталь поворачивается на угол Ф2, допускаемый кромками j и k в направлении '2y.Это означает, что параметры кромок j и k в радиальном направлении примут значения:
E2jH = R1j – R2j; 2ejH = '2y , (26)
E2kH = R1k – R2k; 2ekH = '2y +π. (27)
Положение точки касания кромок j вдоль оси определяется углом '2y. Известны параметры кромок j 1-й детали Ф1j, 1y. Параметры кромок j 2-й детали определяются из векторного уравнения
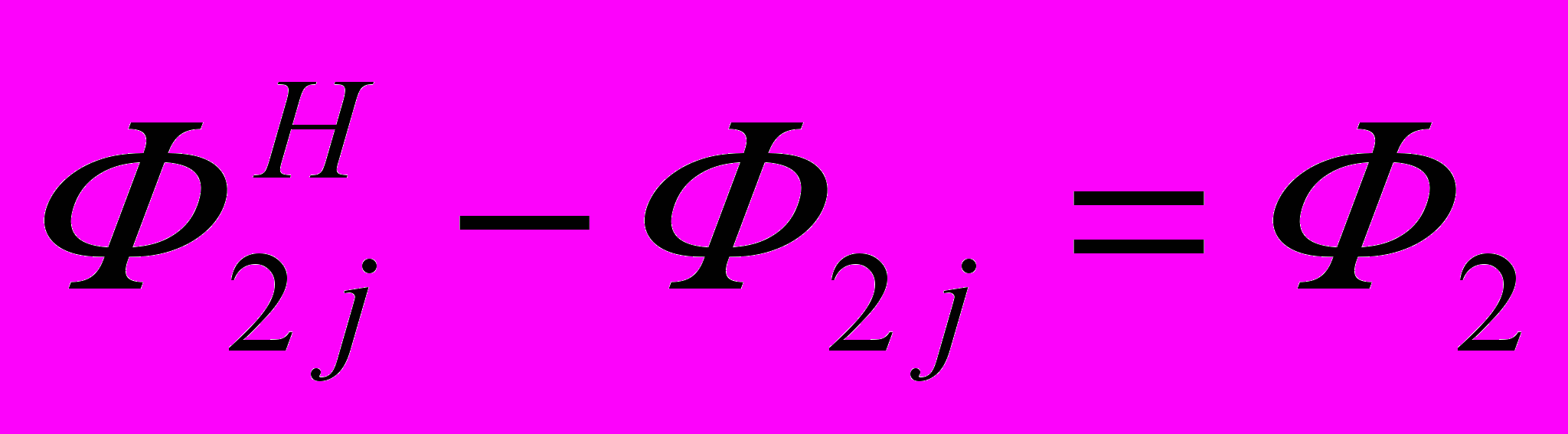 (рис. 12б).
(рис. 12б).Уравнения кромок будут (по малости углов принято tgФ=Ф):
z1j= S01j + R1jФ1jcos ( – 1yj), (28)
z2j= S20j + R2jФ2jHcos ( – 2yjH). (29)
При = 2y' эти значения равны, откуда
S2oj = So1j+ R1jФ1j cos (2y'– 1yi) – R2jФ2jH cos (2j'– 2yjH). (30)
Таким образом, найдены выражения для параметры S20j, Ф2yjH, 2yjH, E2jH, 2ejH, (E2kH, 2ekH), по которым можно определить значения теоретических параметров остальные кромок 2-й детали после соединения.
3. Задача расчета технологических параметров (размеров, эксцентриситетов и наклонов кромок) при механической обработке.
Во многих случаях в единичном и мелкосерийном производстве на этапе базирования и закрепления детали производится выверка положения заготовки. Однако обычная выверка может обеспечить нулевые отклонения доступных для выверки поверхности детали, и практически непригодна для обеспечения нулевых или заданных отклонений недоступных для выверки поверхностей детали. В этом случае может быть применена выверка на основе применения кромочной модели деталей.
С теоретической точки зрения задача выверки сводится к приведению теоретических параметров кромок детали к новой оси, если заданы новые требуемые параметры одной или нескольких кромок. Например, заданы для i-й
и j-й кромки параметры i, ei j, ej (эксцентриситеты кромок и их углы) или параметры i, ei j, yj (эксцентриситет и наклон кромки и их углы). В этом случае положение новой оси определено однозначно. Наиболее важным является вариант, при котором требуется обеспечить i=0 и j=0, то есть поверхность, на которой лежат кромки i и j не должна иметь отклонения относительно оси. Обычно это условие i=0, j=0, необходимо выполнить при выверке обрабатываемых деталей, а величины углов e в этом случае не имеют значения. Рассмотрим решение задачи математического моделирования выверки по варианту i=Еi2зд, Еj=Еj2зд, частным случаем которого является вариант i1=0, j1=0. Известны для всех кромок значения теоретических параметров, среди которых: i1, ei1, j1, ej1, k1, ek1, k1, yk1, Sij, Sik. Известны требуемые новые значения i, ei, j, ej. Нужно найти величины k, ek, k, yk, по которым будет осуществляться выверка. Значения Sij, Sik не изменяются при переходе к новой оси. Здесь i, j – номера кромок, ограничивающих выверяемую поверхность, k – номер кромки, по которой производится выверка. Верхний индекс 1 обозначает параметры кромок до выверки.
Подход к определению искомых величин аналогичен тому, который используется при решении задачи перехода к новой оси: нужно так мысленно двигать деталь в пространстве, чтобы сначала параметр i1 стал равным нулю, а затем равным i при ei при неизменных i1 и yi1 (параллельный перенос детали) при этом изменятся j1, ej1- станут j1n, ej1n; затем, чтобы параметр j1n стал равным нулю и, далее, стал равным j при ej и при неизменных i1, ej (поворот детали). В процессе этих движений будут изменяться значения k1, ek1, k1, yk1, так что в результате получим требуемые значения k, ek, k, yk, при реализации которых путем выверки, будут обеспечены параметры i-й и j-й кромок.
На основе кромочной модели решается задача учета взаимного влияния перекоса и радиального смещения поверхностей детали при расчете технологических размеров. Решение данной задачи изложено в третьей главе работы.
4. Задача построения изображений деталей, сборочных единиц, заготовок, операционных эскизов, схем припусков.
Одной из важнейших задач технологии машиностроения является расчет технологических размеров и обоснование требований взаимного расположения поверхностей. Вспомогательной задачей расчета является визуализация или формирование с помощью ЭВМ исходных данных и результатов – изображений деталей, заготовок и операционных эскизов на всех этапах процесса обработки, схем припусков, сборочных единиц, в частности, с целью проверки правильности данных. В случае деталей типа тел вращения данная задача решается на основе применения структурных изображений через описание кромок деталей, обрабатываемых заготовок, сборочных единиц. При построении математической модели используется не вся информация о детали, а только часть, связанная с теми задачами, которые необходимо решить путем моделирования. В соответствии с этим особенностью предлагаемого подхода является то, что строится изображение не конкретного рабочего чертежа детали, эскиза обрабатываемой заготовки, чертежа сборочной единицы, а их геометрических моделей.
Геометрическая модель детали представляет собой эскиз детали, на котором показаны контуры ее с указанием только торцов и цилиндрических поверхностей, имеющих общую ось, с простановкой всех линейных конструкторских размеров, соединяющих торцы детали. Эскиз дополняется номерами всех поверхностей, указываемых в возрастающем порядке при обходе всего контура детали по часовой стрелке, и сопровождается таблицами, содержащими следующую исходную информацию: а) о количестве участков замкнутого контура детали и номерах поверхностей, образующих участки контура; б) о линейных и диаметральных конструкторских размерах составляющих геометрическую модель детали; в) о границах размеров. Для описания модели заготовки и технологического процесса дополнительно задаются номера поверхностей заготовки, базовых и обрабатываемых поверхностей, границ операционных размеров. Для описания модели сборочной единицы дополнительно к моделям составляющих деталей задается информация о контактах и замыкающих звеньях.
При этом все модели информационно связаны путем применения сквозной нумерации поверхностей, единой для всех моделей.
Разработка программы изображения контура детали включает, во-первых, преобразование данной конкретной информации к виду, который является исходным для изображения контуров деталей, технологических операционных эскизов других графических элементов, во-вторых, собственно построение изображения по преобразованной информации. При изображении детали – выявление количества кромок, количества вертикалей и горизонталей (торцов и цилиндрических поверхностей); определение, на каких горизонталях и вертикалях расположены кромки; определение координат вертикалей и горизонталей; определение последовательности обхода кромок. При изображении заготовки – определение количества кромок, последовательности поверхностей заготовки, количества горизонталей и вертикалей и их координат. При изображении операционного эскиза – добавление к поверхностям заготовки обрабатываемых поверхностей; выделение обрабатываемых поверхностей и изображение на базовых поверхностях значков баз; добавление на каждой операции обработки новых обрабатываемых поверхностей к уже имеющимся поверхностям; оформление операционных эскизов и схемы припусков. При изображении сборочной единицы – выявление размерных связей между деталями.
В результате проведенных теоретических исследований получены следующие новые научные результаты:
- совершенствование теоретических основ размерного анализа объектов машиностроения путем введения в число объектов размерного анализа новых элементов формы деталей – кромок;
- описание формы деталей типа тел вращения кромочной моделью, охватывающей большее число возможных отклонений взаимного расположения поверхностей за счет описания отклонений расположения кромок;
- математическая модель точности деталей типа тел вращения на основе понятия кромки с соответствующим аппаратом теоретических и измеряемых параметров и их преобразования и метод его применения для решения технологических задач обеспечения точности деталей и сборочных единиц;
- предложены методы решения задач размерного анализа на основе применения кромочной модели детали с использованием геометрических моделей объектов размерного анализа.
