Программа дисциплины «Программирование»

Вид материала

Содержание

Задачи к теме «Внешняя сортировка»
Задачи к теме «Хэширование»
Mail, book, man, www, rino, room, paris, lima, kit, phone
Дополнительные материалы для подготовки к контрольнойпо теме «Оценка сложности алгоритмов» Оценка алгоритмов, содержащих ветвлен
Средняя сложность программы

Подобный материал:

1 2 3 4 5 6 7

Задачи к теме «Внешняя сортировка»

1. Сколько отрезков будет в файле записей с ключами

47, 9, 8, 76, 7, 6, 61, 5, 3, 4, 6, 58, 13, 24, 6, 7, 5, 6, 8, 42, 37, 55, 74, 6, 9, 11, 5, 4, 74, 5, 45, 37, 42, 5, 6, 3, 5, 3, 4

после 2-го слияния при использовании метода

а) трехпутевого слияния;

б) двухпутевого сбалансированного слияния файлов;

в) фибоначчиевой сортировки?

Задачи к теме «Хэширование»

2. Пусть коды букв имеют значения:

A-1, B-2, C-3, D-4, E-5, F-6, G-7, H-8, I-9, J-10, K-11, L-12, M-13, N-14, O-15, P-16,
Q-17, R-18, S-19, T-20, U-21, V-22, W-23, X-24, Y-25, Z-26.

Размер хэш-таблицы N=37. Строки нумеруются с 0. Хэш-функция для идентификатора равна сумме кодов букв, составляющих его.

Показать состояние таблицы после записи в нее последовательности идентификаторов:

MAIL, BOOK, MAN, WWW, RINO, ROOM, PARIS, LIMA, KIT, PHONE,

если используется

а) линейное рехеширование;

б) метод цепочек.

Сколько коллизий было разрешено?

Дополнительные материалы для подготовки к контрольной
по теме «Оценка сложности алгоритмов»

Оценка алгоритмов, содержащих ветвления

Для определения максимальной и минимальной сложность необходимо вычислить вес каждой ветви как сумму весов всех входящих в нее вершин и найти максимальное и минимальное значения по всем ветвям соответственно.

Для определения средней сложности необходимо оценить частоты выбора ветвей.

Под частотой ветви понимается отношение числа выполнений программы (алгоритма), при которых исполнились операторы, принадлежащие данной ветви, к общему числу исполнений этой программы.

Средняя сложность программы (ее алгоритма) вычисляется как сумма произведений весов ветвей на их частоты.

Если в программе имеются вложенные ветвления, то можно предложить метод оценки, основанный на оценке частоты, с которой встречаются определенные комбинации входных данных. Рассмотрим его.

Пусть управляющий граф программы содержит ветвления, где выбор ветвей определяется условиями C₁, C₂, C₃, …, C_n. Вид управляющего графа представлен на рис. 1.

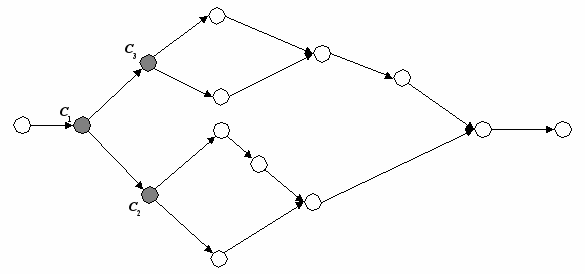
Рис. 1. Пример управляющего графа с ветвлениями

Проверка условия C₁ выполняется всегда, таким образом оно разбивает все ветви на две группы: для первой условие истинно, для второй – ложно. Условие C₂ разбивает группу ветвей, для которых условие C₁ истинно, еще на две группы, для которых истинны условия (C₁ and C₂) и (C₁ and not C₂) соответственно. Условие C₃ также разбивает группу ветвей, для которых условие C₁ ложно, еще на две группы, удовлетворяющих условиям (not C₁ and C₃) и (not C₁ and not C₃) соответственно. Для следующих ветвлений (до C_n) этот процесс «разбиения» ветвей на группы можно было бы продолжить.

Выбор ветвей определяется комбинацией входных данных D. Множество комбинаций исходных данных D также можно разбить на две части D₁ и D₂ (два подмножества), порождаемые условием C₁. В свою очередь D₁ делится на D₃ и D₅, а D₂ разбивается на D₅ и D₆ (рис. 2). Каждая область (подмножество D), которая не разбивается больше ни на какие другие более мелкие части, соответствует ветви в управляющем графе (ветви пересекаются в начальной части графа – для общих условий, определяющих их выбор). Все такие подмножества комбинаций входных данных (областей на рисунке) обозначим d_i. В том случае, когда все комбинации исходных данных являются равновероятными, частоту исполнения i й ветви можно оценить как отношение мощности подмножества d_i к мощности всего множества D: p_i = | d_i | / | D |. Если имеются оценки l_i веса (сложности) i й ветви, то сложность такого алгоритма  с ветвлениями можно оценить величиной

,

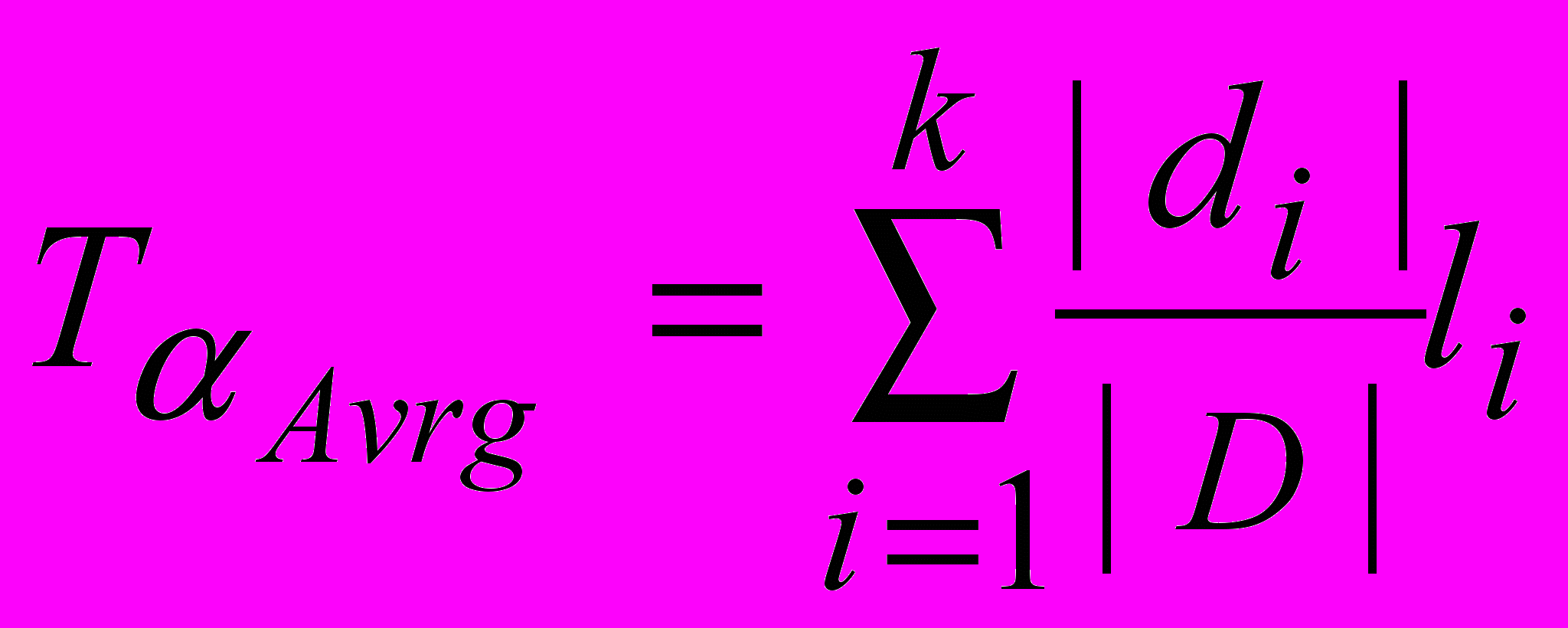где k – количество всех ветвей.

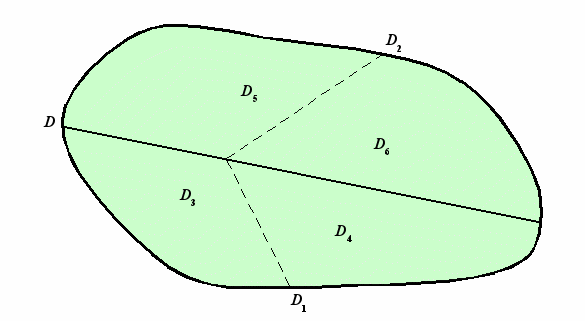
Рис. 2. Разбиение множества комбинаций входных данных, соответствующее
примеру управляющего графа с ветвлениями (рис. 1)

Пример. Пусть алгоритм с ветвлением имеет вид

read(X);

if X < 0.5 then Y := (X + 0.5) * 2

else if X < 0.75 then Y := X * 2 + 0.5 + X**2 + X**3

else Y := X

Допустим, что значение переменной X может принадлежать диапазону [0.00, 1.00], причем ввод любого значения из указанного диапазона равновероятен. Тогда вероятность того, что значение X  [0.00, 0.50), примерно равна вероятности того, что X  [0.50, 1.00]. В приведенном примере вероятность выбора ветви Y := (X + 0.5) * 2 равна 0.5. При невыполнении условия X < 0.5 выбор ветви определяется проверкой условия X < 0.75. Причем ветви выбираются также равновероятно, поэтому частота выбора каждой равна примерно 0.25. Разбиение всего множества комбинаций (в данном случае каждая комбинация определяется только значением переменной X) показано на рис. 3.

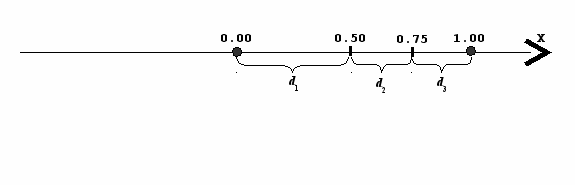
Рис. 3. Геометрическая вероятность ввода значений переменной, определяемая
длинами отрезков числовой прямой (значения равновероятны)

Таким образом, при выполнении программы возможен выбор трех ветвей:

1) ветви Y := (X + 0.5) * 2, соответствующей условию X < 0.5, вес (сложность) которой составляет 5 (ввод, проверка условия, вычисление выражения (2 операции) и присваивание), а вероятность выбора – 0.5;

2) ветви Y := X * 2 + 0.5 + X**3, соответствующей условию not(X < 0.5) and (X < 0.75), вес (сложность) которой составляет 10 (ввод, проверка условия X < 0.5, проверка условия X < 0.75, вычисление выражения (6 операций) и присваивание), а вероятность выбора составляем 0.25;

3) ветви Y := X, соответствующей условию not(X < 0.5) and not(X < 0.75), вес (сложность) которой составляет 4 (ввод, проверка условия X < 0.5, проверка условия X < 0.75, и присваивание), а вероятность ее выбора – примерно 0.25.

Средняя сложность алгоритма составляет

T_Avrg = 0,5  5 + 0,25  10 + 0,25  4 = 2,5 + 2,5 + 1 = 6.

Определите максимальную и минимальную сложность приведенного алгоритма.