Тема 25. Анализ и обработка геофизических данных методом
| Вид материала | Реферат |
- Анализ и обработка геофизических данных методом управляемой эмпирической модовой декомпозиции, 781.33kb.
- Информатизации структур государственной службы реферат, 60.69kb.
- Тема: Обработка данных средствами электронных таблиц. Excel 2010 (2ч), 32.95kb.
- «Математические методы в химии» Общая трудоёмкость дисциплины составляет, 22.21kb.
- Тема доклада, 466.55kb.
- 1352. 08. 02;LS. 01, 19.55kb.
- Тема : Обработка данных, вводимых в виде символьных строк (написать программу средней, 287.53kb.
- Разработка алгоритмов решения обратных задач промышленной диагностики аппроксимационным, 228.31kb.
- Тема: обработка конструкционных материалов лекция 16 Обработка конструкционных материалов, 82.83kb.
- Цель любой программы обработка данных, т е. надо грамотно построить структуры данных, 165.23kb.
ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ
ТЕМА 25. АНАЛИЗ И ОБРАБОТКА ГЕОФИЗИЧЕСКИХ ДАННЫХ МЕТОДОМ
УПРАВЛЯЕМОЙ ЭМПИРИЧЕСКОЙ МОДОВОЙ ДЕКОМПОЗИЦИИ СИГНАЛОВ
Всякой истине суждено одно мгновение торжества между бесконечностью, когда ее считают неверной, и бесконечностью, когда ее считают тривиальной.
Жюль Анри Пуанкаре. Французский математик, физик. 1854-1912 г.
Если снять ограничение тривиальности, то мгновение торжества обращается в ноль, равно как и сама истина. Весьма действенный метод естественного отбора новых истин! Не стала тривиальной, для технического прогресса не годишься.
Игорь Бреднев. Уральский геофизик.
Содержание.
Введение.
1. Частотное управление эмпирической модовой декомпозицией сигналов. Модель сигнала. Условия очистки. Принцип управления EMD. Оценка качества.
2. Очистка периодических сигналов от шумов и флюктуаций. Частотные методы. Ширина переходной зоны частотных фильтров. OEMD при очистке от шумов.
3. Выделение локальных частотных составляющих информации. Передаточные функции OEMD.
4. Очистка от шумов произвольных непериодических сигналов. Условия очистки. Частотный диапазон информации. Очистка от высокочастотных шумов. Оптимальные границы отсева шумов. Устойчивость отсева шумов.
Введение
Адаптивность формирования ортогонального базиса эмпирической модовой декомпозиции (EMD) сигналов для ряда задач анализа создает определенные трудности. В лекции рассматриваются возможности управления процессом эмпирической модовой декомпозиции при анализе геофизических данных. Для управления процессом декомпозиции используется оперативная информация по спектральному составу сигналов и внутренних модовых функций преобразования.
Задачу создания управляемой (operated) эмпирической модовой декомпозиции (OEMD) разделим на две части:
- Очистка сигналов от статистических шумов и флюктуаций.
- Распределение локальных колебательных процессов по уровням IMF.
Разделение вызвано тем, что результаты практически всех методов геофизических исследований природных сред отличаются большими уровнями естественных шумов и статистических флюктуаций измеряемых величин как в силу физической природы самих регистрируемых процессов (например, в методах ядерной геофизики), так и в силу многочисленных физических микро- и макроструктурных неоднородностей геологических сред и дестабилизирующих факторов регистрации физических данных. Очистка геофизических данных от шумов относится к типовой задаче первичной обработки и подготовки данных к интерпретации. Основная задача на этом этапе – отсеять в первую (шумовую) IMF все составляющие сигнала, которые не несут полезной информации.
Что касается второй задачи, то она является естественным продолжением первой задачи применительно к методам активной геофизики (сейсмические, акустические, электромагнитные и т.п.), имеющими дело с сигналами определенной периодичности. Для решения этой задачи необходимо разработать метод управления процессом EMD, позволяющий целенаправленно изменять формирование IMF на всех уровнях разложения таким образом, чтобы получать максимально адекватное представление о процессах в анализируемых данных при сохранении ортогональности базиса разложения.
25.1. ЧАСТОТНОЕ УПРАВЛЕНИЕ ЭМПИРИЧЕСКОЙ МОДОВОЙ ДЕКОМПОЗИЦИЕЙ СИГНАЛОВ
Модель сигнала. Для рассмотрения процесса OEMD зададим (рис. 25.1.1) математическую модель зашумленного сигнала fk с локальными нестационарными частотными составляющими (сигналами) f1k – f4k, которые в сумме образуют полезную информацию f0k и которые необходимо выделить из сигнала в раздельной форме. Мощность шумов соизмерима с мощностью локальных сигналов.
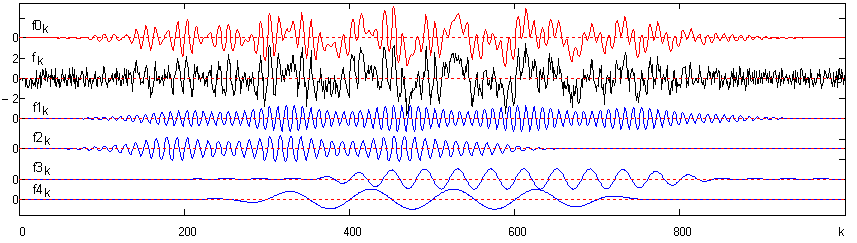
Рис. 25.1.1. Математическая модель сигнала.
Локальные сигналы представляет собой радиоимпульсы с несущими частотами -, два первых из которых амплитудно-модулированы. Белый шум постоянной мощности распределен по всему частотному диапазону сигнала. Амплитудно-частотная характеристика (АЧХ) сигнала fk (модуль частотного спектра в правой части главного частотного диапазона) приведена на рис. 25.1.2. Здесь и в дальнейшем для перевода функций в частотную область представления используется быстрое преобразование Фурье (БПФ).

Рис. 25.1.2. Амплитудно-частотный спектр
модельного сигнала
Условия очистки. В принципе, когда сигнал не зашумлен и в спектре сигнала хорошо выделяются все частотные составляющие (а равно и при априорно известном частотном составе полезной информации), нет необходимости в применении EMD. Разделение частотных компонент может быть выполнено полосовыми частотными фильтрами. Однако для произвольных сигналов при наличии шумов, в спектре сигнала можно уверенно идентифицировать только главные несущие частоты, а все нестационарности сигнала и боковые модуляционные частоты маскируются шумом.
На результаты EMD влияет также отношение мощности шумов к мощности сигнала. Увеличение мощности шумов вызывает «дробление» и искажение даже монотональных функций IMF, т.к. частотные составляющие шума влияют на процесс отсеивания EMD, и на отдельных временных (координатных) интервалах возникает процесс «просачивания» из соответствующих масштабных функций IMF части главных частот на соседние IMF. При близких несущих частотах стандартное EMD может не разделять радиоимпульсы и отсеивать их в одну IMF даже при анализе чистых сигналов. В зашумленных сигналах может наблюдаться искажение всех локальных составляющих, о чем наглядно свидетельствует EMD сигнала fk на рис. 25.1.3.
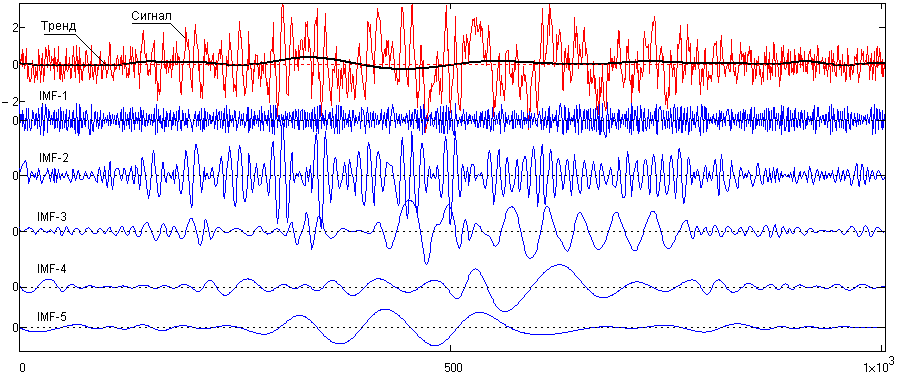
Рис. 25.1.3. Стандартное EMD модельного сигнала
Принцип управления EMD. Для разделения радиоимпульсов в различные IMF необходимо вмешаться в процесс EMD, что можно выполнить с использованием априорной информации о спектральном составе сигналов или непосредственно по оперативной информации о спектре сигнала и спектрах выделяемых IMF.
С учетом следования уровней IMF от высоких частот к низким, на первый уровень в IMF-1 отделяются высокочастотные шумы сигнала за пределами высоких частот полезной информации, что будет рассмотрено ниже. На второй уровень в IMF-2 в принятой нами модели сигнала необходимо отделить сигнал f1. Для этого низкочастотным НЧ-фильтром с граничной частотой среза c ниже частот радиоимпульса f1 (рис. 25.1.2) отфильтруем все частоты сигнала в интервале 0-c и используем результат в качестве начальной функции итераций выделения второй IMF [1]. Аналогично на следующий уровень IMF может быть отсеян радиоимпульс f2, и т.д.
Оценка качества. На модельном сигнале оценку качества разделения сигналов можно проводить вычислением коэффициента взаимной корреляции () между информационными функциями и их IMF-образами или угла расхождения векторов (vectors divergence angle - VDA) = argcos этих функций. Наиболее удобным для сравнения различных вариантов можно считать параметр VDA, который имеет линейный характер изменения своих значений от 0о при полном совпадении функций до 90о при их полной ортогональности (нулевой корреляции).
В этом и заключается сущность частотного управления процессом EMD (метод OEMD), эффективность которого исследуем ниже.
25.2. ОЧИСТКА ПЕРИОДИЧЕСКИХ СИГНАЛОВ ОТ ШУМОВ И ФЛЮКТУАЦИЙ
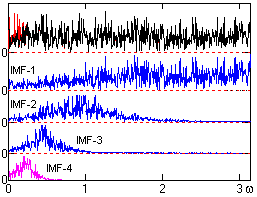
Рис. 25.2.1. Частотная избирательность EMD
по уровням разложения функций IMF
Шумы не относятся к типу колебательных в прямом смысле этого понятия, но они полностью удовлетворяют определениям функций IMF. При распределении спектра шумов по всему частотному диапазону сигнала частотные составляющие шумов распределяются по всем функциям IMF в зависимости от их относительной частотной избирательности. Пример распределения отсева шумов по уровням IMF в главном частотном диапазоне приведен на рис. 25.2.1.
Частотные методы. Очистка от шумов гармонических, квазигармонических и произвольных периодических сигналов при обработке числовых рядов геофизических данных обычно выполняется низкочастотной фильтрацией сигнала, вейвлет-преобразованием данных с исключением из вейвлетного спектра шумовых уровней разложения, и полосовыми частотными фильтрами при непосредственном выделении периодических сигналов по априорным данным о составе сигнала. Следует заметить, что понятие «шума» является относительным, т.к. шумовая составляющая регистрируемых данных также формируется определенными физическими процессами и может содержать определенную информацию об изучаемых объектах и/или условиях их регистрации, которая в дальнейшем (после выяснения природы и характера шумов или степени их корреляции с какими либо процессами/параметрами среды) может использоваться как для повышения точности интерпретации основной информации, так и для получения совершенно новой информации о среде. С этих позиций при очистке главных информационных сигналов от шумов можно считать целесообразным выделение шумов в отдельную составляющую частотно-координатного разложения сигнала.

Рис. 25.2.2. АЧХ сигналов f1 и f2.
Если в спектре сигнала хорошо выражена или априорно известна самая высокая частота max информационной составляющей, то прямой способ очистки сигнала – вырезание ВЧ-фильтром высокочастотных шумов из спектра сигнала от этой границы (c1 модели сигнала, рис. 25.2.2) до частоты Найквиста N с переводом в координатную область в качестве первой функции IMF-1. При использовании для очистки OEMD, с учетом частоты сигнала f1 и частотной избирательности EMD (рис. 25.2.1) для той же операции требуется (3-4)-х кратный последовательный отсев шумов с суммированием результатов отсева в одну функцию IMF-1, если не требуется частотно-координатного анализа шумовых составляющих.

Рис. 25.2.3. Сигнал f1, выделенный
из модельного сигнала.
Для сравнительной оценки качества очистки модельного сигнала от шумов при известных частотных границах локального сигнала f1 выполним выделение сигнала в интервале c1-c2 полосовой фильтрацией (ПФ) и методом OEMD (в IMF-2) и вычислим параметр VDA между выделенными сигналами и модельной функцией f1. Результаты операции приведены на рис. 25.2.3. Качество очистки от шумов обоих методов практически одинаково.
Но амплитудные, частотные или фазовые изменения информационных частот на пространстве задания сигнала эквивалентны их модуляции и появлению у главных пиков несущих частот боковых частот, которые могут не выделяться на спектре, а их вырезание приведет к частичной потере информации. Так, для нашего модельного сигнала корректная установка среза высокочастотного фильтра на очистку от шумов соответствует (по априорно известному значению частоты модуляции сигнала f1) частоте с1, что совершенно не фиксируется на спектре сигнала (рис. 25.2.2).
Ширина переходной зоны частотных фильтров. Исследуем еще один параметр, непосредственно влияющий на процесс EMD – ширина переходной зоны (ПЗ) фильтра tb.
Применительно к ВЧ-фильтрам для выделения шумов ширина ПЗ является отрицательным фактором. При расширении значения ПЗ влево от c1 на рис. 25.2.2 в выделяемые шумы начинают попадать и исключаться из главной информации модуляционные частоты сигнала f1. При использовании OEMD характер влияния ПЗ изменяется на прямо противоположный. При расширении ПЗ вправо от c1 (см. рис. 25.2.4) часть шумов из зоны ПЗ начинает оставаться в интервале сигнала f1 и параметр VDA начинает увеличиваться, но все модуляционные частоты в сигнале f1 сохраняются. Этот фактор начинает играть положительную роль, если ширина боковой полосы сигнала f1 априорно неизвестна и при установке границы c1 НЧ-фильтра может быть допущена ошибка.
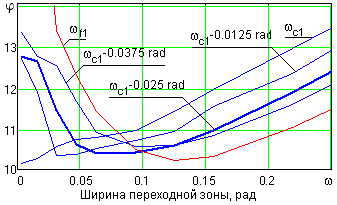
Рис. 25.2.4. Зависимость параметра от ширины переходной зоны НЧ-фильтра при установке разных границ среза фильтра.
На рис. 25.2.4 приведены зависимости параметра VDA для модельного сигнала f1 от ширины переходной зоны НЧ-фильтра (по уровням 0.9-0.1) при разных установках границы среза фильтра в интервале от c1 – верхней границы модуляционных частот, до f1 – несущей частоты сигнала f1 (сдвиг относительно c1 показан в обозначениях кривых).
При установке границы среза НЧ-фильтра OEMD в пределах модуляционных частот выделяемого сигнала при ширине ПЗ, много меньшей ширины боковой полосы модуляционных частот, параметр VDA за счет потери части модуляционных частот возрастает по отношению к минимально возможному (при границе по c1). Но при увеличении ширины ПЗ параметр VDA начинает уменьшаться (уменьшаются потери боковых частот) и достигает определенного минимума (при полном включении боковых частот в состав выделяемого сигнала), близкого к абсолютному минимуму, после чего начинает снова увеличиваться за счет включения в состав сигнала все большей доли шумовых частот. Для полного включения всех боковых частот в состав выделяемого сигнала значение ПЗ должно быть таким, чтобы коэффициент передачи НЧ-фильтра на границе боковых частот был не ниже 0.707 (ширина ПЗ порядка двух значений ширины верхних боковых частот сигнала, tb ≈ 2(c1-f1)). Широкие зоны минимумов VDA по зависимости от ширины переходных зон делают процесс OEMD устойчивым к ошибкам установки границ и ширины переходных зон.
OEMD при очистке от шумов. Отсюда следует простая логика установки НЧ-фильтров OEMD для очистки от шумов. Граница среза фильтра устанавливается непосредственно после пика максимальной частоты очищаемого от шумов сигнала, который обычно хорошо фиксируется по спектру сигнала или известен по априорным данным. Ширина переходной зоны устанавливается по априорным данным или по ожидаемым амплитудно-частотным нестационарностям сигнала.
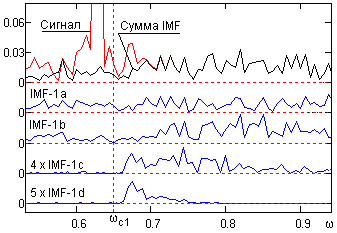
Рис. 25.2.5. АЧХ шумовых функций OEMD.
На рис. 25.2.5 приводятся модули спектров 4-х последовательно отсеянных OEMD функций IMF-1 (c1=0.65 rad, ПЗ 0.075 rad), а также спектр суммы этих функций в сопоставлении со спектром сигнала в области локального сигнала f1 (функции IMF-1c и 1d в увеличенном масштабе).
На рисунке можно видеть, что в функциях IMF появляются низкочастотные составляющие спектров в интервале 0-c1. Эти составляющие не отображают каких-либо шумовых частот в сигнале, а формируются интерференцией выделенных высокочастотных шумов. Это позволяет обнулить значения спектров в интервале 0-c1, что дает дополнительное уменьшение VDA на (3-5)%.
При очистке от шумов OEMD имеет возможность раздельной установки частоты срезов и ширины переходных зон фильтров при отборе функций IMF-1 (т.е. фильтров с разными параметрами для отсева в IMF-1a, IMF-1b и др.), что позволяет повысить управляемость процессом очистки сигналов с особо сложной структурой боковых частот (в диалоговом режиме контроля за спектрами IMF-1).
25.3. ВЫДЕЛЕНИЕ ЛОКАЛЬНЫХ ЧАСТОТНЫХ СОСТАВЛЯЮЩИХ ИНФОРМАЦИИ
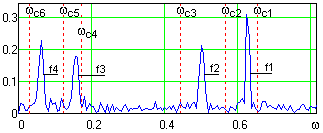
Рис. 25.3.1. Частотные границы процесса OEMD.
Частотные параметры OEMD. Аналогичная методика установки границ срезов НЧ-фильтров и ширины переходных зон OEMD может применяться при последовательном выделении локальных частотных групп по всему частотному диапазону сигнала. На рис. 25.3.1 приведен модуль спектра тестового сигнала fk (рис. 25.1.1) и установленные частотные границы локализации выделения модовых функций IMF. Результат OEMD тестового сигнала приведен на рис. 25.3.2.
Эффект использования OEMD наглядно виден при сравнении рис. 25.3.2 и 25.1.3. Отметим некоторые особенности выполнения декомпозиции сигналов.
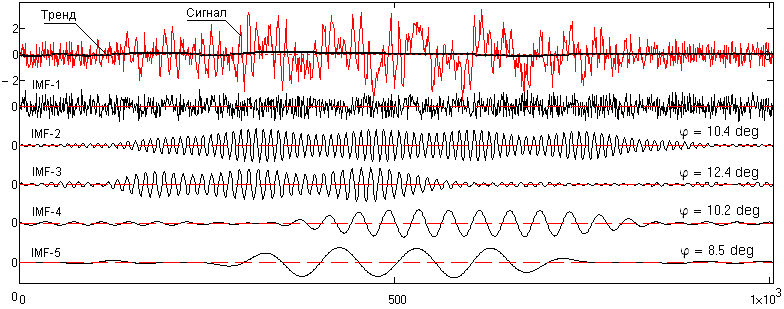
Рис. 25.3.2. Результаты OEMD модельного сигнала.
При выделении модулированных или нестационарных сигналов (f1 и f2) границы НЧ-фильтров целесообразно устанавливать за пределами боковых полос сигналов с малой шириной переходной зоны (c3 и c2). Если ширина боковых полос неизвестна, то можно отодвигать в область более низких частот левые границы выделения соответствующих сигналов (c3 для f2, c2 для f1) с расширением переходной зоны вплоть до несущей частоты сигнала.
Если в спектре сигнала встречаются достаточно протяженные «пустые» зоны (как например, интервал между сигналами f3 и f2), то целесообразно эти интервалы также отсеивать в отдельные IMF или выделять и суммировать с шумовым IMF-1. В противном случае они войдут в состав последующего выделяемого сигнала (f3).

Рис. 25.3.3. Отсечка «хвостов» монотональных IMF.
На рис. 25.3.3 приведены модули спектров IMF-4 и IMF-5. По априорным данным функции f3 и f4 однотональные, следовательно, «хвосты» IMF - низкочастотные шумы сигнала. Для IMF-4 это остаточный шум из интервала c4-c3, не отсеянный в предыдущую «пустую» IMF вследствие его значительного размера, т.е. для полного исключения шума требовался, как минимум, двойной отсев (как при очистке от шумов). Для IMF-5 это шумы межчастотного интервала f4-f3. «Хвосты» шумов однотональных IMF всегда односторонние, в сторону высоких частот, что позволяет идентифицировать их на спектрах IMF и отсекать с переводом a шумовую IMF-1.
На рис. 25.3.4 приведено семейство графиков эквивалентной частотной передаточной функции процесса OEMD при выделении всех информационных сигналов f1-f4 с разными реализациями наложенного шумового сигнала (8 реализаций).
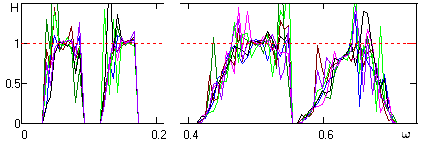
Рис. 25.3.4. Частотные передаточные функции OEMD.
Передаточные функции OEMD вычислялись по отношению суммы модулей спектров функций IMF-2, IMF-3, IMF-4 и IMF-5 (рис. 25.3.2) к модулю спектра реализации сигнала fk (рис. 25.1.1). Все функции IMF вычислялись в однотипном режиме, описанном выше, с одной установкой параметров OEMD для всех реализаций сигнала fk.
Таблица 25.3.1.
| | рад | ∓, рад |
| ∑ fN | 15.92 | 0.72 |
| f1 | 10.98 | 0.96 |
| f2 | 12.13 | 0.93 |
| f3 | 10.11 | 0.98 |
| f4 | 9.14 | 0.90 |
В таблице 25.3.1 приведены данные статистической обработки результатов OEMD этих 8-ми реализаций по углу расхождения с модельными функциями f1-f4 и их суммой.
По этим данным можно сделать заключение, что OEMD сохраняет адаптивность к содержанию исходного сигнала, «изменяя» эквивалентную частотную передаточную характеристику в зависимости от конкретной реализации шумовых сигналов, при этом обеспечивается устойчивость выделения сигналов с погрешностью не более 10%.
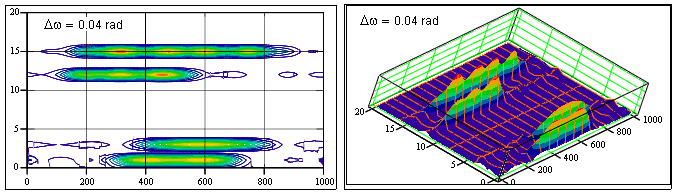
Рис. 25.3.5. Спектр мгновенных частот выделенного сигнала без IMF-1
На рис. 25.3.5 приведено частотно-временное распределение мгновенных частот преобразования (спектр Гильберта-Хуанга) данного модельного сигнала без шумовой IMF-1.
25.4. ОЧИСТКА ОТ ШУМОВ ПРОИЗВОЛЬНЫХ НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Условия очистки. Рассмотрим применение OEMD для решения типовой задачи геофизических измерений - очистку от шумов произвольных сигналов, представленных числовыми рядами в линейном варианте y(x) = f(x, p), где х – координата среды (профиль съемки, ствол скважины), р – произвольный зарегистрированный или вычисленный физический параметр среды (интенсивность излучения, напряженность поля, плотность горных пород, и т.п.). В методах регистрации отклика среды при активном воздействии на нее периодическими излучателями (электромагнитные, акустические и т.п.) под f(x, p) понимается какой-либо физический параметр, выделенный или определенный обработкой из этого отклика.
Полезная информация в таких числовых рядах определяется геологическим строением среды и является преимущественно низкочастотной с гармониками более высоких частот в локальных областях аномалий и резких границ разнотипных геологических сред. Шумовой сигнал, как правило, нелинейный и нестационарный, спектр шумов перекрывается со спектром сигнала, а мощность шумов может быть соизмеримой с мощностью сигнала. В этих условиях задачей первичной обработки данных обычно является подавление шумов с сохранением линейной разрешающей способности интерпретации данных. Но в такой постановке задача относится к числу некорректных, а ее решение во многом имеет субъективный характер и не имеет каких-либо критериев оценки оптимальности для каждой конкретной реализации. Последнее прямо относится к методам выделения полезной информации из данных низкочастотными фильтрами, поскольку требует априорного задания среза фильтров.
Возможности метода OEMD для решения поставленной задачи, с учетом его адаптации под характер сигналов, требуют изучения. Однако задание какой-либо обобщенной математической модели сигнала под поставленные условия весьма проблематично, и поэтому исследование выполним на реальных каротажных диаграммах.
Частотный диапазон информации. Стандартный линейный интервал дискретизации при цифровой регистрации данных в скважинной геофизике составляет 10 см, при этом требования к пространственной разрешающей способности интерпретации данных по минимальной мощности пластов обычно не менее 50-100 см. Отсюда следует, что ожидаемая полезная информация является низкочастотной и занимает не более 5-10% главного частотного диапазона измерений. Естественно, что этот диапазон может быть и много меньше, если геологический разрез по скважине представлен пластами (более или менее однородными интервалами) с гораздо большей мощностью. Но в любом случае следует ожидать, что очистка от шумов потребует проведения трехкратного отсева шумов, т.е. формирование IMF-1 = IMF1a + IMF1b + IMF1c.

Рис. 25.4.1. Диаграмма нейтронного каротажа скважины

Рис. 25.4.2. Спектр нейтронного каротажа.
Очистка от высокочастотных шумов. На рис. 25.4.1 приведен пример диаграммы нейтронного каротажа. Спектр сигнала приведен на рис. 25.4.2. Сделать какое-либо заключение о границе информационной части сигнала по данному спектру не представляется возможным. Для установки границы шумов была использована априорная информация о минимальной мощности однородных интервалов скважин порядка 0.7-1 м, что согласуется с визуальным контролем примерно однородной мощности шумов на спектре сигнала с порога порядка 0.2 рад.
Задаем границы трех фильтров Н1-Н3 при c1 > c2 > c3 с шагом между границами срезов c = 0.02 рад (можно рекомендовать порядка (5-10)% ожидаемой ширины спектра информационной части сигнала). Ширина переходных зон фильтров установлена равной 3c для Н1, 4c для Н2 и 5c для Н3, при этом граница полного подавления высокочастотных составляющих для всех трех фильтров примерно одна и та же. Входной и очищенный сигнал, а также выделенные шумы, приведены на рис. 25.4.3.
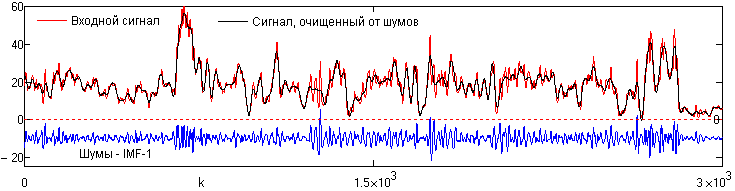
Рис. 25.4.3. Входной сигнал, выходной сигнал, и выделенные шумы нейтронного каротажа.
На спектре сигнала (рис. 25.4.2) довольно четко отмечается также группа низких частот в интервале 0-0.04 рад. На рис. 25.4.4 приведен результат очистки сигнала от шумов при сдвиге порогов всех фильтров на 0.15 рад влево. Естественно, что при этом увеличилась степень сглаживания сигнала и уменьшилась линейная разрешающая способность. Но какой именно из очищенных сигналов, на рис. 25.4.3 или 25.4.4, принять для дальнейшей обработки и интерпретации, можно решить уже только на этапе сопоставления с другими геофизическими и геологическими данными по этому интервалу скважины.

Рис. 25.4.4. Входной сигнал, выходной сигнал, и выделенные шумы нейтронного каротажа при сдвиге среза НЧ-фильтра в область низких частот.
На рис. 25.4.5. приведен еще один пример - диаграмма резистивиметрии (Mud Resistivity). Диаграмма центрирована для обработки.

Рис. 25.4.5. Центрированная диаграмма резистивиметрии по стволу скважины.
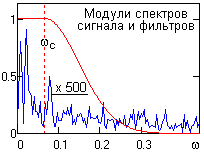
Рис. 25.4.6. АЧХ резистивиметрии
Информационный сигнал резистивиметров обычно является еще более низкочастотным и занимает не более 3-5% главного диапазона на уровне мощных шумов по всему диапазону спектра. В этих условиях можно использовать фильтры отсева шумов с равными частотами срезов и переходных зон. Модули спектров сигнала и передаточных функций НЧ-фильтров приведены на рис. 25.4.6.
На рис. 25.4.7 и 25.4.8 приведены очищенные от шумов диаграммы с порогами отсева с = 0.066 и 0.1 рад. Параллельно очистка сигнала проводилась низкочастотными фильтрами с теми же границами среза c.
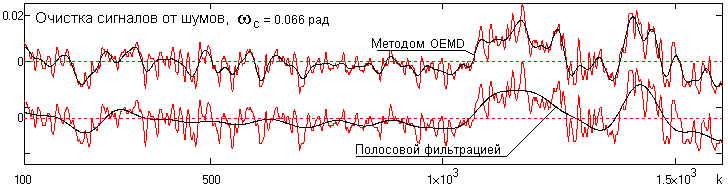
Рис. 25.4.7. Очистка диаграммы резистивиметрии от шумов, срез НЧ-фильтра 0.066 рад.

Рис. 25.4.8. Очистка диаграммы резистивиметрии от шумов, срез НЧ-фильтра 0.1 рад.

Рис. 25.4.9. Гистограммы шумов.
Как можно видеть по результатам сравнения диаграмм, метод OEMD обеспечивает более высокую разрешающую способность очищенного сигнала, причем устойчивость очистки, в отличие от частотной фильтрации, сохраняется при достаточно большом изменении порога отсева шумов и вариациях переходных зон.
Это определяется тем, что при отборе шумов процесс OEMD, протекающий в координатном пространстве, в большей степени учитывает динамику локальных неоднородностей распределения отсчетов (локальную статистику отсчетов), в отличие от частотной фильтрации. Свидетельством этого являются гистограммы выделенных «шумовых» сигналов, приведенные на рис. 25.4.9.
Оптимальные границы отсева шумов. Однако и визуальные, и априорные методы установки границ отсева шумов в определенной степени являются субъективными. Возможность установки оптимальных границ фильтров на основе объективных оценок динамики спектра сигнала рассмотрим на реальном и достаточно типовом сигнале - каротажной диаграмме ПС (Spontaneous Potential) f(k), k = 0 … K, k = 10 см, приведенной на рис. 25.4.10.

Рис. 25.4.10. Каротажная диаграмма ПС и модуль ее спектра.
Как видно на графике спектра ПС в низкочастотной части главного частотного диапазона, какого-либо визуального критерия установки частоты среза c низкочастотного фильтра для очистки сигнала от шумов в данном случае не имеется. Оценку регулярности и значимости информации, выделяемой НЧ-фильтром, можно выполнить по углу расхождения векторов (VDA) отфильтрованной информации и исходного сигнала fk методом «Последовательного Расширения окна Фильтра» (ПРФ). Метод можно применять как в координатном, так и в частотном представлении сигнала. ПРФ по спектру является более быстрым.
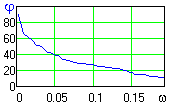
Рис. 25.4.11. График VDA в зависимости от среза НЧ-фильтра.
Просканируем низкочастотную часть спектра сигнала НЧ-фильтром с последовательным сдвигом границы среза фильтра с интервалом (min= 2/(K+1)), начиная с первого отсчета спектра. VDA выделенной части спектра вычисляем с полным спектром сигнала, или (для повышения чувствительности) со спектром сигнала с обнуленной высокочастотной шумовой частью. Полученный график углов расхождения приведен на рис. 25.4.11.
Интегральный характер вычисления VDA резко снижает влияние статистических шумов на результаты вычислений. Угол максимален для первого положения фильтра при c= и постепенно уменьшается по мере увеличения c (в пределе стремится к 0). Но в силу неравномерности спектра это уменьшение также неравномерно и замедляется после пересечения срезом фильтра наиболее значимых регулярных гармоник спектра. Положение этих замедлений может быть зафиксировано по локальным минимумам производной VDA.
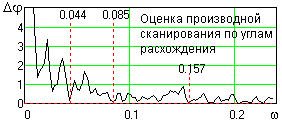
Рис. 25.4.12. Производная VDA в зависимости от среза НЧ-фильтра.
На рис. 25.4.12 приведен график оценки производной VDA (рис. 25.4.11). После прохождения границей среза фильтра всех регулярных гармоник информационной части сигнала при постоянной мощности статистических шумов по спектру сигнала градиент уменьшения углов расхождения также стремится к постоянному статистически флюктуирующему значению и кривая оценки производной выполаживается.
По графику на рис. 25.4.12 могут быть отмечены две возможно оптимальных границы низкочастотной фильтрации c=0.085 и 0.157рад, и одна граница с явной утратой части полезной низкочастотной информации. Естественно, что какая-то часть информации будет теряться и при границе c=0.085, но ее значимость может быть оценена только интерпретатором по критерию степени сглаживания кривой при сохранении линейной разрешающей способности выделения характерных информационных точек. Общий характер степени сглаживания диаграммы с выделенными границами НЧ-фильтрации приведен на рис. 25.4.13.
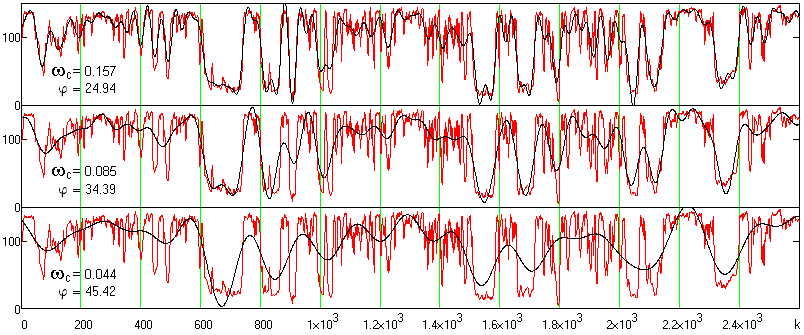
Рис. 25.4.13. Результаты OEMD диаграммы ПС с разными срезами НЧ-фильтра.
Устойчивость отсева шумов. Метод OEMD позволяет производить более гибкую настройку очистки от шумов с визуальным контролем результатов очистки. Для рассматриваемых данных оказалось достаточным применить трехкратный отсев шумов в функцию IMF-1. Пример нескольких вариантов очистки с параметрами настройки приведен на рис. 25.4.14.
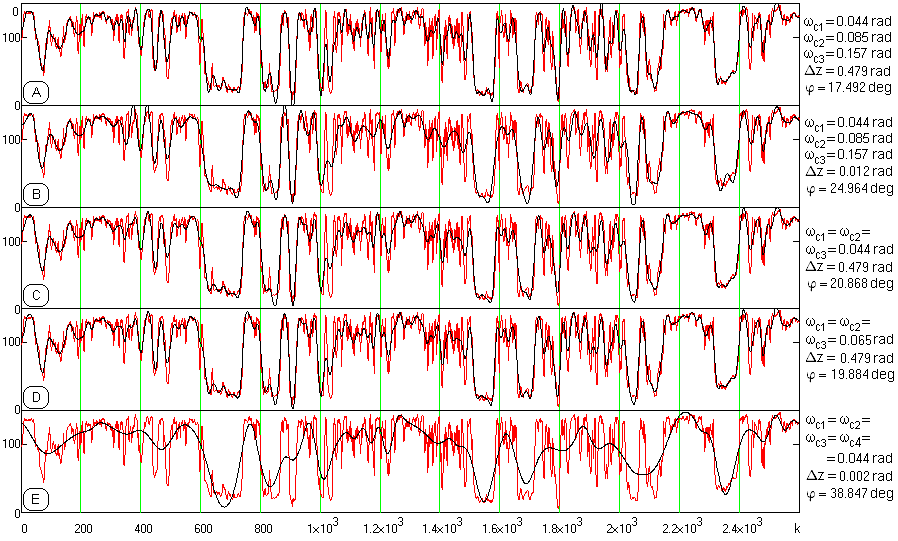
Рис. 25.4.14. Очистка диаграммы ПС от шумов при разных настройках параметров НЧ-фильтра.
С учетом малой критичности OEMD к границам среза фильтров относительно информационной части сигнала, срезы фильтров c были установлены по графику на рис. 25.4.12 с нарастанием от первого локального минимума (0.044 рад) до третьего (0.157 рад) с шириной переходной зоны z = 0.479 рад, одинаковой для всех трех фильтров (кривая А на рис. 25.4.14). При сравнении с первой кривой на рис. 25.4.13 наглядно видна ее более высокая детальность выделения разнородных локальных объектов. Изменением ширины переходной зоны можно изменять степень сглаживания кривой (кривая В). Адаптивность метода позволяет ему достигать практически таких же результатов при одной установке границы среза для всех фильтров (кривая С), при этом допускаются существенные вариации значения границы среза как в большую (кривая D), так и в меньшую стороны.
При включении четвертого фильтра отсева шумов в IMF-1 степень сглаживания сигнала существенно увеличивается (кривая Е), но с этого уровня она также может регулироваться изменением границ фильтров и ширины их переходных зон.
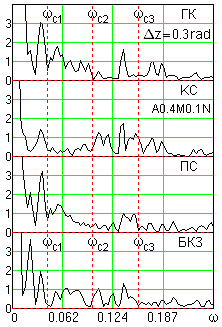
Рис. 25.4.15. Графики ПРФ разных методов каротажа для одного интервала скважины
В целом по результатам сравнения диаграмм можно сделать вывод, что метод OEMD обеспечивает более высокую разрешающую способность очищенного сигнала, причем устойчивость очистки, в отличие от частотной фильтрации, сохраняется при достаточно большом изменении порога отсева шумов и вариациях значений переходных зон.
Частотный диапазон информационной части каротажных диаграмм на изучаемых интервалах скважин определяется геологическим разрезом по стволу скважины и практически одинаков для всех методов каротажных исследований, направленных на детализацию геологического разреза. Это позволяет оптимальные частотные параметры фильтров для управления процессом EMD устанавливать по какому-либо методу с наиболее выразительным характером графика ПРФ и применять эти параметры (учитывая высокую степень адаптации процесса OEMD к характеру сигналов) для обработки других методов каротажа по данному интервалу скважины, а также других интервалов и скважин с аналогичным геологическим строением. Пример графиков ПРФ по каротажным диаграммам одного интервала скважины комплекса ГК, КС, ПС и БКЗ (1 зонд) приведен на рис. 25.4.15, а на рис. 25.4.16 приведены результаты очистки от шумов этого комплекса диаграмм с параметрами фильтрации, установленными по диаграмме ГК.
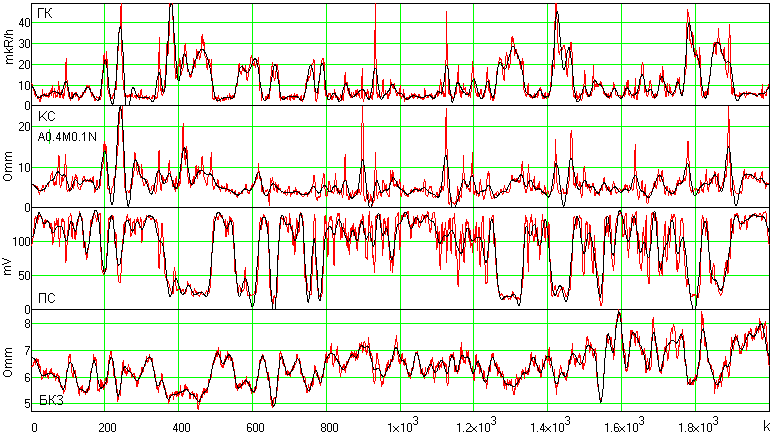
Рис. 25.4.16. Результаты OEMD разных методов каротажа при однотипной установке
параметров НЧ-фильтра
Все вычисления OEMD выполнены программой, разработанной в среде Mathcad [3]. С дополнительными материалами по преобразованию Гильберта-Хуанга и эмпирической модовой декомпозицией сигналов можно познакомиться в работах [2].
Заключение
Изложенная методика свободна как от физической сущности обрабатываемых данных, так и статистики распределения шумовых сигналов и дестабилизирующих флюктуаций, и может эффективно использоваться для очистки от шумов геофизических данных практически всех геофизических методов и детального инструментального анализа информации в активных методах геофизики.
Литература.
1. Давыдов В.А., Давыдов А.В. Очистка геофизических данных от шумов с использованием преобразования Гильберта-Хуанга.// Электронное научное издание "Актуальные инновационные исследования: наука и практика", 2010, № 1. lresearch.ru.
2. Преобразование Гильберта-Хуанга для анализа нелинейных и нестационарных сигналов. ссылка скрыта, ссылка скрыта
3. Давыдов В.А., Давыдов А.В. Эмпирическая модовая декомпозиция сигналов с управлением по частотам разложения. ссылка скрыта, ссылка скрыта
ссылка скрыта ~ ссылка скрыта ~ ссылка скрыта
О замеченных опечатках, ошибках и предложениях по дополнению: davpro@yandex.ru.
Copyright © 2010 Davydov А.V.
