Раздзел VI. Навучанне разважанням
| Вид материала | Документы |
- Раздзел I. Асновы канстытуцыйнага ладу (артыкулы 1 20) раздзел, 554.42kb.
- Раздзел I. Старажытнае грамадства на тэрыторыі беларусі. Фарміраванне этнічных супольнасцей, 6321.57kb.
- Публикация Журнал «Пачатковае навучанне: сям я, дзіцячы сад, школа», 105.64kb.
- Планы- канспекты творчых урокаў І прадметных тыдняў Гісторыя Беларусі, 1850.94kb.
- Раздзел Выкарыстанне асобасна-арыентаваных тэхналогій навучання, 855.87kb.
- Тлумачальная запіска, 170.51kb.
- Тлумачальная запіска, 170.54kb.
- Раздзел Нетрадыцыйныя формы ўрокаў, 388.54kb.
- Нормы ацэнкі вынікаў вучэбнай дзейнасці вучняў па вучэбным прадмеце «Беларуская мова», 489.22kb.
Раздзел VI. НАВУЧАННЕ РАЗВАЖАННЯМ
Да ведама настаўніка
У падручніках матэматыкі пад рэдакцыяй А.А. Столяра вылучаецца асобны раздзел "Вучыся разважаць правільна".
Пад разважаннем разумеюць паслядоўнасць вывадаў. Найкарацейшыя разважанні складаюцца з аднаго вываду. Напрыклад:
(1) Ніхто не абвяргае, што ўменне разважаць з'яўляецца вельмі карысным для паспяховага навучання.
Значыць, кожны настаўнік жадае, каб яго вучні ўмелі разважаць.
(2) Калі вучні будуць ведаць правілы вываду, то развіццё лагічнага мыслення будзе ажыццяўляцца больш эфектыўна. Пазнаёмім вучняў з некаторымі правіламі вываду.
Значыць, уздзеянне на развіццё лагічнага мыслення вучняў будзе больш выніковым.
Вывад - гэта форма мыслення, пры дапамозе якой з аднаго або некалькіх выказванняў атрымліваецца новае.
Раней вядомыя, зыходныя выказванні, на падставе якіх робяць вывад (на якія ў вывадзе спасылаюцца), называюць пасылкамі. Новае выказванне, атрыманае з пасылак, называюць заключэннем.
Такім чынам, лагічныя вывады і разважанні даюць магчымасць набываць новыя веды без непасрэднага звароту да пачуццёвага вопыту і наглядных уяўленняў.
Зразумела, што карыснымі з'яўляюцца толькі такія разважанні, якія прыводзяць да праўдзівых або, у крайнім выпадку, праўдападобных заключэнняў. Таму ўсе вывады падзяляюцца на дэдуктыўныя і недэдуктыўныя (праўдападобныя або імавернасныя). Апошнія маюць эўрыстычны характар, г. зн. садзейнічаюць паяўленню здагадак, дапушчэнняў, гіпотэз (напрыклад, вывад (2)). Яны яшчэ патрабуюць вопытнага або лагічнага абгрунтавання. Да атрымання бясспрэчна праўдзівых ведаў прыводзяць толькі дэдуктыўныя вывады. Менавіта таму яны адыгрываюць у матэматыцы вядучую ролю.
Пералічым істотныя адметныя прыметы дэдуктыўных вывадаў:
1) пасылкі заўсёды праўдзівыя;
2} лагічны пераход ад пасылак да заключэння ажыццяўляецца па пэўных правілах - правілах лагічнага вываду;
3) атрыманае такім шляхам заключэнне абавязкова будзе праўдзівым.
Існуюць разнастайныя правілы лагічнага вываду. Разгледзім найбольш распаўсюджаныя з іх:
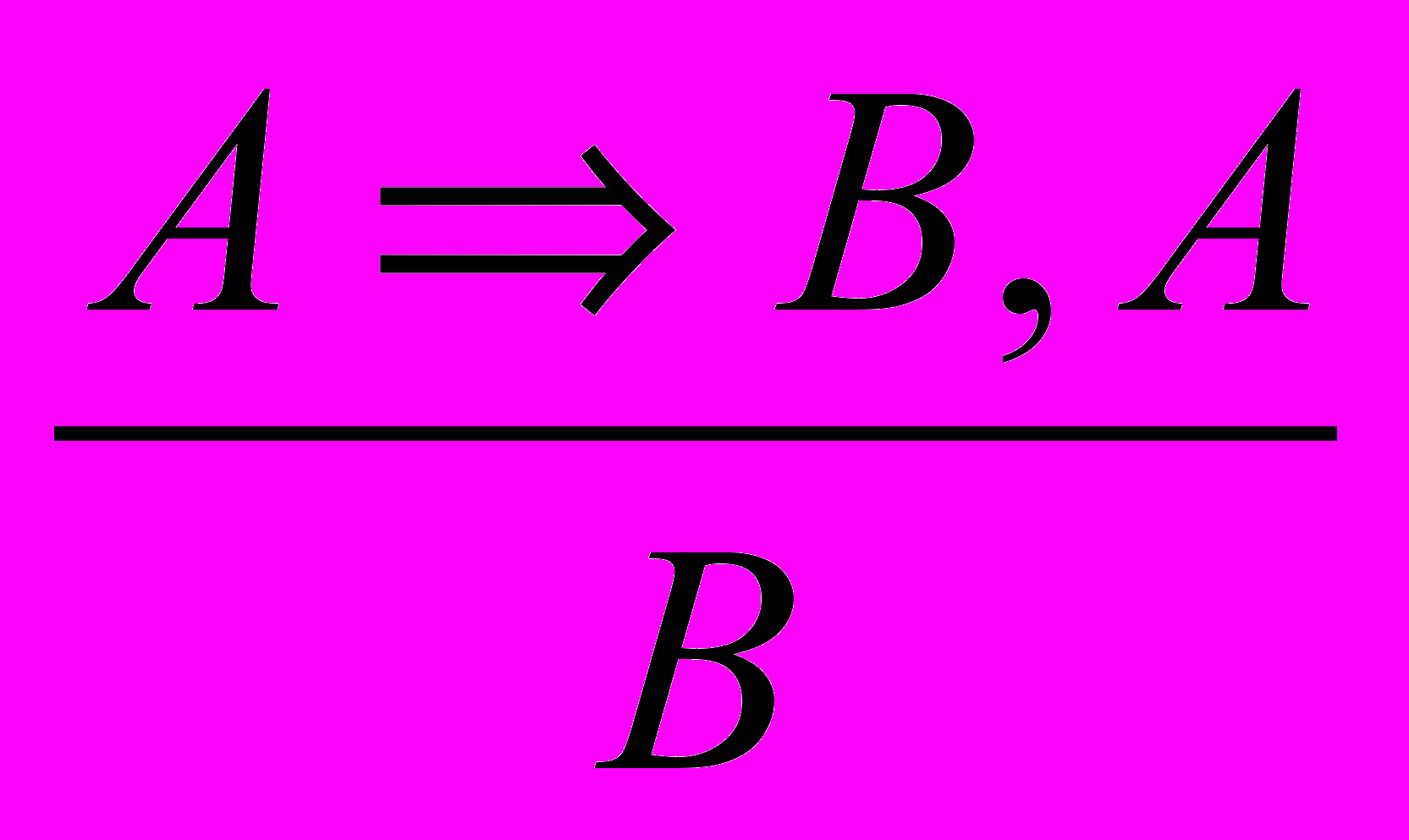- правіла заключэння;
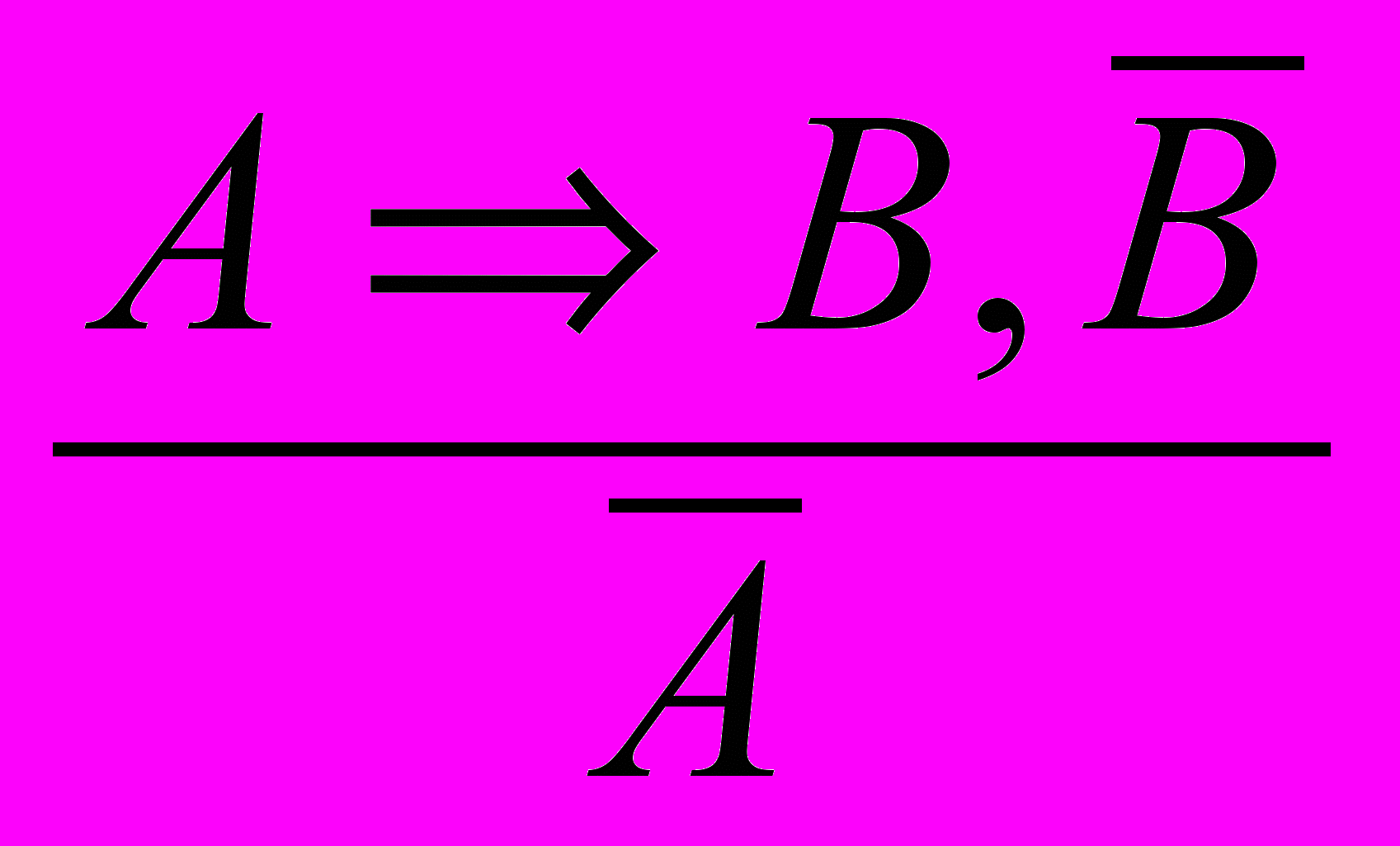- правіла адмаўлення;
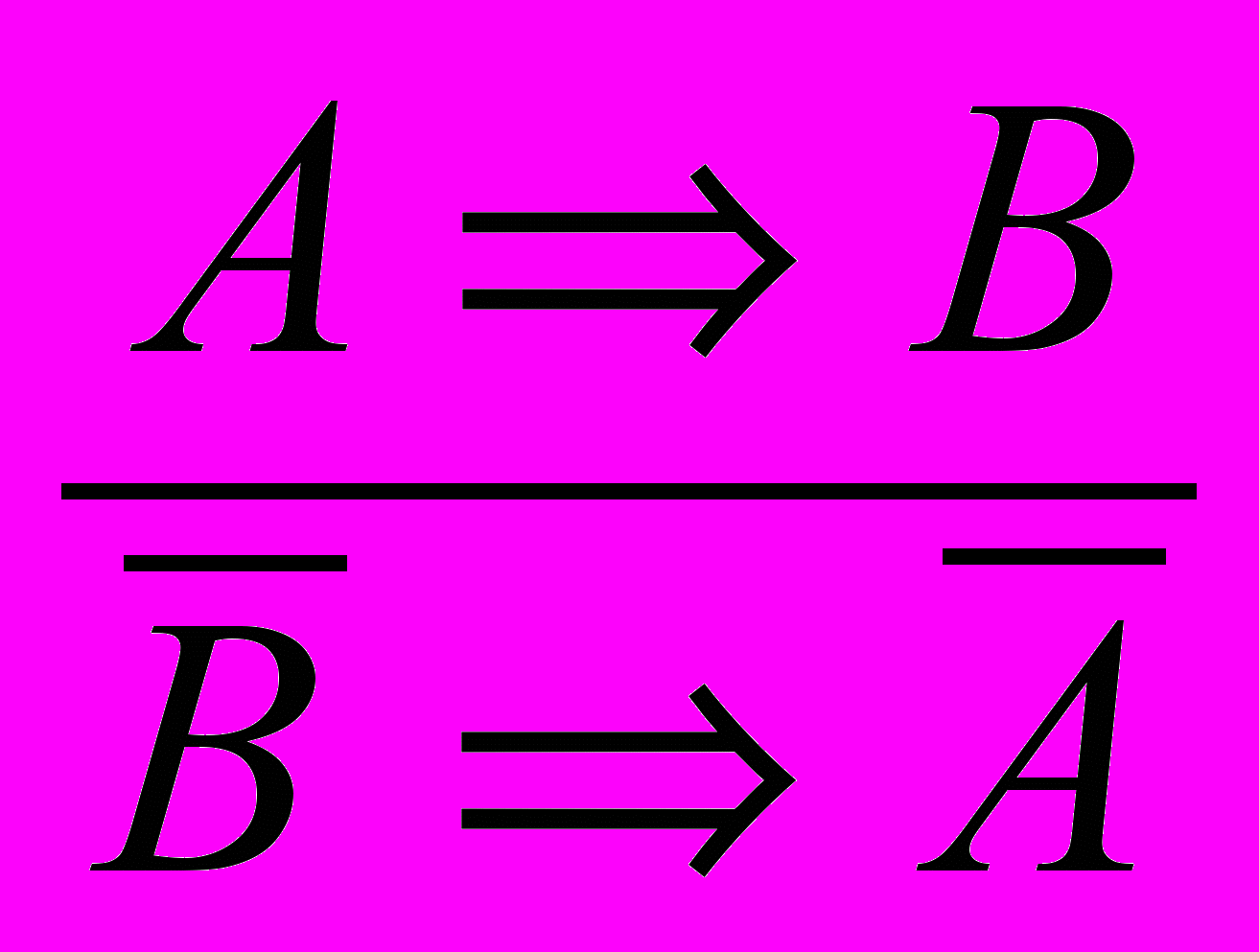- правіла контрапазіцыі;
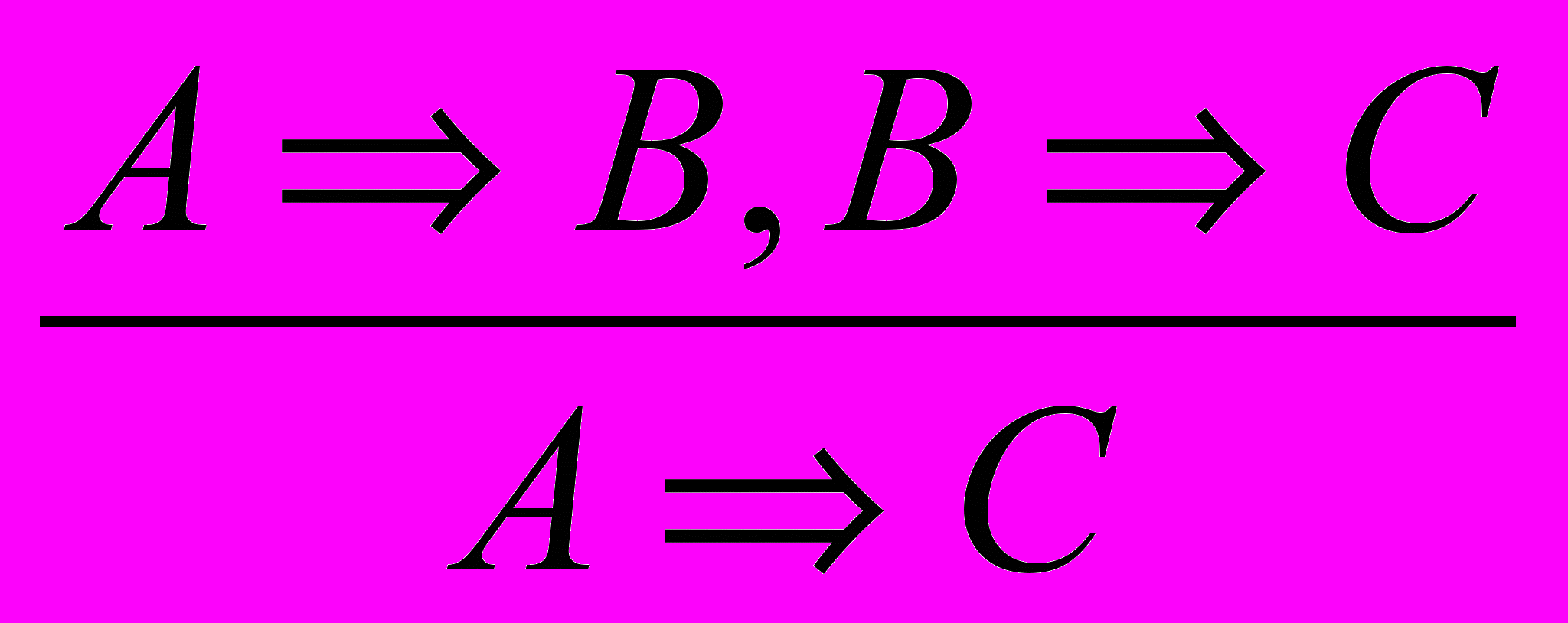- правіла сілагізму.П
ад літарамі А, В, і С разумеюць выказванні. Стрэлкай абазначаюць словазлучэнне "калі..., то ...", рысачкай над літарай (В) - адмаўленне адпаведнага выказвання (В). Запіс правіл у выглядзе схем дазваляе выразна і дакладна вылучыць форму вываду, што вельмі зручна для пабудовы разважанняў і іх аналізу.Пры пабудове разважанняў над гарызантальнай рысай запісваюць пасылкі, а пад ёй - заключэнне. Напрыклад:
Калі вучань умее правільна разважаць, то яму лёгка вучыцца.
Наташа ўмее правільна разважаць.
Наташы лёгка вучыцца.
Форма дадзенага разважання адпавядае правілу заключэння (1). Пасылкі падзяляюць на вялікую і малую. У вялікай пасылцы (А В) зафіксавана некаторая агульная інфармацыя. Малая пасылка (А) датычыцца прыватнага факта - не абстрактны вучань, а зусім канкрэтная дзяўчынка Наташа ўмее правільна разважаць. У заключэнні (В) сцвярджаюцца новыя звесткі таксама аб гэтай жа дзяўчынцы: "Наташы лёгка вучыцца".
Прааналізуем наша разважанне:
1) вялікая і малая пасылкі праўдзівыя;
2) разважанне праведзена па правілу - правілу заключэння, значыць, заключэнне праўдзівае, а разважанне правільнае.
Па гэтых жа прычынах правільным з'яўляецца і наступнае разважанне:
Калі мы вывучаем матэматыку, то адначасова ў пэўнай ступені
авалодваем і ўменнем разважаць.
Вучні пачатковых класаў вывучаюць матэматыку.___________
Вучні пачатковых класаў на ўроках матэматыкі ў пэўнай ступені авалодваюць уменнем разважаць.
Словы "ў пэўнай ступені" падкрэсліваюць абмежаванасць і выпадковасць уздзеяння традыцыйнага навучання на развіццё лагічнага мыслення вучняў. Матэматычны матэрыял з яго лагічнай арганізацыяй стварае для гэтага спрыяльныя перадумовы, але рэалізацыя закладзеных у ім магчымасцей залежыць ад пабудовы навучання. Узнікае дапушчэнне, што калі вучні будуць не толькі разважаць па ўзорах, дадзеных настаўнікам або ў падручніку, а на даступным для іх узроўні пазнаёмяцца таксама з правіламі, па якіх праводзяць разважанні, то значна ўзрасце эфектыўнасць выхавання такіх якасцей мыслення, як дакладнасць, лаканічнасць, строгасць, даступнасць і адназначнасць у перадачы думкі, яе доказнасць. Закладзены пры такім навучанні падмурак культуры мыслення прывядзе да ўзмацнення пераемнасці выкладання матэматыкі ў пачатковых, сярэдніх і старшых класах. Набытыя лагічныя ўменні, зразумела, распаўсюджваюцца і на пазнавальную дзейнасць увогуле. Калі мы станоўча адказваем на пытанне аб карыснасці азнаямлення малодшых школьнікаў з правіламі лагічнага вываду, то адразу ж узнікае праблема дыдактычный апрацоўкі адпаведнага вучэбнага матэрыялу.
Задача дадзенага раздзела заключаецца менавіта ў спробе вырашыць гэта пытанне, вызначыць шэраг напрамкаў, па якіх адбудзецца мэтанакіраванае ўздзеянне на развіццё малодшых школьнікаў. Вызначэнне сістэмы задач, мэты і зместу навучання правільным разважанням, а таксама рацыянальных метадаў, прыёмаў, форм і сродкаў, якія найлепшым чынам адпавядаюць вырашэнню дадзенай праблемы, дапамогуць настаўніку пачатковых класаў у яго рабоце.
Раздзел "Навучанне разважанням" змяшчае практыкаванні, прапаноўваць якія рэкамендуецца толькі пасля засваення матэрыялу папярэдніх раздзелаў, што маюць на мэце падрыхтоўку да выхавання разумовай культуры, развіццё неабходных якасцей дзіцячага мыслення для авалодвання больш складанай ступенню разумовай дзейнасці. Такім чынам, вынікі выканання заданняў гэтага раздзела будуць адлюстраваннем якасці закладзеных падмуркаў лагічнага мыслення, з аднаго боку, і магчымасці пераходу да больш значнай яго якаснай ступені - з другога.
§ 1. Агульныя пытанні методыкі навучання правільным разважанням
Разважанне лічыцца правільным, калі яно праведзена па правілах лагічнага вываду, таму што прымяненне гэтых правіл да праўдзівых пасылак заўсёды прыводзіць да сапраўды праўдзівага заключэння. Адсюль вынікае, што праблема пачатковага навучання правільным разважанням зводзіцца да сістэмы наступных задач:
1) вызначэнне праўдзівасці выказванняў;
2) вылучэнне формы правільных разважанняў і азнаямленне з некаторымі правіламі лагічнага вываду;
3) аналіз разважанняў і вызначэнне адпаведнасці іх структуры таму ці іншаму правілу вываду;
4) фарміраванне ўмення карыстацца ў разважаннях правіламі вываду, абапіраючыся толькі на форму сувязі паміж пасылкамі і заключэннем;
5) аналіз памылак у разважаннях;
6) пабудова найпрасцейшых дэдуктыўных доказаў. Менавіта гэта праграма навучання правільным разважанням рэалізуецца ў падручніках матэматыкі пад рэд. А.А. Столяра.
Праблема навучання правільным разважанням павінна вырашацца не адасоблена ад вывучэння праграмнага матэрыялу па матэматыцы ці іншых дысцыплінах. Яна разглядаецца як неад'емная частка выкладання вучэбных прадметаў. Заканамерны вынік такога падыходу да навучання - павышэнне якасці засваення праграмных ведаў, з аднаго боку, і ўзмацненне накіраванага ўздзеяння на развіццё вучняў - з другога.
Пасля азначэння мэты і зместу навучання правільным разважанням засяродзім увагу на асвятленні рацыянальных метадаў, прыёмаў, форм і сродкаў, якія б найлепшым чынам адпавядалі акрэсленым задачам навучання і ўзроставым магчымасцям малодшых школьнікаў.
Для вылучэння правіл лагічнага вываду найбольш падыходзіць метадычны прыём параўнання: на падставе аналізу разважанняў аднолькавай формы, якія адрозніваюцца толькі зместам пасылак, ствараюцца ўмовы для абагульнення назіранняў і абстрагавання правіла. На этапе азнаямлення для параўнання прапануюцца вывады, што адпавядаюць наступным патрабаванням:
1) у сваім змесце яны адлюстроўваюць жыццёвы вопыт, засвоены дзецьмі ў штодзённай практыцы;
2) маюць выразную структуру: вялікая пасылка, малая пасылка і аддзеленае ад іх заключэнне (з дапамогай слова "значыць" у вуснай мове або гарызантальнай рысай у пісьмовым выглядзе);
3) будуюцца адпаведна аднаму і таму ж правілу вываду;
4) усе сказы, якія ўваходзяць у вывад, гранічна кароткія. Колькасць разважанняў павінна быць дастатковай для абагульнення і абстрагавання формы, г. зн. для "адкрыцця" правіла лагічнага вываду. Напрыклад:
1. Калі гарыць зялёнае святло святлафора, то можна пераходзіць вуліцу.
Гарыць зялёнае святло святлафора.
Можна пераходзіць вуліцу.
- Калі на ўроку ты хочаш адказаць, то павінен падняць руку.
На ўроку ты хочаш адказаць.
Ты павінен падняць руку.
- Калі ідзе дождж, то на вуліцы мокра.
Ідзе дождж.
На вуліцы мокра.
Абраныя для параўнання вывады неабходна запісаць на дошцы, каб успрыманне адбывалася праз розныя органы пачуццяў. Вучні чытаюць вывады і канстатуюць праўдзівасць іх заключэння. Настаўнік паведамляе, што гэтыя разважанні правільныя, і прапануе параўнаць іх.
- Чым адрозніваюцца разважанні? (Зместам. У іх гаворыцца аб розных рэчах).
- Але ўсе яны і вельмі падобныя. Што ў іх агульнага?
Пад кіраўніцтвам настаўніка вучні паслядоўна вылучаюць усе прыметы падабенства дадзеных разважанняў:
1) усе яны складаюцца з трох сказаў;
2) першы і другі сказы запісваюцца над рысай, а трэці сказ - пад рысай;
3) у першым сказе ёсць саюз "калі ..., то ...";
4) другі сказ - гэта частка першага сказа ад слова "калі" да слова "то" (да коскі);
5) трэці сказ - гэта другая, заключная частка першага сказа ад слова "то" (ад коскі) да кропкі ў канцы сказа.
Такім чынам, мы арыентуем вучняў на вылучэнне і абагульненне ўзаемасувязі паміж пасылкамі і заключэннем. У далейшым навучанні правільным разважанням правіла заключэння павінна стаць аб'ектам засваення, таму неабходна надаць яму пэўнае графічнае афармленне, зручнае для ўспрымання, запамінання і практычнага выкарыстання. Форму правільных разважанняў па правілу заключэння можна зафіксаваць, напрыклад, з дапамогай наступных умоўных каляровых сігналаў:
Я
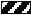ны ўводзяцца пры непасрэдным аналізе разважання аб правіле дарожнага руху. Зялёнай карткай п
ры гэтым замяняецца выказванне "Гарыць зялёнае святло святлафора", а заштрыхаванай карткай - "Можна пераходзіць вуліцу". П
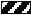
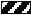
а схеме (1) вучні паўтараюць першае разважанне цалкам. Абстрагаванню ўведзеных каляровых сігналаў ад канкрэтнага сэнсу разважання і першаснаму замацаванню формы разважанняў па правілу заключэння садзейнічае напаўненне тых жа каляровых сігналаў новым зместам пры паўторным аналізе двух астатніх разважанняў. Напрыклад, дзеці яшчэ раз чытаюць разважанне аб правіле паводзін на ўроку. Вылучаецца першы сказ: "Калі на ўроку ты хочаш адказаць, то павінен падняць руку". Гэты сказ суадносіцца з першым радком у схеме (1) і вызначаецца, што картка у ім азначае: "На ўроку ты хочаш адказаць", а картка - "Ты павінен падняць руку". Далей высвятляецца, што замест малой пасылкі: "На ўроку ты хочаш адказаць" таксама ўзялі картку , а карткай зашыфравалі трэці сказ: "Ты павінен падняць руку".Аналагічным чынам з апорай на схему (1) аналізуецца апошняе разважанне аб дажджы.
Далейшае замацаванне "адкрытага" дзецьмі правіла лагічнага вываду можна арганізаваць у выглядзе індывідуальнай практычнай работы з карткамі:
а) Расфарбаваць адпаведным чынам картку з правілам вываду:
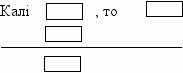
б) Раскласці каляровыя сігналы па сваіх месцах:
Калі . . . , то . . .
. . .
___________________
. . .
Т
акім чынам, для засваення правіла заключэння мы прапануем наступныя сродкі навучання: карткі, на якіх правіла "запісана" з дапамогай каляровых сігналаў (а), карткі з пустымі месцамі для каляровых сігналаў (б), а таксама падвоены набор каляровых сігналаў:
Увесь названы дыдактычны матэрыял павінен быць падрыхтаваны ў двух варыянтах: для дэманстрацыі настаўнікам і для індывідуальнай работы вучняў за партамі. Для вучняў можна таксама зрабіць гэта ў выглядзе перфапапак, дзе на месцах каляровых сігналаў выразаюцца "акенцы".
Фарміраванне ўмення разважаць па правілах лагічнага вываду ажыццяўляецца праз сістэму разнастайных практыкаванняў, у якіх трэба:
- вызначыць адпаведнасць зададзенага правільнага разважання правілу вываду;
- правесці класіфікацыю разважанняў на правільныя (якія праведзены па правілу) і няправільныя (у якіх ёсць парушэнні правіла);
- упарадкаваць паслядоўнасць дадзеных суджэнняў, каб атрымалася разважанне па правілу;
- дапоўніць разважанне адным з элементаў, якога ў ім не хапае; заключэннем, малой пасылкай, вялікай пасылкай;
- самастойна пабудаваць правільнае разважанне, калі зададзена толькі вялікая пасылка;
- знайсці памылку ў разважанні і выправіць яе.
Такім чынам, навучанне правільным разважанням ажыццяўляецца па наступнай схеме:
1) "адкрыццё" пад кіраўніцтвам настаўніка правіла вываду (аналіз і параўнанне некалькіх правільна пабудаваных разважанняў, абагульненне іх канструкцый);
2) абстрагаванне формы разважання (запіс з дапамогай каляровых сігналаў);
3) замацаванне правіла вываду (раскладванне каляровых сігналаў па сваіх месцах або расфарбоўка гэтых месцаў адпаведным чынам);
4) фарміраванне ўмення будаваць правільныя разважанні (разнастайныя практыкаванні).
Аналагічным чынам можа быць арганізавана работа і над іншымі правіламі лагічнага вываду, напрыклад над правіламі адмаўлення або правіламі контрапазіцыі.
На заканчэнне адзначым некаторыя асаблівасці методыкі навучання малодшых школьнікаў правільным разважанням, якія абумоўлены ўзроставымі магчымасцямі дзяцей.
1. Правілы лагічнага вываду не называюцца сваімі імёнамі. Тэрміны "вялікая пасылка", "малая пасылка", "заключэнне" мэтазгодна ўвесці на ўроку азнаямлення з правілам заключэння.
2. Дапушчальнасць правіл лагічнага вываду не абгрунтоўваецца, а проста канстатуецца настаўнікам і знаходзіць пацвярджэнне пры аналізе разважанняў.
3. Навучанне правільным разважанням ажыццяўляецца не на спецыяльна адведзеных для гэтага ўроках. Сістэма адпаведных практыкаванняў размяркоўваецца па розных занятках і выкарыстоўваецца пры вывучэнні не толькі матэматыкі, але і іншых вучэбных прадметаў, а таксама ў пазакласнай рабоце.
4. Трэба шырока ўжываць наглядныя і практычныя метады навучання. Напрыклад, доказ правільнасці канкрэтнага разважання карысна спалучаць з практычнай работай па накладванню адпаведных каляровых сігналаў на асобныя сказы, пасля чаго атрыманы "ўзор" неабходна параўнаць з карткай, на якой з дапамогай каляровых сігналаў зафіксавана правіла лагічнага вываду.
5. Неабходна стварыць умовы для таго, каб кожны вучань меў рэальную магчымасць на ўроку вымаўляць разважанні ўслых. Для гэтага можна прапанаваць чытанне - гудзенне, чытанне парамі, індывідуальнае чытанне.
6. Трэба прыкласці пэўныя намаганні, каб выклікаць цікавасць да навучання правільным разважанням і абудзіць актыўнасць дзяцей. Зрабіць гэта можна, напрыклад, з дапамогай герояў казак або іншых фантастычных персанажаў, якія спрабуюць разважаць, праз стварэнне гульнявых сітуацый.
7. Паступовы пераход да больш складаных заданняў ажыццяўляецца праз:
а) змест пасылак (ад добра вядомага да мала вядомага і зусім новага);
б) структуру разважання (ад стандартнай формы разважання да нестандартнай);
в) далучэнне новых правіл вываду.
§ 2. Лагічны вывад па найпрасцейшых правілах
Да ліку правіл лагічнага вываду, з якіх можна пачынаць навучанне правільным разважанням, звычайна адносяць:
1) правіла заключэння
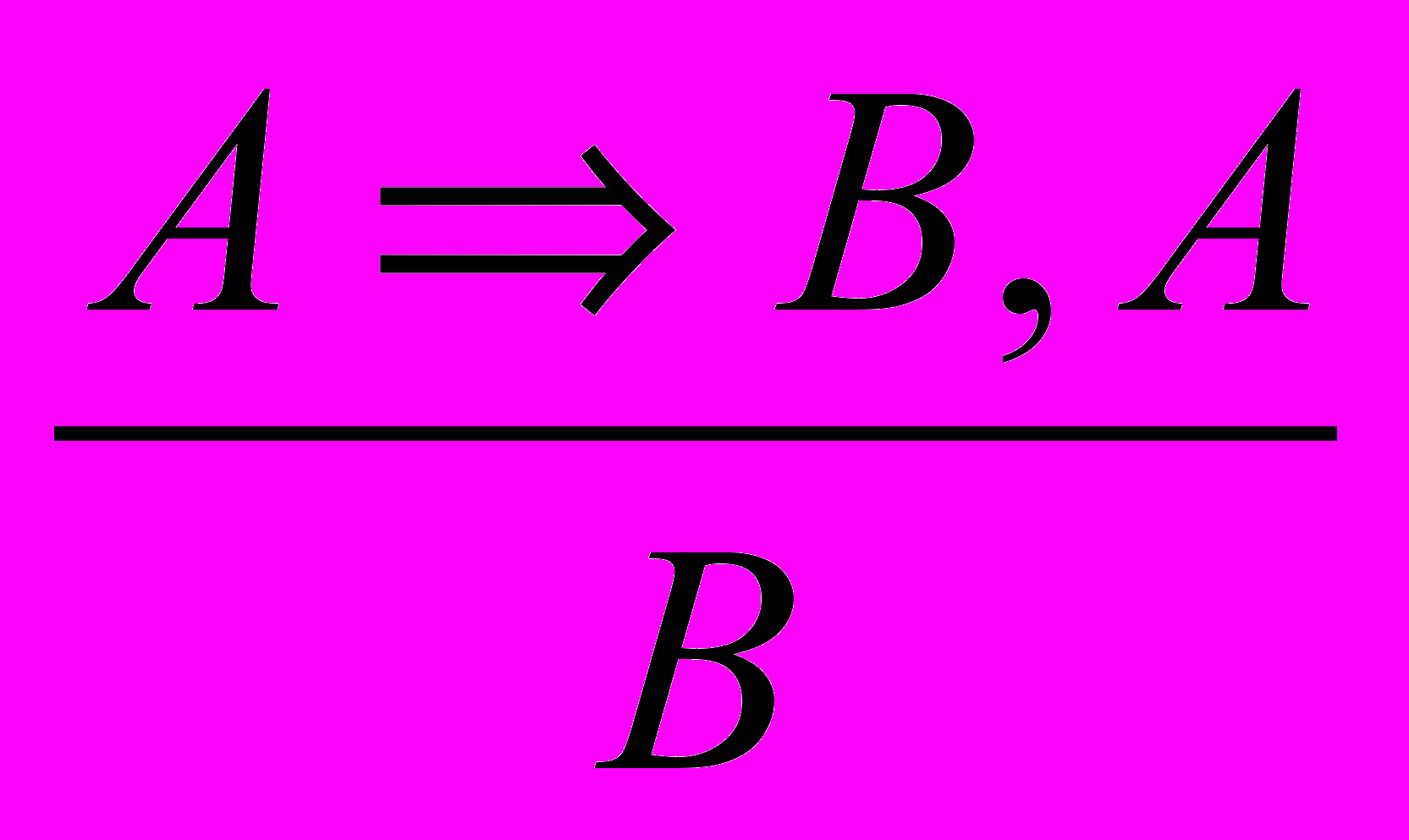
Калi
, то
2) правіла адмаўлення
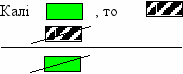
3) правіла контрапазіцыі
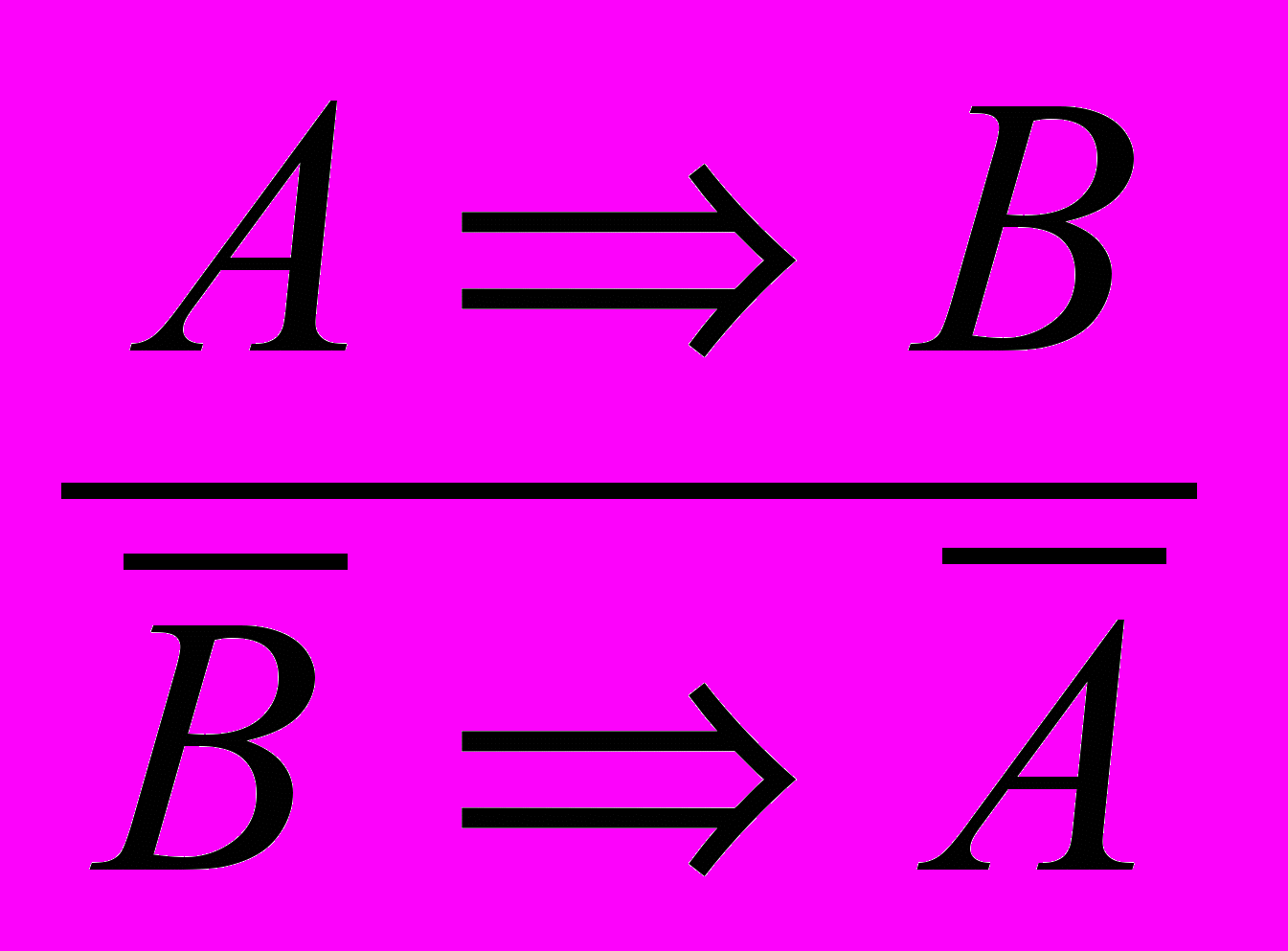
Пры выкананні практыкаванняў у разважаннях трэба, каб адпаведныя схемы - апоры былі перад вачамі вучняў. Прапанаваныя ніжэй заданні размеркаваны па наступных прыметах:
1) спосабы разважанняў, г. зн. правілы лагічнага вываду;
2) змест суджэнняў адпаведна пэўнаму вучэбнаму прадмету ("Свет вакол нас", "Матэматыка", "Прыродазнаўства", "Беларуская
мова").
Да кожнага разважання, што дадзена ў поўнай форме, настаўнік у залежнасці ад мэт, якія ён ставіць, мае магчымасць вар'іраваць патрабаванні і ўмовы. Вучням належыць:
1) праверыць, ці з'яўляецца разважанне правільным;
2) дапоўніць разважанне: а) заключэннем; б) малой пасылкай; в) малой пасылкай і заключэннем; г) вялікай пасылкай;
3) пабудаваць разважанне па правілу, калі зададзена толькі
вялікая пасылка;
4) з дадзеных у адвольным парадку трох суджэнняў пабудаваць
разважанне па правілу.
Напрыклад, прааналізуем разважанне Віні-Пуха:
"Калі каля дупла дрэва раяцца пчолы, то ў гэтым дупле павінен
быць мёд.
Каля дупла дуба раяцца пчолы._________________________
У дупле дуба павінен быць мёд".
Да яго можна прапанаваць наступныя заданні.
1. Ці правільна разважае Віні-Пух?
2. Да якога заключэння прыйшоў Віні-Пух?
Калі каля дупла дрэва раяцца пчолы, то ў гэтым дупле павінен
быць мёд.
Каля дупла дуба раяцца пчолы.
. . .
3. Які сказ адсутнічае ў разважаннях Віні-Пуха?
Калі каля дупла дрэва раяцца пчолы, то ў гэтым дупле павінен
быць мёд.
. . .
У дупле дуба павінен быць мёд.
4. Аб чым падумаў Віні-Пух спачатку?
. . .
Каля дупла дуба раяцца пчолы._____
У дупле дуба павінен быць мёд.
5. Як разважаў Віні-Пух, убачыўшы, што каля дупла дуба раяцца пчолы?
Калі каля дупла дрэва раяцца пчолы, то ў гэтым дупле павінен быць мёд.
. . .
. . .
6. Ад радасці ўсе думкі ў галаве Віні-Пуха пераблыталіся. Дапамажыце яму пабудаваць правільнае разважанне.
У дупле дуба павінен быць мёд.
...
...
Калі каля дупла дрэва раяцца пчолы, то ў гэтым дупле павінен
быць мёд.
Каля дупла дуба раяцца пчолы.
ПРАКТЫКАВАННІ
I. Па правілу заключэння А В
А_________
В
СВЕТ ВАКОЛ НАС
1. Калі на вуліцы многа снегу, то можна катацца на санках.
На вуліцы многа снегу.___________________________
Можна катацца на санках.
- Калі будзе дождж, то мы не пойдзем на прагулку.
Ідзе дождж.
Мы не пойдзем на прагулку.
- Калі чалавек загартоўваецца, то ён рэдка хварэе.
Вова загартоўваецца.
Вова рэдка хварэе.
4. Калі ў чалавека высокая тэмпература, то ён хворы.
У Алёшы высокая тэмпература.
Алёша хворы.
5. Калі ты добра адносішся да людзей, то і яны добра адносяцца да цябе.
Дзіма добра адносіцца да людзей.
Людзі добра адносяцца да Дзімы.
6. Калі ты зрабіў дрэнны ўчынак, то павінен папрасіць прабачэння.
Алёша зрабіў дрэнны ўчынак.
Алёша павінен папрасіць прабачэння.
- Калі сустракаешся са знаёмымі, трэба прывітацца.
Сяргей сустрэўся са знаёмым хлопчыкам.
Сяргею трэба прывітацца са знаёмым хлопчыкам.
- Калі паеў, трэба абавязкова падзякаваць за снеданне.
Коля паеў.
Коля павінен падзякаваць за снеданне.
9. Калі кожны дзень раніцай і вечарам чысціць зубы, яны будуць здаровымі.
Міша чысціць зубы кожны дзень раніцай I вечарам._________
У Мішы будуць здаровыя зубы.
МАТЭМАТЫКА
- Калі вугал большы за прамы, то ён тупы.
Вугал А большы за прамы.
Вугал А тупы.
2. Калі ў трохвугольніка ёсць прамы вугал, то гэта прамавугольны трохвугольнік.
У трохвугольніка АВС вугал А прамы.______________________
Трохвугольнік АВС прамавугольны.
3. Калі ў трохвугольніка ёсць прамы вугал, то два астатнія вуглы ў ім вострыя.
У трохвугольніка АВС вугал А прамы.______________________
У трохвугольніка АВС вуглы В і С вострыя.
4. Калі ў прамавугольніка ўсе стораны роўныя, то ён квадрат.
У прамавугольніка АВСD усе стораны роўныя.
Прамавугольнік АВСD - квадрат.
- Калі адна фігура цалкам змяшчаецца ўнутры другой, то плошча першай фігуры меншая за плошчу другой фігуры.
Трохвугольнік цалкам змяшчаецца ўнутры круга.____________
Плошча трохвугольніка меншая за плошчу круга.
- Калі фігуры роўныя, то іх плошчы роўныя.
Дзве фігуры роўныя паміж сабой.
Плошчы гэтых фігур роўныя.
7. Калі лік дзеліцца на 2, то ён цотны.
Лік 18 дзеліцца на 2._____________
Лік 18 цотны.
8. Калі запіс ліку заканчваецца лічбай 0, то гэты лік дзеліцца на 5.
Запіс ліку 12 340 заканчваецца лічбай 0._________
Лік 12 340 дзеліцца на 5.
- Калі сума лічбаў ліку дзеліцца на 3, то гэты лік дзеліцца на 3.
Сума лічбаў ліку 7215 роўна 15. 15 дзеліцца на 3.
Лік 7 215 дзеліцца на 3.
10. Калі лік дзеліцца на 2 і дзеліцца на 3, то гэты лік дзеліцца на 6.
Лік 72 150 дзеліцца на 2 і дзеліцца на 3.
Лік 72 150 дзеліцца на 6.
11. Калі памяншаемае паменшыць на 1, то рознасць таксама паменшыцца на 1.
360 - 60 = 300, 359 меншы за 360 на 1._________________
359 - 60 = 299.
12. Калі адымаемае павялічыць на 1, то рознасць паменшыцца на 1.
341 - 241 = 100.___________________________
341 - 242 = 99.
13. Калі памяншаемае павялічыць на 2, а адымаемае паменшыць на 2, то рознасць павялічыцца на 4.
800 - 800 = 0._________________________________________
802 - 798 = 4.
14. Калі складаемыя памяняць месцамі, то сума не зменіцца.
7 + 2 = 9.__________________
Значыць, 2 + 7 таксама будзе 9.
15. Калі здабытак падзяліць на адзін з множнікаў, то атрымаецца другі множнік. 6 • 4 = 24.
Дзялю здабытак 24 на першы множнік 6.
(Дзялю здабытак 24 на другі множнік 4.)__________________
Значыць, 24 : 6 = 4 (24 : 4 = 6).
БЕЛАРУСКАЯ МОВА
1. Калі словы маюць агульную частку і блізкі сэнс, то яны з'яўляюцца роднаснымі.
Словы "стол", "столік", "сталяр" маюць агульную частку - "стол" - і блізкі сэнс.
Словы "стол", "столік", "сталяр" роднасныя.
2. Калі да назоўніка можна паставіць словы "ён", "мой", то гэты назоўнік мужчынскага роду.
Да назоўніка "вецер" можна паставіць словы "ён", "мой".
Назоўнік "вецер" мужчынскага роду.
3. Калі слова з'яўляецца першым у сказе, то яго трэба пісаць з вялікай літары.
Слова "хлопчык" у сказе "Хлопчык зрабіў урокі" стаіць на першым месцы.
Слова "хлопчык" у гэтым сказе трэба пісаць з вялікай літары.
4. Калі слова абазначае дзеянне прадмета і адказвае на пытанні "што робіць?", "што робяць?", то гэта дзеяслоў.
Слова "вучыцца" абазначае дзеянне і адказвае на пытанне "што робіць?".
Слова "вучыцца" - дзеяслоў.
5. Калі слова абазначае імя, то яго трэба пісаць з вялікай літары. Вася - гэта слова абазначае імя хлопчыка.
Слова "Вася" трэба пісаць з вялікай літары.
6. Калі ў сказе пра што-небудзь паведамляецца, то ён з'яўляецца апавядальным.
У сказе "Дзеці вучацца" паведамляецца аб дзейнасці дзяцей.
Сказ "Дзеці вучацца" апавядальны.
ПРЫРОДАЗНАЎСТВА
1. Калі заяц "апрануў" белае футра, то хутка прыйдзе зіма. Заяц "апрануў" белае футра._______________________
Хутка прыйдзе зіма.
2. Калі буслы лятаюць кругамі каля сваіх гнёздаў, то будзе вецер. Буслы лятаюць кругамі каля сваіх гнёздаў.
Будзе вецер.
- Калі вельмі душна, парыць, прыпякае, то будзе дождж.
Вельмі душна, парыць, прыпякае.___________________
Будзе дождж.
- Калі зімою грыміць гром, то летам будзе засуха.
Зімою грыміць гром.
Летам будзе засуха.
- Калі певень стаіць на адной назе, то будзе мароз.
Певень стаіць на адной назе.
Будзе мароз.
- Калі качкі крычаць, то будзе навальніца.
Качкі крычаць.
Будзе навальніца.
- Калі снег перастаў скрыпець пад нагамі, то будзе пацяпленне.
Снег перастаў скрыпець пад нагамі._________________
Будзе пацяпленне.
8. Калі ў расліны можна вылучыць галоўнае сцябло - ствол з галінамі, то гэта дрэва.
У таполі можна вылучыць галоўнае сцябло - ствол з галінамі.
Таполя - дрэва.
9. Калі планета ўваходзіць у Сонечную сістэму, то яна круціцца вакол Сонца.
Марс - планета Сонечнай сістэмы.
Марс круціцца вакол Сонца.
10. Калі расліна занесена ў Чырвоную кнігу, то яе нельга зрываць.
Венерын чаравічак занесены ў Чырвоную кнігу.____________
Венерын чаравічак нельга зрываць.
II. Па правілу заключэння А В
В_________
А
СВЕТ ВАКОЛ НАС
- Калі ідзе дождж, то на дварэ сыра.
На дварэ суха.__________________
Дождж не ідзе.
- Калі чалавек шмат чытае, то ён шмат ведае.
Коля мала ведае._____________________
Коля мала чытае.
3. Калі прыбраць кватэру, то ў ёй будзе чыста.
У Машынай кватэры брудна.______________
Маша не прыбрала кватэру.
- Калі надыходзіць ноч, то на вуліцы цёмна.
На вуліцы светла.
Ноч яшчэ не надышла.
- Калі чалавек думае толькі пра сябе, то ён эгаіст.
Вася не эгаіст.
Вася не думае толькі пра сябе.
6. Калі гарыць зялёнае святло святлафора, то можна пераходзіць вуліцу.
Нельга пераходзіць вуліцу.
Гарыць не зялёнае святло святлафора, а чырвонае або жоўтае.
7. Калі чалавек загартоўваецца, то ён рэдка хварэе.
Алесь часта хварэе.
Алесь не загартоўваецца.
- Калі перапынак скончыўся, звініць званок.
Званок не звініць.
Перапынак не скончыўся.
МАТЭМАТЫКА
- Калі лік дзеліцца на 2, то ён цотны.
Лік 37 няцотны.
Лік 37 не дзеліцца на 2.
- Калі лік дзеліцца на 4, то ён дзеліцца і на 2.
Лік 37 не дзеліцца на 2.
Лік 37 не дзеліцца на 4.
3. Калі адыманне выканана правільна, то сума рознасці і адымаемага роўна памяншаемаму.
46 - 39 = 13, 13 + 39 = 52, 52
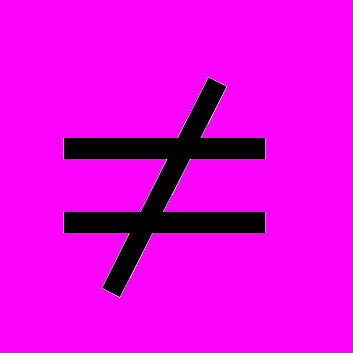46. Адыманне выканана няправільна.
4. Калі дзяленне выканана правільна, то здабытак дзелі і дзельніка роўны дзялімаму.
624 : 3 = 28, 28 • 3 = 20 • 3 + 8 • 3 = 60 + 24 = 84, 84
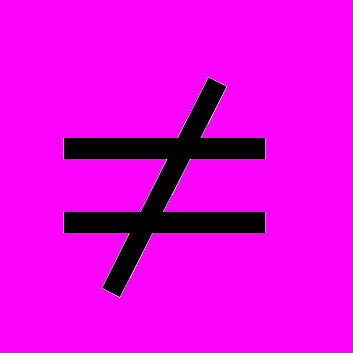624. Дзяленне выканана няправільна.
5. Калі хоць бы адзін з множнікаў роўны нулю, то іх здабытак роўны нулю.
а • b
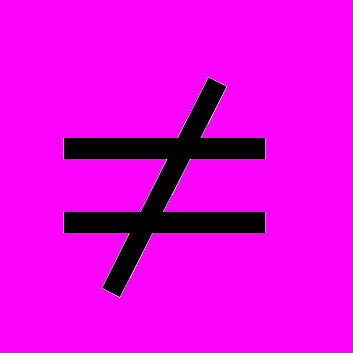0.___________________________________ а
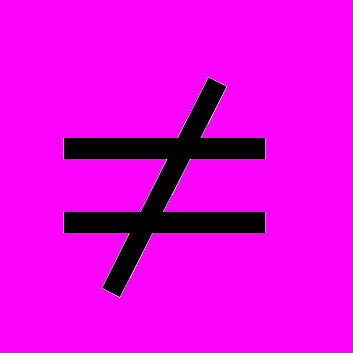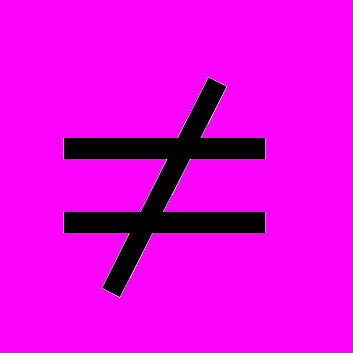0 і b 0.6. Калі фігура з'яўляецца многавугольнікам, то яна мае стораны, вуглы і вяршыні.
Фігура А не мае старон, вуглоў і вяршынь.
Фігура А не з'яўляецца многавугольнікам.
- Калі трохвугольнік раўнабедраны, то яго стораны роўныя.
Стораны трохвугольніка няроўныя.
Трохвугольнік нераўнабедраны.
8. Калі фігура квадрат, то яе вуглы прамыя.
Вуглы фігуры АВСD непрамыя._________
Фігура АВСD неквадрат.
- Калі фігуры роўныя, то іх плошчы роўныя.
Плошчы дадзеных фігур няроўныя.
Дадзеныя фігуры няроўныя.
- Калі прамыя паралельныя, то яны ніколі не перасякаюцца.
Прамыя а і b перасякаюцца.___________________________
Прамыя а і b непаралельныя.
11. Калі ўсе складаемыя аднолькавыя, то складанне можна замяніць множаннем.
Складанне нельга замяніць множаннем.
Не ўсе складаемыя аднолькавыя.
12. Калі дзяленне з астачай выканана правільна, то астача меншая за дзельнік.
34 : 4 = 7 (аст. 6). Астача 6 не меншая за дзельнік 4.
Д
III. Па правілу заключэння А В
В А
зяленне выканана няправільна. БЕЛАРУСКАЯ МОВА
1. Калі словы з'яўляюцца роднаснымі, то яны маюць агульную частку і блізкі сэнс.
Словы "жоўты", "сіні", "зялёны" не маюць агульнай часткі і блізкага сэнсу.
Словы "жоўты", "сіні", "зялёны" не з'яўляюцца роднаснымі.
- Першае слова ў сказе пішацца з вялікай літары.
Слова "стол" пішам у сказе з маленькай літары.
Слова "стол" у сказе займае не першае месца.
3. Калі назоўнік жаночага роду, то да яго можна паставіць словы "яна", "мая".
Да назоўніка "сабака" нельга паставіць словы "яна", "мая".
Назоўнік "сабака" не жаночага роду.
4. Калі ў сказе выказваецца моцнае пачуццё, то ён з'яўляецца клічным.
Сказ не з'яўляецца клічным.
У сказе не выказваецца моцнае пачуццё.
5. Калі сказ складаны, то ў яго ўваходзяць два або некалькі простых сказаў.
У сказе "Прыйшла зіма" няма двух або некалькіх простых сказаў.
Сказ не складаны, а просты.
6. Калі слова з'яўляецца дзейнікам, то яно абазначае, пра каго або пра што гаворыцца ў сказе.
Слова не абазначае, пра каго або пра што гаворыцца ў сказе.
Слова не з'яўляецца дзейнікам.
7. Калі слова з'яўляецца выказнікам, то яно абазначае, што гаворыцца пра дзейнік.
Слова не абазначае, што гаворыцца пра дзейнік.
Слова не з'яўляецца выказнікам.
ПРЫРОДАЗНАЎСТВА
1. Калі ў расліны можна вылучыць галоўнае сцябло - ствол з галінамі, то гэта дрэва.
Гэта расліна - куст.
У куста нельга вылучыць галоўнае сцябло - ствол з галінамі.
2. Калі будзе бура, то ластаўкі лятаюць уверх і ўніз.
Ластаўкі спакойна лятаюць у паветры.
Буры не будзе.
- Калі збіраецца навальніца, то птушкі заціхаюць.
Птушкі весела шчабечуць.
Навальніцы не будзе.
4. Калі набліжаецца дождж, то матылькі перастаюць лятаць і хаваюцца.
Матылькі лятаюць._________________________________
Дажджу не будзе.
- Калі прадмет драўляны, то ён не тоне ў вадзе.
Кубік патануў у вадзе._____________________
Кубік недраўляны.
6. Калі год высакосны, то ў ім 366 дзён.
У 1995 годзе не 366, а 365 дзён.
1995 год невысакосны.
СВЕТ ВАКОЛ НАС
1. Калі хочаш быць здаровым, то рабі зарадку.
Калі не робіш зарадку, то (не хочаш быць здаровым)
2. Калі гарыць зялёнае святло святлафора, то можна пераходзіць вуліцу.
Калі нельга пераходзіць вуліцу, то (гарыць не.зялёна святло святлафора).
3. Калі ўрок закончаны, то звініць званок.
Калі званок не звініць, то (урок не закончаны)
4. Калі заўтра нядзеля, то сёння субота.
Калі сёння не субота, то (заўтра не нядзеля).
МАТЭМАТЫКА
1. Калі фігура - прамавугольнік, то яна - чатырохвугольнік.
Калі фігура - нечатырохвугольнік, то яна і непрамавугольнік.
2. Калі ў прамавугольніка ўсе стораны роўныя, то ён квадрат.
Калі прамавугольнік - неквадрат, то ў яго не ўсе стораны роўныя.
3. Калі ў запісе ліку дзве лічбы, то ён двухзначны._____
Калі лік недвухзначны, то ў яго запісе не дзве лічбы.
4. Калі трохвугольнік можна размясціць унутры круга, то плошча трохвугольніка меншая за плошчу круга.
Калі плошча трохвугольніка большая за плошчу круга, то трохвугольнік нельга размясціць унутры круга.
- Калі ў чатырохвугольніка ўсе вуглы прамыя,
то ён прамавугольнік.
Калі чатырохвугольнік - непрамавугольнік, то ў яго не ўсе вуглы прамыя.
6. Калі фігуры роўныя, то іх плошчы роўныя.
Калі плошчы фігур няроўныя, то фігуры няроўныя.
7. Калі лік дзеліцца на 2, то ён цотны.
Калі лік няцотны, то ён не дзеліцца на 2 .
8. Калі сума лічбаў ліку дзеліцца на 3, то лік дзеліцца на 3.
Калі лік не дзеліцца на 3, то сума яго лічбаў не дзеліцца на 3.
9. Калі запіс ліку заканчваецца на 0 або на 5, то лік дзеліцца на 5.
Калі лік не дзеліцца на 5, то яго запіс не заканчваецца на 0 або на 5.
10. Калі лічнік дробу не меншы за назоўнік, то гэты дроб няправільны.
Калі дроб правільны, то яго лічнік меншы за назоўнік.
11. Калі трохвугольнік роўнастаронні, то ўсе вуглы ў яго роўныя.
Калі не ўсе вуглы ў трохвугольніка роўныя, то ён няроўнастаронні.
БЕЛАРУСКАЯ МОВА
1. Калі склад слова вымаўляецца з большай сілай, то ён націскны.
Калі склад слова ненаціскны, то ён не вымаўляецца з большай сілай.
2. Калі назоўнік абазначае адзін прадмет, то гэта назоўнік адзіночнага ліку.
Калі назоўнік множнага ліку, то ён абазначае два або некалькі прадметаў.
3. Калі сказ з'яўляецца клічным, то ў ім выказваецца моцнае пачуццё._________________________________________
Калі ў сказе не выказваецца моцнае пачуццё, то ён не з'яўляецца клічным.
4. Калі сказ з'яўляецца складаным, то ён будуецца з двух або некалькіх простых сказаў.
Калі сказ не будуецца з двух або некалькіх простых сказаў, то ён не з'яўляецца складаным.
ПРЫРОДАЗНАЎСТВА
1. Калі ў расліны можна вылучыць галоўнае сцябло - ствол з галінамі, то гэта дрэва.
Калі расліна не дрэва, то ў яе нельга вылучыць галоўнае сцябло - ствол з галінамі.
2. Калі глеба не ахавана раслінамі, то вада можа ўтвараць яр.
Калі вада не ўтварае яр, то глеба ахавана раслінамі.
3. Калі вераб'і хаваюцца пад страху, то чакай буру.
Калі буры не будзе, то вераб'і не хаваюцца пад страху.
4. Калі набліжаецца навальніца, то качкі крычаць.
К
IV. Па правілу выдалення квантара агульнасці
алі качкі маўчаць, то навальніцы не будзе.
У адпаведнасці з гэтым правілам, з таго, што ўсе прадметы некаторай вобласці разважання маюць пэўную ўласцівасць, можна рабіць вывад аб тым, што любы адзінкавы прадмет гэтай вобласці таксама мае тую ж уласцівасць. Напрыклад:
1) Усе рыбы дыхаюць жабрамі.
Карась - рыба.
Карась дыхае жабрамі.
2) Здабытак любога ліку на нуль роўны нулю.
7-0 = 0.
СВЕТ ВАКОЛ НАС
- Кожная бабуля старэйшая за сваіх унукаў.
Валянціна Паўлаўна - бабуля.
Валянціна Паўлаўна старэйшая за сваіх унукаў.
- Усе хакеісты добра катаюцца на каньках.
Кастусь - хакеіст.
Кастусь добра катаецца на каньках.
- Усе музыканты ведаюць нотную грамату.
Пётр Іванавіч - музыкант.
Пётр Іванавіч ведае нотную грамату.
- Усе хлопчыкі нашага класа гуляюць у футбол.
Васіль - вучань нашага класа.
Васіль гуляе ў футбол.
- Усе ўрокі працягваюцца 45 хвілін.
Урок матэматыкі працягваецца 45 хвілін.
МАТЭМАТЫКА
1. Сума любога ліку і ліку 1 роўна наступнаму ліку.
9 + 1 = 10.
2. Здабытак любога ліку на 0 роўны нулю.
164 - 0 = 0.
3. Усе двухзначныя лікі большыя за адназначныя.
17 - двухзначны лік, 7 - адназначны лік.______
17 > 7.
4. Усе квадраты - прамавугольнікі.
АВСD - квадрат.
АВСD - прамавугольнік.
5. Усе прамыя вуглы роўныя.
У прамавугольніка чатыры прамыя вуглы.
Вуглы прамавугольніка роўныя.
6. Кожны роўнастаронні трохвугольнік мае роўныя вуглы.
Трохвугольнік АВС роўнастаронні.__________________
Трохвугольнік АВС мае роўныя вуглы.
7. Усе здабыткі з табліцы множання ліку 3 дзеляцца на 3.
6, 9, 12, 15, 18, 27 - здабыткі з табліцы множання ліку 3.
6, 9, 12, 15, 18, 27 дзеляцца на 3.
8. Кожны здабытак можна замяніць сумай.
37 • 2 - здабытак.
Значыць, 37 • 2 = 37 + 37.
9. Кожны мнагазначны лік можна запісаць у выглядзе сумы разрадных складаемых
306 - трохзначны лік.
Значыць, 306 можна запісаць у выглядзе сумы разрадных складаемых:
306 = 300 + 6.
БЕЛАРУСКАЯ МОВА
- Кожны беларус павінен ведаць беларускую мову.
Ваня - беларус.
Ваня павінен ведаць беларускую мову.
- Усе назвы гарадоў і вёсак пішуцца з вялікай літары.
Брэст - горад.________________________________
Слова "Брэст" пішацца з вялікай літары.
- Усе назоўнікі абазначаюць прадметы.
Слова "кніга" - назоўнік.
Слова "кніга" абазначае прадмет.
4. Усякі назоўнік, які абазначае адзін прадмет, з'яўляецца назоўнікам адзіночнага ліку.
Назоўнік "парта" абазначае адзін прадмет.___________
Назоўнік "парта" адзіночнага ліку.
5. Усе словы, якія адказваюць на пытанні "які?", "якая?", "якое?", "якія?", абазначаюць прыметы прадметаў.
Слова "зялёны" адказвае на пытанне "які?".
Слова "зялёны" абазначае прымету прадмета.
6. Любы прыметнік мае той самы род, што і назоўнік, да якога ён адносіцца.
У словазлучэнні "прыгожае дрэва" назоўнік "дрэва" ніякага
роду.______________________________________________
У словазлучэнні "прыгожае дрэва" прыметнік "прыгожае" ніякага роду.
7. "Жы", "шы" заўсёды пішуцца з літарай "ы".
У словах "машына", "жыццё" пасля "ш" і "ж" трэба пісаць літару "ы".
ПРЫРОДАЗНАЎСТВА
- Усе пералётныя птушкі адлятаюць у вырай.
Бусел - пералётная птушка.
Бусел адлятае ў вырай.
- Кожнае ліставое дрэва скідвае на зіму лісце.
Таполя - ліставое дрэва.
Таполя скідвае на зіму лісце.
- Усе расліны паглынаюць вуглякіслы газ.
Бэз - расліна.
Бэз паглынае вуглякіслы газ.
- Усякае пустазелле - вораг культурных раслін.
Пырнік - пустазелле.
Пырнік - вораг культурных раслін.
5. Кожная расліна, занесеная ў Чырвоную кнігу, ахоўваецца дзяржавай.
Венерын чаравічак - кветка, занесеная ў Чырвоную кнігу.
Кветка венерын чаравічак ахоўваецца дзяржавай.
- Кожная пара года складаецца з трох месяцаў.
Лета - пара года.
Лета складаецца з трох месяцаў.
- Кожная гара мае вяршыню, схіл, падножжа.
Эльбрус - гара.
Эльбрус мае вяршыню, схіл, падножжа.
- Усе птушкі нясуць яйкі.
Верабей - птушка.
Верабей нясе яйкі.
9. Кожная планета Сонечнай сістэмы круціцца вакол Сонца.
Марс - планета Сонечнай сістэмы.___________________
Марс круціцца вакол Сонца.
10. Усе свойскія жывёлы прыносяць карысць чалавеку.
Конь - свойская жывёла.
Конь прыносіць карысць чалавеку.