Вопросы к экзамену по философии

Вид материала

Вопросы к экзамену

Содержание Запишите в порядке возрастания числа: 1101 2. Найти все числа вида , кратные 36. Признаки делимости.

Подобный материал:

• Вопросы к экзамену по философии, 27.88kb.
• Вопросы к экзамену по философии, 485.43kb.
• Вопросы к экзамену по философии, 215.77kb.
• Вопросы к экзамену по "философии, 27.97kb.
• Примерные вопросы к кандидатскому экзамену по Истории и философии науки, 33.95kb.
• Вопросы к экзамену по философии науки для магистрантов (доц. Палей Е. В.), 14.96kb.
• Вопросы к вступительному экзамену по дисциплине, 120.62kb.
• Вопросы к вступительному экзамену в аспирантуру по философии общей, 33.7kb.
• «Философия. Часть I. История философии», 1572.94kb.
• Примерные вопросы к кандидатскому экзамену по истории и философии науки, 17.94kb.

Задание 2

Запишите в порядке возрастания числа: 1101₂, 126₈, 122₃.

Для выполнения этого задания необходимо знать запись числа в системе счисления с основанием р и правило перевода числа из системы счисления с основанием р в десятичную систему счисления.

«Записью натурального числа х в системе счисления с основанием р называется его представление в виде: х=а_пр^п+а_п-1р^п-1+…+а₁р+а₀, где коэффициенты а_п,а_п-1,…а₁,а₀ принимают значения 0,1,2,…,р-1 и а_п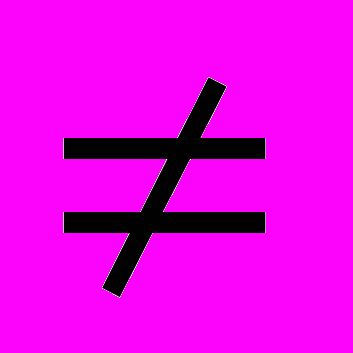0».

Пусть дана запись числа х в системе счисления с основанием р. Найдем запись этого числа в десятичной системе счисления. Так как в записи числа х числа а_п,а_п-1,…а₁,а₀ и р представлены в десятичной системе счисления, то, выполнив над ними действия по правилам, принятым в нем, получим десятичную запись числа х.

Решение: 1101₂= 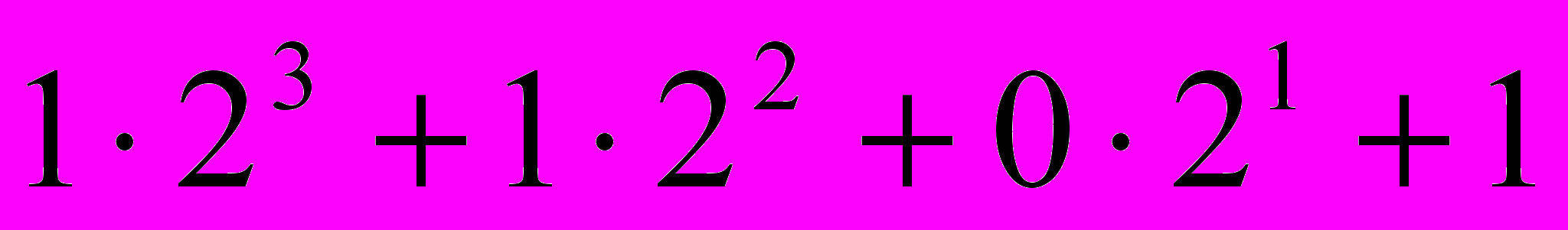=13₁₀

126₈=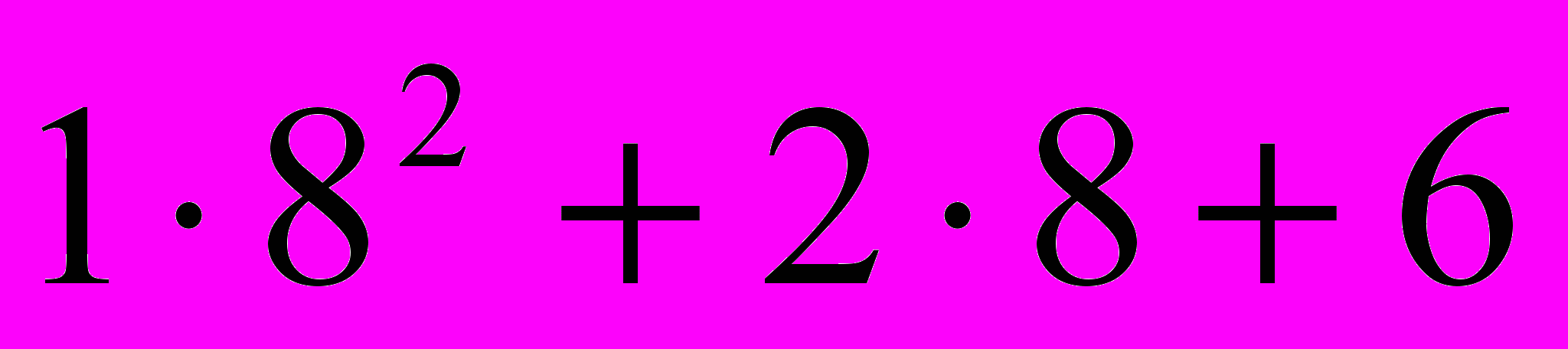=86₁₀

122₃=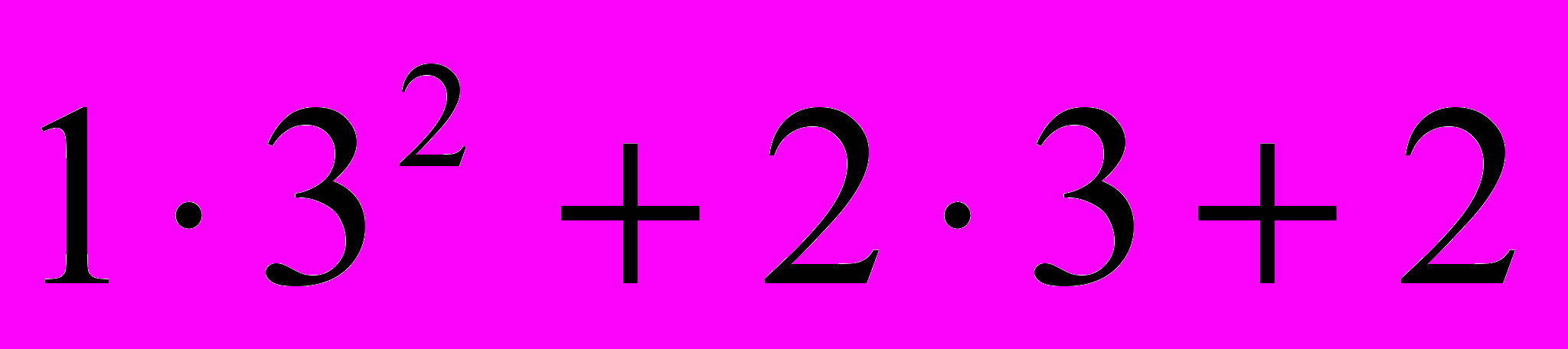=17₁₀

13<17<86 1101₂<122₃<126₈


Задание 3

Числа 412₅ и 524₇ перевести в девятеричную систему счисления и выполнить сложение, вычитание, умножение и деление.

Для правильного выполнения этого задания надо знать запись натурального числа в р-ичной системе счисления, перевод чисел из р-ичной системы счисления в десятичную и из десятичной в р-ичную, таблицы сложения и умножения в р-ичной системе счисления.

Запись натурального числа в р-ичной системе счисления имеет вид:

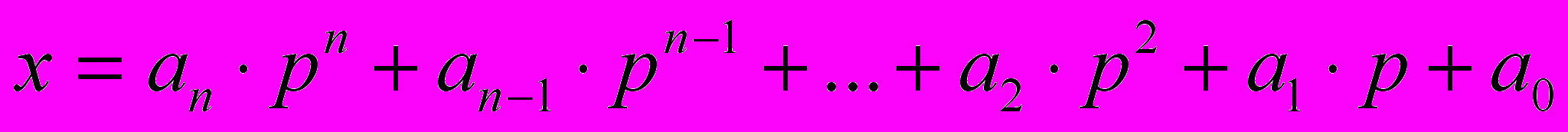, где 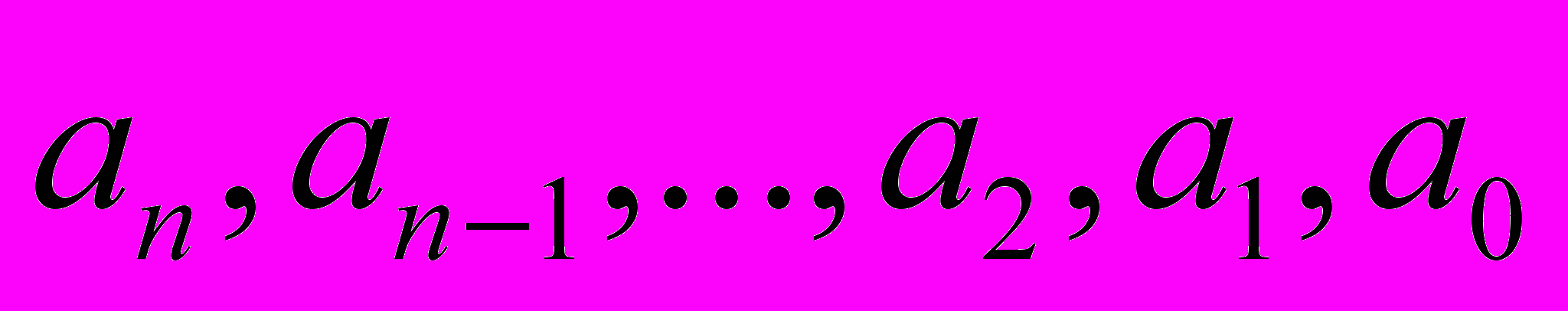числа от 1 до р – 1, и 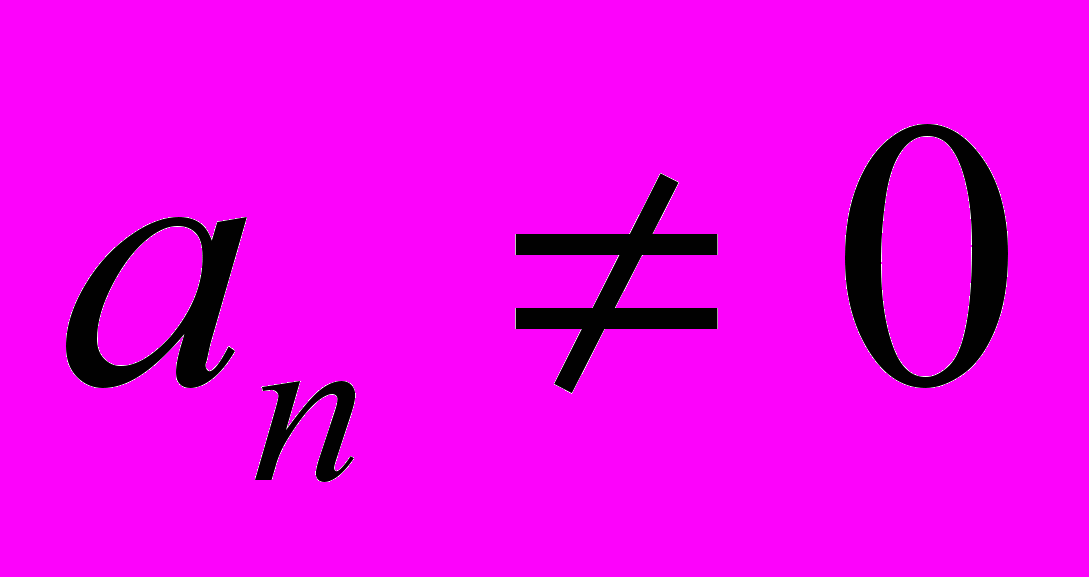, р – любое натуральное число, р ≥ 2.

Запишем числа 412₅, 524₇ в десятичной системе счисления.

412₅ = 4  5² + 1  5 + 2 = 100 + 5 + 2 = 107.

524₇ = 5  7² + 2  7 + 4 = 245 + 14 + 4 = 263.

Переведем число 107 и 263 в девятеричную систему счисления.

_107 _9__ _263 _9_

9 11 _9_ 18 29 _9_

_17 9 1 83 27 3

_9 3 81 2

8 2

Получим: 412₅ = 138₉ и 524₇ = 322₉.

Составим таблицы сложения и умножения в девятеричной системе счисления.

+	0	1	2	3	4	5	6	7	8
0	0	1	2	3	4	5	6	7	8
1	1	2	3	4	5	6	7	8	10
2	2	3	4	5	6	7	8	9	11
3	3	4	5	6	7	8	9	10	12
4	4	5	6	7	8	9	10	11	13
5	5	6	7	8	9	10	11	12	14
6	6	7	8	9	10	11	12	13	15
7	7	8	9	10	11	12	13	14	16
8	8	9	10	11	12	13	14	15	17

	0	1	2	3	4	5	6	7	8
0	0	0	0	0	0	0	0	0	0
1	0	1	2	3	4	5	6	7	8
2	0	2	4	6	8	10	13	15	17
3	0	3	6	10	13	16	20	23	25
4	0	4	8	13	17	22	26	31	35
5	0	5	11	16	22	27	33	38	44
6	0	6	13	20	26	33	40	46	53
7	0	7	15	23	31	38	46	54	62
8	0	8	17	26	35	44	53	62	71

Используя таблицу сложения, выполним сложение и вычитание чисел в девятеричной системе счисления. Имеем:

₊128₉ _ 322₉

322₉ 128₉

451₉ 185₉

Используя таблицу умножения, найдем произведение и частное данных чисел в девятеричной системе счисления:

_128₉ _ 329₉ 128₉ Т. о., 128₉  322₉ = 42437₉ и

322₉ 257₉ 2₉ 322₉ : 128₉ =2₉ (ост. 56₉)

257₉ 56₉

+ 257₉

385₉

42437₉


Задание 4


Числа a и b при делении на 13 дают соответственно остатки 8 и 5. Какой остаток при делении на 13 даст их сумма, разность, произведение?

При выполнении данного задания надо воспользоваться формулой деления с остатком.

Определение. Пусть a и b – натуральные числа. Неполным частным q и остатком r при делении a на b называются такие целые неотрицательные числа, что a = bq + r, причем

0 ≤ r ≤ b.

Число а при делении на 13 дает остаток 8, поэтому а = 13q + 8. Число b при делении на 13 дает остаток 5, поэтому b = 13р + 5. Найдем сумму чисел a и b.

Имеем: a + b = (13q + 8) + (13р + 5) = (13q + 13р) + (8 +5) = 13(q + р) + 13 = 13(q + р + 1) = 13g, где g = (q + р + 1). Таким образом, сумма чисел a и b при делении на 13 дает остаток 0, т.е. кратна 13.

Найдем разность чисел a и b. Имеем a – b = (13 q + 8) × (13р + 5) = (13q – 13р) + (8 - 5) = 13(q + р) – 3 = 13g – 3. Таким образом, разность чисел a и b при делении на 13 дает остаток 3, т.е. r = 3.

Найдем произведение чисел a и b .Имеем: a – b = (13q + 8) × (13p + 5) = 169pq + 104p + 65q + 40 = (169pq + 104p + 65q + 39) + 1 = 13(13pq + 8p + 5q + 3) + 1, где g = 13pq + 8p + 5q + 3.

Таким образом, произведение числа а и b при делении на 13 дает остаток 1, т.е. r = 1.


Задание 5

Используя метод математической индукции, доказать, что при любом натуральном n: 1. 8ⁿ + 6 делится на 7; 2. n⁵ – n делится на 15.

1. Докажем, что при любом натуральном n 8ⁿ + 6 делится на 7. Доказательство приведем методом неполной математической индукции. Этот метод заключается в следующем.

Пусть дано некоторое утверждение A(n), надо доказать, что оно истинно при любом натуральном n.

Для этого надо:

а) доказать, что данное утверждение истинно при n = 1, т.е. что А(1) истинно;

б) предположить, что это утверждение истинно при n = k, т.е. А(k) истинно;

в) доказать, что это утверждение истинно при n = k + 1, т.е. А(k + 1) истинно.

При выполнении этих условий утверждение A(n) будет истинно при любом натуральном n.

Покажем, что при n = 1 наше утверждение 8ⁿ + 6 истинно. Для этого в данное выражение вместо n подставим 1. Имеем: 8¹ + 6 = 14. 14 делится на 7. Следовательно, при n = 1 наше утверждение истинно.

Допустим, что наше утверждение истинно при n = k, т.е. 8^k + 6 делится на 7.

Докажем, что при n = k + 1 наше утверждение истинно, т.е. 8^k+1 + 6 делится на 7.

Имеем: 8^k+1 + 6 = 8^k × 8 + 6 = 8^k × 8 + 6 × 8 – 6 × 8 + 6 = (8^k × 8 + 6 × 8) – (6 × 8 -6) = 8(8^k + 6) – 42.

В данной разности уменьшаемое 8(8^k + 6) делится на 7, т.к. (8^k + 6) делится на 7 по предположению, вычитаемое 42 = 7 * 6 делится на 7. Следовательно, вся разность 8(8^k + 6) – 42 делится на 7. таким образом, 8^k+1 + 6 делится на 7. Следовательно, при n = k + 1 данное утверждение также справедливо.

Таким образом, наше утверждение справедливо при любом натуральном п.

2. Докажем справедливость утверждения: n⁵ – n делится на 15 при любом натуральном п.

Преобразуем выражение к следующему виду: n⁵ – n = n (n⁴ - 1) = n(n² - 1)(n² + 1) = n(n - 1)(n + 1)(n² + 1). Нам надо доказать, что данное выражение делится на 15. Ног 15 составное число, 15 = 5 * 3. Поэтому докажем, что данное выражение делится и на 3 и на 5, тогда оно будет делится и на 15. Доказательство приведем методом полной математической индукции. При n = 1 имеем: 1  (1 - 1) (1 + 1)  (1² + 1) = 0 делится на 3 и на 5.

Докажем, что данное выражение делится на 3 при любом натуральном п  1.

Для этого рассмотрим три возможности: а) n делится на 3 без остатка; б) n при делении на 3 дает остаток 1; в) n при делении на 3 дает остаток 2.

а) Пусть n делится на 3 без остатка. Тогда n = 3k. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = 3k(3k - 1)(3k + 1)((3k)² + 1) – делится на 3.

б) Пусть n при делении на 3 дает остаток 1. Тогда n = 3k + 1. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = (3k + 1)((3k + 1) - )((3k + 1) + 1)((3k + 1)² + 1) = 3k(3k + 1)(3k + 2)((3k + 1)² + 1) – делится на 3.

в) Пусть n при делении на 3 дает остаток 2. Тогда n = 3k + 2. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = (3k + 2)((3k + 2) - 1)((3k + 2) + 1)((3k + 2)² +1) = (3k + 2)(3k + 1)(3k + 3)((3k + 1)² + 1) = 3k(3k + 2)(3k + 1)((3k + 2)² + 1) – делится на 3.

Таким образом, выражение n⁵ – n = n(n - 1)(n + 1)(n² + 1) делится на 3 при любом натуральном п  1.

Докажем, что данное выражение делится на 5 при любом натуральном п  1.

Для этого рассмотрим пять возможностей: а) n делится на 5 без остатка; б) n при делении на 5 дает остаток 1; в) n при делении на 5 дает остаток 2; г) n при делении на 5 дает остаток 3; д) n при делении на 5 дает остаток 4.

а) Пусть n делится на 5 без остатка. Тогда n = 5k. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = 5k(5k - 1)(5k + 1)((5k)² + 1) – делиться на 5.

б) Пусть n при делении на 5 дает остаток 1. Тогда n = 5k + 1. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = (5k + 1)((5k + 1) - 1)((5k + 1) + 1)((5k + 1)² + 1) = 5k(5k + 1)(5k + 2)((5k + 1)² + 1) – делится на 5.

в) Пусть n при делении на 5 дает остаток 2. Тогда n = 5k + 2. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = (5k + 2)((5k + 2) - 1)((5k + 2) + 1)((5k + 2)² + 1) = (5k + 2)(5k + 1)(5k + 3)((25k² + 20k + 4) + 1) = (5k + 1)(5k + 2)(5k + 3)(25k² + 20k + 5) = 5(5k + 1)(5k + 2)(5k + 3)( 5k² + 4k + 1) – делится на 5.

г) Пусть n при делении на 5 дает остаток 3. Тогда n = 5k + 3. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = (5k + 3)((5k + 3) - 1)((5k + 3) + 1)((5k + 3)² + 1) = (5k + 3)(5k + 4)(5k + 2)(25k² + 30k + 10) = 5(5k + 3)(5k + 4)(5k + 2)( 5k² + 6k + 2) – делится на 5.

д) Пусть n при делении на 5 дает остаток 4. Тогда n = 5k + 4. Подставим данное значение n в выражение n(n - 1)(n + 1)(n² + 1) = (5k + 4)((5k + 4) - 1)((5k + 4) + 1)((5k + 4)² + 1) = (5k + 4)(5k + 3)(5k + 5)((5k + 4)² + 1) = 5(k + 1)(5k + 4)(5k + 3)(25k² + 20k + 5) = 5(k + 1)(5k + 4)(5k + 3)((5k + 4)² + 1) – делится на 5.

Таким образом, выражение n⁵ – n = n(n - 1)(n + 1)(n² + 1) делится на 5 при любом натуральном п  1.

А это значит, что n⁵ – n = n(n - 1)(n + 1)(n² + 1) делится на 15 при любом натуральном п  1.

Задание 6

Найти наименьшее общее кратное и наибольший общий делитель (двумя способами) чисел: 64260 и 75735.

Общим делителем натуральных чисел a и b называется число, на которое одновременно делятся числа a и b. Наибольший из всех общих делителей чисел a и b называется их наибольшим общим делителем. Обозначается НОД(a,b).

Кратным натуральных чисел a и b называется число, которое кратно числу a и числу b одновременно. Наименьшее из всех кратных чисел a и b называется их наименьшим общим кратным. Обозначается НОК(a,b).

Наибольший общий делитель чисел a и b можно найти двумя способами:

1. Чтобы найти наибольший общий делитель чисел a и b, надо разложить эти числа на простые множители, т.е. представить их в каноническом виде: 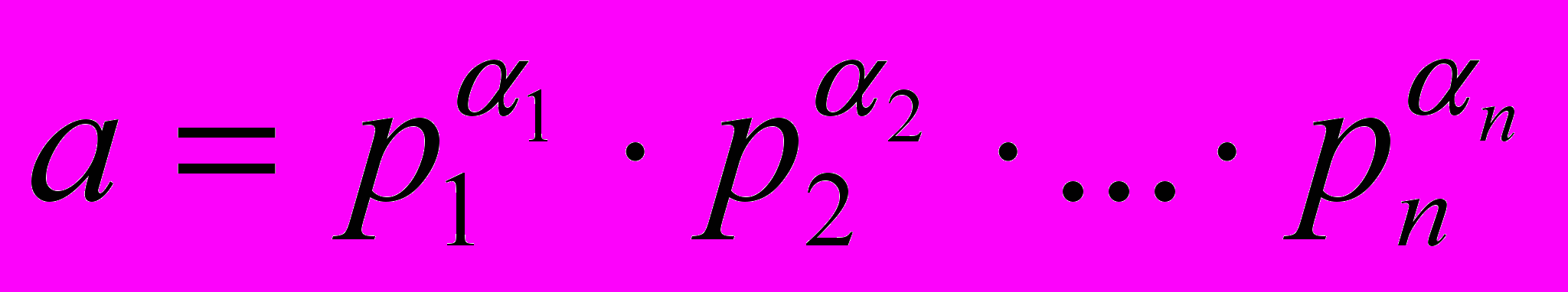и 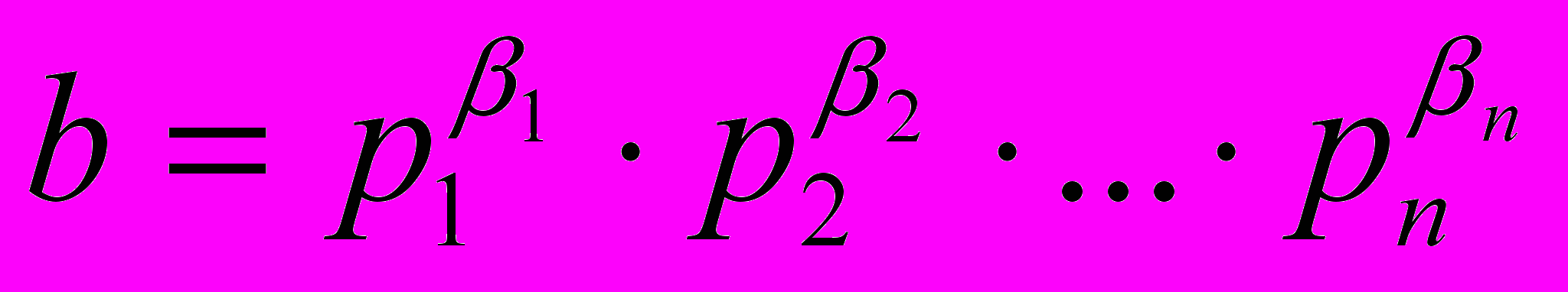. Наибольший общий делитель натуральных чисел a и b равен произведению одинаковых простых множителей, входящих в данные разложения, с наименьшими показателями степени.

2. Наибольший общий делитель натуральных чисел a и b находят с помощью алгоритма Евклида. Он основан на следующих трех утверждениях:

а) Если а делится на b, то делитель чисел a и b равен b.

б) Если при делении а на b получается остаток r, то делитель чисел a и b равен делителю чисел b и r, и задача сводится к отысканию наибольшего общего делителя чисел b и r.

в) Если b делится на r, то наибольший общий делитель чисел b и r равен r. Тогда и наибольший общий делитель чисел a и b равен r. Если же при делении b на r получается остаток r₁, тогда делитель чисел r и r₁ такой же, что и делитель чисел b и r, и, следовательно, такой же, как делитель чисел a и b.

Продолжая описанный процесс, получаем все меньшие и меньшие остатки. В конце концов, дойдем до остатка, на который будет делиться предыдущий остаток. Этот наименьший, отличный от 0 остаток и будет наибольшим общим делителем чисел a и b.

Наименьшее общее кратное тоже можно найти двумя способами.

1. Чтобы найти наименьшее общее кратное чисел a и b, надо разложить эти числа на простые множители, т.е. представить их в каноническом виде: 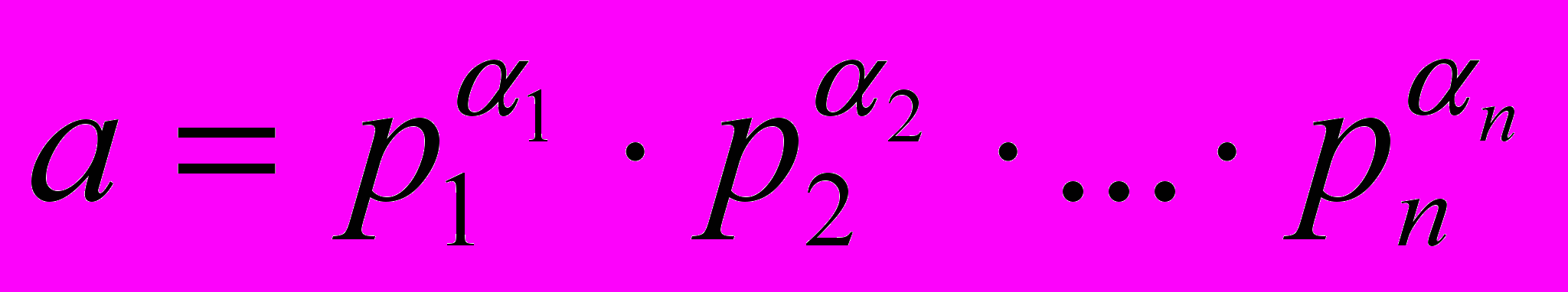и 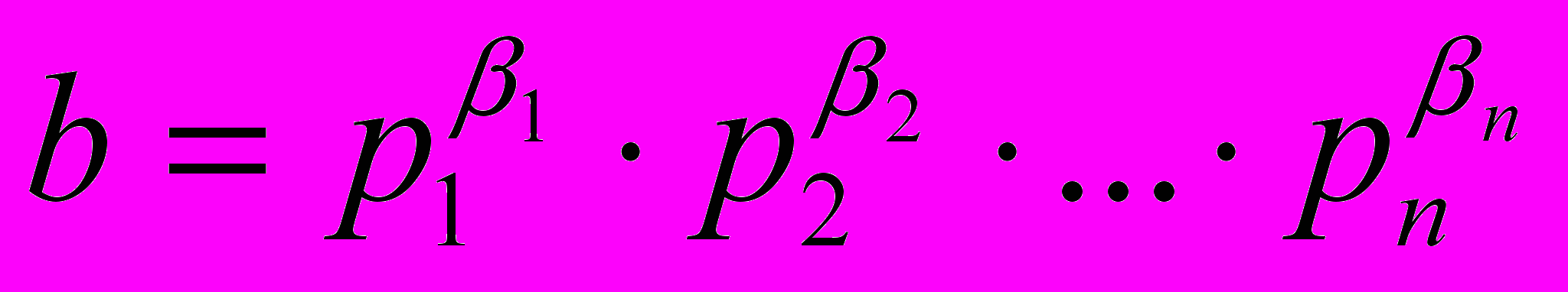. Наименьшее общее кратное натуральных чисел а и b равно произведению всех простых множителей, входящих в данные разложения, с наибольшими показателями степени.

2. Известно, что наименьшее общее кратное и наибольший общий делитель чисел а и b связаны соотношением: НОК (a,b) НОД (a,b) = а  b. Отсюда находим .

Используя приведенные выше теоретические положения, найдем наибольший общий делитель и наименьшее общее кратное чисел а и b.

Найдем наибольший общий делитель (НОД) и наименьшее общее кратное (НОК) чисел 64260 и 75735 двумя способами.


1 способ. Разложим числа 64260 и 75735 на простые множители. Имеем:

64260 2 75735 3

32130 2 25245 3

16065 3 8415 3

5355 3 2805 3

1785 3 935 5

595 5 187 11

119 7 17 17

17 17


Таким образом, получил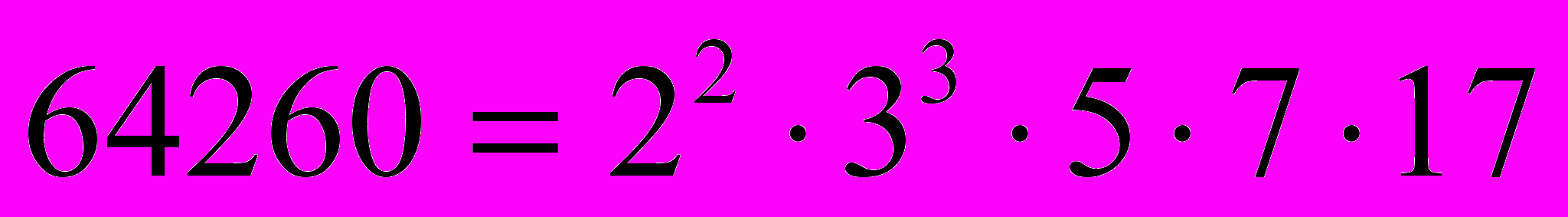и: и 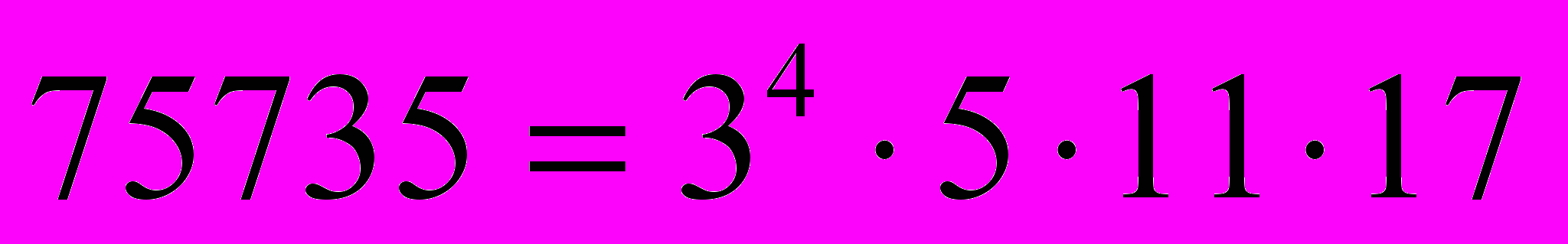. Отсюда получаем, что НОД(64260, 75735) = = 2295 и НОК(64260, 75735) = 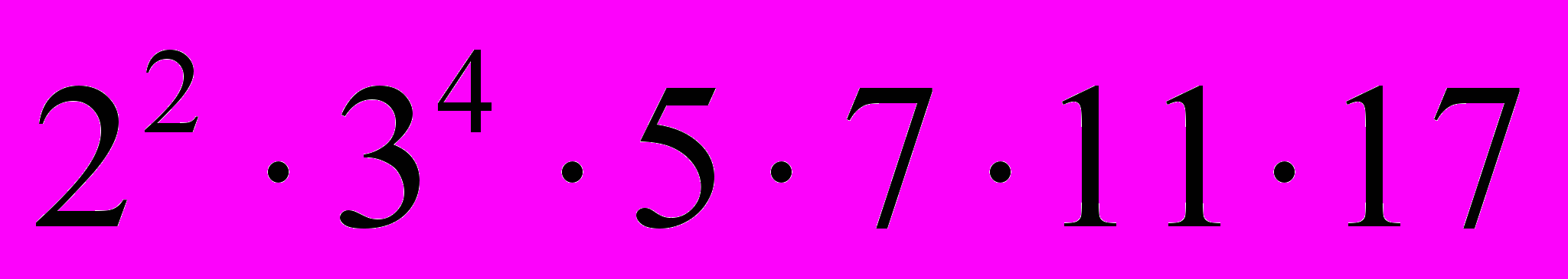= 2120580.

2 способ. Найдем наибольший общий делитель чисел 64260 и 75735 с помощью алгоритма Евклида. Разделим 64260 на 75735 с остатком. Имеем:

_75735 64260 _64260 11475 _11475 6885 _6885 4590 _4590 2295

64260 1 57375 5 6885 1 4590 1 4590 2

11475 = r₁ 6885 = r₂ 4590 = r₃ 2295 = r₄ 0 = r₅

Таким образом, последний, отличный от 0 остаток r₄ = 2295.

Следовательно, НОД(64260, 75735) = 2295.

Найдем НОК(64260, 75735). Имеем а  b = 64260  75735, тогда НОК(64260, 75735) = .

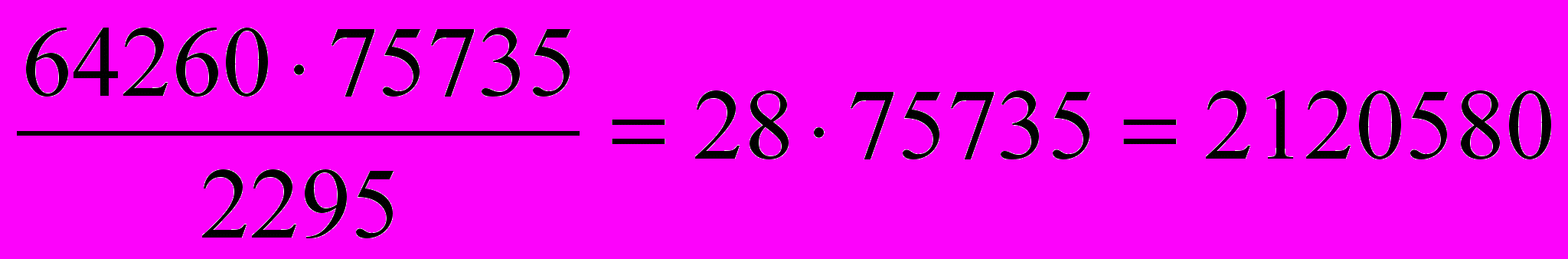Задание 7

1. Среди данных чисел найти простые: 4869, 279, 8345, 223, 847;

2. Найти все числа вида 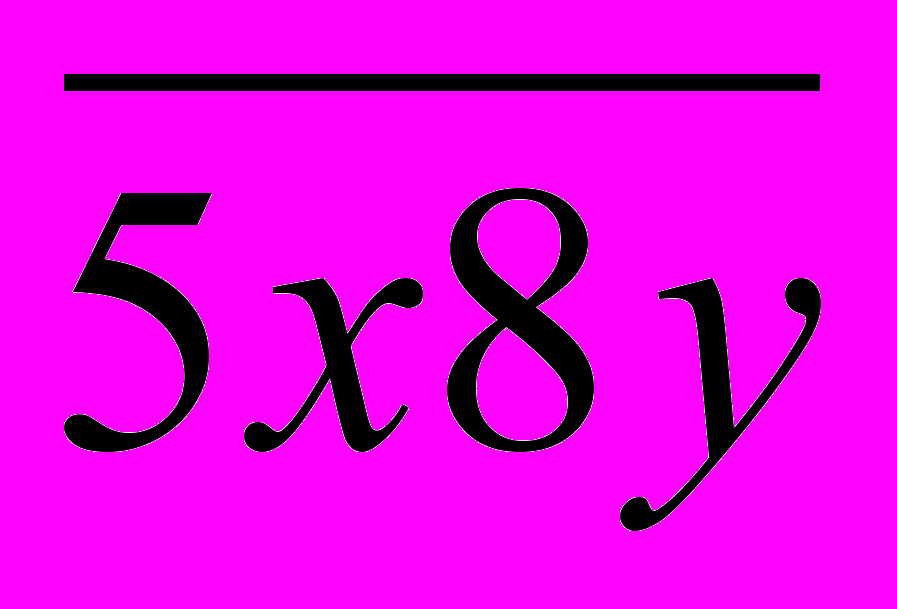, кратные 36.

1. Для выполнения этого задания надо знать определение простого и составного числа, признаки делимости на 2, 3, 5, 9, 11 и способ нахождении простых чисел.

Число называется простым, если оно имеет ровно два делителя, единицу и само себя. Число называется составным, если оно имеет больше двух делителей.

Признаки делимости. Натуральное число делится на два, если оно оканчивается на 0, 2, 4, 6, 8.

Натуральное число делится на 3 (на 9), если сумма цифр в десятичной записи этого числа делится на 3 (на 9).

Натуральное число делится на 5, если оно оканчивается на 0 или 5.

Натуральное число делится на 7, 11, 13, если …?

Теорема. Наименьший простой делитель составного числа а не превосходит .

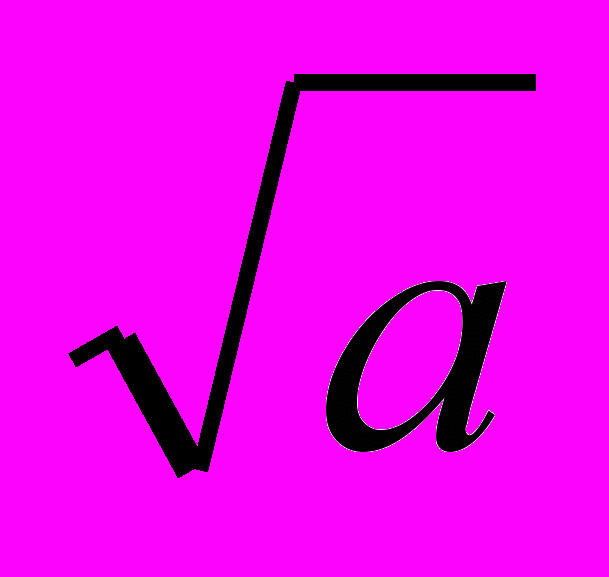Найдем среди чисел 486, 279, 8345, 223 и 847 простые. По признаку делимости на 2 заключаем, что число 8345 делится на 5.

Проверим, делятся ли числа 279, 223, 847 на 3. Найдем сумму цифр числа 279: 2+7+9=18, 18 делится на 3, следовательно, число 279 делится на 3. Найдем сумму цифр числа 223: 2+2+3=7, 7 не делится на 3, следовательно, число 223 не делится на 3. Найдем сумму цифр числа 847: 8+4+7=19, 19 не делится на 3, следовательно, число 847 не делится на 3.

Проверим делимость чисел 223 и 847 на 7. Так как числа трехзначные, проверить их делимость на 7 можно непосредственно делением. Проверка показывает, что число 223 не делится на 7, а число 847 делится на 7. Следовательно, число 847 составное.

Рассмотрим число 223. 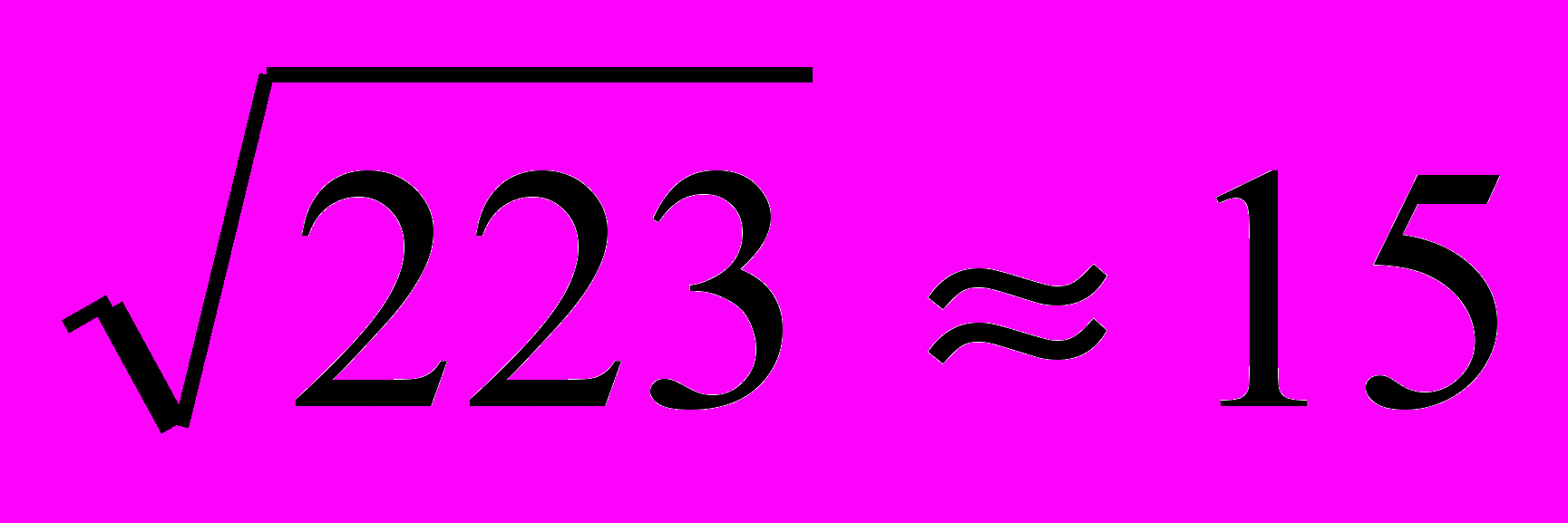. Выпишем все простые числа, меньше 15: 2, 3, 5, 7, 11, 13. Число 223 не делится на 2, 3, 5, 7. проверим, делится ли оно на 11 или 13. Непосредственным делением убеждаемся, что 223 не делится на 11 и 13. Следовательно, данное число простое.

2. Найдем все числа вида 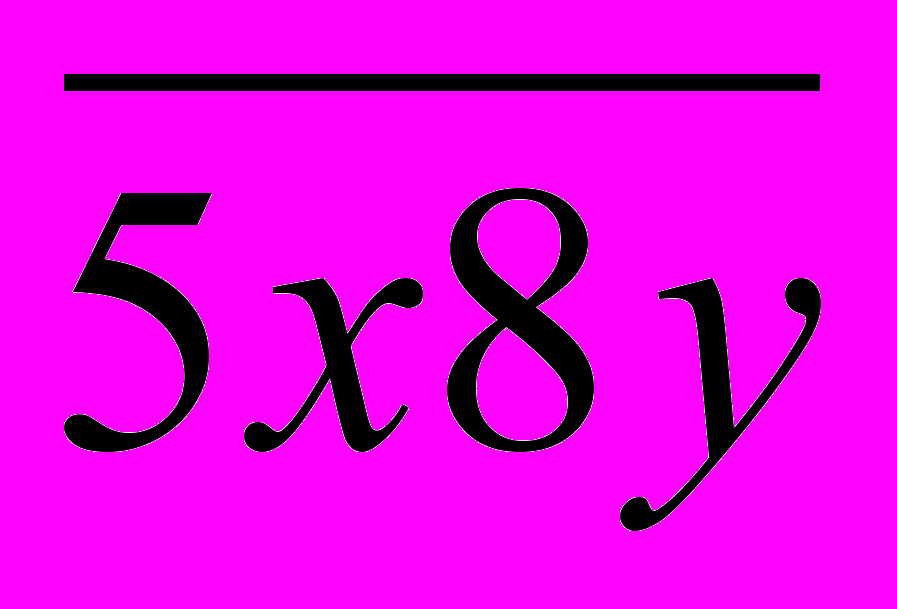, кратные 36. 36 – составное число, 36=4·9. Следовательно, чтобы число было кратно 36, надо, чтобы оно было кратно 4 и 9.

Найдем, при каких значениях у данное число будет кратно 4. Воспользуемся признаком делимости на 4: данное число делится на 4, если число, образованное двумя последними цифрами в его десятичной записи, делится на 4.

Число, образованное двумя последними цифрами в его десятичной записи нашего числа, будет 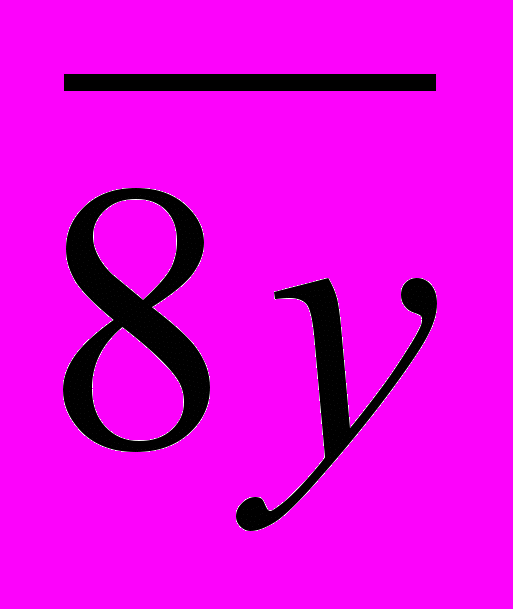. Оно будет делиться на 4 тогда, когда у = 4 и у = 8. Подставив найденные значения у в число 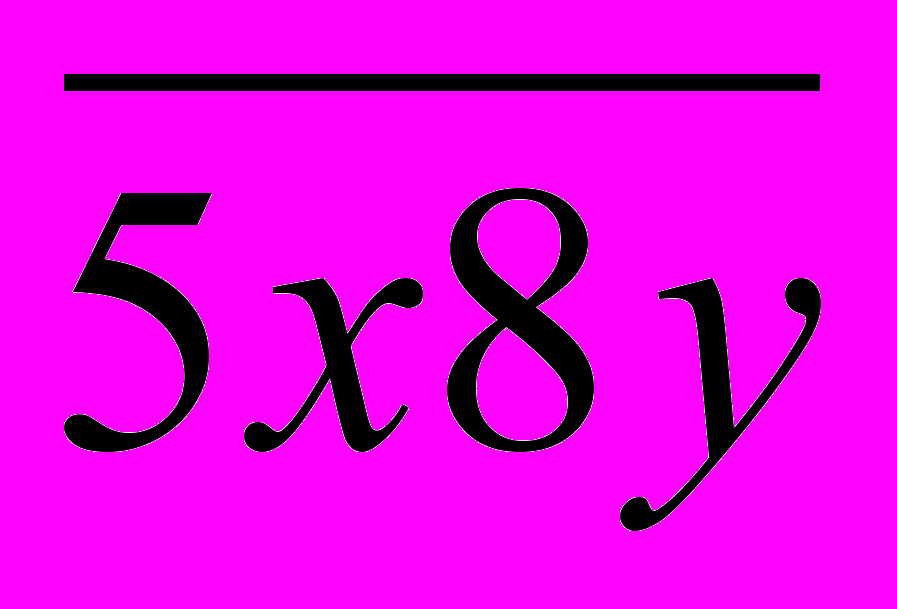получим два числа: 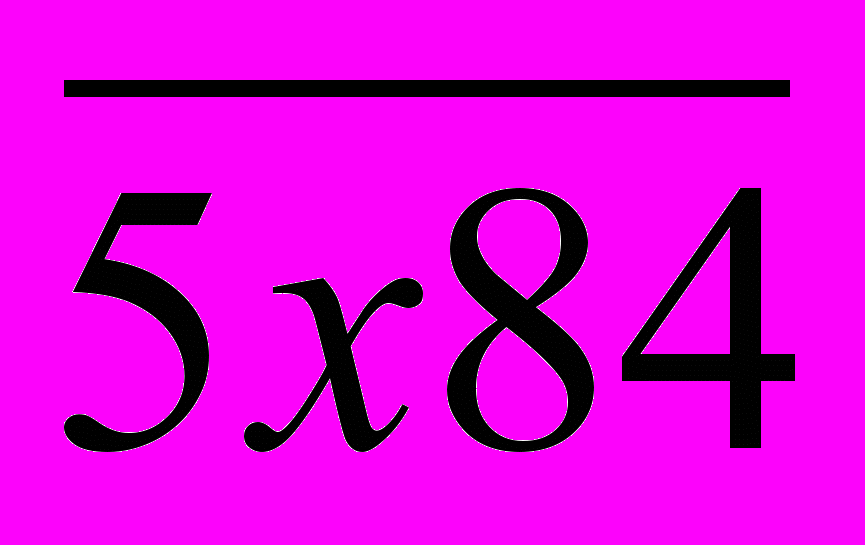и .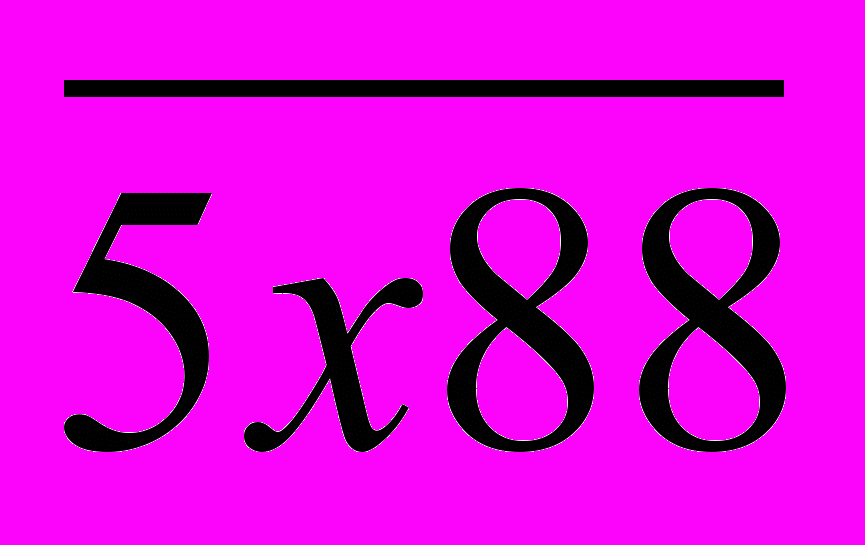

Чтобы число делилось на 9, необходимо, чтобы сумма цифр в его десятичной записи была кратна 9. Найдем сумму цифр числа 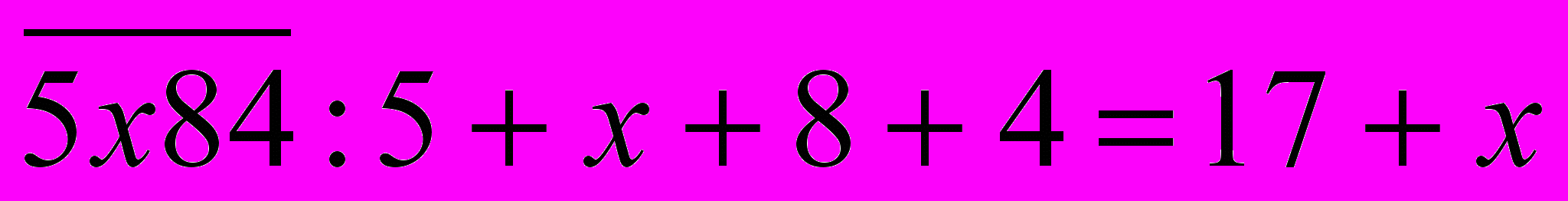. Данная сумма кратна 9 при х = 1 (17 + 1 = 18). Подставив найденное значение х в 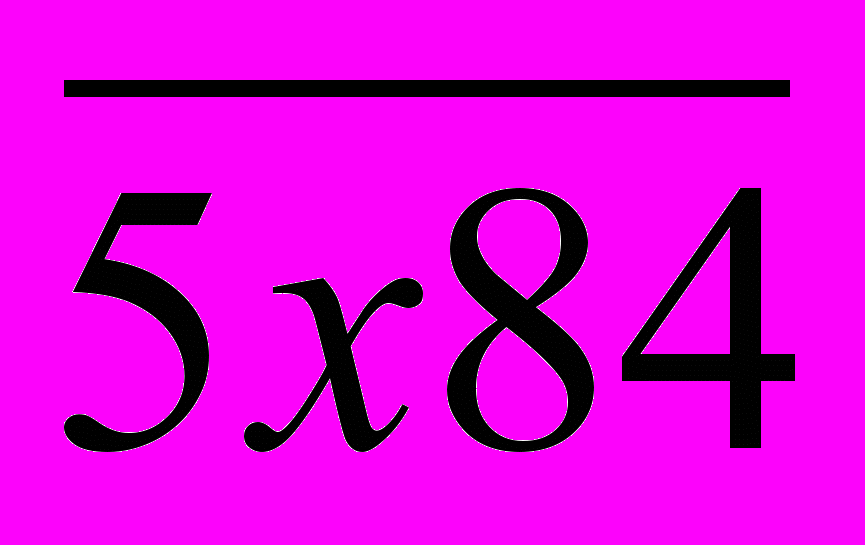, получим число 5184, которое будет делиться на 9. А так как это число делится и на 4, то оно будет делиться на 36. Других значений х нет, так как х должно быть однозначным числом. Рассмотрим число 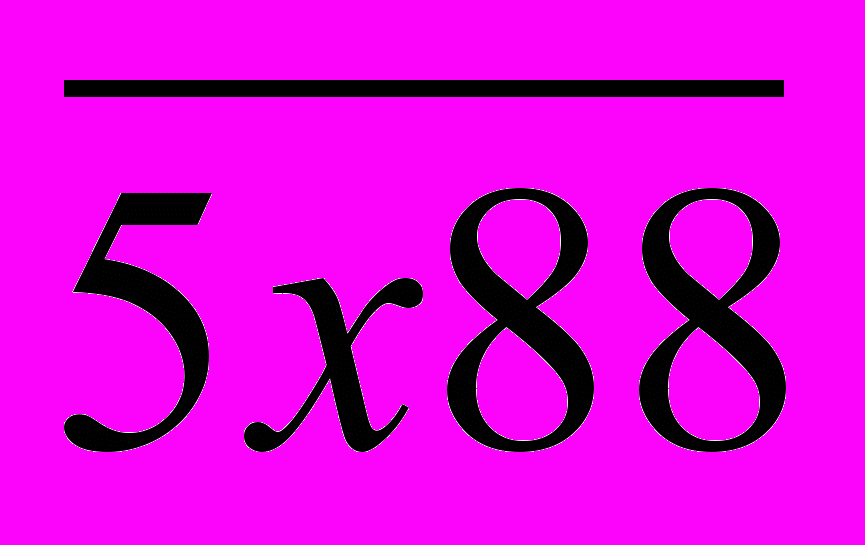, найдем сумму его цифр: 5 + х + 8 + 8 = 21 + х. Данная сумма кратна 9 только при х = 6. подставив найденное значение х в 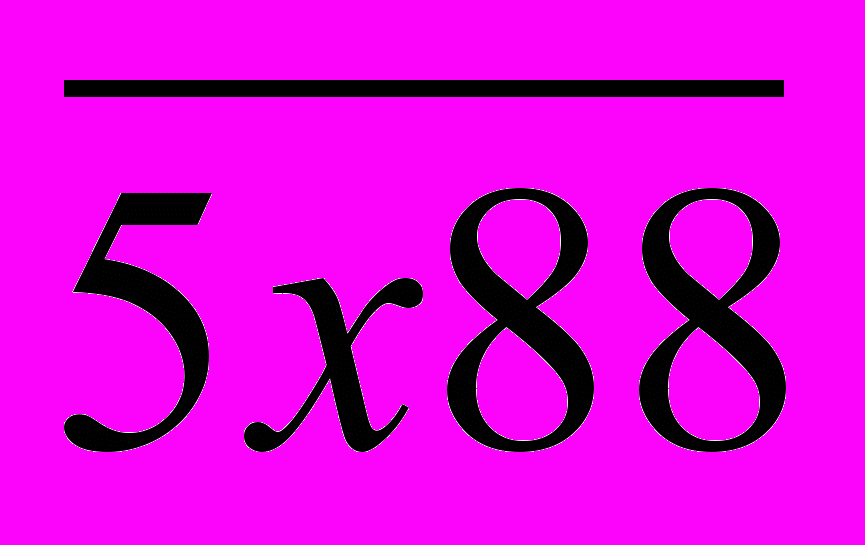, получим число 5688, которое будет делиться на 9. А так как это число делится и на 4, то оно будет делиться на 36.

Таким образом, числами, кратными 36, будут: 5184 и 5688.

Вопросы к экзамену по методике преподавания интегративного курса «Окружающий мир»

1. Предмет и задачи методики преподавания естествознания.

2. Методологические основы методики начального естествознания, ее связь с другими науками.

3. История развития МПЕ в начальной школе в XVIII-XIX вв.

4. В.Ф.Зуев и его учебник по естествознанию. А.Я.Герд - основоположник русской методики.

5. Развитие методики обучения естествознанию на современном этапе. Авторы современных программ и учебников.

6. Содержание начального естествознания. Принципы отбора содержания.

7. Формирование природоведческих представлений и понятий. Образование естественнонаучных понятий.

8. Межпредметные связи. Реализация межпредметных связей на уроках природоведения.

9. Обусловленность и задачи ознакомления младших школьников с природой.

10. Педагогическое значение естественнонаучного образования в развитии личности младшего школьника.

11. Экологическое образование и воспитание младших школьников.

12. Современные программы по природоведению. Общая характеристика программ.

13. Вопросы экологии в программах по природоведению.

14. Материальная база уроков естествознания: учебное оборудование, пришкольный участок и географическая площадка. Значение материальной базы.

15. Уголок живой природы, уголок краеведения. Значение, организация уголка живой природы и уголка краеведения в начальной школе.

16. Средства обучения естествознанию, их классификация. Натуральные объекты.

17. Наглядно-образные средства, модели, приборы. Методика применения на уроках природоведения.

18. Средства обучения естествознанию: учебники, печатные пособия, экранные пособия.

19. Методика обучения. Общая характеристика методов обучения, их классификация.

20. Практические методы обучения естествознанию.

21. Наблюдение как метод обучения естествознанию.

22. Методика работы со схематическими (знаковыми) источниками знаний. Работа с картой.

23. Словесные методы. Устное слово в системе методов обучения естествознанию.

24. Методические приемы и их классификация. Выбор методов и методических приемов.

25. Формы организации обучения естествознанию в начальной школе. Классификация форм обучения.

26. Урок как основная форма организации учебного процесса по естествознанию.

27. Вводные, комбинированные, обобщающие уроки.

28. Образовательные, воспитательные, развивающие задачи, содержание курса природоведения.

29. Требования к уроку в начальной школе. Особенности уроков естествознания.

30. Подготовка учителя к уроку. Планирование учебной работы.

31. Формы, методы и средства ознакомления учащихся с окружающим миром.

32. Построение урока естествознания в начальной школе.

33. Типы уроков естествознания в начальной школе.

34. Методика организации и проведения предметного урока.

35. Уроки с демонстрацией опытов. Организация практических работ на уроках природоведения.

36. Внеурочные формы обучения естествознанию.

37. Методика повторения учебного материала. Проверка и учет знаний учащихся.

38. Значение и методика организации экскурсий по естествознанию.

39. Экологические экскурсии в природу.

40. Игровые формы обучения естествознанию. Значение игры в обучении школьников.

41. Методика подготовки и проведения ролевой игры.

42. Значение внеклассной работы по естествознанию. Организация внеклассной работы.

43. Массовые формы внеклассной работы. Организация тематических вечеров, праздников.

44. Особенности обучения в малокомплектной школе. Специфика урока.

45. Формы, методы и средства ознакомления учащихся младших классов с окружающим миром.