В. П. Казначеев д м. н., академик рамн, президент зсо мса

Вид материала

Документы

Содержание Эволюция природы, человека и общества к тройственной гармонии Ключевые слова; баланс, бытие, небытие, эволюция, гармония, структура, тройственное равновесие, золотая пропорция, хаос, порядок G*- новая функция, мера определенности состояния системы или мера порядка, К Идеальный газ Фрактал «зотолого сечения» Физический опыт и эволюция Новый принцип описания равновесия природы I+G, (15) где 1 – единица - отражает целостность системы, I К является нелинейной мультипликативной изменяющейся функцией: К=К(p)К(q)К(l)= К(p,q,l) Развитие социальных систем

Подобный материал:

• В. П. Казначеев д м. н., академик рамн, президент зсо мса, 4143.24kb.
• В. П. Казначеев д м. н., академик рамн, президент зсо мса, 3704.26kb.
• В президиуме со рамн, 441.3kb.
• Научная программа организационный комитет почетный председатель съезда оганов Рафаэль, 391.06kb.
• Влагалища и шейки матки у детей, 313.83kb.
• Трансфер фактор №, 139.68kb.
• Академик рамн, Президент Российской академии медицинских наук, Директор Российского, 1036.51kb.
• Рецидивы и метастазы гранулезоклеточных опухолей яичников (клиника, диагностика, лечение), 358.95kb.
• Шафрин Ю. А. Информационные технологии: в 2 ч. Ч. 1: Основы информатики и информационных, 264.02kb.
• Галины Чулуевны Махаковой. Приветственное слово директора фгу нии урологии, профессора, 80.37kb.

Эволюция природы, человека и общества к тройственной гармонии

ХаритоновА.С.

Аннотация

В настоящей работе рассмотрен баланс взаимодействия бытия и небытия, описываемый мерами хаоса и порядка в трех классах переменных, как новый способ описания, который указывает на эволюцию объектов природы к тройственной гармонии с целью сохранения ее целостности. Идея гармонии известна со времен Пифагора. Тройственная сущность «мира как органона» рассмотрена Аристотелем. Идея единства и целостности природы, определяемая взаимодействием бытия и небытия, изучалась еще Платоном. Золотая пропорция как характеристика эволюции к гармонии известна со времен Ренессанса. Меры хаоса и порядка в трех классах переменных предложены автором. Показана применимость такого способа описания к исследованию развития природы, человека и общества.


Ключевые слова; баланс, бытие, небытие, эволюция, гармония, структура, тройственное равновесие, золотая пропорция, хаос, порядок, целое и часть.


Профессор химического факультета МГУ Н.И. Кобозев заинтересовал меня в 1968 году проблемой разрешения противоречия в понимании эволюции: биологические и социальные системы возникают, живут, развиваются и, в конечном итоге, элиминируют, а согласно второму закону термодинамики они должны эволюционировать только к максимальному хаосу и деградации своей организации. С тех пор я изучаю эту проблему. В статье приведены промежуточные итоги моего исследования и сформулировано противоречие: мир стремится к гармонии или к максимальному хаосу? Мной установлено, что выбор модели равновесия, используемой в теории, определяет наше представление об эволюции. Модели равновесия объектов природы могут быть разными, и очевидно, что они приводят к разным представлениям об эволюции исследуемых объектов. В работе используется новая модель равновесия природы на основе баланса взаимодействия бытия и небытия. Этот баланс определен равенством мер хаоса и порядка в трех классах переменных, предложенных автором. Тогда, если модель равновесия бинарна, дуальна, дихотомична и построена в двух классах переменных, то теория описывает эволюцию систем к максимальному хаосу. Если модель равновесия тройственна и учитывает взаимодействие трех «сил» в трех классах переменных, то теория будет описывать эволюцию выживающих систем к тройственной гармонии.

Разрешение противоречия («мир стремится к хаосу или гармонии?») имеет относится к развитию социологии. Великие мыслители, например, Цицерон, писали об эволюции общества к гармонии, справедливости и соразмерности. Многие их них рассматривали социологию как физику социальных процессов или физическую социологию /О.Конт, Г.Спенсер/. Однако физика, основанная на статистической механике и термодинамике, указала на эволюцию систем прямо в противоположном направлении - к максимальному хаосу и деградации организации систем. После осознания этого противоречия социология отделилась от физики и стала развиваться как гуманитарная наука, так как математический аппарат физики противоречил ее главным представлениям о законах развития общества. На необходимость собственного математического аппарата для социологии указывали в своих работах В.И.Жуков и Г.С.Жукова, а также многие другие социологи. При этом Э.Андреев и Г.Осипов предлагали вернуться к физике и социологии Аристотеля («Мир как органон», построенный на триединстве природы и стремящийся к тройственной гармонии) [1]. Эти идеи заново востребованы сегодня в социологии («организменный» подход В.И. Франчука и «виталистическое» видение социологии С.И. Григорьева).

Противоречие в понимании эволюции заметили и физики, и они его стали обсуждать сразу после появления термодинамики. С.Карно заметил, что все стремится к равновесию, и, пренебрегая природой вещества, тепловые машины стремятся к теплому равновесию. В. Томсон, один из основателей второго закона термодинамики, заметил в 1842 году: с одной стороны, закон ослабления внешних сил в системах является всеобщим для биологических и косных систем, с другой стороны, «тело животного работает не как термодинамическая машина»[2].

Попытки разрешить это противоречие и понять физическую специфичность живого организма в ХХ веке связаны с развитием двух противоположных подходов в науке. В одном подходе рассматриваются открытые термодинамические системы, так как биологические и социальные организмы обмениваются энергией, веществом и информацией с окружающей средой /Л. Онзагер, И. Пригожин, Г. Хакен/.

В другом подходе Н.И. Кобозев предложил искать разрешение противоречия за рамками постулатов термодинамики, рассматривая диалектику хаоса и порядка в природе /Эпихарм, Н.Макиавелли, А.Ф. Лосев/ и идеи целостности природы и резонансных взаимодействий нелинейных колебаний (А.А. Ухтомский). Последний разработал концепцию доминанты в физиологии человека, где живой организм и окружающая среда рассматриваются как единое целое (И.М.Сеченов и Н.Е.Введенский) [3]. При этом живой организм активно стремится к своему особому равновесию с окружающей средой в отличие от механистических представлений, где живое тело уходит от термодинамического равновесия (Э. Бауэр, Э. Шредингер, И. Пригожин, Н.Моисеев, В.Воейков). Напомним, что в современной синергетике принято за основу механистическое (дихотомическое) равновесие и определение термодинамической энтропии равной мере хаоса в двух классах переменных.

Моя работа под руководством Н.И.Кобозева началась с установления следующего математического факта в 1971 году. Энтропия с вероятностью связана не только мерой хаоса, как показал Л. Больцман 1878году, а суммой мер хаоса и порядка:

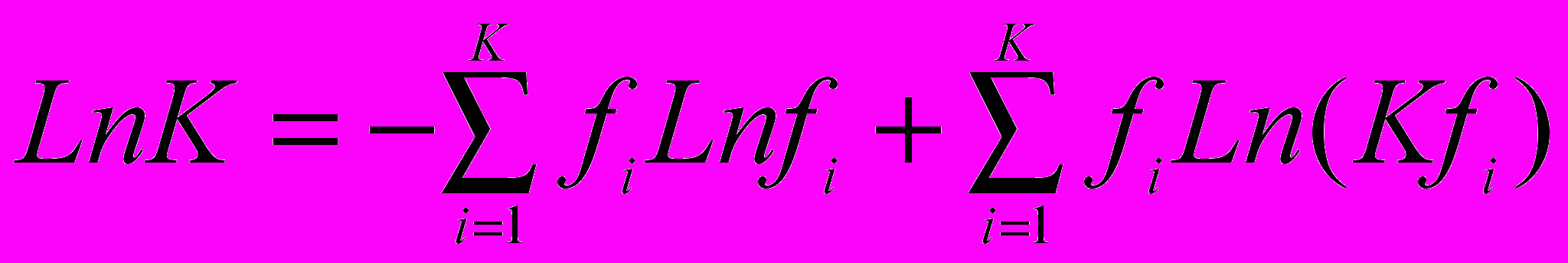= I*+G*, (1)

где LnK – безразмерная статистическая энтропия, I*- мера неопределенности состояния или мера хаоса, G*- новая функция, мера определенности состояния системы или мера порядка, К - число рассматриваемых микросостояний системы, f_i -вероятность i-го микросостояния.

Мои исследования показали [4], что постулат Л.Больцмана о связи энтропии с вероятностью предполагает в статистическом равновесии постоянство числа рассматриваемых микросостояний, К=const, что позволяет пренебречь мерой порядка, G*=0, на основании идеализаций механического равновесия, где тело заменяется его центром тяжести. При замене тел материальными точками механические и термодинамические системы описываются дуально в двух независимых классах переменных: координат и импульсов (скоростей). Поэтому статистическая механика рассматривает частный случай связи энтропии (меры внутреннего превращения) с вероятностью, когда структурой и геометрией динамических частиц (тел) можно пренебречь и также пренебречь процессом концентрации энергии в круговороте природы. /Процесс концентрации энергии определяется изменением структуры и геометрии динамических элементов, доступностью пространства и характером взаимодействия частиц между собой./ С.А. Подолинский обратил внимание в 1880 году на то, что при описании специфичности социальных и биологических систем пренебрегать процессом концентрации энергии, как это делают термодинамика и статистическая механика, нельзя [5].

Н.А. Умов предложил в 1902 году использовать третью переменную, характеризующую структуру динамических элементов, для понимания физической специфичности живой природы. Резонанс структурных параметров между внешними и внутренними круговоротами энергии в природе позволяет объяснить дальнодействие в природе и работу физических, биологических и социальных систем против второго закона термодинамики, и установить возникновение в них внутренних движущих сил [6].

Исследованию скрытых и немеханистических взаимодействий в биологических и социальных системах посвящены исследования А. Гурвича, Н. Бернштейна, К. Тринчера и В. Казначеева.

Поясним дуальную сущность идеализации статистической механики на примере свойств идеального газа. Структура динамических частиц идеального газа задана достоверным или строго упорядоченным образом. Все степени свободы идеального газа только поступательные. Все частицы идеального газа заменены материальными точками с заданными массами, пространство постулируется однородным и изотропным, взаимодействия между частицами считаются постоянными. Всем, что связано со структурой тел, в идеальном газе можно пренебречь и ограничиться двумя сущностями.

Для равновесного идеального газа мера хаоса максимальна по координатам и импульсам и минимальна по типам степеней свободы, так как все частицы обладают только поступательными степенями свободы. Соответственно мера порядка имеет минимальное значение по координатам и импульсам и максимальное значение по типам степеней свободы. Таким образом, для описания идеального газа имеет место диалектика для мер хаоса и порядка, если мы учитываем три сущности частиц:

ИДЕАЛЬНЫЙ ГАЗ:

I*(p,q) - max, I*(l) - min,

G**(p,q) - min , G*(l) - max.

В модели идеального газа К - число микросостояний - задается как постоянная величина, определяемая в двух независимых классах переменных (p) и (q) - импульсов и координат: К=К(p,q)=К(p)К(q). Такое определение числа микросостояний идеального газа справедливо, так как структура (l) и геометрия динамических элементов, пространство и взаимодействия заданы достоверным, строго упорядоченным образом, G*(l) - max. Однако переносить двухсущностную асимметрию эволюции идеального газа к максимальному хаосу, пренебрегая диалектикой или симметрией мер хаоса и порядка, на другие системы вряд ли целесообразно. Хотя именно так описывают эволюцию современные философы, физики и специалисты по синергетике.

Профессор физического факультета МГУ Л.А. Блюменфельд предложил мне в 1978 году исследовать новую связь энтропии с вероятностью для описания макромолекулы, (как более сложно организованной формы материи, чем газ), основы всех известных живых организмов [7].

Макромолекула в термостате может изменять структуру и геометрию (и свою и своих динамических элементов), обладает памятью о предыдущих состояниях, поэтому исходные (двухсущностные) положения статической механики и термодинамики не применимы для нее, как показал И.М.Лифшиц в 1968 [8].

Для описания стационарного состояния макромолекулы я ввел третий класс переменным l – набор типов степеней свободы, характеризующий структуру динамических элементов [9]. Таким образом, кроме движения центра тяжести тел по координатам и импульсам, учтена распределенная структура динамических частиц, которая может изменять взаимодействия и конструкцию макромолекулы. Эти изменения приводят к тому, что плотность вещества в объеме клубка макромолекулы в термостате не является уже достоверной величиной, и по этому признаку макромолекула не является уже замкнутой термодинамической системой. Макромолекула в термостате может не стремиться к термодинамическому равновесию, но обладать самодвижением и осциллировать около равновесия мер хаоса и порядка в трех классах переменных.

Три класса переменных привели к введению трех энтропий, как трех внутренних движущих «сил» системы с распределенными параметрами, и к учету впервые взаимодействий, описываемых этими энтропиями с помощью нового выражения свободной энергии образования системы, как общей движущей «силы» системы к равновесию мер хаоса и порядка.

Свободная энергия образования сложной системы (на примере макромолекулы) с распределенной структурой динамических частиц описывается с помощью трех энтропий в трех классах переменных:

F_min = E- kT {S(p)+S(q)+S(l)}_max, (2)


где F_min – свободная энергия образования системы с переменной внутренней организацией, E – полная энергия такой системы, kT – температура в единицах энергии, S(p) - энтропия импульсного пространства микросостояний, S(q) - энтропия координатного пространства микросостояний, S(l) - энтропия структурного пространства микросостояний, характеризующая структурное многообразие динамических элементов [9,10].

Свободная энергия образования макромолекулы осциллирует (даже при постоянстве внешних условий) около положения своего равновесия за счет изменения структуры динамических элементов, которую можно характеризовать структурной энтропией. Внешние факторы могут только подавлять или усиливать внутренние осцилляции в макромолекуле, и только взаимодействие внешних и внутренних осцилляций может приводить к развитию организации макромолекулы [9].

Самодвижение и осцилляция объектов природы около равновесия хаоса и порядка не учитываются в современной физике, где пренебрегается процессом концентрации энергии в силу принятых исходных упрощений. Поэтому известная физическая модель равновесия задается минимумом свободной энергии образования без учета изменения структуры динамических элементов в круговороте энергии по формуле:

F_min = U- kT S(p,q)_max , (3)

где U – внутренняя энергия системы, kT –температура, выраженная в единицах энергии, и S(p,q) – энтропия или мера хаоса, определенная в двух независимых классах переменных: координат q и импульсов p.

Соответственно, на основе формулы (3) замкнутые системы эволюционируют только к максимальному хаосу и деградации, согласно второму закону термодинамики, а осцилляции и изменения состояния возможны только за счет изменения внутренней энергии системы U, если она является открытой системой и взаимодействует с окружающей средой.

Итак, из сравнения формул (2) и (3) можно видеть, что сначала надо определить внутренние три «силы» - энтропии объектов природы, а потом уже исследовать влияние на них внешних воздействий.

Важно, что «трехсущностное» выражение свободной энергии (2) содержит эволюцию отношения последующих структур к золотой пропорции, которую впервые описал Л. Пачоли в книге «Божественная пропорция», Венеция, 1508(9), с иллюстрациями Леонардо да Винчи вместо формул [11]. Этот факт эволюции последующих структур к гармонии подтверждается экспериментально большим числом современных исследований [12]. Кроме того, Л. Пачоли обратил внимание на определяющую роль небосвода, устроенного как додекаэдр по золотой пропорции, без которого невозможно понимание эволюции живой природы, устроенной также по золотой пропорции [11].

Кроме того, важно, что это описание эволюции к гармонии с учетом изменении структуры динамических элементов построил Л. Пачоли во внутренней системе отсчета и на рекуррентной последовательности чисел, то есть на других исходных аксиомах математики, чем те, которые используются в физике, описывающей эволюцию к хаосу. Поэтому рассмотрим ниже закономерности математического описания эволюции систем к золотой пропорции.


ФРАКТАЛ «ЗОТОЛОГО СЕЧЕНИЯ»

Под фракталом понимается объект, имеющий общий алгоритм построения и разветвленную неповторяющуюся структуру, где любая часть фрактала подобна в своей организации всему объекту.

Основы описания эволюции к гармонии заложил Лука Пачоли в книге [11], иллюстрации к которой сделал Леонардо да Винчи вместо формул. Фактически Л. Пачоли математически описал эволюцию систем к гармонии на принципе триединства природы во внутренней системе отсчета. А Леонардо да Винчи, говоря современным научным языком, указал на фрактальную сущность эволюции природы к гармонии.

Само число А в арифметике уже тройственно по своей практической сути. Согласно опыту число А имеет не менее трех разных смыслов. Число А может характеризовать количество элементов в системе, порядковый номер события в системе и отношение между соизмеряемыми величинами в системе. Для характеристики этих смыслов числа есть универсальная числовая закономерность. Каждое число можно определить как сумму двух других чисел на основе уравнения рекурсии:

А_n+2= A_n+1+A_n. (4)

Такая числовая последовательность обладает универсальным свойством (при условии, когда A₁ ≥0 и A₂>0,): отношение между последующими числами 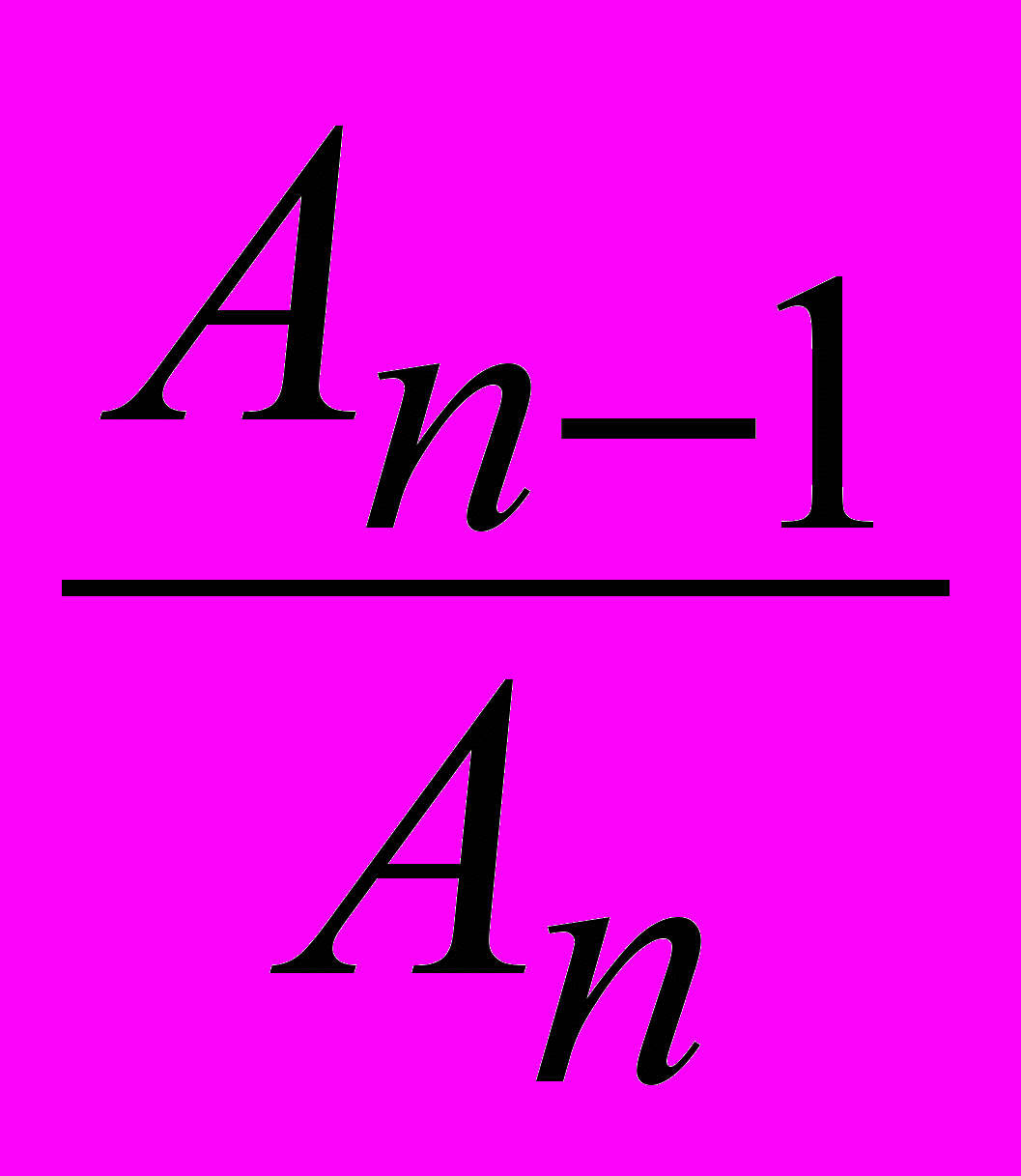стремится к золотому сечению ф при n→∞, где n=1,2,3,….∞:

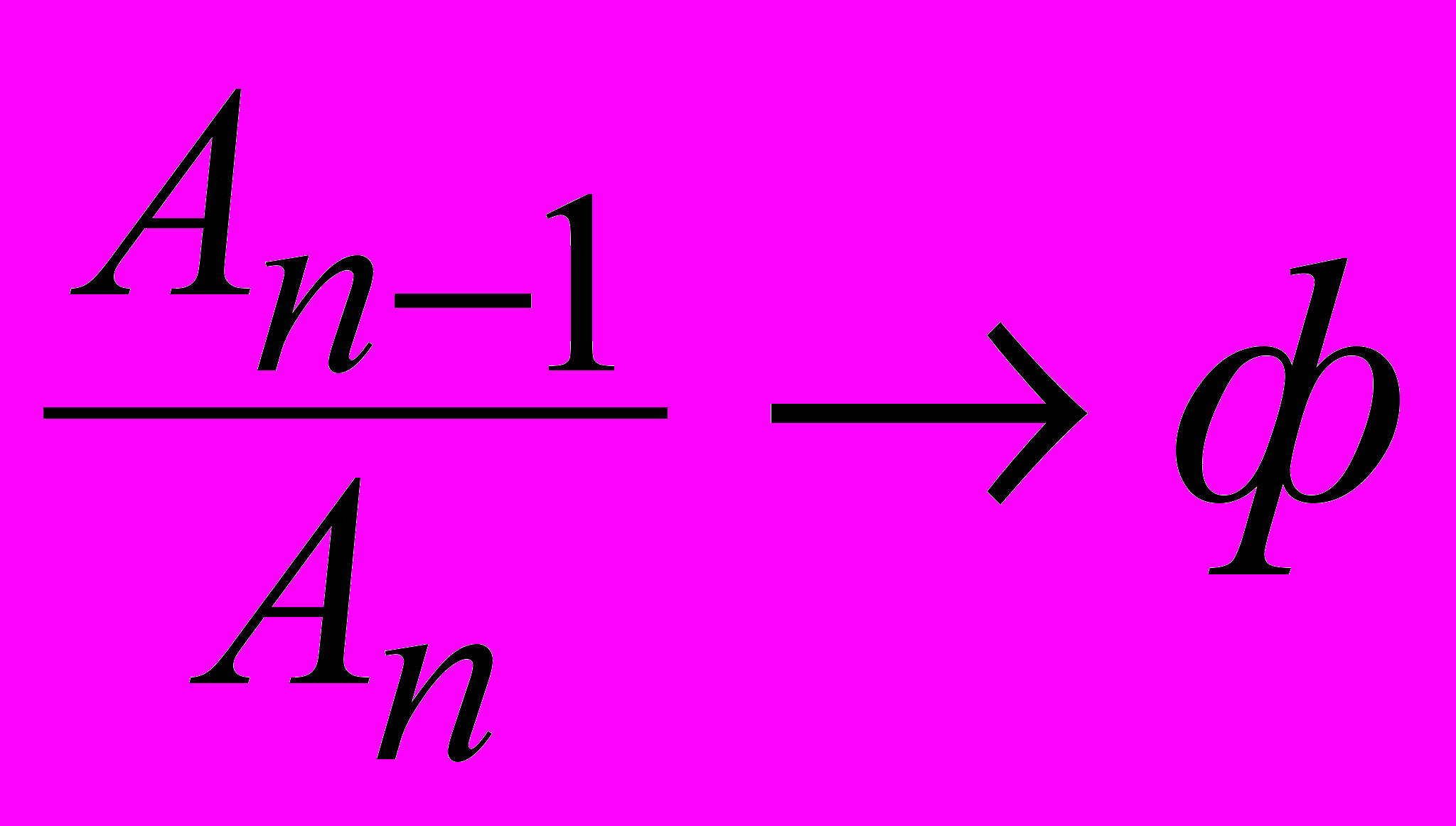. (5)

В биологии примером такой последовательности служит ряд Фибоначчи F_n /1202год/:

0, 1, 1, 2, 3, 5,8,13,21,34,55,89,144,… (6)

Последовательная рекурсия чисел по формуле (4) описывает естественную эволюцию явлений природы к золотому сечению (или к гармонии). Если под n понимать какое-то движение во времени, то уравнение рекурсии (4) описывает временную эволюцию (отношение последующих чисел) к гармонии.

В общем виде, золотое сечение ф разделяет интервал [0,1] на части: [0,ф] и [ф,1], так что три отрезка связаны между собой одним отношением ф, к которому эволюционирует система. Выделение на интервале от нуля до единицы [0,1] особой иррациональной точки ф и бесконечная осцилляция и стремление к ней эволюции отношения последующих чисел является важнейшим элементом «трехсущностной» математики.

Каждое последующее отношение чисел в ряде Фибоначчи больше или меньше числа ф и никогда не повторяется. Математика, имеющая в своем основании три выделенных числа 0, ф , 1, и бесконечную циклическую закономерность приближения к числу ф, позволяет описывать закономерности (фрактальные) эволюции природы, которые математике, основанной на натуральном ряде чисел и геометрии, не доступны. В видимом мире и в геометрии фрактальные закономерности эволюции - скрытые.

Ряд Фибоначчи и золотая пропорция определены также в традиционной бинарной математике, но с второстепенным смысловым значением, как одно из правил комбинаторики и как одно из отношений отрезков и фигур в геометрии. Чисто геометрическое толкование золотой пропорции широко использовалось архитекторами во все времена и у многих народов [12].

О недооценке (или непонимании) аксиом, приводящих к «Божественной пропорции», можно судить по тому, что «физике сегодняшнего дня неизвестно, что такое энергия»[13]. Такая наука не может отличить живое тело от неживого [7]. Соответственно не разрешены парадокс «возникновения порядка из хаоса» и противоречие в понимании эволюции: мир стремится к хаосу или к гармонии?

Подчеркнем еще раз. В современных динамических теориях, пренебрегающих триединством числа, триединством физических тел и целостностью природы, законы гармонии отсутствуют [12], в них нет места развитию природы, человека и общества без божественного промысла. Факты же проявления золотого сечения воспринимаются как одно из равноправных свойств комбинаторики и свойств геометрических фигур. А математика Луки Пачоли как раз основана на триединстве числа и тел в целостной природе и описывает скрытые (фрактальные) закономерности эволюции человека, общества и природы к тройственной гармонии.

Однако в отечественной науке преподаются только те бинарные разделы математики и физики, которые привели к парадоксу «тепловой смерти Вселенной» и исключают понимание цели и смысла эволюции человека и общества.

Взаимодействия, основанные на золотой пропорции, допускают бесконечные внутренние изменения в системе, которые не нарушают ее целостности, а только изменяют ее внутреннюю организацию за счет изменении структуры динамических элементов.

Например, при умножении самой на себя золотая пропорция описывается биномом Ньютона:

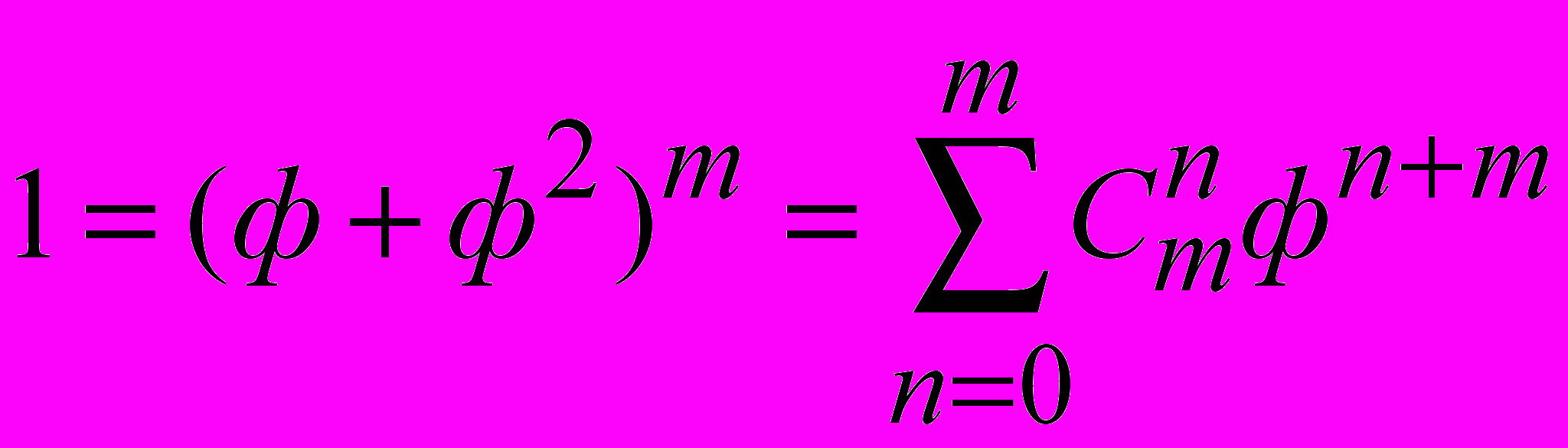, (7)

где 0£n£m£¥; С – число сочетаний из m элементов по n.

При усреднении «золотого сечения»



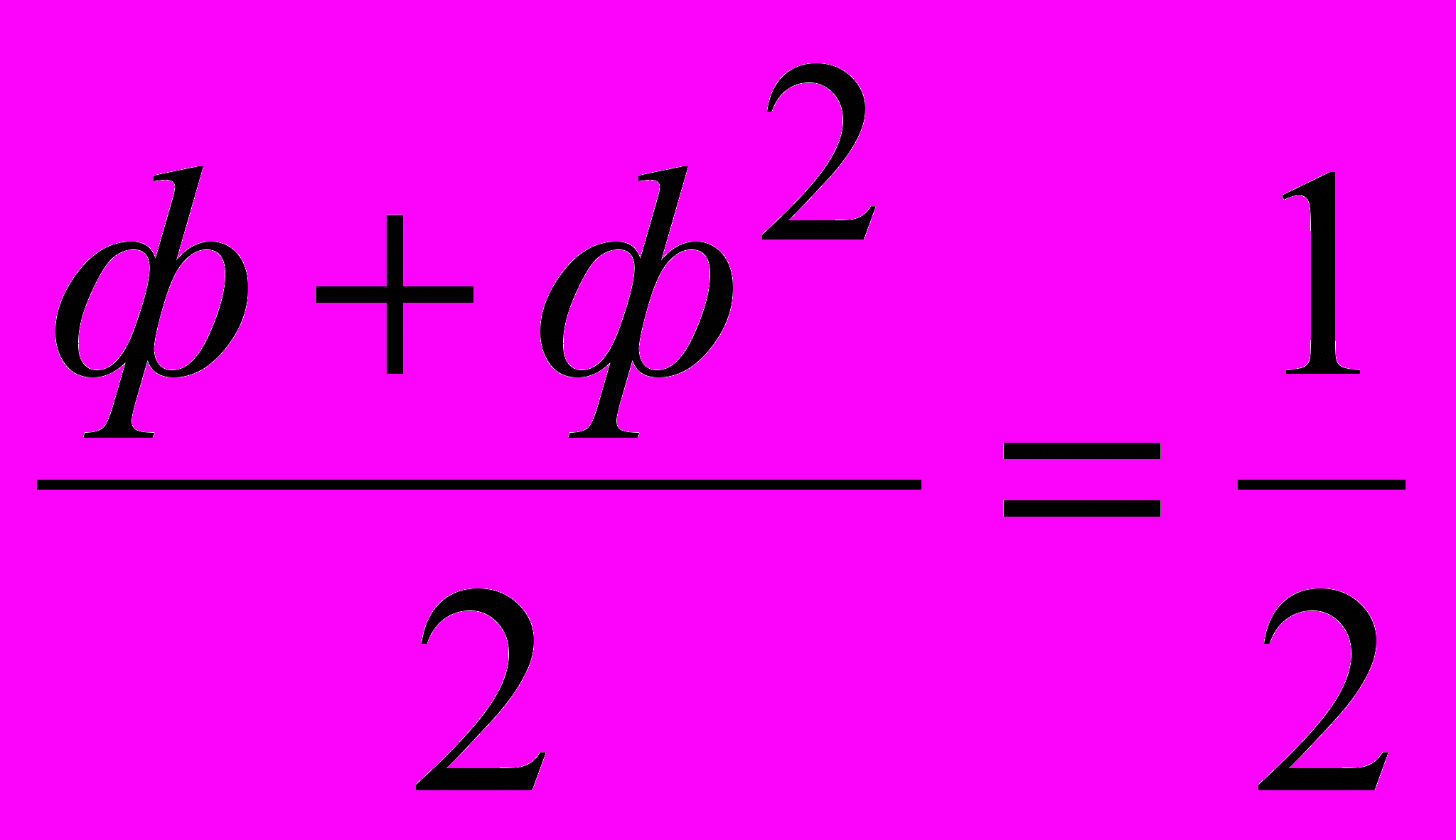
формула (7) вырождается в известное биномиальное распределение:

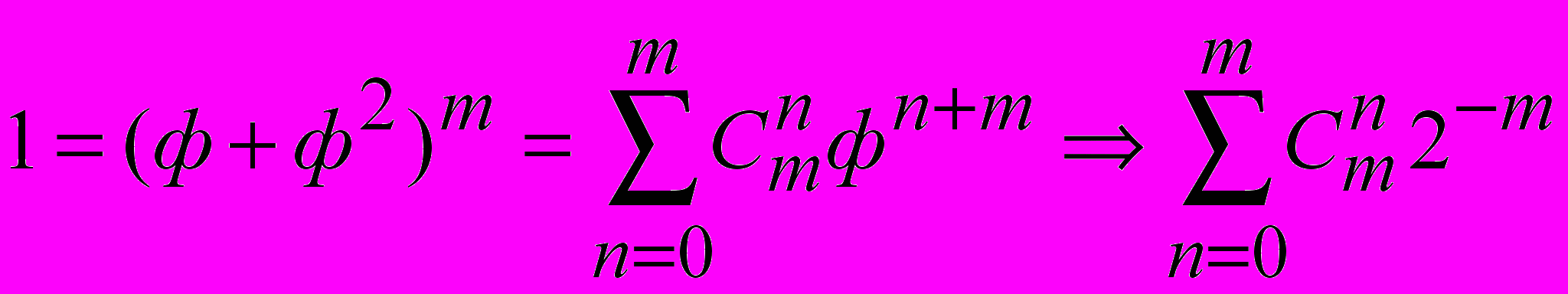, (8)

происходит вырождение триединства (1) в дихотомию.

Другая последовательность операций умножения на «золотую пропорцию» приводит к другим свойствам разбиения целого на части. При умножении получаем:

.

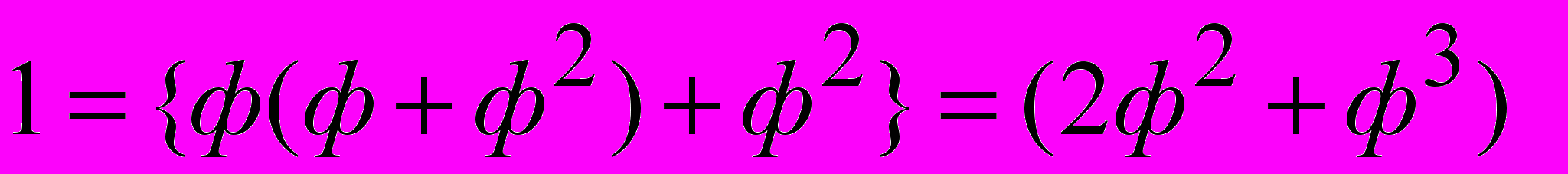На следующем шаге получаем:

.

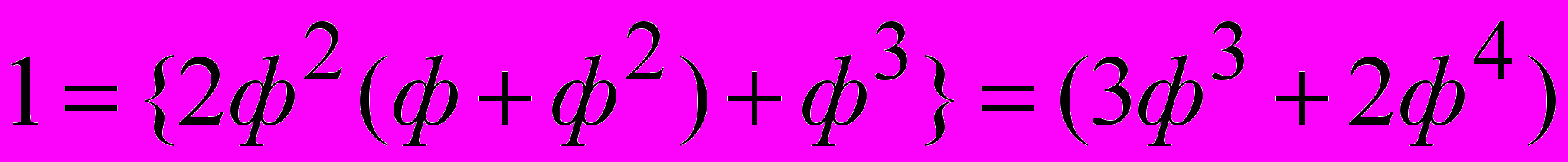В итоге - оптимальное разбиение единицы на две части:

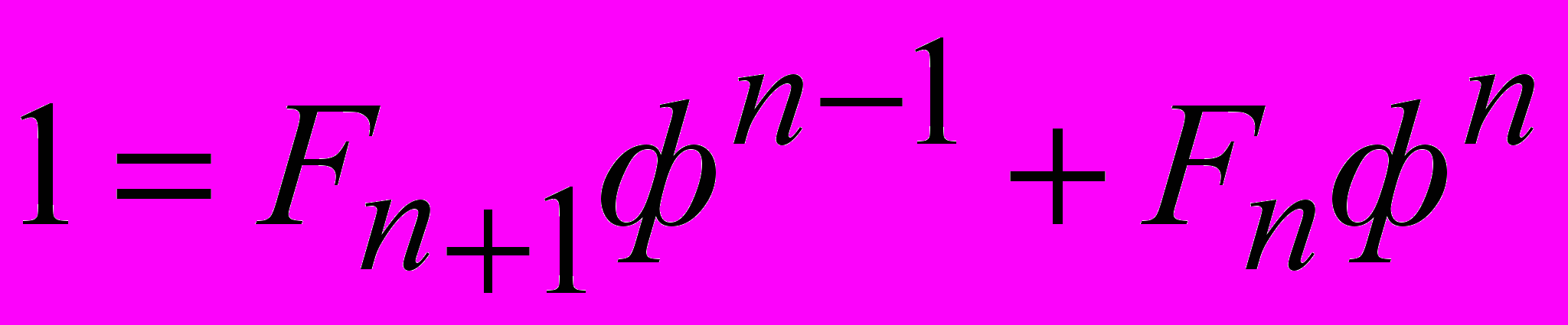, (9)

где F_n - ряд Фибоначчи (6) не постулируется как исходное положение математического описания, а выводится из общего случая (4) через скрытые действия с «золотой пропорцией».

Ряд Люка равен сумме двух рядов Фибоначчи, сдвинутых на два шага: L_n-1= F_n+F_(n-2) ,

и он представляет собой другой типичный ряд чисел:

2,1,3,4,7,11, 18, 29,47, 76, 123, 199,….

Числа ряда Люка описывают другое часто встречаемое разбиение целого на части:

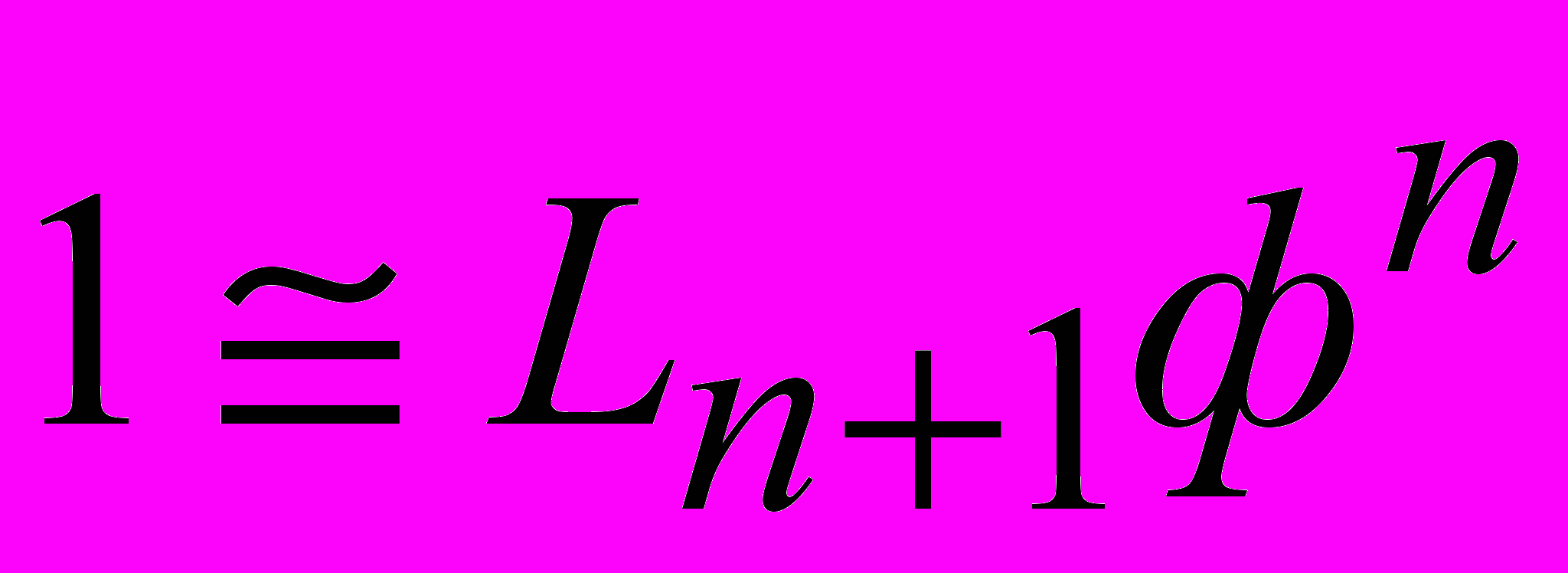. (10)

Традиционно золотое сечение определяют как недостижимую цель из отношения последующих членов ряда Фибоначчи:

,

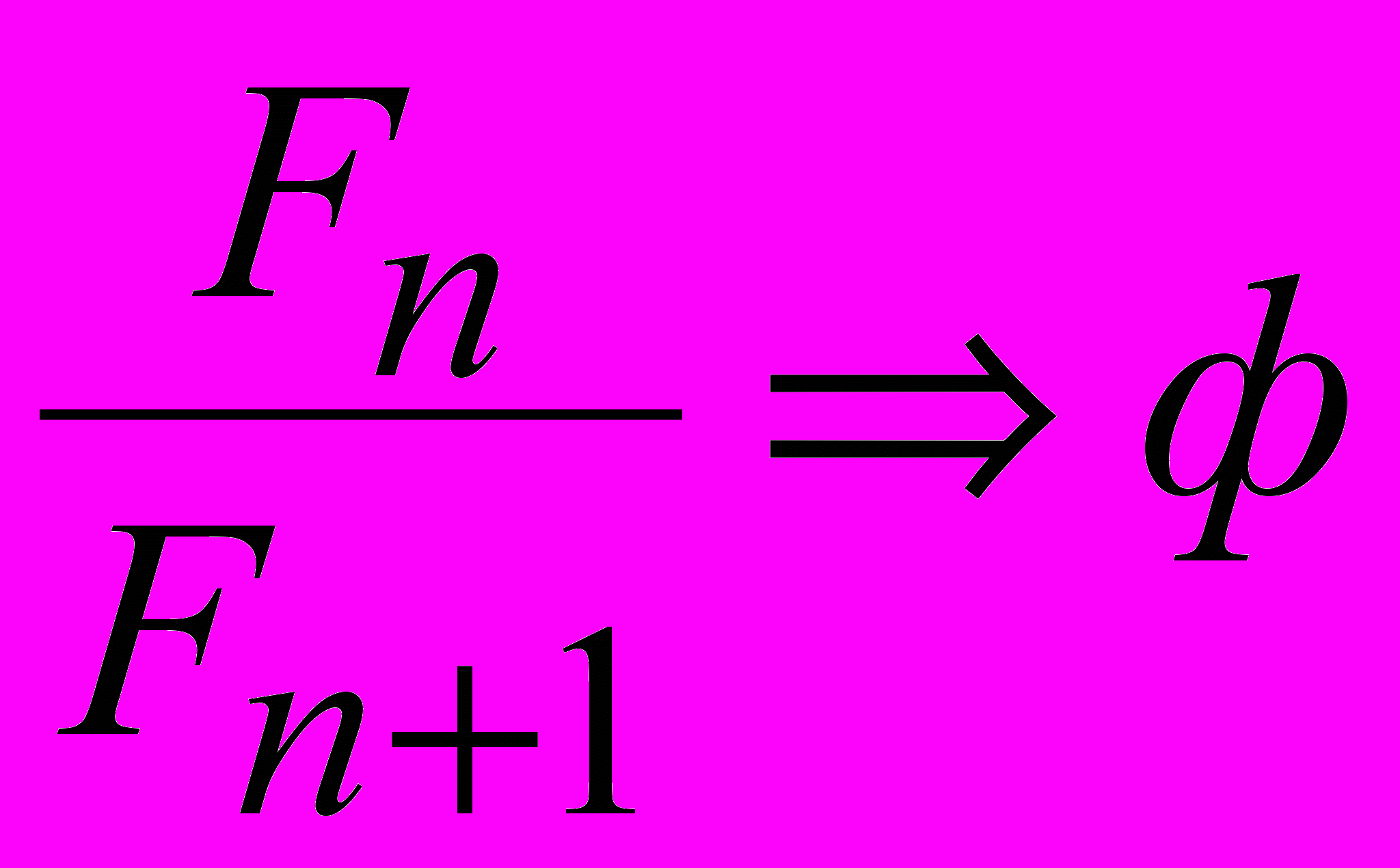или членов ряда Люка:

.

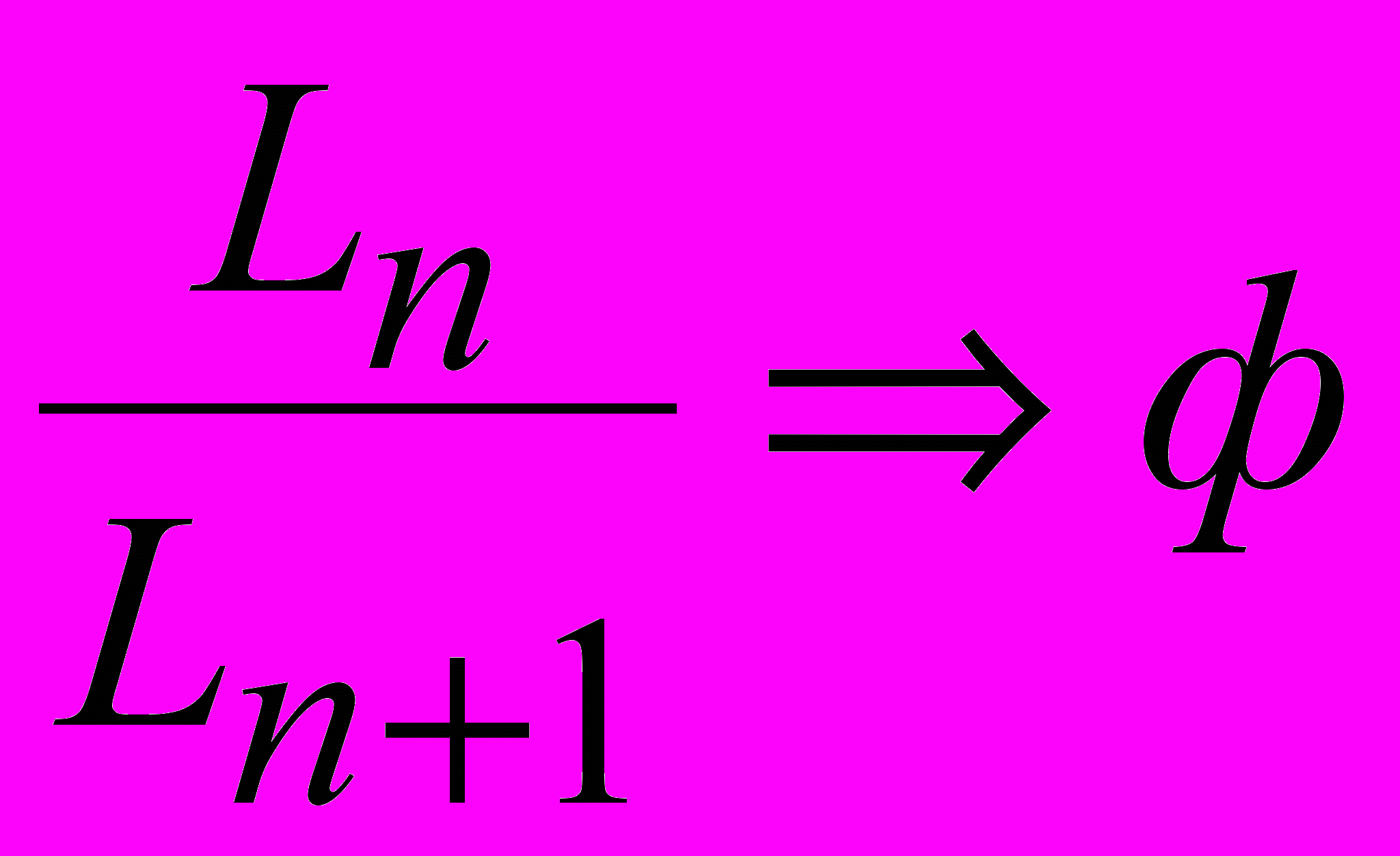Второй способ получения золотого сечения связан с квадратами чисел этих рядов. Последующие числа ряда Фибоначчи порождают следующие числовые квадратичные закономерности:



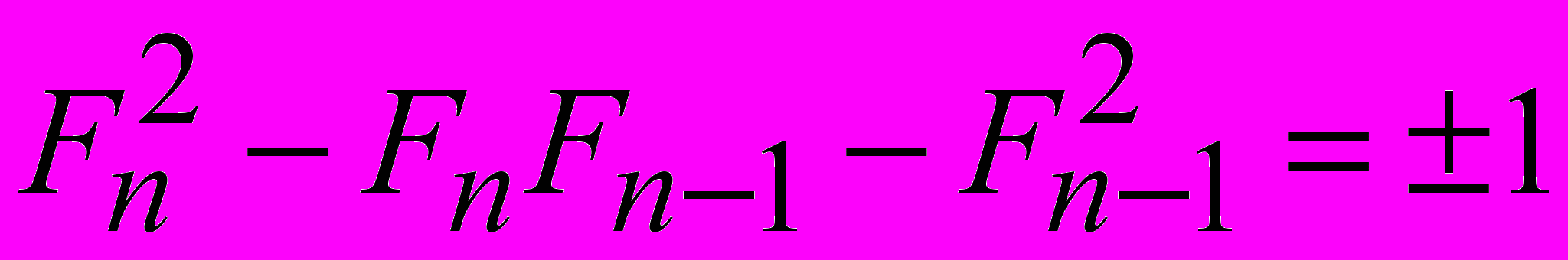
и .

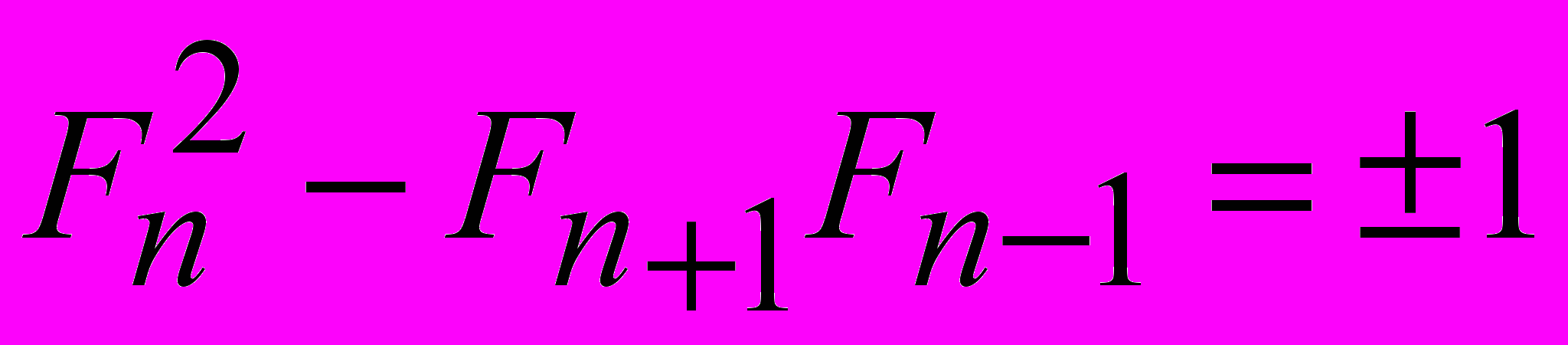Последующие числа ряда Люка порождают следующие числовые квадратичные закономерности:

,

.

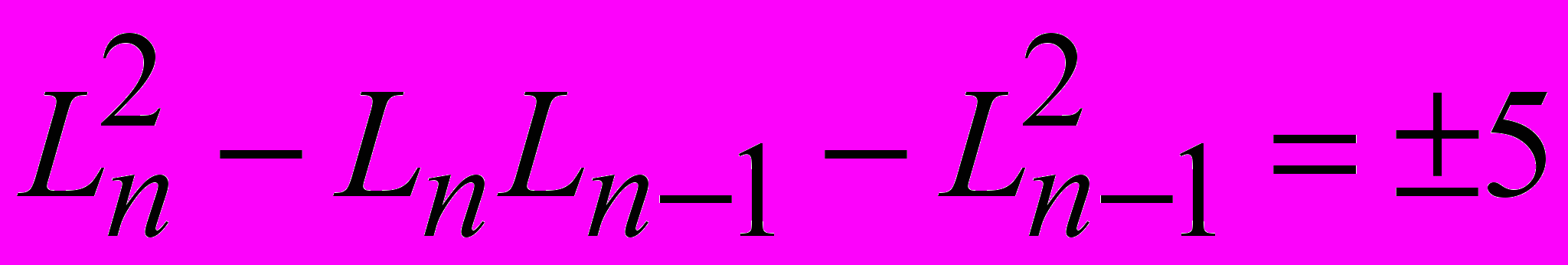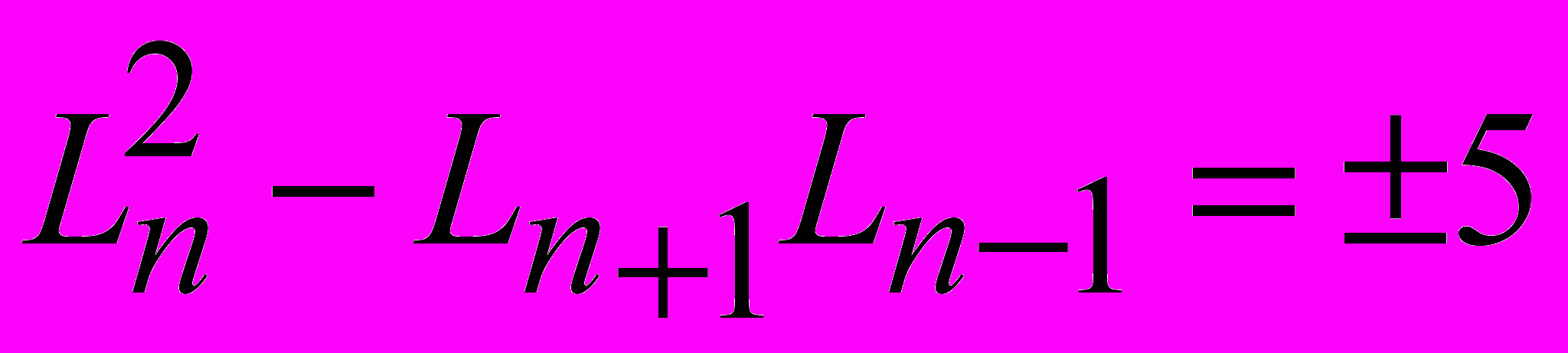Из определения «золотого сечения»:



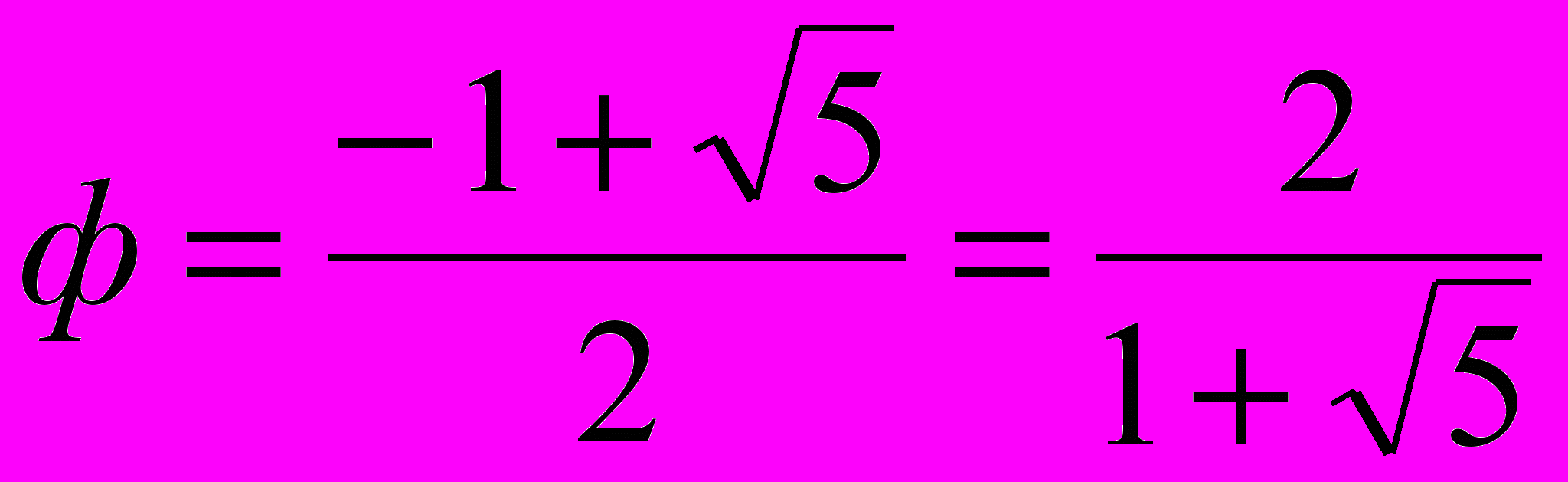
следует, что взаимодействия, описываемые квадратами последующих чисел рядов Фибоначчи и Люка, могут порождать строгое значение золотого сечения.

Третий способ следует из определения «золотого сечения», как четырехбуквенного кода по И.Шевелеву:

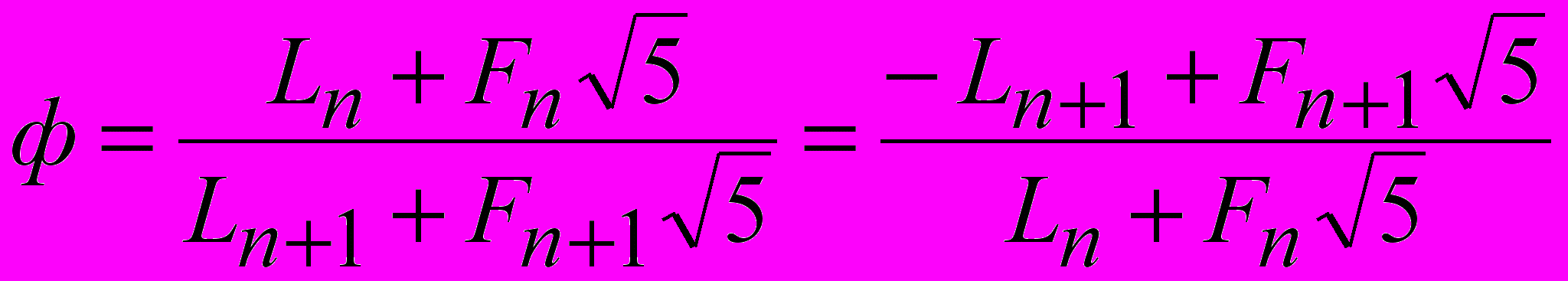. (11)

Число 3 может быть представлено бесконечным числом способов через ф и числа рядов Фибоначчи и Люка:

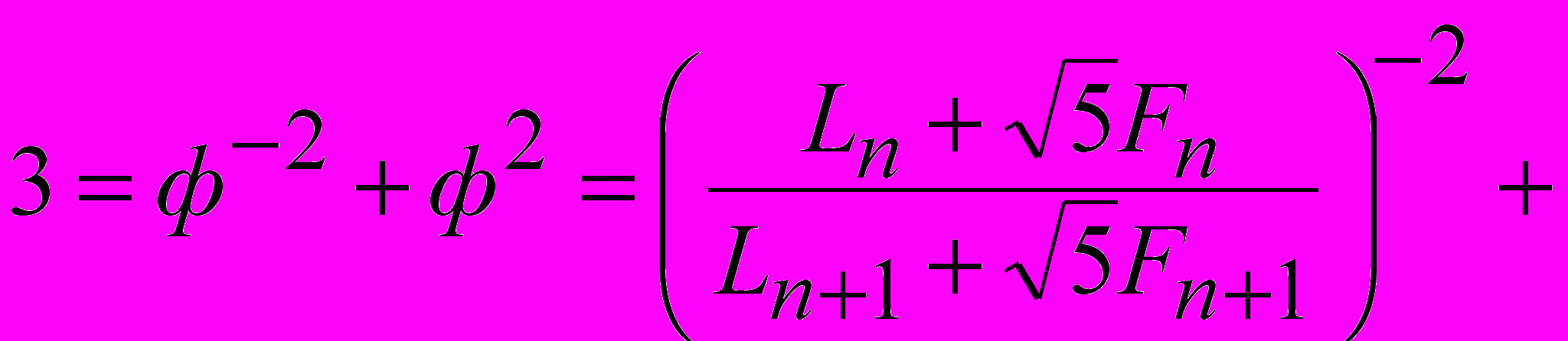
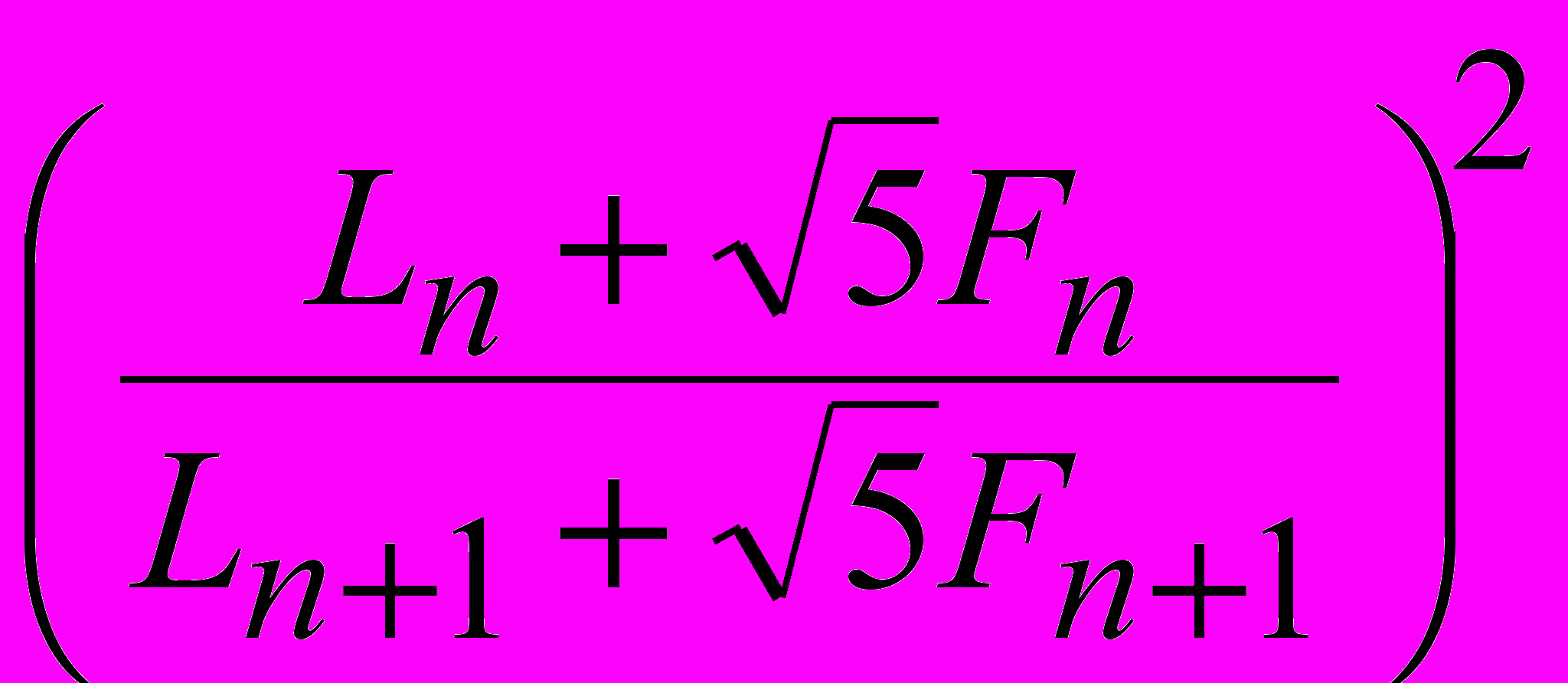. (12)


Число 2 можно представить как фрактал:

₂₌.

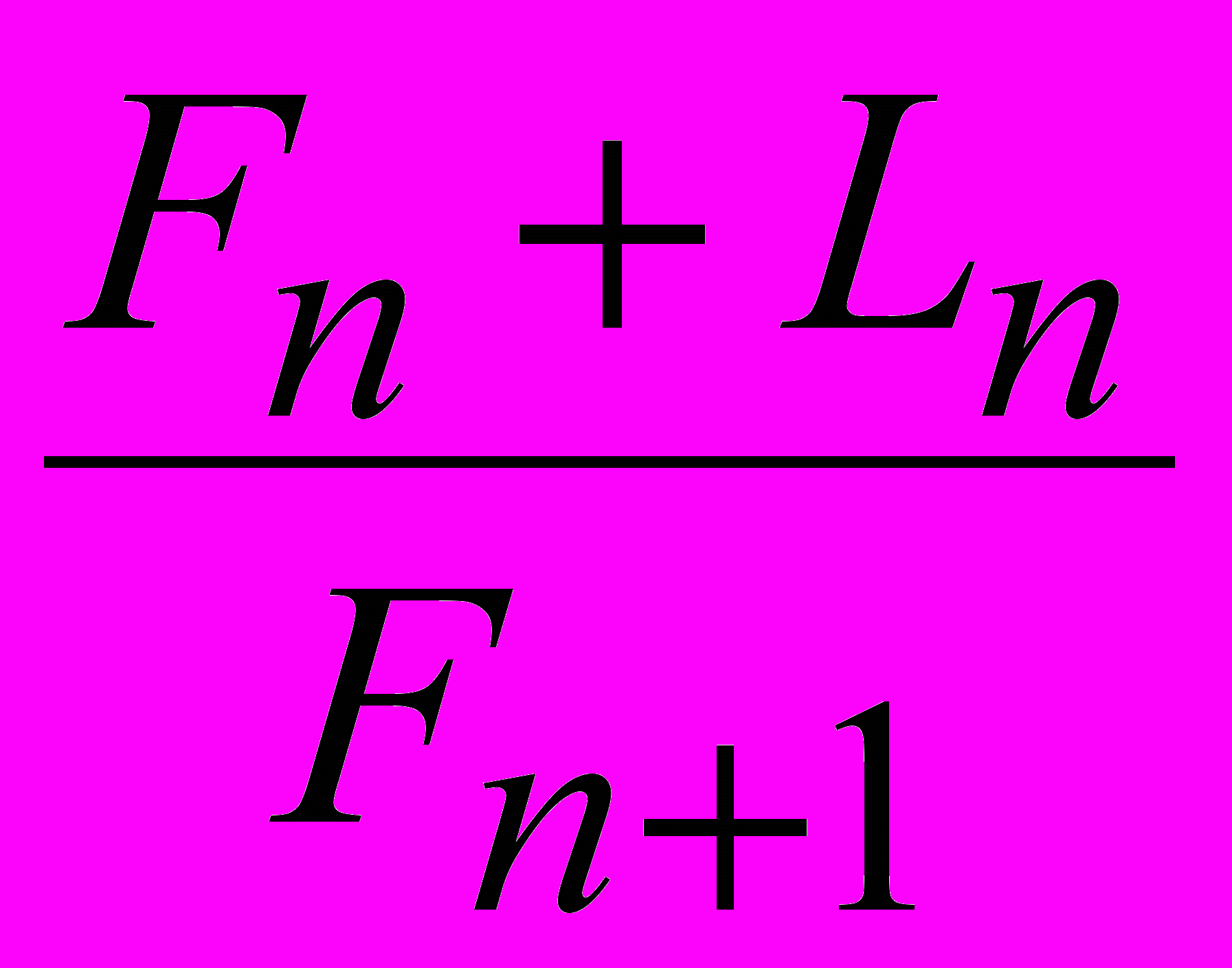Ряды Фибоначчи и Люка порождают золотое сечение тремя разными способами, и при n→∞ возникает фрактал, который, с одной стороны, характеризует одну и ту же эволюцию к золотому сечению, а с другой стороны, - уникальные числовые отношения и новые внутри фрактальные взаимодействия. Это свойство подобия частей и целого позволяет говорить об алгебраическом фрактале золотого сечения, где под фракталом понимается объект, имеющий общий алгоритм построения и разветвленную неповторяющуюся структуру, где любая часть фрактала подобна в своей организации всему объекту и стремится к золотому сечению. Фрактал золотого сечения, на который указывают криптограммы Леонардо да Винчи, оказался потерянным в современном математическом описании систем, основанном на механистической картине мира. Из свойств этого фрактала следуют равновесное распределение, множество числовых отношений, удовлетворяющих теореме Пифагора, и числа натурального ряда:

А=А{ф,[F_n , L_n(ф, … I(p,q,l) = G(p,q,l)]} , (13)


где n = 0,1,2,3,….∞.

Л.А. Шелепин помог мне установить связь канонического распределения энергии в статистической физике с золотой пропорцией в 1996 году и рассмотреть определяющую роль золотой пропорции в социальных и биологических системах [15].

Фрактал золотой пропорции позволяет пересмотреть наши представления о пространстве, времени, веществе и эволюции с тройственной сущности природы.

Математическое описание эволюции к гармонии использовал И.Кеплер в книге «Гармония мира», /1619 г/. В 1695 году Г.Лейбниц провозгласил: «Миром правит Предустановленная гармония». На идее гармонии Ш.Фурье предложил основывать социальное управление в книге «Всемирная гармония» /1803г/. Ф.М.Достоевский, прочитавший труды Ш.Фурье, завещал, что предназначение России - восстановить гармонию для себя и для других народов /1857г/.

Ниже рассмотрим аргументацию для построения новой модели равновесия, которая удовлетворяет формуле (1) и фракталу золотой пропорции. Начнем с анализа взаимосвязи выбранной модели равновесия системы и цели ее эволюции.


ФИЗИЧЕСКИЙ ОПЫТ И ЭВОЛЮЦИЯ

Внешние силы всегда ослабевают в системе, как это установлено физическим опытом и его частным описанием во втором законе термодинамики [2]. Поэтому можно утверждать, что объекты природы эволюционируют (после возмущения) к исходным условиям своего равновесия для сохранения своей целостности. Из этого следует, что физическая теория описывает эволюцию неравновесных процессов к исходным выбранным условиям равновесия системы. Поясним этот факт следующими примерами.

Если в теории за исходную модель равновесия природы принять баланс взаимодействия бытия и небытия, то такая теория будет описывать эволюцию систем (после возмущения) к равновесию бытия и небытия [9].

С позиции такой модели равновесия: все объекты природы стремятся (после возмущения) к равновесию бытия и небытия, имеют единую цель эволюции: сохранить целостность природы, но стремятся к этой цели своими разными способами.

Если взята частная дуальная модель равновесия сил (действия и противодействия), как в механике И.Ньютона, где тело заменено его центром тяжести, то механика описывает эволюцию систем после внешнего возмущения к балансу приложенных сил. На основе механики в термодинамике принята модель теплового равновесия системы, и термодинамика описывает эволюцию своих систем к «тепловой смерти Вселенной». На основе идеализаций механики и термодинамики в статистической механике принята модель равновесия идеального газа, и такая теория описывает эволюцию замкнутых систем к максимальному хаосу.

Опыт существования биологических и социальных систем противоречит механистическому и термодинамическому пониманию эволюции природы, а, следовательно, для их описания известные физические дуальные модели равновесия являются неприемлемыми и слишком упрощенными. Жизнь существует в определенных формах организации круговорота энергии и борется за свое будущее, изменяя, в первую очередь, структуру своих динамических элементов, стремясь к тройственному равновесию (гармонии) внутри себя, со своей окружающей средой и своим предназначением.

Из этого следует, что дуальные модели равновесия механики, термодинамики и статистической механики нельзя применять для исследования эволюции физических, биологических и социальных систем. Следовательно, необходимо рассматривать феномен эволюции в тройственной модели равновесия на основе баланса взаимодействия бытия и небытия с учетом изменения трех «сил» природы.


НОВЫЙ ПРИНЦИП ОПИСАНИЯ РАВНОВЕСИЯ ПРИРОДЫ

Мои исследования показали, что нельзя к двум известным сущностям природы координатам и импульсам просто добавить третью сущность природы – структуру, о которой давно известно в науке. При добавлении третьей переменной в описание объектов природы понятие температуры лишено смысла, производная от функции может не существовать, внешнею систему отсчета параметров определить не возможно. И.Ньютон тщательно оговорил условия, при которых можно пренебрегать триединством сил в природе («врожденной силой инерции») и описывать дихотомической моделью равновесие центра тяжести тел. Поэтому предлагается для описания трехсущностной природы изменить всю систему исходных математических аксиом и физических постулатов, начиная с построения модели равновесия природы. Вместо дихотомии вводим трихотомию, вместо внешней системы отсчета вводим внутреннюю систему отсчета, вместо частиц с заранее заданными свойствами вводим пространство событий, принадлежащих взаимодействию бытия или небытия. На природу в целом ничто не действует, поэтому ее описание надо начитать с модели ее равновесия, и исследовать эволюцию её частей, поддерживающих равновесие взаимодействием бытия и небытия в природе.

Философия эллинов и индусских ведов обращала внимание на то, что видимый мир есть иллюзия и чувственным ощущениям доверять нельзя. На языке физики это означает, что видимые и измеряемые параметры и их величины есть средние по ансамблю микросостояний. Но известные ансамбли микросостояний построены только для описания движения одинаковых и тождественных частиц в рамках эргодической гипотезы, когда концентрацией энергии и эволюцией системы можно пренебречь. Поэтому ансамбль микросостояний необходимо строить по-новому[9].

Новый способ математического описания природы построен на разбиении целого (единицы) на три различные неравные части с помощью мер хаоса и порядка. Целое – единица - 1 - разбивается на три множества и для описания этого разбиения используем формулу полного набора вероятностей, где три множества объединены операцией сложения в некоторую целостность:

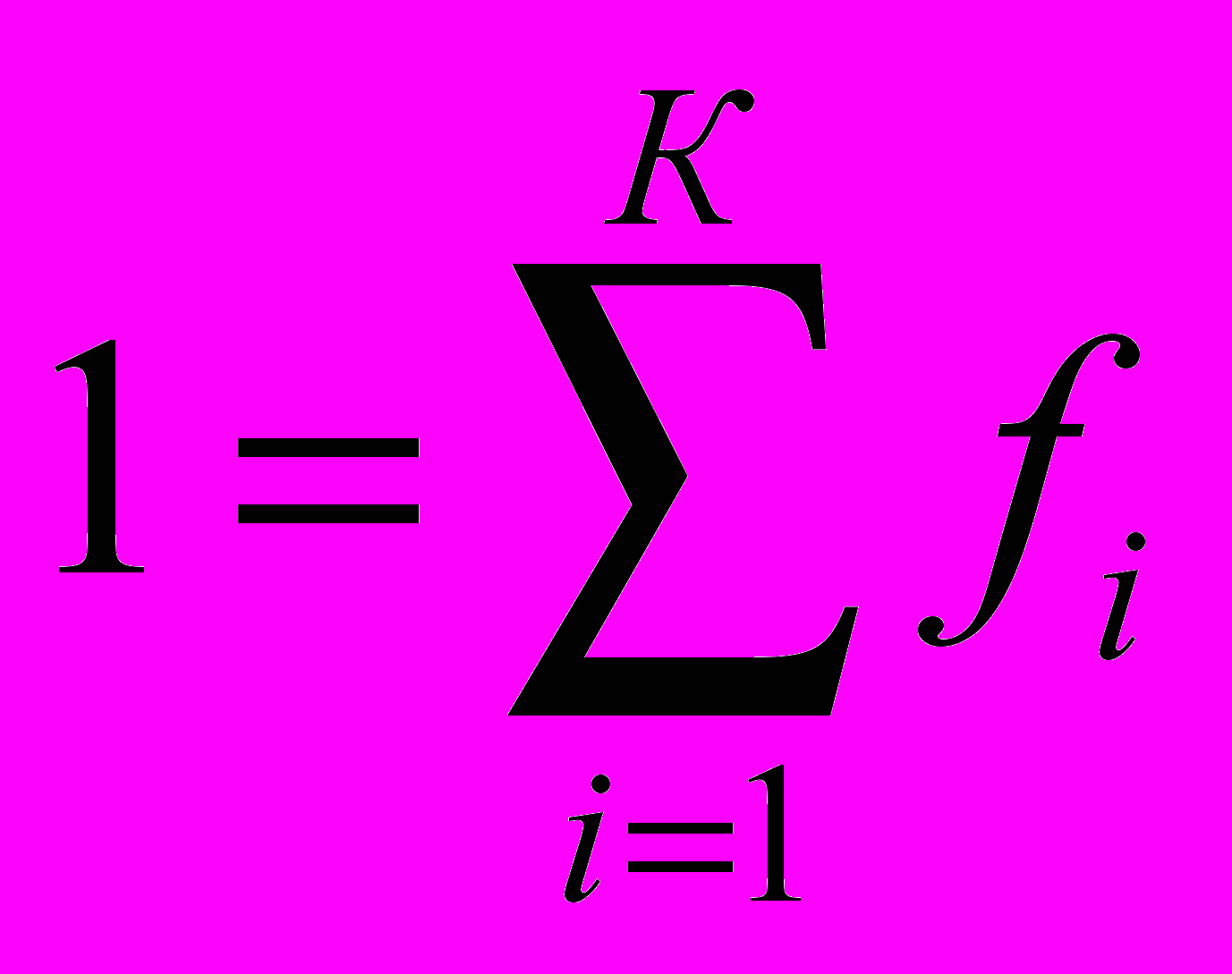(14)

где К - число рассматриваемых состояний системы; f_i - вероятность каждого состояния; последовательность этих состояний i.

Далее учтем, что эти три множества (К, f_i i ) могут изменяться, не нарушая целостности системы. Тогда, учитывая, что К мультипликативная величина и последовательность i не имеет значения, имеем разбиение целого (единицы) на сумму двух функций: мер хаоса и порядка:

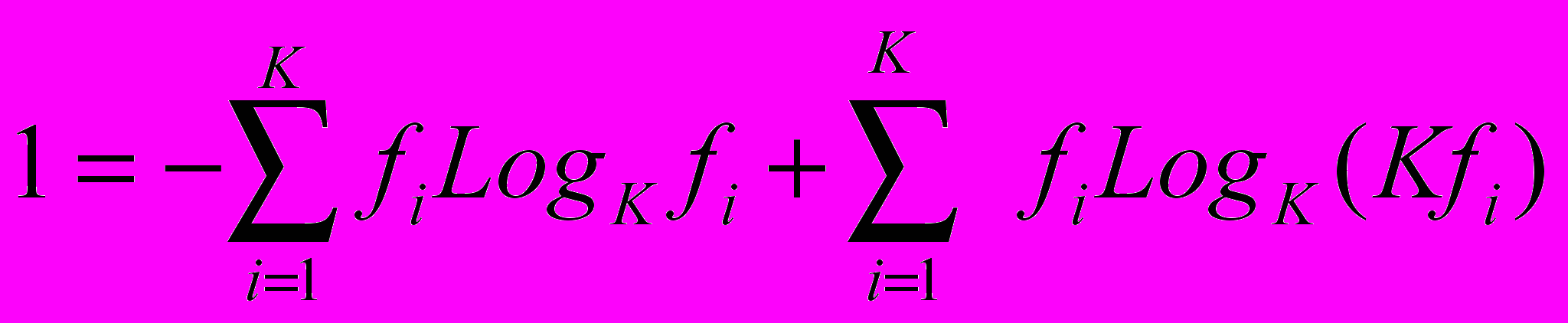= I+G, (15)

где 1 – единица - отражает целостность системы, I – мера хаоса - описывает реализуемые состояния системы или бытие, G – мера порядка - описывает запрещенные для реализации состояния системы или небытие на множестве рассматриваемых состояний К.

Соотношение между мерами хаоса и порядка в общем случае таково, что мера хаоса меньше или равна мере порядка в общем случае:

I ≤ G, (16)

так как всегда можно выбрать такое большое число рассматриваемых состояний К, в котором большая часть событий запрещена для реализации. Число запрещенных состояний в природе всегда больше числа реализуемых состояний. Небытие всегда больше бытия. /«Человечество - это большая часть мертвых и малая часть живущих» ради продолжения своего рода. Человечество - это активное взаимодействие бытия и небытия. Социальное управление направляет это взаимодействие бытия и небытия в интересах своей безопасной организации и своего будущего. Однако если такое управление нарушает гармонизацию интересов народа и власти (гармонию целого и частей), социальный кризис становится неизбежным, и остается только вопрос о сроках и о цене его преодоления./

Постулатом нового описания природы служит равенство мер хаоса и порядка в трех классах переменных:

I (p, q, l) = G (p, q, l), (17)

Этот постулат отражает единство и целостность природы и баланс взаимодействия бытия и небытия.

Природу можно рассматривать как целостную (изолированную) систему со сбалансированным взаимодействием бытия и небытия, где бытие описывается мерой хаоса, а небытие - мерой порядка, или на основе баланса процессов рассеяния и концентрации энергии в круговороте природы. Закон сохранения энергии в круговороте природы выполняется, а организация круговорота энергии может перестраиваться из-за изменения структуры динамических элементов.

В этом случае число рассматриваемых микросостояний К является нелинейной мультипликативной изменяющейся функцией:

К=К(p)К(q)К(l)= К(p,q,l). (18)

Все возможные изменения мер хаоса и порядка, не нарушающие целостность системы, описываются симметрией мер хаоса и порядка:

∆I(p)+∆I(q)+∆I(l)=0. (19)

Насколько возрастает бытие (мера хаоса) по одним переменным, настолько же бытие (мера хаоса) убывает по другим переменным, затрагивая три класса переменных.

Выберем из всевозможных изменений мер хаоса (19) только необратимые изменения. Последние удовлетворяют уравнению рекурсии (4) и описывают эволюцию отношения мер хаоса (или порядка) к гармонии. Тогда новый способ описания природы сводится к описанию свойств фрактала золотой пропорции, которому подчиняется эволюция мер хаоса (и порядка). Из этого фрактала можно заново формировать наши представления о веществе, пространстве и эволюции. Соответственно этот фрактал изменяет цель описания природы. Наука на основе механики Ньютона отвечает на вопрос, как движутся тела с заданной структурой под действием внешней силы. А наука на основе идей Аристотеля и новой теории отвечает на вопрос, для чего происходит движение в природе? Новая теория отвечает, самодвижение в природе происходит для поддержания целостности «органона» - круговорота энергии в природе путем стремления выживающих систем к тройственной гармонии. При этом живое тело и косное по-разному стремятся к тройственной гармонии. Про живой организм обычно писали, что «живое питается отрицательной энтропией» на основе статистической механики Больцмана-Гиббса, а в нашем случае живое тело стремится активно к тройственному равновесию за счет преимущественного роста структурной энтропии, который компенсирует уменьшение обычной энтропии по координатам и импульсам.

Каждый шаг возникновения новой структуры в природе связан с предыдущими структурами и образует рекуррентный процесс развития с памятью [13]. Процесс рассеяния энергии за счет увеличения структурного многообразия динамических элементов описывает развитие систем и может исследоваться на основе фрактала золотого сечения.

Важно, что новое описание впервые установило критерий отбора для выживания эволюционирующих физических, биологических и социальных систем. Те системы, которые в результате эволюции обладают минимумом свободной энергии образования круговорота энергии по формуле (2) или при локальном рассмотрении находятся вблизи к тройственной гармонии по золотой пропорции, имеют преимущества для выживания в процессе эволюции перед другими системами.

РАЗВИТИЕ СОЦИАЛЬНЫХ СИСТЕМ

Для социального управления этих знаний об эволюции природы к тройственной гармонии еще недостаточно, так как эта гармония может быть получена за счет разрушения существующей организации круговорота природы, поэтому необходимо знать еще и условия развития систем при сохранении целостности природы.

Рассмотрим примеры развития потока солнечной энергии и личности на основе применения теории симметрии хаоса и порядка.

Динамическим элементом социальной системы является сам человек. Рассмотрим, как меняются характеристики личности в процессе развития общества. Личность в обществе можно характеризовать, по крайней мере, тремя различными качествами: 1) как потребителя, 2) как производителя и 3) как управленца своего поведения в обществе. Соответственно личность можно характеризовать тремя энтропиями в процессе развитии общества.

При совершенствовании общественных отношений происходит специализация труда – число различных способов трудовой деятельности (n) для каждого индивидуума в среднем уменьшается, каждый ограничивает свою свободу трудовых действий профессиональными интересами:

∆I(n)<0,

а возможности потреблять разнообразный ассортимент (m) товаров и услуг для каждого индивидуума увеличиваются в виде роста энтропии выбора товаров и услуг:

∆I(m)> 0.

Число же разнообразных запретов, характеризующихся культурой и нормами права, растет или энтропия взаимодействия личности с окружающей ее средой уменьшается:

∆I(r) <0.

Взаимосвязанные изменения трех энтропий, характеризующих поведение личности, позволяют их записать на основе теории симметрии хаоса и порядка в виде одного уравнения развития личности:

∆I(m) + ∆I(n) + ∆I(r) = 0. (20)

Насколько в приведенных условных единицах возрастает потребление товаров и услуг личностью, настолько же уменьшается ее трудовое многообразие деятельности и свобода ее поведения.

Это уравнение баланса и развития личности совпадает с уравнением, полученным ранее для описания процесса развития в физических и биологических системах в [4,9,10]. Рассмотренные в работе факторы развития личности (и других социальных систем) в обществе позволили предположить, что математические закономерности развития систем различной природы являются общими и для их описания достаточно знать приращение трех соответствующих энтропий.

На рисунке приведена схема развития потока солнечной энергии в атмосфере Земли. Изменения в потоке происходят для сохранения его целостности, а развитие его структуры подчиняется уравнению симметрии хаоса и порядка, применимому также для описания развития социальных систем и личности в современном обществе.




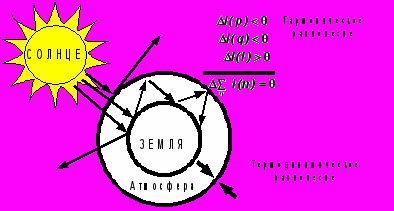
Рис. Схема развития потока солнечной энергии

Итак, развитие потока солнечной энергии в атмосфере Земли характеризуется стремлением к гармонизации отношений трех энтропий и внешнего термодинамического равновесия, и может служить ключом к анализу и прогнозу развития личности и процессов в обществе [15-19], к установлению целей эволюции природы, человека и общества.

ЗАКЛЮЧЕНИЕ

Научное мировоззрение опирается, в конечном счете, на достижения математики, как заметил И.Кант: «В каждой науке столько истины, сколько в ней математики». Однако если аксиомы математики и постулаты физики пренебрегают триединством природы и ее объектов, то такая математика нарушает целостность научной картины мира и искажает цель и смыслы эволюции природы, человека и общества.

Знание цели эволюции природы - поддерживать свою целостность, знание о том, что преимущество для выживания получают те объекты природы, которые оказываются ближе к тройственной гармонии, знание, что специфичность эволюции живого обусловлена процессом развития (ростом структурной энтропии) являются необходимыми интеллектуальными ресурсами для разумных действий человека и социального управления.

Мир единственен и целостен, а эволюция его трехсущностных частей разными способами к тройственной гармонии порождает наблюдаемое многообразие природы.

В природе работает критерий эволюционного отбора: преимущество для выживания имеют те системы, которые ближе к тройственной гармонии и тем самым лучше обеспечивают целостность природы.

Живое возникло, существует и эволюционирует для сохранения целостности организации круговорота энергии в природе. Живое сохраняет свойства круговорота энергии и себя, стремясь к своему равновесию за счет роста структурной энтропии, реализуя процесс развития, а не уходит от равновесия, пренебрегая структурной энтропией [4].

Автор выражает глубокую признательность за неоценимую помощь в работе и поддержку разрабатываемых мной идей В.К.Руденко и профессор д.м.н.н Л.Г.Охнянской, кафедре социального менеджмента и туризма РГСУ и своей жене Н.Т.Харитоновой за создание условий для выполнения научных исследований.

Литература

1. Андреев Э.П., Осипов Г.В. Методы измерения в социологии. Москва: Наука, 1977.
   
2. Томсон В. О проявляющейся в природе общей тенденции к рассеянию механической энергии. Сб. Второе начало термодинамики. М.-Л., ГТТИ. 1934. С.180.
   
3. Охнянская Л.Г., В.П.Мишин, Э.Л.Спектор. А.А.Ухтомский и развитие идей теории нелинейных колебаний в области физиологии. Сб. Учение А.А. Ухтомского о доминанте и современная нейрофизиология. Ленинград. Наука. 1990. С.60-84.
   
4. Харитонов А.С. На принципе триединства бытия. //Сб. Казначеевские чтения 2. Новосибирск. 2009. С. 157- 184.
   
5. Подолинский С.А. М., Ноосфера. 1991.
   
6. Умов Н.А. Физико-механическая модель живого. М., 1902 .
   
7. Блюменфельд Л.А. Решаемые и нерешаемые проблемы биологической физики. М., УРСС, 2002.
   
8. Лифшиц И.М. Некоторые вопросы статистической теории биополимеров // ЖЭТФ.1968. Т. 55. С. 2408.
   
9. Харитонов А.С. Структурные свойства макромолекулы в термостате. //Прикладная физика №1, 2008, С.13 – 166.
   
10. Харитонов А.С. Структурное описание сложных систем. //Прикладная физика №1, 2007, С.5 – 10.
    
11. P a c i o l i L u c a «De divina proportione», Venezia, 1509.
    
12. Сб. Метафизика. Век ХХI, под редакцией Ю.С.Владимирова. М., Бином. 2006.
    
13. Волошинов А.В. Математика и искусство М., Просвещение. 2000.
    
14. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике, «Мир», М., 1977. С.74
    
15. Харитонов А.С., Шелепин Л.А. "Принцип золотой пропорции как характеристика процессов с памятью." Сб."Стратегия жизни в условиях планетарного экологического кризиса" 2002, том. 2, С.378-385.
    
16. Азроянц Э.А., Харитонов А.С., Шелепин Л.А. Немарковские процессы как новая парадигма.// Вопросы философии, 1999, №7, С. 94 – 104.
    
17. Харитонов А.С. Тройственное видение природы войн. //Вестник Академии военных наук.№4(13). 2005.
    
18. Харитонов А.С. Народ и власть: гармония интересов. // Государство, религия, церковь в России и за рубежом. № 3 – 4, 2007. С.18 – 25.
    
19. Харитонов А.С. Скрытые параметры и взаимодействия в природе и обществе. // Государство, религия, церковь в России и за рубежом. 4, 2009.С.69-76.