Потенциальность электростатического поля

Вид материала

Документы

Содержание Потенциал является непрерывной и конечной функцией с конечными производными по координатам. Теорема Ирншоу Замкнутая система неподвижных зарядов не может находиться в состоянии устойчивого равновесия (при условии, что между зарядами де

Подобный материал:

• Программа вступительных экзаменов в магистратуру 210300 "Радиотехника" Профилирующая, 50.13kb.
• Энергия электростатического поля в вакууме, 28.09kb.
• Программа курса "Электричество и магнетизм" Эйхвальд А. И. Краткий исторический обзор, 89.83kb.
• 1 изучение электростатического поля методом моделирования, 117.54kb.
• Физический диктант «Работа сил электростатического поля. Разность потенциалов», 38.51kb.
• Профессор Борис Александрович Луговцов программа курса, 97.88kb.
• Электрическое поле в вакууме, 65.29kb.
• Лекция№1 Электростатическое поле и магнетизм, 24kb.
• Московский государственный технический университет «мами», 64.38kb.
• С. М. Полозов Московский инженерно-физический институт (государственный университет), 16.4kb.

Потенциальность электростатического поля.

1. Условие потенциальности поля.
   

Силовое поле называется потенциальным, если работа сил поля при перемещении в нем зависит только от начальных и конечных точек пути и не зависит от формы траектории.

или:

если работа сил поля при перемещении по замкнутому контуру равна нулю.

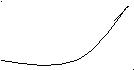
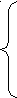В электростатическое поле потенциально.

А 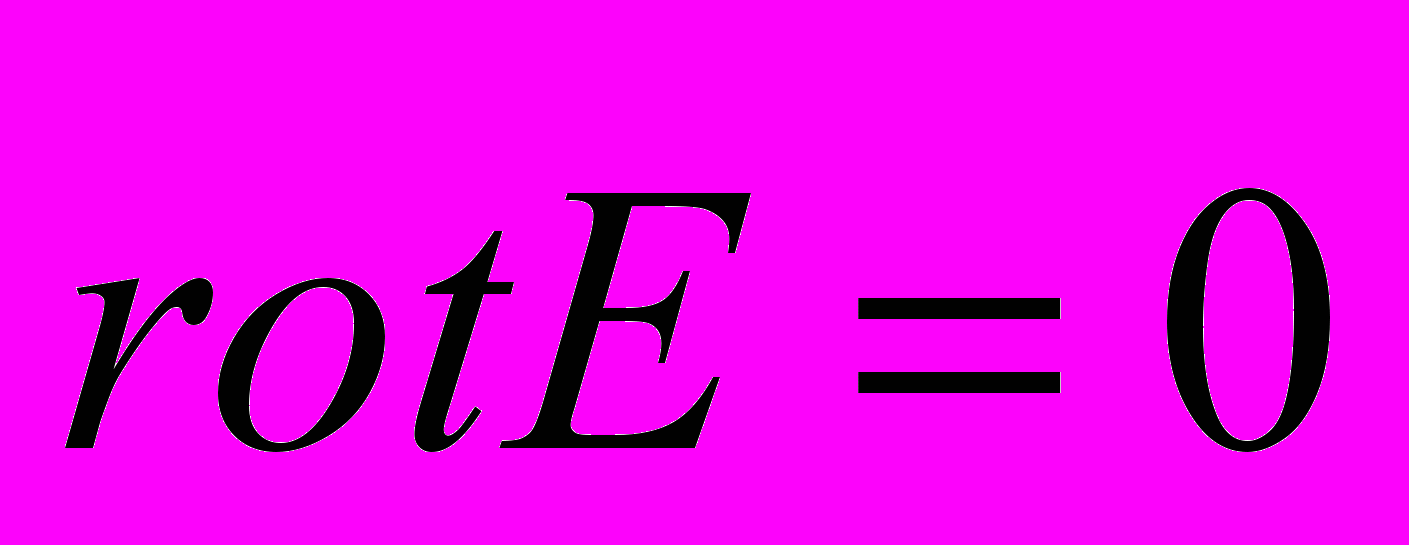- дифференциальная формулировка

потенциальности поля.

2.) Скалярный потенциал

Так как работа при перемещении заряда не зависит от траектории, то ее можно выразить через скалярную функцию , разность значений которой и определяет эту работу.

Так как 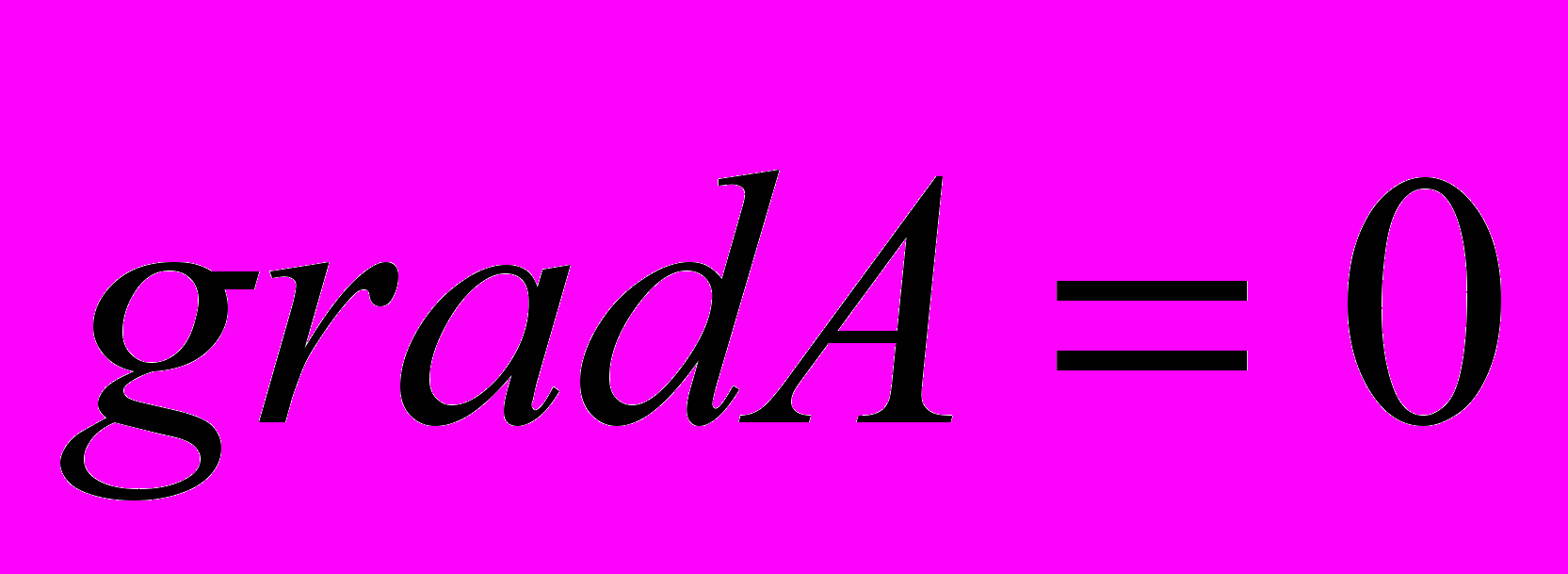всегда, то общим решением уравнения 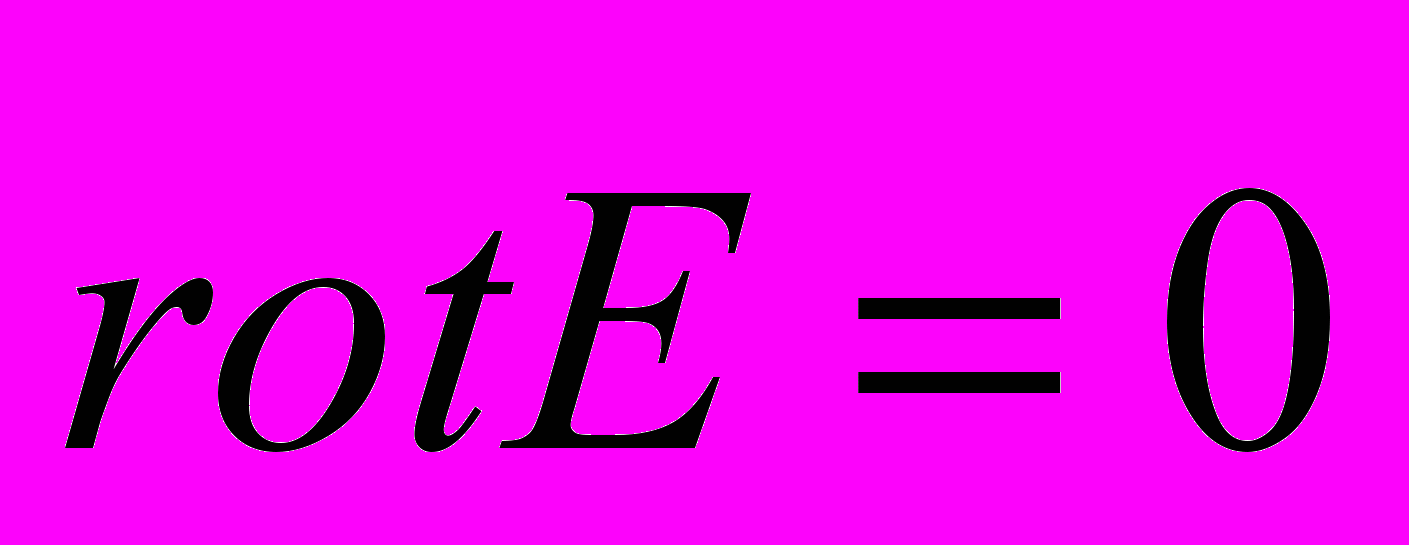будет: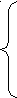

,

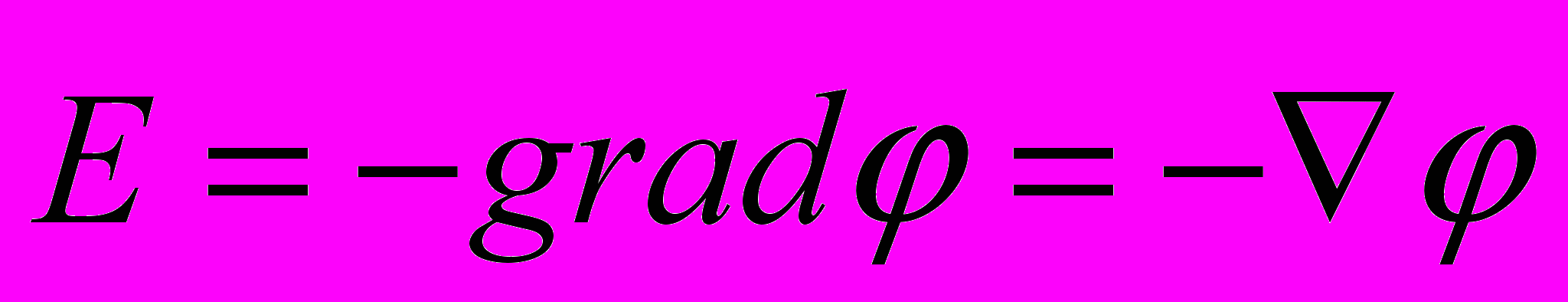где 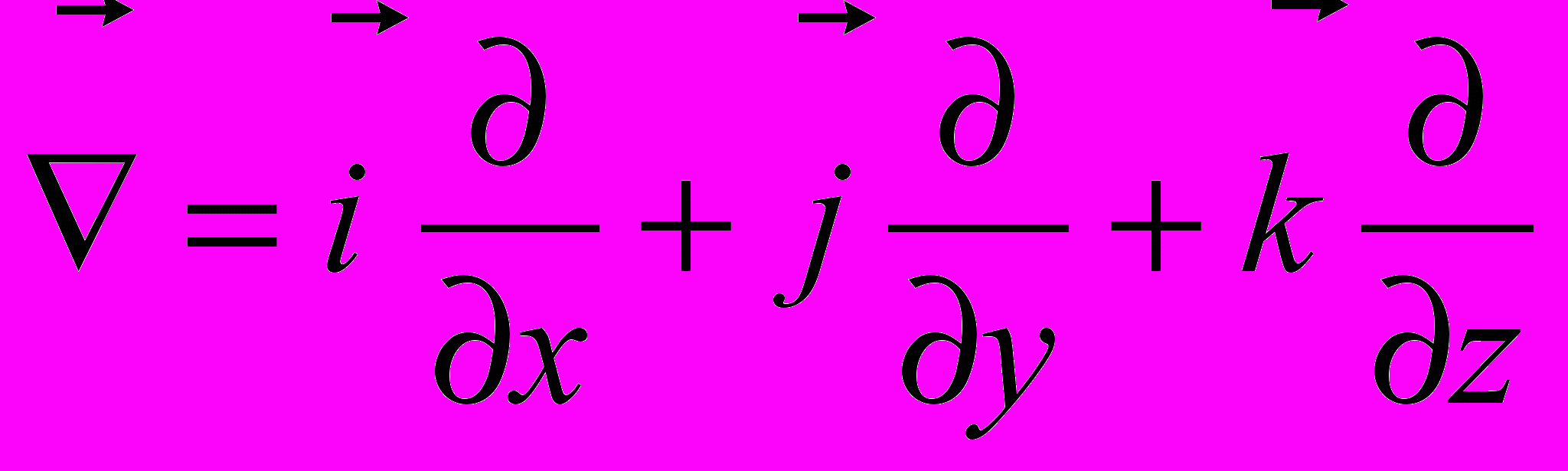(3.1)

Знак «-» в (3.1) возник исторически и означает, что 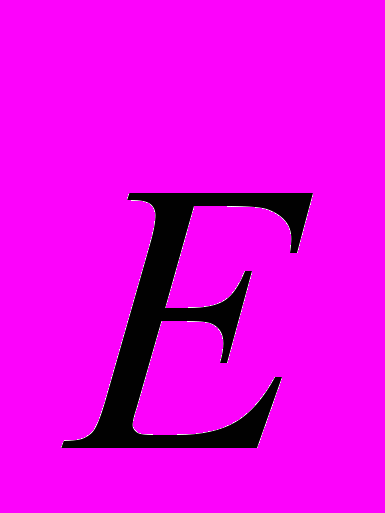направлен в сторону убывания потенциала .

Потенциал 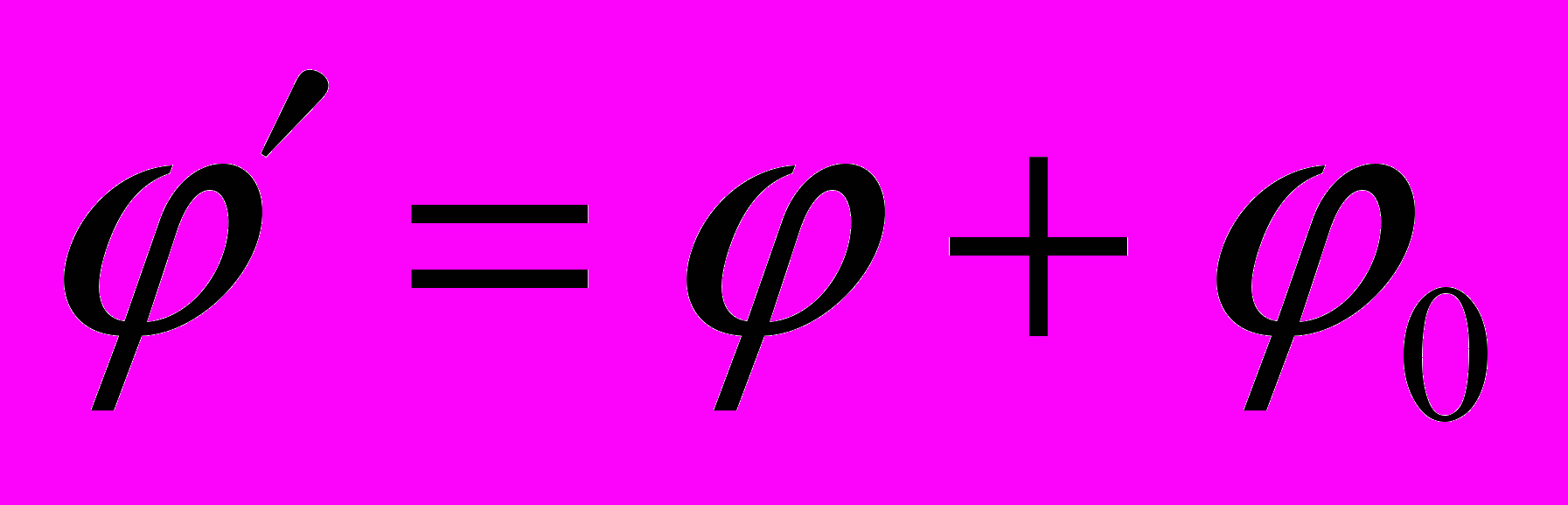описывает тоже поле 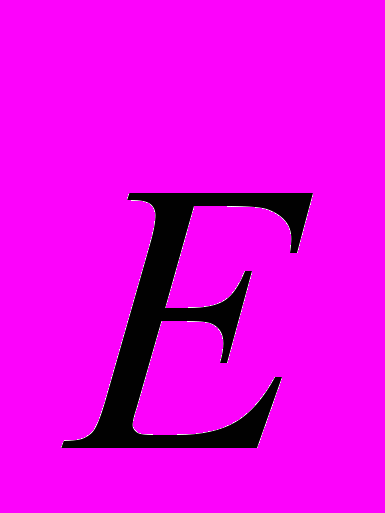, т.е. потенциал определен с точностью до произвольной постоянной φ₀ и не имеет определенного числового значения. Поэтому можно произвольно задать в любой точке пространства. Эта процедура называется нормировкой. Обычно (но не обязательно) полагается 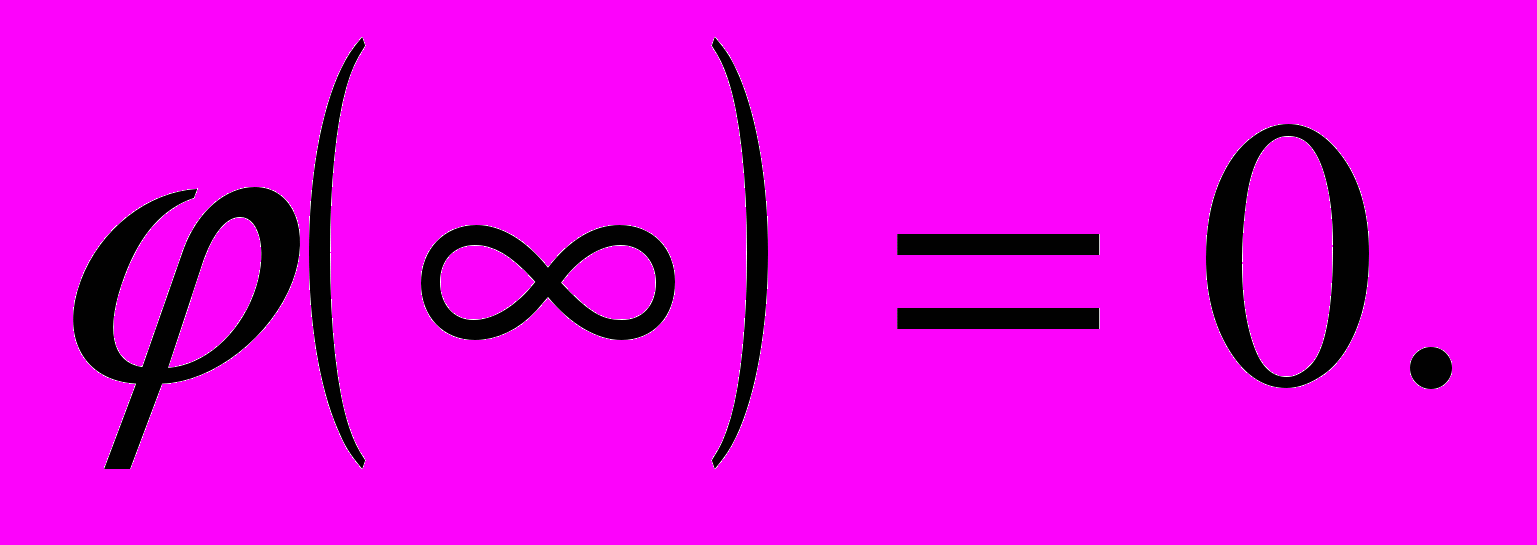или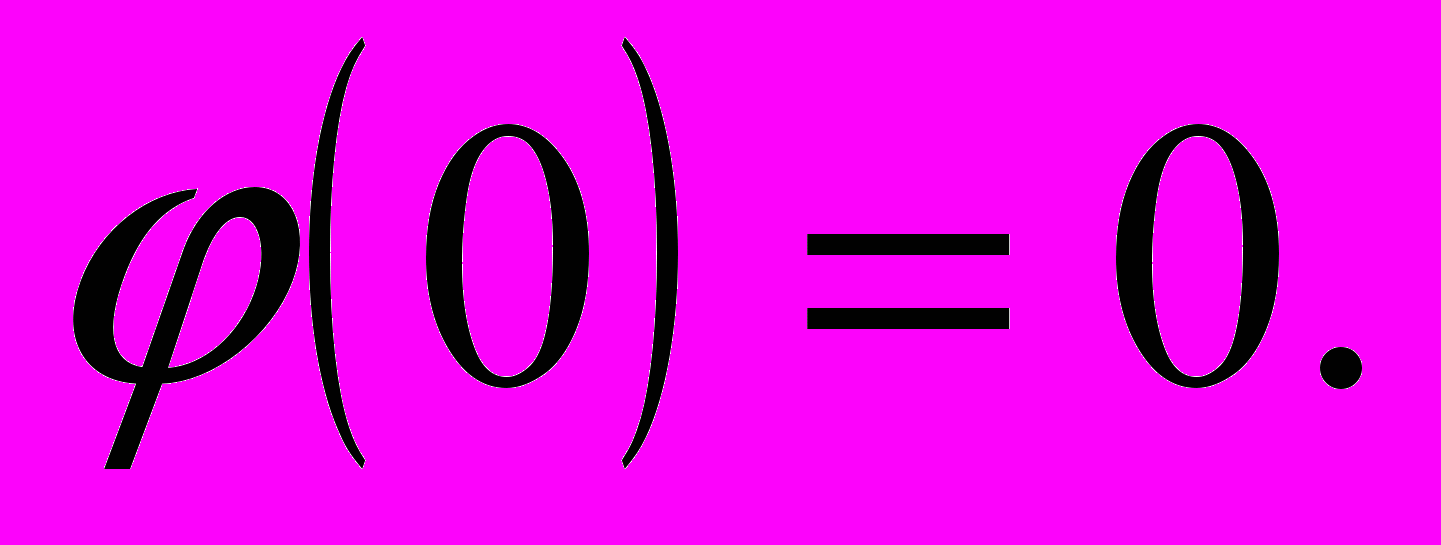

2



1

При перемещении заряда из точки 1 в точку 2 удельная работа:



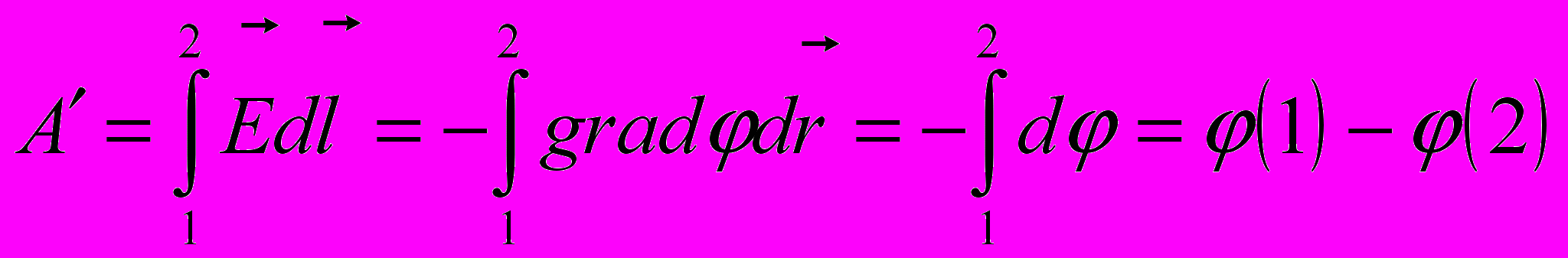
Таким образом, физический смысл имеет не абсолютное значение потенциала, а разность потенциалов между точками: разность потенциалов между двумя точками 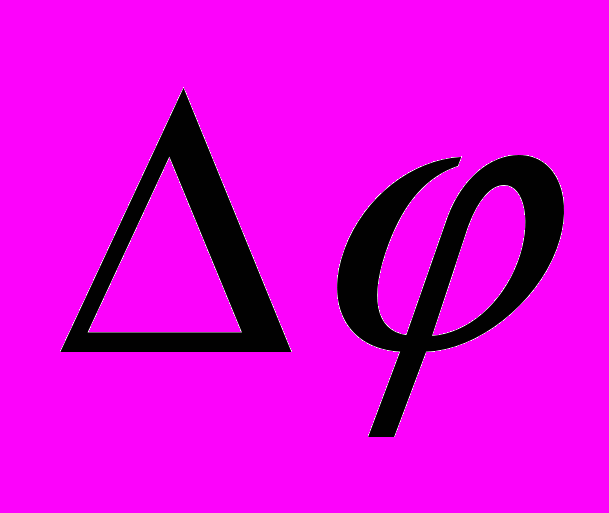равна работе по перемещению единичного положительного заряда между ними.

Здесь мы учли, что

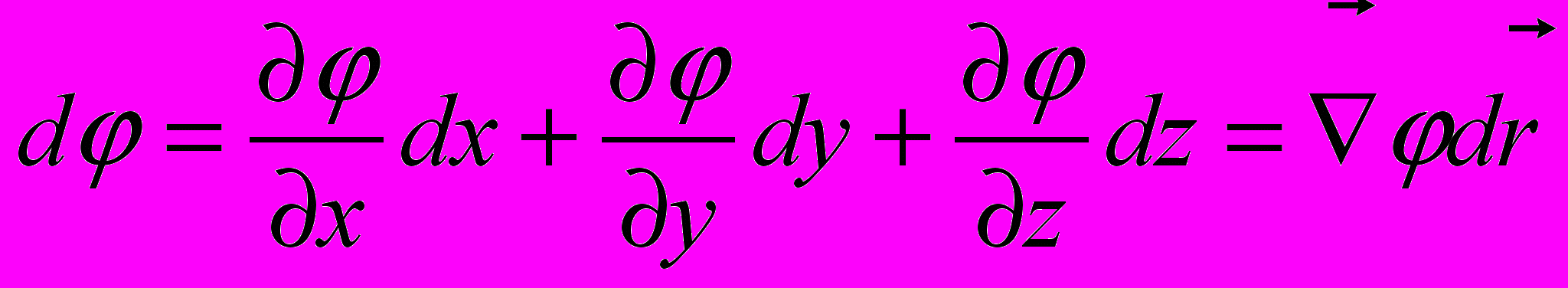
3). Потенциал точечного заряда.




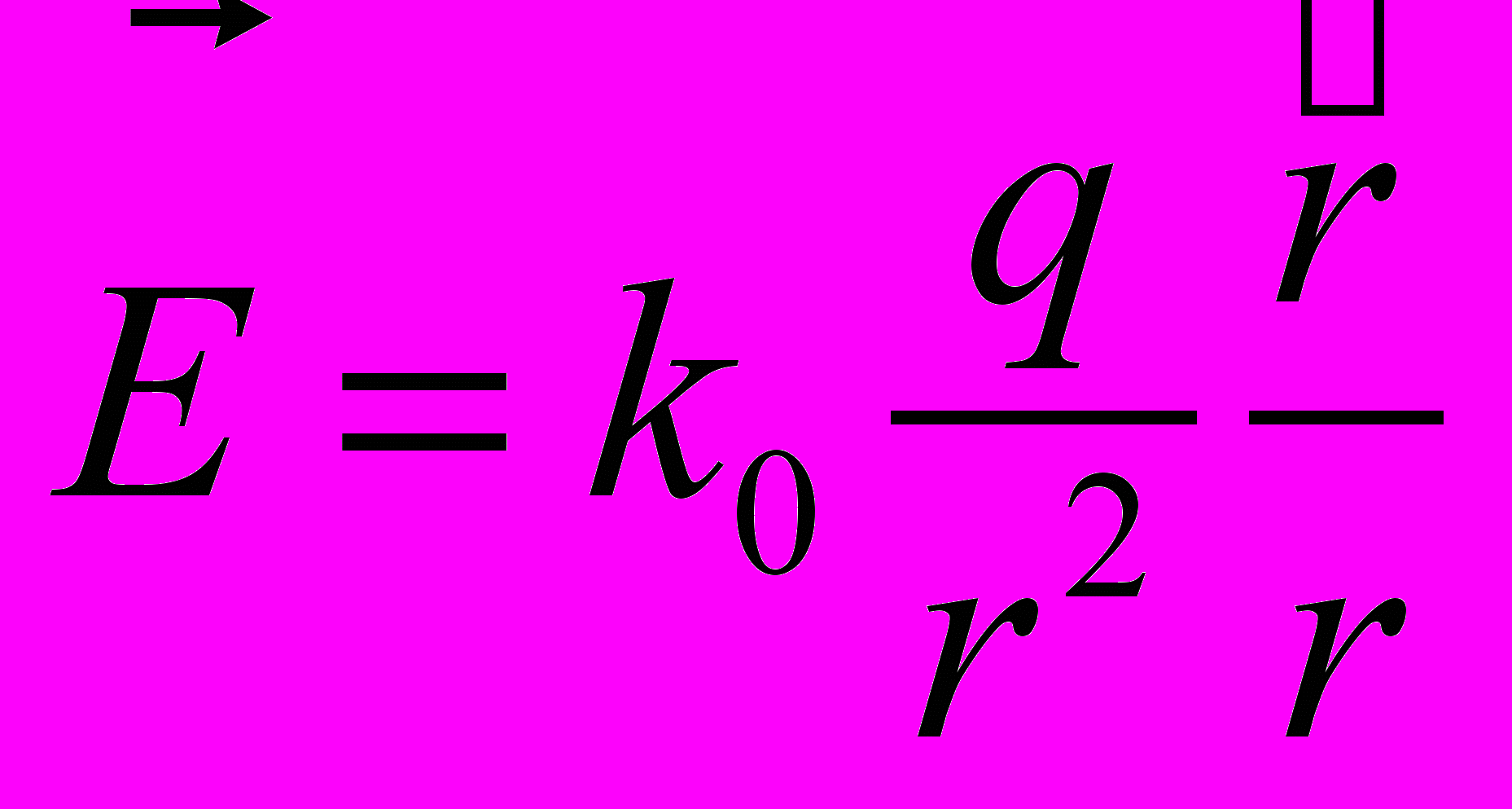
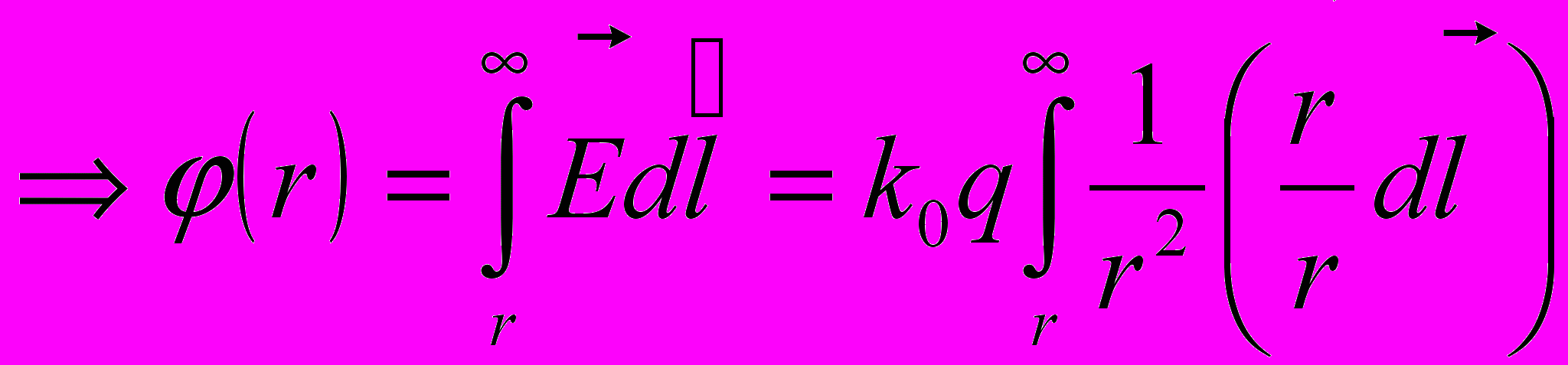
при :

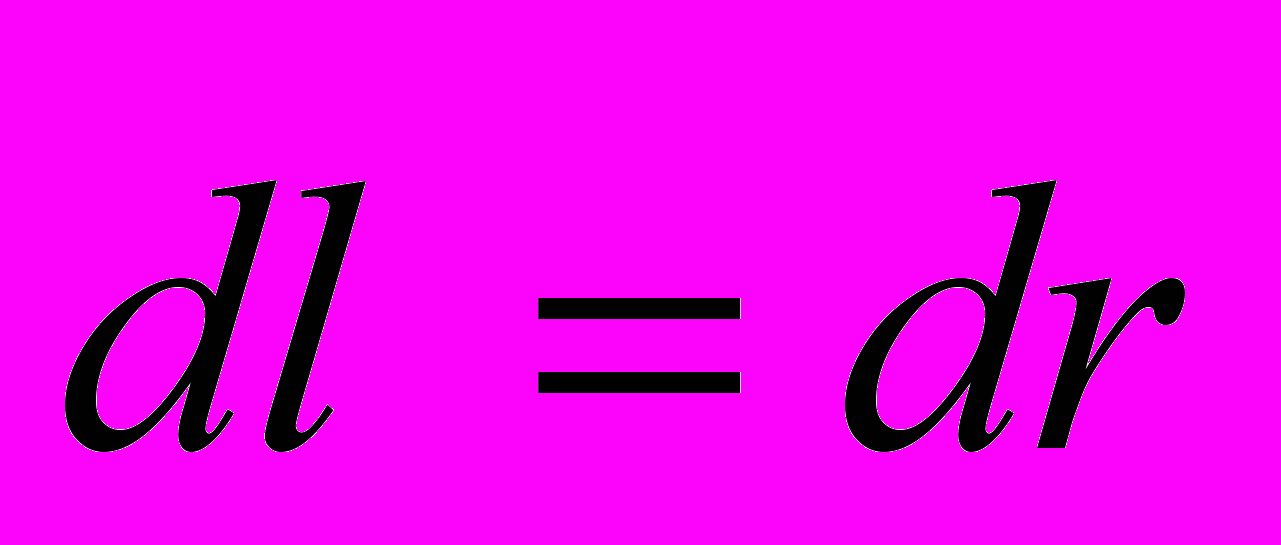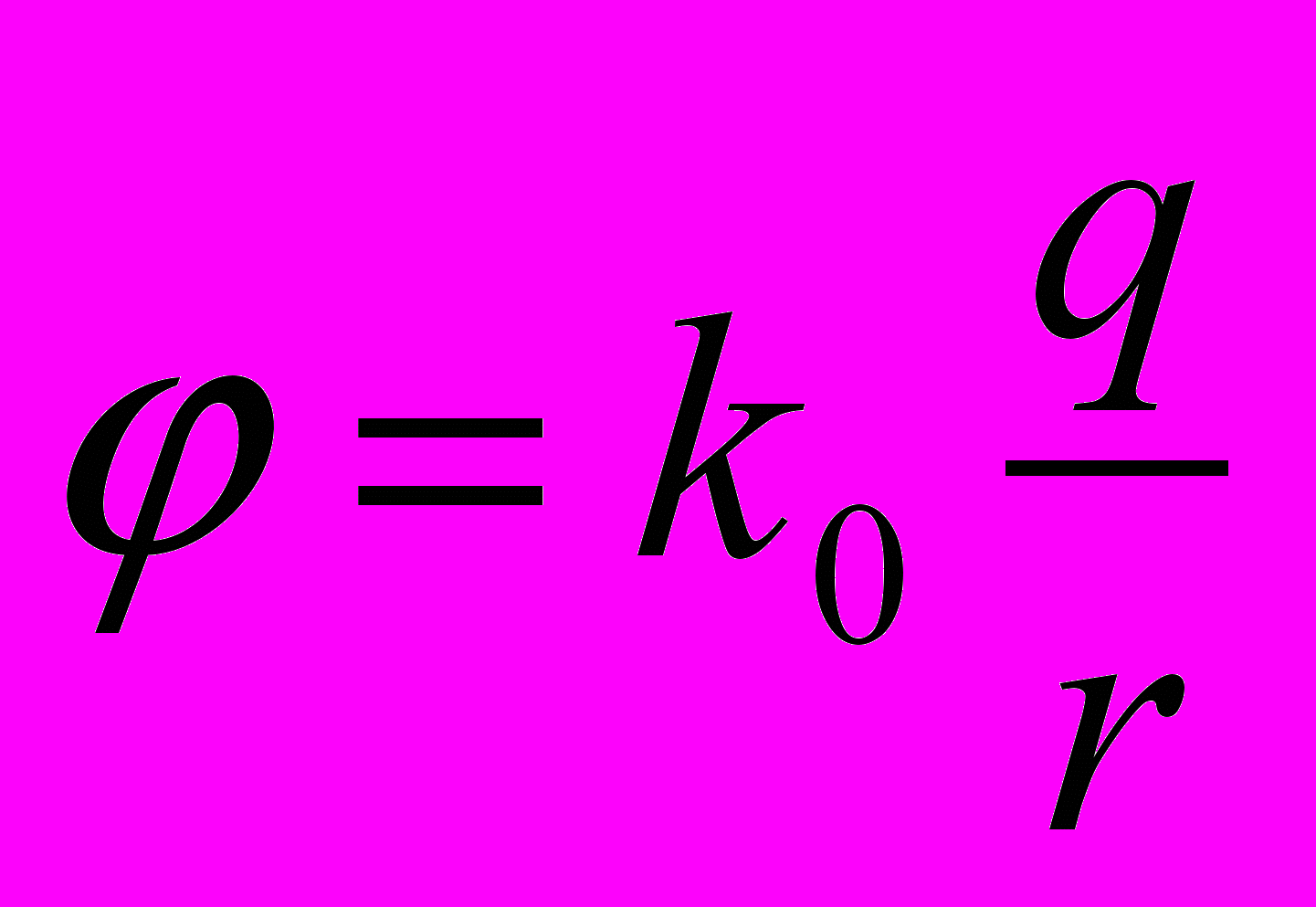
4. Потенциал системы точечных зарядов.
   

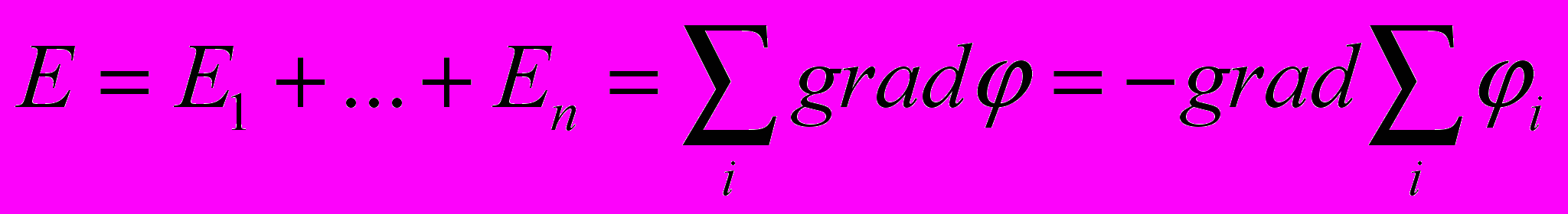
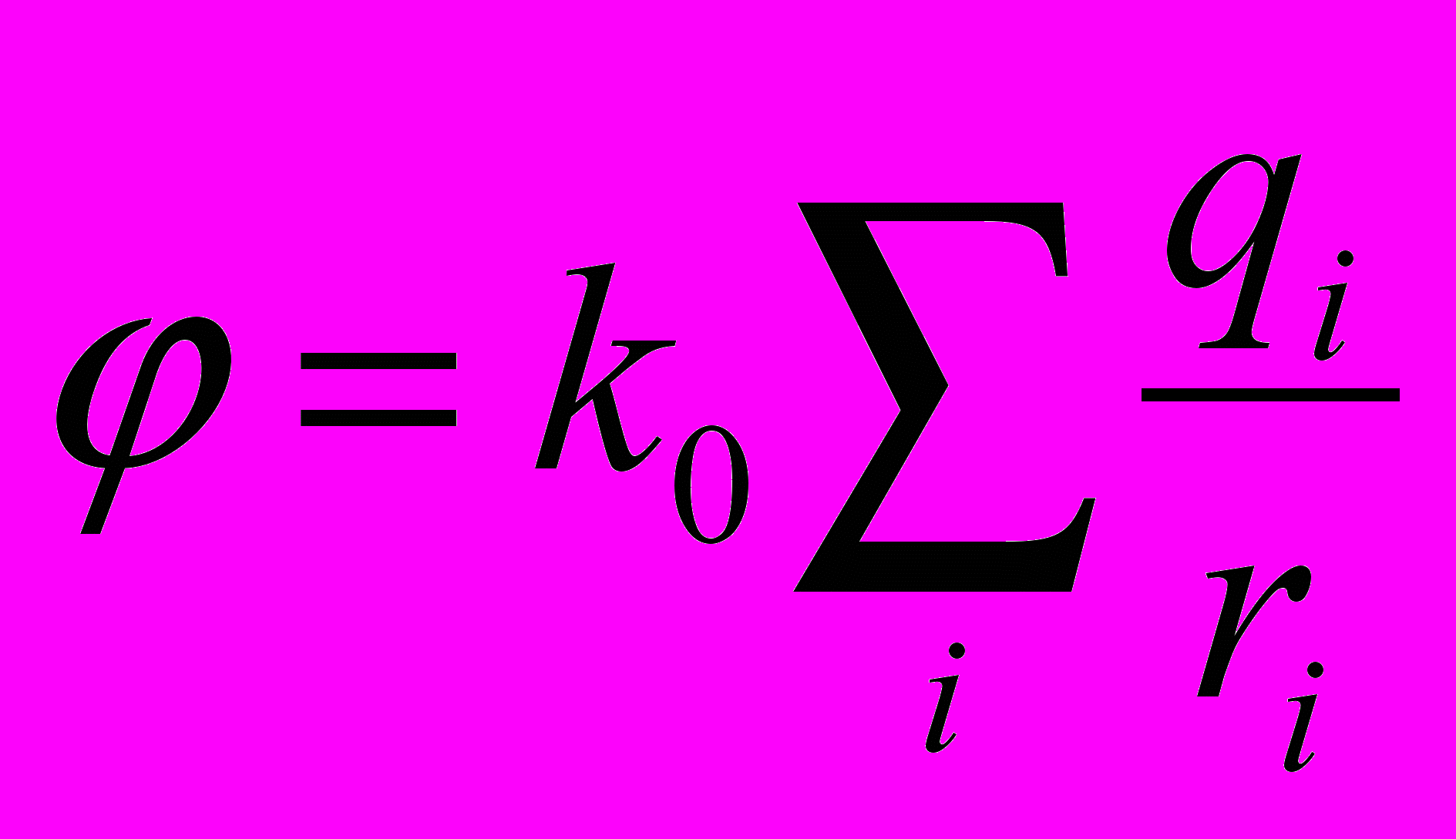, где

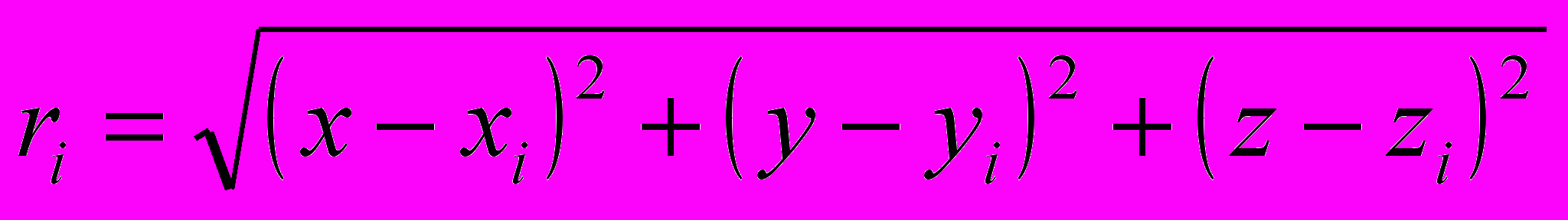
4. Потенциал непрерывно распределенного по объему заряда.
   

Разбиваем весь объем 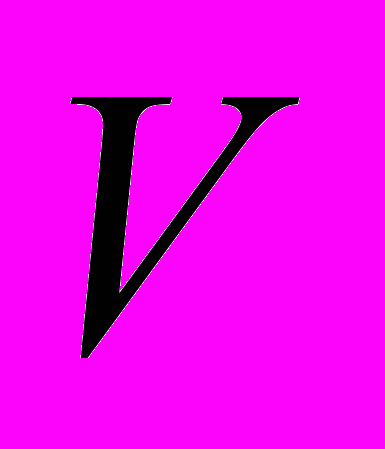на элементы 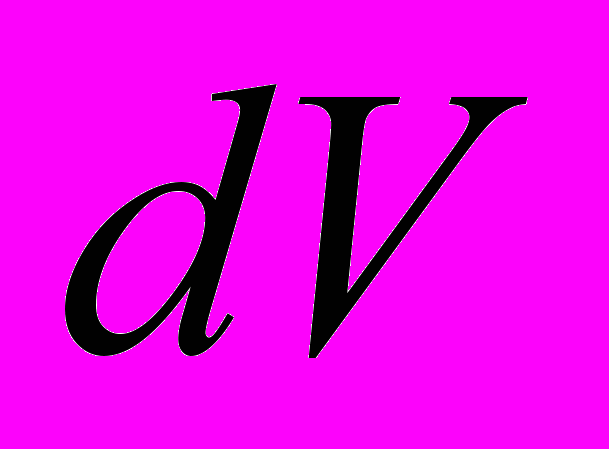, в каждом из которых находится заряд 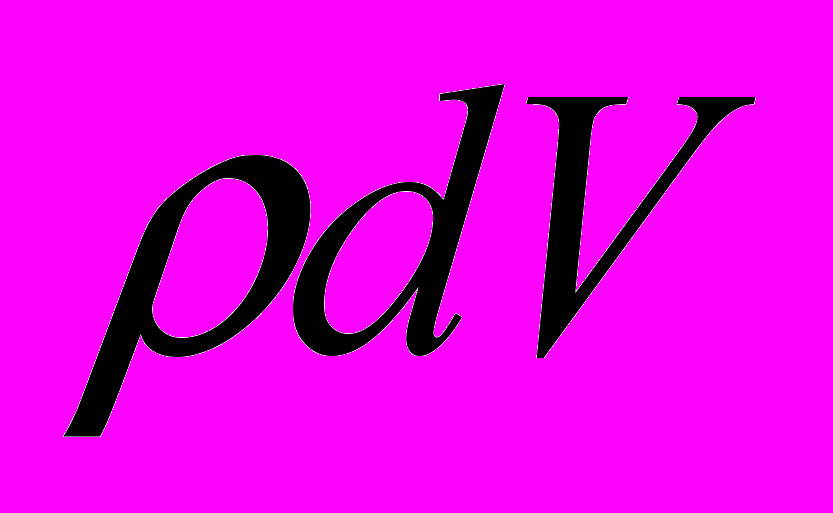, и используем формулу из п.4:

,

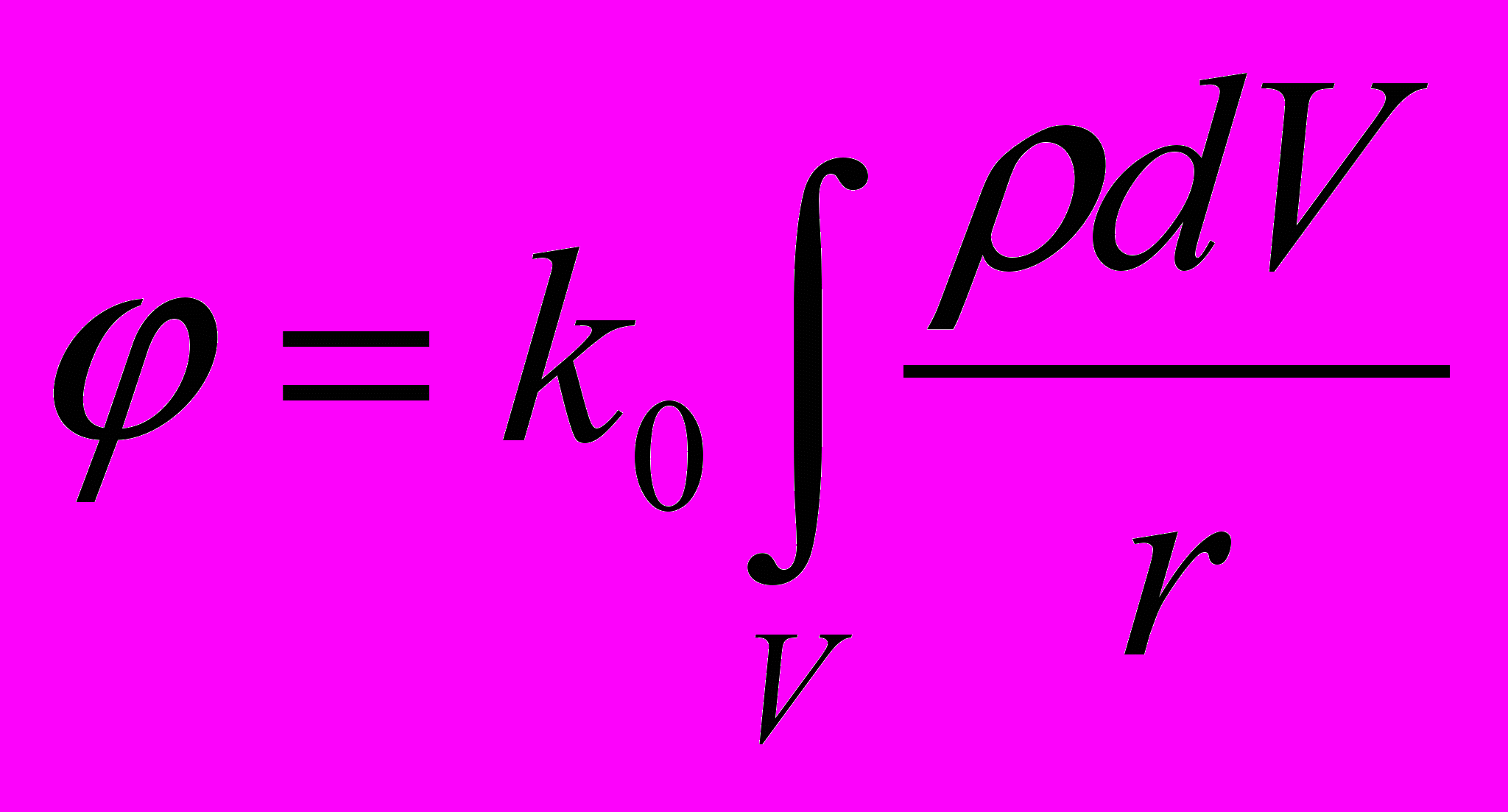где 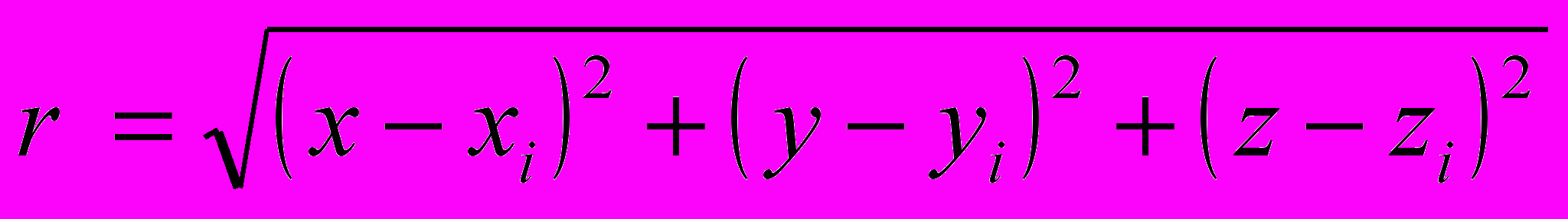- расстояние от объёма 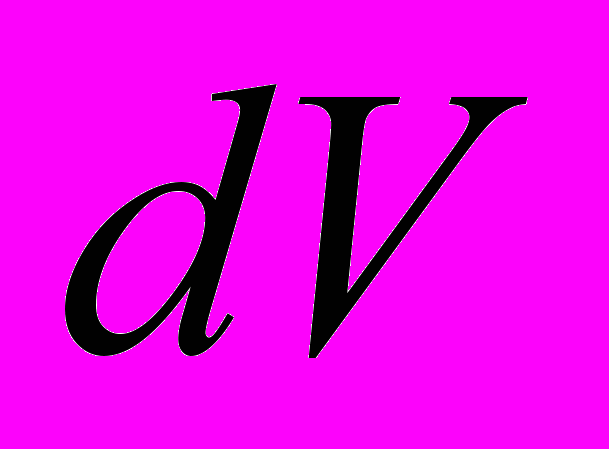до точки вычисления потенциала.

4. Потенциал поля поверхностно распределенного заряда.
   

Аналогично п5:

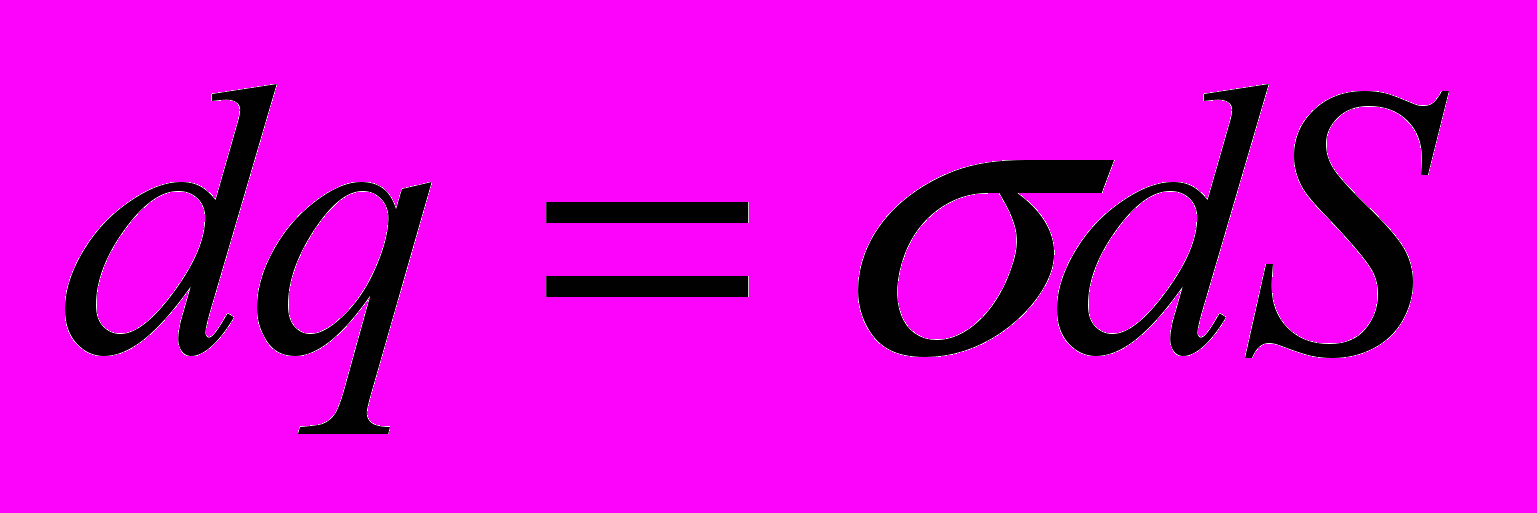
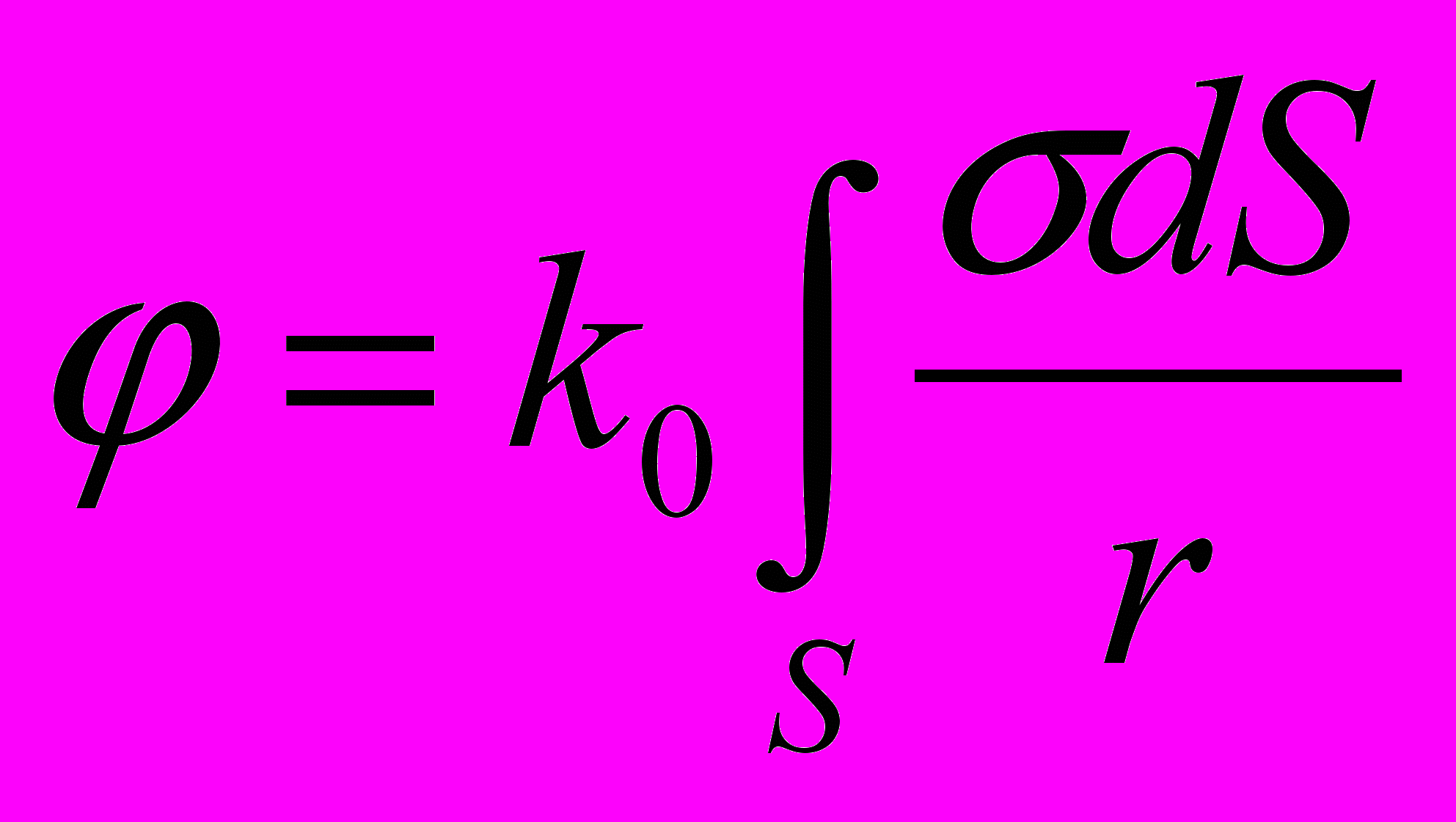
4. Свойства скалярного потенциала:
   

а) Конечность потенциала при распределении заряда с конечной плотностью.

Запишем формулу п.5 в сферических координатах:



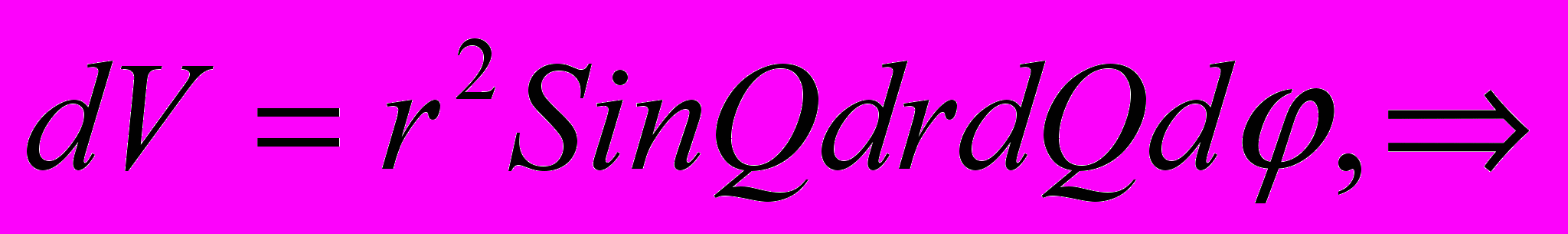
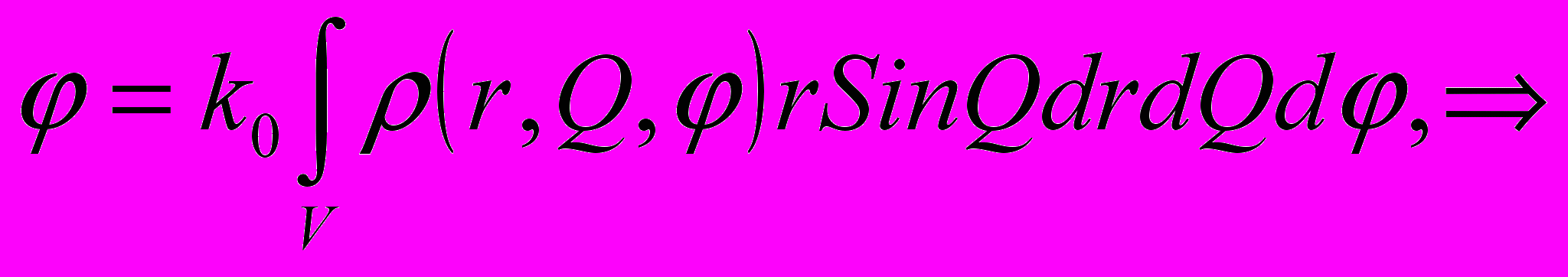
Потенциал системы зарядов, распределенной в конечной области пространства 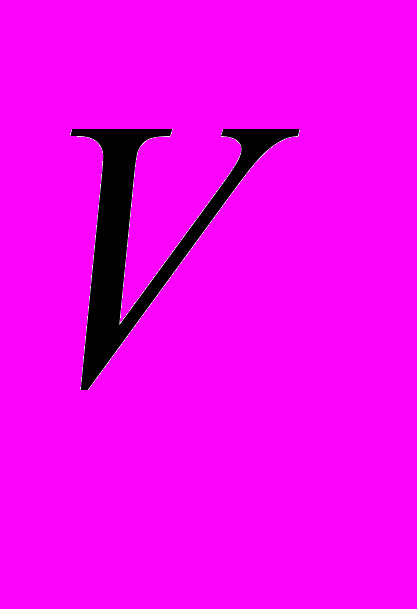с конечной плотностью 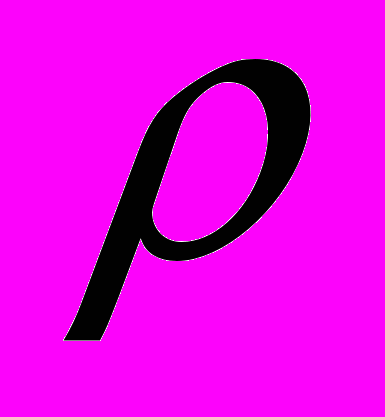- конечен.

Напомним, что бесконечно большой потенциал точечного заряда в точке нахождения заряда обусловлен мнимой бесконечностью его плотности заряда .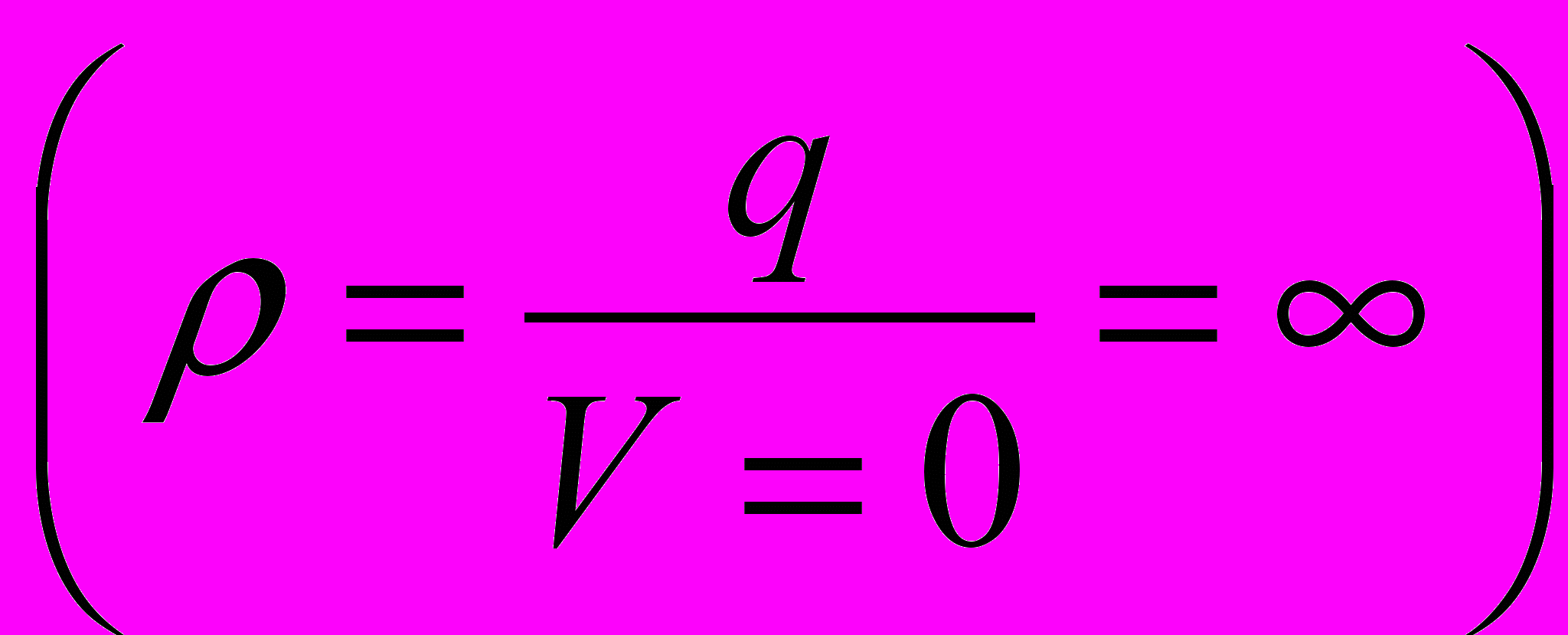

б) Непрерывность потенциала.

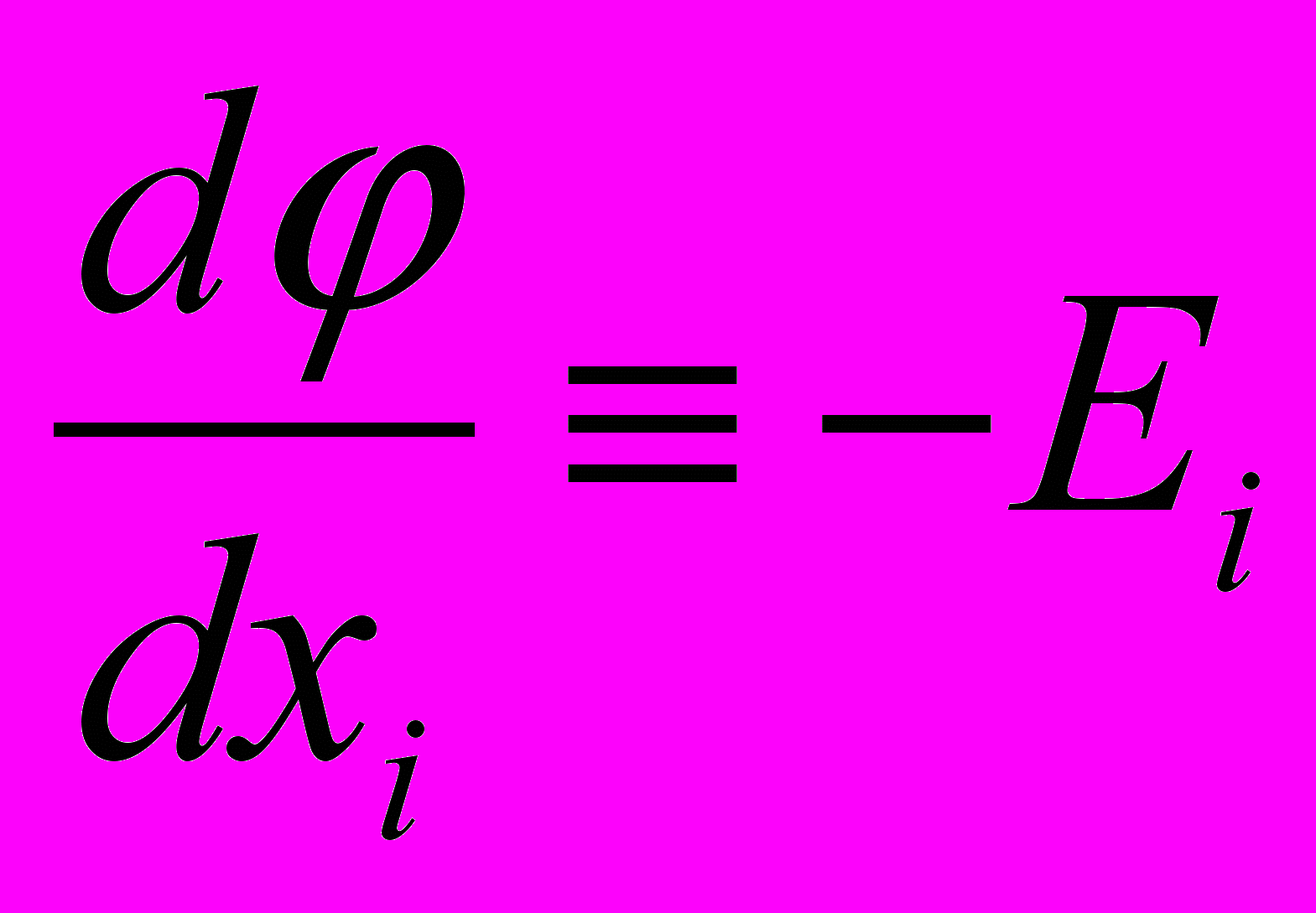, но 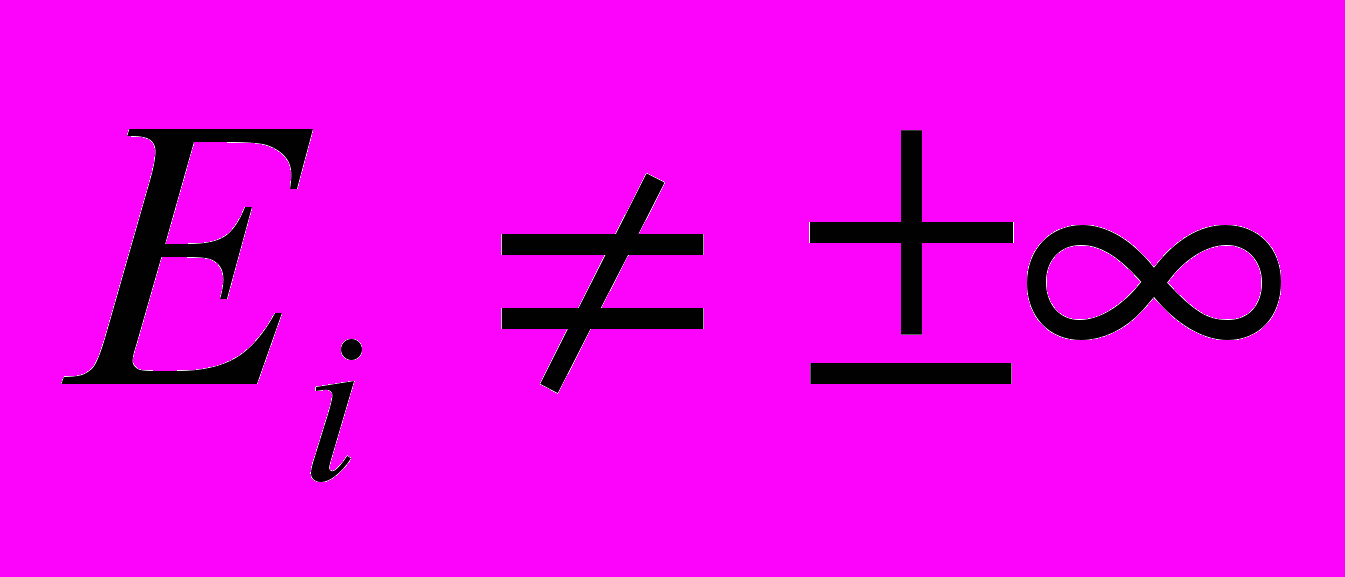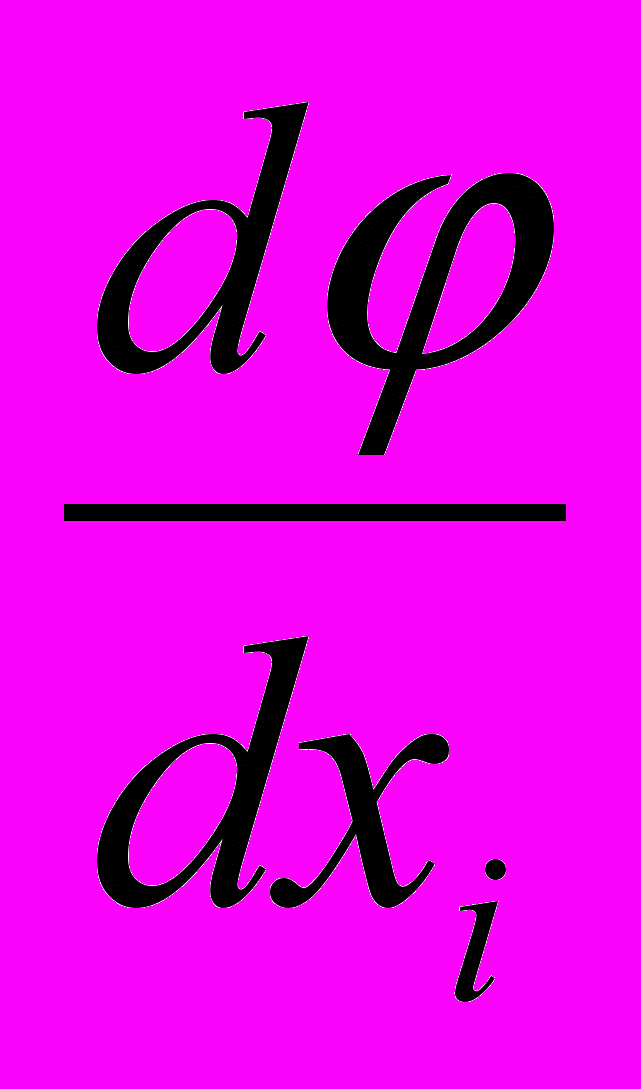- должно быть конечно во всей области пространства.

Т.о. Потенциал является непрерывной и конечной функцией с конечными производными по координатам.


Эти условия и свойства важны при решении дифференциальных уравнений для потенциала .

4. Теорема Ирншоу:
   

Не существует такой конфигурации неподвижных зарядов, которая была бы устойчивой, если нет других сил, кроме кулоновских.

Или:

Замкнутая система неподвижных зарядов не может находиться в состоянии устойчивого равновесия (при условии, что между зарядами действуют только силы Кулона).

Доказательство.

Если положение устойчиво, то при любом смещении должна существовать «возвращающая» сила 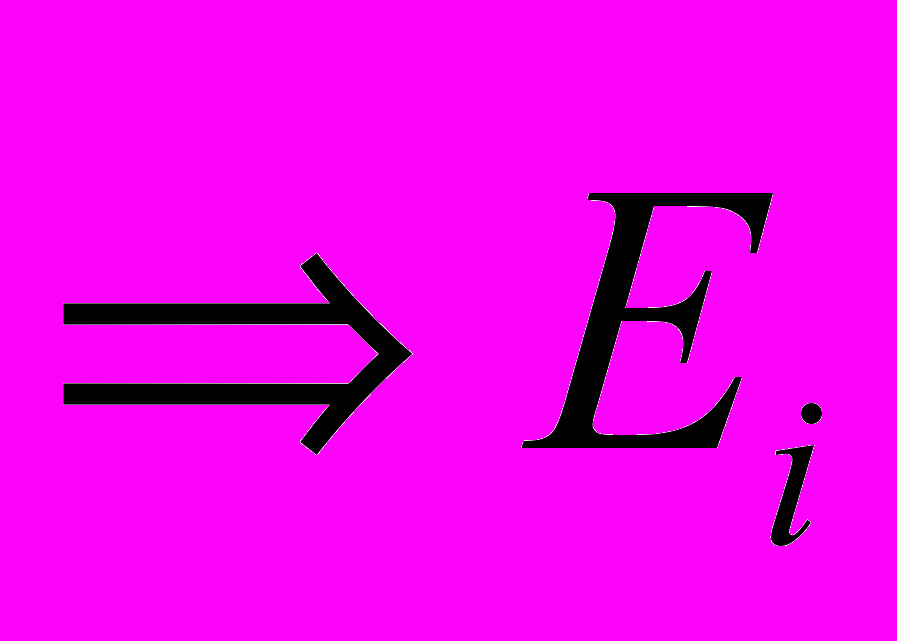вблизи каждого заряда направлена по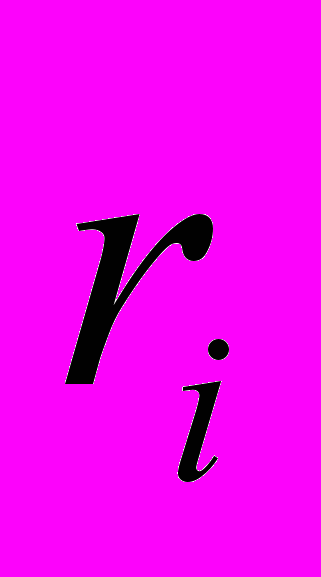

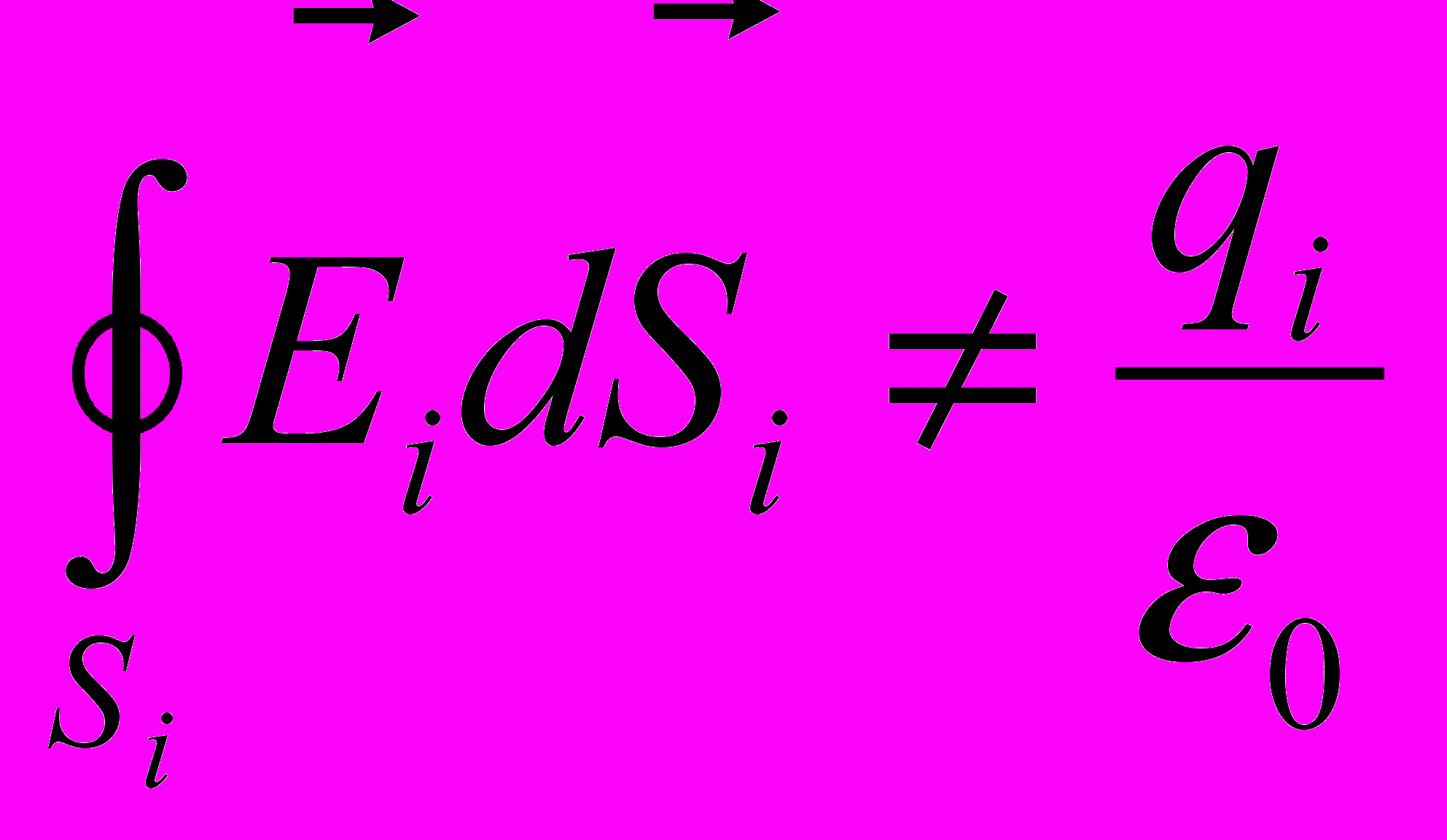
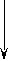- создается зарядом 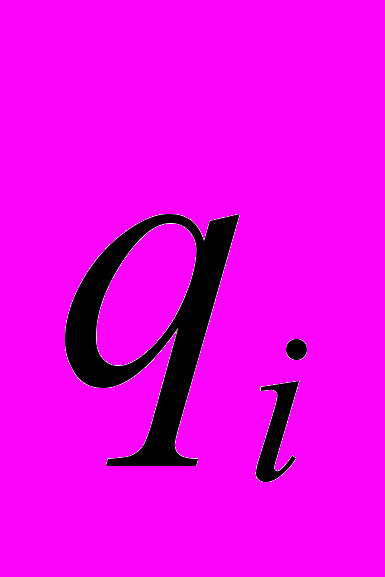внутри объема, что противоречит предложению о создании такого поля зарядами, находящимся вне поверхности.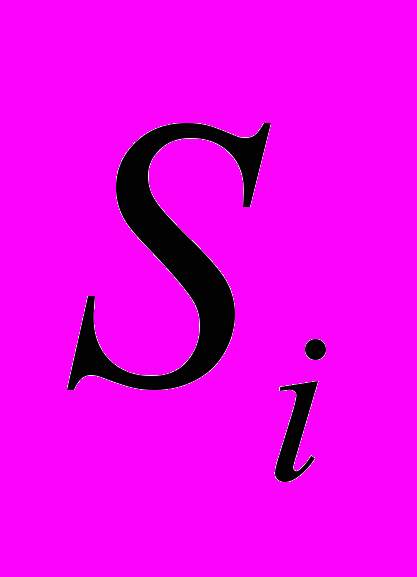