Научно- методическая деятельность

Вид материала

Документы

Содержание Традиционное обучение Специально организованное обучение Система развивающих заданий Логические задачи Нлкиеай (линейка). Проведенная работа по формированию логического мышления у учащихся 5-11 классов позволяет сделать следующие выводы Обоснование выбора учебно–методического комплекта по математике Сравнительный анализ темы «Подобные треугольники» в учебниках по геометрии Гомотетия и её свойства. Определение подобных фигур, свойства подобных фигур. Определение подобных треугольников. Признаки подобия треугольников Метод подобия. Система задач по данной теме. §3. Методические особенности изучения темы «Подобные треугольники» Обоснование выбора используемых технологий, в том числе ИКТ, технологий обучения детей с проблемами в развитии. Сущность модульного обучения Интеграция модульной технологии с разноуровневым обучением предполагает Перестройка на модульной основе позволяет Модульные технологии ... Полное содержание

Подобный материал:

• 2. Научно-исследовательская и научно-методическая деятельность, 656.19kb.
• Положение о научно-практической конференции Методическая и научно-исследовательская, 31.42kb.
• Методическая работа в школе методическая работа, 11.81kb.
• Приказ № от г. Программа развития школы на 2007 2010 годы Санкт-Петербург 2007 год, 940.05kb.
• Творческая деятельность, 1688.28kb.
• Художественно-творческая и научно-методическая деятельность училища, 16.48kb.
• Организация научно – исследовательской деятельности учащихся. Научно-исследовательская, 309.37kb.
• Методическая деятельность библиотек области, 100.16kb.
• Статья Основные понятия, применяемые в настоящем Федеральном законе Научная (научно-исследовательская), 349.52kb.
• Методическая деятельность муниципального общеобразовательного учреждения средней общеобразовательной, 438.03kb.

Раздел 3.Научно- методическая деятельность:

1)Обоснование методической проблемы и план самообразования:


Название проблемы

Формирование логической структуры мышления учащихся 5-6 классов с помощью системы развивающих заданий на уроках математики.


Условия возникновения проблемы, становление опыта

В соответствии с концепцией модернизации Российского образования на период до 2010 года «школа в широком смысле этого слова должна стать важнейшим фактором формирования новых жизненных установок личности».

Среди многих проблем преподавания математики в средней школе все большее внимание привлекает проблема воспитания у учащихся математического мышления. В процессе эволюции математики-науки и педагогики математики естественно изменилось то содержание, которое вкладывалось в понятие «математическое мышление»; то значительно расширился объём этого понятия, и существенно возросла роль проблемы развития мышления в процессе обучения математике. Практика школьного обучения требует от учителя работать над развитием математического мышления учащихся, поэтому и была выбрана данная проблема.

Несмотря на сложность и специфичность проблемы «Формирования логической структуры мышления», учитель математики должен иметь определённые представления о математическом мышление, которые могли бы служить основой для целенаправленной практической работы

Математическое образование учащихся представляет собой сложный процесс, основными компонентами которого являются:

1) приобретение учащимися определённой системы математических фактов и идей;

2)овладение определёнными математическими умениями и навыками;

3) развитие математического мышления.


Актуальность и перспективность опыта, его практическая значимость для повышения качества учебно-воспитательного процесса.

Актуальность и перспективность опыта связана с одним из приоритетных направлений модернизации образования, с предоставлением возможности учащимся заниматься по индивидуальным учебным траекториям. В России, в настоящее время, идёт становление новой системы образования, ориентированной на вхождение в мировое образовательное пространство. Происходят существенные изменения в педагогической теории и практике учебно-воспитательного процесса. Перспективность и практическая значимость опыта заключается в том, что работа учителя спланирована таким образом, что у учащихся появляется возможность приобретать новые умения, развивать способности оперировать информацией, творчески решать проблемы.

Еще одним из приоритетных направлений развития системы образования в России является достижение качества современного образования, отвечающего актуальным потребностям личности, общества и государства. В значительной степени условия эффективной реализации образовательной политики формируются на уровне деятельности образовательного учреждения, в том числе и деятельности каждого конкретного педагога. Образовательная деятельность учителя – предметника регламентируется рамками государственного стандарта и учебной программы. В своей профессиональной деятельности веду поиск ответов не только на вопросы "чему учить?", "зачем учить?", "как учить?", но и на вопрос "как учить результативно?". Актуальность и перспективность опыта проявляются в том, что при снижении интереса учащихся к предмету, предлагается анализ условий, позволяющих стимулировать познавательную и творческую деятельность учащихся, развивать их логическое мышление через использование различных форм развивающего обучения.

Повышается качество успеваемости, формируется творческая личность учащегося, повышается интерес к предмету.


Теоретическая база опыта.

Опыт базируется на концепции модернизации Российского образования на период до 2010 года – Вестник образования (№6- 2002г.).

Теоретическую основу опыта составляют педагогические идеи концепций М.И. Махмутова, М.Н. Скаткина, И.Я. Лернера и др., обоснованно доказавших доминирование развивающего обучения, обеспечивающего развитие целостной личности как индивидуальности.

Были проанализированы и обобщены:

• общие педагогические проблемы дидактики (Ю.В. Бабанский);
  
• общие методические проблемы (В.П. Максаковский, В.В.Сиротин);
  
• проблемы общего развития учащихся (Д.Б. Эльконин, В.В.Давыдов, П.Я.Гальперин, И.Я. Лернер);
  
• проблемы познавательной деятельности и познавательного интереса
  (Г.П. Щукина, И.Я. Лернер, Н.Ф. Талызина);
  
• проблемы проблемного обучения (И.Я. Лернер);
  
• педагогический опыт учителей Курманаевского района.
  

В своей работе опираюсь на личностно – ориентированные развивающие педагогические технологии такие как: система развивающего обучения Л.В. Занкова; технология проблемного обучения (М. Фридман, В. И. Маху и др.), технология блочно – модульного обучения (М.А.Чошанов, П.Я. Юцявичене и др.).

Использованная литература:

• Журнал «Математика в школе» 2004 – 2007г.
  
• Новые педагогические технологии. Пособие для учителя/Под общей редакцией Е. С. Палат. М., 2006г.
  
• С.Л. Рубинштейн О мышлении и путях его исследования. М. 1970.
  
• А.В. Петровский. Общая психология. М.1970.
  
• Я.А. Пономарёв. Психология творческого мышления.1960.с.209
  

Новизна опыта

Новизна опыта заключается в изменении подходов к организации учебно-воспитательного процесса: творческое взаимодействие учителя и учащихся, исходя из принципов сотрудничества и сотворчества с опорой на индивидуальные особенности учащихся.

Новизна предусматривает:

• изменение подходов к преподаванию математики в рамках образовательного учреждения;
  
• изменение статуса ученика как главной фигуры УВП, делающего заказ на обучение;
  
• ориентацию учителя на индивидуальные потребности учащихся;
  
• ориентацию учителя на стандарт как на конечный ориентир обучения, путь к которому индивидуален;
  
• выявление индивидуальных возможностей и интересов учащегося;
  
• оценивание продвижения ученика по личностным и поведенческим параметрам;
  
• составление системы заданий, развивающих логическое мышление в 5-11 классах, программы кружка по математике в 5-11 классах.
  
• контроль, тестирование предполагают развитие логического мышления учащихся и выявление интересов и склонностей учащегося в дальнейшем обучении;
  
• максимальное включение ребенка во все формы активности, расширение его реального опыта по выбранному предмету.
  

Ведущая педагогическая идея опыта.

Ведущей педагогической идеей опыта является формирование ключевых компетенций у учащихся в процессе преподавания математики при овладении технологиями проблемного и блочно-модульного обучения, способствующими всестороннему развитию личности учащихся, в том числе и развитию логического мышления учащегося.

Исходные идеи:

1. Развитие авторской позиции ребенка в образовательном процессе.
   
2. Безоценочный характер реакции на высказывания учащихся в ходе проблемного обучения.
   
3. Целостная включенность ребенка в образовательный процесс, связанная и с рациональным познанием, и с интуитивной, часто неосознаваемой эмоционально-личностной сферой.
   
4. Проблематизация учебного материала (знания возникают в результате удивления и любопытства).
   
5. Активность ребенка (знания должны усваиваться легко).
   
6. Связь обучения с жизнью ребенка, игрой, трудом.
   

Технология опыта.

Развитие мышления при изучении математики состоит в формировании у учащихся характерных для этого предмета приемов мыслительной деятельности. При этом важно, чтобы в структуру умственной деятельности школьников помимо алгоритмических умений и навыков, фиксированных в стандартных правилах, формулах и способах действий, вошли эвристические приемы, которые необходимы для решения творческих задач, применение знаний в новых ситуациях, доказательства высказываемых утверждений.

Процесс обучения предполагает целенаправленное управление мыслительной деятельностью учащихся, что приводит к продвижению учеников в их умственном развитии. Чтобы развить мышление учащихся, нужно показать им как функционирует мышление на практике. Развитие происходит в деятельности, поэтому необходимо создавать ученикам условия соответствующей деятельности, нужно демонстрировать сложную картину поиска решения, всю трудность этой работы. В этом случае ученики становятся активными участниками процесса поиска решения, начинают понимать источники возникновения решения. Как результат – ими легче осваиваются причины ошибок, затруднений, оценивается найденный способ решения и ход логических мыслей, а без этого знания не могут перейти в убеждения.

Системное развитие логического мышления должно быть неотрывно от урока, каждый ученик должен принимать участие в процессе решения не только стандартных заданий, но и задач развивающего характера (активно или пассивно).

На уроках учитель должен моделировать ту умственную деятельность, которая нужна на данном этапе развития (учить анализировать задачи, делать чертежи, выявлять отношения объектов и т.д.). Это имеет обучающее и воспитывающее значение: учащиеся приобщаются к методу поиска, ориентируются не только на результат, но и на процесс его достижения, т.е. учатся мыслить логически.

Можно выделить два подхода к формированию и становлению логико-математического мышления:

1. Традиционное обучение, приводящее в зависимости от воздействия и других объективных причин к формированию либо эмпирического, либо теоретического мышления.

2. Специально организованное обучение, ориентированное на формирование учебной деятельности, приводящее к становлению теоретического мышления.

Для формирования логического мышления приоритетным является второй подход, который и был положен в основу формирования технологии.

Для осуществления формирования логического мышления учащихся 5-11 классов составлена система развивающих заданий по темам:

• аналогия;
  
• исключение лишнего;
  
• «в худшем случае»;
  
• классификация;
  
• логические задачи;
  
• перебор;
  
• задачи с геометрическим содержанием;
  
• задачи «на переливание»;
  
• задачи-шутки;
  
• ребусы и кросснамберы;
  
• занимательные задания.
  

Эти задания можно разделить на группы, учитывая их воздействие на мыслительную деятельность учащихся.

Формирование гибкости ума, освобождение мышления от шаблонов происходит при решении задач-шуток, занимательных заданий, задач на перебор вариантов, т.к. в большинстве своем эти задачи не привязаны к темам и не требуют особой теоретической подготовки.

Задачи на переливание, логические задачи, ребусы, задачи на классификацию учат школьников умению рассуждать, формируют математический стиль мышления, развивают логико-лингвистические способности детей, которые приводят к умению четко мыслить, полноценно логически рассуждать и ясно излагать свои мысли.

Задачи на аналогию и исключение лишнего используются для формирования умений поиска решения задач, интуиции, требуют знания теории и нешаблонного подхода к решению.

Задачи с геометрическим содержанием нацелены на знание геометрических фигур и их свойств как основы для формирования пространственных и изобразительных умений школьников, на расширение кругозора.

Учитель, преподающий в 5-11 классах, может развивать логическое мышление учащихся с помощью созданной системы заданий. Для этого необходимо учитывать следующее:

1. выбранные задания должны быть посильными для детей;

2. задания, отобранные для одного урока, должны быть разнообразными для воздействия на различные компоненты мышления;

3. если ученики не справляются с заданием, то целесообразно оставить его на обдумывание до следующего урока;

4. ученикам можно дать необязательное домашнее задание по составлению аналогичных задач;

5. если на уроке время ограничено, то эти задания можно применять на занятиях математического кружка.

Система развивающих заданий

Аналогия

Аналогия – это сходство между объектами в некотором отношении. Использование аналогии в математике является одной из основ поиска решения задач. Задачи этой серии направлены на отработку таких познавательных приемов, как проведение словесных аналогий и нахождение аналогий между фигурами.

Например:

1.уменьшаемое – разность, множитель - …?

2.продолжите ряд: 1, 5, 13, 29, …

7, 19, 37, 61, …

Исключение лишнего

В каждой задаче этой серии указаны четыре объекта, из которых три в значительной мере сходны друг с другом, и только один отличается от всех остальных.

Например,

1. Сумма, разность, множитель, частное

2. 9, 12, 8, 15

3. см, дм, м², км.

В худшем случае

Это прием решения задачи, где для доказательства какого-либо утверждения можно рассмотреть самый неудобный, худший случай, в котором утверждение выполняется. Если мы докажем утверждение для худшего случая, то тем более оно будет верно и в остальных случаях. Главное – правильно определить этот худший случай.

Например:

1.В классе 37 человек. Докажите, что среди них найдутся четыре человека, родившиеся в один и тот же месяц.

2.Есть три ключа от трех замков. Какое наименьшее количество проб нужно осуществить, чтобы подобрать ключи к замкам?

Классификация

Классификация – это общепознавательный прием мышления, суть которого заключается в разбиении данного множества объектов на попарно непересекающиеся подмножества (классы). Число таких подмножеств, а также их состав зависит от основания классификации (т.е. признака, существенного для данных объектов), которое может принимать различные значения.

Например:

Что объединяет слова длина, площадь, масса? Какое слово к ним подходит: секунда, центнер, величина, метр?

Логические задачи

Логические задачи – это задачи, требующие умения проводить доказательные рассуждения, анализировать.

Например:

1.Ира, Даша, Коля и Митя собирали ягоды. Даша собрала ягод больше всех, Ира – не меньше всех. Верно ли, что девочки собрали ягод больше, чем мальчики?

2.Наташа произнесла истинное утверждение. Лена повторила его дословно и оно стало ложным. Что сказала Наташа?

Перебор

Сущность этого приема заключается в проведении организованного разбора и анализа всех случаев, которые потенциально возможны в ситуации, описанной в задаче.

Например:

1. Сколько имеется двузначных чисел, у которых среди цифр есть хотя бы одна пятерка?

2. В числе 48352 зачеркните такие две цифры, чтобы число, образованное оставшимися цифрами в том же порядке было наибольшим (наименьшим).

Задачи с геометрическим содержанием

1.Нарисуйте два треугольника так, чтобы их общей частью были: а) шестиугольник; б) пятиугольник; в) четырехугольник; г) отрезок; д) точка.

2.Разрезать квадрат на две равные фигуры (10 способов).

3.Деревянный куб покрасили со всех сторон, потом распилили на 27 одинаковых кубиков. Сколько кубиков имеют 3 окрашенные грани, 2 окрашенные грани? Сколько кубиков не окрашено?

Задачи на переливание

1.В первый сосуд входит 10 литров воды. Как, используя еще два пустых сосуда по 5 и 7 литров, разделить воду на две части?

2. Восьмилитровый бидон наполнен водой. Как с помощью трехлитровой и пятилитровой банок отлить 1л воды?

Задачи-шутки

1.Гусь стоит 20 рублей и еще половину того, сколько он на самом деле стоит. Сколько стоит гусь?

2.Сколько концов у двух палок, у трех палок, у пяти с половиной палок?

3.Какой математический знак нужно поставить между 5 и 6, чтобы полученное число было больше 5, но меньше 6?

4.Один поезд отправляется из Москвы в Пермь, одновременно с ним выходит поезд из Перми в Москву, скорость которого в два раза больше. Какой из поездов в момент встречи будет находиться дальше от Москвы?

5.Крышка стола имеет 4 угла. Один угол отпилили. Сколько углов осталось?

Занимательные задачи

1.Чему равно произведение -109*(-108)*…107*108?

2.Чему равна сумма -65+ (-64)+(-63)+…+64+65+66?

3.Вдоль всей траектории забега поставили 15 столбов. После начала забега спортсмен был у третьего столба через три минуты. За сколько минут он пробежит весь путь? (Скорость спортсмена считать постоянной).

Для формирования логического мышления применяются тесты, которые можно разделить на три основные группы:

- словесные,

- символико-графические

- комбинированные.

К первой группе относятся анаграммы и вербальные тесты. Анаграммой называется слово, в котором поменяны местами все или несколько букв. Сущность упражнения состоит в восстановлении «разрушенного» слова, например, НЛКИЕАЙ (ЛИНЕЙКА). Интересны для учащихся и случаи, когда в упражнении включено задание: «Исключить лишнее слово». Например,  МАПРЯЯ, ЧУЛ, РЕЗОТОК, РИПЕТРОМ. Упражнение состоит из двух частей:

1) решить анаграммы (прямая, луч, отрезок, периметр);

2) исключить лишнее слово, т.е. определить логическую закономерность, лежащую в основе подбора этих терминов, и исходя из нее, исключить логически несовместимое слово.

В данном случае лишним словом будет «Периметр», т.к. это величина, а остальные слова – геометрические фигуры. Таким образом, ученики не только усваивают математическую терминологию, но и развивают логическое мышление. Или же, например, нимотро, ансерк, чеврнисрете. (монитор, сканер, винчестер. Лишнее слово: винчестер)
Задания символико-графического типа предназначаются для формирования умений и навыков применения теоретического материала при решении задач, для повторения и закрепления материала, для ее систематизации и обобщения. Вот несколько примеров:



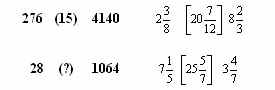
К комбинированным логическим тестам относятся задания, содержащие как вербальную версию, так и символико-графическую. Таким образом, осуществляется связь математики с языковым развитием учащихся. Такие упражнения требуют не только наблюдательности, но и умения устанавливать необычные связи между объектами. Например «Вставьте пропущенное слово»:




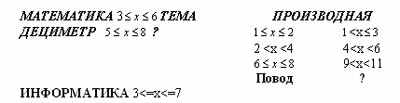
Проведенная работа по формированию логического мышления у учащихся 5-11 классов позволяет сделать следующие выводы:

· логическое мышление развивается интенсивнее, если создавать на уроке атмосферу уважения, поощрять инициативу и стимулировать творчество учащихся;

· система развивающих заданий позволяет привить интерес к предмету, дает более глубокое и полное понимание изучаемых тем, развивает мышление учащихся.


Результативность.

Система заданий является средством повышения уровня логического мышления учащихся 5-11 классов, развивает интеллект. Повышается успеваемость учащихся, прививается интерес к предмету.


Адресная направленность опыта.

Система заданий составлена для учителей, преподающих в 5-6 классах, применяется при решении устных и полуустных заданий, для работы с одаренными детьми, кружковой работы в 5-11 классах и факультативов.

Устойчивые положительные результаты можно получить при выполнении методических рекомендаций к данной системе заданий; при подборе заданий, имеющих отношение к изучаемой теме.


Использованная литература.  

1. Мочалова О.Б. Типология творческих задач. Учебно-методическое пособие для студентов, учителей и учащихся. Уфа, 2001.
   
2. Мочалова О.Б., Мочалова Н.М. Задачи на развитие сообразительности. Учебно-методическое пособие для учителей и учащихся. Уфа, 2001.
   
3. Мочалова О.Б. Учимся рассуждать логически (шаг третий). Учебно-методическое пособие для  учителей и учащихся. Уфа, 2001.
   
4. Нестеренко Ю.В. и др. Задачи на смекалку. – М.: Дрофа, 2006. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. – М.:
   
5. Нестеренко Ю.В. и др. Задачи на смекалку. – М.: Дрофа, 2006. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. – М.: Просвещение, 1988.
   
6. Олехник С.Н., Нестеренко Ю.В., Потапов М.К. Старинные занимательные задачи. – М.: Дрофа, 2006.
   
7. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка. – М.: Просвещение, 1988.
   

Методические пособия.

1. Математика 5 класс. /Зубарева И.И, Мордкович А.Г. 2005 год
   
2. Математика 6 класс /Зубарева И.И., Мордковича А.Г. 2005 год
   
3. Алгебра 7класс./Мордкович А. Г.2005год
   
4. Алгебра 8 класс /Мордкович А.Г.2008год
   
5. Алгебра 9класс/ Дорофеев Г.В., Суворова С.Б.
   
6. Алгебра и начала анализа 10 класс /Мордкович А.Г., Семёнова П.В. 2005год
   
7. Алгебра и начала анализа 11класс/ Мордкович А.Г., Семёнова П.В. 2002 год
   
8. Геометрия 7класс-9 класс /Атанасян Л.С., БутузовВ.Ф. 2002 год
   
9. Геометрия 10-11 класс /Атанасян Л.С., БутузовВ.Ф. 1992,2002 год
   
10. Программа Программы для общеобразовательных учреждений: Алгебр 7 – 9кл. / авт. Г.В.Дорофеев, С.Б. Суворова/ М. Просвещение 2008г. 9.клас
    
11. Программы для общеобразовательных учреждений: математика5.-11класс Мордкович А.Г. Просвещение 2008г.
    
12. Программы для общеобразовательных учреждений: Алгебр 7 – 9кл. / авт. Г.В.Дорофеев, С.Б. Суворова/ М. Просвещение 2008г.
    

Матема- тика	Алгебра	Программы Алгебра и начала анализа. 10-11 классы. Автор И.И. А.Г.Мордкович .-М.: Мнемозима, 2007г.	1.А.Г. Мордкович «Алгебра и начала анализа 10-11кл.»М. Мнемозима 2000г.	1. А.Г. Мордкович» Методическое пособие Мнемозима 2000г.
Матема-тика	Геомет-рия	Программы для общеобразовательных школ, гимназий, лицеев. Математика. 5-11 кл. для общеобразовательных учреждений (Сост. Кузнецова Г.М., Миндюк Н.Г.)– М.: Дрофа, 2001.	1.Л.С. Атанасян «Геометрия 10,11.кл.» М. Просвещение 2004г. 2. Дидактические материалы 2003г.	1.В.А. Яровенко «Поурочные разработки по геометрии 10кл.,11кл М. «ВАКО » 2006г.

Программы государственные, дополненные элективными курсами и кружками. Учебники выбраны так, чтобы учащиеся получили глубокие и прочные знания и подготовились к дальнейшему продолжению учёбы в различных учебных заведениях.


Обоснование выбора учебно–методического комплекта по математике

Из всего многообразия учебно-методических комплексов наиболее приемлемыми для себя и своих воспитанников считаю УМК издательства «Мнемозина», разработанные группой – А.Г.Мордкович и другие. Работаю по ним уже 6-й год. Учебники издательства «Мнемозина» соответствуют основному компоненту государственного стандарта общего образования и входят в Федеральный перечень. В настоящее время я использую учебно-методические комплекты  для 7-9 классов, приоритет в  содержательно-методической линии, которых отдаётся функционально–графическому курсу.

Компоненты УМК:

• Программы  «Алгебра 7-9».
  
• Учебник.
  
• Задачник.
  
• Сборник контрольных работ.
  
• Сборник самостоятельных работ.
  
• Учебное пособие «Тематические тесты».
  
• Методическое пособие для учителя.
  
• Пособие «События. Вероятности. Статистическая обработка данных» – дополнительные параграфы к курсу алгебры 7-9 классов.
  

 Концепция учебника. Математика – гуманитарный предмет, который позволяет субъекту правильно ориентироваться в окружающей действительности, «ум в порядок приводит» и оказывает существенное влияние на развитие речи обучаемых, не только внутри предметной области. Математика описывает реальные процессы на математическом языке в виде математических моделей, поэтому математический язык и математическая модель – ключевые слова в постепенном развёртывании курса. Математика предстаёт перед учащимися не как набор разрозненных фактов, а как цельная развивающаяся и в то же время развивающая дисциплина общекультурного характера. Именно поэтому  из традиционных для любого обучения вопросов: «что?» «как?» «зачем?» – на первое место ставится вопрос «зачем?».

Стиль изложения. Материал учебника интересно читать, он представляет собой развёрнутое повествование, в котором есть интрига. Внутренняя интрига заложена практически в каждой главе и в большинстве параграфов, достигается это за счёт ненавязчивой и естественной постановки проблем, которые по объективным причинам в данном месте курса решены быть не могут, но будут решены в дальнейшем. Стиль изложения во многом расцвечен непривычными для математической рутинной лексики оборотами, и в то же время изложение характеризуется чёткостью, алгоритмичностью, выделяются основные этапы рассуждений, с фиксацией внимания на выделенных этапах.

Психолого-педагогические и методические особенности учебника.

Проблемное изложение материала. Проблема – это то, что мы сегодня решить не можем, то, что мучает нас продолжительное время, к решению чего мы постепенно приближаемся, это то, что, будучи разрешено, даёт эмоциональный заряд, приносит радость. Именно такое понимание проблемного обучения проходит по всему курсу.

Диалектический подход к введению математических понятий. Лишь простейшие понятия даются сразу в готовом виде, остальные же вводятся постепенно, с уточнениями и корректировкой, а некоторые вообще остаются на интуитивном уровне восприятия до тех пор, пока не наступит благоприятный момент для их точного определения.

Развивающее обучение. Особенность учебника не в сухом сообщении математических фактов, а в развитии учащихся посредством продвижения в предмете, иными словами приоритетным является не информационное, а развивающее поле курса. В учебнике практически реализованы принципы развивающего обучения, сформулированные Л.В.Занковым: обучение на высоком уровне трудности; прохождение тем программы достаточно быстрым темпом; ведущая роль теоретических знаний; осознание процесса обучения (ученик должен видеть, как он умнеет в процессе изучения материала – это достигается проблемным обучением); развитие всех учащихся (учитывая уровень каждого). [6]

Работа по УМК А.Г.Мордковича предусматривает использование педагогических технологий: личностно-ориентированного обучения, проблемного и развивающего обучения.

– Использование технологии личностно-ориентированного обучения предполагает «признание ученика главной действующей фигурой всего образовательного процесса», весь учебный процесс строится на основе этого главного положения.

– Проблемное обучение основано на ряде психологических посылок: мышление не сводится лишь к функционированию готовых знаний. Оно процесс продуктивный, творящий новые знания. Начало и источник творческого мышления — это проблемная ситуация. Она вызывает познавательную потребность как внутреннее условие. Через познавательную потребность преподаватель может управлять процессом усвоения учащимися новых знаний.

Цель технологии проблемного обучения – стимулирование интеллектуальной активности учащихся; развитие процесса мышления, индивидуальных особенностей ума; формирование внутренних мотивов учения, способов умственной деятельности учащихся, их творческих способностей; самостоятельный поиск путей решения проблем. Также — формирование творческого, нестандартного мышления, освобожденного от привычных стереотипов и штампов.

– Особенности развивающего обучения:

• обучение на высоком уровне трудности;
  
• ведущая роль теоретических знаний;
  
• обучение быстрым темпом;
  
• осознание школьниками процесса учения;
  
• целенаправленная и систематическая работа над общим развитием всех учащихся, включая слабых.
  

Цель технологии развивающего обучения – общее развитие ученика, не только познавательных процессов; ученик — активный субъект учебной деятельности; учитель — организатор коллективной поисковой деятельности; знания, умения и навыки не есть конечная цель обучения, а средство общего развития.


Обоснование выбора УМК по геометрии:

Сравнительный анализ

1. Атанасян Л. С. Геометрия 7–9 классы;

2. Погорелов А. В. Геометрия 7–9 классы;

3. Шарыгин И. Ф. Геометрия 7–9классы;

В рассмотренных учебниках тема «Теорема Пифагора вводится по-разному.

Например, в учебнике Погорелова изучению теоремы Пифагора предшествует изучение косинуса угла; вводится определение косинуса угла и доказывается теорема: «Косинус угла зависит только от градусной меры угла». И это утверждение используется при доказательстве теоремы Пифагора.

Совершенно иначе вводится теорема Пифагора в учебном пособии Шарыгина И.Ф. Доказательство теоремы Пифагора следует за изучением теоремы о соотношениях в прямоугольном треугольнике: «В прямоугольном треугольнике справедливы следующие соотношения: Высота, опущенная на гипотенузу прямоугольного треугольника, есть среднее пропорциональное между отрезками гипотенузы, на которые она этой высотой разделена; катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу». В результате такого порядка изложения материала, само доказательство теоремы Пифагора укладывается буквально в две строчки. Кроме того только в этом учебнике учащиеся могут познакомиться с обобщённой теоремой Пифагора: «Пусть АВС - прямоугольный треугольник с гипотенузой АВ. Рассмотрим три соответственных отрезка в треугольниках АВС, ACD, CBD (CD – высота в АВС). 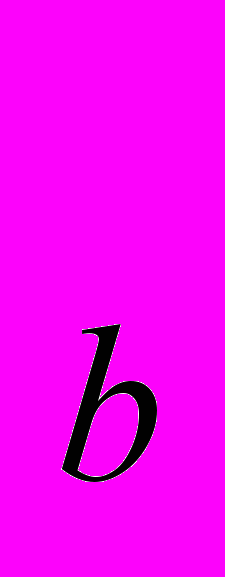Обозначим их через l, lи l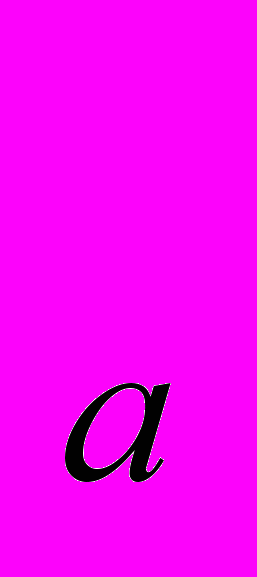 соответственно. Тогда справедливо равенство 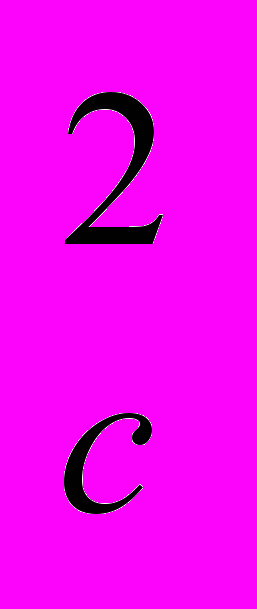l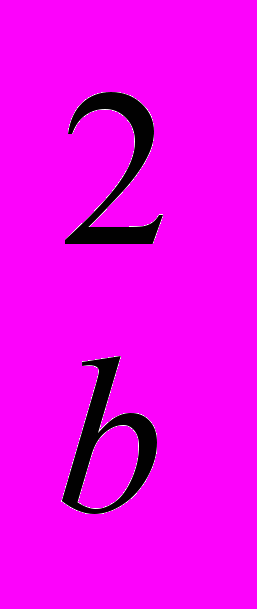=l+l».

В учебнике Атанасяна Л. С. Данная тема вводится после рассмотрения темы «Площади и их свойства». Здесь при доказательстве теоремы Пифагора автор опирается на свойства площадей.

По теме « Теорема Пифагора» в учебниках Атанасяна Л. С., ПогореловаА. В. И Шарыгина И. Ф. рассматривается большое количество задач на построение, на доказательство, на вычисление отношений и другие. Задачи в процессе обучения выполняют дидактические, познавательные, развивающие и воспитательные функции. Относительно перечисленных функций проведём сравнительный анализ систем упражнений.

В каждом учебнике есть своя система задач, отличающая их друг от друга. Например, в учебном пособии Шарыгина И. Ф. больше задач дидактического характера, есть и задачи, несущие развивающую функцию как то «Разрежьте прямоугольный треугольник на три подобных между собой треугольника». Есть задачи познавательного характера: «Докажите, что в данном треугольнике произведение стороны на проведённую к ней высоту постоянно». В этом учебнике почти нет задач прикладного характера. Упражнения расположены вразброс не соответствуя последовательности изложения теоретического. По этому вопросу мы не пришли к общему мнению.

Задачи в учебнике Погорелова А. В. Предлагаются от более простой к более сложной, много задач по готовым чертежам. Большинство упражнений познавательного характера, способствующие получению новых фактов, которые затем используются при решении других, более сложных задач. Только в этом пособии встречаются задачи на построение. Например «даны отрезки a и b. Как построить отрезки

1)√a²+b²

2)√a²+b²

Задачи располагается в соответствии с пунктами теоретического материала.

В учебнике Атанасяна Л. С. предлагаются задачи с решениями. Большое внимание уделяется задачам, несущим дидактическую функцию. Очень интересные познавательные задачи: « Докажите, что площадь квадрата, построенного на катете равнобедренного прямоугольного треугольника, вдвое больше площади квадрата, построенного на высоте, проведённой к гипотенузе. В этом учебном пособии как и пособии Шарыгина И. Ф. нет задач прикладного характера, не указан номер теоретического пункта, но задания расположены в том порядке, в каком идёт изложение теоретического материала.

Во всех рассмотренных учебниках тема «Теорема Пифагора» вводится различно, какой – то материал лучше, какой – то хуже, нет идеальных учебных пособий.

Вывод: Мы считаем, что наиболее доступным, понятным, содержащим большое количество рисунков и упражнений различного характера является учебник Атанасяна Л. С.