Geum.ru

Анкета участника конкурса

Вид материалаАнкета

Содержание


Урок геометрии в 8 классе
Тема урока
Цель урока
Ход урока.
Задачи по индивидуальным карточкам
V. Самостоятельная работа.
VII. Домашнее задание
Подобный материал:
Анкета участника конкурса

  1. Фамилия: Ерилова
  2. Имя: Галина
  3. Отчество: Федоровна
  4. Контактный адрес: 634526, г. Томск, д. Лоскутово, ул. Ленина 27а
  1. E-mail : loskutovo@rambler.ru
  2. Несколько слов о себе: Учитель высшей квалификационной категории, работаю в данной школе 20 лет в 5-11 общеобразовательных классах, веду факультативные курсы по углубленному изучению математики, элективные и профильные курсы.


Описание методической разработки

  1. Название: урок.
  2. Краткая аннотация: Урок геометрии в 8 классе. Тип урока: урок обобщения и систематизации знаний по теме «Подобие треугольников и применение подобия». Урок направлен на проверку знаний теоретического материала по данной теме, на отработку навыков решения задач на подобие треугольников, на применение свойств биссектрисы и медиан треугольника, на нахождение пропорциональных отрезков в прямоугольном треугольнике. Формы работы, применяемые на уроке: фронтальная, индивидуальная, самостоятельная, групповая. Методы обучения, применяемые на уроке: сочетание словестных, наглядных и практических, репродуктивных и проблемно-поисковых; методов работы под руководством учителя и самостоятельной работы учащихся.
  3. Учебный предмет: геометрия
  4. Уровень образования школьников: 8 класс общеобразовательной школы
  5. Форма учебной работы: классно-урочная
  6. Полное описание разработки:

- На данном уроке дети должны приобрести навыки решения задач (хотя бы элементарных в зависимости от возможностей учащихся) с применением подобия треугольников, свойств биссектрисы и медиан треугольника, пропорциональности отрезков в прямоугольном треугольнике; навыки работы с чертежами; навыки составления задач; навыки самостоятельной и групповой работы.

- В связи с типом урока, применением на уроке различных видов деятельности, методов обучения и компьютера особенности роли учителя, считаю, должны состоять в умении учитывать реальные учебные возможности учащихся класса и организации дифференцированного подхода; в умении концентрировать внимание школьников на усвоении важнейших понятий, теоретических положений, закономерностей, выделении главного, существенного в содержании урока; в умении комплексного использования различных средств обучения (учебника, раздаточного материала, наглядных пособий, компьютера); не оставить без внимания слабоуспевающих детей и дать им возможность реализоваться; в умении четко следовать замыслу урока и, возможно, гибко перестроить его ход при неожиданном изменении учебных ситуаций.

- Урок желательно проводить с применением компьютера для показа слайдов по отработке теоретического материала и решению задач на готовых чертежах, для работы с тестом и конфигурацией, заданной рисунком.


Муниципальное общеобразовательное учреждение,

средняя общеобразовательная школа № 33 г. Томска


Ерилова Галина Федоровна


Урок геометрии в 8 классе

Методическое пособие для учителя (план урока)

Удостоено дипломом за участие в конкурсе методических разработок проекта Национального фонда подготовки кадров «Интернет-поддержка профессионального развития педагогов» на Российском общеобразовательного портале


Томск - 2007


Тема урока:

Подобие треугольников и применение подобия к решению задач.

Тип урока: Урок обобщения и систематизации знаний учащихся.

Цель урока:

- Закрепить, обобщить и систематизировать теоретические знания по теме «Подобие треугольников и применение подобия»;

- Закрепить умения и навыки решения задач с применением определения и признаков подобия треугольников, на применение свойств биссектрисы и медиан треугольника, на нахождение пропорциональных отрезков в прямоугольном треугольнике.

Оборудование:

- компьютер;

- раздаточный материал.

Ход урока.

. Повторение теоретического материала по теме “Подобие треугольников и применение подобия к решению задач” по схеме (слайды).



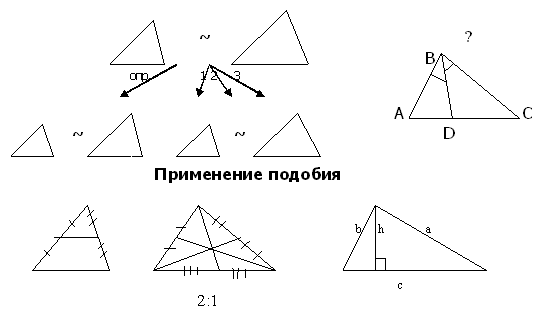
Вопросы учителя и предполагаемые ответы учащихся:
  1. Что могут обозначать на схеме два верхних треугольника? (Это подобные треугольники).
  2. Что обозначают стрелки, проведенные от этих треугольников? (Треугольники могут быть подобны по определению и по трем признакам подобия).
  3. Сформулируйте определение подобия и три признака подобия.
  4. А что за чертеж под знаком вопроса? Что он вам напоминает? (Теорему о биссектрисе угла треугольника).
  5. Сформулируйте эту теорему.
  6. А о чем вам говорят три нижних треугольника? Что за обозначения на них? Опишите каждый из них. (Учащиеся должны ответить, что первый чертеж соответствует теореме о средней линии треугольника, второй выражает свойства медиан треугольника, третий – утверждения о пропорциональных отрезках в прямоугольном треугольнике).
  7. Сформулируйте эти свойства.

II. Устно. Решение задач на готовых чертежах (слайды).
  1. Найдите пары подобных треугольников и определите признак подобия:


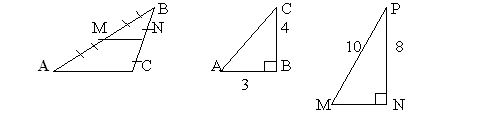
  1. Треугольники ABC и MNP подобны. Периметр треугольника MNP равен 105. Найдите отношение площадей треугольников.



. Тест на установление истинности или ложности высказываний (отвечать “да” или “нет”).
  1. Два треугольника подобны, если их углы соответственно равны и сходственные стороны пропорциональны.
  2. Два равносторонних треугольника всегда подобны.
  3. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
  4. Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?
  5. Периметры подобных треугольников относятся как квадраты сходственных сторон.
  6. Если два угла одного треугольника равны 60 и 50, а два угла другого треугольника равны 50 и 80, то такие треугольники подобны.
  7. Два прямоугольных треугольника подобны, если имеют по равному острому углу.
  8. Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.
  9. Если отрезки гипотенузы, на которые она делится высотой, проведенной из вершины прямого угла, равны 2 и 8 см, то эта высота равна 4 см.
  10. Если медиана треугольника равна 9 см, то расстояние от вершины треугольника до точки пересечения медиан равно 6 см.

(Распределение баллов по заданиям теста: 1. 1б., 2. 1б., 3. 1б., 4. 1б., 5. 1б., 6. 2б.,7. 2б., 8. 2б., 9. 3б., 10. 3б.

Ключ к тесту: 1. да; 2. да; 3. да; 4. нет; 5. нет; 6. нет; 7. да; 8. нет; 9. да; 10. да.

Форма проверки теста – самопроверка).


V. Решение задач на применение подобия треугольников

(Подобраны задачи различного типа на применение подобия треугольников к разным ситуациям и разным геометрическим фигурам для закрепления материала по данной теме).

Наиболее подготовленные ребята решают задачи по индивидуальным карточкам у доски, либо самостоятельно в тетрадях с последующей проверкой учителя, либо «легко поддающиеся» задачи решают только на черновиках с обязательным объяснением учителю (устно «шепотом»), а остальные оформляют в тетради (на усмотрение учителя в зависимости от степени подготовленности учащихся).

Задачи по индивидуальным карточкам:
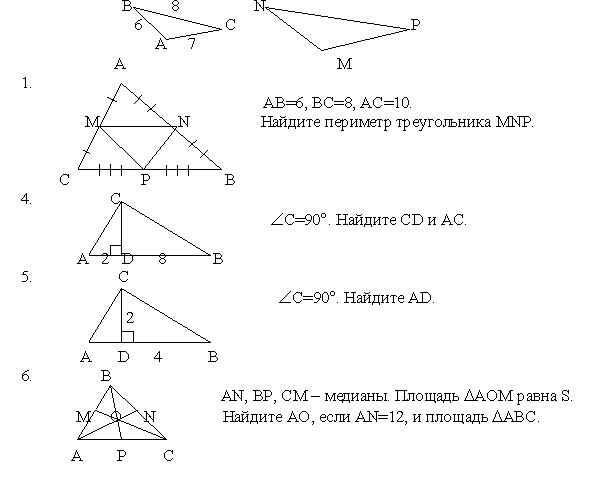
  1. Треугольники ABC и MNK подобны. Их сходственные стороны относятся как 8:5. Площадь треугольника ABC больше площади треугольника MNK на 25 кв.см. Найдите площади треугольников. (Ответ: 16 1/39 и 41 1/39 см 2).
  2. В прямоугольном треугольнике ABC к гипотенузе AC проведена высота BD, BC=2см, AD=3см. Найдите DC, BD, AB. (Ответ: DC = 1см, BD = √3 см, AB = 2√3 см).
  3. Основания трапеции равны 8 и 12 см. Боковые стороны, равные 4,5 см и 5,2 см, продолжены до пересечения в точке M. Найдите расстояния от точки M до концов меньшего основания. (Ответ: 9 и 10,4 см).
  4. В прямоугольном треугольнике с углом 30 и меньшим катетом 6 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями. (Ответ: 9 + 3√3 (см)).
  5. На сторонах AB, BC, AC треугольника ABC отмечены точки D,E,P соответственно, AB=9см, AD=3см, AP=6см, DP=4см, BE=8см, DE=12см.

а) Найдите отношение площадей треугольников DBE и ADP; (Ответ: 4)

б) Докажите, что DE и AC параллельны. (Решение: Рассмотреть соответственно равные углы треугольников DBE и DAP. Равные углы BDE и DAP являются соответственными при параллельных прямых DE и AP и секущей AB. Следовательно прямые DE и AC параллельны).

Остальные учащиеся класса решают задачи, тексты которых должны лежать у них на партах, сопровождая их решение подробным разбором у доски. (Если класс затруднится с решением, учитель открывает на доске сделанный заранее чертеж-заготовку и по нему направляет рассуждения учащихся).

Задачи:
  1. Диагонали выпуклого четырехугольника ABCD пересекаются в точке O так, что OC=5см, OB=6см, OA=15см, OD=18см.

а) Найдите отношение площадей треугольников AOD и BOC; (Ответ: 9)

б) Докажите, что четырехугольник ABCD – трапеция. (Решение: Равные углы OBC и ODA подобных треугольников BOC и AOD являются накрест лежащими при параллельных прямых BC и AD и секущей BD. Следовательно прямые BC и AD параллельны, и четырехугольник ABCD является трапецией).
  1. Высоты, проведенные из вершины тупого угла параллелограмма, относятся как 2:4. Чему равна меньшая сторона параллелограмма, если периметр равен 90 см? (Ответ: 15 см).
  2. Две сходственные стороны подобных треугольников равны 5 см и 6 см. Разность площадей этих треугольников 22 кв.см. Чему равна площадь меньшего треугольника? (50 см2)
  3. Катеты прямоугольного треугольника ABC равны 5см и 12см. К гипотенузе в ее середине восставлен перпендикуляр OD, пересекающий продолжение меньшего катета в точке D. Чему равна длина отрезка CD? (Ответ: 11,9 см)
  4. В прямоугольном треугольнике ABC (C=90) проведен перпендикуляр CD. Чему равна гипотенуза треугольника ABC, если CD=6см, AD=4,5см? (Ответ: 12, 5 см).

V. Самостоятельная работа.

Работа в группах (количество, состав и выбор групп определяет учитель в зависимости от возможностей учащихся, после завершения работы необходимо заслушать отчет каждой группы).

Задание каждой группе: Опишите конфигурацию, заданную рисунком, применив при этом материал сегодняшнего урока, и, используя ее, составьте несколько задач.



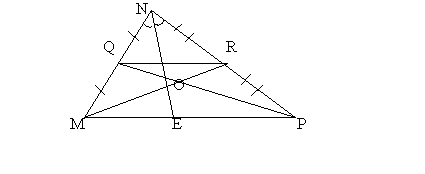
Составьте свою конфигурацию по данной теме и предложите ее для обсуждения.

(Ребята описывают все, что видят на чертеже, используя понятия, теоремы, свойства фигур, изученные ранее по данной теме. Предполагается, что при описании конфигурации учащиеся должны увидеть среднюю линию, биссектрису и медианы треугольника, подобные треугольники, записать отношения, применив свойства биссектрисы и медиан треугольника, составить по чертежу задачи. Тогда можно быть уверенным, что данная тема ими усвоена).

Примеры задач:
  1. Докажите, что QR – средняя линия треугольника MNP.
  2. Докажите, что Δ MNP и Δ QNR подобны. Найдите: a) коэффициент подобия; b) отношение периметров и площадей этих треугольников.
  3. Подобны ли треугольники QOR и MOP? Если «да», то докажите это утверждение.
  4. Найдите ME, если известны MN, NP, EP.
  5. Найдите медианы MR и PQ треугольника MNP, если известны MO и OP и т.д.

VI. Итог урока.
  1. Примерные вопросы учащимся: Понравился ли вам урок? Что вам конкретно понравилось, а что не понравилось? Помог ли вам сегодняшний урок систематизировать знания теоретического материала по данной теме? Помог ли вам сегодняшний урок в приобретении новых знаний или в отработке навыков решения задач по данной теме? Какие пробелы в знаниях по данной теме вы еще не ликвидировали?
  2. Вопросы учащихся.
  3. Слова признательности ученикам за сотрудничество.

VII. Домашнее задание:

Составить кроссворд по теме “Подобие треугольников и применение подобия к решению задач”. Непременное условие при составлении кроссворда – это включение в него двух и более задач.

Литература
  1. Л.С. Атанасян , В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия, 7 – 9: Учеб. для общеобразоват. учреждений. – М.: Просвещение, 2002.
  2. Б.Г. Зив. Дидактические материалы по геометрии для 8 класса. – М.: Просвещение, 2002.
  3. Б.Г. Зив, А.Г. Мейлер, А.Г. Баханский . Задачи по геометрии: Пособие для учащихся 7 – 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2000.