Дифракция
| Вид материала | Лекция |
СодержаниеЗамечание (Рэлей) |
- Дифракция Фраунгофера, 29.62kb.
- Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Дифракция Френеля, 57.78kb.
- Лекция n17 Лекция 17, 369.58kb.
- «Дифракция электронов. Электронный микроскоп», 429.35kb.
- Излучение и дифракция электромагнитных волн в естественных и искусственных неоднородных, 403.99kb.
- Программа по курсу «Атомная и ядерная физика», 28.5kb.
- Реферат Отчет 32 с, 38.18kb.
- Лекция 8 Квантовая механика и концепции неклассического естествознания, 88.7kb.
- Дифракция на круглом отверстии, 97.55kb.
Раздел 2. Дифракция/ 4 а , 4 б /
(6 часов)
Лекция 3 Дифракция
- Принцип Гюйгенса-Френеля
- Дифракция Френеля
- Графическое вычисление амплитуды
- Дифракция на круглом отверстии
- Зонная пластинка
- Дифракция на крае полуплоскости
- Приближение коротких длин волн
Совокупность явлений, наблюдаемых при распространении волн в среде с резкими неоднородностями, связанных с отклонениями от законов прямолинейного распространения т.е. проникновением волн в область геометрической тени и огибанием препятствий.
Наряду с интерференцией дифракция – важнейшее проявление волновой природы явлений => критерий!
Между интерференцией и дифракцией нет существенного отличия – оба явления – суть перераспределения волновой энергии в пространстве в результате суперпозиции волн.
Перераспределение интенсивности, возникающее в результате суперпозиции конечного числа когерентных волн называется интерференцией волн.
Перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, называют дифракцией.
Количественный критерий:
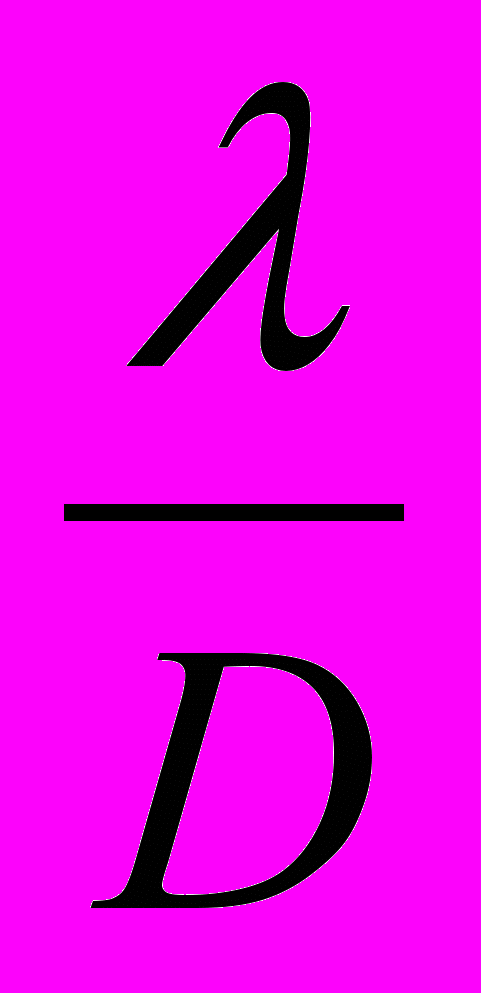 , где λ – длина волны, D – характерные размеры препятствия.
, где λ – длина волны, D – характерные размеры препятствия.-
 → 0 – явлением дифракции можно пренебречь,
→ 0 – явлением дифракции можно пренебречь,
-
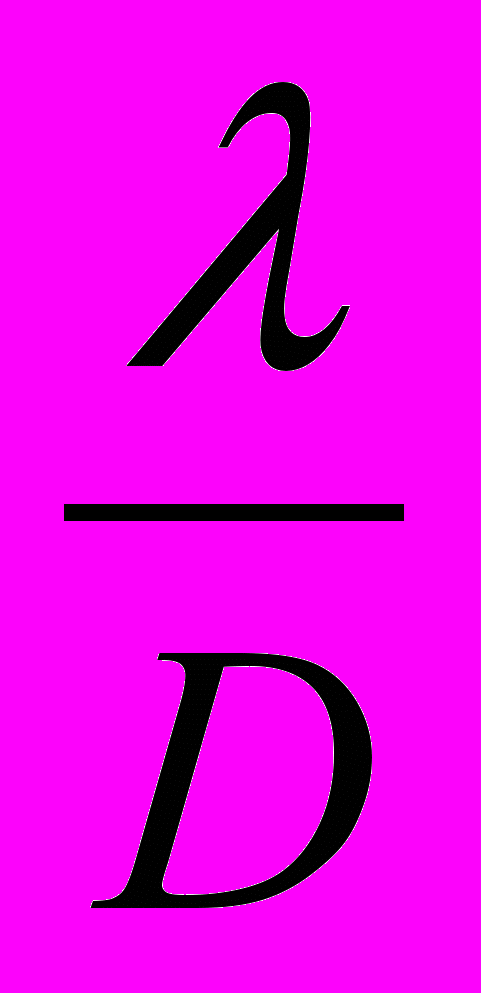 → 1 – явление дифракции необходимо учитывать.
→ 1 – явление дифракции необходимо учитывать.


Принцип Гюйгенса – Френеля
Представление о том, что каждая точка волнового фронта является источником вторичных волн [Гюйгенс] было дополнено [Френель]: эти источники когерентны между собой, а испускаемые ими вторичные волны интерферируют. Т.О. при анализе распространения волн, необходимо учесть их фазу и амплитуду, что позволяет рассчитать интенсивность.

. (3.1)
Количественное выражение принципа Гюйгенса – Френеля:
Каждый элемент волновой поверхности S служит источником вторичной сферической волны, амплитуда которой пропорциональна площади элемента dS и убывает с расстоянием по закону
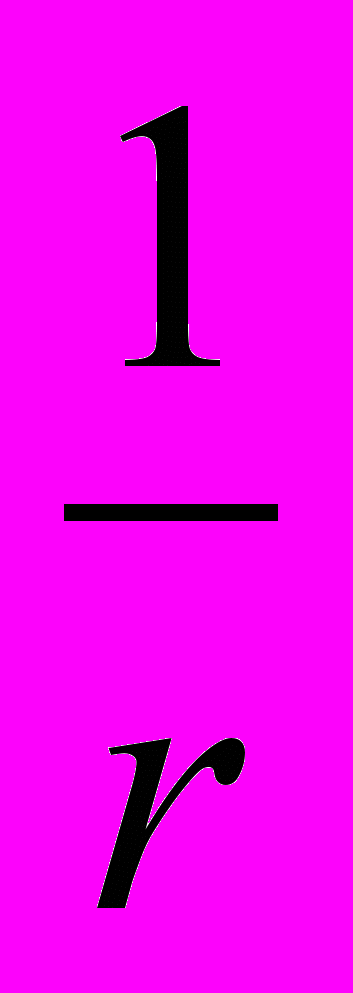 ,
, 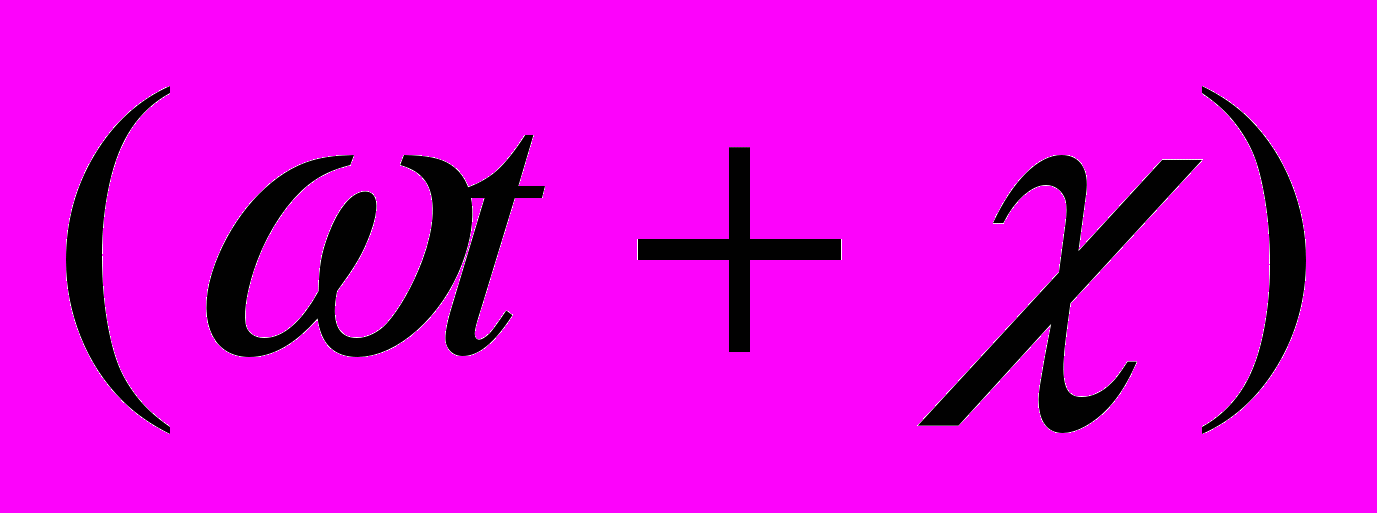 - фаза колебаний на волновой поверхности, к – волновое число, а – определяется амплитудой светового колебания в месте нахождения элемента dS.
- фаза колебаний на волновой поверхности, к – волновое число, а – определяется амплитудой светового колебания в месте нахождения элемента dS.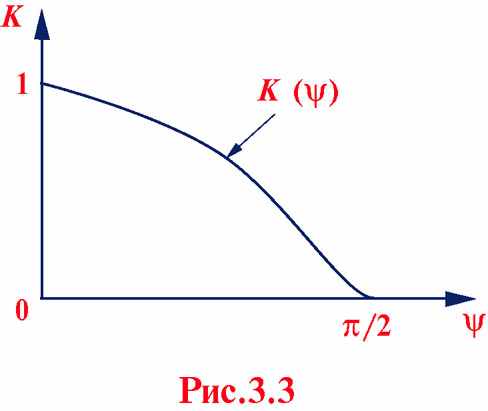
Наконец, фактор
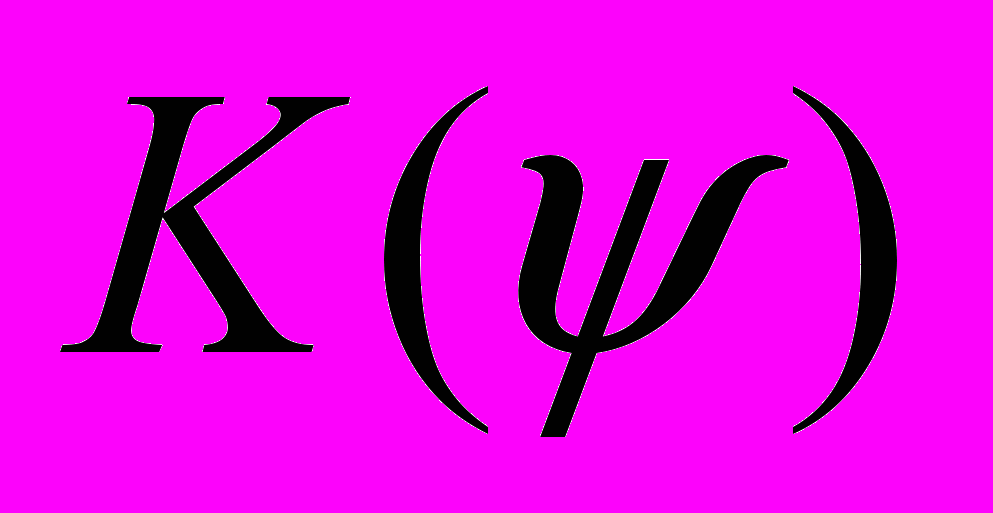 - гладкая функция угла
- гладкая функция угла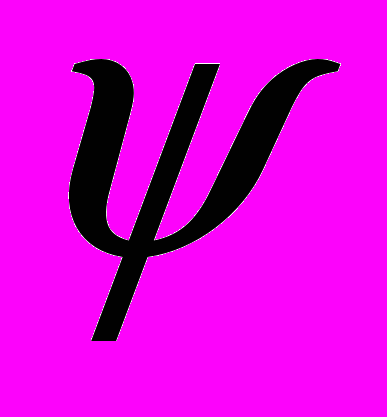 между нормалью
между нормалью 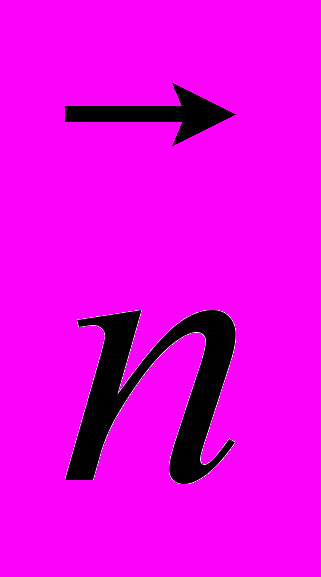 к поверхности dS и направлением от dS к точке наблюдения Р, при этом К(0) = 1, и
к поверхности dS и направлением от dS к точке наблюдения Р, при этом К(0) = 1, и 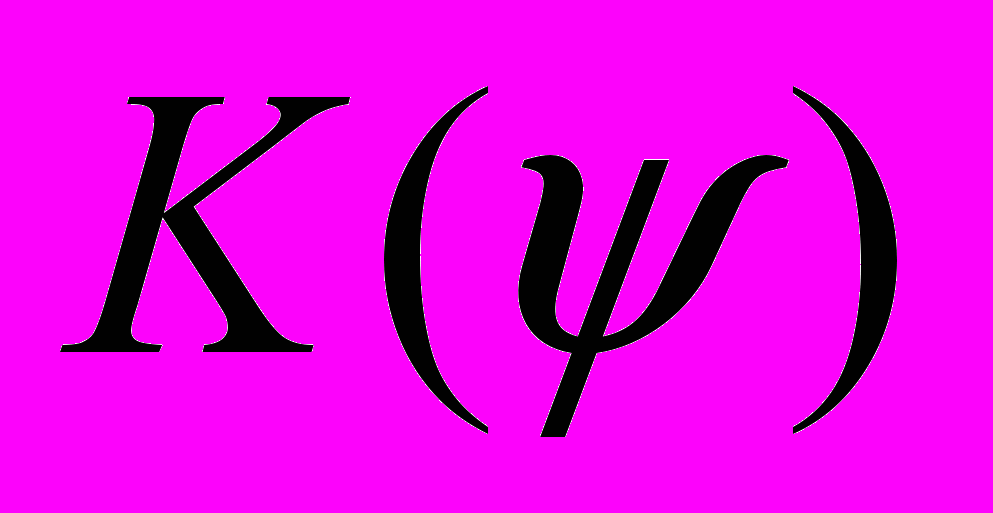 = 0 при
= 0 при 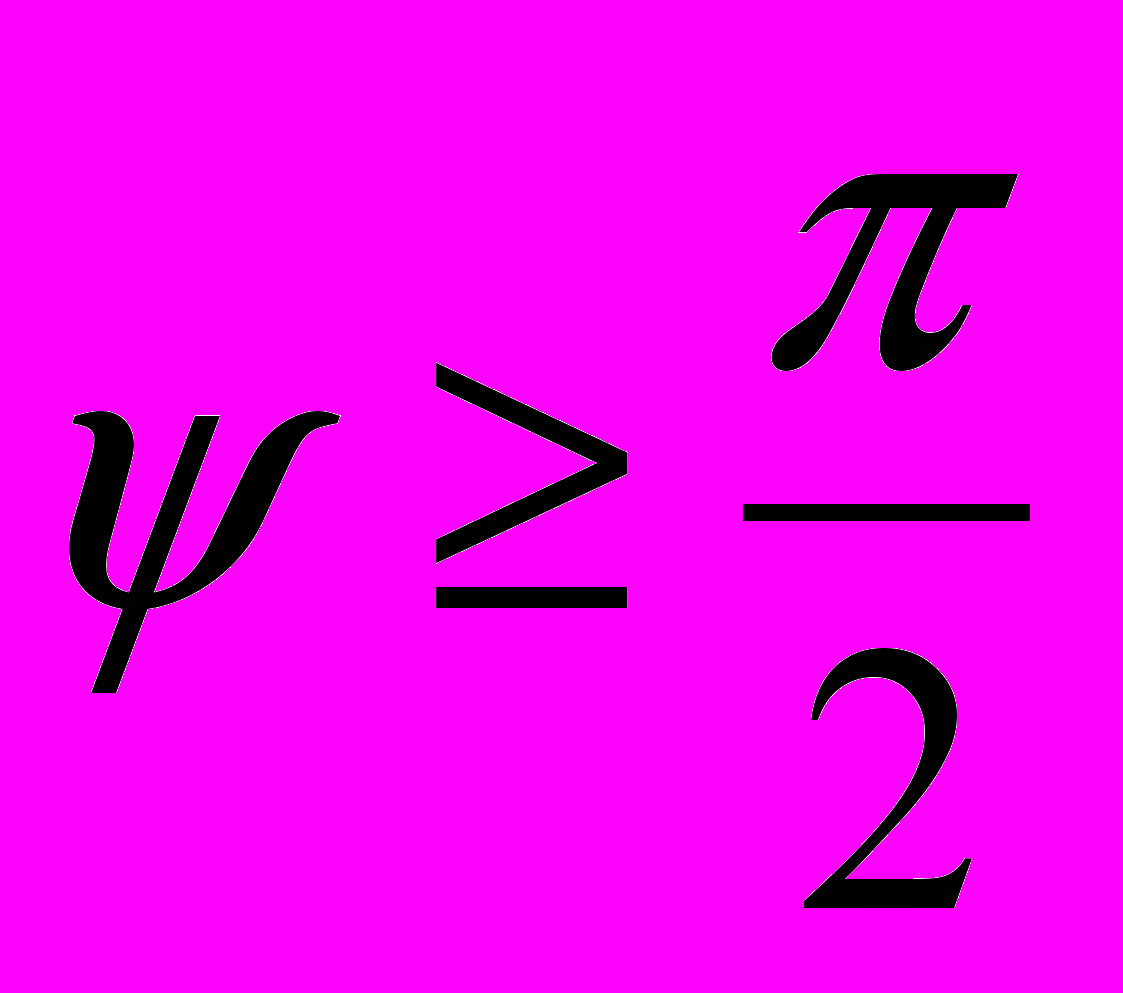 .
.Результирующие колебания в точке Р есть суперпозиция колебаний (3.1), взятых по всей волновой поверхности S за вычетом части, уничтоженной экраном:
(
 3.2)
3.2)Различают два вида дифракции: Френеля и Фраунгофера. Если источник света S и точка наблюдения Р расположены от препятствия достаточно далеко так, что лучи, падающие на препятствие, и лучи, идущие в точку Р, можно считать параллельными, говорят о дифракции Фраунгофера. В противном случае имеем дифракцию Френеля.
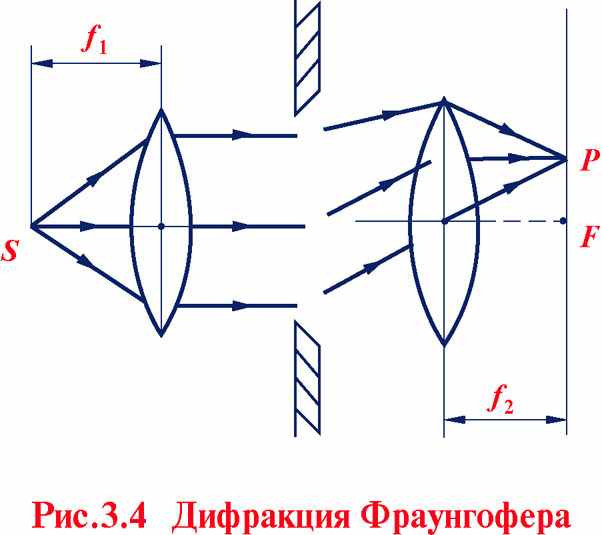
Замечание: Дифракцию Фраунгофера можно смоделировать на конечном расстоянии от точек S и P препятствия. Это делается с помощью двух собирающих линз (см. рис. 3.4). При этом точка S должна находиться в фокусе первой линзы, а точка P в фокальной плоскости второй.
Зоны Френеля
.
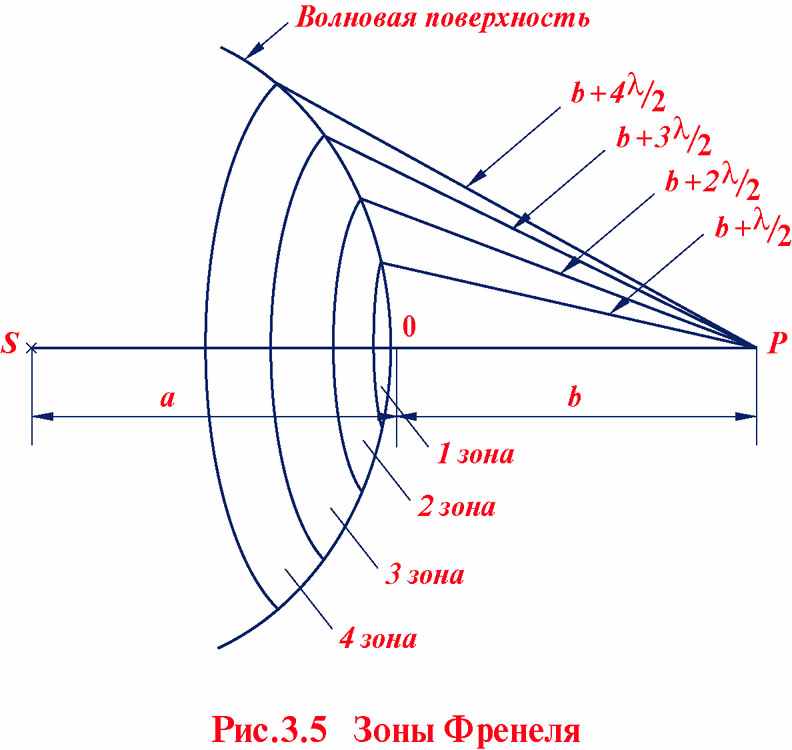
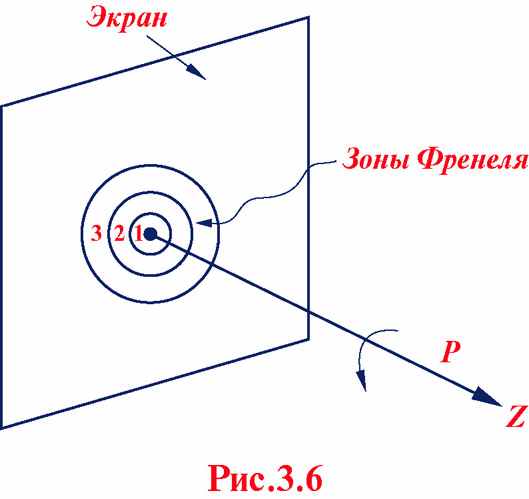
Расчёт амплитуды Ep колебаний в точке Р по формуле (3.2) существенно упрощается в случае наличия симметрии. Если препятствие – отверстие радиусом R в непроницаемой плоскости и центр отверстия лежит на отрезке SP (см. рис. 3.5), система обладает аксиальной симметрией (вращение вокруг оси SP не меняет условия). Волновая поверхность S разбивается на кольцевые зоны – зоны Френеля, построенные так, что расстояние от краёв каждой зоны до точки Р отличается на
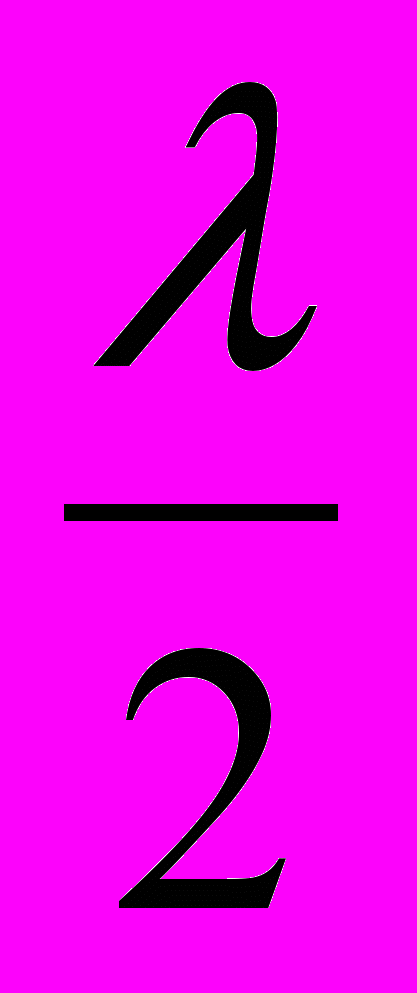 . Каждой точке поверхности любой из зон Френеля соответствует аналогичная точка в соседней зоне, колебания от которой в точке Р отличается по фазе на π. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, находятся в противофазе.
. Каждой точке поверхности любой из зон Френеля соответствует аналогичная точка в соседней зоне, колебания от которой в точке Р отличается по фазе на π. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, находятся в противофазе.
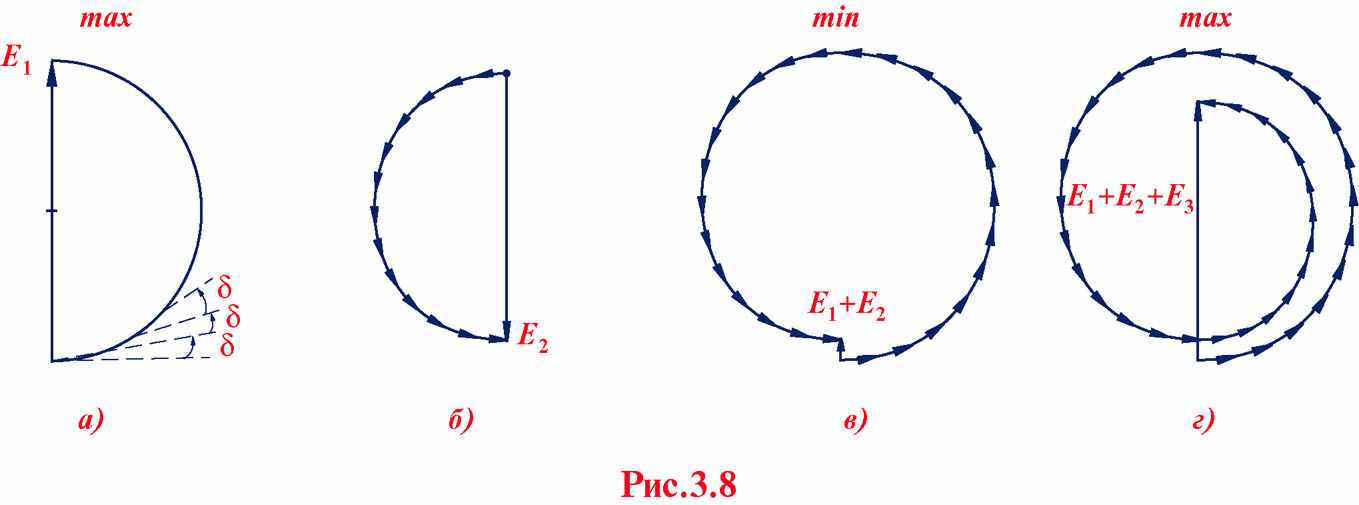
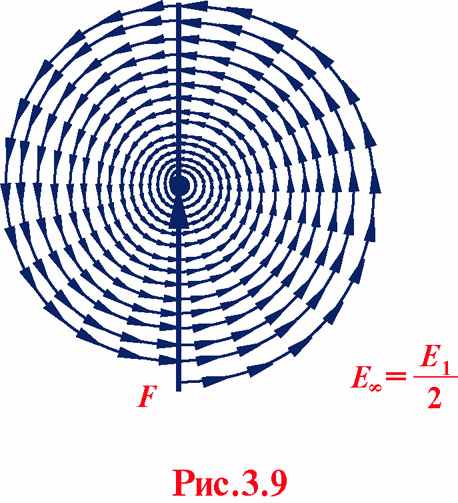
Графический метод сложения амплитуд ( Френель )
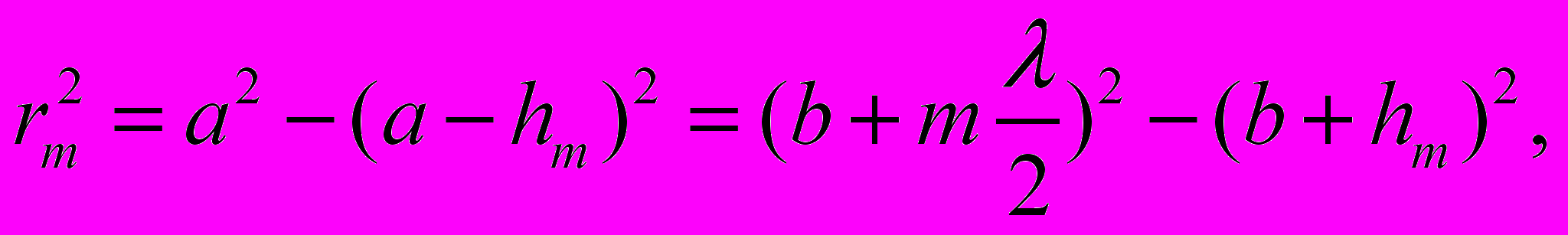 (3.3)
(3.3)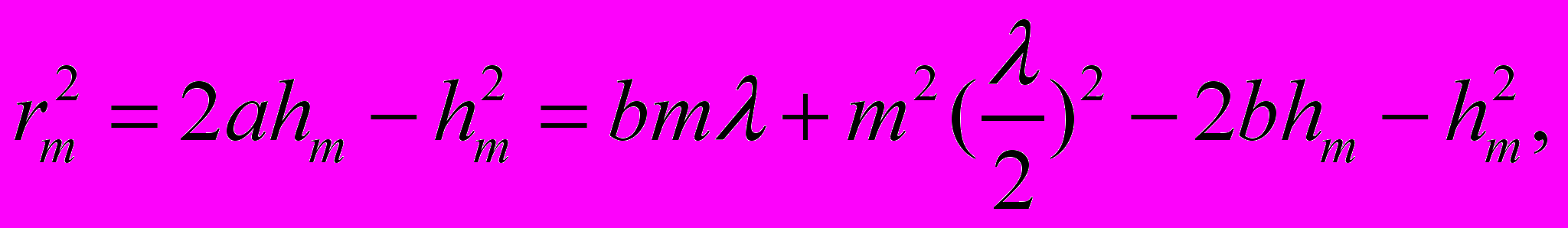 (3.4)
(3.4)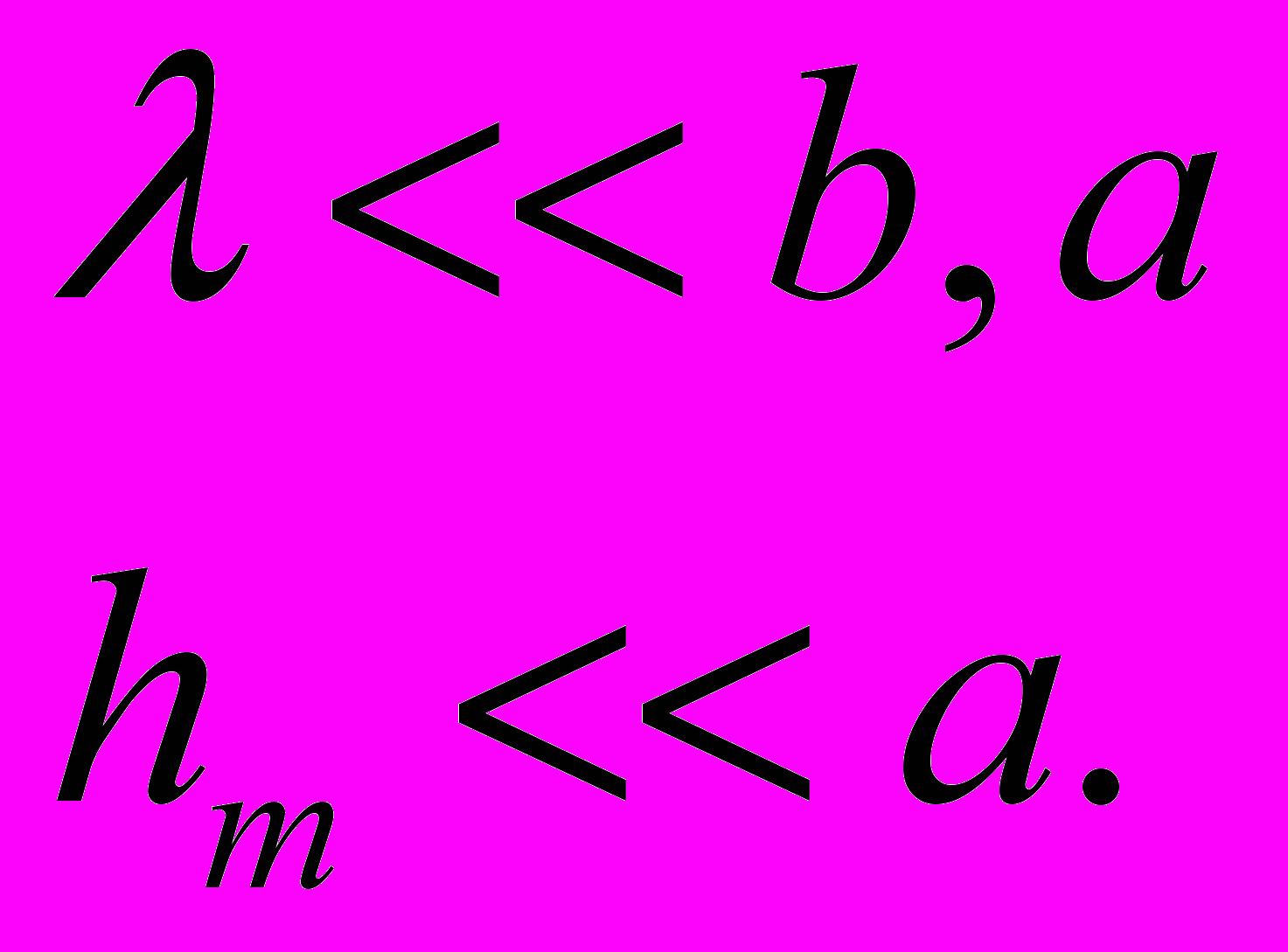
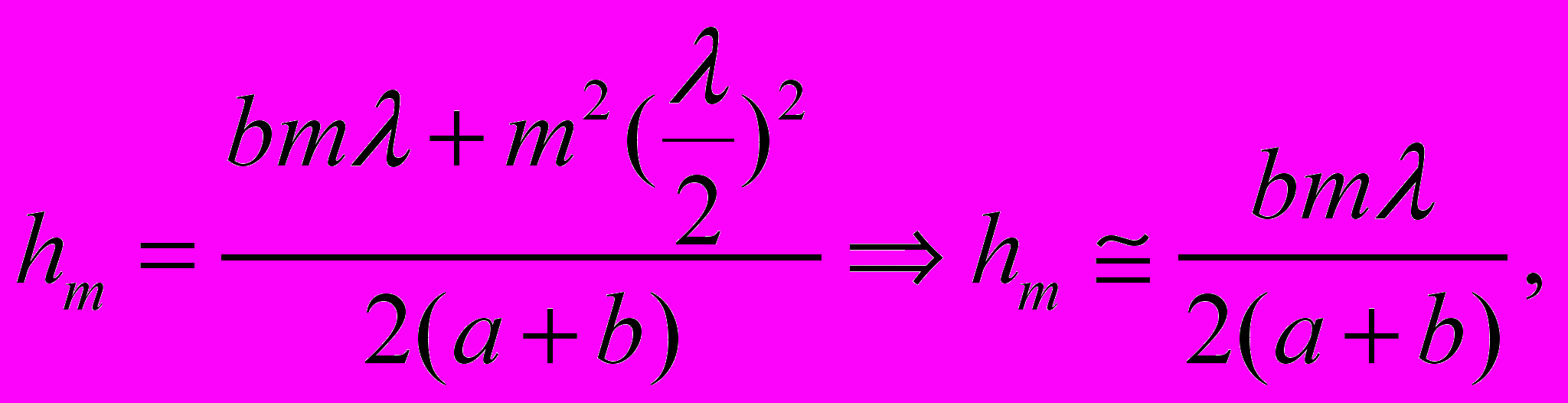 (3.5)
(3.5)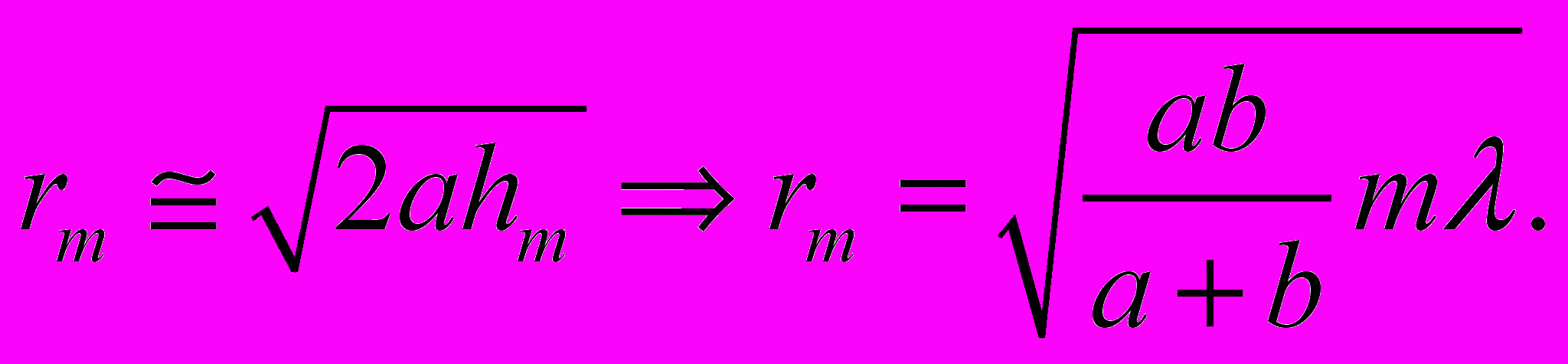 (3.6)
(3.6)| Внешний радиус зоны Френеля  |
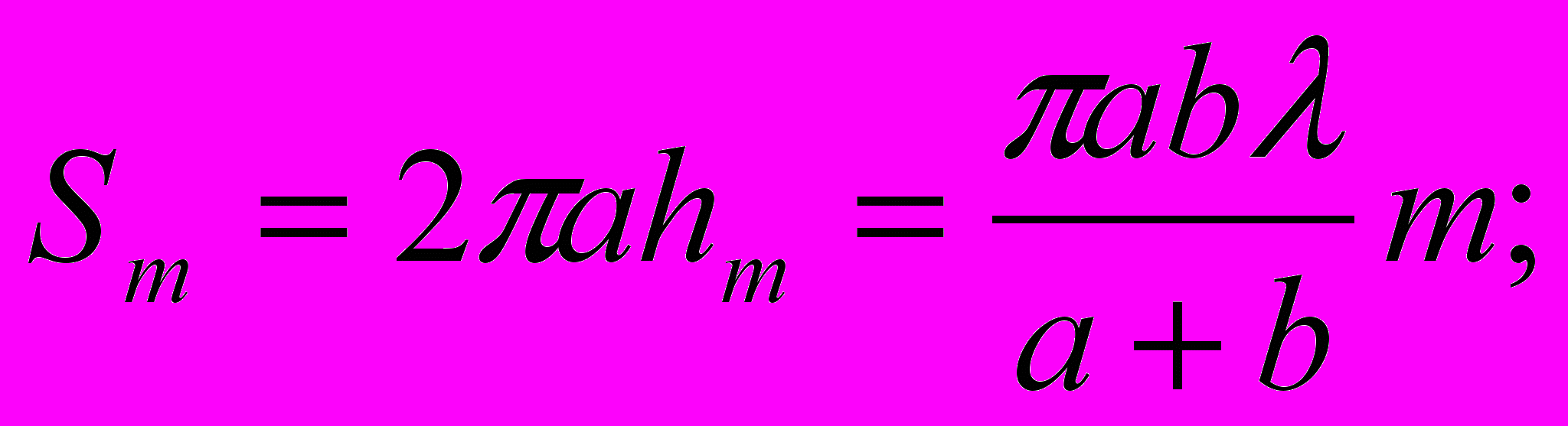
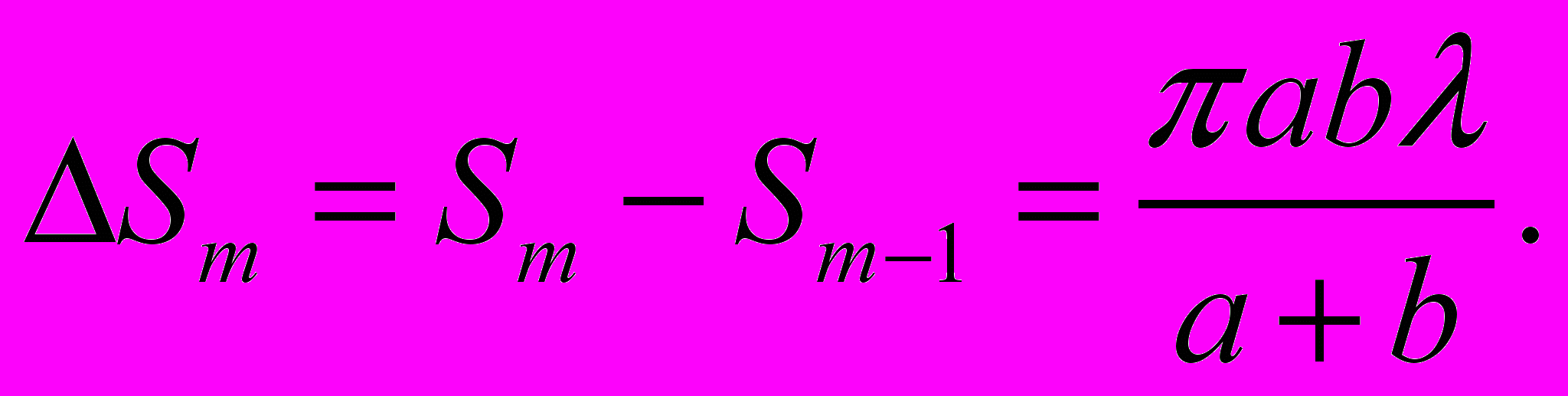 (3.7)
(3.7)Фактор
 (3.8)
(3.8)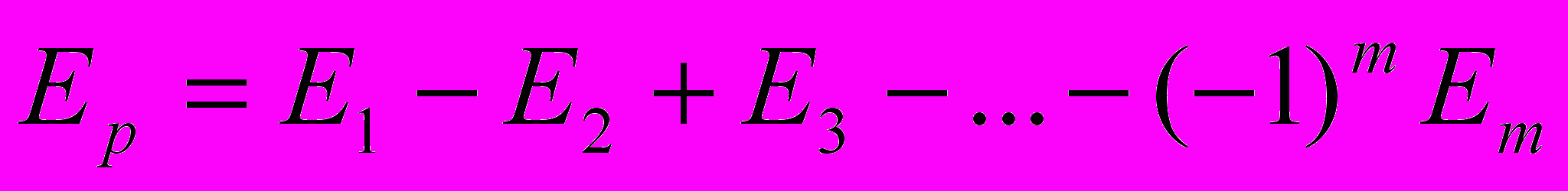 Если
Если 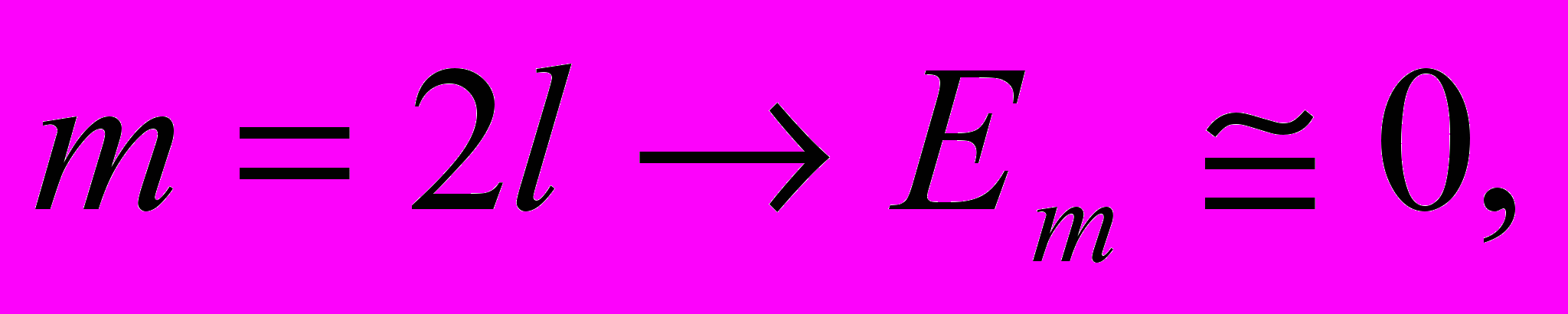 (3.9)
(3.9)Если
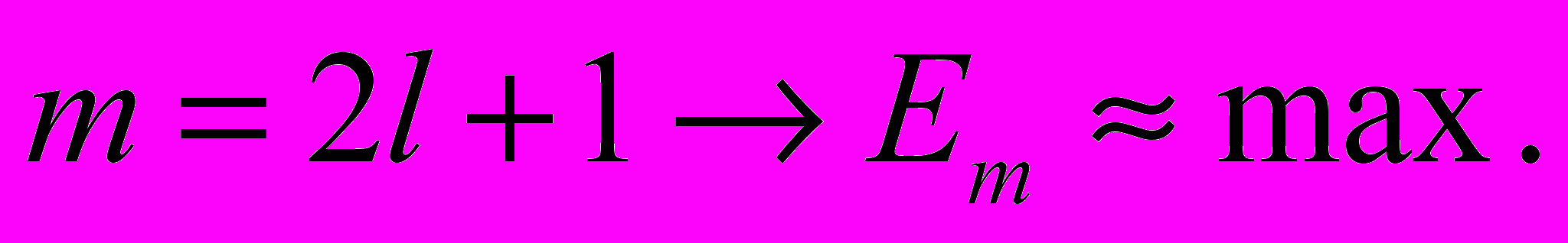
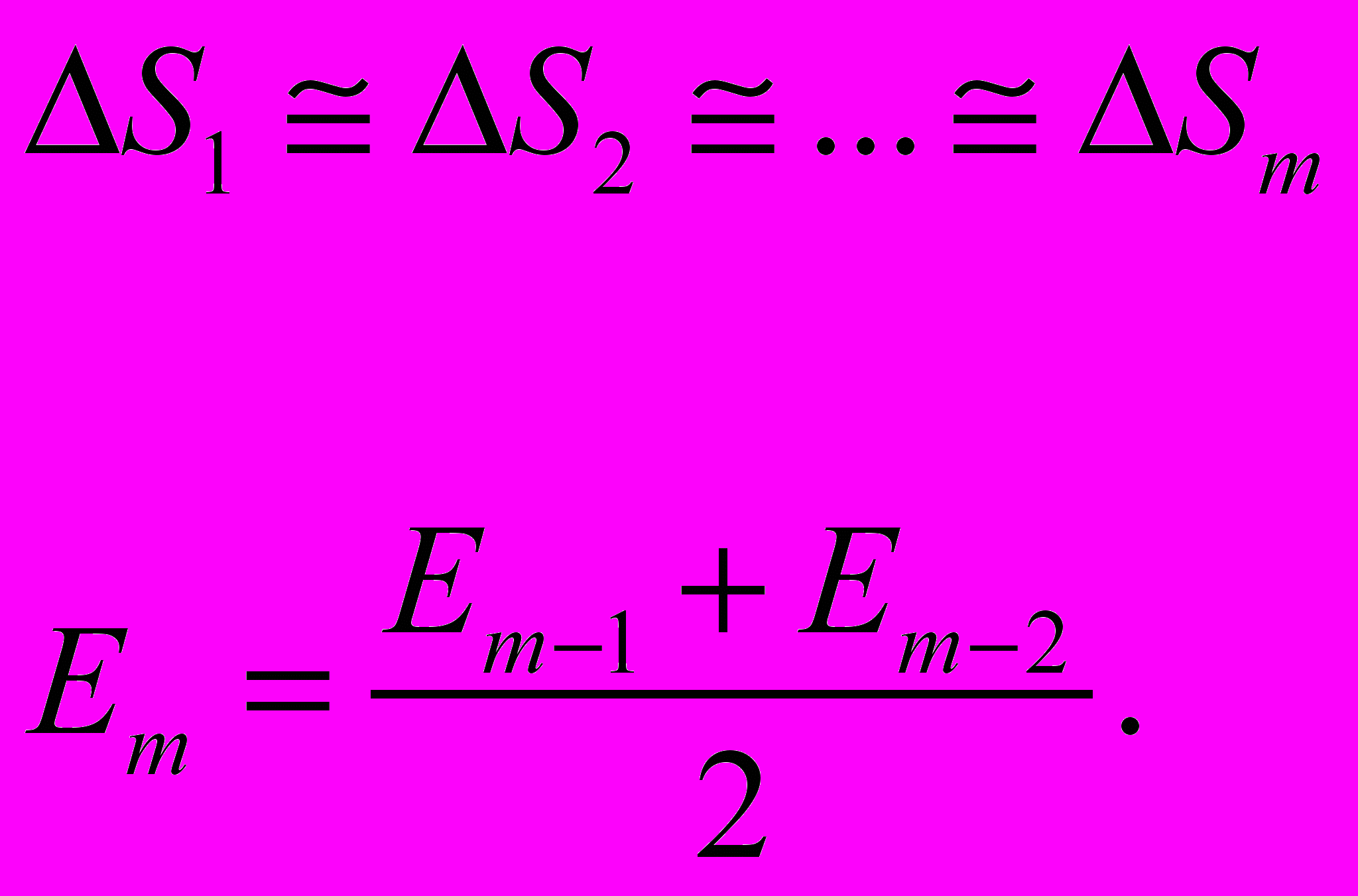
 , (3.10)
, (3.10)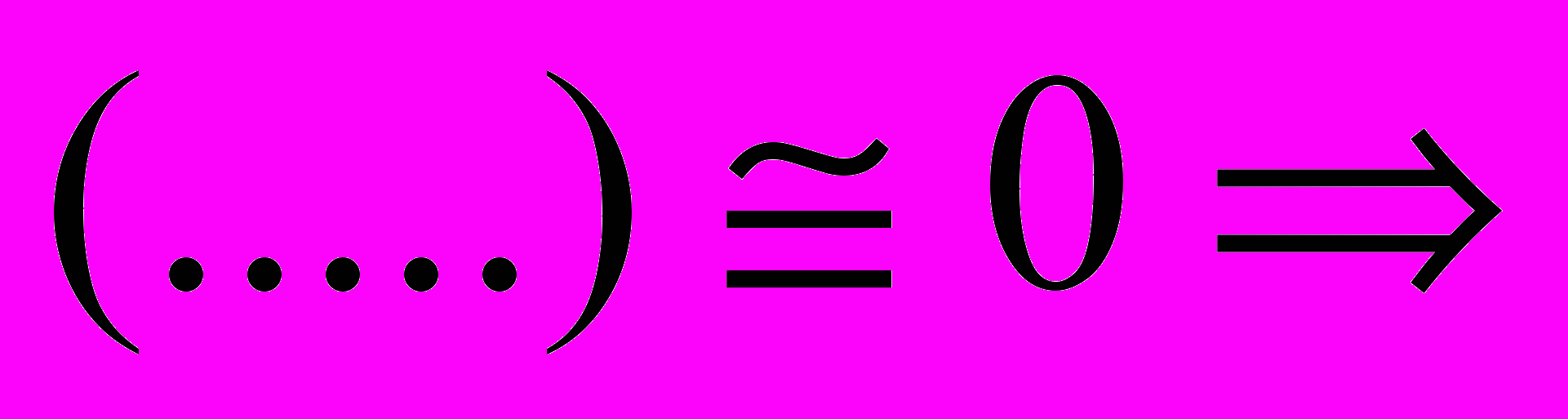
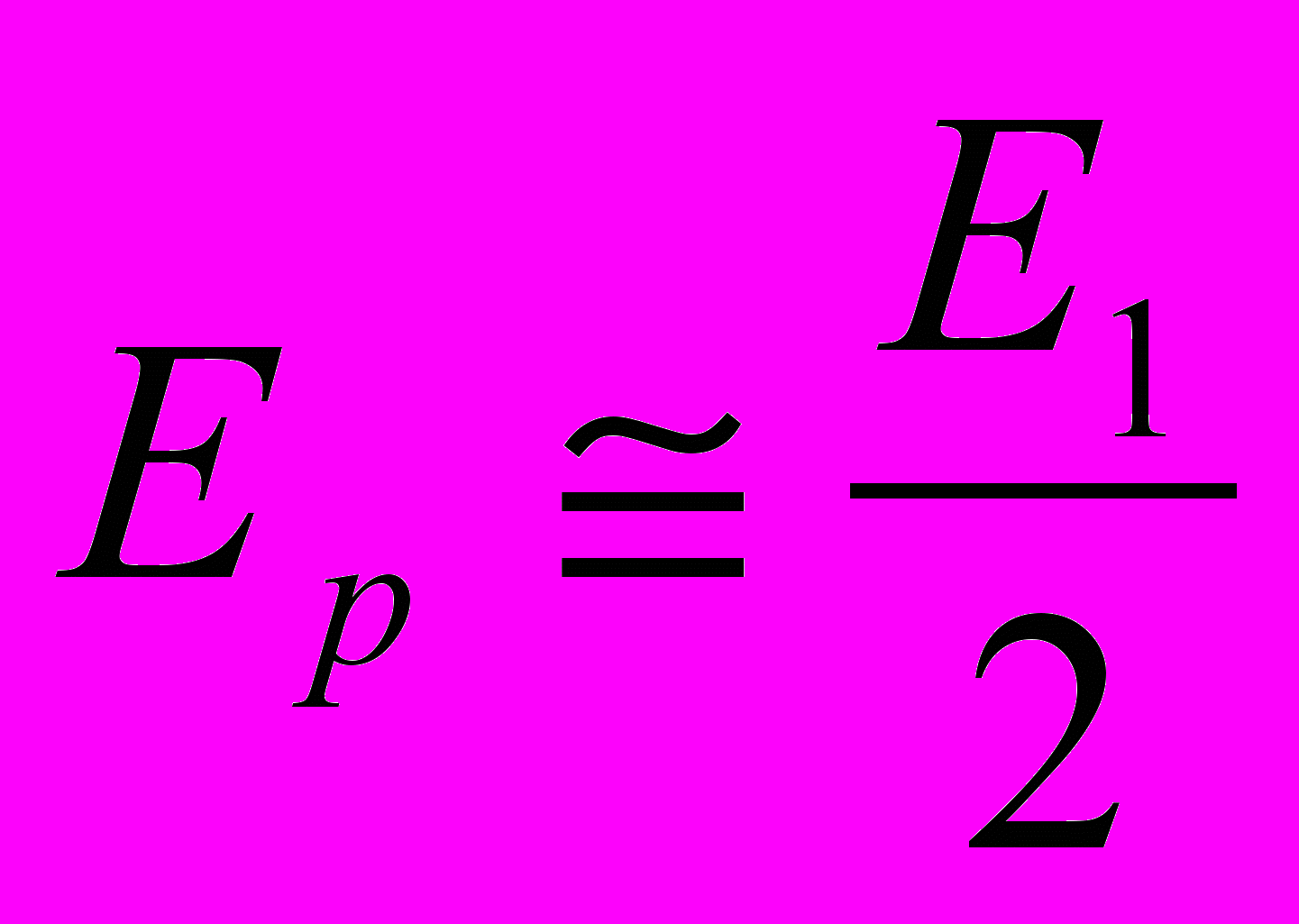 . (3.11)
. (3.11)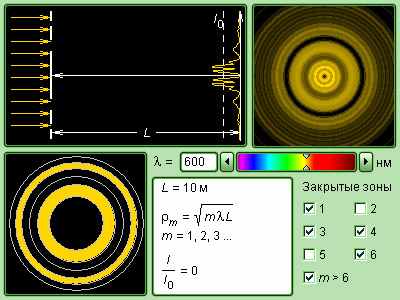
Компьютерное моделирование дифракции Френеля на круглом отверстии курсе «Открытая физика 2.6» под редакцией профессора МФТИ С.М.Козела.
Дифракция на оси от круглого отверстия
- В отверстии помещается только первая зона Френеля, радиус отверстия
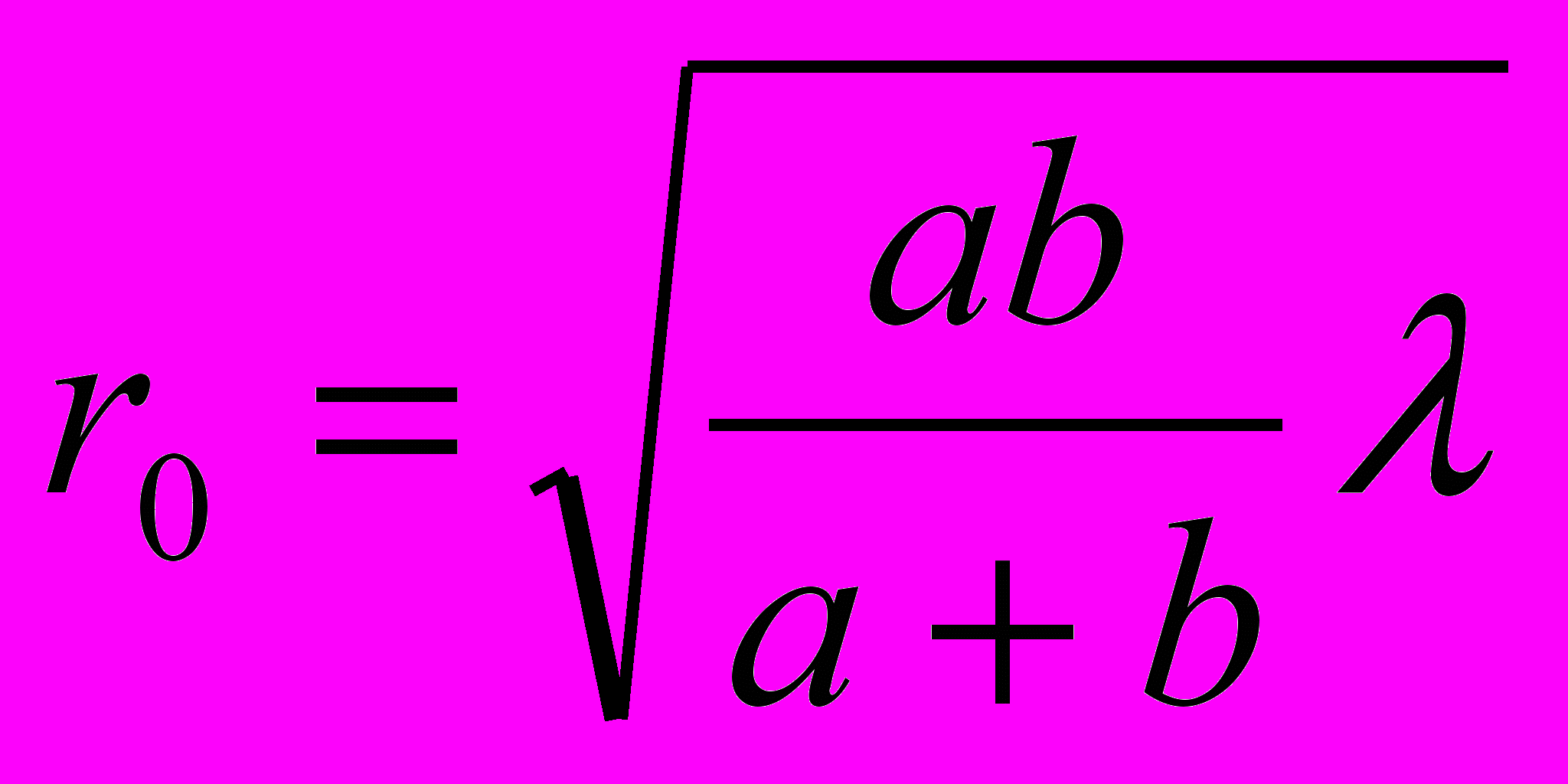 .
. 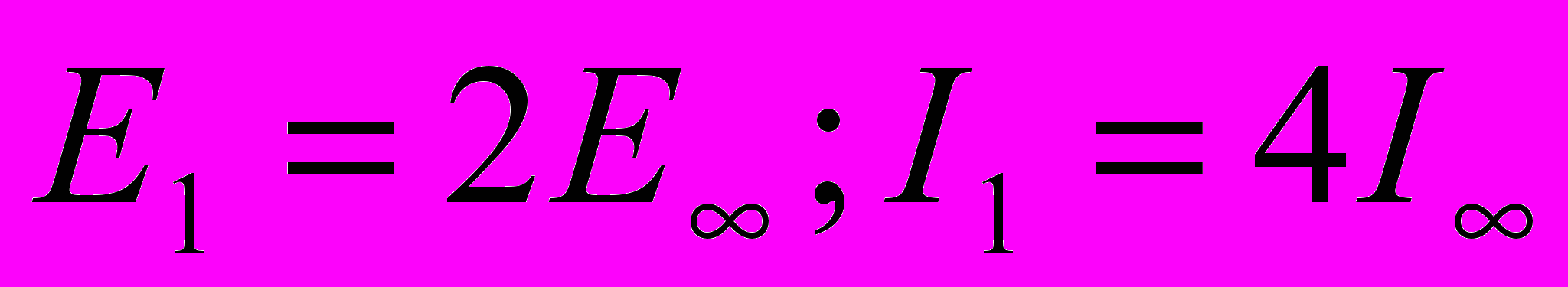 , где
, где - амплитуда колебаний в точке Р в отсутствии препятствия,
- амплитуда колебаний в точке Р в отсутствии препятствия, 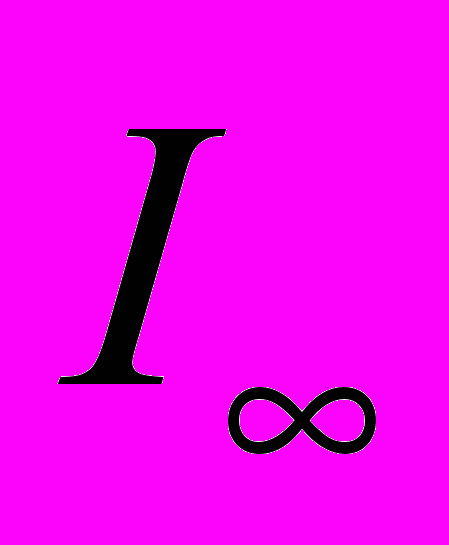 - интенсивность в отсутствии отверстия. В центре (точка Р) – яркое пятно, интенсивность плавно спадает к периферии ( См. Рис. 3.10, N = 1).
- интенсивность в отсутствии отверстия. В центре (точка Р) – яркое пятно, интенсивность плавно спадает к периферии ( См. Рис. 3.10, N = 1).
- В отверстии помещается две первые зоны Френеля,
 .
. 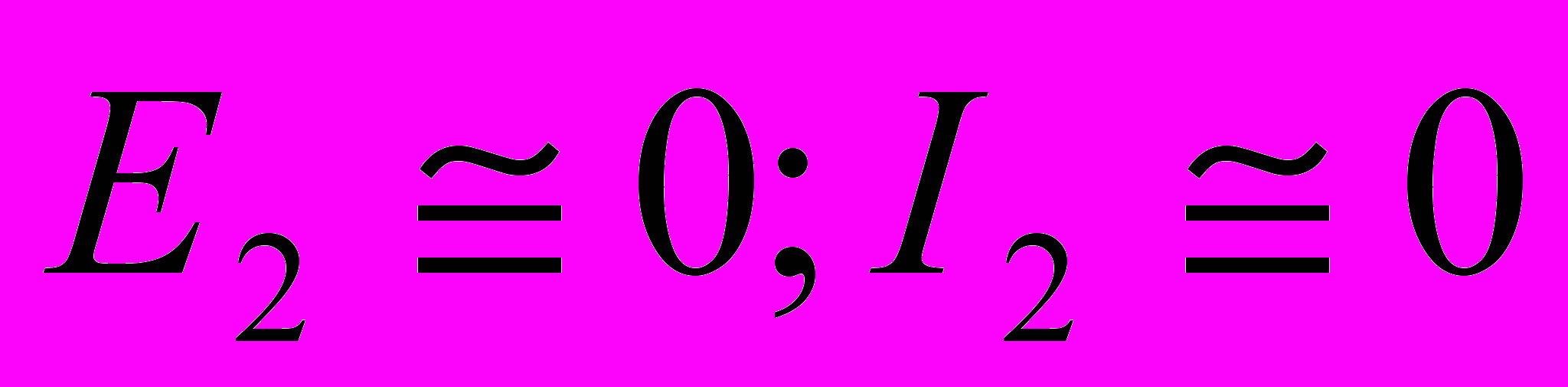 . В точке Р – тёмный кружок, окружённый светлым кольцом ( Cм. Рис. 3.10, N = 2 ).
. В точке Р – тёмный кружок, окружённый светлым кольцом ( Cм. Рис. 3.10, N = 2 ).
- В отверстии помещается три первые зоны Френеля.
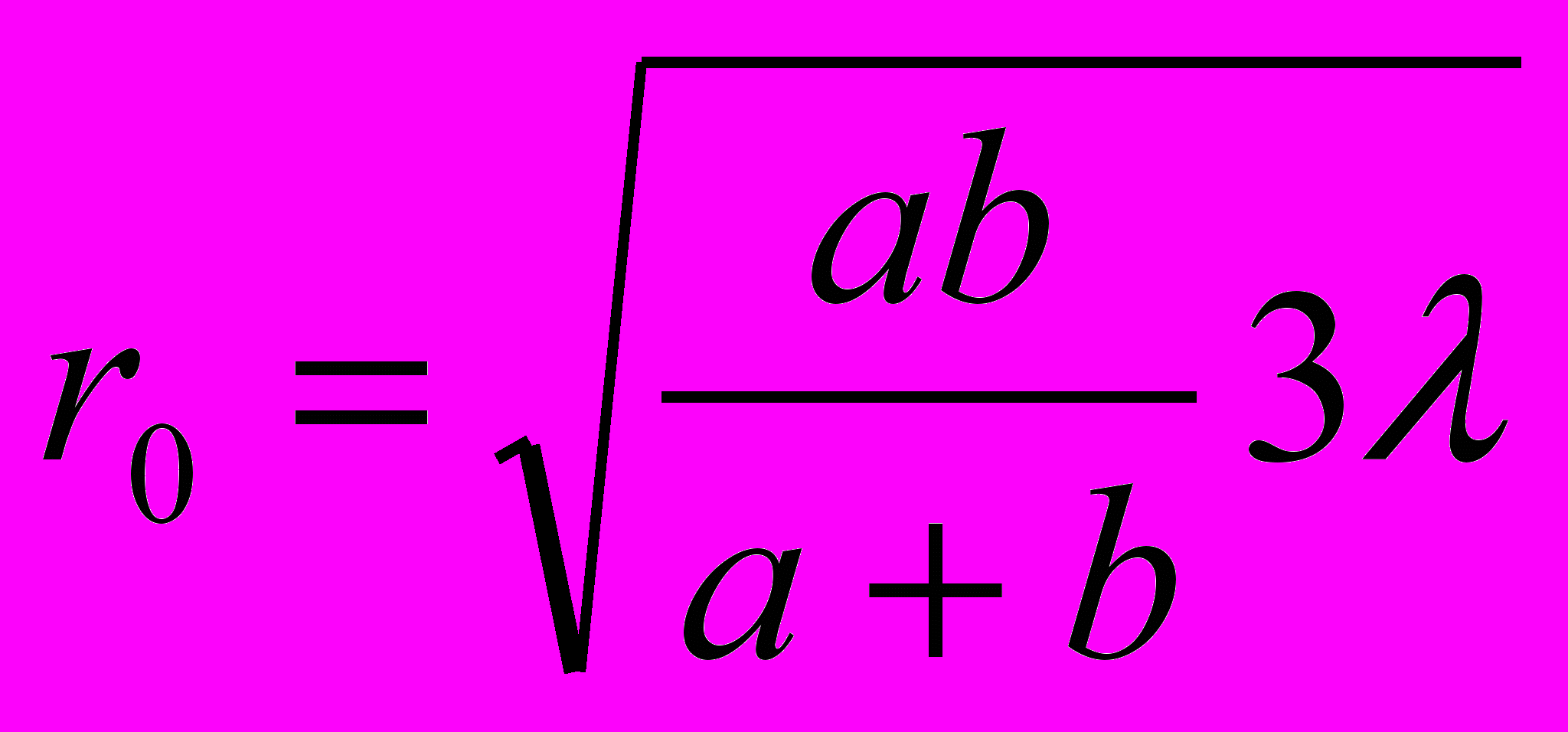 .
. 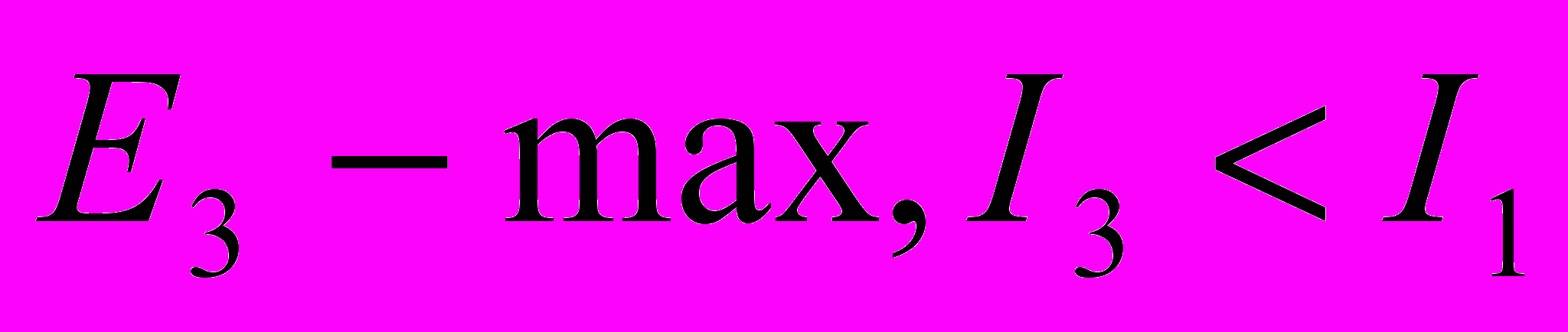 . В точке Р – светлое пятно, менее яркое, чем в пункте 1, далее тёмное кольцо, переходящее в светлое большего радиуса ( См. Рис. 3.10, N = 3 ).
. В точке Р – светлое пятно, менее яркое, чем в пункте 1, далее тёмное кольцо, переходящее в светлое большего радиуса ( См. Рис. 3.10, N = 3 ).


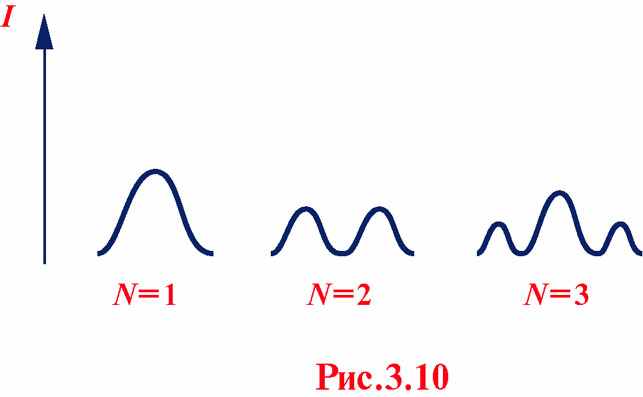
Зональная (зонная) пластинка

 или (3.12)
или (3.12) .
.n открытых нечётных (только!) или n открытых чётных (только!) дают амплитуду колебаний
 , а интенсивность
, а интенсивность  .
.
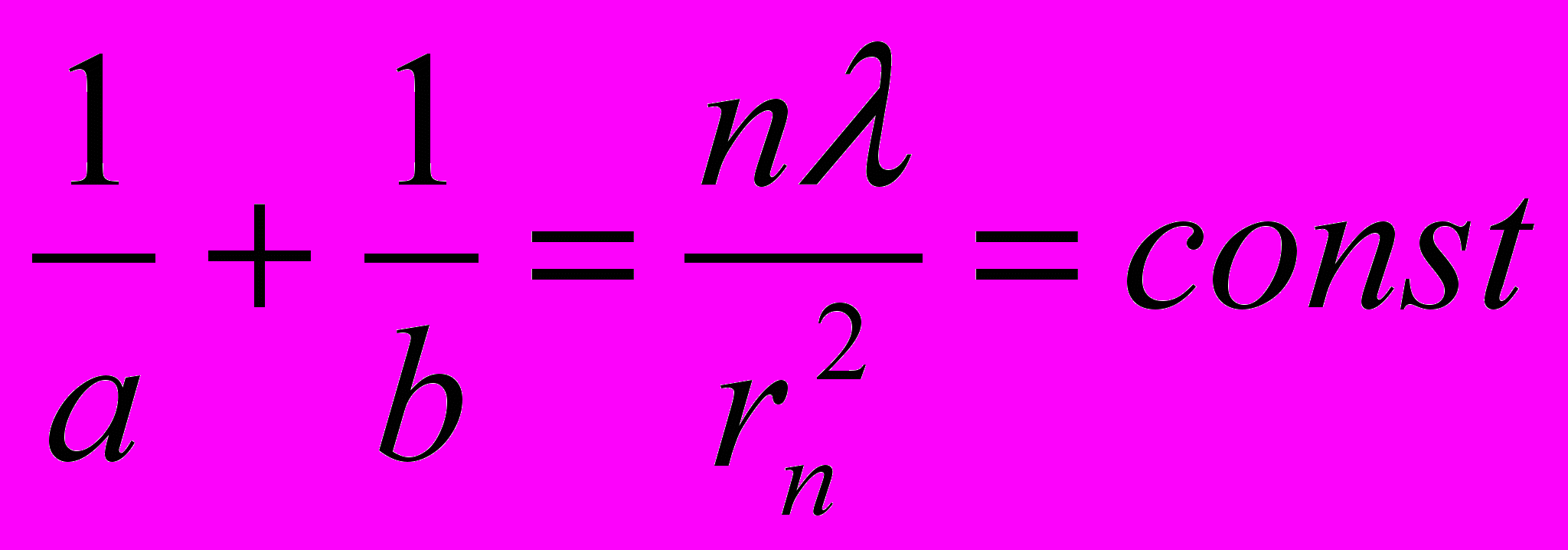 , (3.13)
, (3.13)т.к.
 .
. 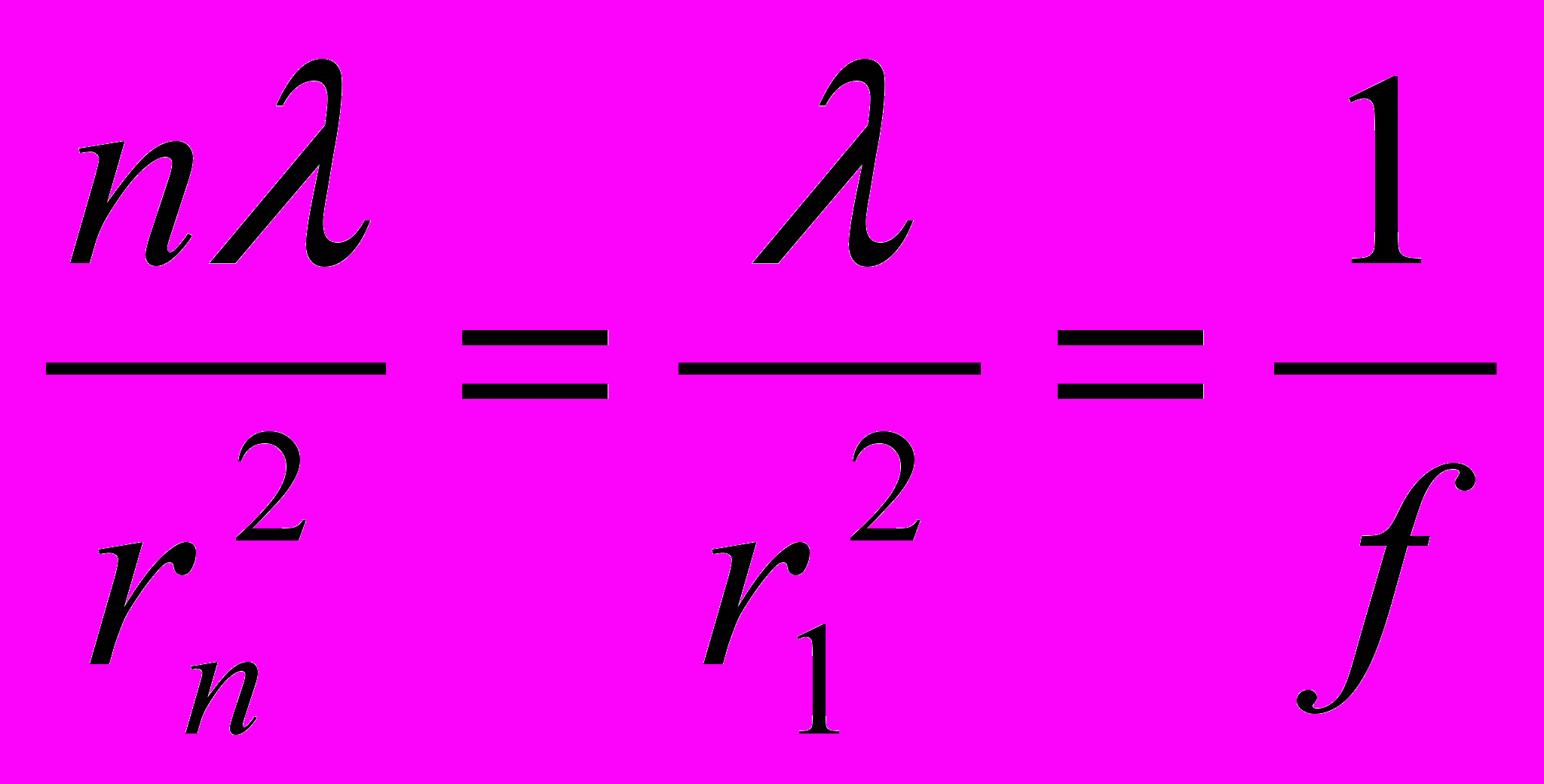 , (3.14)
, (3.14)f – фокусное расстояние зонной пластинки.
Особенности:
- Зонная пластинка (в отличие от линзы) система не таутохронная: колебания, приходящие в фокус от соседних открытых зон, различаются по фазе на 2π (разность хода λ).
- Кроме основного фокуса пластинка имеет бесконечную последовательность фокусов
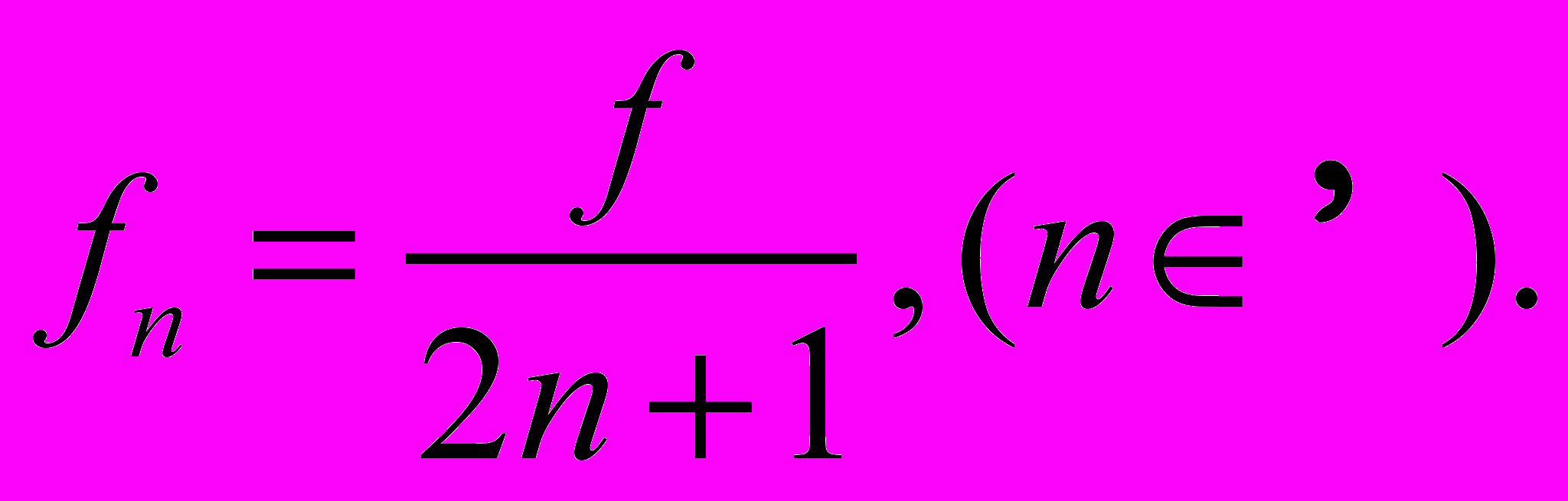 Последовательность точек Fn, в которые колебания от соседних открытых зон приходят с разностью хода 2λ, 3λ и т.д. Дополнительные фокусы имеют освещённость существенно более слабую по сравнению с основным.
Последовательность точек Fn, в которые колебания от соседних открытых зон приходят с разностью хода 2λ, 3λ и т.д. Дополнительные фокусы имеют освещённость существенно более слабую по сравнению с основным.
Замечание (Рэлей): интенсивность в точке наблюдения Р увеличивается в 4 раза, если изменить на π фазы вторичных волн (не уничтожать!), исходящих от всех зон Френеля с чётными (или нечётными) номерами.
Дифракция на непрозрачном диске

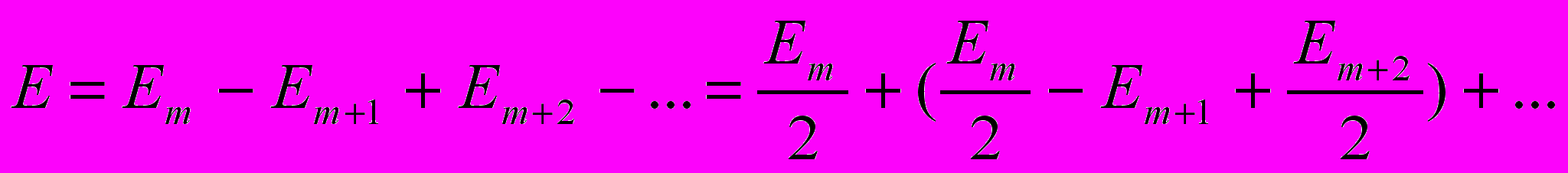 . (3.15)
. (3.15)( … ) = 0 => E = Em / 2 .

Светлое пятно в центре геометрической тени послужило причиной истории, которая прочно вошла в учебники курсов оптики. Парижская Академия Наук предложила объяснение дифракции света в качестве темы на премию за 1818 год. Френель представил мемуар, в котором с волновой точки зрения объяснялись все известные оптические явления.
Пуассон, бывший членом конкурсной комиссии, обратил внимание на то, что из теории Френеля следует абсурдный вывод: в центре геометрической тени, отбрасываемой небольшим диском, должно находиться светлое пятно.
Араго тут же провел эксперимент, который подтвердил существование предсказанного Пуассоном пятна. Это принесло победу и всеобщее признание в научном мире волновой теории света.
Дифракция на крае полуплоскости
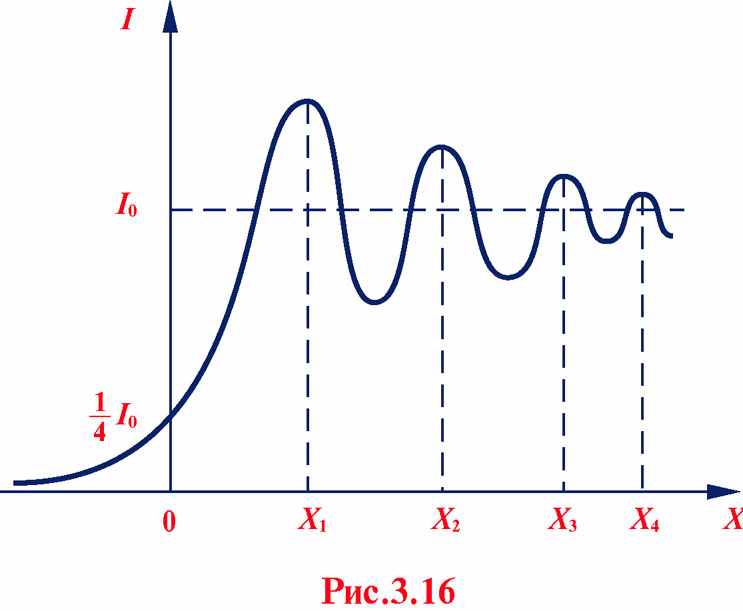
Результат дифракции Френеля на крае полубесконечной плоскости характеризуется проникновением части световой энергии в область геометрической тени. В освещенной области (справа от края полуплоскости) образуется система параллельных краю полос, период и контрастность которых убывают по мере удаления от границы, т.е. в положительном направлении оси Х. По мере роста координаты «х» интенсивность волны приближается к значению
 т.е. значению интенсивности в отсутствие препятствия.
т.е. значению интенсивности в отсутствие препятствия.Все эти качественные особенности легко получить, основываясь на разбиении плоского волнового фронта на полуволновые зоны, так называемые зоны Шустера, аналогичные зонам Френеля по смыслу, но убывающие с ростом номера по площади.
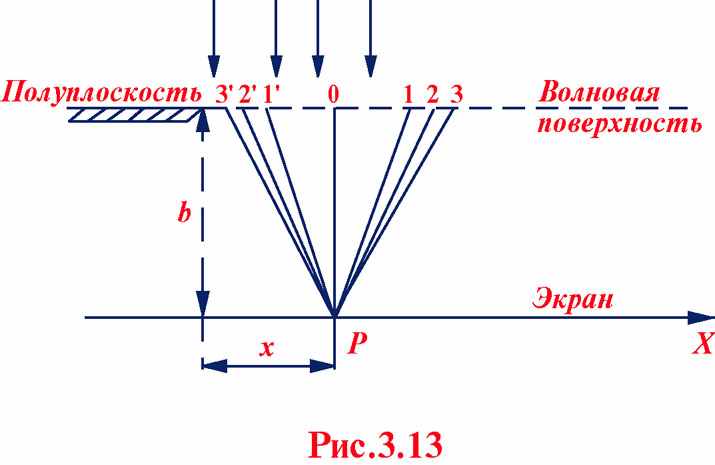
Разбиение на зоны ведется путем последовательного добавления половины длины волны к расстоянию b от точки наблюдения P до границы полуплоскости. Поперечный размер зон быстро убывает, поэтому амплитуды вторичных волн от зон Шустера убывают быстрее, чем в случае круглого отверстия, при этом спираль Френеля на комплексной плоскости трансформируется в спираль Корню, имеющую два фокуса.
Зоны Шустера: ∆ = λ / 2.
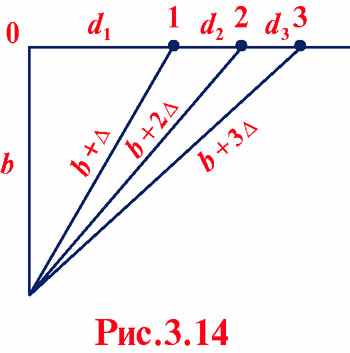
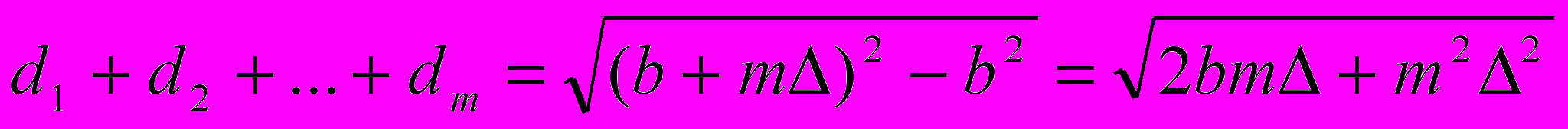 , (3.16)
, (3.16) , (3.17)
, (3.17) , (3.18)
, (3.18)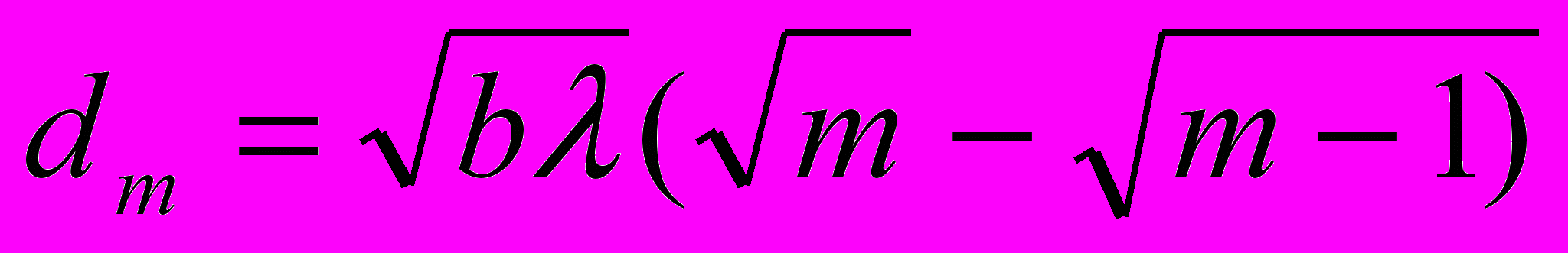 . (3,19)
. (3,19) d1:d2:d3:d4: ...= 1 : 0,41 : 0,32 : 0,27 :… (3.20)
Спираль Корню (клотоида)
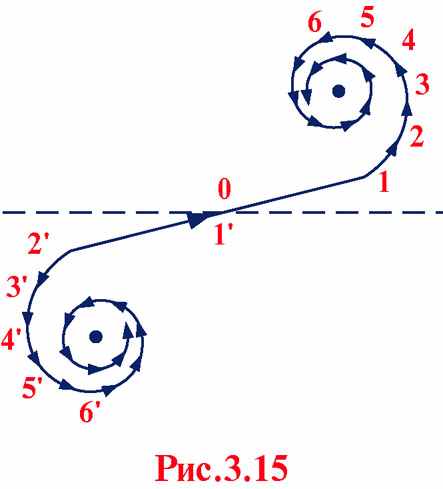
Для точек в области геометрической тени суммарная амплитуда изображается вектором, заканчивающемся в фокусе
 и монотонно возрастающим по мере приближения к точке P, расположенной непосредственно под краем полуплоскости, при этом начало вектора («стрелочки») непрерывно скользит по спирали (см. Рис.3.17 а и б) и длина вектора монотонно растет. В точке P (х = 0) вектор
и монотонно возрастающим по мере приближения к точке P, расположенной непосредственно под краем полуплоскости, при этом начало вектора («стрелочки») непрерывно скользит по спирали (см. Рис.3.17 а и б) и длина вектора монотонно растет. В точке P (х = 0) вектор по модулю вдвое меньше вектора
по модулю вдвое меньше вектора 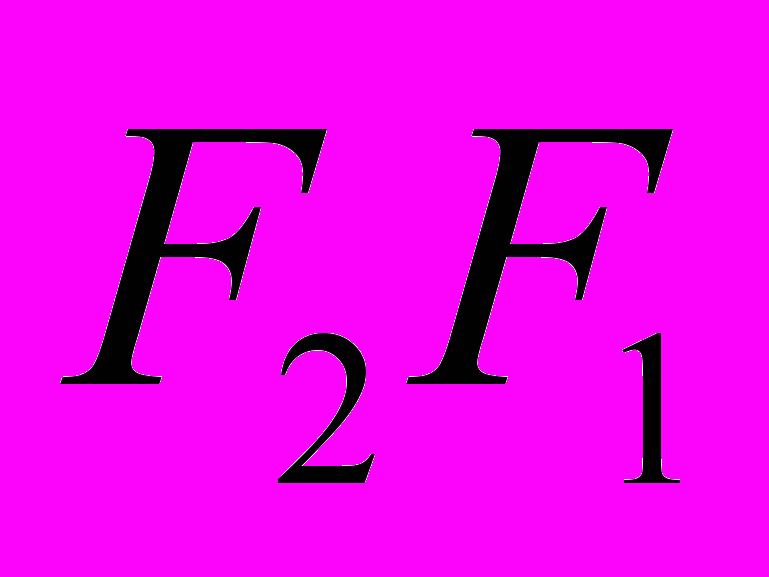 , который соответствует амплитуде волны на большом расстоянии (
, который соответствует амплитуде волны на большом расстоянии ( ) от края полуплоскости. Из этого непосредственно следует, что в точке P интенсивность составляет четверть от
) от края полуплоскости. Из этого непосредственно следует, что в точке P интенсивность составляет четверть от  , интенсивности падающей волны. Здравый смысл подсказывает, что на больших расстояниях от края полуплоскости в освещенной части влиянием экрана на падающую волну можно пренебречь. Очевидно, что при дальнейшем перемещении в освещенной части должны возникать убывающие по размаху осцилляции амплитуды (см. Рис.3.17в,г,д), при этом конец векторной амплитуды по-прежнему зафиксирован в фокусе
, интенсивности падающей волны. Здравый смысл подсказывает, что на больших расстояниях от края полуплоскости в освещенной части влиянием экрана на падающую волну можно пренебречь. Очевидно, что при дальнейшем перемещении в освещенной части должны возникать убывающие по размаху осцилляции амплитуды (см. Рис.3.17в,г,д), при этом конец векторной амплитуды по-прежнему зафиксирован в фокусе , а начало скользит по нижней ветви спирали, неограниченно приближаясь к фокусу
, а начало скользит по нижней ветви спирали, неограниченно приближаясь к фокусу 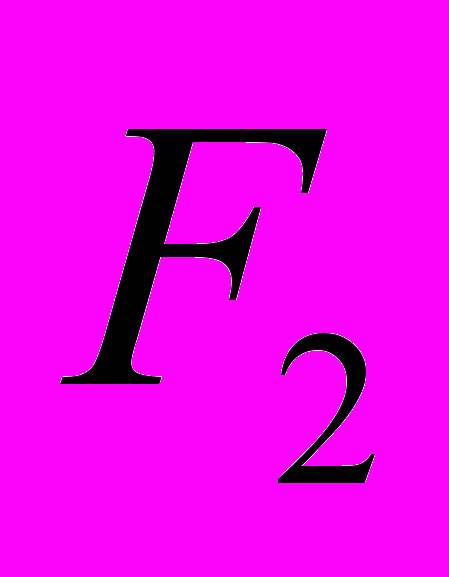 , то есть к амплитуде волны без экрана. На рисунке 3.16 представлен график зависимости интенсивности от координаты х, то есть от положения точки наблюдения P.
, то есть к амплитуде волны без экрана. На рисунке 3.16 представлен график зависимости интенсивности от координаты х, то есть от положения точки наблюдения P. 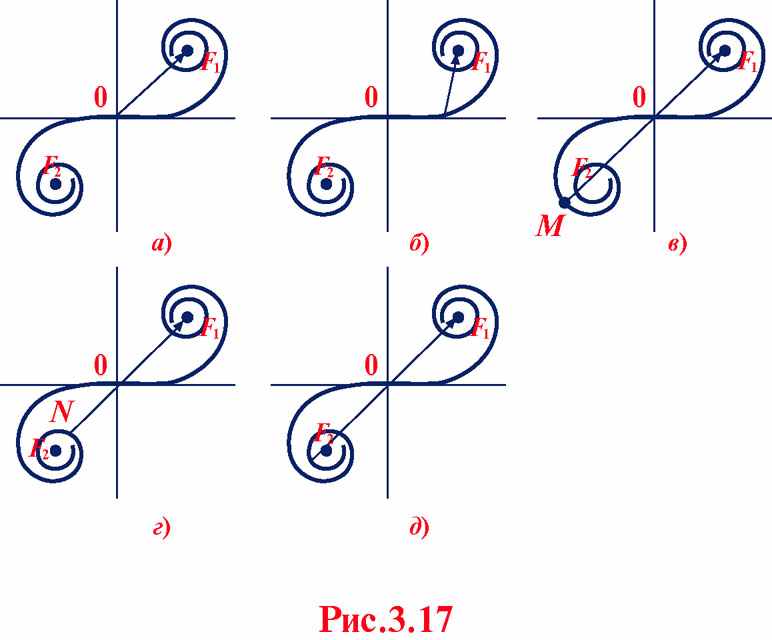

Рис.3.18
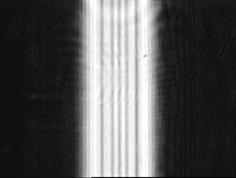



Дифракция Френеля на узкой и широкой щели и распределение интенсивности света, зарегистрированное с помощью видеокамеры (Физический ф-т НГУ, кафедра общей физики, куратор практикума профессор В.Ф.Климкин).
Число Френеля
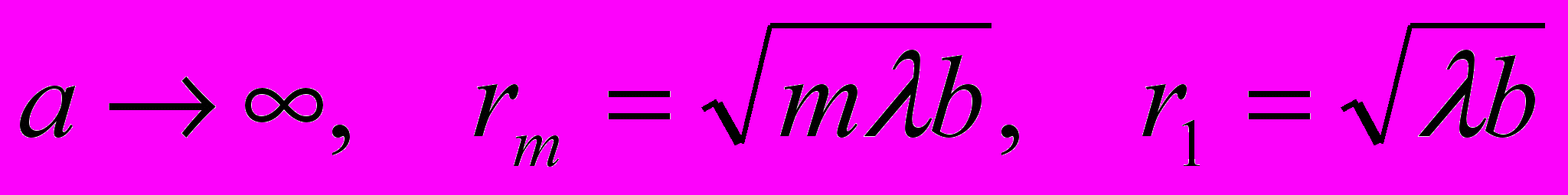 . (3.21)
. (3.21)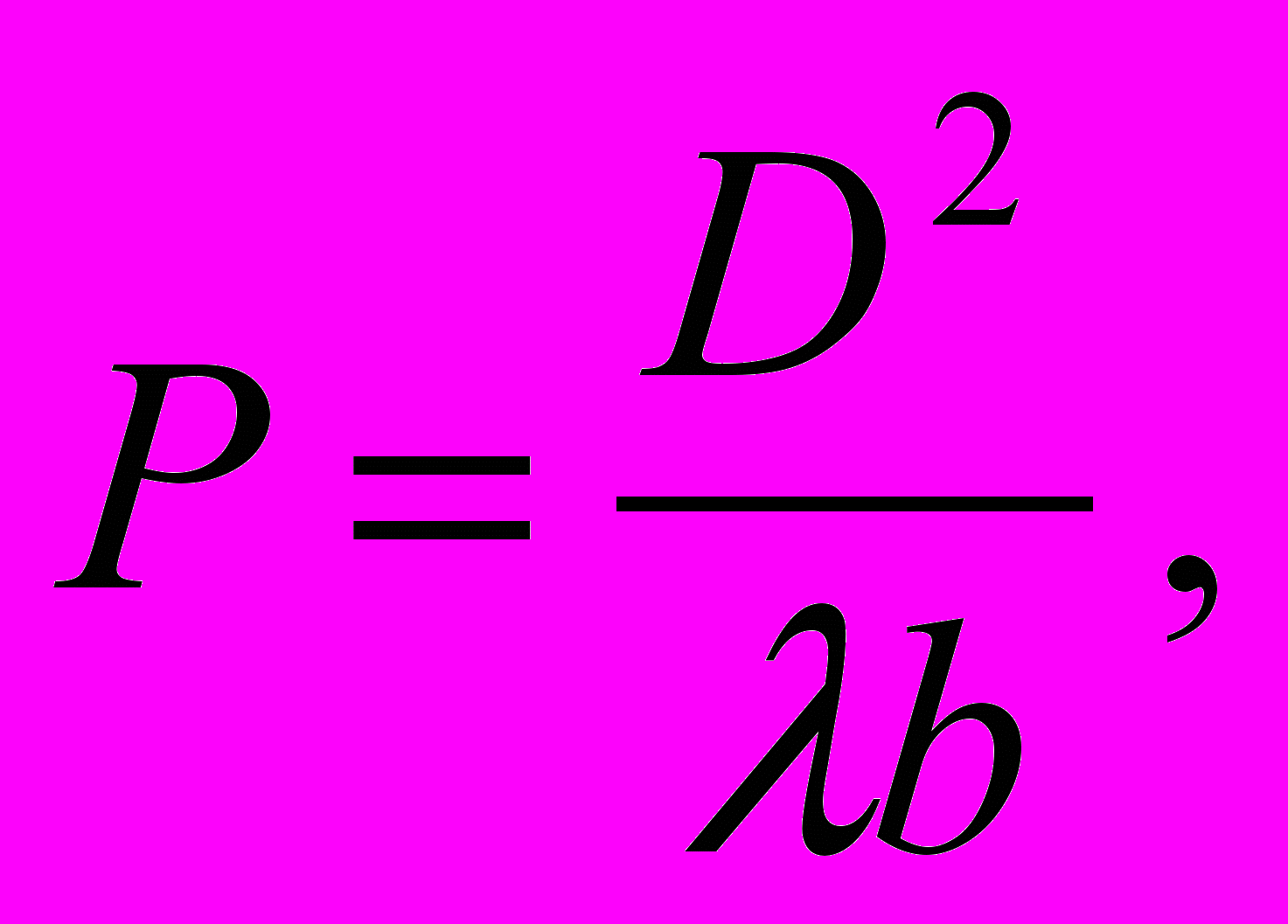 где D – характерный размер препятствия . (3.22)
где D – характерный размер препятствия . (3.22)P << 1 – дифракция Фраунгофера,
P ~ 1 – дифракция Френеля, (3.23)
P >> 1 – приближение геометрической оптики.
Геометрическая оптика
Следствие волновой природы света, полученное предельным переходом
 . При этом линейные размеры препятствий много больше размеров любой зоны Френеля и дифракционные эффекты пренебрежимо малы. В этом случае можно ввести понятие луча как линии, перпендикулярной волновым поверхностям. Траектория луча определяется принципом Ферма, согласно которому свет выбирает из всех возможных путей тот путь, который требует наименьшего времени для его прохождения. Использование принципов Ферма позволяют обосновать многие законы геометрической оптики.
. При этом линейные размеры препятствий много больше размеров любой зоны Френеля и дифракционные эффекты пренебрежимо малы. В этом случае можно ввести понятие луча как линии, перпендикулярной волновым поверхностям. Траектория луча определяется принципом Ферма, согласно которому свет выбирает из всех возможных путей тот путь, который требует наименьшего времени для его прохождения. Использование принципов Ферма позволяют обосновать многие законы геометрической оптики. Дополнение к Лекции 03
С помощью принципа Гюйгенса легко объяснить преломление света на границе раздела двух сред с
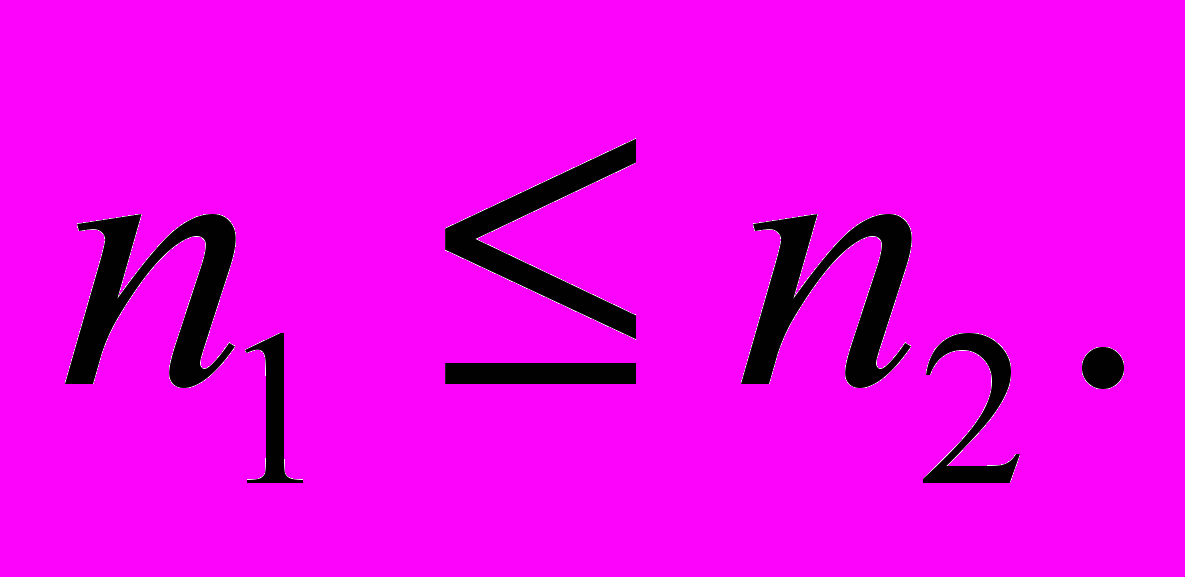 время, пока световой луч в первой среде проходит путь
время, пока световой луч в первой среде проходит путь 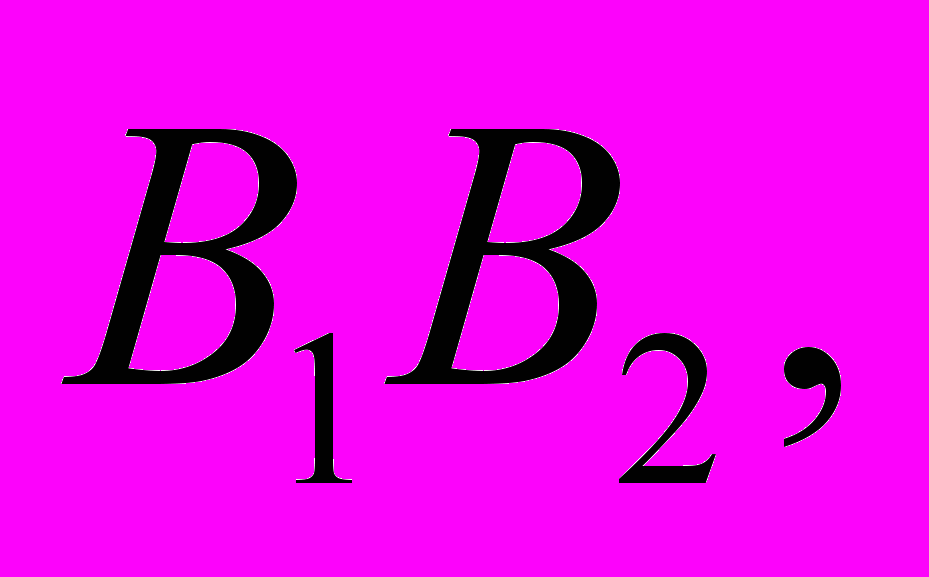 вторичные волны во второй среде проходят меньшее расстояние
вторичные волны во второй среде проходят меньшее расстояние  поскольку скорость света во второй среде по условию меньше. Световые лучи перпендикулярны волновому фронту.
поскольку скорость света во второй среде по условию меньше. Световые лучи перпендикулярны волновому фронту.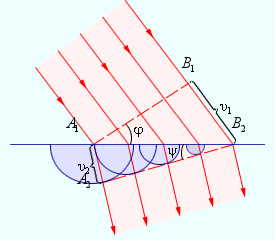
Согласно очевидным геометрическим соотношениям
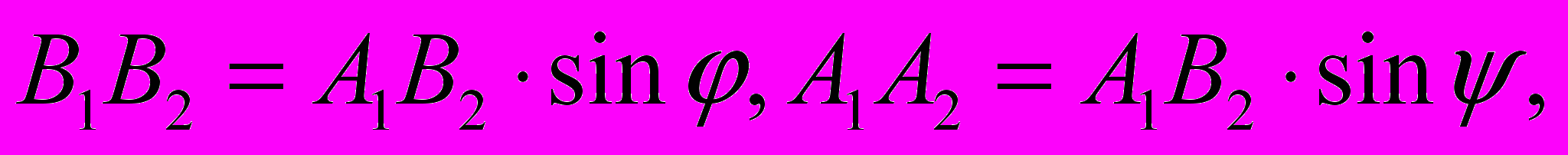 получаем обычный закон преломления (закон Снеллиуса):
получаем обычный закон преломления (закон Снеллиуса):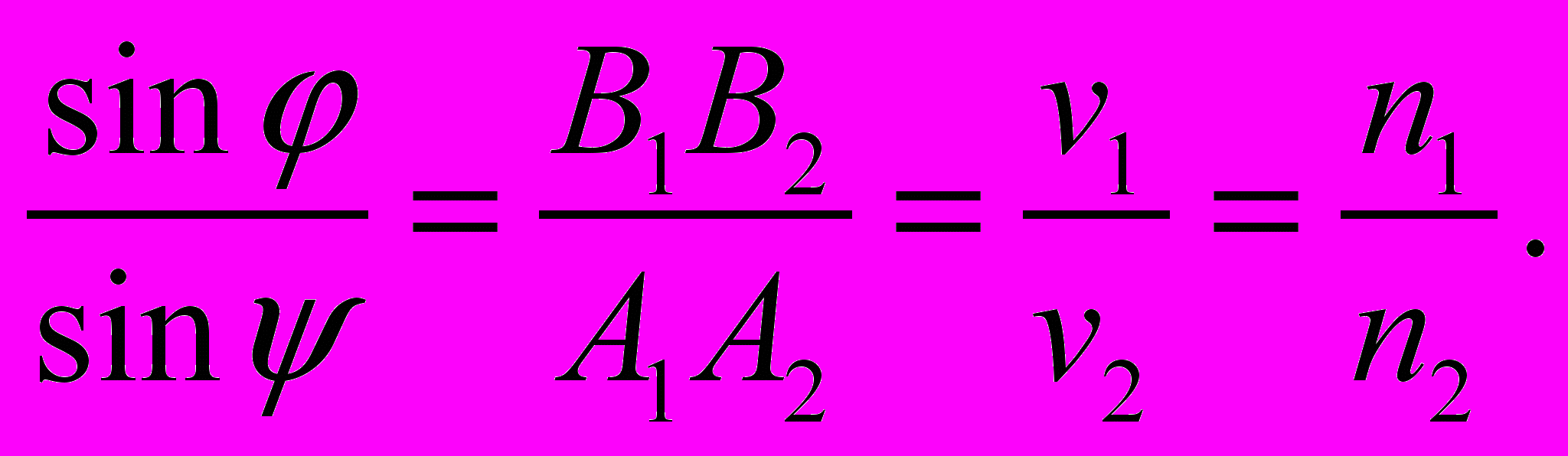
Принцип Гюйгенса позволяет продемонстрировать проникновение световых лучей в область геометрической тени у границ непрозрачного экрана, то есть характерное дифракционное явление.

Ограничивая бесконечную плоскость фронта падающей волны отверстием АВ, мы приводим к искривлению огибающей вторичных волн, и, следовательно, к отклонению от прямолинейного распространения света (особенно в окрестности границ отверстия) и, как следствие, захождение света в область геометрической тени.
