Конспект лекций по сопротивлению материалов Владивосток 2004
| Вид материала | Конспект |
- Конспект лекций Владивосток Издательство вгуэс 2004, 737.28kb.
- Конспект лекциий владивосток 2004 г. Министерство образования и науки Российской Федерации, 822.52kb.
- Конспект лекций прочитанных на кафедре инфекционных болезней для фельдшерского отделения, 1007.39kb.
- Конспект лекций Салов А. Н., к э. н., доцент Владивосток 2005, 724.35kb.
- Конспект лекций 2010 г. Батычко Вл. Т. Муниципальное право. Конспект лекций. 2010, 2365.6kb.
- Конспект лекций 2008 г. Батычко В. Т. Административное право. Конспект лекций. 2008, 1389.57kb.
- Конспект лекций 2011 г. Батычко В. Т. Семейное право. Конспект лекций. 2011, 1718.16kb.
- Конспект лекций 2011 г. Батычко Вл. Т. Конституционное право зарубежных стран. Конспект, 2667.54kb.
- Конспект лекций по курсу "Микропроцессорные устройства": Раздел Микропроцессорный модуль., 281.54kb.
- Конспект лекций 2010 г. Батычко В. Т. Уголовное право. Общая часть. Конспект лекций., 3144.81kb.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВЛАДИВОСТОКСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И СЕРВИСА
ИНСТИТУТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ И ТЕХНИЧЕСКИХ СИСТЕМ
КАФЕДРА ФИЗИКИ, ХИМИИ И ПРИКЛАДНОЙ МЕХАНИКИ
Потехин Б.Б.
Конспект лекций по сопротивлению материалов
Владивосток 2004
В В Е Д Е Н И Е
Сопротивление материалов является основой всех инженерных наук, так как все вопросы этого курса связаны с проблемой прочности инженерных сооружений и долговечностью их эксплуатации.
Все упругие тела обладают в определенной мере прочностью и жесткостью. Сопротивление материалов - наука, изучающая законы прочности и жесткости упругих тел, относящихся к элементам сооружений и машин.
Строительная механика - наука, изучающая прочность и жесткость сооружений в целом и их элементов.
Наряду с сопротивлением материалов и строительной механикой существует наука , называемая теорией упругости. Теория упругости изучает те же законы, что и сопротивление материалов, но в более строгой (точной) постановке с применением большого математического аппарата. Теория упругости является основным теоретическим курсом сопротивления материалов и различных строительных механик.
Наука о сопротивлении материалов, распологая выводами теории упругости, решает основные задачи упрощенным методом.
Сопротивление материалов изучается в курсе "Прикладная механика", как составная его часть специальным разделом для специальностей 23.01.00, 28.08.00, 28.11.00. На изучение сопротивления материалов учебные планы данных специальностей предусматривают 32 часа аудиторных лекционных занятий.
Данный конспект лекций расчитан на 8 часов аудиторных занятий. В нем рассмотрены задачи и методы сопротивления материалов, основные понятия и определения, моменты инерции плоских фигур, устойчивость стержней при продольном изгибе, cовместное действие изгиба и растяжения (сжатия), совместное действие изгиба и кручения, косой изгиб, расчет на прочность и жестскость при кручении сплошного и полого вала. Приведен пример определения критической нагрузки.
Краткая история развития науки о сопротивлении материалов
Проблема прочности упругих тел всегда была в поле зрения человечества, так как с ней связана прочность искусственых сооружений, творцом которых является человек. В древности обходились без расчетов и при выборе расчетов шли ощупью, путем чистого эмпиризма. Так Архимед, живший за 250 лет до нашей эры, на основе интуитивного знания законов упругих тел в сочетании с опытом, сумел создать уникальные машины и снаряды. В дальнейшем типы сооружений видоизменялись медленно, а сами сооружения являлись как бы объектами для опытов. Если сооружение являлось прочным, оно служило образцом для дальнейшего строительства.
Зарождение науки о сопротивлнии материалов относится к XVII веку и связано с работами Галилея (1564 - 1642 гг.). Он впервые поставил вопрос о необходимости проведения аналитических расчетов сопротивляемости стержней действию внешних сил.
В 1678 году Роберт Гук установил зависимость между усилием и удлиннением стержня при растяжении, (известна под названием закона Гука). Этот закон можно рассматривать как основной закон сопротивления материалов, который в общем виде можно сформулировать: какова внешняя сила, такова и деформация.
Значительный вклад в развитие аналитических методов исследования задач сопротивления материалов сделали выдающиеся ученые Бернулли, Сен-Венан, Коши, Ламе и другие.
Следует отметить важные исследования знаминитого руского ученого Л. Эйлера (1707 - 1783 гг.) в области расчетов стержней на устойчивость.
В XIX веке мировую известность приобретают работы русских ученых Д.И. Журавского, Х.С. Головина, А.В. Гадолиса, Ф.С. Ясинского.
С начала XX века роль русских ученых в науке сопротивления материалов еще более возрастает. Появляются замечательные работы И.Г. Бубнова и А.Н. Крылова. Большой вклад в развитие науки о сопротивлении материалов внес С.П. Тимошенко, автор первоклассных учебников и многочисленных научных работ.
После 1917 года в нашей стране была создана большая сеть научно-исследовательских институтов, работающих в области расчета конструкций, в которых были решены многие важные задачи для развития новой техники, созданы новые эффективные методы расчета деталей сложной формы. Следует отметить работы академика С.В. Серенсена по изучению прочности деталей, работающих при переменных нагрузках, академика А.Н. Длишева -по устойчивости конструкций.
Важные исследования в области сопротивления материалов в последнее время выполнены Ю.Н. Робоовым, А.А. Ильюшиным, А.Р. Ржаницыным, А.Ф. Смирновым, В.И. Федосьевым и другими русскими учеными.
Задачи и методы сопротивления материалов
В поготовке высококвалифицированых специалистов важная роль принадлежит инженерным дисциплинам, в частности, сопративлению материалов.
Цель курса сопротивления материалов - дать общие понятия об элементах, применяемых в машиностроительных и строительных конструкциях, о современных элементах расчета этих элементов на прочность, жесткость и устойчивость, научить будущего специалиста инженерному мышлению, пониманию особенностей выбора оптимальных конструктивных решений и объективной оценке условий работы элементов конструкций в процессе эксплуатации.
Сопротивлением материалов называют науку об инженерных методах расчета на прочность, жесткость и устойчивость элементов сооружений и машин.
Для успешного изучения сопротивления материалов необходимы знания теоретической механики, математики и физики.
В качестве основных положений сопротивления материалов используются законы и теоремы общей механики, в первую очередь, законы статики, которые необходимо знать и помнить.
В теоретической механике при рассмотрении ряда вопросов полагают, что тела не изменяют своей формы под действием сил, каковы бы эти силы не были по величине. То есть мы считаем тело абсолютно жестким. Такой подход позволяет вполне удовлетворительно решать большое число вопросов, касающихся рвновесия и движения реальных тел.
Переходя же к практической реализации рассматреваемой конструкции (от схемы к телу) мы неизбежно должны решить две задачи:
1. Из каких материалов следует сделать элементы конструкции.
2. Какие размеры поперечного сечения следует назначить каждому элементу конструкции, чтобы он мог успешно воспринимать действие внешних сил, так как опыт показывает, что даже материалы, обладающие значительным сцеплением своих частиц, могут быть разорваны, раздавлены и т. д., если приложенные силы достигнут некоторых предельных значений.
Другими словами, возникает вопрос об обеспечении прочности конструкции и ее элементов. На этот вопрос статика бессильна дать ответ и эту задачу решают методы и приемы сопротивления материалов.
Обращаясь к опыту, мы прежде всего обнаружим, что всякая внешняя сила, которую в дальнейшем мы будем называть нагрузкой, приложенная к телу, даже весьма малая по величине, производит изменение его формы, являющейся результатом перемещения его частиц под действием нагрузки.
В связи с этим в отличии от теоретической механики сопротивление материалов рассматривает задачи, в которых наиболее существенными являются свойства деформируемых тел. В то же время следствие общности основных положений, сопротивление материалов может рассматриваться как раздел механики, который называется механикой деформируемых тел.
К механике деформируемых тел относятся и другие дисциплины, такие, как математическая теория упругости, где рассматриваются, по существу те же вопросы, только математическая теория упругости изучает поведение деформируемых тел в более точной постановке. Это приводит к необходимости использовать сложный математический аппарат и при решении практических задач производить громоздкие вычислительные операции.
В процессе эксплуатации конструкций и машин их элементы подвергаются внешнему воздействию различных нагрузок. Для обеспечения надежной работы конструкции ее элементы должны обладать достаточной прочностью, жесткостью и устойчивостью при наименьших затратах материала, а, cледовательно, и наименьшей стоимости.
Прочность - способность конструкции и ее элементов выдерживать нормативные нагрузки, не разрушаясь.
Жесткость - способность конструкции и ее элементов работать в условиях нормальной эксплуатации таким образом, чтобы изменение формы и размеров не привышали заданных величин.
Устойчивость - способность конструкции и ее элементов сохранять первоначальную форму или находиться в состоянии устойчивого равновесия.
Реальный объект и расчетная схема
Рассчитывая реальную конструкцию, следует сразу установить, какие факторы, относящиеся к объекту и условиям эксплуатации, существенны, а какие - нет. То есть произвести схемотизацию и отбросить несущественные факторы, которые не могут сколько-нибудь заметно повлиять на работу объекта в целом. Выбор расчетной схемы в сопротивлении материалов начинается со схемотизации свойств материалов. Принято рассматривать все материалы как однородную сплошную среду.
Реальный объект, освобожденный от несущественных особенностей, называется расчетной схемой.
Элементы конструкций и машин
Имеющееся разнообразие конструктивных элементов, которые используются в сооружениях и машинах, можно свести к небольшому числу основных геометрических форм, cовокупность которых лежит в основе их конструктивного оформления.
К ним относят:
1.Стержень ( или брус), когда один размер много больше двух других. Различаются стержни: прямые, кривые, переменного сечения и призматические.
2.Оболочка, когда один размер много меньше двух других. Оболочки бывают сферическими или плоскими, которые называются пластинами.
3.Тело, когда все три размера соизмеримы.
Сопротивление материалов в основном занимается изучением стержневых конструкций.
Основными геометрическими характеристиками стержней являются его размеры, площадь поперечного сечения и ось.
Ось - линия, соединяющая центры тяжестей всех поперечных сечений.
Поперечное сечение - плоская фигура, получаемая при мысленном рассечении стержня плоскостью, перпендикулярной к его оси.
Внешние силы
Все силы, приложенные к элементу конструкции, называются внешними силами или нагрузками.
По связи с материалами элемента внешние силы разделяются на объемные и поверхностные.
Объемные - силы, распределенные по объему тела и приложенные ко всем его частицам (силы тяжести, магнитные силы, cилы инерции). Характеризуются интенсивностью, то есть силой, приходящейся на единицу объема материала.
Поверхностные - силы, приложенные к поверхности тела (давление воды на обшивку корабля, взаимодействие элементов и так далее). Они условно разделяются на сосредоточенные и распределенные.
Когда размеры области приложения нагрузки намного меньше самого элемента, то нагрузку заменяют равнодействующей и называют сосредоточенной силой.
Наиболее широкое распространение из распределенных нагрузок в сопротивлении материалов получили нагрузки распределенные по линии, которые характеризуются интенсивностью, то есть силой, приходящейся на единицу длины.
В расчетах эту нагрузку часто задают эпюрой (графиком), ось которой служит ось стержня, а ординаты в принятом масштабе выражают интенсивность нагрузки в соответствующих точках. На эпюрах ординаты имеют вид стрелок, показывающих направление нагрузки.
По относительной продолжительности действия все внешние силы разделяются на временные (постановка судна в док, случайные нагрузки и так далее) и постоянные, которые в общем-то могут изменяться во времени.
По относительной скорости приложения внешние силы разделяют на статические и динамические.
Статические - медленно возрастают от нуля до конечного значения (вес здания, давление воды).
Динамические - быстро меняют свою величину, а иногда и направление. Они разделяются на мгновенноприложенные, ударные и повторно-переменные.
Понятие о деформациях, внутренних усилиях и упругости
При воздействии внешних сил на конструкцию при превышении их нормативных значений все ее элементы изменяют свои геометрические размеры и форму, то есть деформируются.
Деформация - это изменение геометрических размеров и формы тела.
Любой материал элементов конструкции состоит из бесчисленного множества элементарных частиц. В результате внешней нагрузки между частицами материала элемента появляются силы межатомного взаимодействия, препятствующие их перемещению. Эти силы называют в сопротивлении материалов внутренними силами. Они зависят от физических свойств материала данного элемента и его геометрических размеров.
К внутринним силам относят: продольную силу, поперечные силы, изгибающие моменты, крутящий момент.
Вообще в любом теле между его частицами существуют внутренние силы взаимодействия и до его деформации. Они обуславливают существование тела , как такового. Однако в сопротивлении материалов они не изучаются. Нас интересуют исследования и вычисления дополнительных внутренних сил, которые возникли в результате нагружения тела внешними нагрузками.
Таким образом, внутренними силами (или усилиями), будем называть силы внутри тела между его частицами и обусловленные их смещением в результате деформациии.
Внутренние силы при снятии внешней нагрузки возвращают частицы в исходное положение, деформация исчезает и тело принимает свои начальные размеры и форму.
Свойства тел возвращаться к своей первоначальной форме и принимать первоначальные размеры после удаления внешней нагрузки называются упругостью.
Абсолютно упругое - это такое тело, которое после снятия внешней нагрузки полностью восстанавливает начальные размеры и форму.
Частично упругое - это такое тело, у которого после снятия внешней нагрузки деформация исчезает не полностью.
Упругие свойства обусловлены внутреннеми силами, которые можно назвать внутренними силами упругости.
Опыты показывают, что все материалы могут рассматриваться как абсолютно упругие только в некоторых пределах значений внутренних сил.
Основные допущения, принимаемые в сопротивлении материалов
В сопротивлении материалов используется ряд допущений (предпосылок), упрощающих расчеты. Эти допущения, как показывают эксперименты, а также исследования, проверяются более строгими методами теории упругости, можно использовать при решении задач, рассматриваемых в сопротивлении материалов.
К ним относят :
1.Тела считаются абсолютно упругими.
2.Все тела считаются достаточно жесткими.
3.Все тела считаются однородными и изотропными, то есть все точки тела по всем направлениям обладают одинаковыми физическими свойствами.
4.Все тела следуют закону Гука.
5.Всем телам свойственно пребывать в естественном состоянии.
6.Зоконы механики, применяемые к телам конечных размеров, применимы также и к телам бесконечно малых размеров.
7.Если нет специальной оговорки, то всегда предпологается действие принципа или пастулата Сен-Венана: "Если к ограниченному объему тела приложить две взаимноуравовешенные системы сил, равнадействующие которых одинаковы, а закон распределения сил различен, то в этом месте возникают местные напряжения, быстро затухающие по мере удаления от места приложения уравновешенных сил".
8.Результат воздействия на тело системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности - принцип независимости действия силы.
9.Перемещения от внешних нагрузок малы по срввнению с размерами тел. Это позволяет считать расчетную схему неизменяемой.
В некоторых случаях, специально оговариваемых, часть допущений использовать нельзя.
Моменты инерции плоских фигур. Общие положения и понятия
В данном разделе будут изложены общие положения теории определения моментов инерции и сопративления для площадей плоских фигур. Рассмотрим фигуру произвольного очертания (Рис.1).
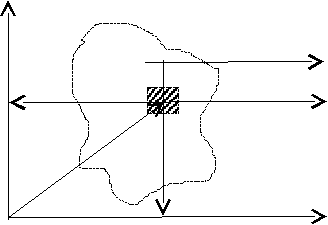 z
z00
y 0y
dF
z
y
Рис.1
Выражение
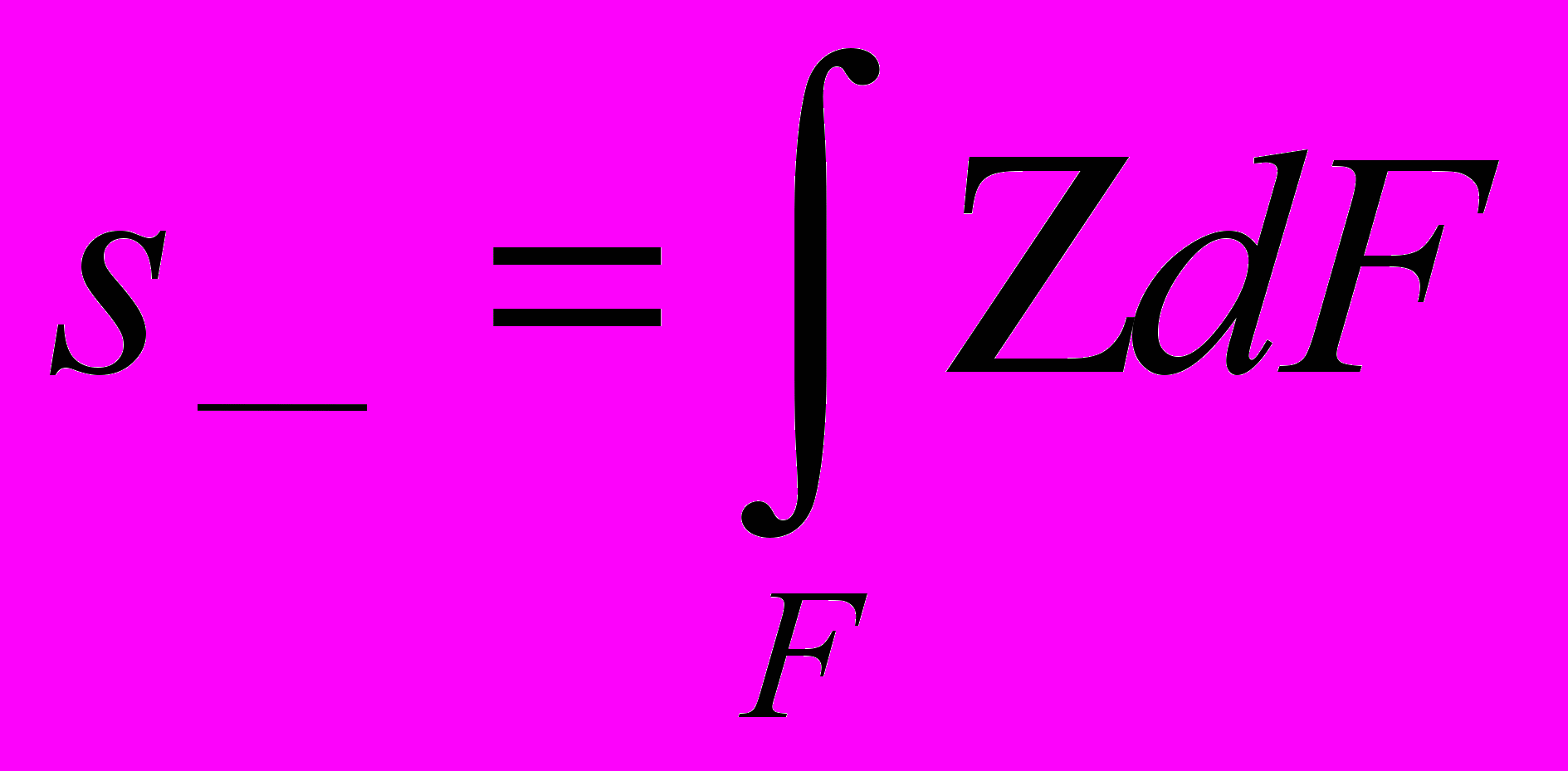 (1)
(1)называется статическим моментом площади сечения относительно оси
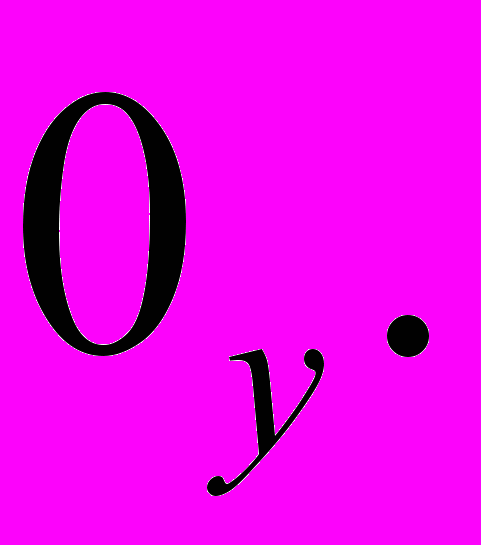
Для оси 00, параллельной оси
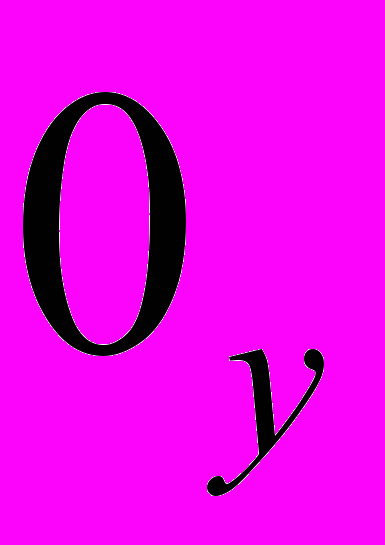 и отстоящей от нее на расстояние ,
и отстоящей от нее на расстояние ,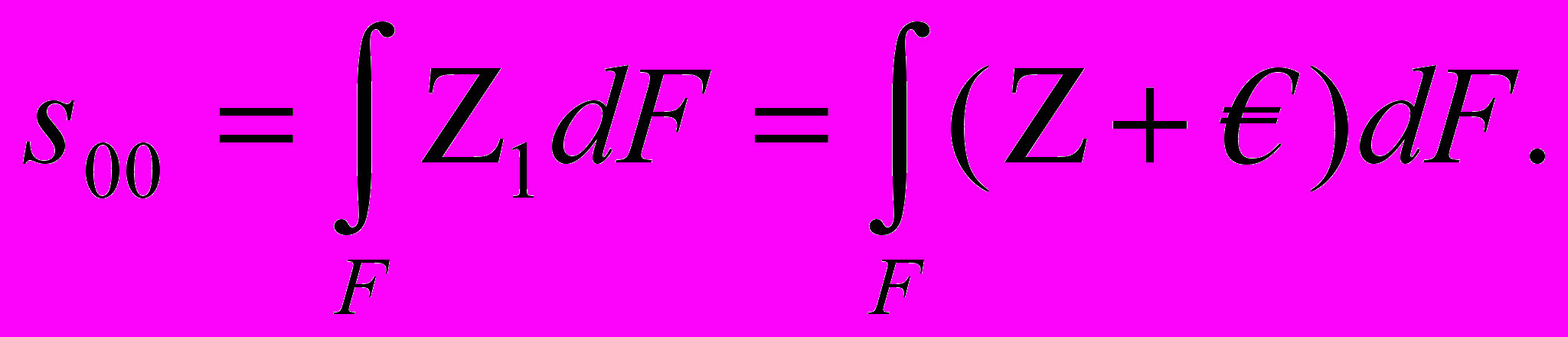 (2)
(2)Статический момент может быть положительным и отрицательным. Статический момент относительно оси, проходящей через центр тяжести площади, равен нулю, то есть
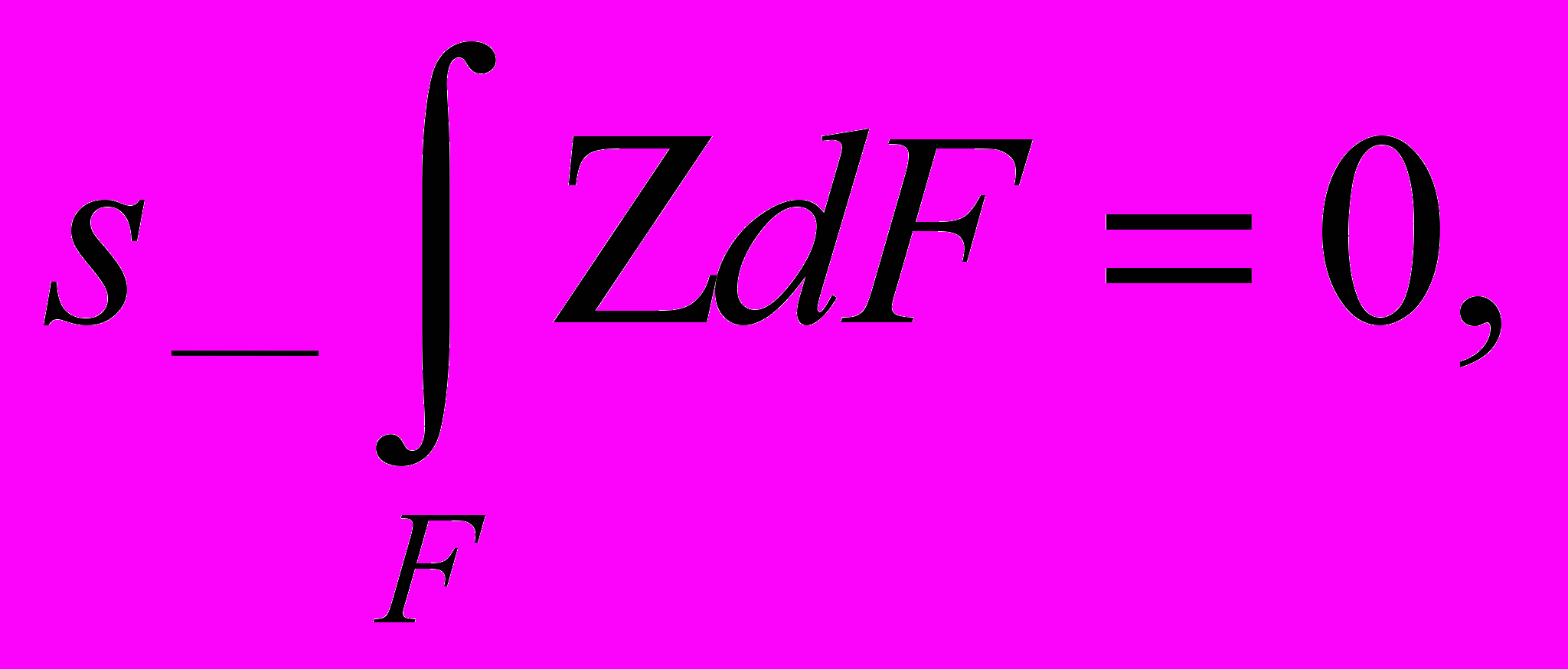 (3)
(3)Если ось у проходит через центр тяжести площади.
Выражение
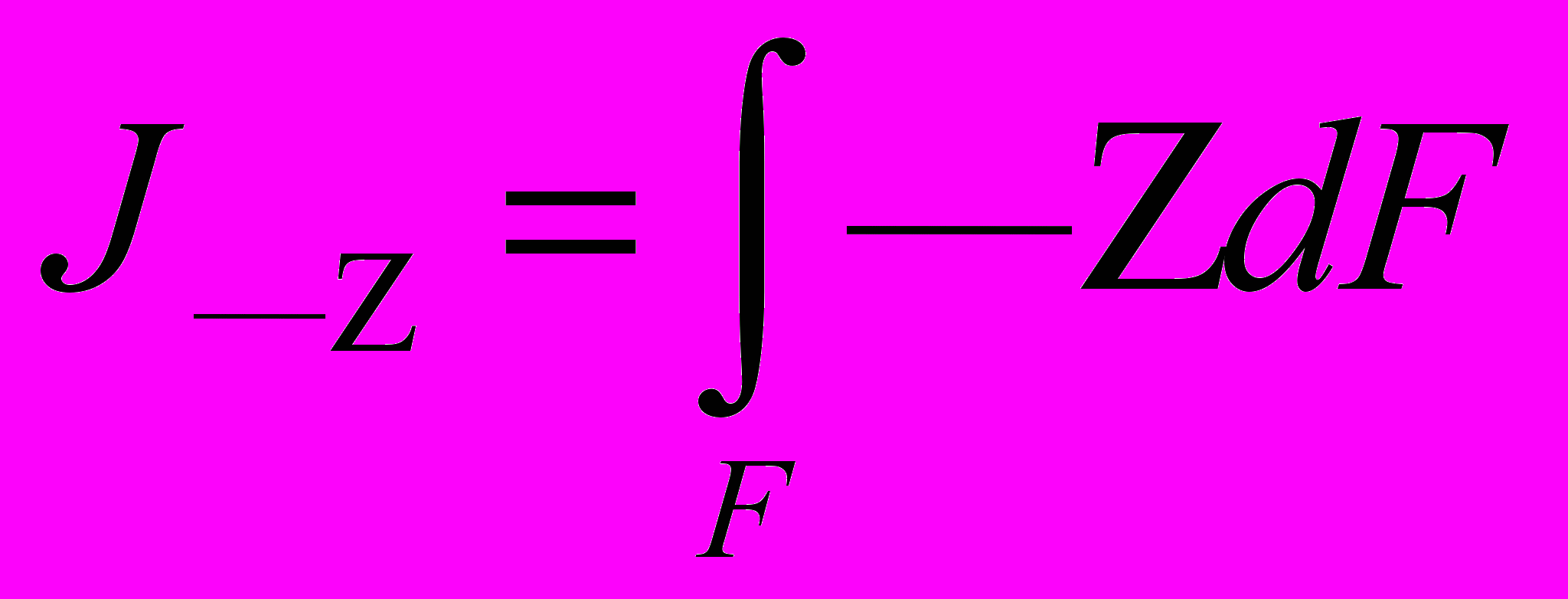 (4)
(4)называется центробежным моментом инерции площади фигуры.
Центробежный момент инерции может быть положительным и отрицательным. Если фигура имеет ось симметрии (например, на рис.2), то центробежный момент инерции относительно осей, из которых одна совмещена с осью симметрии фигуры, всегда равен нулю, то есть
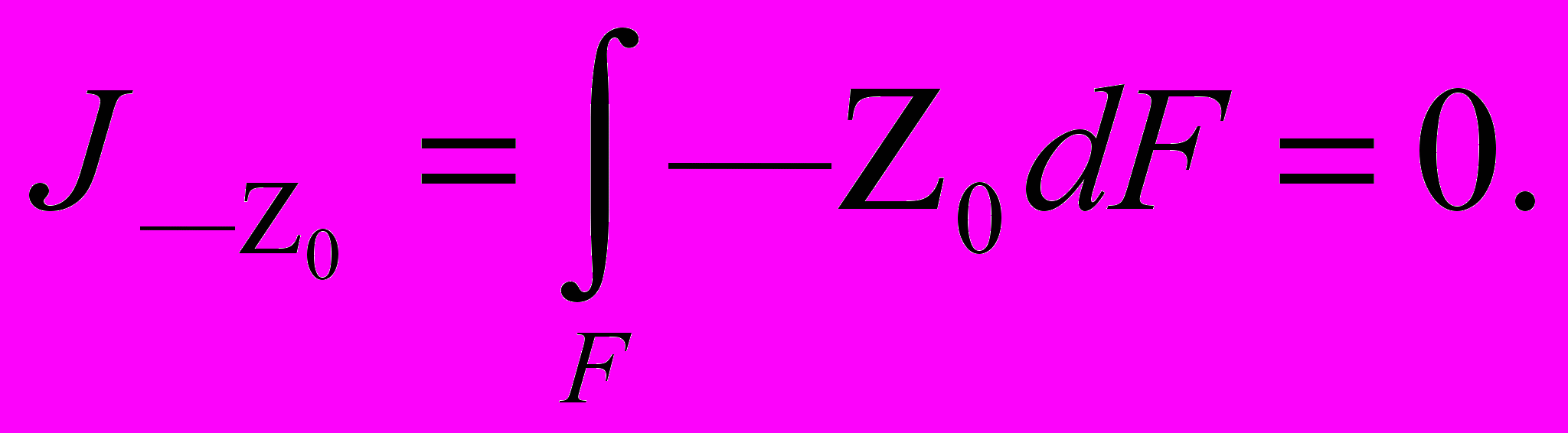 (5)
(5) z
z0 у
Рис.2
Это следует из того, что всякой ординате
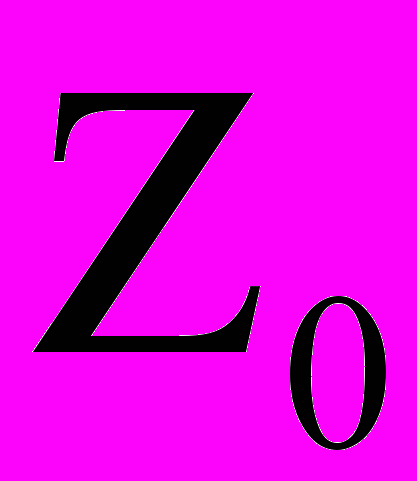 , соответствуют два значения
, соответствуют два значения 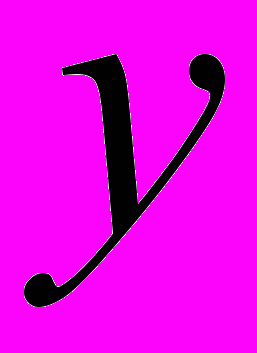 : c "+" и "-".
: c "+" и "-".Выражения
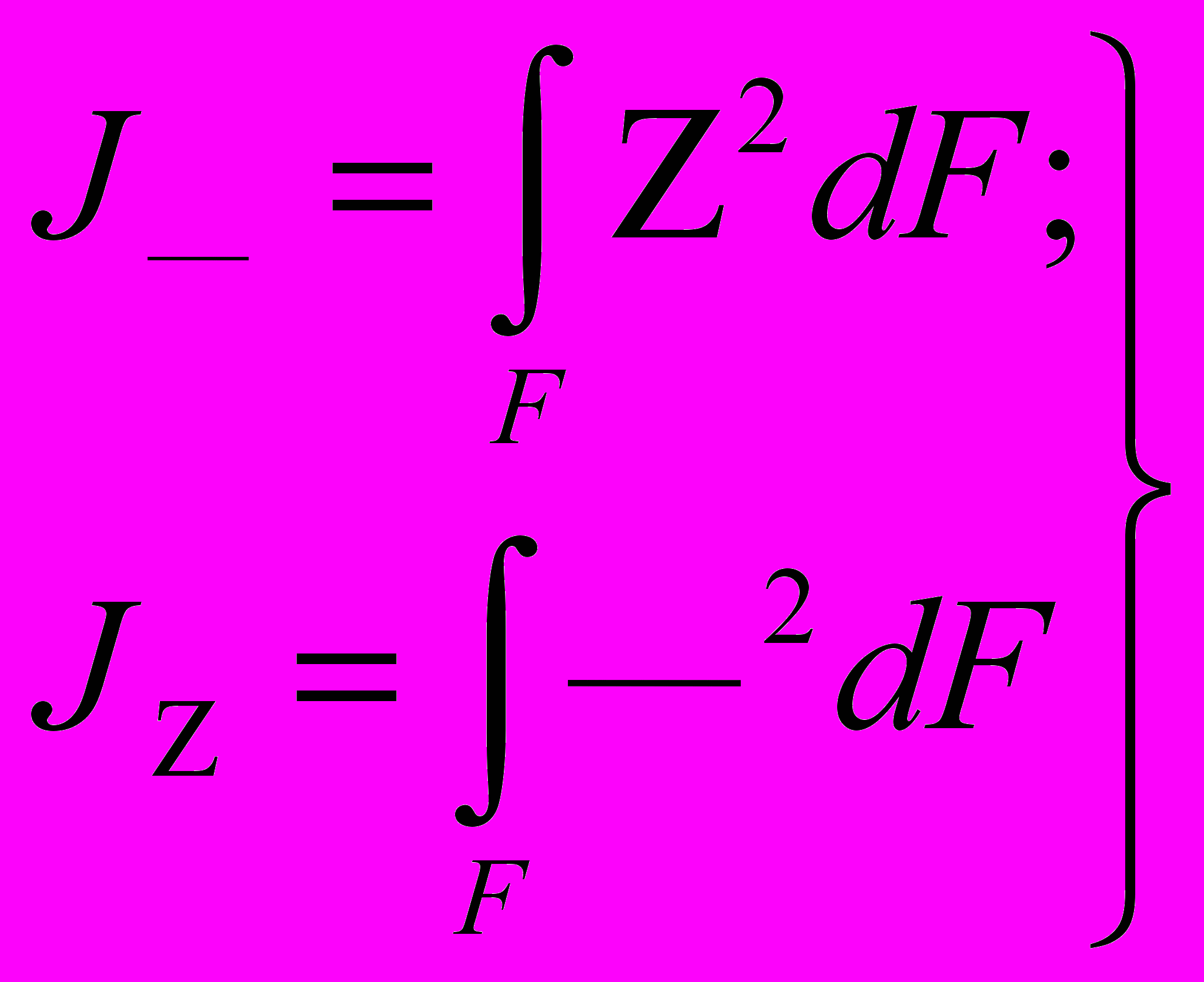 (6)
(6)называют моментами инерции относительно осей или экваториальными моментами инерции.
Момент инерции площади относительно оси всегда положителен.
Выражение
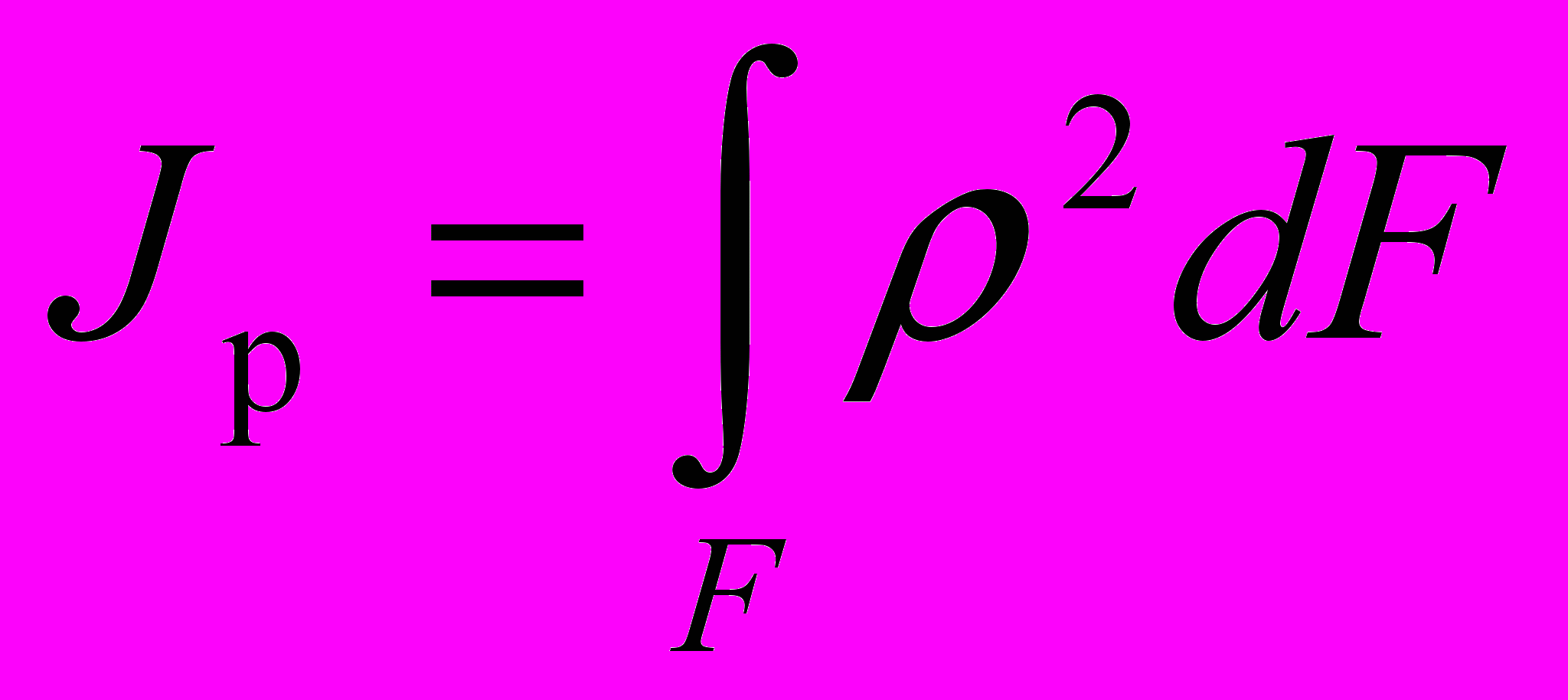 (7)
(7)называется полярным моментом инерции площади фигуры (см. Рис.1).
Полярный момент инерции связан с моментами инерции площади относиительно осей зависимостью вид
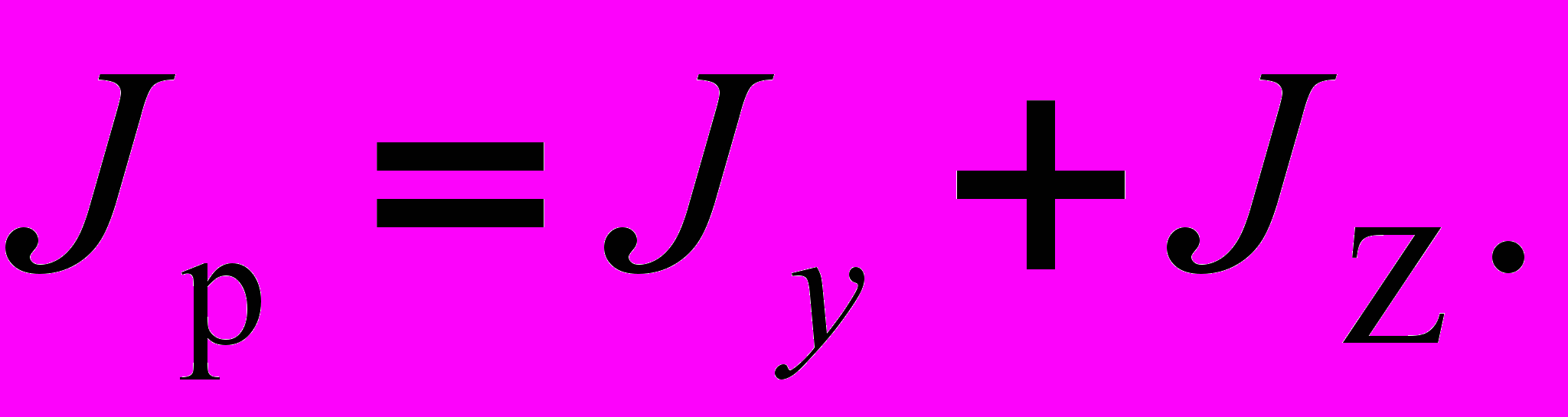 (8)
(8)Оси, проходящие через центр тяжести фигуры, называются центральными осями. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями для данной точки сечения (начала координат). Главные оси, проведенные через центр тяжести площади фигуры, называют главными центральными осями. Главные центральные оси обладают тем свойством, что осевые моменты инерции, относительно этих осей, достигают экстремального значения
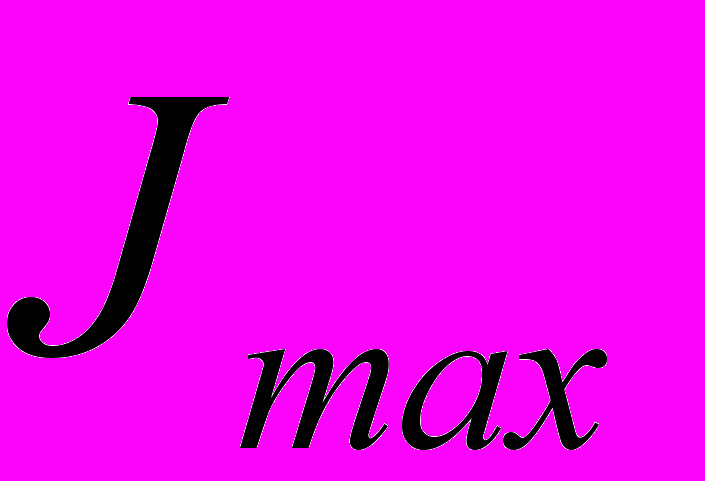 и
и  по сравнению с осевыми моментами инерции относительно всех центральных осей.
по сравнению с осевыми моментами инерции относительно всех центральных осей.Моменты инерции и моменты сопротивления простейших фигур
Прямоугольное сечение
 z
zh 0
y
b
На рисунке показано сечение, для которого нужно определить моменты инерции относительно центральных и моменты сопротивления.
Известно, что:
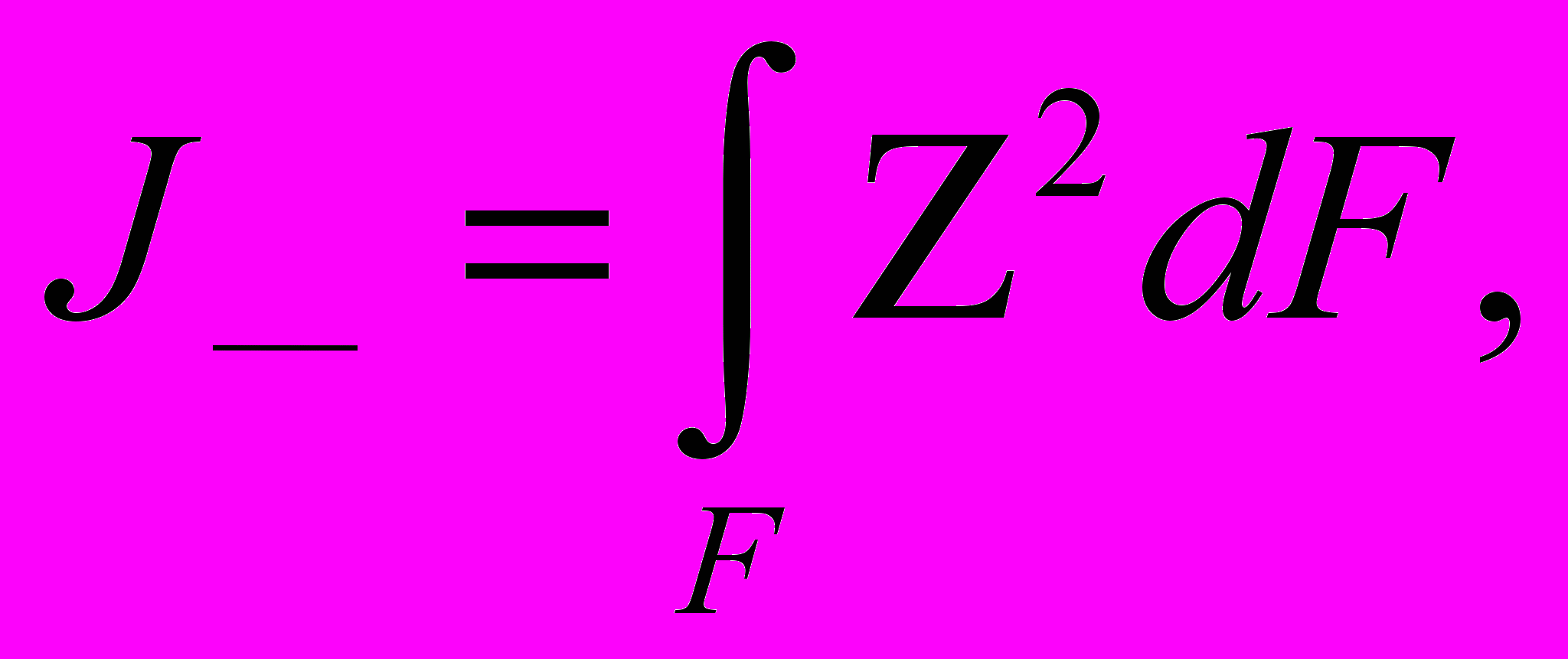
но, как видно из представленного рисунка
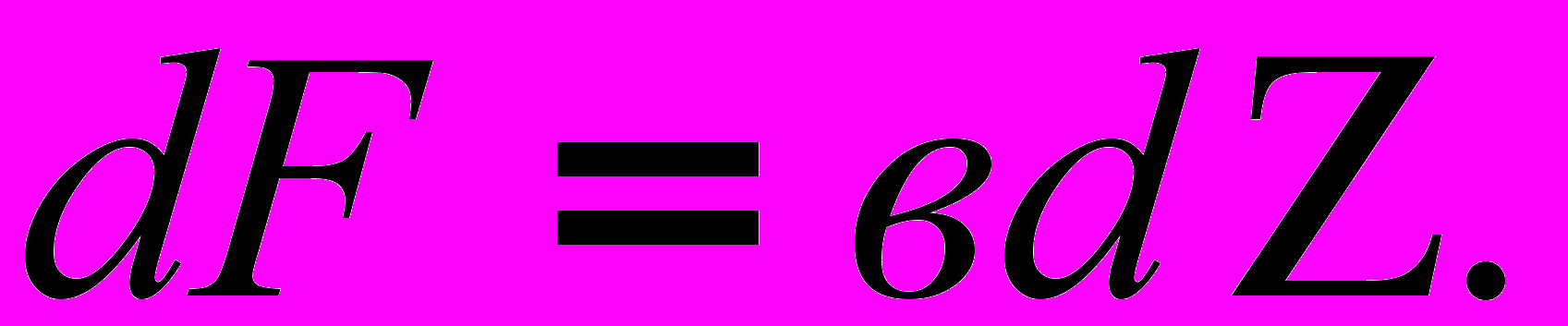
Значит,
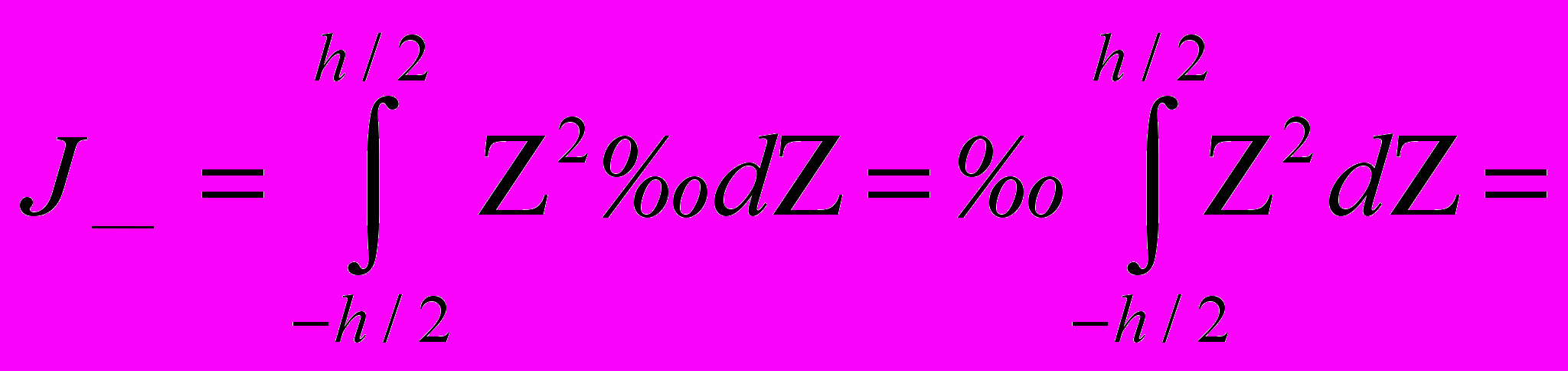
=
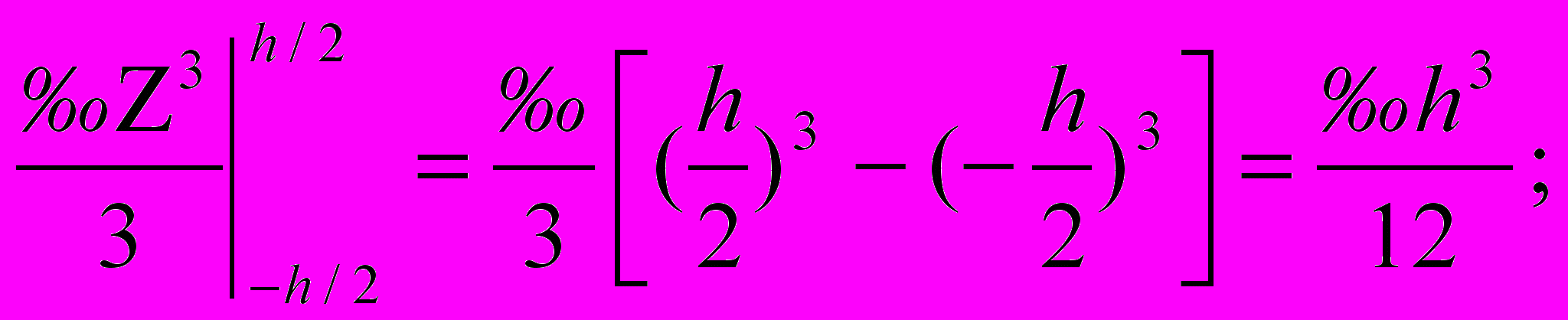
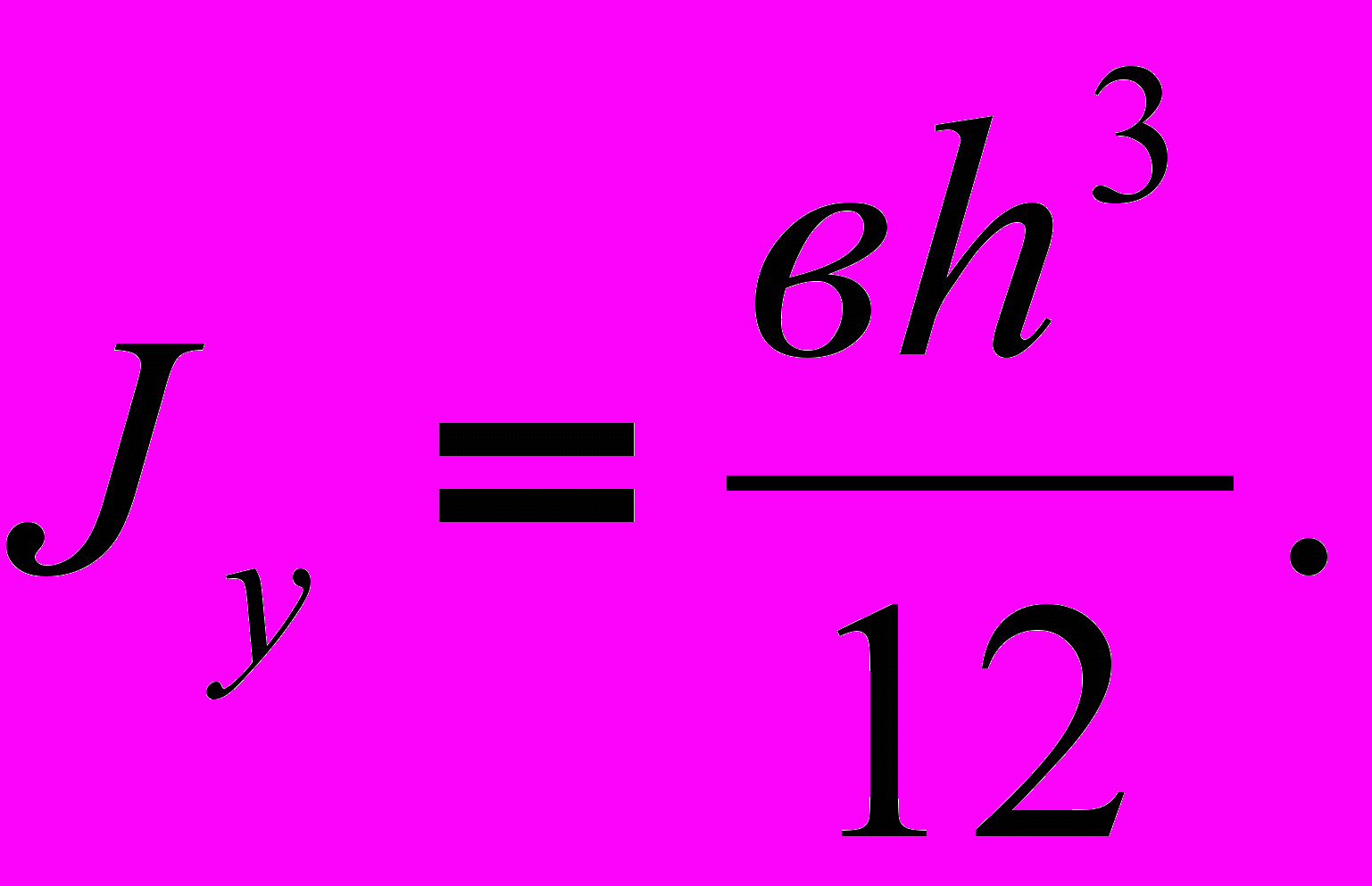 (1)
(1)Зная формулу (1), легко получить
 . Для этого нужно только заменить h на
. Для этого нужно только заменить h на 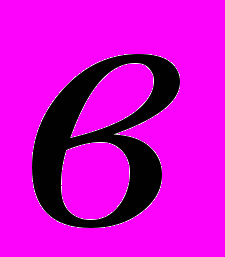 , а
, а 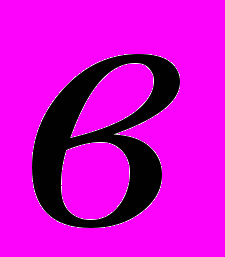 на h:
на h: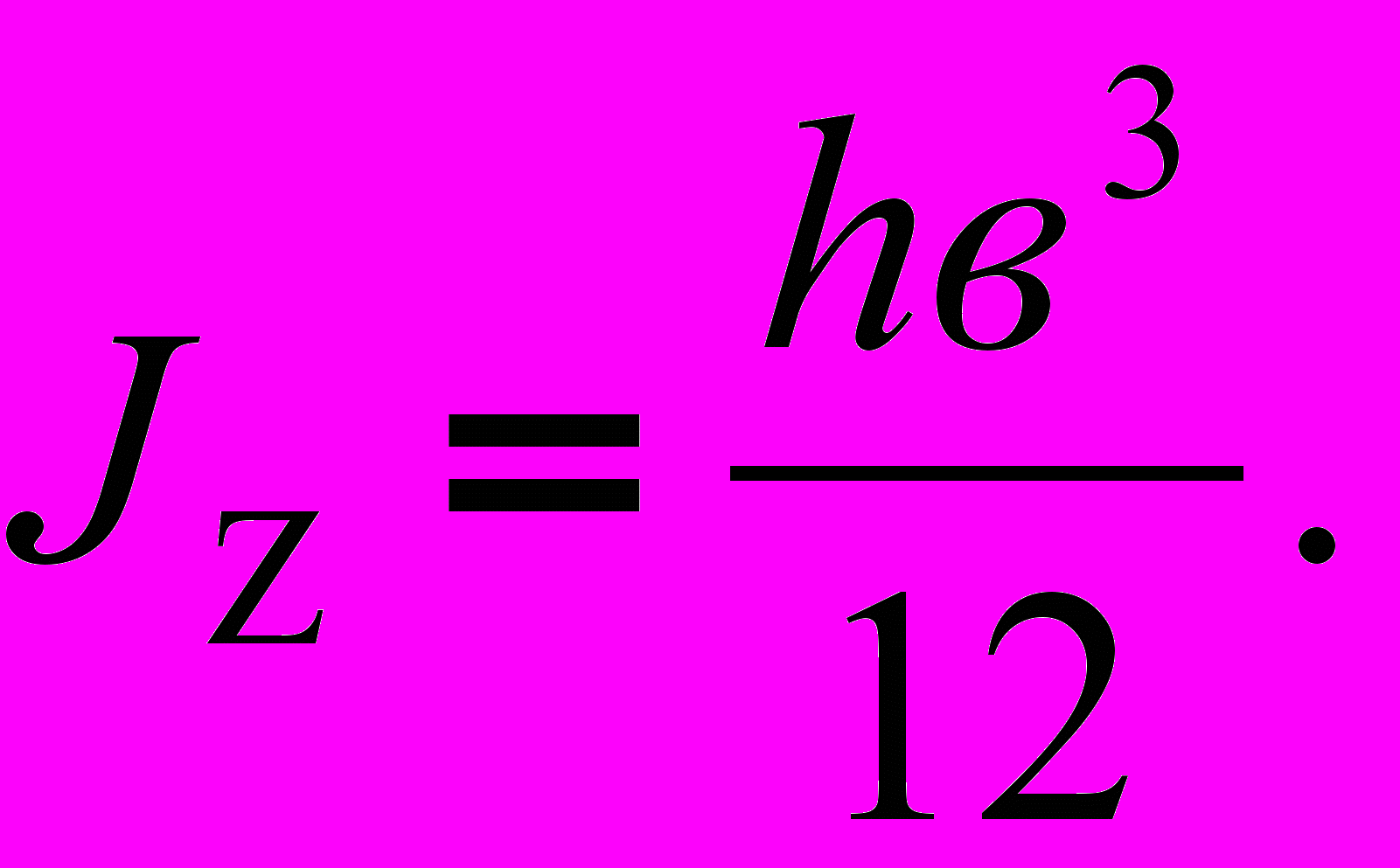 (2)
(2)Моменты сопротивления сечения
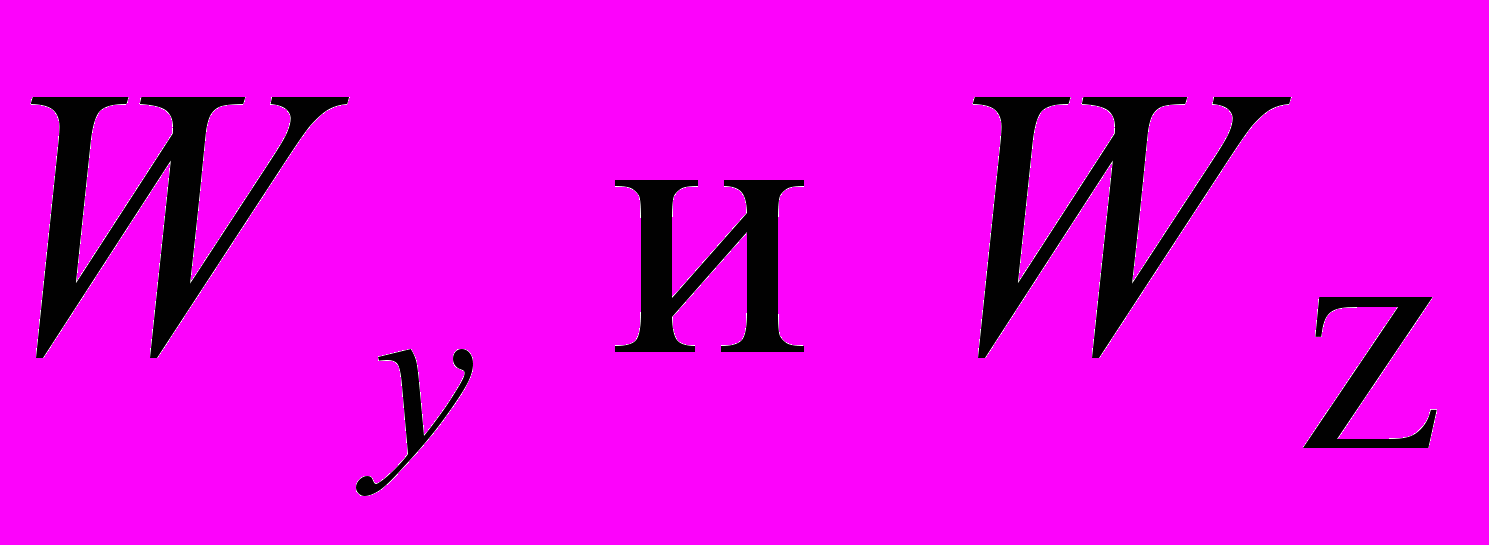 определяются выражениями:
определяются выражениями: (3)
(3)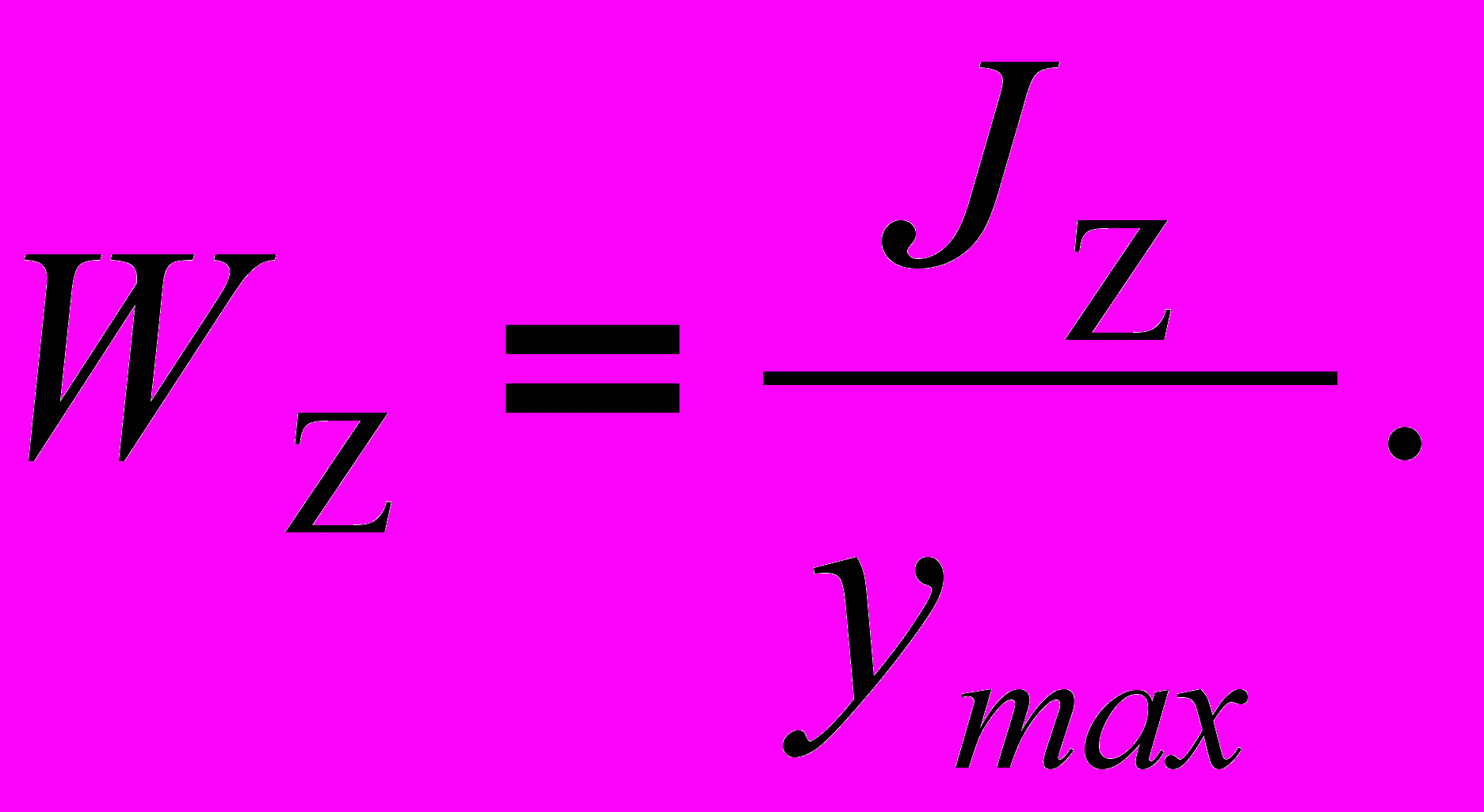 (4)
(4)В нашем случае
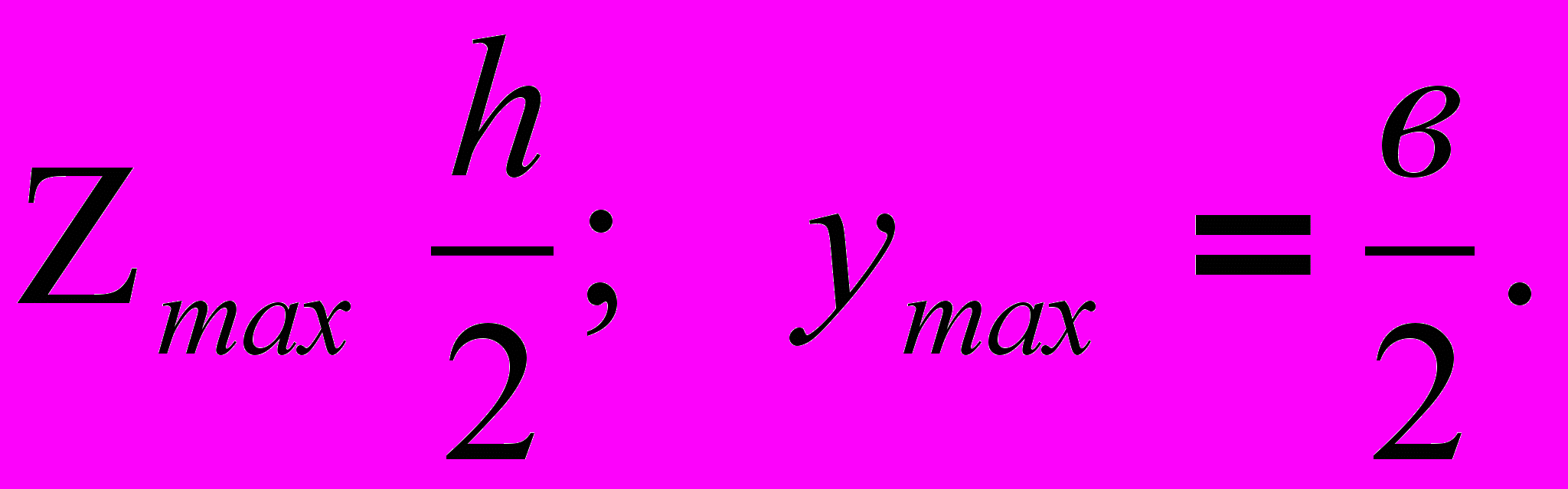
Следовательно:
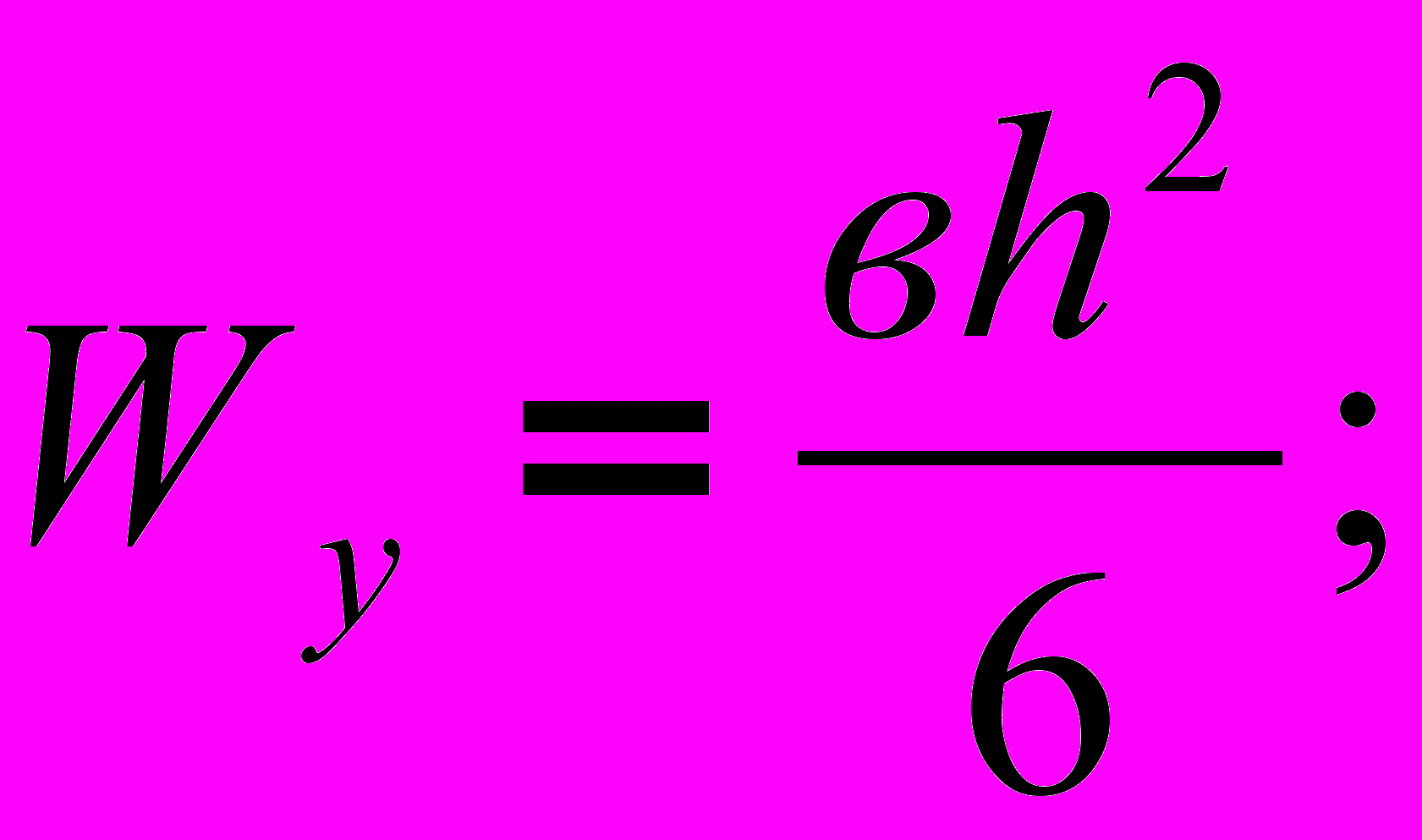 (5)
(5)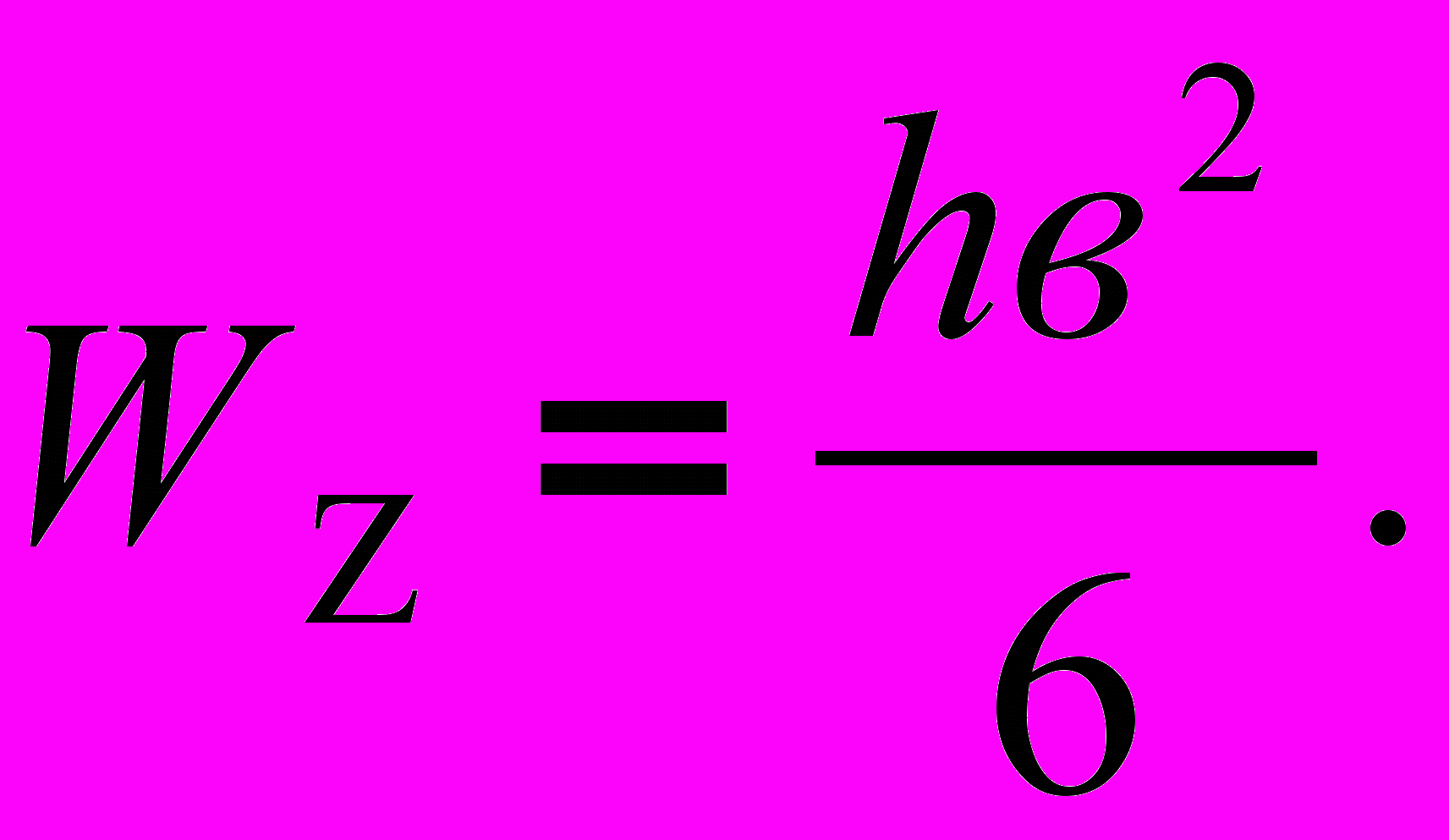 (6)
(6)Круглое сечение
 z
zr
0 y
На рисунке показано круглое сечение. Найдем
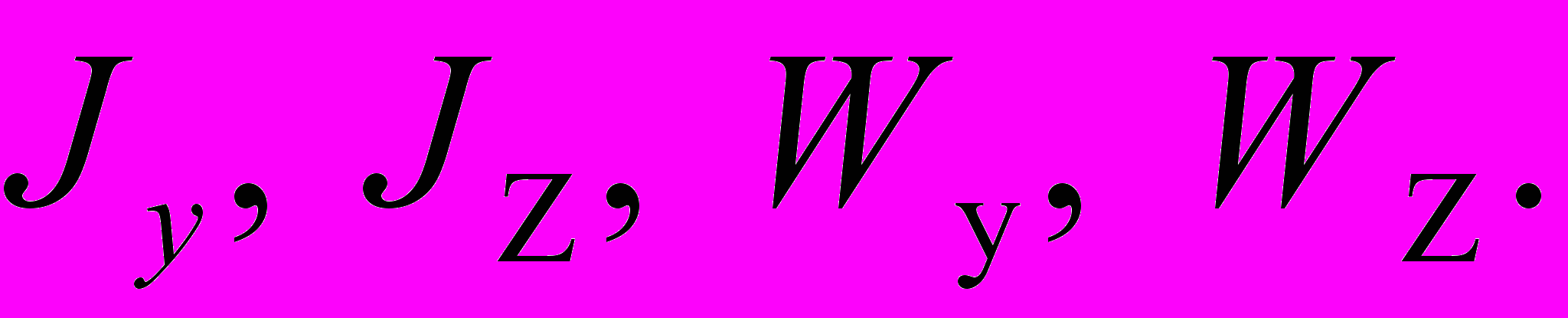 Известно, что
Известно, что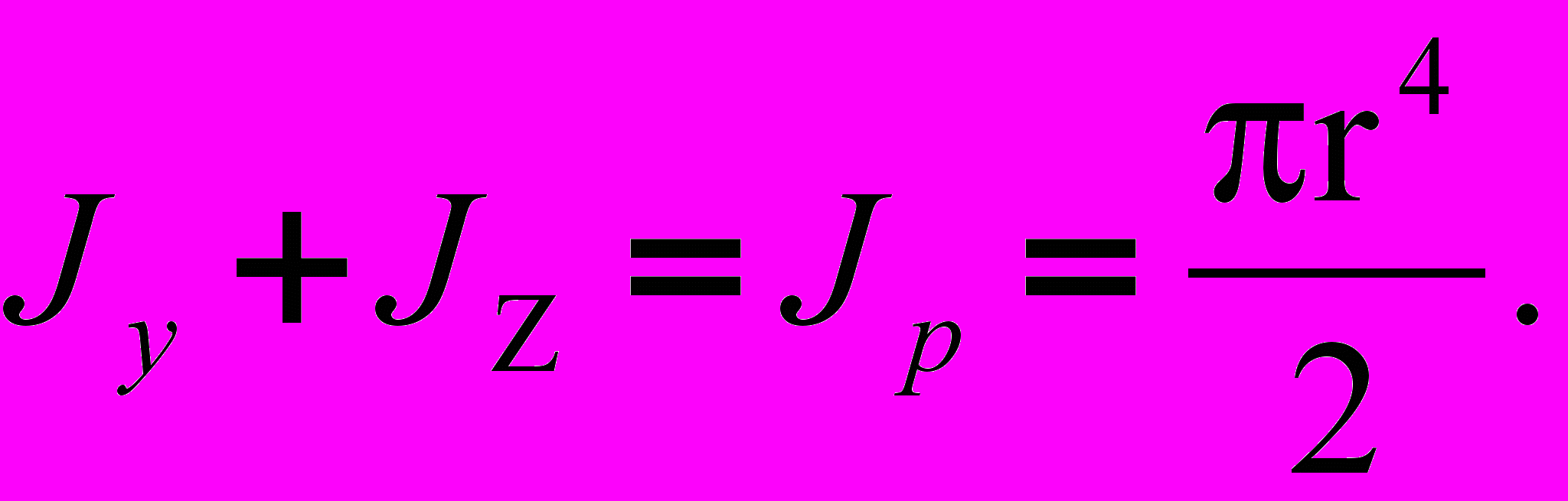 (1)
(1)В силу симметрии
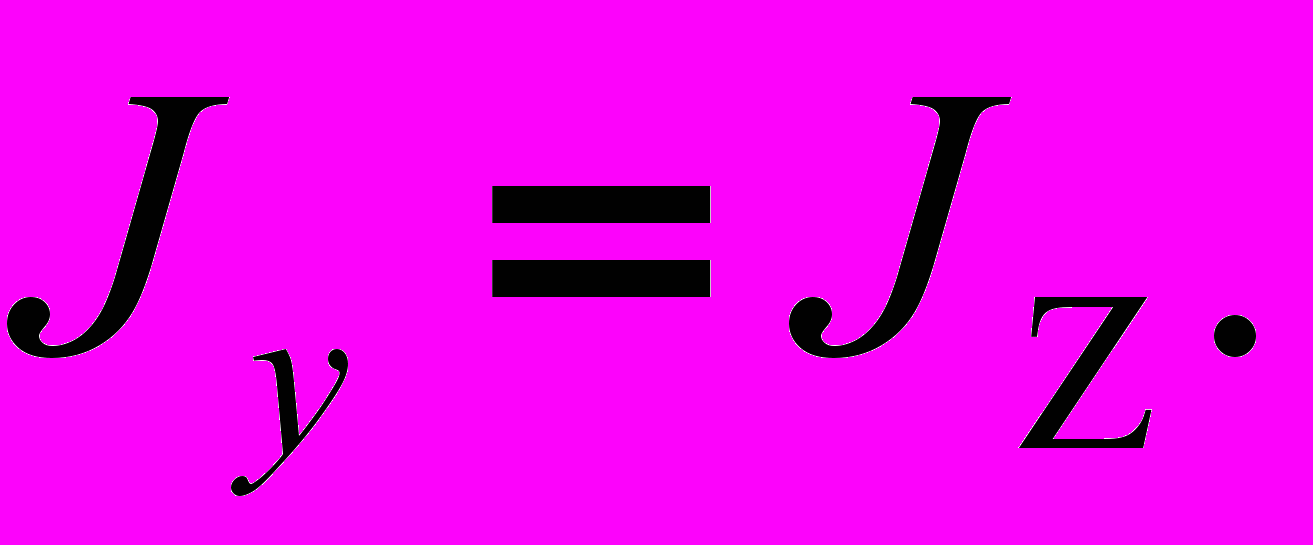 Подставляя это в (1), получим:
Подставляя это в (1), получим: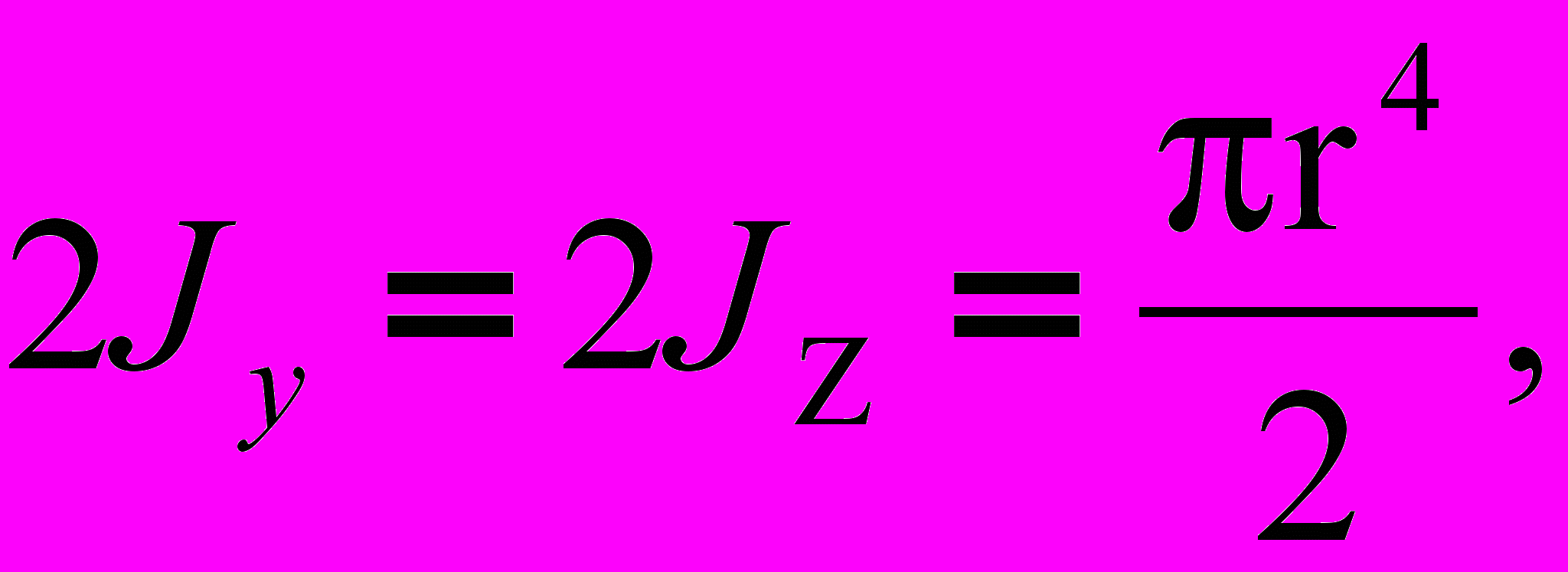 .
.Откуда:
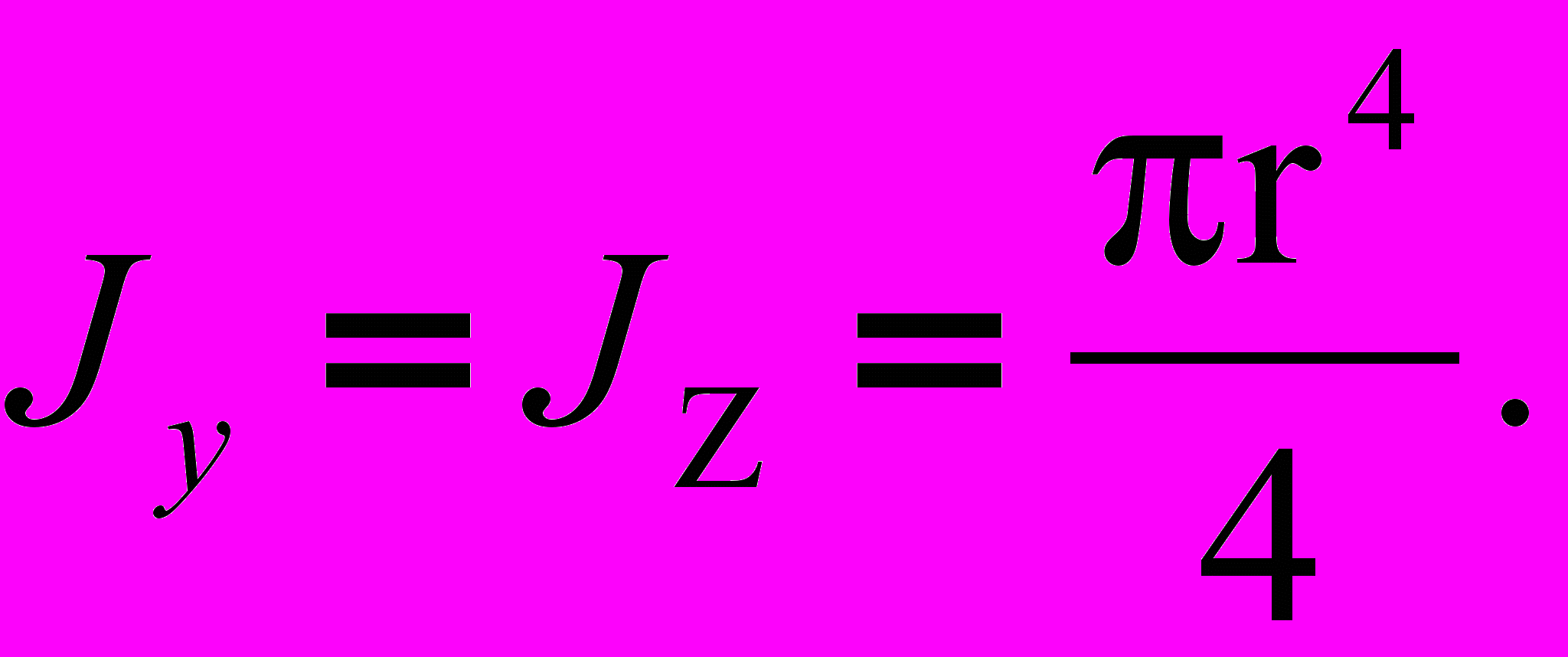 (2)
(2)Соответственно моменты сопротивления будут:
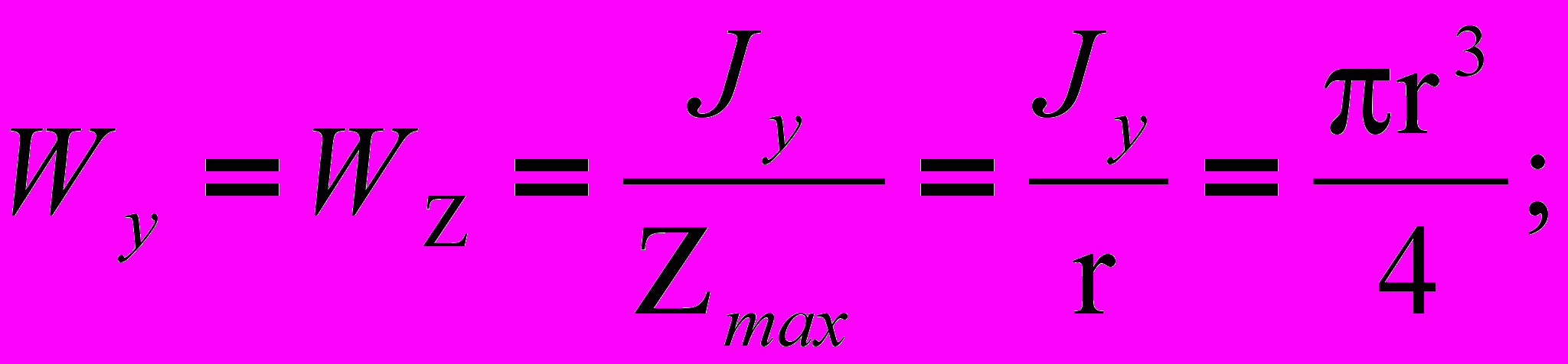
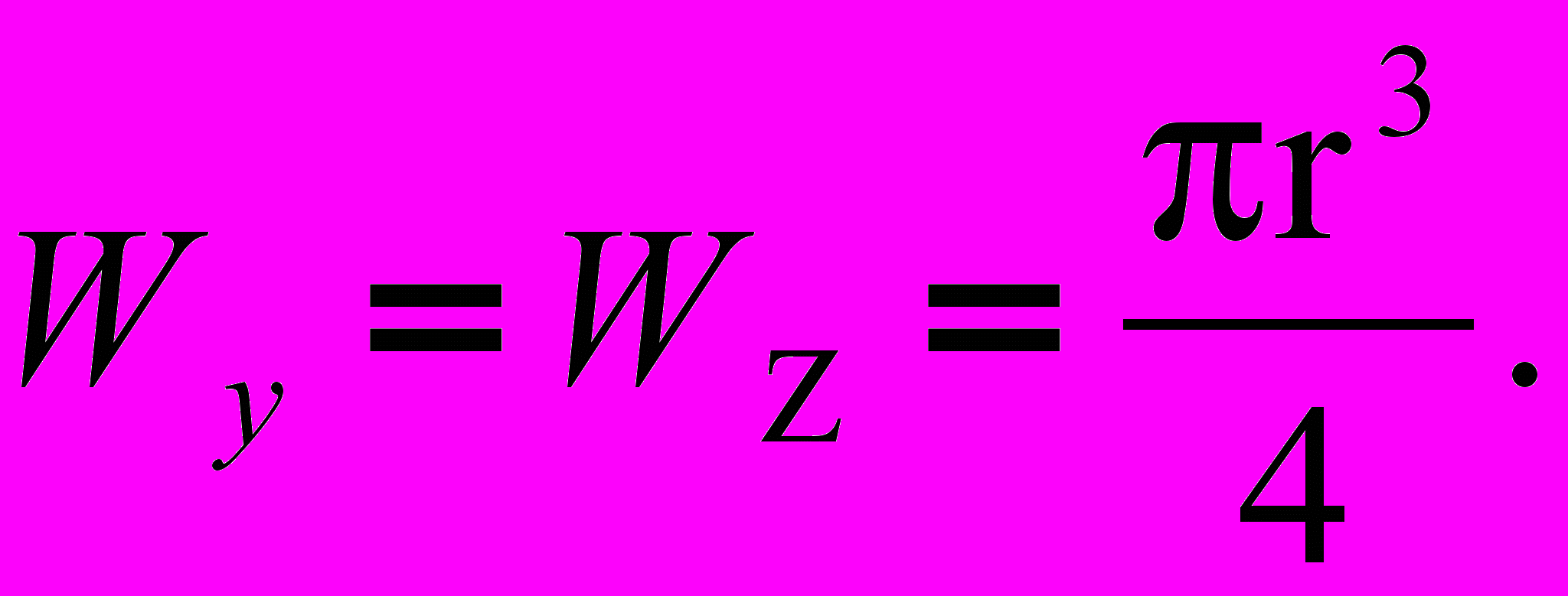 (3)
(3)Треугольное сечение
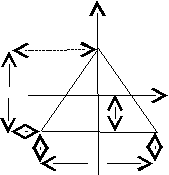 z
zh 0 y
z
A b B
На рисунке показано треугольное сечение, для которого требуется определить момент инерции относительно оси АВ, совмещенной с основанием треугольника.
По определению
 (1)
(1)Из чертежа находим:
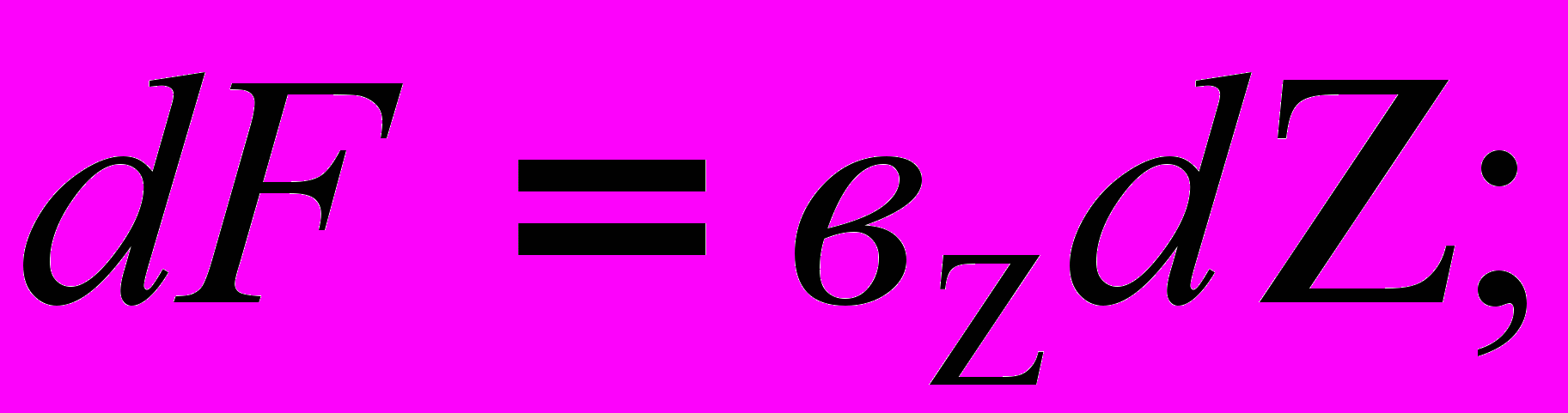
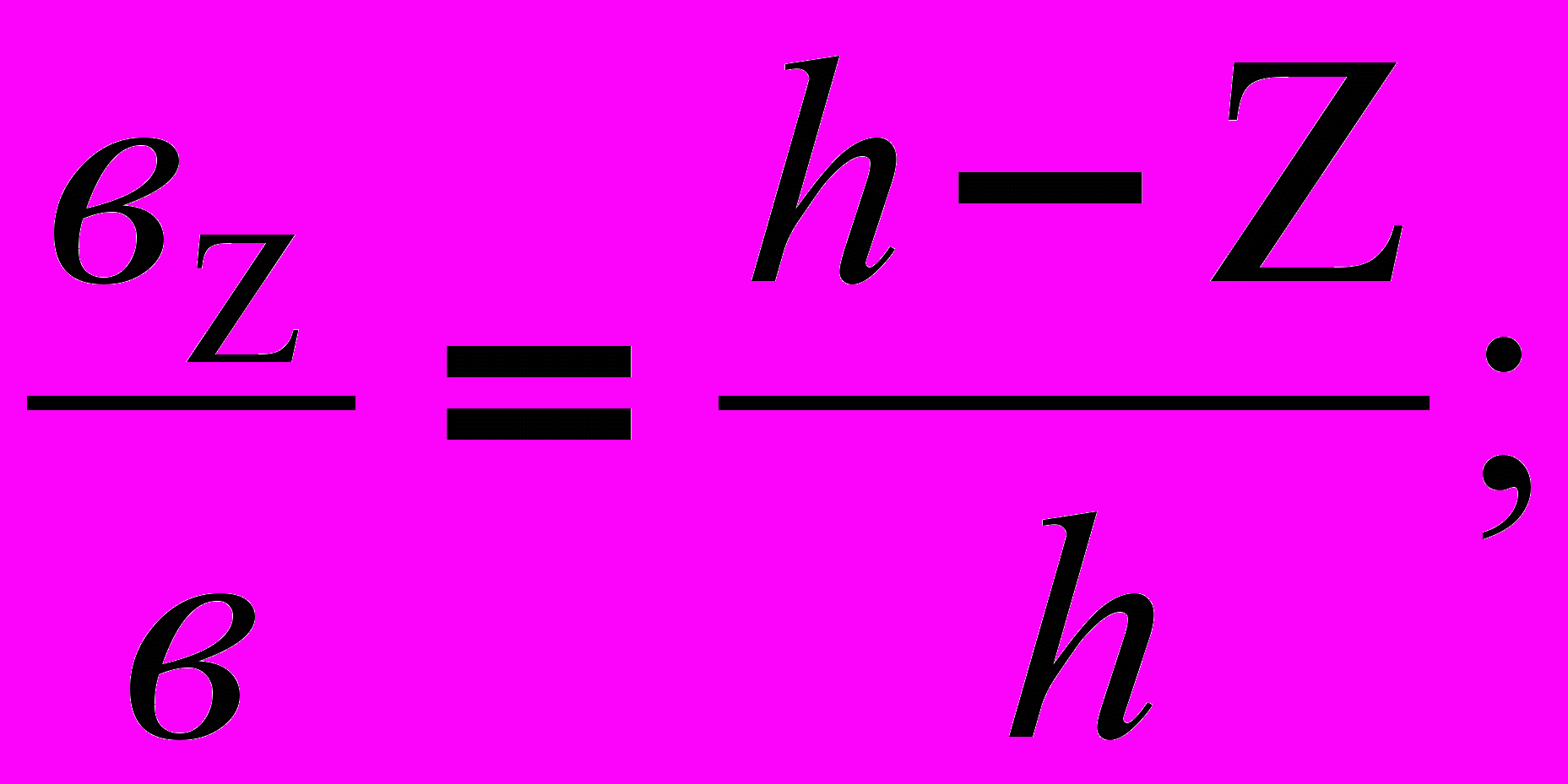
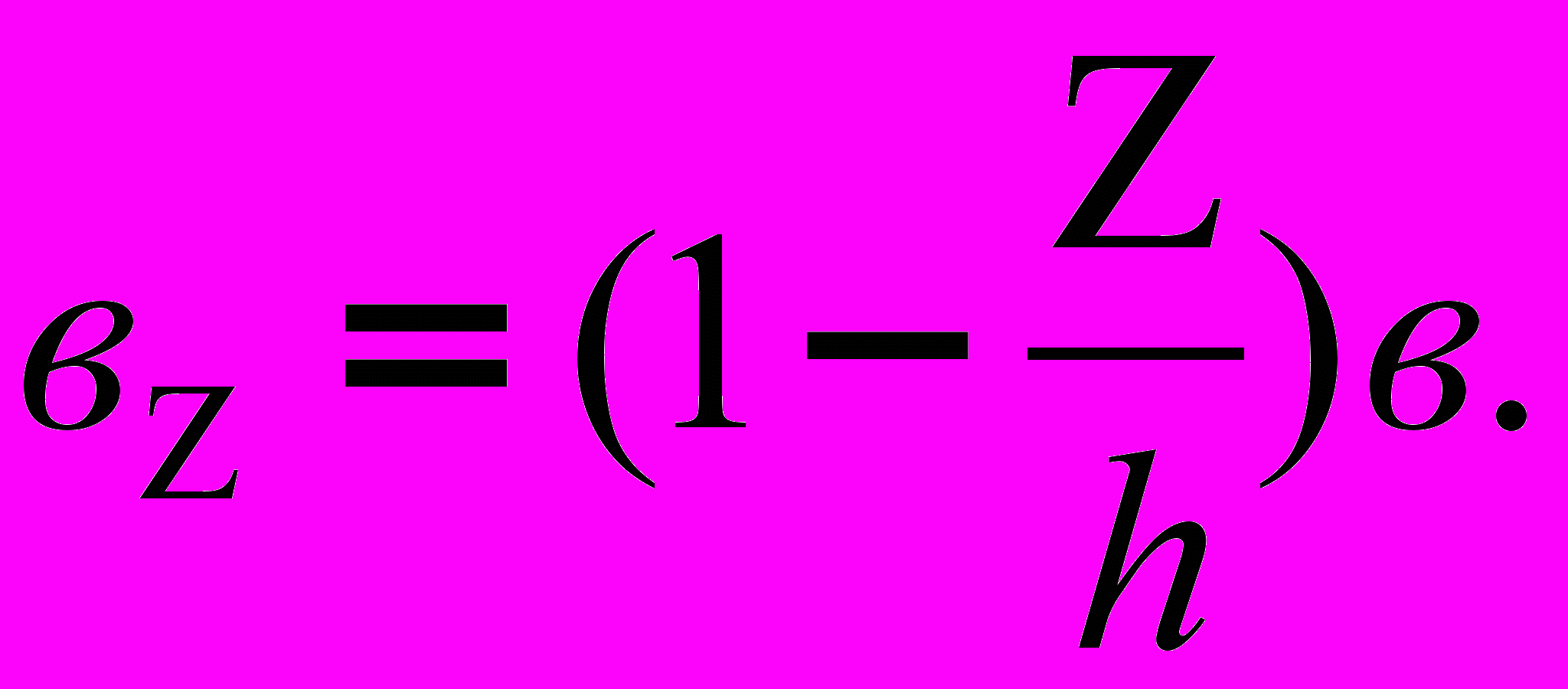
Подставляя значения dF в выражение (1) получим :
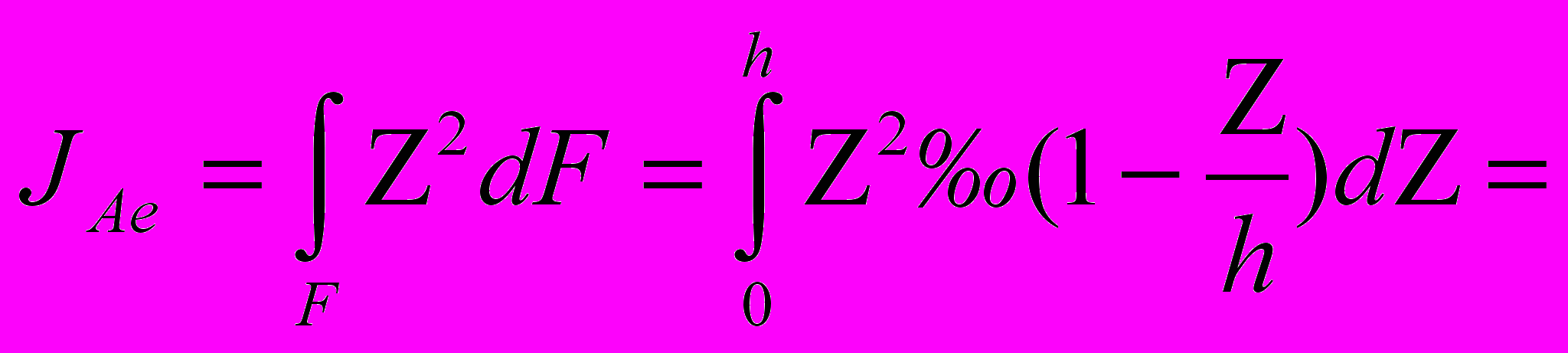
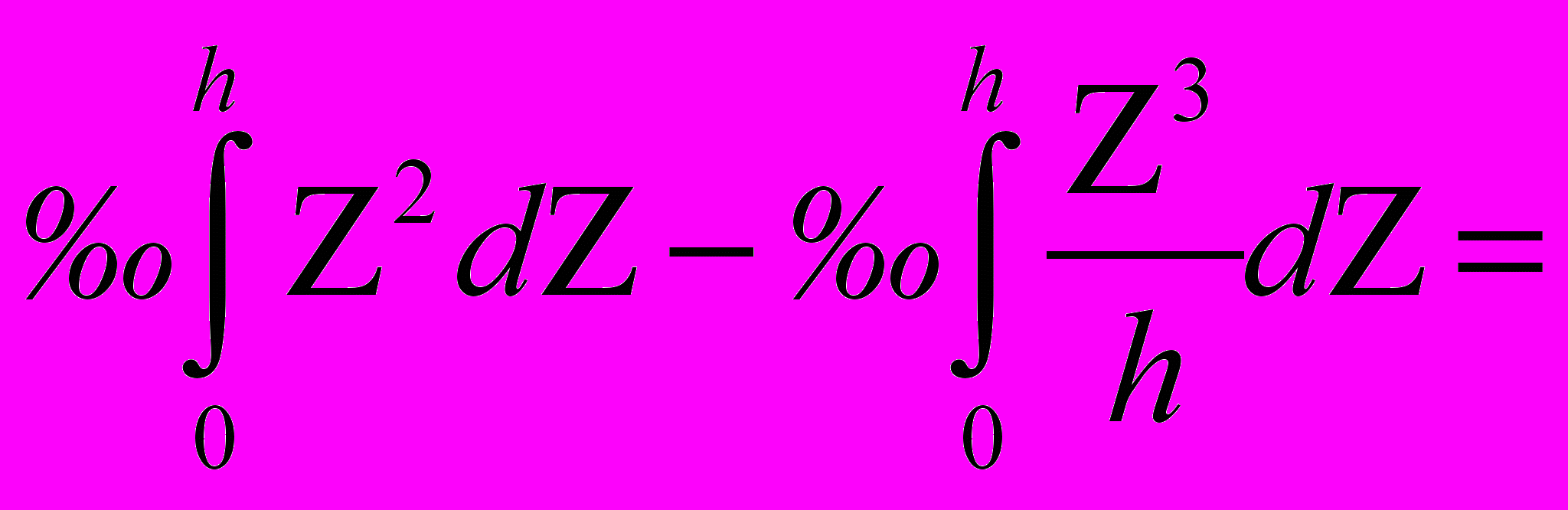
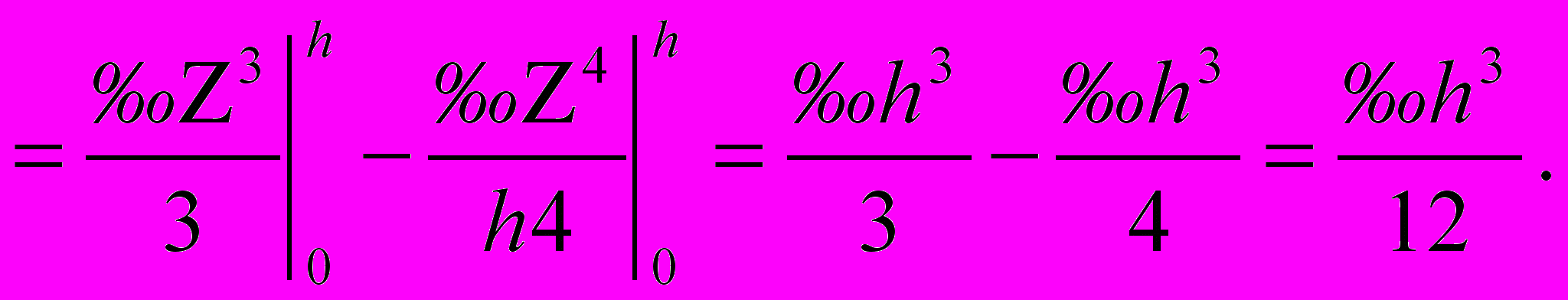
Окончательно
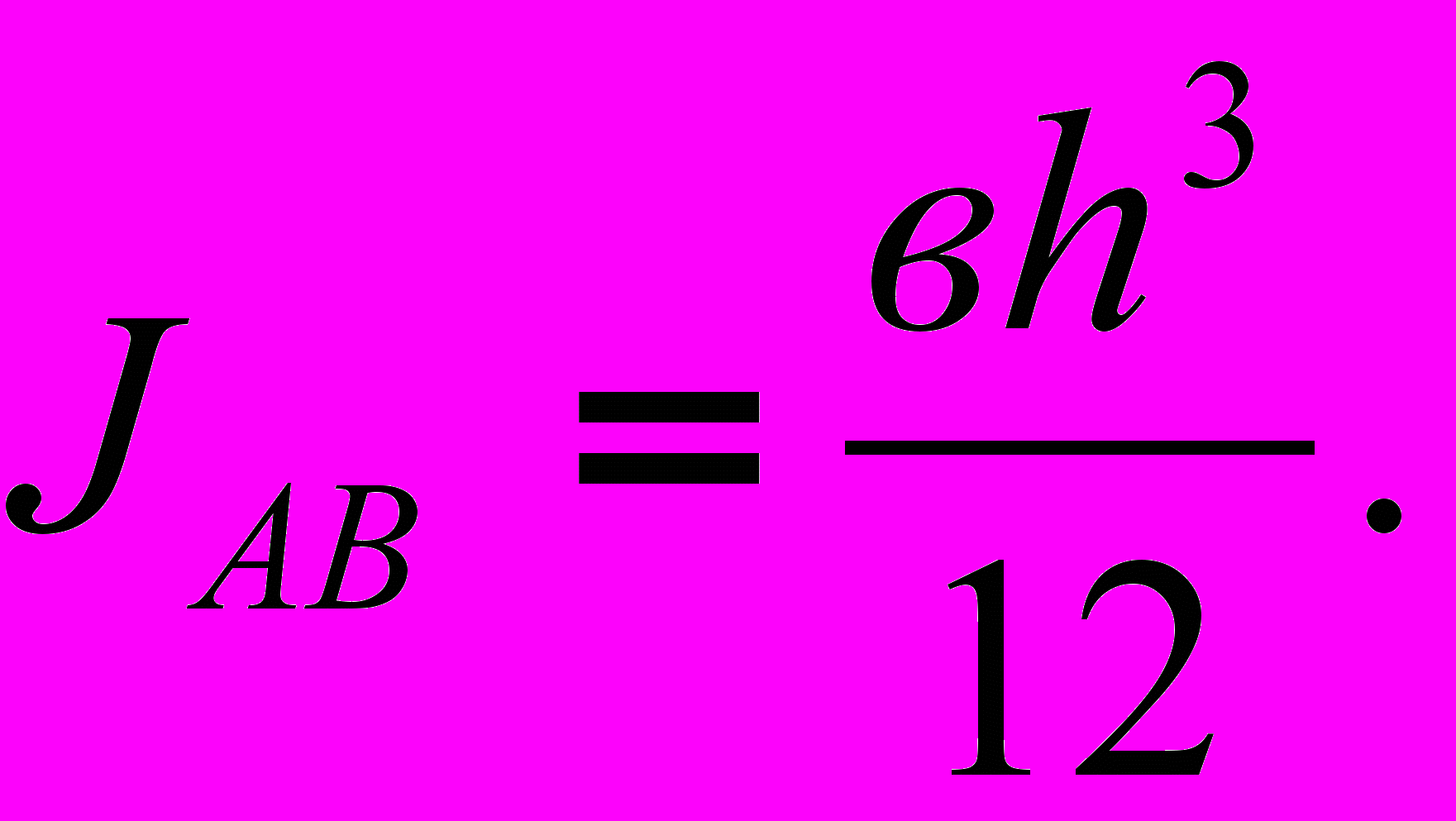 (2)
(2)Устойчивость стержней (продольный изгиб)
Если стержень,( показанный на рис.1 ) сжимать силой R, то при некоторой величине этой силы стержень из устойчивой прямолинейной формы перейдет в неустойчивую криволинейную (см. пунктир). Сила, при которой стержень начинает искривляться (деформироваться), называют критической или эйлеровой силой
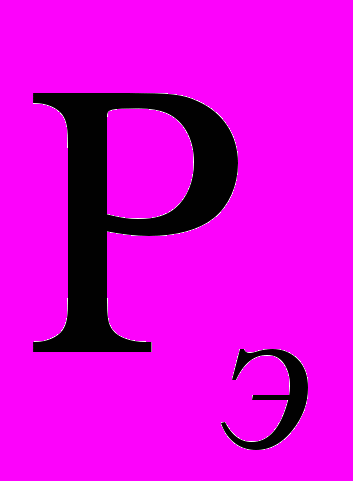 .
.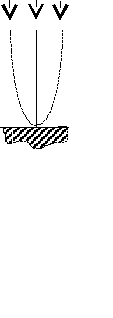 Pэ Р Рэ
Pэ Р РэРис.1
Положение равновесия тела называют устойчивым, если, представленное самому себе после отклонения от этого положения, тело стремится вернуться в исходное положение (рис. 2)

Рис. 2
Положение тела называется неустойчивым, если тело, отклоненное от равновесного и предоставлено самому себе, откланяется от этого положения (рис. 3).

Рис. 3
Положение тел называется безразличным, если оно, откланяется от равновесного положения и представлено самому себе, остается на месте (рис. 4).

Рис. 4
Вывод основного дифференциального уравнения продольного изгиба
Рассмотрим стержень, показанный на рисунке, и будем считать, что сила R доведена до такой величины, что стержень искривляется (см. пунктир)
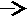











 y
yz
y
P z
l
В этом случае изгибающий момент в текущем сечении запишется в виде

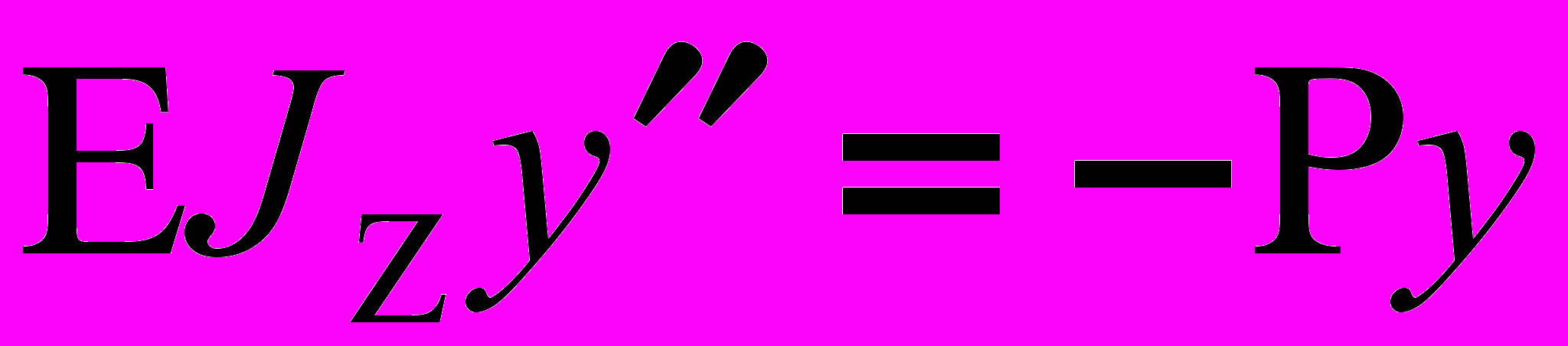 . (1)
. (1)В дальнейшем (для простоты записи) будем считать:
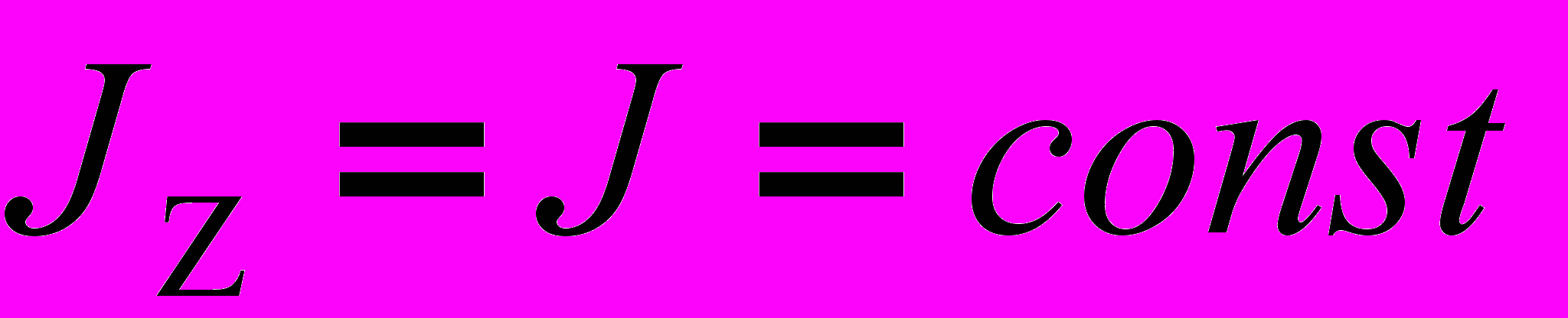 , .
, .тогда:
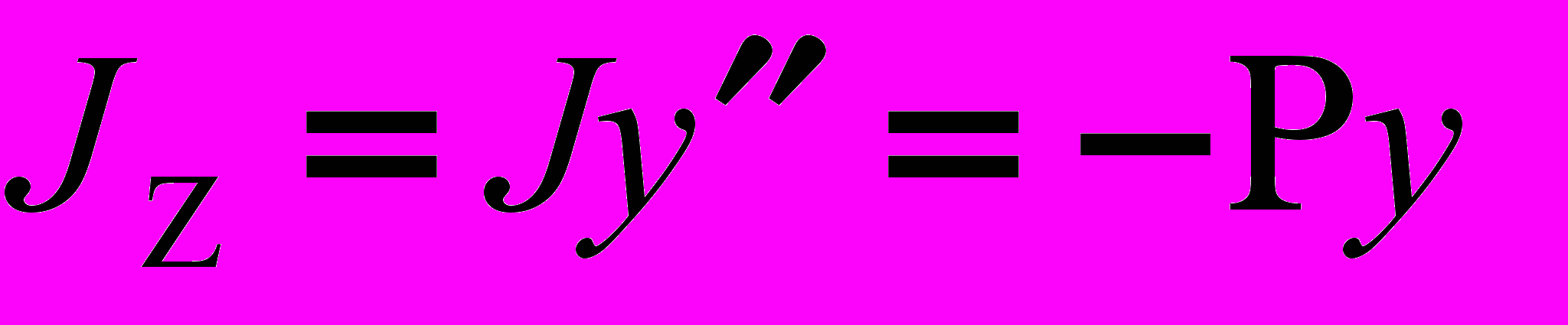 . (1¢)
. (1¢)Дифференцируя дважды уравнение (1), получим:
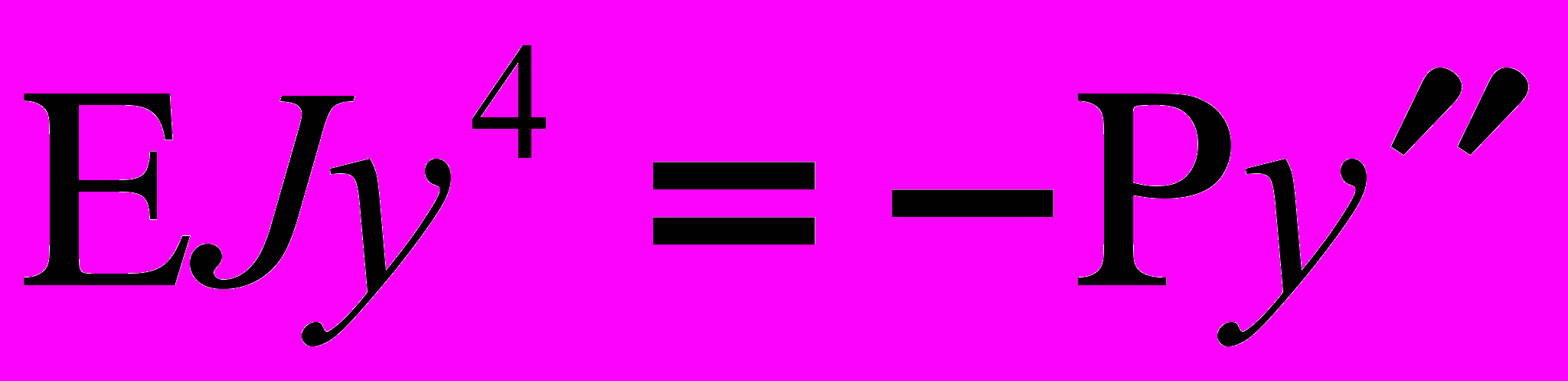 .
.или
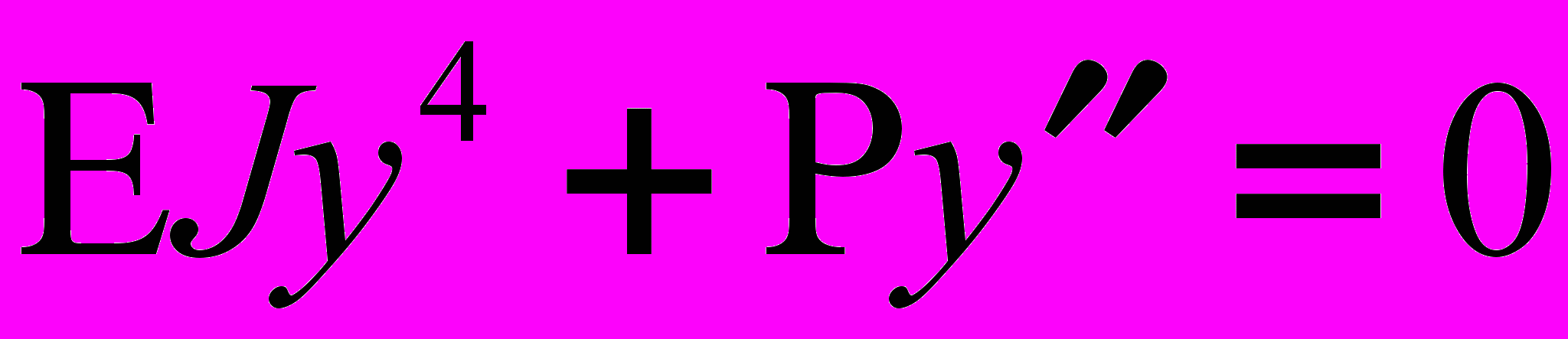 . (2)
. (2)Это и есть дифференциальное уравнение продольного изгиба.
Интегрирование дифференциального уравнения продольного изгиба
Итак, мы получили дифференциальное уравнение продольного изгиба, которое является линеиным дифференциальным уравнением четвертого порядка:
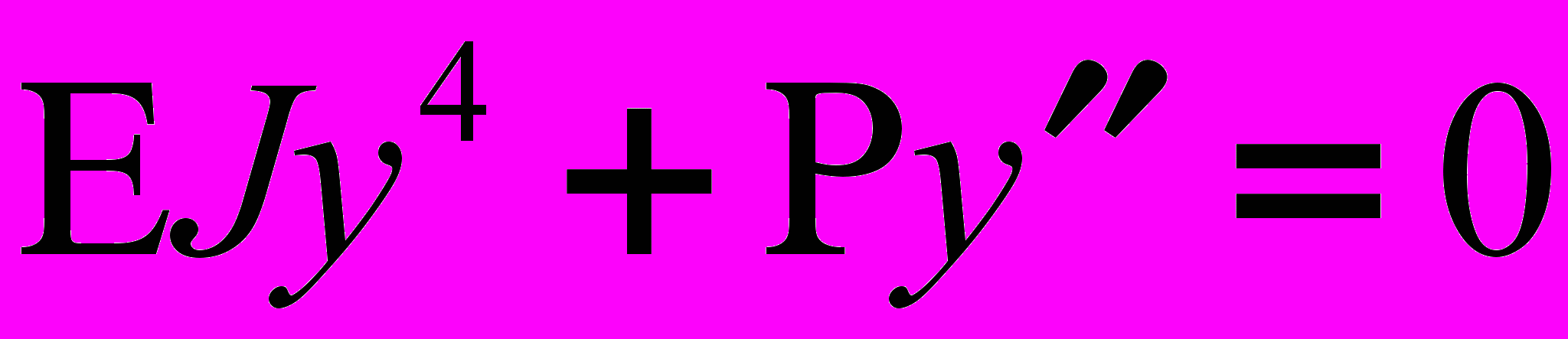 . (1)
. (1)Общий метод решения таких уравнений сводится к решению алгебраического характеристического уравнения. Действительно, будем искать частное решение дифференциального уравнения (1) в форме
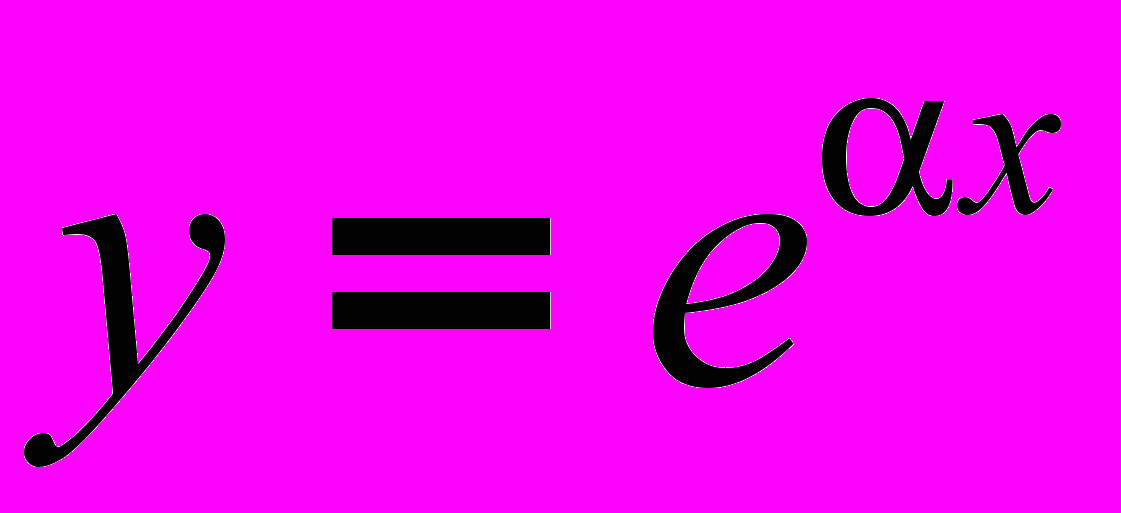 , где a нужно определить.
, где a нужно определить.Подставляя это решение в уравнение (2) получим
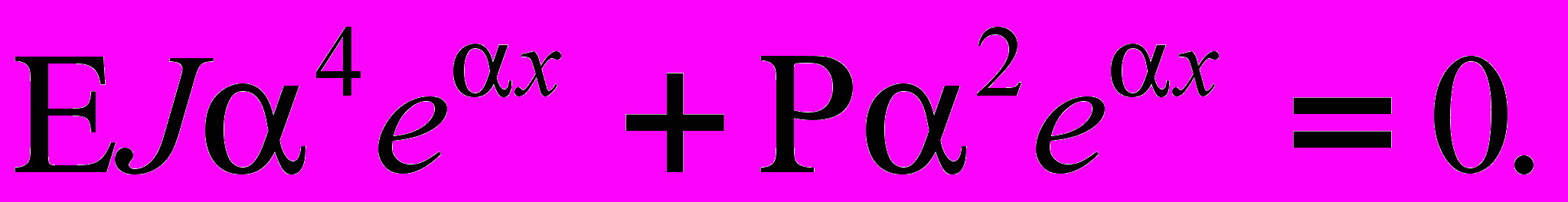 (2)
(2)Так как
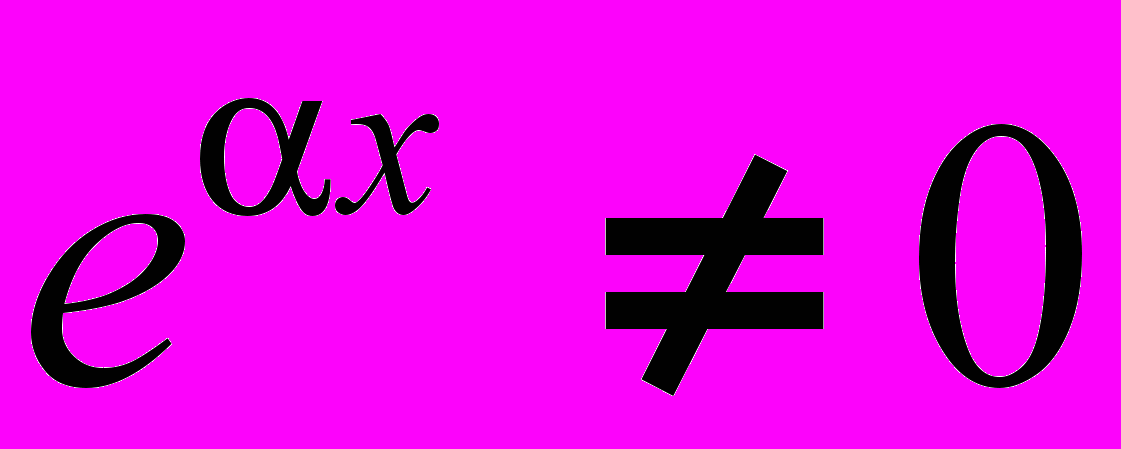 , из (2) получим характеристическое уравнение:
, из (2) получим характеристическое уравнение: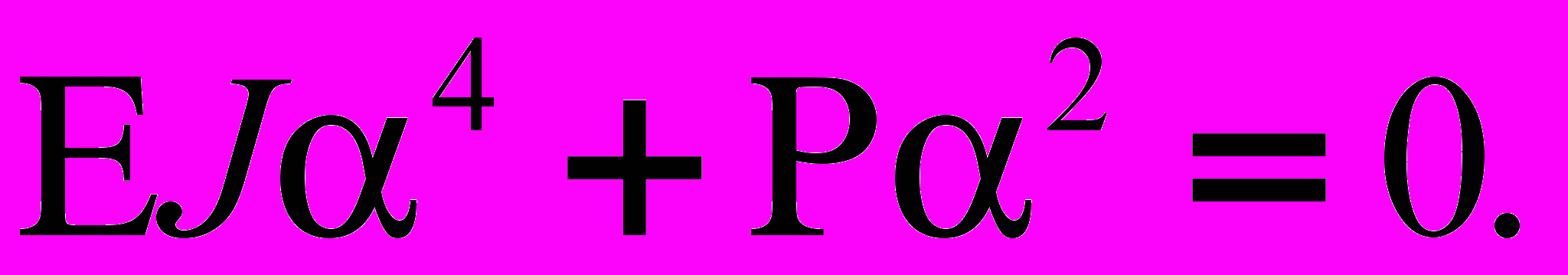 (3)
(3)Найдем корни этого уравнения, переписав его в виде:
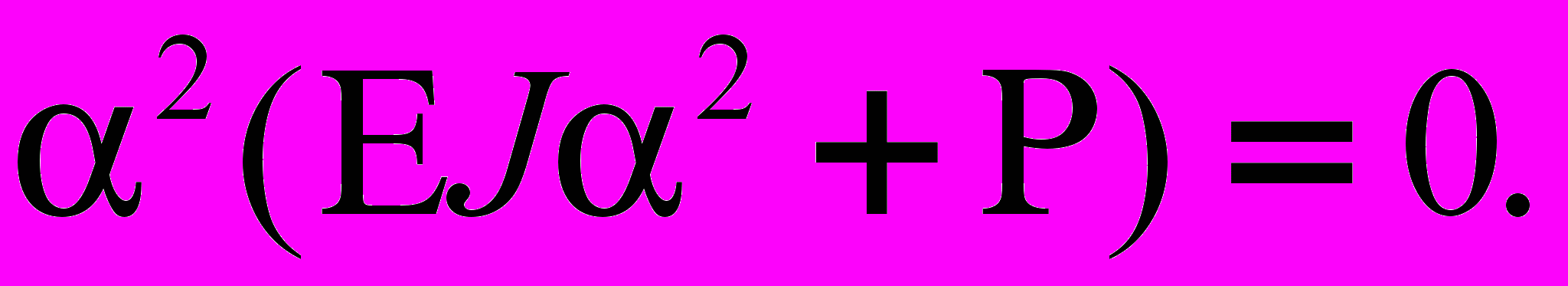 .
.Значит,
 , (4)
, (4)где :
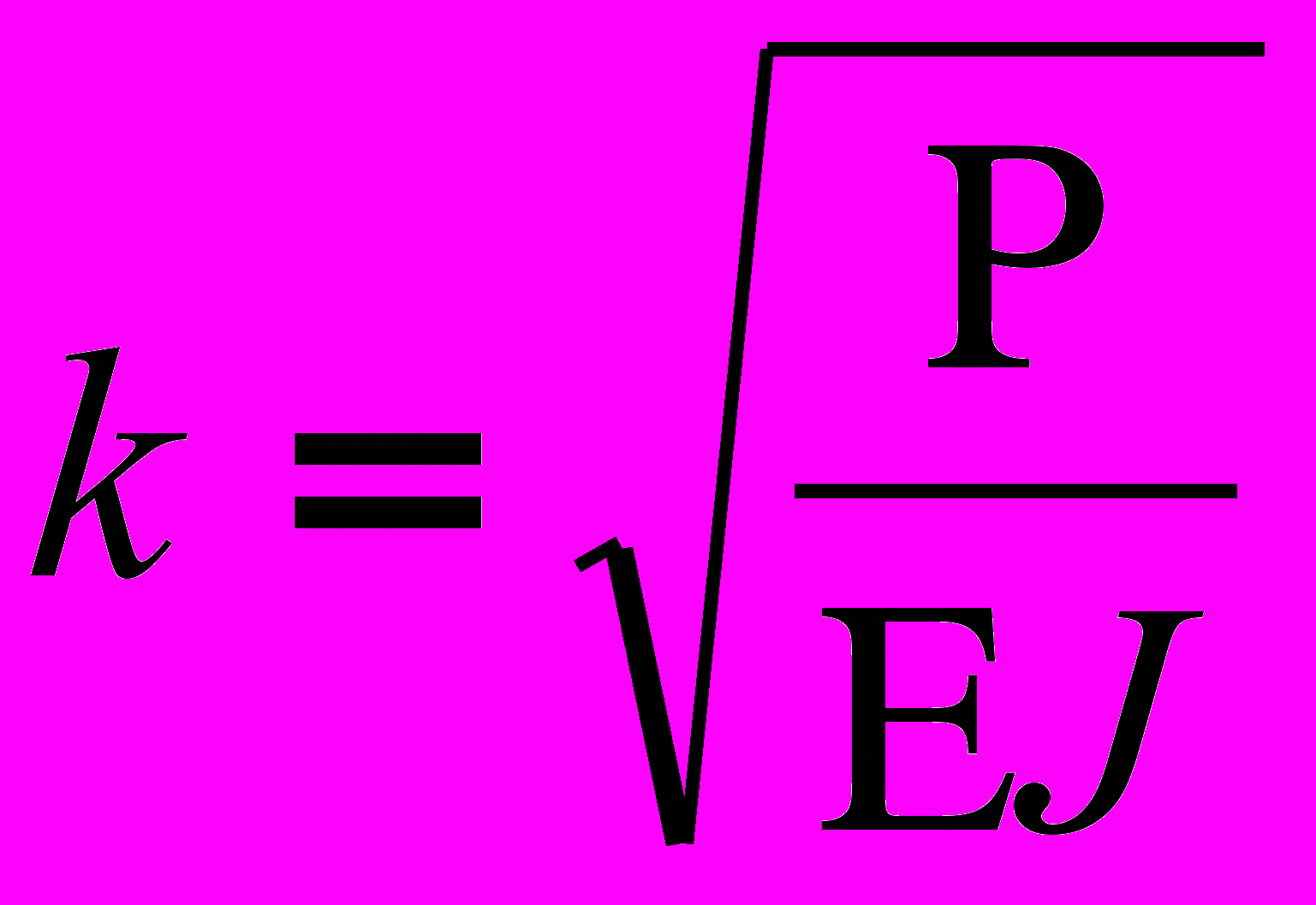 . (5)
. (5)Зная корни характеристического уравнения, можно записать общий интеграл уравнения (2):
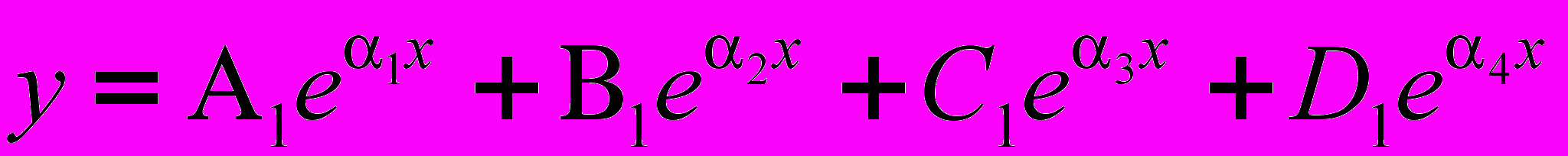 ,
,где
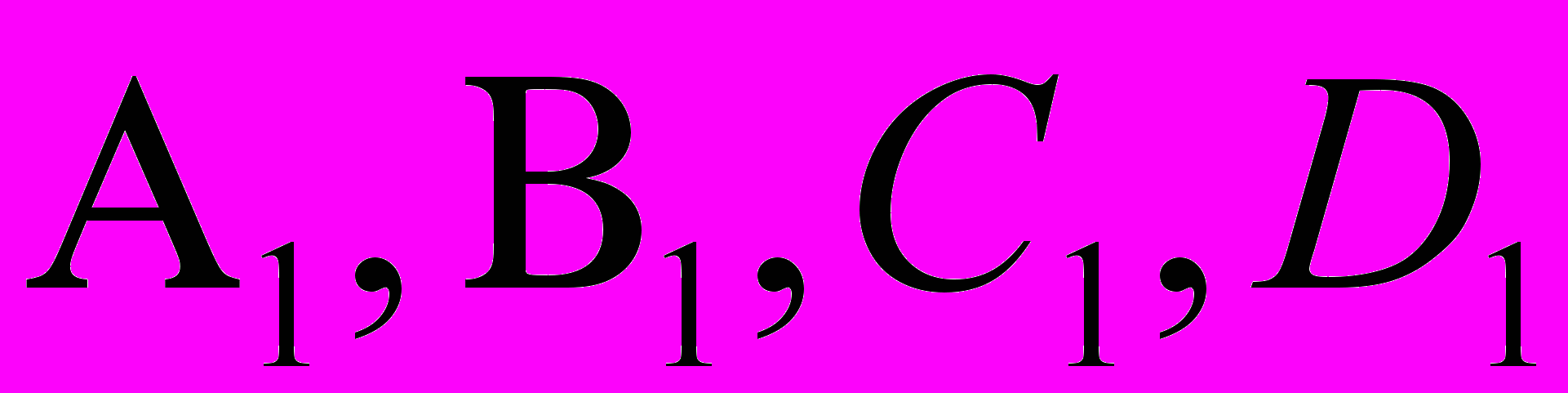 - постоянные интегрирования.
- постоянные интегрирования.Такая форма интеграла будет, если все
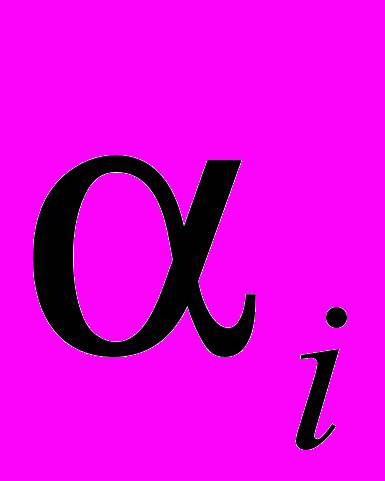 различны. В случае наличая кратных корней (как в нашем случае), когда
различны. В случае наличая кратных корней (как в нашем случае), когда 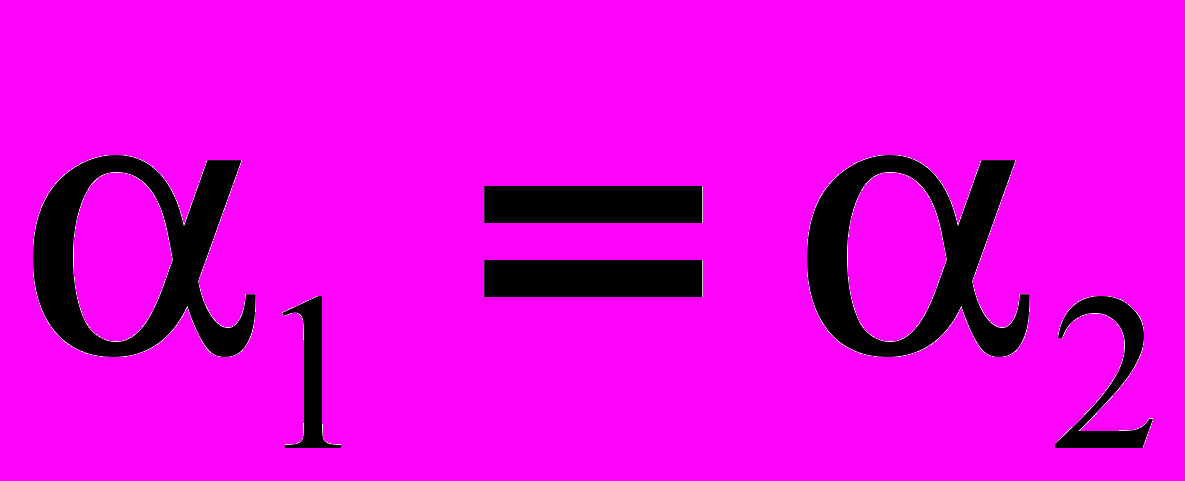 , общий интеграл записывается так:
, общий интеграл записывается так: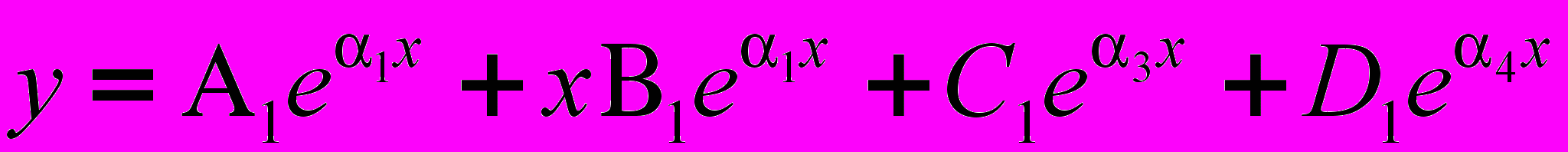 . (6)
. (6)Подставляя (4) в (7), получим
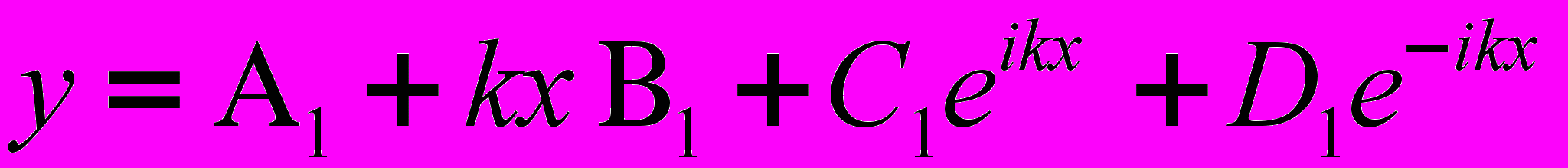 . (7)
. (7)Данному выражению можно придать более удобную форму, если воспользоваться формулами Эйлера:
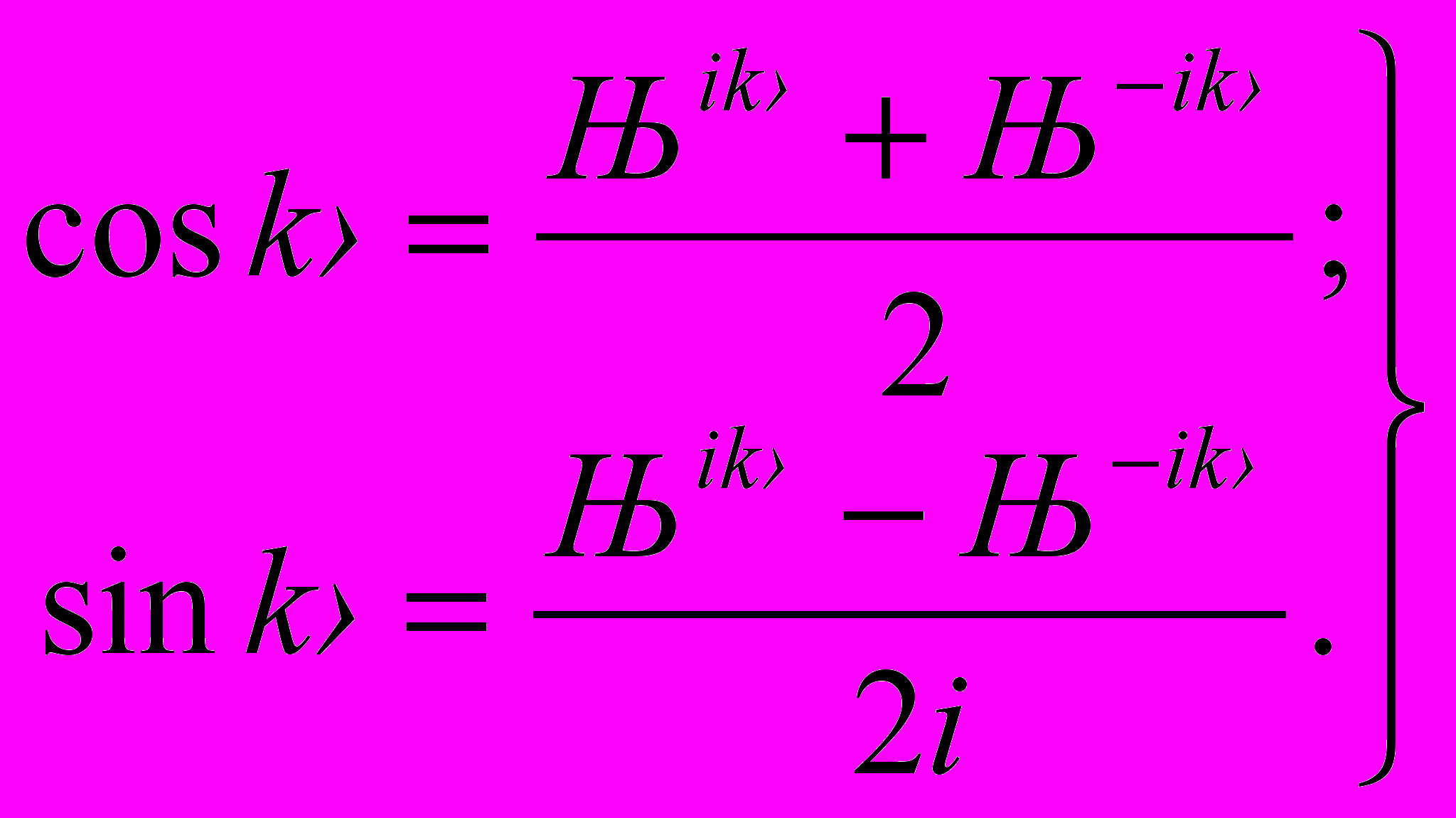 (8)
(8)Складывая и вычитая почленно, получим:
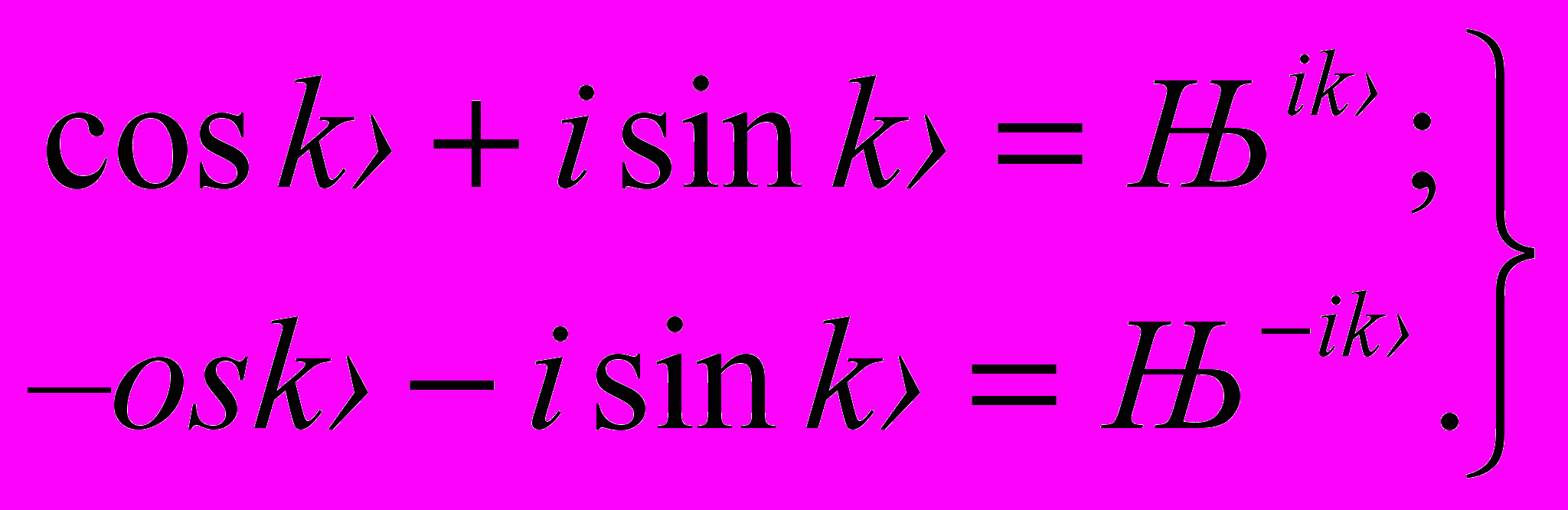
Подстовляя данное выражение в (7) и приведя подобные члены, найдем, что:
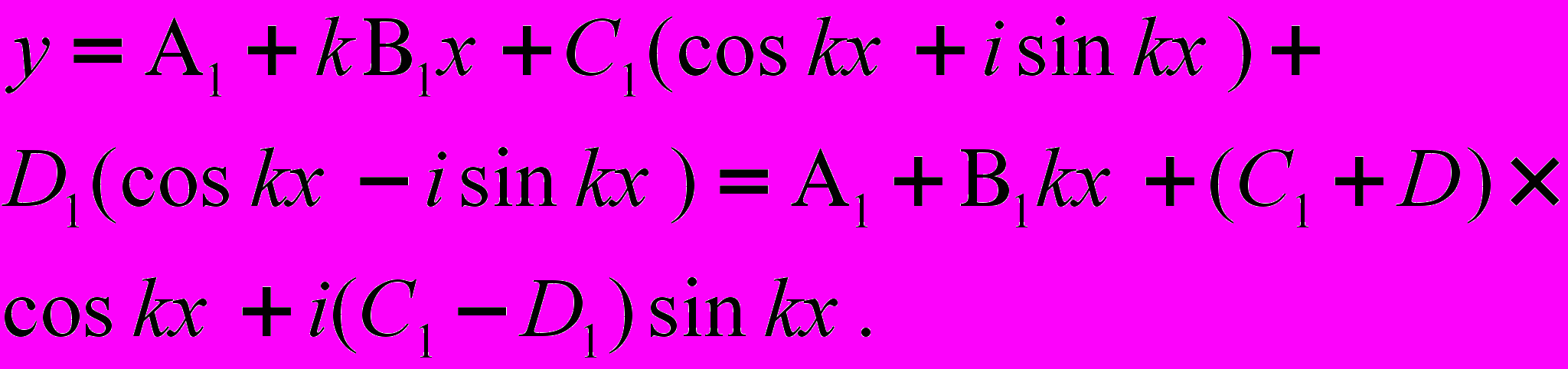
Обозначив:
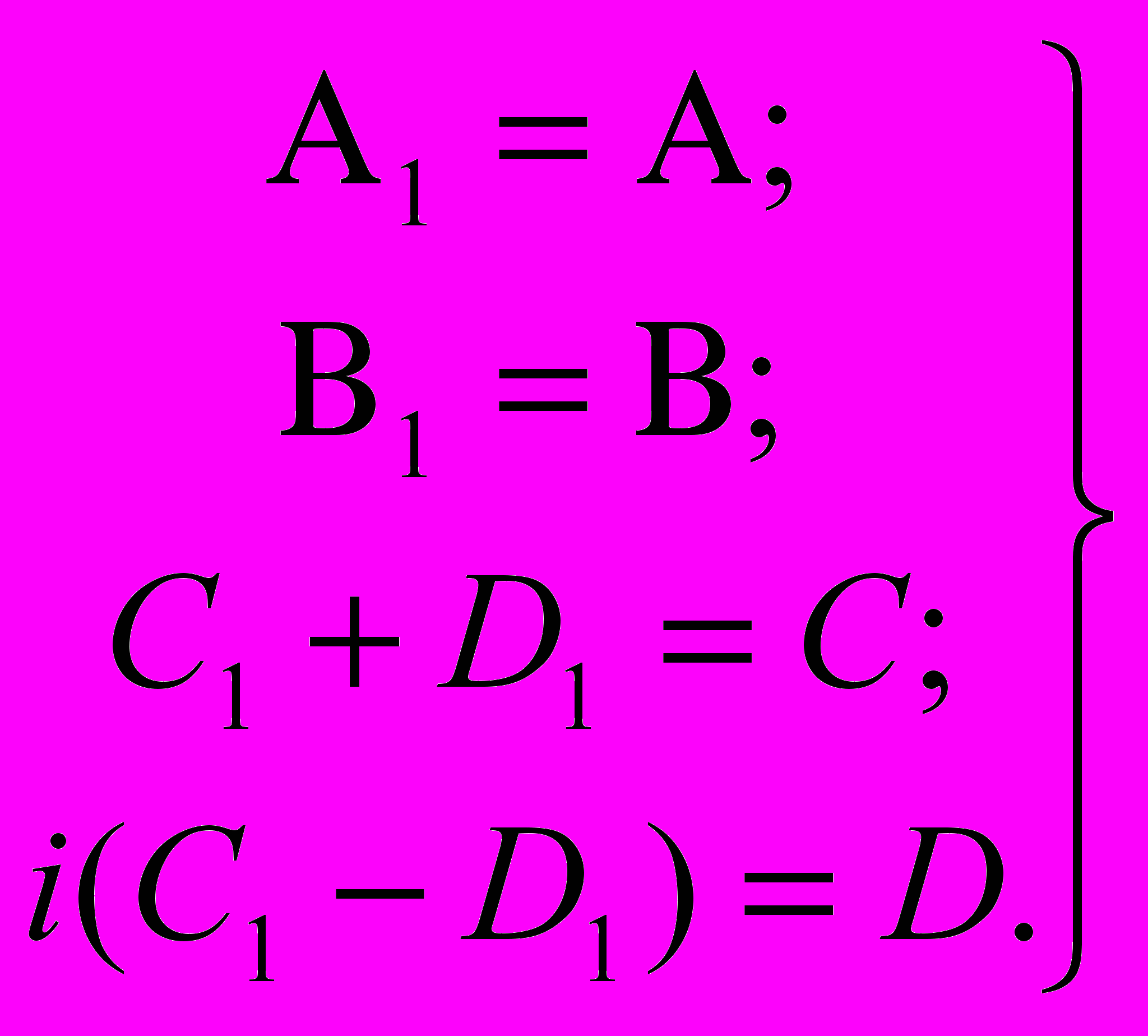
Тогда:
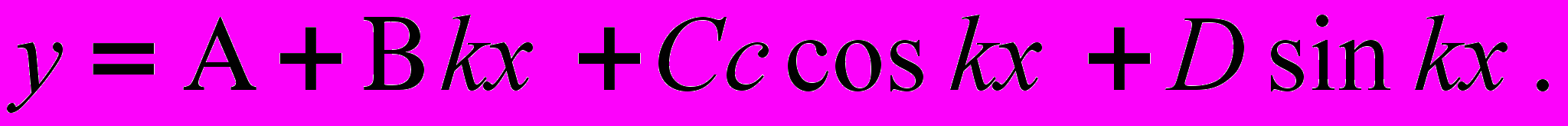 (9)
(9)Эту форму решения необходимо использовать для решения конкретных задач.
Пример: Определение критической нагрузки (силы) для балки, показанной на рис.1
Предположим, что сила R доведена до такой величины, что стержень принял искривленную форму. В этом случае общий интеграл упругой линии стержня будет
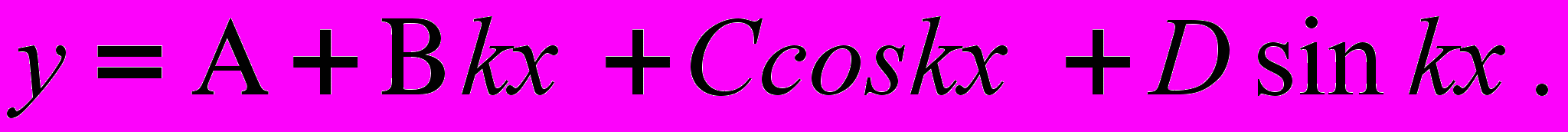 (1)
(1)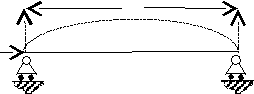 l
lP
Рис.1
Постоянные A, B, C, и D определяются из граничных условий, которые будут:
при
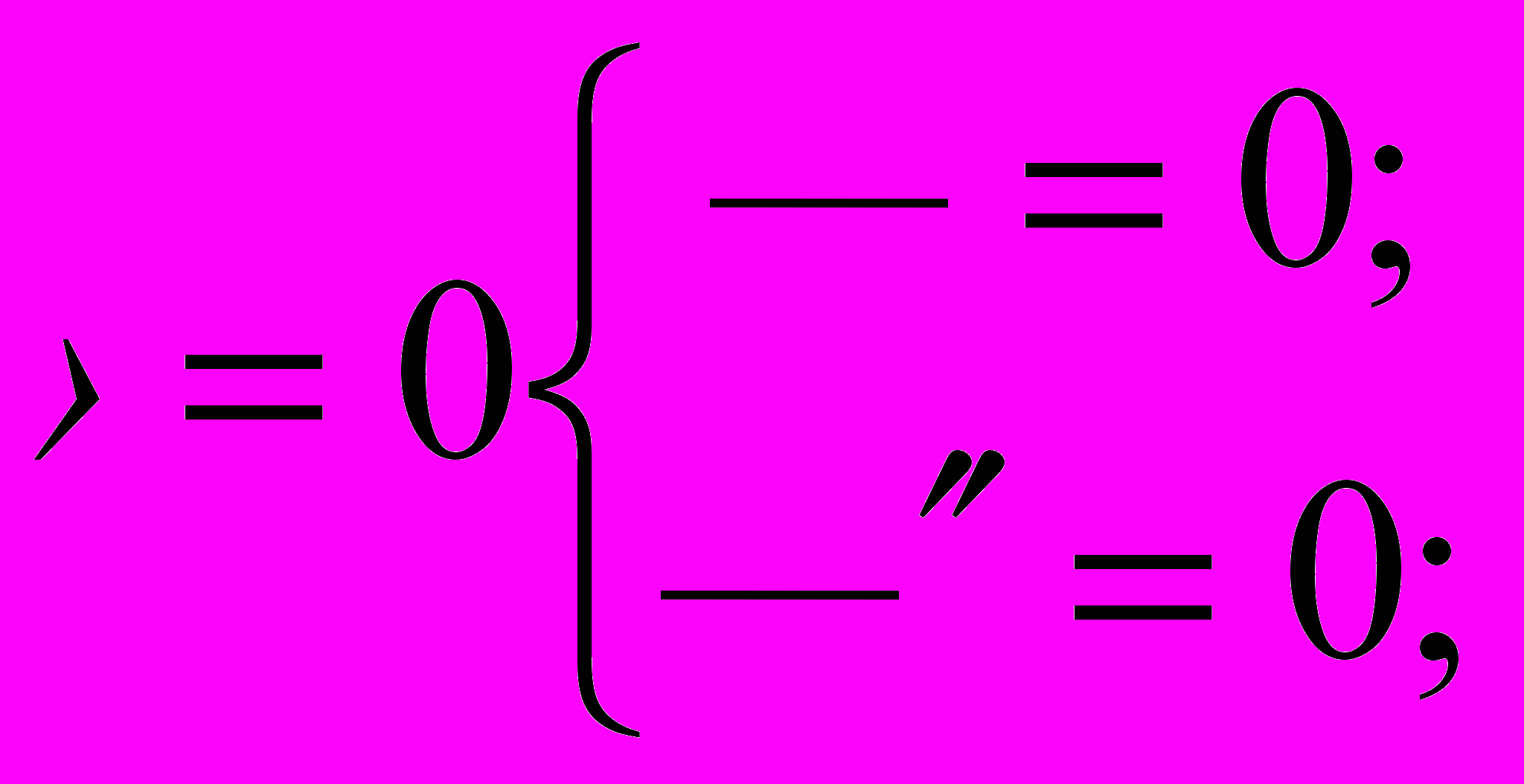
при
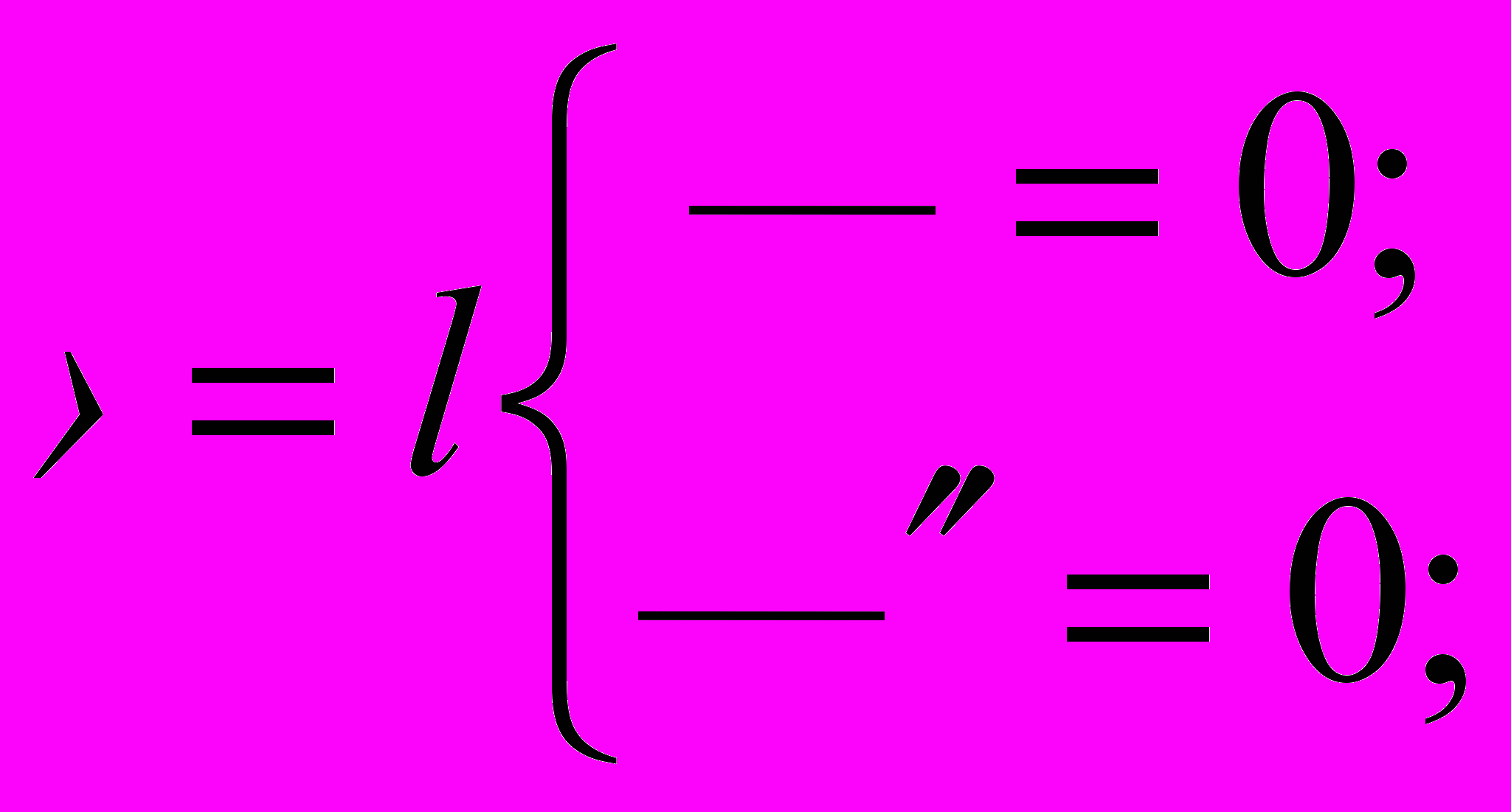
Используя условия при х=0, получим:
A + C = 0; C = 0.
Следоавтельно, A = С = 0.
Значит интеграл (1) примет частный вид
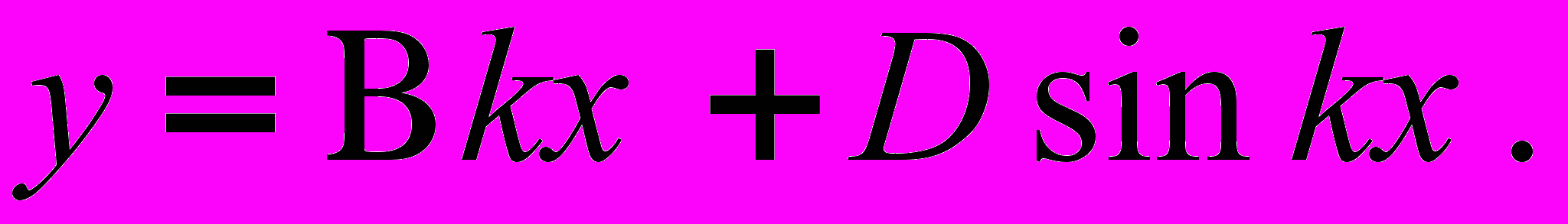 (2)
(2)Воспользуемся условиями при х=
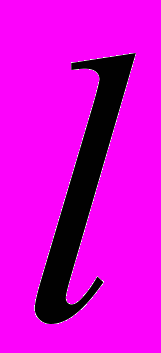 :
: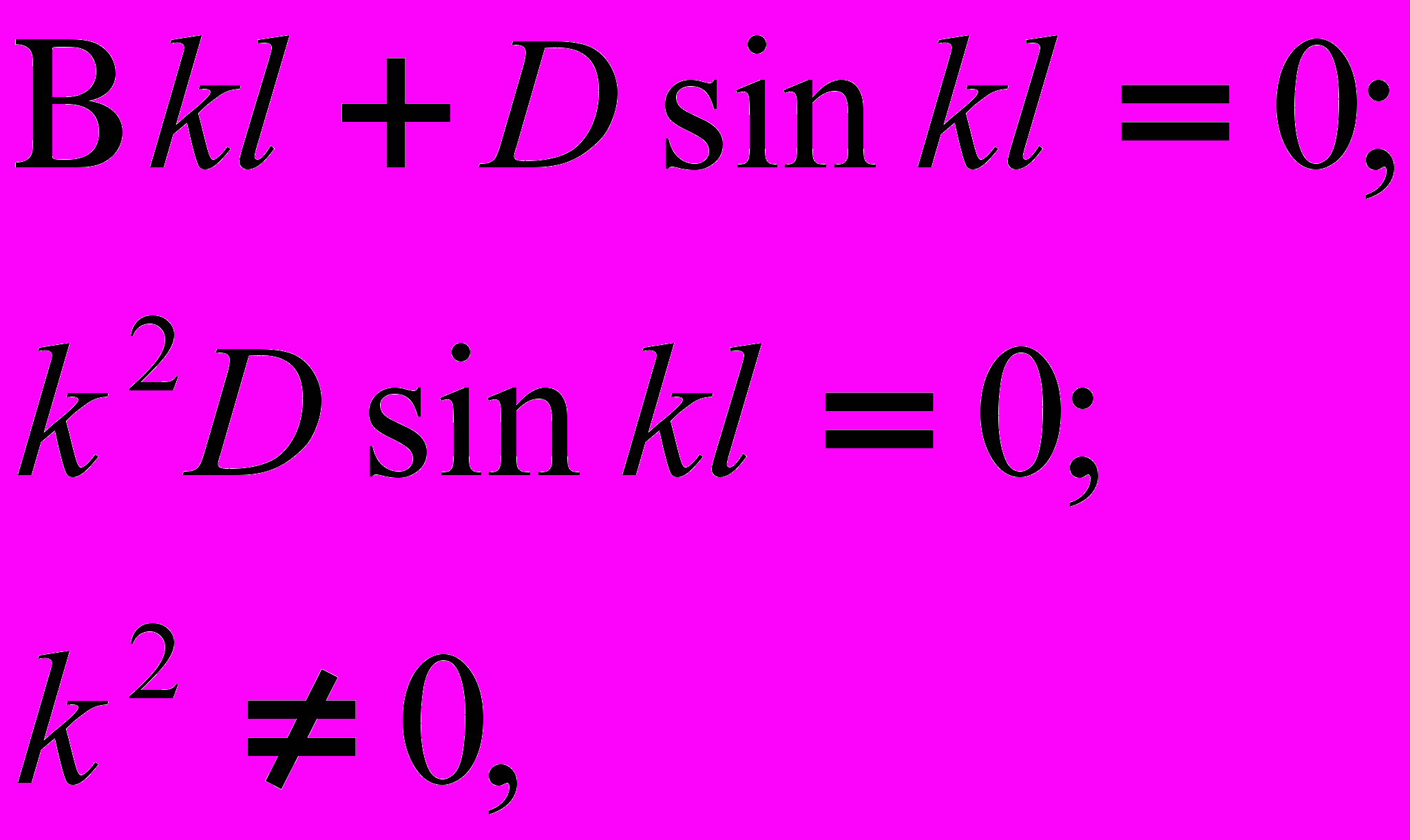
значит последнее уравнение имеет вид:
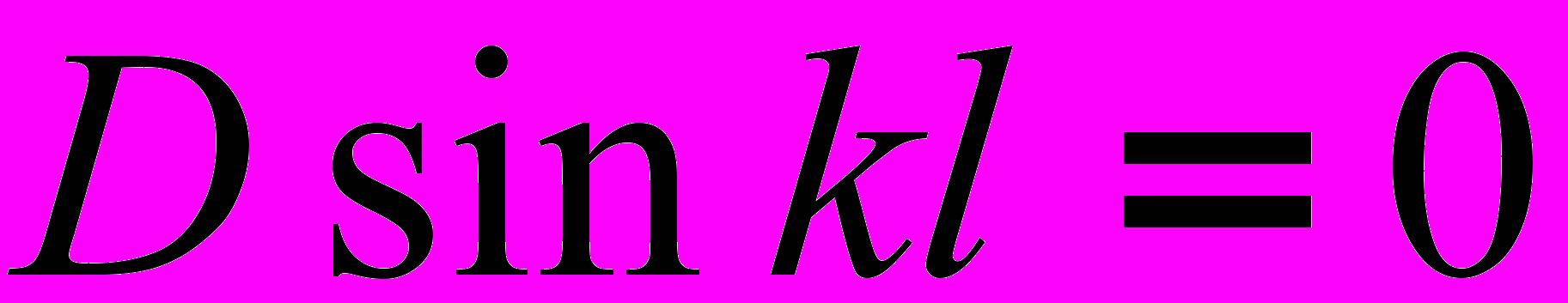 .
.Подставляя это равенство в первое уравнение системы, получим, что В=0.
Итак, остается уравнение
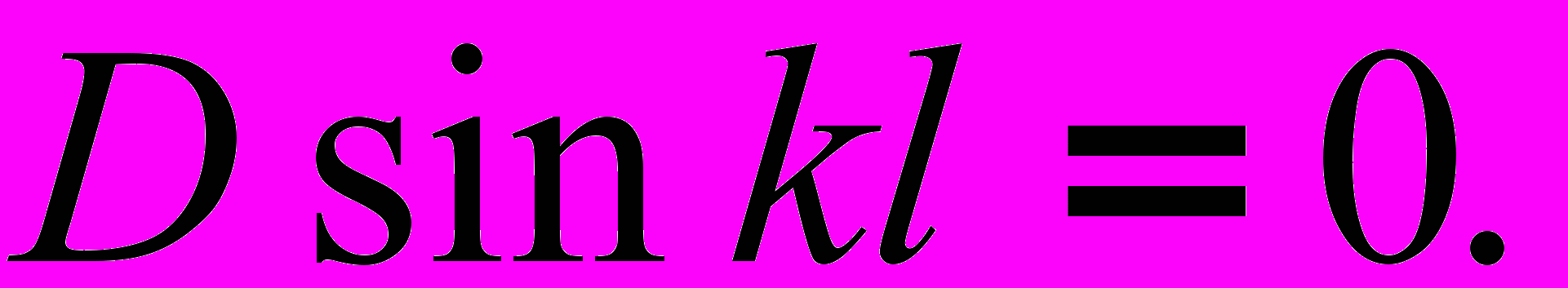 (3)
(3)В уравнений (3) D
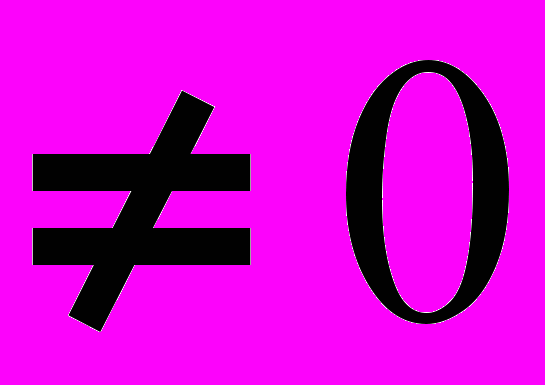 , так как если D = 0, то стержень не будет искривленным, что противоречит исходному условию.
, так как если D = 0, то стержень не будет искривленным, что противоречит исходному условию.Значит,
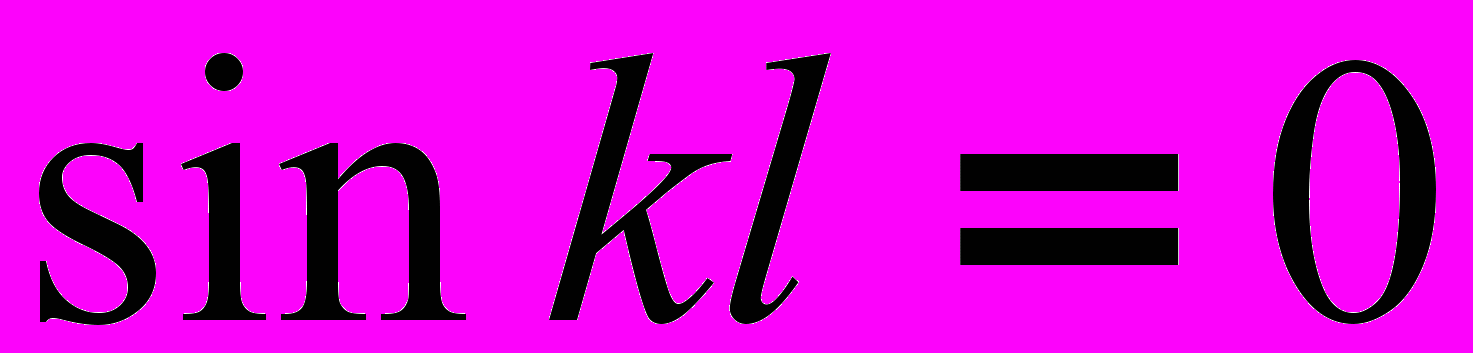
и
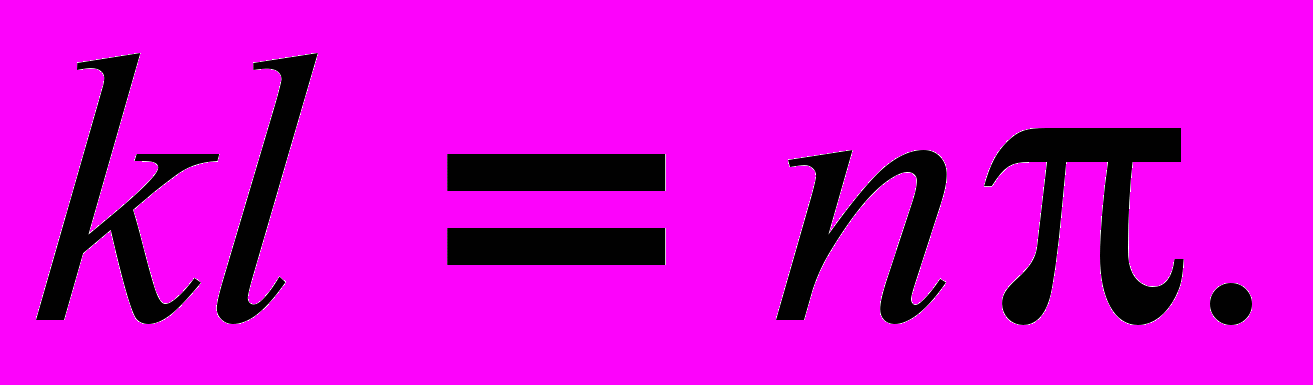
Отсюда
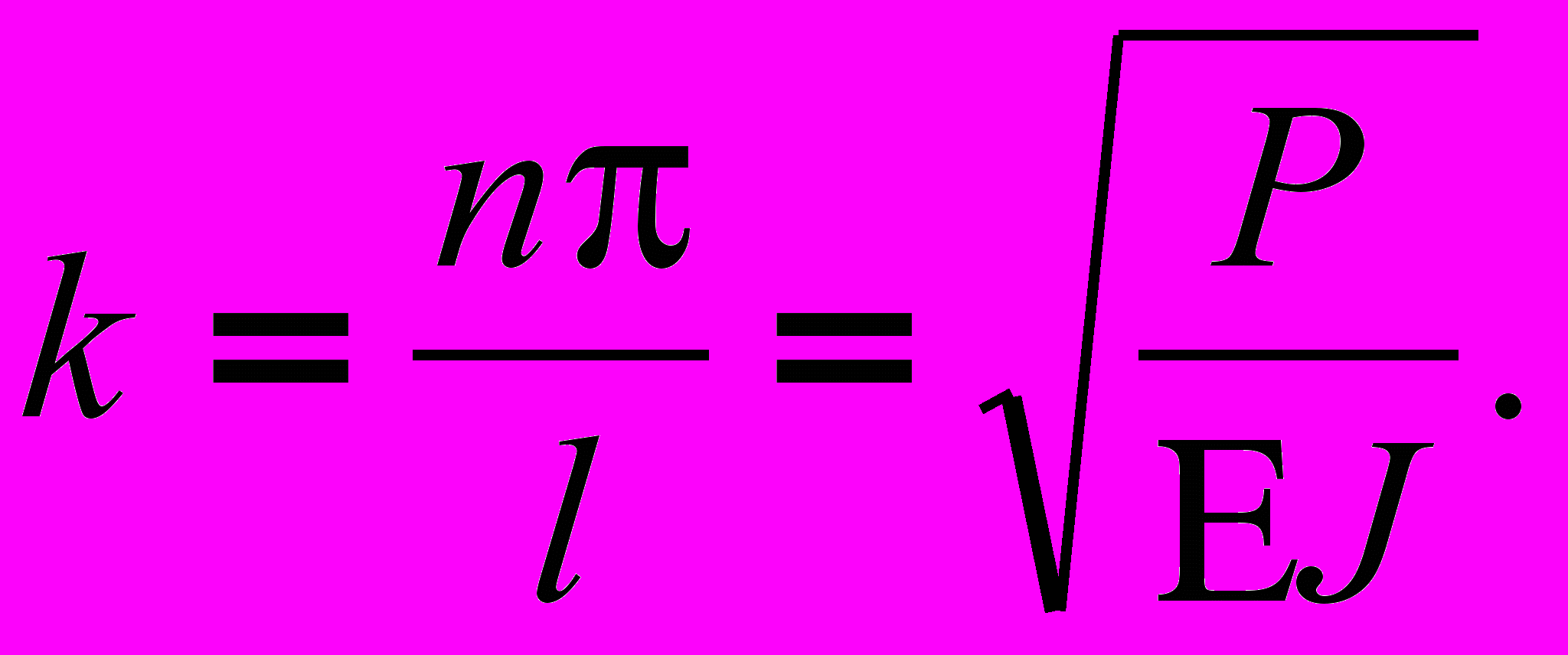
Следовательно,
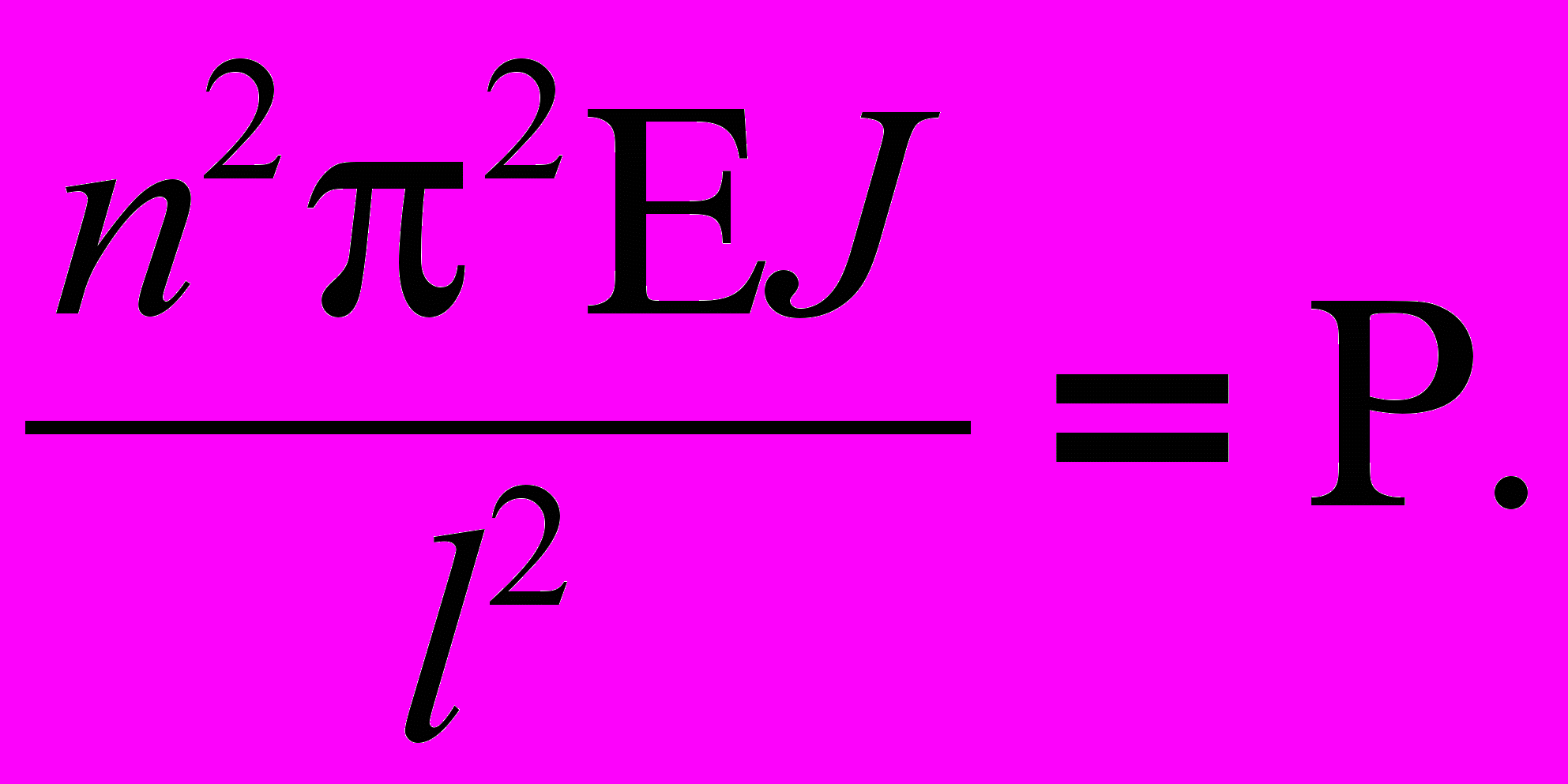 (4)
(4)Критическая нагрузка - минимальная из всех сил R.
Значит,
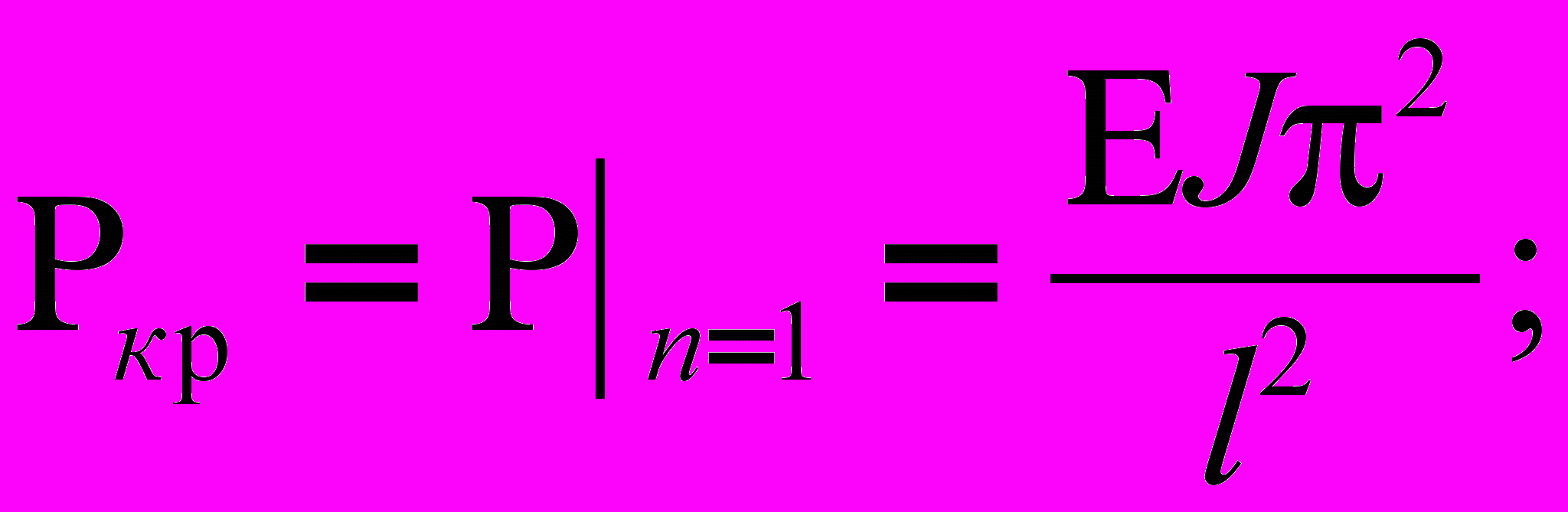
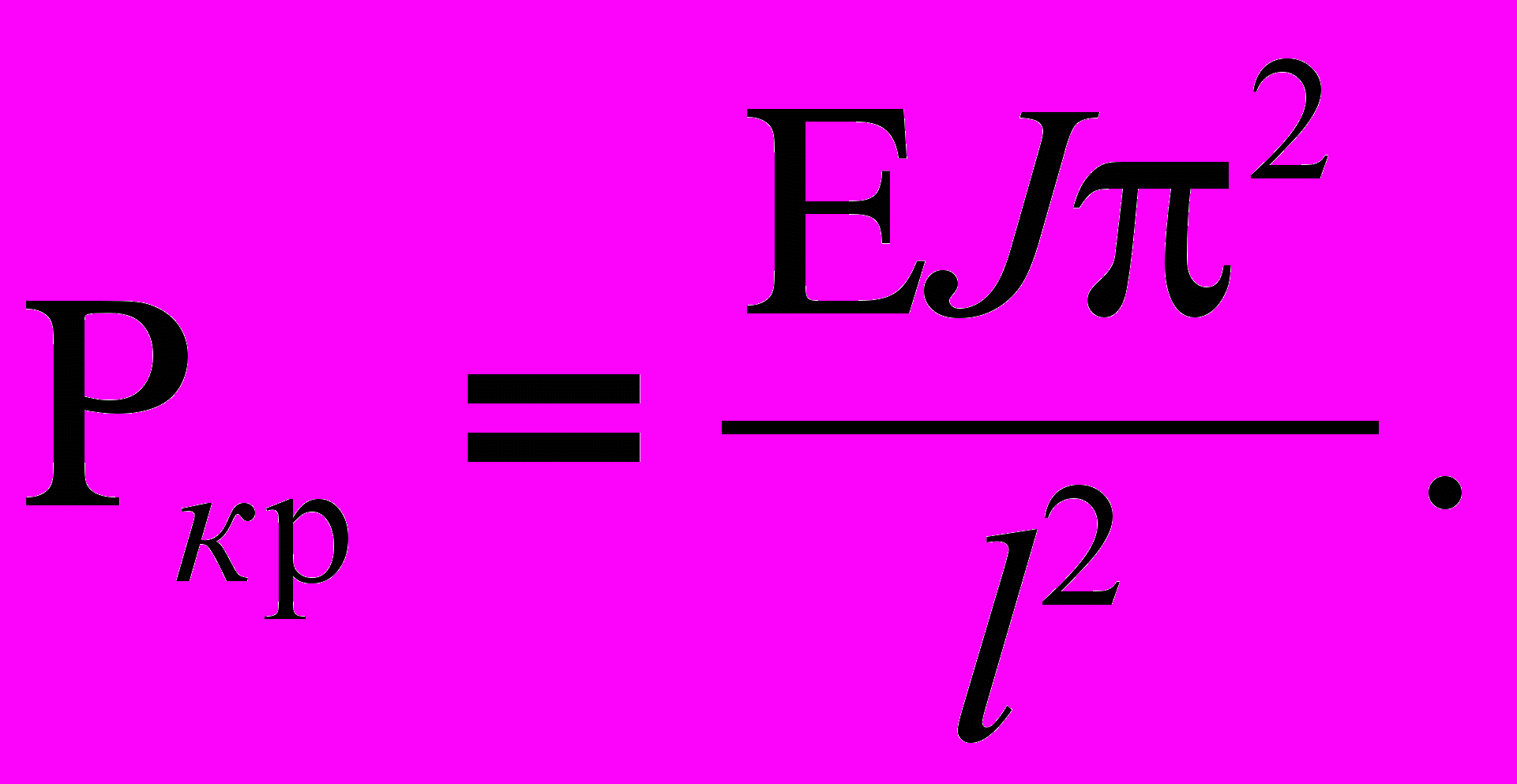 (5)
(5)Сложное сопротивление
Основные понятия
Всякое сочетание простых видов деформации вызывает сложное напряженное состояние упругого тела, которое называют сложным сопротивлением.
То есть сложным сопротивлением принято считать такой вид нагружения элементов конструкций и машин, при котором в их поперечных сечениях деиствует два и более внутренних силовых фактора. Так, грузовые крюки работают не только на растяжение, но одновременно и на изгиб; болты и заклепки наряду со срезом и смятием могут испытовать растяжение; валы подвергаются кручению и изгибу и т.д. Поперечный изгиб также относят к разряду сложного сопротивления, так как в данном случае в поперечных сечениях элементов конструкции под действием внешних нагрузок действует два силовых фактора: чистый изгиб и поперечная сила.
Общим случаем сложного сопротивления является случай, когда в сечениях действует вся совокупность всех внутренних сиоловых факторов, возникающих под действием внешних нагружений, а именно, продольная и поперечные силы, крутящий и изгибающие моменты. При этом при действии нескольких внутренних силовых факторах используют принцип суперпозиции для определения суммарного результата.
В настоящем разделе мы рассмотрим три вида сложного сопротивления: cовместное действие изгиба и растяжения (сжатия), совместное действие изгиба и кручения, косой изгиб.
Совместное действие изгиба и растяжения (сжатия)
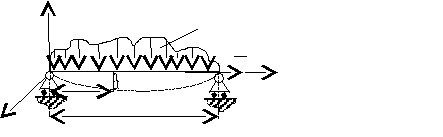
На рис.1 показана схема балки, в которой одновременно возникают напряжения от изгиба и растяжения. Если пренебречь изгибающим моментом от растягивающей силы N в текущем сечении, а это допустимо в силу малости величины
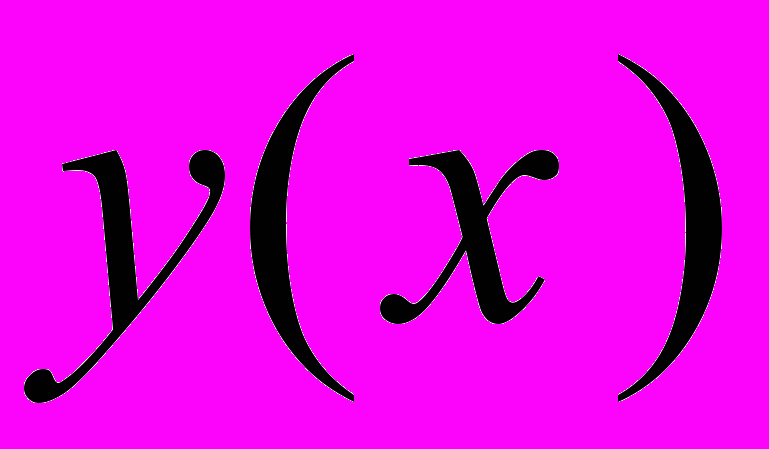 , то напряжение в балке определится формулой
, то напряжение в балке определится формулой (1)
(1)y
q(x)
 N
Nx y(x) x
z l
Рис.1
Формула (1) определяет напряжение в любом сечении балки и в любой точке по высоте поперечного сечения.
Наибольшее напряжение определится формулой:
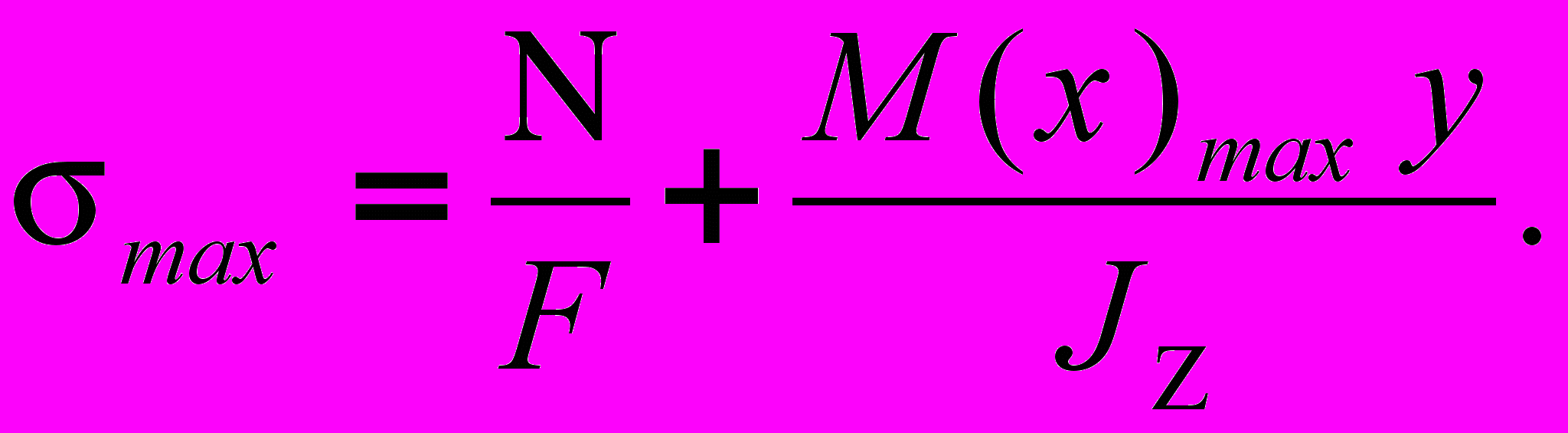 (2)
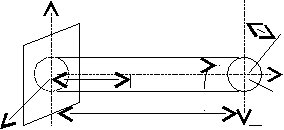
(2)Совместное действие изгиба и кручения
На рис.1 показана балка, одновременно испытывающая изгиб и кручение, при этом каждая точка сечения испытывает одновременно напряжения от изгиба и кручения, то есть в ней возникают
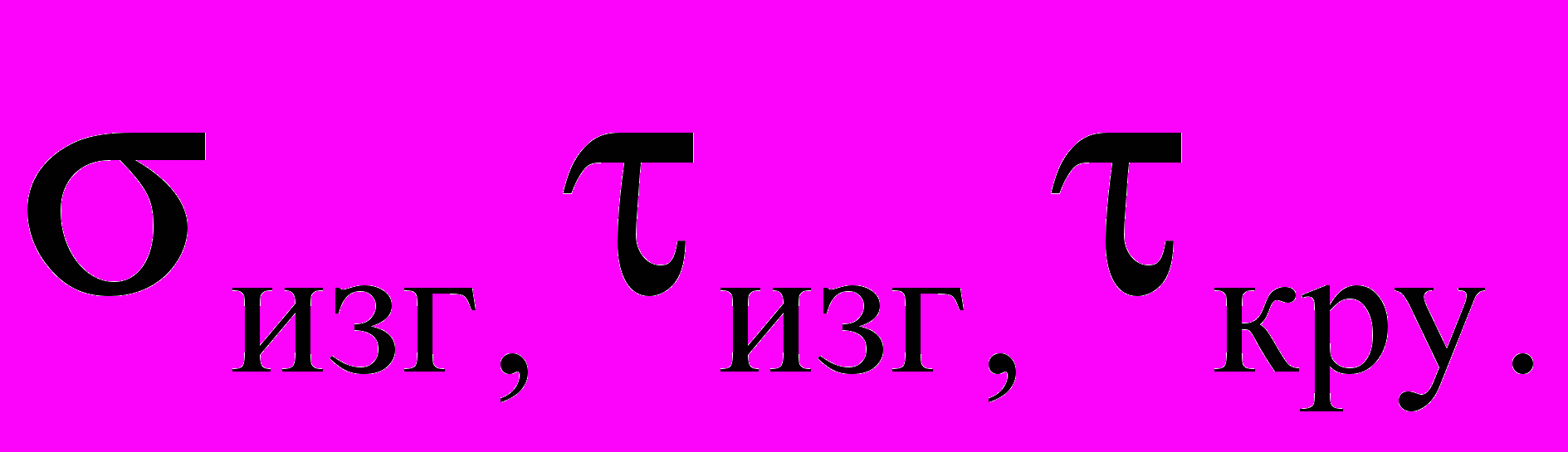 .
.y
 Мкр x
Мкр xx
r
l
z P
Рис.1
Если обозначить изгибающий момент в текущем сечении через
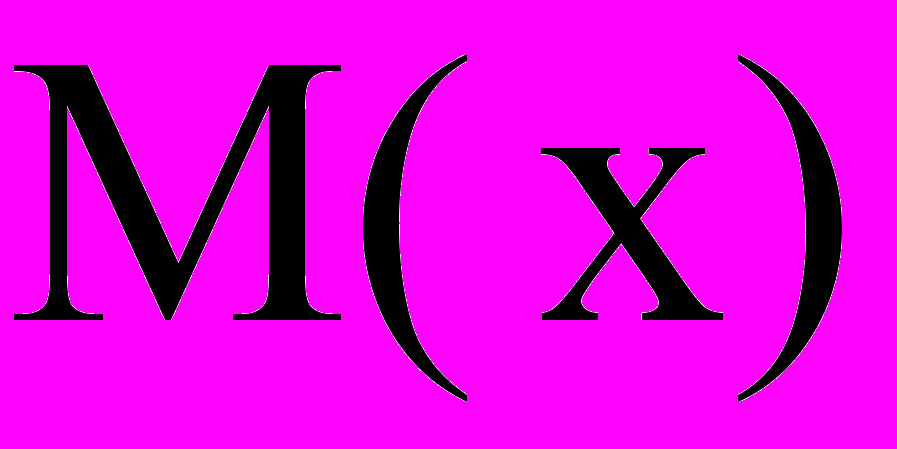 , то
, то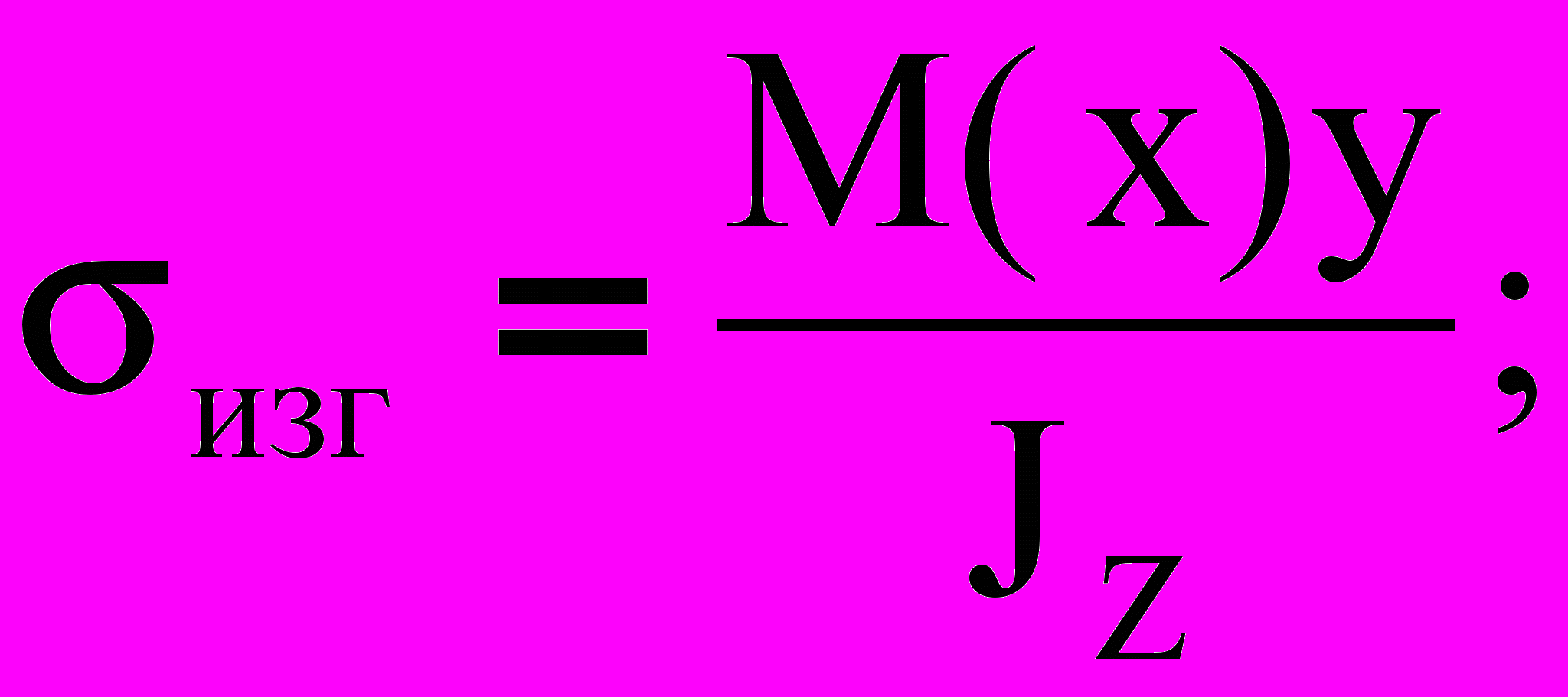 (1)
(1)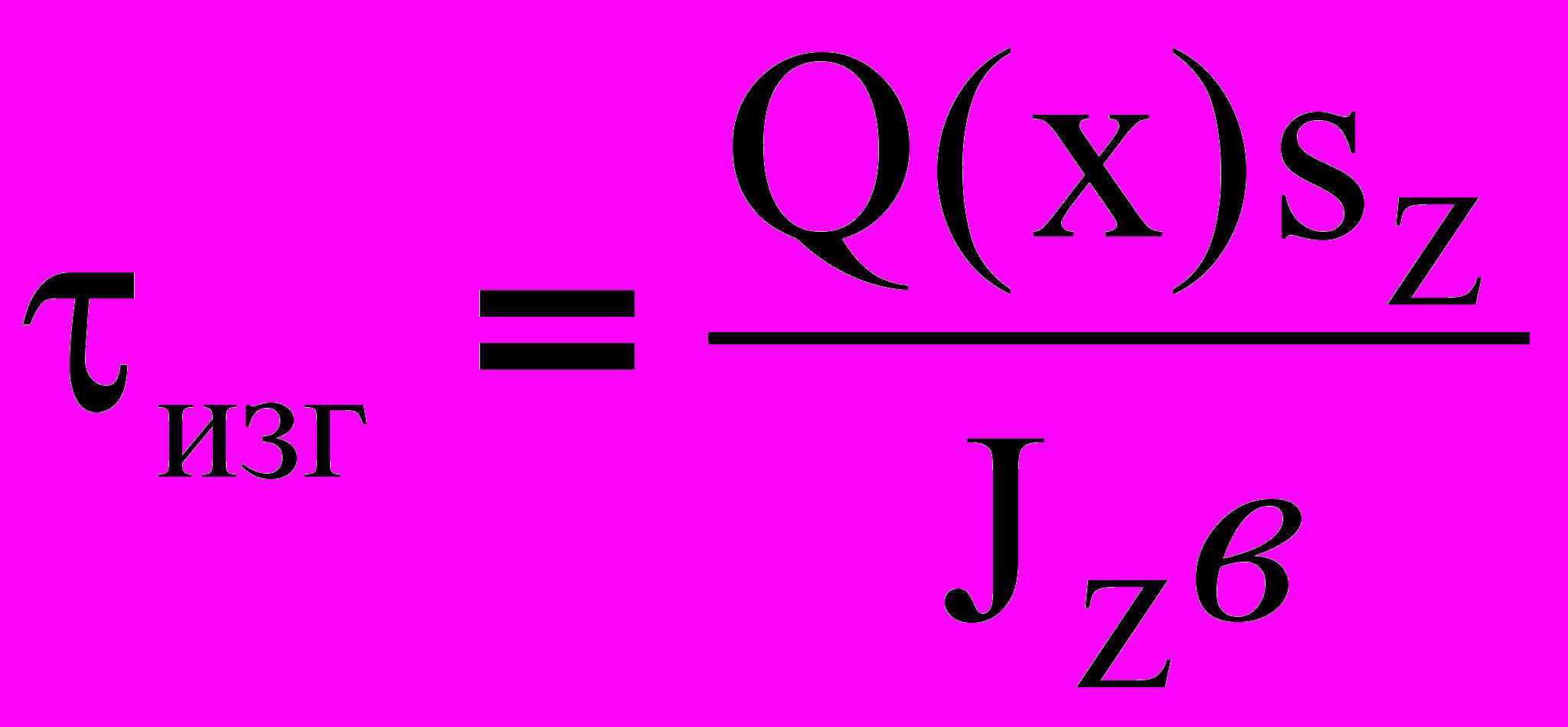 ; (2)
; (2)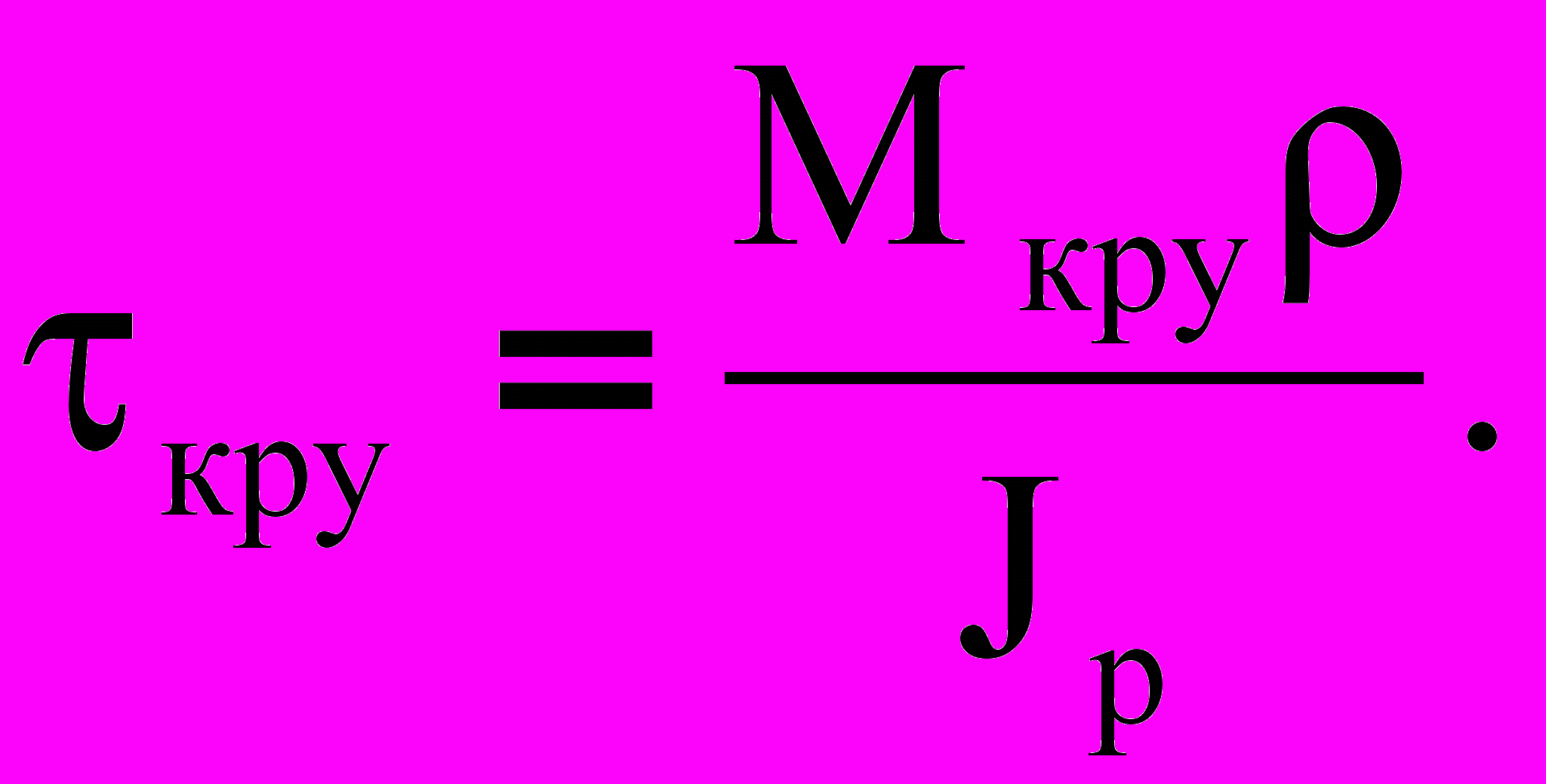 (3)
(3)Соответственно:
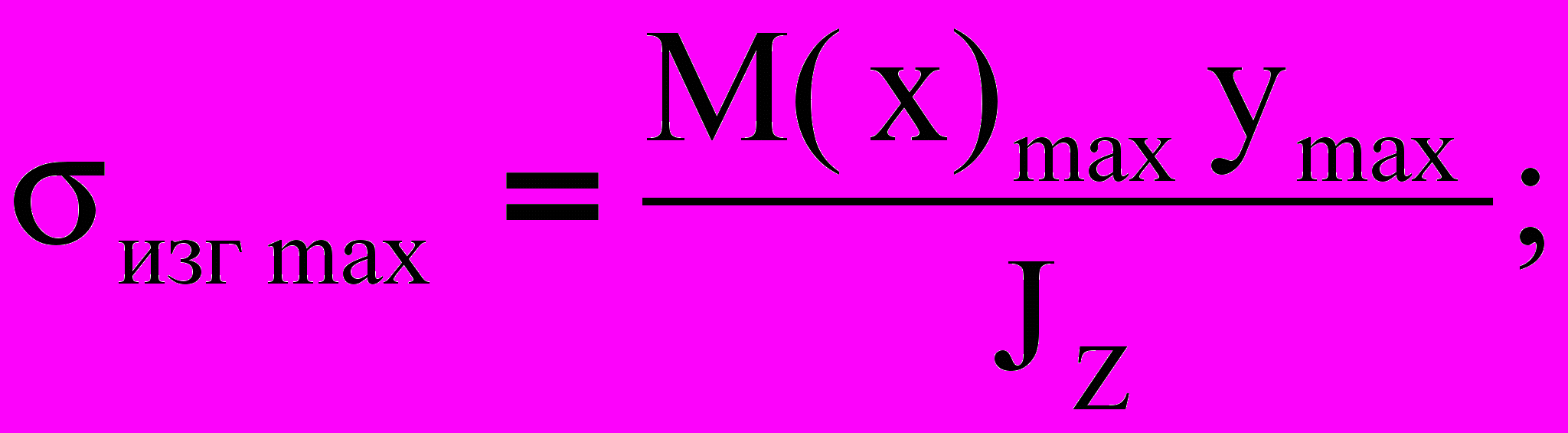 (3¢)
(3¢)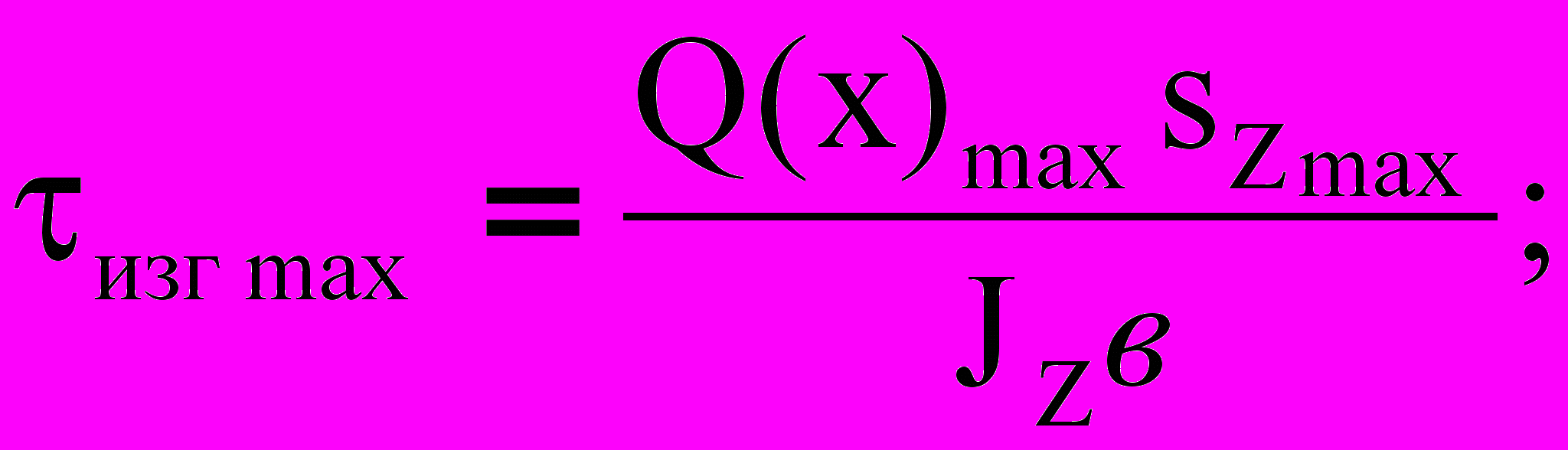 (4¢)
(4¢)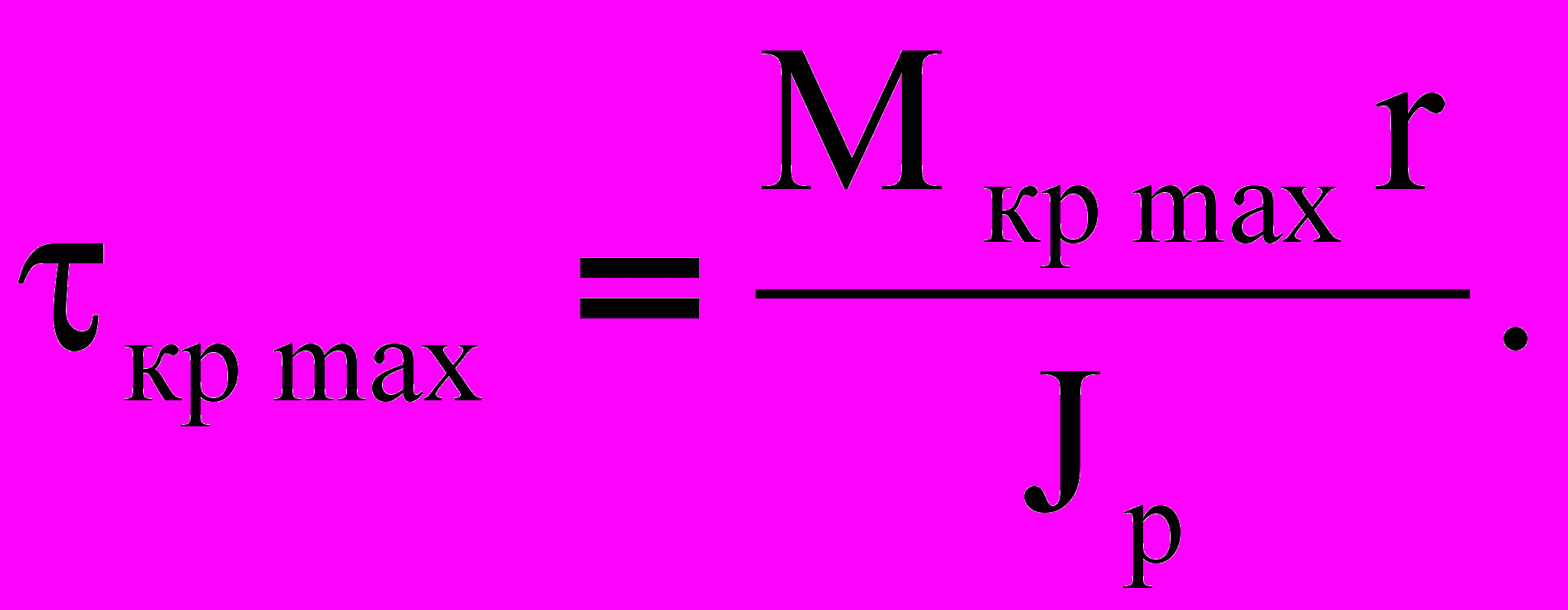 (5¢)
(5¢)Где :
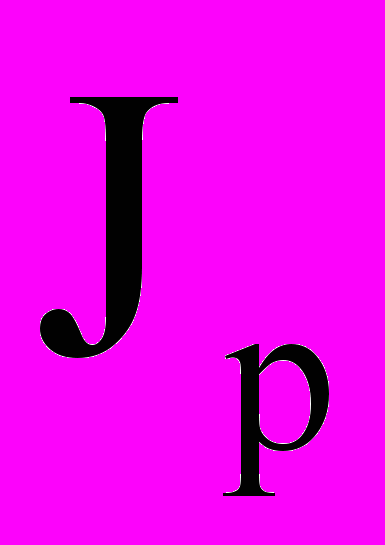 - полярный момент инерции площади поперечного сечения, вычисляется как сумма моментов инерции относительно осей х и у;
- полярный момент инерции площади поперечного сечения, вычисляется как сумма моментов инерции относительно осей х и у;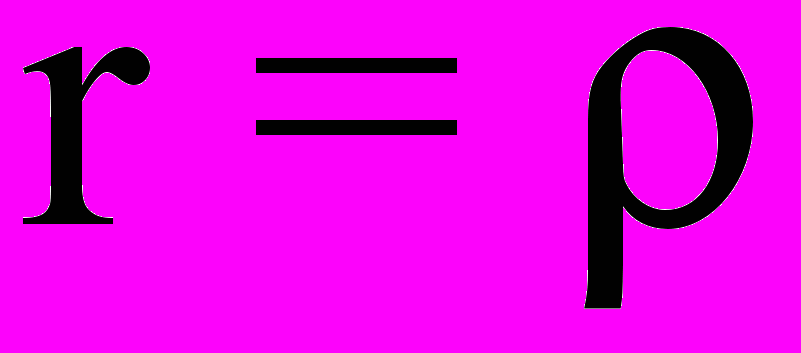 - радиус кривизны круглого сечения;
- радиус кривизны круглого сечения;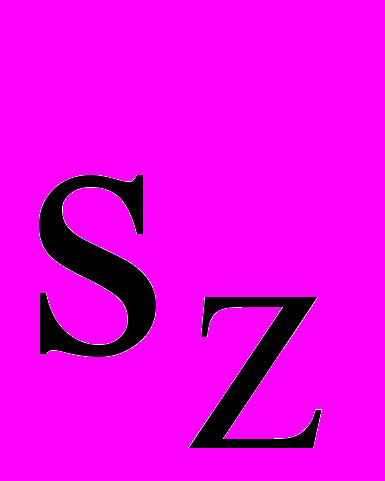 - статический момент площади поперечного сечения относительно оси Z.
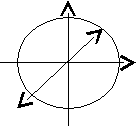
- статический момент площади поперечного сечения относительно оси Z.Из (3¢) - (5¢) следует, что наиболее напряженными окажутся точки 1 и 2 сечения (рис.2)
 y
y1
r
0 x
z 2
Рис.2
Согласно рисунку 1.
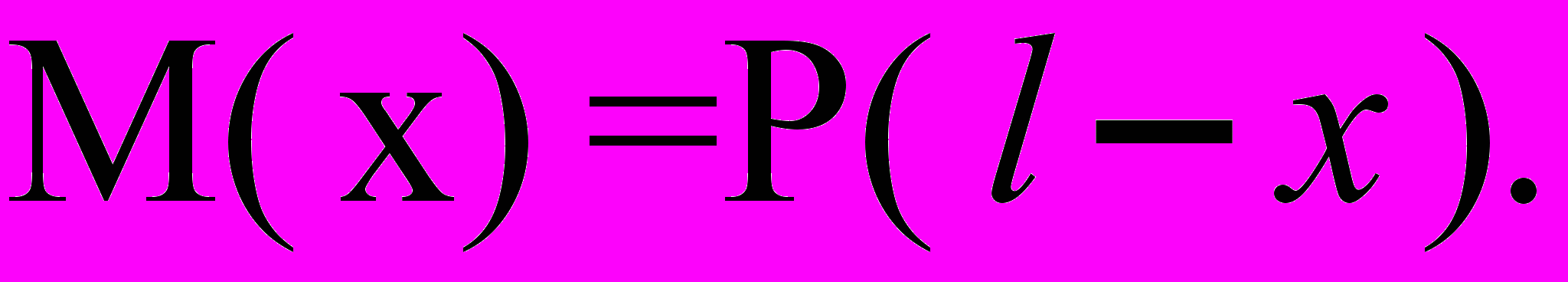 (6)
(6)Следовательно,
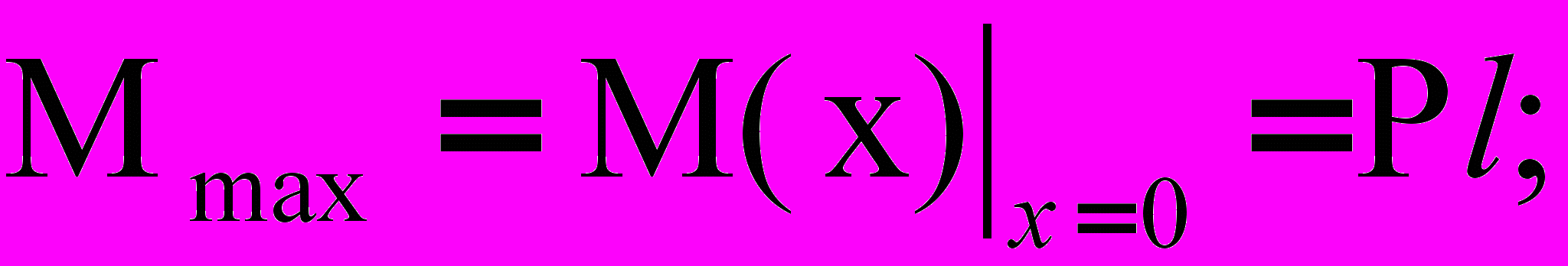 (7)
(7)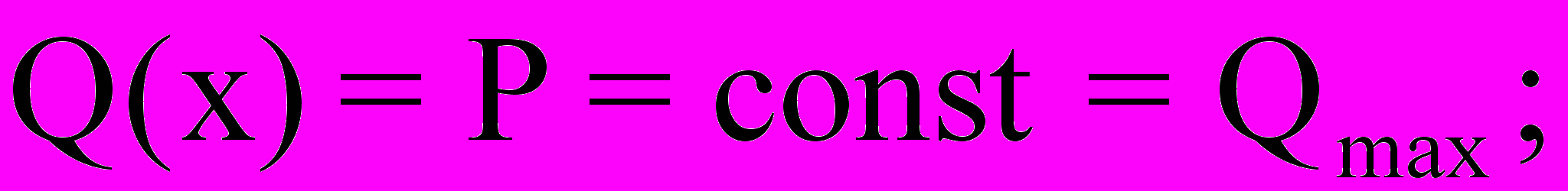 (8)
(8)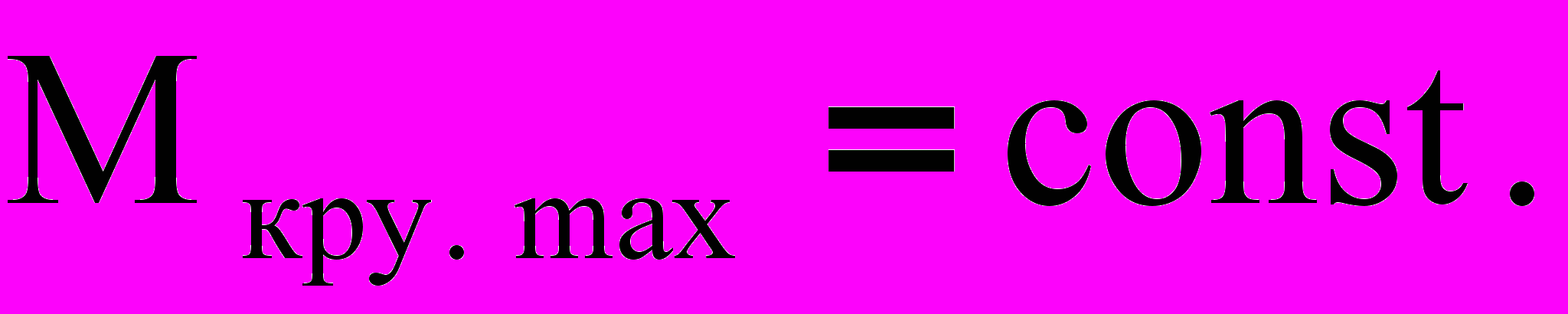 (9)
(9)Таким образом для точек 1 и 2 в сечении заделки напряжения будут:
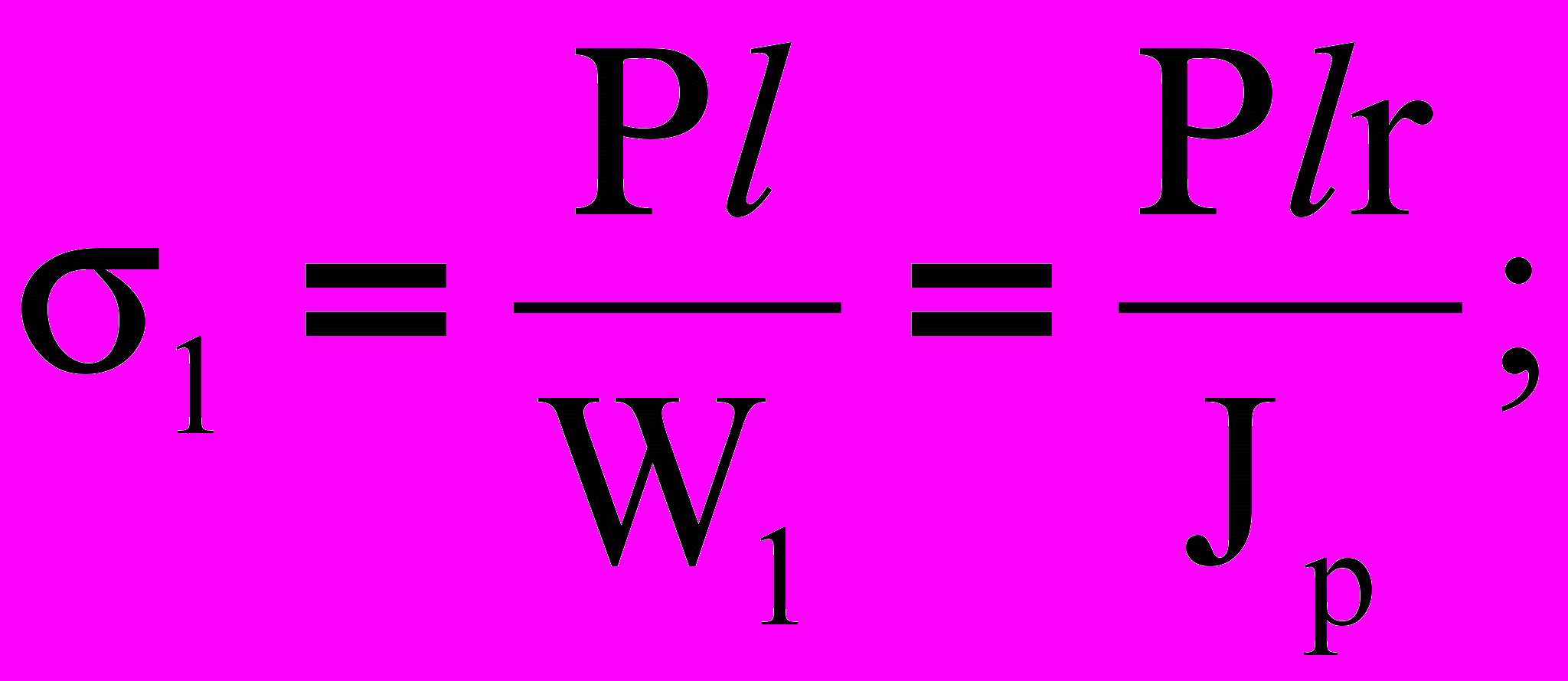 (10)
(10)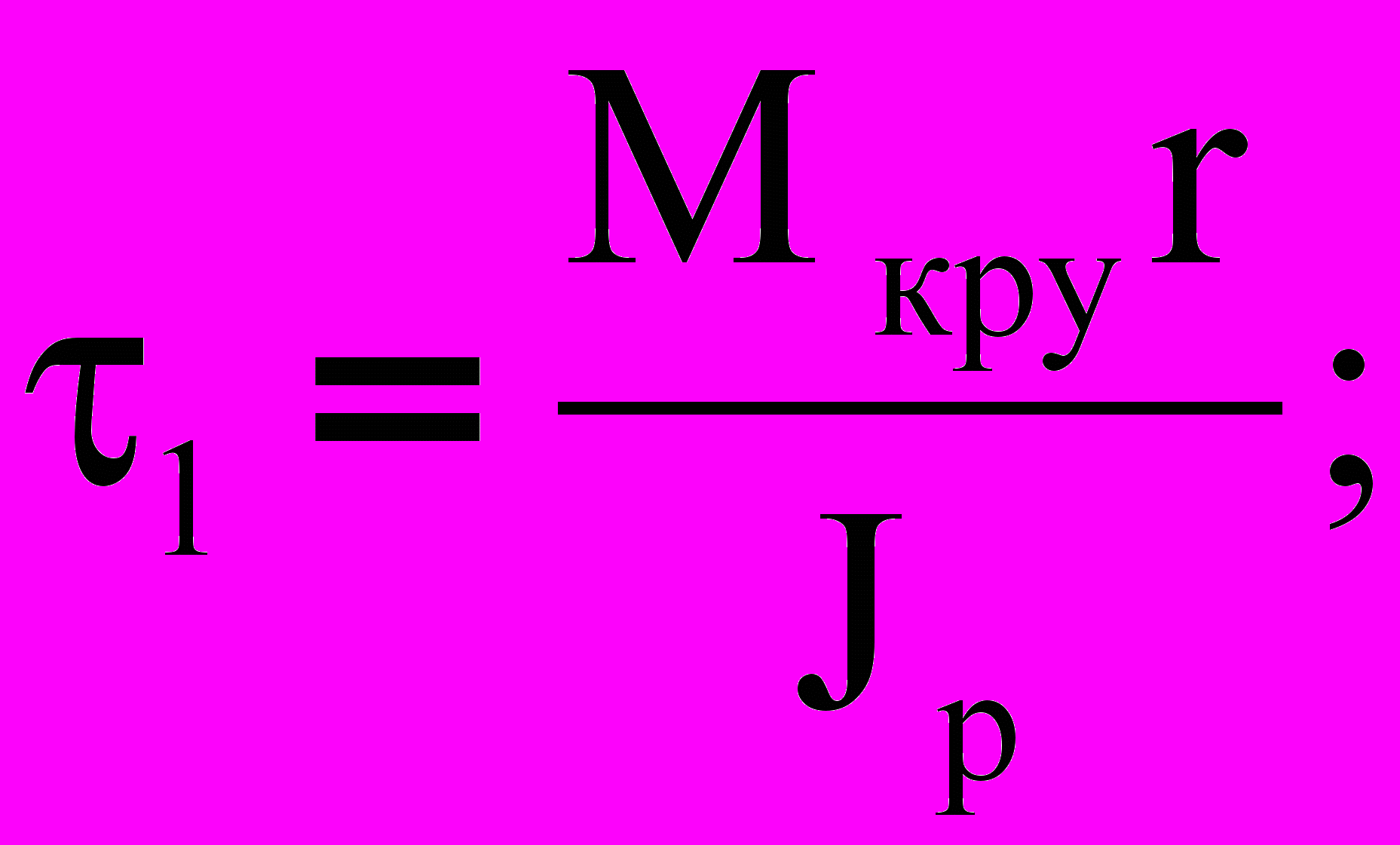 (11)
(11)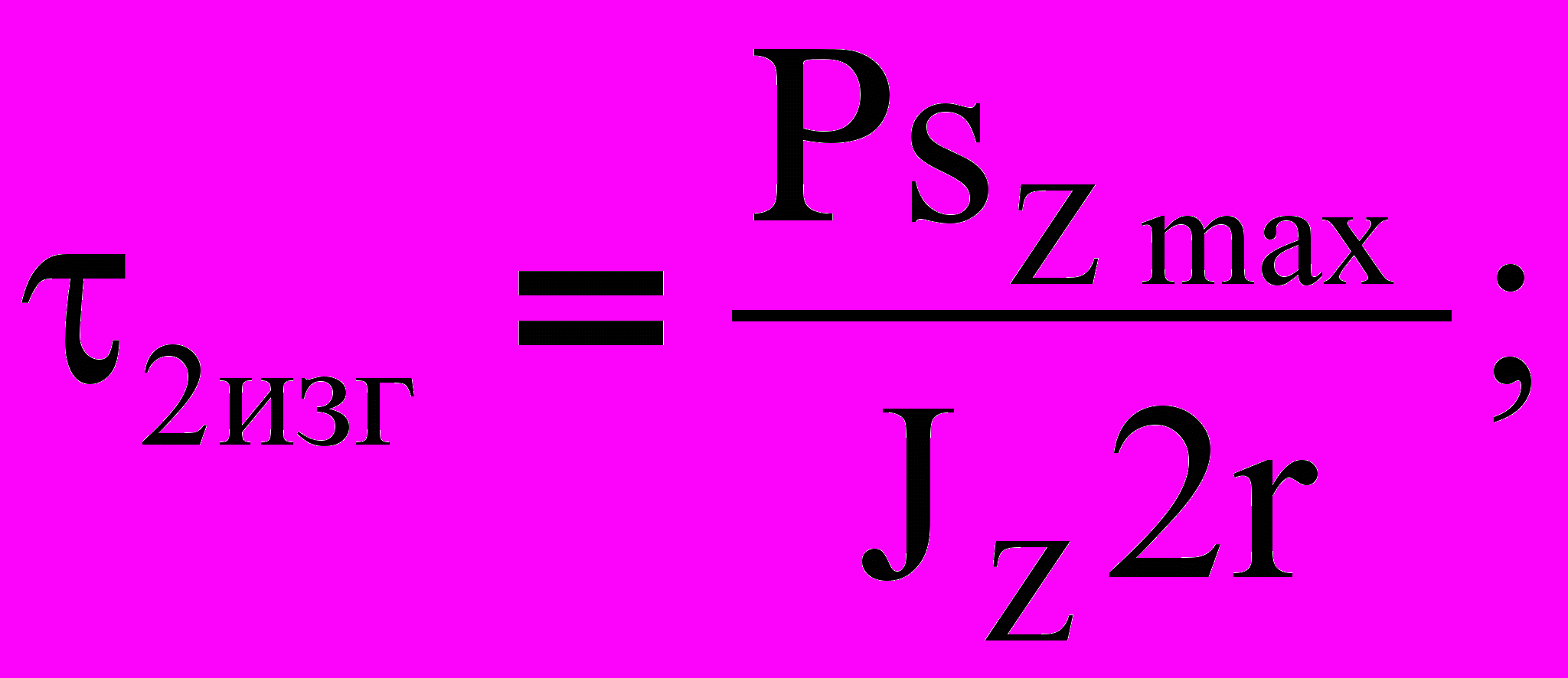 (12)
(12)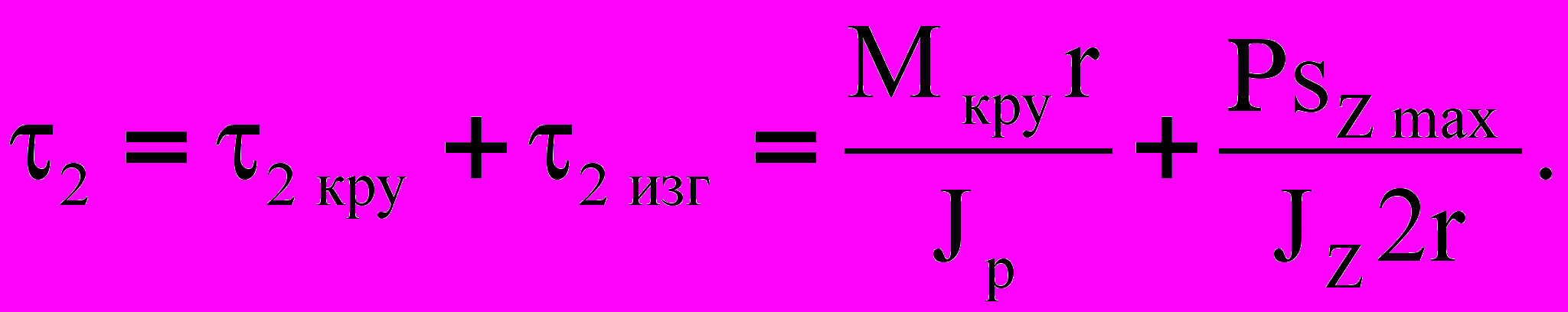 (13)
(13)Для подсчета значений напряжений нужно знать
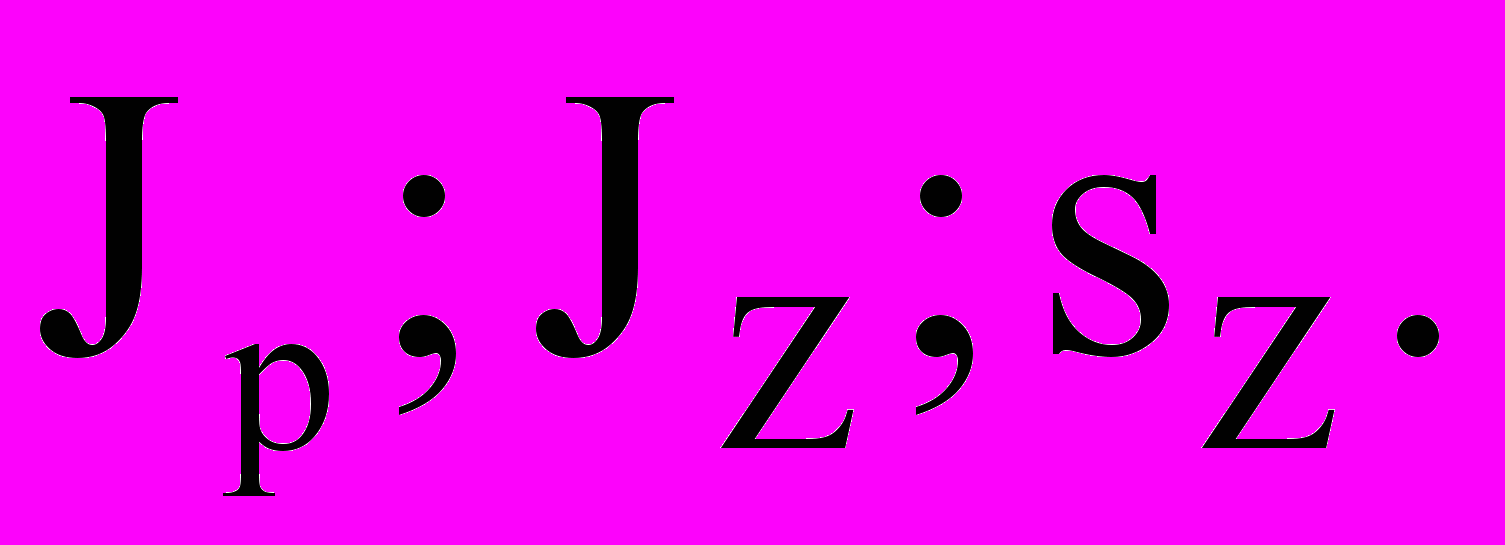 Из теории известно, что:
Из теории известно, что: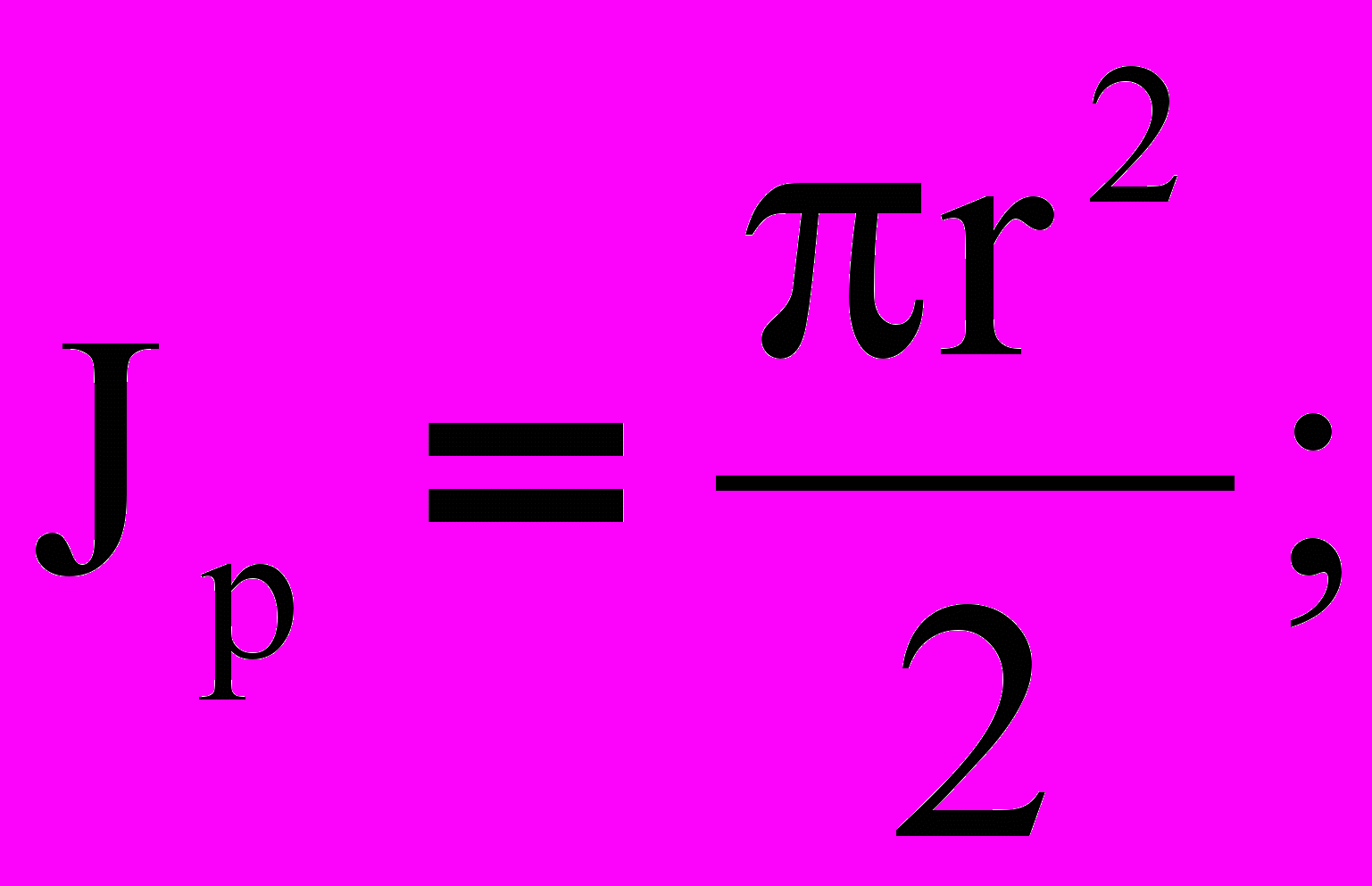
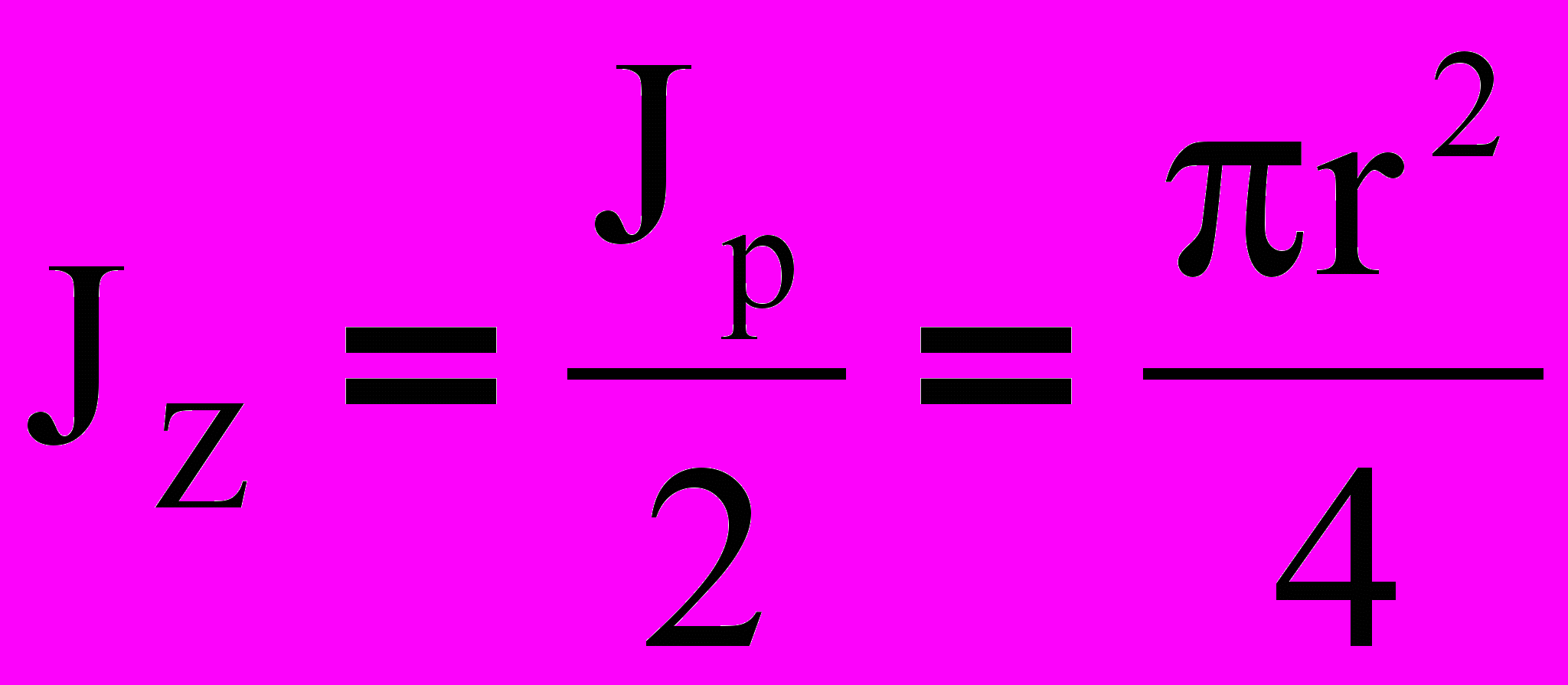 , так как
, так как 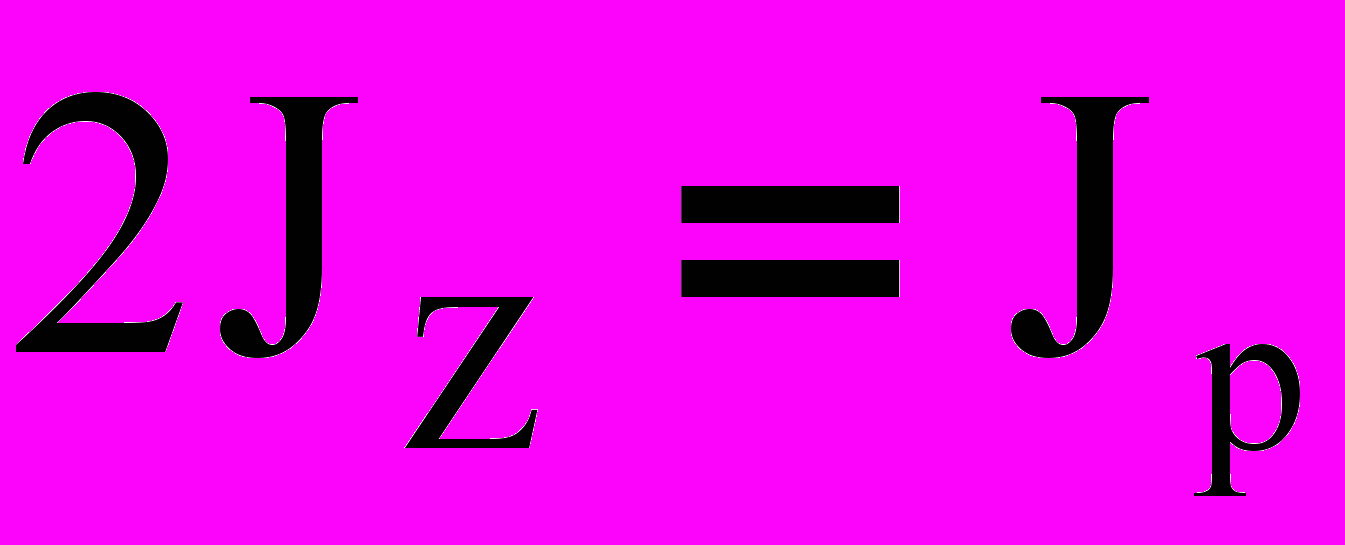 .
.Определим
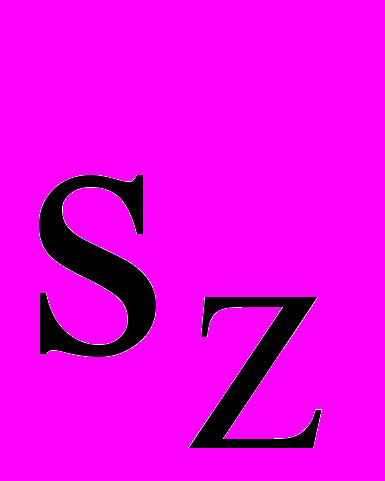 . Согласно теории статический момент площади, отсеченной сечением m - m, определится выражением вида :
. Согласно теории статический момент площади, отсеченной сечением m - m, определится выражением вида :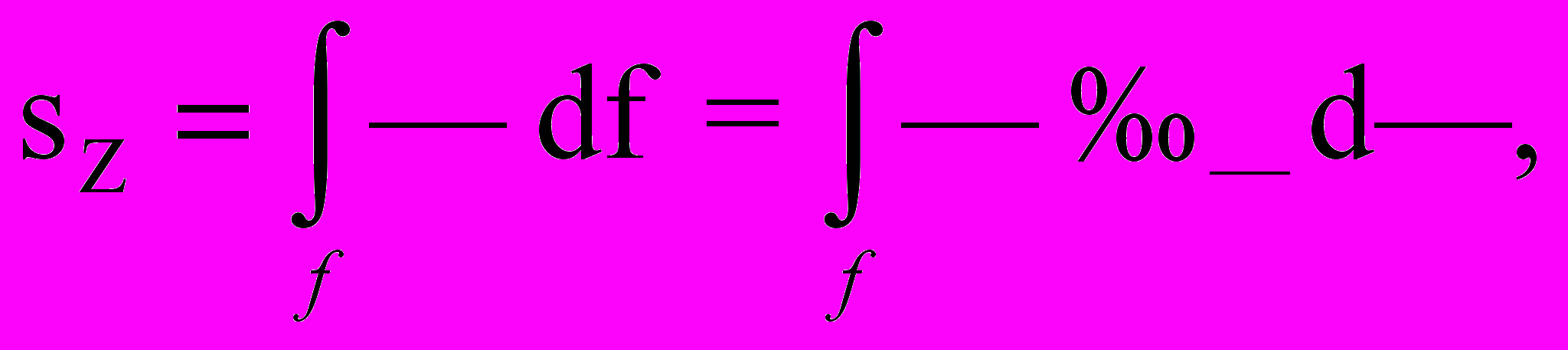
где:

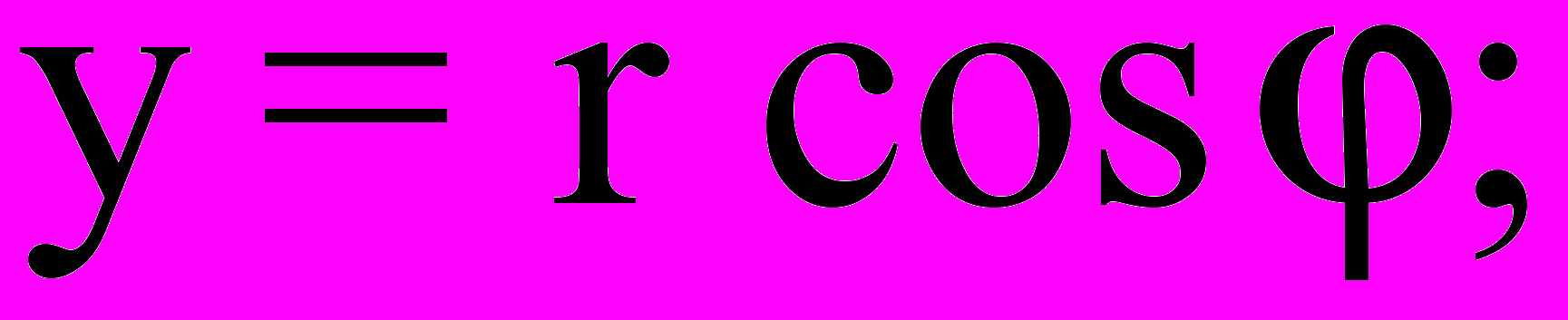
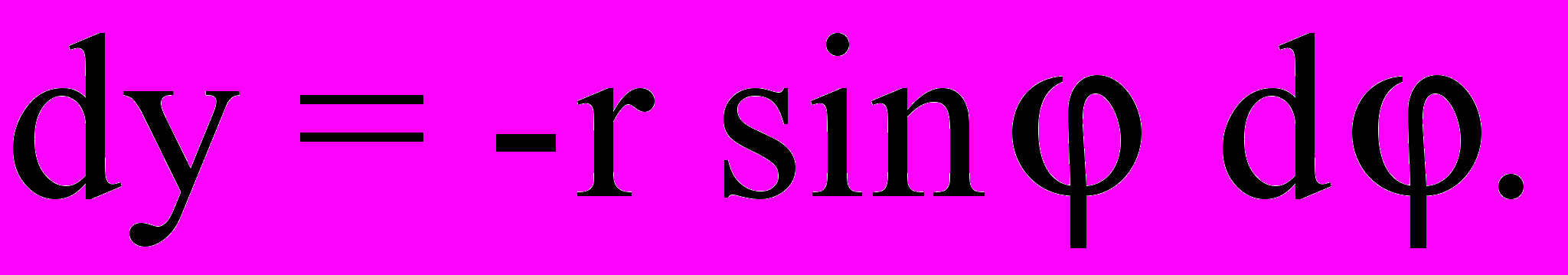
Значит:

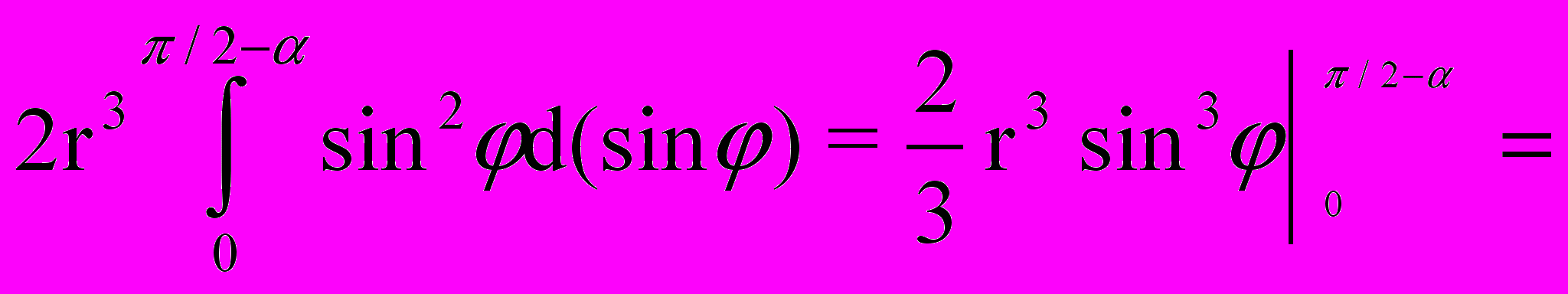
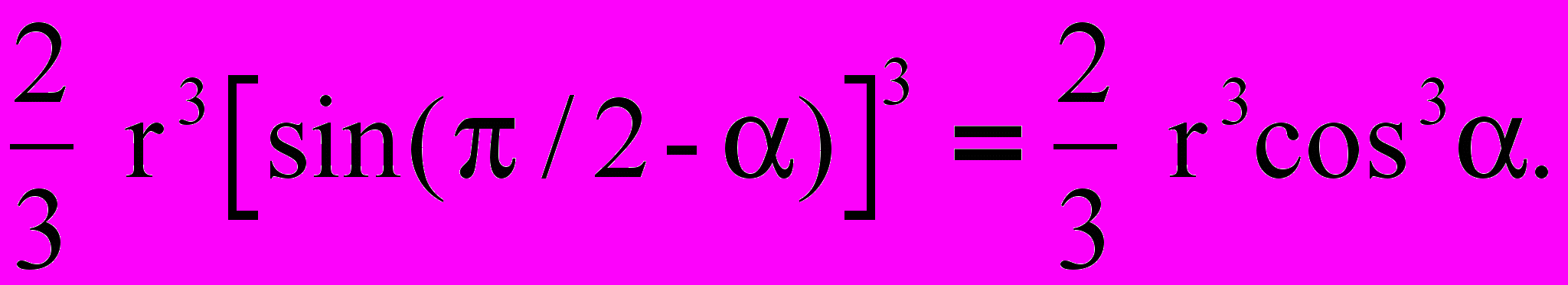 (14)
(14)Величину
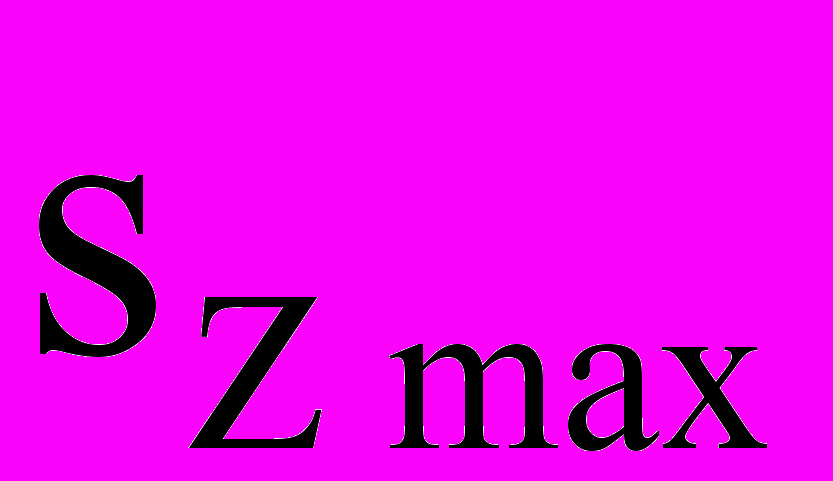 получим, когда m - m пройдет через нейтральный слой (a=0):
получим, когда m - m пройдет через нейтральный слой (a=0):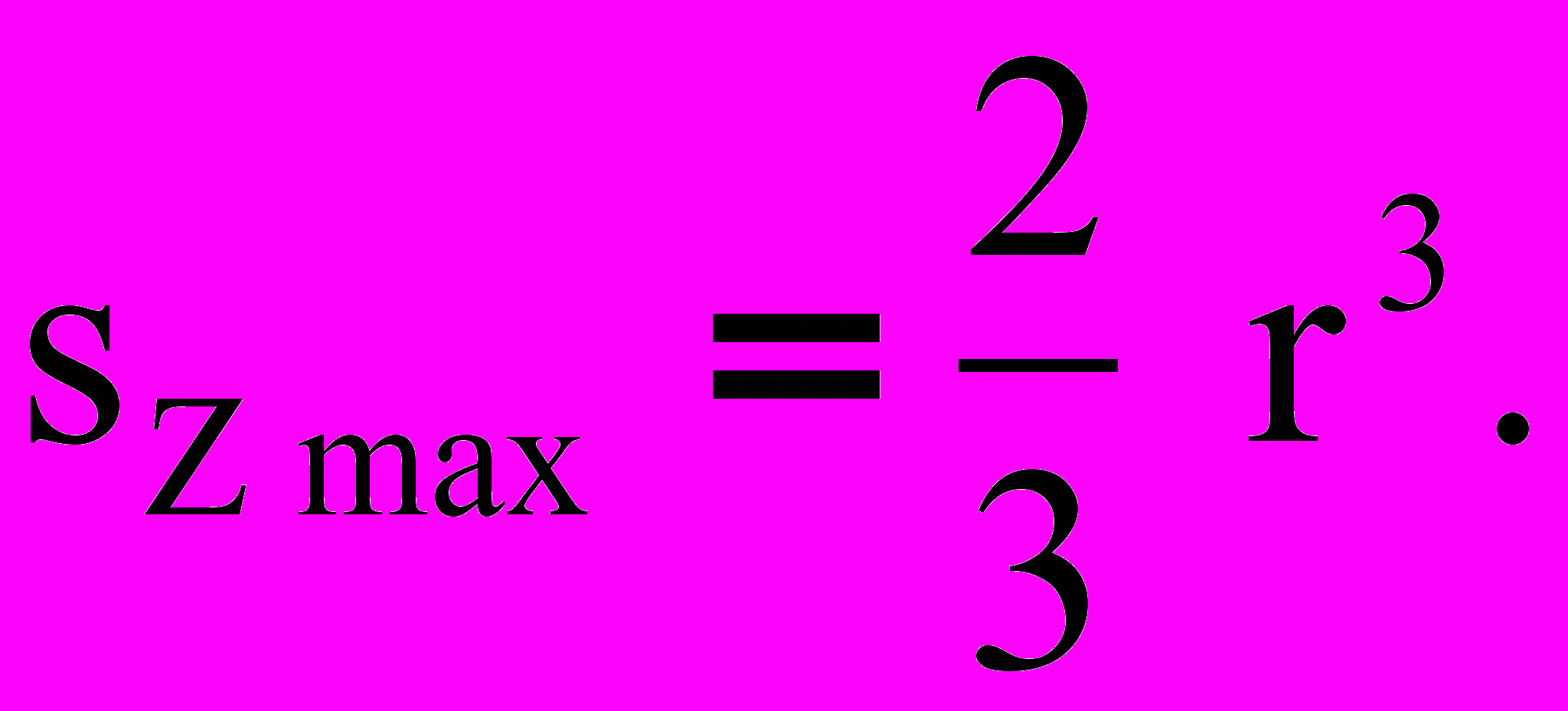 (15)
(15)Косой изгиб
Сила, приложенная вне главных осей поперечного сечения, вызывает так называемый косой изгиб, то есть одновременный изгиб в двух взаимоперпендикулярных плоскостях (рис.1).
 y
yPz z
x
x
l
P Py
Рис.1
Разложим силу Р на две составляющие, параллельные осям у и Z. Получим:
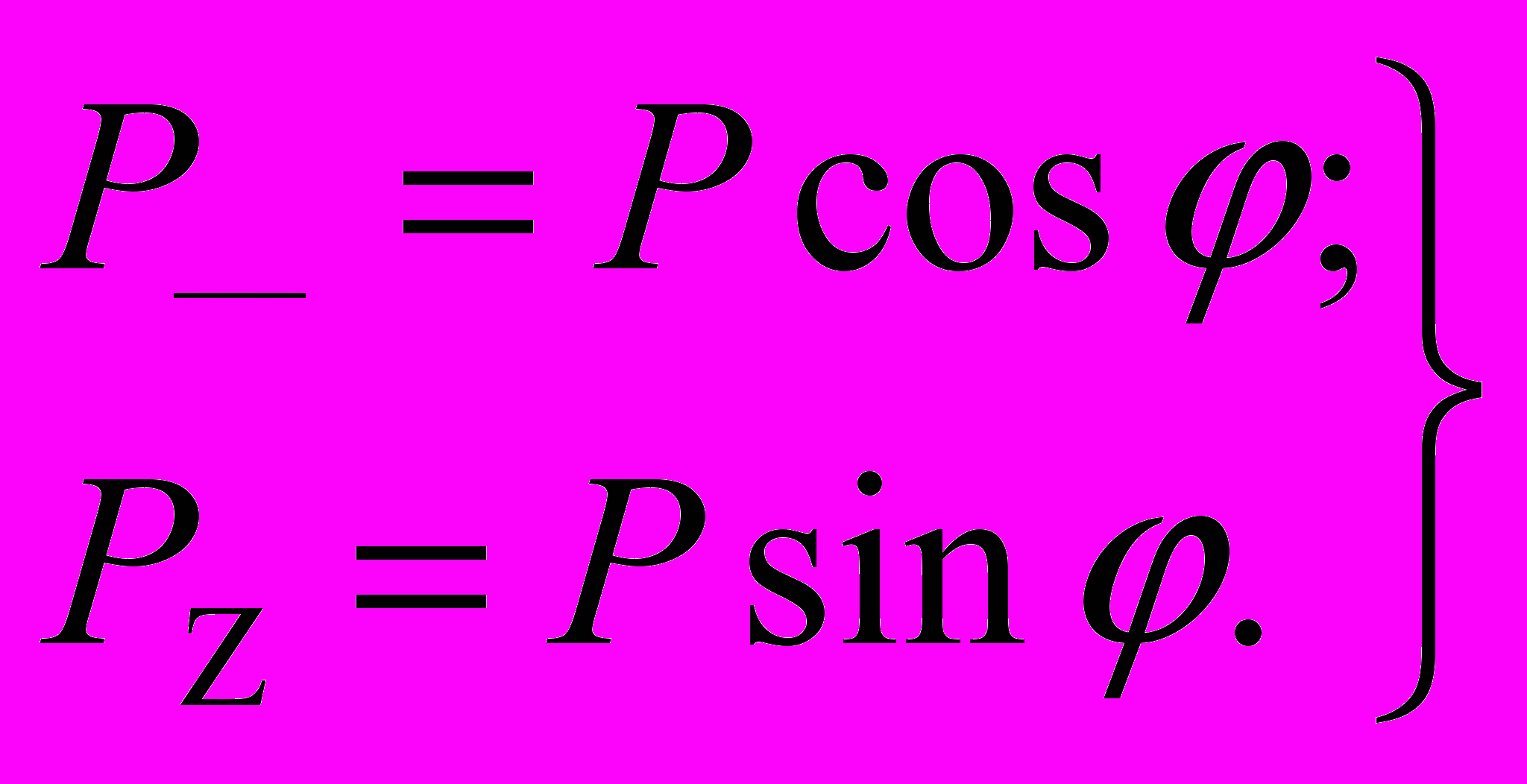 (1)
(1)Силы
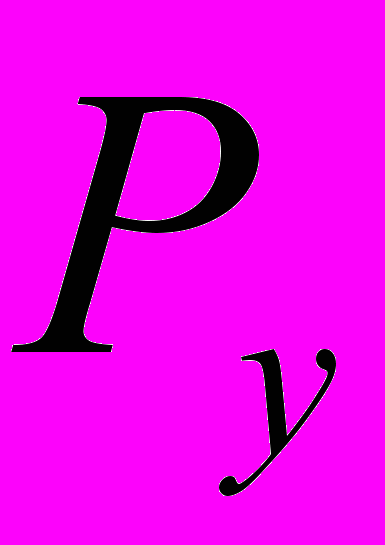 и
и 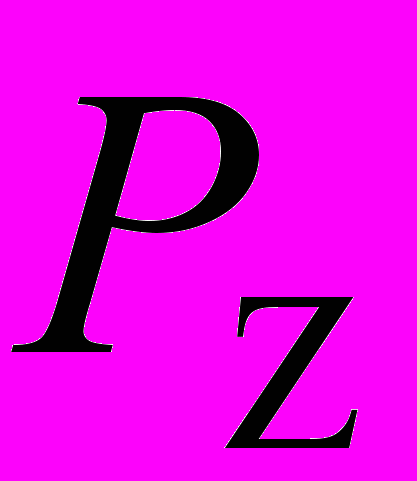 будут вызывать изгиб в двух взаимно перпендикулярных плоскостях. Соответственно изгибающие моменты будут равны:
будут вызывать изгиб в двух взаимно перпендикулярных плоскостях. Соответственно изгибающие моменты будут равны: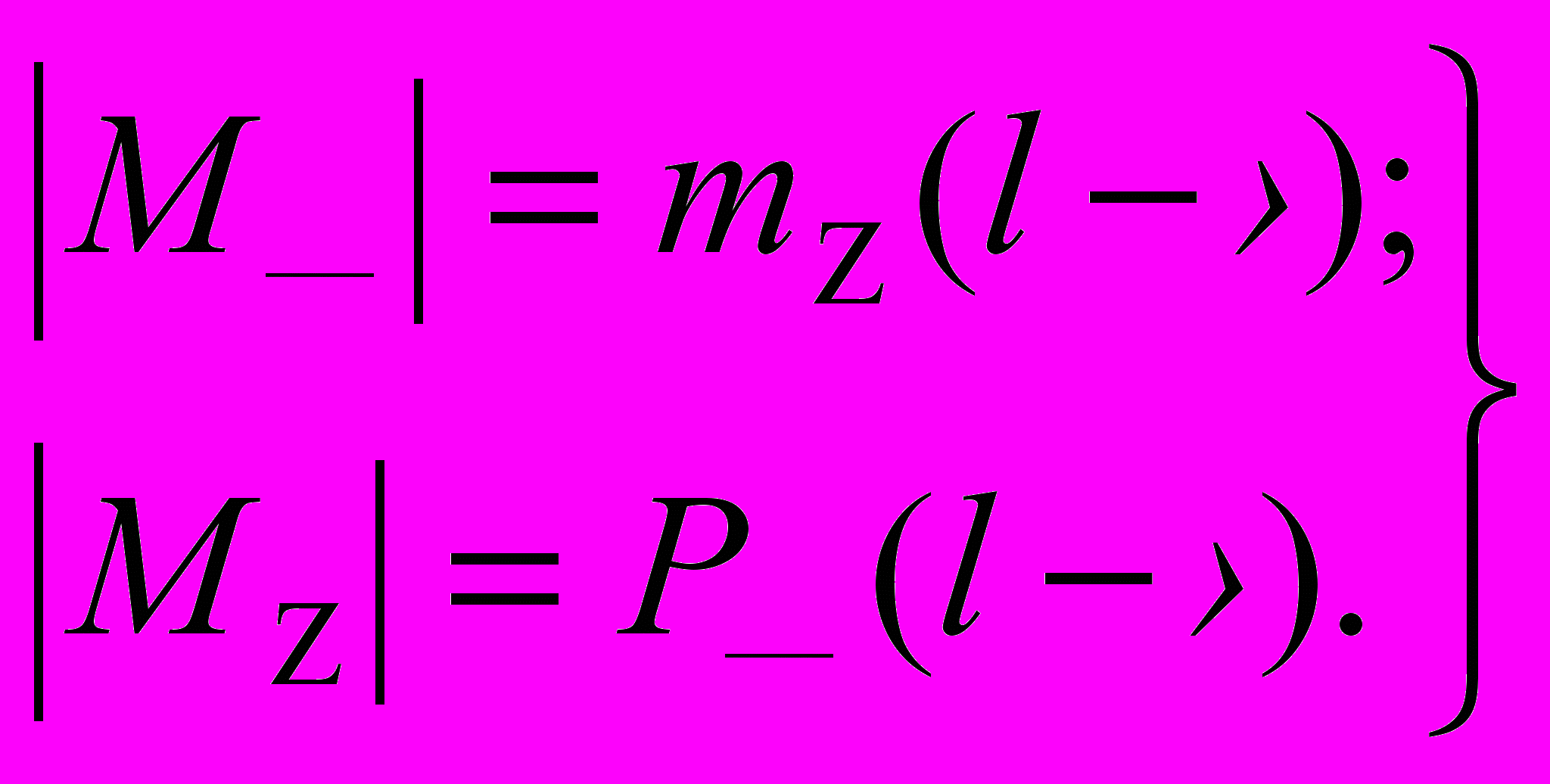 (2)
(2)Подставляя значение (1) в (2), получим:
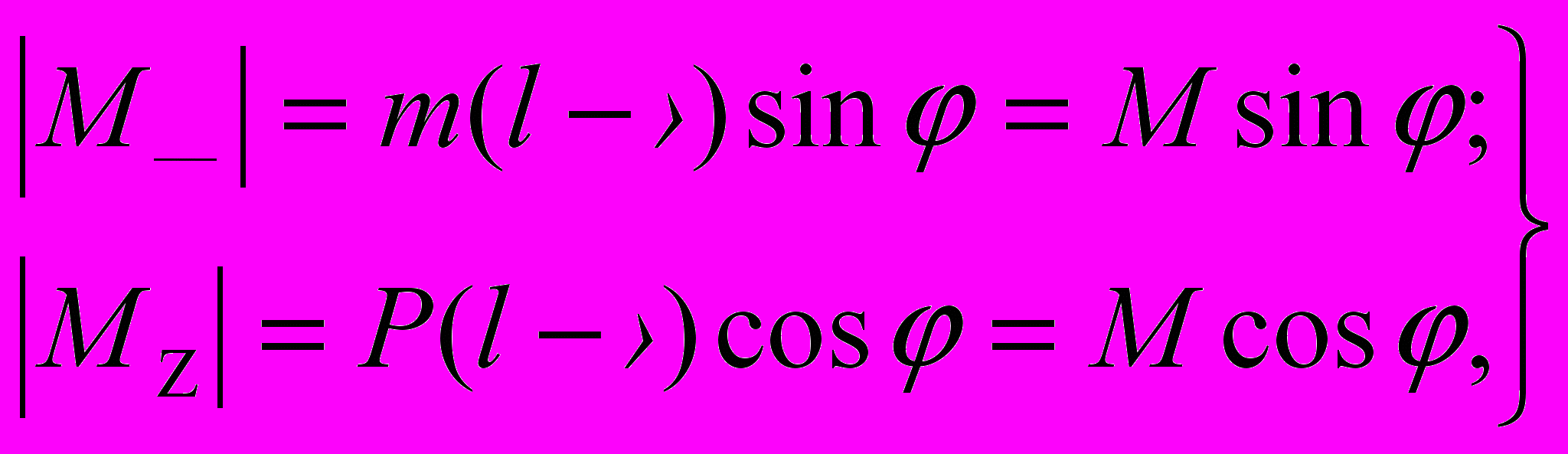 (3)
(3)где:
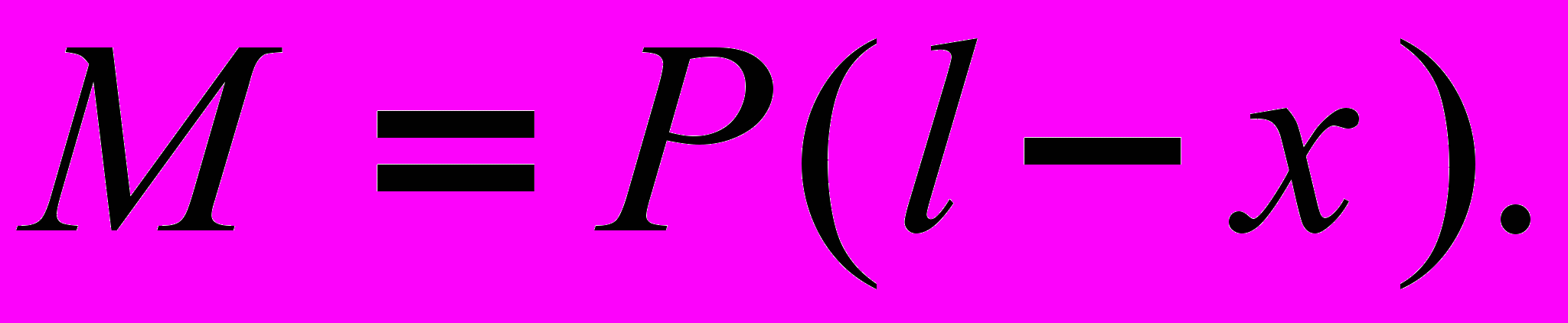 (4)
(4)Нормальные напряжения определяются формулой
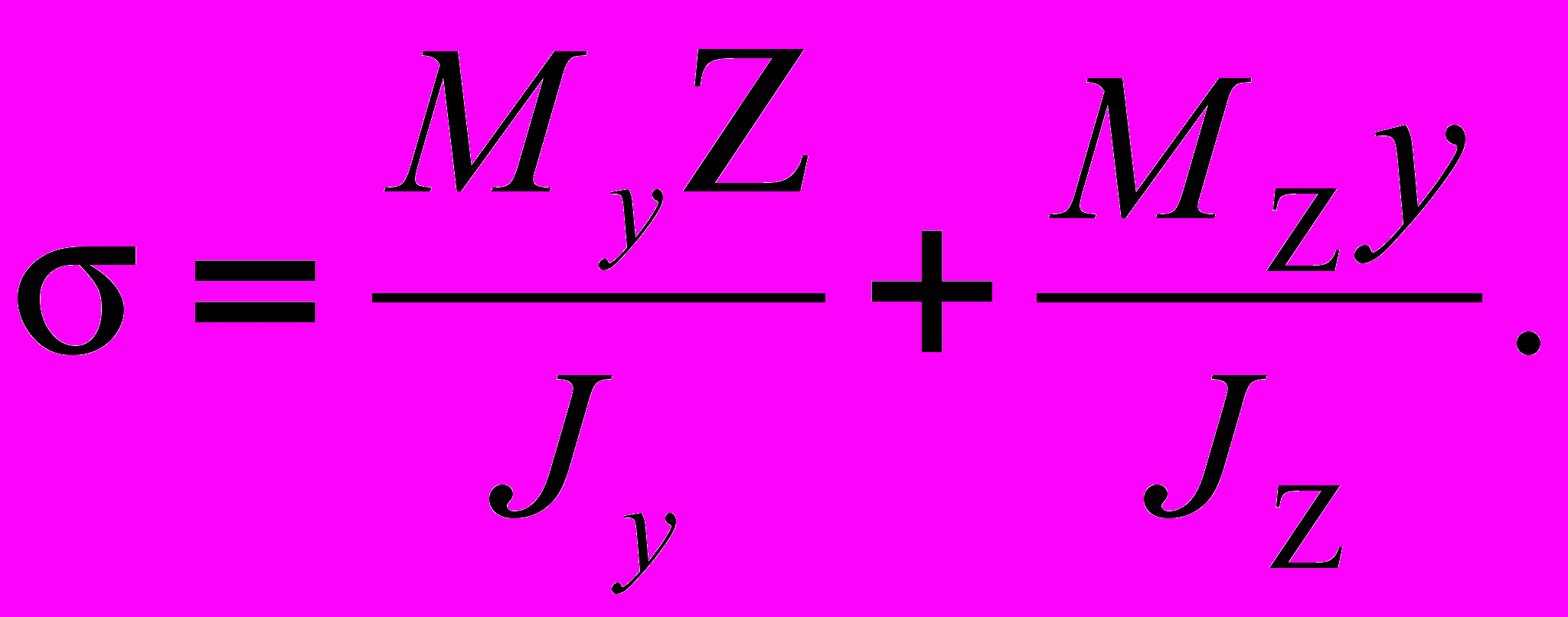 (5)
(5)Подставляя выражение (3) в (5), получим:
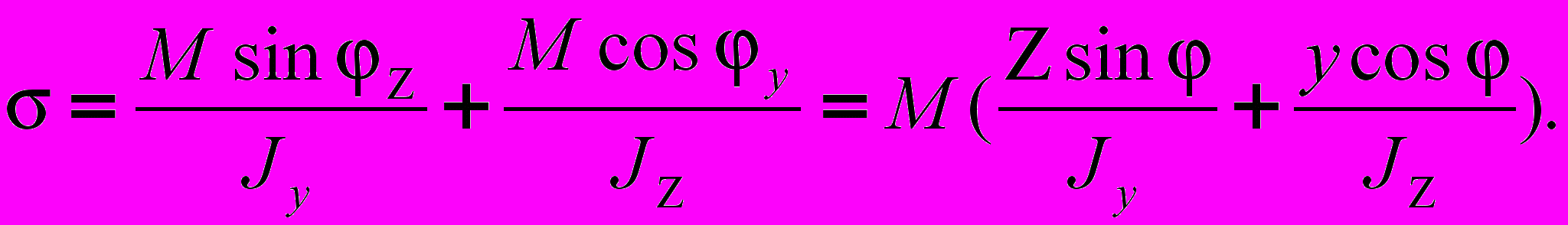 (6)
(6)Соответственно максимальные напряжения будут определяться выражениями вида:
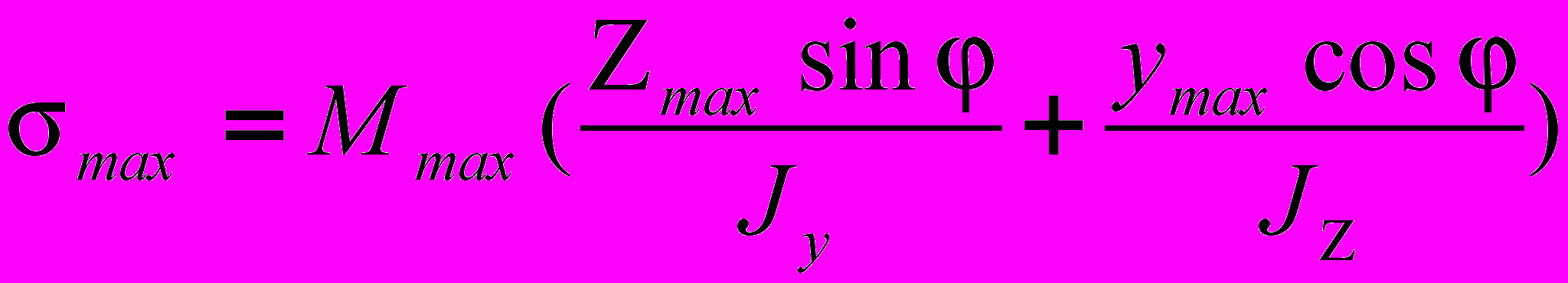
или
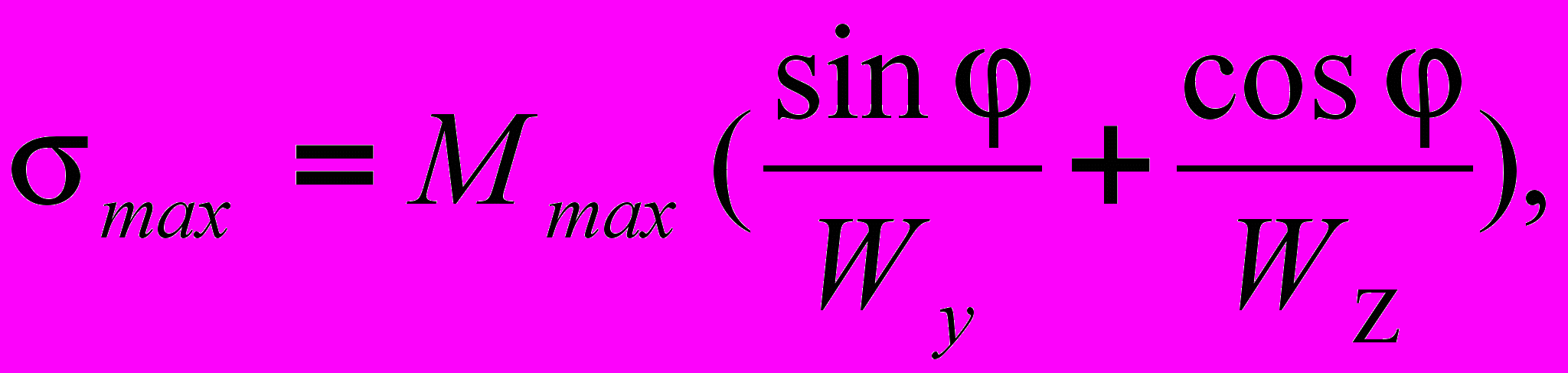 (7)
(7)где:


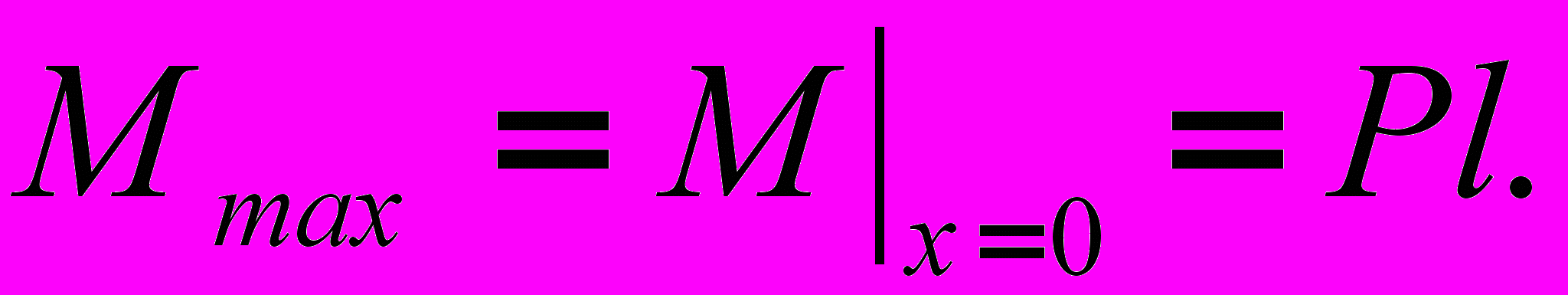
Наряду с нормальными напряжениями в балке возникают касательные напряжения, направленные по осям
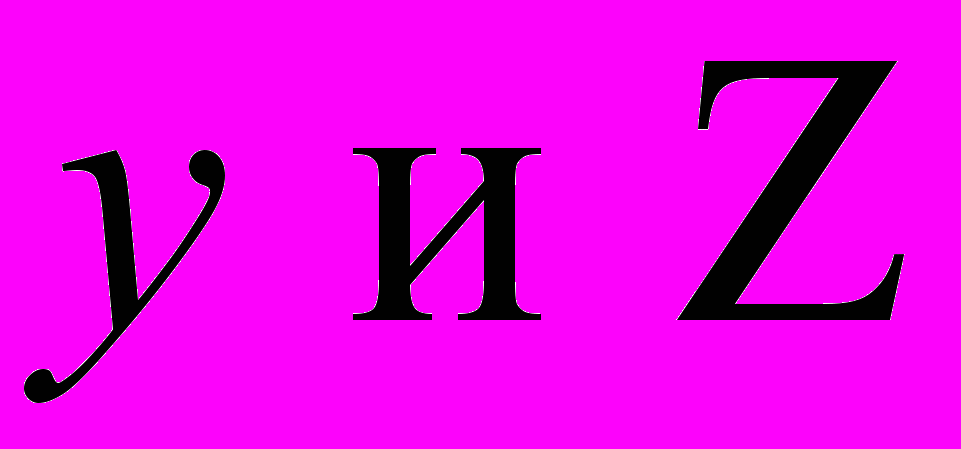 (рис.1), то есть:
(рис.1), то есть: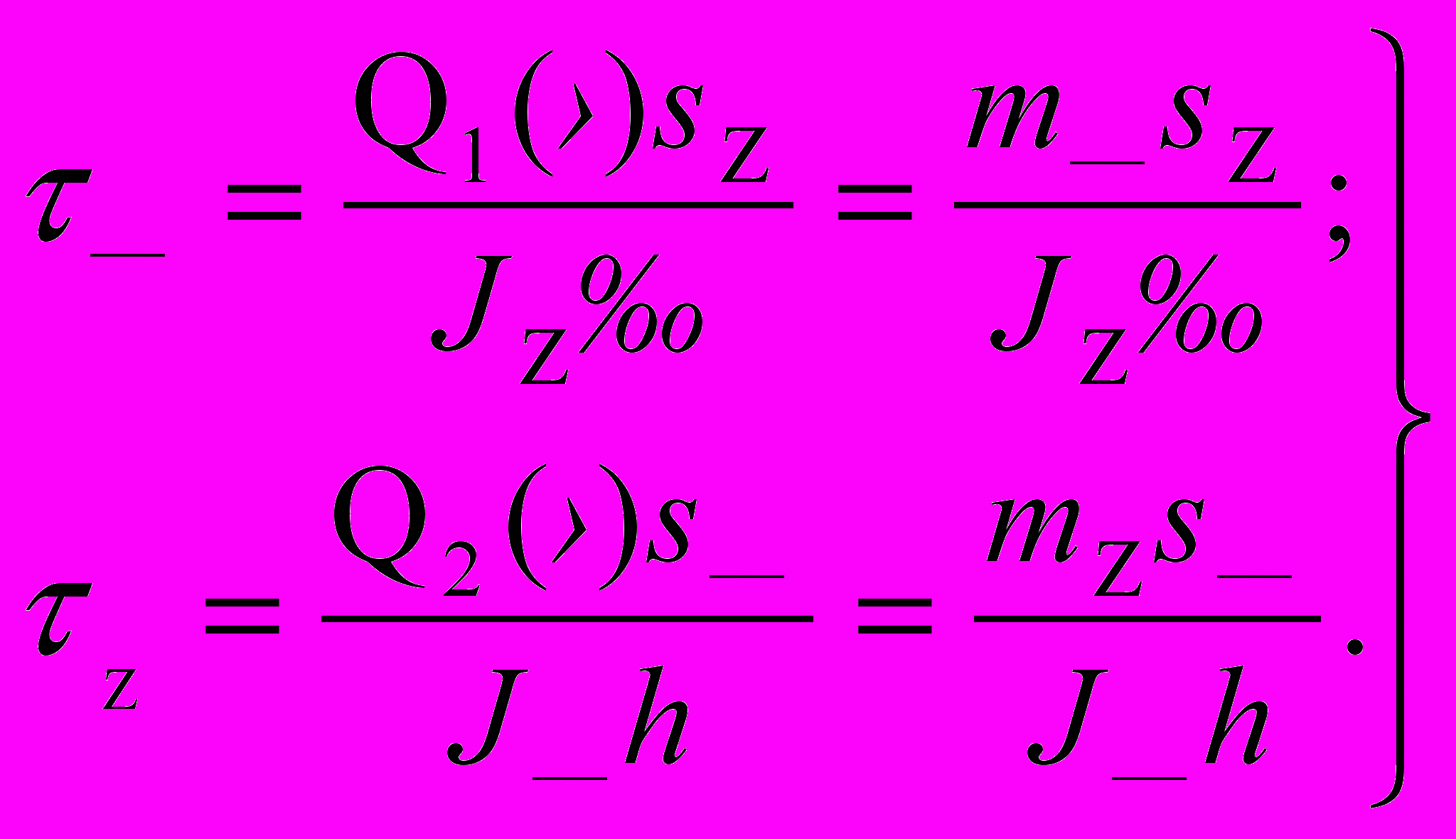 (8)
(8)Полное касательное напряжение будет равно:
 (9)
(9)Наибольшие касательные напряжения равны:
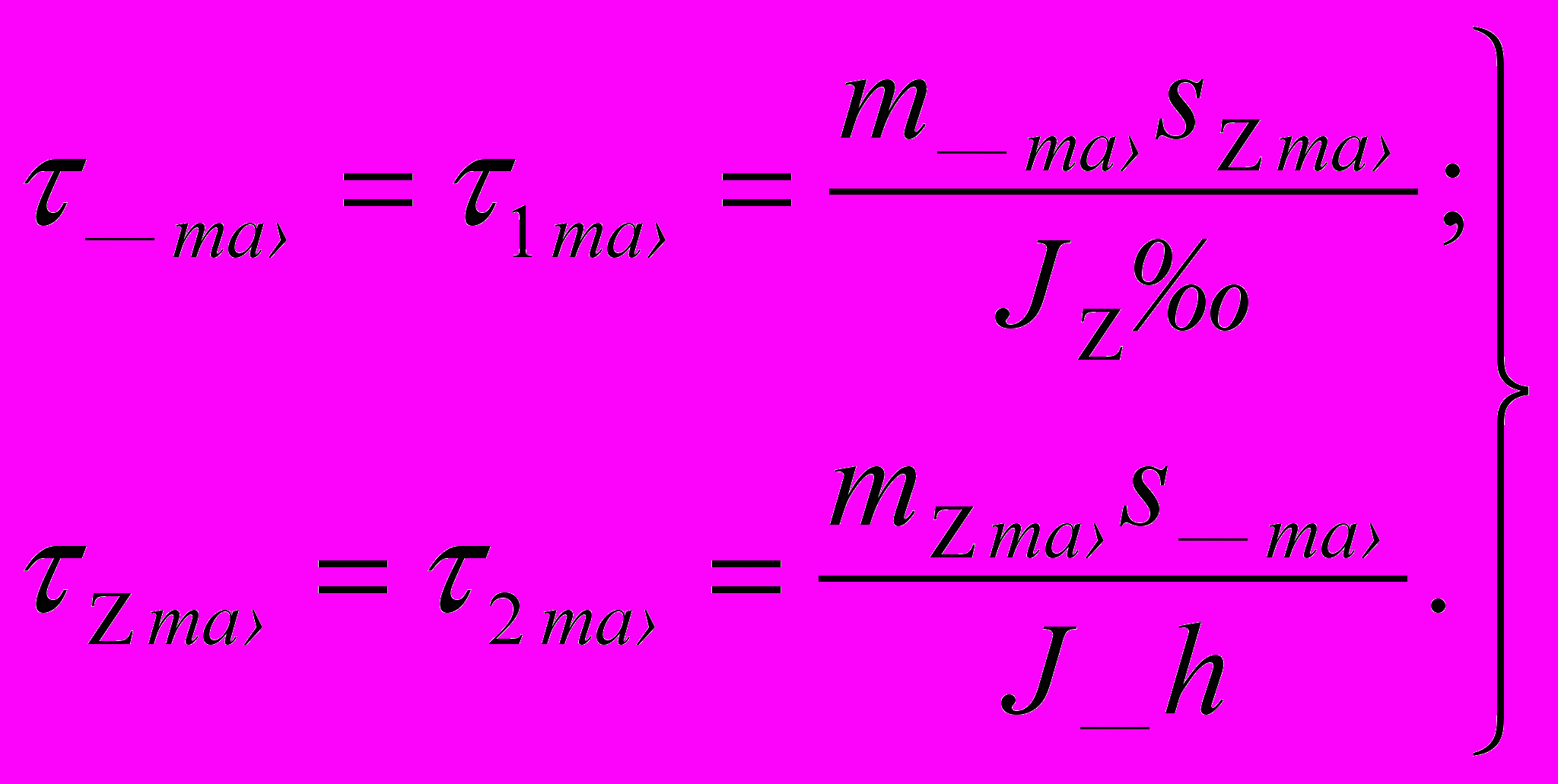 (10)
(10)Следовательно, :
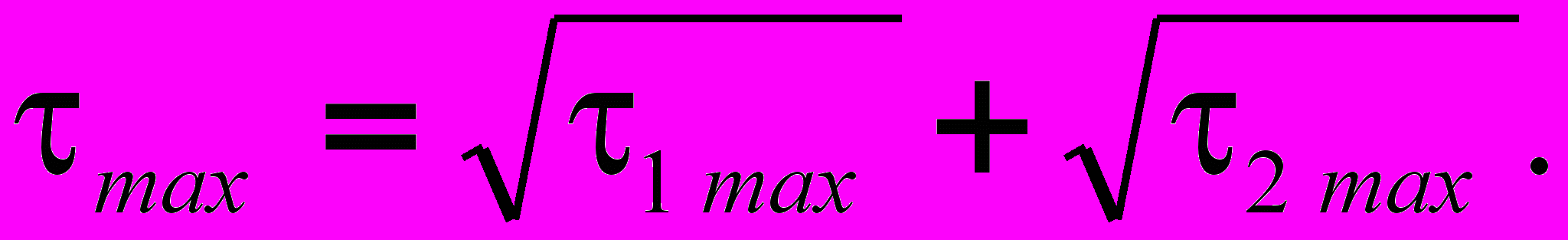 (11)
(11)Из теории известно, что :
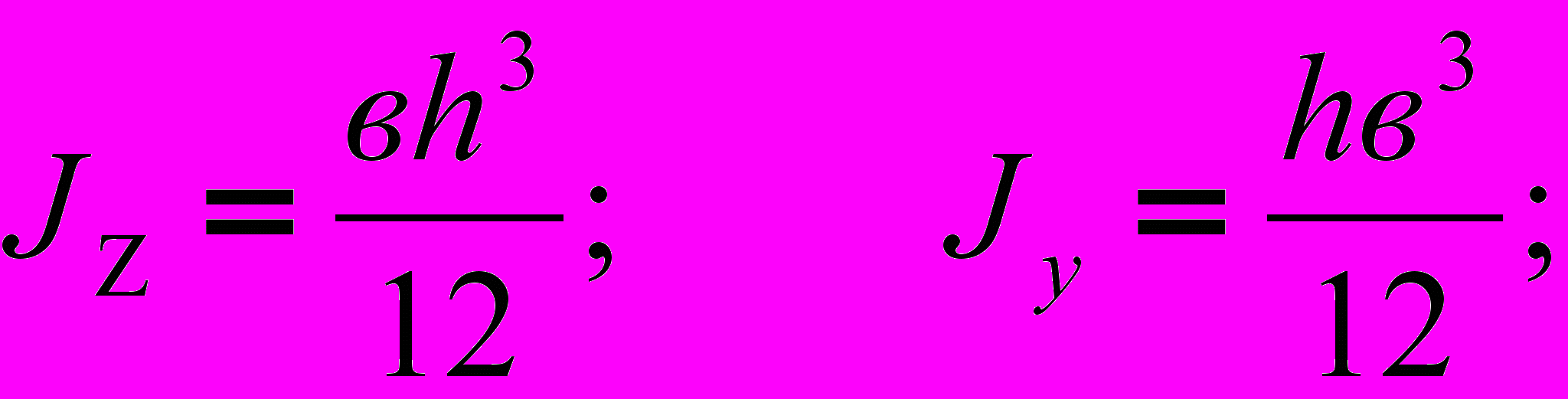
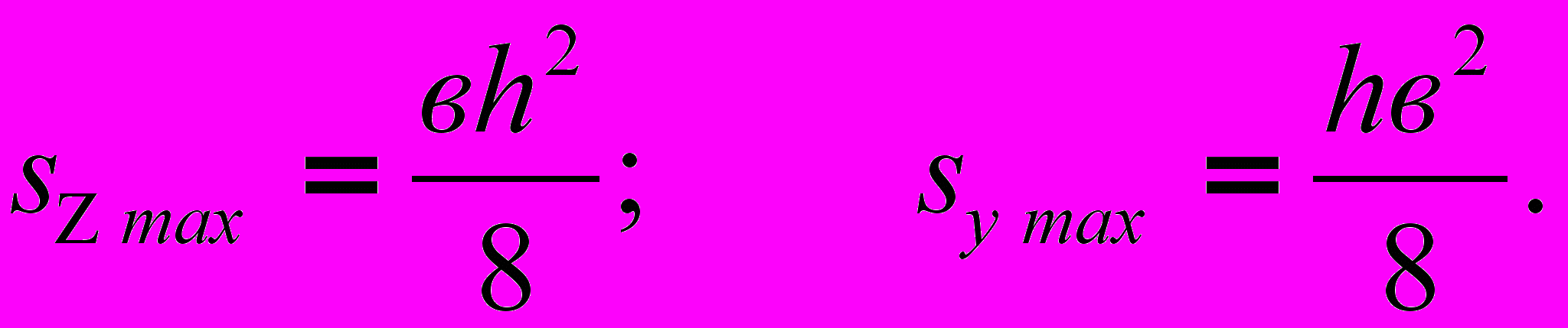
Значит,
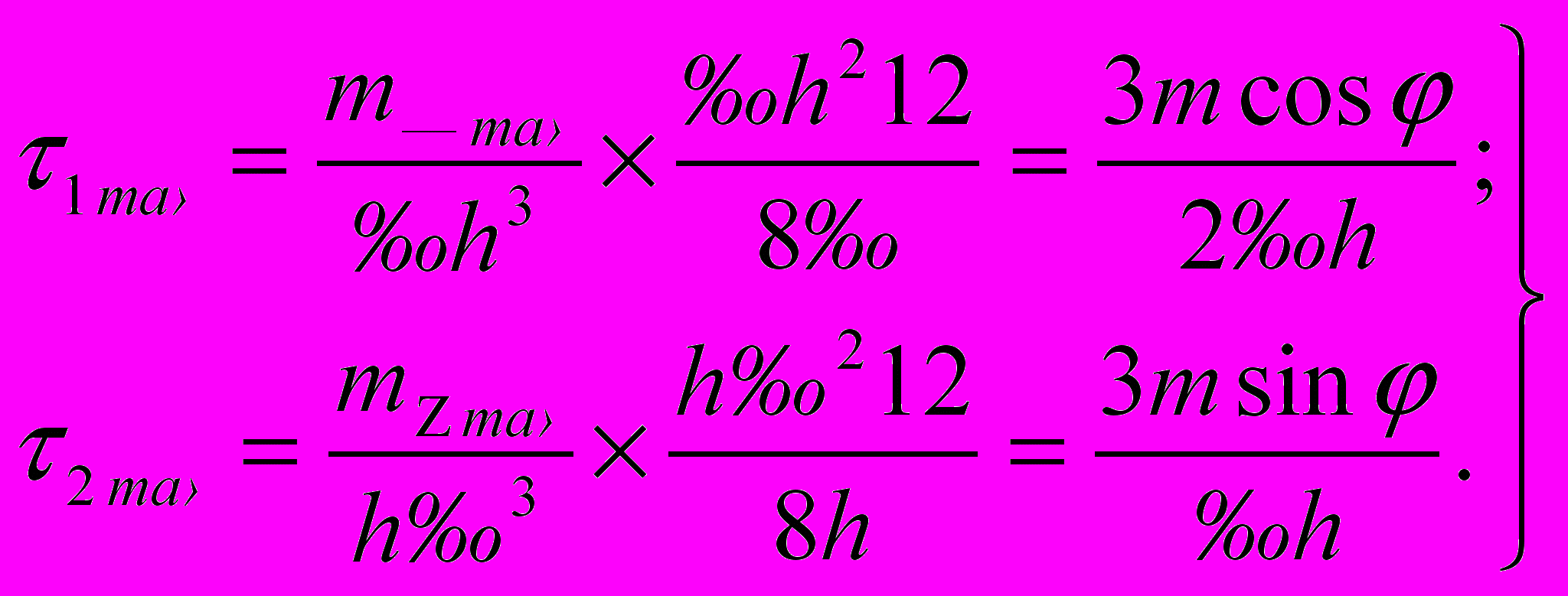 (12)
(12)Подставляя выражение (12) в (11), получим :
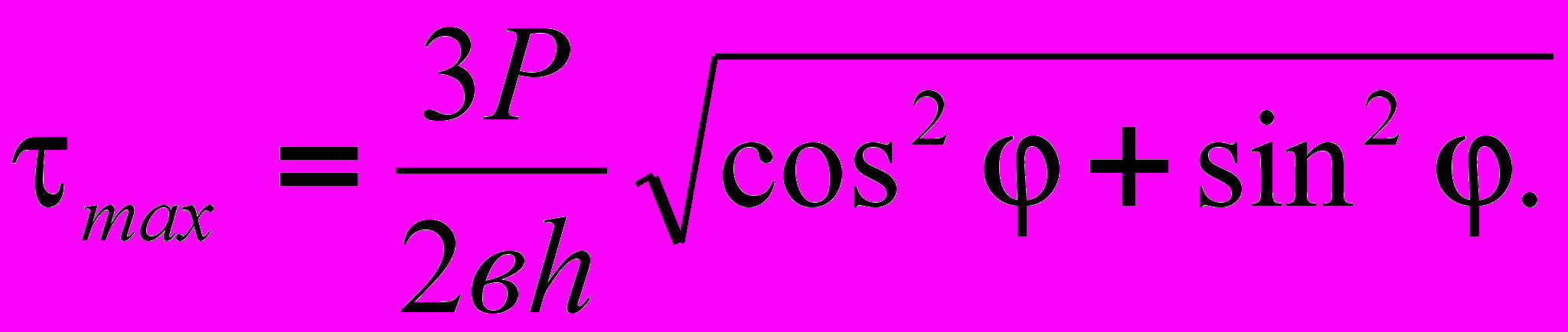 (13)
(13)Из формулы (6) можно получить важное следствие о том, что нейтральный слой при косом изгибе неперпендикулярен направлению силы Р (см. рис.1).
Расчет на прочность и жесткость при кручении сплошных и полых валов
В сопротивлении материалов расчеты стержневых конструкций, в том числе и валов, производится по допускаемым напряжениям.
Условие прочности при кручении заключается в том, что наибольшее касательные напряжения от нормативных внешних нагрузок, возникающих в опасном сечении вала, не должно превышать допускаемого напряжения в этом опасном сечении. Расчет производится по формуле
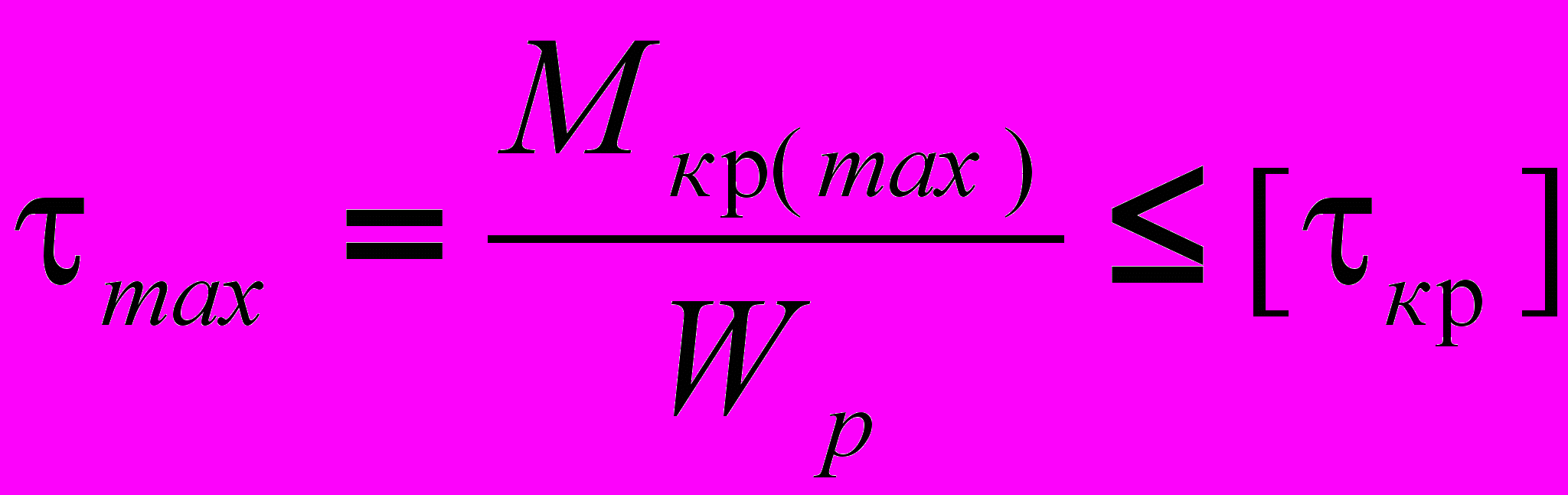 , (1)
, (1)где :
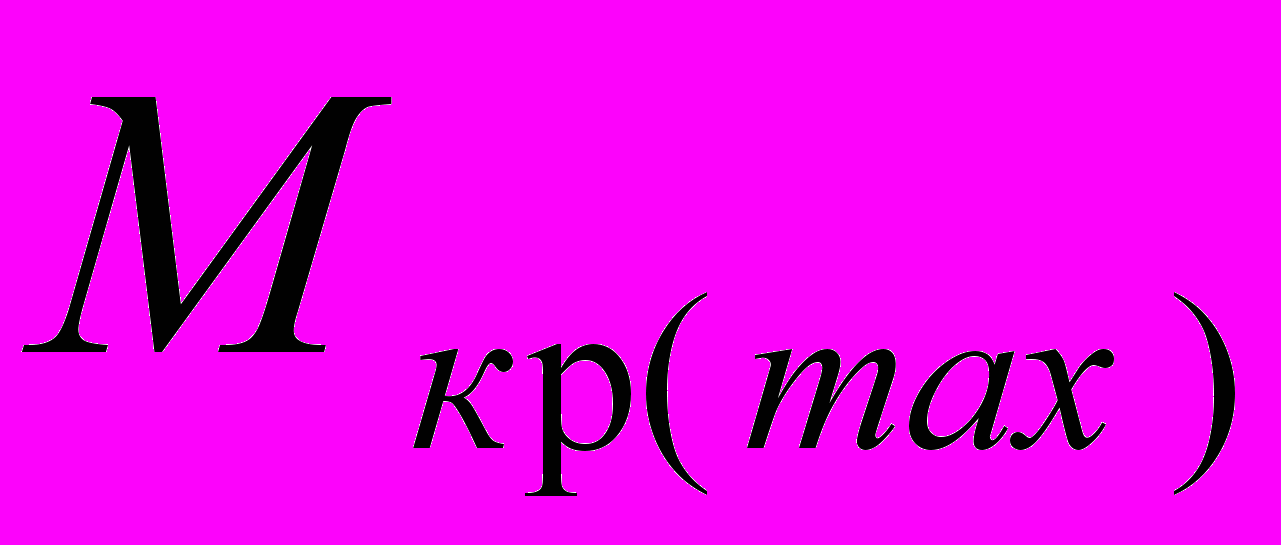 - наибольший нормативный крутящий момент от внешних нагрузок;
- наибольший нормативный крутящий момент от внешних нагрузок;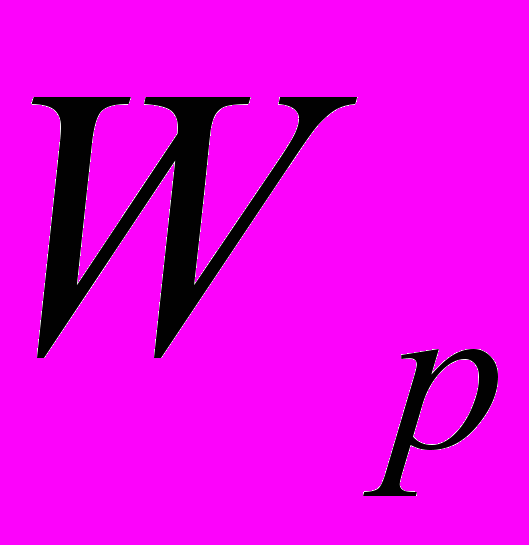 - полярный момент сопротивления сечения круглого вала;
- полярный момент сопротивления сечения круглого вала;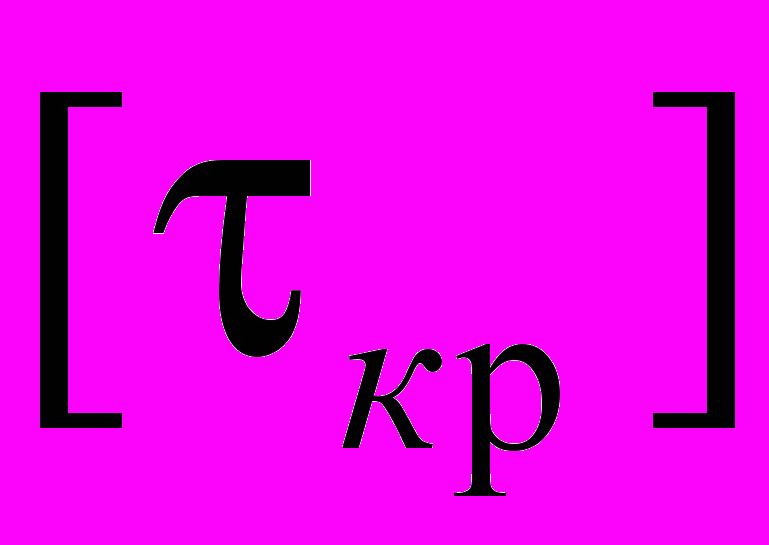 - допускаемое косательное напряжение материала на кручение.
- допускаемое косательное напряжение материала на кручение.Для стали :
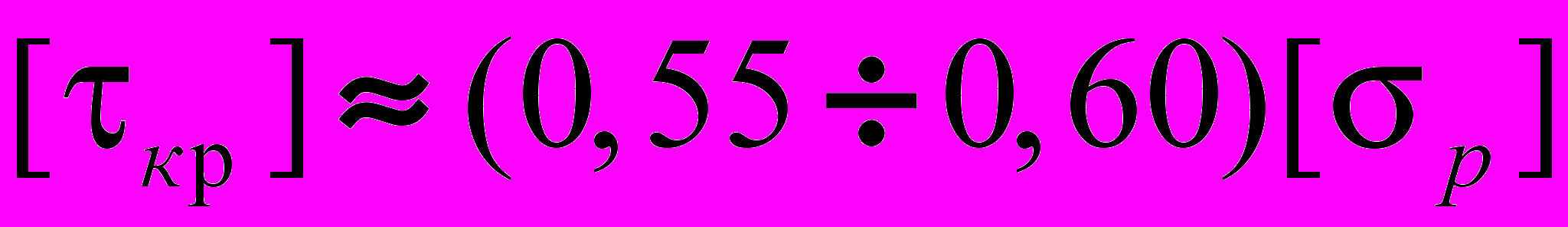 ,
,для чугуна :
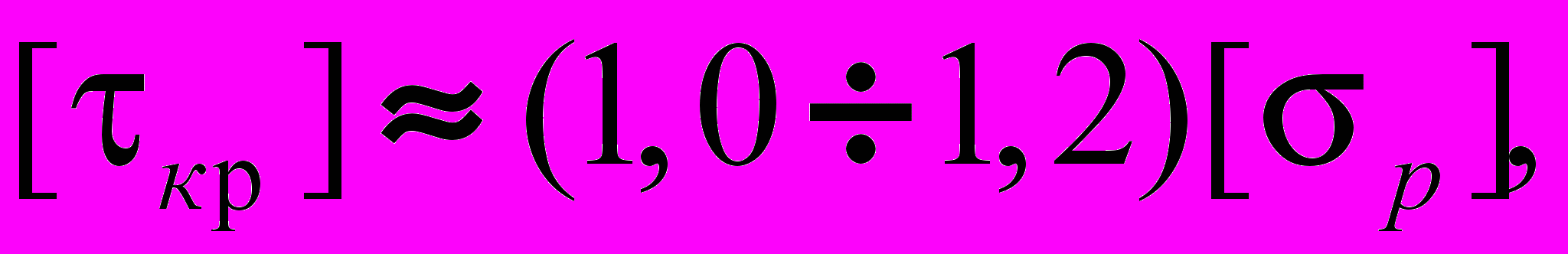
где :
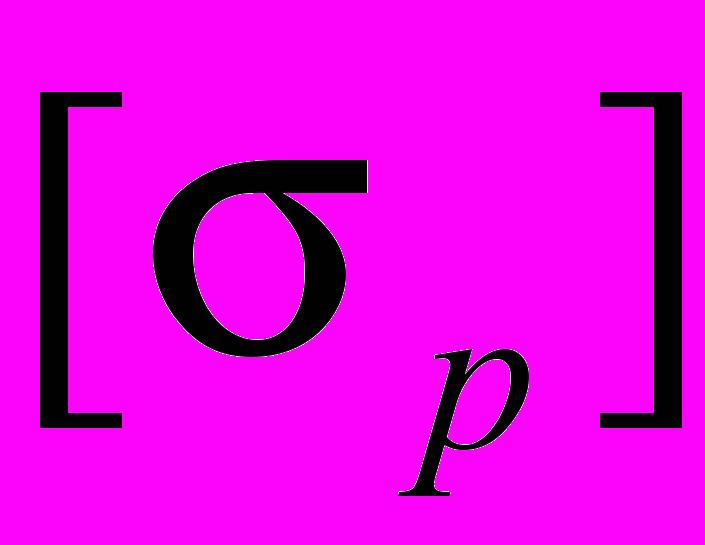 - допускаемое напряжение на растяжение.
- допускаемое напряжение на растяжение.В выражении (1) значение максимального крутящего момента определяют методом сечений после схематизации реальной конструкции. Опасные сечения определяются при расчете и построении эпюры крутящего момента. Значение полярного момента сопротивления сечения сплошного круглого вала рассчитывают по выражению :
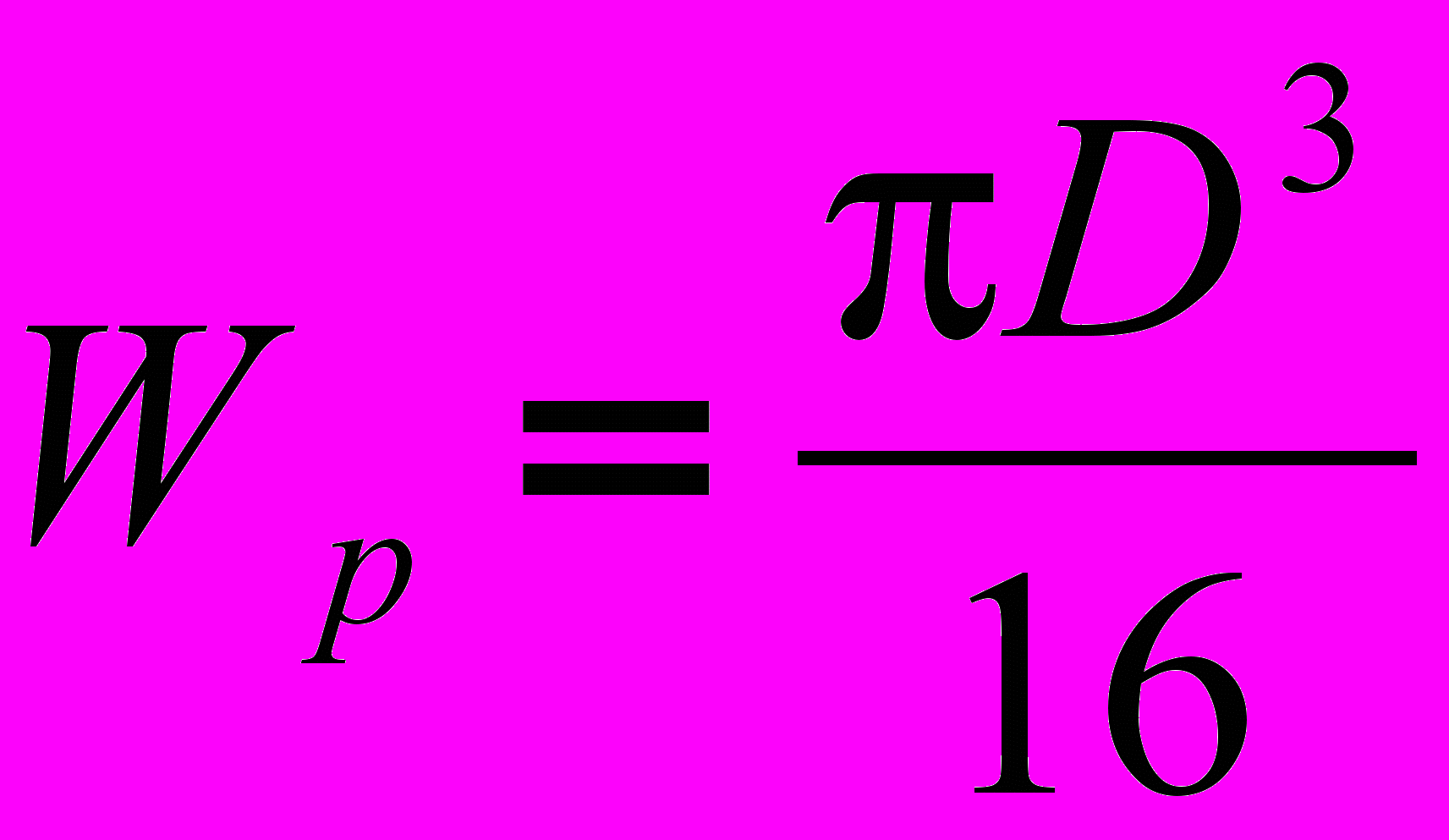 .
.
Экспериментально установлено, что касательные напряжения, возникающие под действием внешних нагрузок в поперечных сечениях, при кручении круглого вала распределяются неравномерно. В центре вала значение касательного напряжения равно нулю. Двигаясь от центра по радиусу окружности к поверхности вала, значения касательных напряжений начинают возрастать и достигают свойх максимальных значений на его переферии (рис.1).
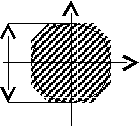 y
yrmax
r=0
D z
Рис.1
Характер распределения касательных напряжений позволяет сделать вывод, что в центральной части круглого вала их значения пренебрежимо малы и целесообразно применять валы кольцевого сечения (трубчатые или полые) с удаленной сердцевиной.
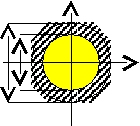 y
yrmax
rp
D d r=0 z
Для расчета максимальных касательных, значений допускаемых касательных напряжений справедливы выше приведенные формулы. Следует лишь вместо значений
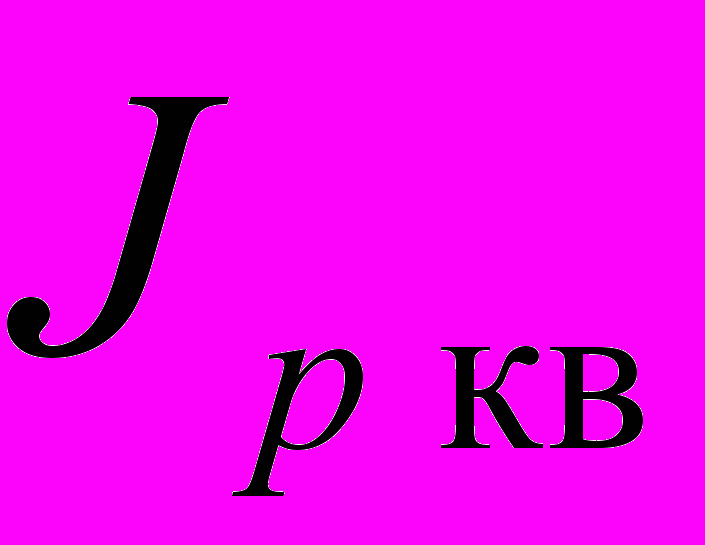 и
и 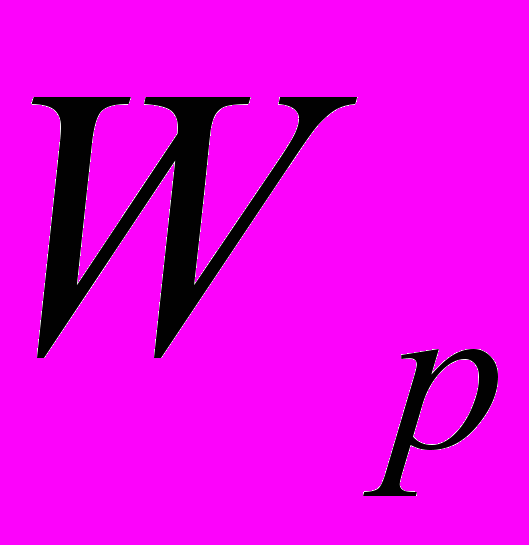 для сплошного вала подставить их значения для кольцевого сечения:
для сплошного вала подставить их значения для кольцевого сечения: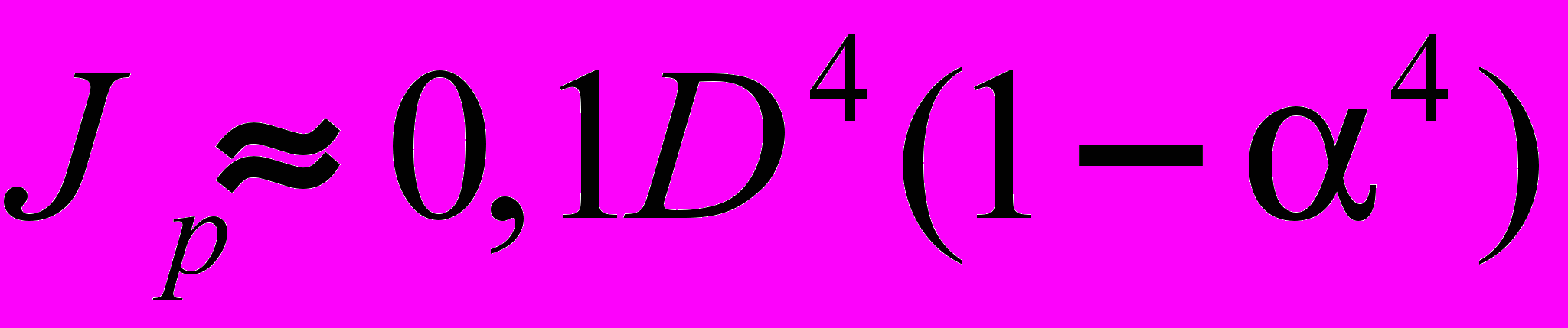 ;
;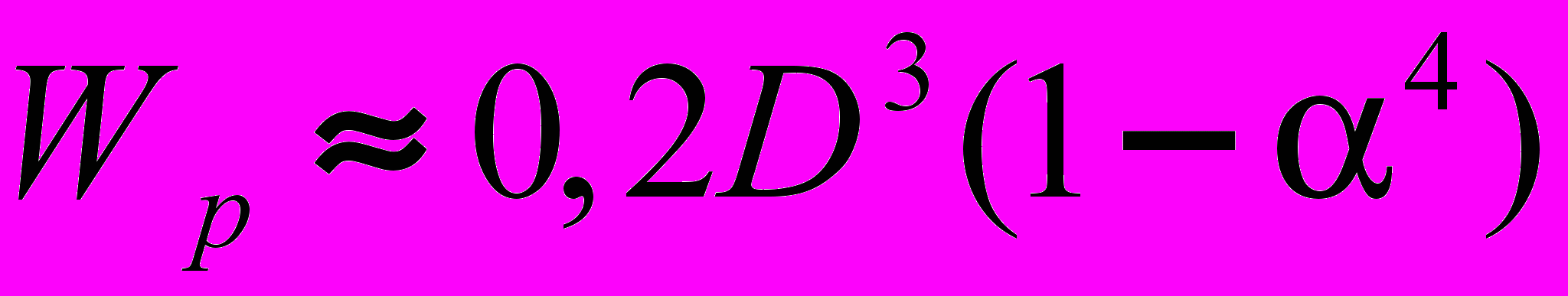 ,
,где :
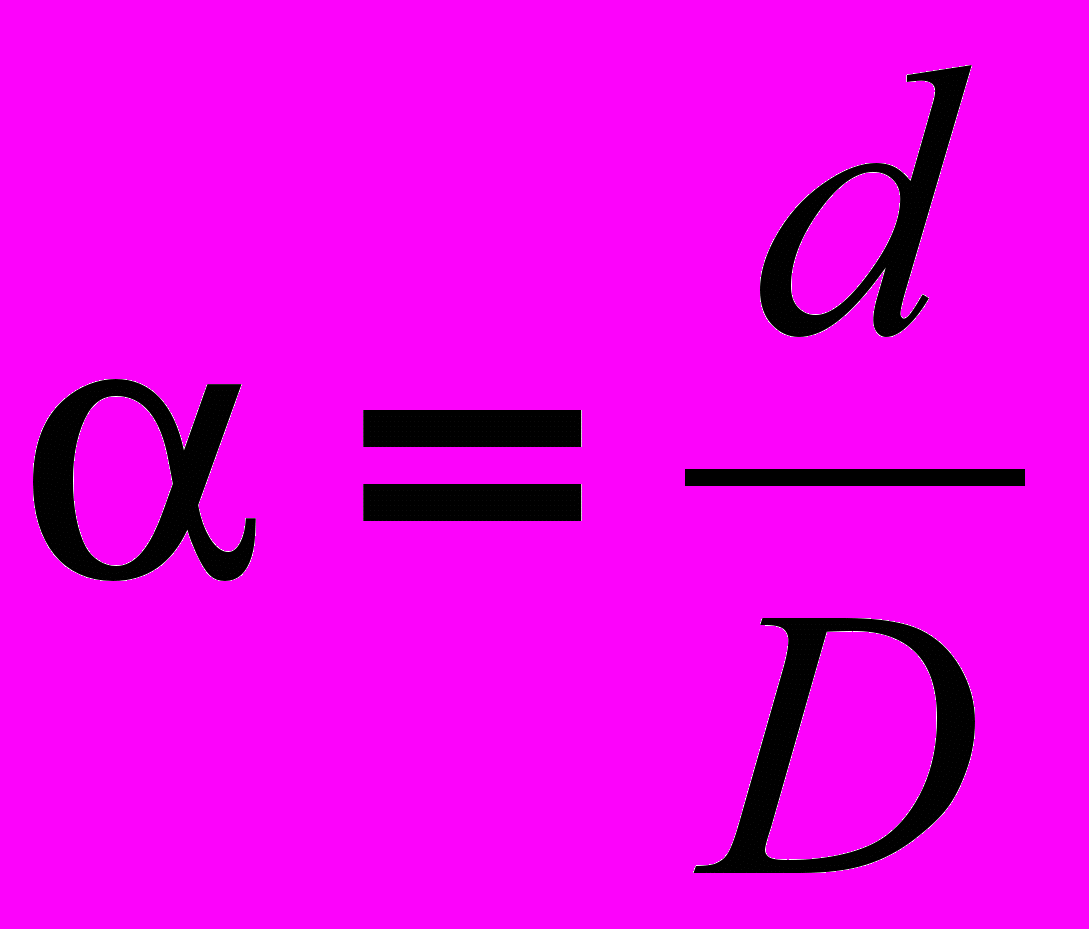 ,
,d - внутренний диаметр сечения, в см;
D - наружный диаметр сечения, в см.
Разность
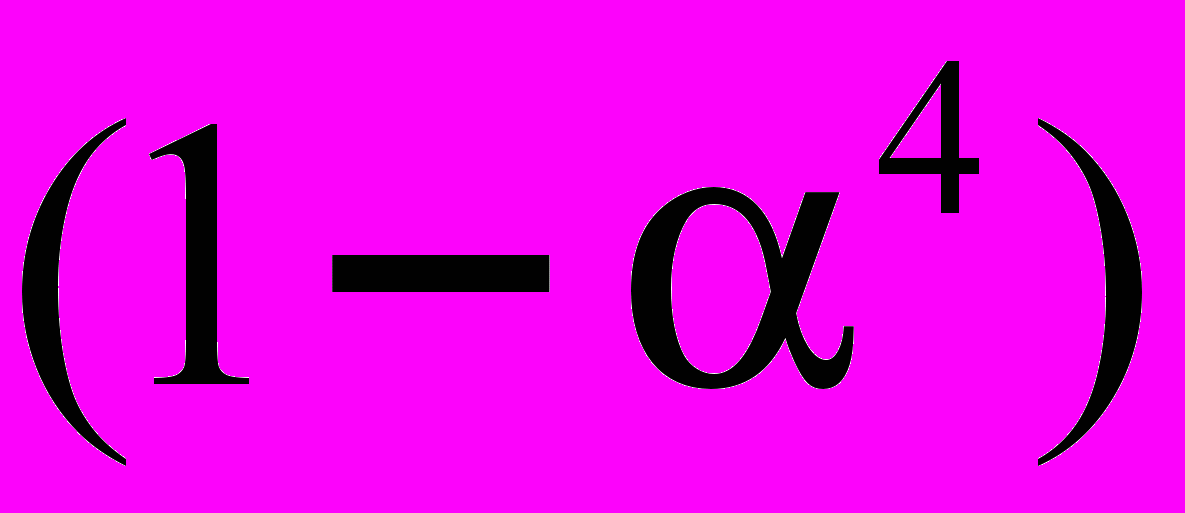 характеризует поправку к значениям
характеризует поправку к значениям 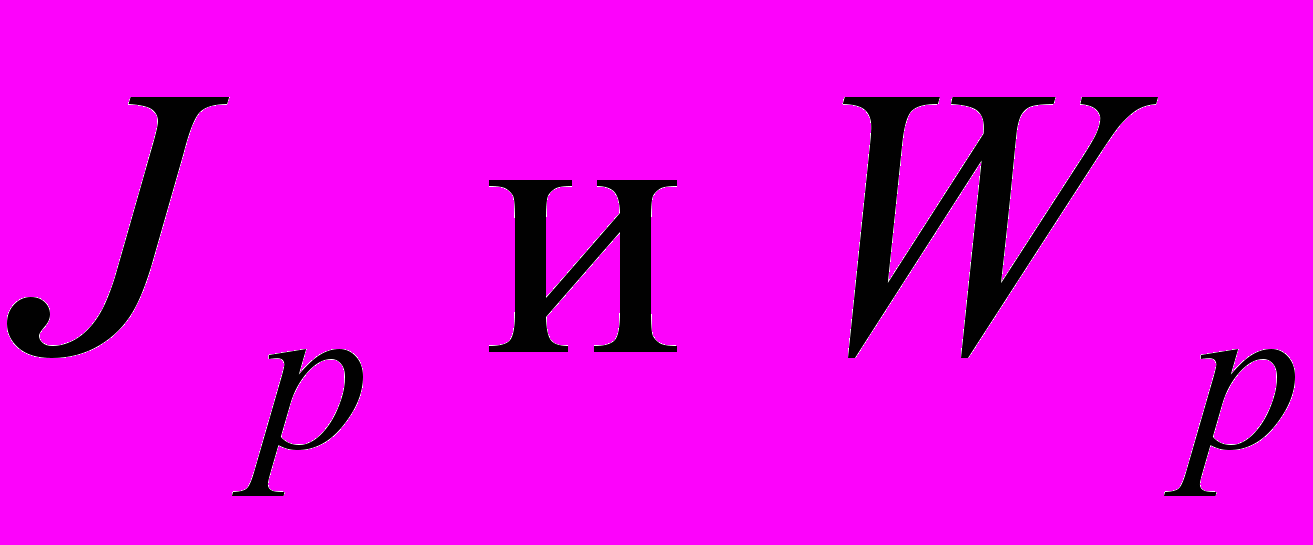 для сплошного круглого сечения, вызванную наличием отверстия.
для сплошного круглого сечения, вызванную наличием отверстия.Кроме проверки валов при кручении на прочность в ответственных узлах машин и аппаратов необходимо проверить работу вала на жесткость при кручении. Жесткость вала при кручении оценивается по наибольшему относительному углу закручивания на единицу его длины. При этом значение угла закручивания не должно превышать допускаемой величины:
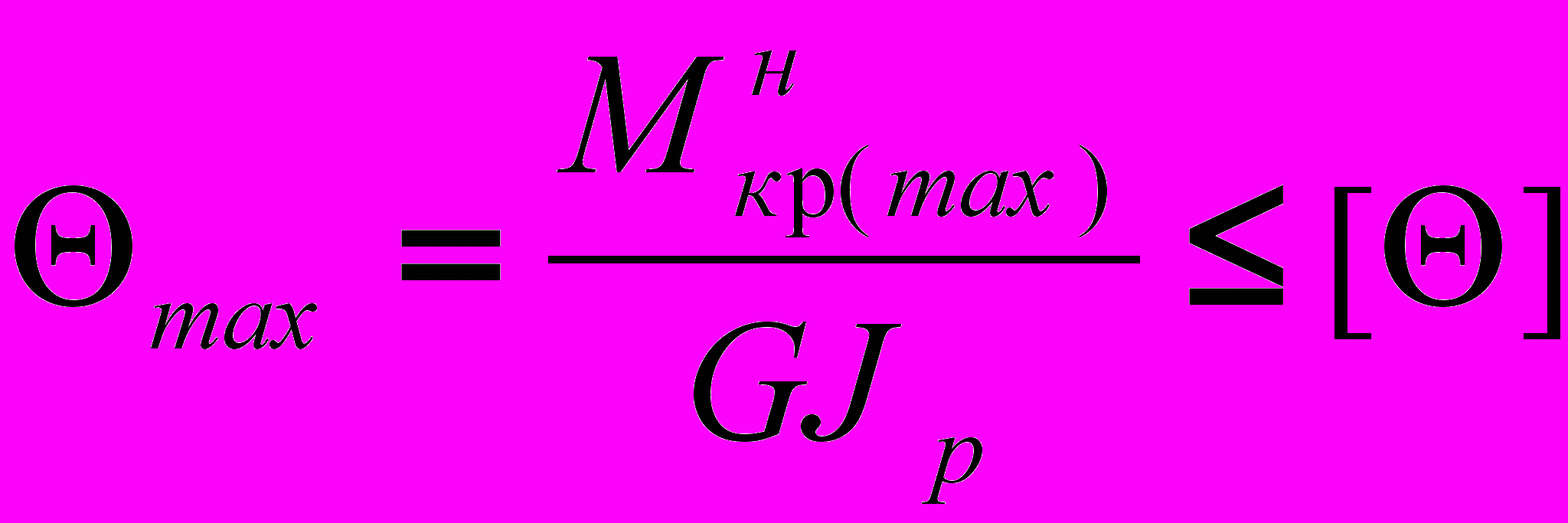 (2)
(2)или
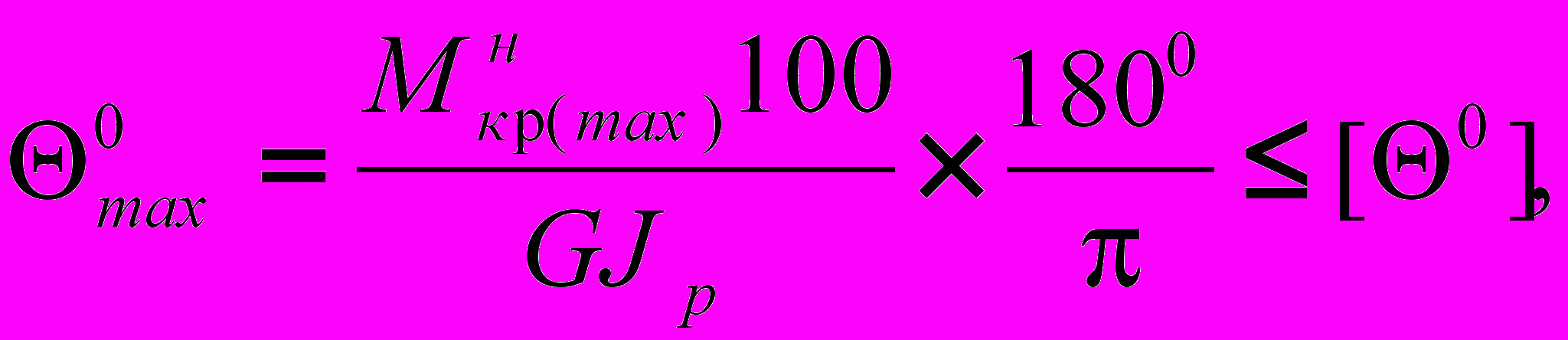 (3)
(3)где :
 - допускаемый относительный угол закручивания, рад/cм;
- допускаемый относительный угол закручивания, рад/cм;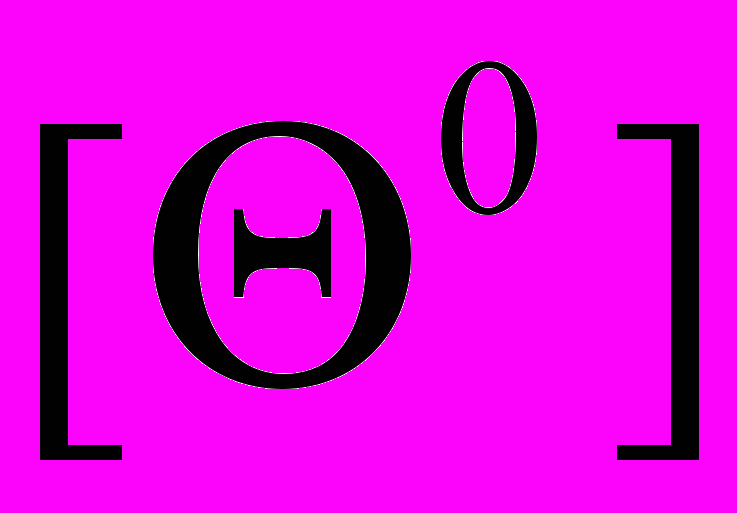 - допускаемый относительный угол закручивания, град/м.
- допускаемый относительный угол закручивания, град/м.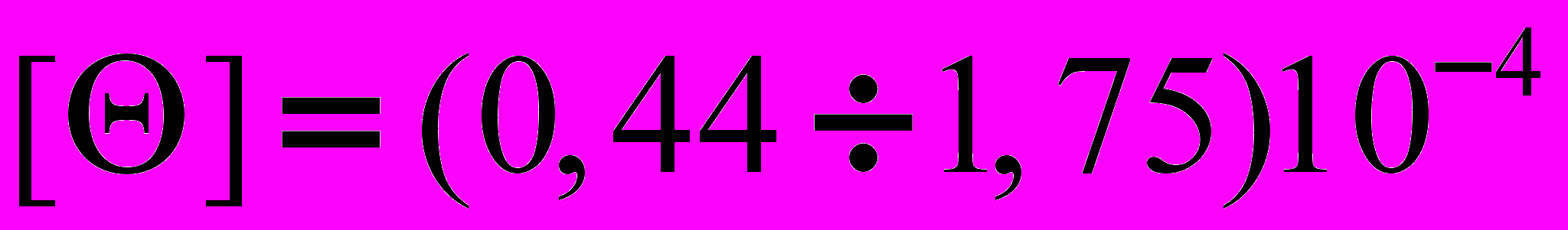 рад/см;
рад/см;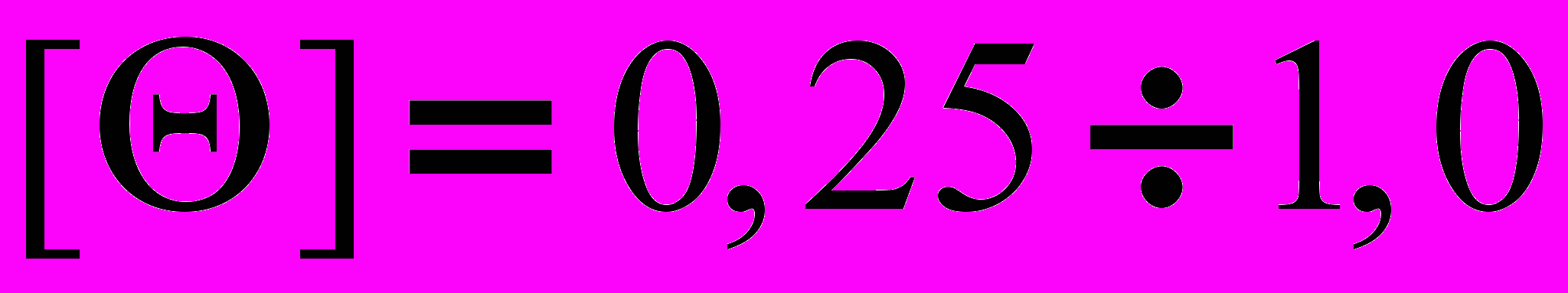 град/м.
град/м.G - модуль сдвига; для стали 8,0´
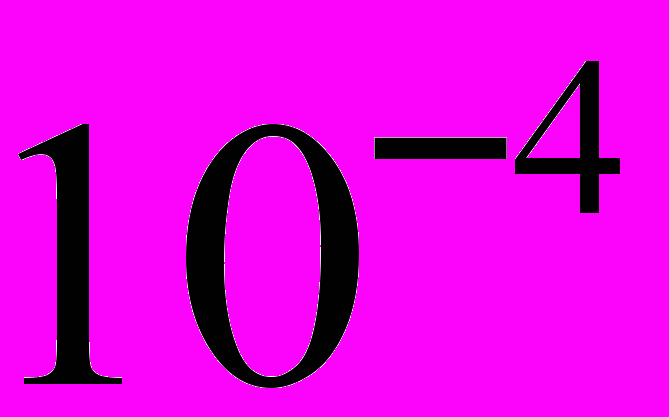 Мн/
Мн/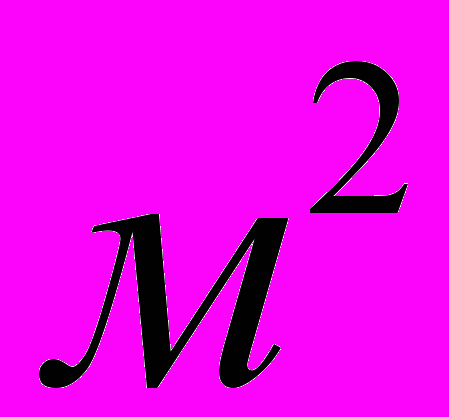 .
.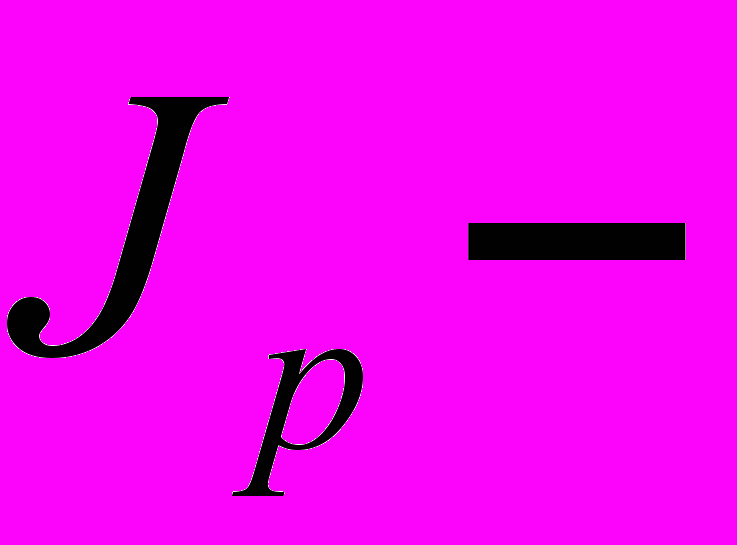 полярный момент инерции;
полярный момент инерции; 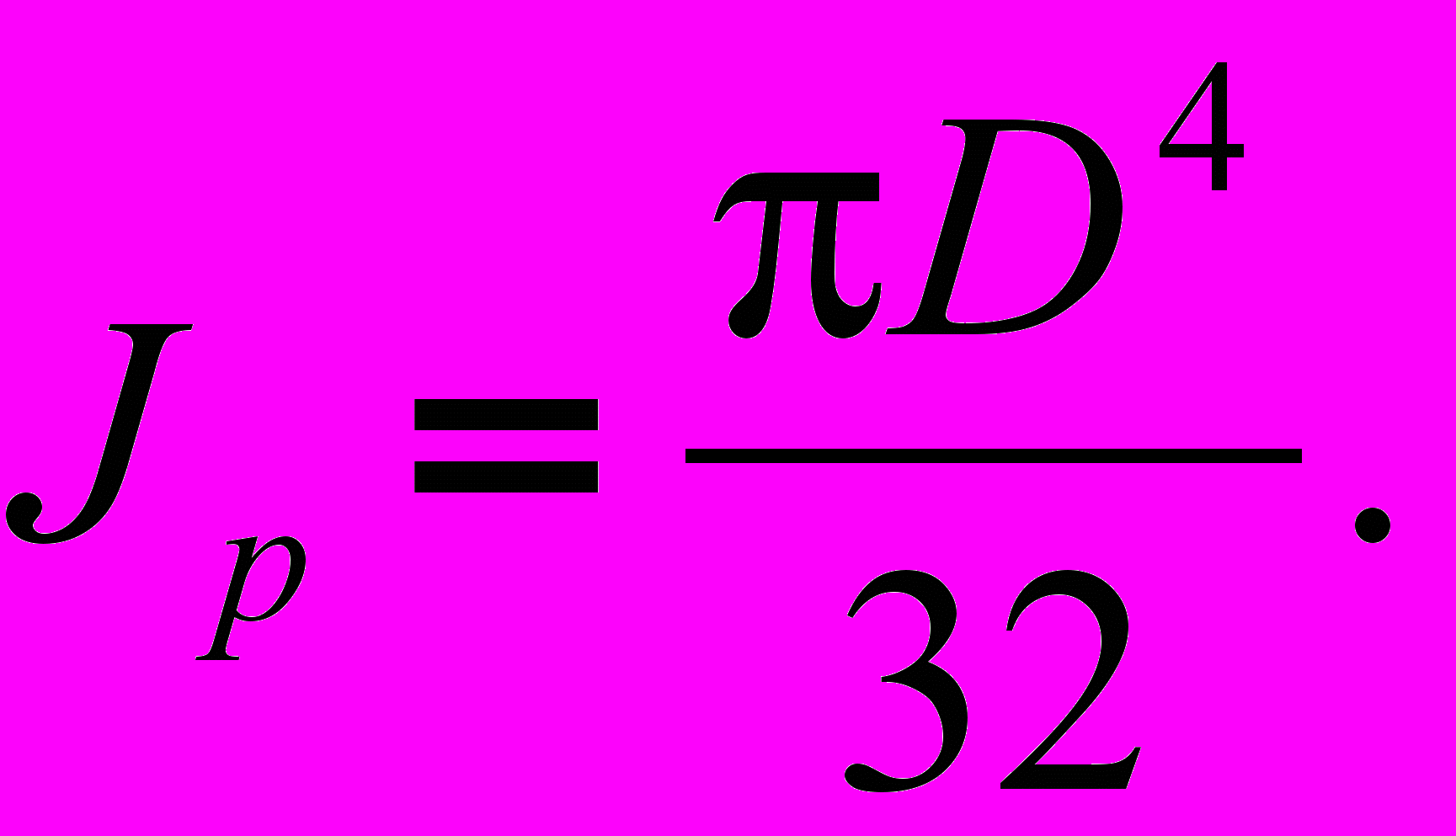
Л и т е р а т у р а
1.Федосьев В.И. Сопротивление материалов. - М.: Наука, 1986.
2.Кинасошвили Р.С. Сопротивление материалов. - М.: Наука, 1975.
3.Иосилевич Г.Б., Строгонов Г.Б., Маслов Г.С. Прикладная механика. - М.: Высшая школа, 1989.
4.Ковалев Н.А. Прикладная механика. - М.: Высшая школа, !982.
5.Сборник задач по сопротивлению материалов. Под редакцией Вольмира А.С. - М.: Наука, 1984.
СОДЕРЖАНИЕ
В В Е Д Е Н И Е 4
Краткая история развития науки о сопротивлении материалов 4
Задачи и методы сопротивления материалов 6
Реальный объект и расчетная схема 7
Элементы конструкций и машин 8
Внешние силы 8
Понятие о деформациях, внутренних усилиях и упругости 9
Основные допущения, принимаемые в сопротивлении материалов 10
Моменты инерции плоских фигур. Общие положения и понятия 11
Моменты инерции и моменты сопротивления простейших фигур 13
Прямоугольное сечение 13
Круглое сечение 15
Устойчивость стержней (продольный изгиб) 18
Вывод основного дифференциального уравнения продольного изгиба 19
Интегрирование дифференциального уравнения продольного изгиба 20
Пример: Определение критической нагрузки (силы) для балки, показанной на рис.1 23
Сложное сопротивление 25
Основные понятия 25
Совместное действие изгиба и растяжения (сжатия) 25
Совместное действие изгиба и кручения 26
Косой изгиб 30
Расчет на прочность и жесткость при кручении сплошных и полых валов 33
Л и т е р а т у р а 37
