Geum.ru

Ярославский Государственный Технический Университет Кафедра менеджмента курсовая

Вид материалаКурсовая

Содержание


2.5. Определение оптимального потока материалов в сети
2.5.2. Определение потока минимальной стоимости (задача Басакера-Гоуэна)
Алгоритм Басакера-Гоуэна
2.6. Построение графика перевозки нерудных материалов Почасовые графики перевозки нерудных материалов приведены в Приложении.ЗАК
Подобный материал:
1   2   3   4   5

2.5. Определение оптимального потока материалов в сети

2.5.1. Расчет пропускных способностей ребер транспортной сети




Cij*=Cij, если 0


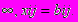
Схема 4. Пропускные способности сети.

Пропускные способности отдельных участков сети определяются исходя из рассчитанной выше суммарной производительности потоков автосамосвалов, идущих по этим участкам сети.

Пропускная способность вычисляется по формуле:

bij=mik*Паik*kа,

где bij - пропускная способность по ребру между двумя пунктами, м3/час

к - число маршрутов;

ka - коэффициент перевыполнения (1,15-1,20);

Пропускная способность ребер, через которые одновременно проходят несколько маршрутов, представляет собой сумму пропускных способностей каждого из этих маршрутов.

Ниже представлен список маршрутов и соответствующих им пропускных способностей.

Е1Е10 - 55м3/час

Е1Е11 - 48м3/час

Е2Е10 - 95,4м3/час

Е3Е11 - 180м3/час

Транспортная сеть с нанесенными на ней пропускными способностями и стоимостями перевозок представлена на схеме 3..

2.5.2. Определение потока минимальной стоимости (задача Басакера-Гоуэна)


Постановка задачи: задана сеть с одним истоком Е0 и одним стоком Е12, и промежуточными вершинами Е1-Е11. Каждому ребру поставлены в соответствие две величины: пропускная способность bij и дуговая стоимость Cij (стоимость доставки единицы потока по ребру Еij). Необходимо найти поток из источника в сток заданной величины В, обладающий минимальной стоимостью.

Целевая функция:

F = ® min

Ограничения:

0£ x £ bij, i ¹ j, i, j = 0,n

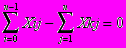— закон сохранения потока

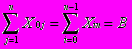— поток, идущий из источника, равен потоку, входящему в сток, и равен максимальному потоку в сети.

При наличии ограничений на пропускные способности ребер можно последовательно находить различные пути минимальной стоимости и пропускать по ним поток до тех пор, пока суммарная величина потока по всем путям не будет равна заданной величине потока.

Алгоритм Басакера-Гоуэна

Положим все дуговые потоки равными нулю (Xij=0).

Находим в сети путь с минимальной стоимостью и определяем модифицированные дуговые стоимости Cij, зависящие от величины найденного потока следующим образом:

С*ij = Cij, если 0£ xij£ bij, и С*ij = ¥, если xij = bij.

Ход решения задачи:
  1. Выбираем путь с минимальной стоимостью. Это маршрут Е1Е11. Максимальная величина потока, равная минимальной пропускной способности, равна v1=48 м3/час. С1=5,28.Q1=min(bij)=min(103;48)=48. Х111=49. Закрываем дугу Е9-Е11.
  2. Выбираем путь с минимальной стоимостью. Это маршрут Е3 - Е11. Максимальная величина потока, равная минимальной пропускной способности, равна v2=180 м3/час. С1=5,28.Q1=min(bij)=min(180;180)=180. Х311=180. Закрываем дуги Е3-Е4,Е4-Е11.
  3. Выбираем путь с минимальной стоимостью. Это маршрут Е1 - Е10. Максимальная величина потока, равная минимальной пропускной способности, равна v3=55 м3/час. С1=6,08.Q1=min(bij)=min(55;55)=180. Х110=55. Закрываем дуги Е1-Е9,Е9-Е10.
  4. Выбираем путь с минимальной стоимостью. Это маршрут Е2 - Е10. Максимальная величина потока, равная минимальной пропускной способности, равна v4=95 м3/час. С1=6,11. Q1=min(bij)=min(95;95)=95. Х210=55. Закрываем дуги Е2-Е5,Е5-Е6, Е6-Е10.

Все ребра закрыты, задача решена.

Пропускные способности каждого ребра:

Маршрут
bij, м3/час

Е1-Е9
103

Е9-Е10
55

Е9-Е11
48

Е2-Е5
95

Е5-Е6
95

Е6-Е10
95

Е3-Е4
180

Е4-Е11
180


Суммарный поток равен сумме всех потоков, проходящих через сечение (см. чертеж). V=Svi= 378 м3/час.

Время выполнения данного объема перевозок:

t = V/m*Па;

где - t - время;

V - объем перевозок;

m*Па - производительность системы;

Е1Е10 - 942,5час

Е1Е11 - 124час

Е2Е10 - 276,72час

Е3Е11 - 558,03час

2.6. Построение графика перевозки нерудных материалов


Почасовые графики перевозки нерудных материалов приведены в Приложении.

ЗАКЛЮЧЕНИЕ


Изучение спроса на транспортные услуги свидетельствует, что важнейшим требованием клиентов к работе автомобильного транспорта является своевременность отправки и доставки грузов. Вызвано это стремлением многих грузовладельцев к сокращению запасов в производстве и в потреблении, поскольку их затраты на содержание запасов по ряду отраслей составляют более 20% на единицу выпускаемой продукции.

Это доказывает важность решения задачи оптимального управления движением потоков грузов. Оптимальность в данном случае выражается в том, что доставка грузов происходит точно в срок и при минимальных затратах на перевозку. Решить эту сложную комплексную задачу позволяют некоторые методы исследования операций, а также теоретические разработки логистической теории.

В настоящее время, при переходе к рыночной экономике, задача минимизации расходов на транспортировку и распространение продукции становится одной из основных задач каждого предприятия, так как успешное ее решение позволяет существенно снизить издержки на изготовление продукции и тем самым повысить прибыльность предприятия.



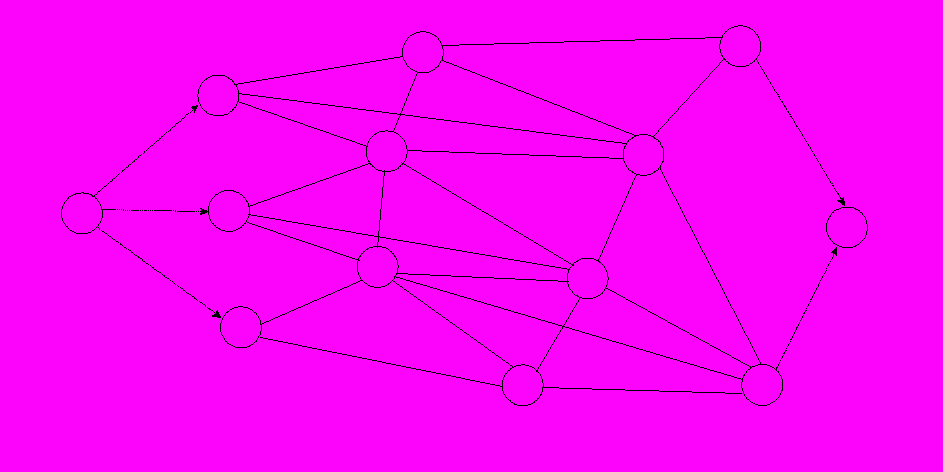
Схема 3. " Определение потока минимальной стоимости".


СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ


1. Яблонский А.А. Моделирование систем управления строительными процессами: Монография. - Москва, 1994. - Федеральная целевая программа книгоиздания России, - 296 с

2. Яблонский А.А., Тризина В.А. Управление потоком автосамосвалов, транспортирующих грунт экскаватора на два участка автодороги: Изв. Вузов.-1991. - №12. - с. 94-98.

3. Кофман А. Методы и модели исследования операций. - М.,Мир, 1996. - 523с.

ПРИЛОЖЕНИЯ