Методические указания для выполнения контрольных работ для студентов специальности 1 53 01 01 05 "Автоматизация технологических процессов и производств (легкая промышленность)"

Вид материала

Методические указания

Содержание 1. введение. цели и задачи курса «основы 2. базовая учебная программа курса «основы 4. работа №1. решение задач линейного 6. методические указания к выполнению 1 Введение. цели и задачи курса «основы исследования операций», его место в образовательном процессе студентов технологических в 2 базовая учебная программа курса «основы исследования операций» Глава 4. элементы теории игр Глава 5. целочисленное линейное программирование Глава 6. нелинейное программирование. Глава 7. дискретное программирование Примерная тематика лабораторных занятий Примерная тематика практических занятий Примерная тематика контрольных работ 3. общие требования к выполнению и оформлению контрольных работ Решение задач линейного программирования графическим методом Решение задач линейного программирования табличным симплекс-методом 6 методические указания к выполнению контрольных работ № 1, 2 Ограничение ЗЛП имеет предпочтительный вид

Подобный материал:

• Методические указания для студентов специальности 210200 «Автоматизация технологических, 273.81kb.
• Методические указания по выполнению дипломных проектов для студентов специальности, 294.98kb.
• Методические указания для выполнения контрольных работ по курсу «Автоматика и автоматизация, 447.92kb.
• Методические указания и индивидуальные задания для студентов идо, обучающихся по направлению, 142.63kb.
• Т. В. Фёдоров методические указания по технологической практике студентов IV курса, 107.4kb.
• Методические указания по выполнению выпускной квалификационной работы для студентов, 470.69kb.
• Методические указания по выполнению лабораторных работ по курсу «Системы автоматизированного, 369.98kb.
• Методические указания по выполнению курсовой работы для студентов специальности 220301, 189.64kb.
• Методические указания к курсовым (семестровым) и выпускным квалификационным работам, 1017.9kb.
• Кафедра микропроцессорных средств автоматизации Вопросы к государственному экзамену, 85.14kb.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

"ВИТЕБСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ"


ОСНОВЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ


МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для выполнения контрольных работ

для студентов специальности 1 – 53 01 01 - 05 "Автоматизация

технологических процессов и производств (легкая промышленность)"


ВИТЕБСК

2008

УДК 621.865.8


Основы исследования операций. Методические указания для выполнения контрольных работ для студентов заочного факультета специальности 1-53 01 01-05 “Автоматизация технологических процессов и производств (легкая промышленность)”.

Витебск: Министерство образования РБ, УО «ВГТУ», 2008 г.


Составитель: доц. каф. АТПП, к.ф.-м.н. Вислобоков Н.Ю.


В методических указаниях предлагается информация для выполнения двух контрольных работ по дисциплине «Основы исследования операций», основные требования к выполнению контрольных работ, варианты заданий, методические указания к выполнению работ и примеры расчетов.

Методические указания составлены в соответствии с учебной программой курса «Основы исследования операций», изучаемого студентами заочной формы обучения специальности 1-53 01 01-05 “Автоматизация технологических процессов и производств (легкая промышленность)”.


Одобрено кафедрой «Автоматизация технологических процессов и производств» УО «ВГТУ» ___.11.2008 г. протокол № _.


Рецензент: ст. преп. Куксевич В.Ф.

Редактор: доц. Смелков Д.В.


Рекомендовано к опубликованию редакционно-издательским советом УО «ВГТУ» ___.11.2008 г., протокол № _


Ответственный за выпуск Букин Ю.А.


Учреждение образования «Витебский государственный технологический университет»

_______________________________________________________________

Подписано в печать___________. Формат_________. Уч.-изд. лист._____. Печать ризографическая. Тираж_____экз. Заказ №_____. Цена_______руб.


Отпечатано на ризографе Учреждения образования «Витебский государственный технологический университет».

Лицензия № 02330/0133005 от 1 апреля 2004 г.

210035, Республика Беларусь, г. Витебск, Московский пр-т, 72.


СОДЕРЖАНИЕ


1. ВВЕДЕНИЕ. ЦЕЛИ И ЗАДАЧИ КУРСА «ОСНОВЫ

ИССЛЕДОВАНИЯ ОПЕРАЦИЙ», ЕГО МЕСТО В

ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ СТУДЕНТОВ

ТЕХНОЛОГИЧЕСКИХ ВУЗОВ…..………………………………………..4


2. БАЗОВАЯ УЧЕБНАЯ ПРОГРАММА КУРСА «ОСНОВЫ

ИССЛЕДОВАНИЯ ОПЕРАЦИЙ»……………...………………………..…4


3. ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ

КОНТРОЛЬНЫХ РАБОТ…...………………………………………………8


4. РАБОТА №1. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО

ПРОГРАММИРОВАНИЯ ГРАФИЧЕСКИМ МЕТОДОМ…………..……8


5. РАБОТА №2. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО

ПРОГРАММИРОВАНИЯ ТАБЛИЧНЫМ

СИМПЛЕКС-МЕТОДОМ…..……………………………………………….9


6. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

КОНТРОЛЬНЫХ РАБОТ № 1 И № 2…………………………………......10


7. ЛИТЕРАТУРА………………………………………………………………18


1 ВВЕДЕНИЕ. ЦЕЛИ И ЗАДАЧИ КУРСА «ОСНОВЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ», ЕГО МЕСТО В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ СТУДЕНТОВ ТЕХНОЛОГИЧЕСКИХ ВУЗОВ.


Целью преподавания основ исследования операций является формирование у студентов знаний и умений по разработке математических моделей, постановке и решению оптимизационных задач.

В результате изучения дисциплины студент должен знать:

- общие принципы и методологию исследования операций;

- математические модели и классификацию типовых задач исследования операций;

- методы аналитического и численного решения задач исследования операций;

Студент должен уметь:

- формулировать оптимизационные задачи, критерии оптимизации, строить математические модели задач исследования операций;

- осуществлять математическую постановку и разрабатывать компьютерные модели оптимизационных задач обоснования принятия решений;

- использовать стандартные алгоритмы и программы решения задач исследования операций.


2 БАЗОВАЯ УЧЕБНАЯ ПРОГРАММА КУРСА «ОСНОВЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ»


Введение


Цель, задачи и структура курса. Связь со смежными дисциплинами. Мировоззренческие вопросы принятия решений, постановки и решения оптимизационных задач, применения вычислительной техники в процессах принятия решений. Профессиональная ориентация.


ГЛАВА 1. Базовые понятия и определения ИССЛЕДОВАНИЯ ОПЕРАЦИЙ


Понятие и определение математической модели задачи исследования операций. Типовые задачи математического программирования и их модели. Факторы и факторные пространства, характеристики. Ограничения на факторы и характеристики, допустимые области решений. Критерий оптимизации – целевая функция. Векторно-матричные формы задач математического программирования. Классификация допустимых областей и задач математического программирования.


ГЛАВА 2. Линейное программирование


Примеры задач линейного программирования (ЗЛП). Формы записи задач линейного программирования, их эквивалентность и способы преобразования. Каноническая форма ЗЛП. Понятия плана, допустимого и оптимального плана. Геометрическая интерпретация ЗЛП и частных случаев решения. Графический метод решения ЗЛП. Понятие симплекса и симплексного метода решения ЗЛП. Симплексная таблица, анализ плана и свойств ЗЛП по симплексной таблице. Симплексные преобразования. Алгоритм симплекс-метода: общая идея, построение начального опорного плана, вычислительные процедуры. Реализация симплекс-метода на ЭВМ. Использование стандартных программ для решения ЗЛП.


ГЛАВА 3. Двойственность в линейном Программирова-нии


Понятие двойственности. Построение двойственных задач и их свойства. Математические модели двойственных ЗЛП, основные теоремы двойственности. Решение двойственной задачи и интерпретация результата.


ГЛАВА 4. ЭЛЕМЕНТЫ ТЕОРИИ ИГР


Понятия и определения теории игр. Стратегия, ход, выигрыш. Матричные игры с нулевой суммой. Платежная матрица. Оптимальные стратегии. Понятие седловой точки и решение матричной игры в чистых стратегиях.

Решение матричных игр в смешанных стратегиях. Сведение матричной игры в смешанных стратегиях к паре двойственных задач линейного программирования. Алгоритм решения матричной игры в смешанных стратегиях.

Статистические игры. Критерии Байеса, Лапласа, Вальда, Сэвиджа, Гурвица для решения статистических игр.


ГЛАВА 5. ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ


Примеры и особенности целочисленных задач линейного программирования (ЦЗЛП). Метод отсечения решения ЦЗЛП. Понятие правильного отсечения. Общий алгоритм метода Гомори.


ГЛАВА 6. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ.

Математические модели задач нелинейного программирования и их классификация. Условия оптимальности задач нелинейного программирования: а) нелинейная задача на безусловный экстремум; б) задача нелинейного программирования с ограничениями равенствами; в) задача нелинейного программирования с ограничениями неравенствами.

Численные методы нелинейной безусловной оптимизации. Градиентные методы поиска безусловного экстремума. Метод наискорейшего спуска, градиентный метод с памятью. Квазиградиентные методы. Метод Ньютона безусловной оптимизации. Области применимости численных методов безусловной оптимизации.

Применение вычислительных схем методов безусловной оптимизации для решения условных задач. Применение функции Лагранжа для решения условной задачи с ограничениями-равенствами. Вычислительная схема градиентного метода для решения условной задачи с ограничениями неравенствами.


ГЛАВА 7. ДИСКРЕТНОЕ ПРОГРАММИРОВАНИЕ


Понятие дискретной величины и дискретной модели. Математические модели задач дискретного программирования.

Графы, математические модели графов. Анализ графов по моделям матрицы инцидентности и матрицы смежности. Примеры задач дискретного программирования.


Заключение


Сравнительный анализ математических моделей и методов исследования операций. Применение методов исследования операций в решении задач оптимального управления. Применение программных библиотек в решении задач исследования операций.


ПРИМЕРНАЯ ТЕМАТИКА ЛАБОРАТОРНЫХ ЗАНЯТИЙ

1. Вводное занятие. Разработка программы симплекс метода и решение задач линейного программирования.
   
2. Разработка процедуры нахождения начального опорного плана ЗЛП.
   
3. Решение матричной игры в смешанных стратегиях.
   
4. Разработка программы градиентного метода и решение безусловной задачи нелинейного программирования.
   
5. Решение условной задачи нелинейного программирования с ограничениями-равенствами.
   

ПРИМЕРНАЯ ТЕМАТИКА ПРАКТИЧЕСКИХ ЗАНЯТИЙ

1. Графический метод решения задачи линейного программирования.
   
2. Анализ симплекс таблицы и решение задач линейного программирования симплекс-методом.
   
3. Нахождение начального опорного плана задачи линейного программирования.
   
4. Решение матричных игр в чистых стратегиях.
   
5. Решение статистических игр.
   
6. Решение безусловных задач нелинейного программирования аналитическим методом.
   
7. Решение задач нелинейного программирования методом множителей Лагранжа.
   
8. Решение задач нелинейного программирования градиентным методом.
   
9. Постановка и решение задач дискретного программирования.
   

ПРИМЕРНАЯ ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ

1.  Решение задач линейного программирования графическим методом при условии максимизации и минимизации целевой функции.
   
2.  Решение табличным симплекс-методом приведенных и не приведенных к каноническомой форме задач линейного программирования.
   

ЛИТЕРАТУРА

1. Вентцель, Е.С. Исследование операций: задачи, принципы, методология / Е.С. Вентцель -М.: Наука, Главная редакция физико-математической литературы, 1980. - 208 с.
   
2. Кузнецов, А.В. Математическое программирование / А.В. Кузнецов, Н.И. Холод -Мн.: Вышэйшая школа, 1994. - 221 с.
   
3. Кузнецов, А.В. Сборник задач по математическому программированию / А.В. Кузнецов и др. -Мн.: Вышэйшая школа, 1985. - 143 с.
   
4. Батищев, Д.И. Методы оптимального проектирования.: Учеб. Пособие для вузов / Д.И. Батищев -М.: Радио и связь, 1984. - 248 с.
   
5. Кузнецова, А. Б. Математика для экономистов на базе Mathcad / А.Б. Кузнецова, О. Мельникова, В. Новикова, А. Черняка С-Пб.: БХВ -Санкт-Петербург, 2003. - 485 с.
   
6. Таха, Х.А. Введение в исследование операций Вильямс / Х.А. Таха, - ISBN: 5-8459-0180-4, 2001. -127 с..
   
7. Хэмди, А. Введение в исследование операций / А. Хэмди – 6-е издание, 2006.
   
8. Кузнецов, О.П. Дискретная математика для инженера / О.П. Кузнецов, Г.М. Адельсон-Вельский - М.: Энергия, 1988.- 480с.
   
9. Прохоров, Г.В. Математический пакет Maple. / Г.В. Прохоров, и др. -М.: Петит.-1997.-200 с.
   
10. Норенков, И.П. Учебный курс “Оптимизация” / И.П. Норенков, -М.: Петит.-2007.-188 с.
    
11. Королев, В.А. Лекции по курсу "Иследование операций" / В.А. Королев, - М.: Энергия, 2003.- 180с.
    

3. ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ


При выполнении и оформлении контрольных работ следует:

• на титульном листе указать название университета, кафедры, номер учебной группы, фамилию, имя и отчество студента, название и номер работы;
  
• использовать стандартные листы бумаги формата А4;
  
• при расчетах пользоваться международной системой единиц СИ;
  
• в формулах и на графиках пояснять все используемые обозначения;
  
• перечень литературы должен быть оформлен в полном соответствии с требованиями библиографического описания документов.
  

4. РАБОТА № 1

РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ГРАФИЧЕСКИМ МЕТОДОМ


Графическим методом решить задачу линейного программирования (ЗЛП) на максимум вариантам 1–16 (номер задачи в таблице 1 соответствует номеру варианта) и на минимум вариантам 17–32 (номер задачи соответствует номеру варианта, уменьшенному на 16). Решить ЗЛП на максимум/минимум означает найти экстремальное значение целевой функции и план, при котором достигается экстремум.


Таблица 1 – Задания к контрольной работе № 1

Задача № 1	Задача № 2	Задача № 3	Задача № 4
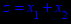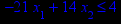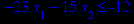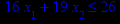x1 ≥ 0; x2 ≥ 0.	x1 ≥ 0; x2 ≥ 0.	x1 ≥ 0; x2 ≥ 0.	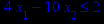x1 ≥ 0; x2 ≥ 0.
Задача № 5	Задача № 6	Задача № 7	Задача № 8
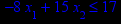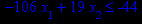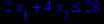x1 ≥ 0; x2 ≥ 0.	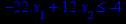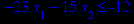x1 ≥ 0; x2 ≥ 0.	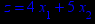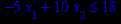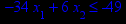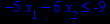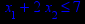x1 ≥ 0; x2 ≥ 0.	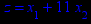x1 ≥ 0; x2 ≥ 0.
Задача № 9	Задача № 10	Задача № 11	Задача № 12
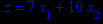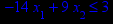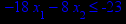x1 ≥ 0; x2 ≥ 0.	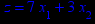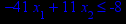x1 ≥ 0; x2 ≥ 0.	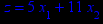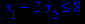x1 ≥ 0; x2 ≥ 0.	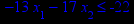x1 ≥ 0; x2 ≥ 0.
Задача № 13	Задача № 14	Задача № 15	Задача № 16
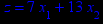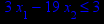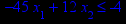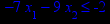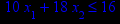x1 ≥ 0; x2 ≥ 0.	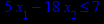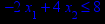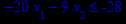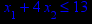x1 ≥ 0; x2 ≥ 0.	x1 ≥ 0; x2 ≥ 0.	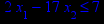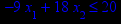x1 ≥ 0; x2 ≥ 0.