Методические указания для выполнения контрольных работ для студентов специальности 1 53 01 01 05 "Автоматизация технологических процессов и производств (легкая промышленность)"

Вид материала

Методические указания

Содержание Решение задач линейного программирования табличным симплекс-методом 6 методические указания к выполнению контрольных работ № 1, 2

Подобный материал:

• Методические указания для студентов специальности 210200 «Автоматизация технологических, 273.81kb.
• Методические указания по выполнению дипломных проектов для студентов специальности, 294.98kb.
• Методические указания для выполнения контрольных работ по курсу «Автоматика и автоматизация, 447.92kb.
• Методические указания и индивидуальные задания для студентов идо, обучающихся по направлению, 142.63kb.
• Т. В. Фёдоров методические указания по технологической практике студентов IV курса, 107.4kb.
• Методические указания по выполнению выпускной квалификационной работы для студентов, 470.69kb.
• Методические указания по выполнению лабораторных работ по курсу «Системы автоматизированного, 369.98kb.
• Методические указания по выполнению курсовой работы для студентов специальности 220301, 189.64kb.
• Методические указания к курсовым (семестровым) и выпускным квалификационным работам, 1017.9kb.
• Кафедра микропроцессорных средств автоматизации Вопросы к государственному экзамену, 85.14kb.

5 РАБОТА № 2

РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ТАБЛИЧНЫМ СИМПЛЕКС-МЕТОДОМ


Привести ЗЛП к канонической форме и решить её табличным симплекс-методом (варианты заданий соответствуют номерам задач в таблице 2).


Таблица 2 – Задания к контрольной работе № 2

Задача № 1	Задача № 2	Задача № 3
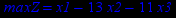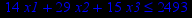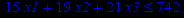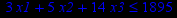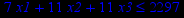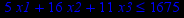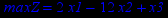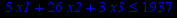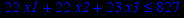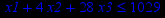Задача № 4	Задача № 5	Задача № 6
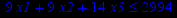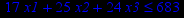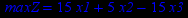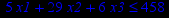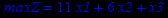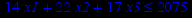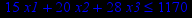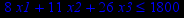Задача № 7	Задача № 8	Задача № 9
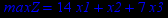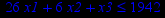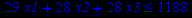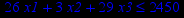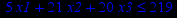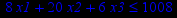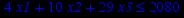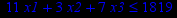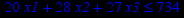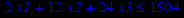Задача № 10	Задача № 11	Задача № 12
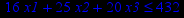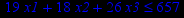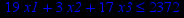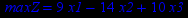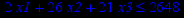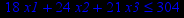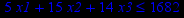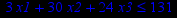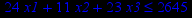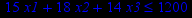Задача № 13	Задача № 14	Задача № 15
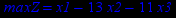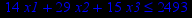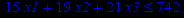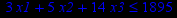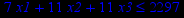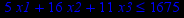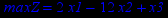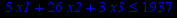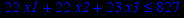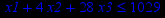Задача № 16	Задача № 17	Задача № 18
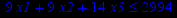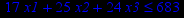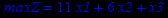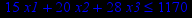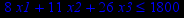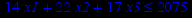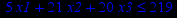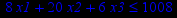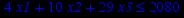Задача № 19	Задача № 20	Задача № 21
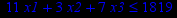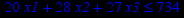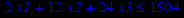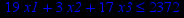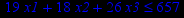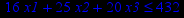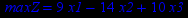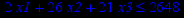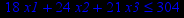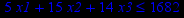Задача № 22	Задача № 23	Задача № 24
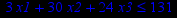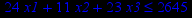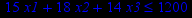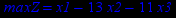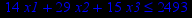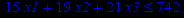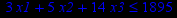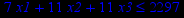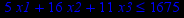Задача № 25	Задача № 26	Задача № 27
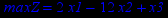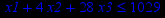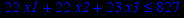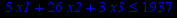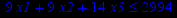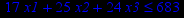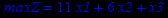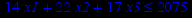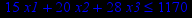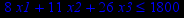Задача № 28	Задача № 29	Задача № 30

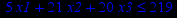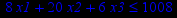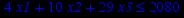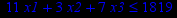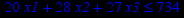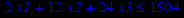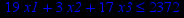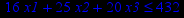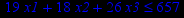6 МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ № 1, 2


В рекомендованной литературе достаточно полно представлены теоретические и практические материалы, необходимые для изучения данной дисциплины и понимания способов решения и выполнения заданий контрольных работ.

Здесь рассматривается ряд ключевых моментов, которые необходимо знать для выполнения данных контрольных работ, а также примеры использования изложенной учебно-методической информации для решения задач исследования операций.


Общая задача ЛП (ОЗЛП) – задача по отысканию целевой функции записанной в виде:


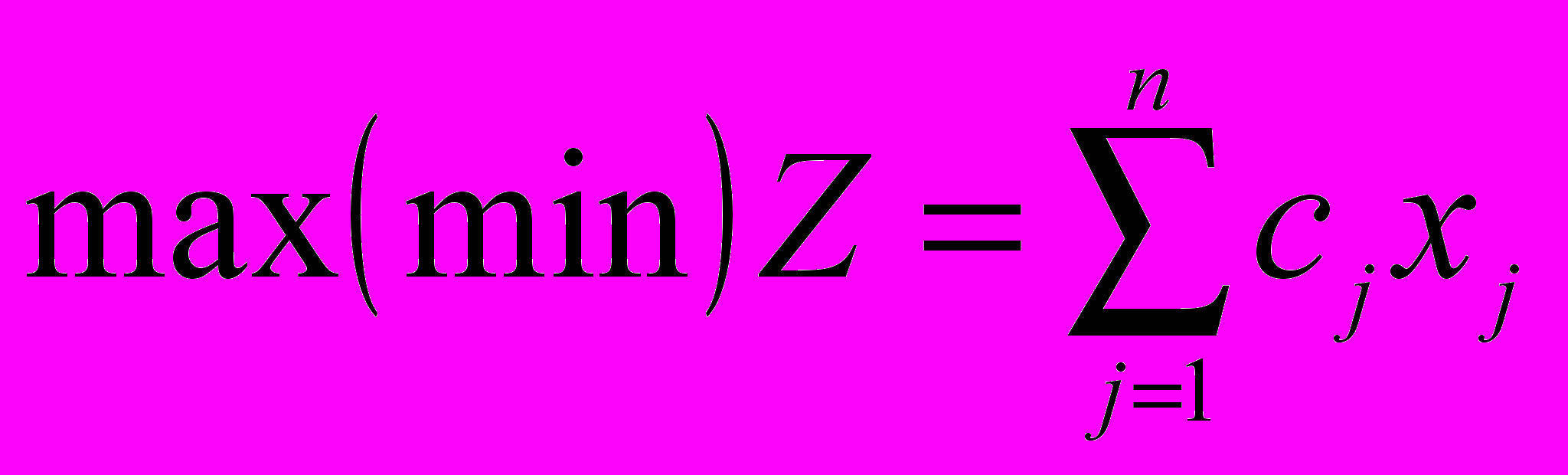(1)

при ограничениях:



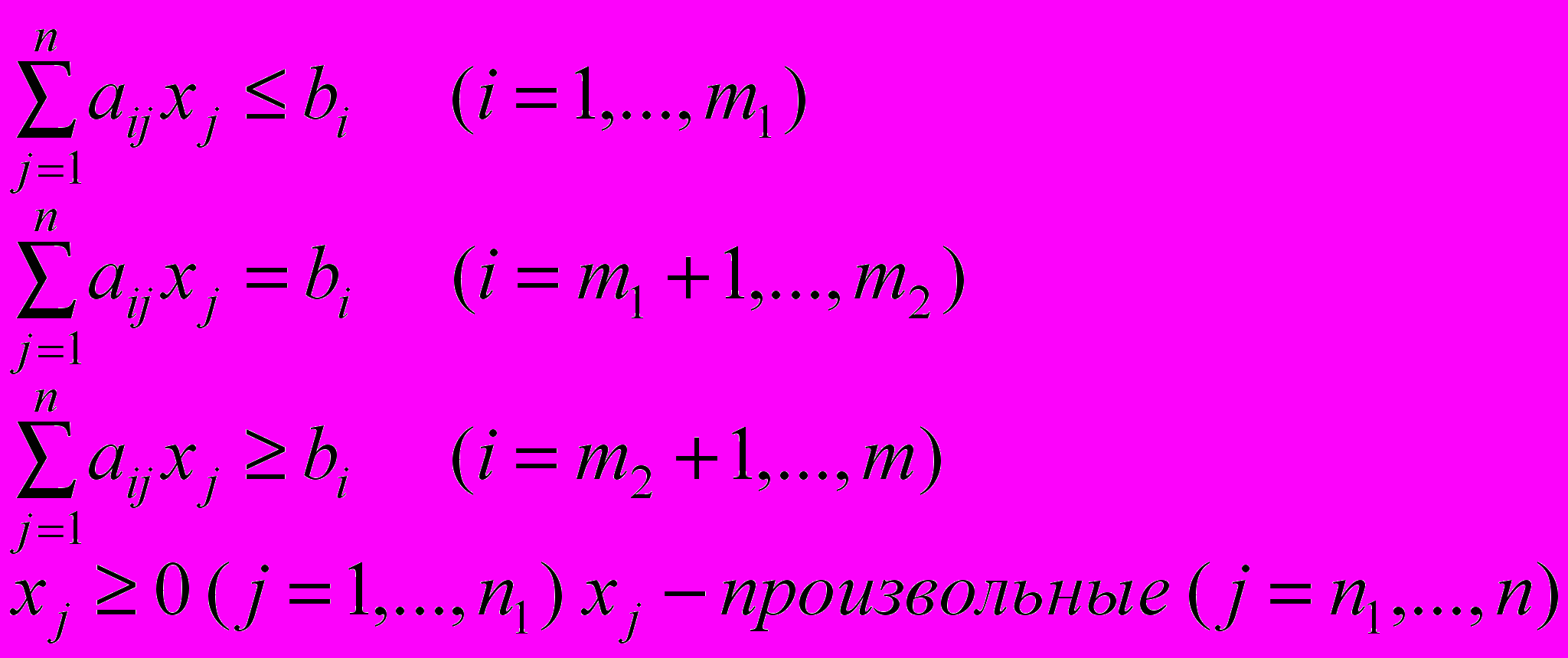
где c_j , a_ij , b_j – заданные действительные числа; а х = (x₁ ,; ...; x_n ) – план задачи.

Каноническая форма записи ЗЛП:

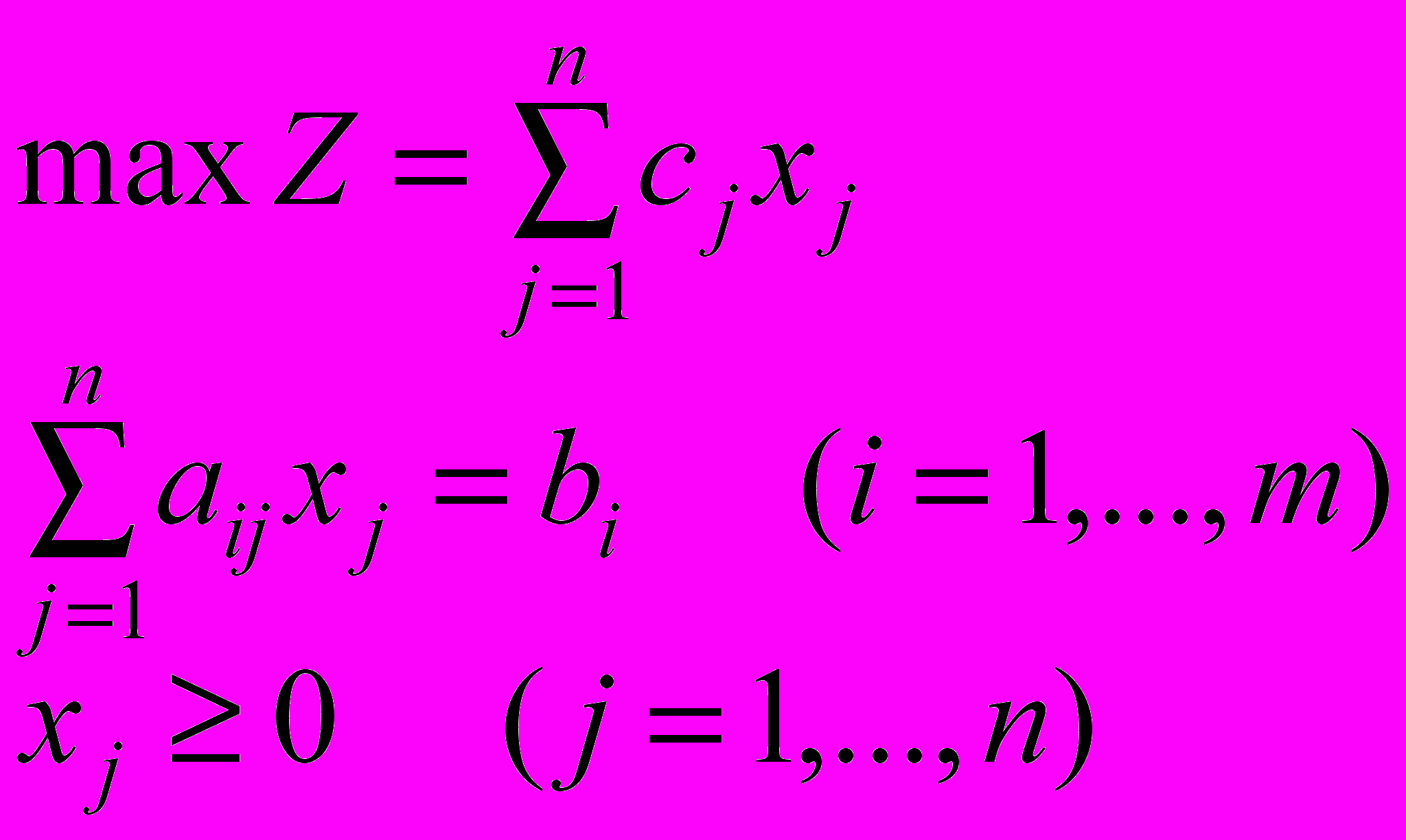(2)


Эквивалентность и способы преобразования

Наиболее же широко используемые методы решения ЗЛП применяются к задачам, записанным в канонической форме. Поэтому приходится переходить от любой формы ЗЛП к ее каноническому виду, причем нужно быть уверенным, что эти формы эквивалентны.

Пусть исходная ЗЛП имеет вид

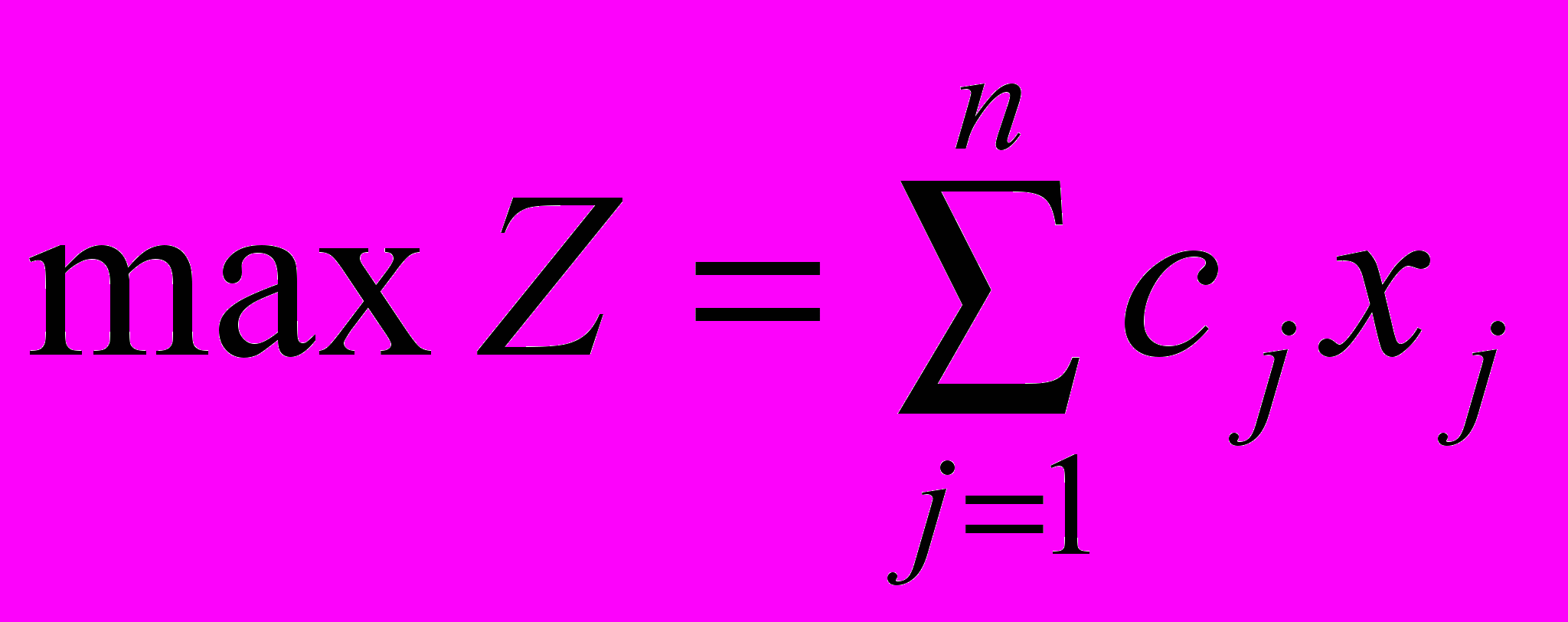(3)

(4)


Далее ЗЛП преобразуется к каноническому виду. Вводятся т дополнительных (балансовых) неотрицательных переменных x_n+i ≥ 0 (i = 1, …, m). Для того чтобы неравенства ограничений типа 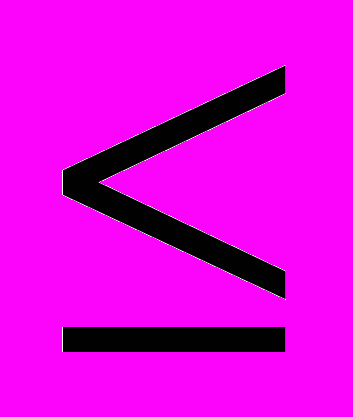преобразовать в равенства, к их левым частям прибавляются дополнительные переменные x_n+i (i = 1, …, m₁); для того чтобы неравенства ограничений типа 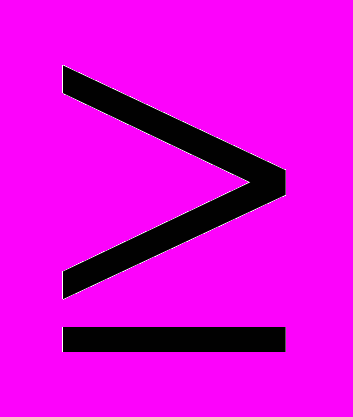преобразовать в равенства, из их левых частей вычитаются дополнительные переменные x_n+i (i = m₁+1, …, m). В целевую функцию балансовые переменные вводятся с коэффициентами, равными нулю.

Получается задача в канонической форме:

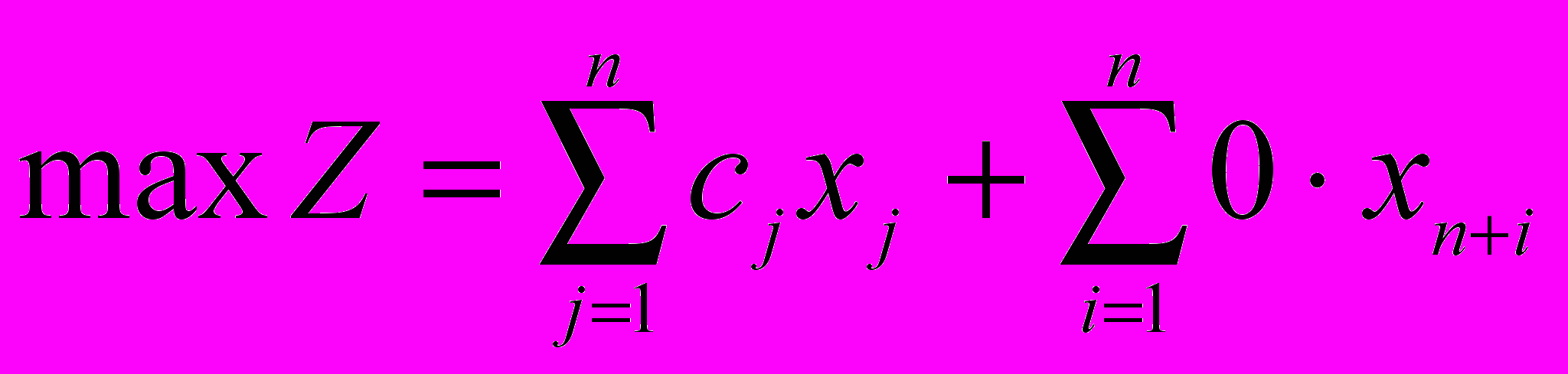(5)

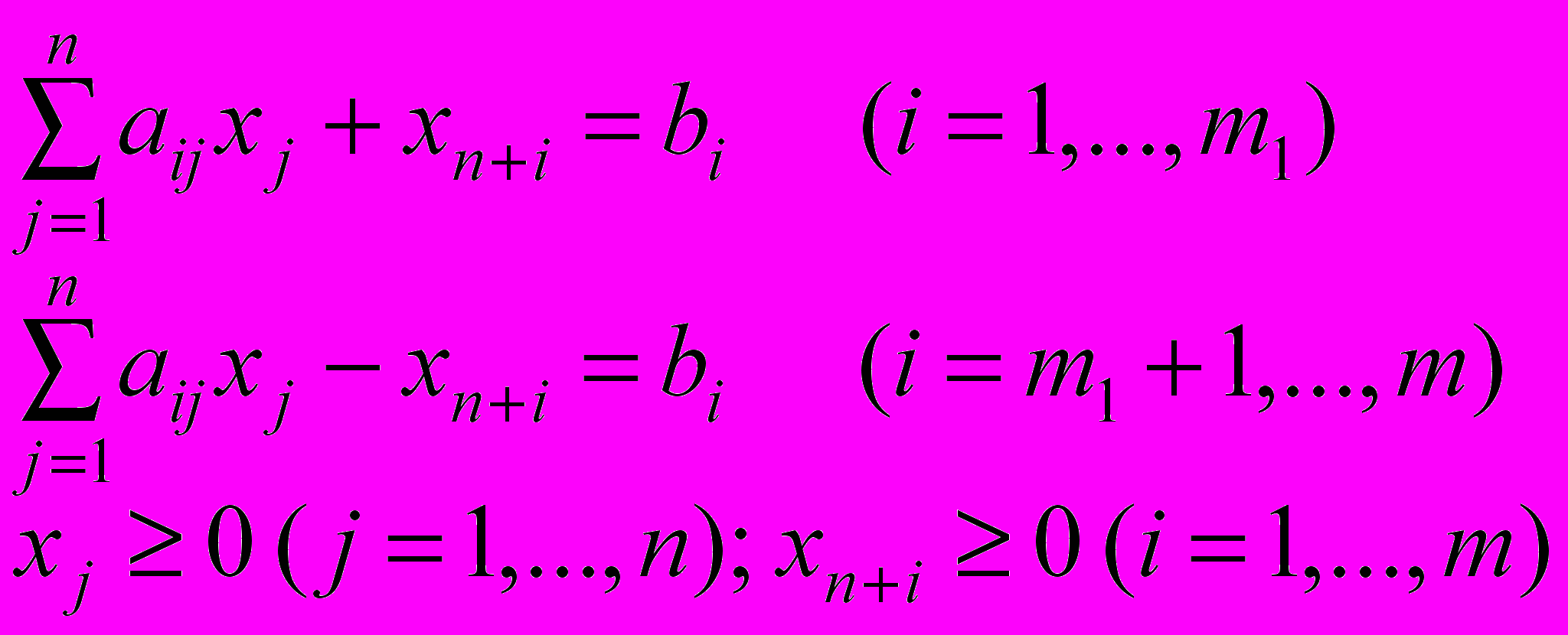(6)

Система уравнений (6) эквивалентна системе неравенств (4), т.е. оптимальному решению ( x₁⁰ ; …; x_n⁰ ) задачи (3)–(4) соответствует оптимальное решение ( x₁⁰ ; …; x_n⁰ ; x_n+1⁰ ; …; x_n+m⁰) задачи (5)–(6).


Геометрическая интерпретация и графическое решение ЗЛП

Геометрическая интерпретация задач исследования операций (оптимизационных задач) дает возможность наглядно представить их структуру, выявить особенности. ЗЛП с двумя переменными всегда можно решить графически.

Пусть дана задача 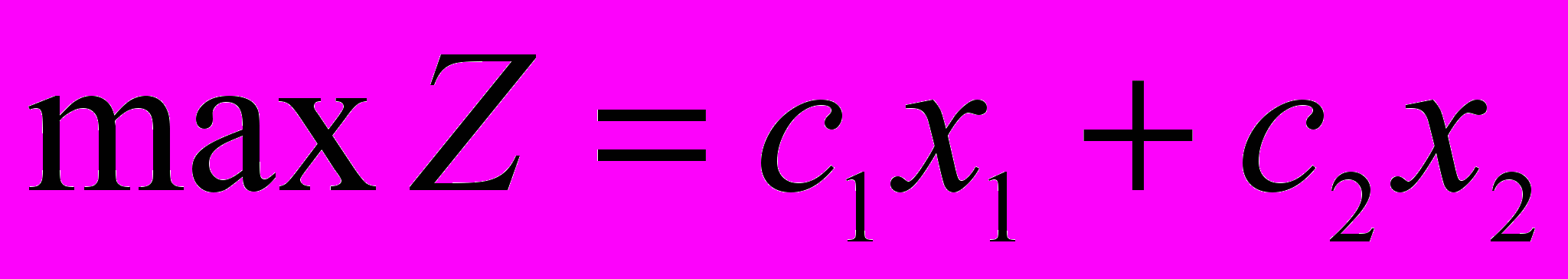(7)

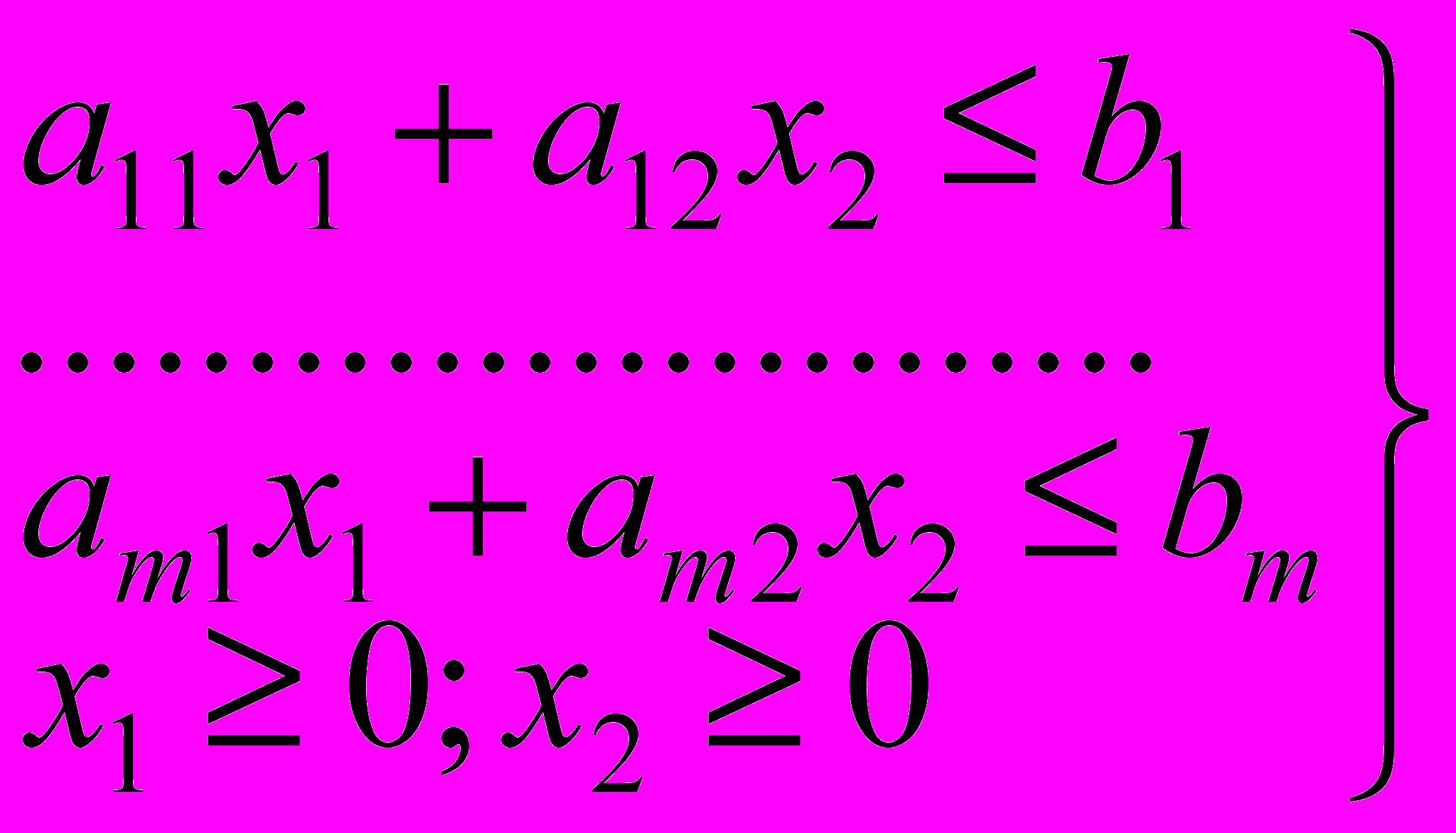(8)

Геометрическая интерпретация ограничений. Каждое из ограничений (3.36) задает на плоскости x₁Ox₂ некоторую полуплоскость, пересечение которых является областью допустимых решений задачи.

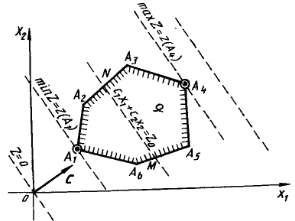Рисунок 1 – Геометрическая интерпретация целевой функции ЗЛП

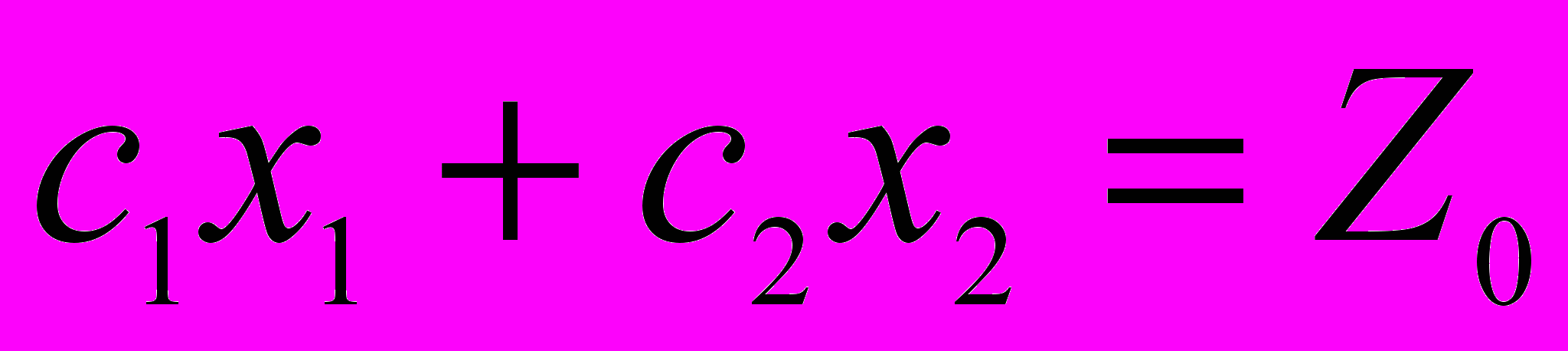Переход к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП – непустое множество, например многоугольник A₁ A₂ A₃ A₄ A₅ A₆ на рисунке 1. Выберается произвольное значение целевой функции Z = Z₀ . Получается . Это уравнение прямой линии. В точках прямой N M целевая функция сохраняет одно и то же постоянное значение Z₀ . С учётом того, что в равенстве (7) Z–параметр, получается уравнение семейства параллельных прямых, называемых линиями уровня целевой функции.

Теперь необходимо определить направление возрастания (убывания) целевой функции. Пусть .

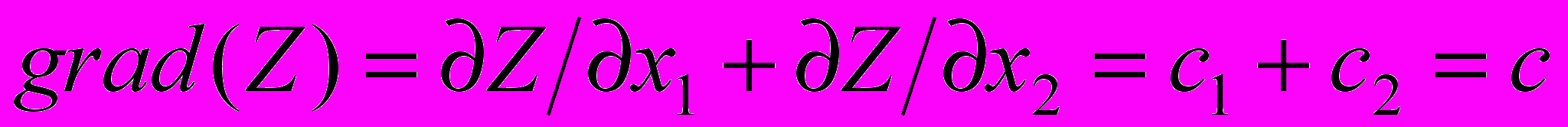Тогда с₁ и с₂ – скорости возрастания Z вдоль осей ОX₁ и OX₂ , а вектор градиента показывает направление наискорейшего возрастания целевой функции (вектор антиградиента – наискорейшего убывания целевой функции).

Порядок графического решения ЗЛП:

1. строится область допустимых решений Ω.
   
2. строится вектор градиента/антиградиента.
   
3. проводится произвольная линия уровня.
   
4. при решении задачи на максимум линия уровня перемещается в направлении вектора градиента так, чтобы она касалась границы области допустимых решений (A₄ на рис. 1). В случае решения задачи на минимум линию уровня перемещается в антиградиентном направлении (А₁ на рис. 1).
   
5. Определяется оптимальный план х* и экстремальное значение целевой функции Z = z(х*).
   

Пример решения ЗЛП графическим методом

Графическим методом решить задачу линейного программирования на максимум и минимум