Пособие разработано ст преп. Зубко Т. Я., доцентом Седовой С. М., доцентом Сулавко Т. С одобрено методической комиссией кафедры «Высшая математика»
| Вид материала | Документы |
СодержаниеИсходное уравнение запишем в матричной форме Исходное уравнение запишем в матричной форме Индивидуальные задания |
- Учебно-методическое пособие Москва 2003 Учебно-методическое пособие разработано коллективом, 523.99kb.
- Программа итогового междисциплинарного экзамена по специальности 080105 «финансы, 564.94kb.
- Философия эпохи Возрождения, 674.41kb.
- Философия западноевропейского Средневековья, 680.27kb.
- Настоящее пособие ставит своей целью дать студентам краткое руководство к философскому, 764.48kb.
- Учебно методическое пособие «Глоссарий по биосоциологии» разработано кандидатом философских, 360.43kb.
- Учебное пособие историко-культурные туристские ресурсы Северного Кавказа для студентов, 671.13kb.
- Учебное пособие историко-культурные туристские ресурсы Северного Кавказа для студентов, 496.84kb.
- Методические указния к семинарским занятиям по философии для студентов факультета «Сестринское, 1401.94kb.
- Общая патология, 627.07kb.
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Матрицы и определители
Индивидуальные задания
-
Пособие разработано ст. преп. Зубко Т. Я., доцентом Седовой С. М., доцентом Сулавко Т. С..
Одобрено методической комиссией кафедры «Высшая математика»
© 2007, каф. «Высшая математика» ПГТУ
Пермь 2007
Задание к работе
1. Вычислить определитель 3-го порядка, используя метод Саррюса (или метод треугольников) и метод разложения по минорам какого-нибудь ряда.
2. Вычислить определитель высшего порядка.
3. Привести матрицу к ступенчатому виду и вычислить ранг матрицы.
4. Выполнить действия с матрицами.
5. Вычислить значение многочлена от матрицы
 .
.6. Найти неизвестную матрицу
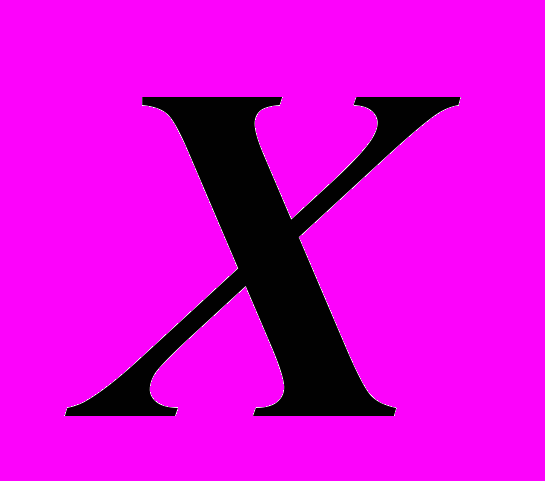 из уравнения.
из уравнения.Образец решения варианта.
1.Вычислить определитель 3-го порядка 1) по правилу Саррюса (правило треугольников). Это правило заключается в равенстве
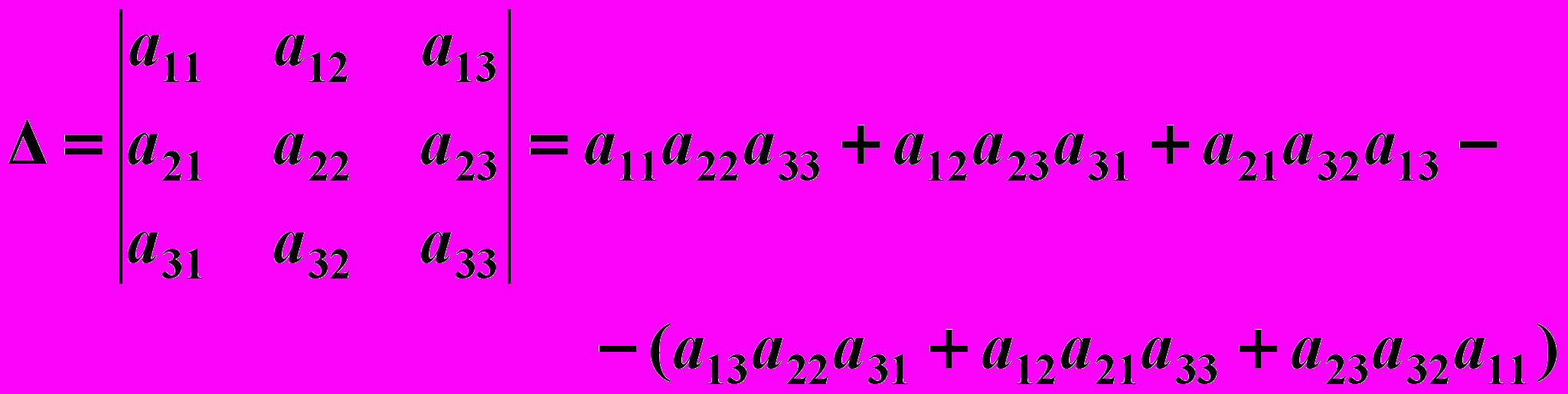 .
.Таким образом,

2) Второе правило вычисления
 называется разложением
называется разложением  по элементам некоторой строки (или столбца). Например, разложение по элементам первой строки имеет вид
по элементам некоторой строки (или столбца). Например, разложение по элементам первой строки имеет вид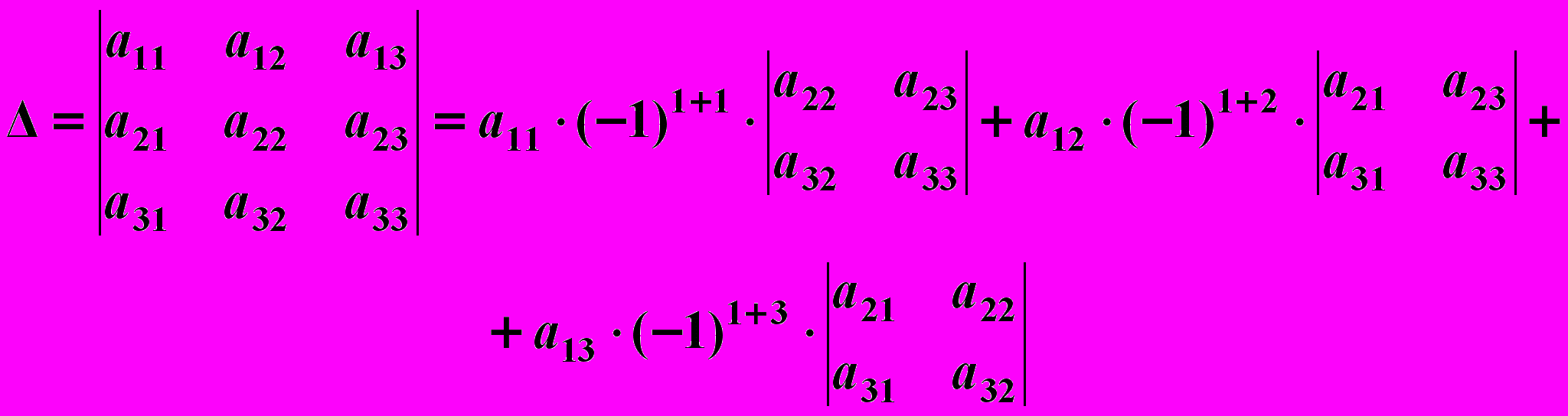 .
.Определитель

разложим по элементам третьего столбца, т.е.
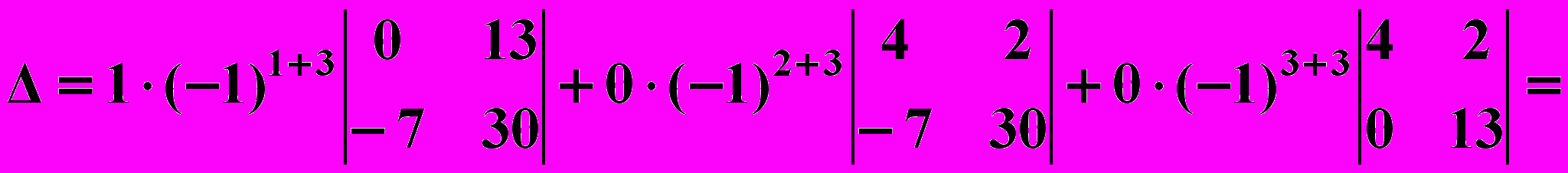
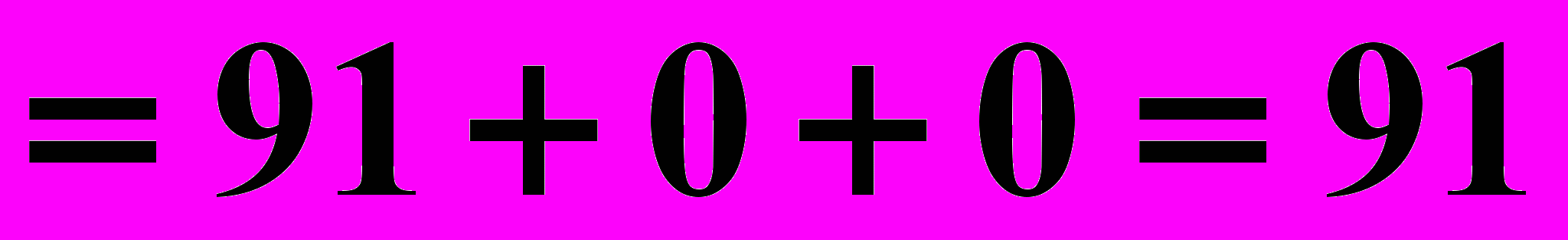 .
.Как видно из приведенных примеров, вычисление определителей значительно упрощается, если какой-нибудь ряд определителя имеет только один элемент, отличный от нуля. Это можно всегда достигнуть, используя свойства определителей. В определителе

умножим первую строку на 2 и прибавим ко второй, прибавим первую строку к третьей, получим
 .
.2. Вычислить определитель высшего порядка
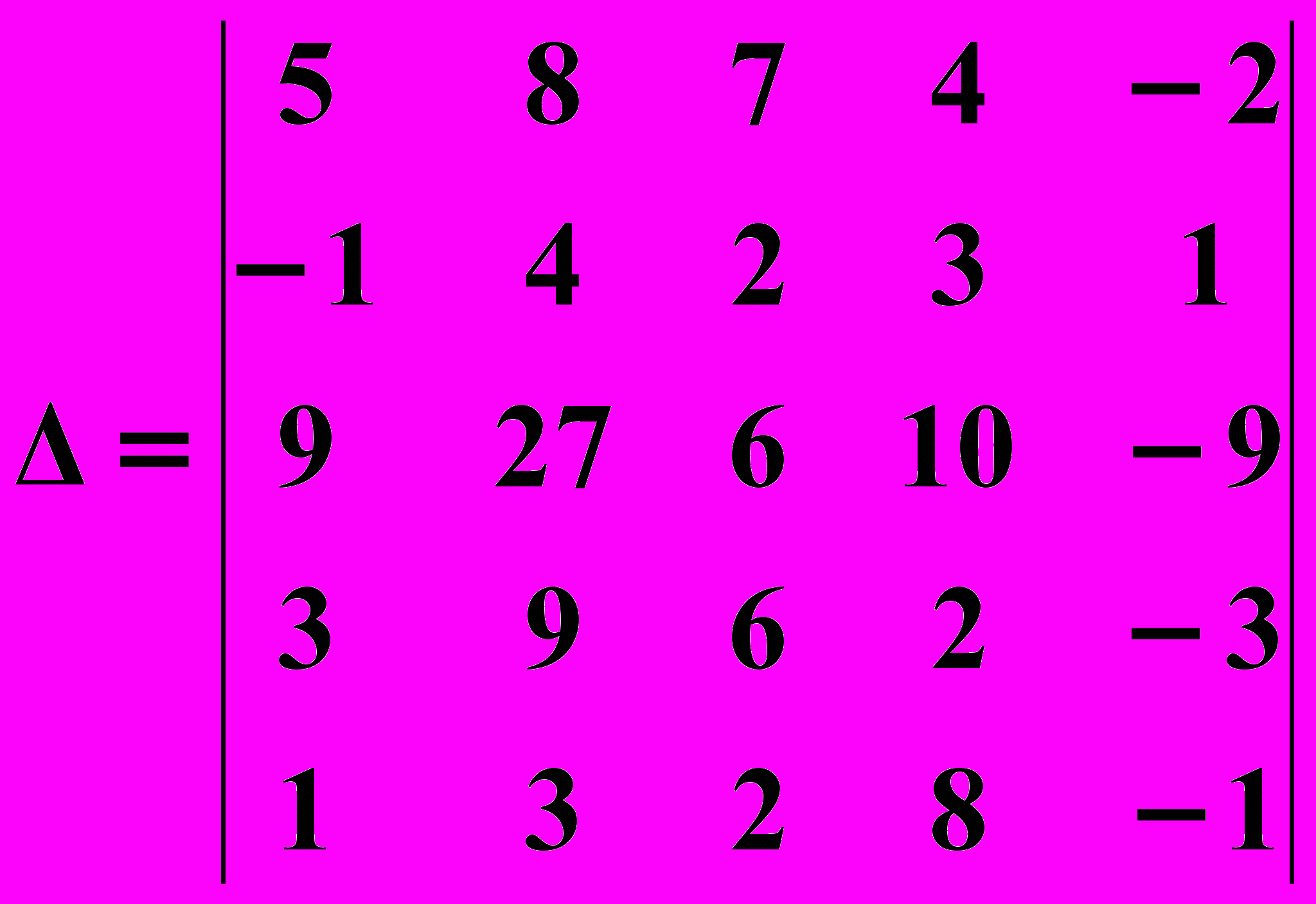 .
.Решение :
Используя свойства определителя, понизим порядок определителя. С этой целью прибавим пятый столбец к первому :
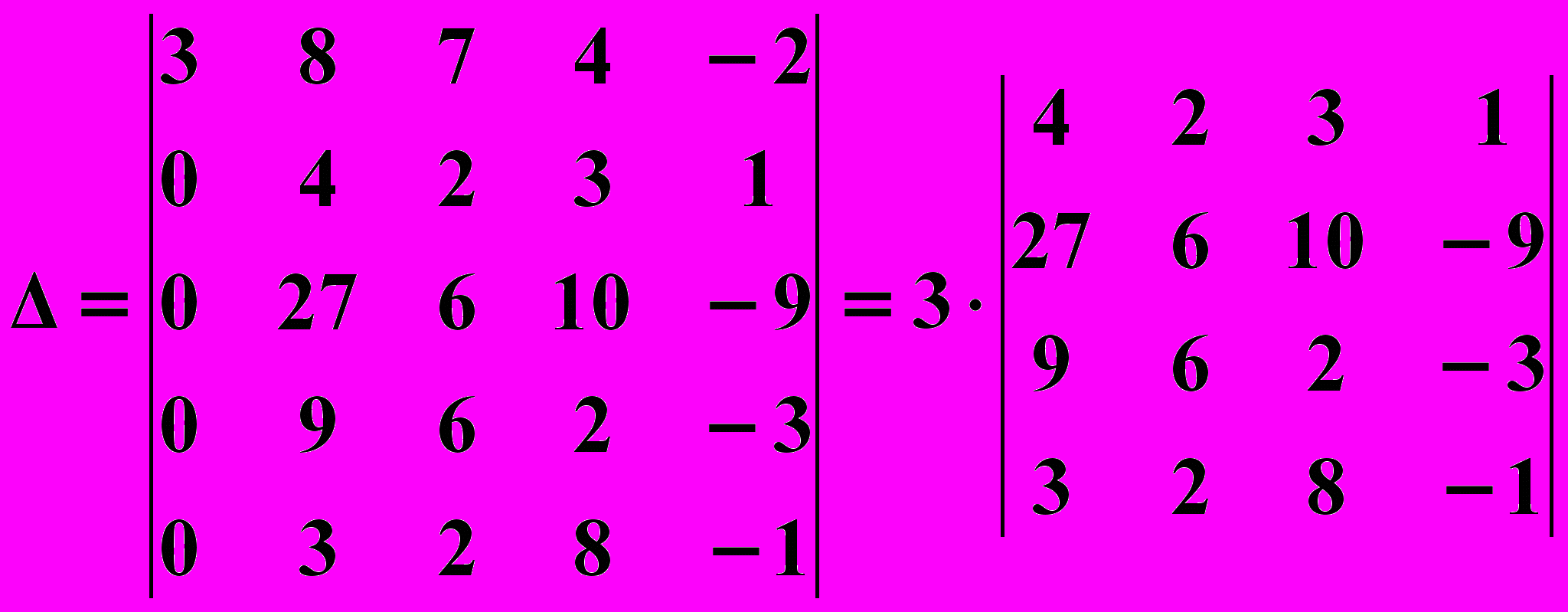 ;
;в полученном определителе 4-го порядка четвертый столбец умножим на 3 и прибавим к первому столбцу, затем умножим его на 2 и прибавим ко второму столбцу, умножим его на 8 и прибавим к третьему столбцу, получаем
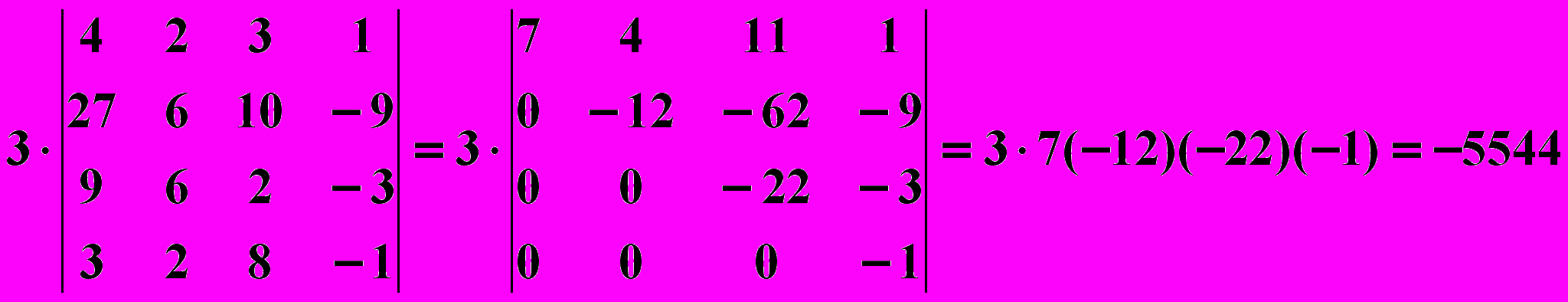 .
.Из приведенного примера очевидно, что вычисление определителей высших порядков значительно упрощается, если определитель привести к треугольному виду.
3. Привести матрицу к ступенчатому виду и вычислить ранг матрицы
 .
.Решение.
Говорят, что квадратная матрица имеет ступенчатый вид, если ниже ее главной диагонали стоят нулевые элементы. Матрица приводится к ступенчатому виду с помощью элементарных преобразований : а) перестановка строк, б) умножение строки на число, в) прибавление к одной строки другой, умноженной на некоторое число. Ранг матрицы
 ,
,  , равен количеству ненулевых строк эквивалентной ей матрицы ступенчатого вида.
, равен количеству ненулевых строк эквивалентной ей матрицы ступенчатого вида. В первом столбце данной матрицы
 ниже первого элемента получим нулевые элементы с помощью преобразования в). Последовательно умножим первую строку матрицы на (–2) и прибавим ко второй строке, умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим
ниже первого элемента получим нулевые элементы с помощью преобразования в). Последовательно умножим первую строку матрицы на (–2) и прибавим ко второй строке, умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим .
.В полученной матрице во втором столбце во второй строке и ниже второй строки отсутствуют единицы. Единицу можно получить, умножив вторую строку на (
 ), или поделив на (–5) , а затем во втором столбце ниже второго элемента получить нули с помощью преобразования в), при этом будут возникать дробные числа. Во избежание вычислений над дробями получим единицу во втором столбце второй строки иначе: ко второй строке прибавим третью строку, умноженную на (–1), результат запишем на месте второй строки. Далее, поделим третью строку на (–2), четвертую строку на (–1), имеем
), или поделив на (–5) , а затем во втором столбце ниже второго элемента получить нули с помощью преобразования в), при этом будут возникать дробные числа. Во избежание вычислений над дробями получим единицу во втором столбце второй строки иначе: ко второй строке прибавим третью строку, умноженную на (–1), результат запишем на месте второй строки. Далее, поделим третью строку на (–2), четвертую строку на (–1), имеем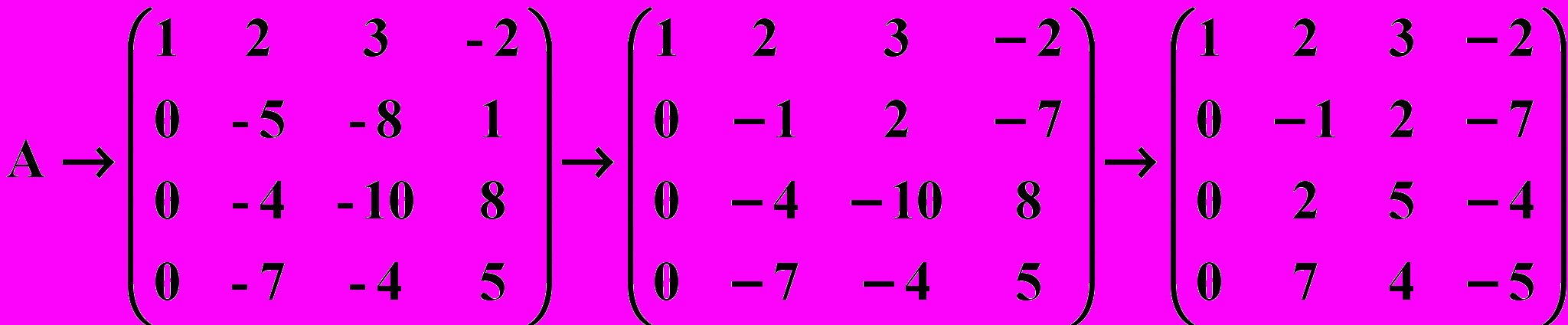 .
.Во втором столбце полученной матрицы ниже второго элемента получим нулевые элементы. Последовательно умножим вторую строку полученной матрицы на 2 и прибавим к третьей строке, умножим на 7 и прибавим к четвертой строке, затем третью строку поделим на 9 , четвертую строку поделим на 18. Во вновь полученной матрице в третьем столбце ниже третьего элемента получим нулевой элемент: третью строку умножим на (–1) и прибавим к четвертой строке, имеем
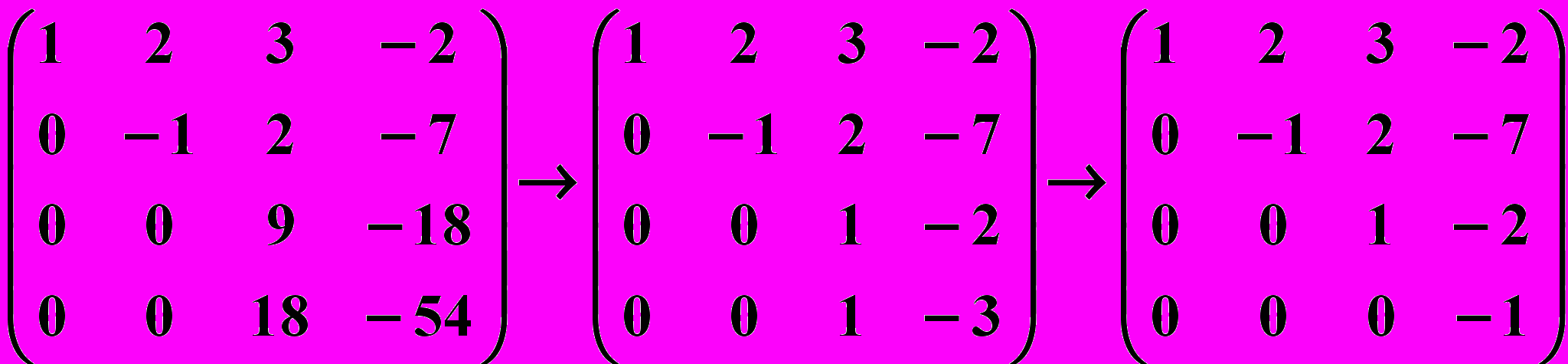 .
.Отсюда заключаем, что
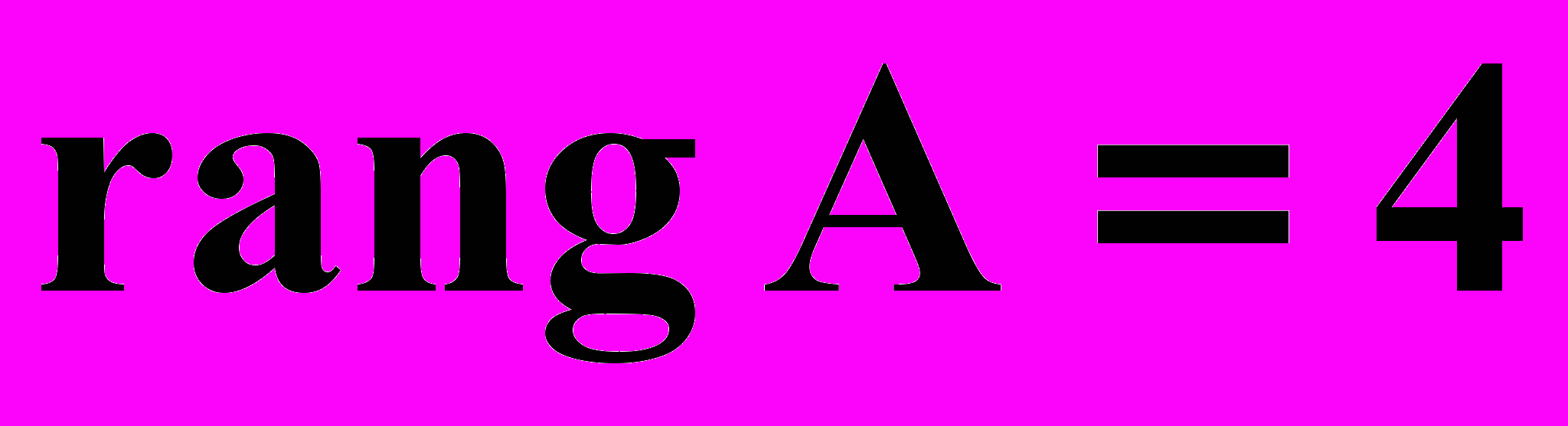 .
.4. Выполнить действия с матрицами
 .
.Решение. Обозначим
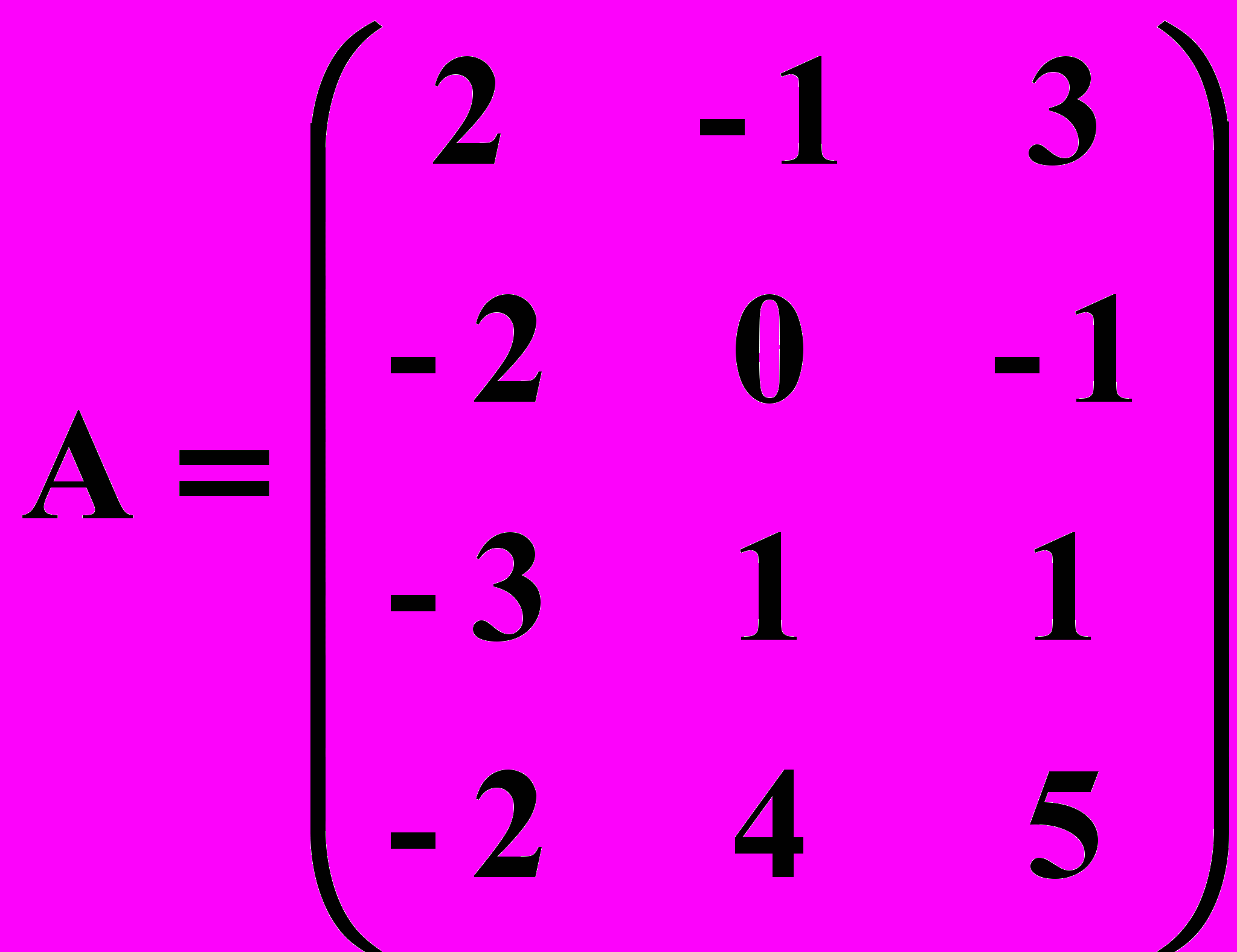 ,
, 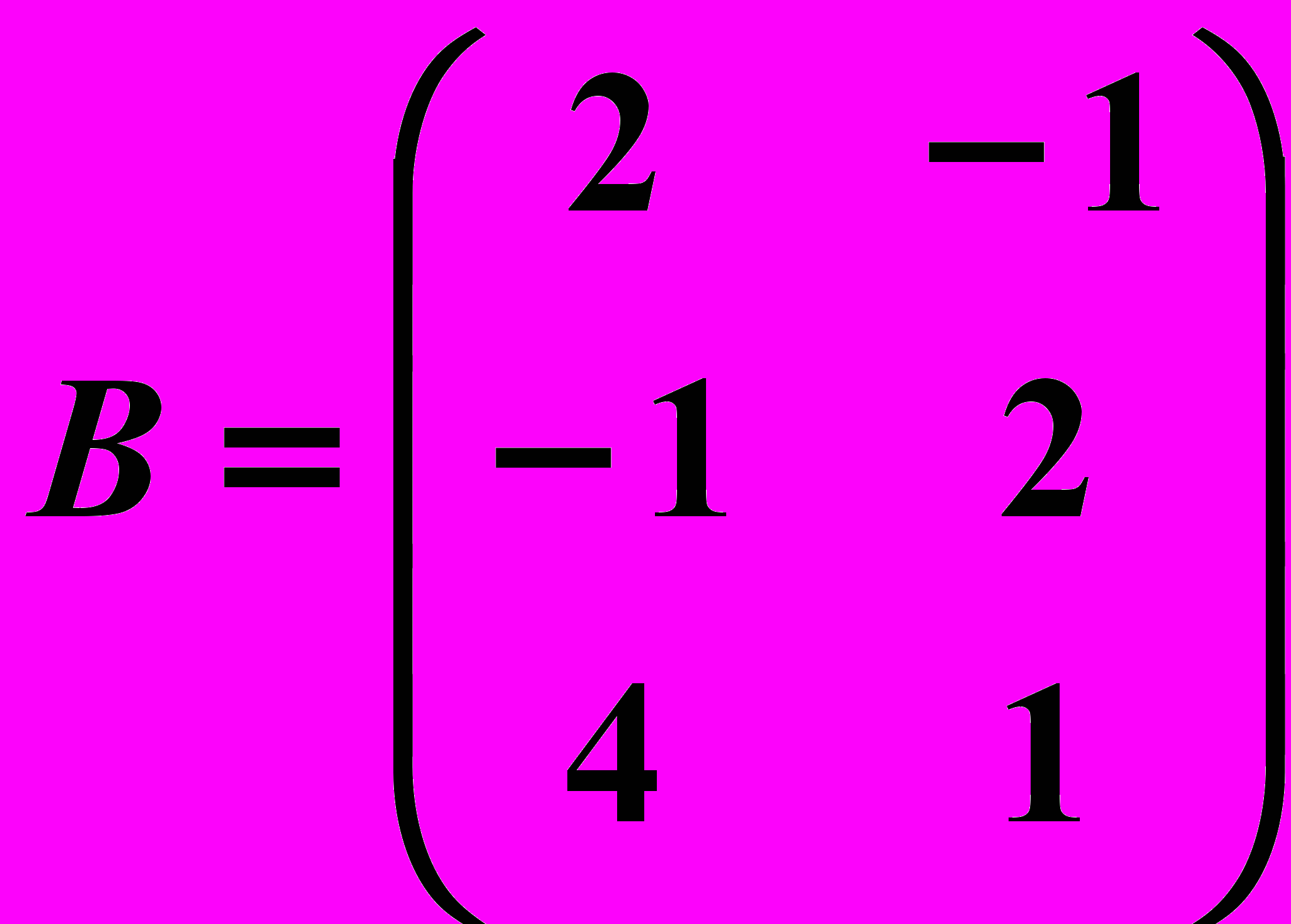 ,
,  ,
,  .
.Произведение
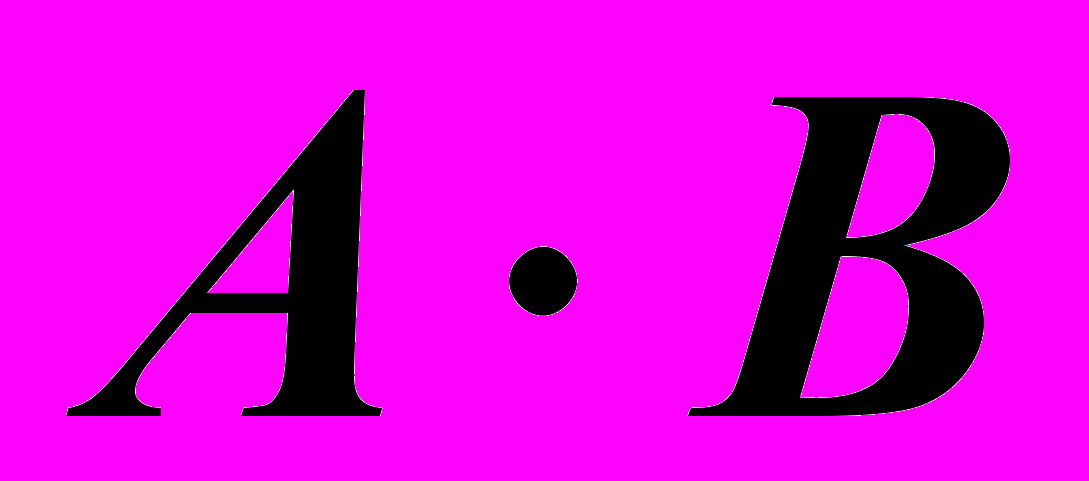 имеет смысл, так как число столбцов матрицы
имеет смысл, так как число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы 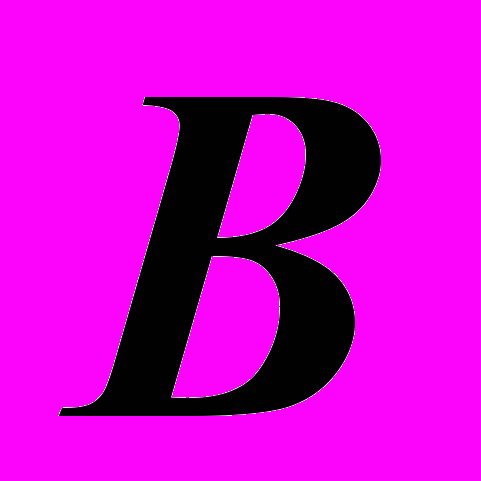 . Находим матрицу
. Находим матрицу 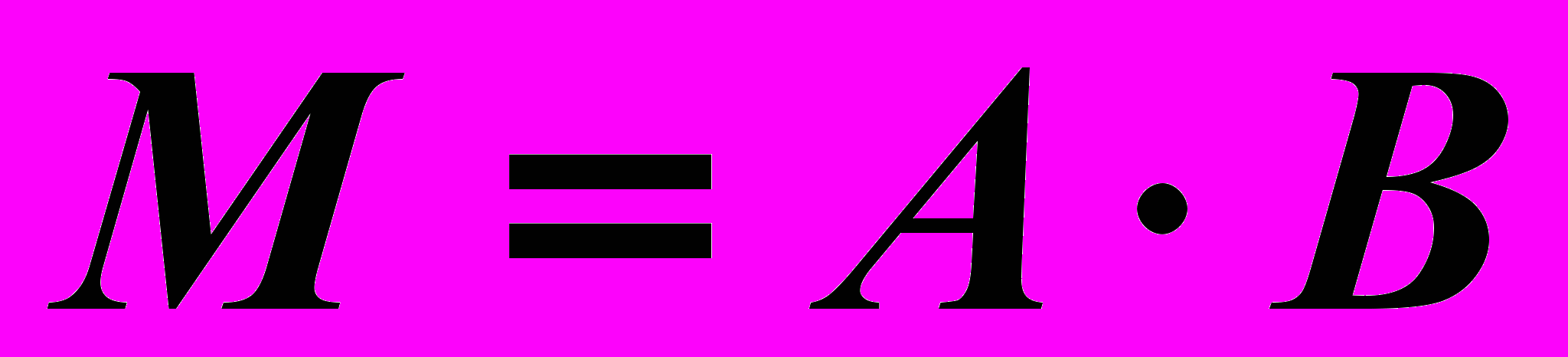 , элементы которой
, элементы которой 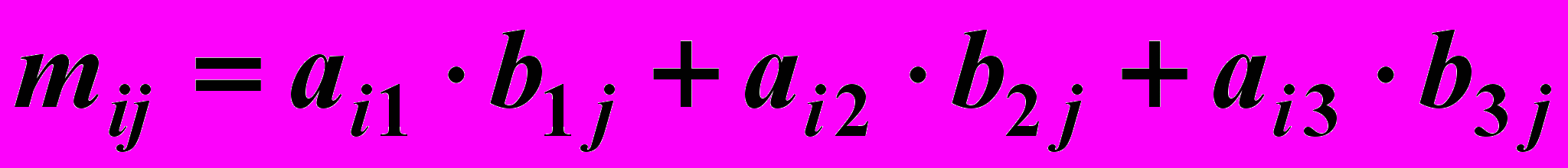 ,
,  . Имеем
. Имеем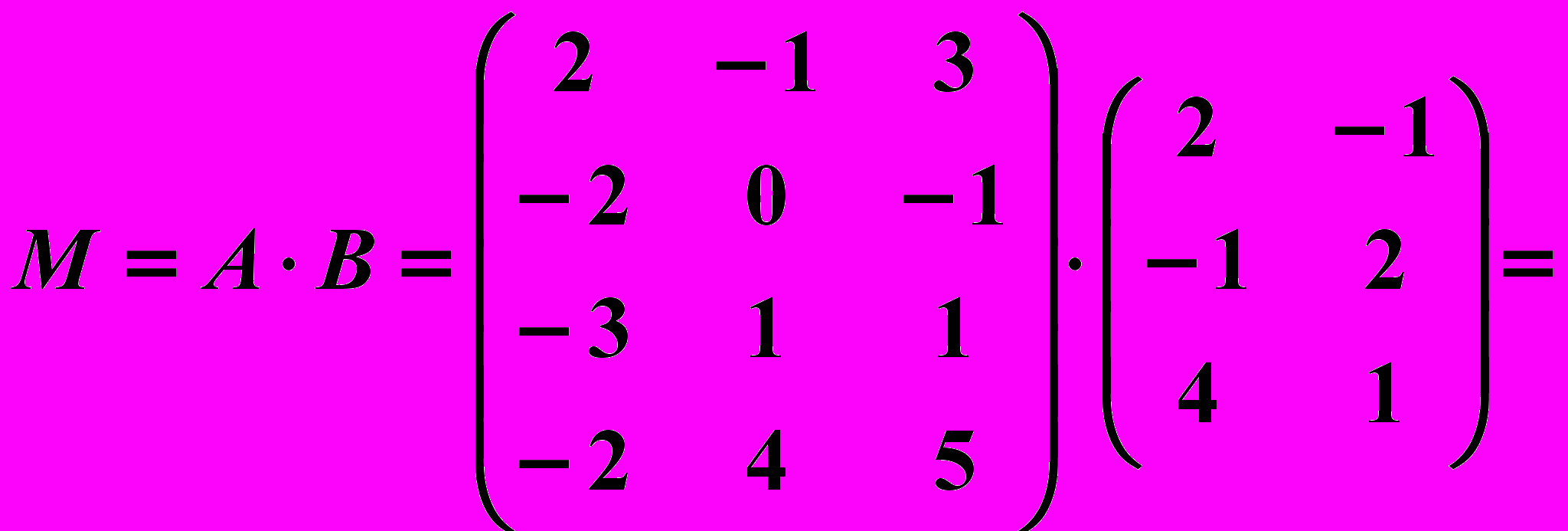
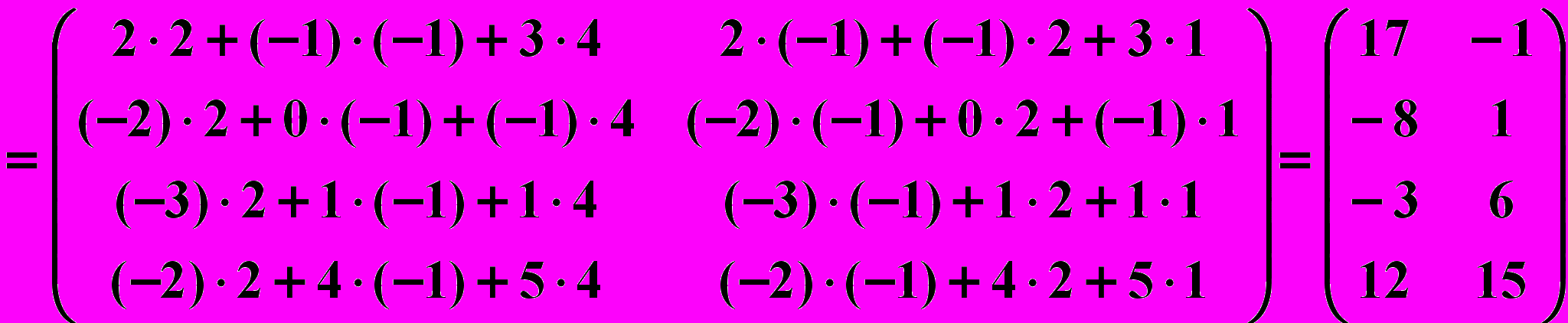 .
.Произведение
 имеет смысл, так как тоже число столбцов матрицы
имеет смысл, так как тоже число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  . Находим матрицу
. Находим матрицу 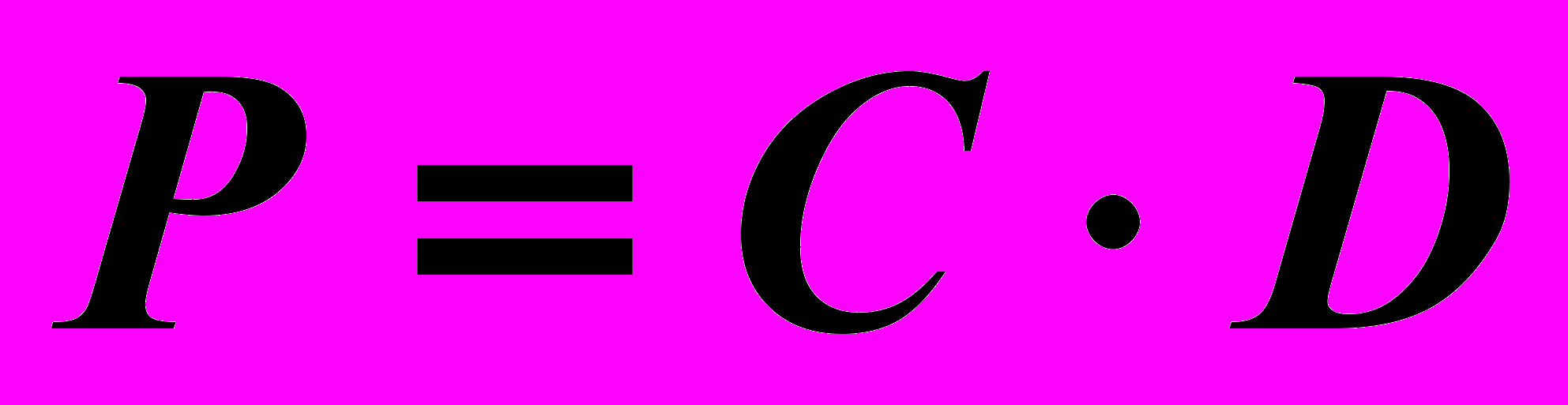 , элементы которой
, элементы которой  ,
,  . Имеем
. Имеем
 .
.Разность
 имеет смысл, так как матрицы
имеет смысл, так как матрицы 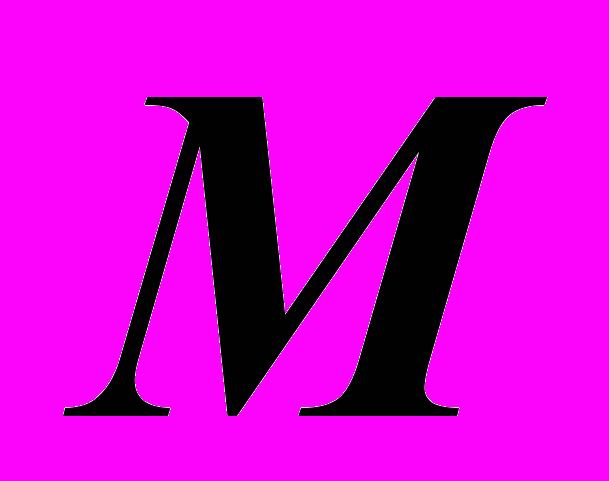 и
и  имеют одинаковую размерность
имеют одинаковую размерность  . Находим искомую матрицу
. Находим искомую матрицу  , элементы которой
, элементы которой  ,
,  . Имеем
. Имеем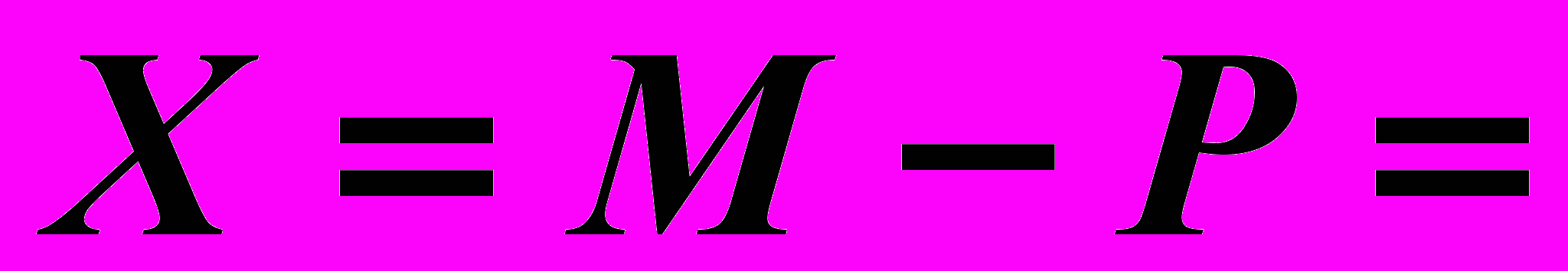
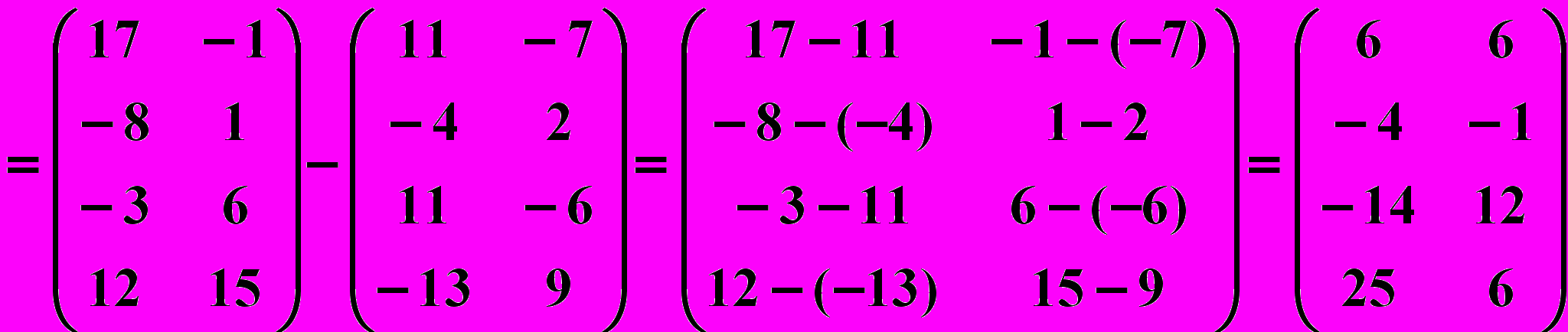 .
.Ответ : Результатом действия данных матриц является матрица
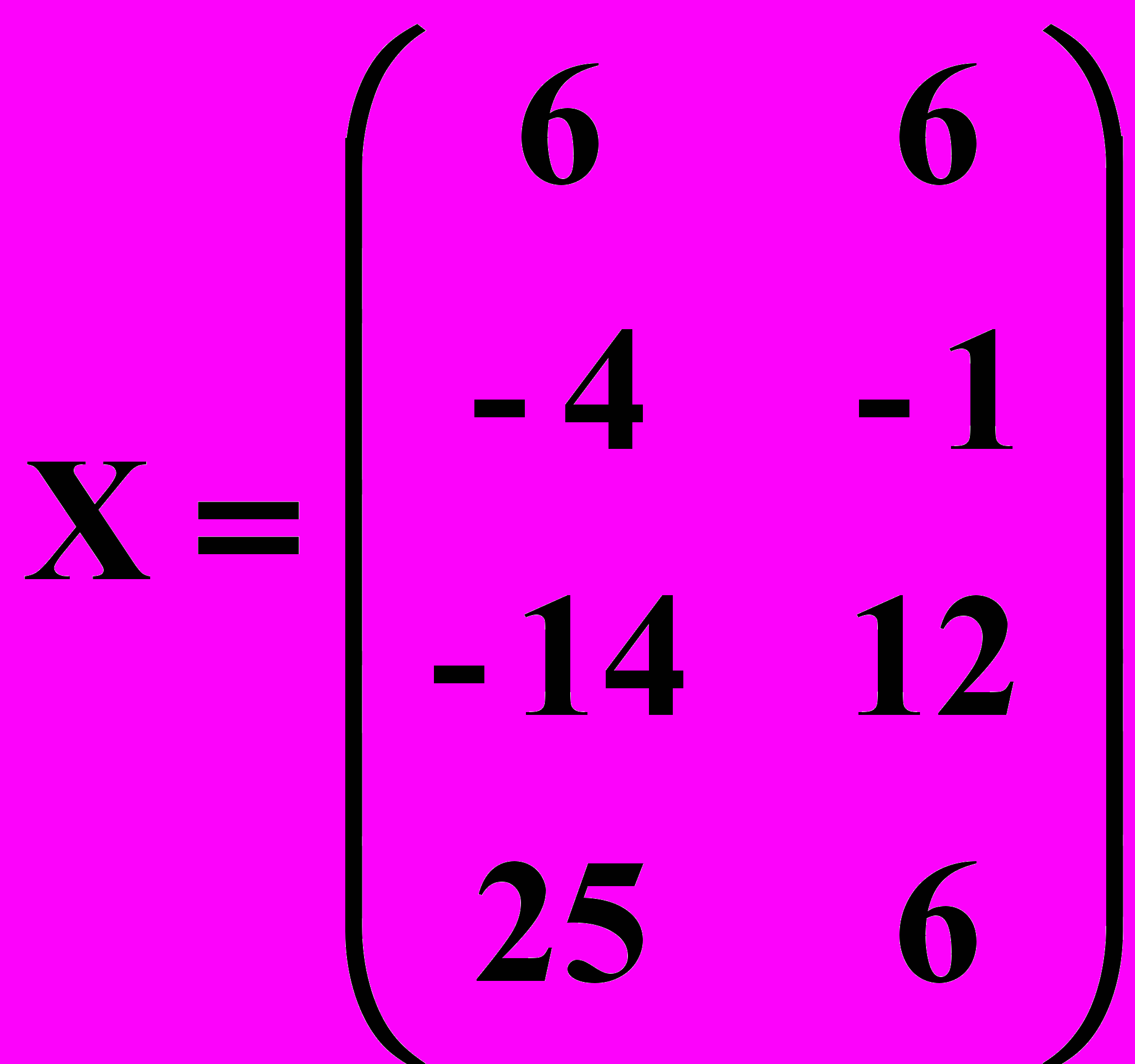 .
.5. Вычислить значение многочлена
 от матрицы
от матрицы  , где
, где ,
, 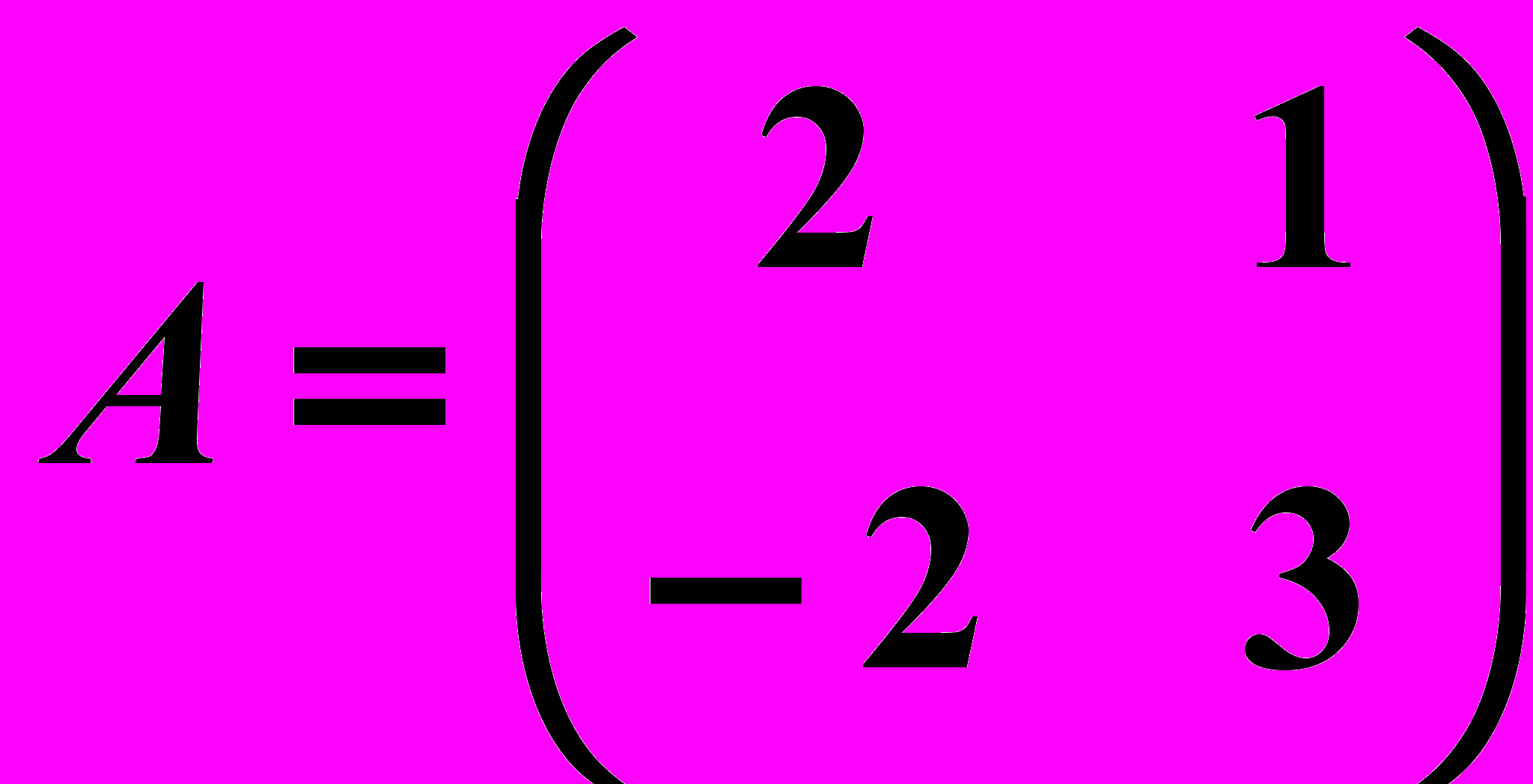 .
.Решение.
При вычислении значения многочлена
 от матрицы
от матрицы  вместо
вместо 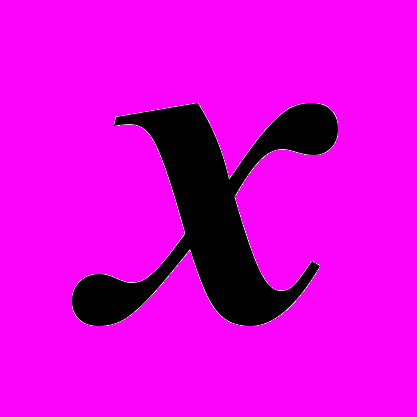 подставляем данную матрицу
подставляем данную матрицу  , а свободный член многочлена записываем в матричной форме, т.е. в виде
, а свободный член многочлена записываем в матричной форме, т.е. в виде 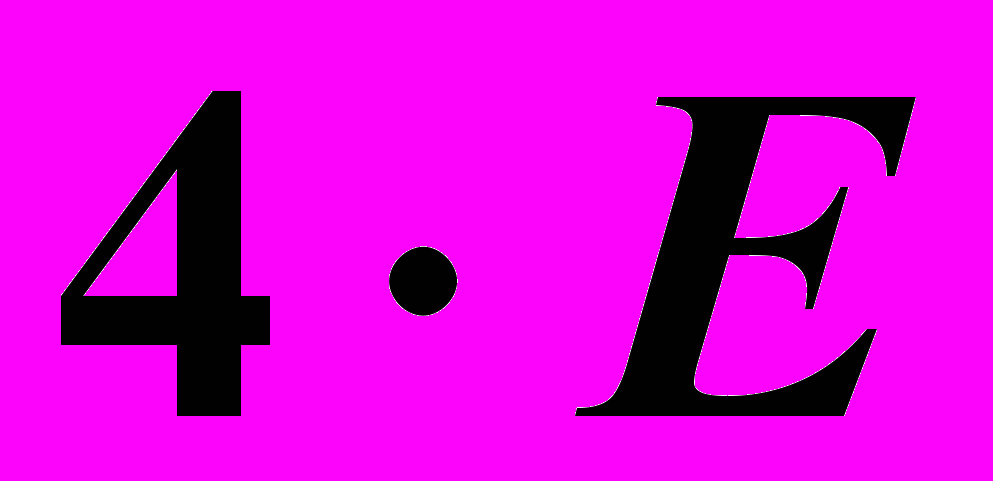 , где
, где  единичная матрица того же порядка, что и данная матрица
единичная матрица того же порядка, что и данная матрица  . Таким образом,
. Таким образом,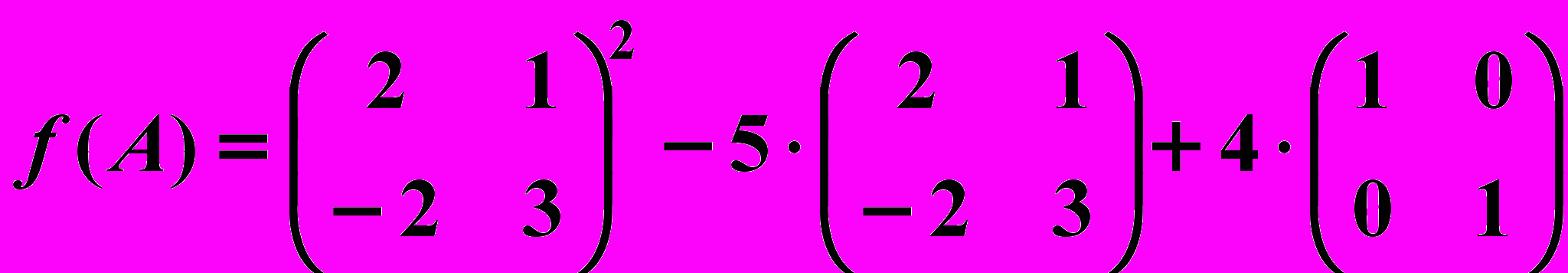 ,
,1)

 ,
,2)
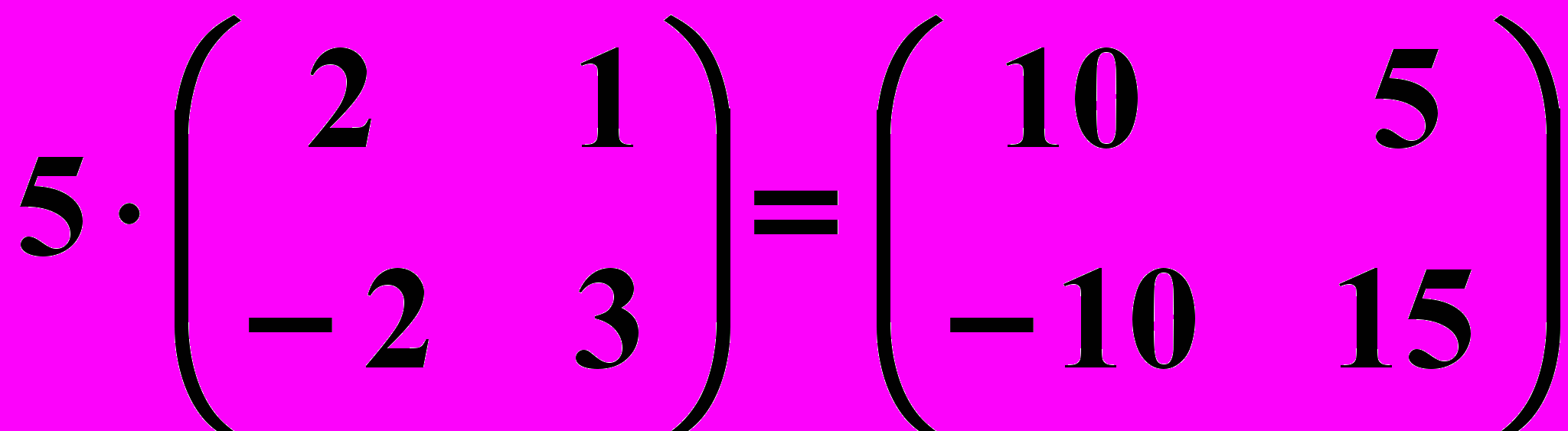 ,
,3)
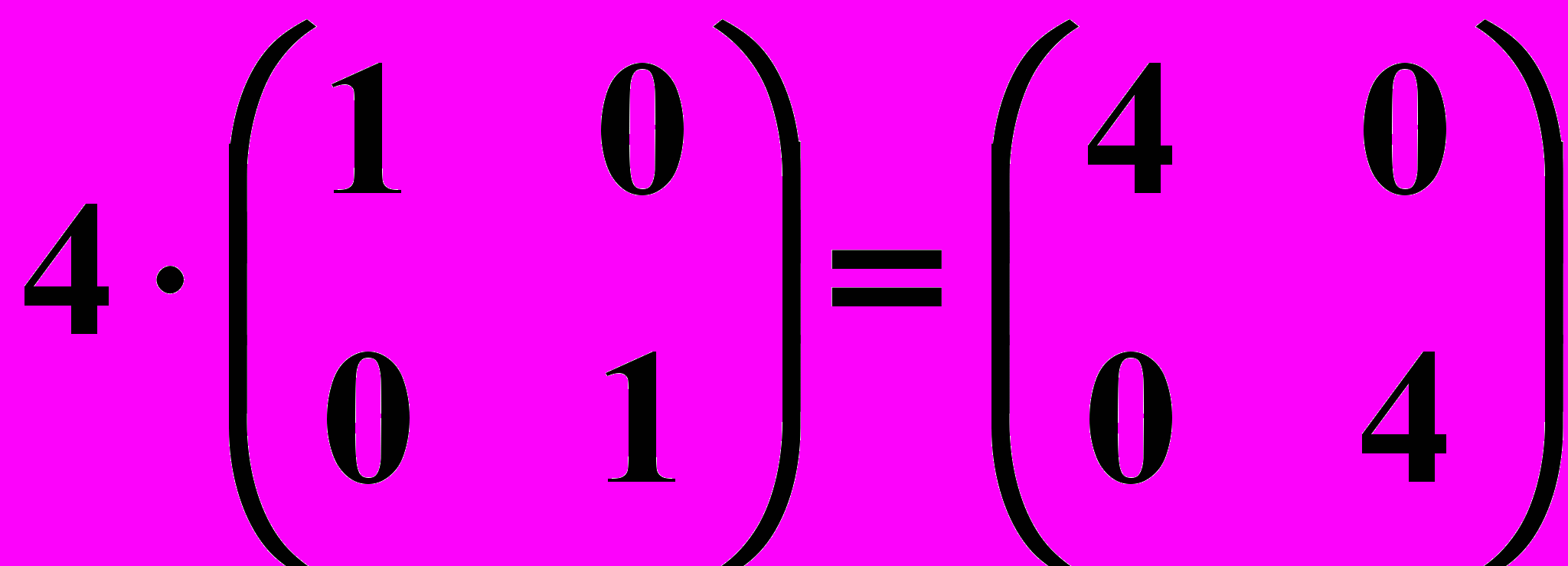 .
.Имеем
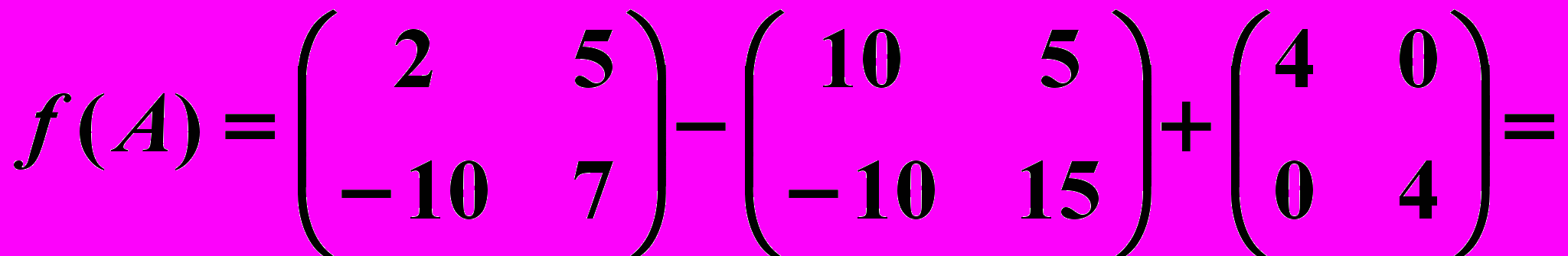
 .
.Ответ :
 .
.6. 1) Найти неизвестную матрицу
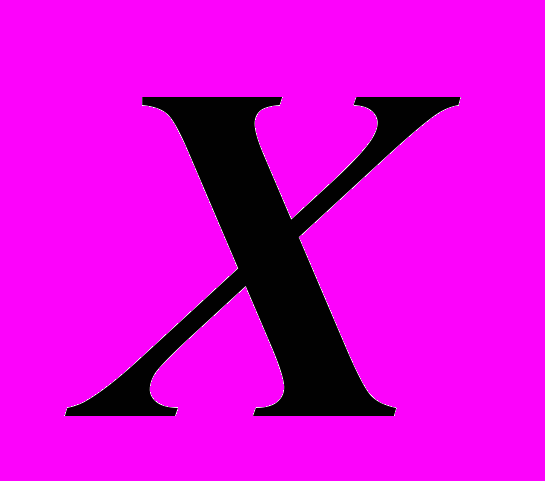 из уравнения
из уравнения .
.Решение.
Исходное уравнение запишем в матричной форме
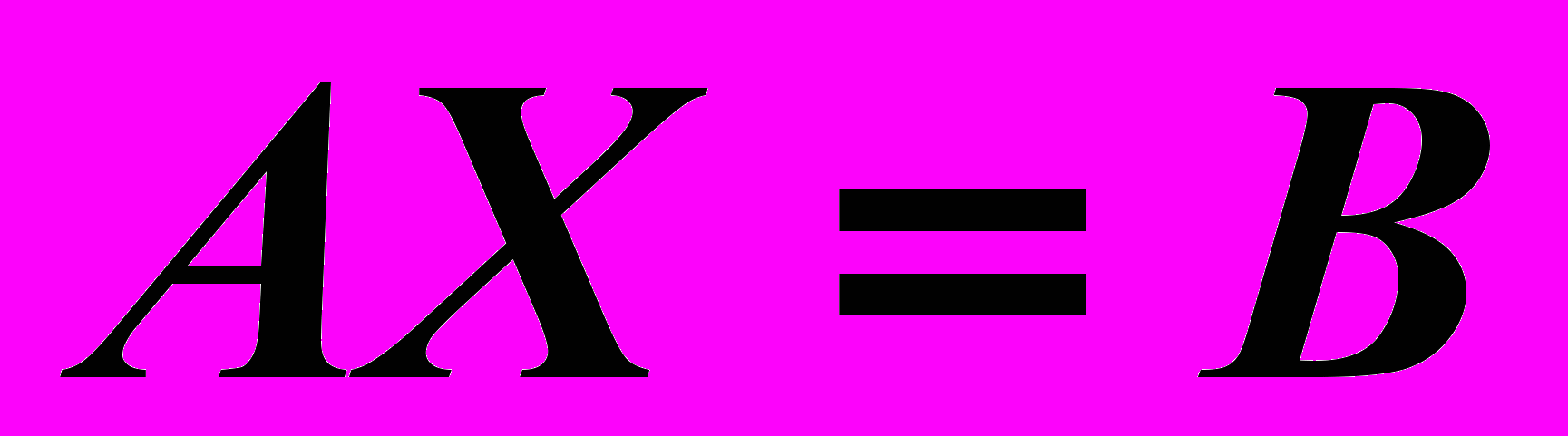 , где
, где 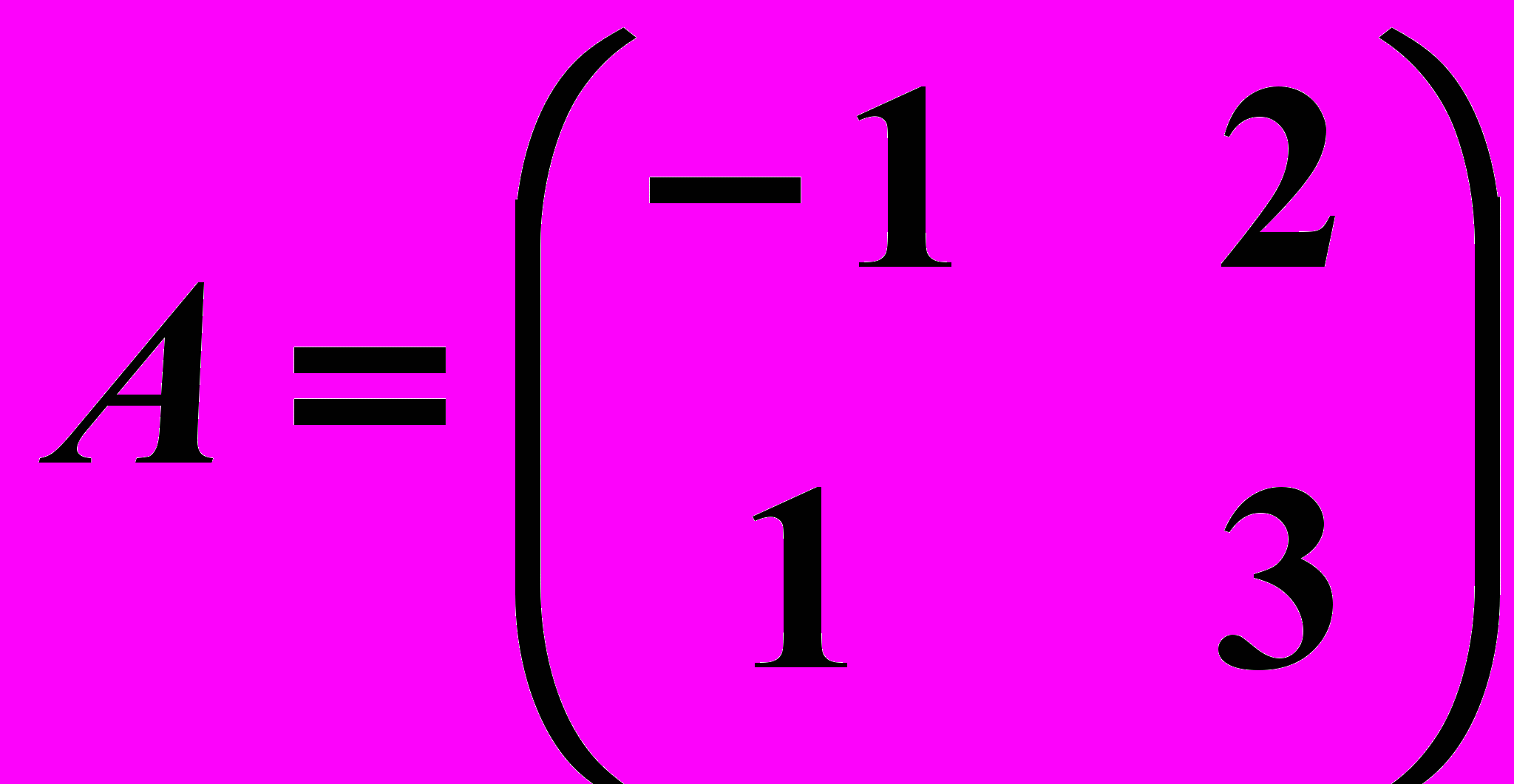 ,
,  .
.Матричное уравнение вида
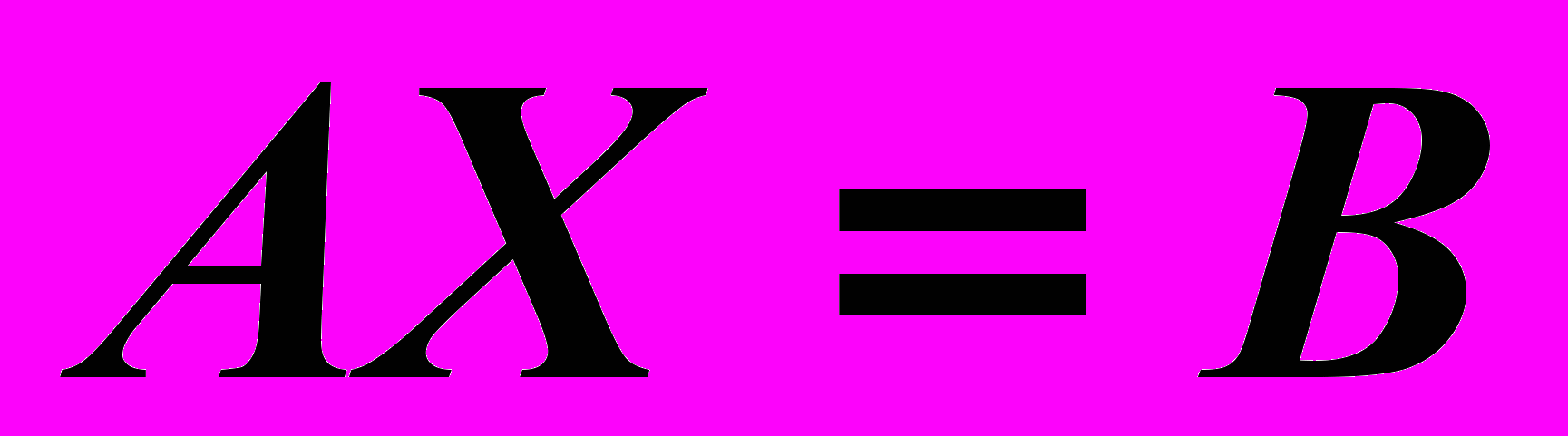 имеет решение, если матрицы
имеет решение, если матрицы  и
и 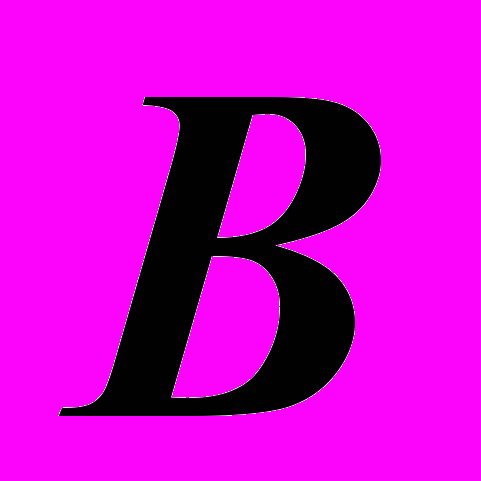 – квадратные матрицы одинакового порядка и матрица
– квадратные матрицы одинакового порядка и матрица  – невырожденная, т.е.
– невырожденная, т.е.  . В этом случае для матрицы
. В этом случае для матрицы  существует обратная матрица
существует обратная матрица 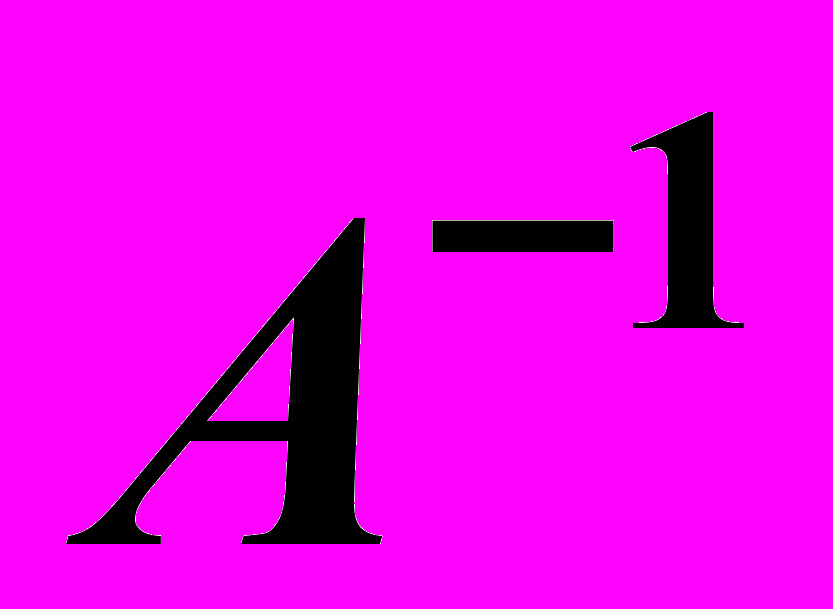 . Умножая слева обе части уравнения
. Умножая слева обе части уравнения 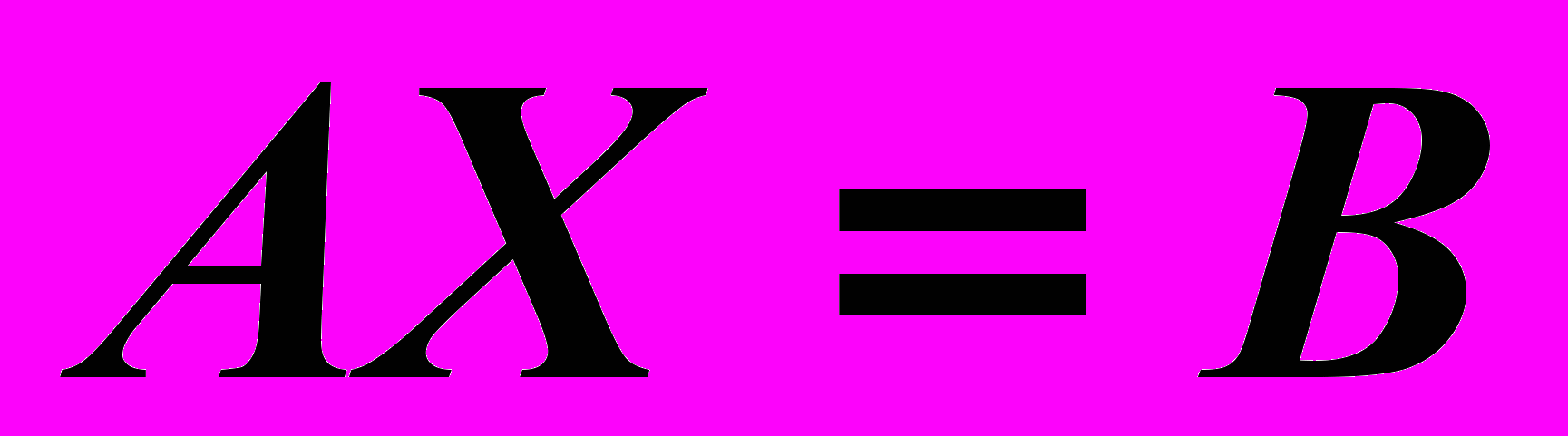 на
на 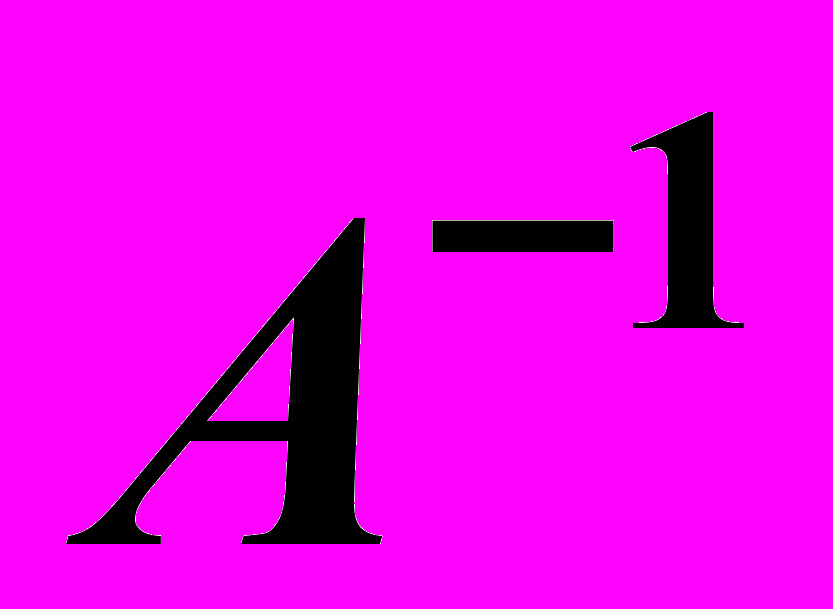 , получим
, получим  , где
, где 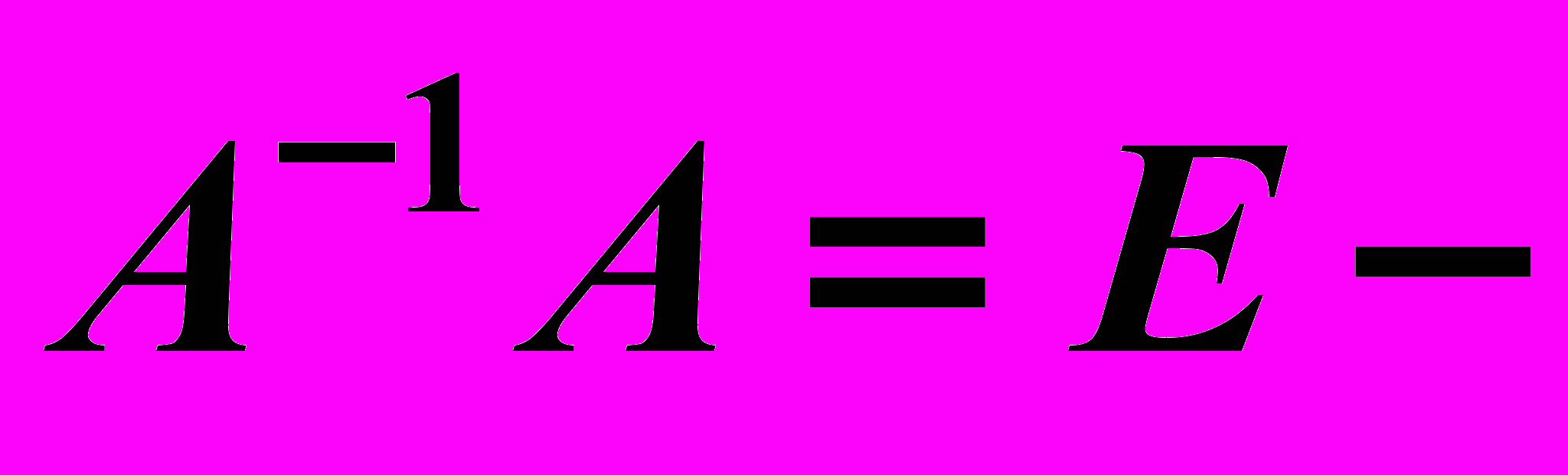 единичная матрица,
единичная матрица,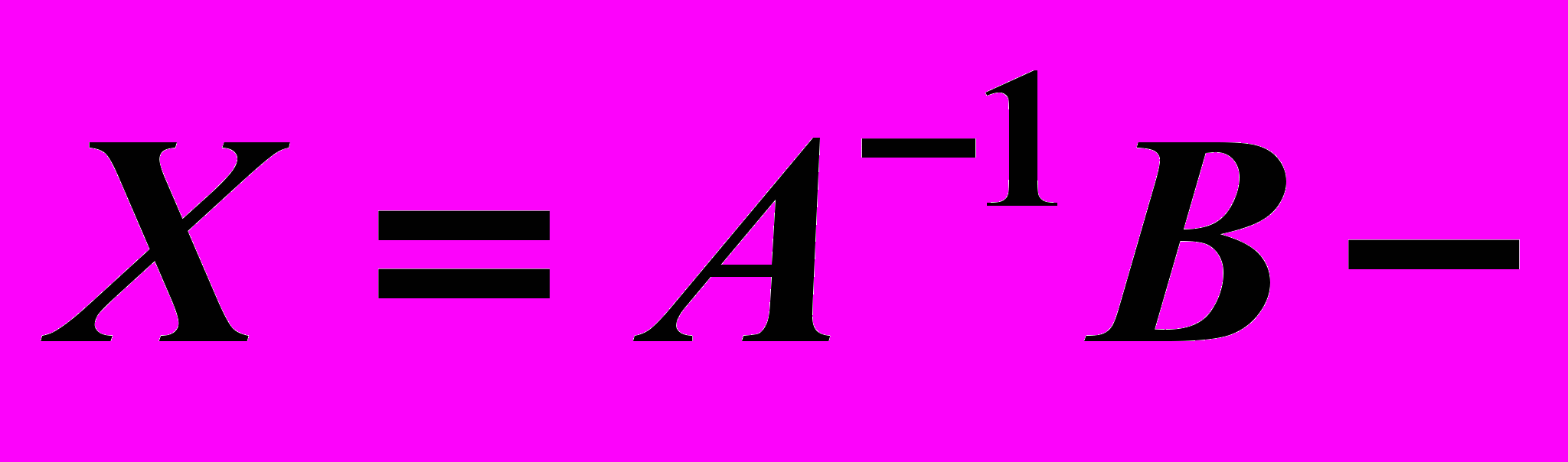 искомая матрица.
искомая матрица.Для данной матрицы
 :
:  . Следовательно, существует
. Следовательно, существует 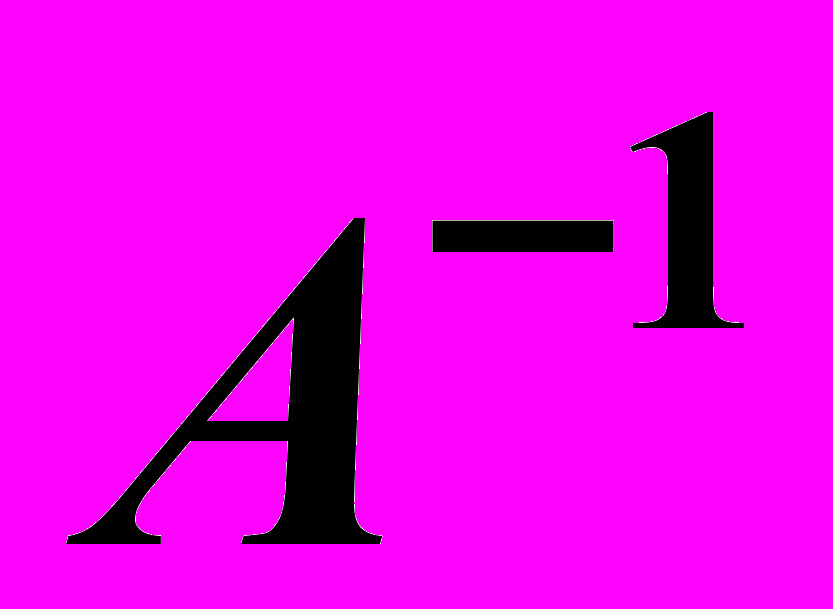 . Найдем ее по формуле
. Найдем ее по формуле 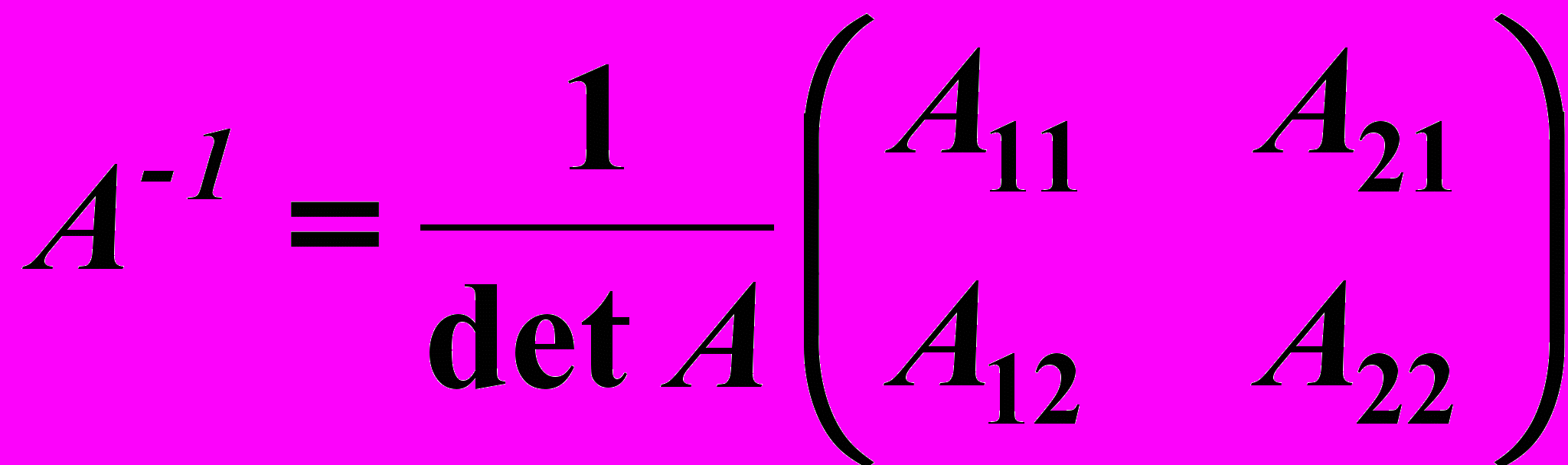 , где
, где  алгебраическое дополнение элемента
алгебраическое дополнение элемента  матрицы
матрицы  . Для данной матрицы
. Для данной матрицы  :
:  . Тогда
. Тогда 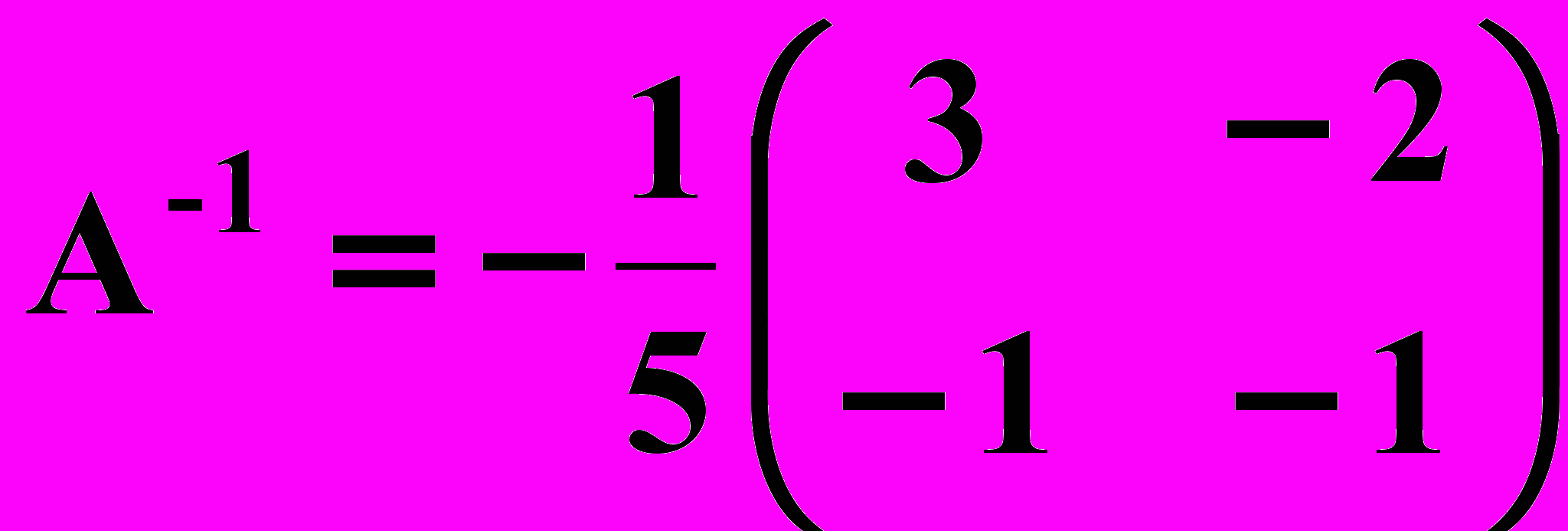
и

 .
.Ответ :
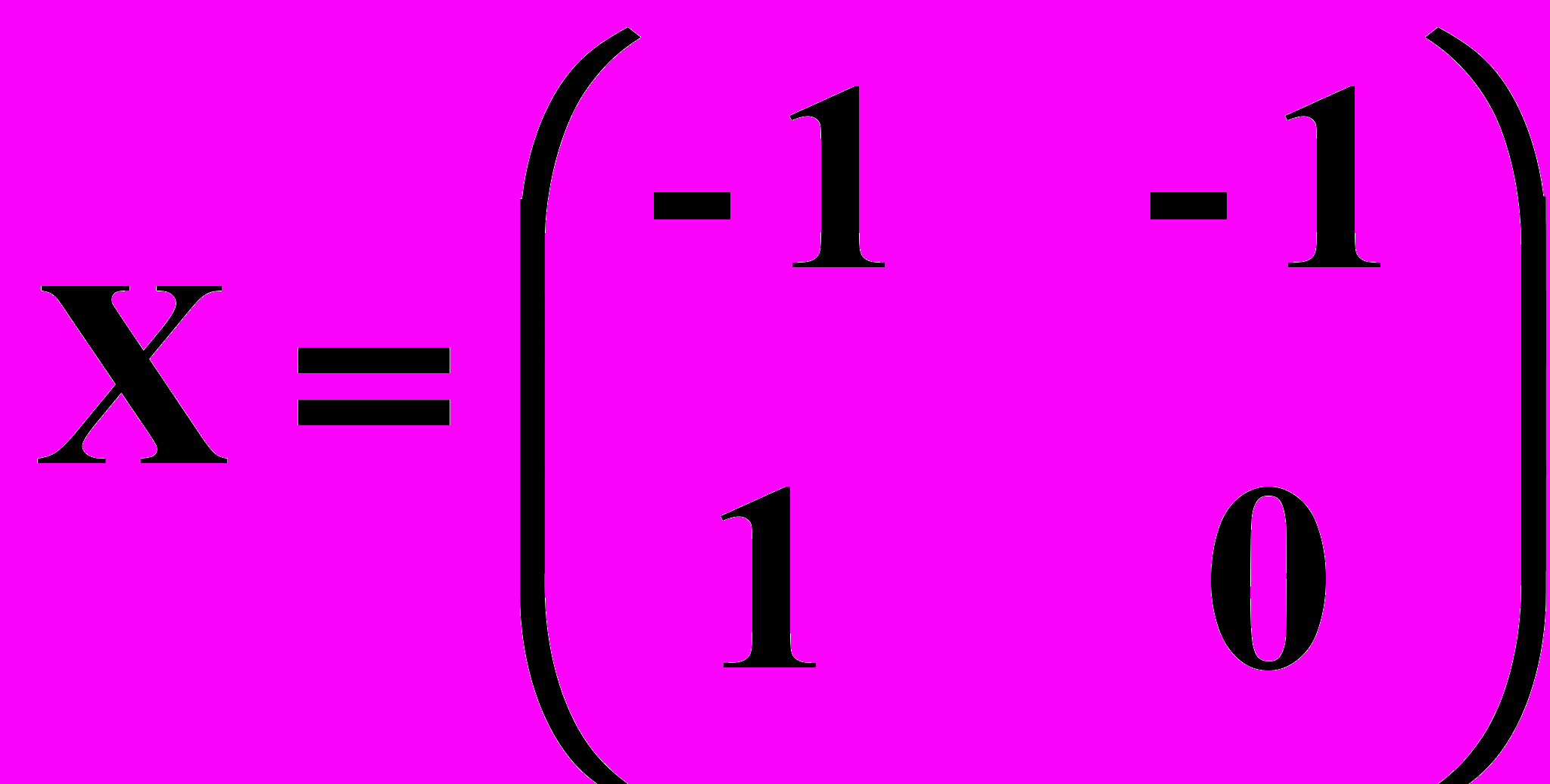 .
.2) Найти неизвестную матрицу
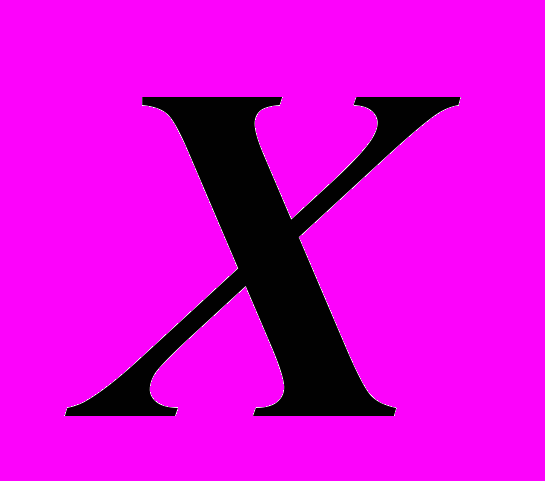 из уравнения
из уравнения .
.Решение.
Исходное уравнение запишем в матричной форме
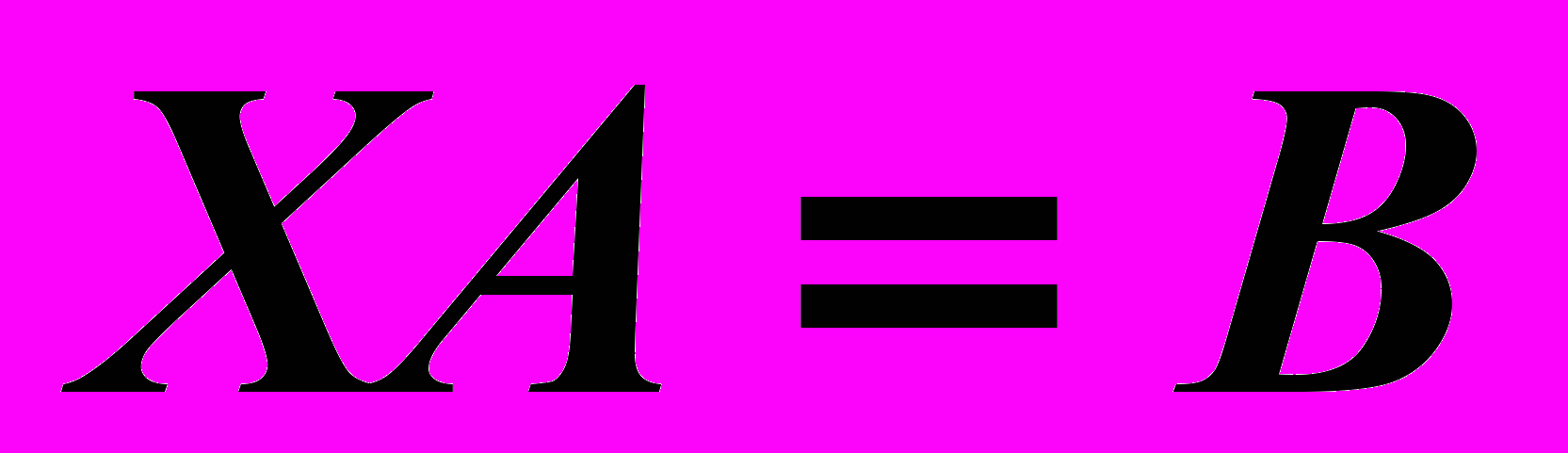 , где
, где  ,
,  .
.Матричное уравнение вида
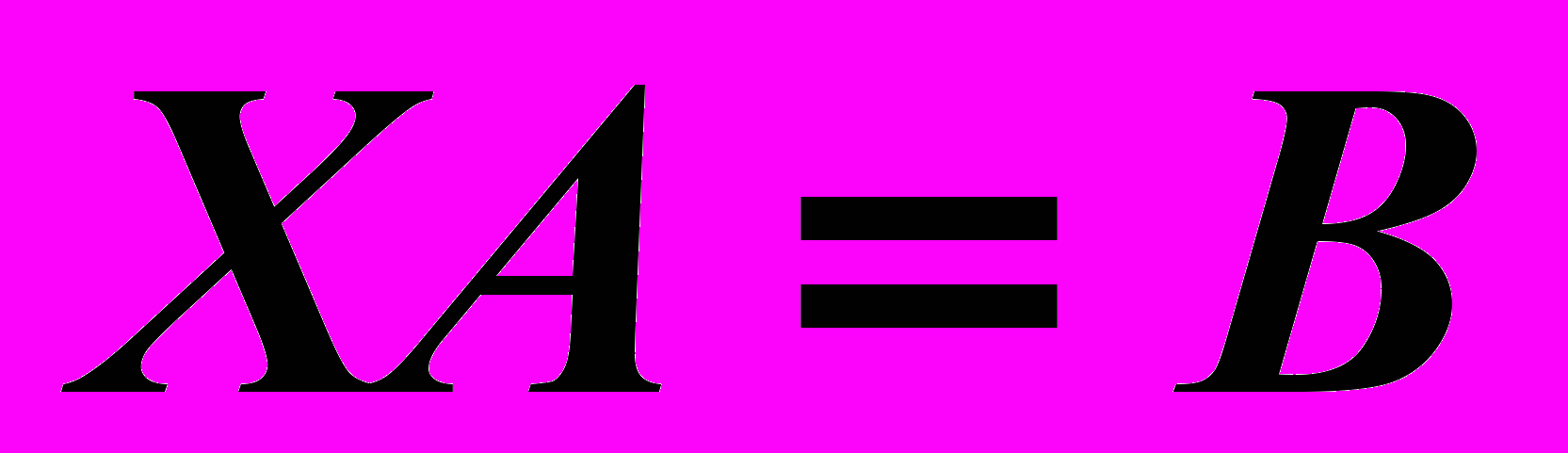 имеет решение, если матрицы
имеет решение, если матрицы  и
и 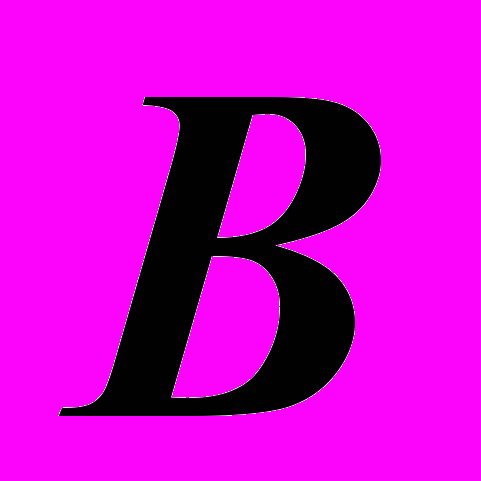 – квадратные матрицы одинакового порядка и
– квадратные матрицы одинакового порядка и  , т.е. для матрицы
, т.е. для матрицы  существует обратная матрица
существует обратная матрица 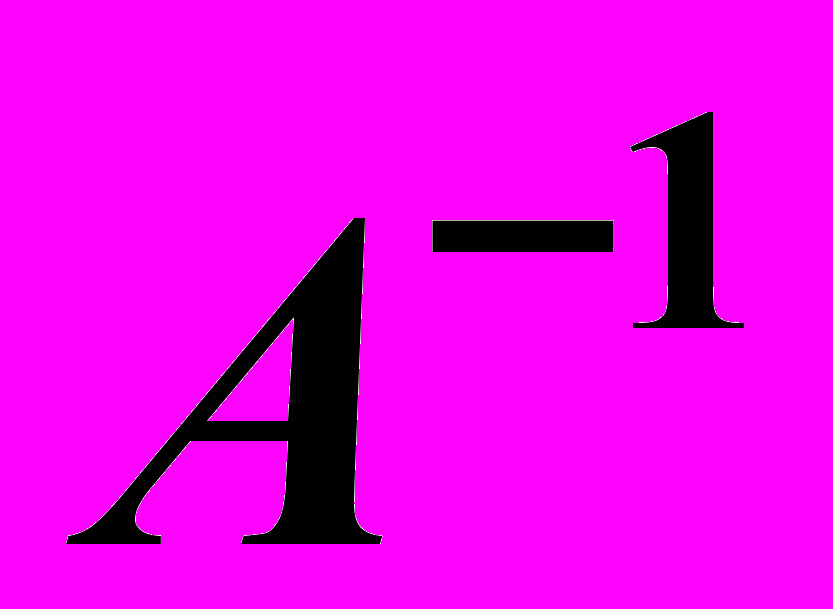 . Умножая справа обе части уравнения
. Умножая справа обе части уравнения 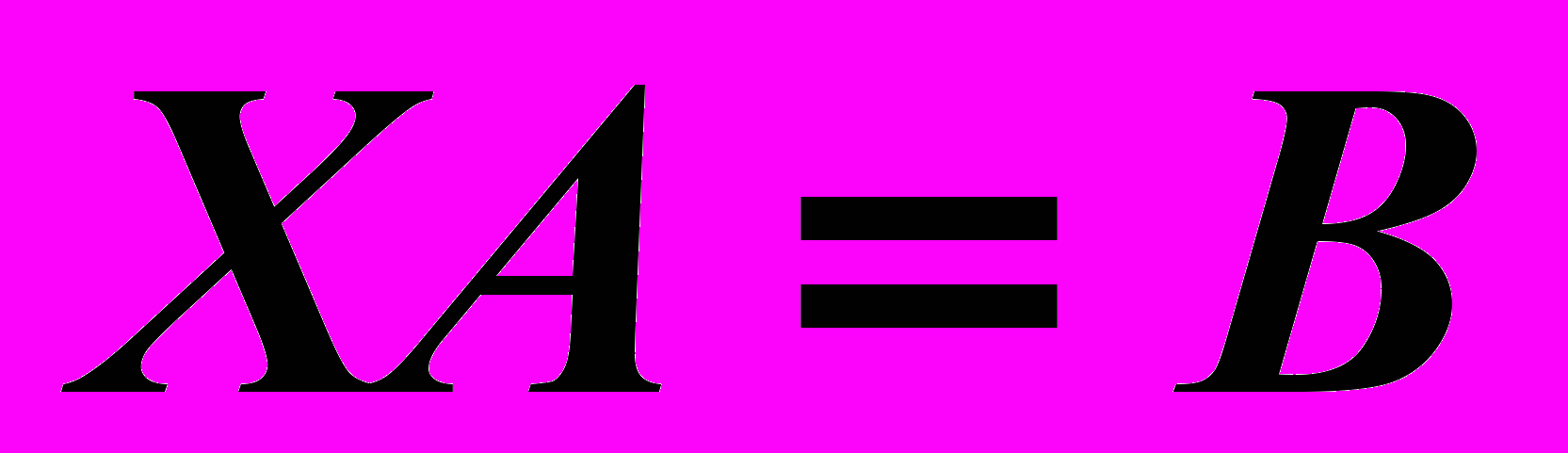 на
на 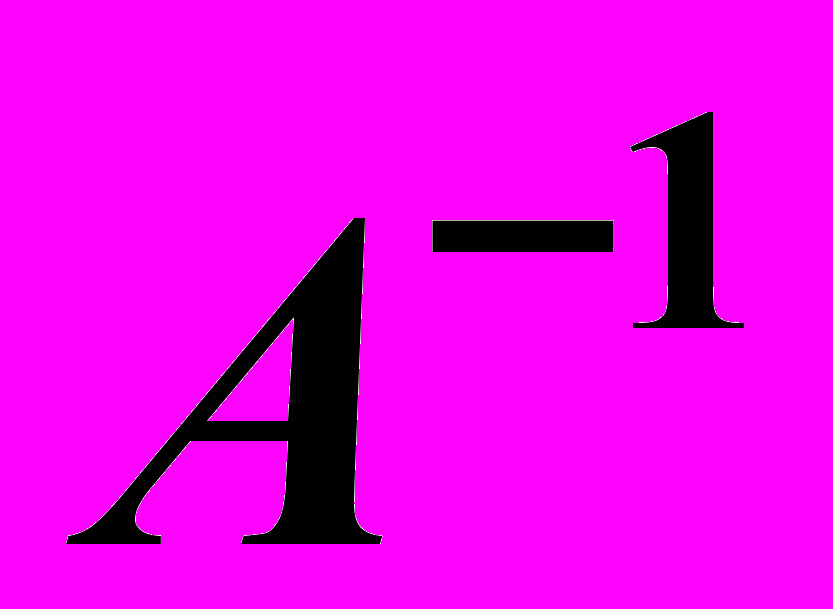 , получим
, получим 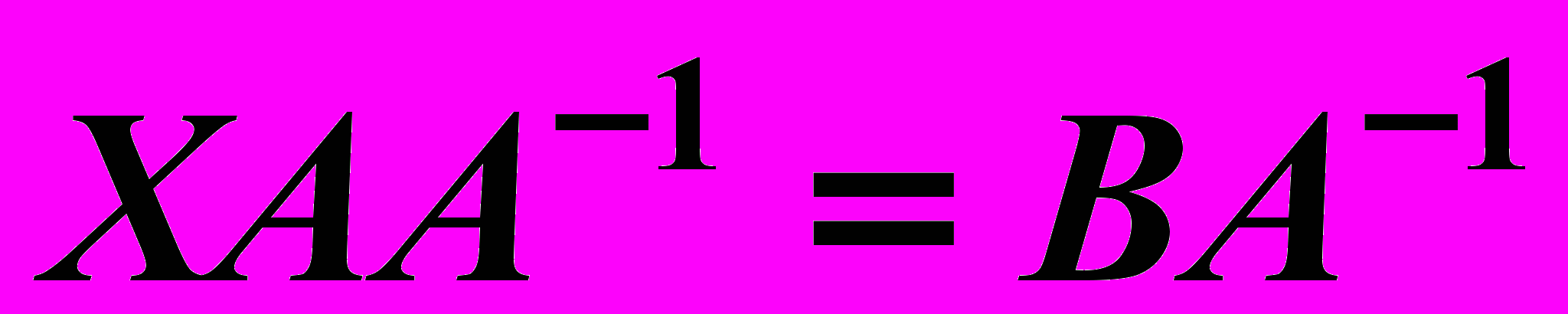 , где
, где 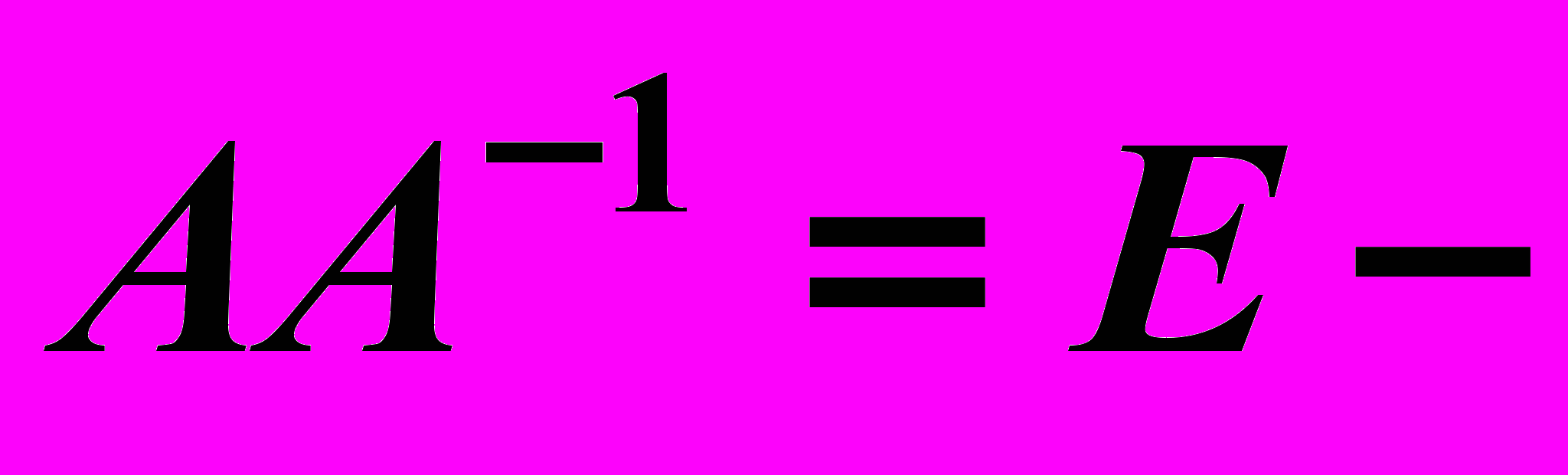 единичная матрица, или
единичная матрица, или  , или
, или искомая матрица.
искомая матрица.Для данной матрицы
 :
:  . Следовательно, существует
. Следовательно, существует 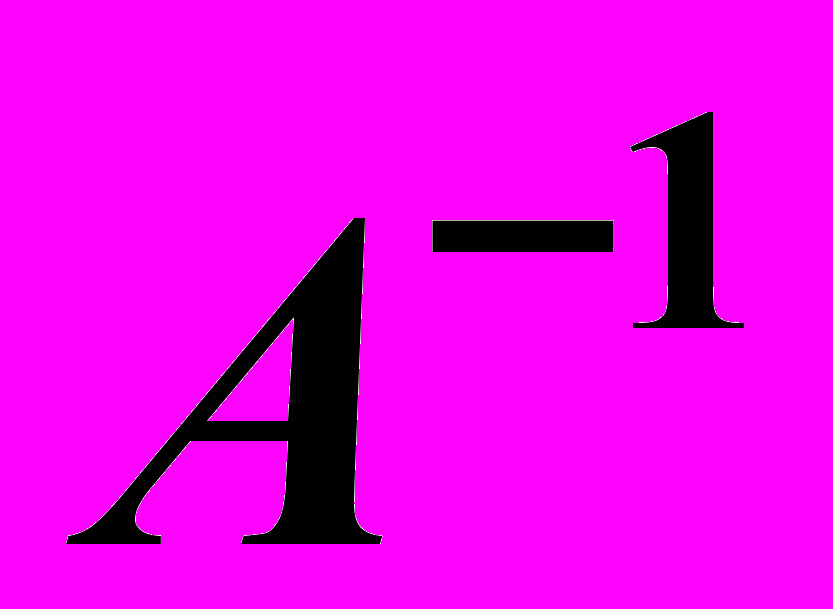 . Найдем ее по формуле, указанной в примере 1), имеем
. Найдем ее по формуле, указанной в примере 1), имеем 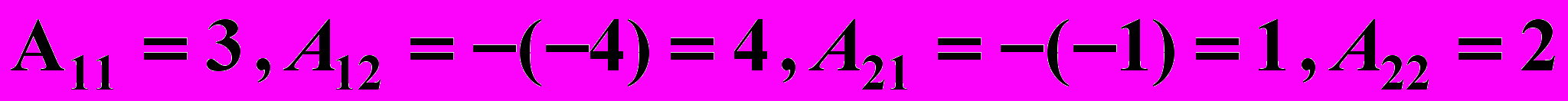 и
и .
.Тогда
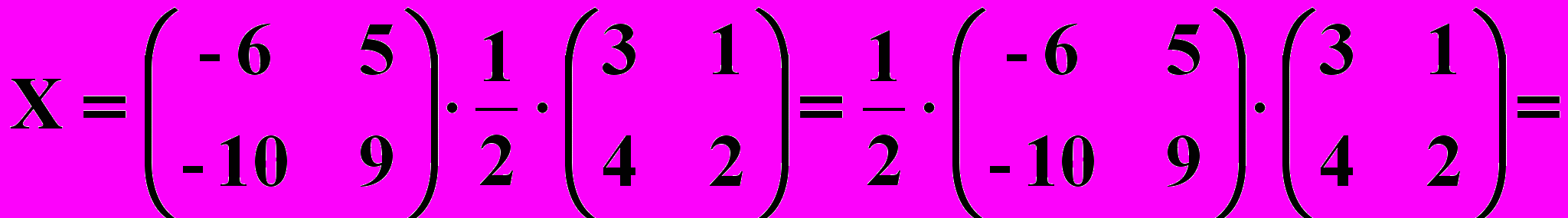
 .
.Ответ :
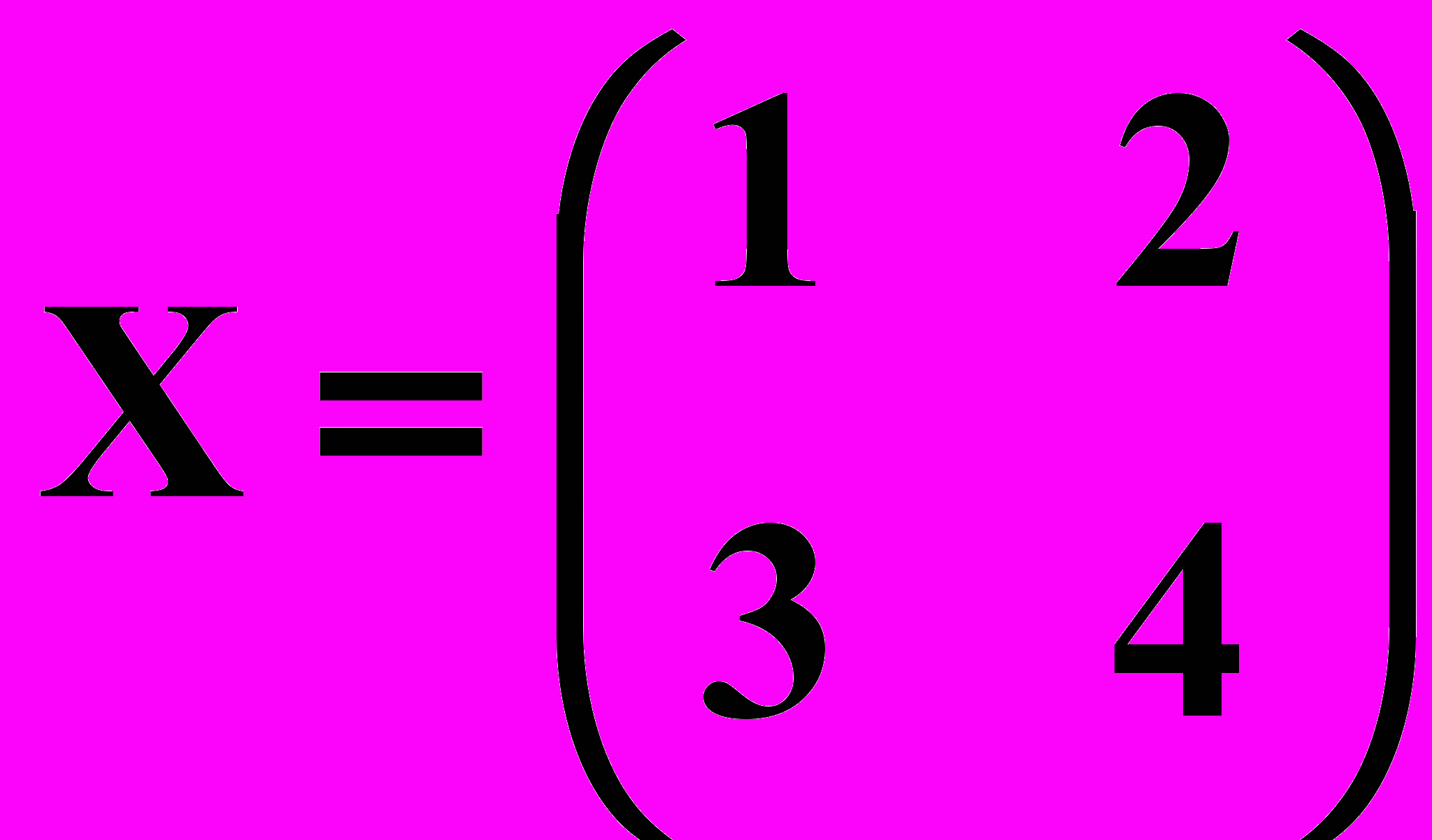 .
.Индивидуальные задания
Вариант № 1
1.1.
 1.2.
1.2.  1.3.
1.3. 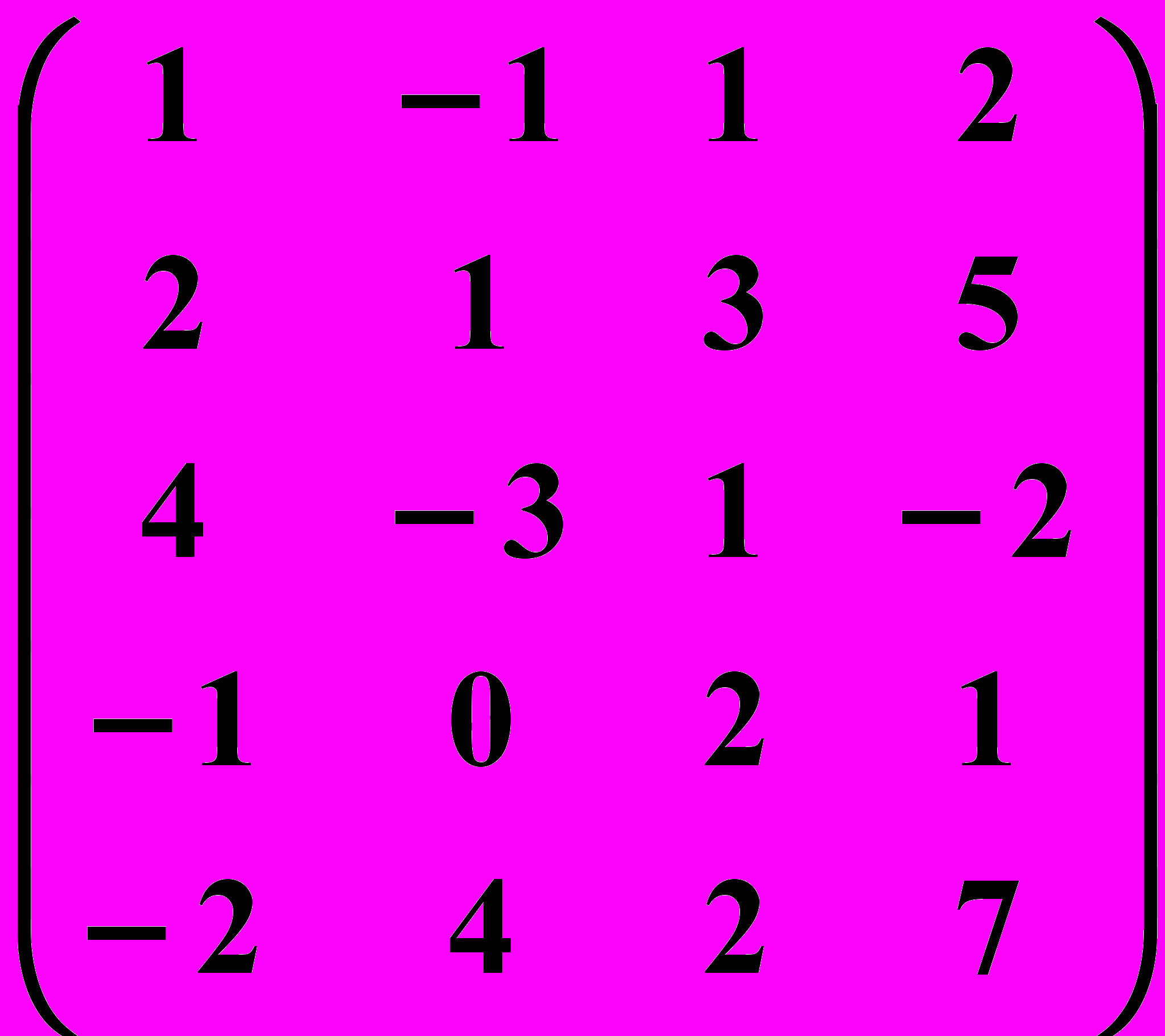
1.4.

1.5.
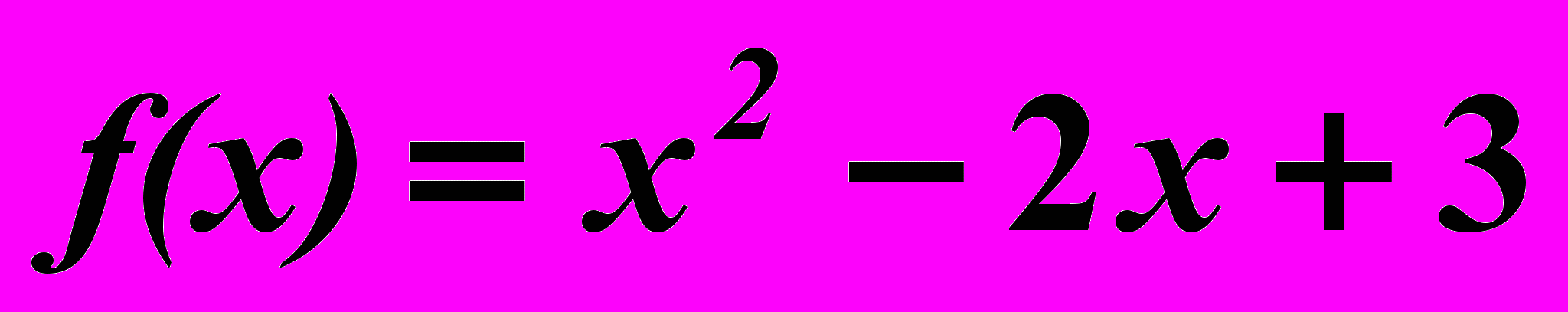 ,
, 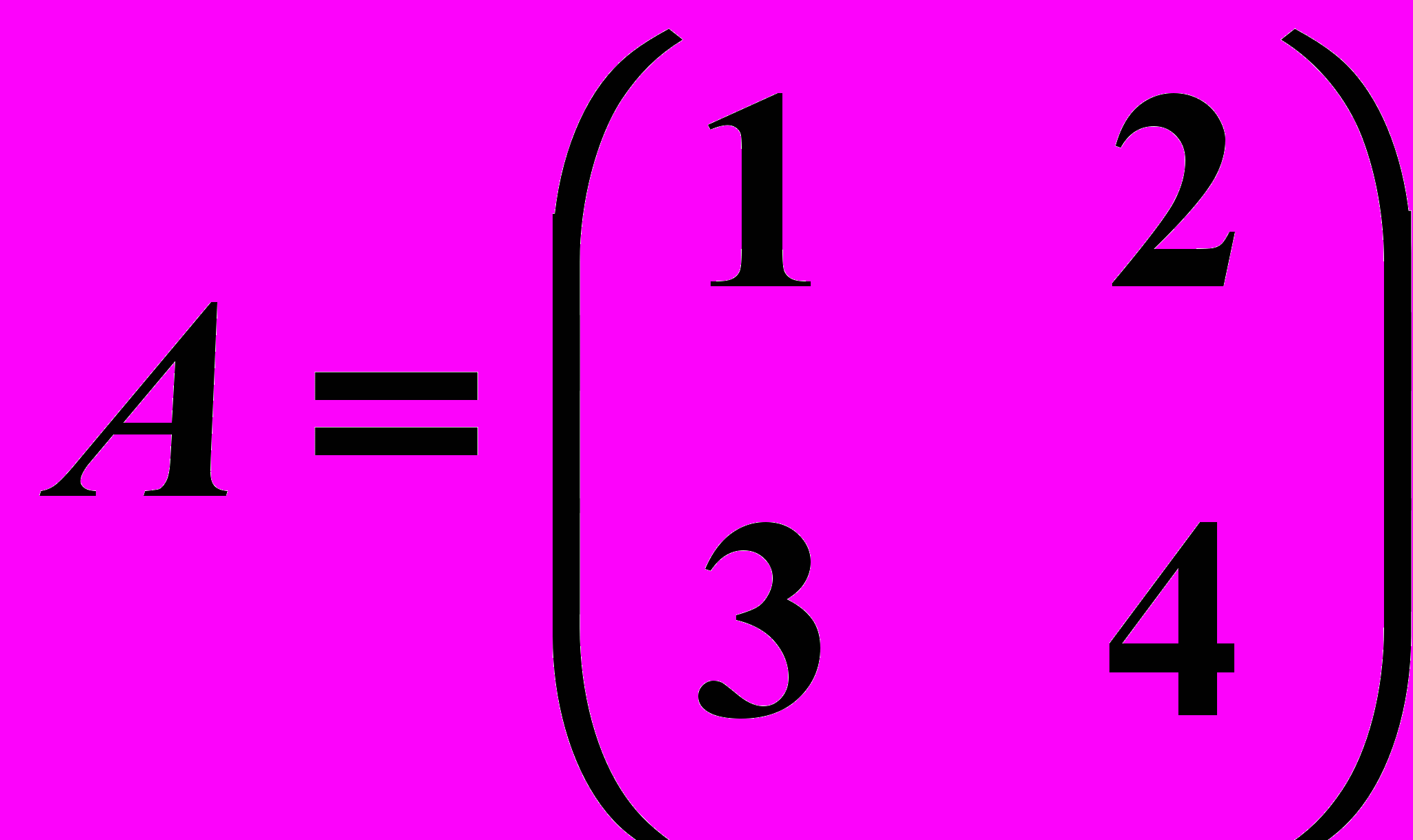 1.6.
1.6.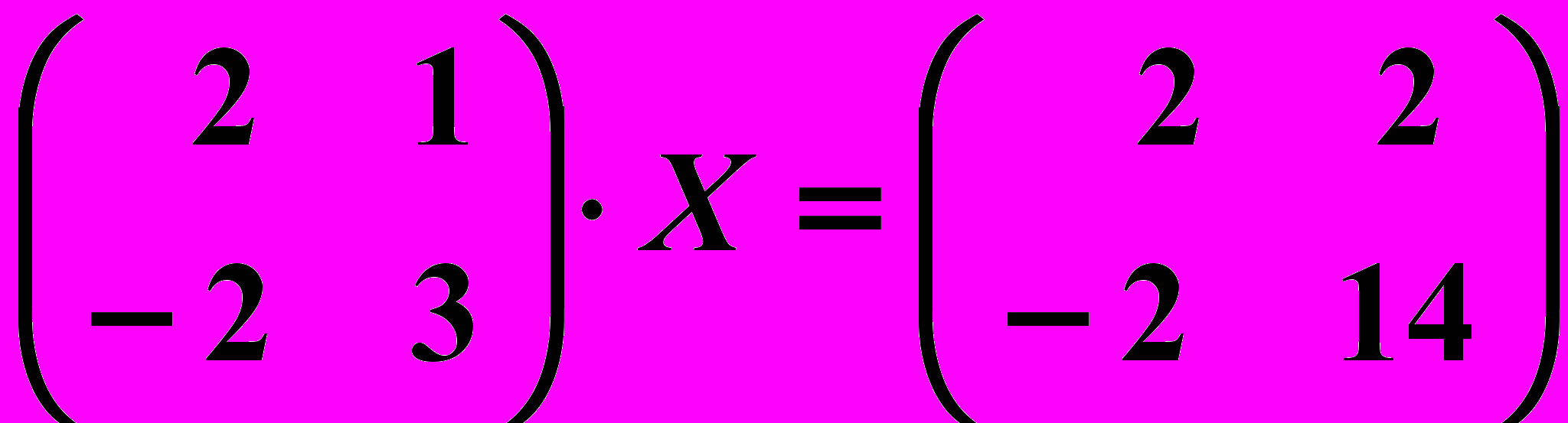
Вариант № 2
2.1.
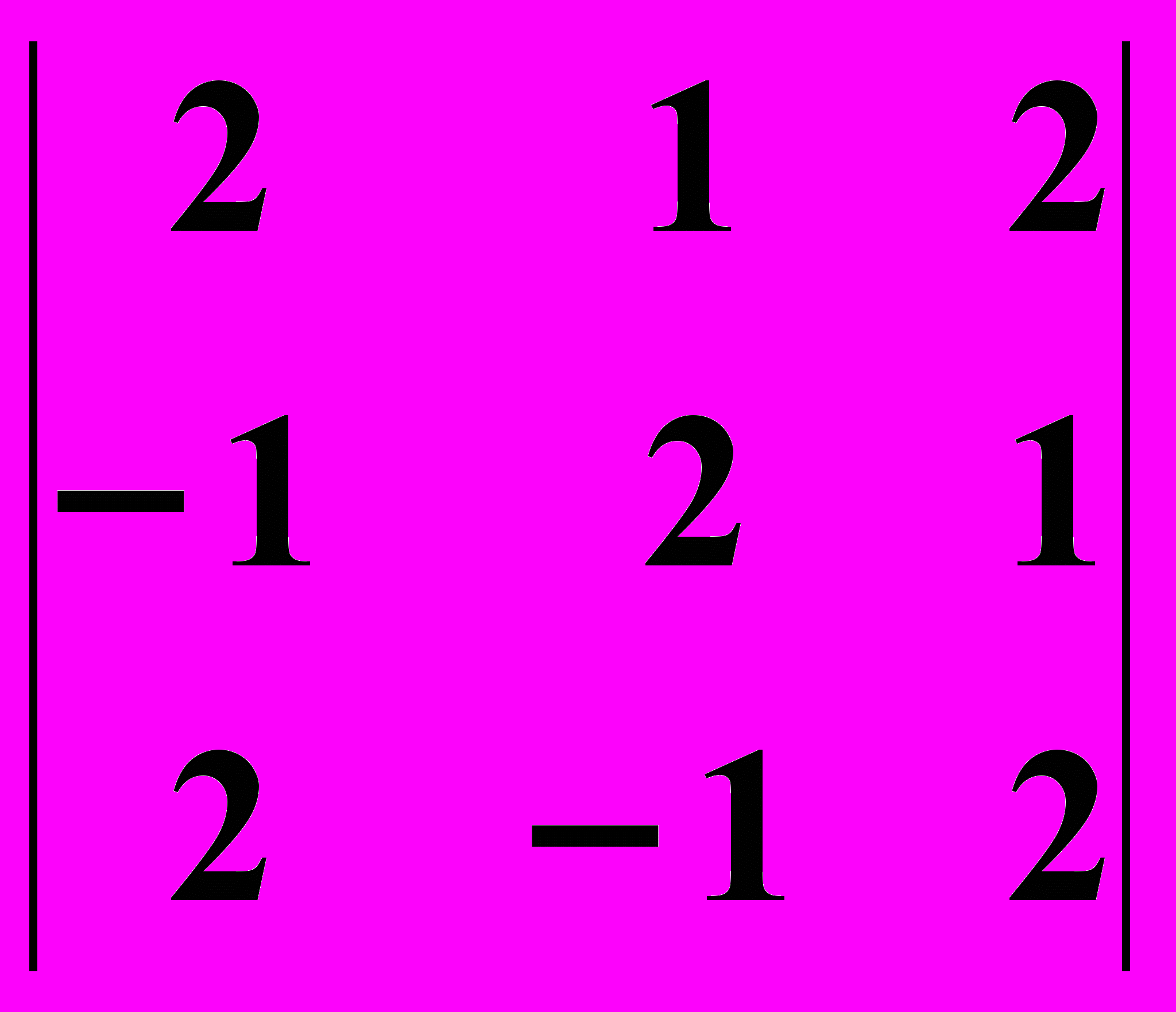 2.2.
2.2. 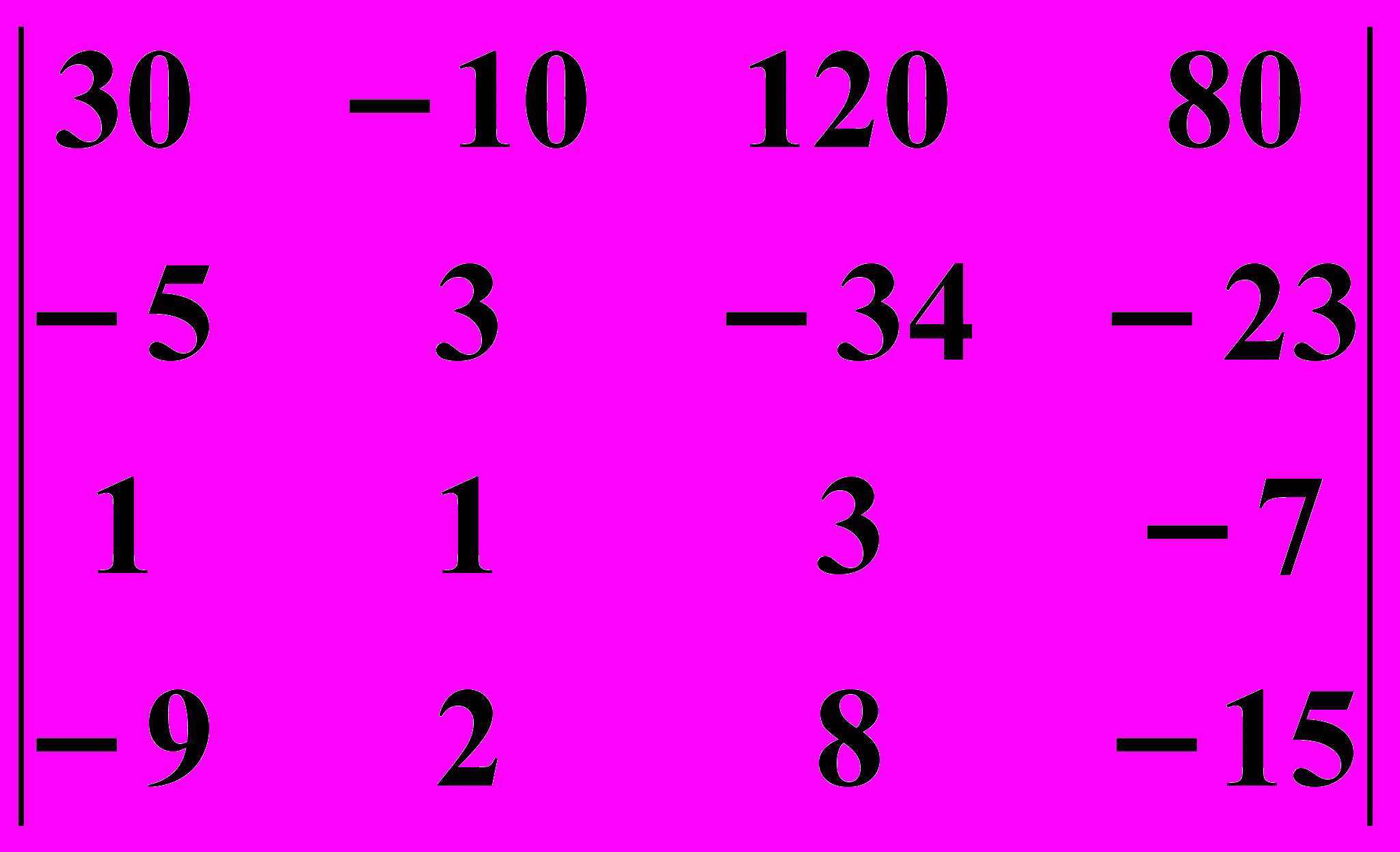 2.3.
2.3. 
2.4.

2.5.
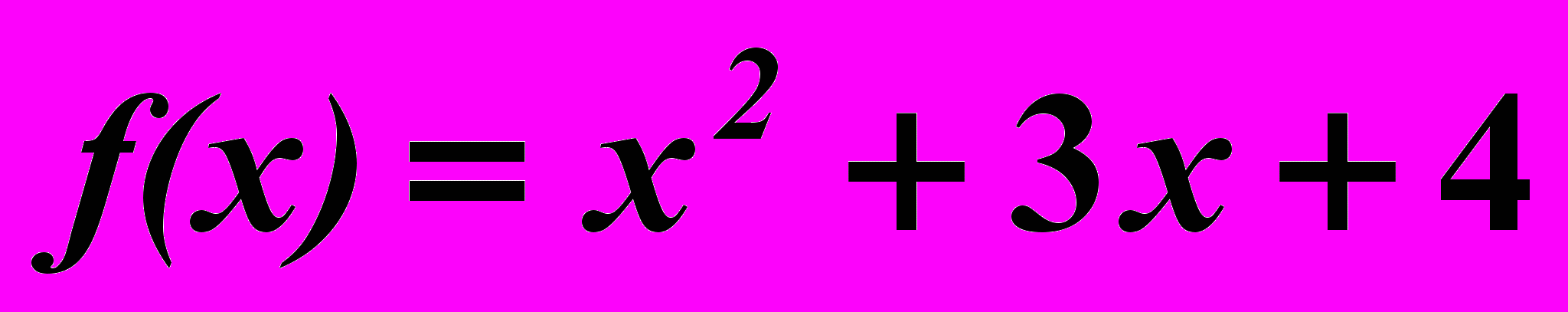 ,
, 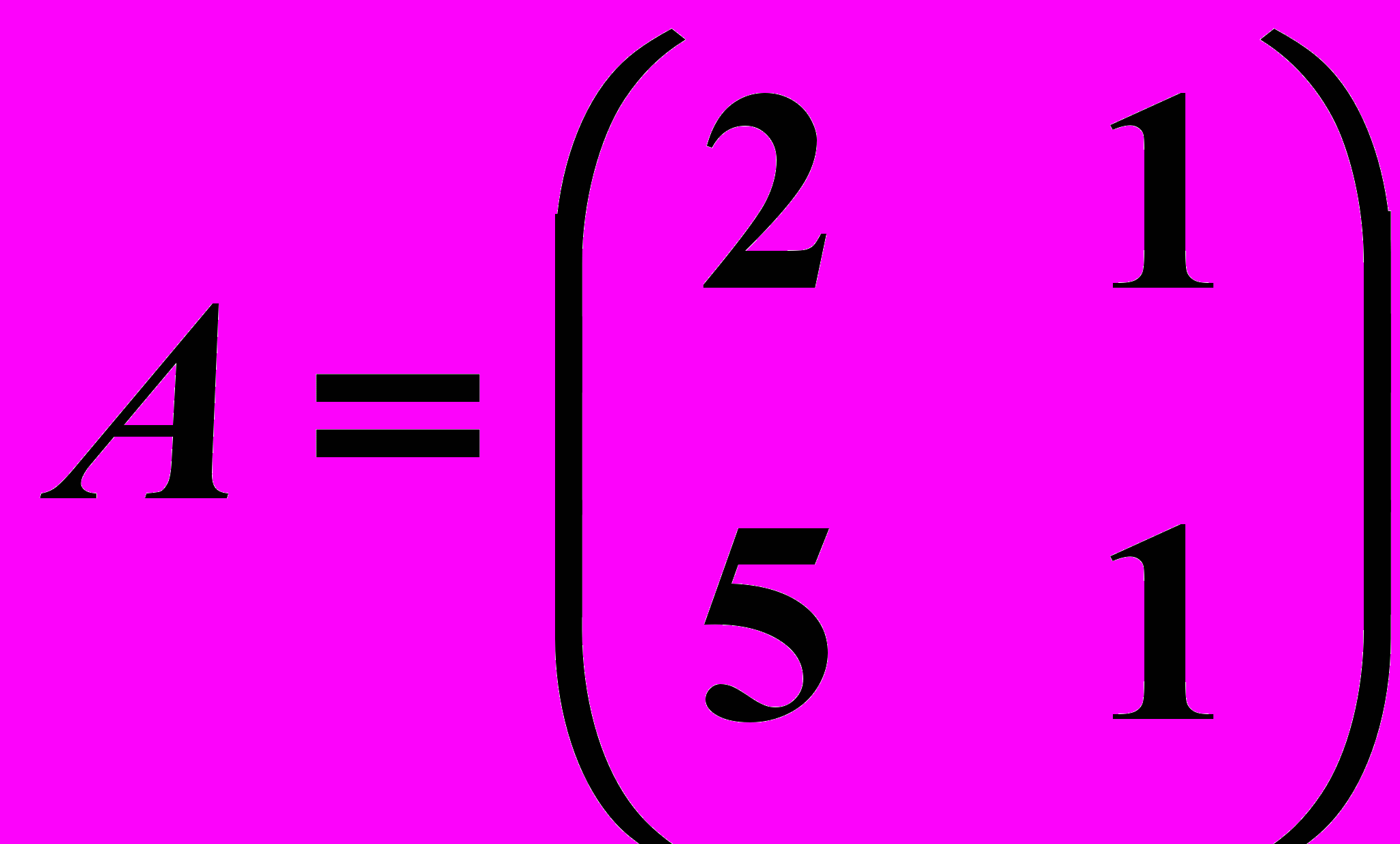 2.6.
2.6. 
Вариант № 3
3.1
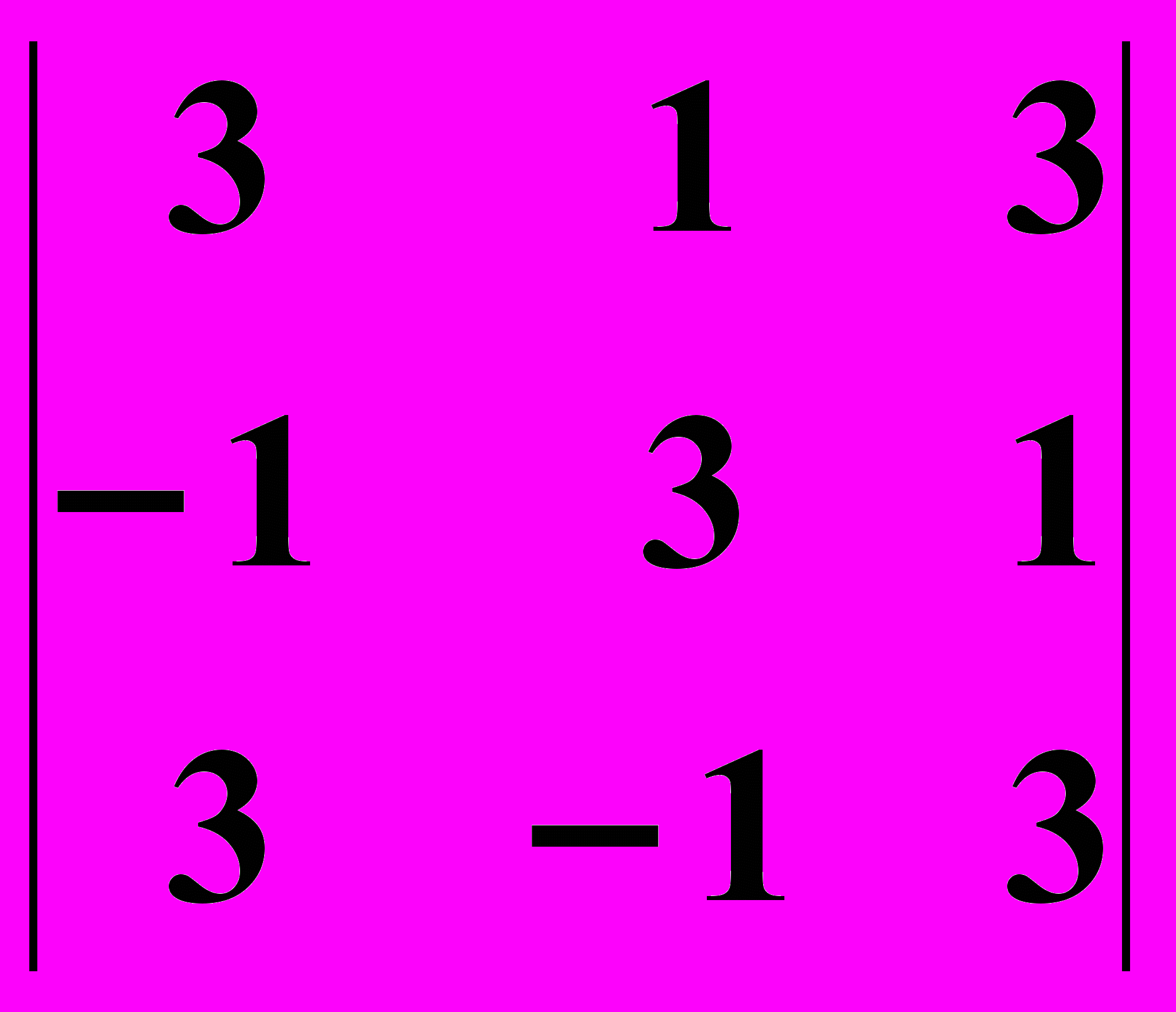 3.2.
3.2.  3.3.
3.3. 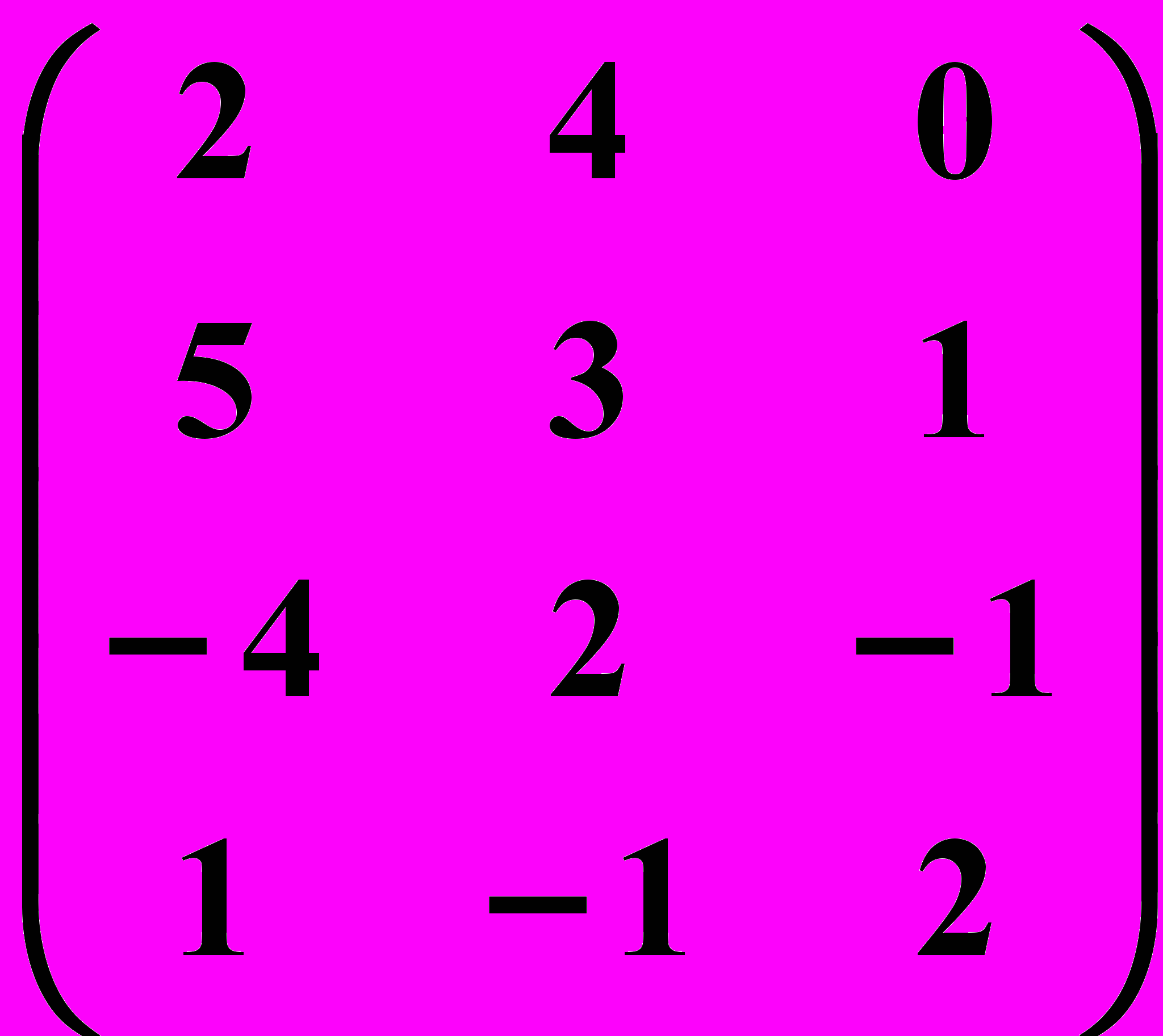
3.4.
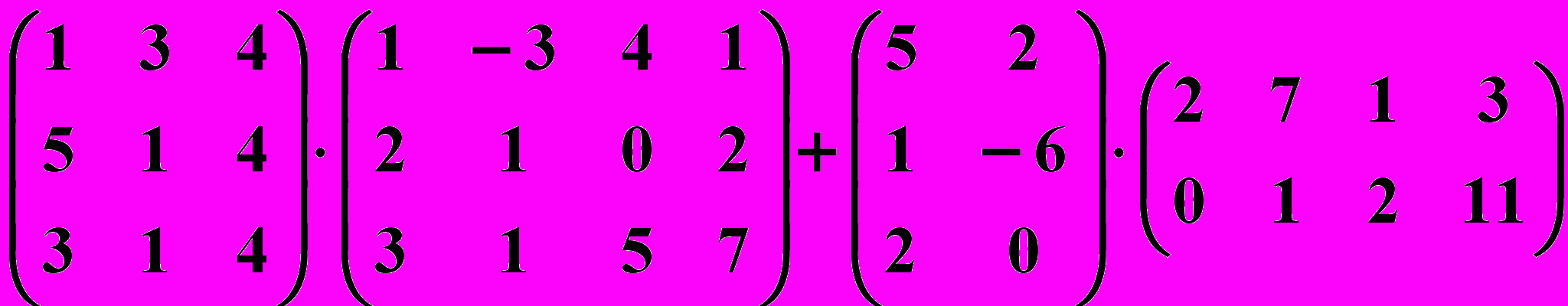
3.5.
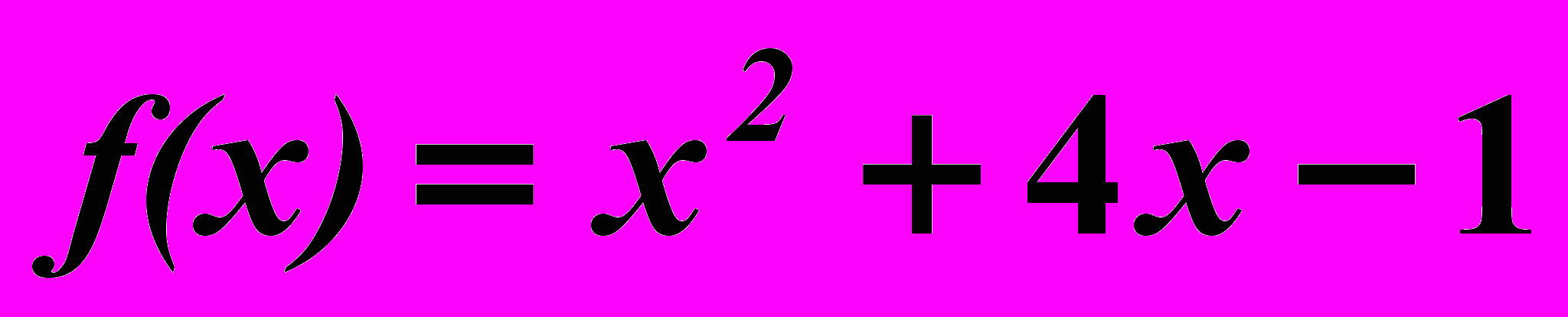 ,
,  3.6.
3.6.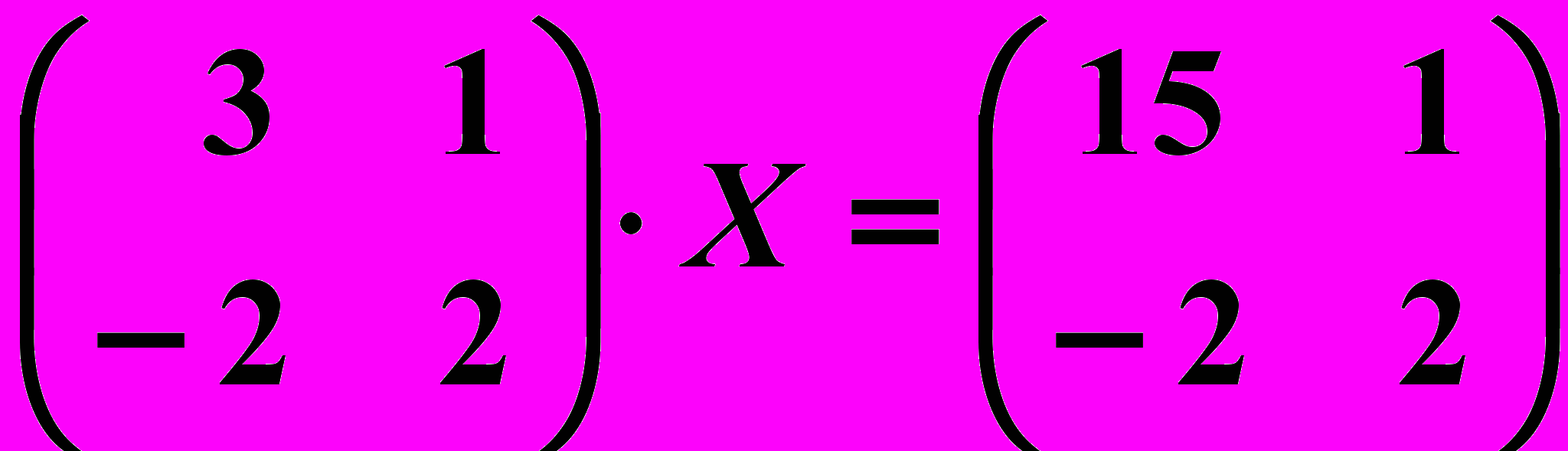
Вариант № 4
4. 1.
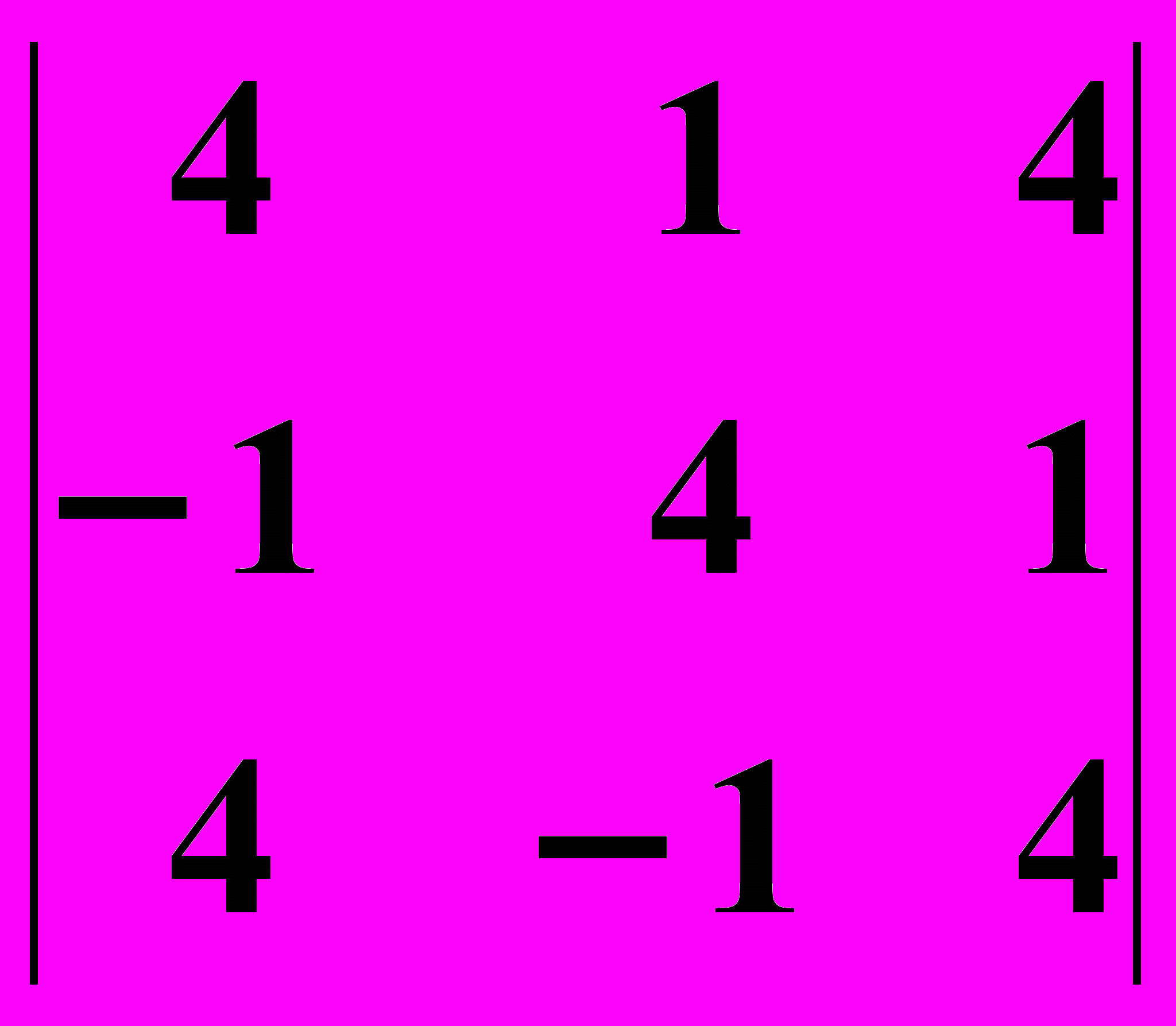 4.2.
4.2. 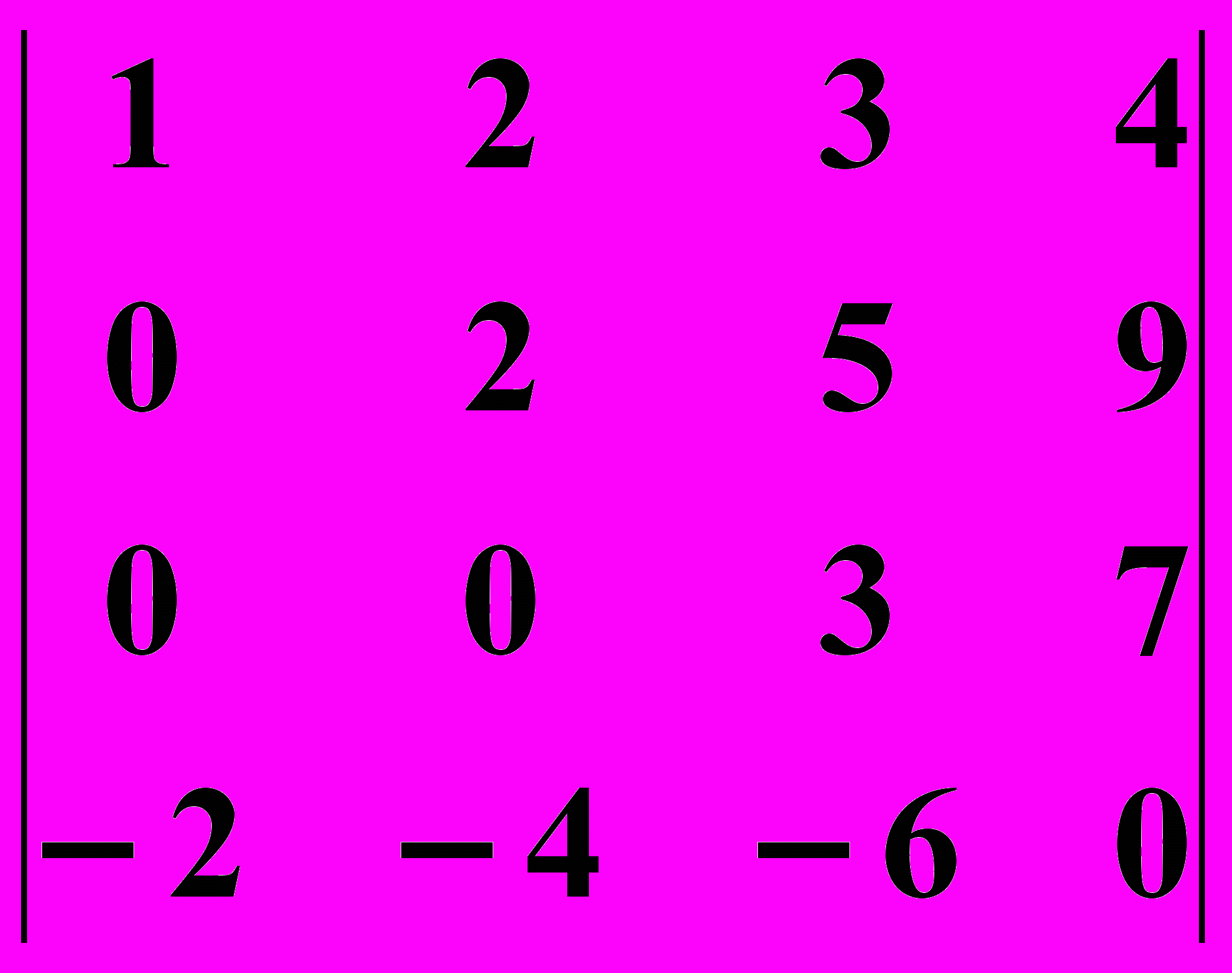 4.3.
4.3. 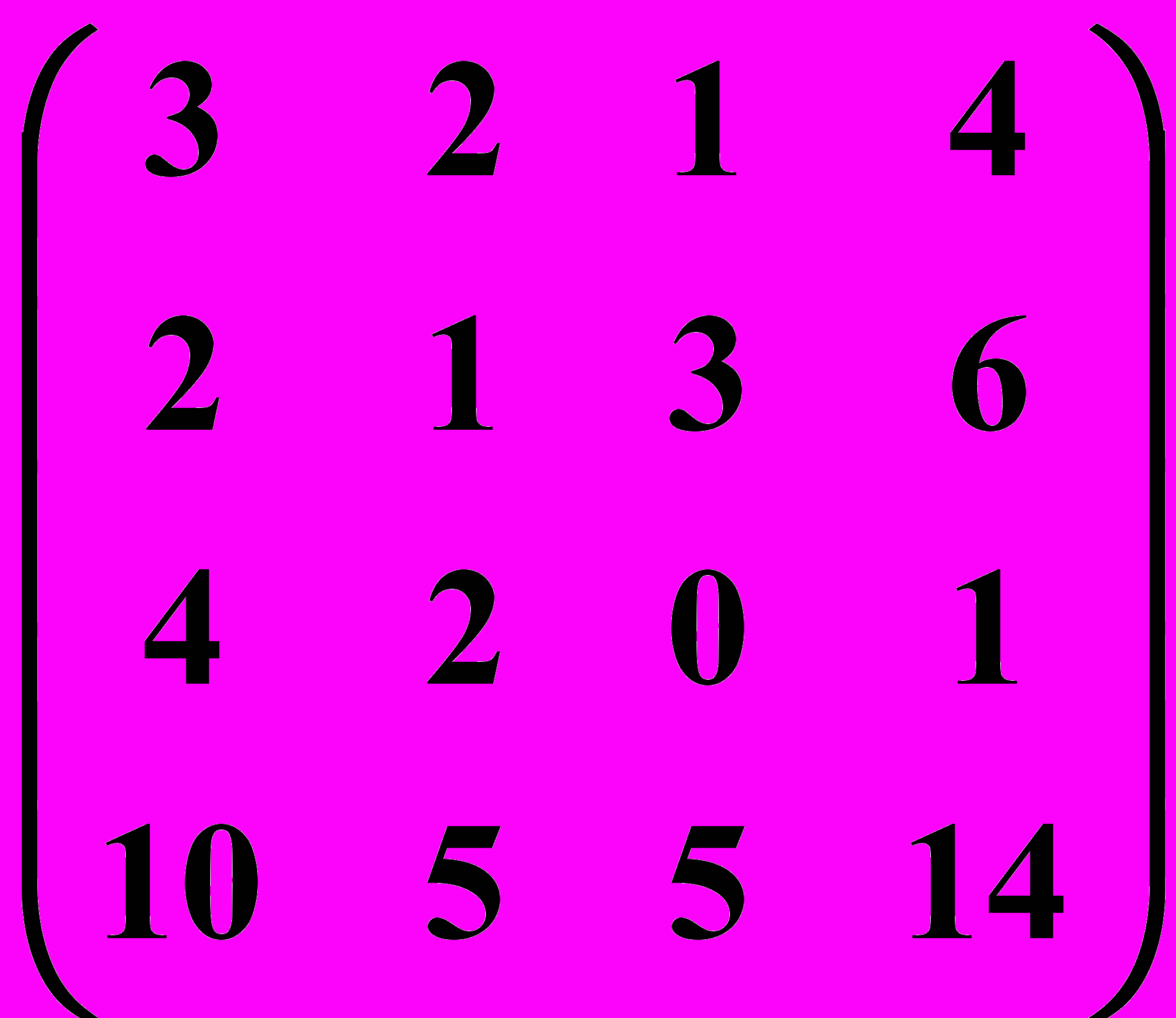
4.4.

4.5.
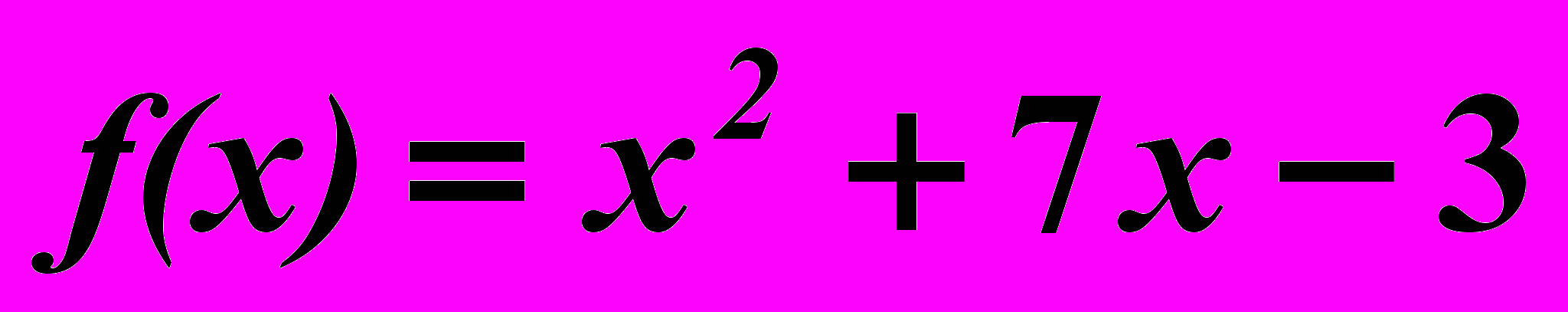 ,
, 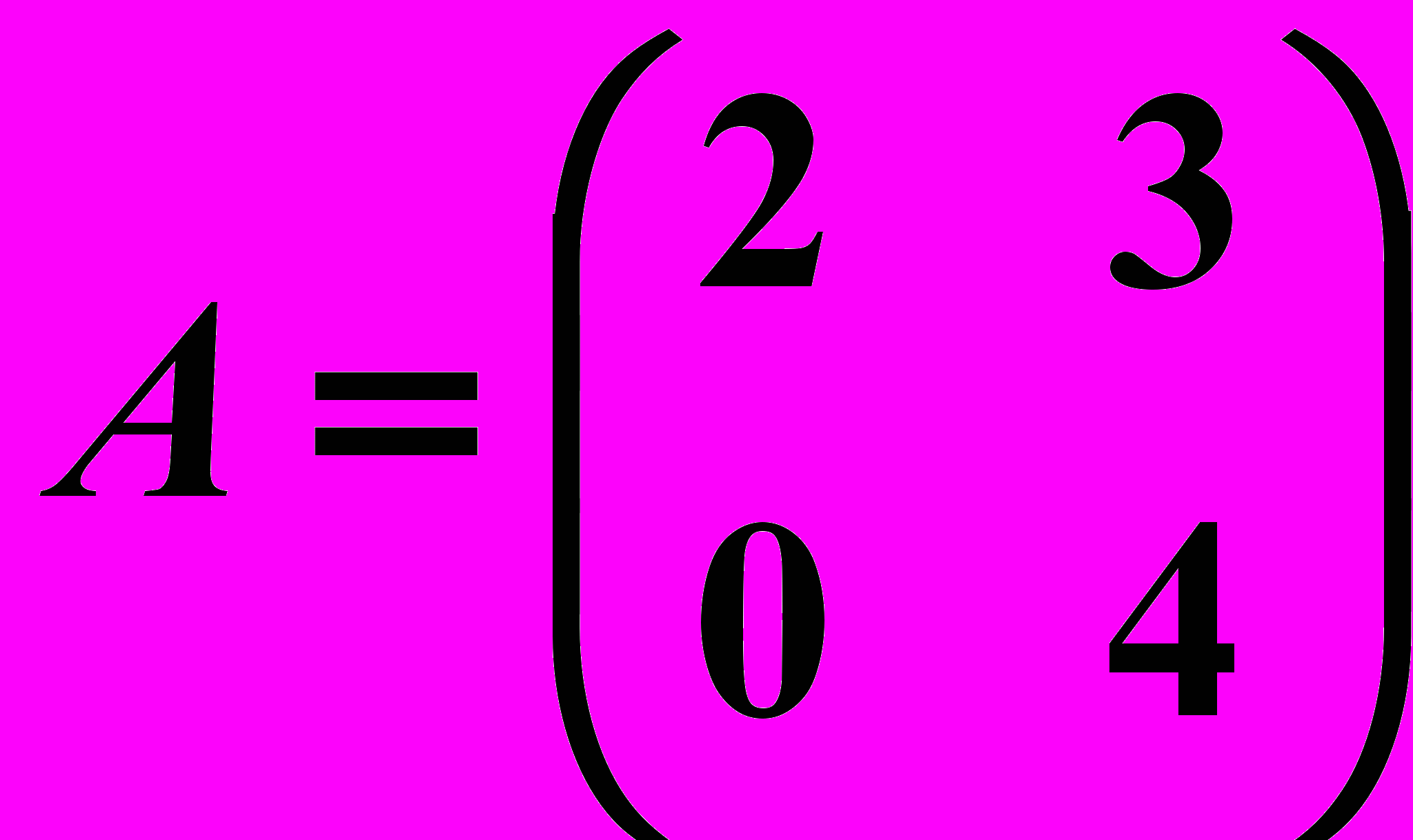 4. 6.
4. 6. 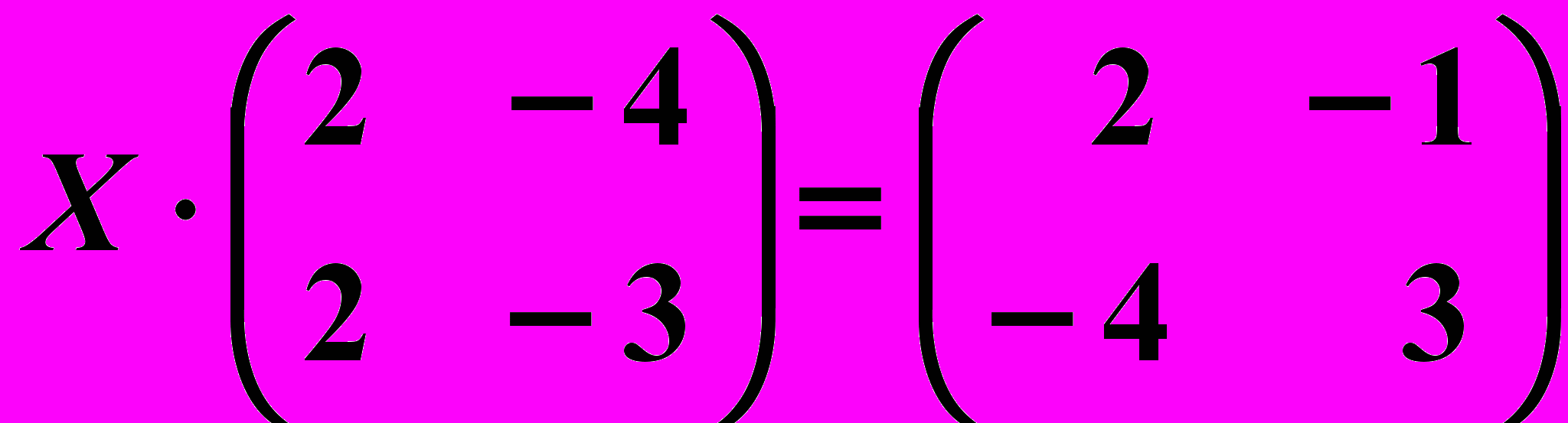
Вариант № 5
5.1.
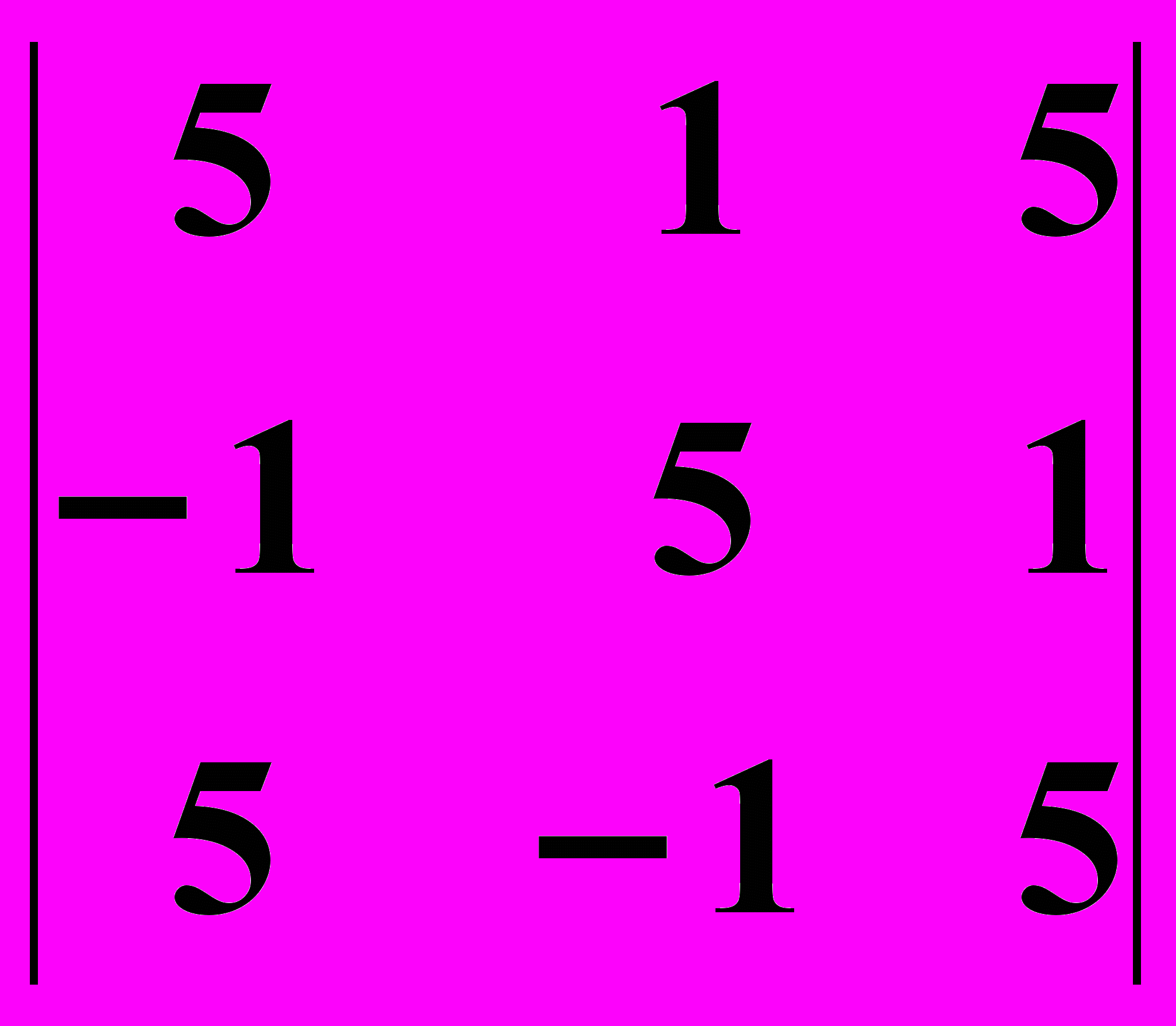 5.2.
5.2.  5.3.
5.3. 
5.4.
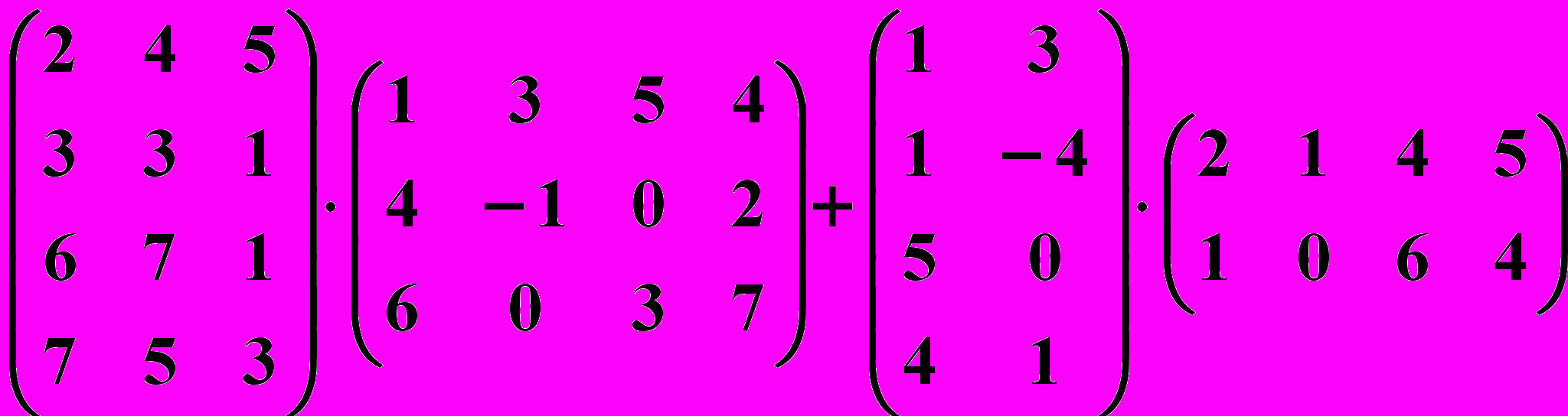
5.5.
 ,
,  5.6.
5.6.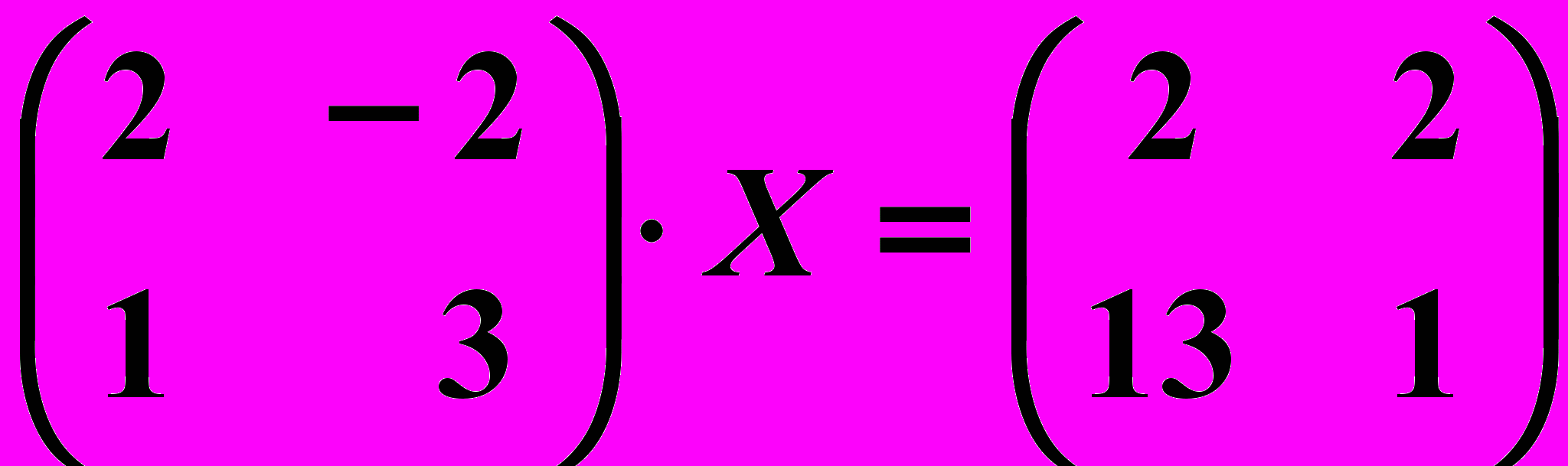
Вариант № 6
6.1.
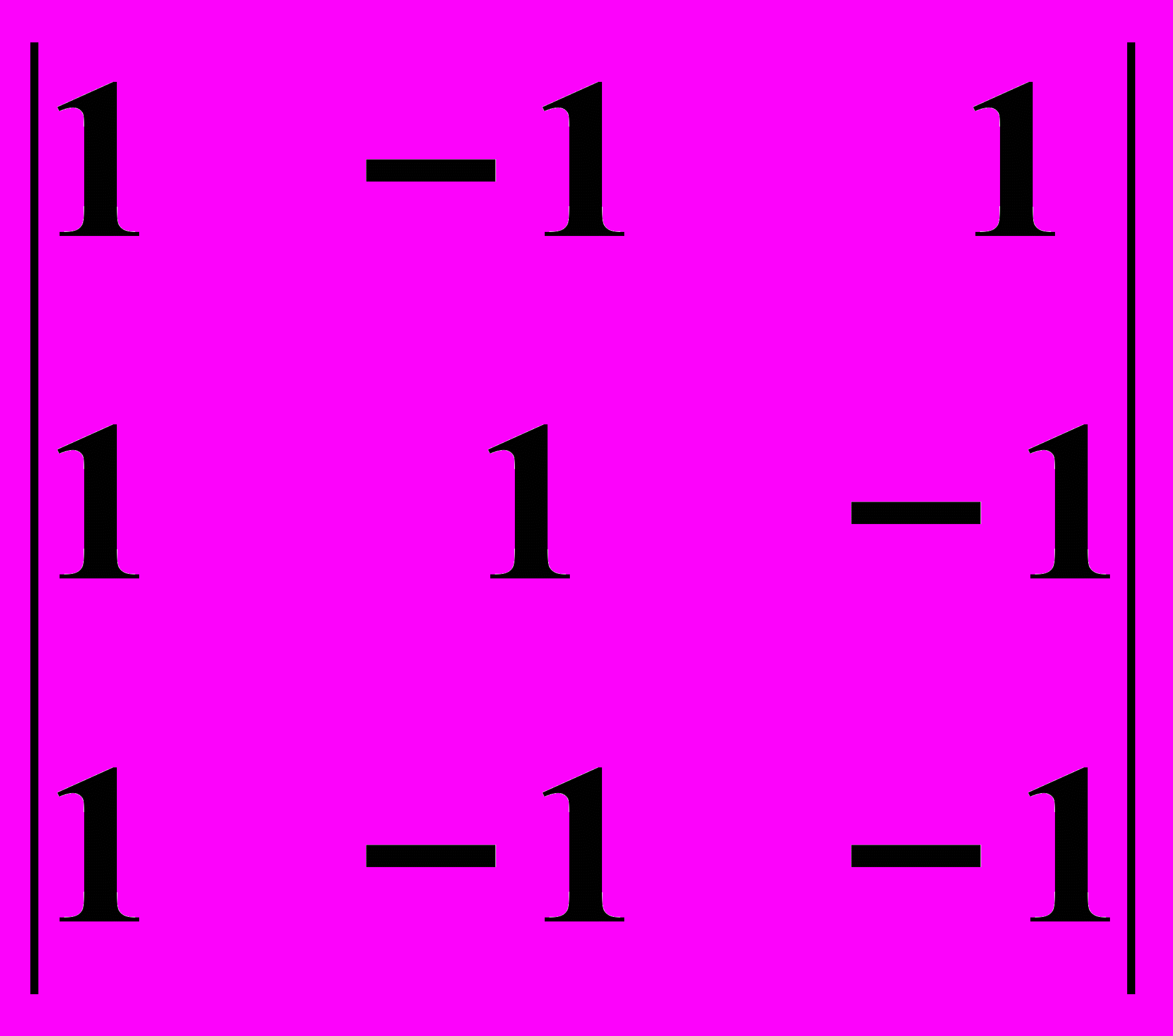 6.2.
6.2.  6.3.
6.3. 
6.4.

6.5.
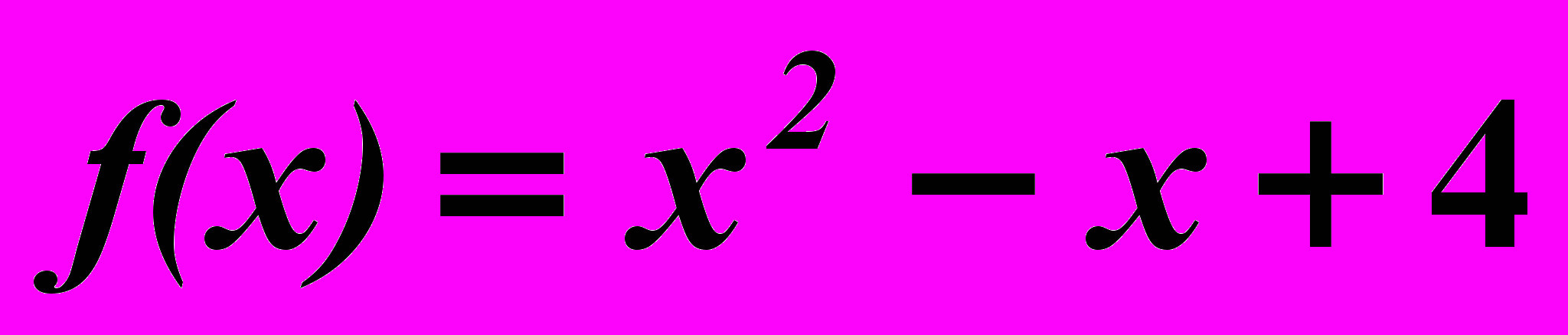 ,
, 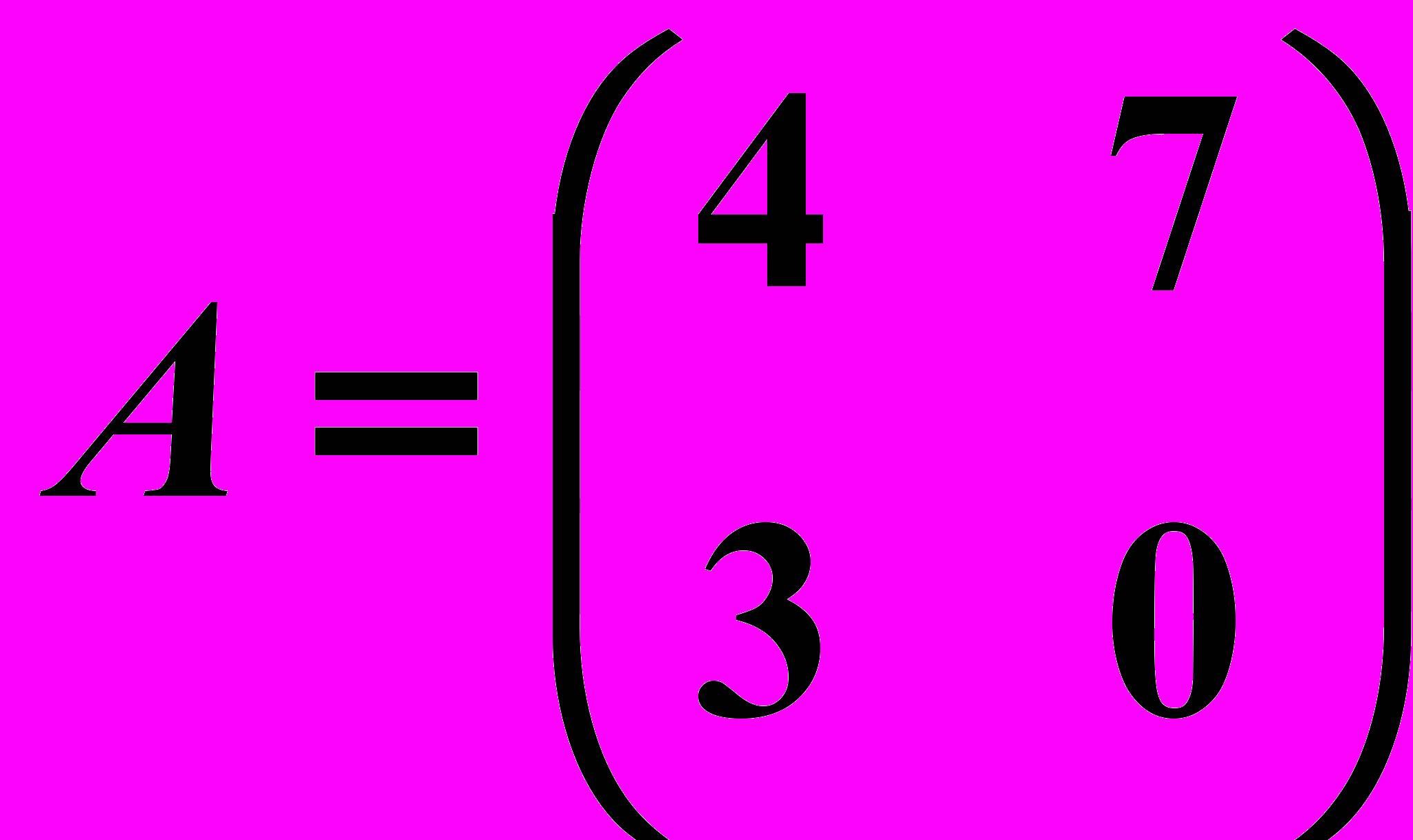 6.6.
6.6. 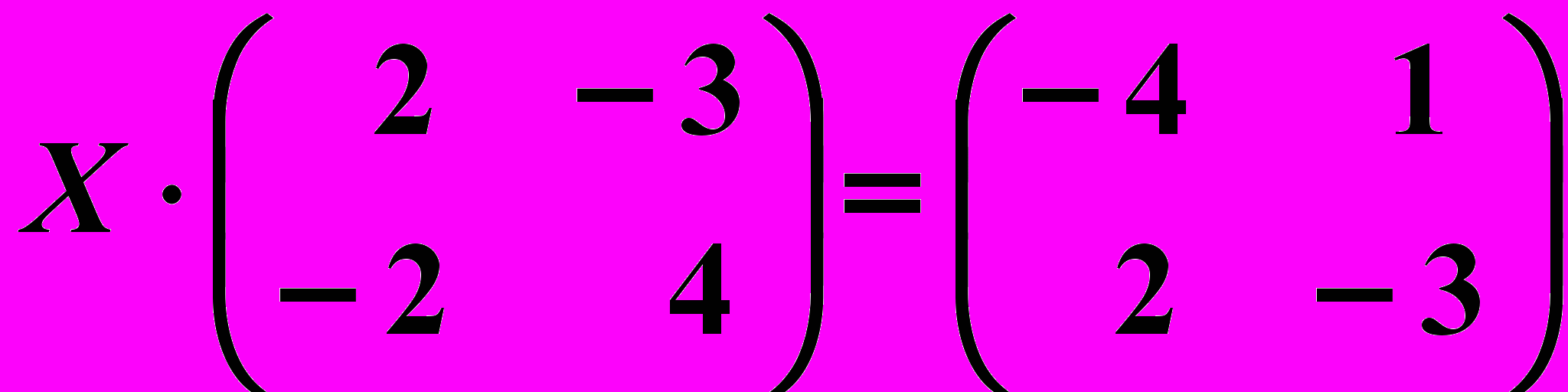
Вариант № 7
7.1.
 7.2.
7.2. 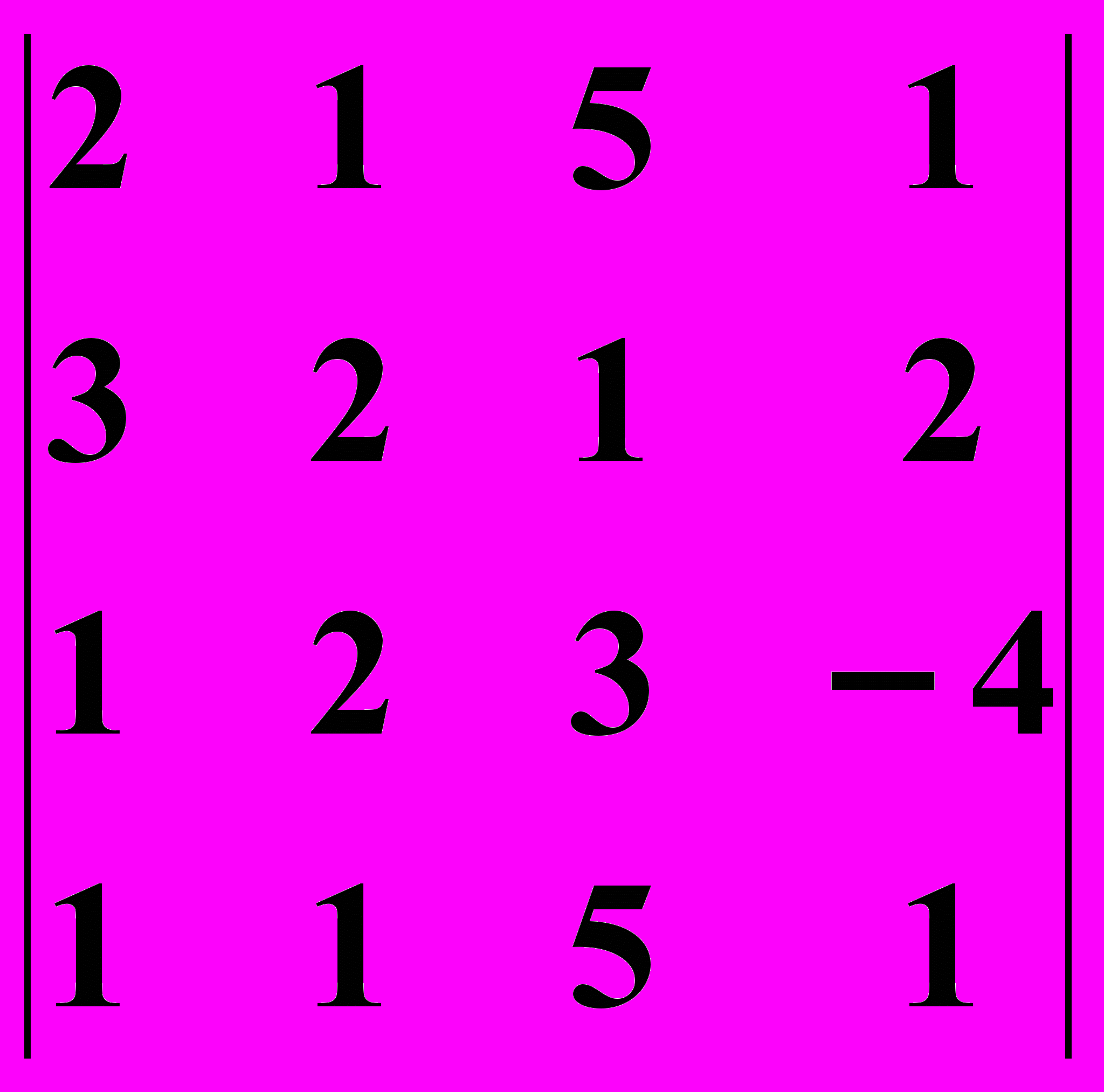 7.3.
7.3.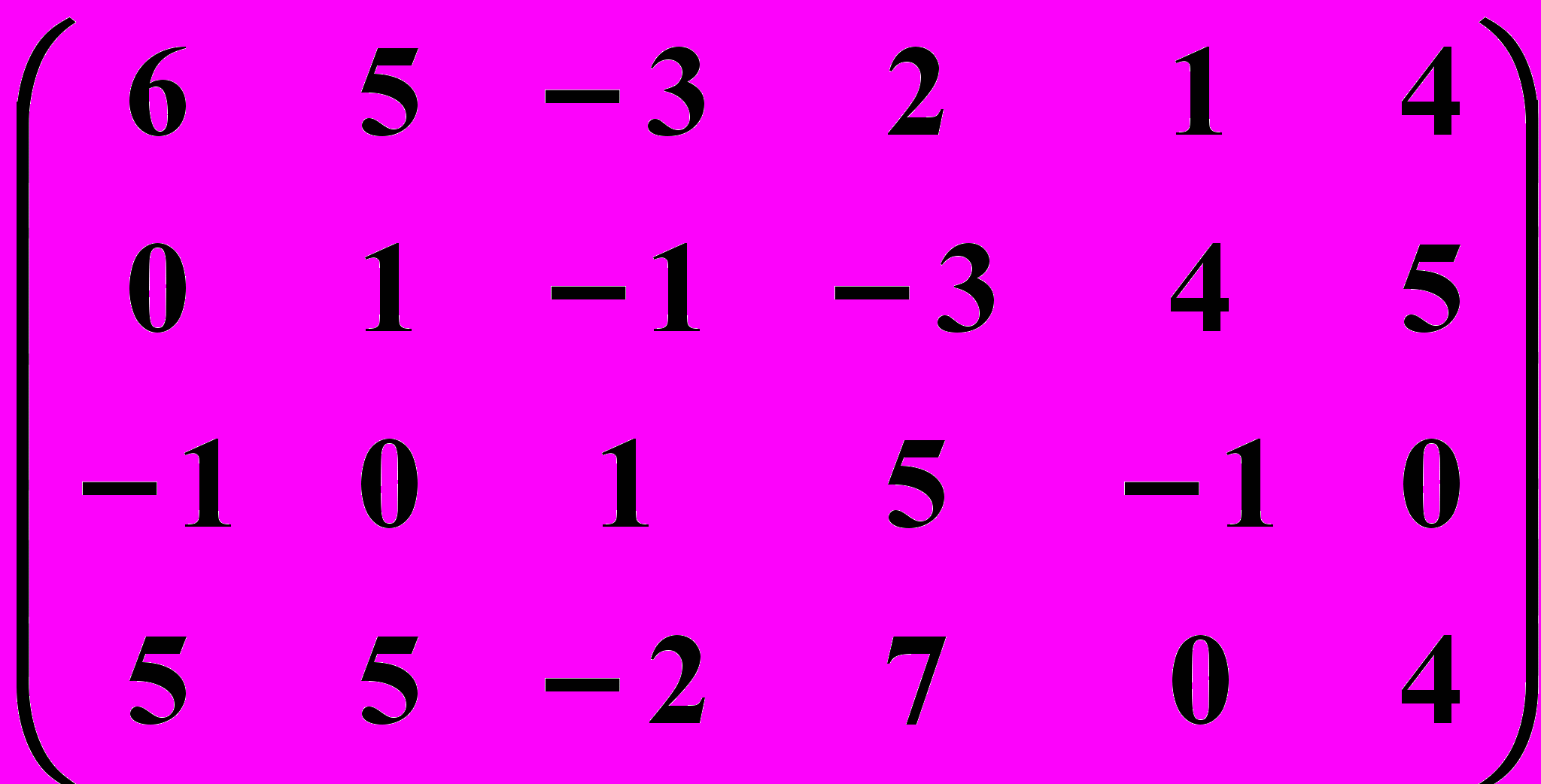
7.4.

7.5.
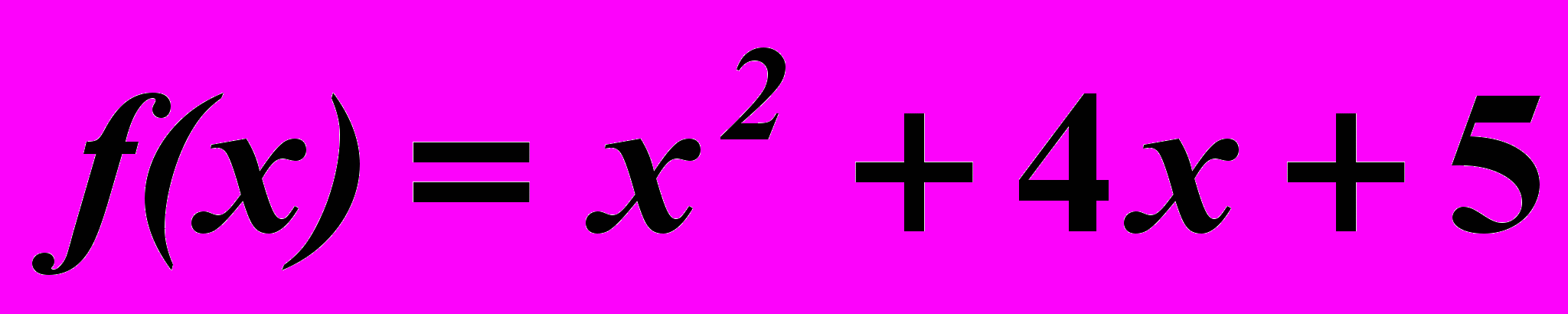 ,
,  7. 6.
7. 6. 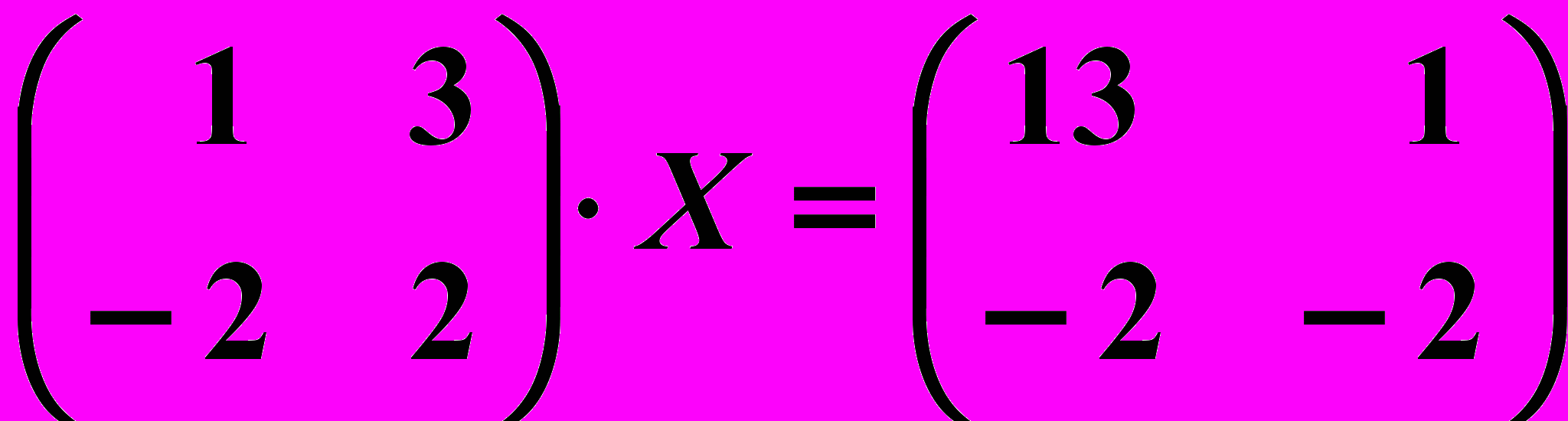
Вариант № 8
8.1.
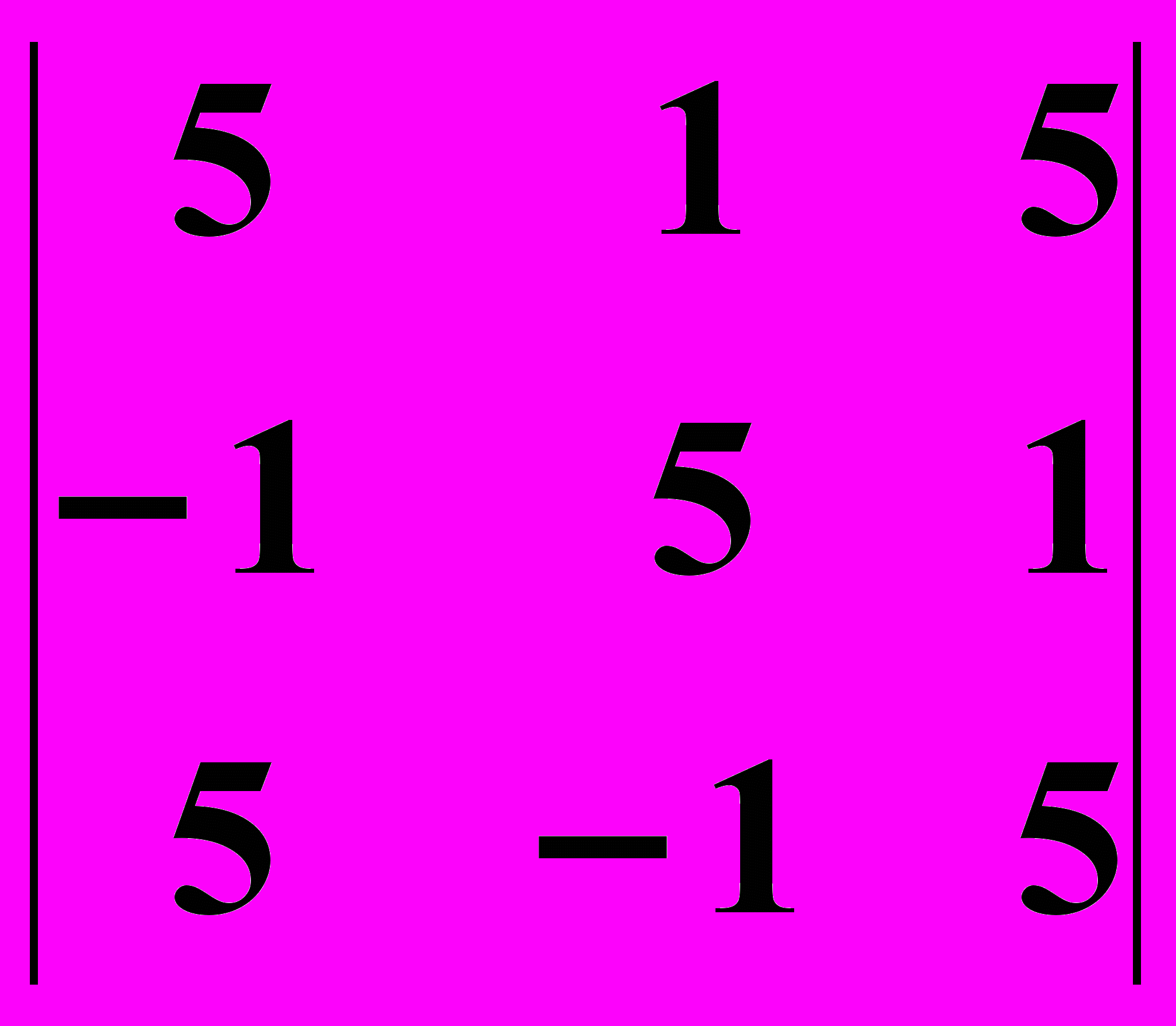 8.2.
8.2.  8.3.
8.3. 
8.4.

8.5.
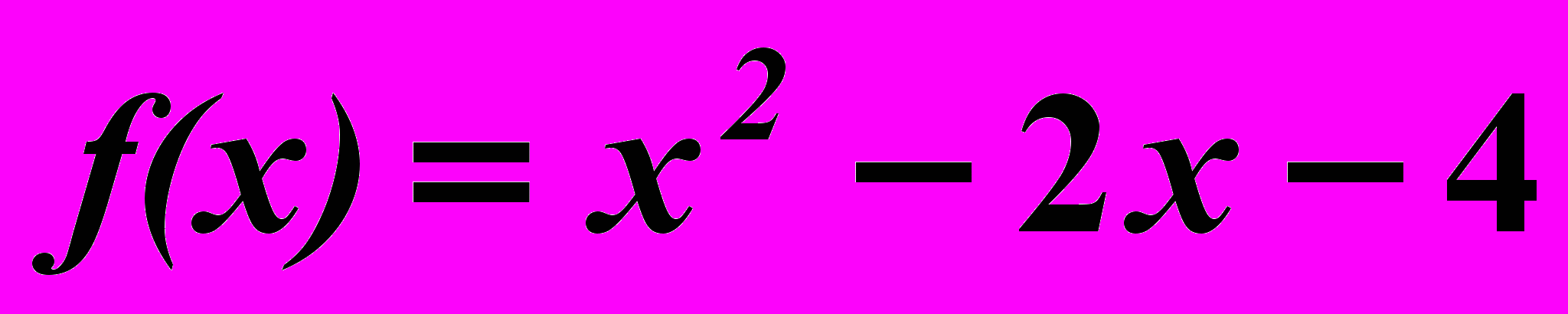 ,
,  8.6.
8.6. 
Вариант № 9
9.1.
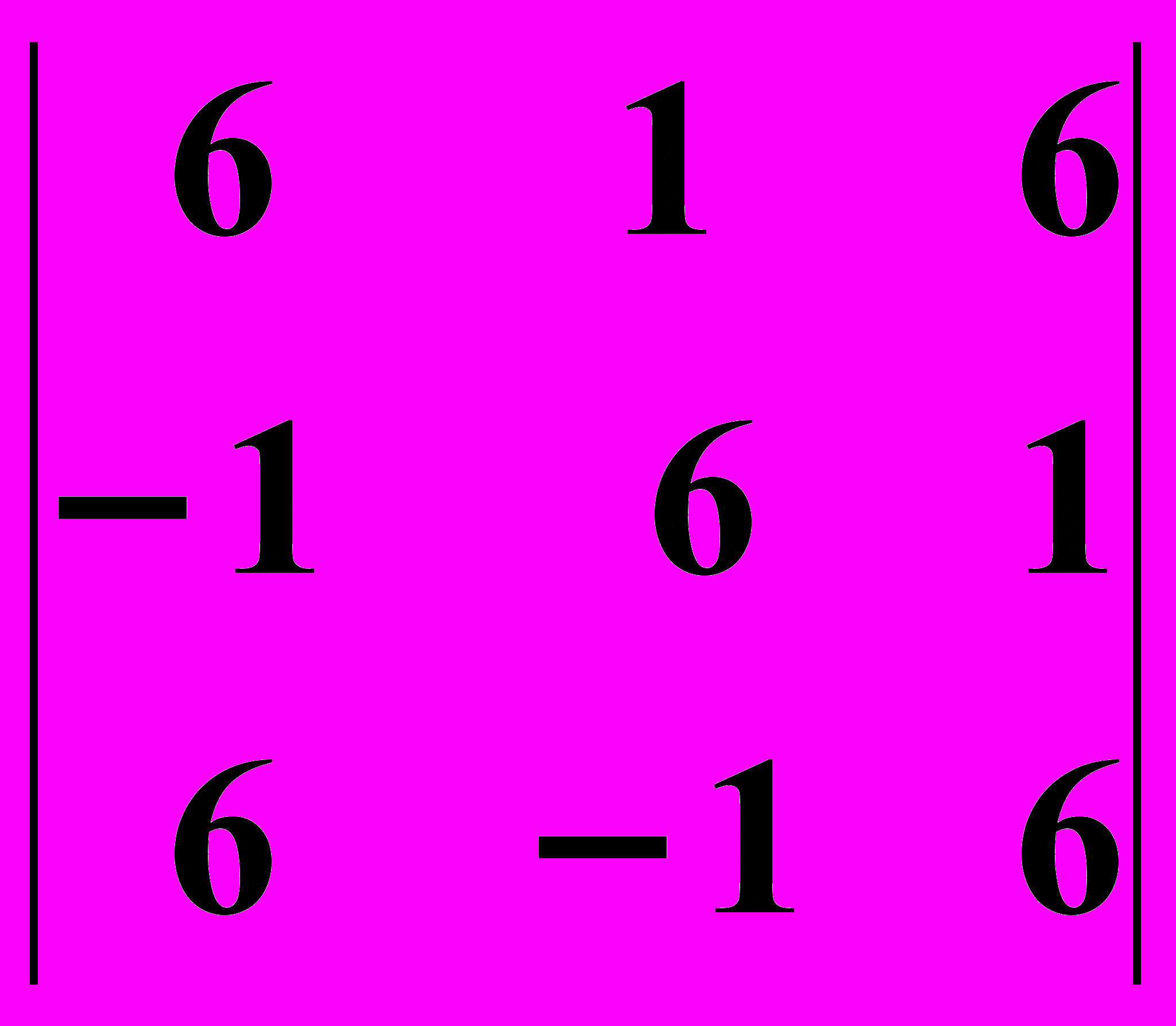 9.2.
9.2. 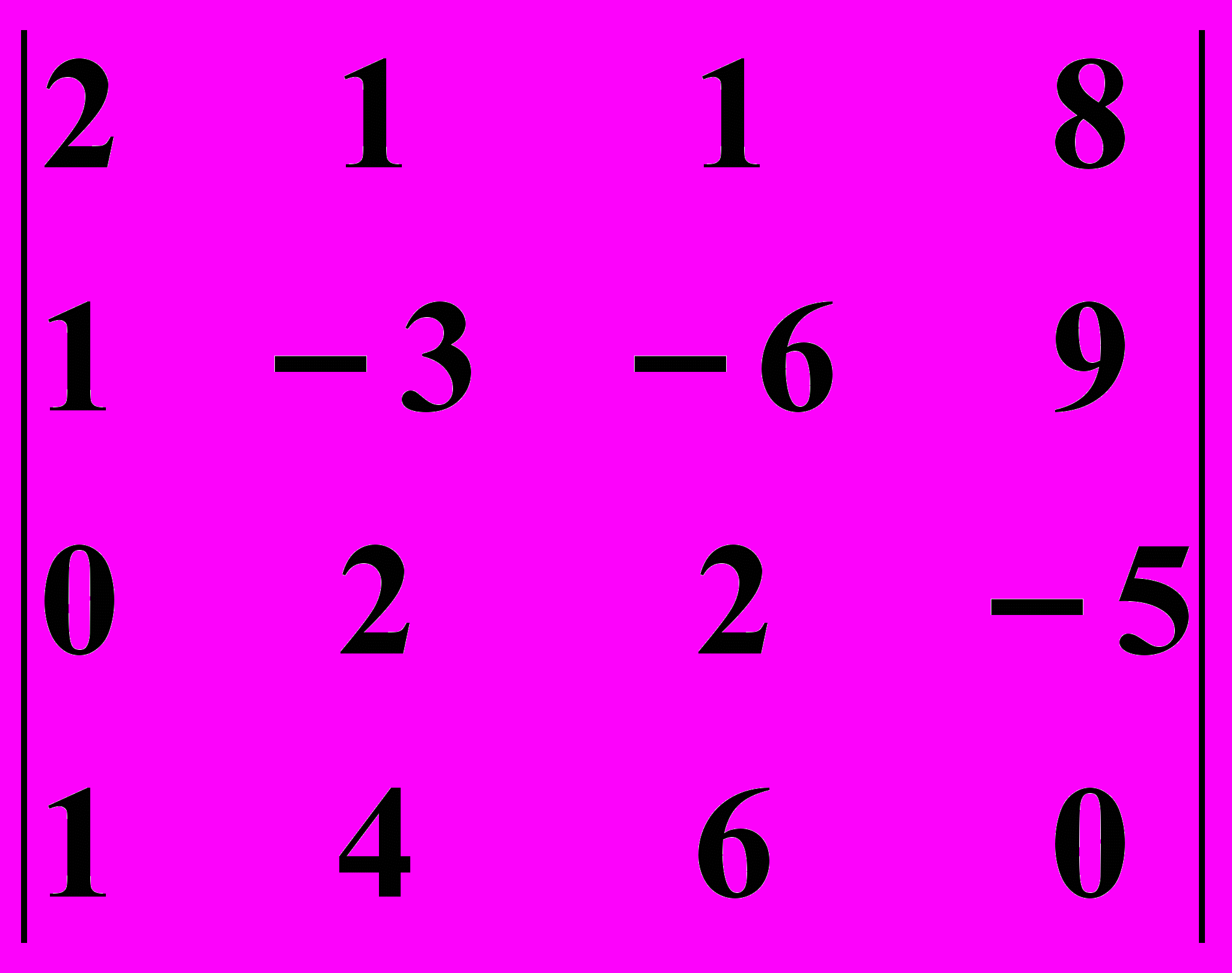 9.3.
9.3. 
9.4.

9.5.
 ,
,  9.6.
9.6. 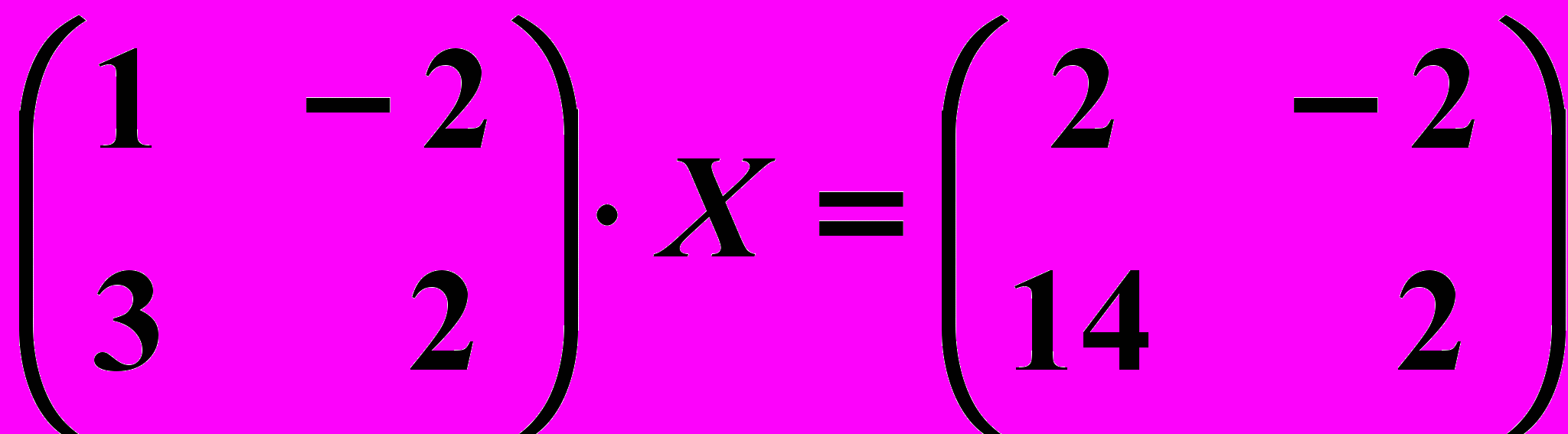
Вариант № 10
10.1.
 10.2.
10.2.  10.3.
10.3.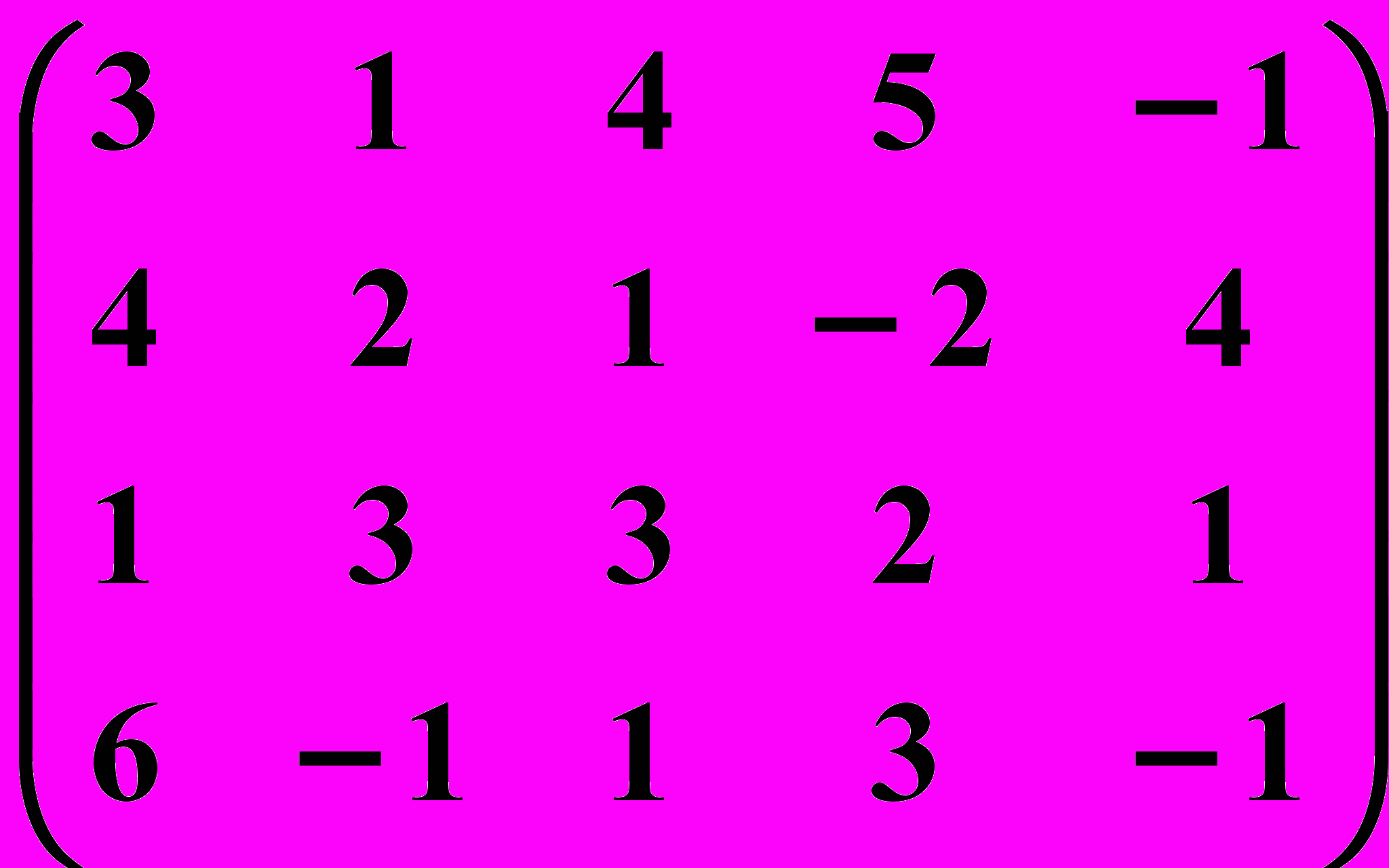
10.4.
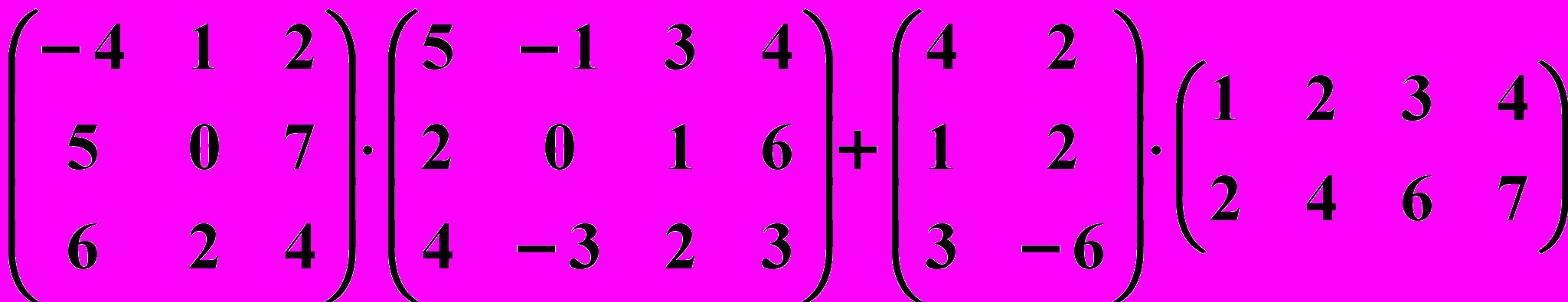
10.5.
 ,
, 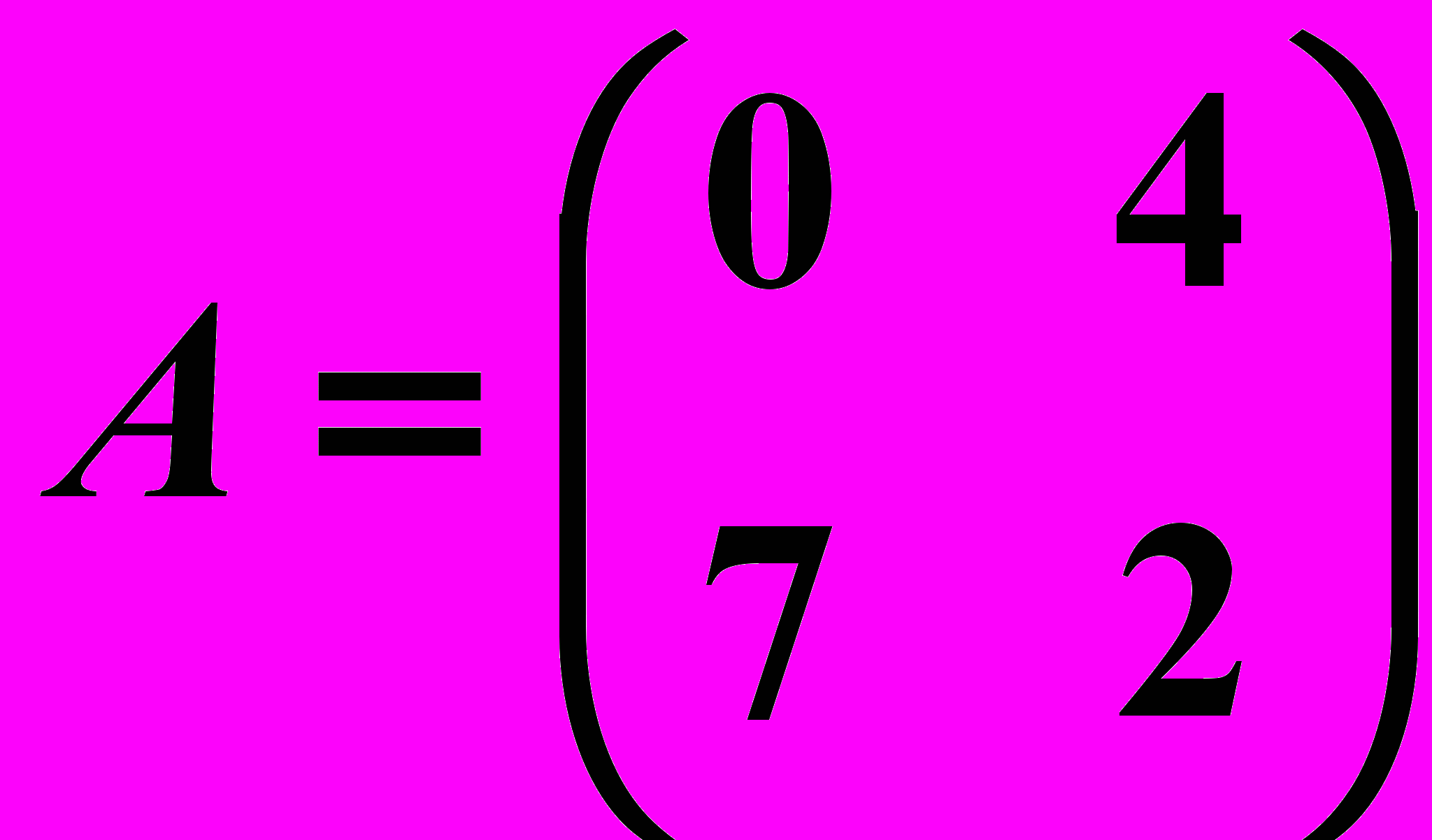 10.6.
10.6. 
Вариант № 11
11.1.
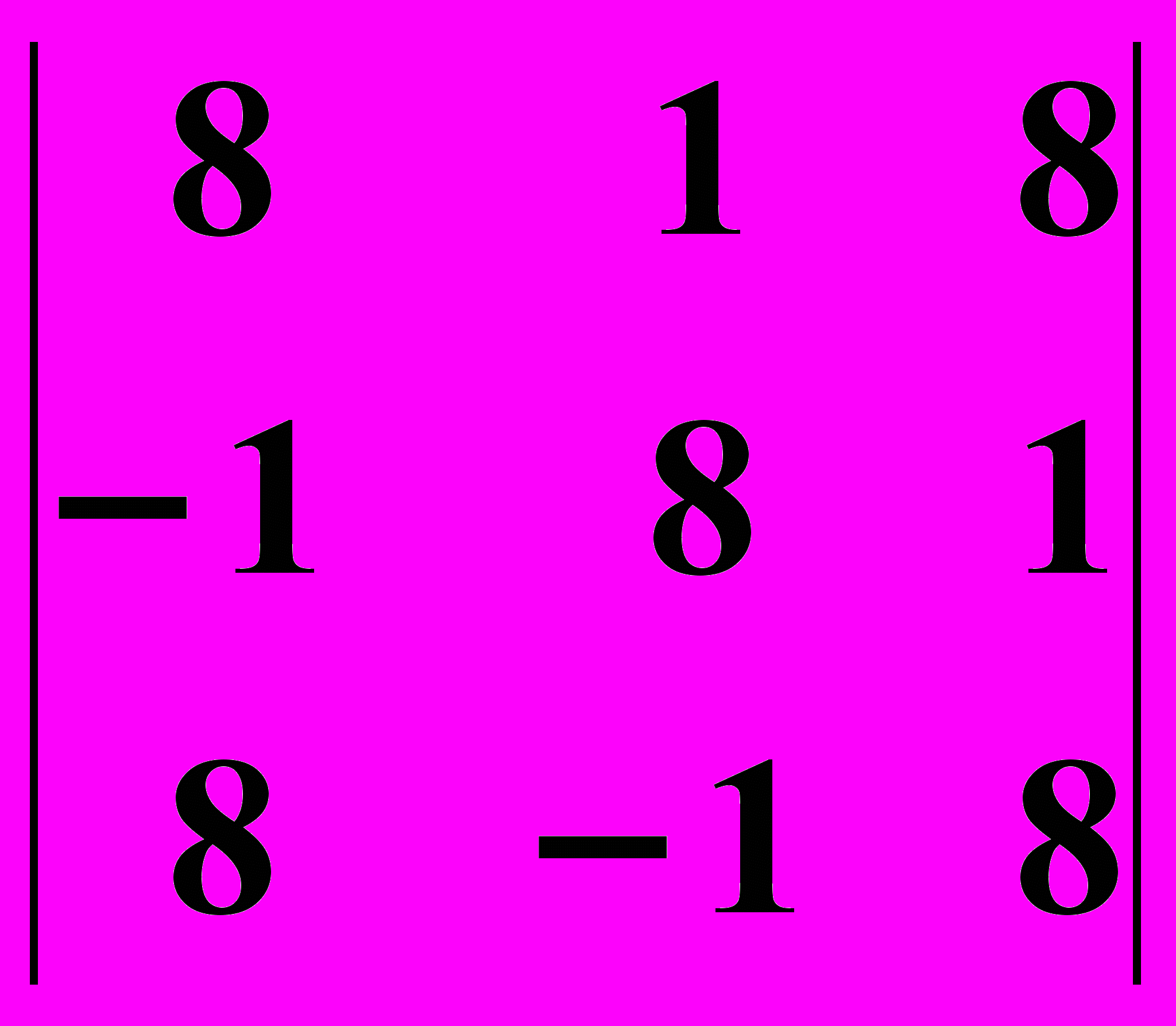 11.2.
11.2.  11.3.
11.3. 
11.4.
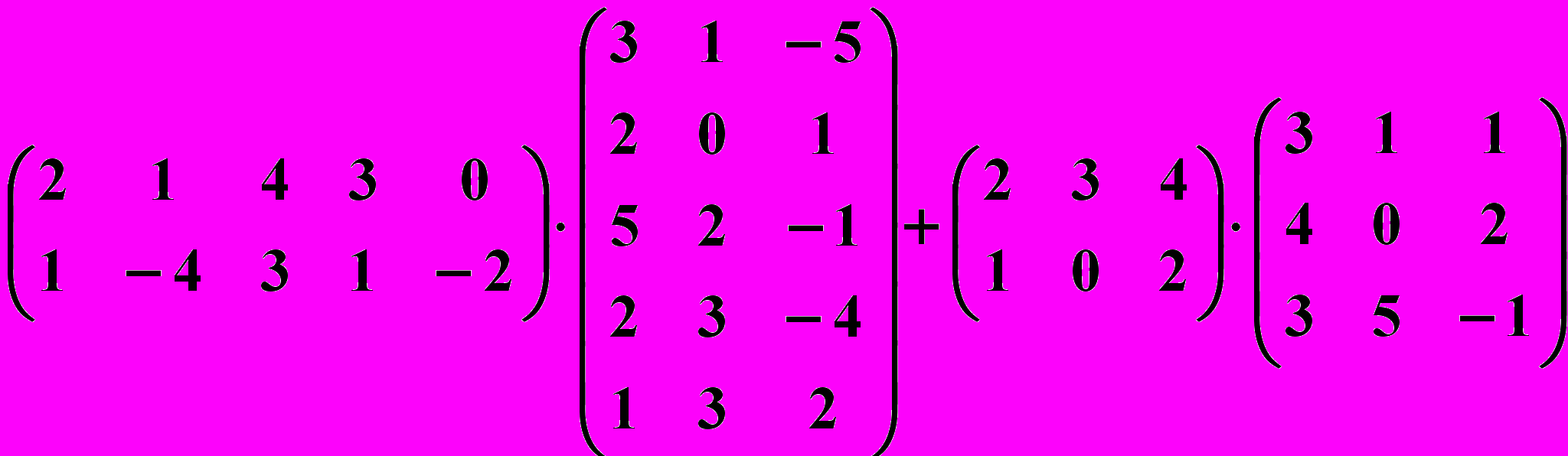
11.5.
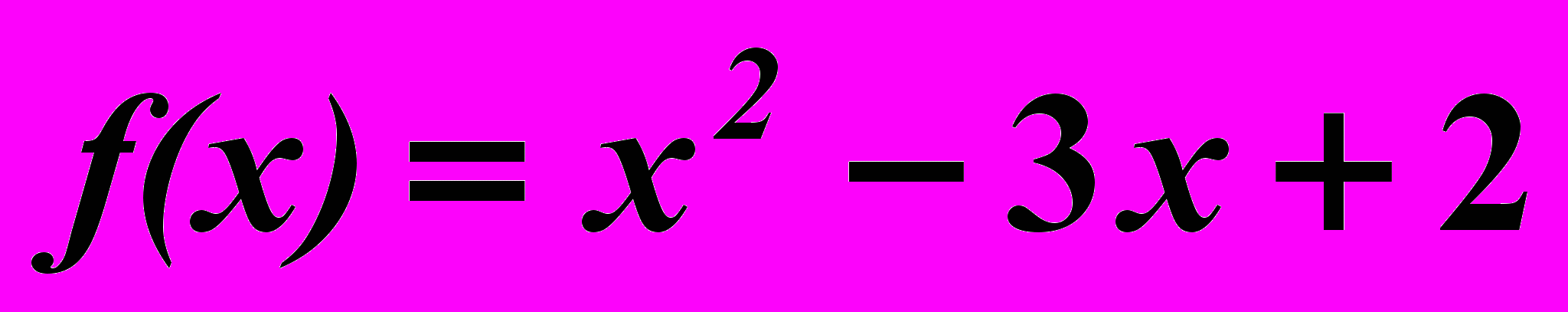 ,
,  11. 6.
11. 6. 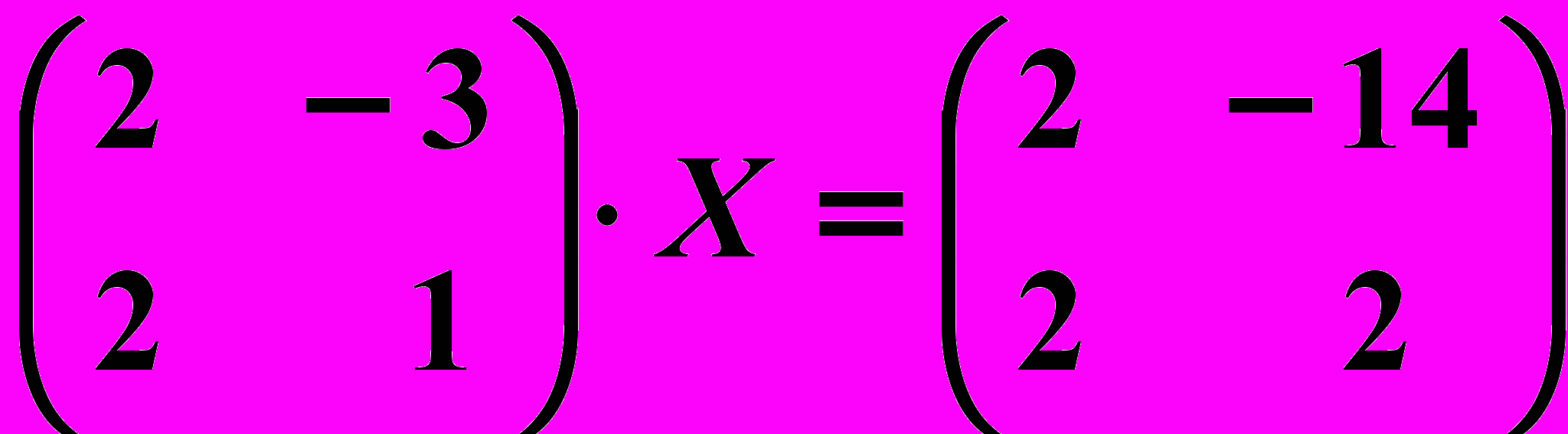
Вариант № 12
12.1.
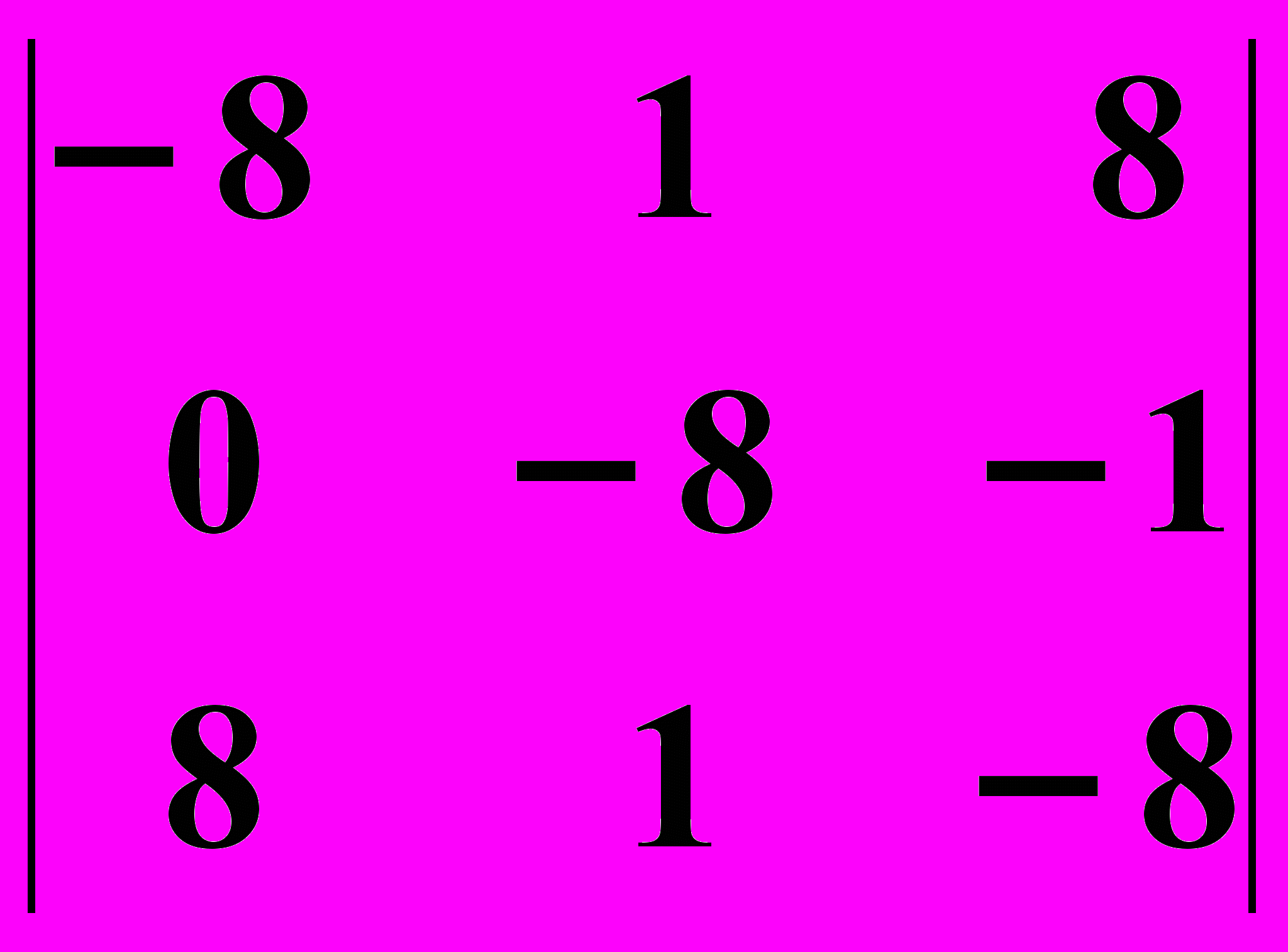 12.2.
12.2.  12.3.
12.3. 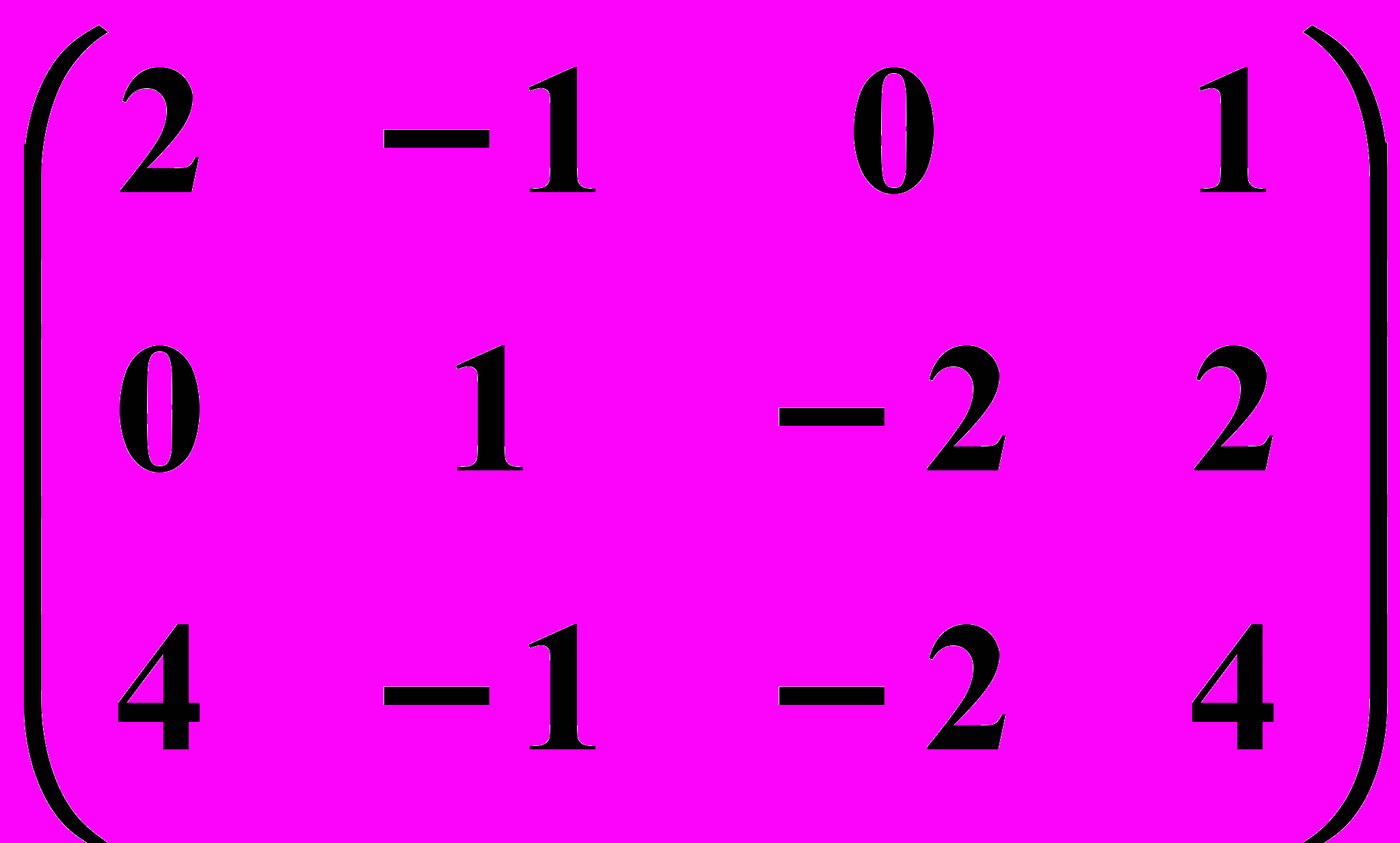
12.4.

12.5.
 ,
, 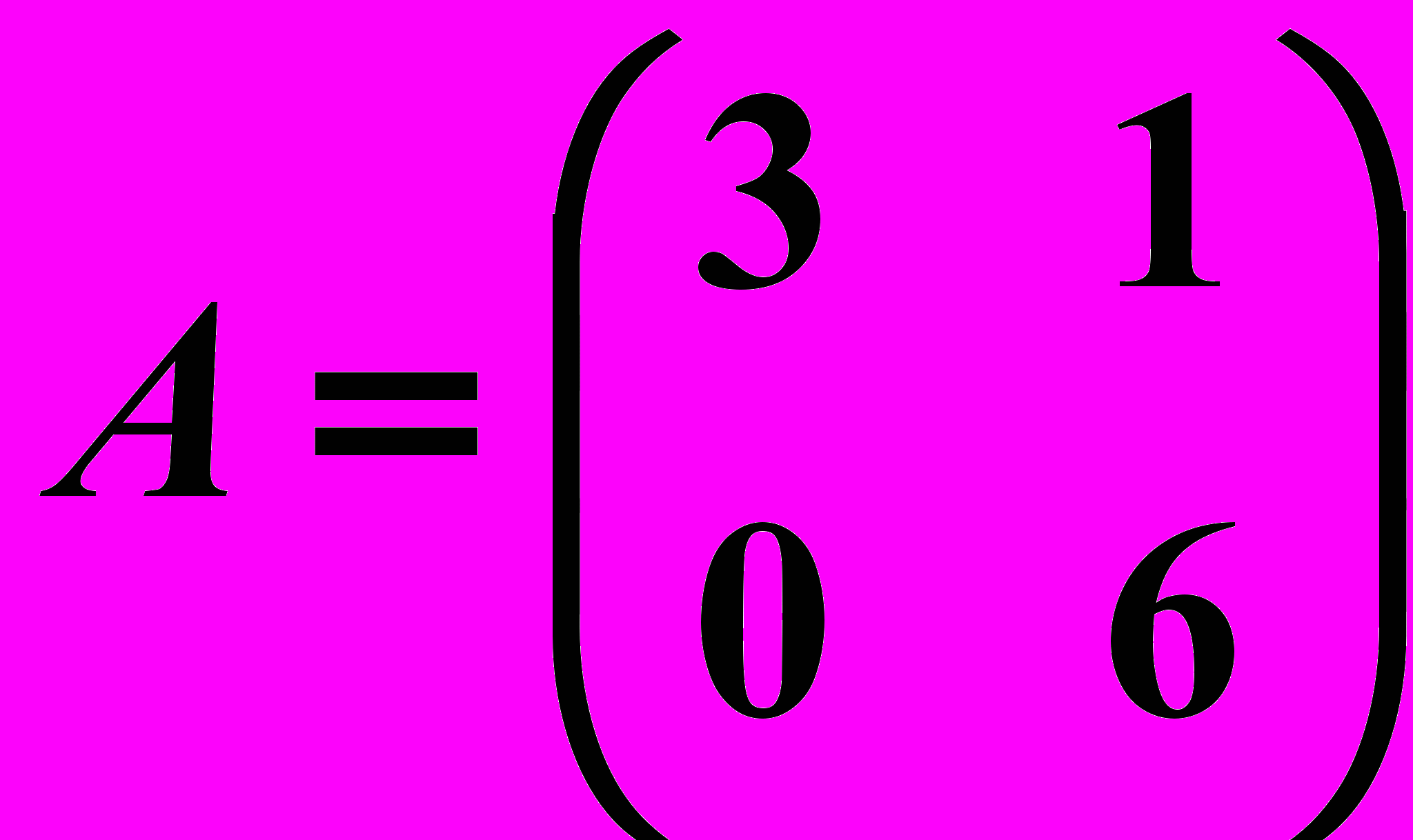 12.6.
12.6. 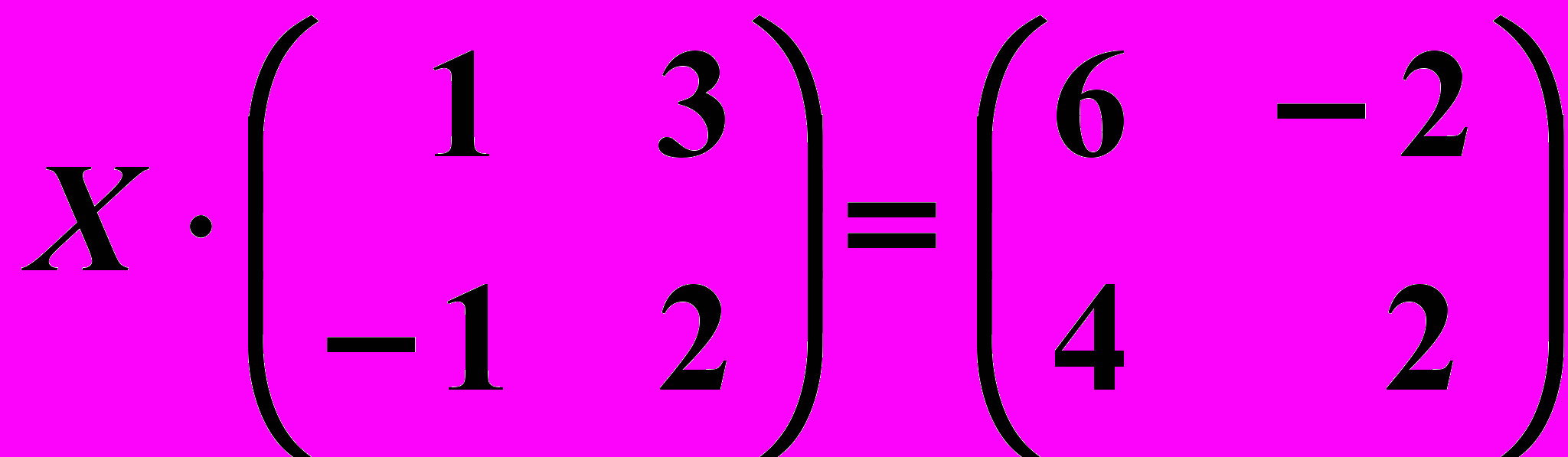
Вариант № 13
13.1.
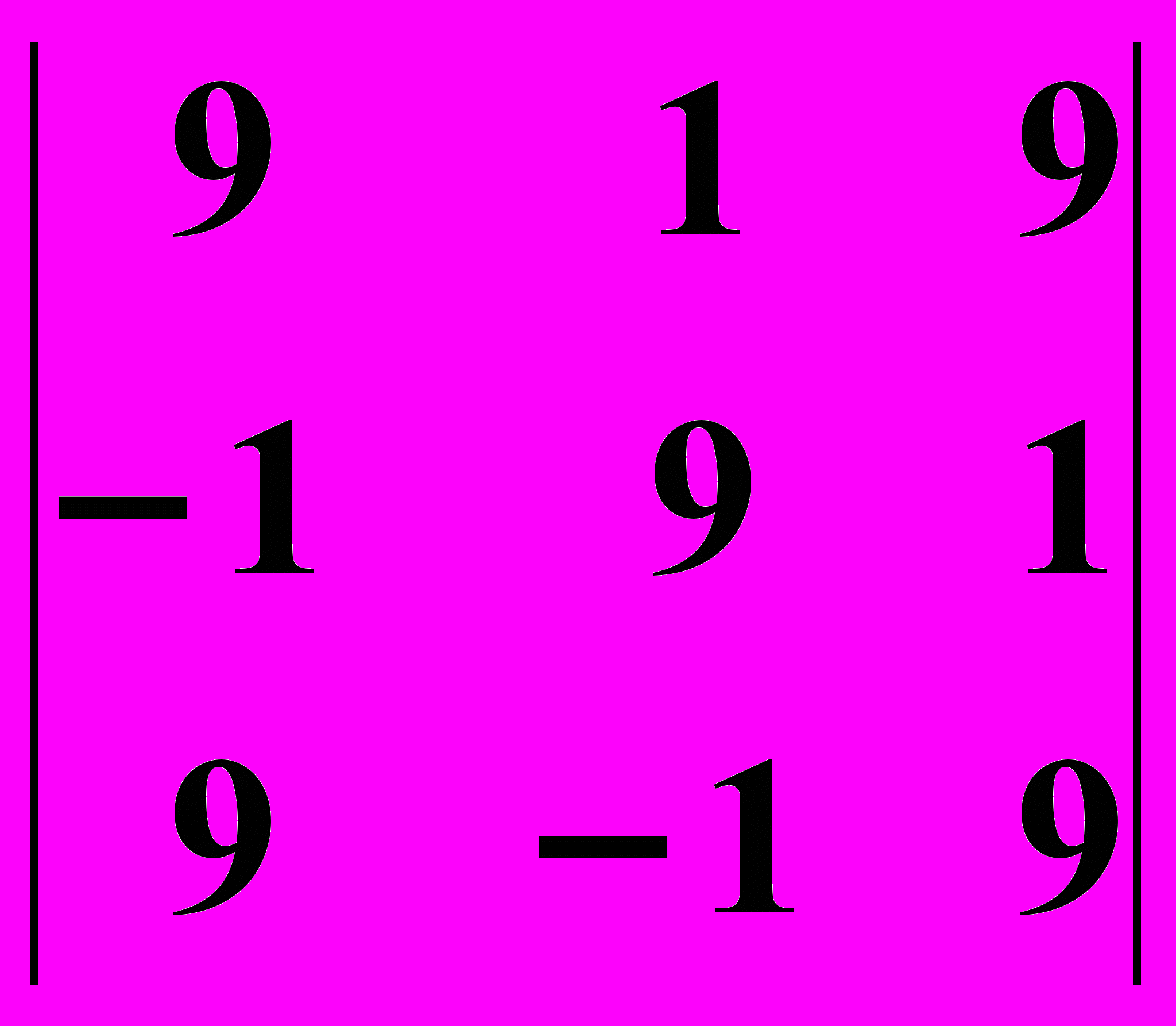 13.2.
13.2. 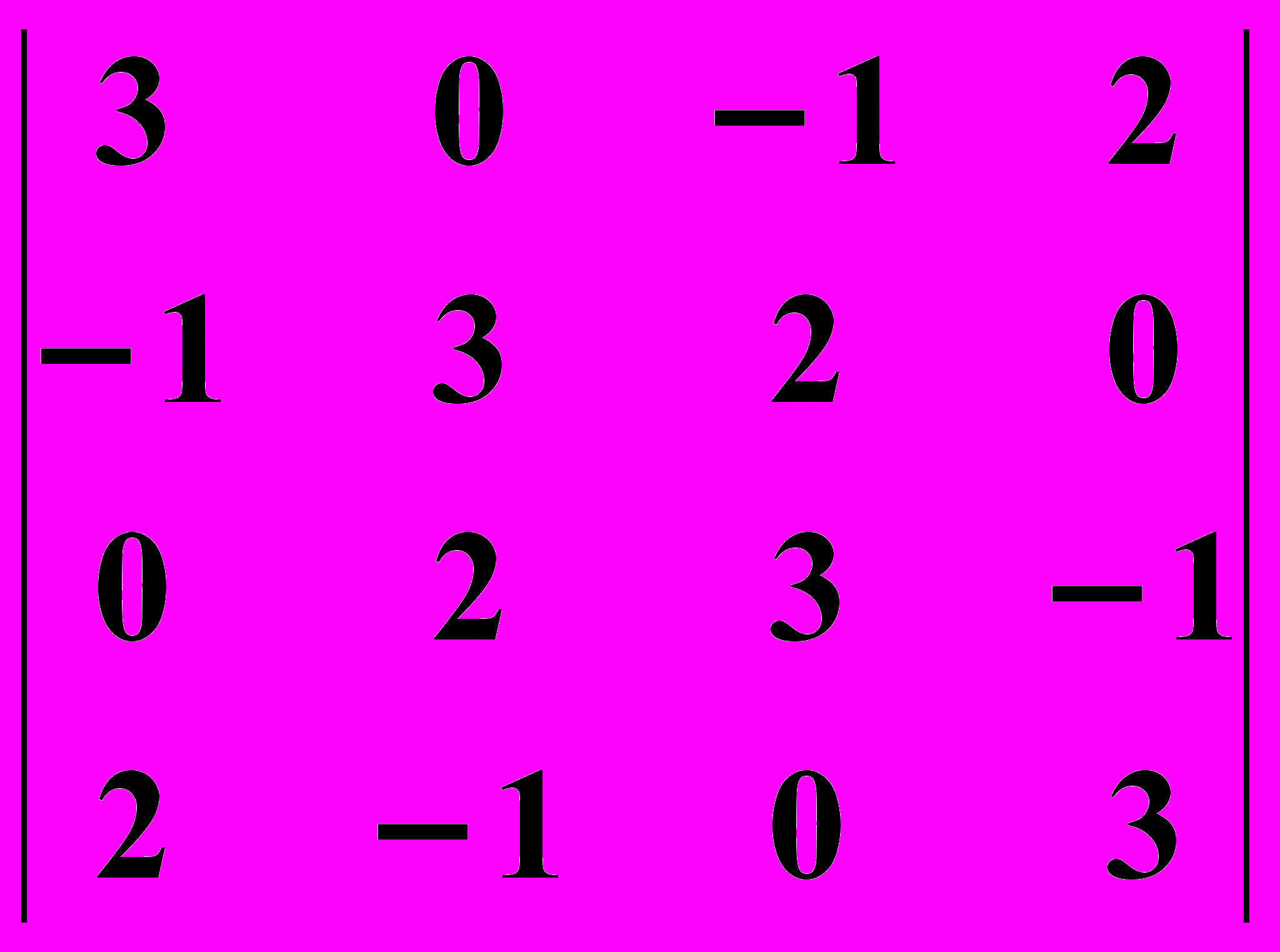 13.3.
13.3.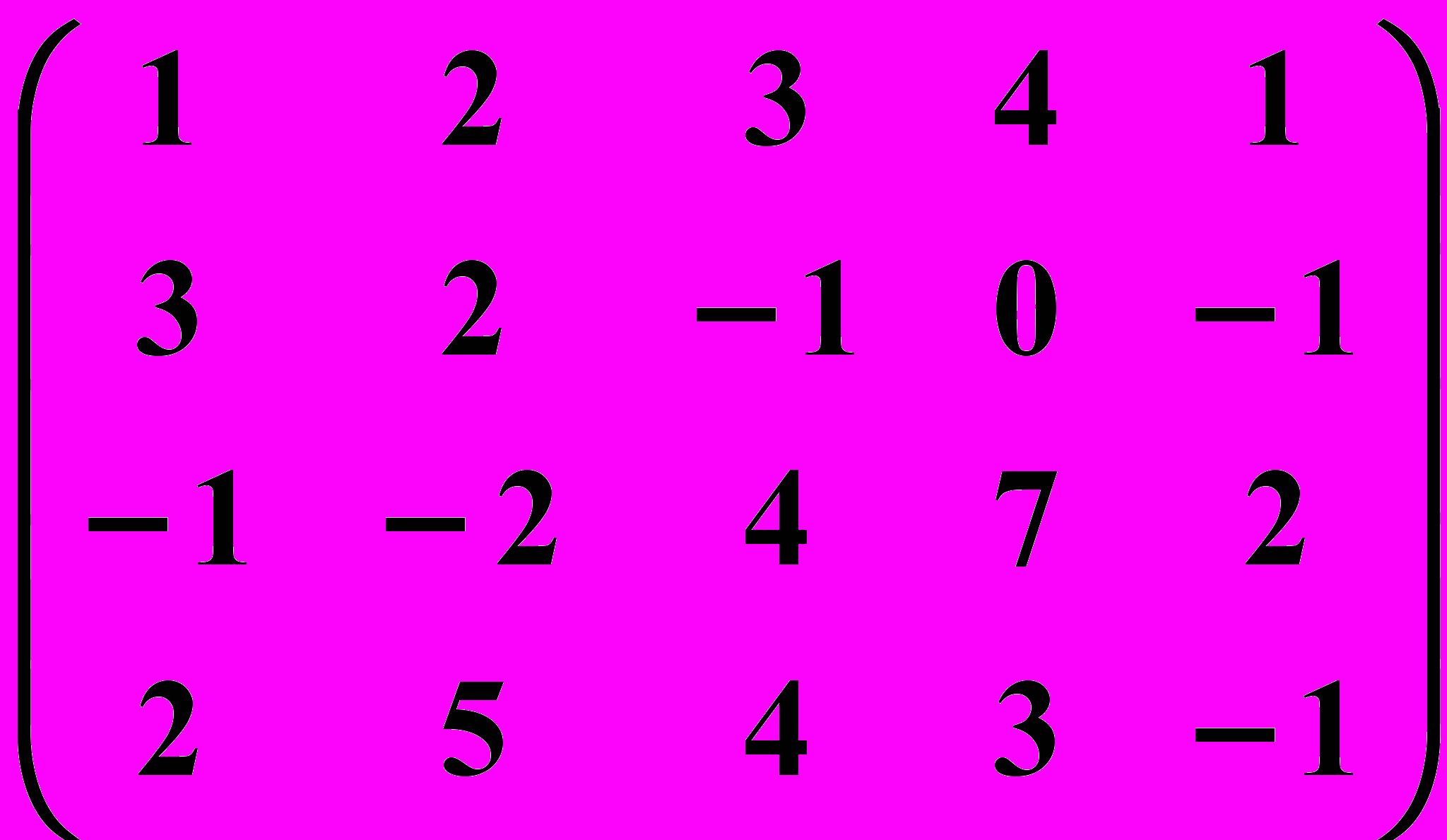
13.4.
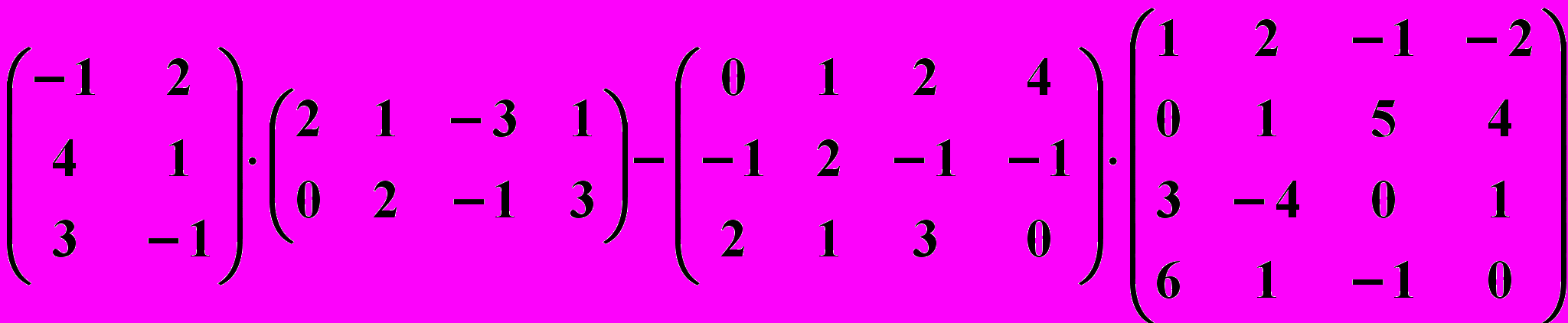
13.5.
 ,
, 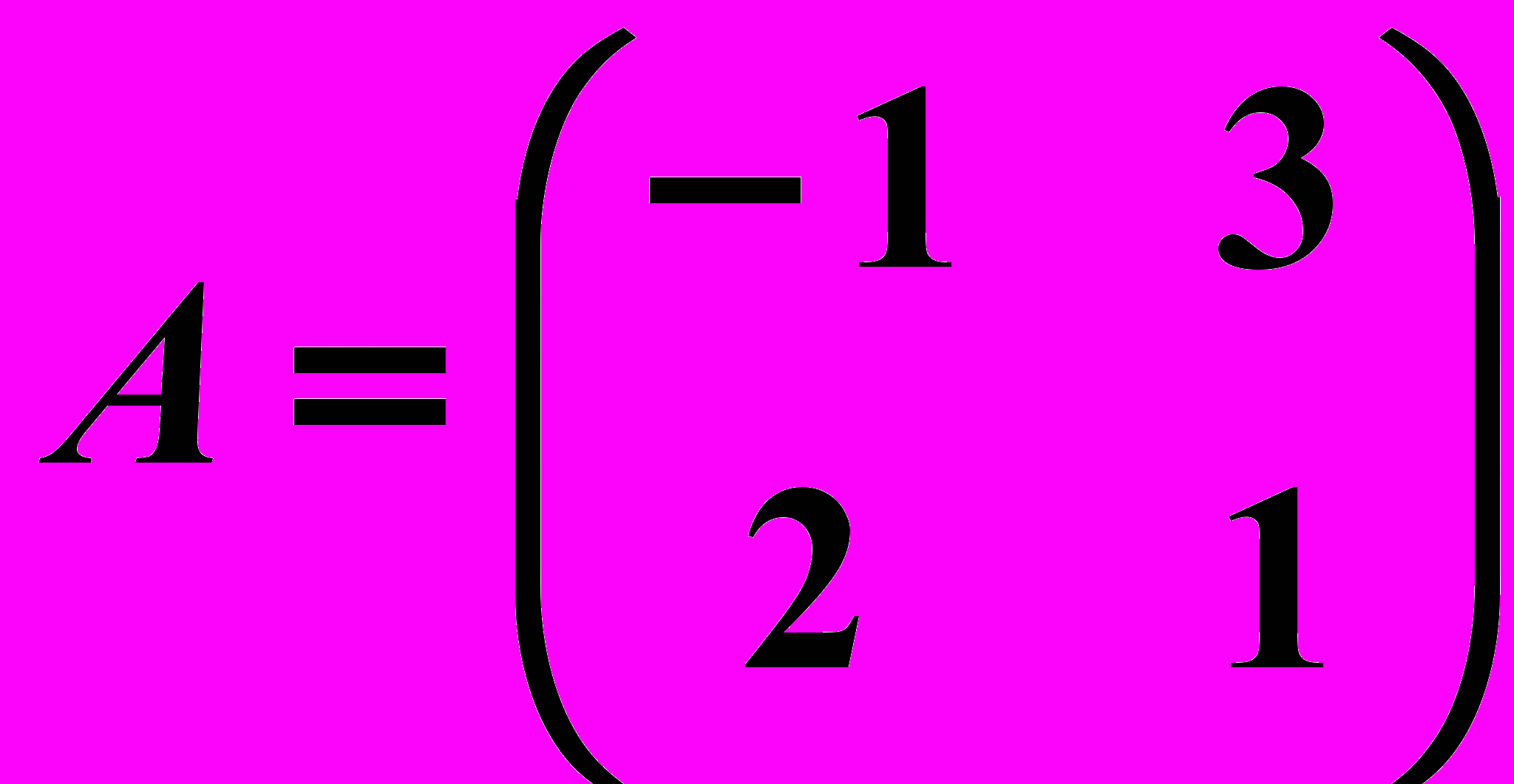 13.6.
13.6. 
Вариант № 14
14.1.
 14.2.
14.2. 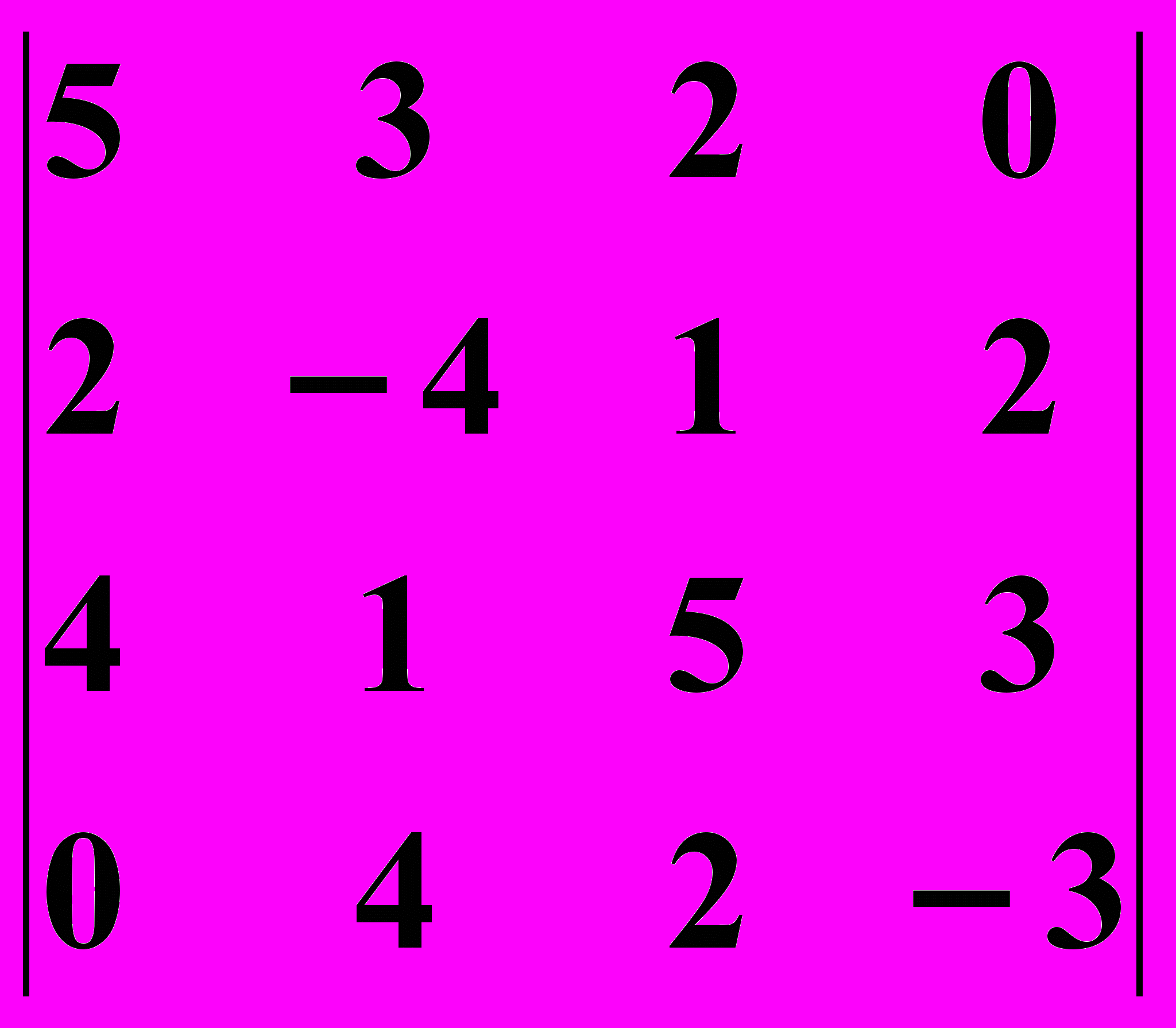 14.3.
14.3. 
14.4.
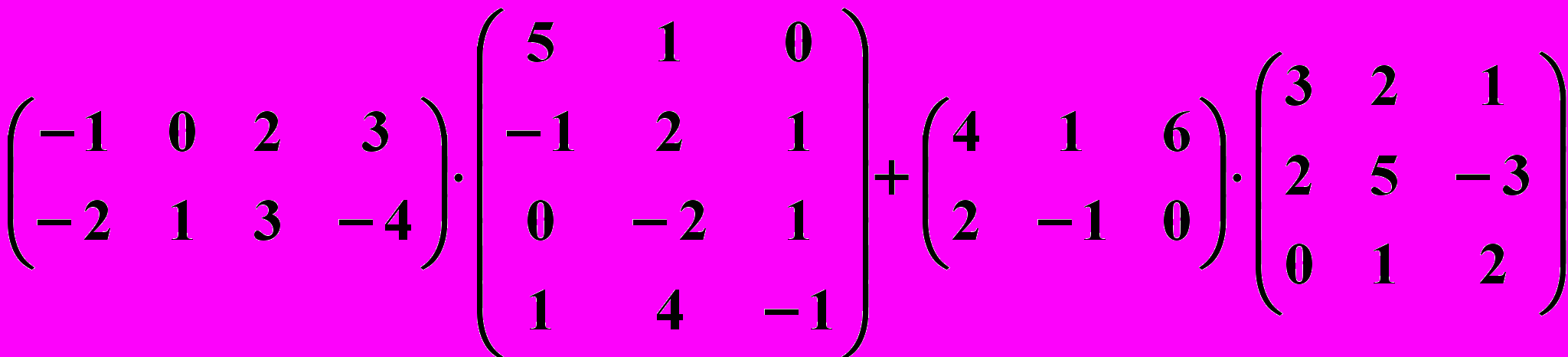
14.5.
 ,
,  14.6.
14.6. 
Вариант № 15
15.1.
 15.2.
15.2.  15.3.
15.3. 
15.4.
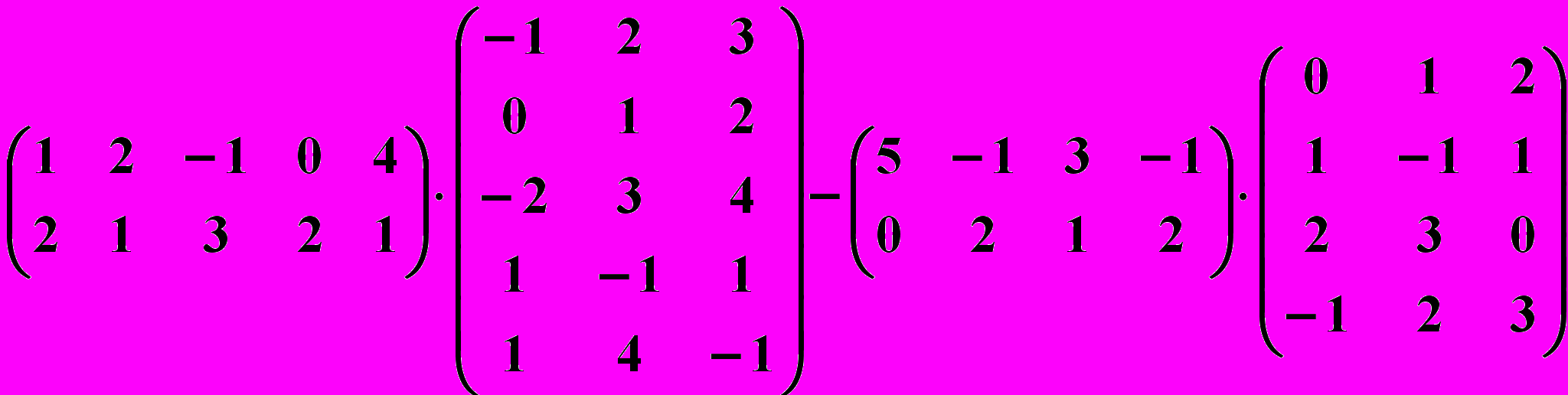
15.5.
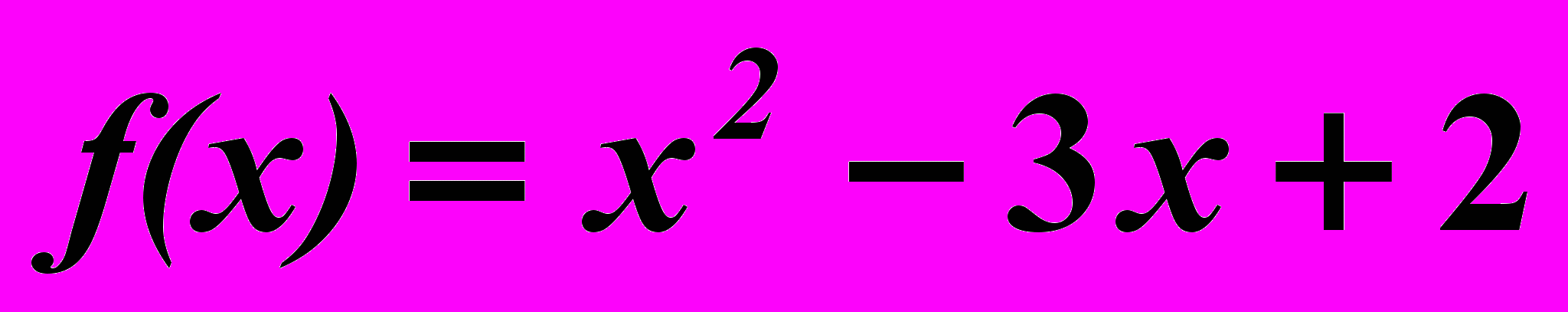 ,
,  15.6.
15.6. 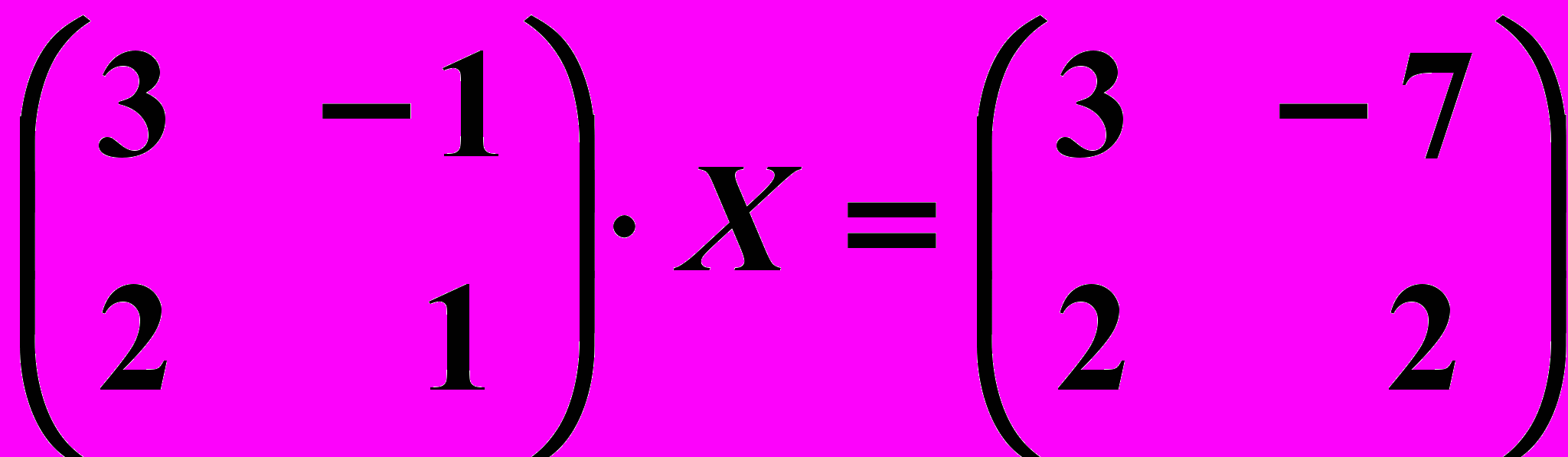
Вариант № 16
16.1.
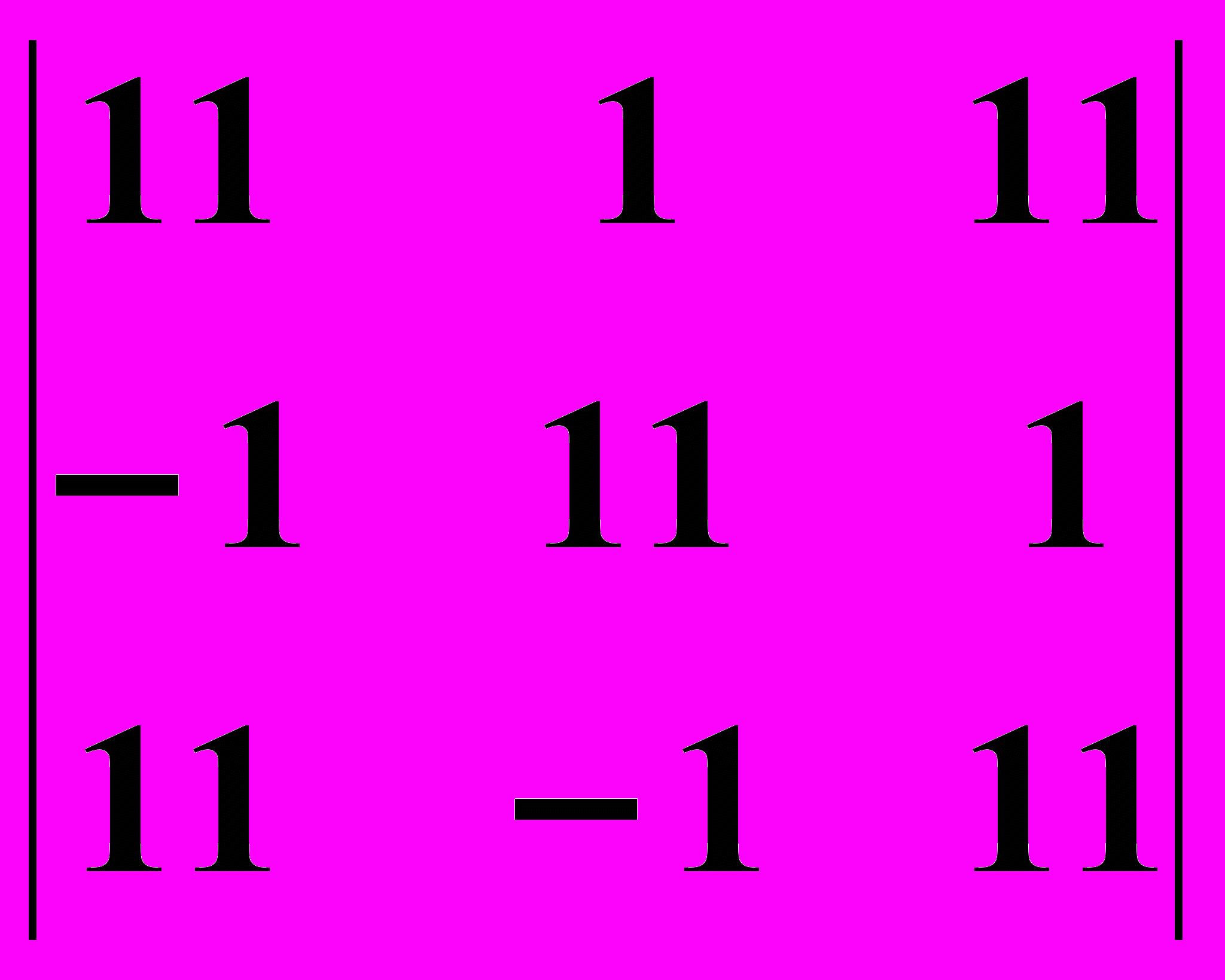 16.2.
16.2.  16.3.
16.3. 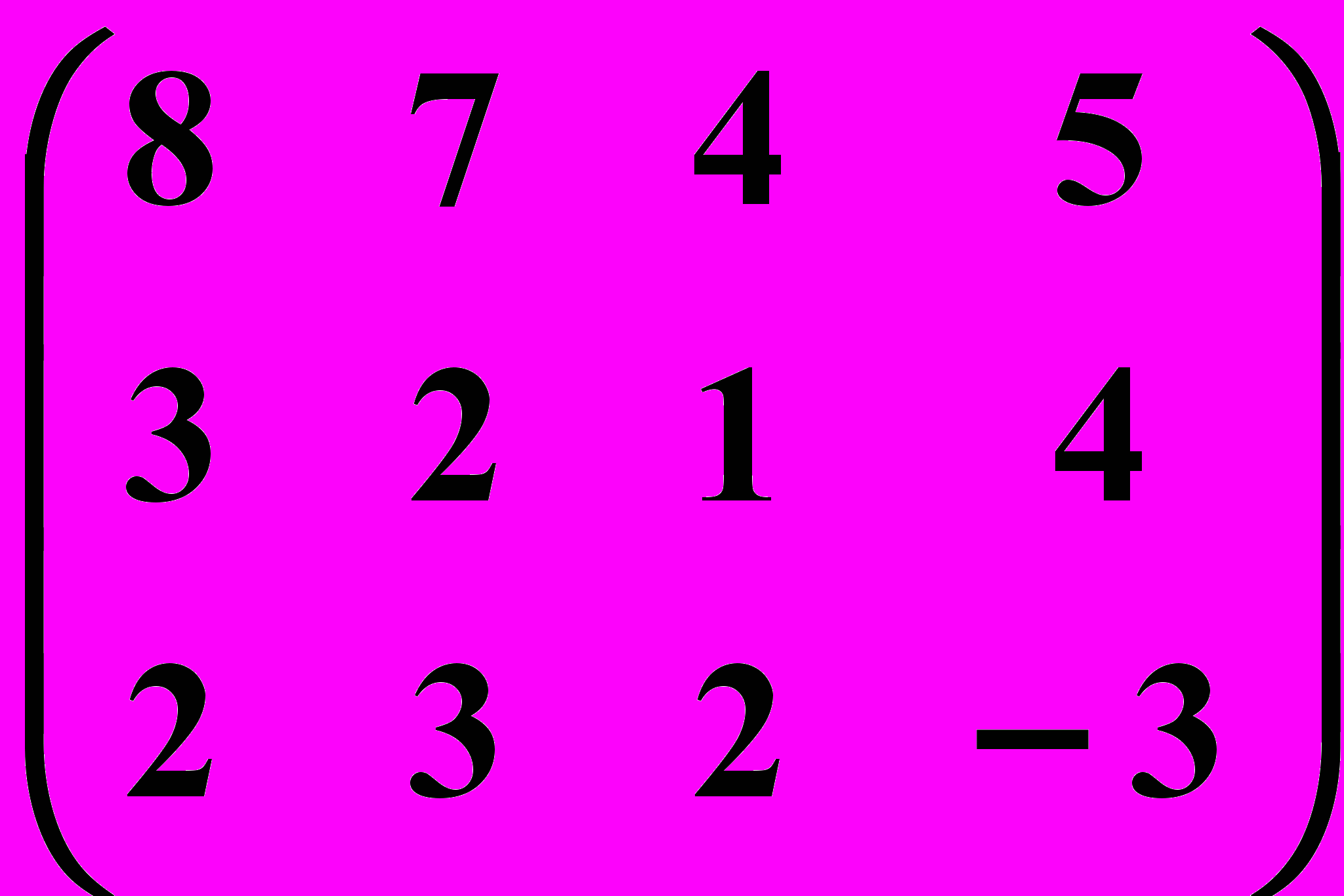
16.4.

16.5.
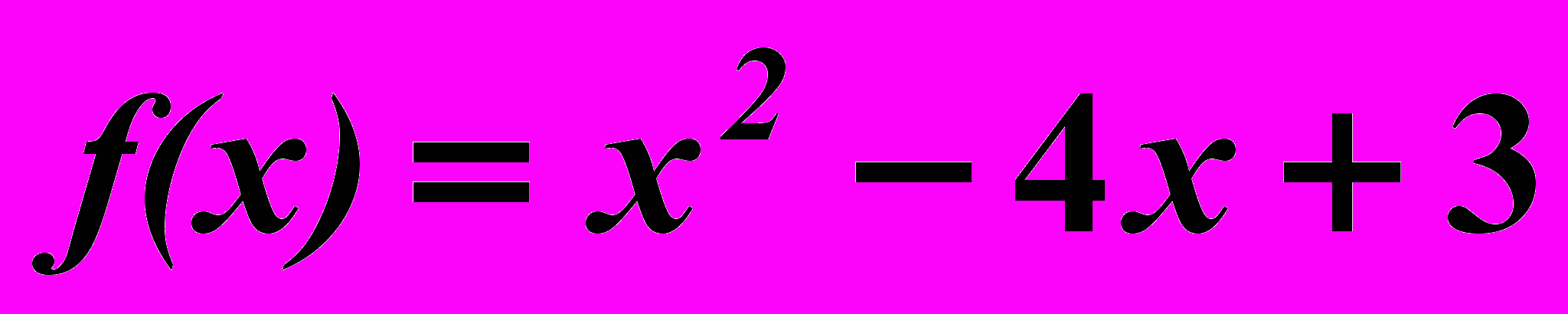 ,
,  16.6.
16.6. 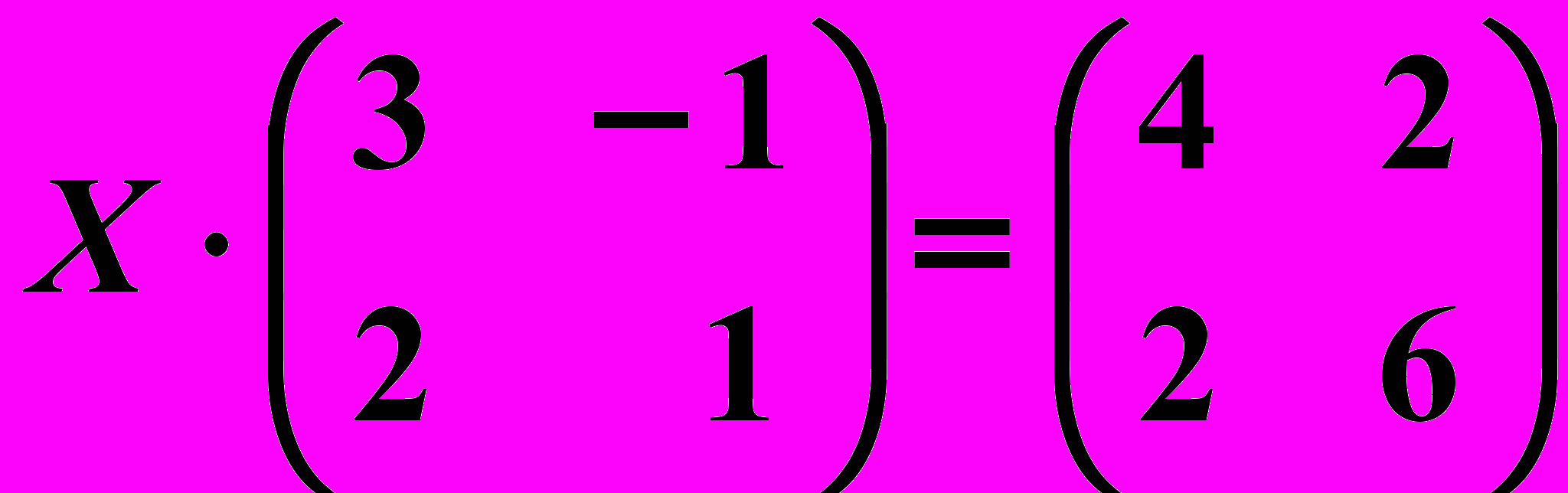
Вариант № 17
17.1.
 17.2.
17.2. 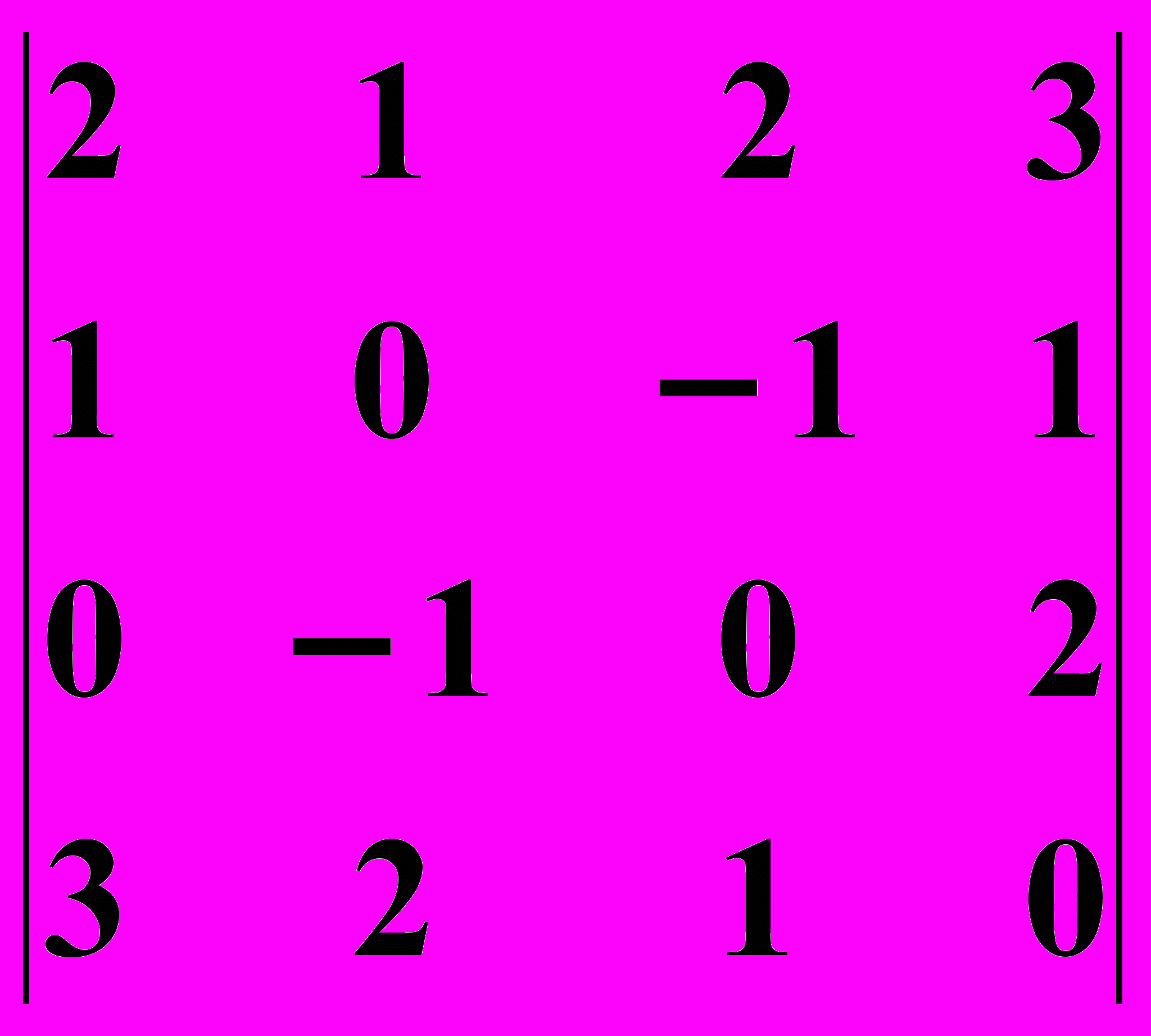 17.3.
17.3. 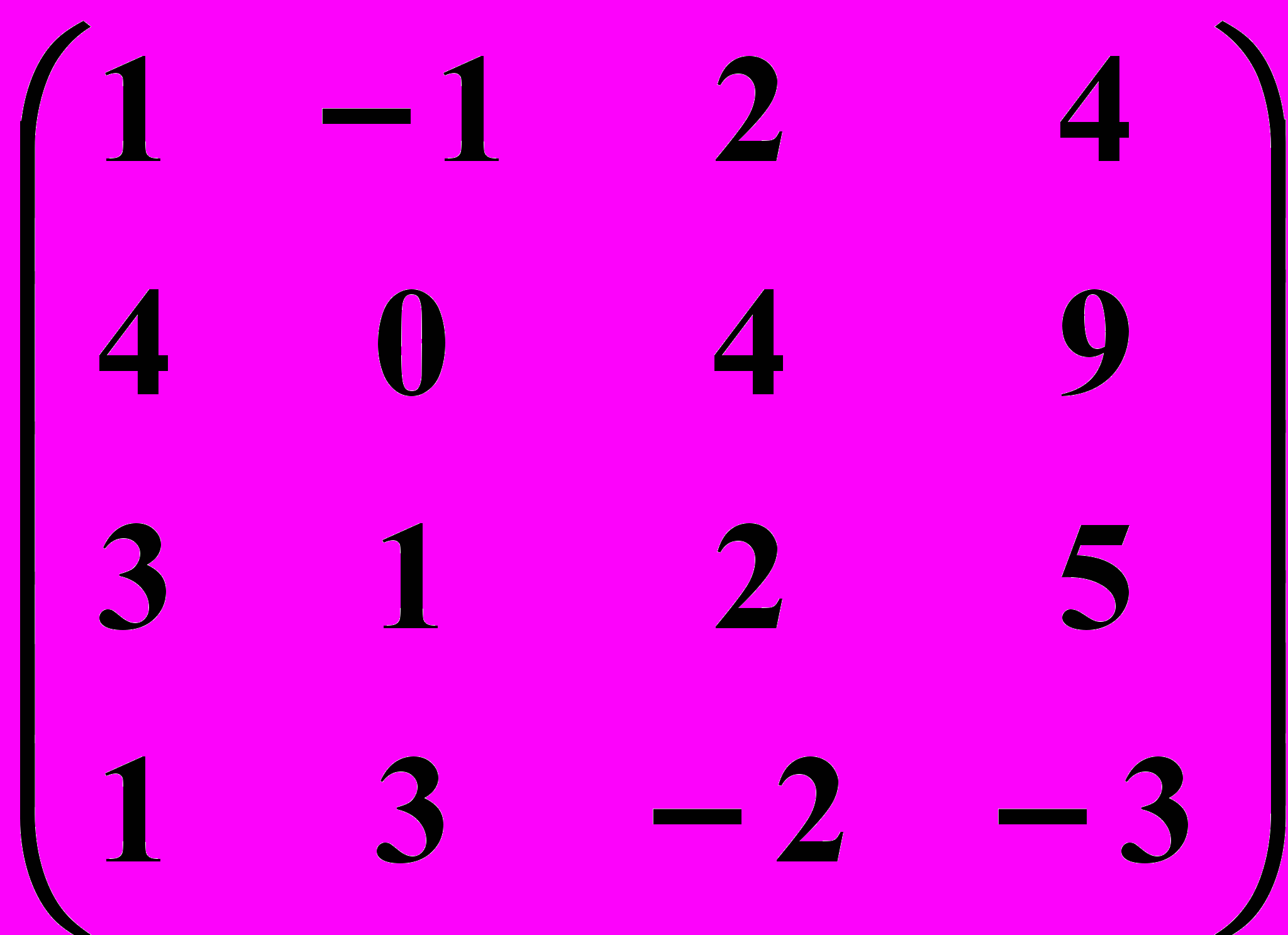
17.4.

17.5.
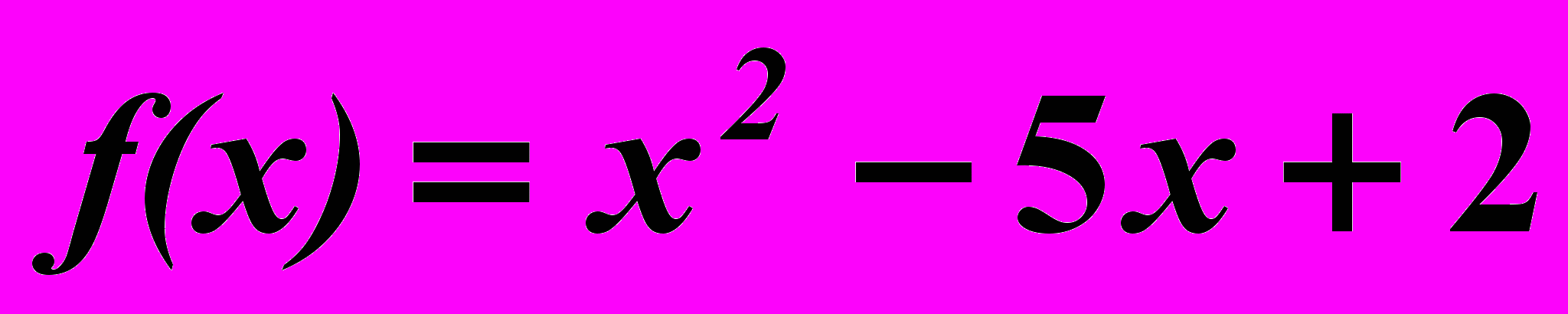 ,
, 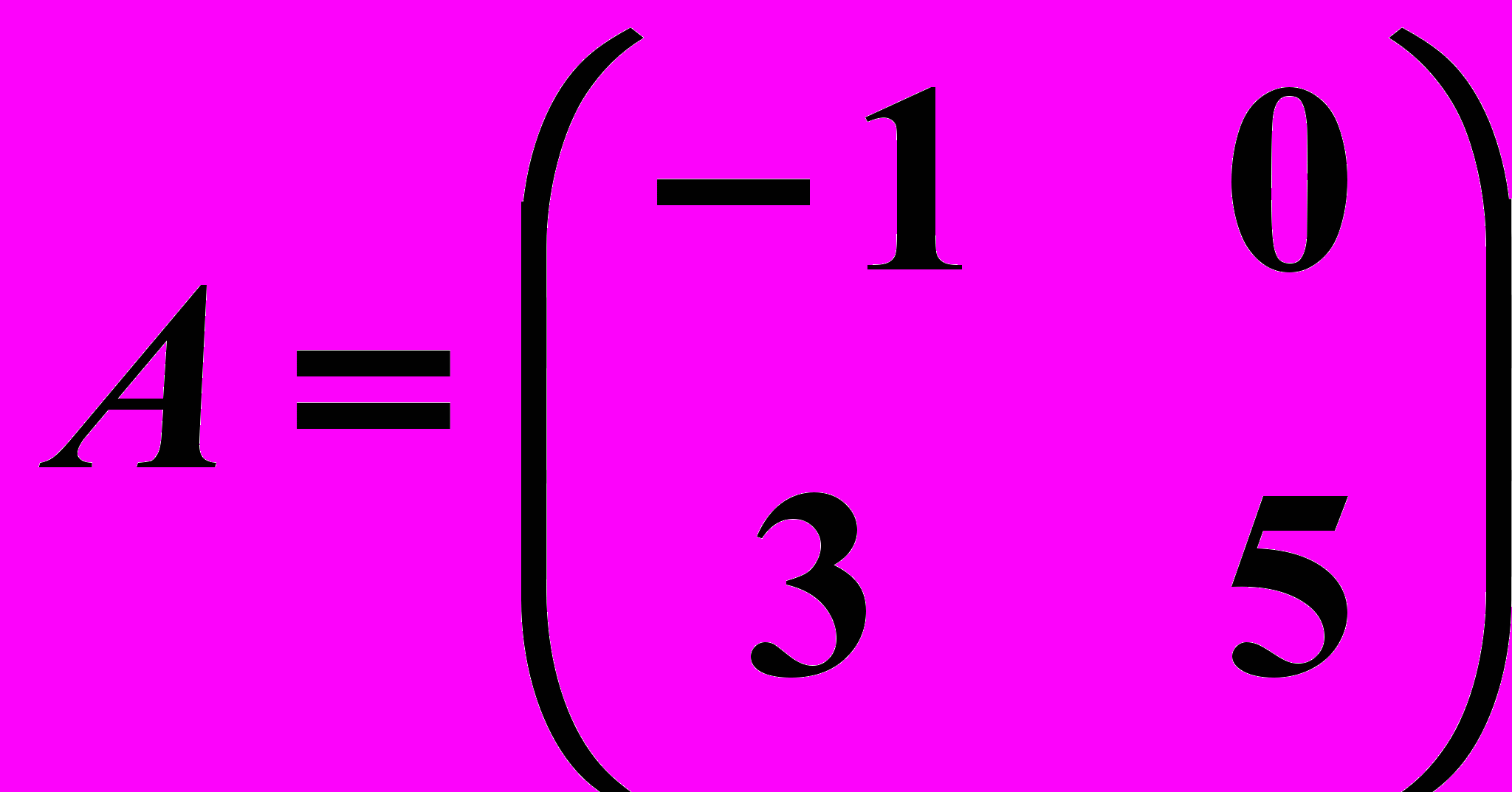 17.6.
17.6. 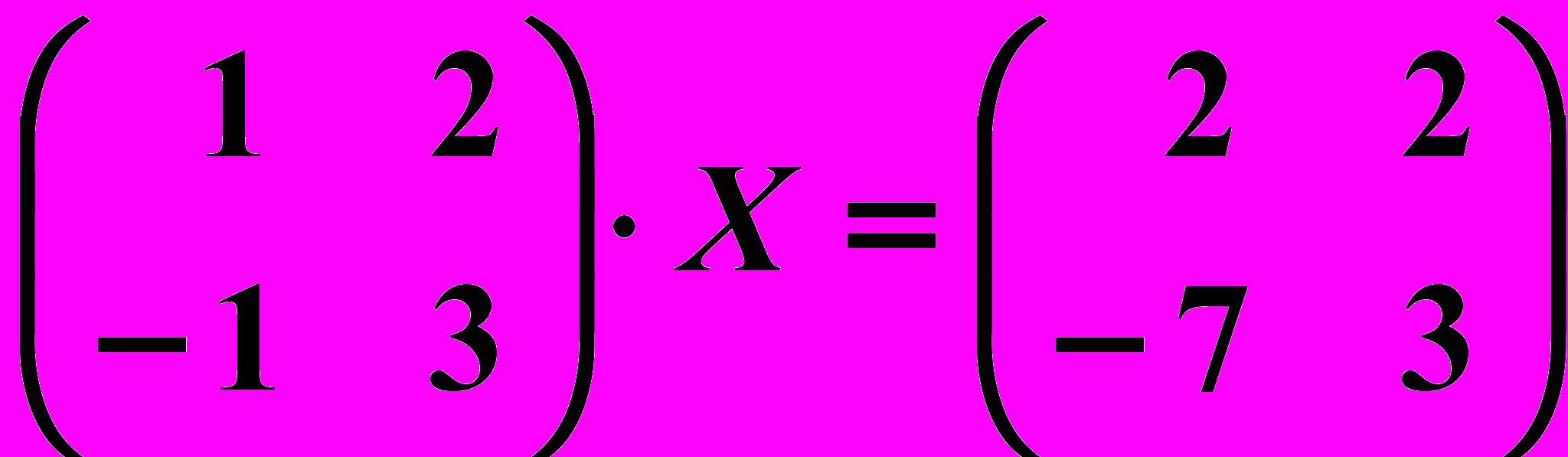
Вариант № 18
18.1.
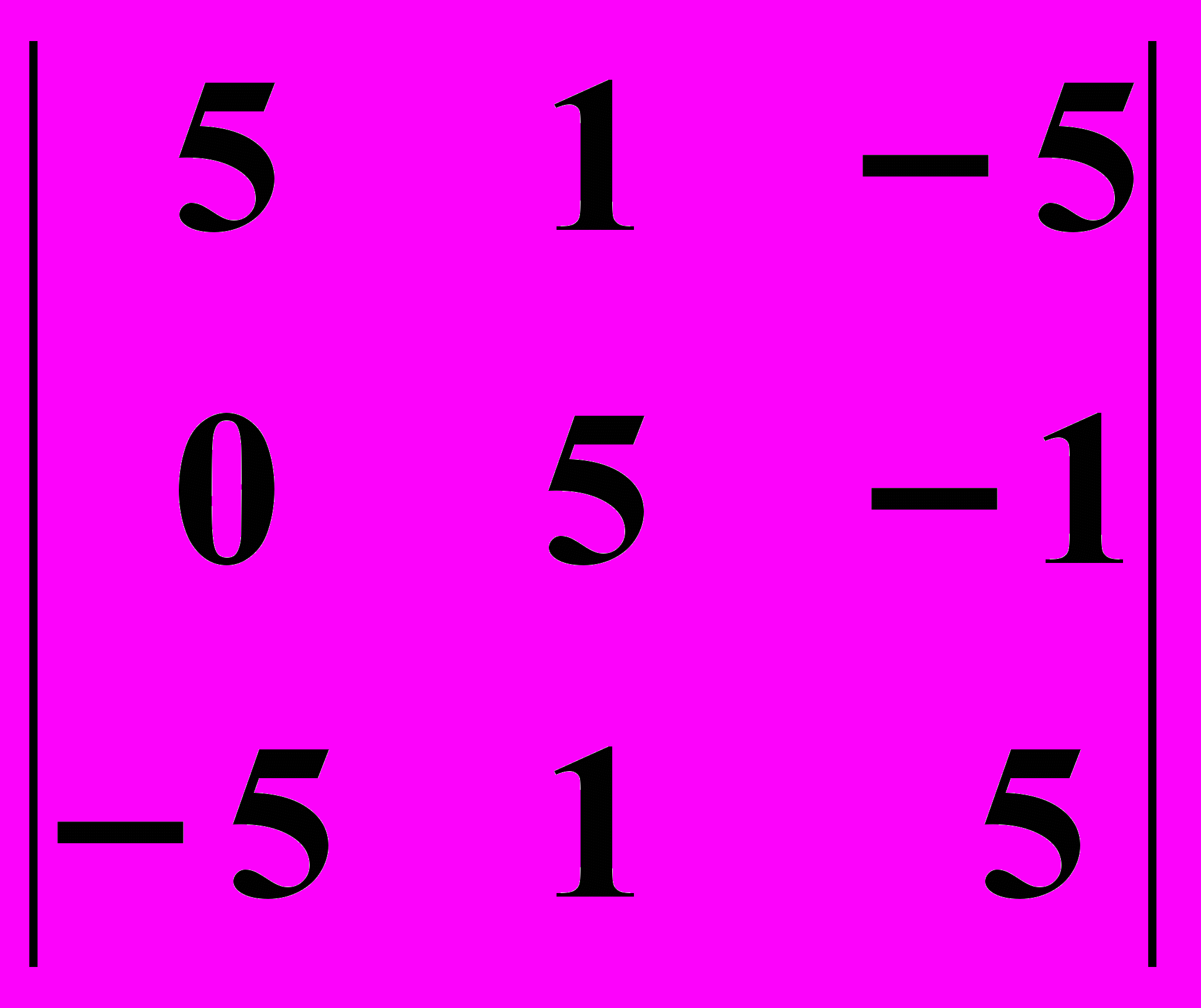 18.2.
18.2. 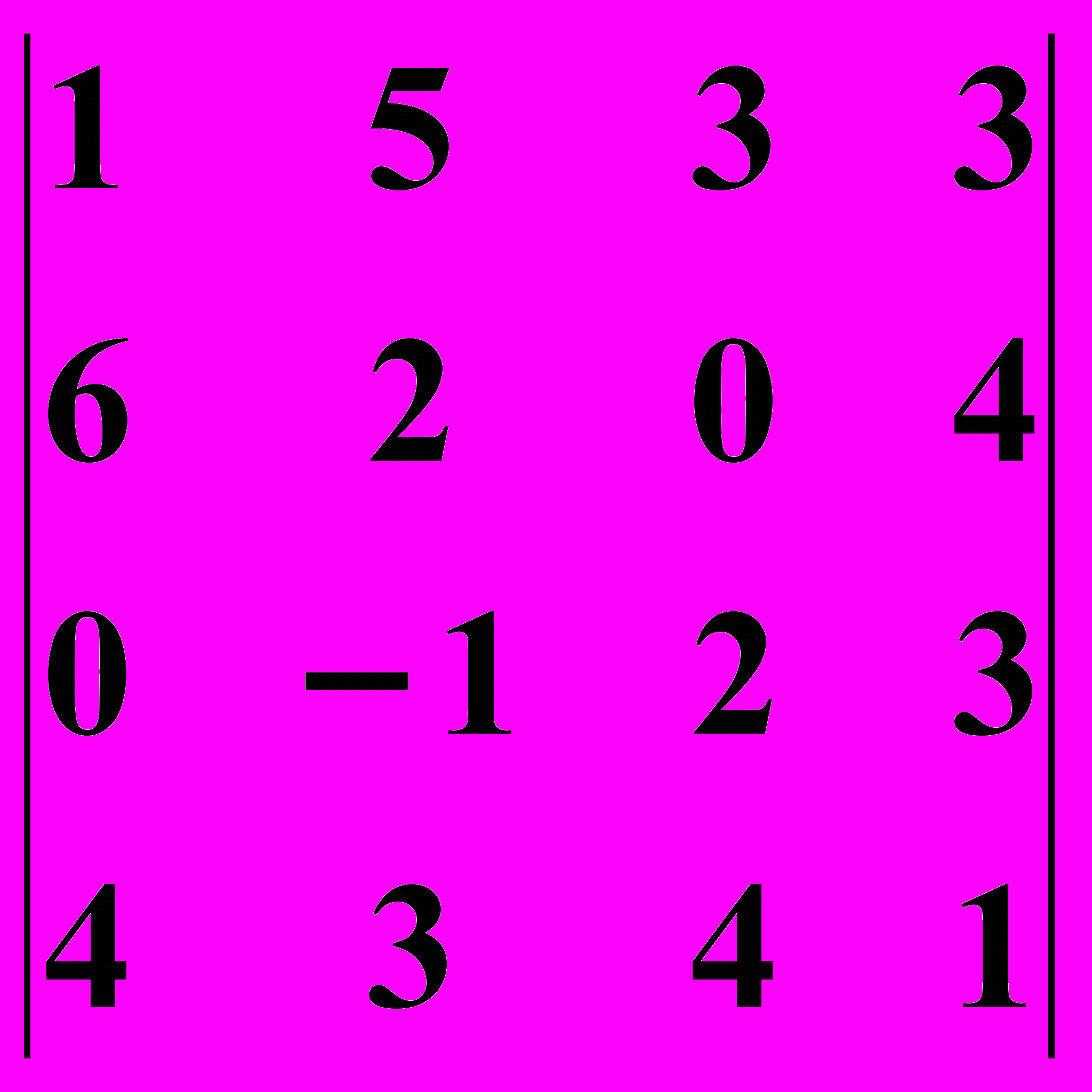 18.3.
18.3. 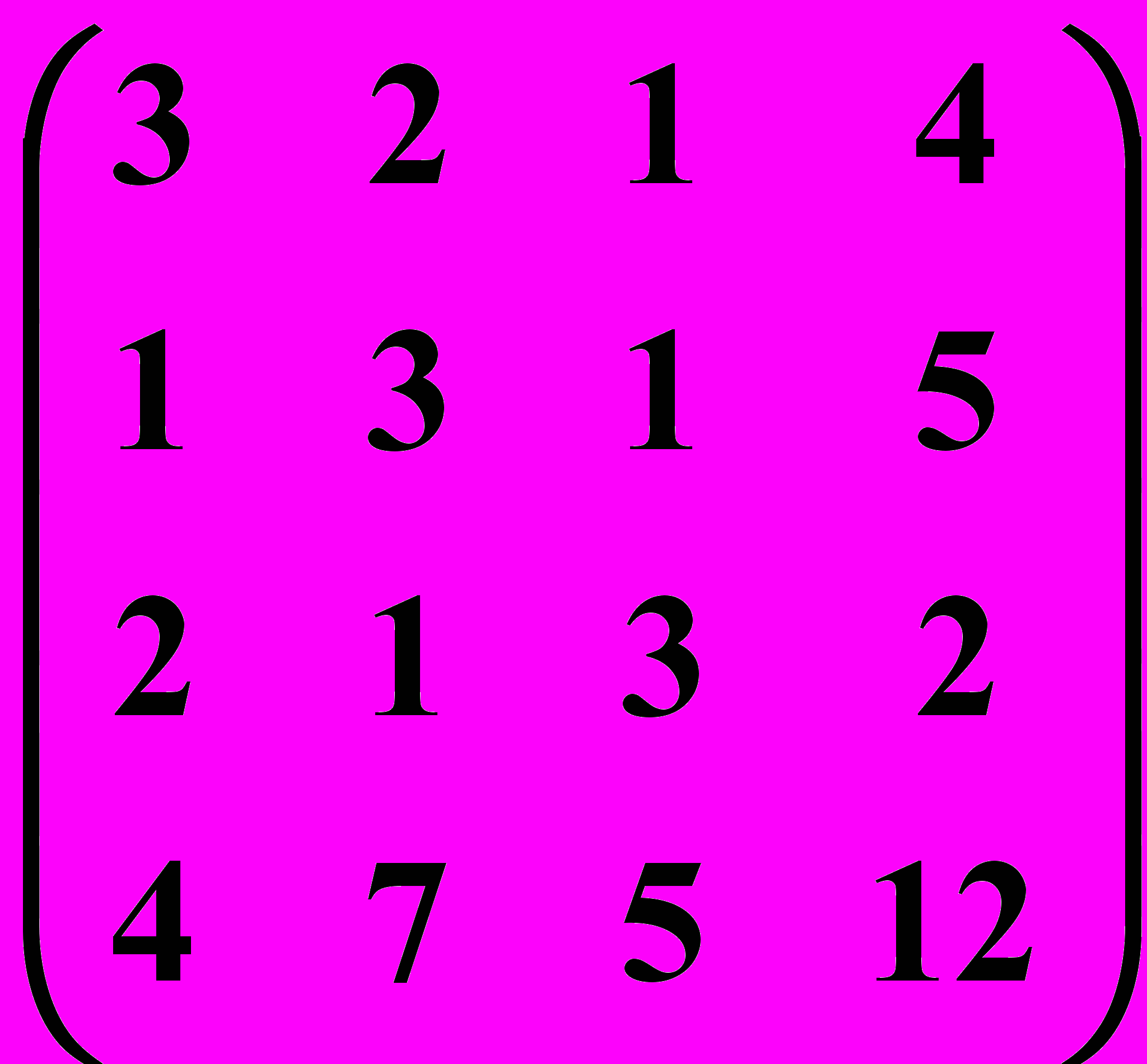
18.4.

18.5.
 ,
, 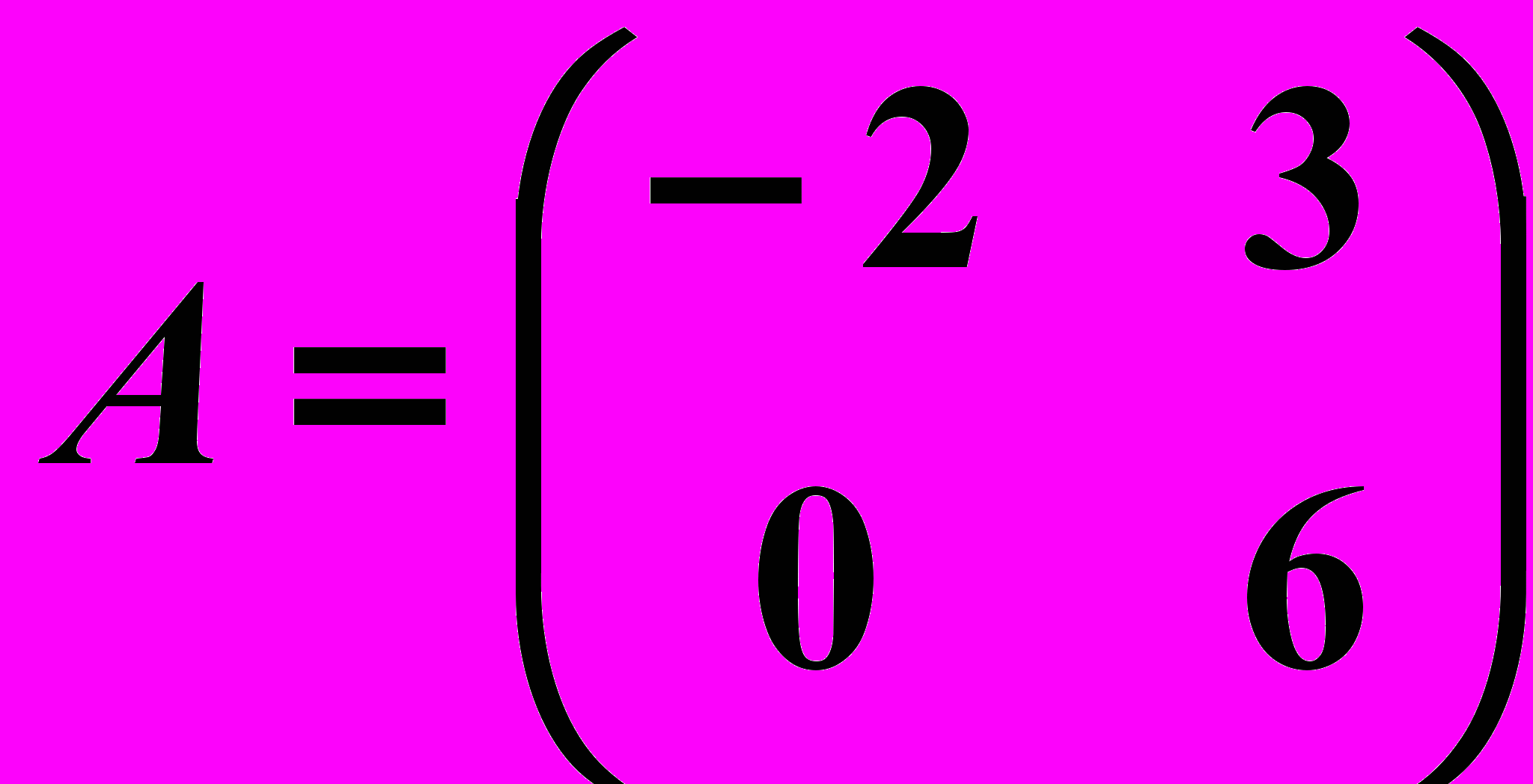 18.6.
18.6. 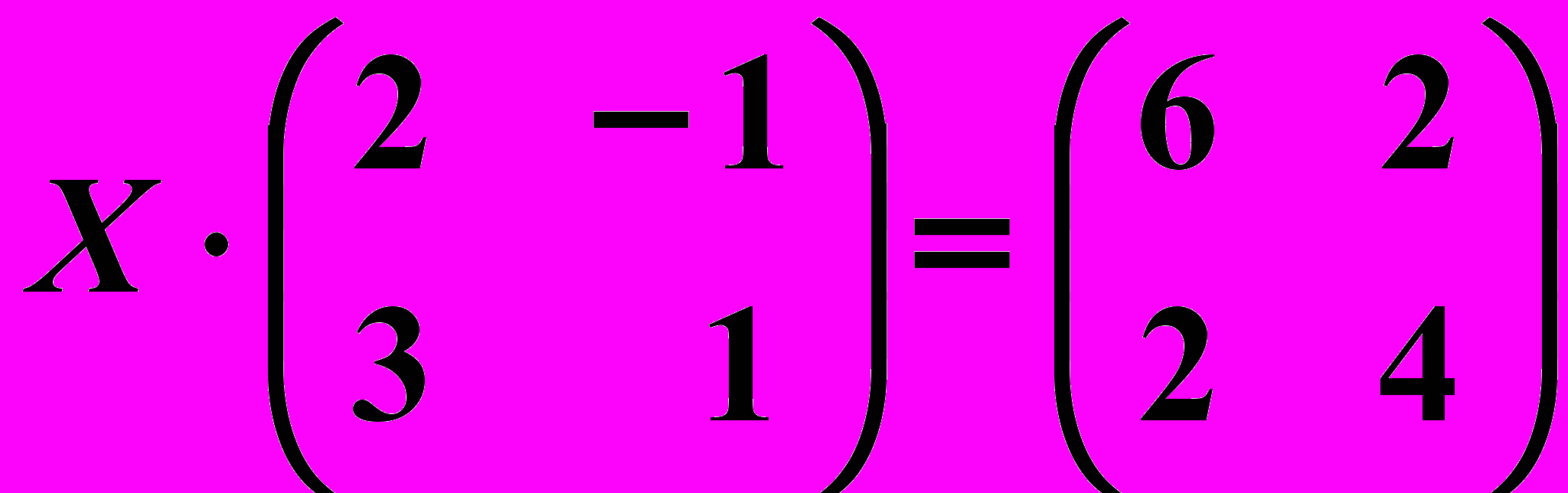
Вариант № 19
19.1.
 19.2.
19.2.  19.3.
19.3. 
19.4.

19.5.
 ,
, 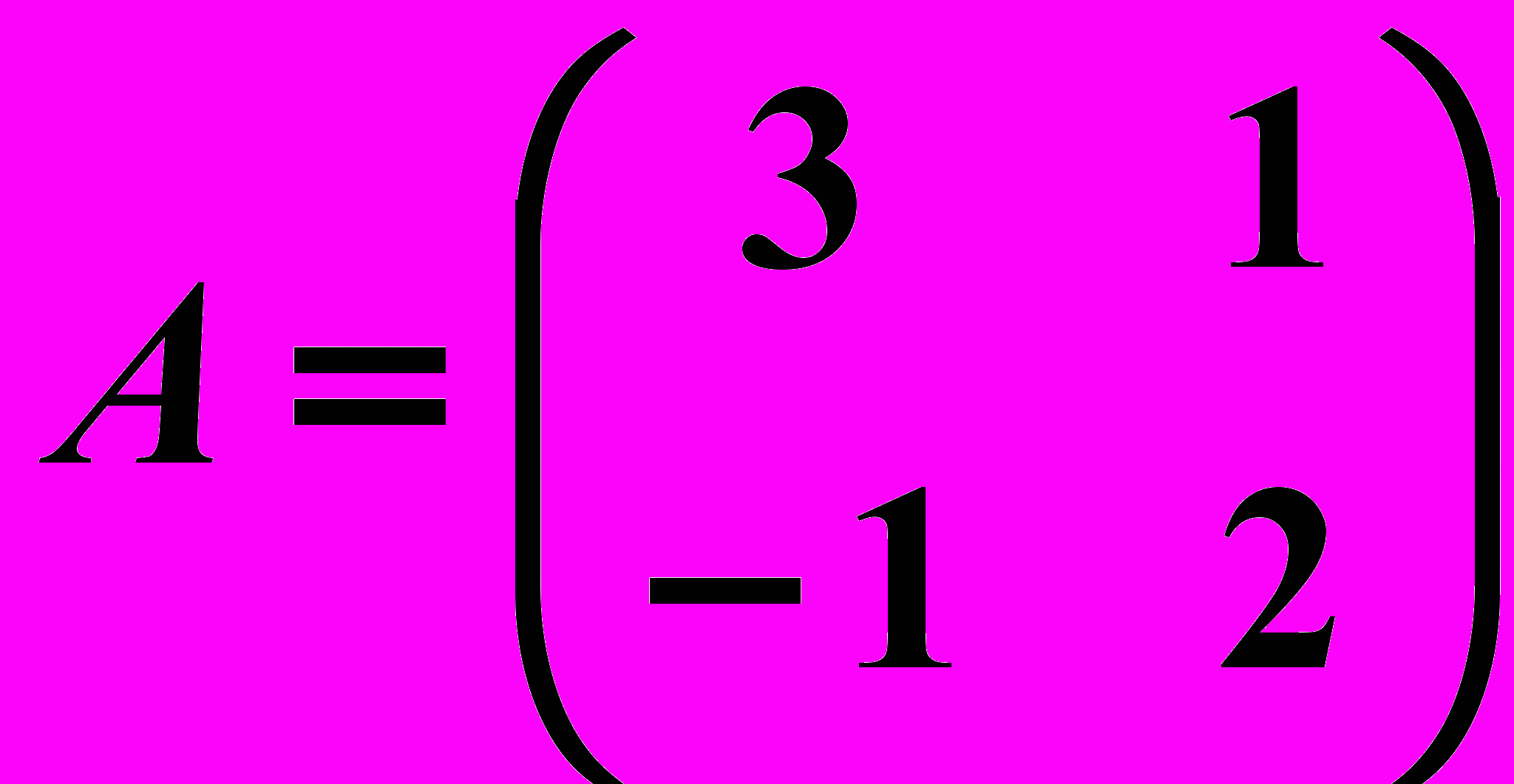 19.6.
19.6. 
Вариант № 20
20.1.
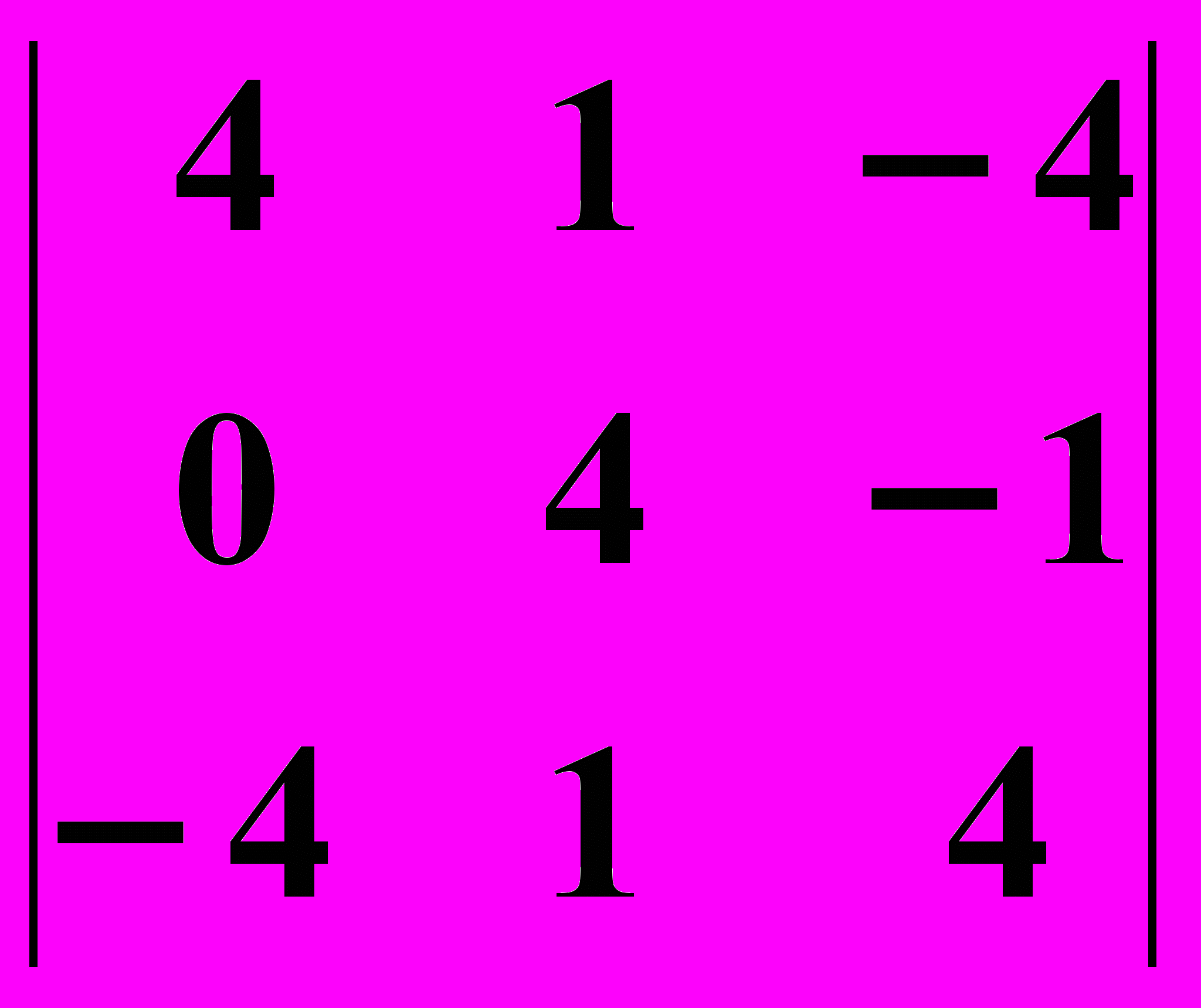 20.2.
20.2. 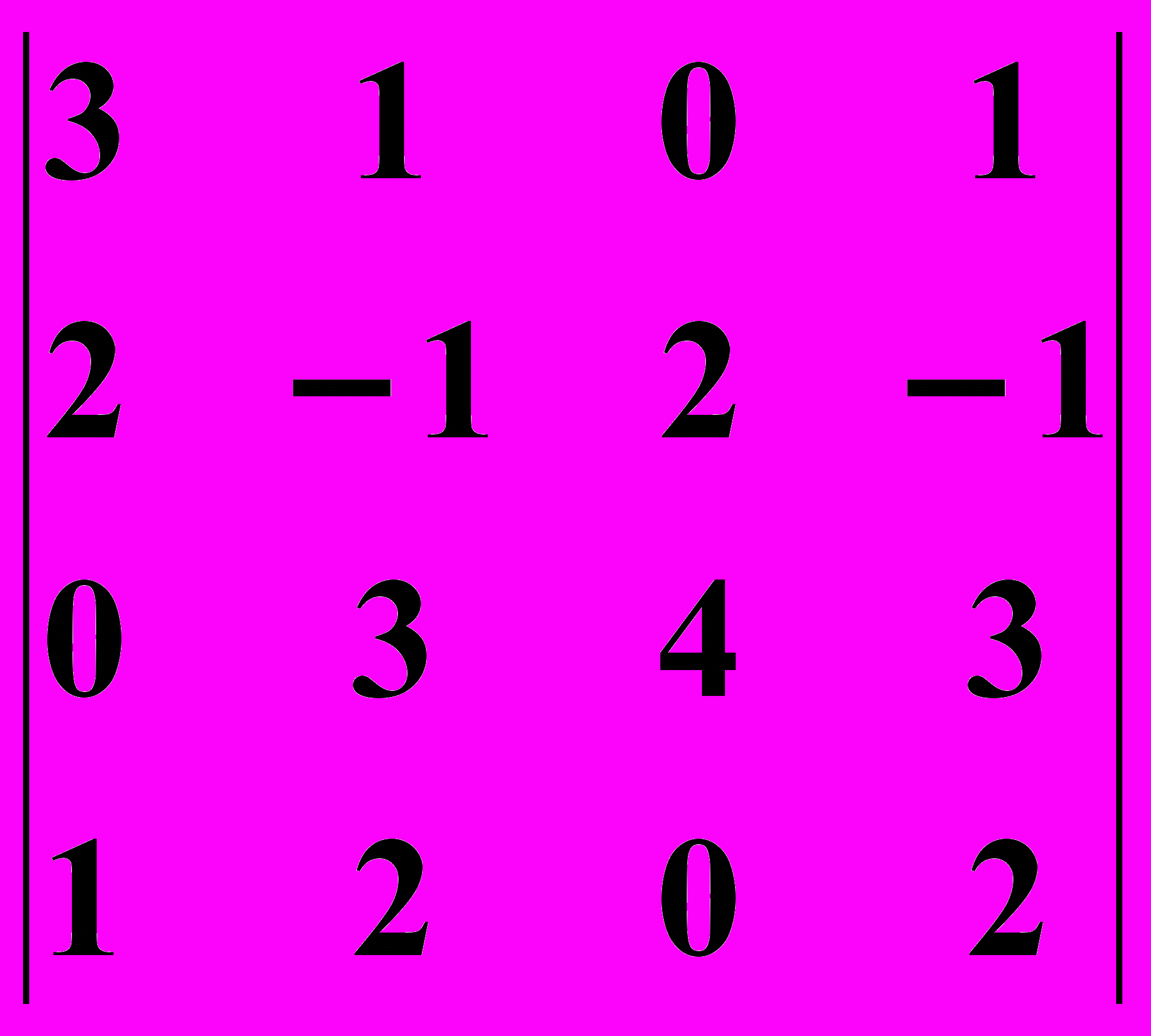 20.3.
20.3. 
20.4.

20.5.
 ,
, 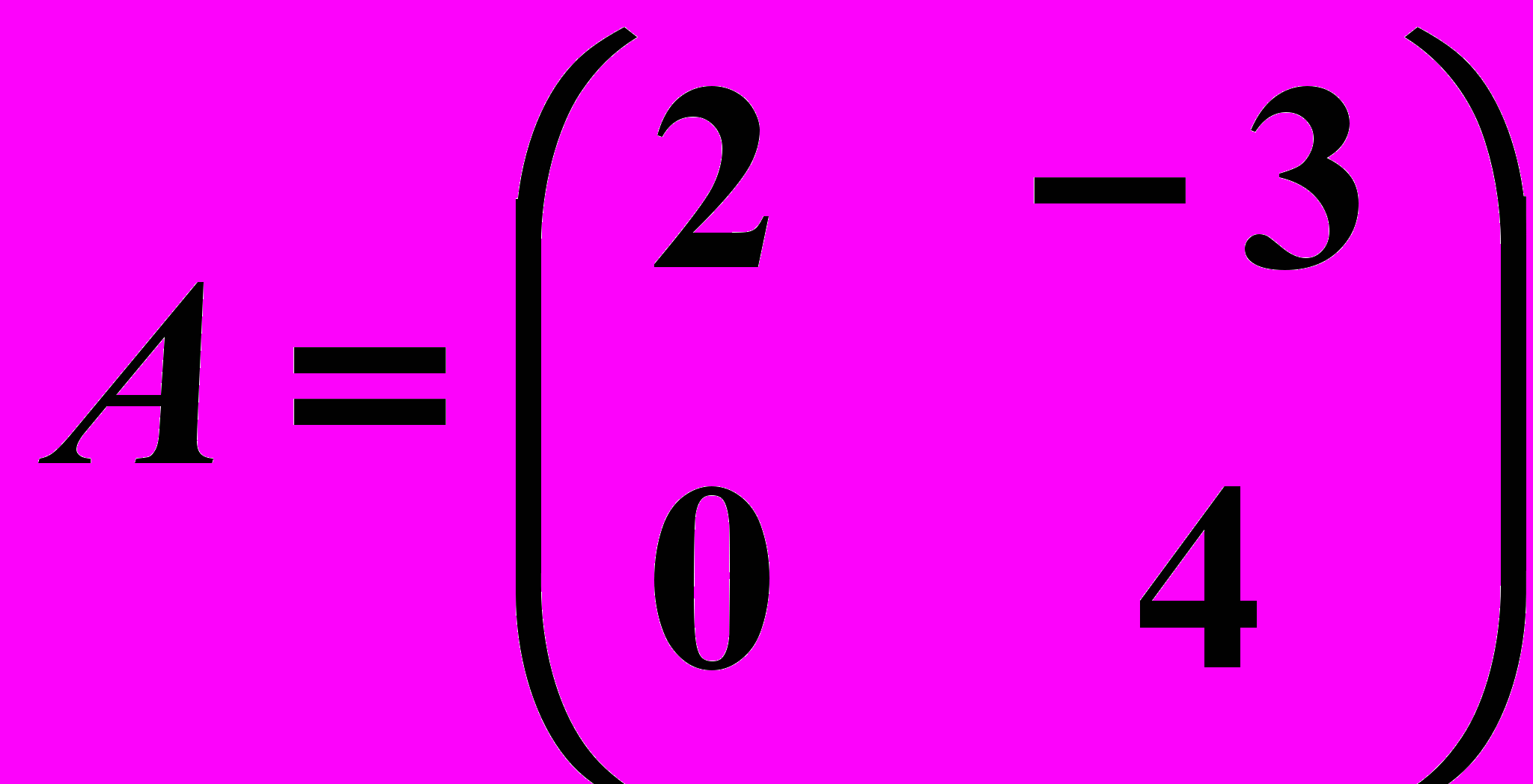 20.6.
20.6. 
Вариант № 21
21.1.
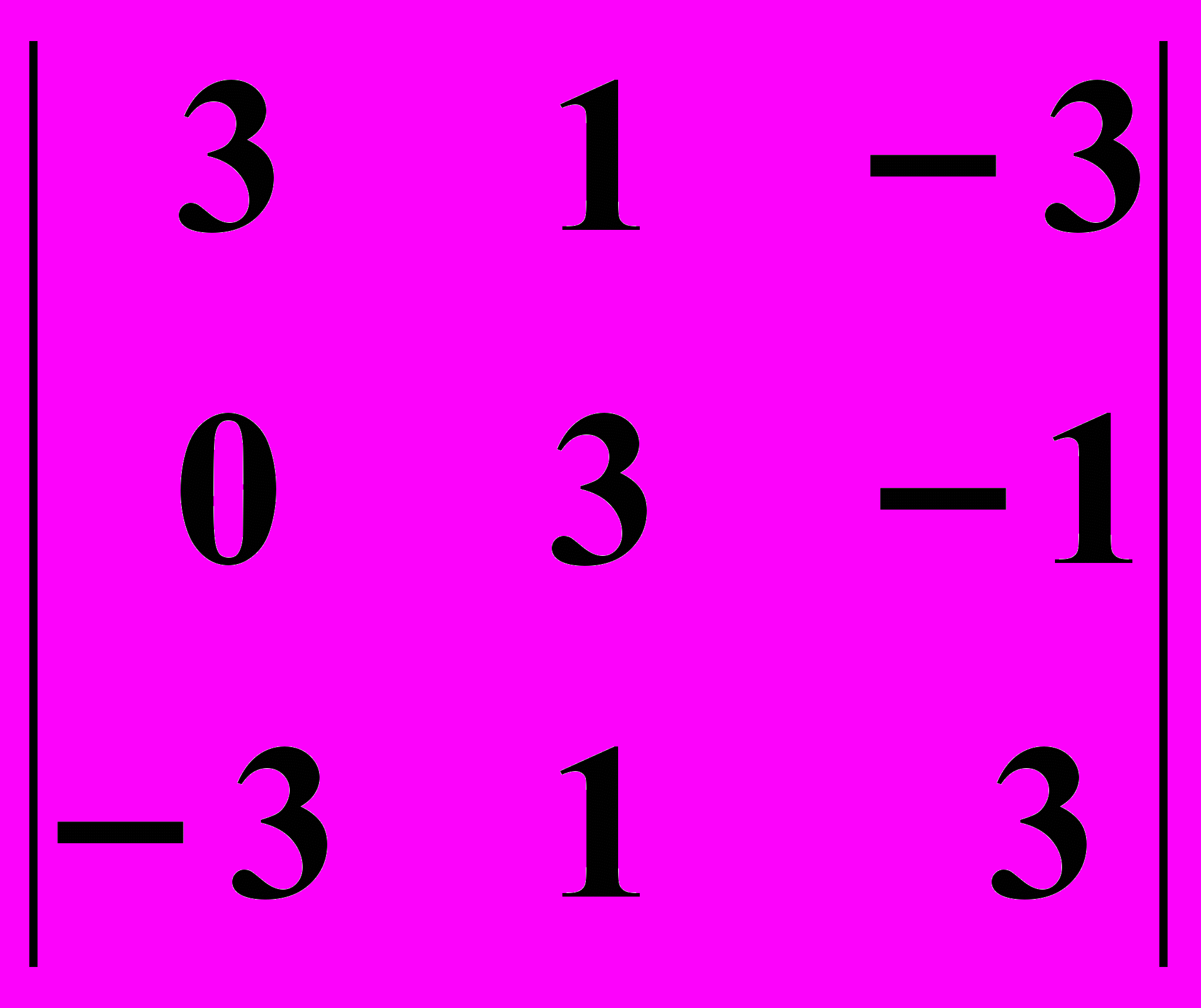 21.2.
21.2. 
 21.3.
21.3. 
21.4.
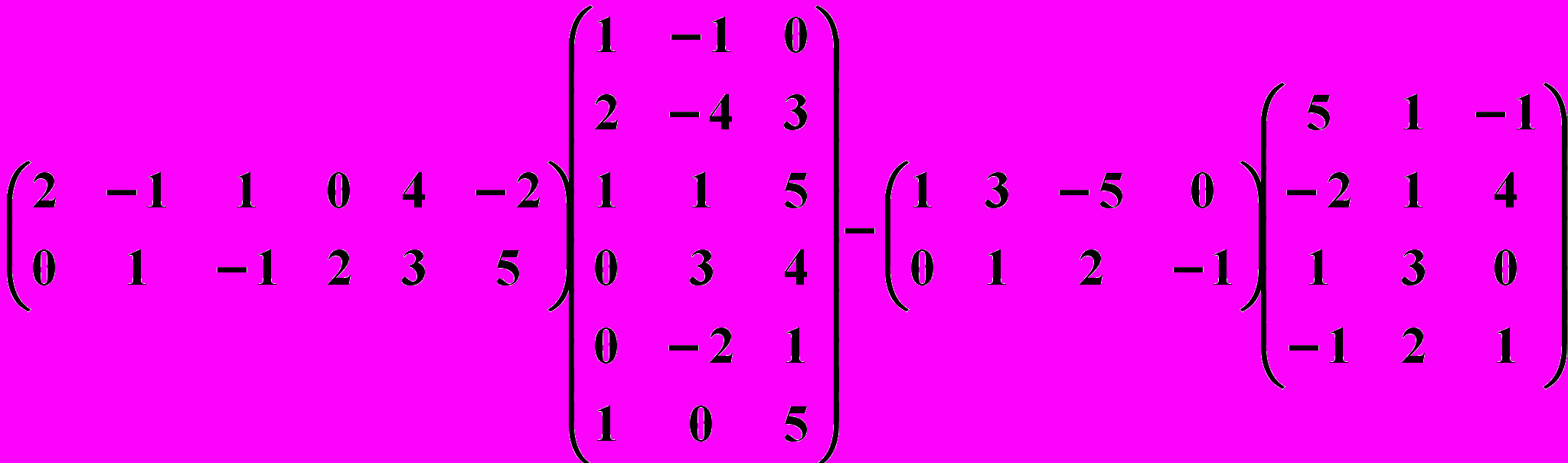
21.5.
 ,
,  21.6.
21.6. 
Вариант № 22
22.1.
 22.2.
22.2.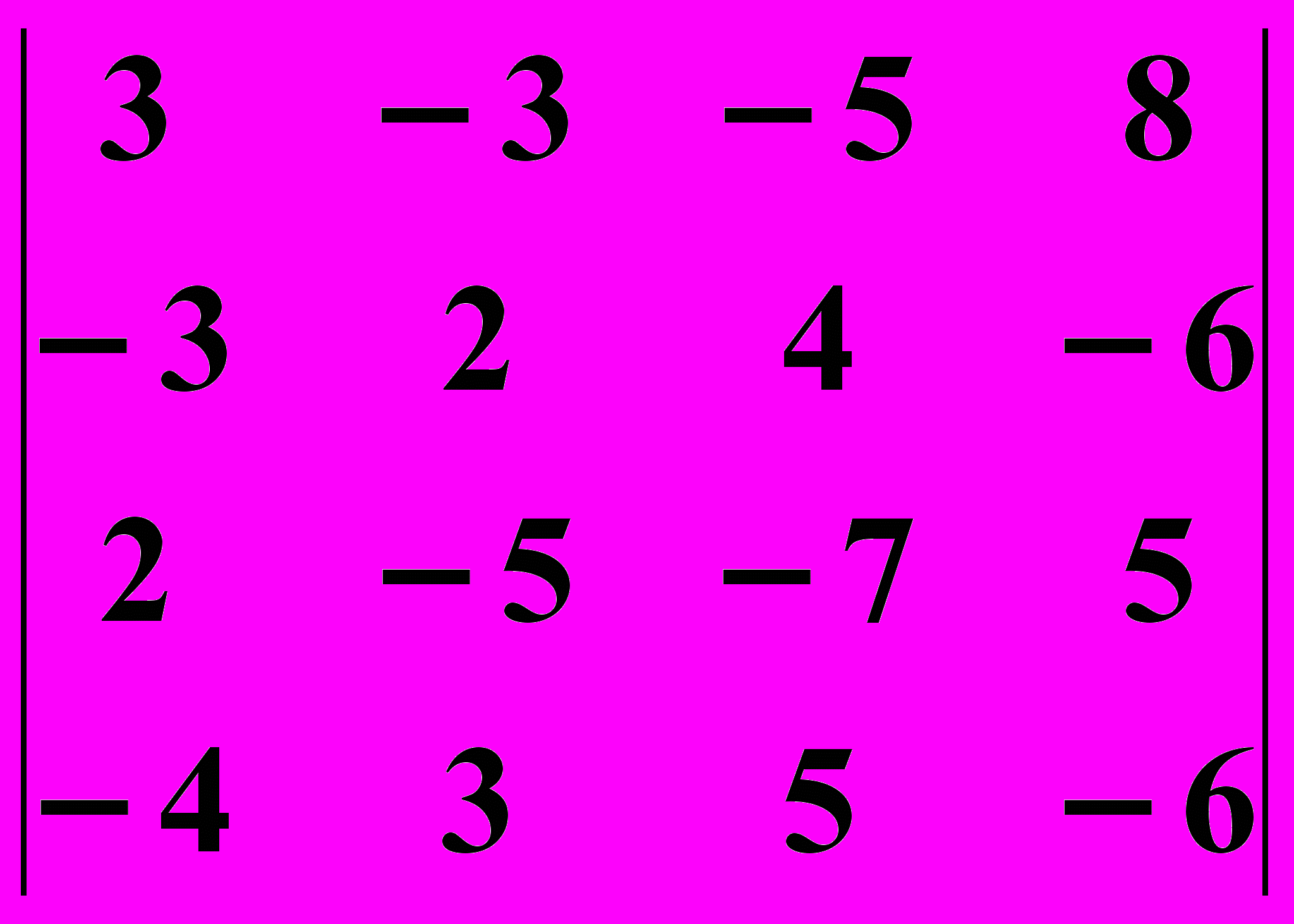 22.3.
22.3. 
22.4.

22.5.
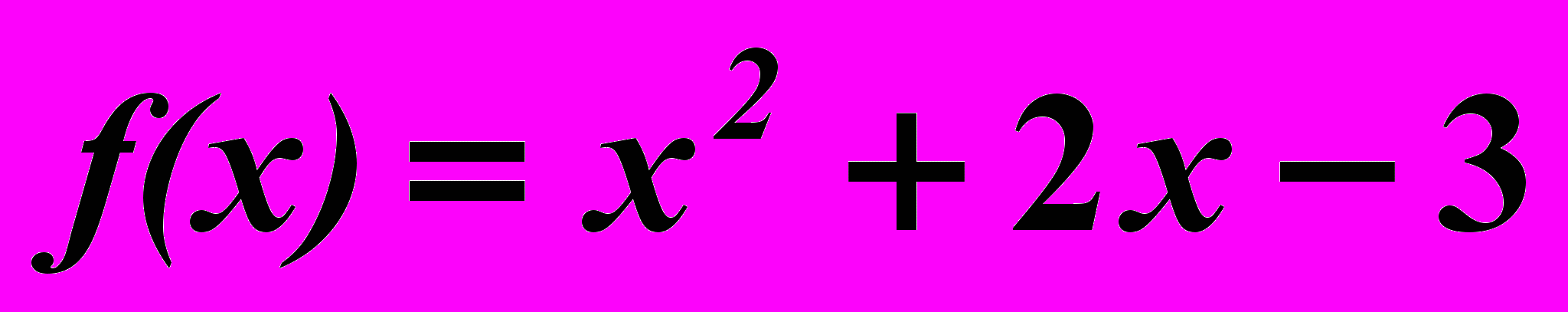 ,
, 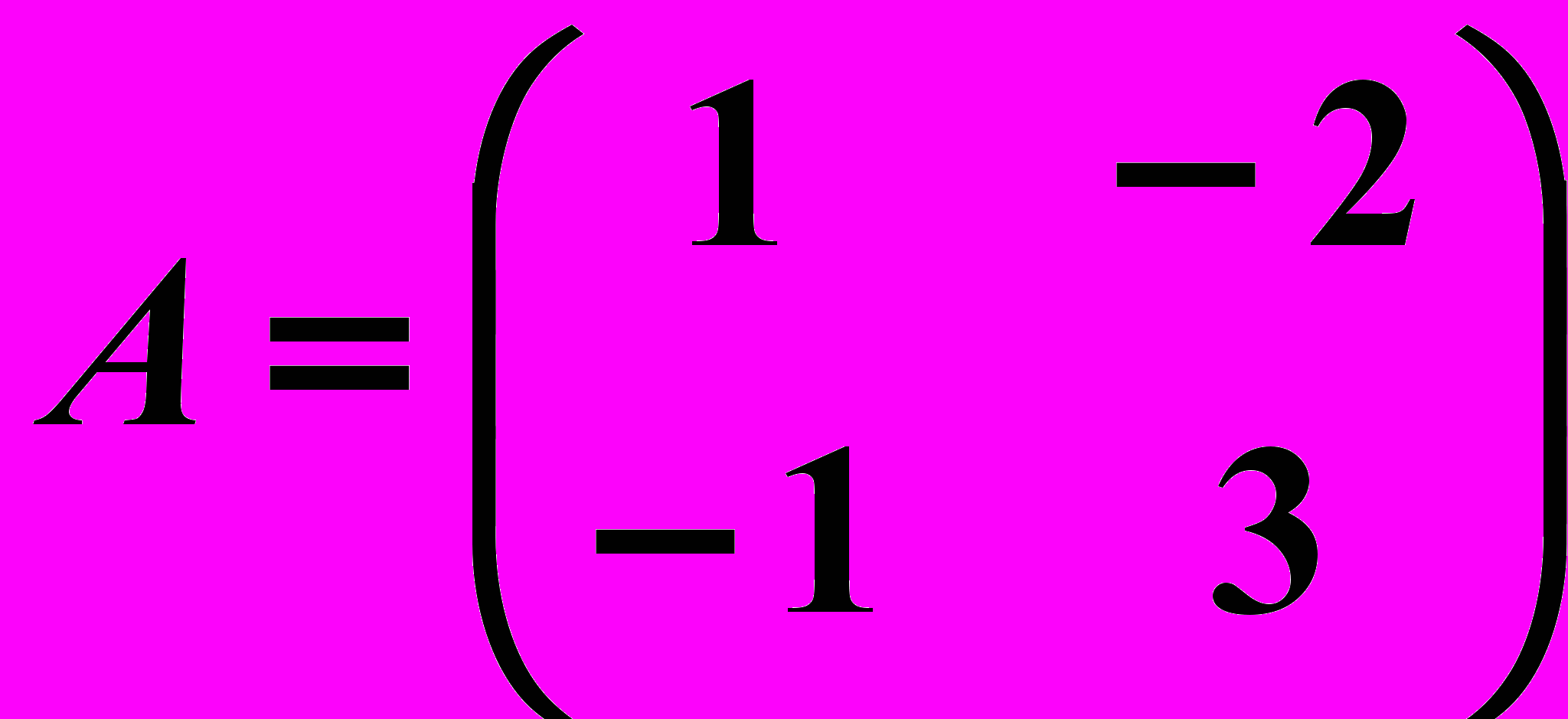 22.6.
22.6. 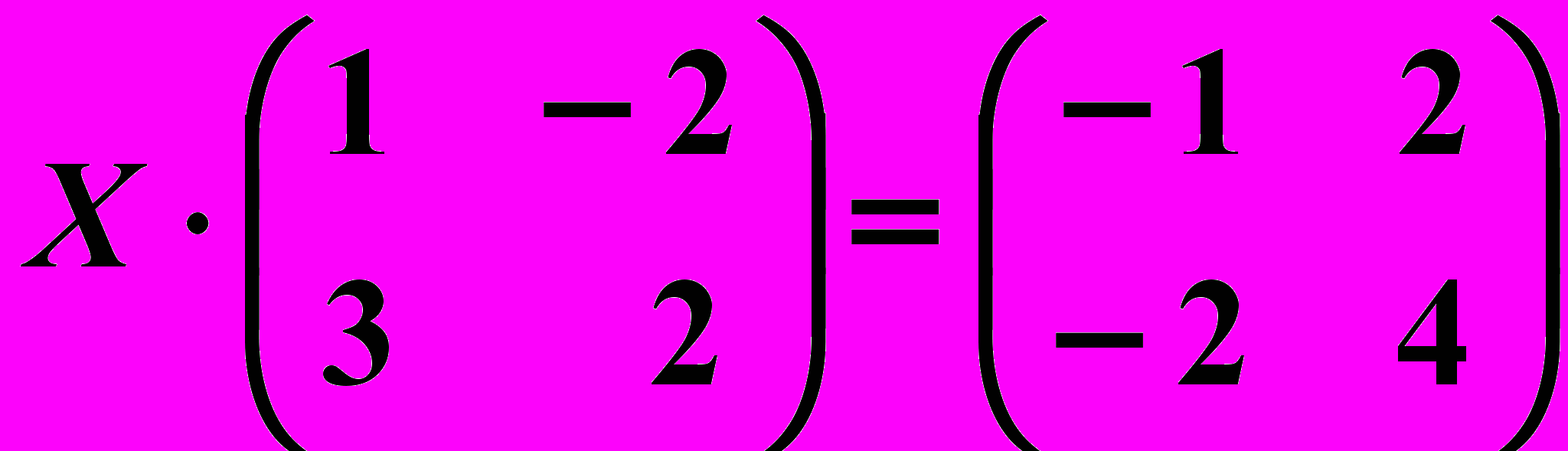
Вариант № 23
23.1.
 23.2.
23.2. 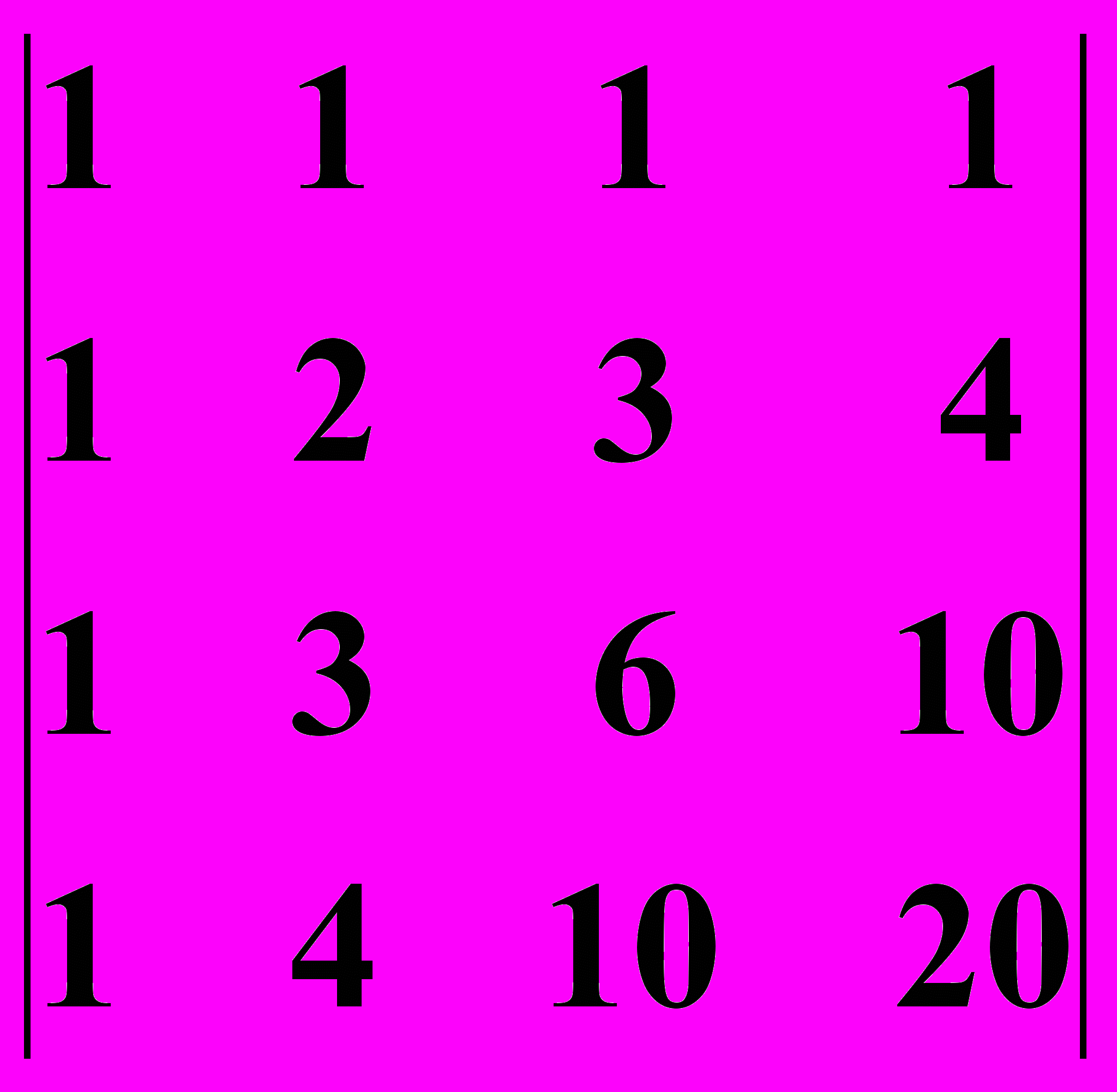 23.3.
23.3. 
23.4.

23.5.
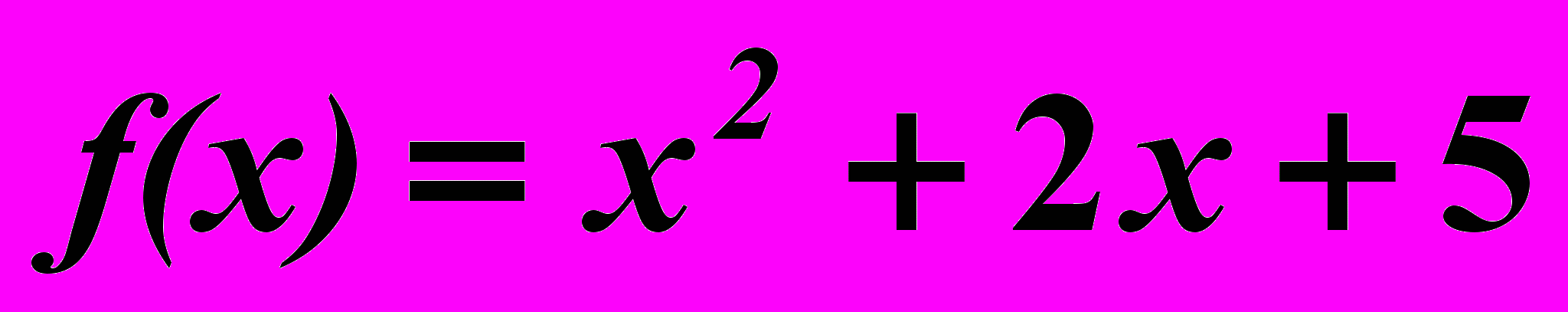 ,
,  23.6.
23.6. 
Вариант № 24
24.1.
 24.2.
24.2. 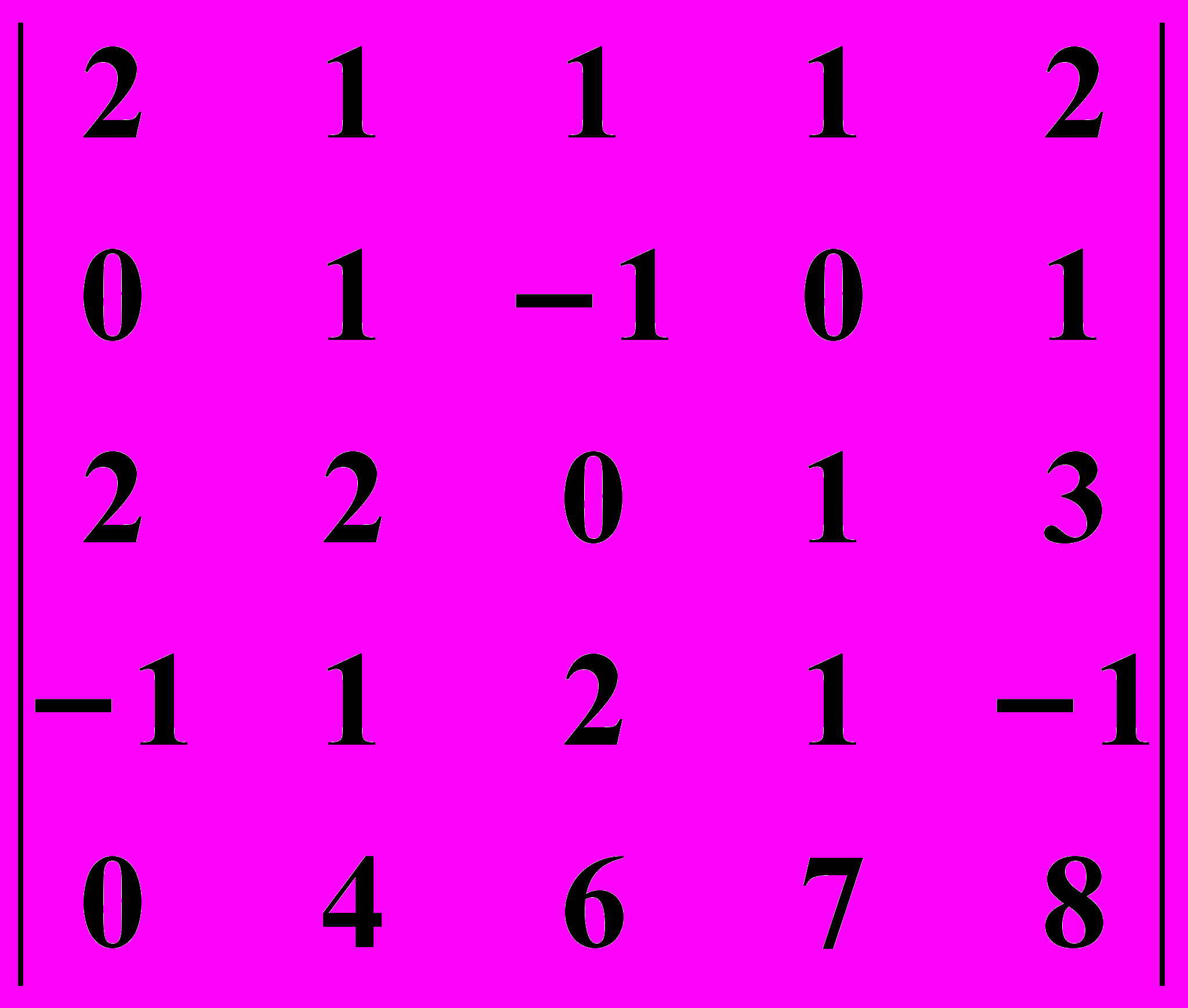 24.3.
24.3. 
24.4.

24.5.
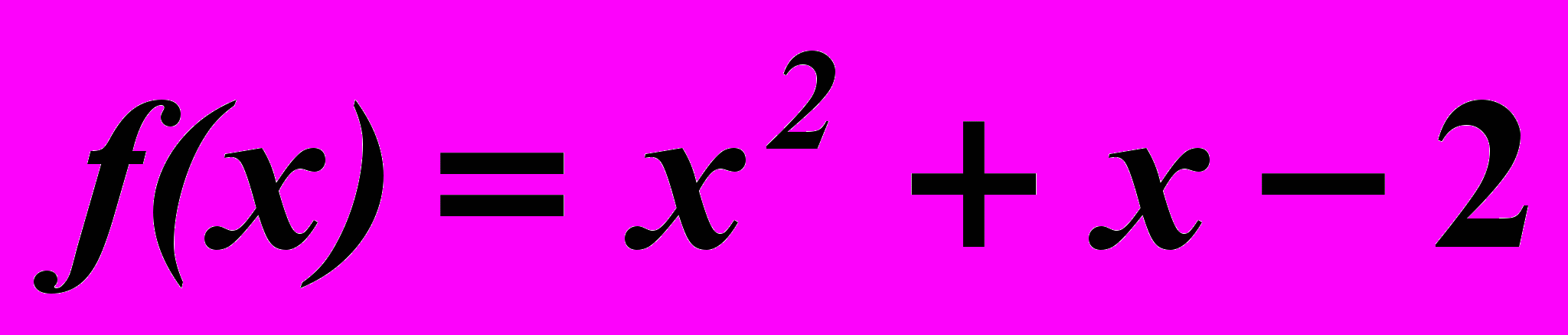 ,
, 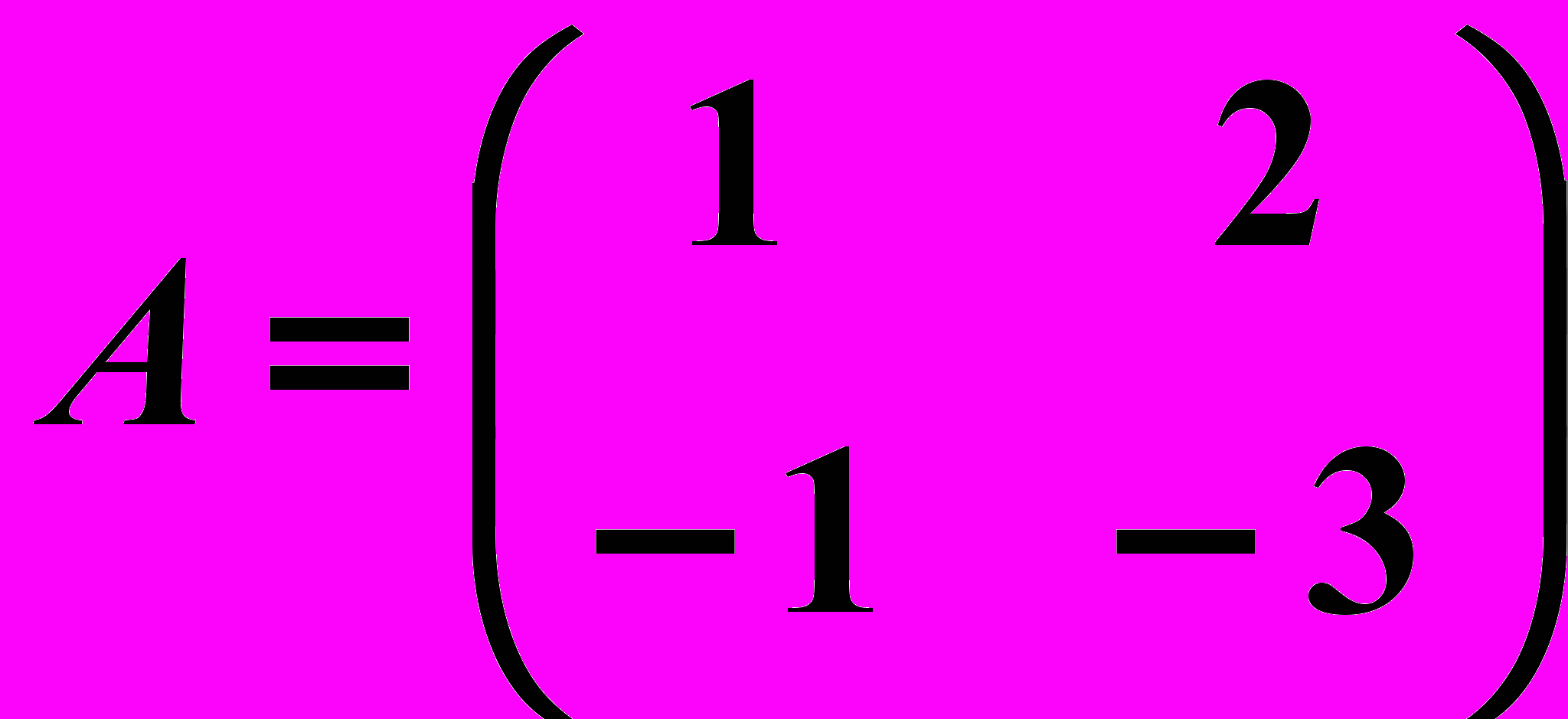 24.6.
24.6. 
Вариант № 25
25.1.
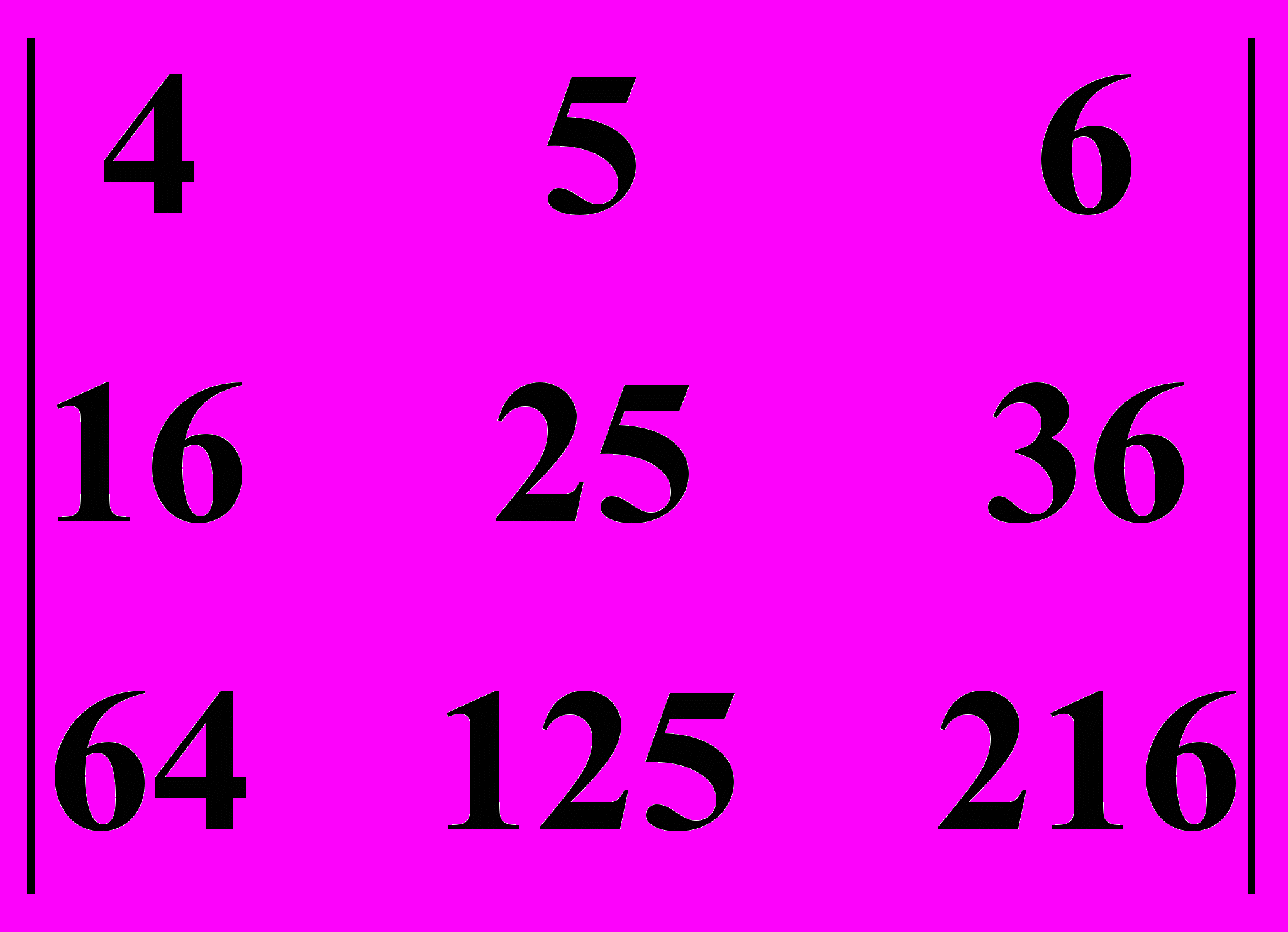 25.2.
25.2. 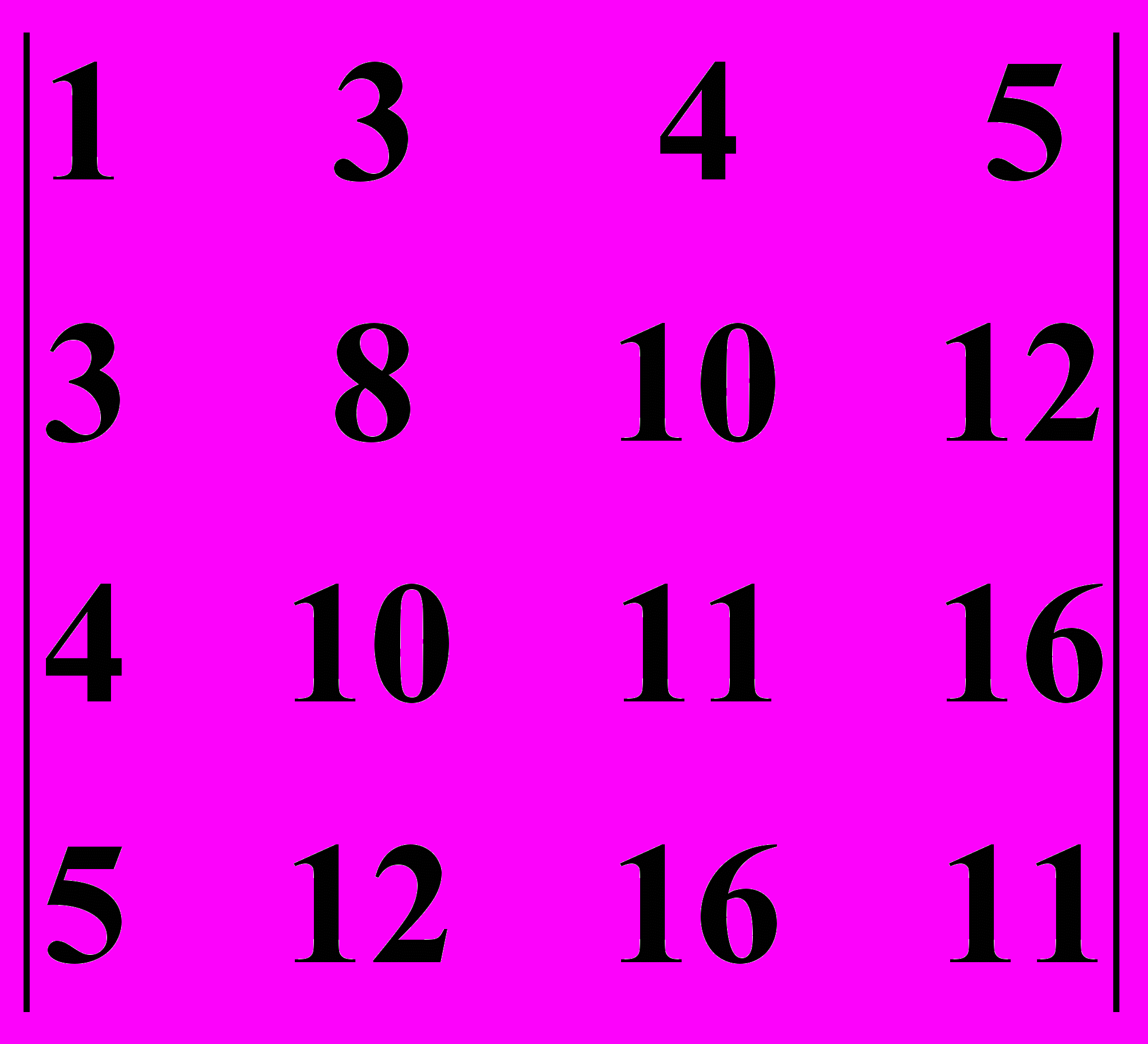 25.3.
25.3. 
25.4.

25.5.
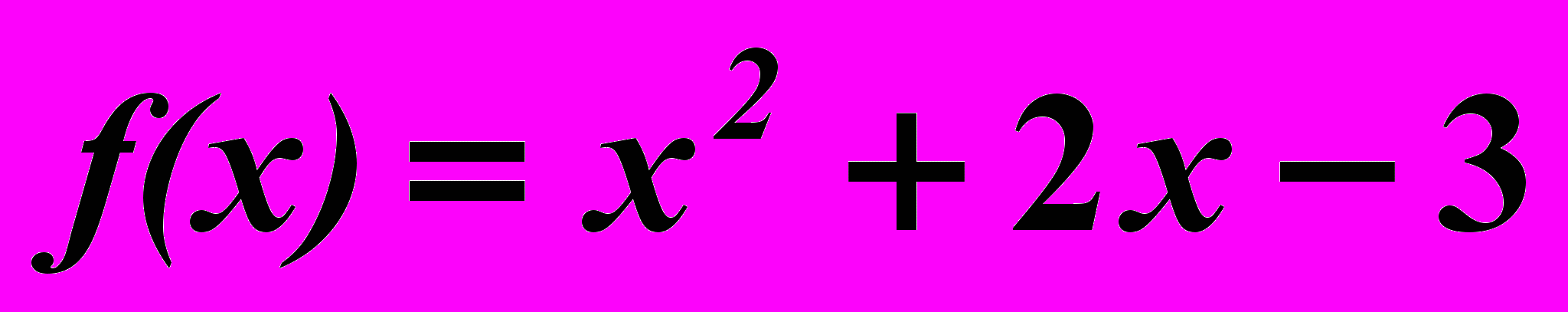 ,
,  25.6.
25.6. 
Вариант № 26
26.1.
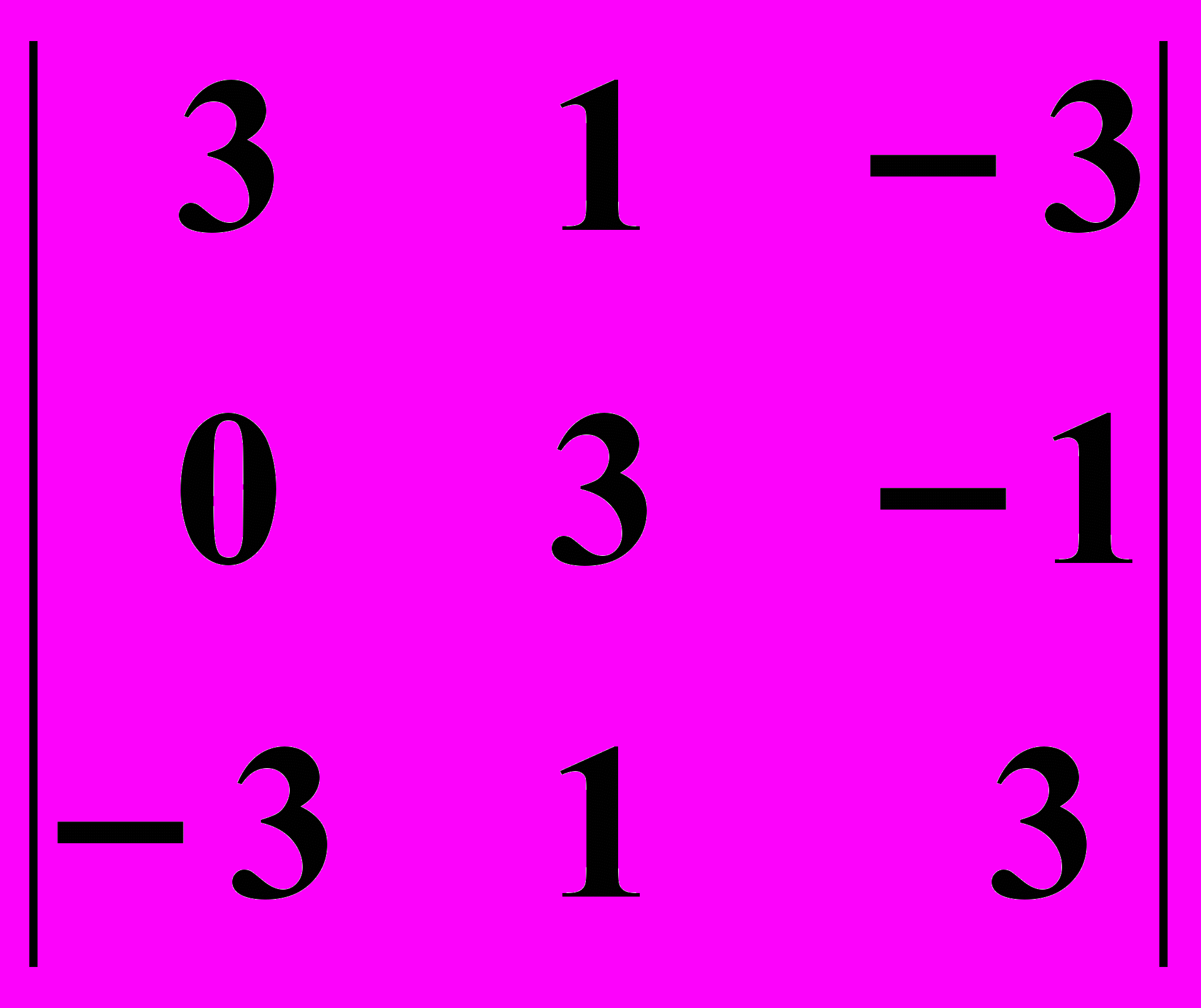 26.2.
26.2.  26.3.
26.3. 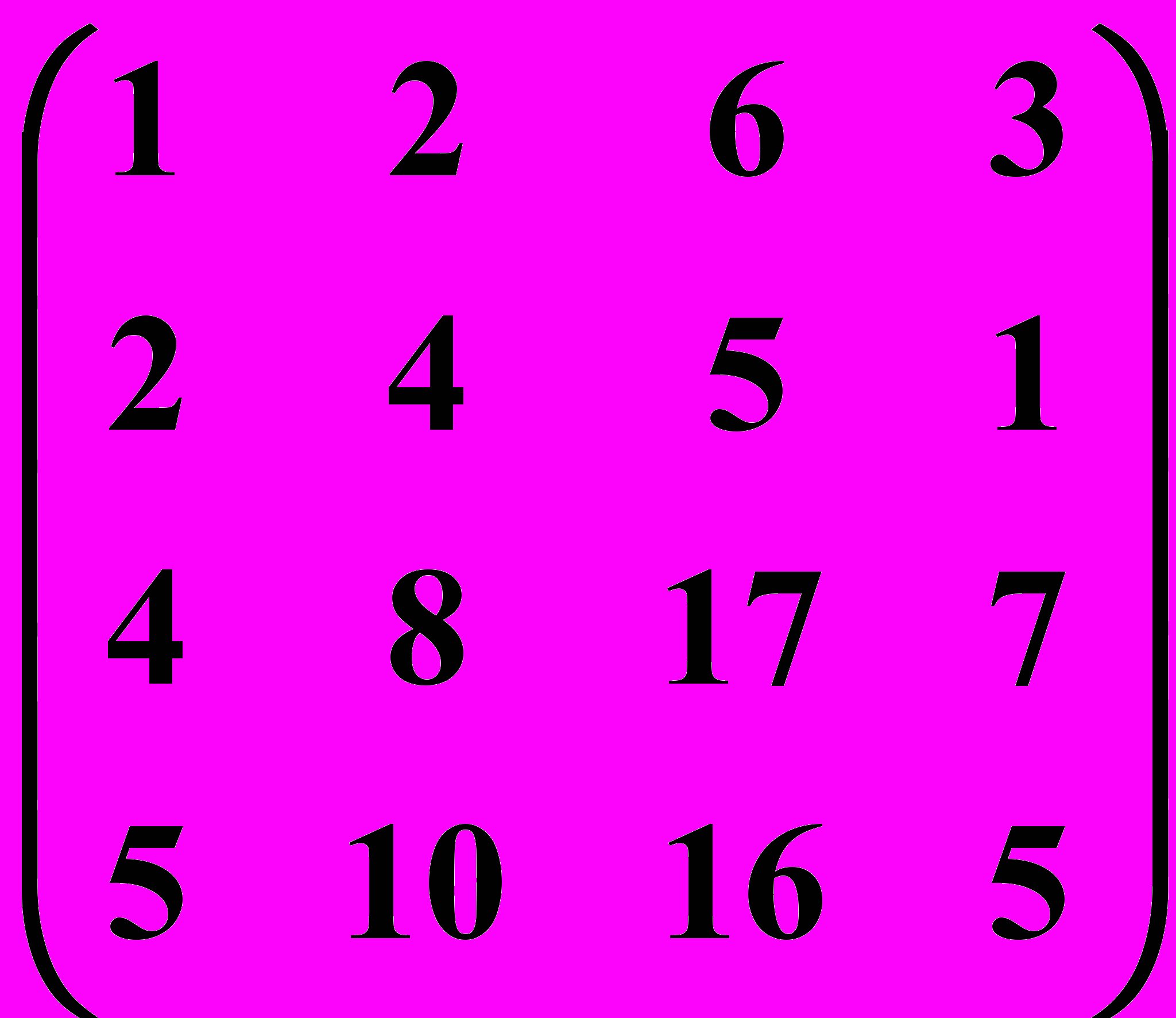
26.4.
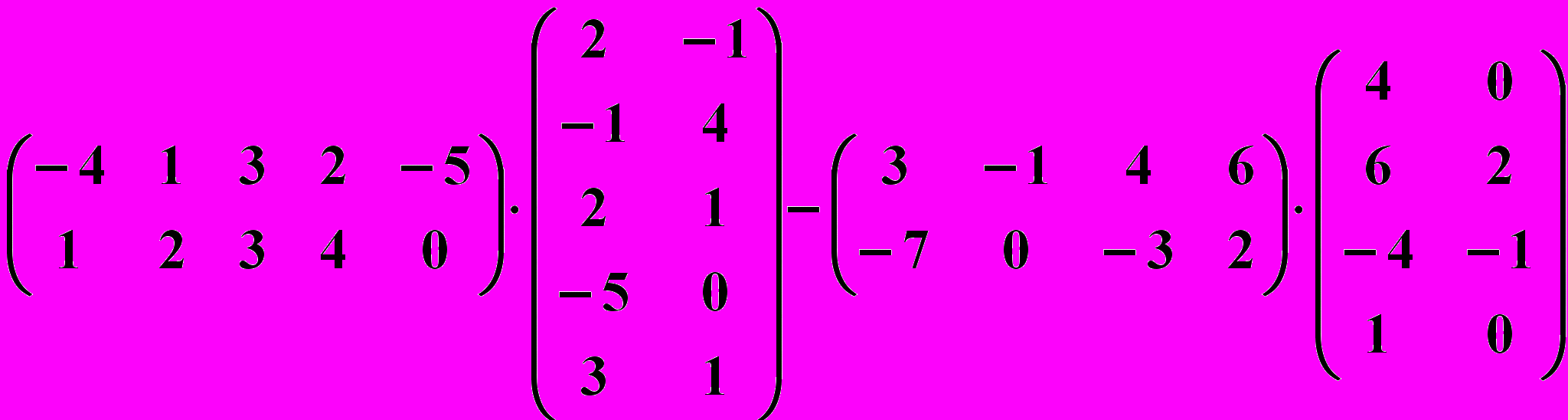
26.5.
 ,
, 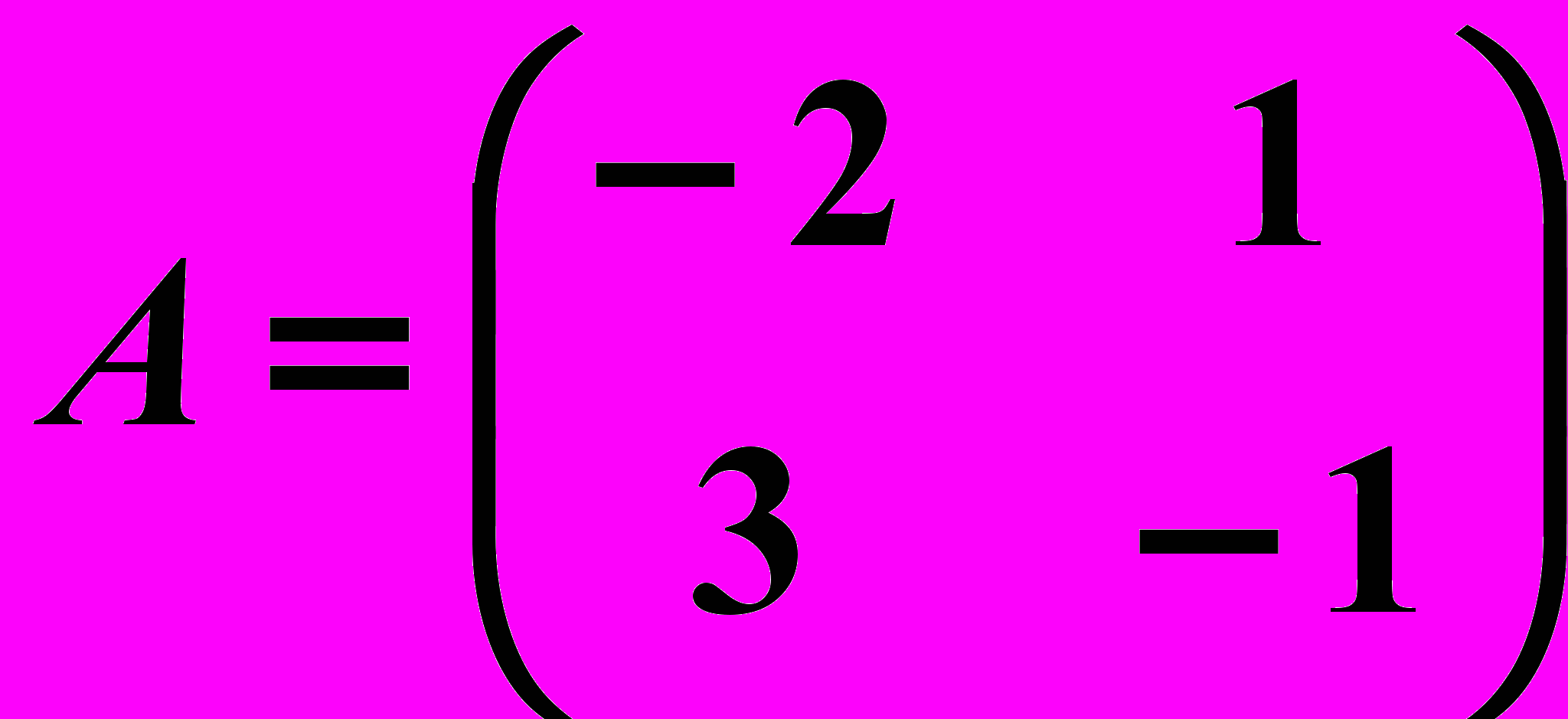 26.6.
26.6. 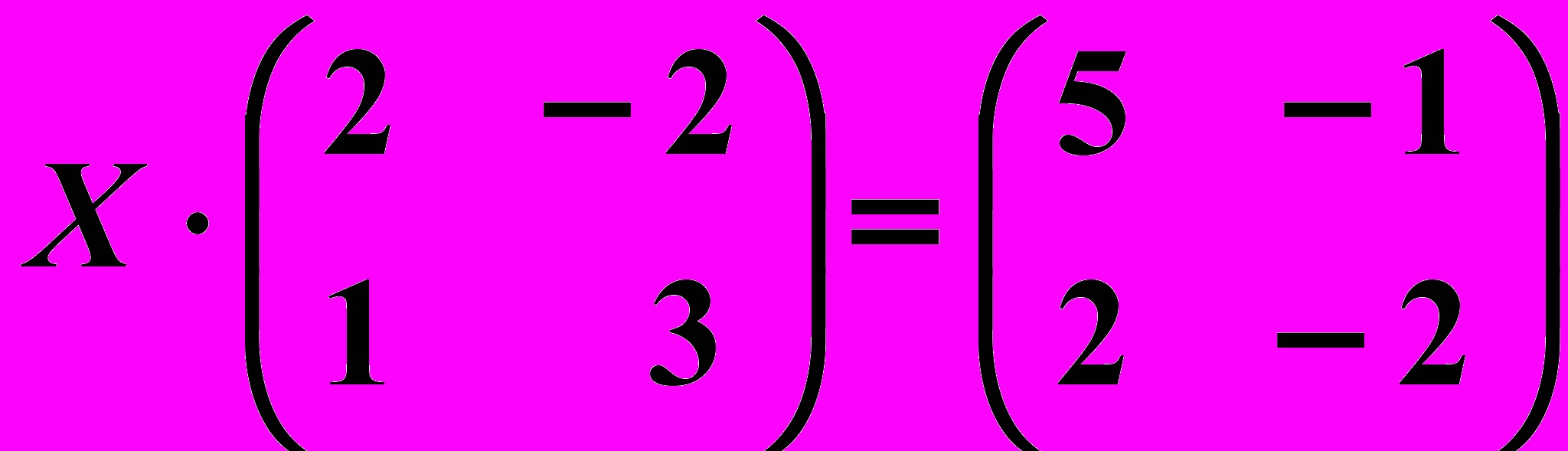
Вариант № 27
27.1.
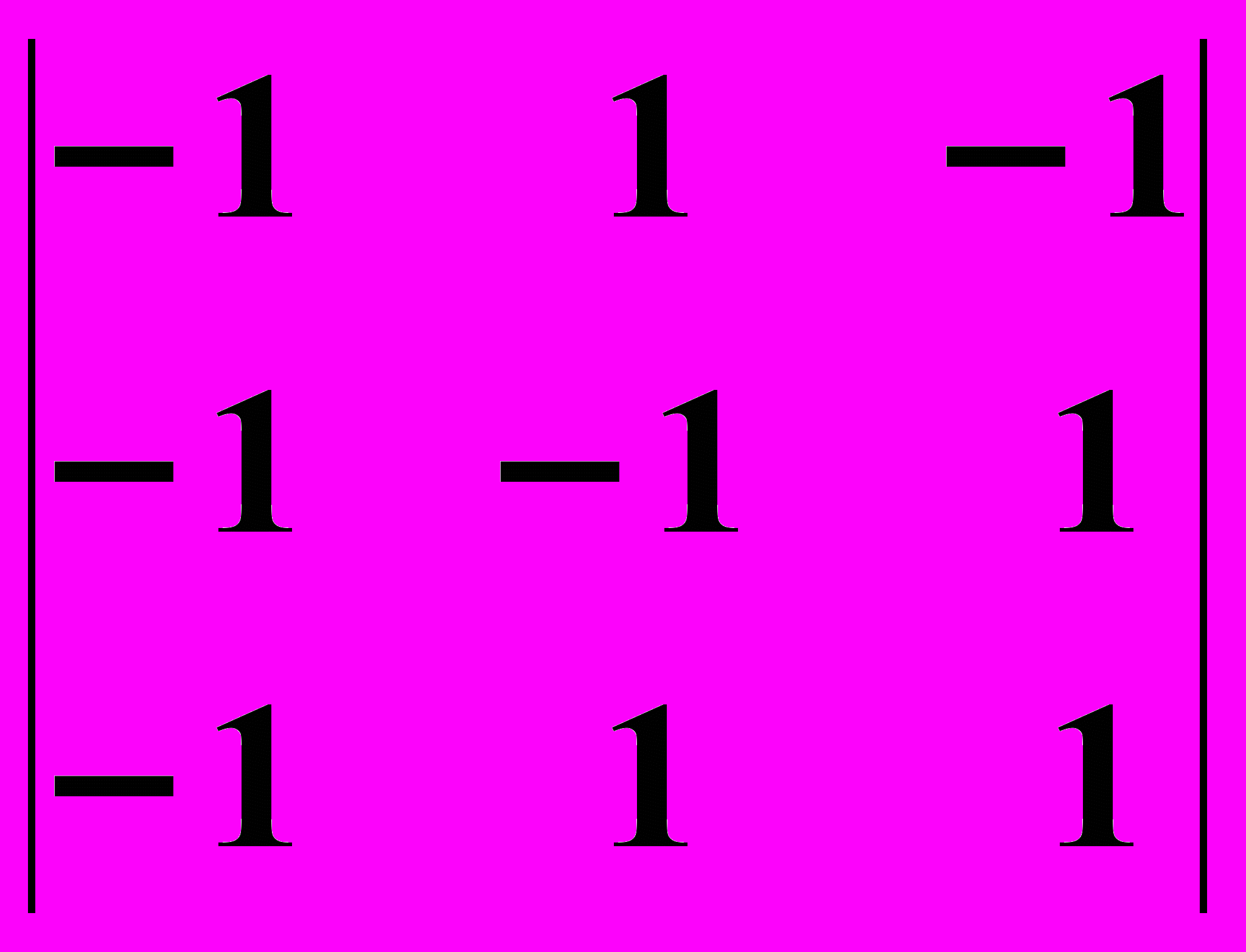 27.2.
27.2. 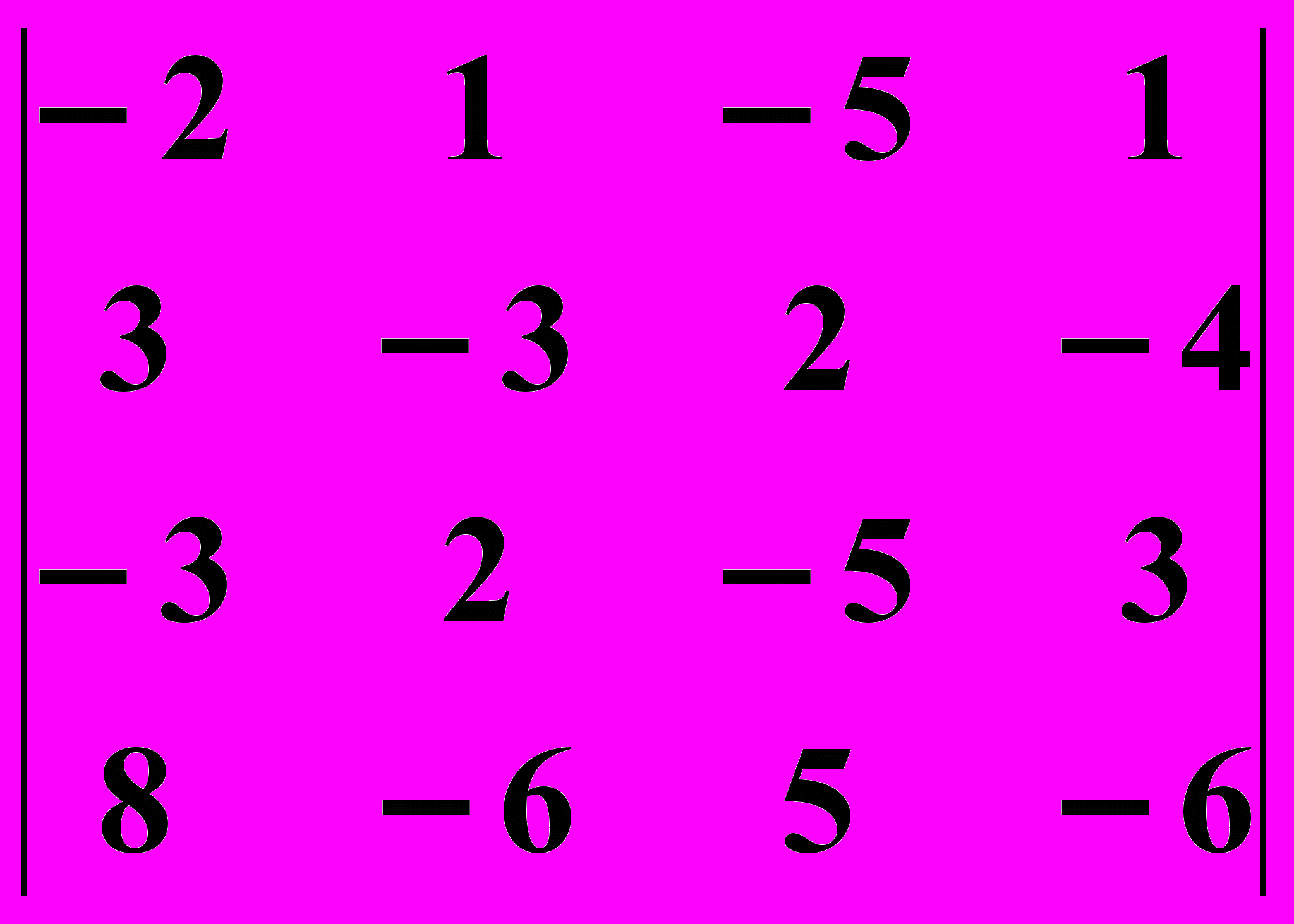 27.3.
27.3. 
27.4.
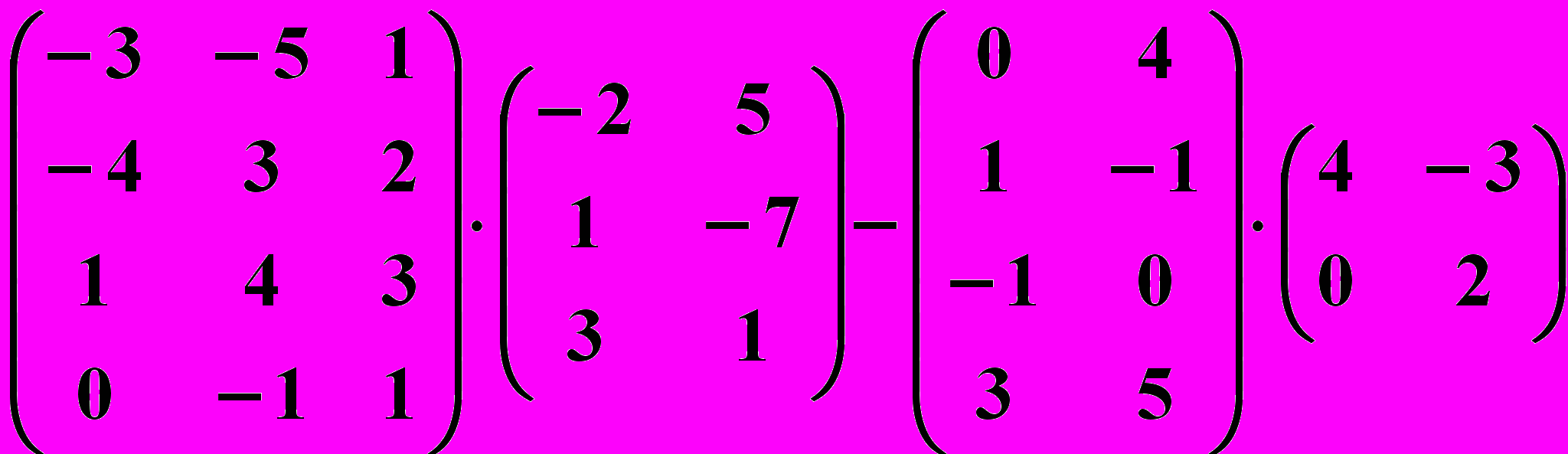
27.5.
 ,
,  27.6.
27.6. 
Вариант № 28
28.1.
 28.2.
28.2.  28.3.
28.3. 
28.4.

28.5.
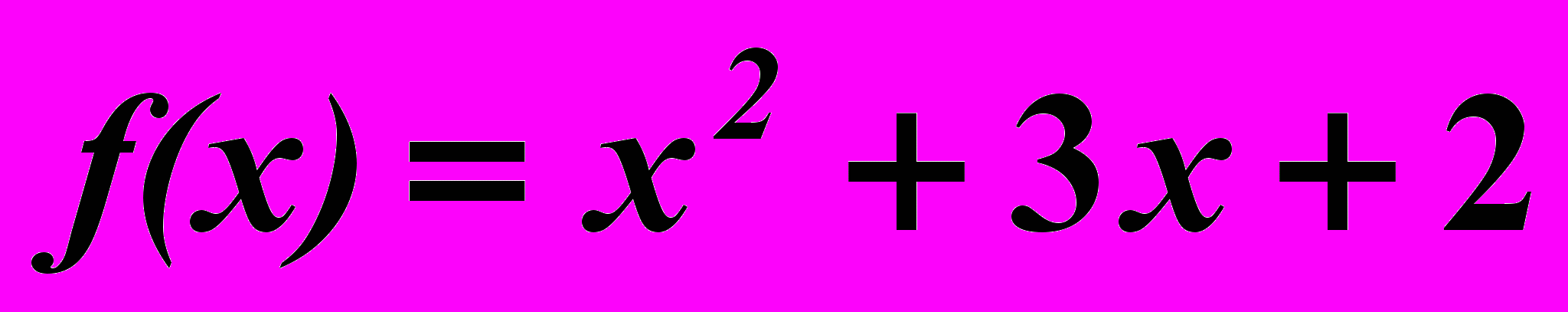 ,
,  28.6.
28.6.
Вариант № 29
29.1.
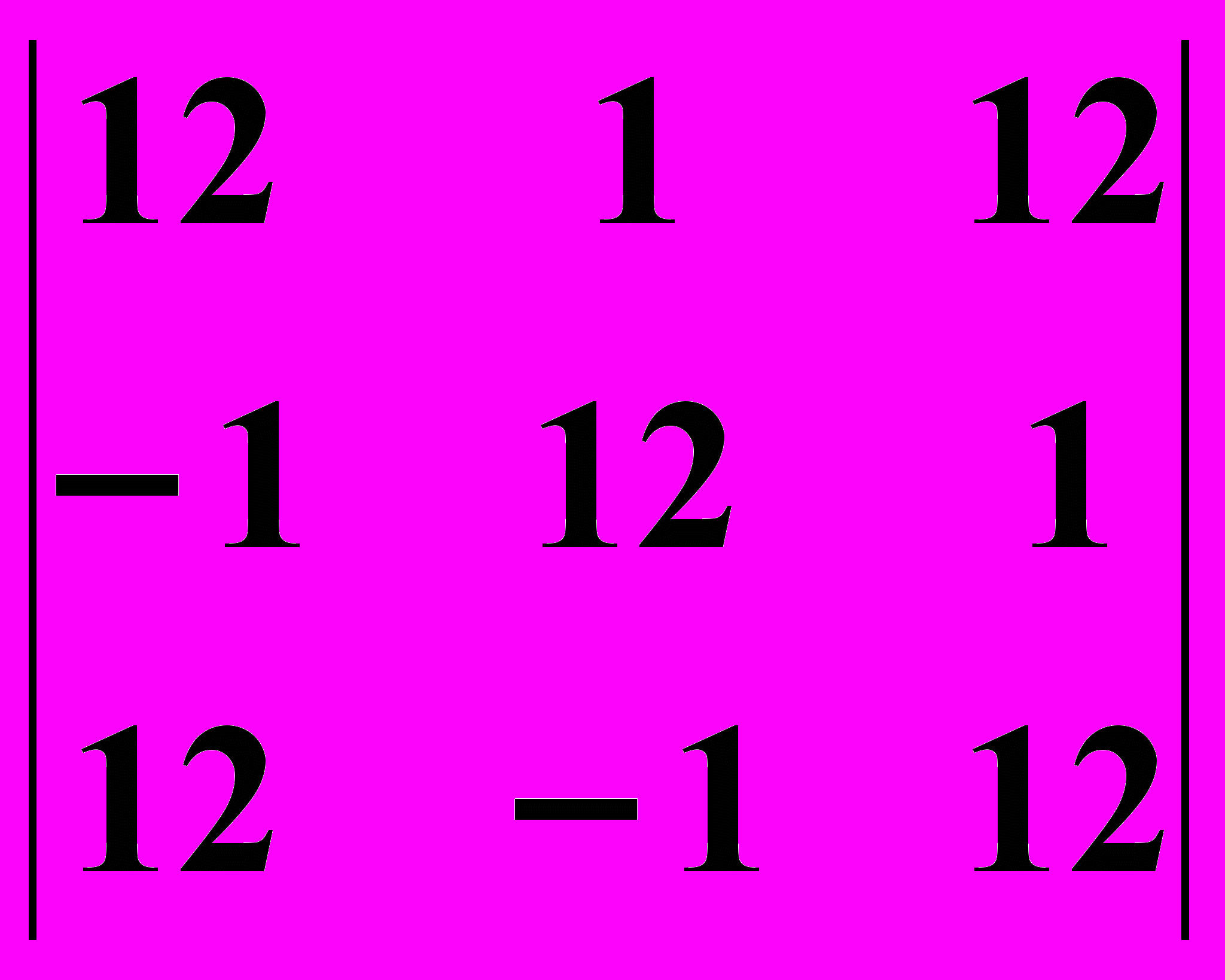 29.2.
29.2. 29.3.
29.3. 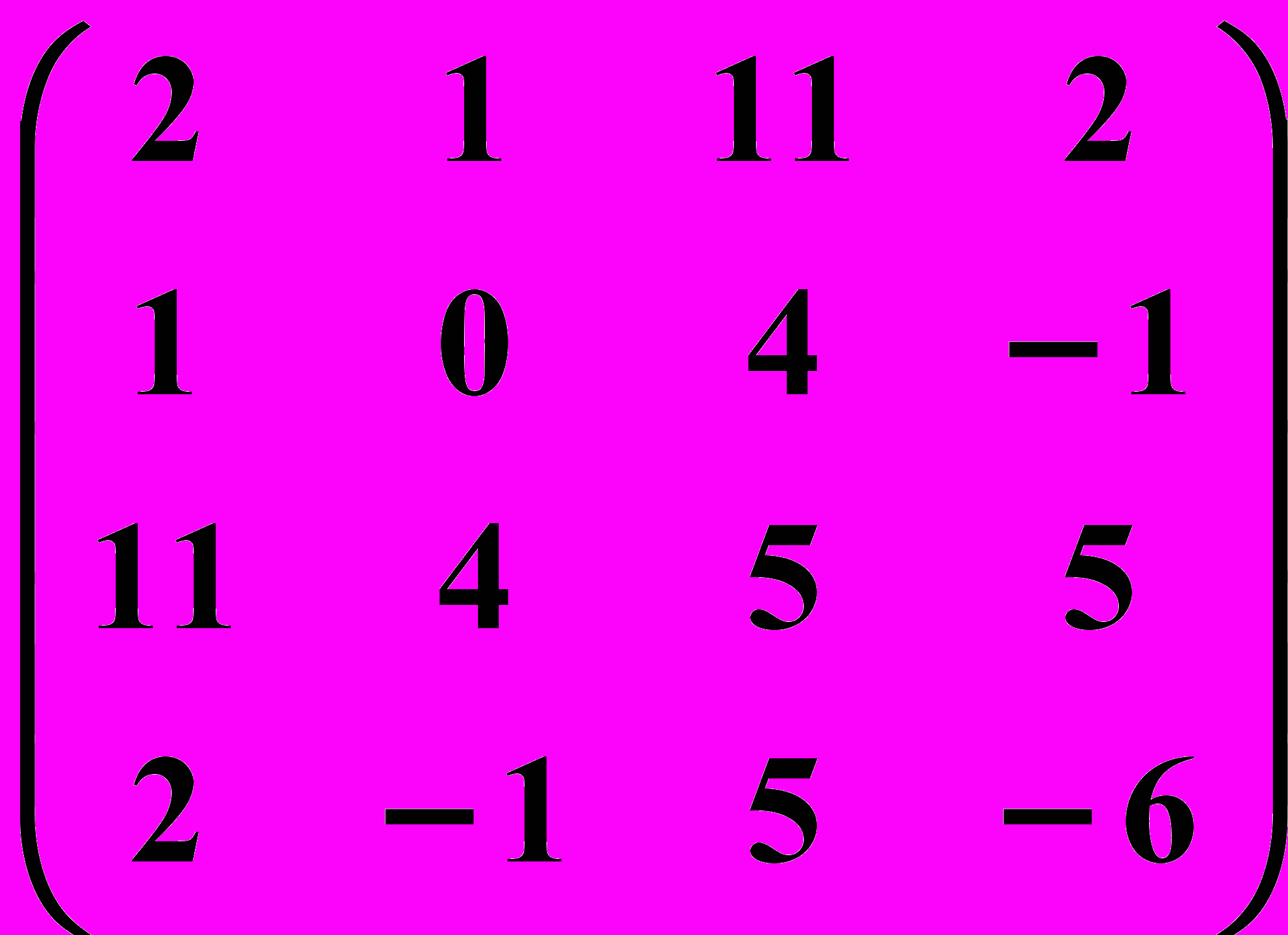
29.4.

29.5.
 ,
, 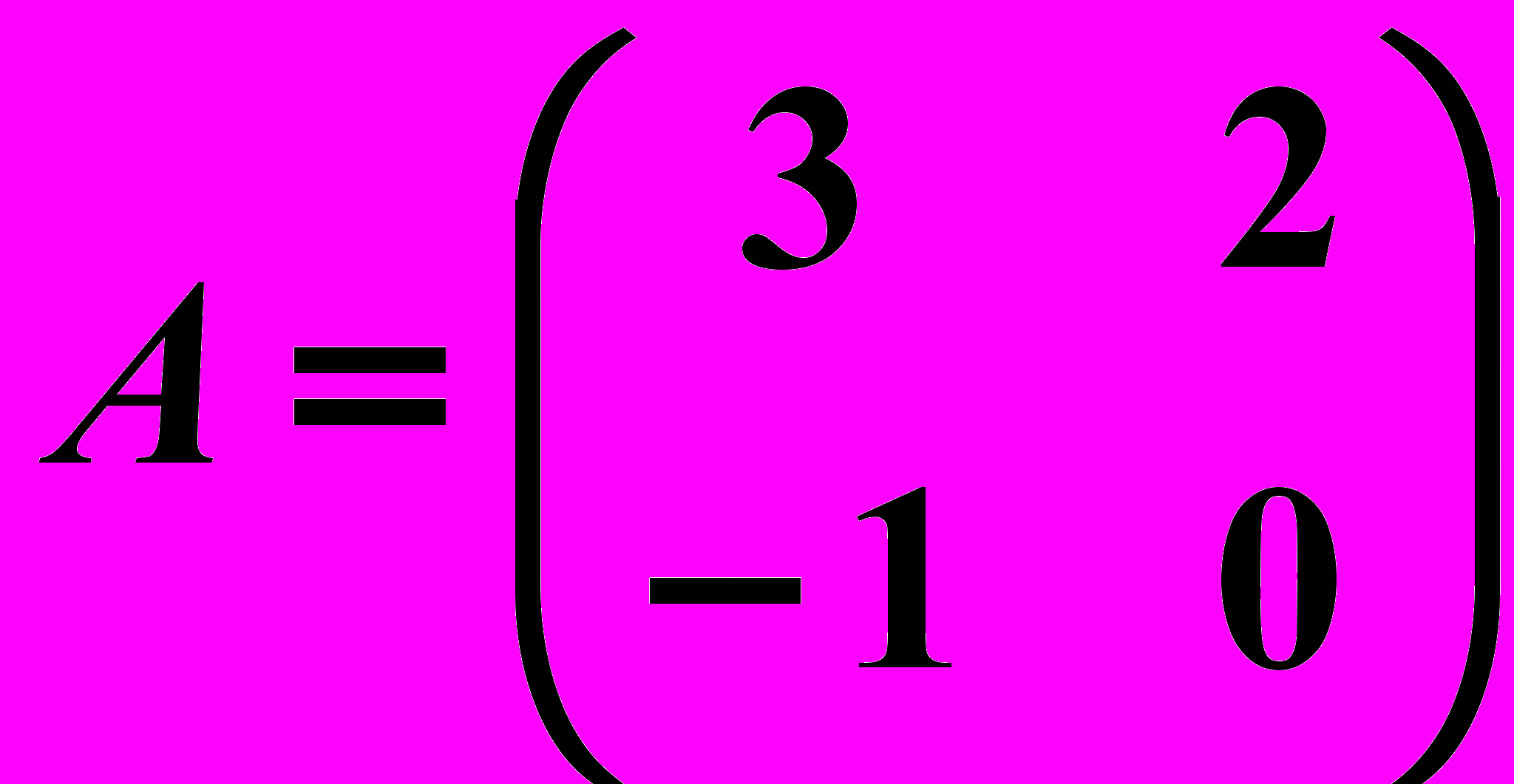 29.6.
29.6.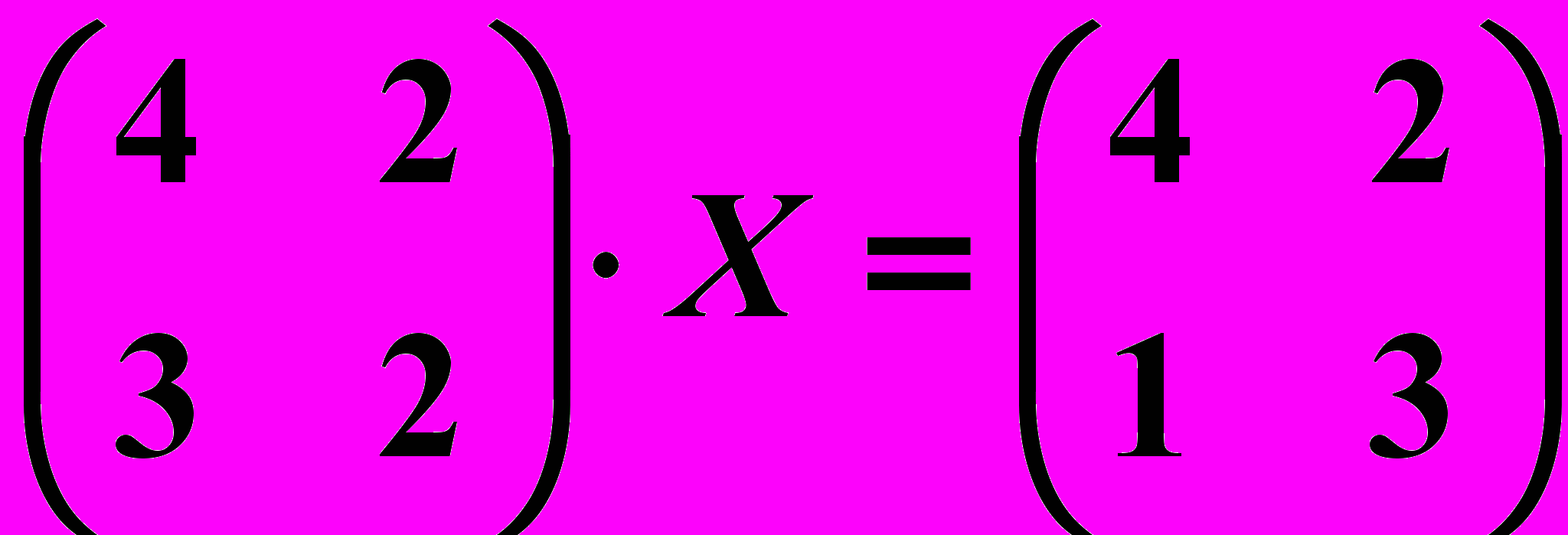 .
.Вариант № 30
30.1.
 30.2.
30.2.  30.3.
30.3. 
30.4.
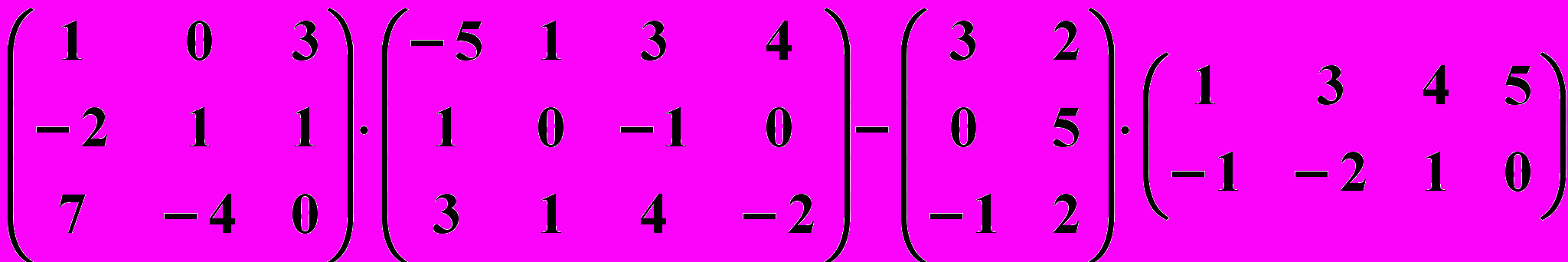
30.5.
 ,
,  30.6.
30.6.  .
.