Geum.ru

Аннотация научно-образовательного материала (ном)

Вид материалаДокументы
Подобный материал:
Аннотация

научно-образовательного материала (НОМ)

«Комплекс учебных пособий по курсу”Дифференциальные уравнения”»,

представленного кафедрой Математического моделирования (ММ).


Для проведения в 2010 году мероприятий в сфере образования для населения города Москвы в целях повышения качества образовательных услуг кафедра ММ выполнила

работу по созданию комплекса учебных пособий по курсу «Дифференциальные уравнения ». Этот комплекс предназначен для использования в системе повышения

квалификации и может быть использован также в системе дополнительного образования.

Он состоит из следующих учебных пособий :

1. Амосов А.А., Зубков П.В., Перескоков А.В. Лекции по вариационному исчислению.-

М.: Издательский дом МЭИ. 2011.

2. Амосов А.А., Игнатьева Н.У., Перескоков А.В. Задачи по вариационному

исчислению. – М.: Издательский дом МЭИ. 2008. 72 с.

3. Григорьев В.П., Перескоков А.В. Расчётные задания по курсу «Дифференциальные

уравнения ». – М.: Издательский дом МЭИ. 2011.

Все эти учебные пособия написаны на высоком научно-методическом уровне , и

закрывают имеющийся в учебной литературе пробел по данному курсу и тем самым

они повышают качество образовательных услуг.

Первое учебное пособие подготовлено на основе лекций читаемых кафедрой ММ

по вариационному исчислению – одной из важнейших дисциплин, связанной с прило-

жениями теории дифференциальных уравнений. Эта, одна из наиболее трудных частей курса, до подготовки этого пособия была очень слабо методически обеспеченной, что приводило к трудностям в изучении всего курса «Дифференциальные уравнения ». В учебном пособии с достаточной полнотой изложены все основные вопросы вариационного исчисления : 1) Функционалы. Сильная и слабая дифференцируемость. Необходимое условие дифференцируемости.

2) Простейшая задача вариационного исчисления. Уравнение Эйлера. 3) Случаи интегрируемости уравнения Эйлера. 4) Задача со свободными концами. 5) Задача с подвижными концами. 6) Задача Больца. 7) Функционалы вида .

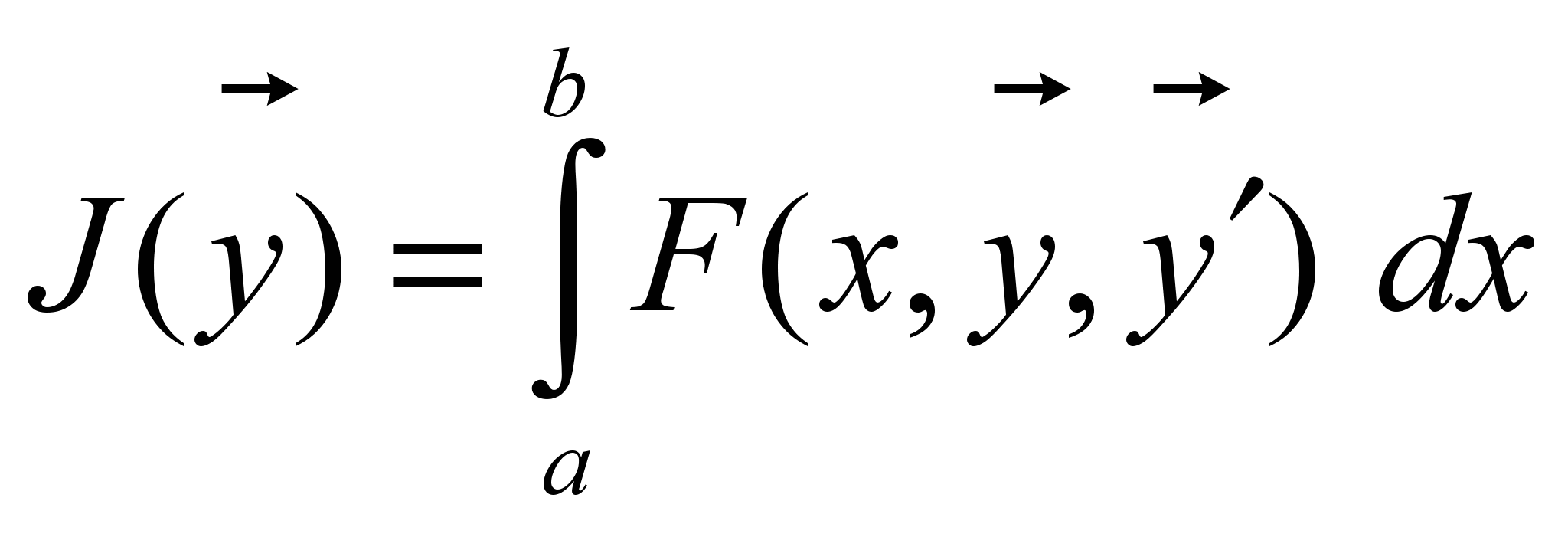8) Функционалы вида 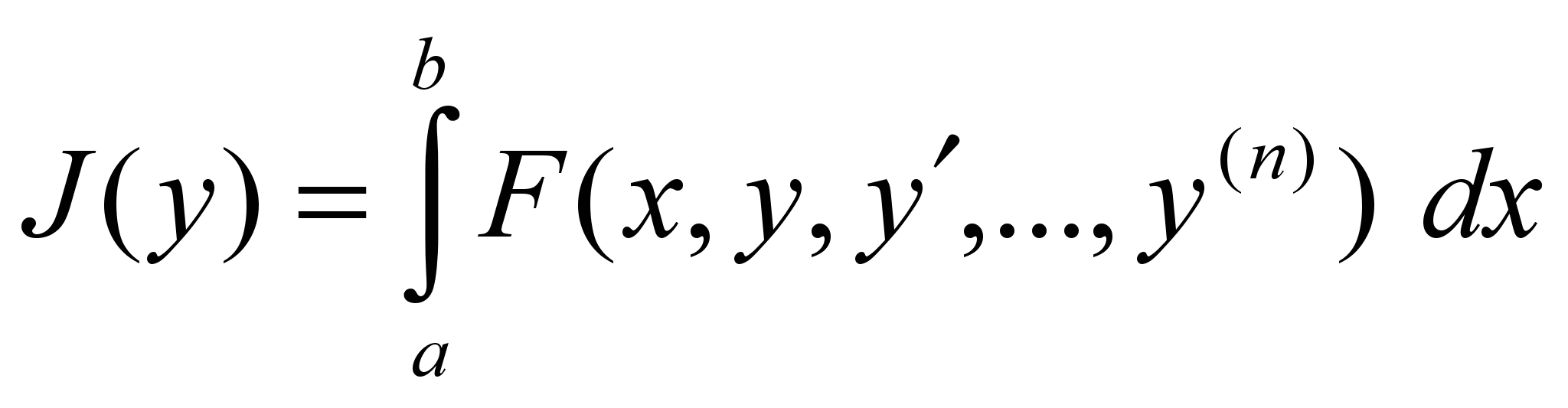. 9) Минимизация выпуклых функ-ционалов. 10) Вторая вариация функционала. Необходимое условие экстремума в терминах второй вариации. Условие Лежандра. 11) Классические достаточные условия


экстремума. 12) Изопериметрические задачи. 13) Вариационные задачи на условный экстремум с голономными и неголономными условиями связи.

Все результаты приведены с чёткими доказательствами и снабжены поясняющими

примерами.

Второе учебное пособие : Амосов А.А., Игнатьева Н.У., Перескоков А.В. Задачи по вариационному исчислению; представляет собой сборник задач по вариационному исчислению, полностью согласованный с научно-образовательным материалом

первого пособия. Его отличает большое число задач различного уровня трудности,

подробные теоретические указания, что в современной учебной литературе по

данной дисциплине не имеет места. Апробация этого методического ресурса при

изучении курса «Дифференциальные уравнения » в МЭИ (ТУ) в течение 2010 года

показала его безусловную полезность и эффективность.

Третье учебное пособие: Григорьев В.П., Перескоков А.В. Расчётные задания по курсу «Дифференциальные уравнения »; представляет собой материал, не имеющий

аналогов в учебной литературе. Он посвящён расчётным заданиям по такому, тра-

диционно трудному разделу теории дифференциальных уравнений, как теория

систем дифференциальных уравнений. Практические задания по этому разделу мож-

но найти в задачниках, но при выдаче индивидуального задания преподаватель

сталкивается с трудностями, которые призвано разрешить данное пособие. Важное

обстоятельство ещё заключается в том, что в число задач расчётного задания вклю-

чены задачи по теории устойчивости решений дифференциальных уравнений, что

также позволяет получить поддержку при преподавании и изучении этих вопросов

в курсе «Дифференциальные уравнения ». НОМ прошёл апробацию в МЭИ (ТУ) и

показал высокую эффективность.

В целом, НОМ «Комплекс учебных пособий по курсу ”Дифференциальные урав- нения”» представляет собой научно-методическую разработку важных разделов матема- тического образования современного инженера всех технических специальностей. Он

может применяться в любой образовательной схеме, в частности в системе повыше-ния квалификации и в системе дополнительного образования.


И.о. заведующего кафедрой ММ

профессор Дубинский Ю.А.


Контактный адрес E-mail : pereskokov @ comail.ru