Автор программы и лектор : к т. н, доцент Рейнов Ю. И, препод. Слуцкая Ю. Л статус курса

Вид материала

Лекции

Содержание I. Целевая установка II. Организационно-методические указания. Тема 1 Элементы теории множеств и математической логики. Тема 4. Числовые множества и числовые функции Тема 1 Элементы мат. логики, теории множеств. Тема 3. Системы линейных уравнений. Тема 4. Числовые множества и числовые функции Зачет по материалам 1 – 15 лекции Тема 6. Основы дифференциального исчисления и его приложения Тема 7. Основы интегрального исчисления и его приложения Тема 6. Основы дифференциального исчисления и его приложения Тема 7. Основы интегрального исчисления и его приложения Типовые примеры зачетных (экзаменационных) и контрольных заданий VI. Распределение дисциплины по темам учебных занятий Название темы

Подобный материал:

• Автор программы и лектор : Караваева Ирина Владимировна, e-mail: ikaravaeva30@yandex, 232.54kb.
• Курс: 1 Статус дисципліни: обов’язкова Стаціонарне навчання Години на тиждень Триместр, 432.82kb.
• Анализ Авторы программы: академик Ильин В. А., доцент Леонтьева Т. А. Лектор 2010/11, 60.87kb.
• Вопросы теории, практики и методики изучения, 1714.38kb.
• Учебное пособие Под редакцией Л. М. Шипицыной Москва Санкт-Петербург 2007 Авторы: Шипицына, 2318.2kb.
• Программа дисциплины «Бизнес и власть: конституционно-правовые основы лоббизма и взаимодействия», 308.22kb.
• Программа дисциплины «конституционно-правовые проблемы судебного нормоконтроля в российской, 307.09kb.
• Учебного курса численные методы для студентов факультета Прикладной математики и информатики, 34.19kb.
• Оао «Слуцкая мебельная фабрика», 277.7kb.
• Календарный план учебных занятий по обязательной дисциплине «Алгебра и геометрия»,, 105.72kb.

М а т е м а т и к а

(100 аудиторных часов, в том числе 50 часов - лекции, 50 часов – семинары (практические занятия); 116 – самостоятельная работа)

Автор программы и лектор : к.т.н , доцент Рейнов Ю.И, препод. Слуцкая Ю.Л..

Статус курса: курс является обязательным, читается на 1 курсе в 1 и 2 (3, 4 модули) семестре.

Организация курса: курс читается в течение 1 и 2 семестра, контроль знаний организован в форме контрольной работы (четыре), домашнего задания, дифференцированного зачета и экзамена. Зачет проводится по окончании 1-го семестра, а экзамен – по окончании 4 модуля 2-го семестра.


I. Целевая установка


Курс «Математика» является одной из базовых дисциплин, обеспечивающих математическую подготовку студентов по направлению «Социология».

В курсе сделан акцент на изложение базовых понятий дисциплины, что даст возможность студентам в дальнейшем самостоятельно изучать приложения курса к задачам статистики и социологии.

Сведения, содержащиеся в данном курсе, необходимы для изучения следующих дисциплин

• Теория вероятностей и мат. статистика
  
• Общая статистика и социология
  
• Основы экономики
  

Курс может быть использован для разработки и применения численных методов решения задач из многих областей знаний, для построения и исследования математических моделей таких задач.

Все разделы программы излагаются так, чтобы привить студентам навыки математического мышления. Программа предусматривает чтение лекций и проведение практических (семинарских) занятий. От студентов требуется систематическое посещение лекций и семинаров.

Курс в 1-м семестре завершается зачетом, во 2-м – экзаменом.


II. Организационно-методические указания.


Организационная структура курса – лекционные занятия сопровождаются практическими занятиями. Задачей практических занятий является развитие у студентов практического преломления теоретических знаний, полученных на лекционных занятиях, что достигается только с помощью решения прикладных задач.

Промежуточная оценка знаний осуществляется по результатам контрольных работ (по 2 в каждом семестре) и проверочных работ (т.н. «летучек») (в количестве не менее 5 в каждом семестре). Также производится дифференцированный контроль выполнения домашних заданий (не менее 2 за семестр). Домашние задания даются студентам после каждого практического и (или) лекционного занятия и выполняются ими в часы, отведенные для самостоятельной работы.

Зачет и экзамен представляют собой письменный открытый тест, содержащий 2 теоретических и 4-6 практических вопросов. Продолжительность зачета и экзамена -2ч.

Итоговая семестровая оценка является результатом накопленных за семестр баллов по контрольным работам, проверочным работам, домашним заданиям и итогового экзаменационного (зачетного) тестирования. Вычисляется итоговая оценка по следующей формуле: О_итог= к/\р №1 * 0,2 + к/р №2 * 0,2+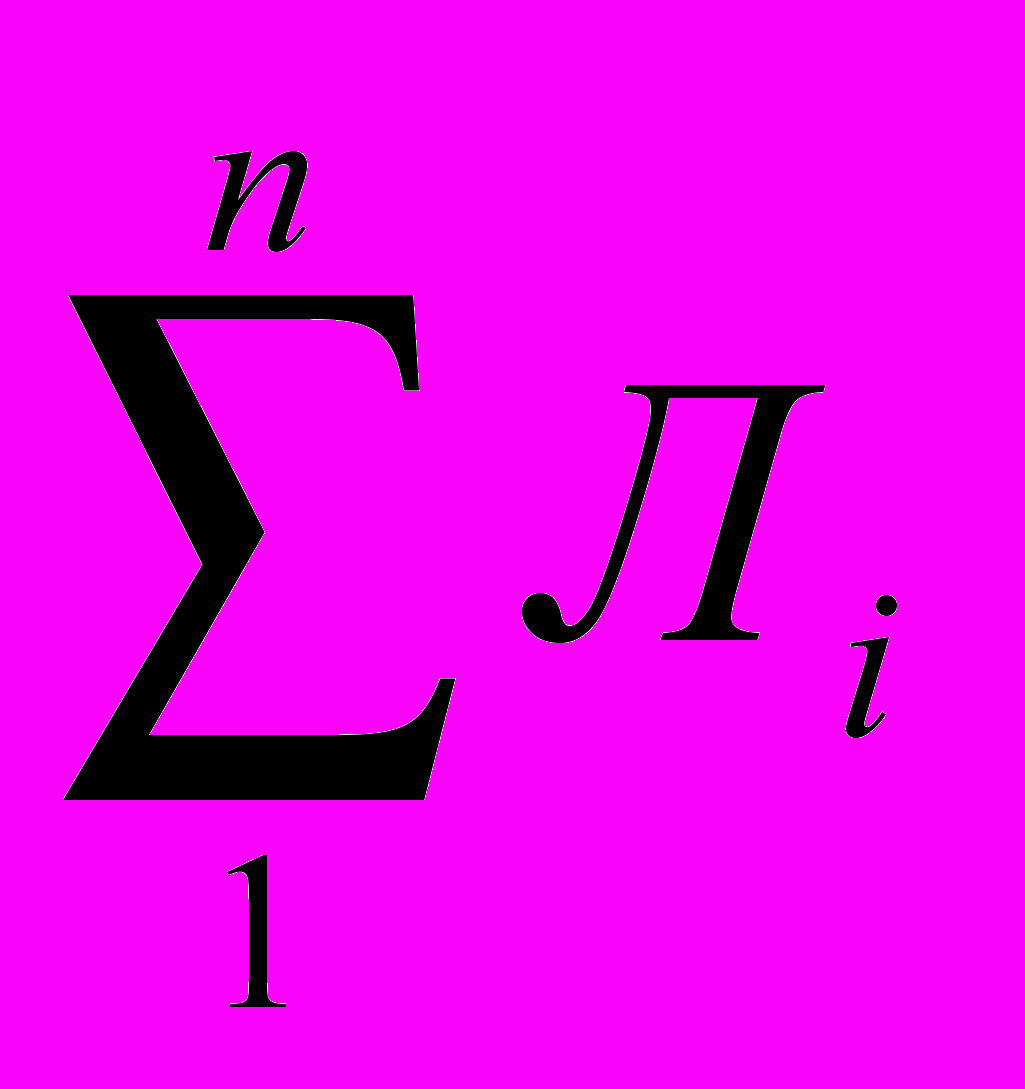:n * 0,1+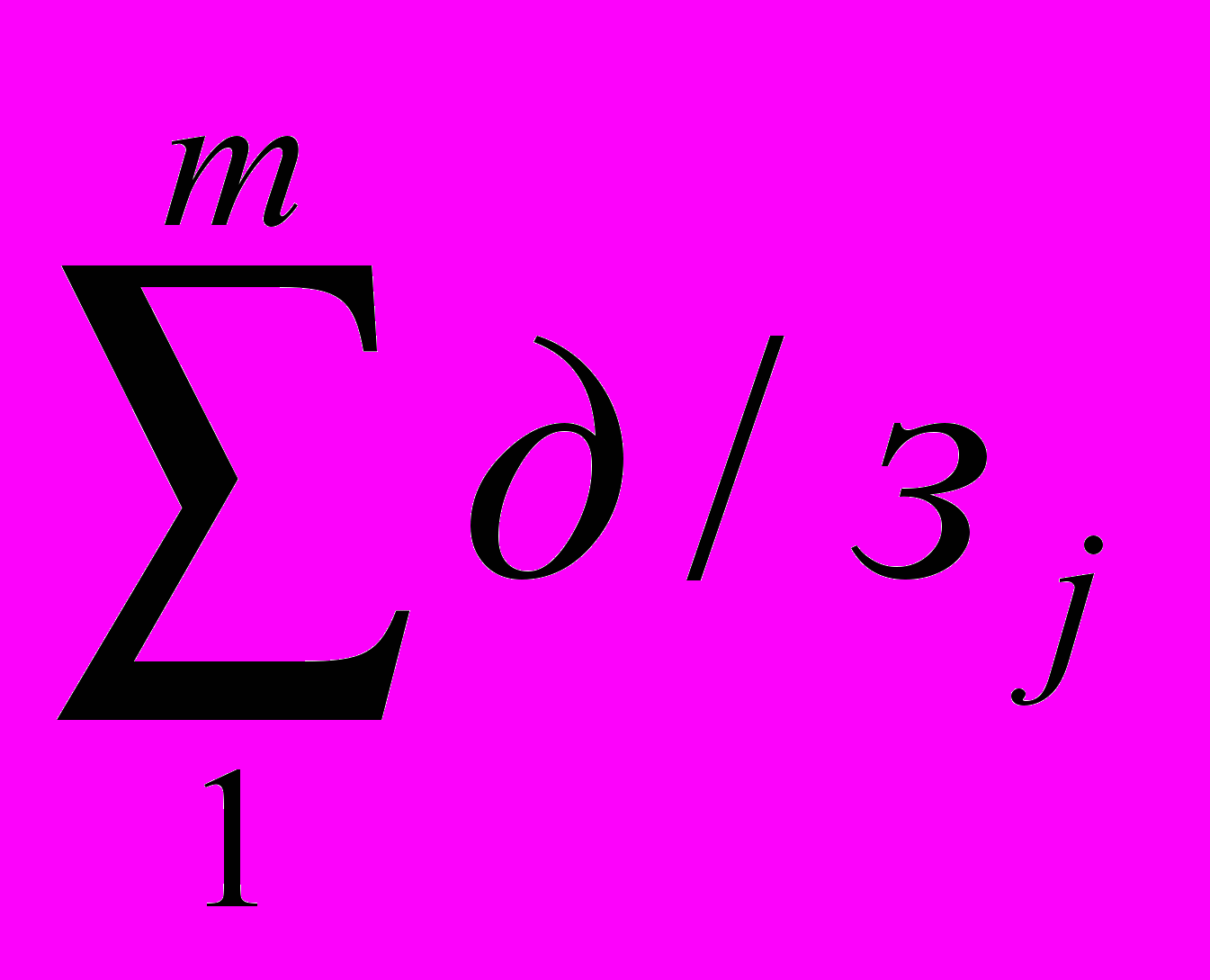:n*0,1+ Э*0,4, где к/\р №1(№2)- оценка в 10-балльной шкале за контрольную работу №1(№2), Л_i (i=)- оценка в 10-балльной шкале за каждую проверочную работу, д/з_j (j=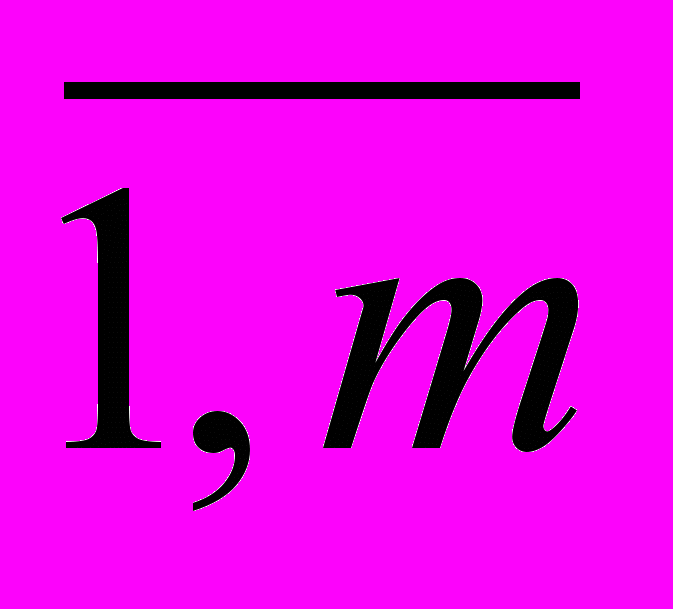)- оценка в 10-балльной шкале за каждую домашнюю работу, Э – оценка в 10-балльной шкале за экзамен (зачет).

Итоговая оценка за семестр вычисляется в соответствии с правилами округления с учетом активности работы студентов на практических занятиях (дополнительно 0,1-0,4 балла).

Во втором семестре студенты, набравшие по накопительной системе в течение семестра максимально возможный балл (5,5 – 6 баллов) получают, по желанию, итоговую оценку 9 баллов, не сдавая экзамен.


III. Содержание дисциплины.


Лекционные занятия 1 семестр

Тема 1 Элементы теории множеств и математической логики.

Лекция 1. Множества и подмножества, способы задания множеств. Операции над множествами и их свойства. Прямое произведение множеств. Взаимно однозначное соответствие и мощность множеств.

Лекция 2. Отображения на множествах и виды отображений (сюръективное, инъективное и биективное). Композиция и суперпозиция отображений. Обратное отображение. Отношения, виды отношений. Свойства отношений (рефлексивность, симметричность, транзитивность). Отношения эквивалентности, отношения строгого и нестрогого порядка.

Лекция 3. Простые высказывания и умозаключения. Логические операции над высказываниями. Формулы исчисления и тавтологии. Правила вычисления логических формул. Основные тавтологии и равносильные формулы.

Лекция 4. Логика предикатов. Операции над предикатами. Кванторы, операции с кванторами. Связь между логическими и теорико - множественными операциями.

Тема 2. Матрицы и определители.

Лекция 5. Понятие матрицы. Виды матриц. Линейные операции над матрицами. Свойства линейных операций. Умножение матриц. Перестановочные и симметричные матрицы. Свойства умножения матриц. Транспонирование матриц. Свойства транспонированной матрицы.

Лекция 6. Определители 1, 2, 3 порядка. Перестановка, инверсия. Определитель n-го порядка. Свойства определителя.

Лекция 7. Минор элемента, алгебраическое дополнение элемента матрицы. Разложение определителя по строке (столбцу). Минор матрицы. Ранг матрицы. Элементарные преобразования матрицы. Свойства элементарных преобразований матрицы:

Лекция 8. Обратная матрица, особенная и неособенная матрица. Взаимная матрица. Теорема о взаимной матрице. Теорема об обратной матрице. Свойства обратной матрицы. Алгоритм нахождения обратной матрицы. Матричные уравнения.


Тема 3. Системы линейных уравнений

Лекция 9. Системы линейных уравнений. Совместные и несовместные системы. Трапециевидная матрица. Теорема о преобразовании всякой матрицы в трапециевидную матрицу. Элементарные преобразования системы линейных уравнений. Равносильные системы. Теорема о переходе системы при элементарных преобразованиях в равносильную систему. Алгоритм метода Гаусса.

Лекция 10. Теорема Крамера (без доказательства). Метод решения системы уравнений с помощью обратной матрицы; его связь с формулами Крамера.

Лекция 11. Условие совместности системы линейных уравнений (теорема Кронекера-Капелли). Теорема о числе решений. Системы линейных однородных уравнений. Условие существования ненулевых решений однородной системы.

Тема 4. Числовые множества и числовые функции

Лекция 12. Натуральные, рациональные, вещественные и комплексные числа. Действия над комплексными числами, геометрический смысл комплексного числа, алгебраическая и тригонометрическая форма к.ч. Возведение в рациональную степень комплексного числа.

Лекция 13. Окрестность и  - окрестность. Граничные и внутренние точки. Ограниченные множества, точная верхняя и нижняя граница.

Вещественная функция, ее область определения и множество значений. Способы задания числовых функций. Обратные функции. Композиция функций. Основные свойства функций.

Лекция 14. Основные элементарные числовые функции. Элементарные числовые функции (рациональные, дробно-рациональные, показательные, логарифмические, тригонометрические и обратно тригонометрические). Свойства элементарных функций и правила построения их графиков.


Тема 5. Предел числовой последовательности и предел функции.

Лекция 15. Числовые последовательности. Операции над последовательностями. Ограниченные и неограниченные последовательности. Бесконечно малые и бесконечно большие последовательности. Их свойства. Сходимость последовательностей и свойства сходящихся последовательностей. Предельный переход в неравенствах. Монотонные последовательности. Второй замечательный предел последовательности. 1-ая и 2-ая теорема Вейерштрасса (ограниченность и достижение точных верхних и нижних граней) – без доказательств.


Программа практических занятий 1-го семестра

Тема 1 Элементы мат. логики, теории множеств.

Практика 1. Основные операции над множествами.

Практика 2. Отображения на множествах .

Практика 3. Логические операции над высказываниями. Формулы исчисления и тавтологии. Основные тавтологии и равносильные формулы

Практика 4. Операции над предикатами. Операции с кванторами.


Тема 2. Теория определителей и матриц.

Практика 5. Линейные операции над матрицами. Умножение матриц и нахождение перестановочной матрицы для заданной. Примеры на матричные уравнения с использованием операций транспонирования, умножения и сложения матриц.

Практика 6. Примеры на вычисление определителей 2 и 3 - го порядка.

Практика 7. Примеры вычисления определителя 3 - 4 порядка с помощью алгебраического дополнения. Вычисления определителей с применением основных свойств определителя.

Контрольная работа №1 (Элементы мат. логики, свойства элементарных функций, вычисление определителей).

Практика 8. Построение взаимной матрицы. Нахождение обратной матрицы. Решение матричных уравнений с использованием обратных матриц.


Тема 3. Системы линейных уравнений.

Практика 9 Вычисление ранга матрицы с помощью ее приведение к трапециевидной форме. Решение систем линейных уравнений методом Гаусса

Практика 10. Примеры на решение уравнений 4-5 порядка по формулам Крамера и методом обратной матрицы.

Практика 11. Исследование систем уравнений на совместность и количество решений. Решение однородных систем.

Контрольная работа № 2 (нахождение обратной матрицы, матричные уравнения, системы линейных уравнений)

Тема 4. Числовые множества и числовые функции

Практика 12. Комплексные числа. Действия с комплексными числами. Геометрический смысл корня из комплексного числа.

Практика 13. Свойства числовых функций (четность, периодичность, монотонность)

Практика 14. Правила построения эскизов графиков элементарных функций.

Практика 15. Нахождение точной верхней и нижней грани. Пределы числовых последовательностей. Вычисление пределов последовательности с помощью определения .


Зачет по материалам 1 – 15 лекции


Лекционные занятия 2 - ой семестр


Тема 5. Предел функции.

Лекция 16. Основные определения и свойства пределов функции. Первый замечательный предел (с доказательством). Второй замечательный предел. Пределы сложных функций. Бесконечно большие и бесконечно малые функции. Сравнение бесконечно больших и бесконечно малых функций. Важнейшие эквивалентности.

Лекция 17. Непрерывность в точке. Основные определения и свойства непрерывных функций. Неопределенности. Разрывы функций и их классификация.

Тема 6. Основы дифференциального исчисления и его приложения

Лекция 18. Понятие производной. Геометрический смысл производной. Примеры вычисления производных. Таблица производных элементарных функций. Производная обратной и сложной функции. Производная суммы, произведения и частного.

Лекция 19. Основные теоремы о дифференцируемых функциях: Ролля, Лагранжа, Коши. Правило Лопиталя для раскрытия неопределенностей. Понятие дифференциала. Геометрический смысл дифференциала . Приближенные вычисления с помощью производной.

Лекция 20. Асимптоты функции и способы из нахождения. Теорема о существовании наклонной асимптоты. Нахождение областей возрастания и убывания функции. Теорема Ферма. Экстремумы функции. Необходимое и достаточное условие экстремума.

Лекция 21. Нахождение областей выпуклости и вогнутости функции. Точки перегиба. Необходимое условие перегиба функции. 1-ое и 2-ое достаточное условие перегиба функции. Принципы исследования и построения графиков функции с помощью производных. Наибольшее и наименьшее значение функции на промежутке

Тема 7. Основы интегрального исчисления и его приложения

Лекция 22. Первообразная и ее свойства. Неопределенный интеграл и его свойства. Таблица основных неопределенных интегралов. Прямое интегрирование.

Лекция 23. Интегрирование с помощью замены переменных.

Интегрирование по частям. Интегрирование простейших дробей. Основные преобразования многочленов и рациональных функций. Интегрирование многочленов и рациональных функций.

Лекция 24. Криволинейная трапеция. Определенный интеграл и его свойства. Необходимое и достаточное условие интегрируемости. Теорема о среднем значении. Формула Ньютона–Лейбница. Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла.

Лекция 25. Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур и объемов тел вращения. Несобственные интегралы первого рода. Достаточные признаки сходимости. Абсолютная и условная сходимость. Несобственные интегралы второго рода. Связь между несобственными интегралами первого и второго рода. Примеры.

Практические занятия 2-го семестра

Тема 5. Предел функции.

Практика 16 Примеры на определение и свойства пределов. Пределы сложных функций.

Практика 17. Вычисление пределов. Раскрытие неопределенностей. Сравнение бесконечно больших и бесконечно малых функций. Разрывы функций и их классификация

Тема 6. Основы дифференциального исчисления и его приложения

Практика 18. Примеры на вычисление производных простых функций и сложных функций.

Практика 19. Вычисление пределов с помощью правила Лопиталя. Дифференциал. Приближенные вычисления.

Практика 20. Нахождение асимптот графиков функций. Нахождение экстремумов. Исследование графика функций с помощью производных.

Практика 21. Исследование графика функций с помощью производных. Нахождение наибольшего и наименьшего значения функции на отрезке.

Контрольная работа № 3(вычисление предела функции, исследование и построение графика функции)

Тема 7. Основы интегрального исчисления и его приложения

Практика 22. Вычисление неопределенного интеграла с помощью замены переменной. Интегрирование рациональных дробей.

Практика 23. Интегрирование по частям.

Практика 24. Вычисление определенных интегралов с помощью определения и теоремы Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле.

Практика 25. Вычисление площадей плоских фигур и объемов тел вращения.

Контрольная работа № 4 ( первообразная и определенный интеграл).

4. Типовые примеры зачетных (экзаменационных) и контрольных заданий
   

Cеместр 1


Логические высказывания. Логические операции над высказываниями. Свойства логических операций (2б.)

Числовые множества. Комплексные числа. Алгебраический и тригонометрический вид комплексного числа. Действия над комплексными числами. (2б.)

Для матрицы А= 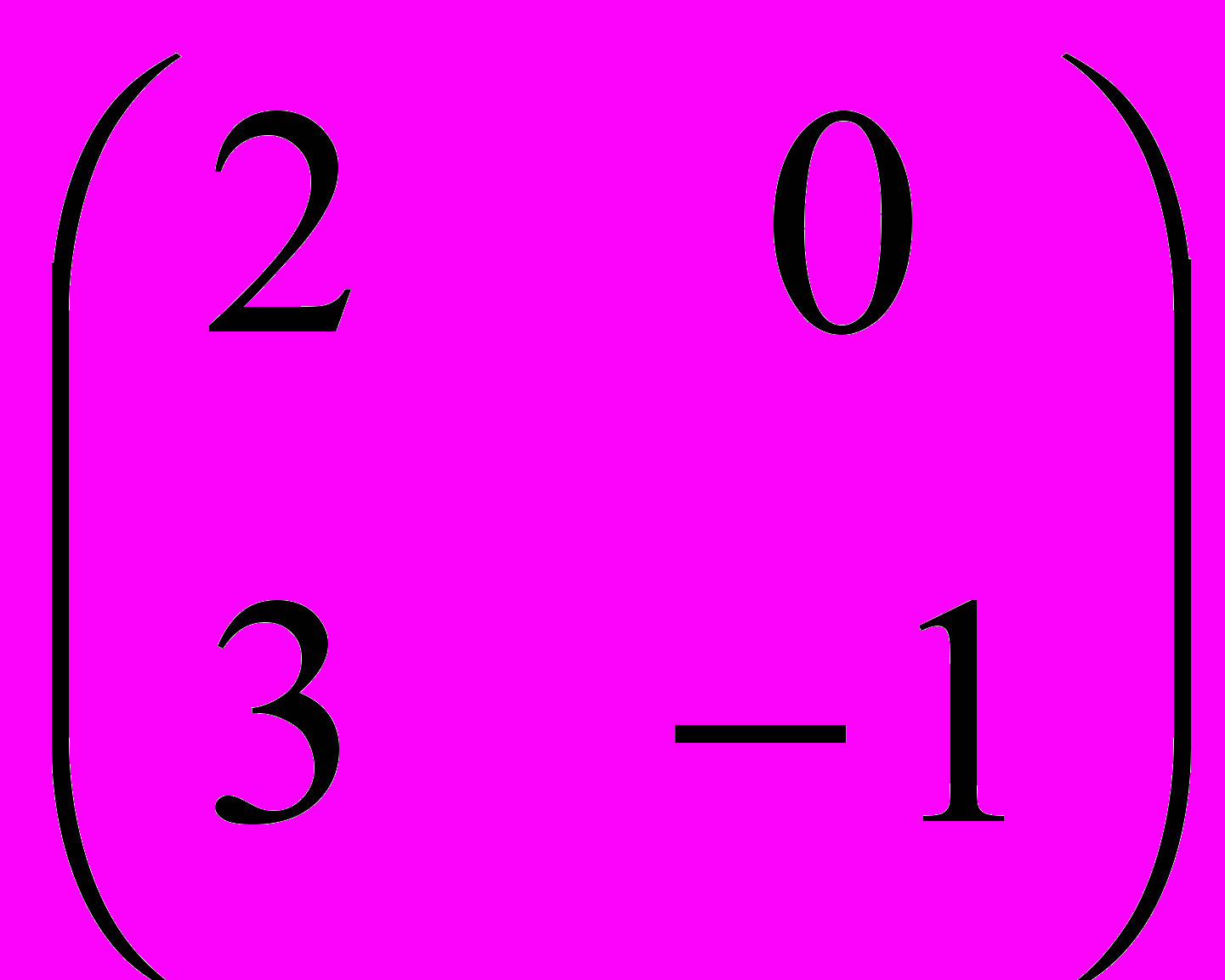найдите все перестановочные матрицы размера 2х2. (1б.)

Определите, является ли формула тавтологией: . (1б.)

Исследуйте систему на количество решений и найдите их. 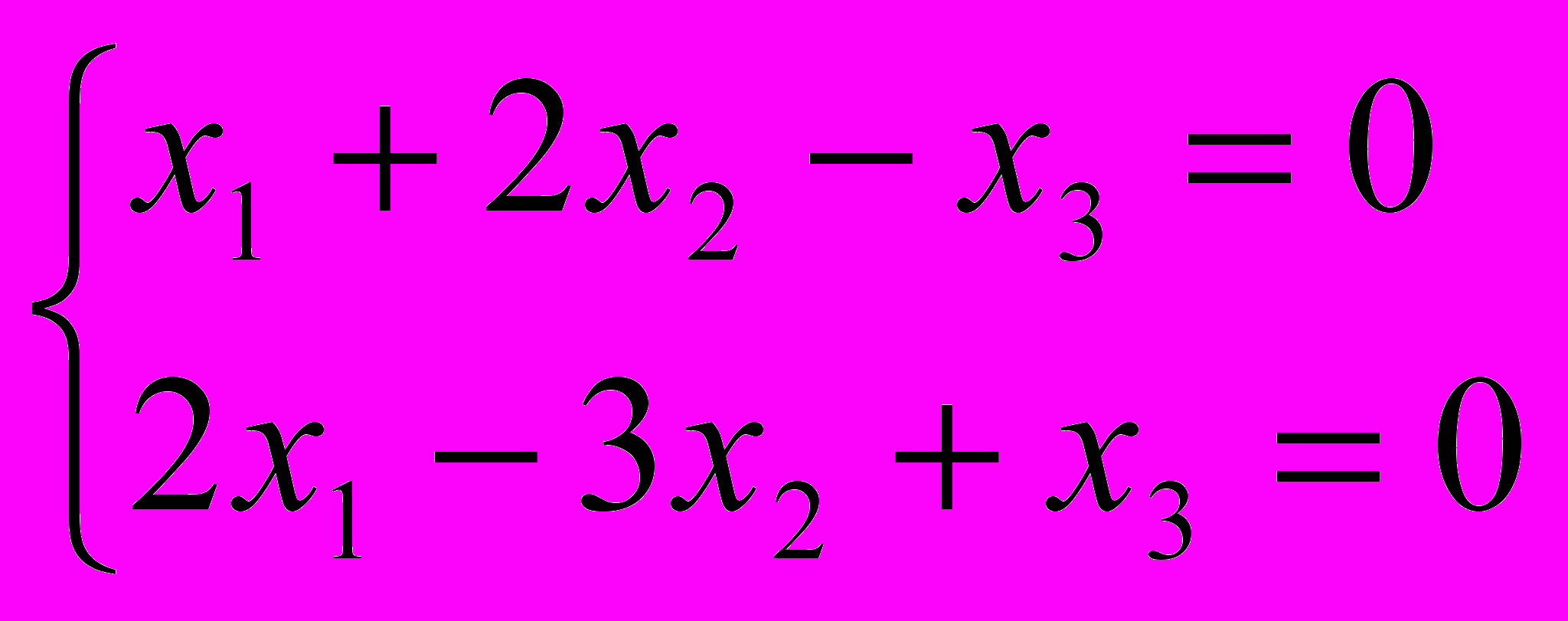(2б.)

Выполните возведение в степень: (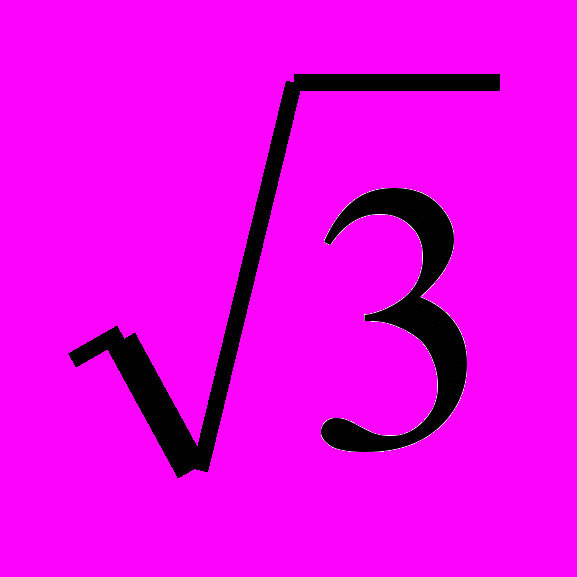-i)¹⁰⁰ (2б.)


Семестр 2

1. Первообразная и ее свойства. Неопределенный интеграл и его свойства. Таблица основных неопределенных интегралов. (2б.)
   

2. Экстремумы функции. Необходимое и достаточное условие экстремума. (2б.)

3. Вычислите предел: (1б.)

4.Найдите площадь фигуры, ограниченной функциями f(x) = x² – 4 и g (x) = x + 2 и осью Ох при х  0. (2б.)


5.Найдите 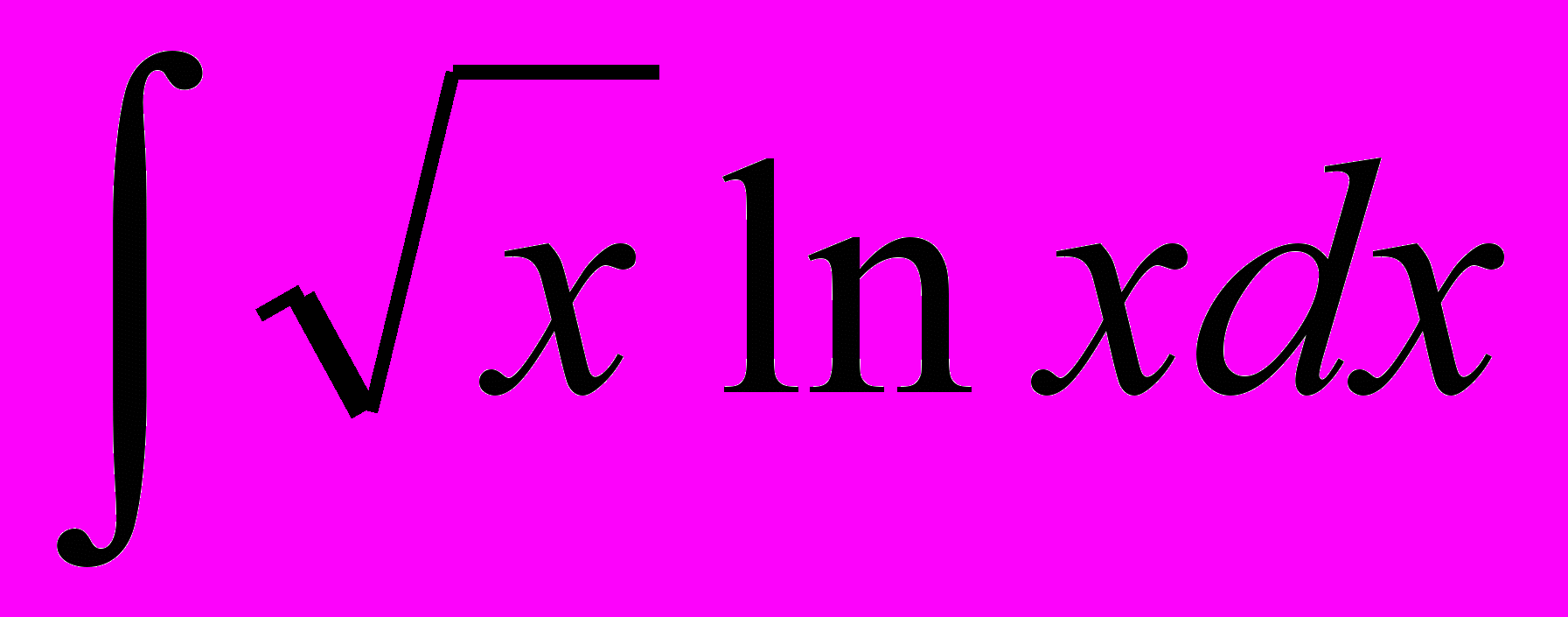(2б.)

6. Периметр прямоугольника равен 16. Какую наибольшую площадь может иметь такой прямоугольник? (1б.)


Контрольные работы :


Семестр 1

1 контрольная

2 контрольная


Семестр 2


1 контрольная

2 контрольная


Примерный вариант контрольной работы № 2. Работа рассчитана на 2ч.


1.Для матрицы А= 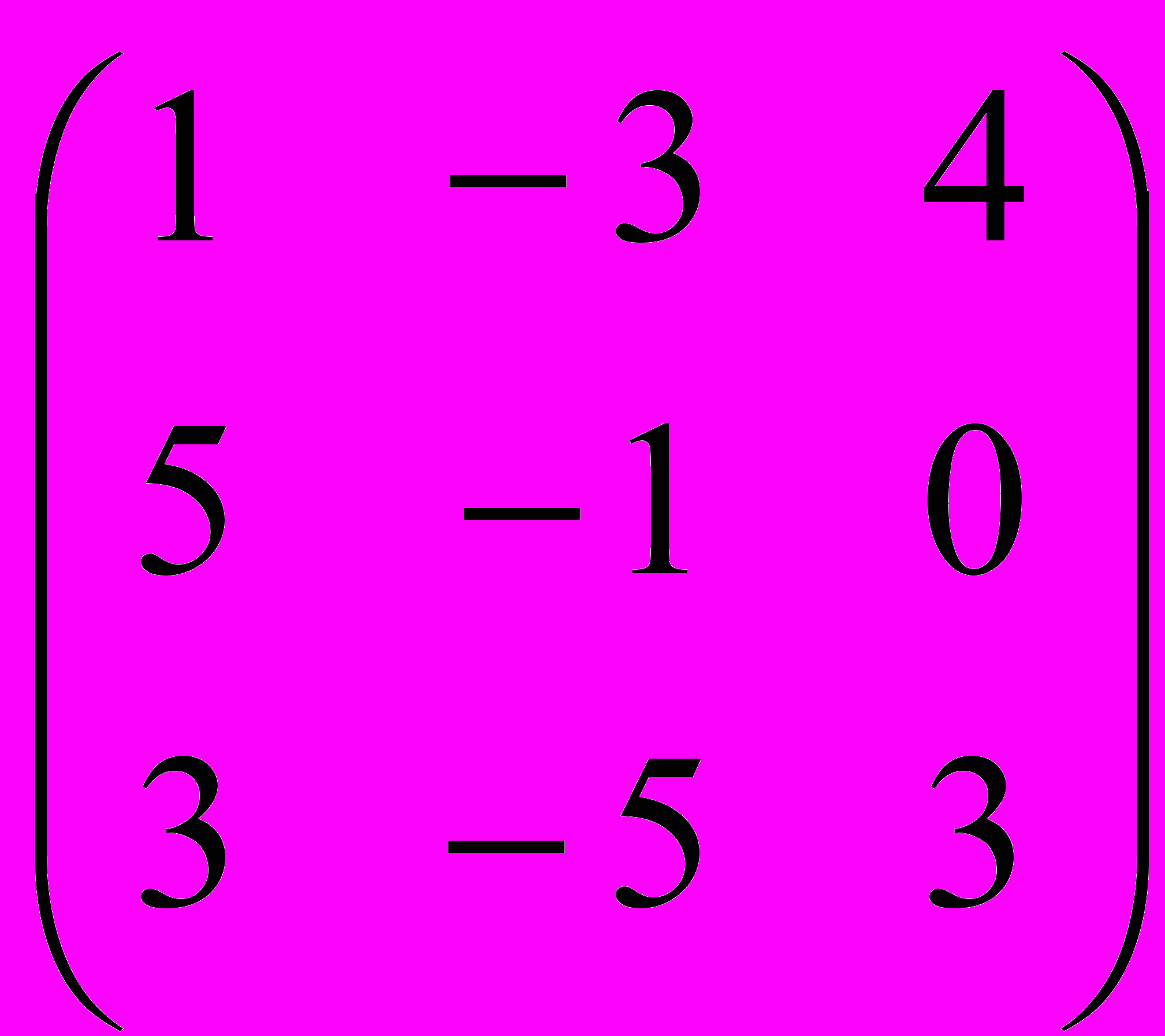найдите обратную. (2 балл)

2. Вычислите ранг матрицы А=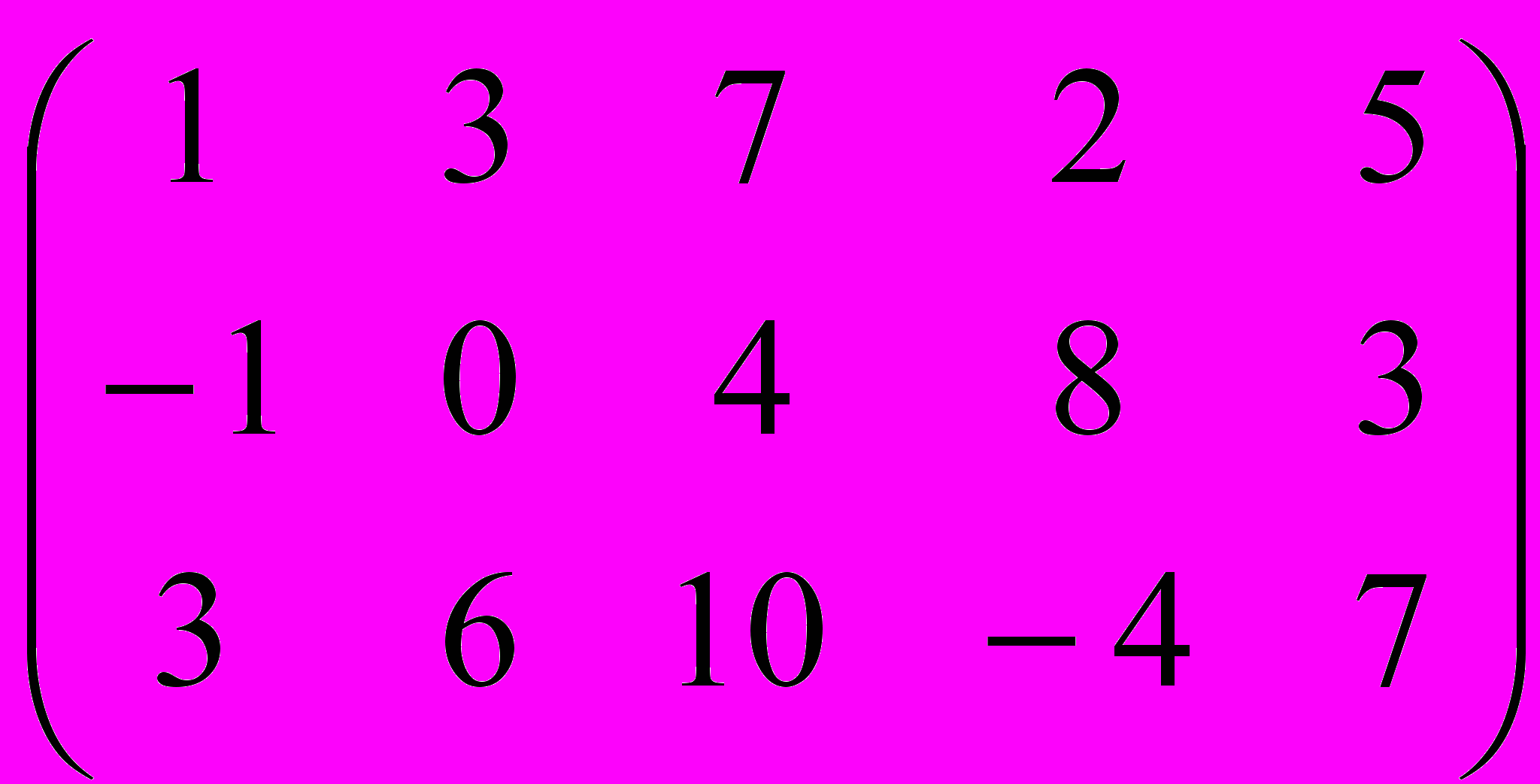. (2 балл)


3.. Исследуйте систему на совместность и количество решений и найдите их, если она совместна.

x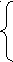₁ + x₂ - 2x₃ - x₄ + x₅ =1,

3x₁ - x₂ + x₃ + 4x₄ + 3x₅ =4,

x₁ + 5x₂ - 9x₃ - 8x₄ + x₅ =0.

(3 балла)


4.. Решите матричное уравнение АХ=В, где А=, В=. (2 балл)


5. Сколько решений имеет система уравнений 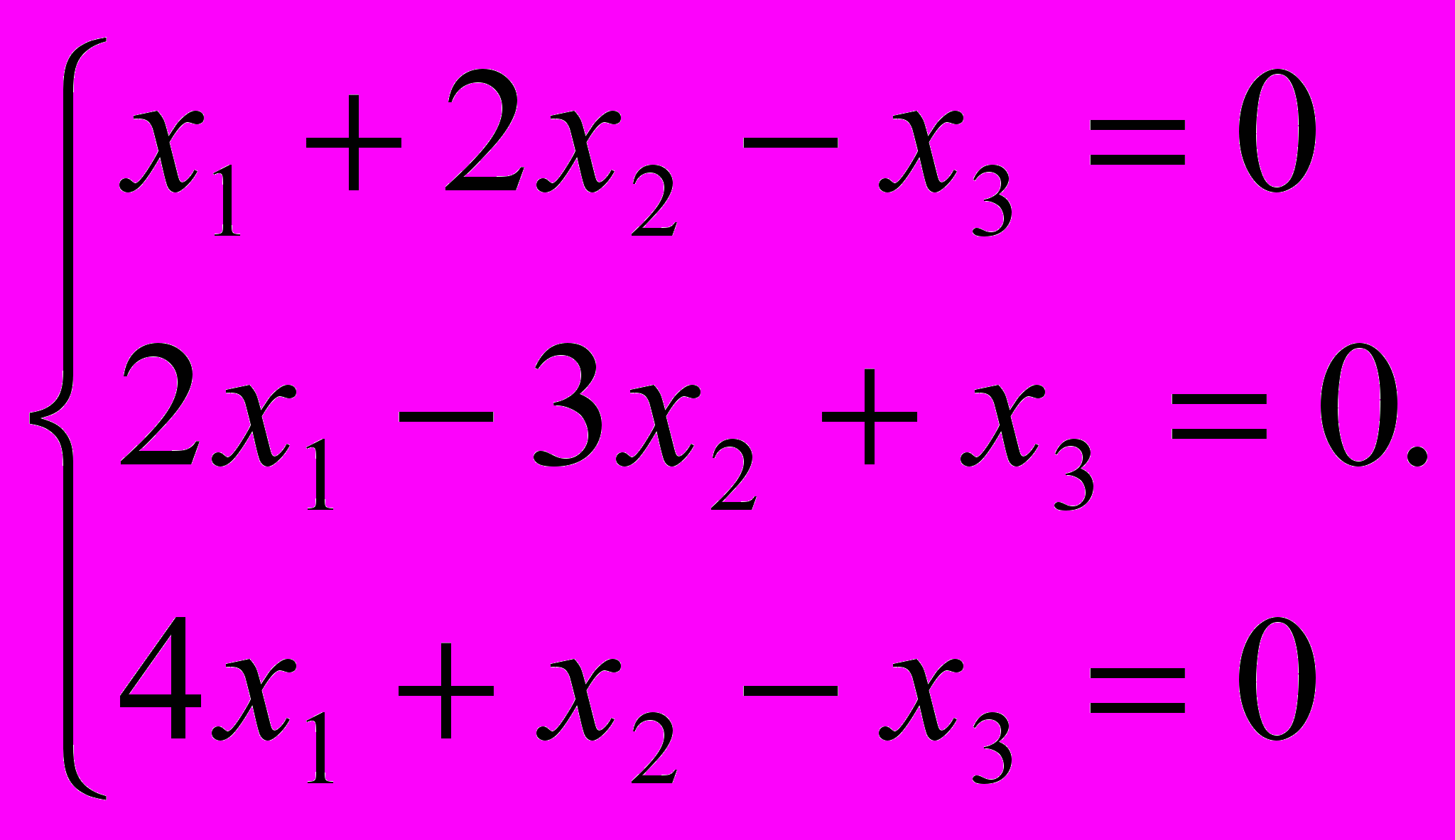? (1 балл)

4. Учебно – методическое обеспечение программы
   

Базовая литература:

1. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Изд.
   
2. Физматлит, 2006г.
   
3. Л.С. Понтрягин. Математический анализ. М.,Наука,1988
   
4. В.А. Ильин, Г.П. Поздняк. Основы математического анализа. М., Наука, 1991
   
5. Г.Н.Берман. Сборник задач по курсу математического анализа. Изд. Лань, 2007г.
   
6. Боревич З.И. Определители и матрицы М. Наука 1988
   
7. Ильин В.А., Поздняк Э.Г. Линейная алгебра М.,Наука, 1974
   
8. П.С. Новиков. Элементы математической логики. М., Наука, 1973
   
9. Ильин В.А., Поздняк Э.Г. Аналитическая геометрия М.,Наука, 1988
   

Основная литература:

1. Бурмистрова Е.Б., Лобанов С.Г. Линейная алгебра с элементами аналитической геометрии: Учебное пособие. – М.: Изд - во ГУ-ВШЭ, 1998.
   
2. Фаддеев Д.К., Сломинский И.С. Сборник задач по высшей алгебре. М. Наука, 1988
   
3. Гусак А.А. Аналитическая геометрия и линейная алгебра. Минск, Тетра Систем, 1998
   
4. Л.С. Понтрягин. Анализ бесконечно малых. М.,Наука,1980
   
5. Бугров С.Я., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М. Наука. 1984
   
6. Бугров С.Я., Никольский С.М. Задачник по линейной алгебре и аналитической геометрии. М. Наука. 1984
   
7. Высшая математика для экономистов под ред.Н.Ш. Кремера. М. Юнити, 1998г.
   

Дополнительная литература:

1. Д.Гильберт, В. Аскерман. Введение в теоретическую логику. М., Мир,1965
   
2. А.Тарский. Введение в логику. М., ИЛ, 1969
   
3. М.Е. Драбкина. Логические упражнения по элементарной логике. Минск, Высшая школа, 1978
   
4. П.С. Александров. Введение в теорию множеств и функций. М., Гостехиздат,1941
   
5. Н.Бурбаки. Теория множеств. М., Мир, 1969
   
6. Ф. Хаусдорф. Теория множеств. М., ИЛ, 1971
   
7. Н.Я. Виленкин. Рассказы о множествах. М., Наука, 1972
   
8. Н.Н. Лузин. Теория функции вещественного переменного. М., Наука,1968
   
9. И.Б. Абельсон. Максимум и минимум. М.,Наука, 1967
   
10. А.Л. Брудно. Введение в теорию функций. М.,Физмат,1972
    
11. Г.П. Толстов. Элементы математического анализа. М., Наука, 1971
    
12. В.Г. Болтянский. Что такое дифференцирование ? М., Физматгиз, 1960.
    
13. Р. Курант. Дифференциальное и интегральное исчисление. М.,Наука, 1970.
    
14. Г.Е. Шилов. Математический анализ М., Наука,1971
    
15. Г.Е. Шилов. Как строить графики ? М., Просвещение,1976
    
16. И.Х.Сивошанский. Элементарные функции и графики.М.,Просвещение,1967.
    
17. И.П. Гурский. Функции и построение графиков.М.,Наука,1968
    
18. 27. М.А. Смолянский. Таблицы неопределенных интегралов. М.,Наука,1979
    
19. Ефимов Н.В. Краткий курс аналитической геометрии. М, Наука, 1975
    
20. Идельсон А.В., Блюмкина И.А. Аналитическая геометрия и линейная алгебра. М. Инфра-М, 2000
    
21. Кострикин А.И. Введение в алгебру. Основы алгебры. М. Наука, 1994
    
22. Погорелов А.В. Аналитическая геометрия. М., Наука, 1978
    
23. Проскуряков И.В. Сборник задач по линейной алгебре. М. Наука 1977
    
24. Тышкевич Р.И., Феденко А.С. Линейная алгебра и аналитическая геометрия. Минск, Высшая школа, 1976
    

VI. Распределение дисциплины по темам учебных занятий

Название темы	Всего аудиторных часов	Лекции	Семинары	Самостоятель- ные занятия
Тема 1 Элементы математической логики и теории множеств	16	8	8	16
Тема 2. Теория определителей и матриц.	18	10	8	20
Тема 3. Системы линейных уравнений	14	6	8	14
Тема 4. Числовые множества и числовые функции	14	6	6	14
Тема 5. Предел функции	8	4	4	12
Тема 6. Основы дифференциального исчисления	18	8	8	20
Тема 7. Основы интегрального исчисления.	18	8	8	20
Всего часов	100	50	50	116

Авторы программы Рейнов Ю.И.

Слуцкая Ю.Л.