27. ЗадаЧа двух тел

Вид материала

Задача

Содержание Приведенная масса Приведенная частица

Подобный материал:

• Урок 5/11     Тема: Определение расстояний до тел сс и размеров этих небесных тел, 73.09kb.
• П. П. Порешин московский инженерно-физический институт (государственный университет), 23.75kb.
• Задача геометрического моделирования сплошных тел является важной областью машинной, 96.16kb.
• Г. Москва, пер. Б. Черкасский, д. 4 стр. 6, офис 7 Тел. +7 (495) 504-9127, 504-9132, 83.04kb.
• Вопросы к экзамену по учебному курсу «Нейрокомпьютерные системы» (первый семестр), 24.51kb.
• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
• Задание по начертательной геометрии для студентов 1 курса   Задание №1 Задача №1 , 909.02kb.
• Е. С. врач-гастроэнтеролог мц «Семейная клиника династия» Екатеринбург Вработе гастроэнтеролога, 244.51kb.
• Туристический оператор "Имеджин Тревел" г. Киев, ул. Искровская 18 Тел.: (044) 248, 62.02kb.

27. ЗадаЧа двух тел.

Задача двух тел – отыскание закона движения системы двух тел 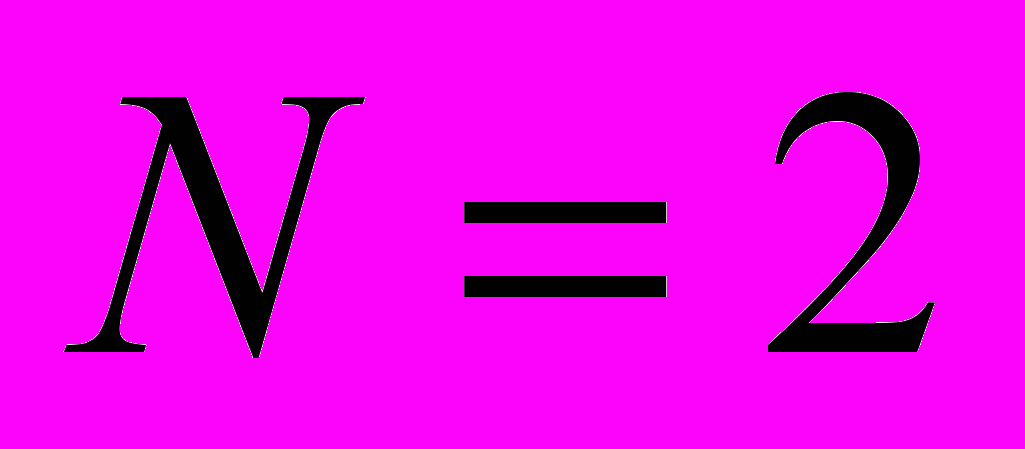материальных точек 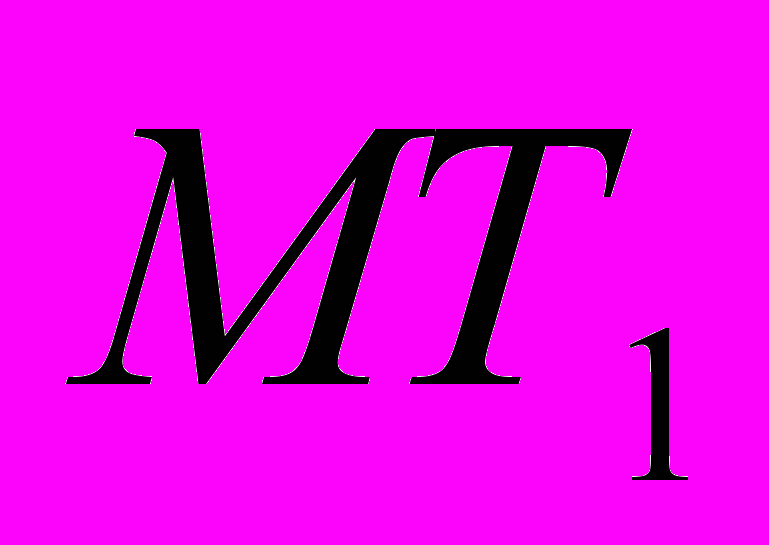с массой 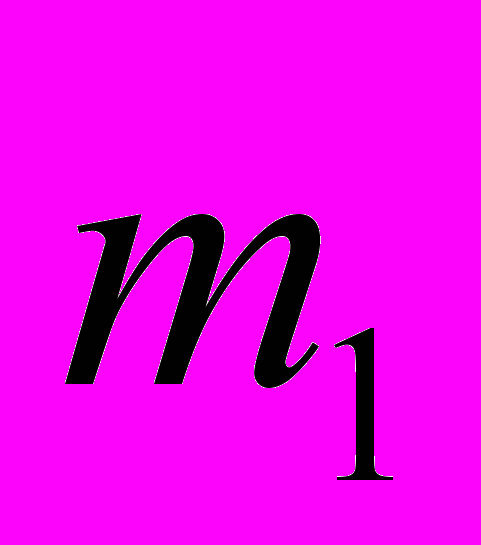и радиус-вектором 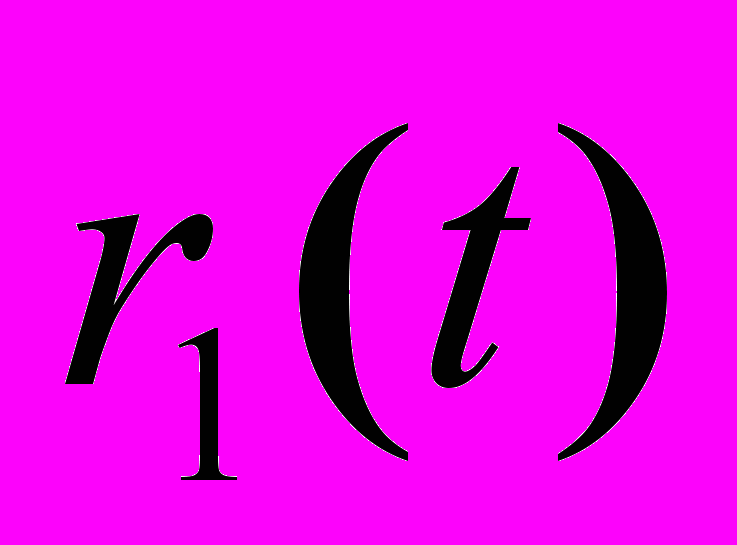и с массой 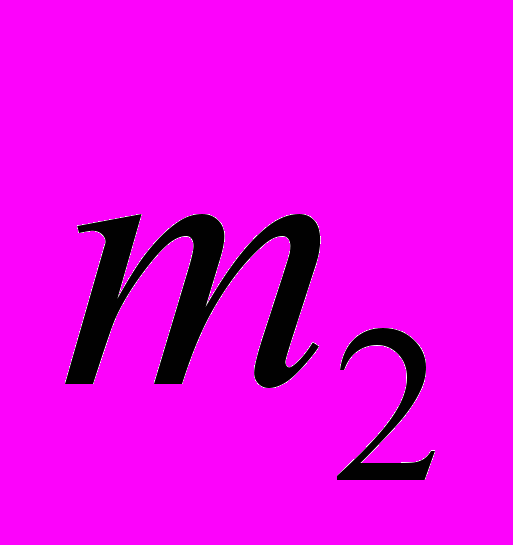и радиус-вектором 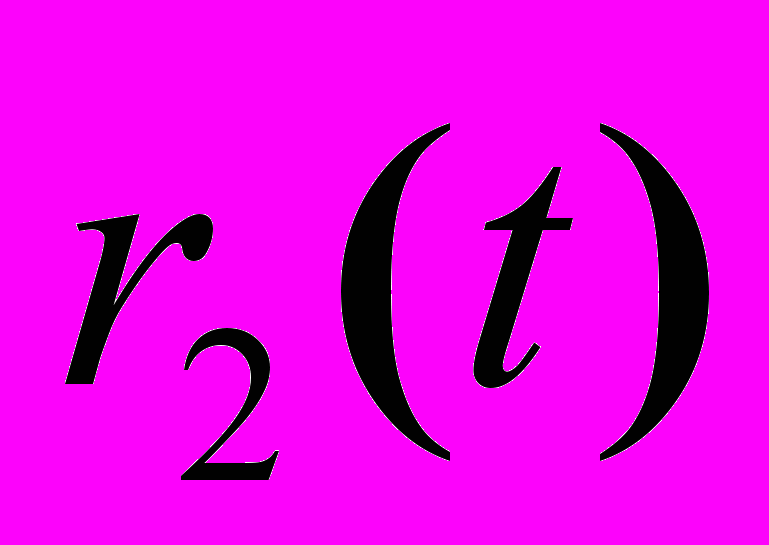, взаимодействующих через поле потенциальных сил с потенциальной энергией взаимодействия

,

выражающийся через радиус-вектор относительного движения 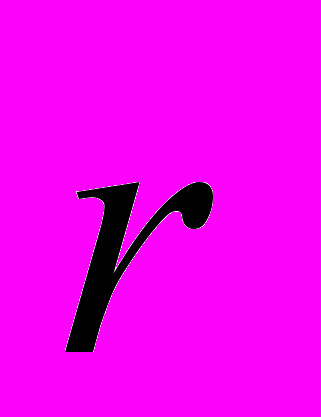. Она равнозначна отысканию всех интегралов движения системы, в частности – полного импульса центра масс с радиус-вектором

,

который в системе центра масс 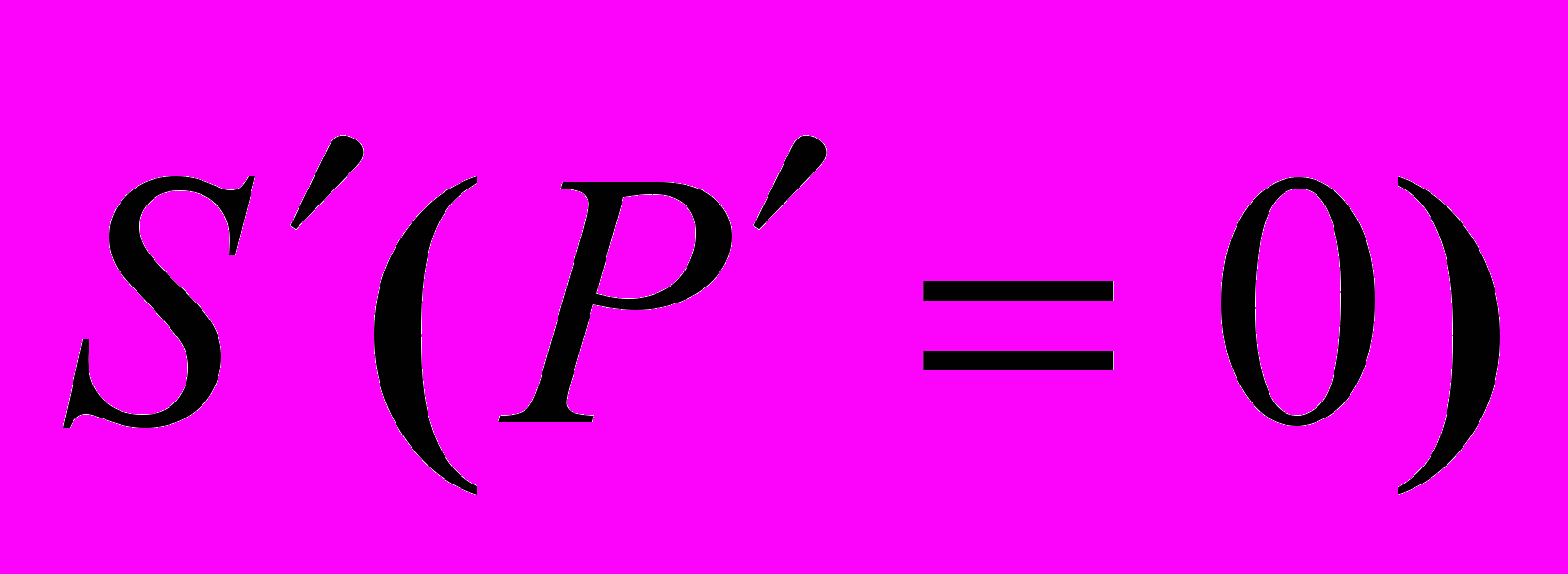равен нулю, так что

,

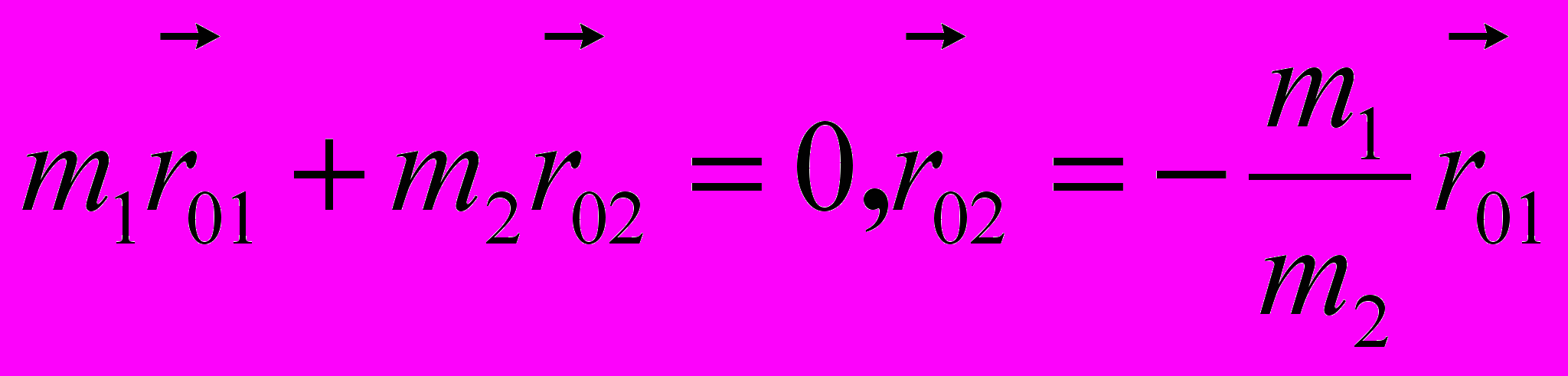а радиус-вектор относительного движения в СЦМ



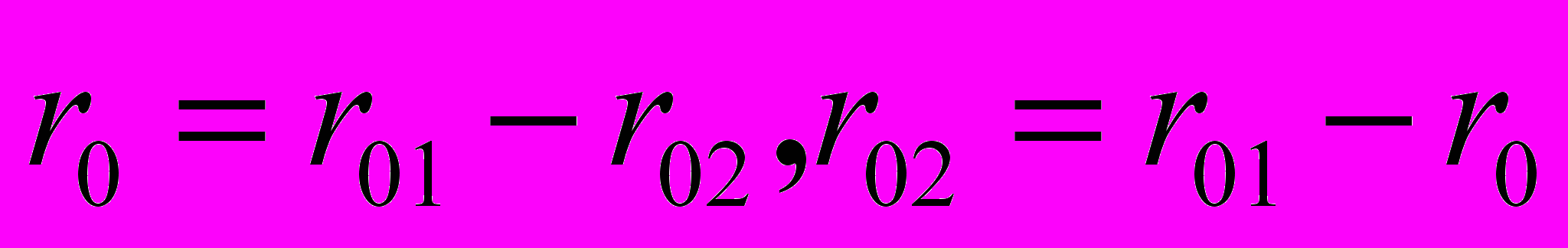
из



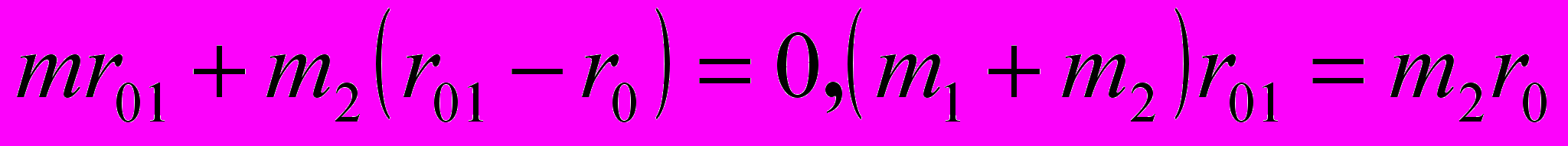
определяет

,

из

_, .

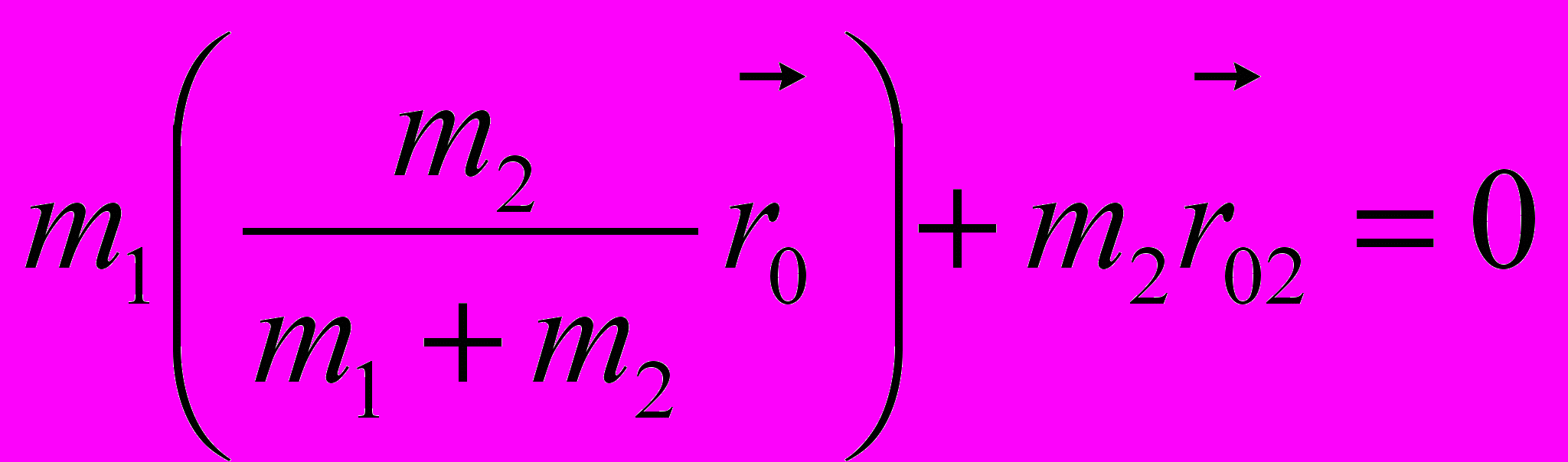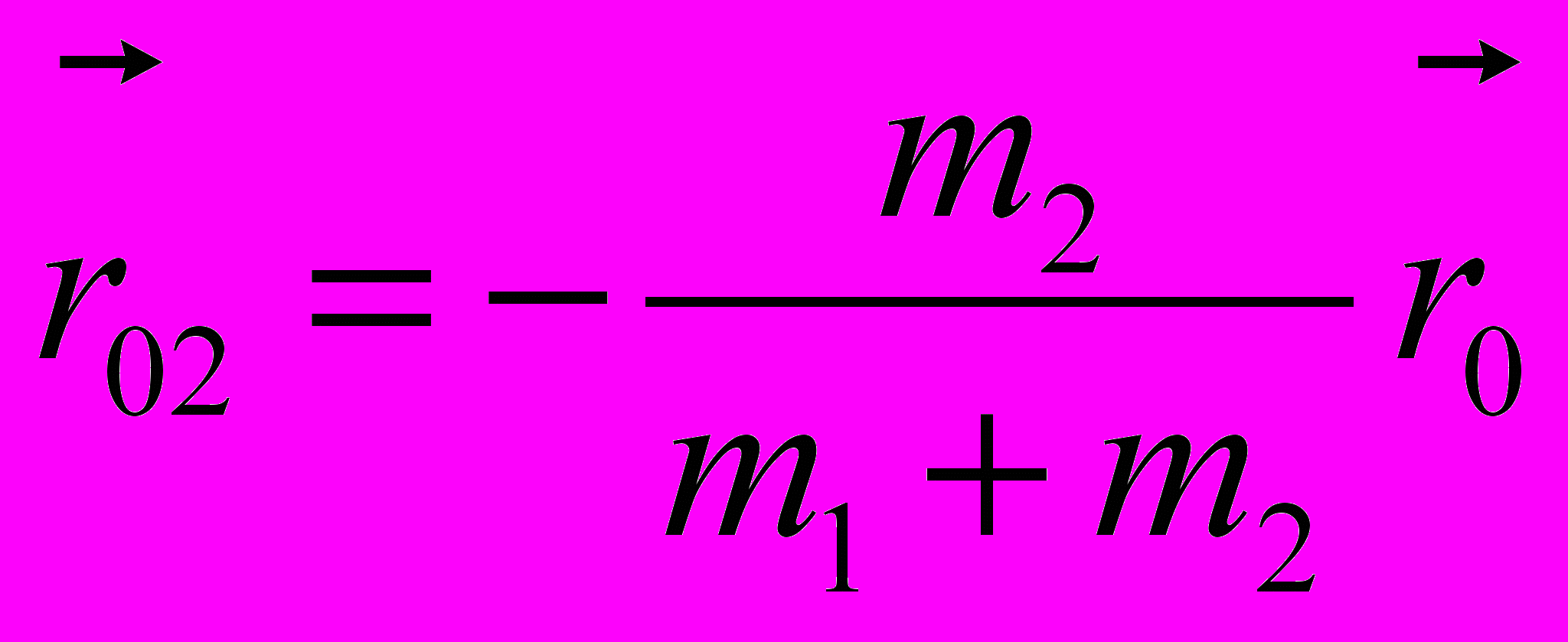Скорости материальных точек выражаются через относительную скорость дифференцированием

.

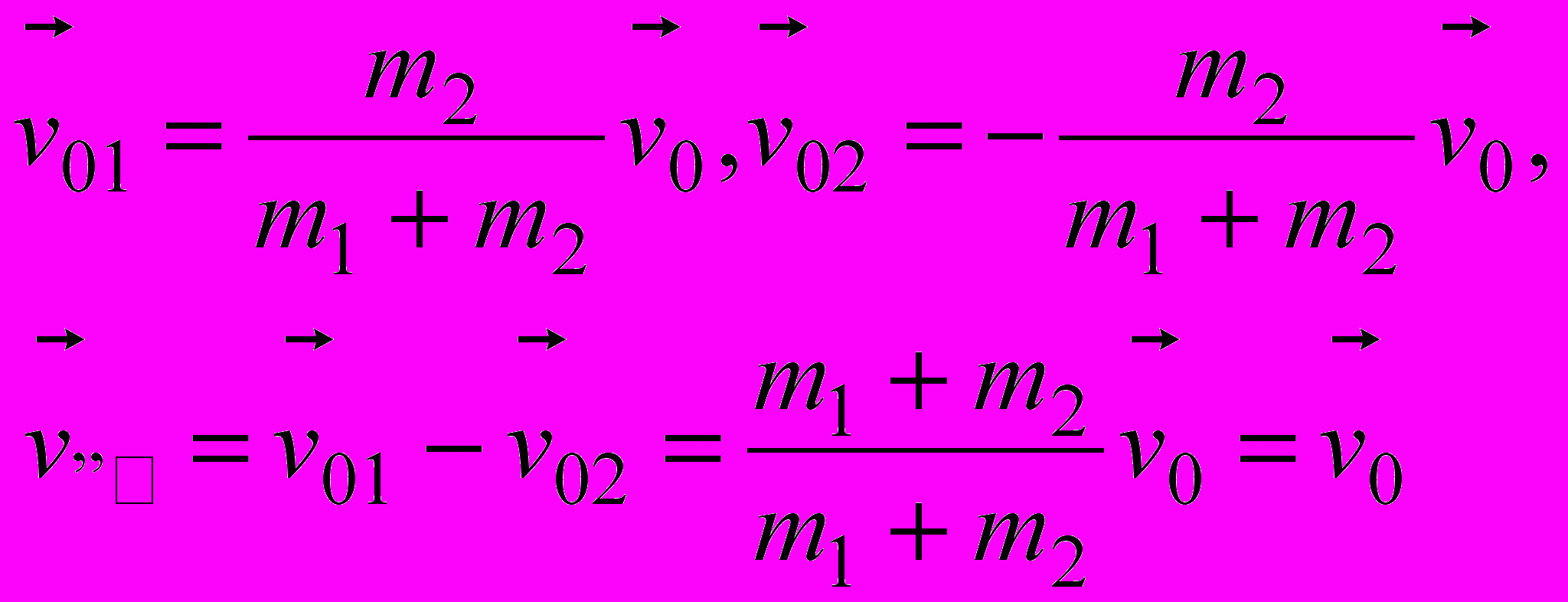Они противоположны и изменяются вместе с импульсами вследствие взаимодействия. На каждую со стороны другой действуют силы



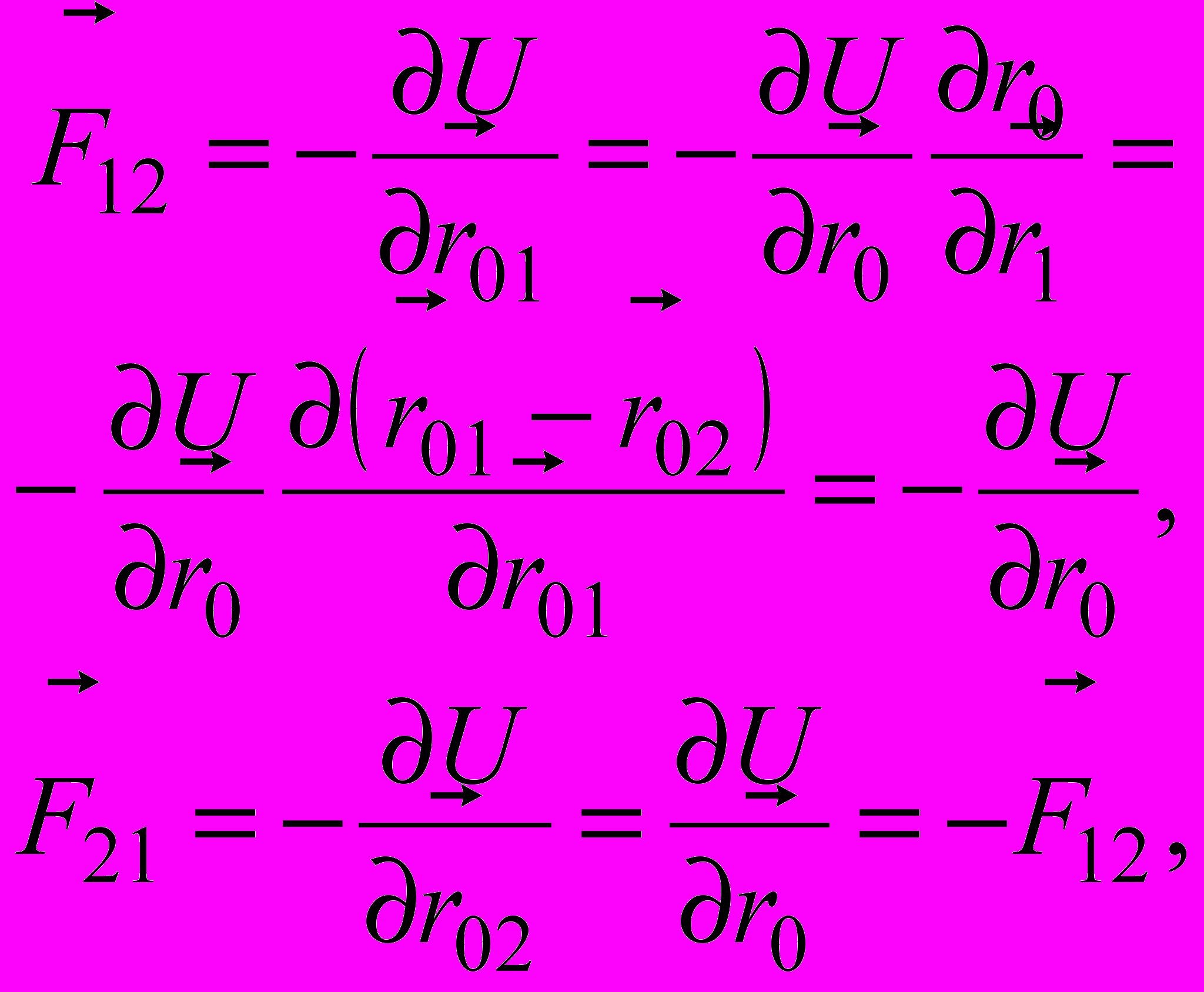
так что уравнения движения системы двух тел есть система уравнений движения каждой материальной точки в СЦМ



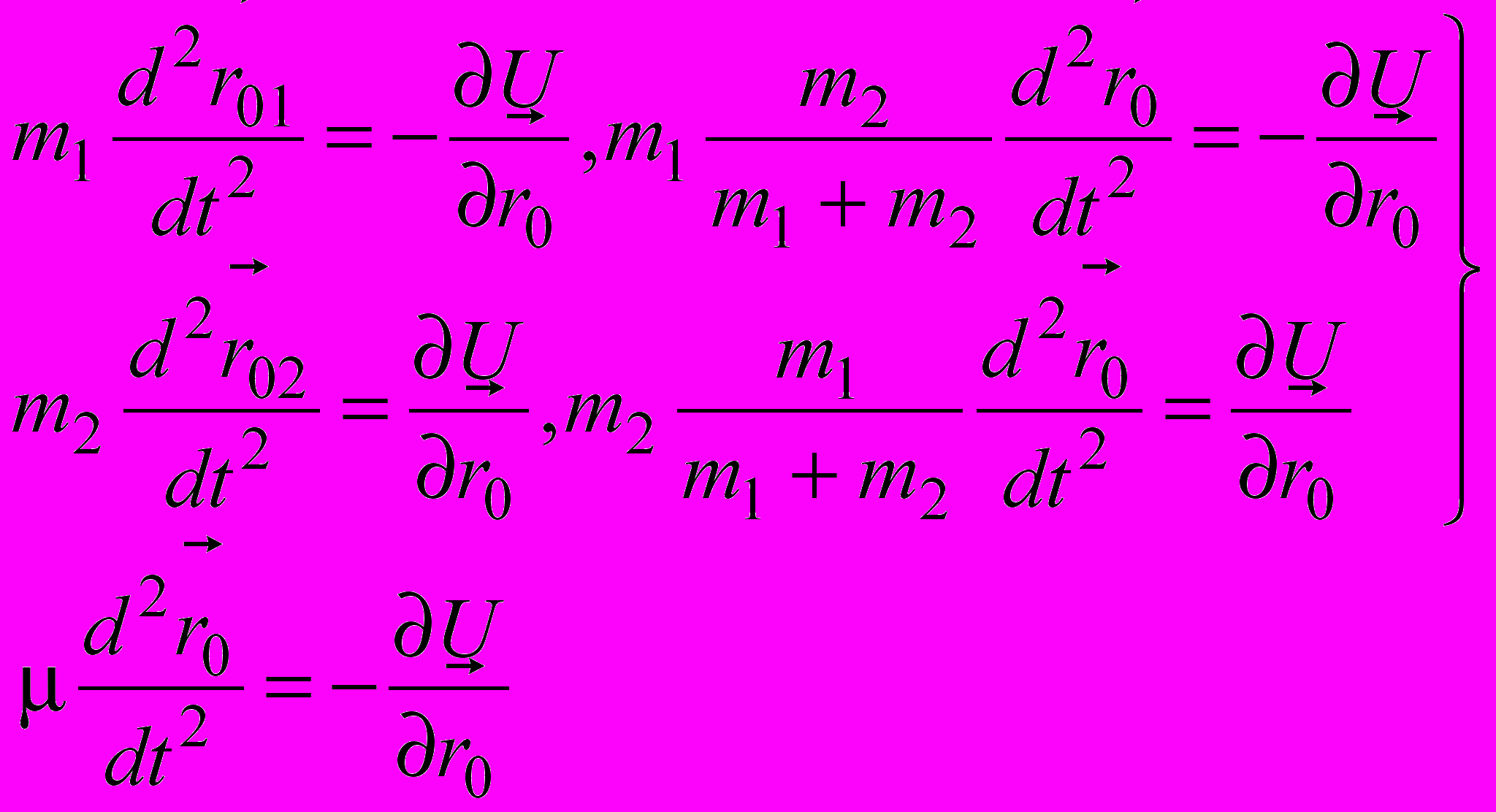
одинаковых для относительного движения каждой из них.

Приведенная масса системы двух материальных точек – множитель при ускорении относительного движения системы в уравнении их относительного движения.

Приведенная частица - материальная точка с массой, равной приведенной массе системы двух тел, движущаяся согласно уравнению их относительного движения в системе отсчета центра масс.

Решение этого уравнения дает закон движения приведенной частицы 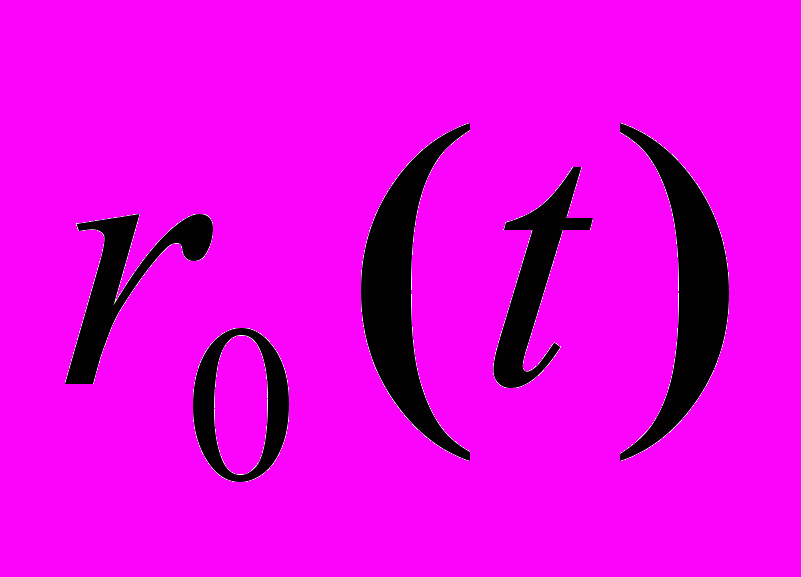, т.е. закон относительного движения системы двух тел в СЦМ. Согласно закону сложения перемещений из него следует закон движения системы в ЛСО по теореме о движении центра масс

,

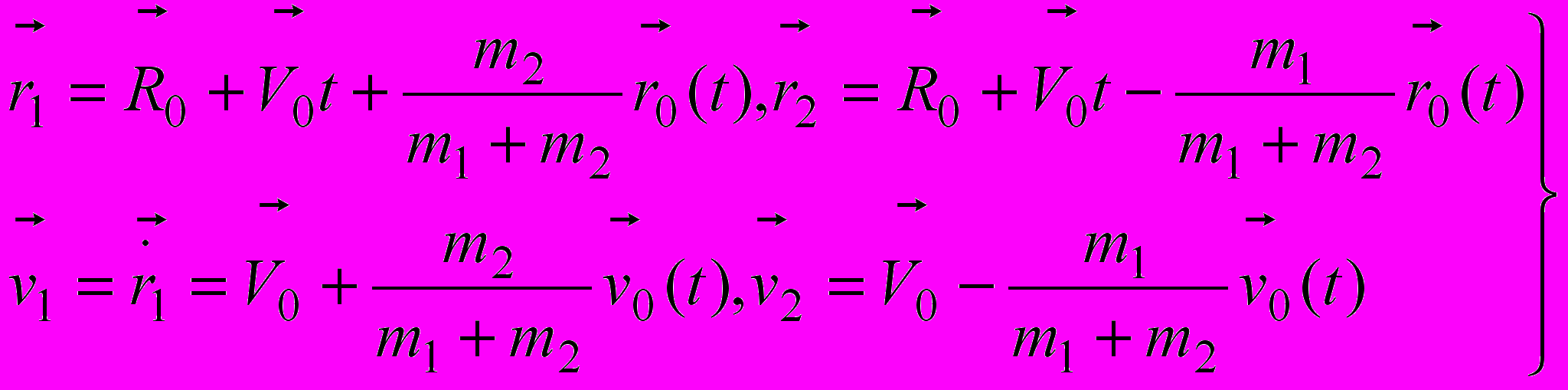выраженный через скорость относительного движения

.

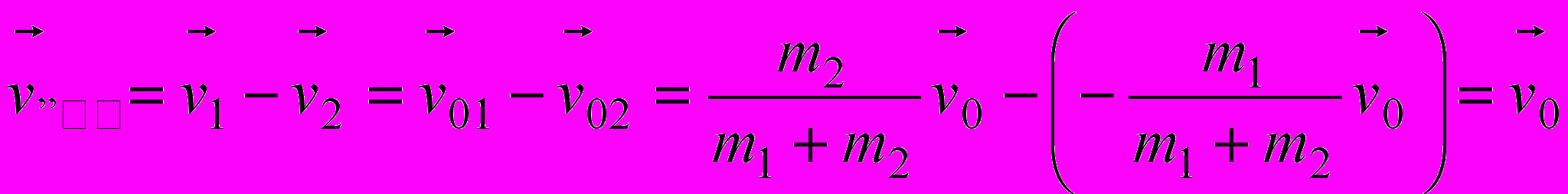Законы движения материальных точек в СЦМ, а с ними их траектории, подобны друг другу



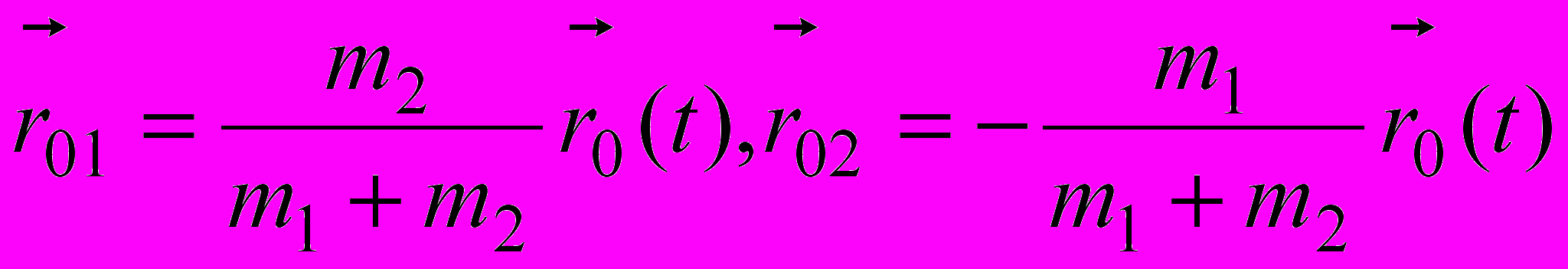
С множителем подобия - 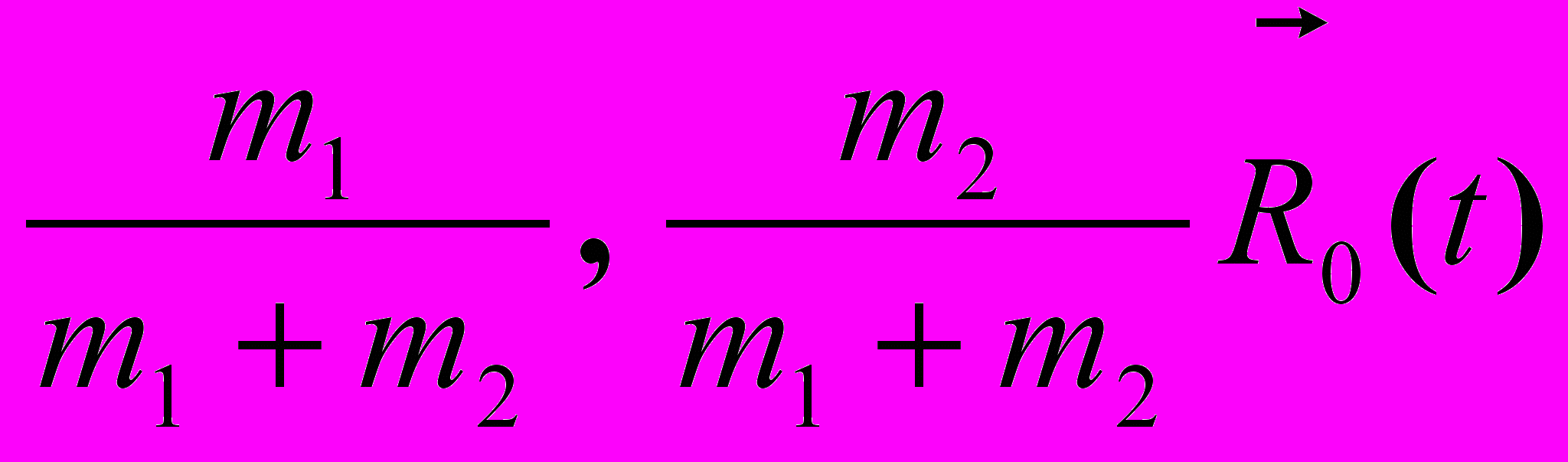, а их скорости пропорциональны и противоположны.

Если масса одного из тел гораздо больше, чем другого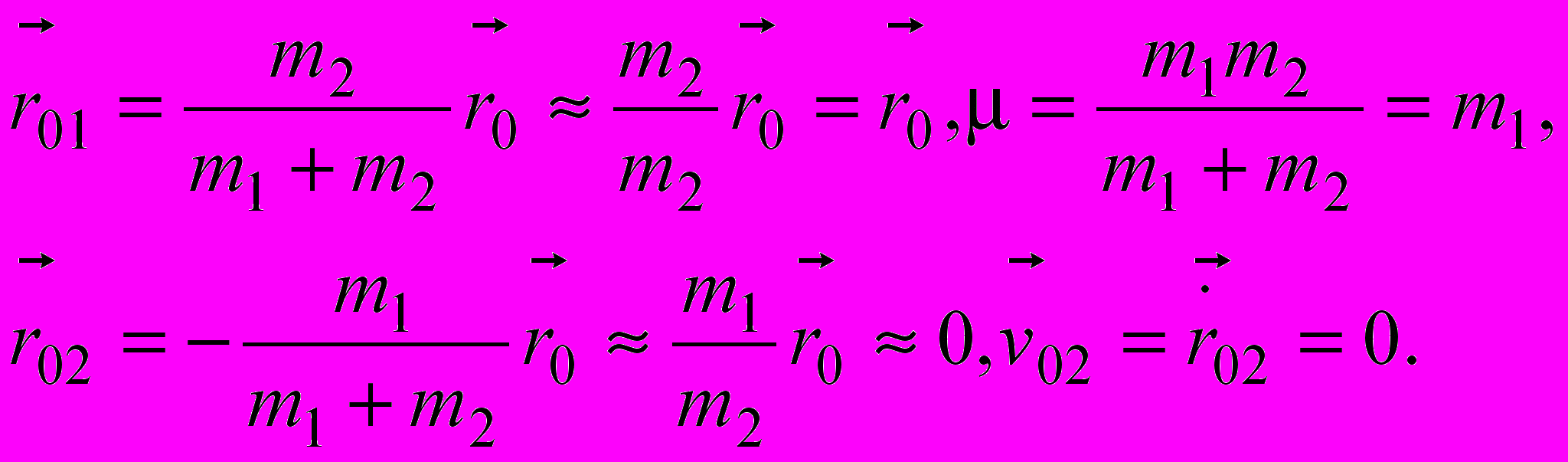



Массивная, тяжелая материальная точка почти неподвижна в центре масс, а легкая (безмассивная) движется вокруг нее в создаваемой массивной частицей центральном силовом поле.

2. Если 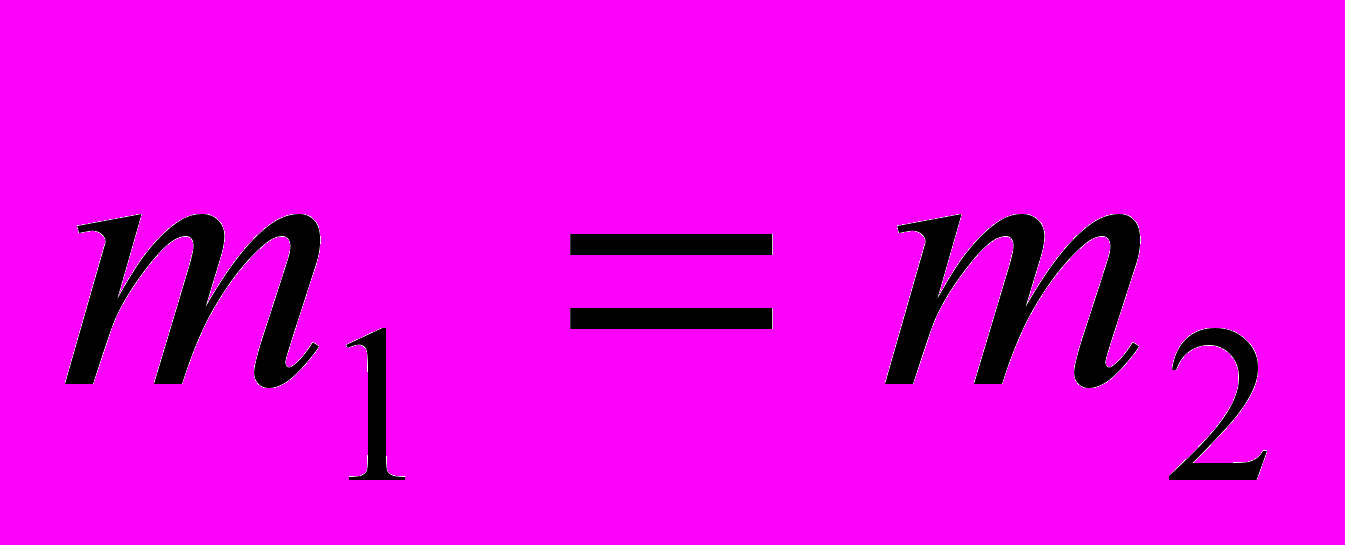массы тел одинаковы, то
   

.

Оба тела движутся по одной траектории в СЦМ с противоположными радиус-векторами и скоростями друг за другом вокруг центра масс, которой согласно теореме о движении центра масс движется независимо с полным импульсом

,

,

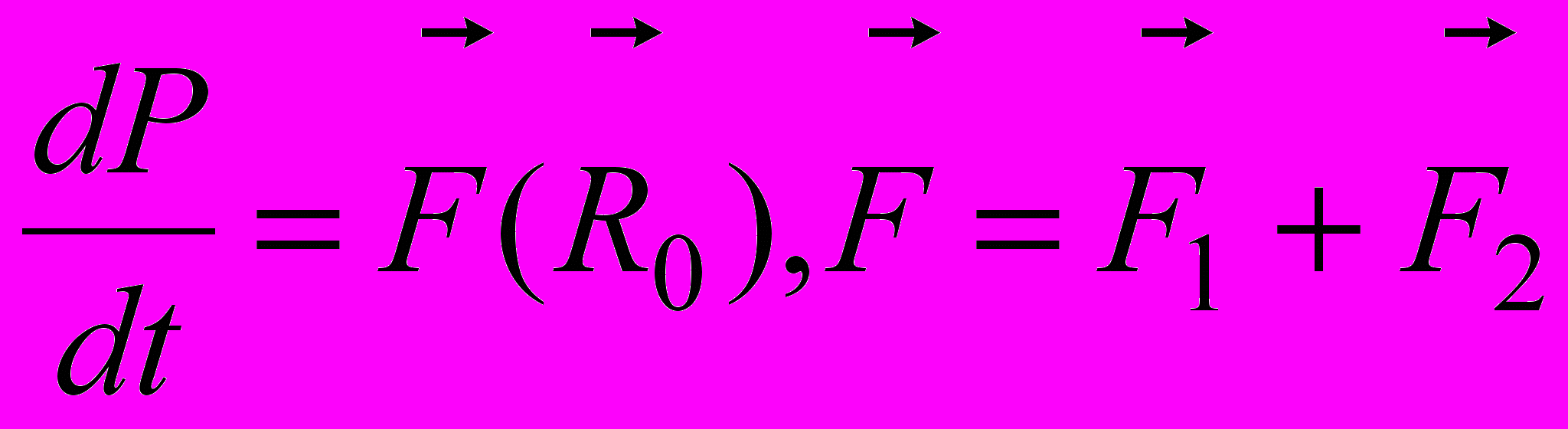решение которой (теоремы) даст закон движения центра масс .

3) При произвольном соотношении масс закон движения системы двух тел определяется из полной системы интегралов движения.

По теореме о движении центра масс для полного импульса как первого векторного интеграла движения



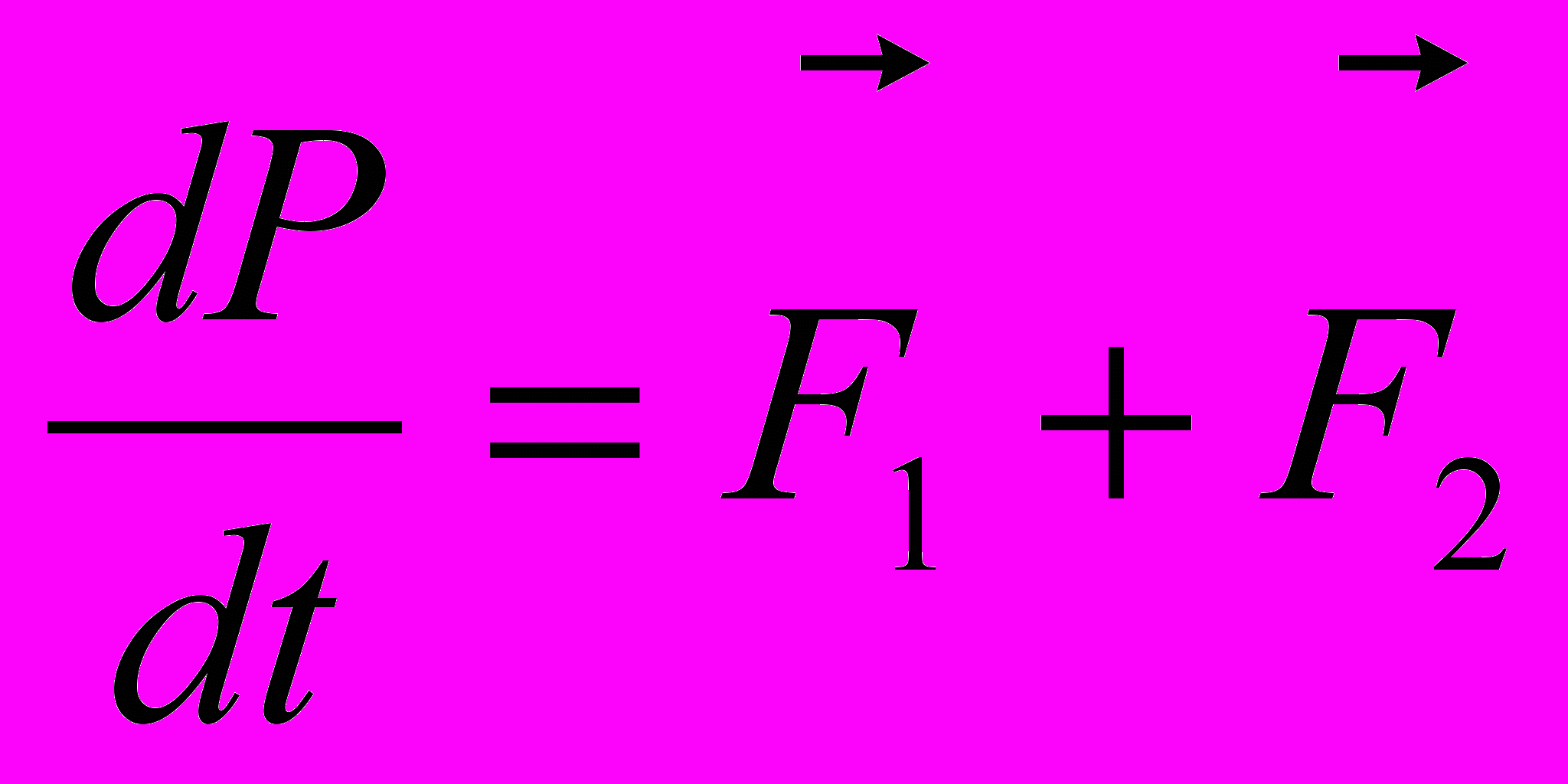
определяется закон движения центра масс .

По закону сохранения и превращения полной механической энергии



,



.

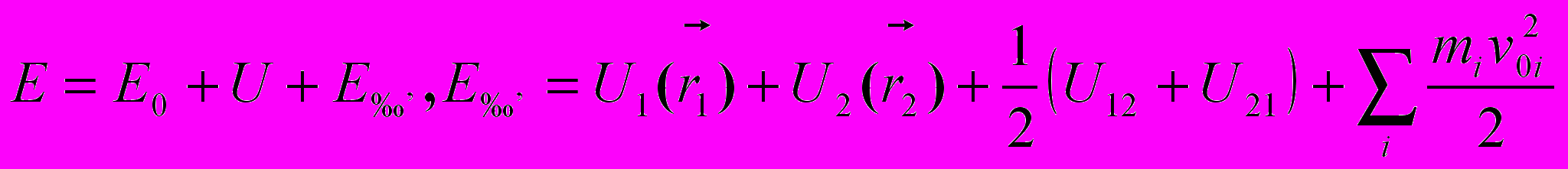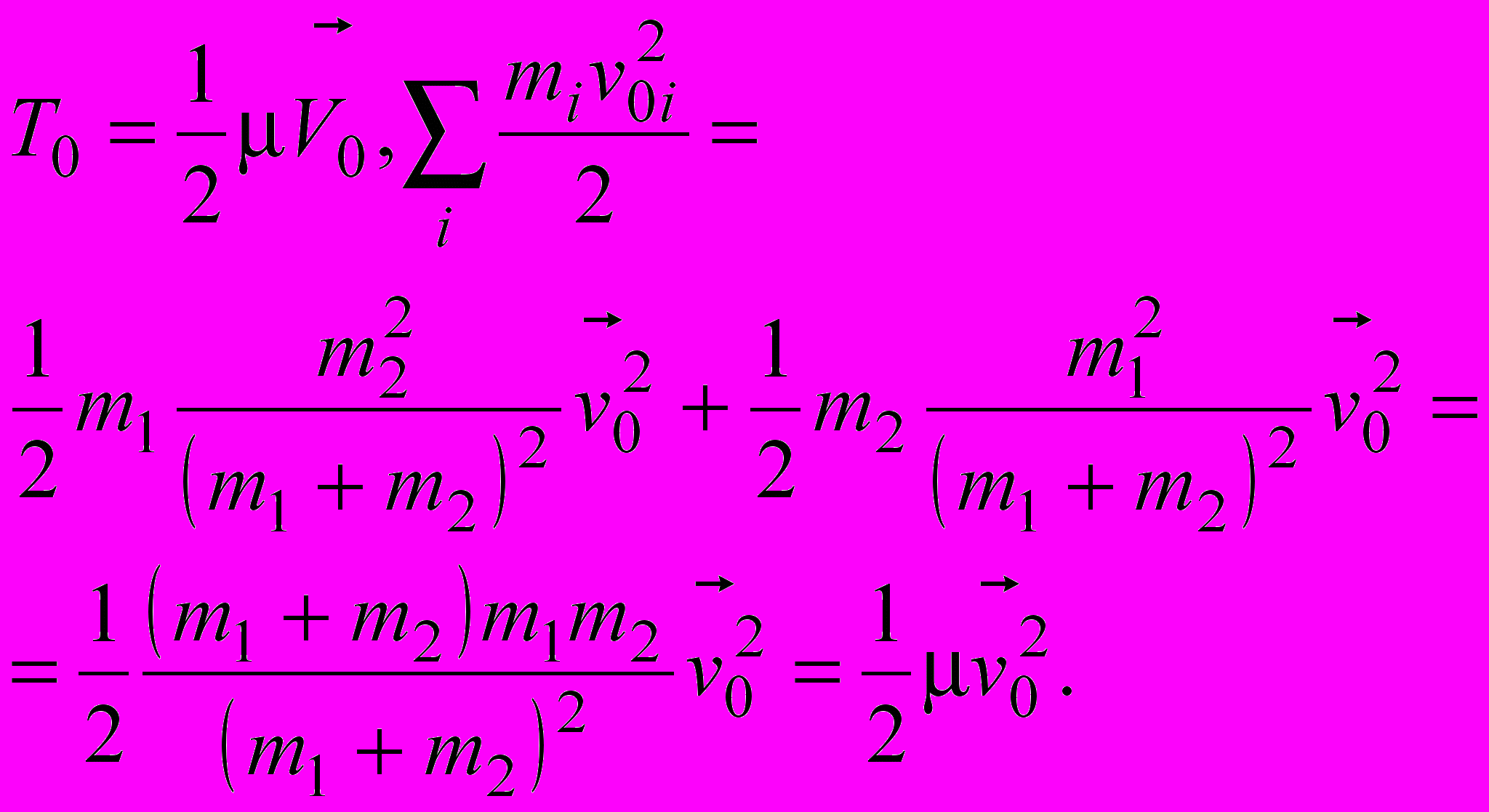
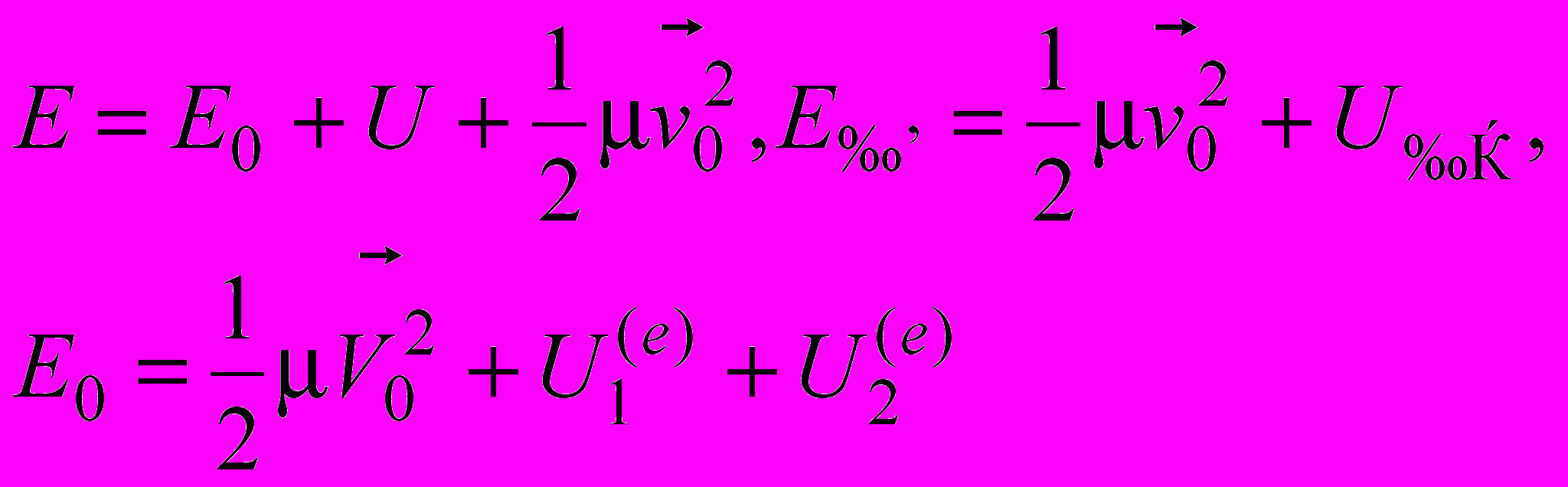Полная энергия системы двух тел равна сумме энергии центра масс 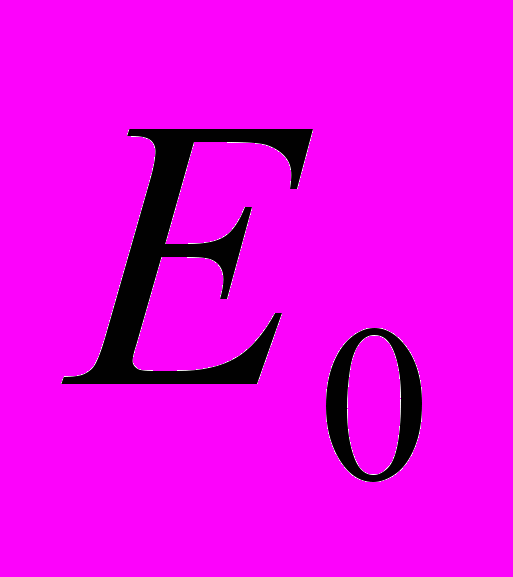и внутренней энергии, которая равна сумме кинетической энергии приведенной частицы и потенциальной энергии взаимодействия

.

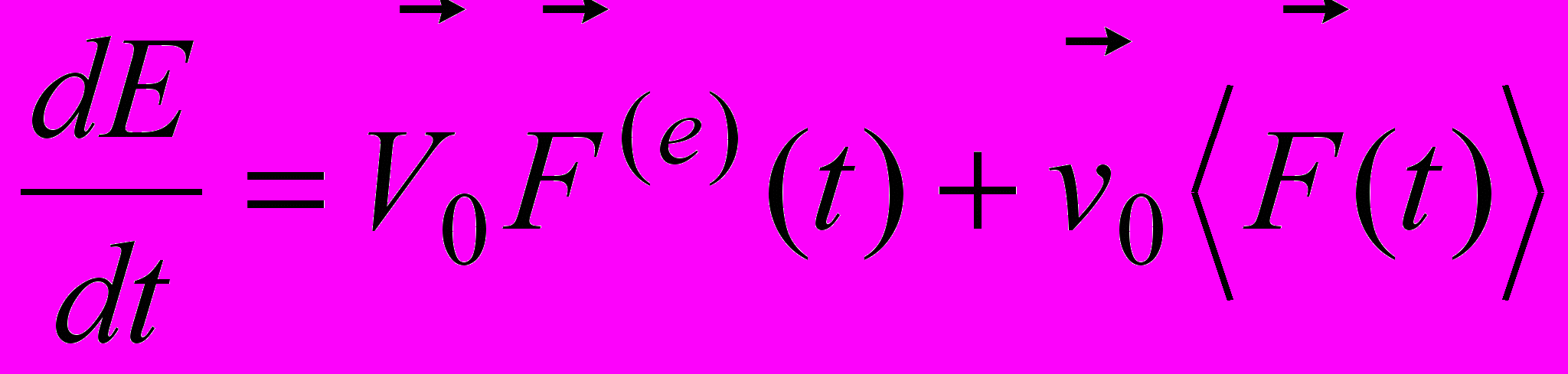3. По закону сохранения и превращения момента импульса, т.е. еще одного интеграла движения системы двух тел
   

,

,

,

.

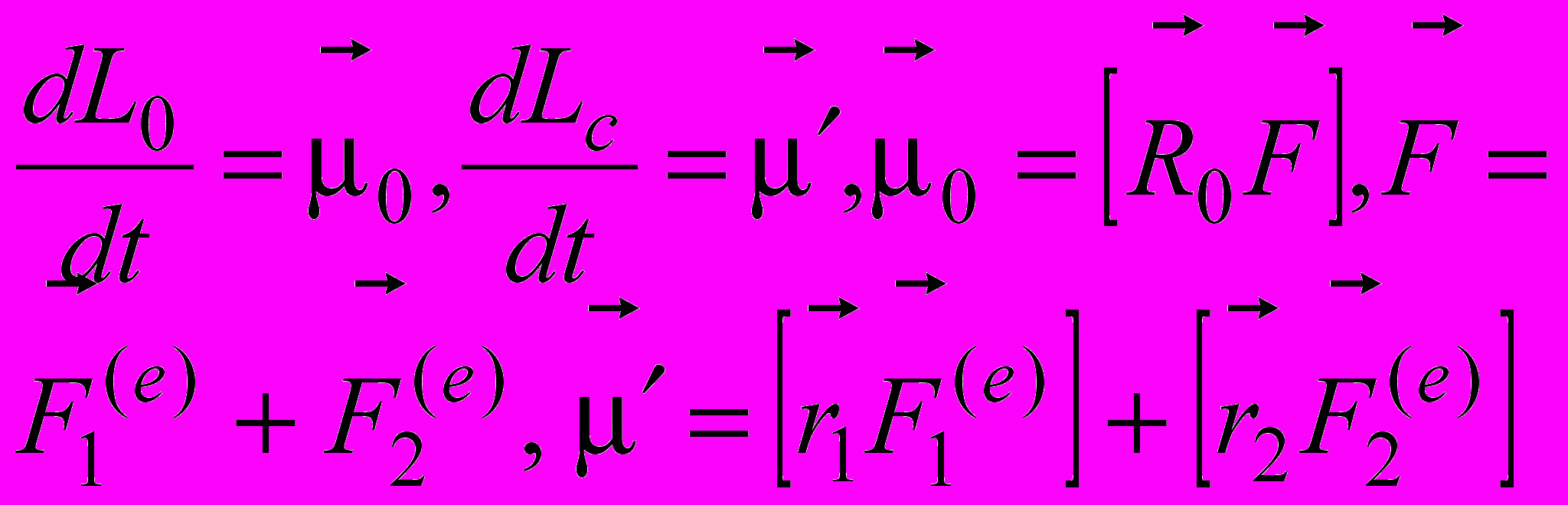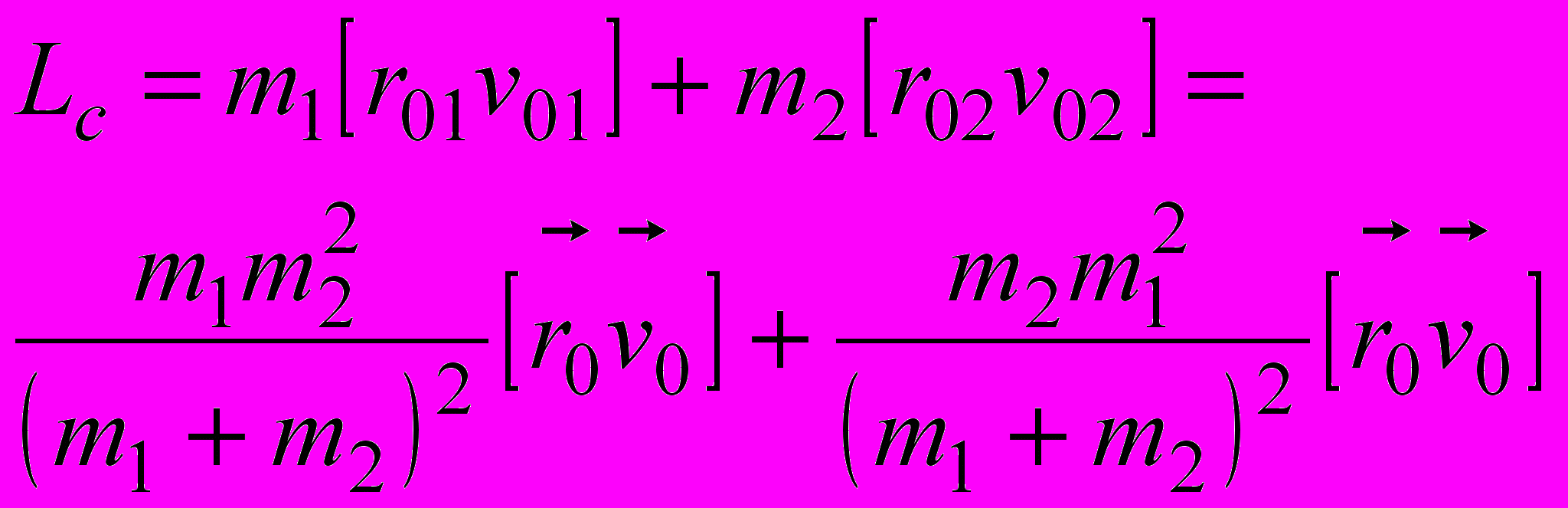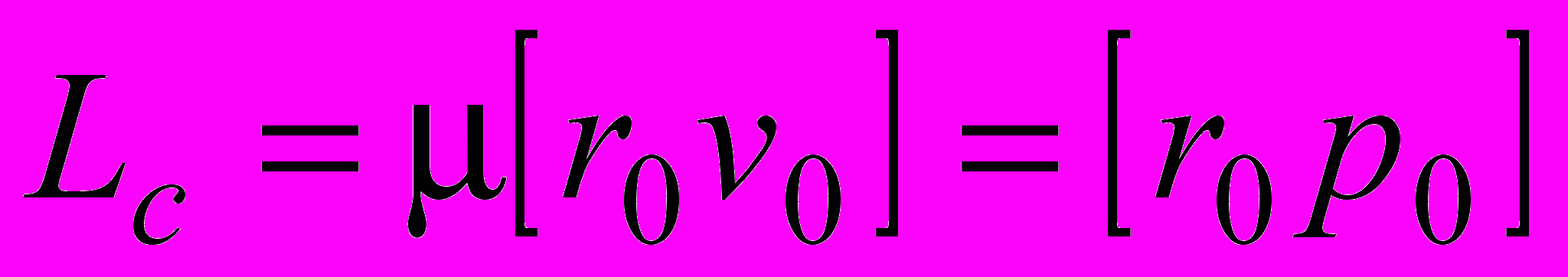Собственный момент импульса равен моменту импульса приведенной частицы относительно СЦМ.

Закон движения системы двух тел есть наложение закона движения центра масс и закона относительного движения приведенной частицы в системе отсчета центра масс, который определяется законами сохранения и превращения энергии и момента импульса



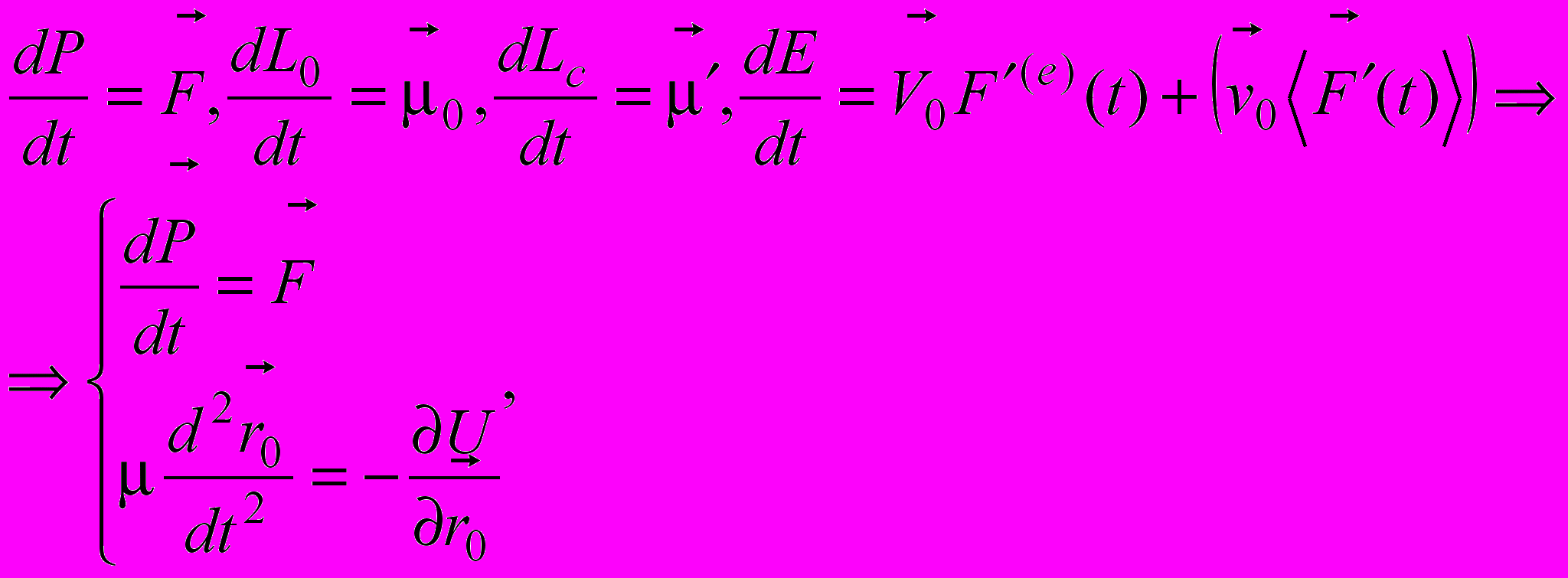
а в консервативной системе двух тел – уравнениями движения относительно СЦМ.