Задачи урока: обучающая научить учащихся решать оптимизационные задачи в среде электронных таблиц ms excel развивающая

Вид материала

Урок

Содержание Тип урока Задачи урока Объяснение нового материала Пусть в колхозе требуется распределить площадь пашни между двумя культурами в соответствии со следующими данными Урожай, ц/га Сервис выбираем Поиск решения Поиск решения Практическая работа по закреплению изученного материала. Виды кормов

Подобный материал:

• Задачи урока: образовательная знакомство учащихся с основными приемами построения графиков, 115.56kb.
• Урок №2. Тема: Знакомство с электронной таблицей ms exsel, 109.12kb.
• Контрольная работа №1 для 9 класса. Задание №1: вычислить значения следующих выражений, 35.07kb.
• Задачи урока: Обучающая: помочь учащимся осмыслить понятие молитвы как разговора человека, 368.66kb.
• Программа ms excel входит в пакет Microsoft Office и предназначена для подготовки, 127.81kb.
• Задачи урока: образовательная знакомство учащихся с основными приемами построения графиков, 91.98kb.
• Назначение программы Microsoft Excel (или просто Excel ) и создание и обработка электронных, 184.32kb.
• Как научить младших школьников решать текстовые задачи?, 124.64kb.
• Конспект урока математики в 3 классе по теме «Виды треугольников. День космонавтики», 79.5kb.
• Сцепленное с полом наследование, 139.03kb.

Урок разработала

учитель информатики

МОУ СОШ №12 г.Геленджика

Третьякова Н.И.


Интегрированный урок (инф.технологии – экономика, математика)

«Решение оптимизационных задач в среде электронных таблиц Excel.»


Тема урока: Решение оптимизационных задач в среде электронных таблиц.


Цели урока: изучение возможностей MS Excel по решению оптимизационных задач и практическое освоение соответствующих навыков и умений.


Тип урока: комбинированный – урок изучения нового материала и практического закрепления полученных знаний, умений и навыков.


Вид урока: сдвоенный, продолжительность1 час 20 минут.


Задачи урока:

• обучающая – научить учащихся решать оптимизационные задачи в среде электронных таблиц MS Excel.
  
• развивающая – познакомить учащихся с применением компьютеров в качестве помощников для экономического расчета наилучшего использования ресурсов;
  
• воспитательная – выработать у учащихся умение рационально использовать ресурсы.
  

Оборудование урока:

• Компьютеры с ОС MS Windows;
  
• Приложение MS Windows – MS Excel;
  
• 
  
• Карточки с задачами для самостоятельной работы.
  

Ход урока


В начале урока в ходе опроса повторяются приёмы эффективной работы в Excel – заполнение ячеек, копирование и редактирование формул.

Объяснение нового материала происходит на фоне практической работы учащихся за компьютерами. В ходе урока ребята выполняют на компьютерах задания, как устно предлагаемые учителем, так и представленные на розданных им карточках. Некоторые из этих заданий выполняются фронтально (т.е. учитель объясняет, что надо сделать, комментирует выполнение задания, ребята обсуждают выполненные действия), другие задания учащиеся выполняют самостоятельно, учитель только даёт индивидуальные консультации.


Объяснение нового материала


Учитель: Вы уже знакомы со многими функциями, которые имеются в программе электронных таблиц MS Excel. Но следует отметить, что возможности современных электронных таблиц не ограничиваются вычислениями по формулам и построением диаграмм и графиков. С помощью надстроек ЭТ можно решать самые разнообразные задачи.

Некоторые из надстроек не инсталлируются по умолчанию и требуют дополнительной установки. Так, для установки надстройки Поиск решения необходимо:

• выбрать команду Сервис, Надстройки;
  
• установить флажок около пункта Поиск решения;
  
• щелкнуть на кнопке ОК.
  

Поиск решения является надстройкой, которая позволяет решать задачи оптимизированного моделирования. Процедура поиска решения дает возможность найти оптимальное значение формулы, содержащейся в ячейке, которая называется целевой. Это процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке искомый результат, процедура изменяет значения во влияющих ячейках. Чтобы сузить множество значений, используемых в модели, применяются ограничения. Эти ограничения могут содержать ссылки на другие влияющие ячейки.

Рассмотрим решение задачи линейного программирования с использованием указанной возможности.

Пусть в колхозе требуется распределить площадь пашни между двумя культурами в соответствии со следующими данными:

чения во влияющих ячейках. построением диаг

Культура	Площадь, га	Урожай, ц/га	Затраты, руб./га	Цена за 1 ц, руб.	Затраты, человеко-дней на 1 га.
1	x	10	50	6	2
2	y	15	80	8	10

Кроме того, заданы ресурсы производства:

земли – 1800 га, человеко-дней – 8000.

Величины x и y являются неизвестными и подлежат определению.


Построение математической модели задачи включает в себя:

• задание целевой функции (ее надо максимизировать или минимизировать);
  
• задание системы ограничений в форме линейных уравнений и неравенств;
  
• требование неотрицательности переменных.
  

Решим задачу по оптимизации критерия, а именно по максимуму прибыли.

Ограничения задачи имеют следующий вид:

ограничение по площади: 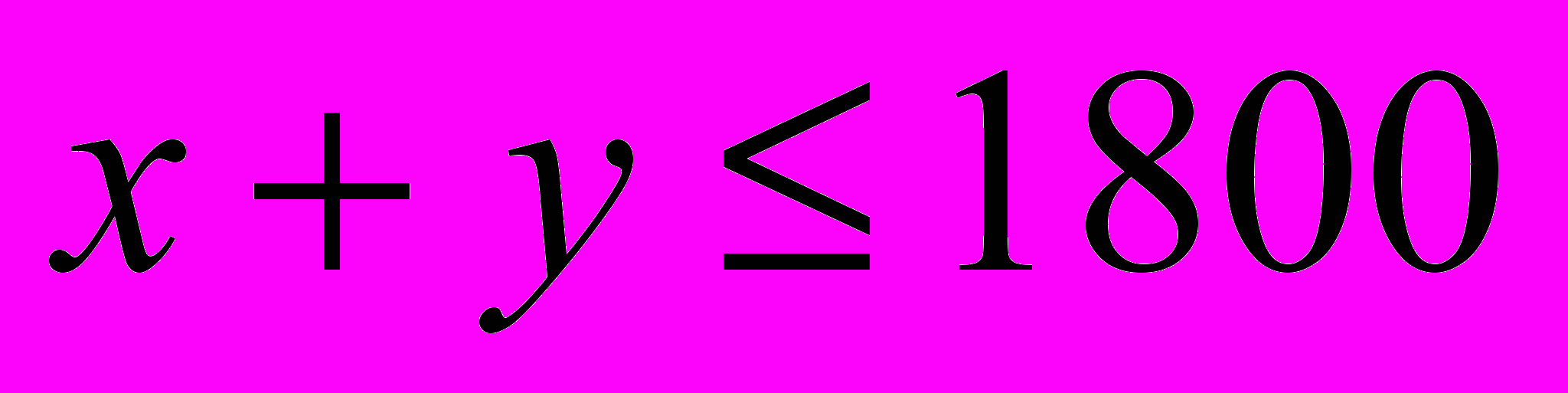; (1)

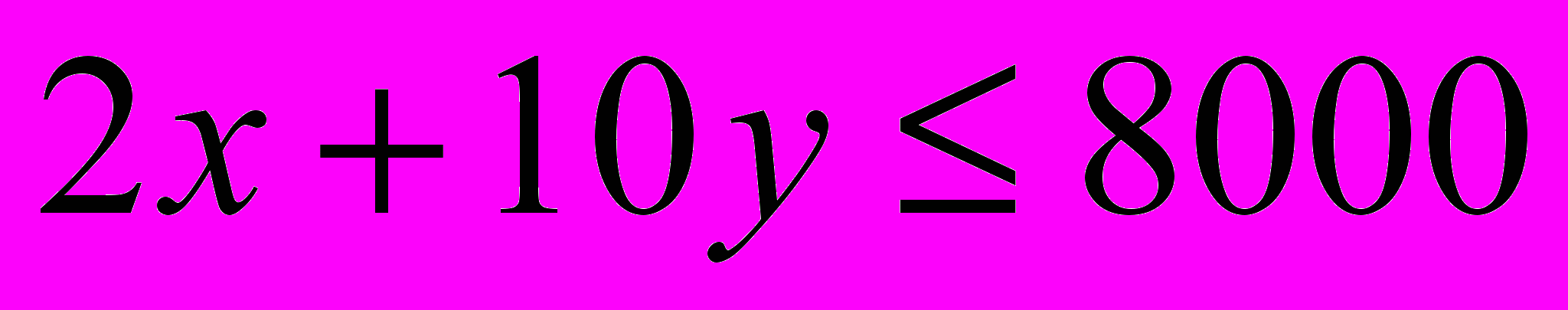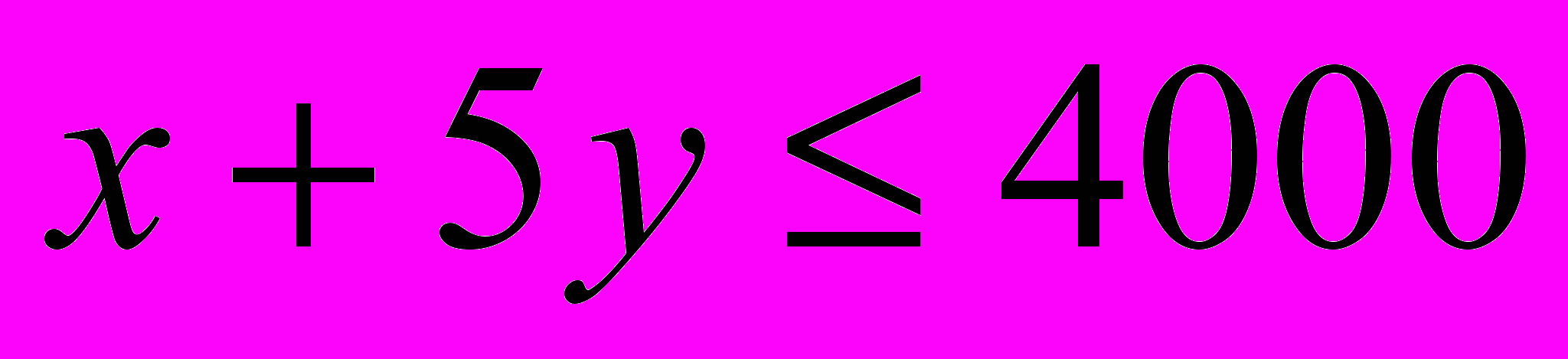ограничение по человеко-дням: , или (2)

Кроме того, ясно, что 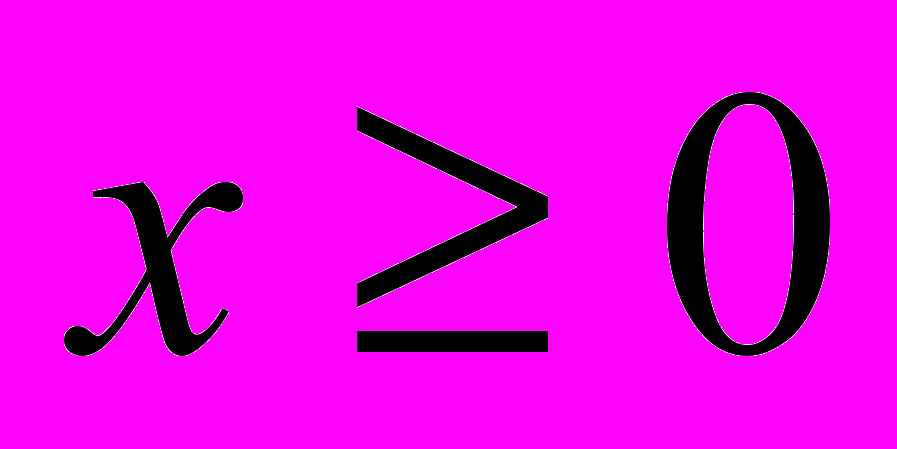, 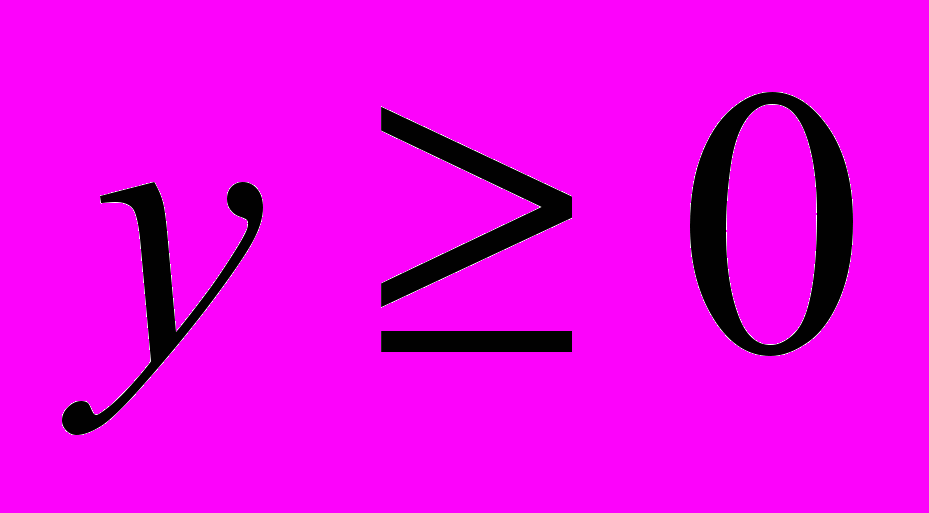(3)

Для прибыли (согласно данным таблицы) имеем формулу:

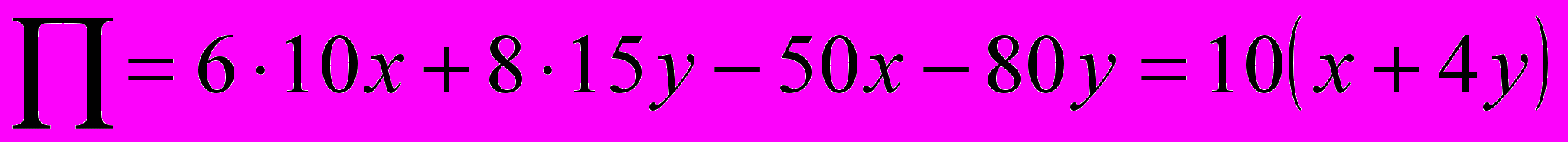. (4)

Учтя все условия задачи, приходим к её математической модели неотрицательных целочисленных решений системы линейных неравенств



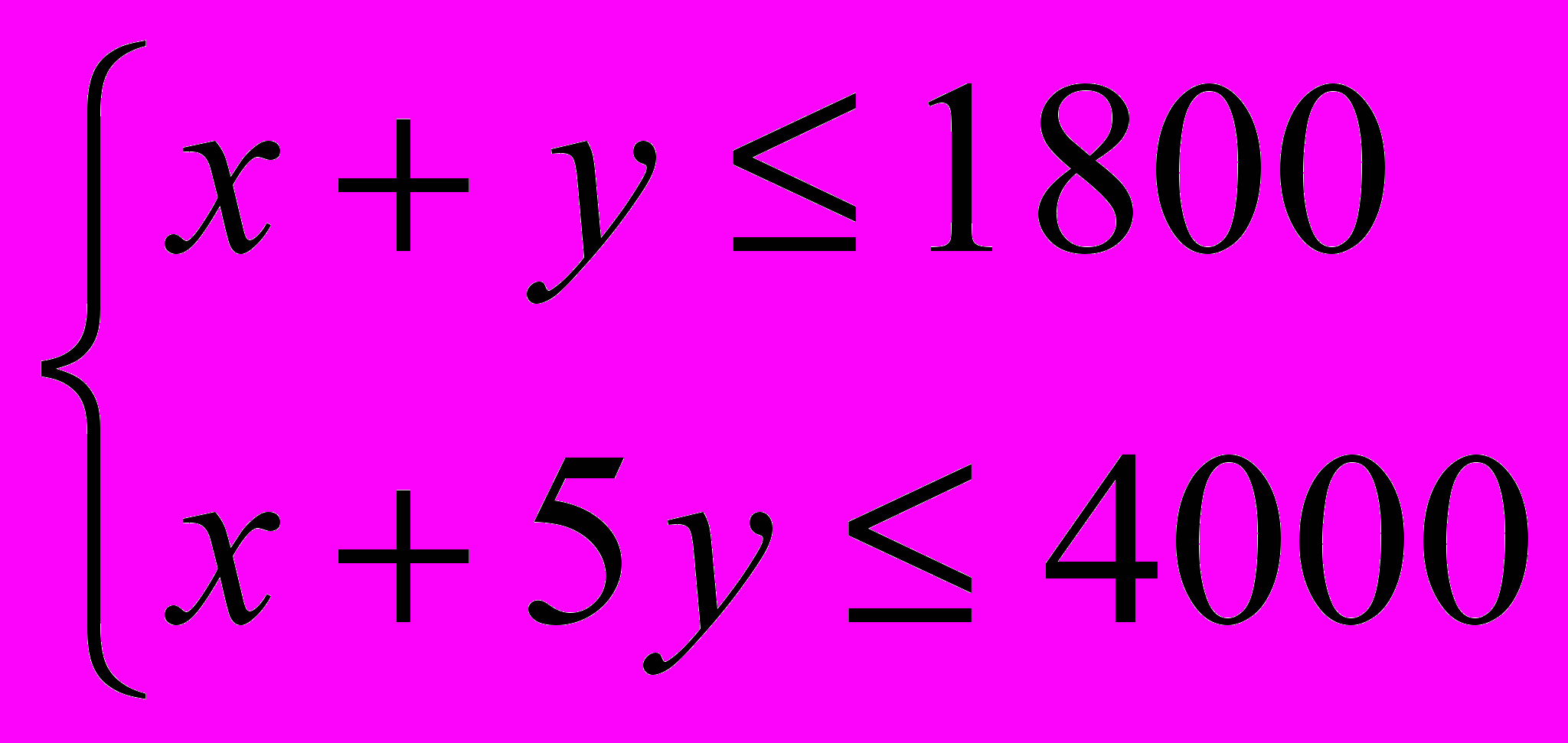
найти такое, которое соответствует максимуму линейной функции .

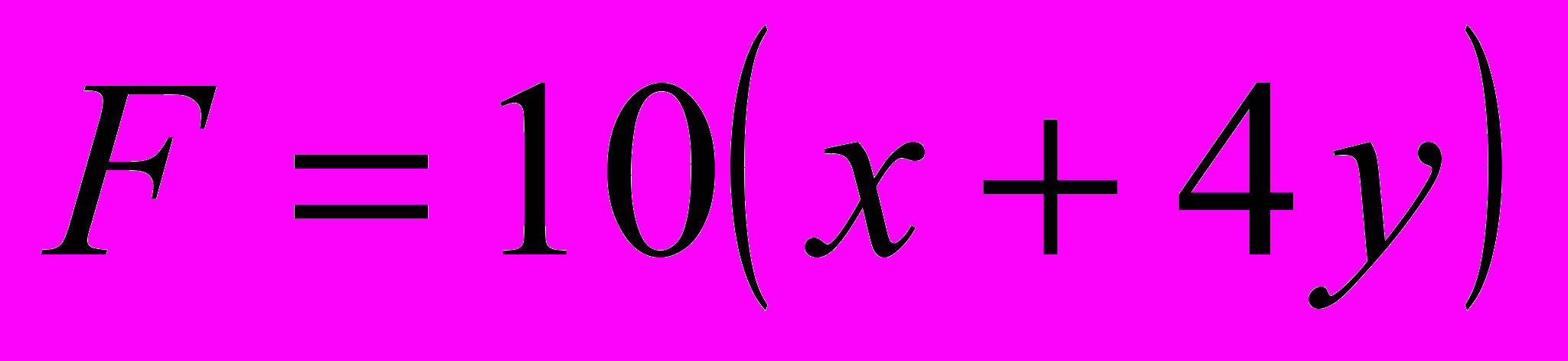Теперь заполним расчетную форму в табличном процессоре Excel.

Введем:

в столбец А - подписи к величинам и расчетным формулам,

в столбец В – расчетные формулы (отображаются вычисленные по этим формулам значения),




В меню Сервис выбираем Поиск решения и заполняем открывшееся диалоговое окно следующим образом:





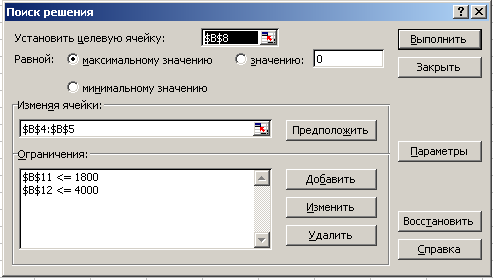
Далее щелкаем в этом окне на кнопке Параметры и в открывшемся диалоговом окне Параметры поиска решения устанавливаем флажки Линейная модель и Неотрицательные значения. Щелкаем по кнопке ОК.




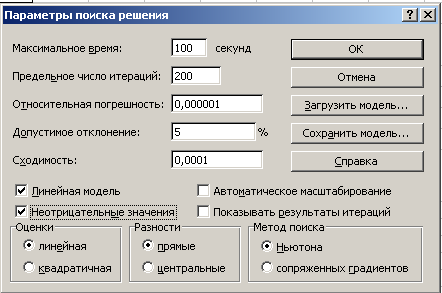
В окне Поиск решения щелкаем на кнопке Выполнить.


Оптимальное решение найдено:



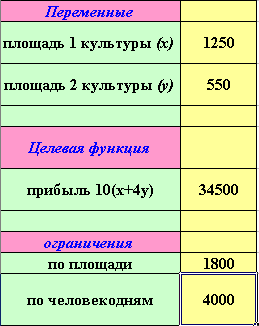
Таким образом, x = 1250 (га), y = 550 (га) - искомый оптимальный вариант распределения площади пашни между двумя культурами, при котором достигается максимальная прибыль, и выполняются все условия задачи.

Самостоятельно сохранить найденное решение, используя различные типы отчета.



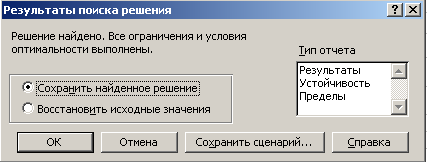
Практическая работа по закреплению изученного материала.


Учащимся предлагается самостоятельно решить одну из следующих задач (в зависимости от уровня подготовки).


Задача 1.

Предполагается, что рацион коров составляется из двух видов кормов – сена и концентратов. Суточная потребность кормов на 1 корову равна 20 кормовых единиц. В таблице приведены числовые данные о себестоимости кормов в данном хозяйстве.

Виды кормов	Содержание кормовых единиц в 1 кг кормов	Себестоимость кормов, в рублях.
Сено	0,5	1,5
Концентраты	1,0	2,5

Найти самый дешевый рацион, если ежедневный рацион кормления сельскохозяйственных животных должен включать не менее 16 кг. сена.

(Ограничения:





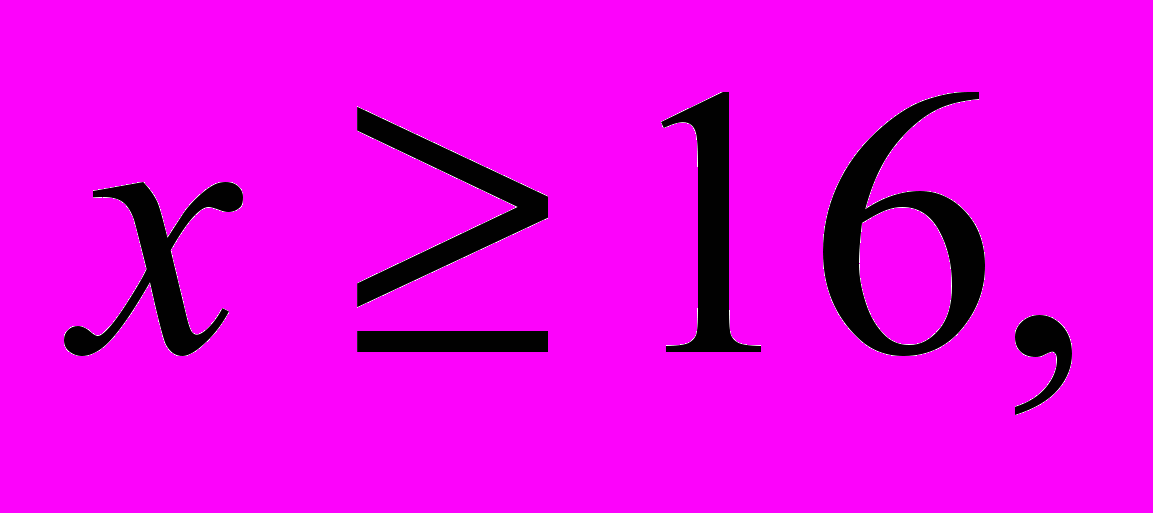
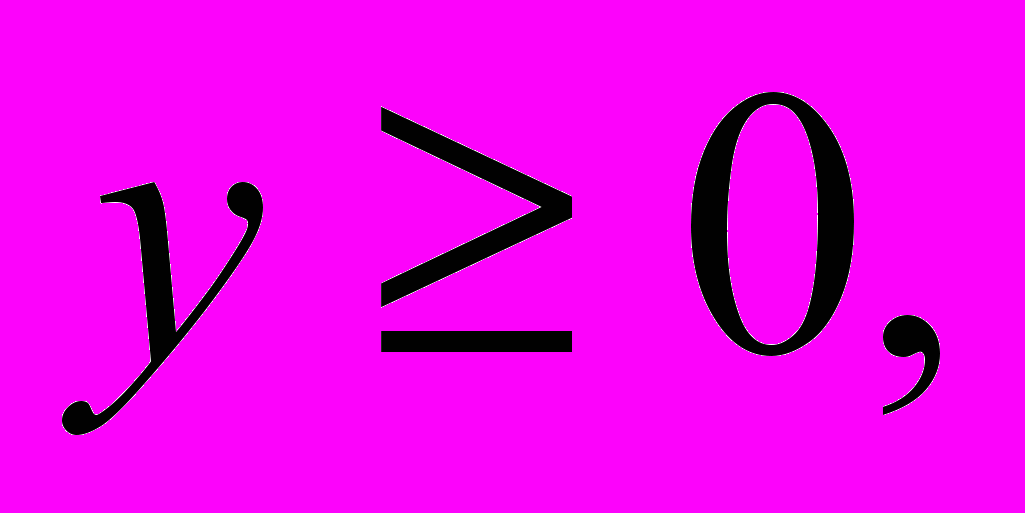
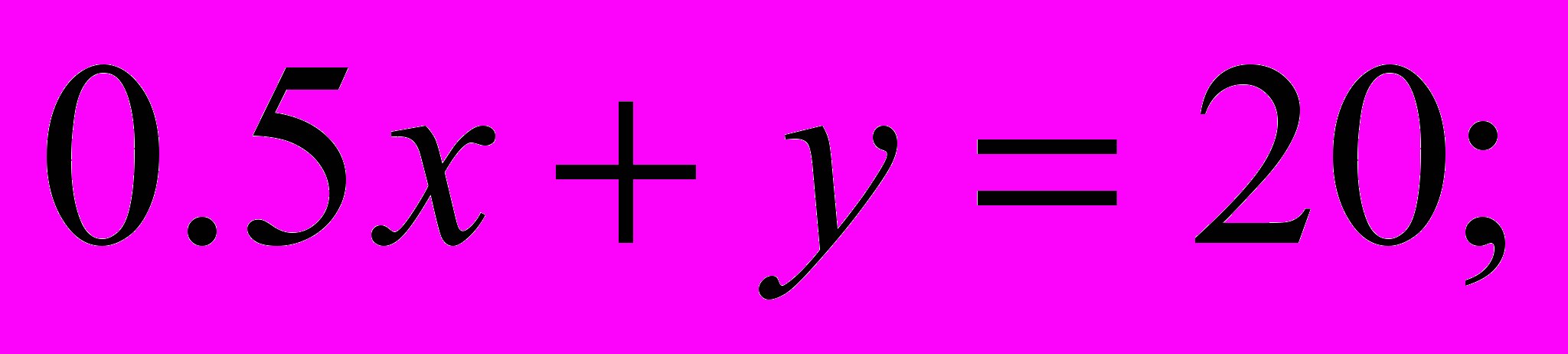
Целевая функция: )


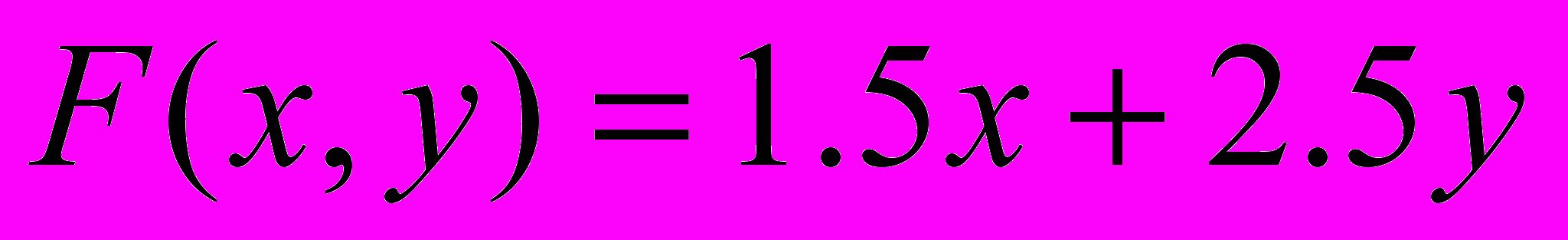Задача 2.

Мебельная фабрика выпускает кресла двух типов. На изготовление кресла первого типа расходуется 2 м досок стандартного сечения, 0,8 м² обивочной ткани и затрачивается 2 человеко-часа, а на изготовление кресла второго типа – соответственно 4 м, 1,25 м² и 1,75 человеко-часа. Известно, что цена одного кресла первого типа равна 1500 рублей, второго типа – 2000 рублей. Сколько кресел каждого типа надо выпускать, чтобы стоимость выпускаемой продукции была максимальной, если фабрика имеет в наличии 4400 м досок, 1500 м² обивочной ткани и может затратить 3200 человеко-часов рабочего времени на изготовление этой продукции?

(Ограничения:









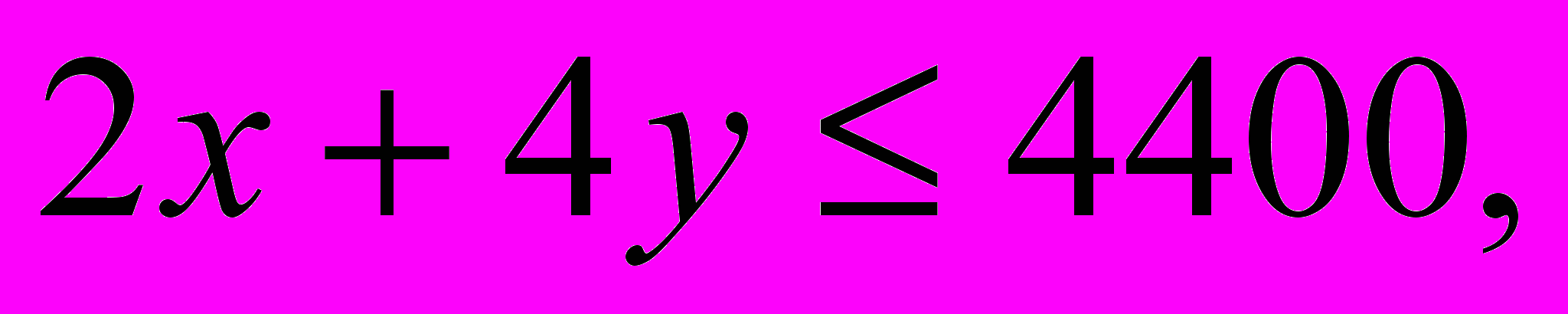
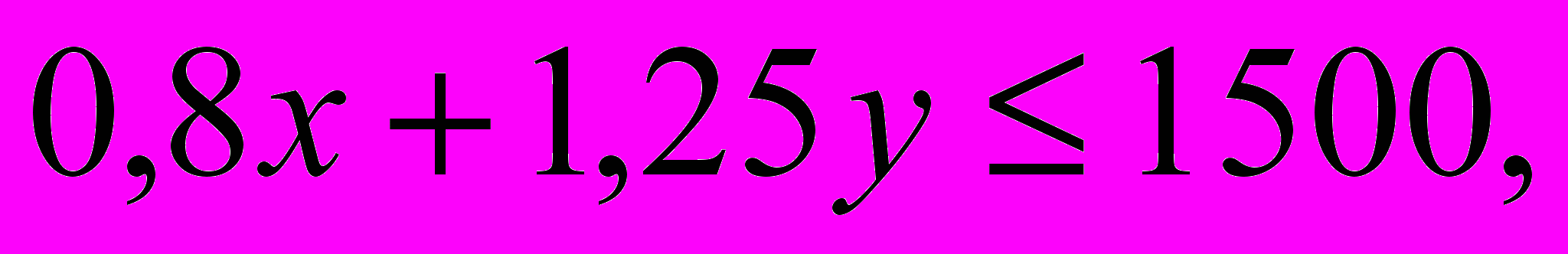
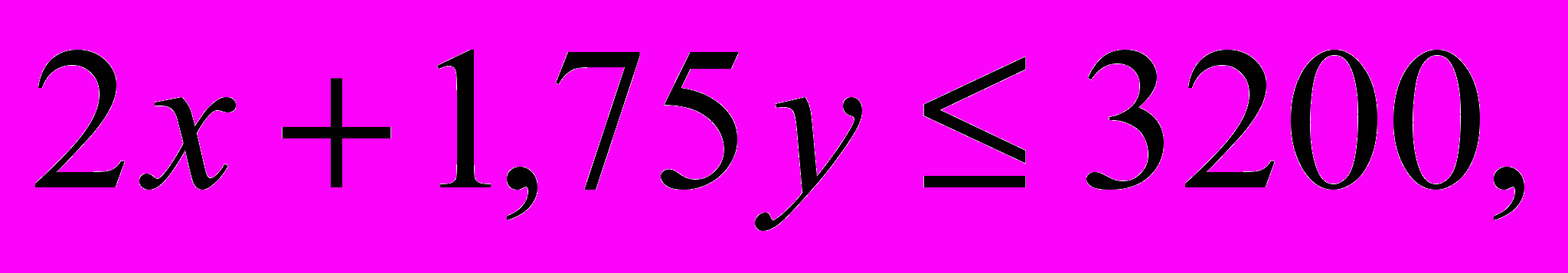
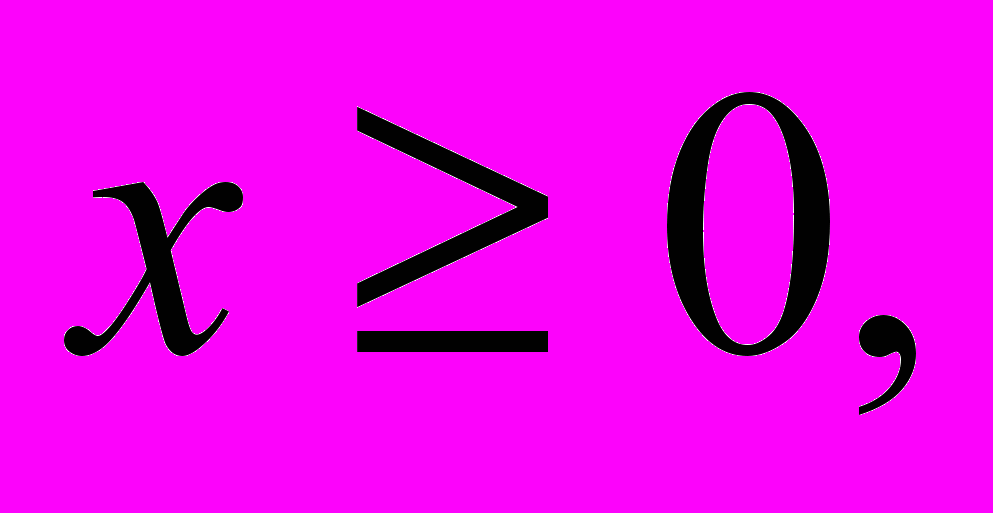
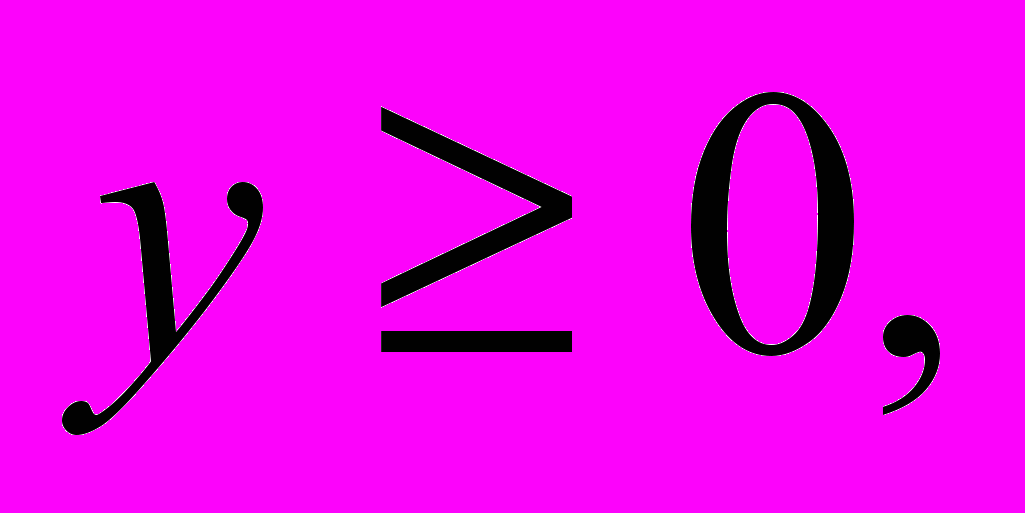
Целевая функция: )


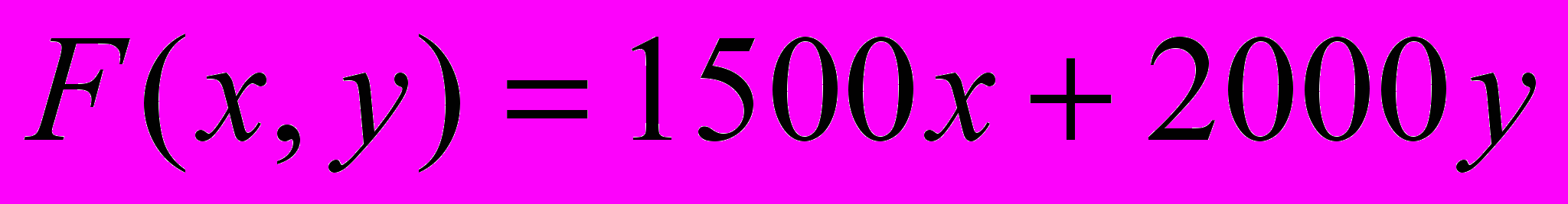Задача 3

Хозрасчетной бригаде выделено для возделывания кормовых культур 100 га пашни. Эту пашню предполагается занять кукурузой и свеклой, причем свеклой решено занять не менее 40 га. Как должна быть распределена площадь пашни по культурам, чтобы получилось наибольшее число кормовых единиц? При этом должно быть учтено следующее: 1 ц кукурузного силоса содержит 0,2 кормовой единицы, 1 ц свеклы – 0,26 кормовой единицы, на возделывание 1 на кукурузного поля необходимо затратить 38 человеко-часов труда механизаторов и 15 человеко-часов ручного труда, а на возделывание 1 га поля, занятого свеклой, соответственно 43 и 185 человеко0часов, ожидаемый урожай кукурузы – 500 ц с 1 га, а свеклы – 200 ц с 1 га, наконец, всего на возделывание кормовых культур можно затратить 4000 человеко-часов механизаторов и 15000 человеко-часов ручного труда.


(Ограничения:









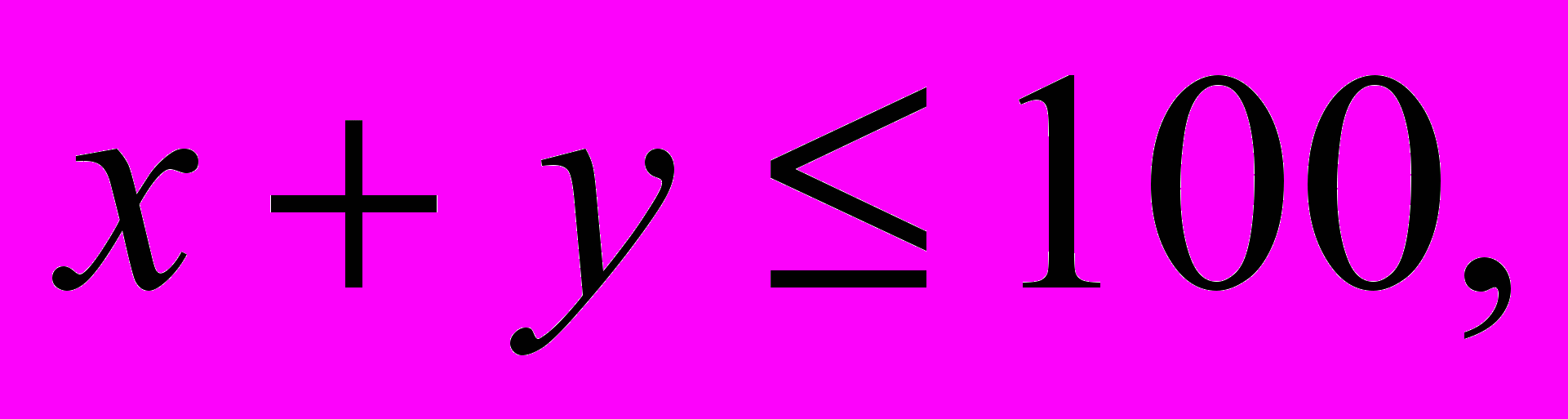
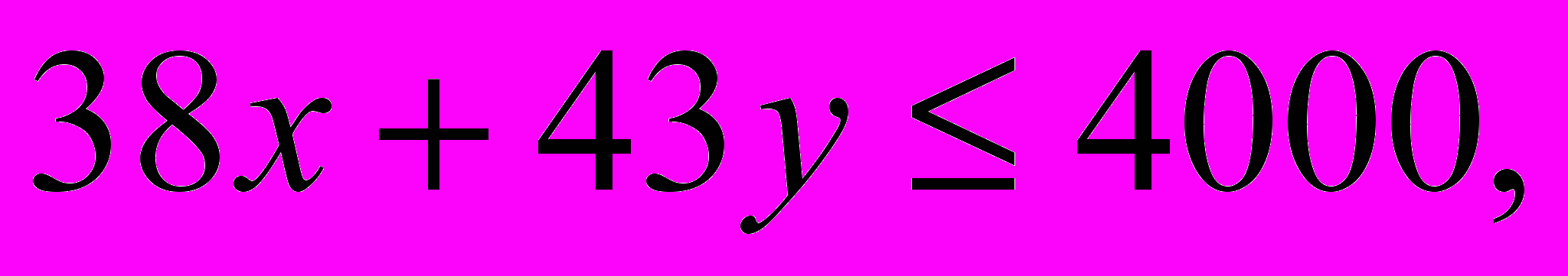
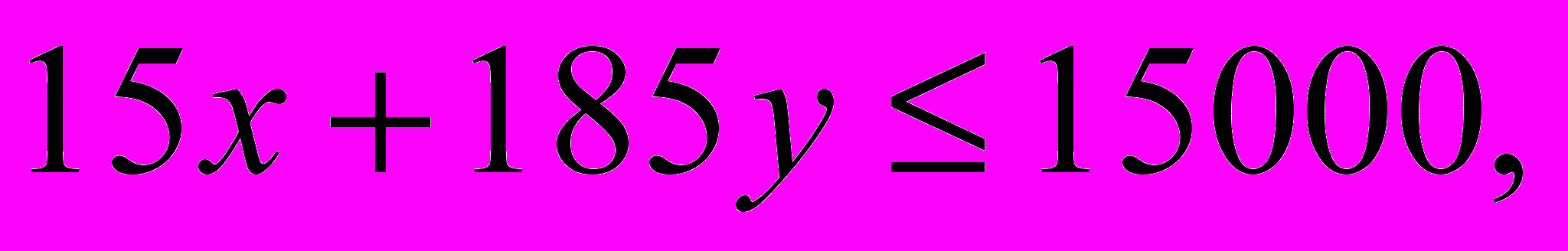
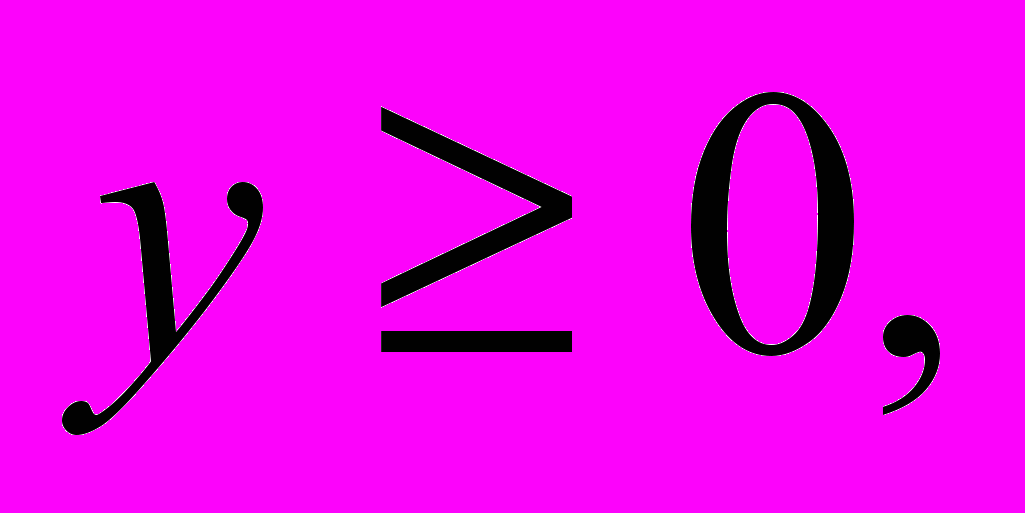
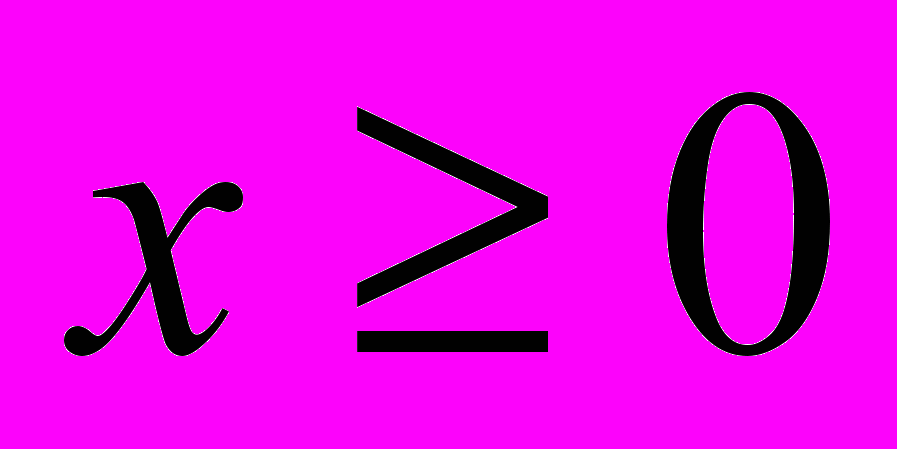
Целевая функция: )


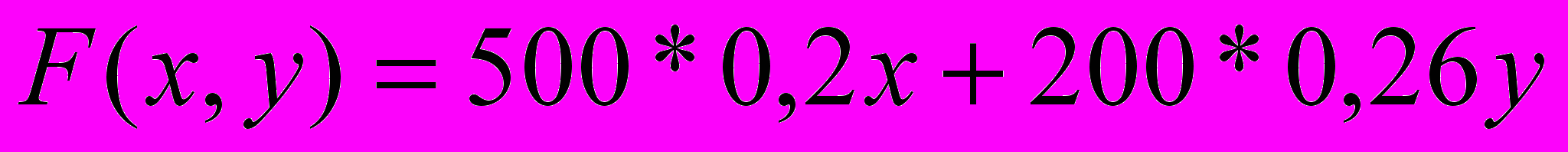Урок проводила

учитель информатики МОУ СОШ № 12 Третьякова Наталья Ивановна 07.12.2006г.