Сівак В. М., к т. н., доцент
| Вид материала | Документы |
- Культурология, 395.24kb.
- Рабочая программа по философии для специальности, 379.23kb.
- Охорона праці в галузі, 1878.5kb.
- Методические рекомендации по выполнению, оформлению и защите выпускных квалификационных, 445.38kb.
- Учебно-методические указания по дисциплине отечественная история для студентов неисторических, 762.11kb.
- З виробничої практики, 169.38kb.
- Основные направления конференции, 72.62kb.
- Хмельницького Магістратура "Затверджую", 292.99kb.
- Программа всероссийской научно-практической конференции «проблемы современной экономики:, 87.2kb.
- Зачеты, 37.94kb.
УДК 66-966:628.3:557.31
Сівак В.М., к.т.н., доцент (Національний університет водного господарства та природокористування, м. Рівне)
СТІЙКІСТЬ ПРОЦЕСУ БІОЛОГІЧНОГО ОЧИЩЕННЯ СТІЧНИХ ВОД В БІООКИСЛЮВАЧ В ЗАЛЕЖНОСТІ ВІД КІНЕТИЧНИХ МОДЕЛЕЙ
Пропонується механізм стійкості процесу біологічного очищення стічних вод у біоокислювачах з урахуванням кінетичних моделей.
The mechanism of biological purification and instability of sewage waters in bio-oxygenation tanks with kinetic models assumption is presented.
Постановка задачі. Проблема стійкості біологічних процесів в біоокислювачах є дуже складною. Про це нами аналізувалося у роботах [1,3].
Виходячи з того, що чим складнішим є процес, тим складнішим є пошук припустимих спрощень і аналітичних рішень. Тому у даній статті ми скористаємося такими спрощеними математичними моделями біоокислювачів, щоб можна було б розв‘язувати рівняння в аналітичному вигляді, нехтуючи відношенями між багатьма несуттєвими параметрами. Такий підхід має певні переваги: він полегшує розуміння і дає змогу отримати загальне уявлення про проблему, а результати, отримані в рамках цих моделей, мають більшу ступінь узагальненості і можуть бути використанні при побудові математичних моделей біоокислювачів більш високої розмірності.
Найпростіша модель біоокислювача для умов ідеального перемішування мулового середовища, яка враховує процес росту мікроорганізмів і утилізацію забруднень, що знаходяться у стічній воді, має вигляд
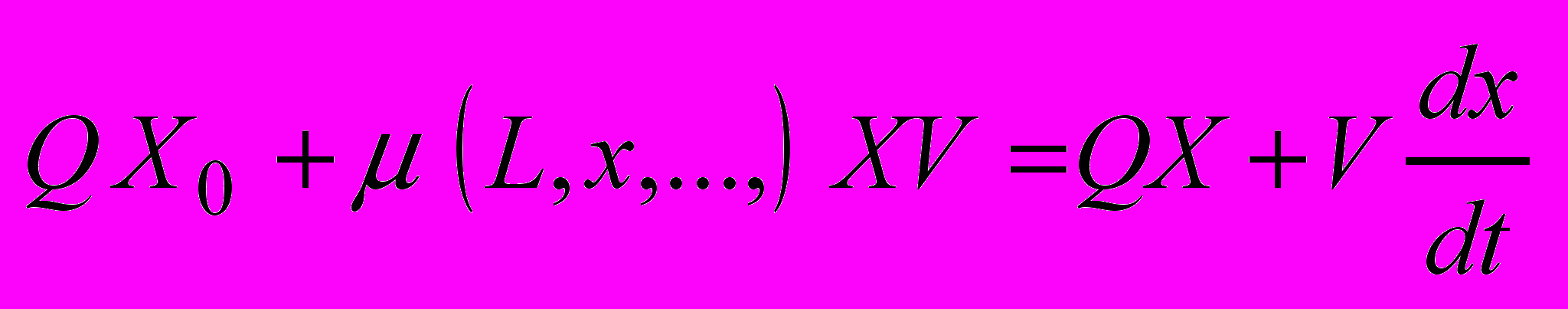, (1)
,
(2)де V - об‘єм середовища у біоокислювачі, м3; Q - витрати стічної води, що проходить через біоокислювач, м3/год; X,L - концентрація мікроорганізмів і забруднюючих речовин у муловому середовищі (індекс ”0” відноситься до початкових концентрацій);
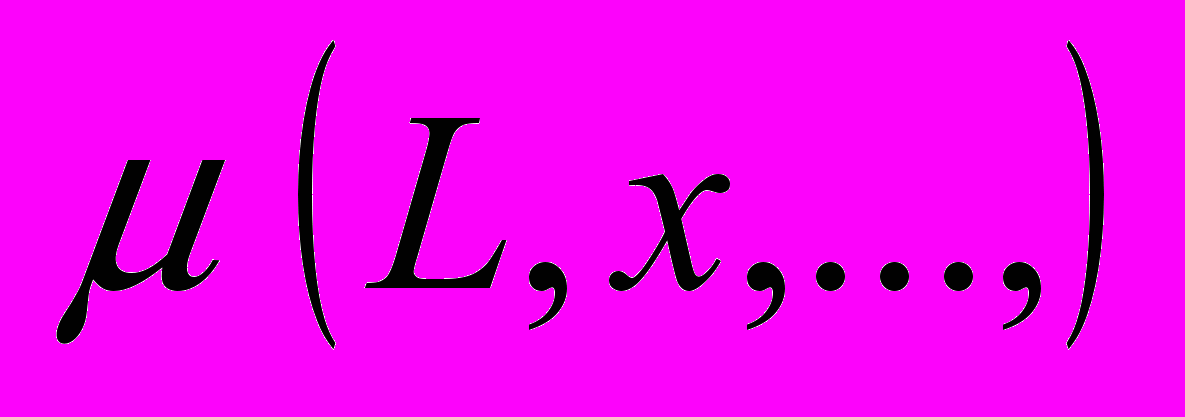- питома швидкість росту мікроорганізмів, мг/м3год; 
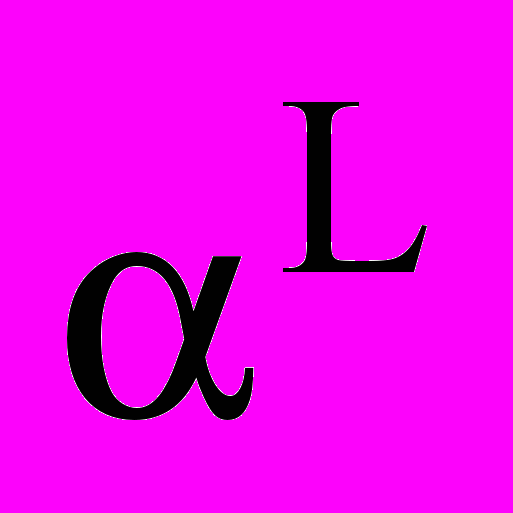- витратний коефіцієнт по забрудненню, мг/м.На питому швидкість росту мікроорганізмів
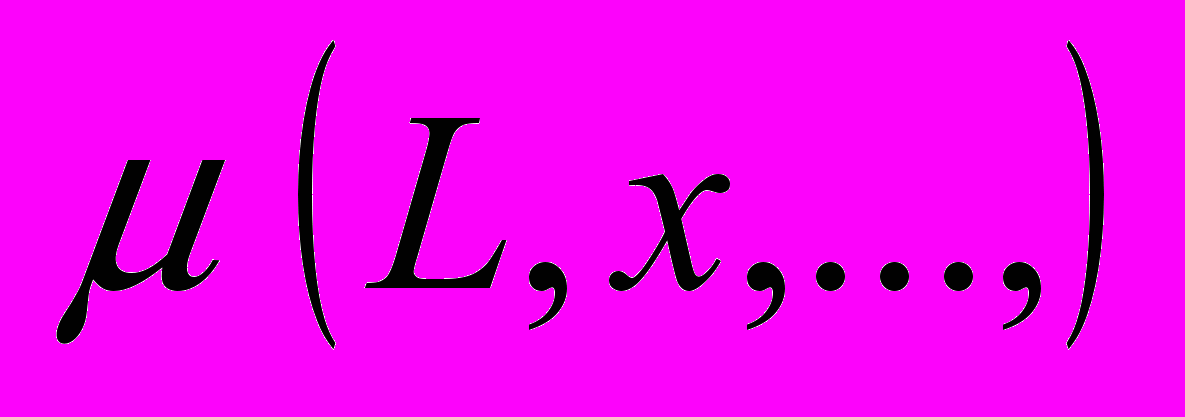впливають такі параметри, як концентрація забруднюючих речовин L, кисню 
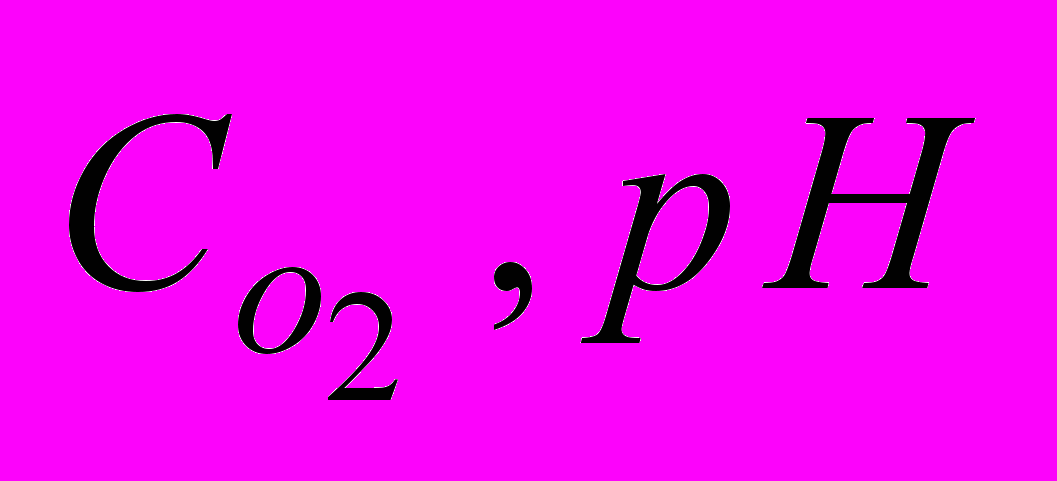, температура, вміст токсичних речовин, концентрація азоту і фосфору. Тоді залежність 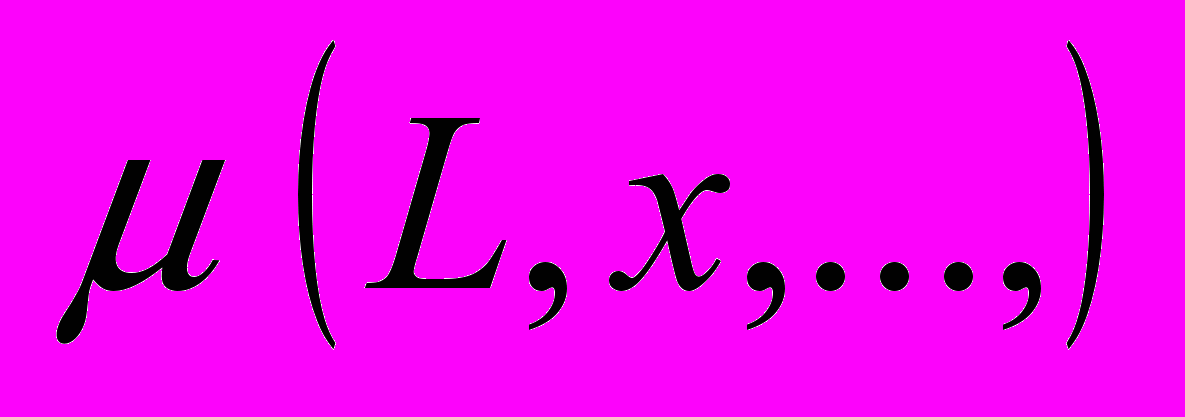від названих параметрів можна представити у такій загальній формі:
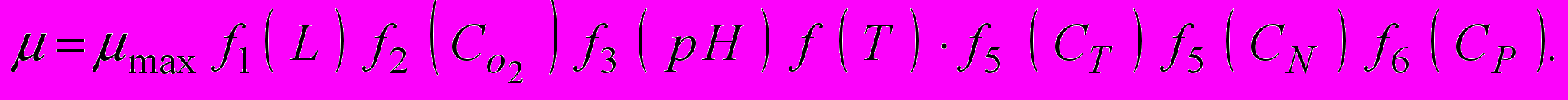, (3)де f2 (...)...f6 (...) - функціональні залежності
від концентрації забруднюючих речовин ( L ), концентрації розчиненого у воді кисню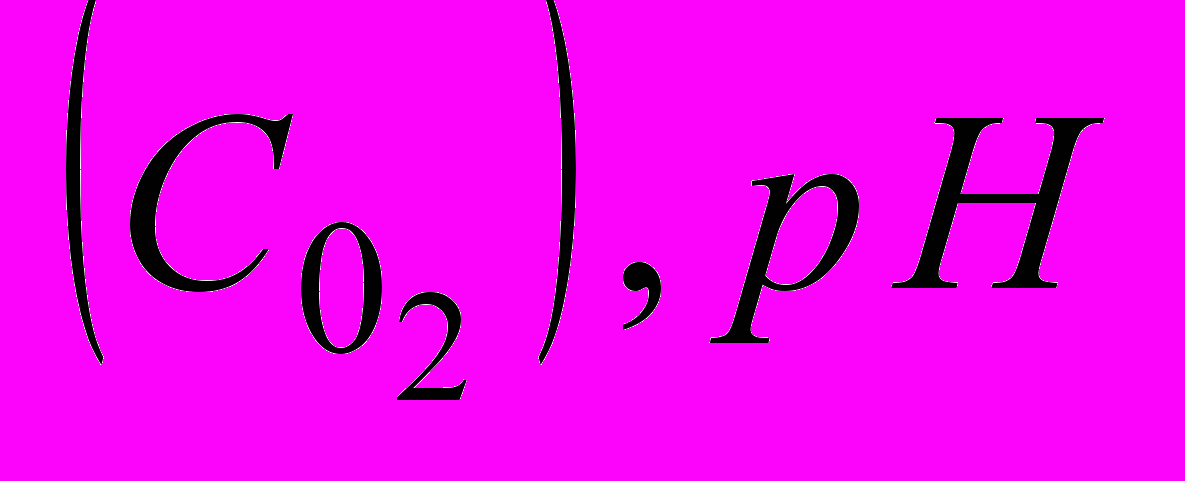 
, температури (T), концентрації токсичних речовин (CT), азоту (CN) і фосфору (Cp).Залежність
від окремих параметрів рядом авторів розглядаються [4-6], але в загальному вигляді, така залежність у відомій нам науково-технічний літературі не зустрічалася. ЇЇ можна отримати математичними засобами за умов, коли відомі частинні залежності. Такі частинні залежності за своєю структурою, яка є аналогічною загальновідомому рівнянню Моно.Кінетика росту мікроорганізмів у біоокислювачах в залежності від органічних забруднюючих речовин L , представляє собою рівняння Моно:
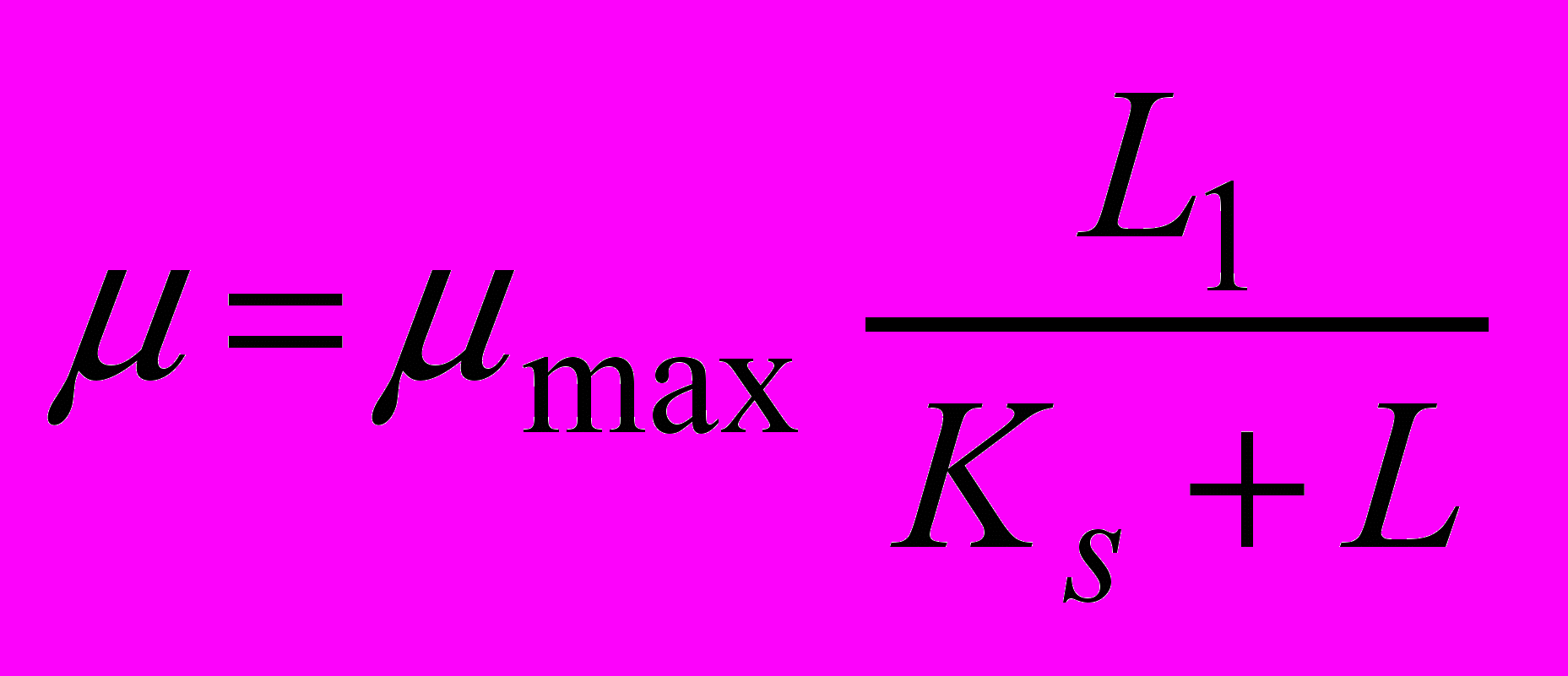, (4)де
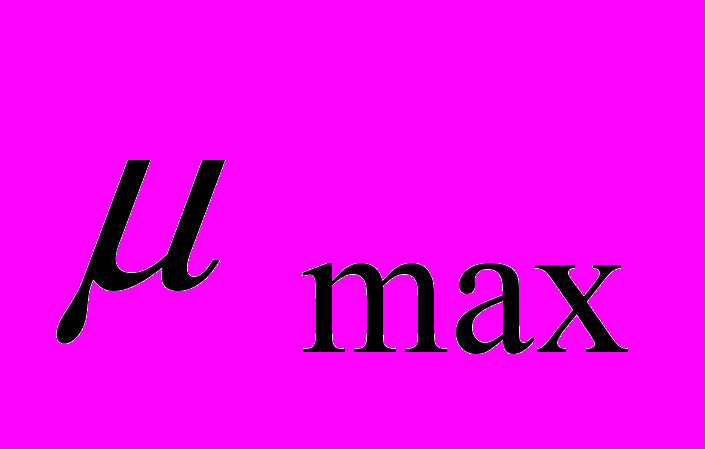- максимальна питома швидкість росту 
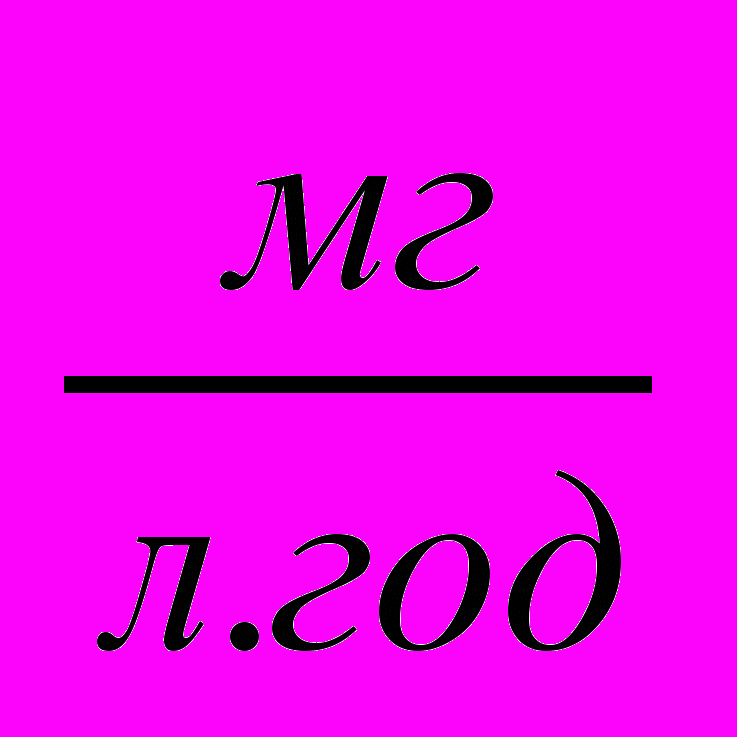; L - концентрація забруднюючих речовин (субстрату) в біоокислювачі, мг/л; Ks - константа насичення за субстратом, мг/л.Вплив температури на кінетику росту мікроорганізмів можна описати відомим рівнянням Вант-Гофора:
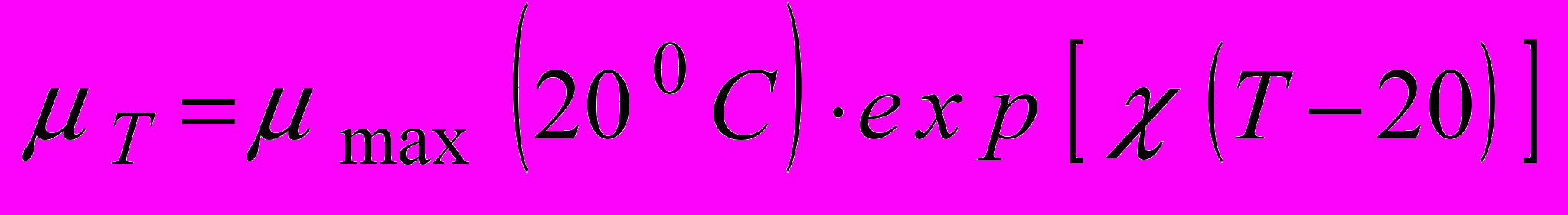, (5)де
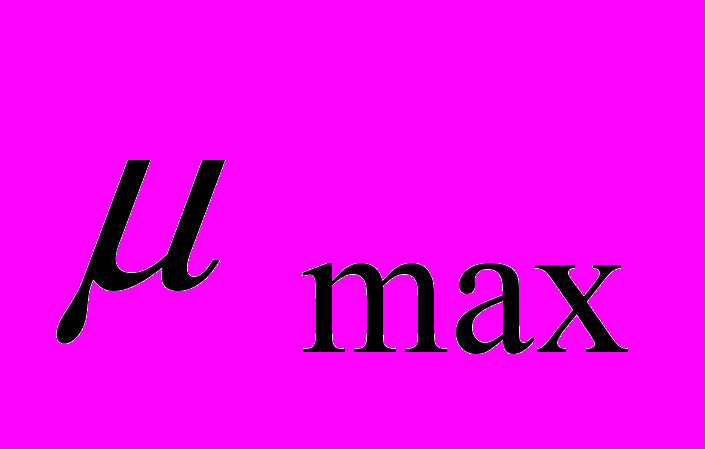(200С) – максимальна питома швидкість росту мікроорганізмів при температурі 200С, ; 
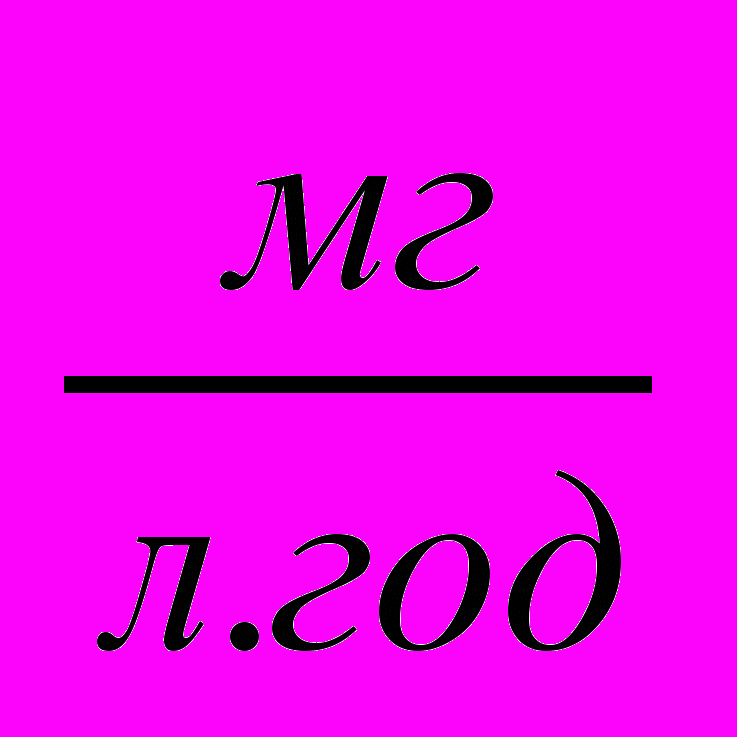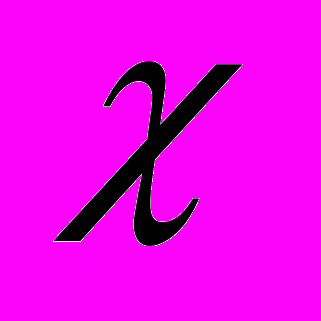- температурна константа для 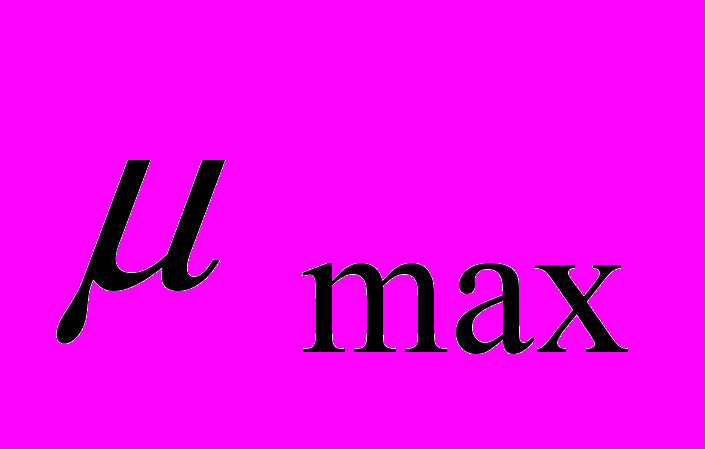град -1. T– температура, 0С.Залежність швидкості аеробного процесу від концентрації кисню
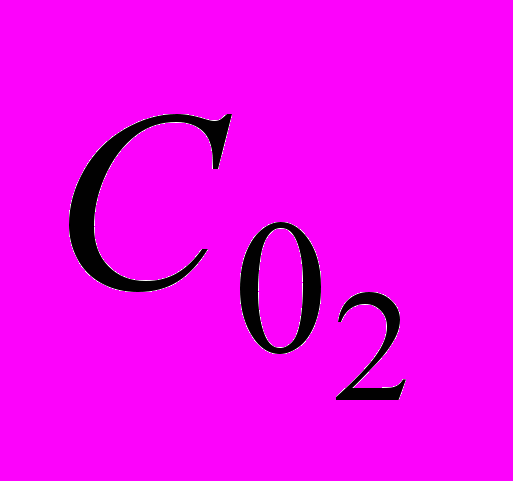можна описати рівнянням, аналогічним рівнянню Моно.
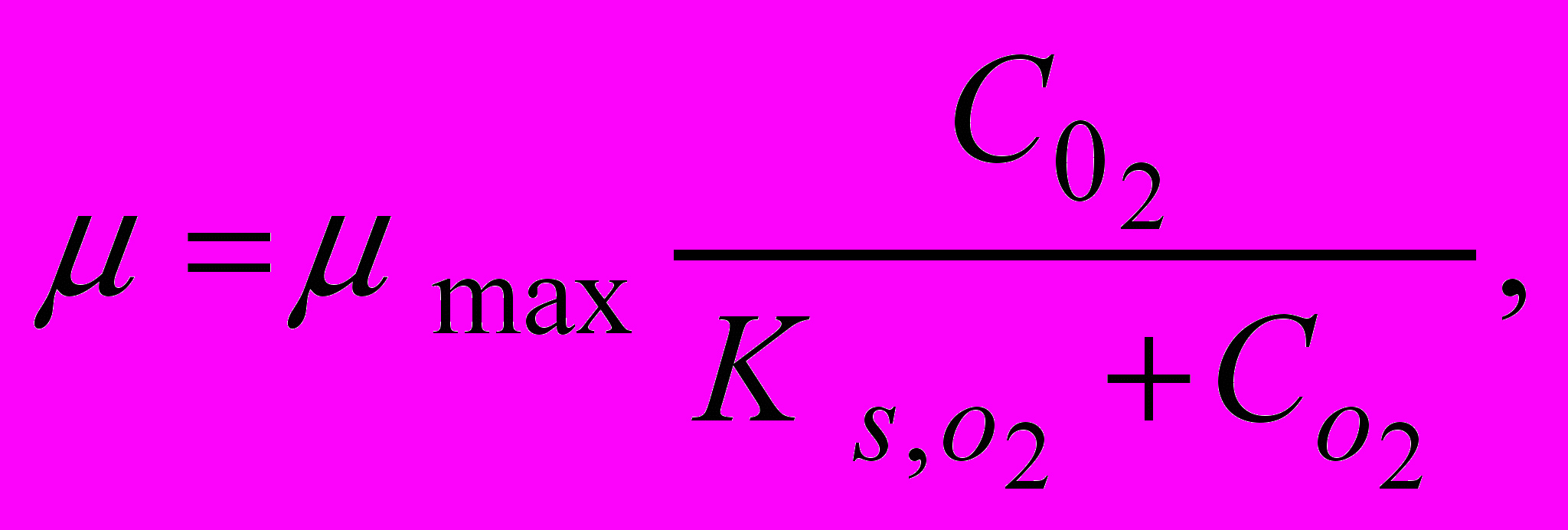(6)де
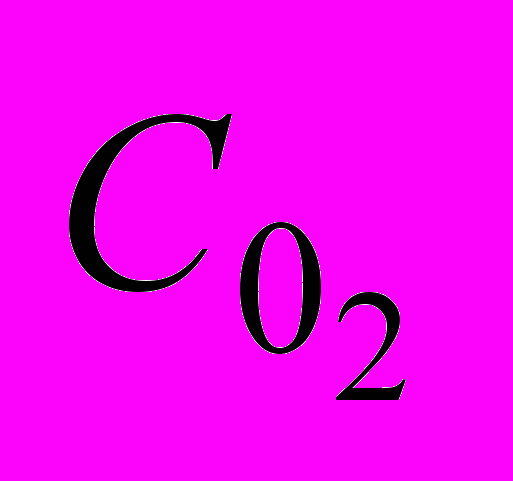- концентрація кисню у біоокислювача, мг/л; 
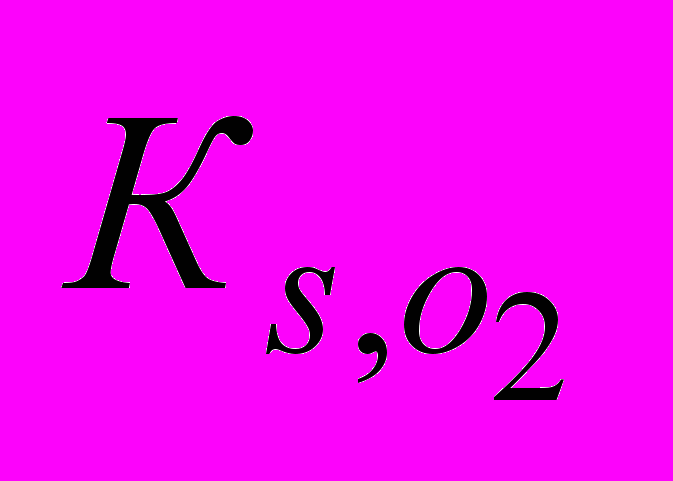- константа насичення за киснем, мг/л.Об‘єднуючи рівняння (4) і (6) отримуємо подвійне рівняння Моно:
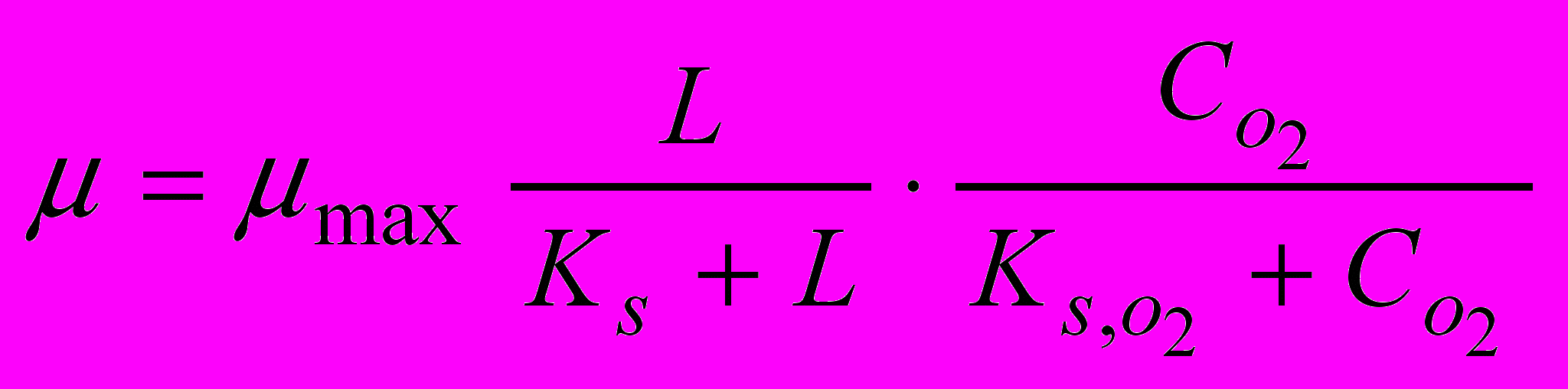, (7)У дещо в іншій формі аналогічне рівняння було отримано І.В. Скірдовим і інші. (ВОДГЕО) [7]:
Константа насичення
залежить від розміру пластівців активного мулу (товщини біоплівки) і від температури, оскільки температура обумовлює обмеження на дифузію кисню всередину пластівців активного мулу (біоплівки).Кінетична залежность
від pH описується рівнянням [6]: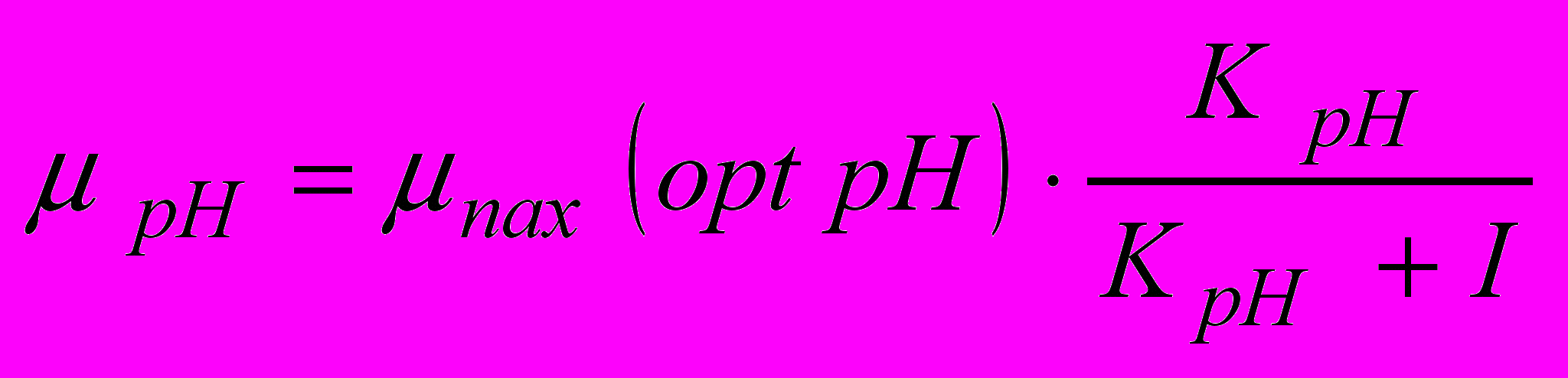
, (8)де KpH - pH - константа;
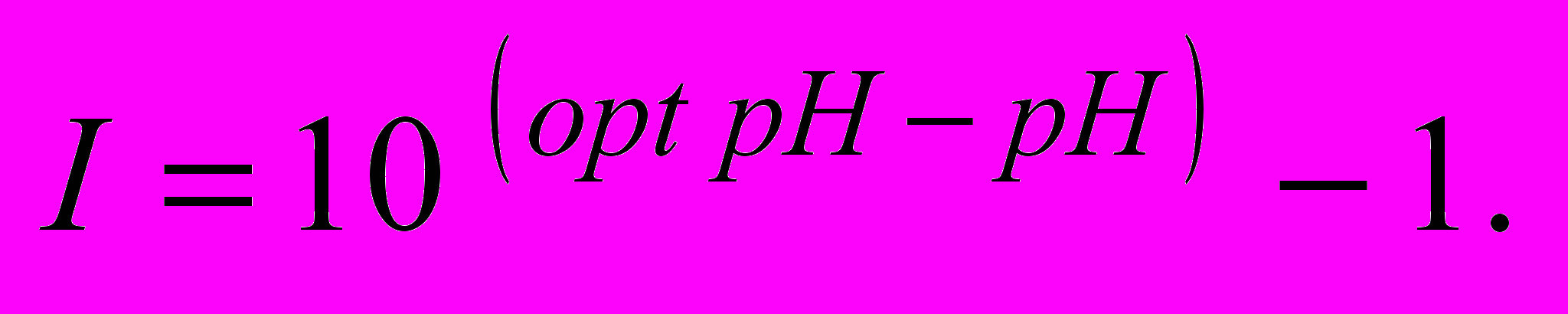
Максимальна питома швидкість росту мікроорганізмів
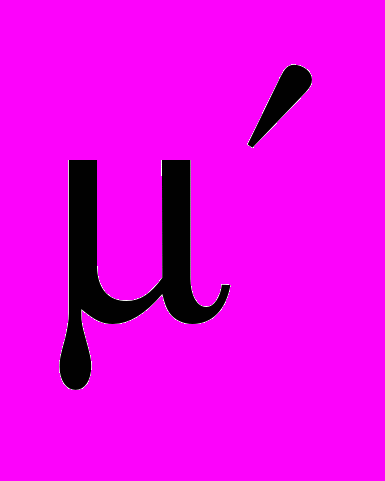у присутності токсичних речовин (інгібіторів процесу) описується рівнянням:
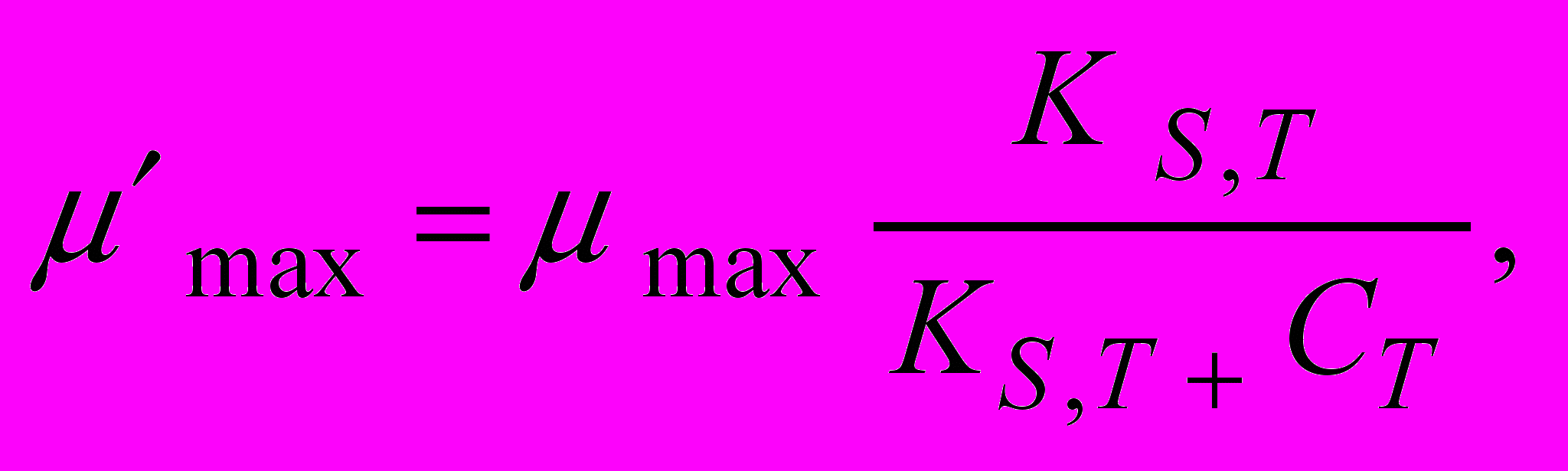(9)де
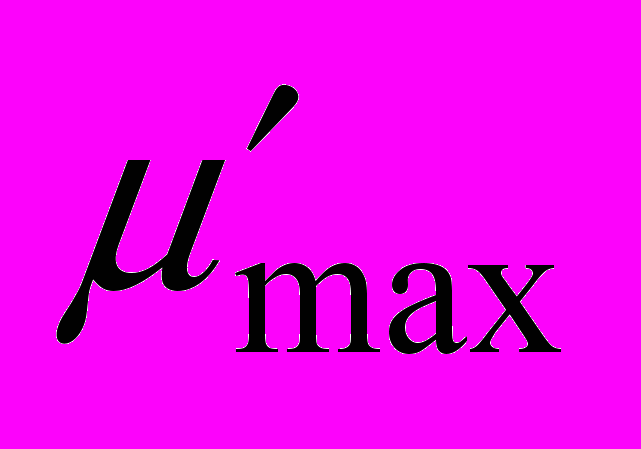- максимальна питома швидкість росту мікроорганізмів у присутності токсичних речовин (інгібіторів) ; 
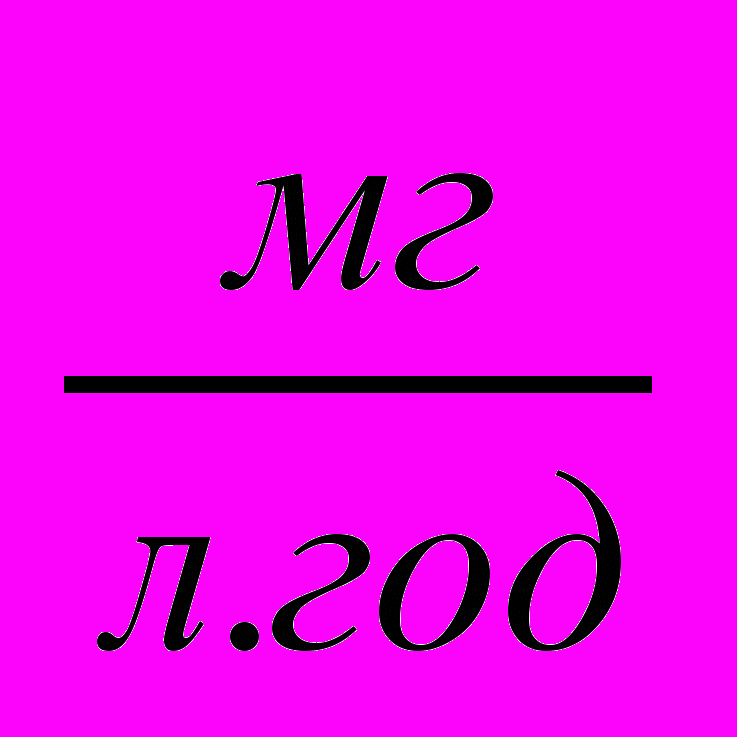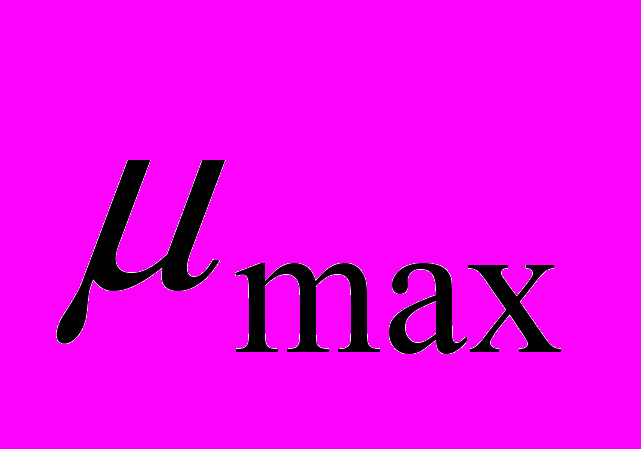- те ж саме, без інгібітора, 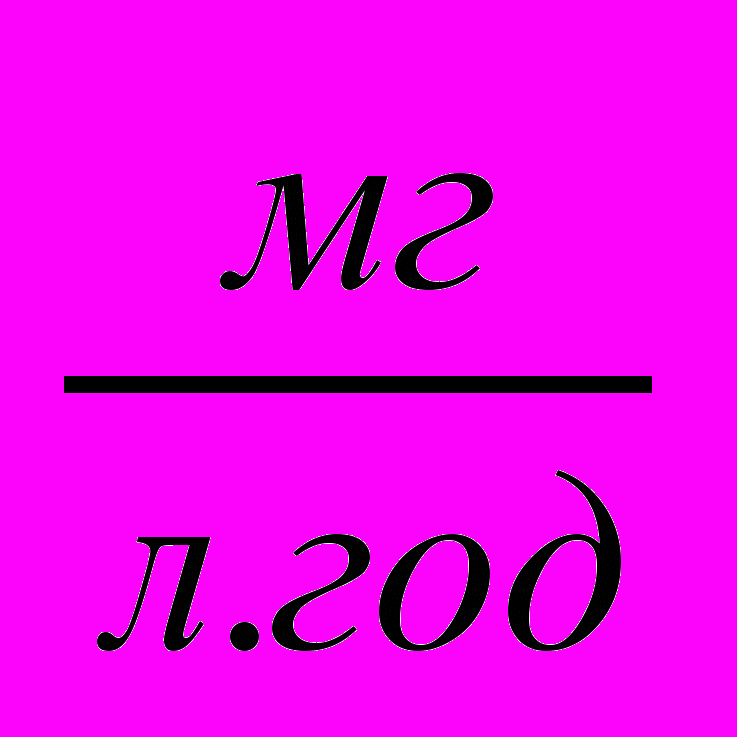; KS,T - константа інгибування, мг/л; CT - концентрація інгібітора, мг/л;Кінетика росту мікроорганізмів у присутності азоту і фосфору в біоокислювачах при аеробному очищенні стічних вод можна описати подвійним рівнянням Моно [6] .
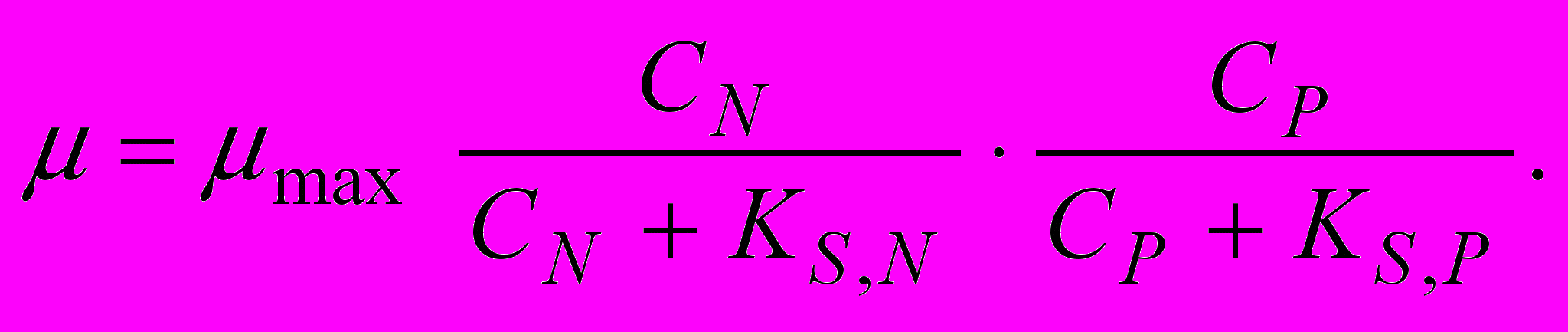(10)де CN - концентрація азоту, мг/л; CP - концентрація фосфору, мг/л; KS,N - константа насичення по азоту, мг/л ; KS,P - константа насичення по фосфору, мг/л.
Для використання рівнянь (4) – (10) як “робочих” формул при проектуванні біоокислювачів для очищення міських стічних вод можна використати такі дані [6]:
Таблиця
Значення констант в рівняннях (4) – (10), при аеробному очищенні міських стічних вод [6].
| Характеристика процесу | Позначення | Розмірність | Величина |
| Максимальна питома швидкість росту | 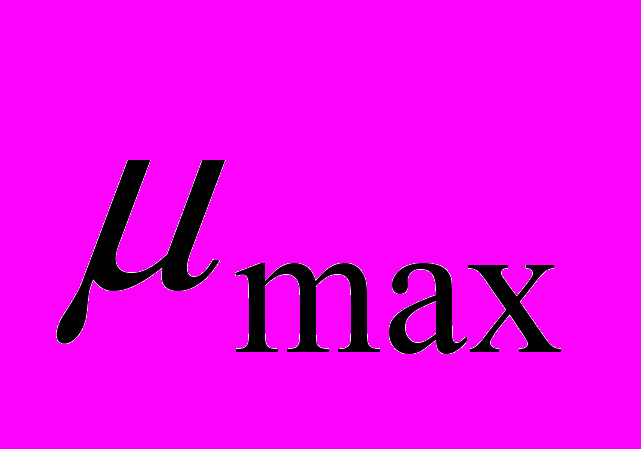| доб-1 | 4 - 8 |
| Константа насичен-ня по субстрату | KL,ХПК | г ХПК/м3 | 5 - 30 |
| Константа насичен-ня по кисню | 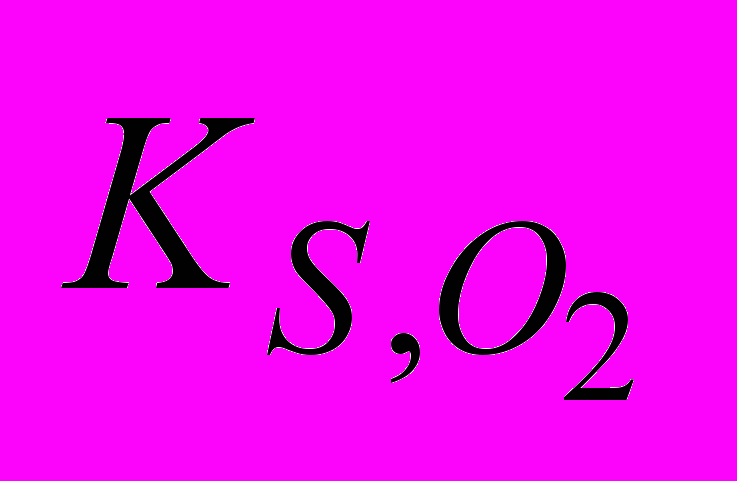 | г О2/м3 | 0,5 - 1 |
| Максимальний коефіцієнт приросту біомаси | Y | г ХПК/г ХПК | 0,5 - 0 ,7 |
| Температурна константа | 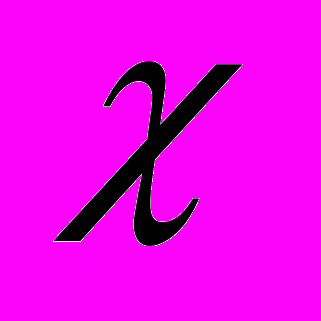| град-1 | 0,06 – 0.1 |
| pH - константа | KpH | - | 150-250 |
| Константа насичення по азоту | KS,N | г N/м3 | 0,1 - 0,5 |
| Константа насичення по фосфору | KS,P | г P/м3 | 0,1 – 0,2 |
Розглянемо математичну модель (1), яка відображає біологічний процес аеробного очищення стічних вод в біоокислювачах ідеального змішування, основи для дослідження стійкості процесу біологічного очищення стічних вод у біоокислювачах.
Умови ідеального змішування реалізуються переважно у біоокислювачах невеликого об‘єму із інтенсивним механічним змішуванням середовища, яке виключає утворення застійних зон або байпасних потоків.
Диференціальні рівняння, що входять у систему рівнянь (1, 2), представляють собою баланс речовин для Х і L і визначають той факт, що стан біоокислювача повністю описується концентраціями забруднюючих речовин L і мікроорганізмів Х.
Визначення можливих умов стаціонарних станів, стійкість цих стаціонарних станів до малих збурень системи (тобто до малих змін величин Q або Lo) а також при яких початкових умовах система приходить до розрахункового стаціонарного режиму, а при яких – ні, залежить від використання конкретних кінетичних залежностей для досліджуванного процесу очищення, тобто від рівнянь (3-10).
Крім емпіричного підходу щодо побудови кінетичних моделей процесів очищення стічних вод у біоокислювачах, розвиток математичного моделювання здійснюються за трьома напрямками для опису кінетики процесу біологічного очищення стічних вод.
Перший напрямок зв‘язаний із використанням для опису дослідних даних простих моделей, аналогічних рівнянням кінетики нульового, першого або n-го порядків. На цій основі розроблені відомі у теорії і практиці біологічного очищення моделі Гаррета, Сойєра і Екенфельдера [4]. Згідно даним моделям процес росту мікроорганізмів має дві характерні фази: у першій ріст клітин не залежить від концентрації забруднюючих речовин (субстратів), оскільки їх величина перевищує лімітуюче значення, у другій фазі швидкість росту клітин активного мулу знижується по мірі утилізації субстрату. Ця система рівнянь має вигляд:
- перша фаза, (11)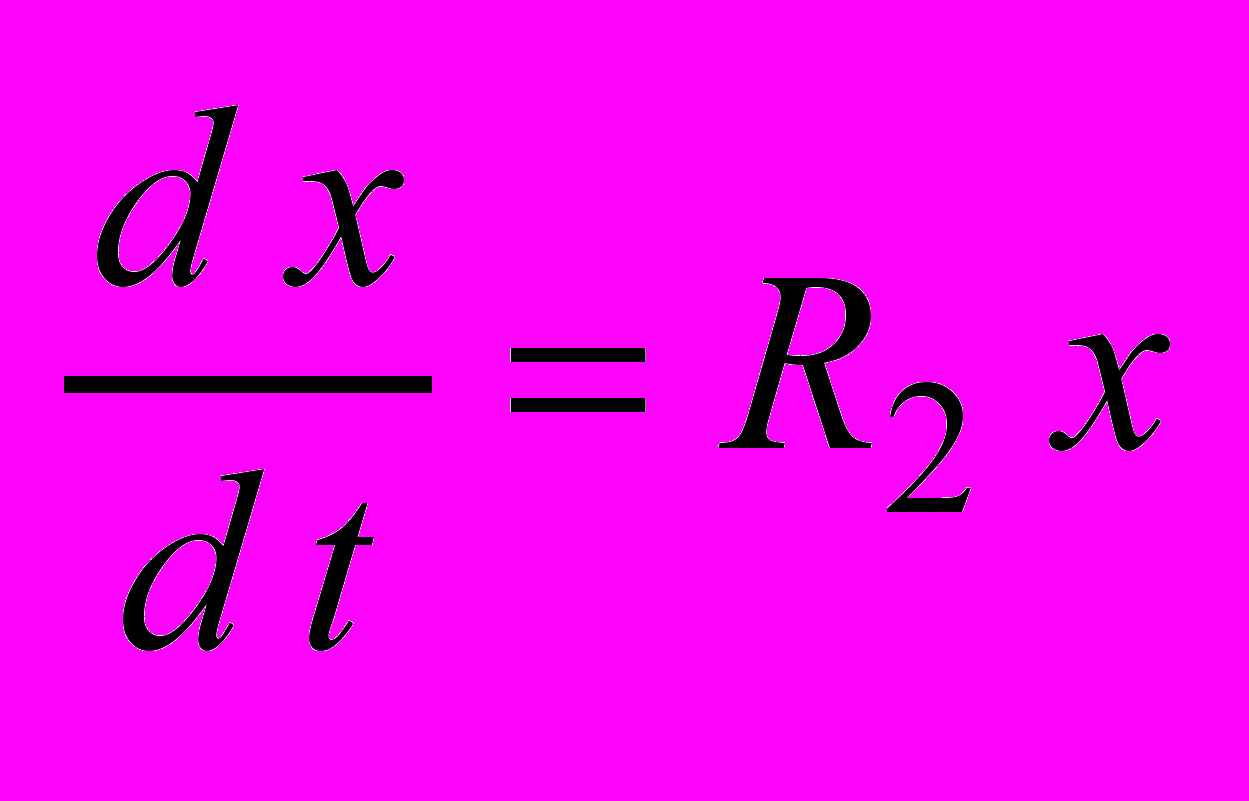
- друга фаза, (12)Другий напрямок моделювання кінетики біологічного очищення стічних вод зв‘язаний із використанням рівнянь ферментативних реакцій: із урахуванням лімітуючого впливу субстрата (рівняння Моно); із урахуванням лімітуючого і інгибуючого впливу субстрата (рівняння Ієрусалимського); із урахуванням інгибуючого впливу дії субстрата (рівняння Халдейна); із урахуванням загибелі мікроорганізмів-самоокислювання клітин (модель Герберта).
Третій напрямок оснований на врахуванні гетерогенного видового складу мікроорганізмів, трофічних зв‘язків біоценозу активного мулу. При цьому використовується трофічна схема зв‘язків виду: органічні забруднення (субстрат) – бактерії активного мулу (біомаса) – простіші (хижаки). Цей напрямок представляється моделлю Кенела.
Ставиться задача як будуть змінюватися можливі умови стаціонарних станів, стійкість цих стаціонарних станів до малих збурень (тобто до малих змін величин Q і L ), до початкових умов при яких біоокислювач приходить до розрахункового стаціонарного режиму, а при яких ні.
Використовуючи залежність питомої швидкості росту мікроорганізмів
від концентрації забруднюючих речовин L (модель Моно) на основі рівнянь (1) і (2) отримаємо систему звичайних нелінійних диференціальних рівнянь: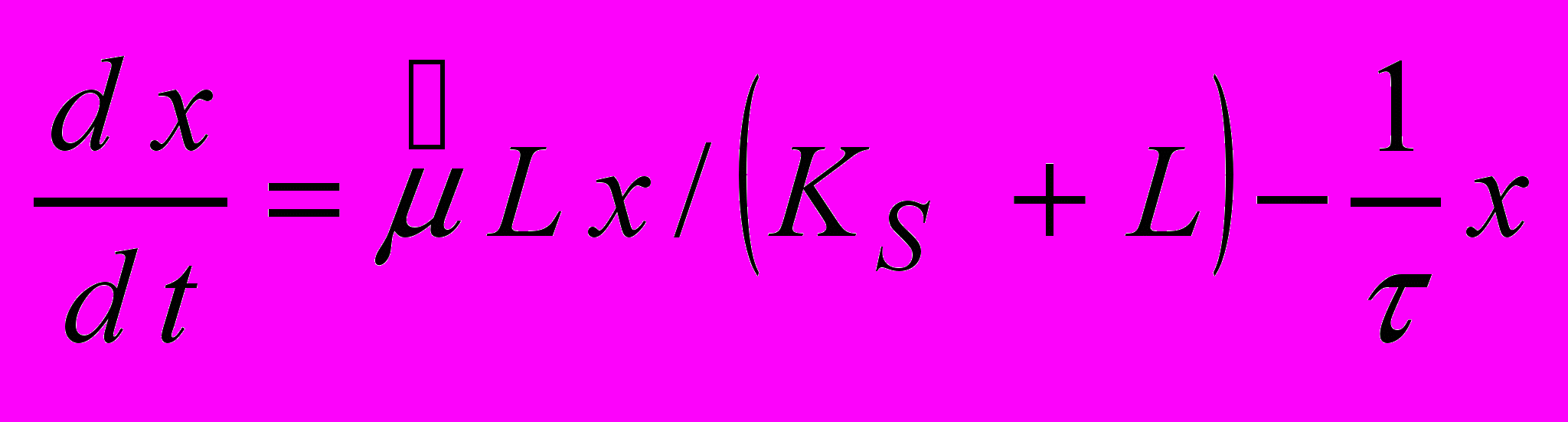
, (13)
(14)де
- максиамальна питома швидкість росту мікроорганізмів, ;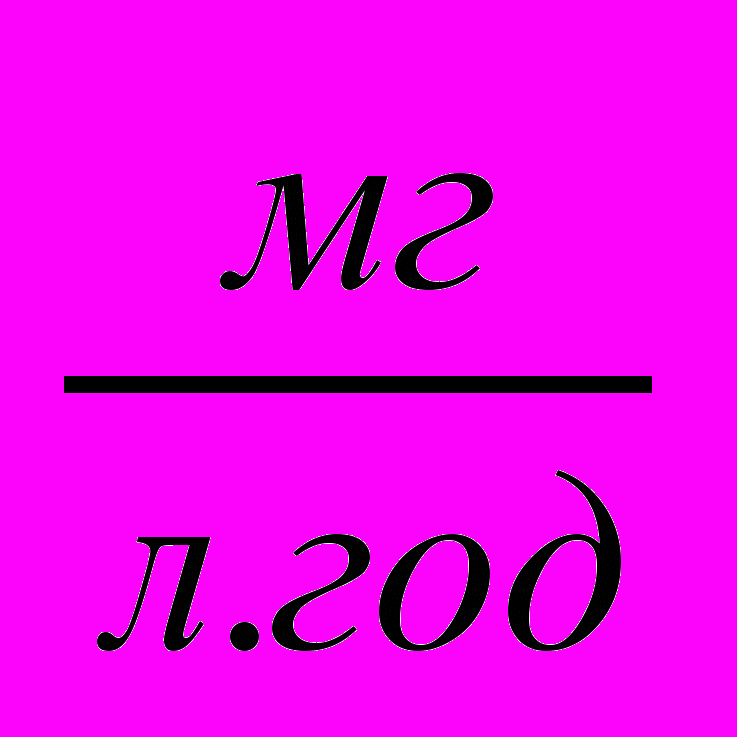 
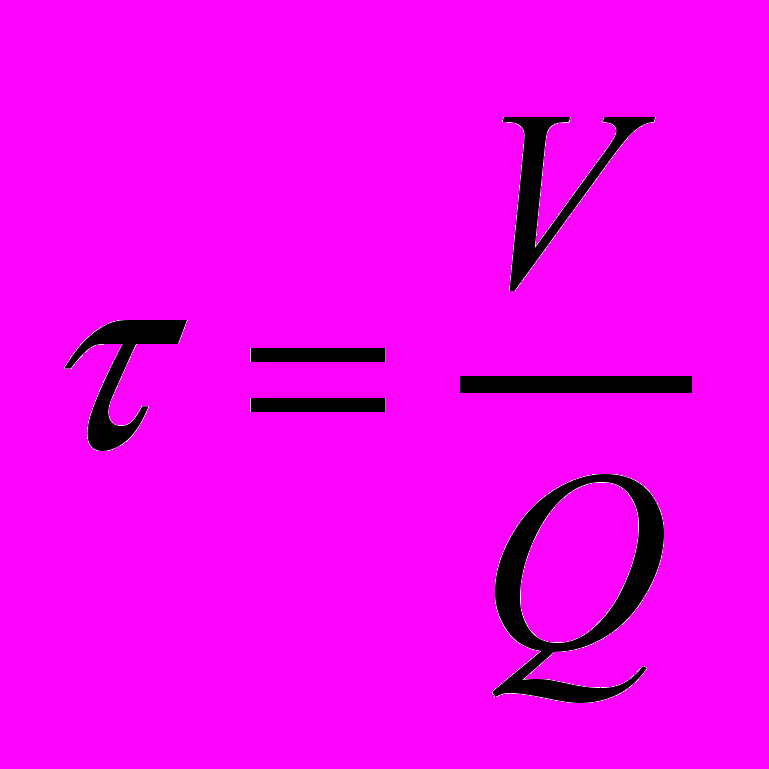- середній час перебування (або час затримки у біоокислювачі), год.Аналізуючи представлену математичну модель, яка моделює процес біологічного очищення стічних вод в біоокислювачах, можна відзначити, що таке моделювання здійснена за концепцією “чорного ящика”. Тут входи (концентрація L0 і Х0); виходи (L і Х) зв‘язані деякою математичною операцією, яка моделює реакцію системи. Крім того дана математична модель не враховує розподіл часу перебування елементів стічної води у біоокислювачі і є нелінійною.
Незважаючи на вказані зауваження, дана математична модель може дати багато інформації, не роз‘язуючи її чисельно. Це можна здійснити використовувати теорію якісного рішення диференціальних рівнянь [8].
Стаціонарний стан у біоокислювачі буде мати місце тоді, коли похідні
і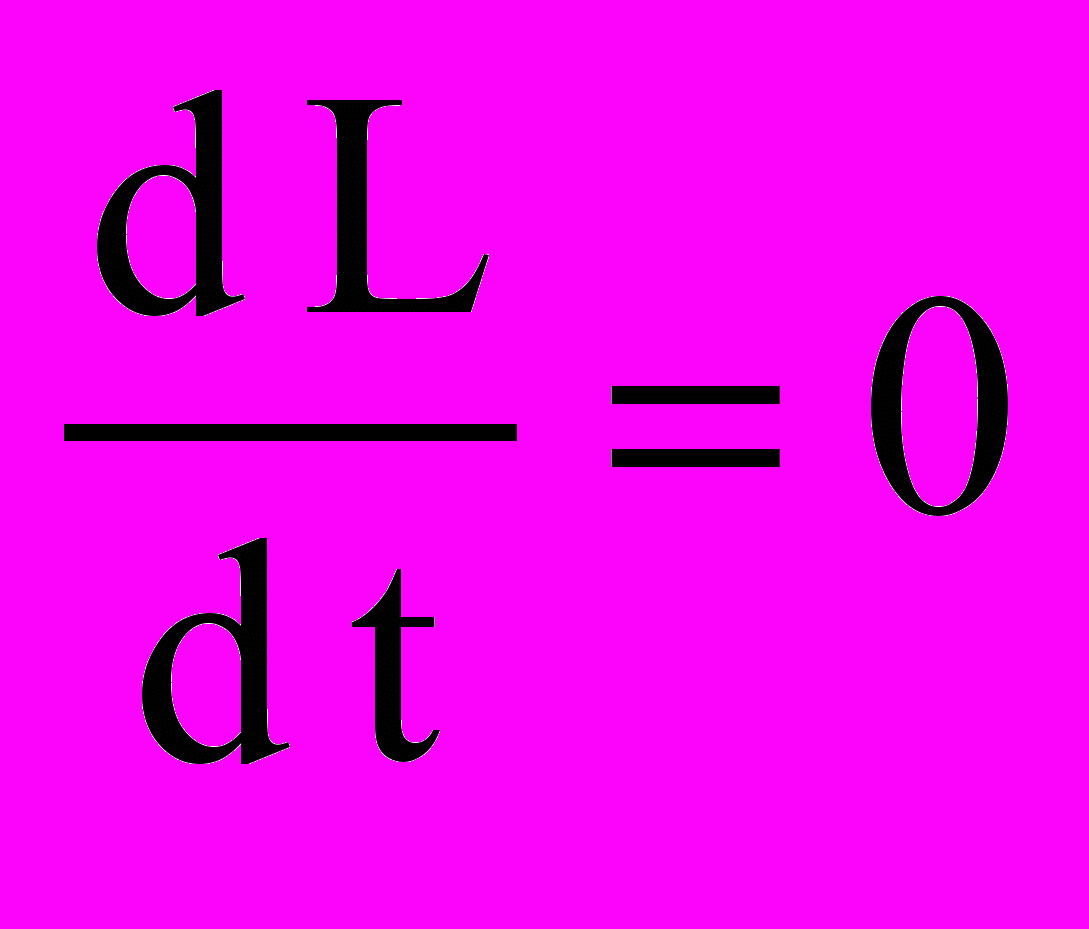 
. Отже, нам потрібно знайти такі значення Х* і L* , для яких праві частини рівнянь математичної моделі (13,14) будуть одночасно перетворюватися в нуль. Ця система має два можливих рішення, а отже, і два стаціонарних стани:
(15)
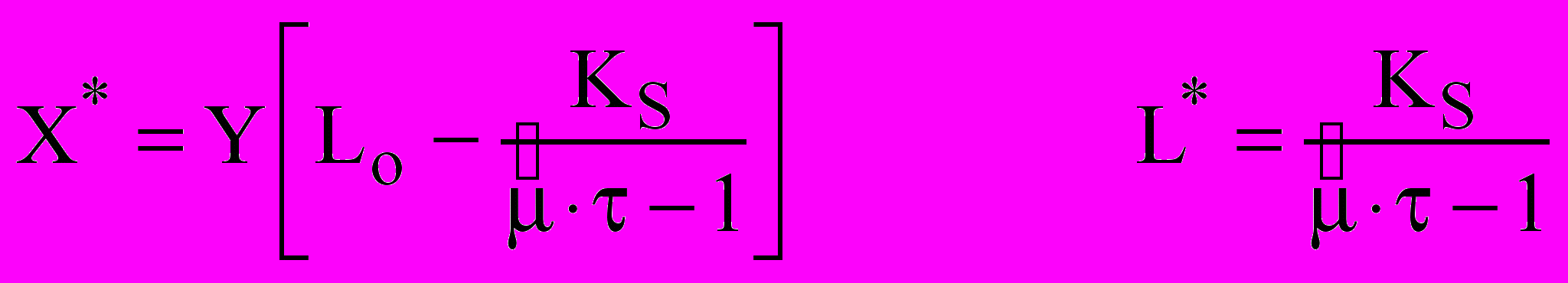(16)Перше рішення відповідає вимиванню всіх мікроорганізмів, тому не має фізичного змісту, друге - є єдиним, якому відповідає бажаний (можливий) стаціонарний режим. Тому першим кроком є перевірка можливості фізичної реалізації цього режиму (оскільки цей режим має смисл тільки при позитивних значеннях Х* і L* ). Далі ми можемо зробити спробу вияснити стійкість цього режиму, а отже, і здійснити його на практиці.
Із припущення, що всі параметри є позитивними, то позитивність L* означає, що
, а позитивність Х* - що 
. Звідси отримаємо верхню границю для витрат стічної води Q при фіксованих значеннях V і Lo , а саме: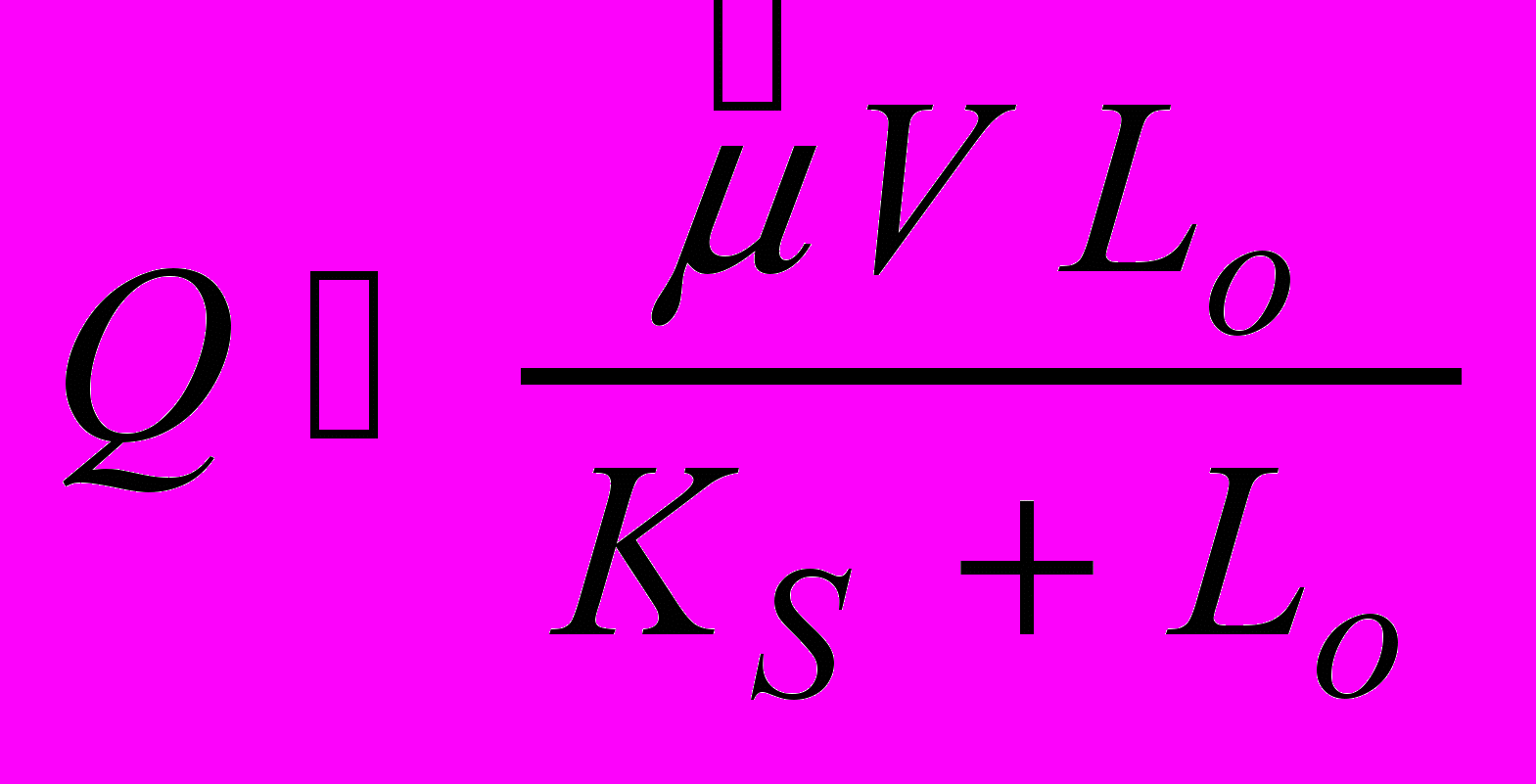
. (17)З іншої сторони, можна вважати Q фіксованим і визначити граничне значення концентрації забруднюючих речовин L0, яка необхідна для підтримання популяції мікроорганізмів у біоокислювачі. Тоді ми отримаємо
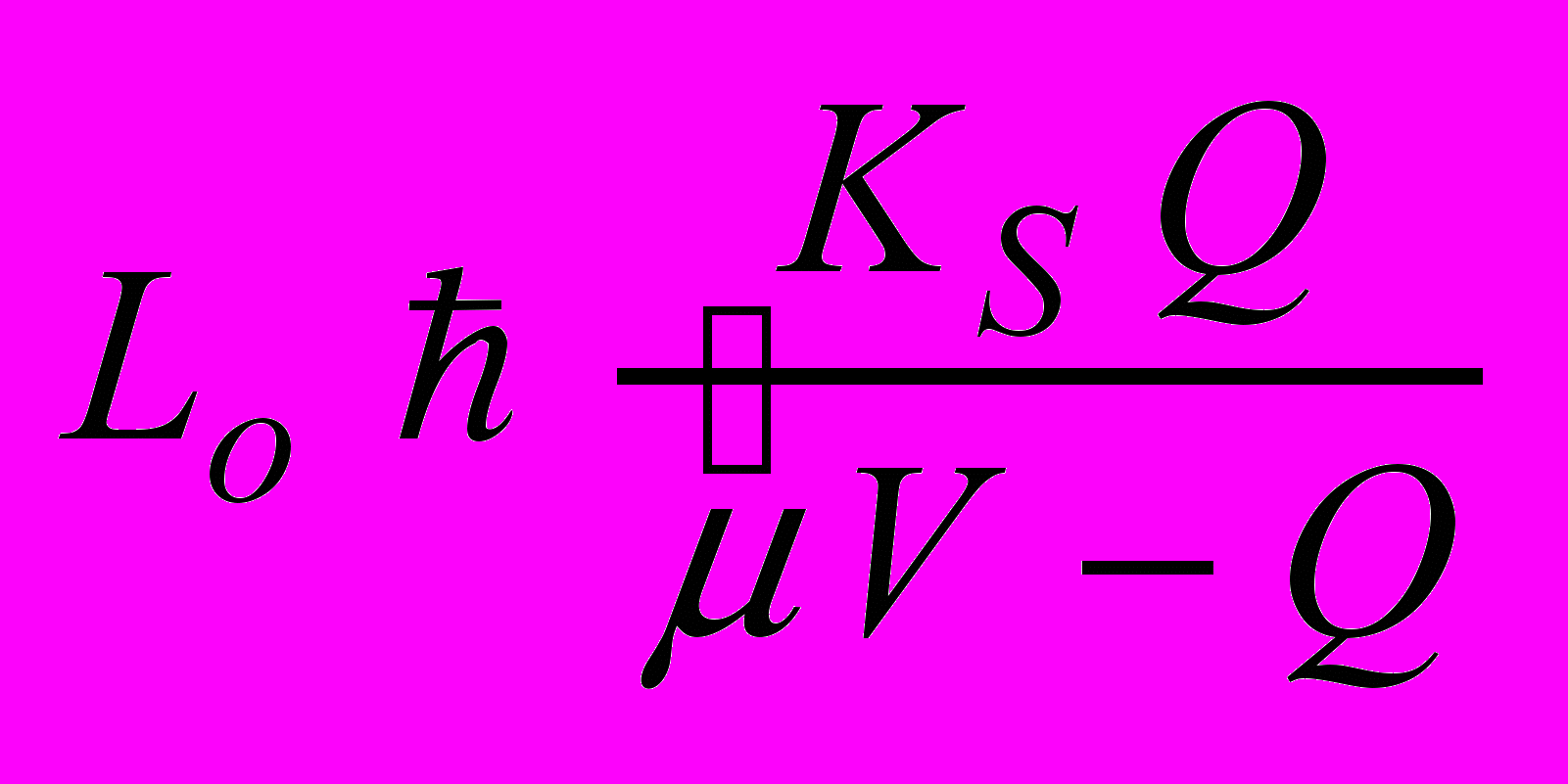(18)Тут передбачається, що V,
, KS і Y - є фіксованими величинами і лише тільки Q і Lo є змінними параметрами, які можуть або змінювати самі, або бути зміненими автоматичними засобами.Зрозуміло, що якщо прийняти інші припущення, то рівняння можуть бути перетворені до необхідного виду.
Для визначення локальної стійкості бажаного режиму мінімізуємо систему (математичну модель) в околі стаціонарної точки і за допомогою стандартних методів отримаємо необхідну і достатню умову стійкості щодо малих збурень:
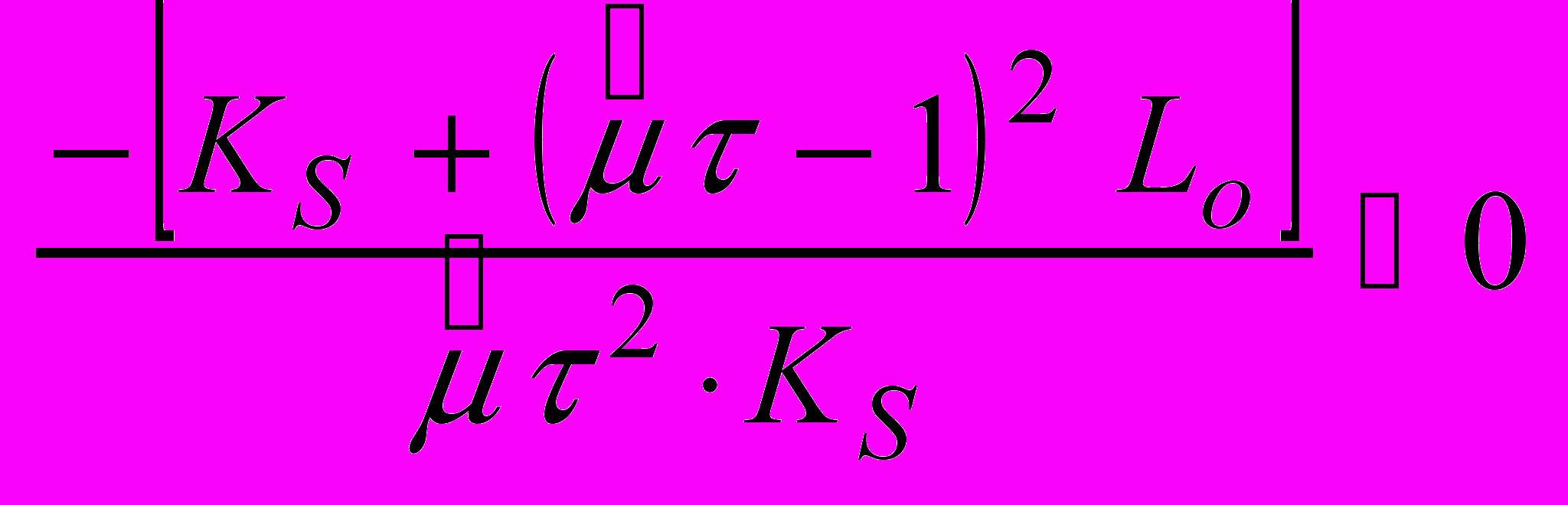(19) 
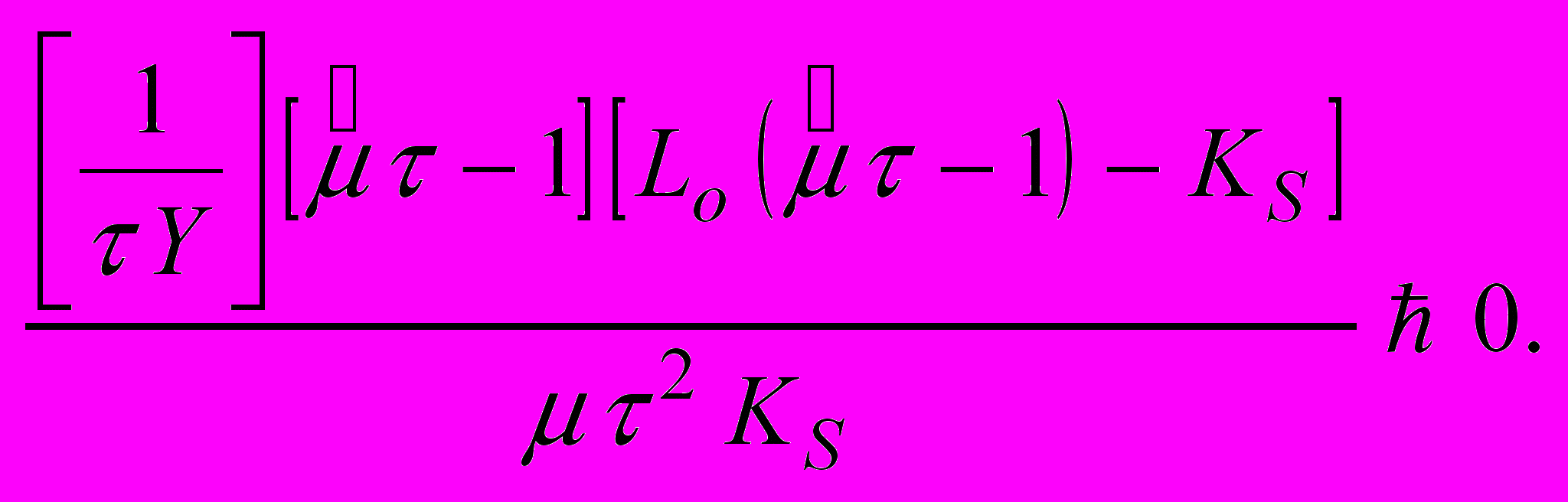(20)Аналіз нервностей (19) і (20) показує, що вони задовільняються, якщо
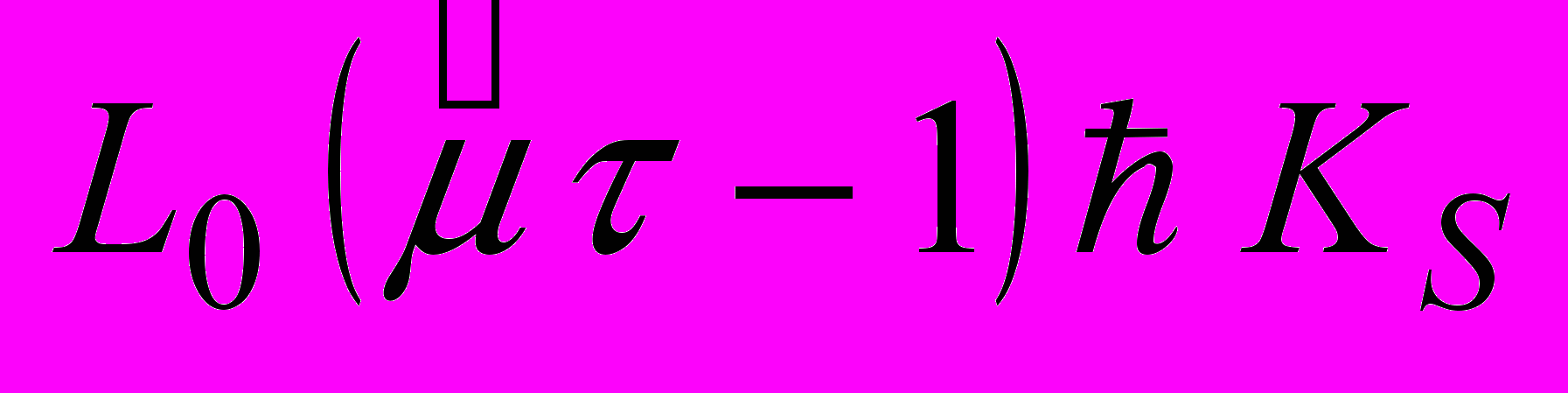, тобто якщо виконується вже сформульована умова фізичної здійсненості стаціонарного режиму. Таким чином, дана модель передбачаєстійксть стаціонарного стану для всіх значень параметрів, які дають любий стаціонарний стан, крім вимивання.Необхідно відмітити, що при аналізі ми користувалися рівняннями, лінеаризованими в околі стаціонарних станів, тому висновки є дійсними тільки для малих відхилень від цих станів. Формально ми розглядали малі відхилення величин L і Х, однак розповсюдження наших висновків на малі зміни інших параметрів – не є важкою задачею. Ми розглядали квазістаціонарний процес зміни цих параметрів, тому що зміна, скажимо, величина Lo лише зсуває стаціонарний стан, Значення Х* і L* старого стаціонарного стану тепер є збуреними значеннями для нового стаціонарного стану.
Методи дослідження стійкості стосовно великих відхилень є більш складними, тому що вони зв‘язані із ідеями фазової площини [9,10].
Ймовірно, великий інтерес як для інженера, так і для дослідника були б ідеї стосовно змінення моделі або модифікації процесу, які випливають із вище проведеного аналізу. Наприклад, до ідеї щодо регенерації мікроорганізмів і повернення їх у біоокислювач для зменшення втрат, зв‘язаних із вимиванням їх із системи. Другим використанням математичного моделювання до процесу проектування біоокислювачів могло б стати автоматичне регулювання системи. Регулювання бажано для того. щоб гарантувати, що змінення Q і L0 на вході біоокислювача не викличуть можливого катастрофічного впливу на функціонування системи.
Цікавим є дослідження стійкості процесу біологічного очищення стічних вод у біоокислювачах, при врахуванні ефекту інгибування росту мікроорганізмів і при високих концентраціях субстрату. Для цього скористаємося моделлю кінетики, яка запропонована Ендрюсом [2]:
(21) де K1 - визначає концентрацію сустрата, при якій починає виявлятися інгибування. У граничному випадку при K→ ∞ рівняння переходить у рівняння Моно [4].
Ввівши у рівняння (13) і (14) рівняння (21) і дослідивши їх на стійкість отримаємо наступні висновки.
Перший висновок – існує стійкий стаціонарний стан, який описується такими співвідношенням:
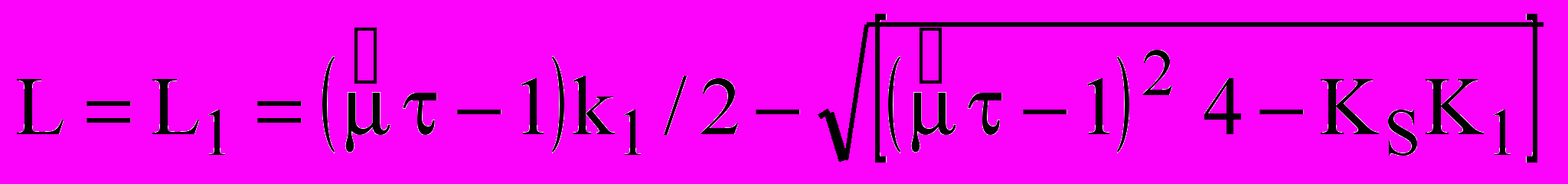(22) 
за умов, що
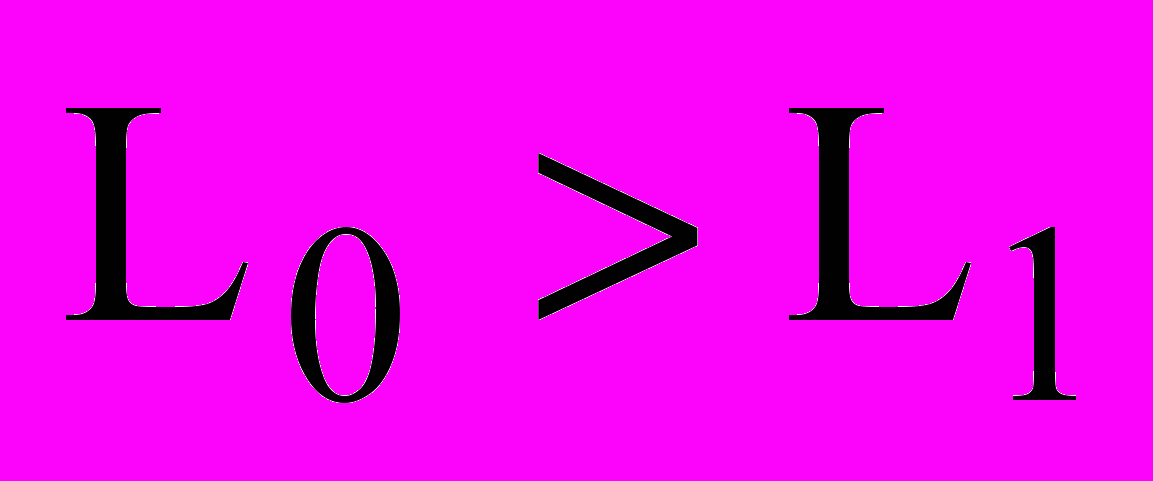(23) 
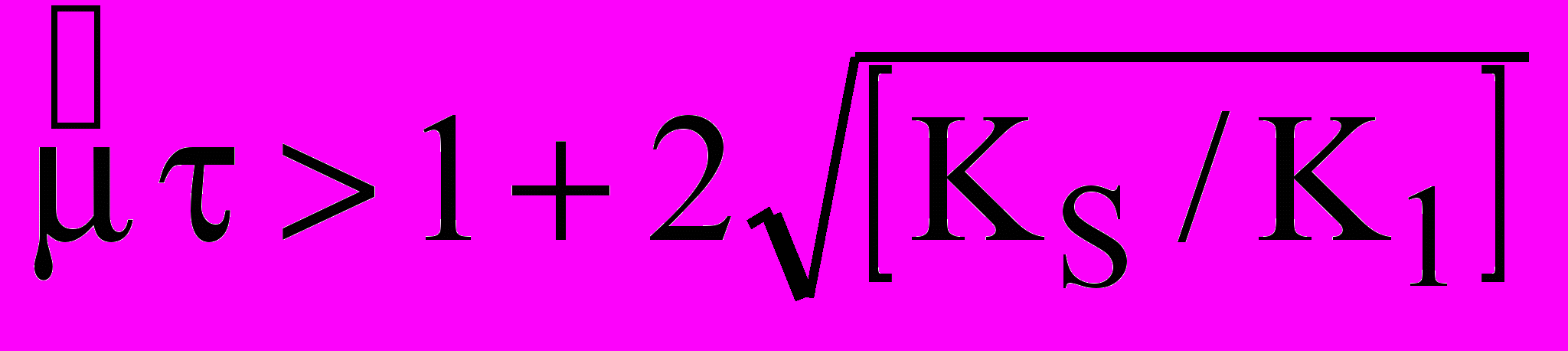(24) Крім того є ще один нестійкий стаціонарний стан
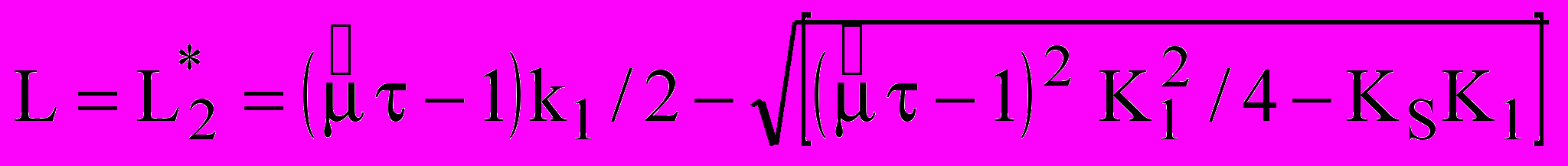(25)Висновки: При проектуванні та розрахунку біоокислювачів для очищення стічних вод, доцільно побудувати області стійкості режимів роботи біоокислювачів і знайти сукупні значення параметрів при яких робота біоокислювачів є не тільки стійкою, але й забезпечується необхідним запасом стійкості.
Проблема стійкості очисних споруд взагалі і очищення стічних вод зокрема має технічні, фізико-хімічні і біохімічні аспекти.
Причини потенційної нестійкості очисних споруд умовно можна розділити на зовнішні і внутрішні збурення. Зовнішні збурення - температура, рН, швидкості протікання стічних вод. Внутрішні – це генетична нестійкість (нестабільність) мікроорганізмів, їх автоселекція.
Кінетика – це основа розв’язку задач по розрахунку оптимальних умов ведення процесу, умов масштабного переходу. Крім того, при визначені стійкості біохімічних процесів очищення стічних вод, мають значення три головні системи, які забезпечують мікробіальну кінетику високоенергетичними сполуками, а саме: система Емдена-Мейєрглфа-Пірсона; цикл Крепса і ланцюг фосфарування. На співвідношення шляхів метаболізму, обумовлених цими системами (на різних стадіях розвитку мікроорганізмів) впливає кисень.
1. Сівак В.М. Міждисциплінарні підходи в методології математичного моделювання систем водоочищення// Вісник НУВГП. – 2002. – Вип.4(23). –с.178-183. 2. Сівак В.М. Побудова концептуальної моделі водоочищення на основі загальної теорії систем// Вісник НУВГП. – 2007. – Вип.1(37). –с.181-188. 3. Сівак В.М. Методологічні аспекти визначення дифузійної і кінетичної області біохімічних процесів очищення стічних вод // Гідромеліорація та гідротехнічне будівництво. – Збірник неук.праць. НУВГП – Вип.31. –с.402-408. 4. Вавилин В.А., Васильев В.Б. Математическое моделирование процессов биологической очистки сточных вод активным илом. – М.: Гаука, 1978.-118с. 5. Andrews I.F. Kinetic models of biological waste treatment processes-Biotechnol.and Bioeng.Symp.N02,1971, p.5. 6. Хекце М. Очистка сточных вод: Пер с англ. /Хекце М., Армоэс П., Ля-Кур-Янсек И., Арван Э.-: Мир, 2004.-С.111. 7. Скірдов И.В., Шведов В.Н., Морозова К.М. и др. Применение технического кислорода для очистки концентрированных сточных вод // Труды института "ВОДГЕО". Научные исследования в области механической и беологической очистки промышленных сточных вод.–М.:Изд.во. "2ВОДГЕОя. – С.134-145. 8. Демидович Б.П. Лекции по математической теории устойчивости. –М.: Наука, 1967, - 475 с. 9. Ляпунов А.М. Общая задача об устойчивости движения. – М.-Л.:Гостехиздат, 1950,-472 с. 10. О кривых, определяемых дифференциальными уравнениями . – М.-Л.:Гостехиздат, 1947, - 392 с.