Geum.ru

Выделяют пять общих требований к тестам контроля знаний: валидность; определенность (общепонятность)

Вид материалаДокументы

Содержание


Метод наибольшего правдоподобия
Точность исходных измерений
Проверка адекватности модели Раша с помощью χ2 - критерия Пирсона
Проверка равномерности распределения дистракторов и эффективности их работы
Влияние числа дистракторов на точность оценивания уровня знаний
Дифференцирующая (разрешающая) способность теста
Оценка различающей способности тестовых заданий с помощью точечно-бисериального коэффициента
Шкалы оценок в диагностическом тестировании
Шкала первичных баллов
Дробная и политомическая оценка результатов тестирования
Нормативная шкала
Метрическая шкала
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11

Метод наибольшего правдоподобия



Данный метод основывается на использовании функции правдоподобия [6,8]. В применении к тестированию функция правдоподобия L дискретной случайной величины балла aij будет функцией аргументов и , представляющей произведение вероятностей для всевозможных значений i и j:





В качестве точечных оценок латентных параметров принимают такие значения и , при которых функция правдоподобия достигает максимума),кие оценки называют оценками наибольшего правдоподобия). Необходимо отметить, что функции и достигают максимума при одних и тех же значениях своих аргументов, поэтому более удобно искать максимум функции . В данном случае:


,


где и - соответственно первичные баллы участников и заданий.

Логарифмическая функция правдоподобия зависит только от первичных баллов и , являющихся достаточными статистиками исходных наблюдений. Для нахождения максимума функции правдоподобия приравняем нулю частные производные логарифмической функции правдоподобия по каждому из аргументов:


, i=1, 2, 3, ……N


, j=1, 2, 3, ……K


Данная система нелинейных уравнений называется системой уравнений правдоподобия и содержит (N+K) уравнений с (N+K) неизвестными латентными параметрами . Эта система имеет единственное решение, соответствующее максимуму логарифмической функции правдоподобия. В случае модели Раша наблюдается совпадение систем уравнений, получаемых в методе моментов и методе максимального правдоподобия. Следовательно, решение этих уравнений можно выполнить, используя все выше изложенные рассуждения. Для другой функции успеха уравнения правдоподобия будут иметь иной вид.

Метод наибольшего правдоподобия обладает следующими свойствами:

Получаемые оценки являются состоятельными, несмещенными и эффективными.

Оценки подчиняются нормальному распределению с параметрами:


,


,

,


и имеют наименьшую дисперсию по сравнению с другими нормальными оценками. Дифференцирование по представленным формулам позволяет оценить в рамках модели Раша нижние границы дисперсий оценок латентных параметров:


,


3) Если эффективные оценки существуют, то метод наибольшего правдоподобия дает именно эти оценки.

4) Метод наибольшего правдоподобия наиболее полно использует данные выборки об оцениваемом параметре и позволяет найти достаточные оценки, если они существуют. Однако, несмотря на 40-летний опыт применения этой модели во многих областях, прежде всего в образовании и психологии, до сих пор продолжаются дискуссии об истинной ценности и эффективности модели Раша. До сих пор существуют две крайние точки зрения на эту модель.

Наиболее убежденные сторонники модели Раша утверждают: "Можно ли собрать или построить или сформулировать данные так, чтобы они соответствовали определению измерения (модели Раша)? Если нет, — то такие данные бесполезны".

Их наиболее последовательные оппоненты утверждают следующее: "Данные — это данные, а модель — это конструкция исследователя, которая подвержена ошибкам". Например, при построении регрессии, выбрасывая те или иные данные, можно получить любую зависимость, но мы тем самым ограничиваем реальный мир данных. Таким образом, создается искусственная переменная, о которой мало что известно.

Для практики одним из наиболее важных критериев является точность оценивания. Чем больше точность, тем лучше работает модель. В случае отсутствия ошибок измерения любая модель в смысле точности измерения работает идеально. Но на практике ошибки всегда есть и поэтому важно знать, насколько точные оценки позволяет получать та или иная модель.

На основе имитационного моделирования можно исследовать точность оценивания уровня знаний и трудностей заданий. А также число итераций, требуемых для вычисления этих оценок (методом наибольшего правдоподобия) в многофакторной ситуации в зависимости от:
  • диапазона уровней знаний испытуемых;
  • диапазона трудностей заданий;
  • степени соответствия диапазонов уровней знаний испытуемых и трудностей заданий;
  • числа испытуемых;
  • числа заданий;
  • степени соответствия данных модели;
  • доли пропущенных данных.

Для статистической обработки результатов моделирования используется многофакторный дисперсионный анализ.


Анализ точности оценивания параметров функции успеха

Точность исходных измерений



При диагностике знаний исходными величинами в модели Раша являются вероятности () верного решения j- задания участниками, набравшими один и тот же первичный балл b. Эти вероятности определяются соответствующими несмещенными оценками – относительными частотами - , имеющими дисперсию :





Однако последняя оценка является смещенной, поскольку





Символ M обозначает математическое ожидание.


,


где .


Поэтому: и

несмещенная оценка дисперсии относительной частоты определяется формулой:


,


где - количество участников, набравших балл b и правильно выполнивших задание с номером j. Таким образом:


, ,


Оценим дисперсию оценки функции успеха () решить задание с номером- j, участником, набравшим b – баллов [6]:


.


После дифференцирования данного уравнения получим:





Дифференциалы можно заменить средними квадратичными ошибками (корень квадратный из дисперсии):





- средневзвешенное значение, причем: .


Величина является статистическим весом (весовым коэффициентом) набранного балла b, т.е. она показывает, как часто данный набранный балл, встречается у участников тестирования среди различных комбинаций набранных баллов (0≤≤1). Последнее равенство в формуле среднеквадратичной оценки предполагает, что является хорошей оценкой для . Однако





и поэтому оценка является смещенной. В случае биноминального распределения несмещенное оценивание 1/p невозможно [6, 9]. Однако [12]





Следовательно, (N+1)/(b+1) является асимптотически несмещенной оценкой для 1/p. Поэтому, выражение:





является (по N) асимптотически несмещенной оценкой для и





где - количество участников, решивших j – задание и набравших по b – баллов, - общее количество участников набравших балл – b.


,


Легко заметить, что заметное отличие





от


наблюдаются только при малых значениях . Предположив некоррелированность случайных величин, для статистических оценок соответствующих дисперсий можно получить следующие формулы:


,


,


,





Последняя формула получена без учета ковариации между и . Величина является статистическим весом (весовым коэффициентом) набранного балла b, т.е. она показывает, как часто данный набранный балл встречается у участников тестирования среди различных комбинаций набранных баллов (0≤≤1).


Проверка адекватности модели Раша с помощью χ2 - критерия Пирсона


Если предположить справедливость модели Раша то разности [6] позволяют вычислить теоретические вероятности того, что i-участник испытания правильно выполнит j-задание:


.


Первичные баллы делят всех N испытуемых на K+1 группу в зависимости от числа правильно выполненных заданий в тесте, причем уровень подготовленности одинаков для всех участников, набравших одинаковый первичный балл- b. Введем следующие обозначения: Nb – количество испытуемых набравших по b – баллов, Nbj – количество испытуемых набравших b- баллов и правильно выполнивших j-задание (j=1, 2, 3, …. K).





Для каждого значения b и j экспериментальное и теоретическое значение вероятностей будут соответственно равны:


и .


Возникает вопрос, насколько значимы различия между экспериментальными и теоретическими значениями вероятностей? Какие расхождения связанны со случайными отклонениями и ограниченностью данных, позволяющими считать, что модель Раша не противоречит исходной матрице ответов, а какие противоречат модели Раша.

Необходимо проверить при определенном уровне значимости α следующую нулевую статистическую гипотезу Ho: генеральная совокупность участников испытания и тестовых заданий такова, что вероятность адекватно моделируется формулой Раша:





В качестве меры согласия теоретической и экспериментальной величины вероятности выбирают χ2 – критерий Пирсона:


.


Число степеней свободы (ν) χ2 – распределения равно g-1, где g – количество групп, на которые разбиваются участники испытания в зависимости от набранного балла (g=K+1), таким образом, ν=K. Следует учесть, что число участников тестирования должно быть относительно велико. Статистика имеет K(K+1) число степеней свободы.

Поскольку в условиях нулевой гипотезы статистика χ2 должна иметь определенное конкретное вероятностное распределение, то появляется возможность сравнить наблюдаемое значение и критическое (взятое из соответствующих таблиц для χ2 распределения).

Если ≥ , то модель Раша не согласуется с опытными данными.

Если ≤ , то модель Раша согласуется с опытными данными.

При проведении тестирования возникает необходимость обработки матрицы ответов, состоящей из элементов аij принимающих случайные значения 0 (неправильно) или 1(правильно). Математическое ожидание и дисперсия будут соответственно равны:


, ,


где i=1, 2, 3, ……..N (N-число участников тестирования), j=1, 2, 3, …….K (К-число заданий в тесте), - вероятность правильного решения i- участником с уровнем подготовленности задания j с уровнем трудности .


,


Статистические оценки и , математическое ожидание и дисперсии уровней подготовленности участников тестирования и уровней трудности заданий позволяют вычислить нормированное уклонение (ν(аij)) элемента аij матрицы ответов:


.


Согласно модели Раша для и получим:


,


,


.


Если сумма квадратов указанных нормированных уклонений для всех значений аij матрицы ответов составляющих единую строку (ответы i- участника на все задания) или единый столбец (ответы всех участников на j-задание) подчиняются распределению χ2 , то модель Раша применима к результатам данного тестирования. Иными словами должны выполняться следующие равенства:


, ,


где K-1 и N-1 соответствующее число степеней свободы нормированного уклонения. На практике и рассчитывают, используя следующие выражения:


,


.


Если вычисления значения критерия или не превосходят критических значений при заданном уровне значимости α и соответствующем числе степеней свободы, то можно считать, что анализируемая строка или столбец полученных результатов не противоречит модели Раша и следовательно, эта модель применима. Более подробную информацию по данному вопросу можно найти в работе [13].


Проверка равномерности распределения дистракторов и эффективности их работы


Дистракторы являются очень важным элементом тестовых заданий в закрытой форме, с выбором одного или нескольких правильных ответов. При этом остальные ответы не являясь правильными должны выглядеть правдоподобными (их принято называть дистракторами). Оказывается, что при удачном подборе дистракторов, испытуемые, неправильно отвечающие на задание выбирают их с одинаковой частотой. Равномерность распределения дистракторов является показателем надежности и валидности задания. Рассмотрим следующий пример расчета равномерности распределения дистракторов [6]. Пусть, на какое то из заданий теста, содержащее 5 вариантов ответов, 642 человека дали неправильные ответы. Теоретическая частота выбора каждого из дистракторов составляет 642/4=160,5. Составим следующую таблицу 1:


Таблица 1

Частоты
Номер дистрактора
Σ

1
2
3
4

Экспериментальная частота выбора (n)
140
179
180
143
642

Теоретическая частота выбора (n*)
160,5
160,5
160,5
160,5
642

(n-n*)
-20,5
18,5
19,5
-17,5
0



Для получим: . Критическое значение критерия, соответствующее трем степеням свободы и уровню значимости α=0,05 . Поскольку, , то гипотезу о равномерном выборе дистракторов следует отвергнуть, однако при α=0,02 .

Анализ выбора дистракторов данным испытуемым может представлять не менее важную задачу, чем анализ равномерности распределения. Поскольку, он позволяет в ряде случаев выявить характер “незнания” тестируемого и составить представления о мере эклектичности его знаний.

Для оценки равномерности распределения дистракторов, а по существу определения эффективности их работы могут быть использованы отличные от определения коэффициента подходы. В частности можно использовать подход [14], основанный на модели Раша, согласно которой вероятность того, что i- участник тестирования с уровнем подготовленности правильно выполнит j – задание с уровнем трудности определяется формулой:


,

а вероятность неправильного ответа (выбора одного из дистракторов данного задания):

.


Предположим, что вероятность выбора одного из r – дистракторов (), предлагаемых в данном тестовом задании, является монотонно убывающей функцией уровня подготовленности участника, и линейно связанна с вероятностью неправильного ответа, например:


,


где некоторый коэффициент линейной связи. Нахождение значения коэффициента при использовании выборок испытуемых порядка нескольких тысяч человек в сравнении с результатами работы дистракторов, полученными другими методами, показывает, что величина для хороших дистракторов варьируется от 0,98 до 1,02, а для плохих < 0,90. При этом наблюдается очень хорошее согласование результатов, что показывает возможность использования коэффициента для оценки работы дистракторов.


Влияние числа дистракторов на точность оценивания уровня знаний



При проведении педагогических измерений очень важным является вопрос о выборе оптимального числа дистракторов и их влиянии на точность оценки латентных параметров. Для решения этого вопроса, можно, например, использовать имитационное моделирование [15]. При котором результаты тестирования можно задать в рамках модели Бирнбаума, приписав всем заданиям дифференцирующую способность равную 1,7, а трудность заданий и подготовленность испытуемых разделить на 17 уровней от -4,0 до +4,0 логита с шагом 0,5. В зависимости от числа ответов на задание, вероятность угадывания может составлять от 0,5 (два варианта) до 0,1 (десять вариантов ответов с одним правильным). Точность оценивания уровня знаний в данном случае определяется по числу пар, внутри которых уровни значимо отличаются друг от друга, и по ширине 95%-ого доверительного интервала для моделируемых уровней знаний. Результаты имитационного моделирования показывают, что оптимальным является 5-6 вариантов ответов на задание теста, т.к. точность оценки уровня знаний повышается незначительно, при использовании более 5 дистракторов, а при использовании менее 4 резко снижается.


Дифференцирующая (разрешающая) способность теста


Разрешающая способность теста является одним из ключевых понятий современной теории тестирования, поскольку разделение испытуемых по рейтингу или по группам, при аттестации, является основной задачей любого тестирования. В связи с этим вводится понятие коэффициента дискриминации (или различающей способности), который может характеризовать как весь тест в целом, так и отдельные тестовые задания, и рассчитывается на основании полученных результатов. Основное влияние при вычислении разрешающей способности теста оказывает число заданий – К, поскольку число заданий, как правило, меньше числа участников – N. При заданном конечном числе заданий – К, первичные баллы принимают конечное число значений 0,1, 2, 3, ……..К с шагом ∆b=1. Общепринято, что разрешающей способностью теста (ξ) называется длина промежутка ∆θ в логитах на латентной шкале уровня подготовленности, который соответствует шагу ∆b=1, т.е.

Если , то тест не в состоянии различить θ1 и θ2 . В реальной жизни величину разрешающей способности теста (ξ) желательно знать заранее при составлении теста, что можно сделать [11] используя следующий метод.

Продифференцируем по ():


, тогда .


Принимая dbi=1 получим:





Разрешающая способность теста в окрестности балла bi будет тем больше, чем больше информации содержится в i- строке матрицы ответов. Минимальное значение ξ (ξmin) ξmin=4/K достигается при для любого j=1, 2, 3, …….K. Поскольку максимального значения коэффициента разрешающей способности ξ не существует, то практически ограничиваются величиной ξ=11/K [11], соответствующего маловероятному случаю для любого j=1, 2, 3, …….К. На практике используют значения ξ удовлетворяющие неравенству: 4/K<ξ<11/K (K-число заданий), а для приближенных вычислений брать ξ≈7/K логит. Для средней квадратичной ошибки определения ξ () можно воспользоваться формулой:


(логит).


Соотношение позволяет установить взаимосвязь между соответствующими среднеквадратичными ошибками и :




Таким образом, для среднеквадратичной ошибки оценки уровня подготовленности i- участника, можно получить, что логит (bi –первичный балл, набранный участником), для среднеквадратичной ошибки оценки уровня сложности задания логит (Nj – число участников успешно выполнивших данное j- задание). Для более строгих расчетов, вероятности и вычисляют по модели Раша, используют следующее выражение:


.


В диапазоне от 0 до 1 коэффициент различающей способности имеет следующую интерпретацию [2]:

- больше 0,40(задание является эффективным);

- от 0,30 до 0,39 (задание является удовлетворительным);

- от 0,20 до 0,29 (задание требует переработки);

- менее 0,20 (задание необходимо полностью заменить).


Оценка различающей способности тестовых заданий с помощью точечно-бисериального коэффициента



Очень часто для оценки различающей способности заданий используют так называемый точечно-бисериальный коэффициент корреляции , который выражает связь между результатами ответов на данное задание с индивидуальными баллами выборки испытуемых [2,6]:


,


где - среднее значение индивидуальных баллов испытуемых, правильно ответивших на j – задание, - среднее значение индивидуальных баллов всей выборки испытуемых, - стандартное отклонение индивидуальных баллов всей выборки испытуемых, и соответственно доли участников выполнивших и не выполнивших j- задание.

Точечно-бисериальная корреляция является значимой, если:


.


При практических вычислениях считается приемлемым, если коэффициент точечно-бисериальной корреляции имеет значение больше или равное 0,3 [16].

Для исследования показателей качества тестовых заданий необходима достаточно большая выборка испытуемых, порядка 200-300 человек. В реальных условиях эта задача бывает трудно реализуемой, что существенно осложняет работу по разработке качественных заданий.


Шкалы оценок в диагностическом тестировании


С математической точки зрения, процесс измерения уровня подготовленности должен являться отображением реальных состояний системы на некоторое множество действительных чисел, называемых шкалой. Причем, между ее элементами должен наблюдаться содержательный смысл, позволяющий проводить разумное объяснение результатов.

Порядковые шкалы применяются для сравнения результатов между собой по типу: лучше – хуже. Примером такой шкалы может служить лингвистическая оценка знаний: неудовлетворительно (2)-удовлетворительно (3)-хорошо (4)-отлично (5). При таком типе оценивания бессмысленно говорить о том, что знания на “3” отличаются от знаний на “2” так же как знания на “5” и “4” (т.е. “3”-“2”≠”5”-“4”). Преимуществом данной шкалы является традиционность ее использования, а существенным недостатком субъективизм измерения. Один и тот же студент может получить у разных преподавателей за одни и те же знания существенно различные оценки. Арифметические операции с оценками типа: “неудовлетворительно - удовлетворительно-хорошо-отлично” являются не корректными и имеют размытые качественные экспертные значения.

Метрические или интервальные шкалы имеют метрики и являются шкалами более высокого уровня. В данном случае содержательный смысл имеет не только сравнение элементов (меньше, больше, равно), но и разность, трактуемая, как “расстояние” между двумя элементами. Однако отсутствие начала отсчета делает эту шкалу непригодной для абсолютных измерений.

Метрические или интервальные шкалы, в которых определено начало отсчета, называются нормированными. Такая шкала является наиболее привлекательной, и ее построение позволяет преодолеть зависимость оценок от используемого теста и выборки испытуемых.

Номинальные шкалы основаны на использовании качественных переменных, не поддающихся количественному измерению (например, пол испытуемых и т.д.). При использовании таких шкал имеет смысл только равенство или неравенство элементов между собой, а разность между ними не имеет никакого смысла.

Использование любой из рассмотренных шкал подразумевает использование определенных математических методов. Например, для переменных, измеряемых метрической шкалой, где возможны количественные оценки, можно использовать регрессионный или корреляционный анализ.


Шкала первичных баллов



В отличие от шкал измерения физических величин (длина, масса, время и т.д.) первичные баллы, полученные при диагностике знаний не имеют для интерпретации решающего значения, поскольку тестирование, как правило, ориентируется на получение либо критериально-ориентированных, либо нормативно-ориентированных результатов 2,6,17]. Необработанные (первичные) баллы показывают количество правильно выполненных заданий без учета коррекции на случайное угадывание в закрытых формах тестовых заданий. Для коррекции первичных баллов используют следующую формулу [18]:


,

где - результат i-испытуемого, - количество правильных ответов i- испытуемого, - количество неправильных ответов i- испытуемого, k- число ответов в задании с выбором ответа (закрытая форма). Данная формула используется в тесте SAT (Scholastic Aptitude Test). Однако результаты показывают, что при очень большой длине теста обработка данных с использованием формулы коррекции баллов и без ее использования приводит к практически одинаковым результатам.

Шкала первичных баллов является порядковой шкалой и позволяет ранжировать испытуемых только по отношению к выполнению данного теста. Первичный балл при необходимости может быть переведен в 100 – бальную или процентную шкалу следующим образом: , где N – число заданий в тесте. Аналогичным образом можно охарактеризовать трудность каждого задания теста: , где М- число участников испытания, - первичный балл j – задания. Подход, использующий шкалу первичных баллов, не позволяет оценивать данного участника в зависимости от результатов других участников и уровня трудности решенных заданий. Например, если два участника решили по 5 заданий из 20, то их первичный балл будет равен 5, но один из участников решил более трудные задания и, следовательно, его балл должен быть выше.

Дробная и политомическая оценка результатов тестирования



Введение дробной оценки результатов тестирования является весьма продуктивным и интересным, поскольку позволяет провести более селективное распределение участников тестирования по баллам, чем использование целочисленных шкал, в которых число возможных значений рейтинга равно максимальному баллу.

Простая алгебраическая модель оценивания результатов тестирования [19,20] предполагает, что каждое из заданий может быть оценено в некоторой дробной шкале имеющей следующий вид:


, где .


Необходимо ввести некоторые обозначения:

N-число участников тестирования;

К-количество заданий в тесте;

Пусть в результате тестирования получена матрица первичных баллов ( первичный балл i-участника за j –задание, соответственно равный 1, если задание выполнено верно, и 0, если задание выполнено неправильно). Введем дополнительно следующие параметры:

- степень решенности j – задания i – участником (в дробной шкале );

степень нерешенности j – задания i – участником (в дробной шкале );

матрица результатов тестирования в дробной шкале , размера ;

- матрица размера , двойственная к матрице результатов тестирования ;

- вектор столбец трудности заданий;

- вектор столбец уровней подготовленности тестируемых.


Модель дробной оценки результатов тестирования основывается на следующих предположениях:


трудность заданий является экспериментально определяемой величиной;

окончательный (сертификационный) балл () i -участника определяется как сумма основного балла (за “широту” знаний) () и призового (за “глубину”) () ;

основной балл тестируемого , где α > 0 некоторая константа;

трудность заданий теста пропорциональна сумме ненабранных на этом задании тестовых баллов с учетом основных баллов испытуемых , β>0;

призовой балл тестируемого пропорционален количеству полностью решенных им заданий: , где , γ>0.


На основании изложенных предположений для вектора – столбца трудности заданий можно записать:


,

где , - квадратная матрица К – ого порядка.


Вектор – столбец трудности заданий является неотрицательным правым собственным вектором матрицы , соответствующим положительному собственному значению λ. Неотрицательный правый собственный вектор () матрицы и его собственное значение λ могут быть найдены после обработки результатов тестирования. Если для оценки трудности заданий ввести R –бальную шкалу, то вектор трудности заданий в такой шкале рассчитывается по формуле:


,


основной балл (, α=1/2):


,


призовой балл (, γ=1/2):


,


для окончательного (сертификационного) балла () получим:


.

Близкий по идеологии подход может быть реализован, если оценивать выполнение не всего тестового задания в целом (0 или 1), а результат выполнения каждого шага j –задания i –участником тестирования дихотомической оценкой. При этом все задание получит политомическую оценку, величина которой будет находиться в интервале от 0 до , где - количество шагов в j- задании теста [21]. Таким образом, если учитывать степень трудности каждого шага результаты тестирования N –участников с помощью K – заданий, каждое из которых состоит из - шагов, будут представлять 3-х мерную матрицу, состоящую из N- строк, К – столбцов и - “подстолбцов”. Однако, если трудность каждого шага выполнения заданий не учитывать, то получится матрица результатов в которой, для каждого участника будет свое (целое) количество баллов за каждое задание. Такая матрица ответов может быть обработана исходя из любой существующей модели тестирования.

Однако, наиболее адекватные результаты, в случае политомической оценки заданий, дает модель Partial Credit [22-24]. Которую можно рассматривать как обобщение модели Раша. Элементы матрицы ответов при тестировании с использованием политомически оцениваемых заданий принимают значения от 0 до (где - максимальный балл за j- задание) и являются случайными величинами. Можно выбрать одно, какое либо задания j и проверить адекватность модели Partial Credit для экспериментально полученных результатов. Если вероятность получения i –участником тестирования - баллов за j –задание, то математическое ожидание балла - полученного i –участником тестирования за данное задание –j определяется по следующей формуле:


,


а дисперсия величины :


.


Математическое ожидание и дисперсия величины позволяют проверить адекватность модели Partial Credit с помощью критерия χ2 –Пирсона. Для этого необходимо найти случайную величину :





Если модель Partial Credit является адекватной полученным при тестировании данным (для данного задания j), то величина подчиняется распределению (с N-1 степенью свободы). Для более точной оценки возможности применения модели Partial Credit необходимо использовать несколько различных заданий теста. Проверка данной модели, проведенная Центром тестирования Министерства образования РФ показала, что она является достаточно адекватной для обработки результатов тестирования с политомически оцениваемыми заданиями.


Нормативная шкала



Более приемлемыми для оценки достижений учащихся являются нормативные шкалы. Нормативная шкала разрабатывается на основе предположения о нормальном законе распределения баллов. Одной из причин применения нормативной шкалы является то, что линейная трансформация первичных (необработанных) баллов зависит от характеристик заданий в тесте. Перевод в нормативную шкалу предполагает, что знания испытуемых в их произвольной выборке подчиняются нормальному закону распределения, и равные отрезки под кривой распределения соответствуют равному количеству правильных ответов. При данном подходе используется следующая процедура. Сначала, на случайной выборке из генеральной совокупности проводится тест. Далее строится распределение первичных баллов, при этом стараются добиться их нормального распределения. Соответствие закона распределения экспериментально полученных первичных баллов нормальному закону распределения можно проверить методами статистической проверки гипотез распределения. В данном случае окончательный балл выставляется в зависимости от относительных успехов данного испытуемого в сравнении с остальными участниками. В результате тестирования получается экспериментальная функция распределения (F(x)) вероятности (p(x)) наблюдения тех или иных первичных баллов . Далее необходимо определить число интервалов, на которые делится числовая прямая, определяющая оценку. Если деление происходит на 2 промежутка, соответствующих оценкам: ”зачет - незачет”, то находится 50 ая процентиль, называемая медианой. Если осуществляется деление на 5 интервалов (что соответствует оценкам: 1, 2, 3, 4, 5), то необходимо определить соответствующие пентели (4 индекса делят числовую прямую на 5 частей) и т.д. Характер частотного распределения первичных баллов [25,26] отражается на значениях соответствующих процентилей и поэтому, например, пентили можно использовать в качестве окончательной оценки балла по 5 балльной шкале, децили по 10-ти балльной, центили по 100 бальной и т.д. В таком случае балл участника с номером i выражает процентную долю испытуемых, первичный балл которых ниже первичного балла данного испытуемого. Подобные шкалы называют процентильными или шкалами первичных процентилей. Эти шкалы, как и шкала процентов, имеют ранговый смысл и поэтому их трудно сравнивать между собой, если они получены по разным выборкам. Стандартизация достигается путем преобразования всех экспериментальных функций плотности распределения баллов к нормальному закону. Для нормального закона распределения медиана совпадает с математическим ожиданием. Расстояние между нижней и верхней квартилями равно 0,675σ а соответствующая р-ая квантиль определяется по формуле:


.


Если получаемое экспериментально распределение баллов отличается от нормального закона распределения, то его подвергают принудительной нормализации [53], однако отклонение от нормального закона говорит об неудачно подобранных тестовых заданиях. Если принудительной нормализации не требуется, то достаточно выполнить центрирование и нормирование экспериментально полученного распределения первичных баллов по формуле:


,


где - математическое ожидание, а - среднеквадратичное отклонение, . Полученные значения Z не являются удобными для использования в качестве баллов, однако их можно преобразовать в более наглядный вид, чтобы избавится от отрицательных баллов и изменить единицы измерения. Для чего можно использовать например следующую формулу:


,


где , , . Характеристикой точности измерения индивидуального балла служит среднеквадратичная оценка :


,


где r- коэффициент надежности теста.

На основании первичного балла возможно построение следующих нормативных шкал:

-процентная шкала (выставляемый балл прямо пропорционален первичному баллу);

-шкала первичных процентилей (выставляемый балл соответствует квантилям экспериментально полученного распределения частот первичных баллов);

-нормализованные шкалы (экспериментально полученное распределение первичных баллов подвергается нормализации и преобразованию к модельному распределению вида );

-шкалы нормализованных процентилей (выставляемый балл соответствует квантилям модельного распределения вида

);

-нормализованные шкалы с постоянным шагом (индексы шкалы выставляемого балла соответствуют равноудаленным значениям стандартной переменной Z).

При оценивании результатов с использованием нормативной шкалы в ряде случаев целесообразно использовать задания с заранее известным распределением уровней трудности, отличным от нормального закона. Например, при аттестационном тестировании предпочтительнее, чтобы распределение трудности заданий имело “крутое левое крыло” и растянутое “правое крыло” (см. рис.2). Данный характер распределения может быть обеспечен за счет повышения доли простых заданий (и/или повышении оценок простых заданий) в тесте, чего можно добиться предварительной нормировкой.





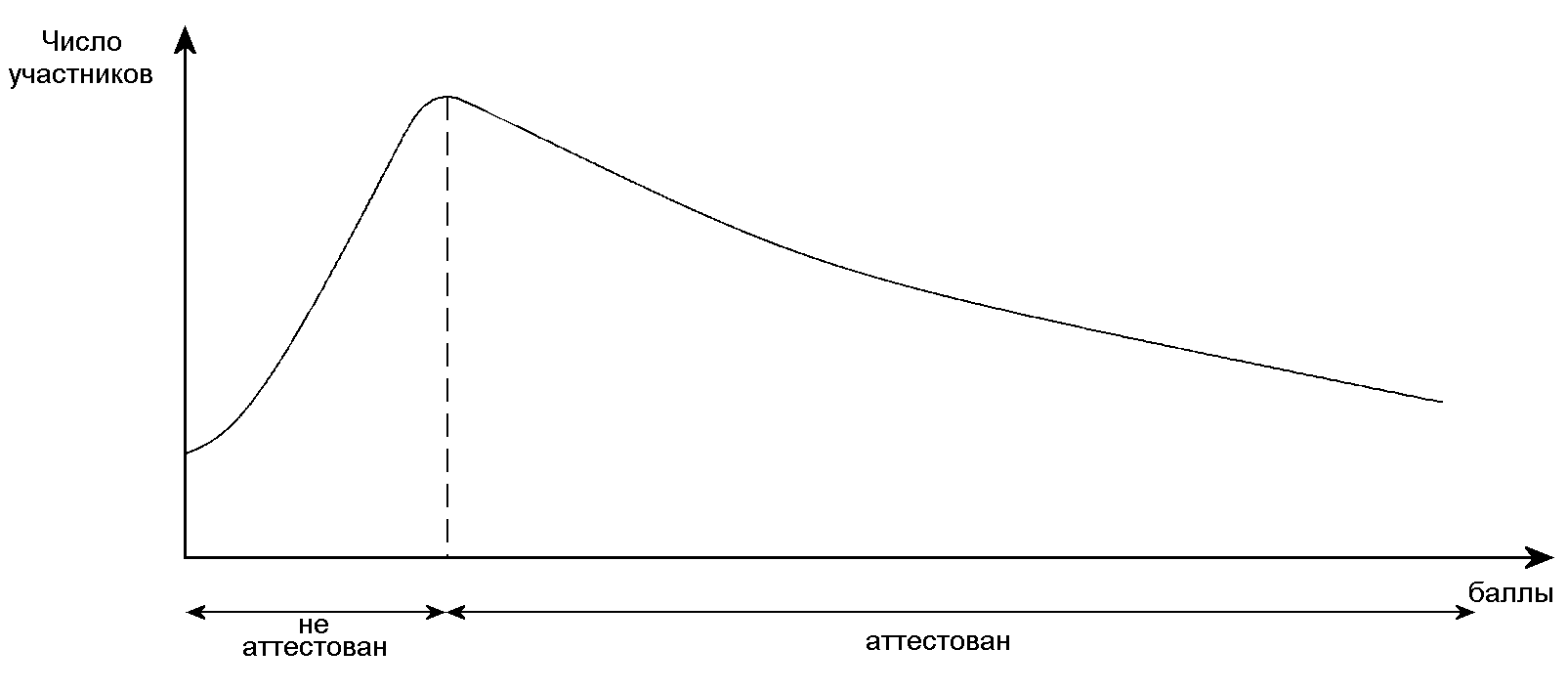
Рис.2. Кривая распределения результатов аттестационного тестирования с растянутым “правым крылом”


Метрическая шкала



Основным достоинством теории Раша является возможность построить не порядковую, а метрическую шкалу выставляемых баллов, т.е. произвести измерение уровня их подготовленности, а не ранжирование участников [6,27,28].

Пусть имеется матрица ответов N участников тестирования на К заданий теста, и полученные результаты полностью описываются моделью Раша. Тогда пересчет окончательного балла в 100 бальную шкалу можно осуществить линейным преобразованием, например, приравняв самый маленький уровень подготовленности нулю, а самый большой - 100 баллам. Кроме того, можно пойти следующим путем:


,


где - окончательный тестовый балл на 100 бальной шкале, - среднее значение уровня подготовленности, - уровень подготовленности i – участника, - среднеквадратичное отклонение, - некоторые эмпирические коэффициенты подбираемые вручную (например , ).