Наименование и краткое содержание лекций в соответствии с Рабочей программой Тема лекций, краткое содержание

Вид материала

Краткое содержание

Содержание 1. Основы автоматизированного проектирования РЭС 1.1. Цель и задачи курса. Основные термины и определения 2. Автоматизация схемотехнического проектирования РЭС Многовариантный анализ. 2. Анализ чувствительности Статистический анализ Анализ на наихудший случай Спектральный анализ. 2.2. Компонентные и топологические уравнения. Математические модели компонентов, основные требования, характеристики, модели пас I=GU+Iq (l.l) Если в ветви присутствует только проводимость, то I R = 0, в линейный источник тока невозможно (в этих случаях применяют модифицированный метод УП). Пример составления уравнений для расчета линейной цепи постоянного тока (расчет статического режима). 2.4. Моделирование переходных процессов и частотных характеристик 2.4.2. Расчет частотных характеристик схемы F(jω) при разных значениях ω F(jω) - комплексная А ЧХ. 2.5. Структурное, функциональное и логическое моделирование 4. Программные средства автоматизированных систем 4.1. Обзор современных САПР электроники и машиностроения, EDA,CAD, CAM системы 5.1. Структура технического обеспечения. Аппаратура рабочих мест в автоматизированных системах, связь с технологическим оборудов 2. Автоматизация схемотехнического проектирования РЭС 3 3. Автоматизация конструкторского проектирования РЭС 14

Подобный материал:

• Наименование и краткое содержание лекций № Тема лекций. Краткое содержание. Количество, 67.09kb.
• Наименование и краткое содержание лекций (5 семестр) № Тема лекций. Краткое содержание., 135.39kb.
• Наименование и краткое содержание лекций № лек. Тема лекции, краткое содержание Количество, 72.86kb.
• Краткое содержание лекций по курсу «Минералогия и геохимия», 491.68kb.
• Наименование и краткое содержание лекций №№ п/п Тема лекции, краткая аннотация Кол-во, 44.79kb.
• Текст лекций «Мировой и российский мембранный рынок». Содержание Раздел Введение. Рынок, 1644.63kb.
• Краткое содержание информационного сайта муниципального образования, 693.73kb.
• Краткое содержание лекций Раздел Мировая валютная система Тема, 38.03kb.
• Краткое содержание дисциплины (конспекты лекций) Тема 1 Смысл жизни как вызов, 927.24kb.
• Темы лекций и краткое содержание. Вопросы к семинарским занятиям. Литература. Примерные, 338.41kb.

Лекции по Основам компьютерного проектирования и моделирования

разработчик – Большаков А.П. ссылка скрыта

Наименование и краткое содержание лекций в соответствии с Рабочей программой

Тема лекций, краткое содержание	Кол. часов
1. Основы автоматизированного проектирования РЭС Цель и задачи курса. Основные термины и определения. Этапы проектирования РЭС и возможности их автоматизации, виды обеспечения САПР.	2
2. Автоматизация схемотехнического проектирования РЭС. 2.1. Задачи схемотехнического моделирования. Моделирование статических режимов, моделирование во временной и частотной области, анализ чувствительности, статистический и спектральный анализ. 2.2. Компонентные и топологические уравнения. Математические модели компонентов, основные требования, характеристики, модели пассивных и активных элементов. 2.3. Формирование топологических уравнений методом узловых потенциалов. Моделирование статического режима. 2.4. Моделирование переходных процессов и частотных характеристик 2.5. Структурное, функциональное и логическое моделирование.	10
3. Автоматизация конструкторского проектирования РЭС. 3.1. Общие сведения о задачах конструкторского проектирования. Возможность автоматизации задач конструкторского проектирования.	2
4. Программные средства автоматизированных систем. 4.1. Обзор современных САПР электроники и машиностроения, EDA,CAD, CAM системы.	2
5. Техническое обеспечение систем автоматизированного проектирования. 5.1. Структура технического обеспечения. Аппаратура рабочих мест в автоматизированных системах, связь с технологическим оборудованием.	1
ИТОГО:	17

1. Основы автоматизированного проектирования РЭС

1.1. Цель и задачи курса. Основные термины и определения

1.2. Этапы проектирования РЭС и возможности их автоматизации, виды обеспечения САПР

1. Системотехнический

2. Схемотехнический

3. Конструкторский

4. Технолонический

2. Автоматизация схемотехнического проектирования РЭС

2.1. Задачи схемотехнического моделирования. Моделирование статических режимов, моделирование во временной и частотной области, анализ чувствительности, статистический и спектральный анализ

Многовариантный анализ и анализ выходных параметров схем

1. Многовариантный анализ.

Одновариантный анализ позволяет получить информацию о состоянии и поведении проектируемой схемы в одной точке пространства внутренних X параметров и внешних Q параметров. Очевидно, что для оценки свойств проектируемой схемы этого недостаточно. Нужно выполнять многовариантный анализ, то есть исследовать поведение схемы в ряде точек упомянутого пространства, которое для краткости далее будем называть пространством аргументов.

Чаще всего многовариантный анализ в САПР осуществляется в интерактивном режиме, когда разработчик неоднократно меняет в математической модели те или иные параметры из множеств X или Q, выполняет одновариантный анализ и фиксирует значения выходных параметров. Подобный многовариантный анализ позволяет оценить область работоспособности, степень выполнения условий работоспособности, а следовательно, степень выполнения ТЗ на проектирование.

Примечание: Областью работоспособности называют область в пространстве аргументов, в пределах которой значения всех выходных параметров находятся в пределах ТЗ.

Среди процедур многовариантного анализа можно выделить типовые, выполняемые по заранее составленным программам. К таким процедурам относятся анализ чувствительности и статистический анализ.


2. Анализ чувствительности

Цель анализа чувствительности заключается в нахождении тех элементов схемы и параметров X этих элементов, отклонение которых от номинальных значений приводит к наибольшему отклонению выходных параметров схемы Y.

Примеры выходных параметров схем: потребляемая мощность, выходная мощность, помехоустойчивость, динамические параметры (задержка, длительность фронта, ...), частотные параметры (коэфф. усиления, полоса пропускания, ....).

Наиболее просто анализ чувствительности реализуется путем численного дифференцирования. Пусть анализ проводится в некоторой точке Х_ном пространства аргументов, в которой предварительно проведен одновариантный анализ и найдены значения выходных параметров y_{j ном} . Выделяется N параметров-аргументов x_i, (из числа элементов векторов X и Q), влияние которых на выходные параметры подлежит оценить, поочередно каждый из них получает приращение Δ x_i , выполняется одновариантный анализ, фиксируются значения выходных параметров y_j и подсчитываются значения абсолютных:

Аji =( y_j - y_{j ном} ) / Δ x_i,

и относительных коэффициентов чувствительности:

Вji = Аji x_{i ном} ) / y_{j ном.}

Такой метод численного дифференцирования называют методом приращений. Для анализа чувствительности методом приращений требуется выполнить N + 1 раз одновариантный анализ. Результат его применения - матрицы абсолютной и относительной чувствительности, элементами которых являются коэффициенты Аji и Вji.

Примечание: Анализ чувствительности - это расчет векторов градиентов выходных параметров, который входит составной частью в программы параметрической оптимизации, использующие градиентные методы.


3. Статистический анализ

Целью статистического анализа является определение процента выхода годных схем, соответствующих ТЗ, при данном конкретном разбросе параметров X.

В результате анализа определяется вероятность Р(Х) того, что вектор внутренних параметров X, определяющий состояние схемы в момент ее изготовления, находится в области работоспособности G(X).

Исходной информацией являются характеристики законов распределения внутренних параметров X, а результатом расчета - характеристики законов распределения выходных параметров Y. Статистический анализ ограничивается лишь расчетом начальной надежности схемы, без учета старения.

В САПР статистический анализ проводится численным методом - методом Монте-Карло. В соответствии с этим методом осуществляется N статистических испытаний, каждое статистическое испытание представляет собой одновариантный анализ, выполняемый при случайных значениях параметров-аргументов. Эти случайные значения выбираются в соответствии с заданными законами распределения аргументов x_i. Полученные в каждом испытании значения выходных параметров накапливают и обрабатывают. Испытание считается неудачным, если нарушено хотя бы одно условие работоспособности. Если число неудачных испытаний М, то отношение M/N с некоторой точностью характеризует вероятность Р(Х).

В итоге расчета могут быть получены следующие результаты:

- гистограммы выходных параметров;

- оценки матожиданий и дисперсий выходных параметров;

- оценки коэффициентов корреляции и регрессии между избранными выходными и внутренними параметрами, которые в частности модно использовать для оценки коэффициентов чувствительности.

Статистический анализ, выполняемый методом Монте-Карло - трудоемкая процедура, поскольку число испытаний приходится выбирать довольно большим, чтобы достичь приемлемой точности анализа. Другая причина, затрудняющая применение метода Монте-Карло - трудности в получении достоверной исходной информации о законах распределения параметров-аргументов x_i

Более типична ситуация, когда законы распределения x_i не известны, но известны предельно допустимые отклонения Δ x_i параметров от номинальных значений x_{i ном} (такие отклонения указываются в паспортных данных). В таких случаях более реалистично применять метод анализа на наихудший случай.


4. Анализ на наихудший случай.

Согласно этому методу сначала выполняют анализ чувствительности с целью определения знаков коэффициентов чувствительности. Далее осуществляют m раз одновариантный анализ, где m - число выходных параметров. В каждом варианте задают значения аргументов, наиболее неблагоприятные для выполнения условия работоспособности каждого выходного параметра.

Однако следует заметить, что, проводя анализ на наихудший случай, можно получить

завышенные значения разброса выходных параметров, и если добиваться выполнения условий работоспособности в наихудших случаях, то это может привести к неоправданному увеличению стоимости, габаритов и других показателей проектируемых схем.


5. Спектральный анализ.

Спектральный анализ является мощным средством анализа сигналов, особенно распознавания слабых сигналов с яркой периодичностью на фоне посторонних сигналов и шумов. Получаемые на основе расчета спектры, полезны при анализе модулированных сигналов, изучении результатов взаимной модуляции сложных сигналов и искажений, анализе шума и т.д.

На практике для расчета спектров сигналов используют математический аппарат на основе дискретного преобразования Фурье (ДПФ).

Как известно непрерывное прямое преобразование Фурье описывается выражением:


Т/ 2

X(jw)= ∫ x(t)e ^–jwt dt (l)

-Т / 2


где X(jw) - функция спектральной плотности для сигнала x(t).

Выражению (1) можно поставить в соответствие его дискретный аналог. Пусть сигнал x(t) измерен на интервале (0,Т) в N равноотстоящих на Δ t точках t₀, t₁, ...t_n,..., t_N-1 . Тогда дискретное преобразование Фурье описывается выражением:


(2)


где X(k) - спектральная составляющая на частоте кратной основной частоте: ’

k = 0,1,...N-1; W = e-^{j2π N} .

Для восстановления последовательности х(п) (то есть исходных отсчетов) используется обратное ДПФ:

(3)

В случае ДПФ предполагается, что исходная функция х(п) является периодической с периодом Т = N Δ t и дискретной, с шагом дискретизации Δ t. Из свойств преобразования Фурье следует, что результат преобразования будет периодической и дискретной функцией.

Замечание: ДПФ исходит из предположения, что сигнал x(t) имеет ограниченный спектр, то есть в нем отсутствуют частоты больше F_max, а частота дискретизации:


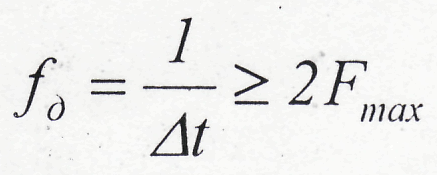(4)




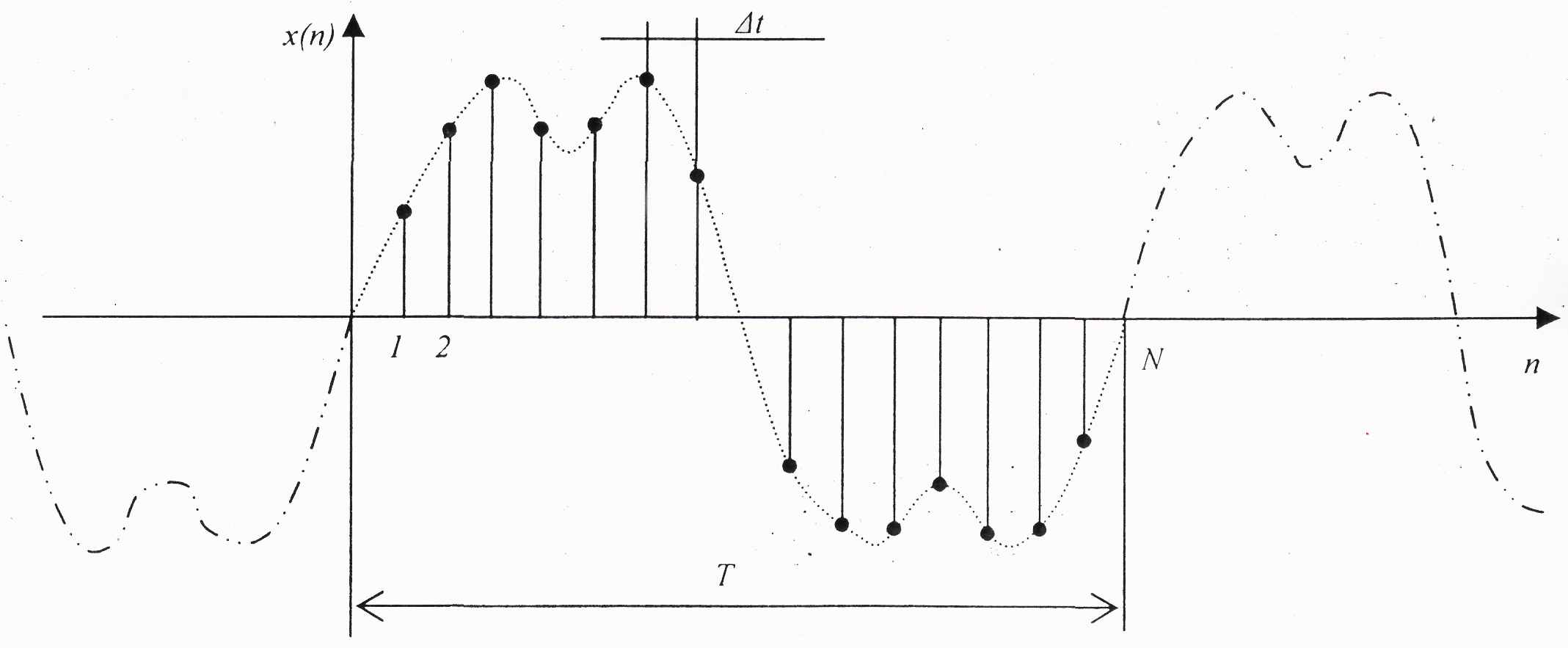
Рисунок 1. Дискретный периодический сигнал.




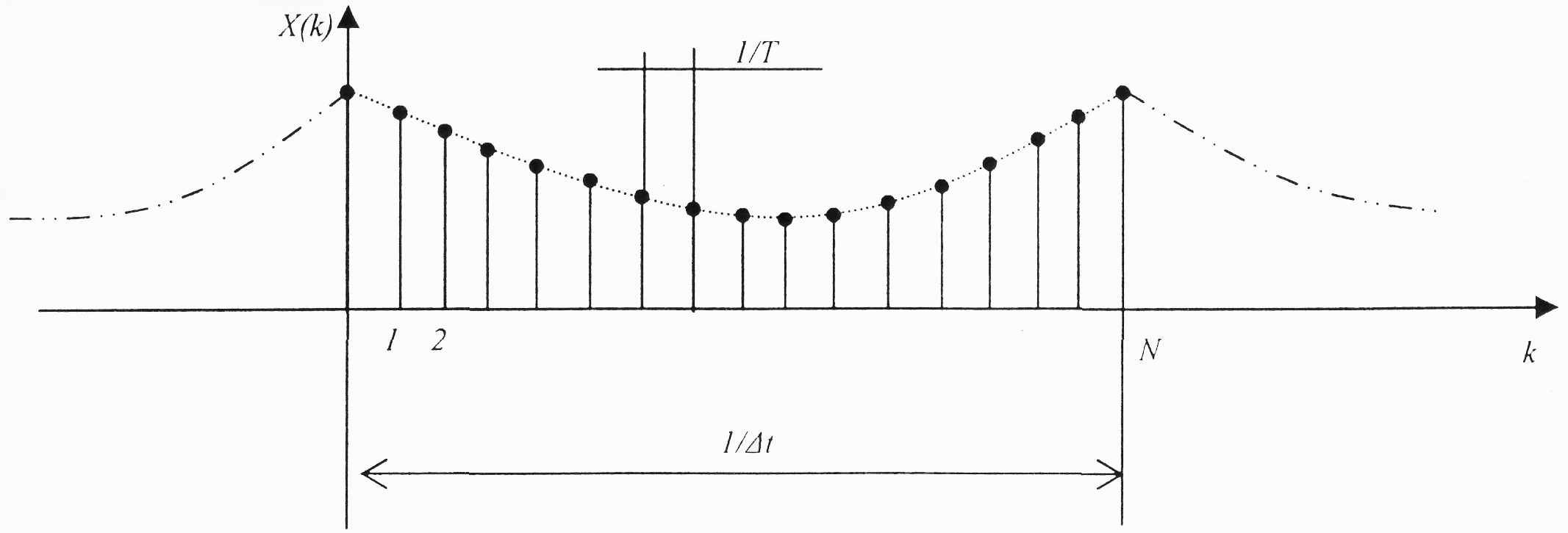
Рисунок 2. Спектр периодического дискретного сигнала.

2.2. Компонентные и топологические уравнения. Математические модели компонентов, основные требования, характеристики, модели пассивных и активных элементов

2.3. Формирование топологических уравнений методом узловых потенциалов. Моделирование статического режима

Формирование топологических уравнений методом узловых потенциалов. Моделирование статического режима

1. Метод узловых потенциалов.

Как было отмечено ранее, топологические уравнения для электронных схем составляются на основе законов Кирхгофа: ЗТК и ЗНК. В большинстве современных программ схемотехнического моделирования при составлении топологических уравнений для схемы применяется метод узловых потенциалов (УП).

Согласно этому методу предусматривается замена каждой ветви схемы линейным источником тока, который представляет собой параллельно включенные идеальный источник тока и проводимость G = const (рисунок 1, а).

В этом случае уравнение ветви выглядит следующим образом:

I=GU+Iq (l.l)

Если в ветви присутствует только проводимость, то I_q = 0, а активное сопротивление R = const можно преобразовать в проводимость G = 1/R. Если ветвь содержит идеальный источник тока, то G = 0.

Линейный источник напряжения (рис.1, б) может быть преобразован в линейный источник тока следующим образом:

I= -Uq/R, (1.2)

G = 1/R. (1.3)

Преобразование идеального источника напряжения, у которого R = 0, в линейный источник тока невозможно (в этих случаях применяют модифицированный метод УП).

Ток Iq и напряжение Uq считаются положительными, если их направления совпадают с направлениями тока и напряжения в ветви.

При анализе методом УП сначала выбирается базовый узел, потенциал которого φ0 = 0. Этому узлу присваивается номер 0,остальные узлы нумеруются по порядку. Каждое напряжение



Рисунок 1.Ветви линейной цепи:

а) линейный источника тока б) линейный источник напряжения

схемы может быть описано как разность потенциалов. При этом напряжение между узлом х и базовым узлом определяется в виде:

, (1.4)

где 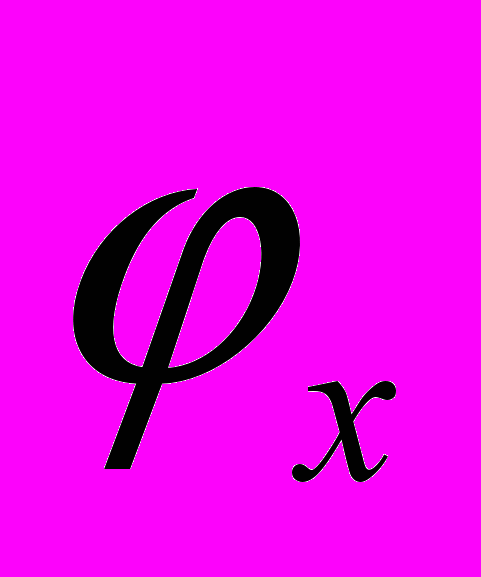- потенциал узла х.

При = 0 узловое напряжение:

, (1.4)

Число уравнений п для цепи без идеальных источников напряжения и базового узла равно числу узлов k. Для всех означенных узлов составляются уравнения Кирхгофа для токов, которые решаются относительно неизвестных узловых напряжений. Зная узловые напряжения можно рассчитать напряжение в каждой ветви.


В соответствии с ЗТК исходная система топологических уравнений в базисе узловых потенциалов имеет вид:

I(φ)=0 (1.5)

где I(φ) - вектор узловых токов.

Вследствие того, что в большинстве случаев для решения систем уравнений используется метод Ньютона (будет рассмотрен ниже), система уравнений соответствующая решению (1.5) формируется в следующем виде:

(1.6)

где G = [dI/dφ]- матрица узловых проводимостей (матрица Якоби); k - номер ньютоновских итераций; 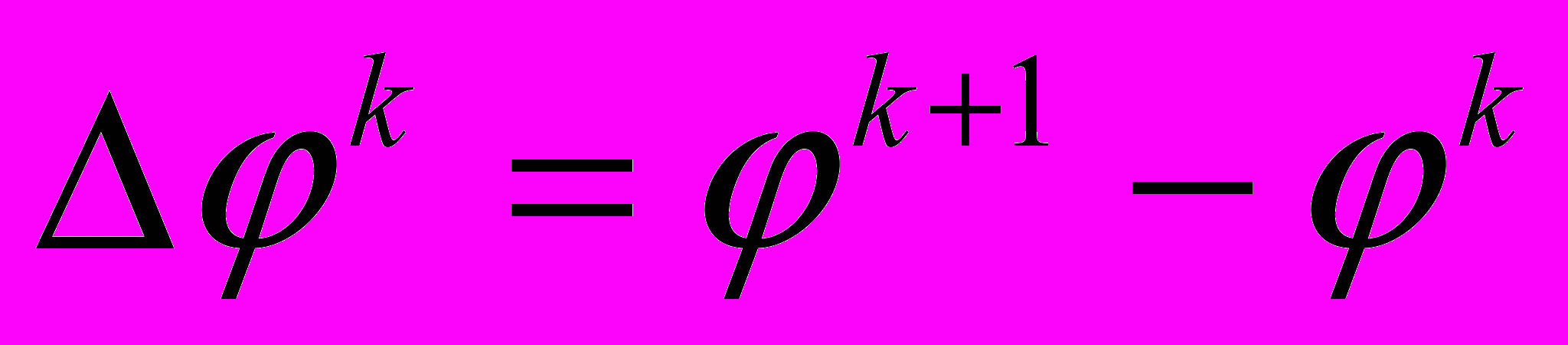- вектор поправок.

Структура матрицы проводимостей подчиняется определенным правилам: в каждом элементе главной диагонали матрицы стоит сумма проводимостей, которые одним своим полюсом соединены с соответствующим узлом. Во всех остальных элементах размещается отрицательная сумма тех проводимостей, которые расположены между узлами. Номера проводимостей в матрице определяются соответствующими номерами строк и столбцов. Формирование вектора узловых токов I(φ) состоит в образовании для каждого узла суммы полюсных токов элементов, соединенных с этим узлом. Вектор узловых токов строится также согласно строгим правилам: ток I_q источника получает отрицательный знак для того узла, из которого он «выходит», и положительный для узла, в который он «входит».

Для включения элемента в модель схемы по методу узловых потенциалов необходимо, чтобы его уравнение имело вид:

i=ƒ(u) (1.7)


Для резистора R: i = u/R , поэтому его вклад в вектор узловых токов I будет u/R, а в матрицу G: 1 /R.

Вклад нелинейного 2-полюсника с уравнением i = ƒ (u) в вектор токов I равен ƒ (u) , а в матрицу G: di / du.

Элементы, уравнения которых отличаются от вида (1.7), считаются неудобными для составления модели схемы в базисе УП. К ним относятся идеальные источники тока и напряжения, а также управляемые источники вида i = ƒ(i), u = ƒ(i), u= ƒ (u). В этом случае можно воспользоваться следующим приемом: в ветвь с неудобным элементом включают дополнительный элемент - последовательное малое сопротивление или параллельную малую проводимость.


2. Пример составления уравнений для расчета линейной цепи постоянного тока (расчет статического режима).

Расчет статического режима может иметь самостоятельное значение, например, при составлении карты режимов схемы по постоянному току, указывающей номинальные значения токов, напряжений и рассеиваемых мощностей в разных точках и элементах схемы. Однако чаще всего моделирование статического режима является основной составной частью других, более сложных задач. Например, расчет переходных процессов в схеме можно представить как последовательность расчетов квазистатических режимов в отдельные моменты времени, в каждый из которых нужно выполнить законы равновесия (ЗТК, ЗНК), то есть найти квазистатический режим.

Методом узловых потенциалов составим систему уравнений для цепи, изображенной на рисунке 2.

Уравнения для узлов 1 - 3 выглядят следующим образом:

I₂ + I₃-I₁ = 0,

I₄ + I₅-I₃ = 0,

I₅ – I₆ = 0.



Рисунок 2. Цепь постоянного тока с шестью ветвями и тремя узлами.


Заменим ток в каждой ветви, использовав уравнение (1.1), тогда:

G₂U₂ + G₃U₃- G₁U₁-I_q = 0,

G₄U4 + G₅U₅-G₃U₃ =0,

G₆U₆ - G₅U₅ = 0.

Напряжение в каждой ветви можно выразить через узловые напряжения (потенциалы):

U₁=- U₁,₀ ; U₂ = U₁,₀ ; U₃ = U₁,₀ - U₂,o;

U₄ = U₂,₀; U₅ = U₂,o-U₃,o; U₆ = U₃,₀ ;


Подставляя полученные выражения в узловые уравнения получаем и объединяя последние,

получаем:

(G₁ + G₂ + G₃) U₁,₀ - G₃U₂,₀ = I_q;

- G₃U₁,₀ + (G₃ + G₄ + G₅)U₂,₀ - G₅U₃,₀ = 0 ;

- G₅ U_2,1 + (G₅ + G₆)U_3,0 = 0.

Запишем теперь систему уравнений в матричной форме:

	1	2	3
1	G1+G2+G3	-G3		U1,0		Iq
2	- G3	G3+G4+G5	-G5	U2,0	=	0
3		G5	G5 + G6	U3,0		0

Таким образом, мы пришли к матричной форме системы уравнений по методу УП, сделав ряд преобразований над исходной системой уравнений. Подобную матрицу можно было бы получить сразу, следуя правилам, описанным в разделе 1. В программах СМ построение матриц проводимости и вектора токов, соответствующих системе уравнений в базисе УП, происходит автоматически по аналогичным (или похожим) правилам.

Полученная система уравнений является линейной. Для решения систем линейных уравнений наиболее известен метод Гаусса, который называют также методом исключений, потому, что неизвестные х₁, х₂, ..., x_n-1 поочередно исключаются до тех пор, пока не останется одно уравнение с неизвестной х_п. После решения этого уравнения путем обратной подстановки определяются неизвестные x_n-1, x_n-2 ..., х₁. Однако, как известно, большинство реальных схем содержит нелинейные элементы (диоды, транзисторы и т.п.), поэтому система уравнений для таких схем будет нелинейной. Для решения систем нелинейных уравнений в программах СМ наибольшее применение нашел метод Ньютона (метод касательных).


Поясним метод Ньютона исходя из геометрических соображений. Исходное уравнение, подлежащее решению, имеет вид:

ƒ(x) = 0. (2)

То есть, нам нужно найти x, при котором значение функции равно 0.




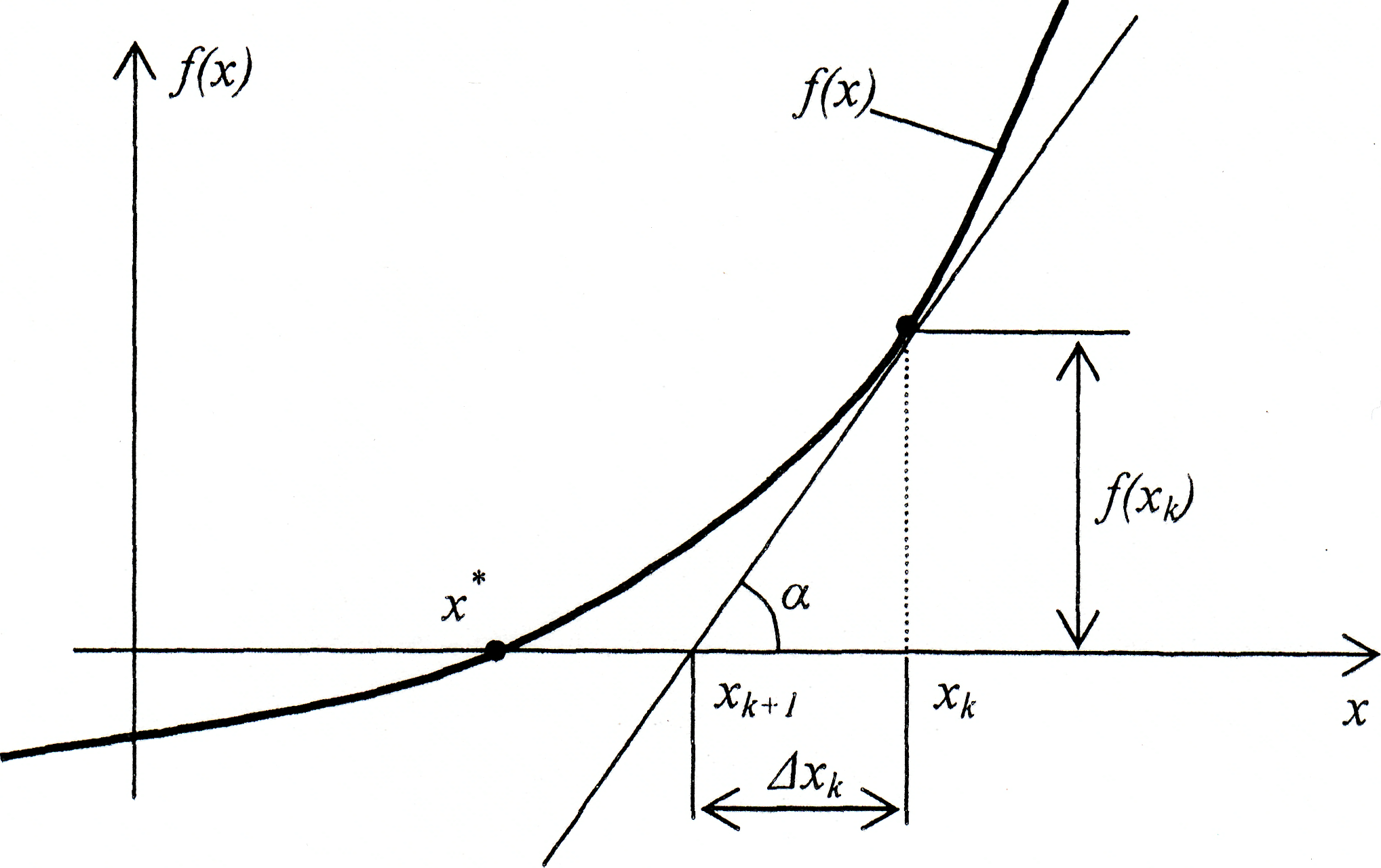
Рисунок 3. Геометрическая интерпретация метода Ньютона.


На рисунке 3 показана геометрическая интерпретация одной итерации по методу Ньютона. Согласно этому методу на каждом шаге k, функцию f(x) в точке x_k аппроксимируем линейной функцией, угол наклона α, которой равен производной f` (x) в этой точке. Чтобы найти следующее, приближающееся к решению значение x_k+1, нужно найти Δ x_k , которое может быть определено из выражения:

tga = f ` (x_k) = .

тогда:



Полученное выражение обычно записывают в виде:

f ` (x_k) Δx_k=-f(x_k),

а в случае системы уравнений:

F'(X_k ) ΔX_k = -F(X_k),

где ΔX_k = X_k+1 - X_k - называется вектором поправок, F(X_k) - вектор невязок, F'(X_k ) -матрица Якоби.

Таким образом, исходную систему нелинейных уравнений приводим к линейной (это называется линеаризацией), новые значения X_k+1 используем как приближенное значение решения, и процесс повторяем до тех пор, пока не будет найдено решение или не станет ясно, что получить его не удастся. Такой процесс нахождения решения является итерационным (что характеризует все численные методы решения уравнений). Процесс прекращается, если | ΔX_k | станет меньше некоторой величины ε (ошибка вычисления).

Недостаток метода Ньютона - это малый размер области сходимости и необходимость задания точки начального приближения достаточно близко к точке решения.

Пример:

2.4. Моделирование переходных процессов и частотных характеристик

2.4.2. Расчет частотных характеристик схемы

Основная задача расчета частотных характеристик схемы состоит в определении амлитудно-частотной (АЧХ) и фазо-частотной характеристик (ФЧХ) схемы.

Перед выполнением расчета в частотной области, сначала рассчитывается режим схемы по постоянному току (расчет статического режима). Затем линеаризуются все нелинейные элементы (диоды, транзисторы, пассивные компоненты с нелинейными параметрами, нелинейные управляемые источники), при этом в схеме замещения постоянные источники напряжения закорачиваются, а постоянные источники тока размыкаются. Далее выполняется расчет комплексных амплитуд узловых потенциалов и токов ветвей для линейной схемы.

В программах СМ получил распространение численный подход решения задачи, когда АЧХ вычисляется как численное значение F(jω) при разных значениях ω, то есть поточечно.

В качестве входного сигнала используется источник напряжения E_ex(jώ) = 1 x e^jώ с

единичной комплексной амплитудой, нулевой начальной фазой и малым внутренним сопротивлением. В базисе узловых потенциалов этот источник преобразуется в единичный источник тока I_вх ( jώ) =1 х e^jώ.

При указанном входном сигнале будет верно соотношение:

(2.1)

где F(jω) - комплексная А ЧХ.

То есть, рассчитывая и_вых(jώ) в любой ветви схемы, мы тем самым рассчитываем АЧХ

этой ветви.

Метод узловых потенциалов позволяет формировать уравнения не только для временной, но и для частотной области. В этом случае вся ранее рассмотренная методика сохраняется, изменяются лишь компонентные уравнения реактивных ветвей:

i_c = jώС(φ_нач -φ_кон), i_L = — ( φ_нач -φ_кон) (2.3)

где φ_нач , φ_кон - потенциалы на концах реактивных ветвей; j - мнимая единица; ω - частота. Соответственно проводимости ветвей равны:

G_c = jώC, G_L =— . (2.4)

Уравнения c i_c используются для формирования вектора узловых токов, c G_c – для матрицы узловых проводимостей.

В результате получим систему уравнений линейной схемы в частотной области:

G(jώ)φ(jώ) = - I(jώ) (* *)

В отличие от (*) для временной области, которое в каждый момент времени нужно решать несколько раз до сходимости, уравнения (* *) на каждой частоте нужно решать лишь один раз, поскольку схема линейная.

Для решения системы уравнений (* *) используются программы оперирующие с комплексными коэффициентами. Для каждой частоты определяются действительные и мнимые части узловых потенциалов, по ним находят амплитуду и фазовый угол каждой спектральной составляющей, что и позволяет построить АЧХ, ФЧХ, найти собственные частоты колебательной системы и т.п.

2.5. Структурное, функциональное и логическое моделирование

3. Автоматизация конструкторского проектирования РЭС

3.1. Общие сведения о задачах конструкторского проектирования. Возможность автоматизации задач конструкторского проектирования

4. Программные средства автоматизированных систем

4.1. Обзор современных САПР электроники и машиностроения, EDA,CAD, CAM системы

5. Техническое обеспечение систем автоматизированного проектирования

5.1. Структура технического обеспечения. Аппаратура рабочих мест в автоматизированных системах, связь с технологическим оборудованием

Оглавление