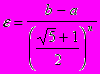Лекция №2 виды моделирования
| Вид материала | Лекция |
- Самостоятельная работа 2 часа в неделю всего часов, 42.13kb.
- Лекция №16, 127.41kb.
- Лекция: Анализ и моделирование функциональной области внедрения ис: Основные понятия, 234.94kb.
- Программа вступительных испытаний (собеседования) для поступающих в магистратуру, 31.28kb.
- 1. Основные понятия теории моделирования, 279.51kb.
- Программа курса «Основы математического моделирования» Осень 2007, 25.35kb.
- Лекция №12, 54.84kb.
- О Конкурса асов компьютерного 3D-моделирования среди предприятий, использующих в проектных, 9.87kb.
- Аннотация дисциплины «основы математического моделирования», 29.01kb.
- Учебной дисциплины «Компьютерное моделирование» для направления 010100. 62 «Математика», 62.26kb.
ЛЕКЦИЯ №2
ВИДЫ МОДЕЛИРОВАНИЯ
Можно выделить следующие виды моделирования:
1. Физическое моделирование, когда в качестве модели исследуемого объекта выбирается реально, физически существующие явление, процесс, реальная установка или их комбинация.
Процесс-модель может быть той же физической или физико-химической природы, что и исходный объект, но, например, осуществляться в меньшем масштабе (лабораторная установка технологического процесса, опытный агрегат и т.п.). Это так называемая прямая аналогия.
2. Математическое моделирование, когда объекту исследования ставится в соответствие система математических уравнений, или логических соотношений, или программа для ЭВМ, отражающие состояние и характеристики объекта исследования в соответствии с теорией и правилами соответствующих разделов математики, в том числе вычислительной.
Строго говоря, моделью в этом случае является не только сама запись, но и ЭВМ с реализованными на ней алгоритмами и программами воспроизведения и анализа указанной записи.
ОБЩИЙ ВИД МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОБЪЕКТА
В самом общем виде математическая модель любого объекта включает выражения для сформулированных целевых функций предстоящего исследования V и соотношения взаимосвязи между переменными объекта в виде fi:
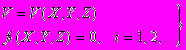 (1).
(1).В подавляющем большинстве случаев целевые функции
 выбираются так, чтобы можно было бы достигнуть максимального улучшения функционирования объекта, поэтому математическая модель объекта в таких случаях представляется в следующей форме:
выбираются так, чтобы можно было бы достигнуть максимального улучшения функционирования объекта, поэтому математическая модель объекта в таких случаях представляется в следующей форме: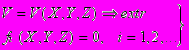 (2),
(2),в этом случае второе выражение в общих математических моделях (1) и (2) часто называют ограничениями.
Различают аналитические математические модели и математические модели алгоритмического типа, которые очень часто называют также имитационными моделями. Аналитические математические модели представляют собой систему математических уравнений и соотношений, обладающих свойствами аналитических математических функций. Математические модели алгоритмического типа представляют собой человеко-машинные системы, информационные системы и другие, большинство переменных которых представляют собой неколичественные переменные.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ОПТИМИЗАЦИИ
Задача оптимизации заключается в том, что заданы множество Х и функция f(x), определенная на X; требуется найти точки минимума или максимума функции f(x) на X. Общий вид задачи оптимизации может быть сформулирован следующим образом:
f(x) min, x X.
hk(x) = 0, k=1,...,K
gj(x) 0, j=1,...,J
При этом f будем называть целевой функцией, X - допустимым множеством, любой элемент x X - допустимой точкой задачи, hk(x) - ограничениями типа равенства, а gj(x) - ограничениями типа неравенств.
Необходимо дать понятие минимума, т.е. той точки, которая является решением оптимизационной задачи
Определение. Глобальным минимумом f(x) называется точка x* такая что: f(x*) f(x) для любого xX.
Если мы заменим слово "минимум" на "максимум", а в неравенстве поменяем знак, то мы получим определение глобального максимума.
Точки минимума или максимума еще называют экстремальными точками, а задачи - экстремальными задачами.
Различают задачи безусловной оптимизации и задачи условной оптимизации. Задача безусловной оптимизации имеет вид:
f(x) min, x X.
Рассмотрим методы решения задач безусловной оптимизации.
Задачи безусловной оптимизации для функций одной переменной
Согласно наиболее простому определению, функция
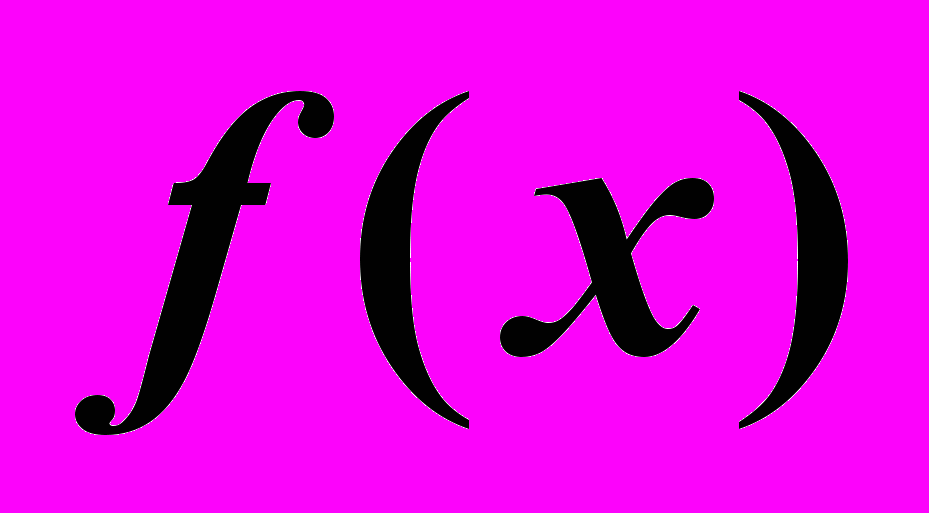 представляет собой правило, которое позволяет каждому значению
представляет собой правило, которое позволяет каждому значению 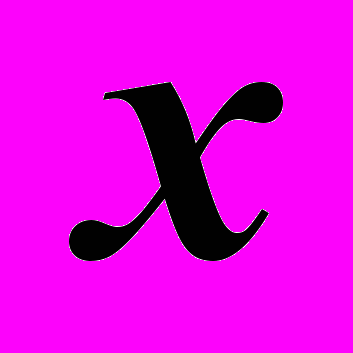 поставить в соответствие единственное значение
поставить в соответствие единственное значение 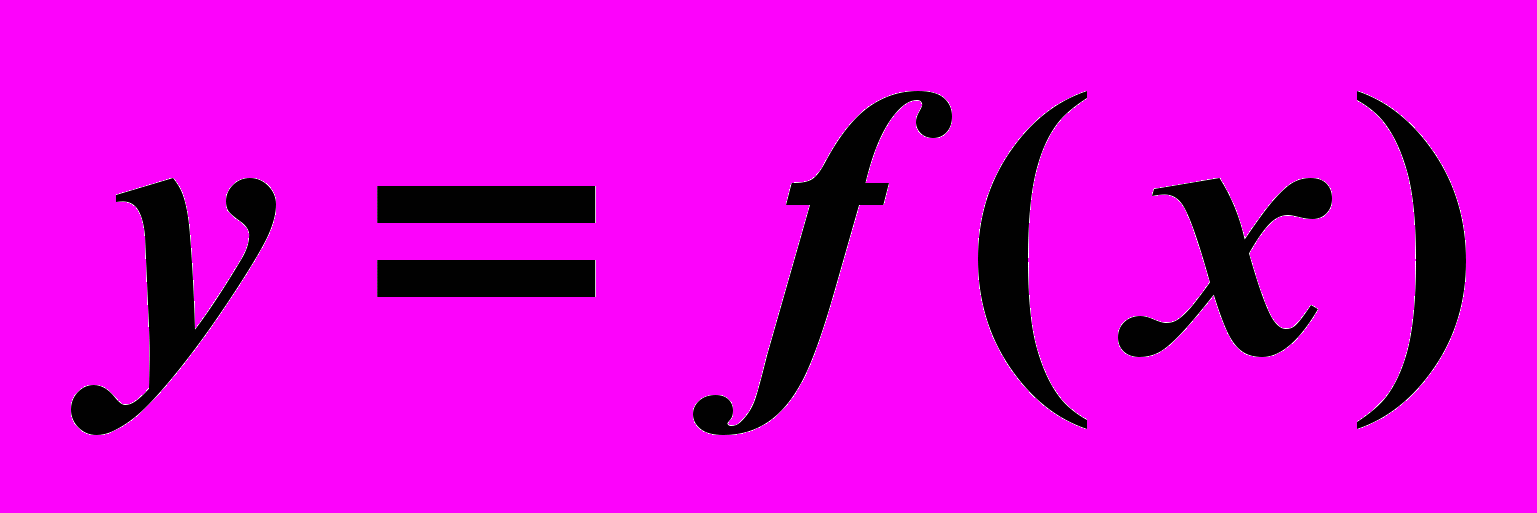 . В этом случае
. В этом случае 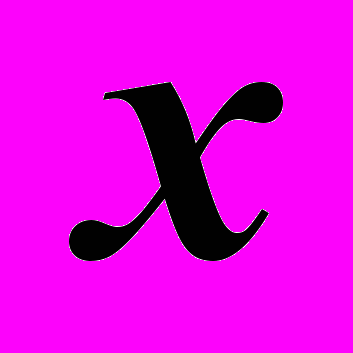 носит название независимой переменной, а
носит название независимой переменной, а  - зависимой переменной.
- зависимой переменной.Ряд физических процессов можно описать (или построить мдели этих процессов) с помощью непрерывных функций, т.е. функций, которые обладают свойством непрерывности в каждой точке
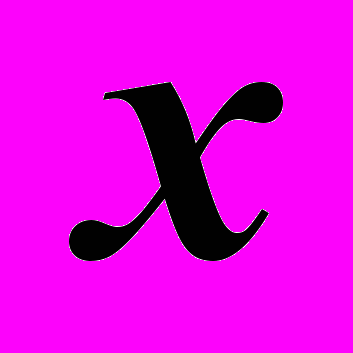 , принадлежащей областям их определения.
, принадлежащей областям их определения.Определение. Функция f, определенная на выпуклом множестве XRn, называется выпуклой, если
f(x1 + (1-)x2) f(x1) + (1-)f(x2)
при всех x1, x2 X, [0,1].
Определение. Функция называется вогнутой, если функция -f является выпуклой.
Рисунок: Пример выпуклой и вогнутой функции.
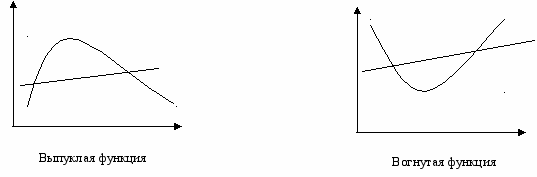
Методы решения задач для функции одной переменной
Метод деления отрезка пополам.
Этот метод применим для выпуклых функций.
Необходимо найти минимум функции f(x) на интервале (a,b) при заданном минимальном значении длины интервала.
Алгоритм.
- Вычислить
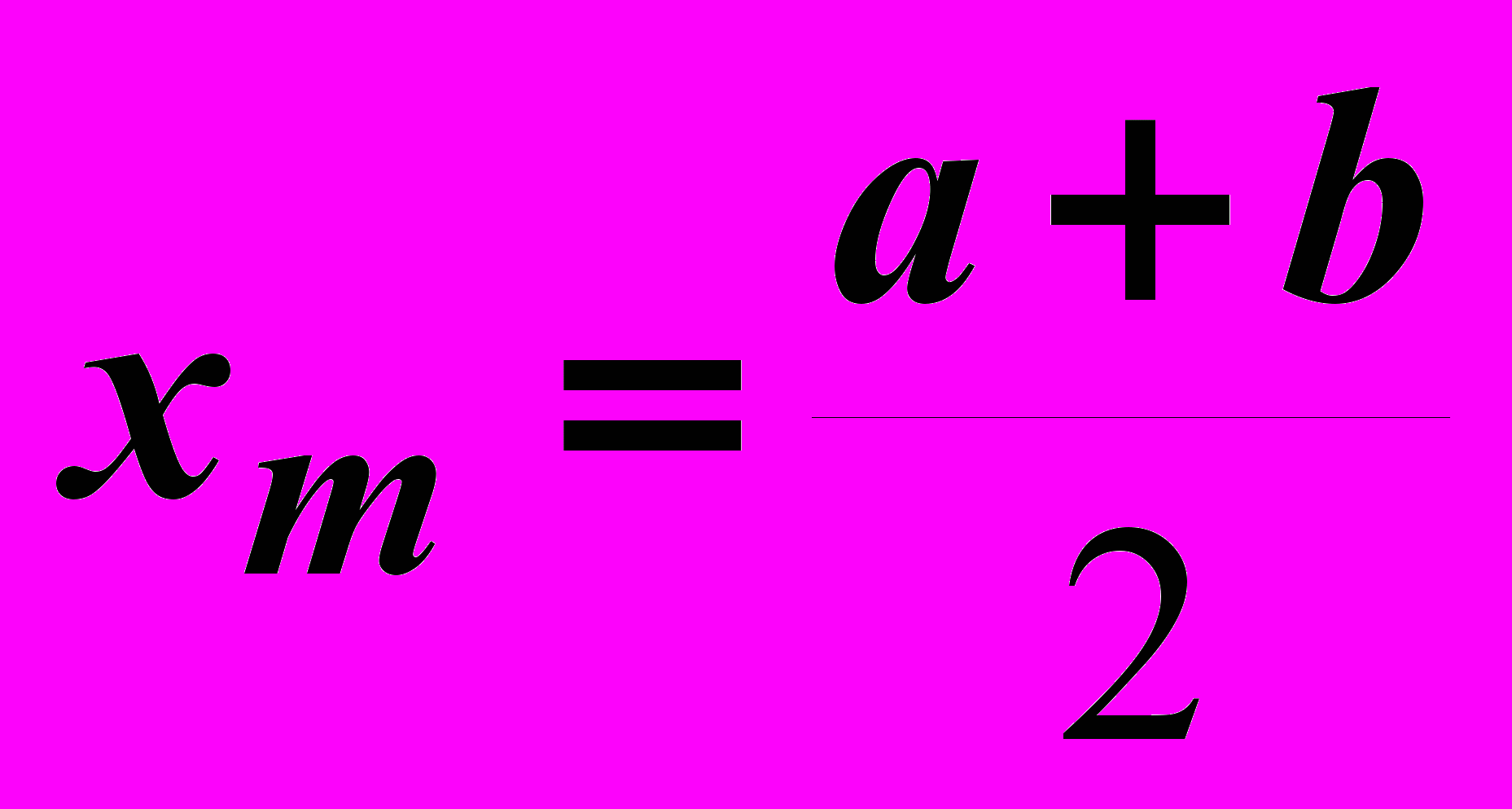 ,
,  ,
, 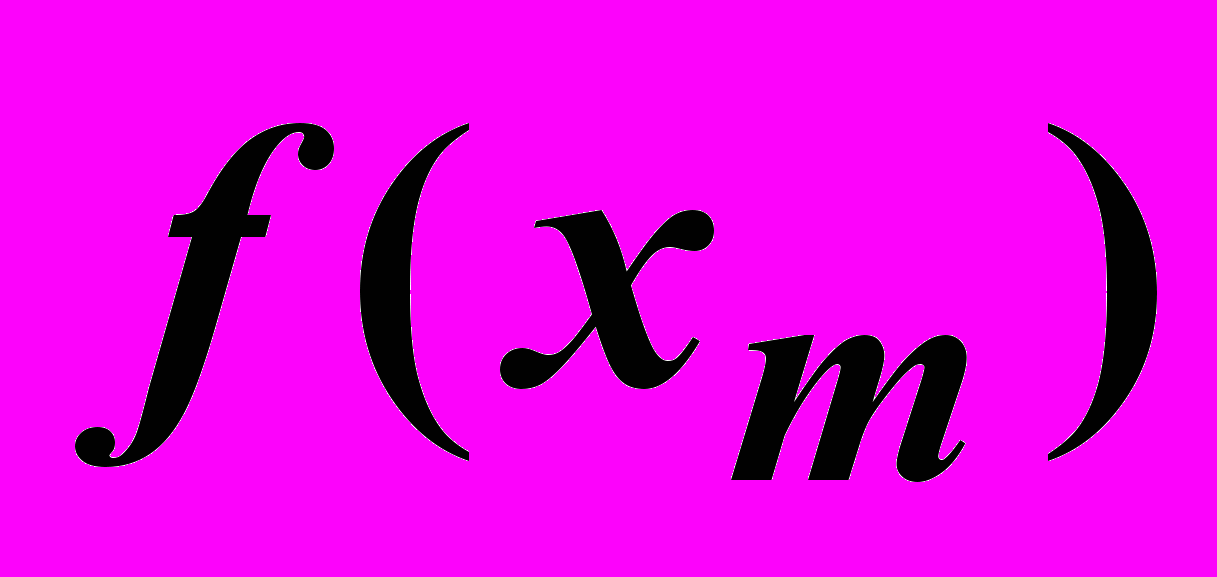 .
.
- Положить
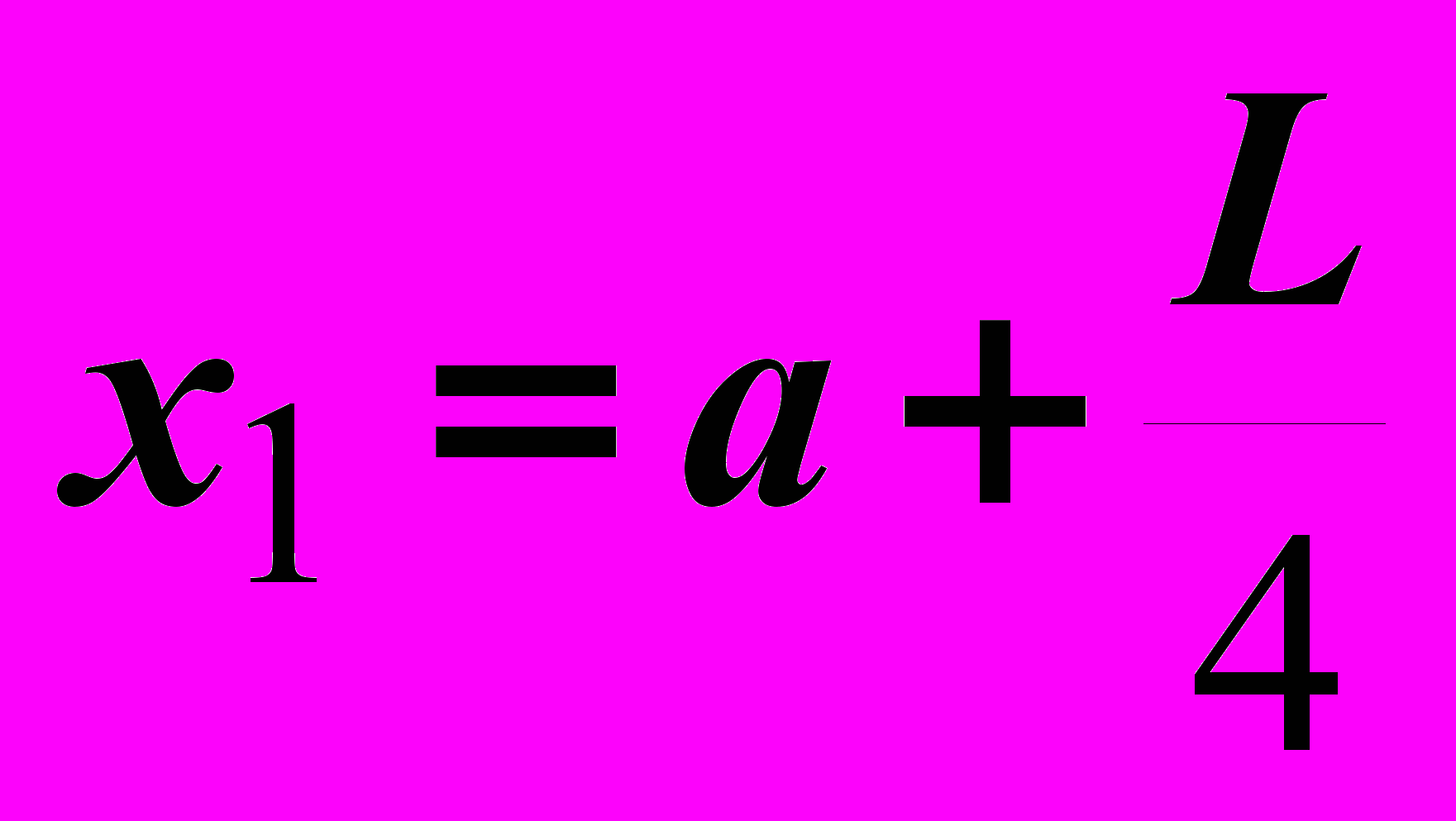 ,
, 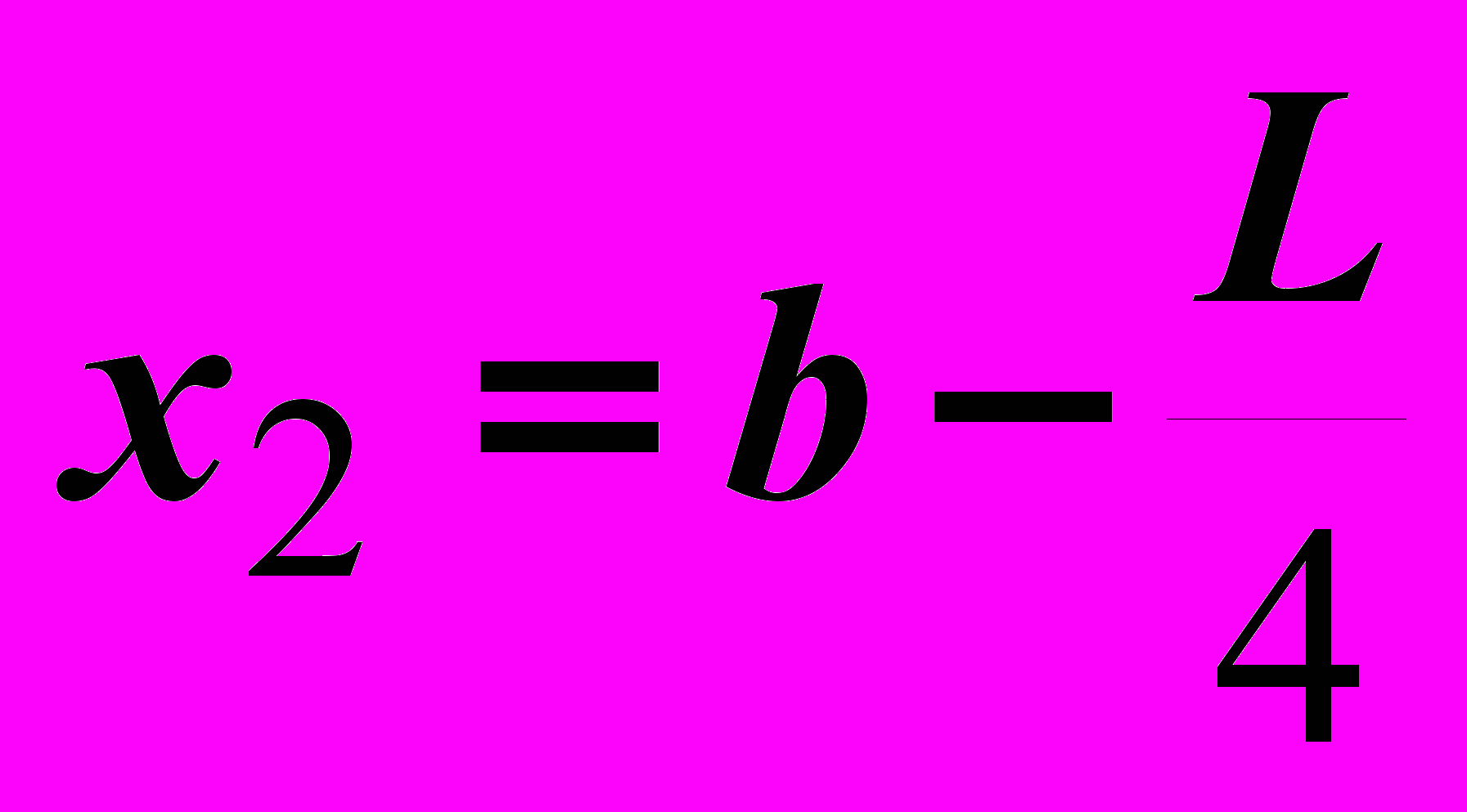 . Вычислить значения функции
. Вычислить значения функции 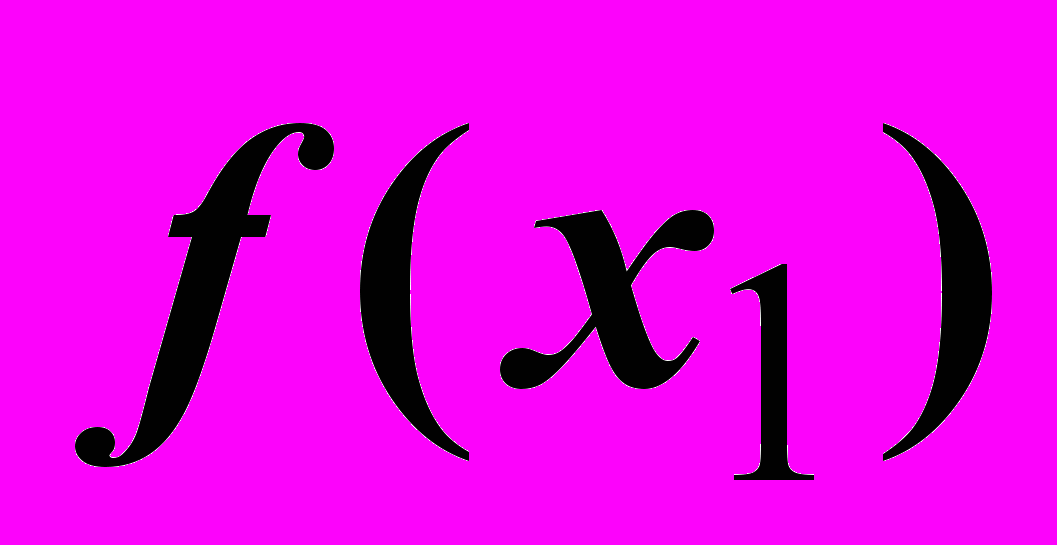 и
и  .
.
- Если
 , то новый отрезок будет
, то новый отрезок будет 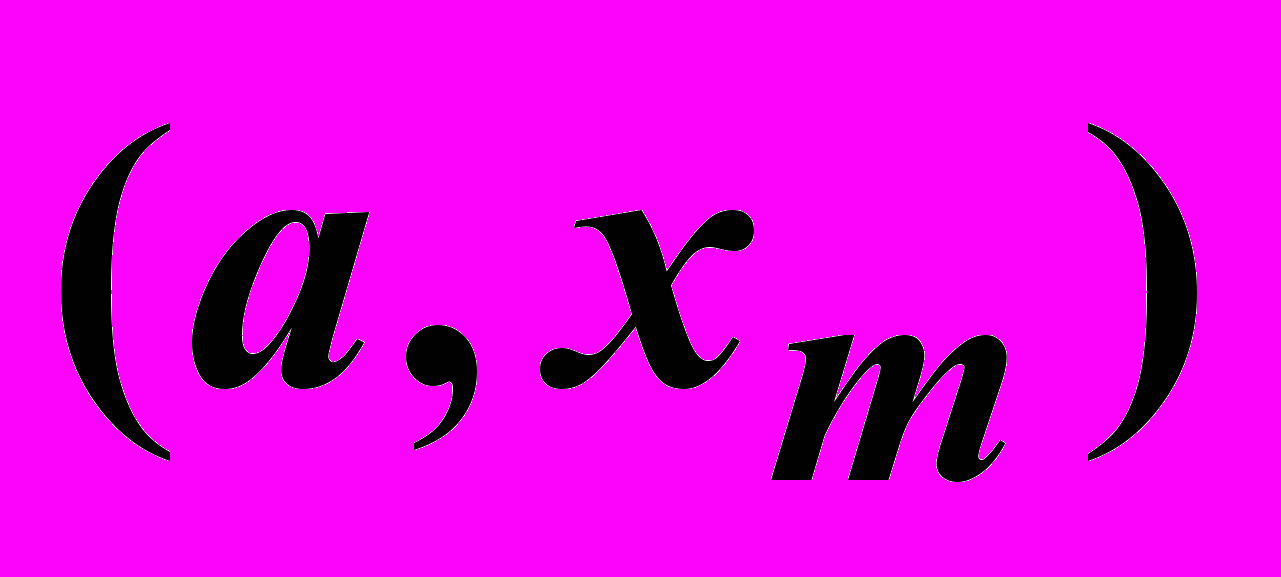 ,
,  .
.
Если
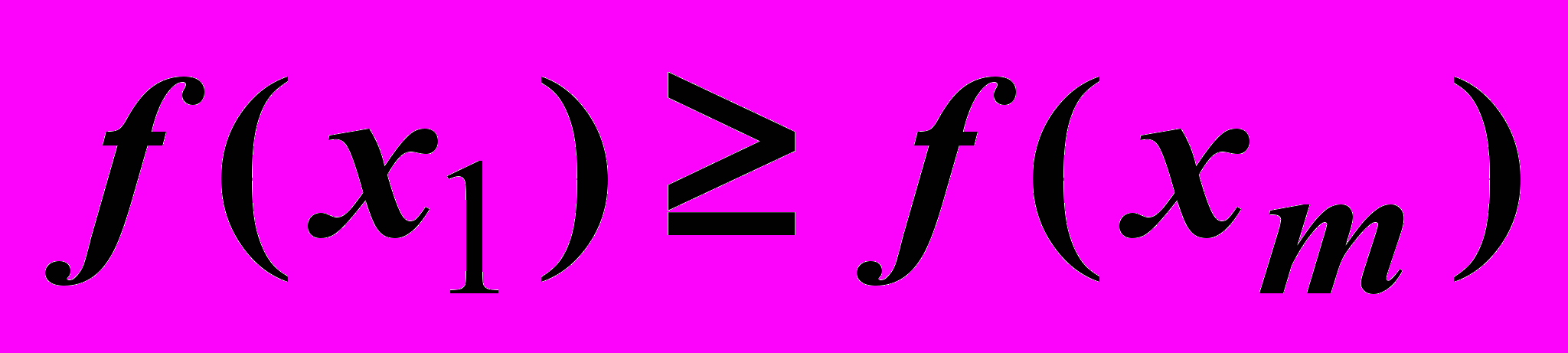 , перейти к шагу 4
, перейти к шагу 4- Если
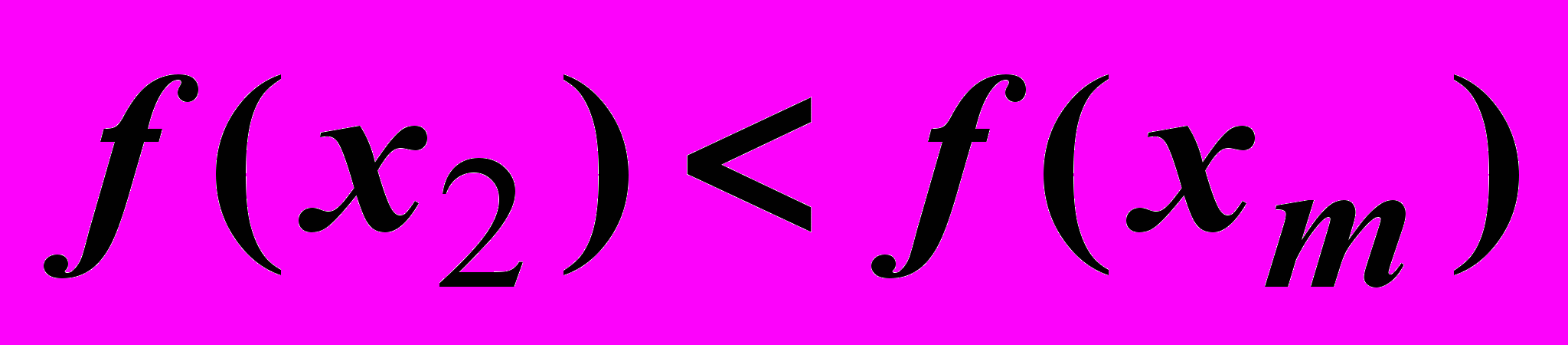 , то новый отрезок будет
, то новый отрезок будет  ,
,  Перейти к шагу 6.
Перейти к шагу 6.
- Если
 , то положить
, то положить  .
.
- Вычислить L=b-a. Если величина длины отрезка меньше заданной, закончить поиск. Точкой минимума будет средняя точка отрезка.
В противном случае вернуться к шагу 2.
Пример. Найти минимум функции f(x)=(100-x)2 в интервале 60 x 150.
Здесь a=60, b=150 и L=150-60=90, xm=(60+150)/2=105, L1=12.
Итерация1: x1=a+(L/4)=60+(90/4)=82,5
x2=b-(L/4)=150-(90/4)=127,5
f(82,5)=306,25 > f(105)=25
f(127,5)=756,25 >f(105)
Таким образом, исключаются интервалы (60, 82.5) и (127.5, 150).
Итерация 2: a=82,5 b=127,5 xm=105 L=127,5-82,5=45
x1=82,5+(45/4)=93,75
x2=127,5-(45/4)=116,25
f(93,75)=39,06 > f(105)=25
f(116,25)=264,06> f(105)=25
Таким образом, интервал неопределенности равен (93.75, 116.25)
Итерация 3: a=93,75 b=116,25 xm=105 L=116,25-93,75=22,5
x1=99,375 x2=110,625
f(99,375)=0,39 < f(105)=25
Интервал неопределенности равен (93.75, 105), его средняя точка есть 99,375 (это точка x1 на итерации 3), которая является точкой минимума на этом отрезке.
Метод Фибоначчи.
Если кроме отрезка задано количество шагов, за которое можно найти экстремум задачи, то для таких задач применим метод Фибоначчи.
Числа Фибоначчи определяются по следующей формуле:
Fn+2=Fn+1 + Fn
F1=1, F2=1
Пример: n=1 F3=2, n=2 F4=3, .....
Однако можно сразу вычислить n-ное значение числа Фибоначчи:
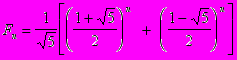
Алгоритм.
- Вычислим значения:
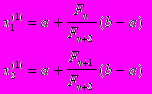
- Если f(x1) < f(x2) , то новый отрезок будет (a, x2), в противном случае - (x1, b).
- На втором шаге имеем следующее выражение для вычисления:
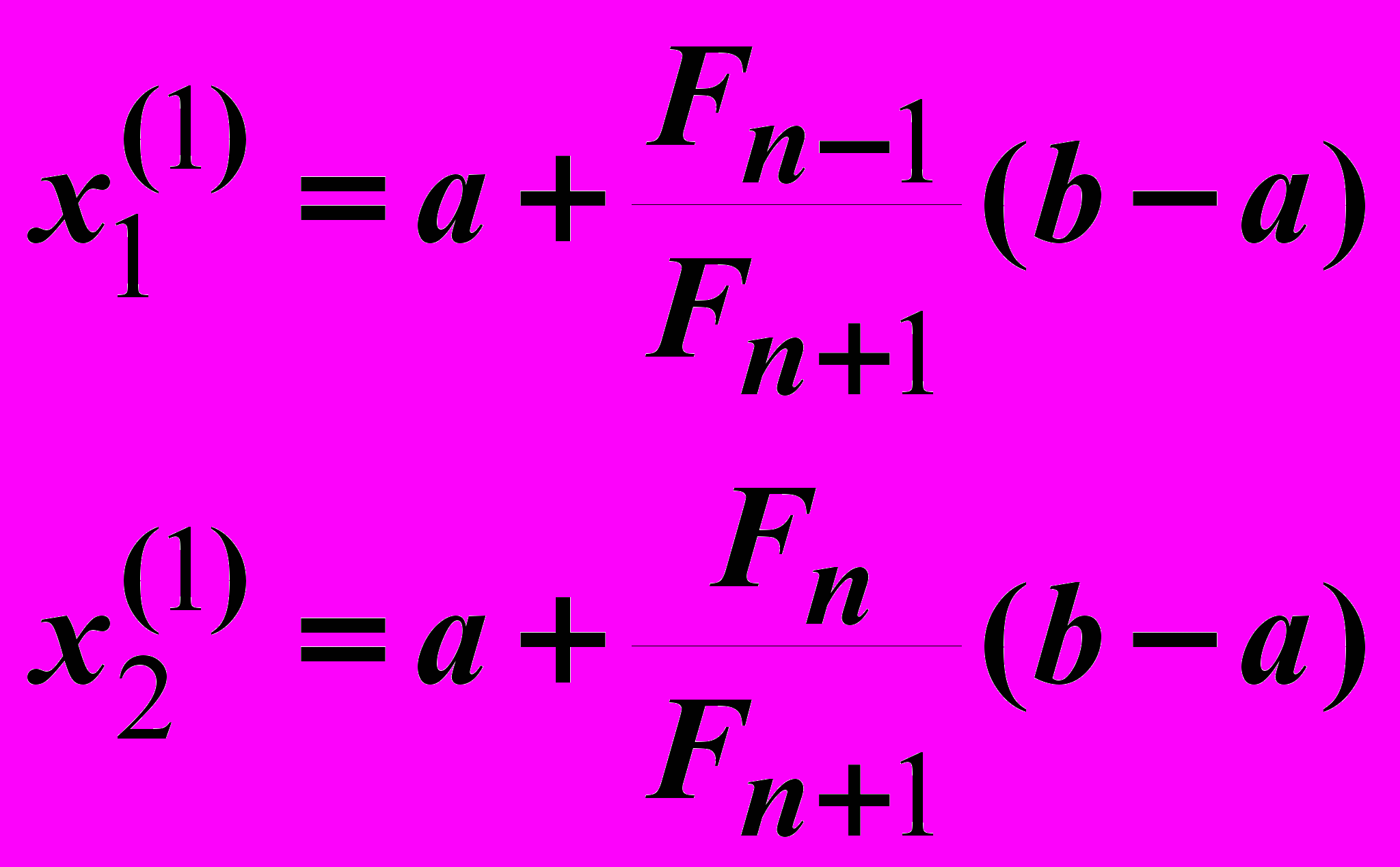
- На n-ном шаге
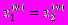 . Эта точка и будет точкой минимума функции.
. Эта точка и будет точкой минимума функции.
Точность метода:
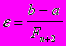
Метод золотого сечения
Определение. Золотым сечением называется такая точка u, в которой отношение всей длины отрезка к большей части отрезка равно отношению этой части к меньшей, т.е.
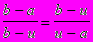
Точка x определяется по следующей формуле:
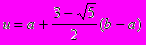
Обозначим точку золотого сечения через x1, тогда x2=b+a-x1.
Дальше поступаем аналогично методу Фибоначчи, т.е. вычисляем значения f(x1) и f(x2). Сужаем отрезок и продолжаем дальше. Поиск продолжается до тех пор, пока длина интервала не станет меньше заданной длины.
Алгоритм.
- Вычислить
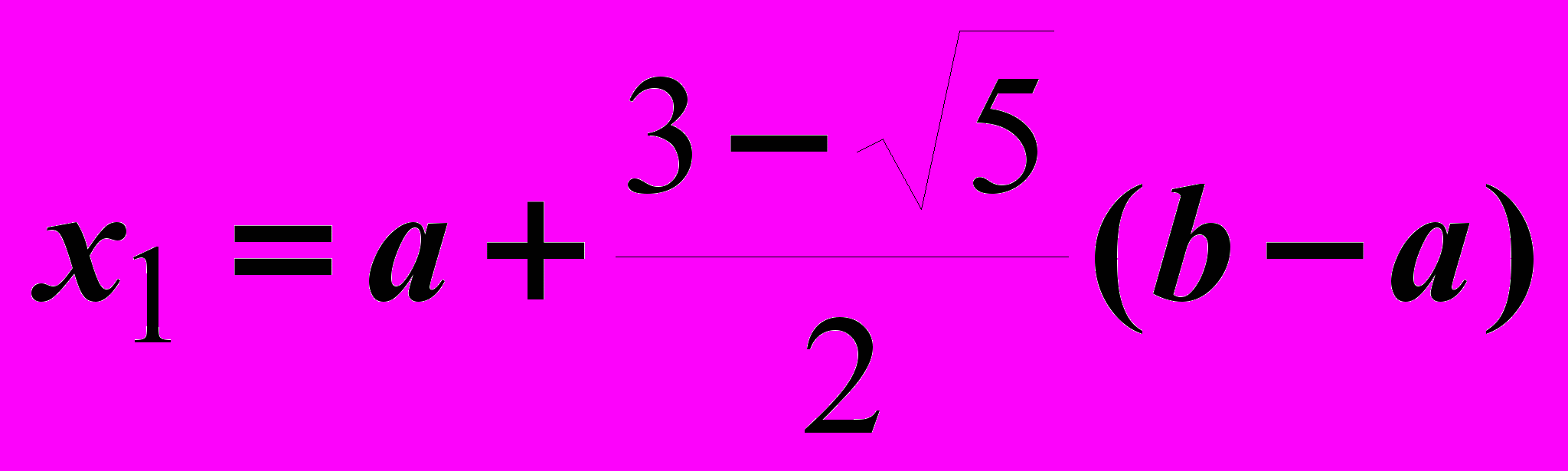 ,
,  .
.
- Вычислить
 .
.
- Если
 , то новый отрезок будет
, то новый отрезок будет  .
.
- Если
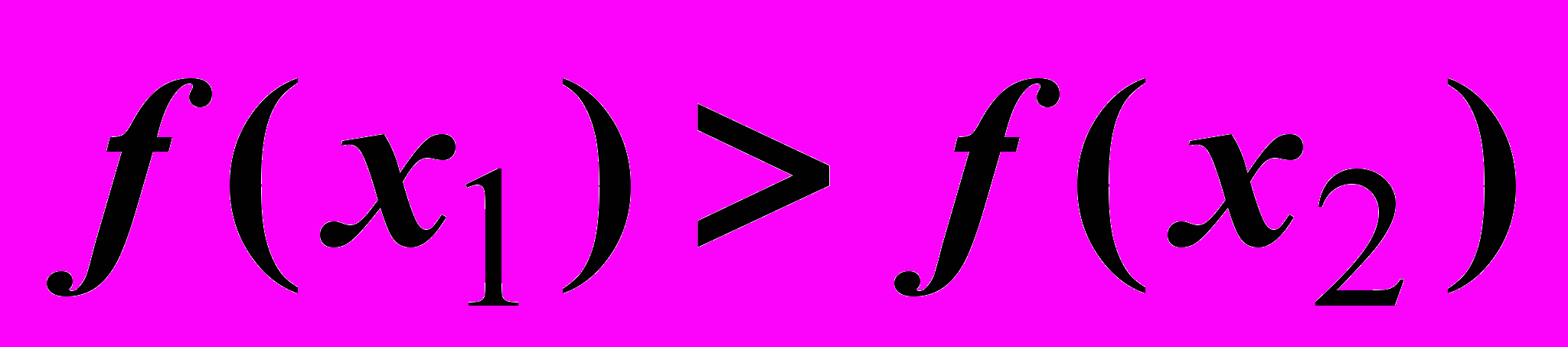 , то новый отрезок будет
, то новый отрезок будет  .
.
- Вычислить
 . Если
. Если 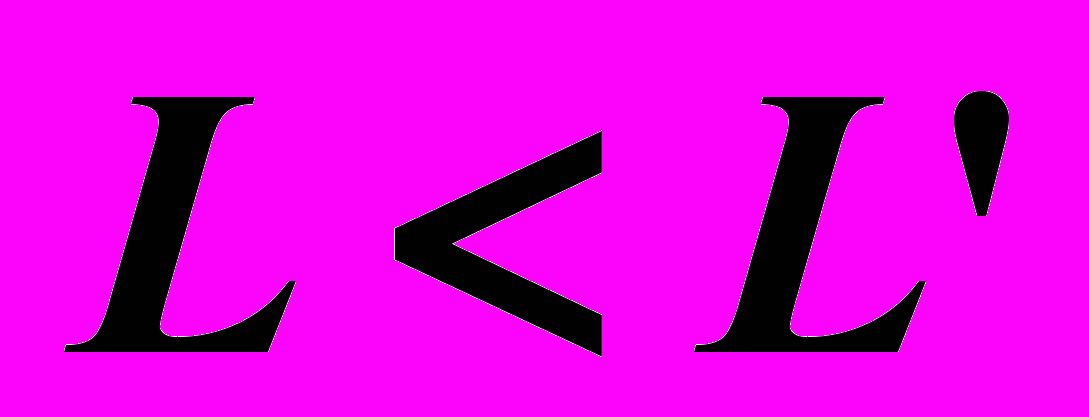 , то найден минимум.
, то найден минимум.
- Если
 , то точка минимума
, то точка минимума  , иначе точка минимума
, иначе точка минимума  .
.
- Если
 , то перейти к шагу 1.
, то перейти к шагу 1.
Точность метода: