Конспект лекций (нф-401) Математическое моделирование. Численный эксперимент

Вид материала

Конспект

Содержание 1) алгоритмические Поисками алгоритмов в математике уделялось большое внимание задолго до того, как появились первые компьютеры. Алгоритм заканчивается после выполнения конечного числа шагов Основные элементы языка fortran-90 (95) Выражения, операции и присваивание Tan(x), cotan(x), atan(x) 4.2. Формула прямоугольников 4.3. Формула Трапеций Заменим подынтегральную функцию на интервале [xn,xn+1] отрезком прямой 4.4. Формула Симпсона Численные методы решения дифференциальных уравнений Постановка задачи Коши. Метод Рунге-Кутта Метод Рунге-Кутта первого порядка (метод Эйлера) Блок-схема алгоритма Модифицированный метод Эйлера (метод Рунге-Кутта второго порядка) Геометрический смысл модифицированного метода Эйлера Метод Рунге-Кутта 4-го порядка

Подобный материал:

• Учебно-методический комплекс учебной дисциплины «численные методы и математическое, 428.92kb.
• Численный алгоритм вариационной инициализации океанологических полей 05. 13. 18 Математическое, 202.48kb.
• Математическое моделирование управляемого движения космических аппаратов, 213.72kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• Математическое моделирование многомерных квазистационарных электромагнитных полей, 380.28kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• И математическое моделирование, 1392.77kb.
• Математическое моделирование термомеханических процессов в системах армированных стержней, 259.01kb.
• Вестник Брянского государственного технического университета. 2007. №4(16) математическое, 61.09kb.
• Программа вступительного испытания собеседования для магистерской программы «математическое, 67.11kb.

Вычислительные методы


Конспект лекций (НФ-401)


1.1. Математическое моделирование. Численный эксперимент.

Одной из характерных черт современных научных исследований стала математизация физического познания, интенсивное применение методов математического моделирования не только в физике, но и других науках (медицина, экология).

В настоящее время практика выдвигает перед учеными различного рода проблемы, достаточно полное исследование которых может быть проведено лишь численным путем или с помощью тщательно поставленного физического эксперимента. Вот почему так важно создание общих численных методов для решения задач математической физики.

Что же такое математическое моделирование?

Это по сути своей определение свойств и характеристик рассматриваемого явления, процесса или состояния путем решения на ЭВМ системы неких уравнений - математической модели.

Важно так сконструировать приближенную модель, чтобы она достаточно полно отражала свойсва рассматриваемого явления и в то же время была доступной для исследования. Последнее обстоятельство очень важно. Часто бывают случаи когда программист (особенно часто этим грешат чистые математики) пытается создать возможно более полную модель, которая потом оказывается нереализуемой. Следует помнить, что ресурсы ЭВМ (память и быстродействие) ограничены.

Таким образом численный эксперимент это моделирование на ЭВМ аналога исследуемого физического (не обязательно) процесса на основе фундаментальных законов, управляющих этим процессом.

Давайте кратко определим основные этапы численного эксперимента и параллельно проведем аналогию с экспериментом физическим.

1). Вначале на основе анализа исследуемого физического объекта разрабатывается алгоритм решения задачи (явления , процесса) и делается его математическое описание (выбирается математическая модель) и. В физическом эксперименте этому этапу соответствует предварительный анализ и выбор схемы эксперимента.

2). Затем для выбранной системы дифференциальных, интегральных или других уравнений составляется код (программа) на одном из языков программирования. В физическом эксперименте на данном этапе осуществляетя изготовление экспериментальной установки и ее отладка.

Результатом этих двух этапов является средство для исследования (программа или экспериментальная установка) интересующего нас явления или процесса.

3). С помощью этих средств проводится машинный счет или серию измерений (диагностики), в результате которых исследователь получает информацию об объекте исследования.

4). Следующим этапом является анализ полученных данных, в результате которого делаются коррективы в математической модели или экспериментальной установке. Такая обратная связь позволяет совершенствовать методологию как вычислительного, так и физического экспериментов.


Численное моделирование особенно важно там, где не совсем ясна картина физического явления, не известен механизм процесса. Например, одним из способов получения многозарядных ионов являетя нагрев пламы при ЭЦР. Хорошо известен механизм ЭЦР, однако что именно происходит в плазме, какие процессы и факторы влияют на эфффективность таких источников до конца не ясно. Зачастую экспериментатор чисто интуитивно работает с установкой. И до сих пор на страницах журналов идут споры о том, какие факторы оказывают наибольшее влияние на параметры ЭЦР плазмы.

Численный эксперимент в определенном смысле представляет собой совершенный эксперимент, так как позволяет независимо менять параметры задачи, более детально изучать те или иные этапы эволюции исследуемого процесса. По образному выражению одного из ученых аналитическое исследование всегда считалось сходным с добычей алмазов. Теперь с появлением мощных ЭВМ возможна добыча другой формы углерода - угля. Хотя и в этом "угле" иной раз встречаются вкрапления алмазов. С помощью численного эксперимента было открыто ряд доселе неизвестных явлений. Следует также заметить, что аналитические и численные методы очень часто сочетаются при решении сложных задач.

Численное моделирование и вычислительный эксперимент являются частью информатики. Становление информатики как научной дисциплины относится к 60-м годам нашего столетия. В общем смысле под информатикой понимают фундаментальную естественную науку, изучающую процессы передачи, накопления и обработки информации.

Термин «Informatique» был введен французами (60-70 гг.). Еще ранее американцы ввели в употребление термин «Computer Science» для обозначения науки, о преобразовании информации, базирующейся на вычислительной технике, В настоящее время термины «Informatique» и «Computer Science» используются в эквивалентном смысле.

Известно широкое определение информатики, данное Международным конгрессом в Японии в 1978 г. Понятие информатики охватывает области, связанные с разработкой, созданием, использованием и материально-техническим обслуживанием систем обработки информации, включая машины, оборудование, математическое обеспечение, организационные аспекты, а также комплекс промышленного, коммерческого, социального и политического воздействия, Отсюда можно выделить главное, что составляет основу современного содержания информатики: ЭВМ и машинную обработку информации.

Содержание информатики определяют три неразрывно связанные между собой части: 1) алгоритмические, 2) программные, 3) технические средства.


1.2. Алгоритмы.

Одним из фундаментальных понятий информатики является понятие алгоритм. Слово алгоритм произошло от имени среднеазиатского ученого аль-Хорезми (IX век) и использовалось в математике для обозначения правил выполнения четырех арифметических действий, С неформальной точки зрения алгоритм – последовательность шагов, которые определяют, каким образом должна быть решена та или иная задача.

Например, алгоритмы конструирования самолетов (описываются в виде некоторых инструкций). Ноты – также являются алгоритмом. Говорят также об алгоритме управления производственным процессом, алгоритме управления полетом ракеты и др.

На основе алгоритма для непосредственного решения задачи создается программа. Собственно программа или программное обеспечение называется Software, в противоположность инструменту, машине, на которой программы выполняются, называемым Hardware. Перед непосредственным решением проблемы алгоритм должен быть представлен в виде программы. Алгоритм (наука об алгоритмах) в информатике, как науке, играет ведущую роль.

Наука об алгоритмах начиналась как одна из ветвей математики. Поисками алгоритмов в математике уделялось большое внимание задолго до того, как появились первые компьютеры.

В качестве примера можно привести один из алгоритмов Евклида (Euclid) для определения наибольшего общего делителя двух целых положительных чисел. Такой алгоритм можно представить словесно.

Step 1. Приписать (задать) переменным M и N соответственно большее и меньшее значение из двух заданных чисел.

Step 2. Разделить M на N и обозначить остаток как R.

Step 3. Если R не 0, приписать M значение N, а N значение R и вернуться к шагу 2. В противном случае наибольший общий делитель равен N.

Обратим внимание на следующие особенности алгоритмов.

1. Алгоритм имеет некоторое число входных величин – аргументов, задаваемых до начала работы, Цель выполнения алгоритма – получение результата, имеющего вполне определенное отношение к исходным данным, То есть алгоритм указывает последовательность действий по переработке исходных данных в результаты. Если один и тот же алгоритм можно применять для решения целого класса однотипных задач, это свойство алгоритма называют массовостью.
   
2. Чтобы алгоритм был выполнен, он должен быть понятен исполнителю. Понятность алгоритма означает знание исполнителя о том, что надо делать для исполнения алгоритма.
   
3. Алгоритм представлен в виде конечной последовательности шагов. Говорят, алгоритм имеет дискретную структуру. Каждый его очередной шаг начинается после выполнения предыдущего.
   
4. Алгоритм заканчивается после выполнения конечного числа шагов, хотя некоторые его шаги могут выполняться многократно. Однако часто при решении математических задач процедура может описывать бесконечный процесс. Приходится прерывать ее искусственно.
   
5. Каждый шаг алгоритма должен быть четко и недвусмысленно определен, не допускать той или иной трактовки. Другими словами, алгоритм рассчитан на чисто механическое исполнение. Это очень важный момент. Если поручить исполнение разным исполнителям, то они придут к одному и тому же результату. Именно эта особенность алгоритма дает возможность поручить его исполнение автомату или машине.
   
6. Алгоритм должен быть выполнен за разумное конечное время. Все о чем мы говорили – лишь интуитивное понятие алгоритма, то есть не четкое и не строгое. Лишь с появлением алгоритмически неразрешимых задач появилась потребность в построении формального определения алгоритма. Но об этом немного позже.
   

Изучение алгоритмов занимает центральное место в информатике, Как только найден алгоритм, решение задачи не требует более понимания принципов, на которых алгоритм построен, Таким образом, если поручить выполнение задачи машине, ее уровень разумности (интеллекта) определяется возможностью «понимания» тот или иного алгоритма. В принципе, как только найден алгоритм, уже можно создать машину для его исполнения, Другое дело, если такого алгоритма нет, тогда решение задачи за пределами возможности компьютера.

3. Скорость вычислений на ЭВМ.
   

Несмотря на бурное развие вычислительное техники, значительное возростание мощности компьютеров (рис. 1), создание многопараметрических численных моделей является сложнейшей задачей. Важно так сконструировать приближенную модель, чтобы она достаточно полно отражала свойсва рассматриваемого явления и в то же время была доступной для исследования. Последнее обстоятельство очень важно. Часто бывают случаи когда программист (особенно часто этим грешат чистые математики) пытается создать возможно более полную модель, которая потом оказывается нереализуемой. Следует помнить, что ресурсы ЭВМ (память и быстродействие) ограничены.




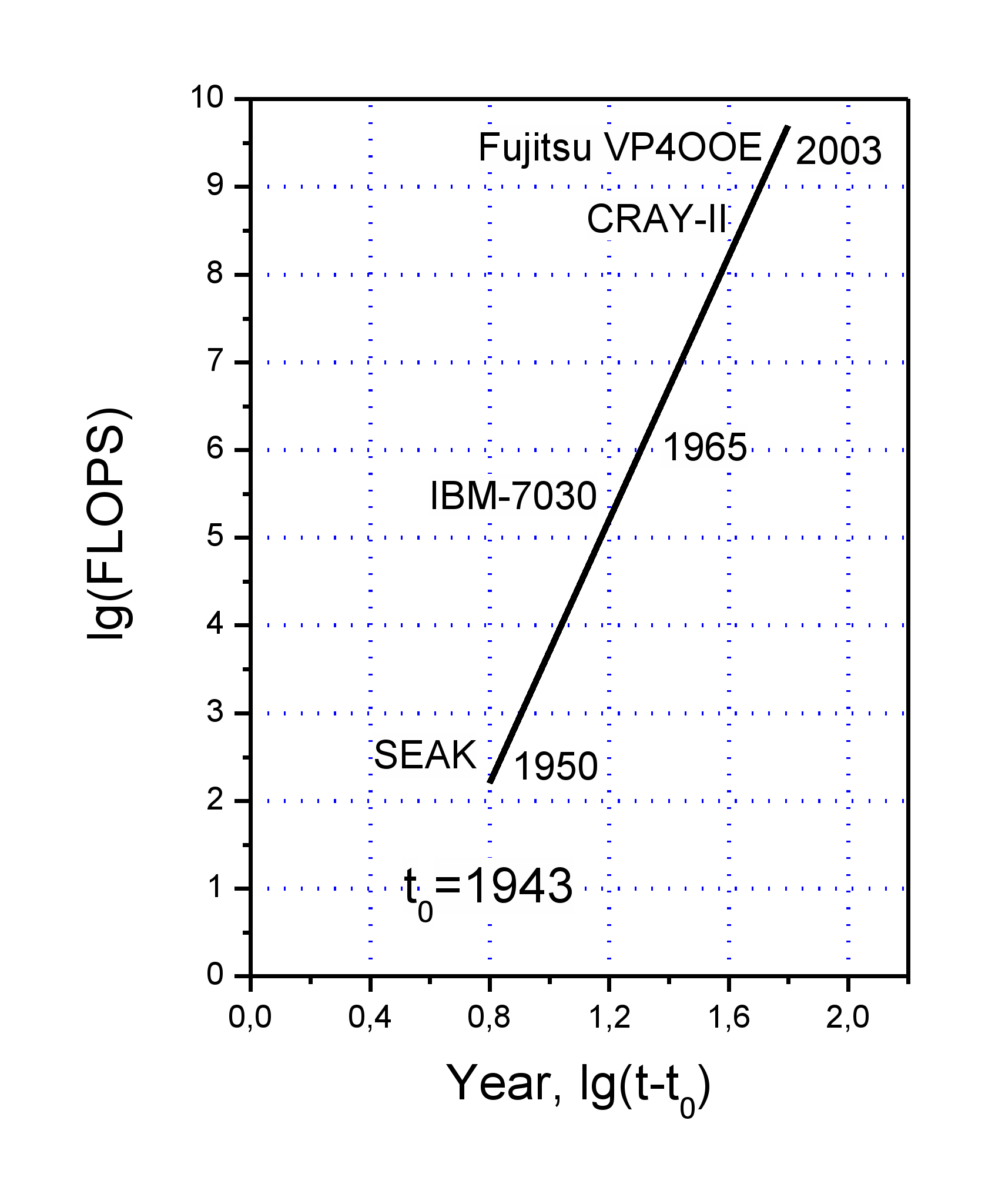
Рис. 1. Рост скорости вычислений на ЭВМ.


При работе с вещественными данными выполняются операции с плавающей точкой (запятой) каждую из которых принято называть флопом. (от floating point operation – “flop” ). Таким образом, общая трудоемкость задачи определяется количеством выполненных при ее решениии флопов.

Например, вычисление суммы ряда, в котором n членов 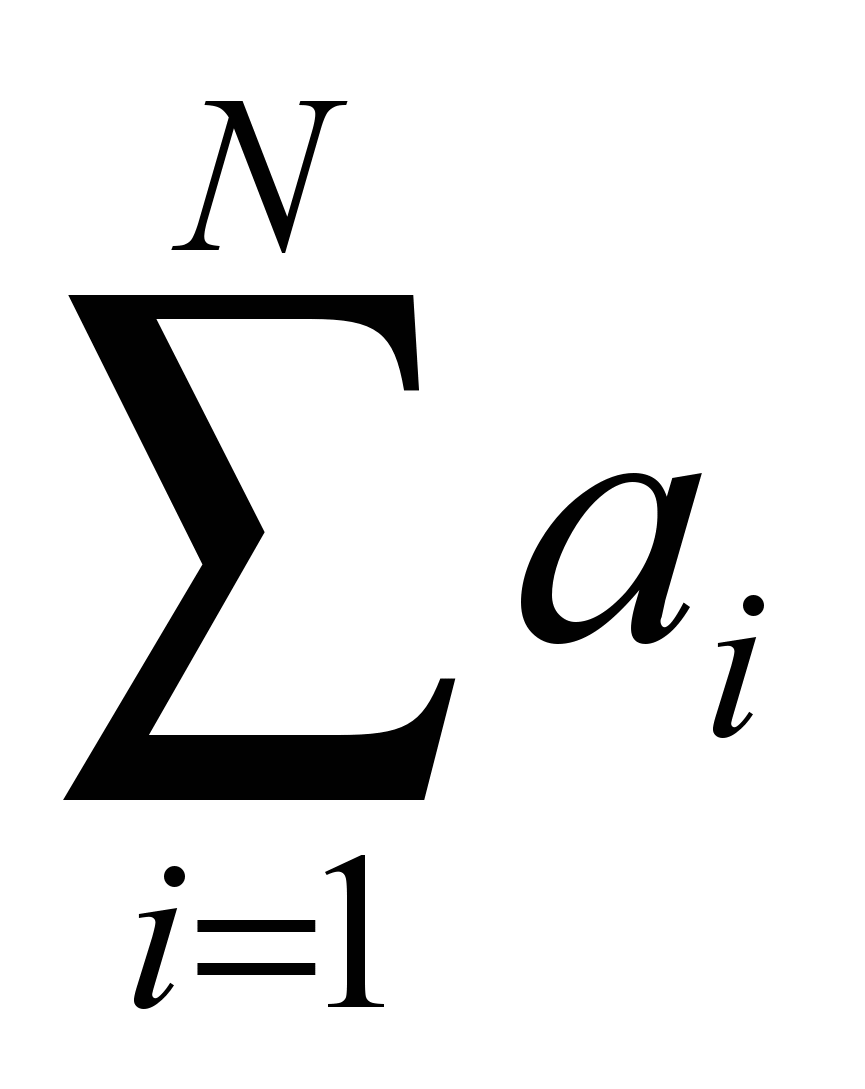, требует N флопов, а скалярное произведение двух векторов размера N требует 2N флопов.

Однако, если даже подсчет флопов выполнен точно, он даст лишь грубую оценку эффективности алгоритма, поскольку не учитывает затраты на индексацию, обмены с памятью и другие программные издержки. При параллельных вычислениях производительность программы существенно зависит от организации данных и оптимизации алгоритма. Коды, имеющие одинаковое число флопов, но разные структуры данных могут серьезно различаться производительностью.


1.4. Об особенностях компьютерной арифметики и точности расчетов.

Не говоря уже о сложных физических процессах, далеко не всегда удается найти аналитическое решение даже на первый взгляд, казалось бы, простой задачи. Примером может служить хотя бы задача взаимодействия трех тел. Пытаясь решить какую-то задачу с помощью численных методов необходимо помнить, что непрерывное описание физических процессов заменяется дискретным. Это одно из коренных отличий численного исследования от аналитического. Помимо этого надо учитывать, что точность записи числа на ЭВМ ограничена. Во-первых ограничен диапазон их представления, а во-вторых, представление вещественных и комплексных чисел не всегда является точным. Например, все вещественные числа типа real(4) расположены в интервале от –3.402328E+38 до 3.402328E+38. Кроме того, между представимыми числами в ЭВМ существуют разрывы, то есть, для каждого числа value > 0 существует минимальное положительное число _min которое в сумме с value даст число большее, чем value. Для положительных чисел  меньших, чем _min

value + value.

Чем меньше value, тем меньше _min.

Это свойство машинной арифметики можно трактовать и по другому. Запись числа производится 7 значащими цифрами для обычной точности real(4) и 15 значащими цифрами для двойной точности real(8).


1.4.1. Ошибки округления

Ограничения, связанные с представлениями вещестсвенных и комплексных чисел.

В любом численном расчете необходимо проводить анализ ошибок, проводится расчет вручную или с помощью ЭВМ. Причиной ошибок являются неточности исходных данных, а также округление данных.

Рассмотрим ставший уже классическим пример вычисления синуса (или косинуса) с помощью разложения в ряд Тейлора:





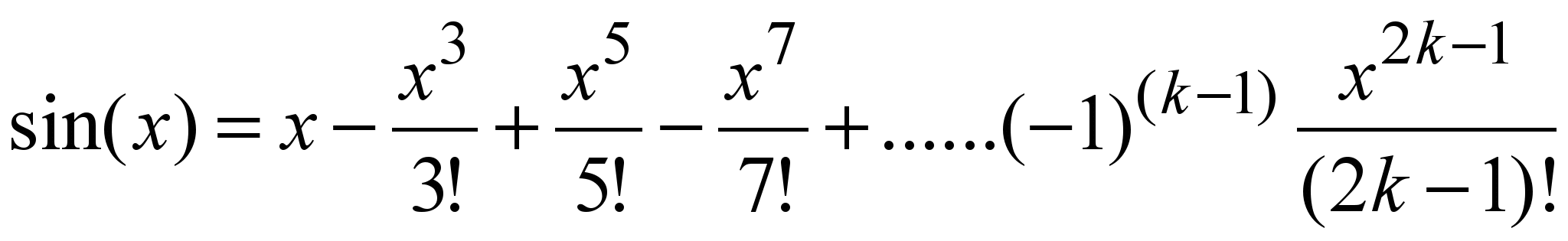
Считается, что этот ряд годится для любого конечного x, а ошибка, происходящая от ограничения ряда конечным числом членов, не превосходит по модулю первого отброшенного члена.

Однако, для больших углов использование этого ряда для численного расчета абсолютно бесполезно. Все теоретические рассуждения относительно обрывания ряда были бы справедливы, если бы вычисления проводились с бесконечным числом значащих цифр. Если, например, попытаться просчитась на ЭВМ значения синуса, проводя расчет с 7 значащими цифрами и остановить счет, когда очередной член ,

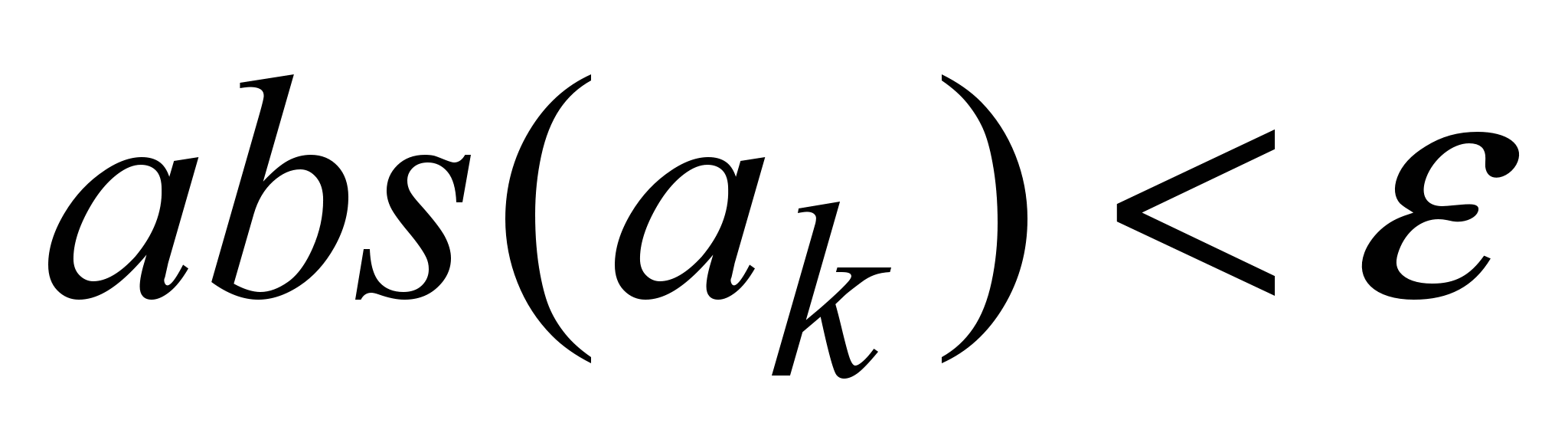то для x=25, sin(x)=24(!). Не на много улучшается результат и при счете с 15 значащими цифрами.

В этом примере ошибочный результат обусловлен тем, что расчет ведется с конечным числом значащих цифр, то есть вследствие ошибок округления. И вообще, без анализа ошибок вычислений нельзя сказать что либо определенное относительно точности результата.


1.4.2. Принято проводить оценку относительной и абсолютной ошибок.

Абсолютная ошибка - разность между истинным значением величины и ее приближенным значением.

Относительная ошибка - отношение абсолютной ошибки к приближенному значению. (Более естественным было бы определить относительную ошибку по отношению к точному значению, но оно не известно).

В процессе проведения численных расчетов возможны различные типы ошибок. Среди них выделим два основных: ошибки ограничения (ошибки метода) и ошибки округления.

Давайте подробнее остановимся на примере расчета синуса угла. Составим алгоритм решения этой задачи в виде блок-схемы. Очевидно, ключевым моментом является определение множителя перехода от члена ряда 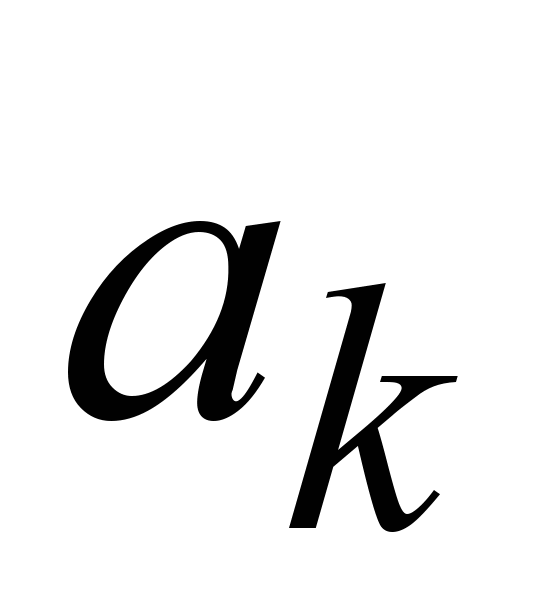к .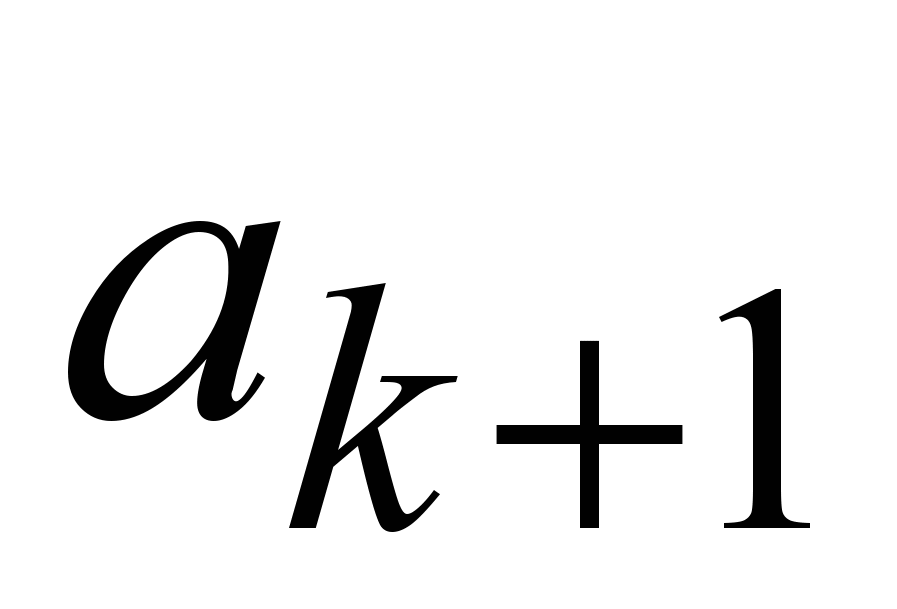

Очевидно, это будет 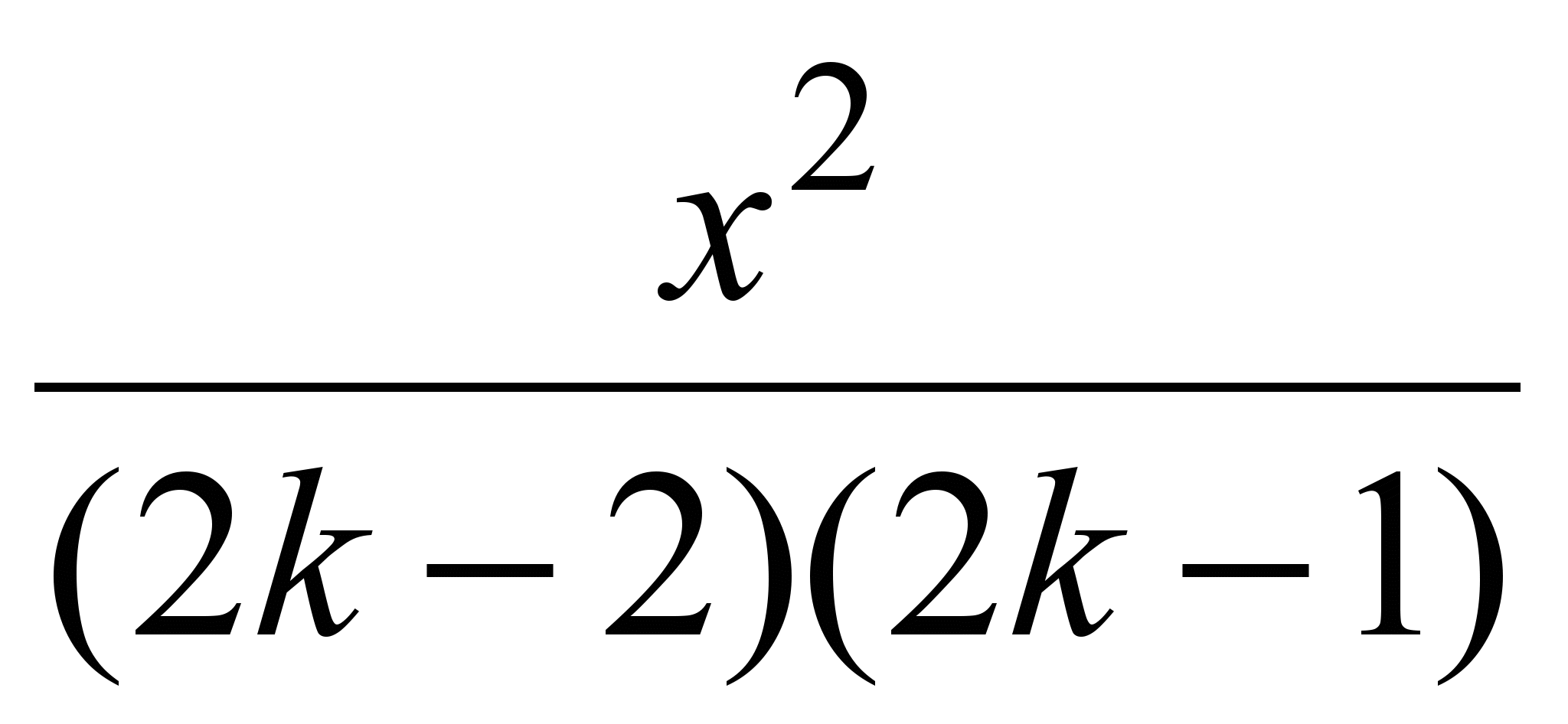с изменением знака на каждом шаге.

Тогда алгоритм в виде блок схемы будет иметь следующий вид.





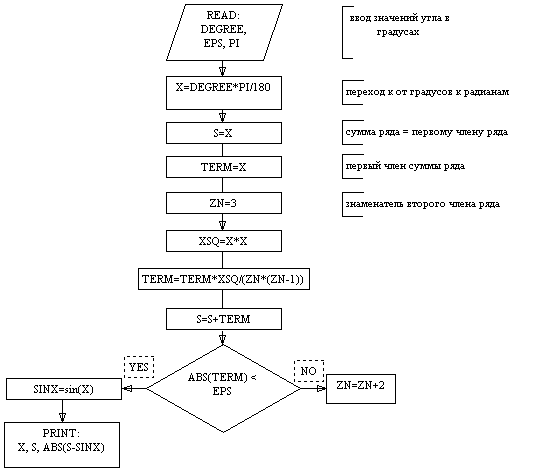
Короткое резюме.

1) Ошибки ограничения

Эти ошибки определяются тем приближенным методом, с помощью производится вычисление. Например, вычисление интегралов по методу трапеций.


2) Ошибки округления.

Так как ЭВМ работает с числами ограниченной длины, то результаты всех арифметических операций округляются.

При работе с двумя целыми числами в Фортране результатом будет также целое число.

Можно дать некоторые рекомендации при работе с ЭВМ с целью уменьшения ошибок при выполнении арифметических операций.

1) Если необходимо произвести сложение и вычитание большой последовательности чисел, нужно начинать вычисления с наименьших по модулю чисел.

2) По возможности следует избегать вычитания двух почти равных чисел.

3) Если задача такова, что в ней фигурируют или очень большие, или очень маленькие числа, то нужно произвести нормировку всех величин, так, чтобы основные величины изменялись где-то около единицы.

1. Методы решения нелинейных уравнений.
   

Пусть задано уравнение вида f(x)=0. Найти его корни. Задачи такого типа разбиваются на два этапа: вначале необходимо локализовать корни, т.е. определить на оси x отрезки, содержащие не более одного корня, затем на обнаруженных интервалах производится уточнение корней, т.е. вычисление с требуемой точностью.

Будем считать, что нам известно, что на отрезке [a,b] уравнение имеет единственный корень.


2.1.1. Метод деления отрезка пополам (метод бисекций).

Делим отрезок [a,b] пополам. Пусть x = (a+b)/2. Теперь, учитывая то что функция f(х) на концах отрезка поиска имеет противоположные знаки, определяем по знакам f(a), f(b) и f(x) какому из двух полученных отрезков принадлежит искомое решение.

С новым отрезком проделываем аналогичную операцию и делаем так до тех пор, пока не выполнится условие (b-a)/2ⁿ  , где  – требуемая погрешность, а n – число половинных делений исходного отрезка.


1-ый шаг. Отрезок делится пополам и производится анализ знака f(x₁) в точках a, x₁ , b. Если знак f(b) совпадает со знаком f(x₁), то очевидно корень находится внутри отрезка x 11 .

2-ой шаг. Делим полученный новый отрезок (a,b) пополам и снова анализируем знаки f(a), f(x₂ ) и f(b). Если знаки f(x₂), f(b) не совпадают, берем b=x₂ .

Процесс будет выполняться до тех пор, пока не выполнится условие a-b   , где  - точность с которой надо найти решение.


2.1.1. Метод последовательных приближений (метод простых итераций).

Представим исходное уравнение в виде x = (x) (ниже будет показано, как это можно сделать, даже когда разрешить его относительно x не удается). Точное решение исходного уравнения x^* обратит, разумеется, это новое уравнение в тождество x^*  (x^*). Построим следующую последовательность x_n+1 =  (x_n) , задавшись некоторым начальным числом x₀ из интервала [a,b]. Оказывается, если функция (x) в окрестности искомого корня удовлетворяет условию Липшица: |  (x) -  (x)|  q |x - x| при q = const < 1,

x,x {| x – x^* |  R}, то построенная последовательность сходится к корню исходного уравнения, и выполняется оценка | x_n – x^* |  qⁿ |x₀ – x^* |, т.е. имеет место сходимость со скоростью геометрической прогрессии. Условие Липшица можно заменить более простым (но и менее сильным!) условием ограниченности первой производной в окрестности корня: |(x)|  q < 1. Искать же подходящую для итераций функцию можно в виде

(x) = x – g(x)f(x), подбирая g(x) так, чтобы удовлетворить требуемым условиям. На практике g(x) часто ищут в виде константы g(x)    const, что приводит к так называемому методу релаксаций.

Отмечая предпочтительность метода простых итераций в виду простоты его реализации и высокой скорости сходимости, следует подчеркнуть необходимость обращения особого внимания на выбор функции (x), так как удачный ее выбор (простота вычисления, q <<1) существенно сокращает число итерационных шагов. Неудачный или вовсе неправильный ее выбор может привести к неоправданным затратам времени. Именно поэтому очень часто применяется метод половинного деления, как требующий меньшего времени на теоретический анализ исходных данных, а также позволяющий проводить и локализацию корней уравнения.


3) Метод Ньютона-Рафсона.


Рассмотрим теперь еще один простой, однако более быстро сходящийся метод. Выберем на отрезке [a,b] некоторое число x₀, которое послужит нам начальным приближением для корня уравнения. Теперь заменим в окрестности этой точки функцию f (x) отрезком касательной:

f (x)  f (x₀) + f (x₀)(x-x₀).

Теперь, решив это линейное уравнение f (x₀) + f (x₀)(x-x₀) = 0, получим x = x₀- f (x₀)/ f (x₀). Этот процесс можно продолжить, трактуя новое решение как новое уточненное значение корня: x_n+1 = x_n- f(x_n)/ f(x_n), что приводит нас к рекуррентному соотношению для вычисления корня. К сожалению вычисление производной на практике в данной ситуации затруднительно, поэтому заменим ее конечной разностью f(x_n)  (f (x_n)- f (x_n-1)) / (x_n-x_n-1), что по сути означает замену касательной на секущую (хорду). Итак мы получили соотношение:

x_n+1 = x_n- f (x_n) (x_n-x_n-1)/ (f (x_n)- f (x_n-1)).

Геометрическая интерпретация метода ясна из Рис.2. Для начала вычислений необходимы две точки x₀ и x₁, в качестве которых можно, например, взять границы отрезка поиска. Вычисления заканчивают, когда два подряд вычисленных приближения отстоят друг от друга не более чем на требуемую величину погрешности: | x_n+1 – x_n |  .










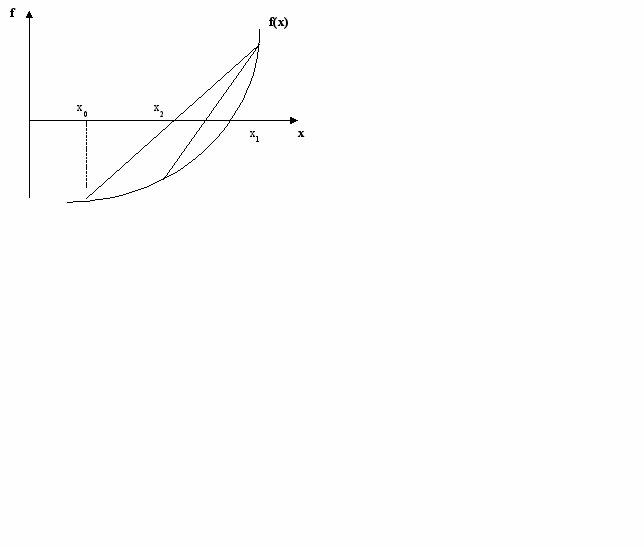
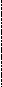
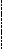
Рис. 2. Геометрическое представление метода Ньютона-Рафсона.


Метод сходится, если

1) выбрано достаточно близко к корню уравнения,

2) производная не становится слишком большой,

3) производная не слишком близк

а к нулю.


ОСНОВНЫЕ ЭЛЕМЕНТЫ ЯЗЫКА FORTRAN-90 (95)

1. Типы данных:
   

3.1.1. Целый – INTEGER(1), BYTE от –128 до 127 INTEGER(2) от –32768 до 32767 INTEGER(4) или INTEGER от 2147483648 до 2147483647 Примеры integer :: a=2, b=4 ! Обязательно наличие разделителя integer a/2/, b/4/ ! Разделитель может отсутствовать integer c(10) /1,2,3,4,5,5,5,5,5,6/ ! статический массив и его инициализация 3.1.2 Вещественный: REAL(4), REAL от –3.4028235Е+38 до –1.1754944Е-38. 0 от 1.1754944Е-38 до 3.4028235Е+38. REAL(8) от –1.797693134862316D+308 До –2.225073858507201D-308 или DOUBLE PRECISION Примеры: integer, parameter :: m=3, n=5, l=4 real :: d(m,n)=15.0, h=3.2 # real a(6,7), d , r ! Объявляет массив a ранга 2 real b(2,3,10) ! Размер массива – 60, форма массива (2,3,10). Если ранг, форма и размер массива совпадают – согласованные массивы. 3.1.3. Комплексный: COMPLEX, COMPLEX(4) – упорядоченная пара вещественных чисел одинарной точности. COMPLEX(8) – упорядоченная пара вещественных чисел двойной точности. Примеры: complex :: c, z=(3.0, 4.0) c=z/2 ! (1.50000, 2.0000)

2. ВЫРАЖЕНИЯ, ОПЕРАЦИИ И ПРИСВАИВАНИЕ
   

3.2.1. Арифметические выражения. Операции, кроме возведения в степень, производятся слева направо в соответствие с приоритетом. Примеры: -a+b+c (((-a)+b)+c) a**b**c (a**(b**c)) Запрещается: делить на нуль, возводить в отрицательную или нулевую степень, возводить отрицательное число в нецелочисленную степень. 3.2.2. Операции отношения. .LT. или < .LE. или <= .GT. или > .GE. или >= ! Пробелы в записях являются ошибкой .EQ. или == .NE. или /= 3.2.3. Логические операции. .NOT. .AND. .OR. Пример. Условие попадания точки в область пересечения эллипса (2,1) и графиками функций y=|x|. if(x**2/4.0+y**2<1.0.and.y>abs(x)) then write(*,*) ‘Inside the region’ else write(*,*) ‘Outside the region’ end if

3.3. Управляющие операторы и конструкции.

Оператор GOTO безусловного перехода (используется для организаций повторных действий, т.е. цикла. integer(1) in 10 continue print*, ‘Введите число от 1 до 10’ read*, in if(in>=1.and.in.<=10) then print*, ‘Вы ввели: ‘, in else print*, ‘Ошибка, повторите ввод‘, in goto 10 end if

3.4. Элементные числовые функции.

ABS(a) – абсолютная величина целого, вещественного или комплексного аргумента. Пример: complex:: z=(3.0,4.0) write (*,*) abs(z) ! 5.0 (тип результата REAL(4) AINT(a) – обрезает вещественную величину a до целого числа. ANINT(a) – выполняет округление а. Real :: a(3)=(/2.8, -2.8, 1.3/) Write(*,*) anint(a) ! 3.000000 3.000000. 3.000000 Write(*,*) nint(2.8), nint(2.2) ! 3 2 Write(*,*) nint(a(2)), nint(2.2) ! -3 -2 Write(*,*) aint(2.6), aint(-2.6) ! -3 -2 CONJG(z) – возвращает комплексно-сопряженное Print*conjg(3.0,5.6) ! (3.000000,-5.600000) DIM(x,y) – возвращает x-y, если x>y и 0, если x<=y. Вычисление max и min. # write(*,*) max(5.2,3.6,9.7) ! 9.7 write(*,*) max1(5.2,3.6,9.7) ! 9 write(*,*) amin0(5,-3,9) ! -3

3.5. Математические элементные функции.

EXP(x) – возвращает ex =e**x в случае комплексного x=(a,b) результат e**a*(cos(b)+i*sin(b)) LOG(x) в случае комплексного x=(a,b), log(x)=(log(sqrt(x**2+b**2)) LOG10(x) SQRT(x) SIN(X), SIND(X), ASIN(X) ASIND(X) – возвращает в интервале от –90 до 90. TAN(X), COTAN(X), ATAN(X) ATAN2(Y,X) – возвращает арктангенс в интервале от –pi до pi.

6. Массивы.
   

Массив – это именованный набор из конечного числа объектов одного типа. В отличие от простых переменных, предназначенных для хранения отдельных значений, массив является составной переменной. Массивы могут быть статическими и динамическими. Под статические массивы выделяется при компиляции заданный объем памяти, которая занимается массивом все время выполнения программы. Память под динамические массивы выделяется во время выполнения программы, при необходимости может быть изменена или освобождена.

4.1. Вычисление определенных интегралов.


Рассмотрим простые и удобные методы, позволяющие проинтегрировать функцию f(x) на некотором интервале [a,b]

_b

J=  f(x)dx.

^a

Далее мы полагаем, что подынтегральная функция ограничена. Разобъем отрезок [a,b] на N отрезков. Точки разбиения x_n (n=0,1…,N) называют узлами, величины h_n= x_n+1- x_n – шагами

_N-1

интегрирования. Ясно, что  h_n=b-a. Удобнее работать с постоянным шагом ⁿ⁼⁰

интегрирования h=(b-a)/N. Обозначим f_nf(x_n). Запишем наш интеграл в виде


_N-1 x_{n+1 N-1} x_n+1

J=   f(x)dx=  J_n, где J_n=f(x)dx.

ⁿ⁼⁰ x_n ⁿ⁼⁰ x_n

4.2. Формула прямоугольников

Полагая h_n достаточно малым, заменим J_n площадью прямоугольника с основанием h_n и высотой f_n+1/2 =f(x_n+h_n/2). В результате мы приходим к формуле прямоугольников:

_N-1

J   h_n f_n+1/2.

ⁿ⁼⁰

4.3. Формула Трапеций

Заменим подынтегральную функцию на интервале [x_n,x_n+1] отрезком прямой

f(x)  f_n+ (f_n+1- f_n) (x- x_n)/ (x_n+1- x_n).


Выполняя далее интегрирование по отрезкам, придем к формуле трапеций:


_N-1

J  (1/2)  h_n (f_n+1+f_n)_.

ⁿ⁼⁰

В случае постоянного шага h формула принимает вид:

h

J  — [f₀+2f₁+…+2f_N-1+f_N].

2

4.4. Формула Симпсона

Заменим подынтегральную функцию на отрезке [x_n,x_n+1] параболой:

f(x)  f_n+1/2+ (f_n+1- f_n) [x- (x_n+1+x_n)/2]/ h_n+ (f_n+1-2f_n+1/2+f_n) [x- (x_n+1+x_n)/2]²/ (h_n²/2)

Выполняя далее интегрирование по отрезкам, придем к формуле Симпсона:

J  (1/6)  h_n (f_n + 4f_n+1/2+f_n+1)_.

На практике используют несколько иное представление этой формулы. При постоянном шаге h, а также беря значения функции из пары соседних отрезков (вместо f_n+1/2 используем f_n ,т.е. N должно быть четным), получим:

h

J  — [f₀+4f₁+2f₂+4f₃+…+2f_N-2+4f_N-1+f_N].

6

Заключение

Для рассмотренных выше квадратурных формул получаются следующие оценки погрешности   J_{приближ} - J_точное при постоянном шаге интегрирования:

формула прямоугольников:   (1/24)(b-a)h² max |f |

^[a,b]

формула трапеций:   (1/12) (b-a)h² max |f |

^[a,b]

формула Симпсона (при использовании пар отрезков):   (1/180)(b-a) h⁴ max |f |

^[a,b]

Разумеется, эти оценки зависят от гладкости подынтегральной функции. Обычно величины производных не удается оценить, тогда контроль точности результатов численного интегрирования можно проводить, выполняя вычисления с меньшим шагом. Если J^(h) – приближение, полученное с шагом h, а J^(h/2) получено с половинным шагом, то оценить погрешность последнего вычисленного значения можно так:

 J^(h/2) - J_точное  J^(h/2) - J^(h).

Для получения требуемой точности  повторяем вычисления при последовательно уменьшающемся шаге до тех пор, пока не выполнится  J^(h/2) – J^(h) .

Можно также использовать автоматическую коррекцию шага для контроля локальной погрешности. Тогда длина интервала h_n, в следствие уменьшения или увеличения начальной длины, выбирается такой, чтобы локальная ошибка удовлетворяла неравенству

 J_n – J_{n точное}  J^(h/2) - J^(h)   h_n / (b-a).

Тогда ошибка по всему отрезку интегрирования не превзойдет сумму локальных ошибок

 h_n / (b-a) = . Автоматическая коррекция шага приводит к его уменьшению в областях резкого изменения функции и к его увеличению там, где функция меняется слабо. Такая процедура вычисления является более эффективной с точки зрения количества выполняемых операций и получаемой точности.


ЛИТЕРАТУРА

1. Калиткин Н.Н. Численные Методы. М., Наука, 1978.
   
2. Федоренко Р.П. Введение в Вычислительную Физику. М., Издательство МФТИ, 1994.
   
3. Форсайт Дж., Малькольм М., Моулер К. Машинные методы Математических Вычислений. М., Мир, 1980.
   
4. Поттер Д. Вычислительные Методы в Физике. М., Мир, 1975.
   

5.1. Конечно-разностные методы.

Идея метода конечных разностей по пространственным переменным:

функции, заданные на континууме 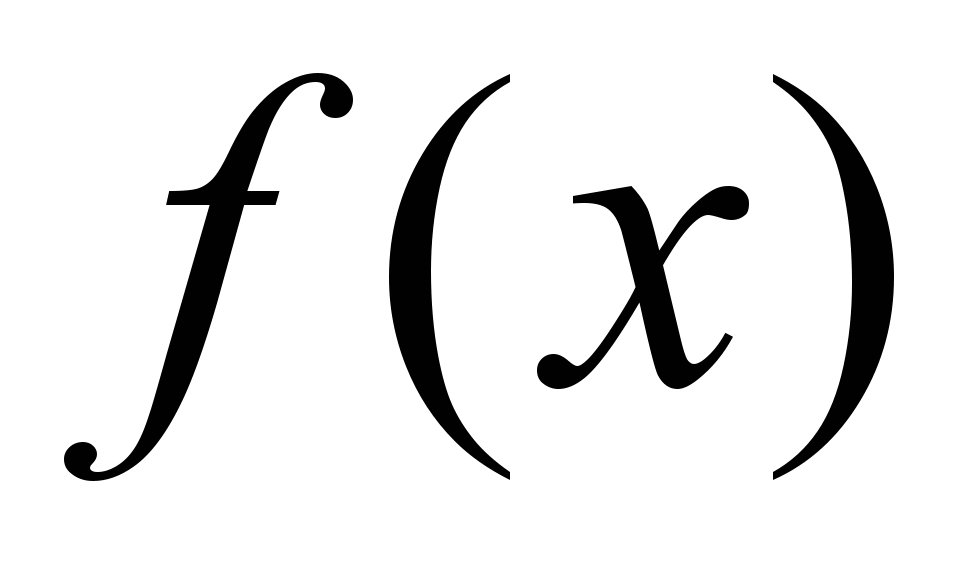заменяются сеточным вектором 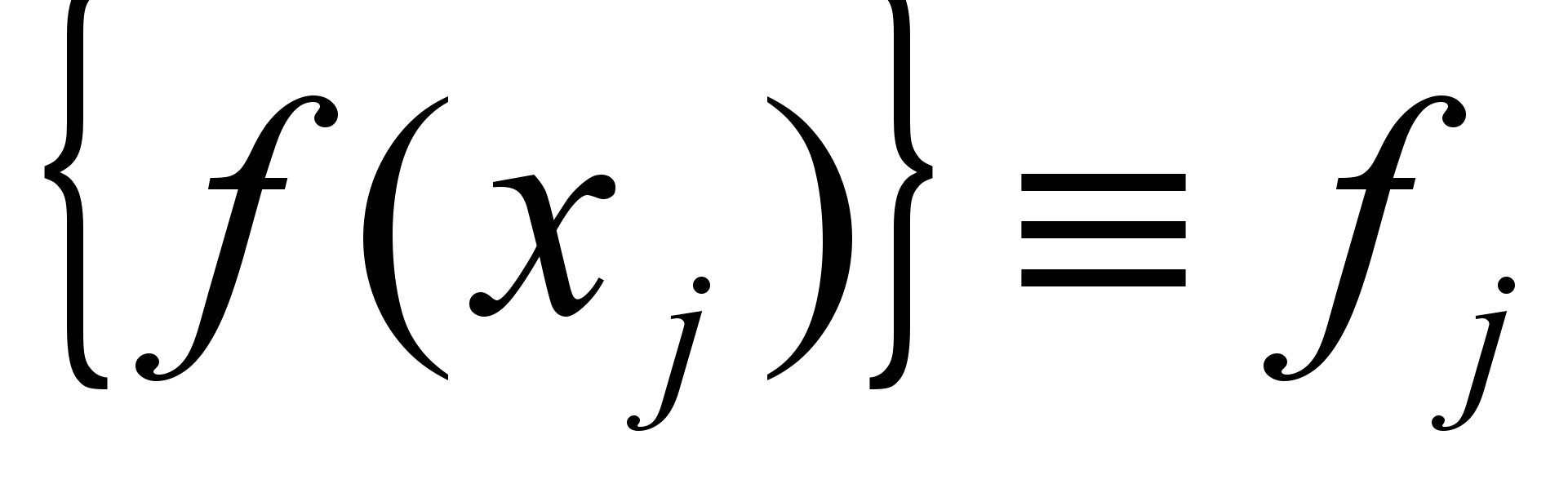. В свою очередь дифференциальный оператор 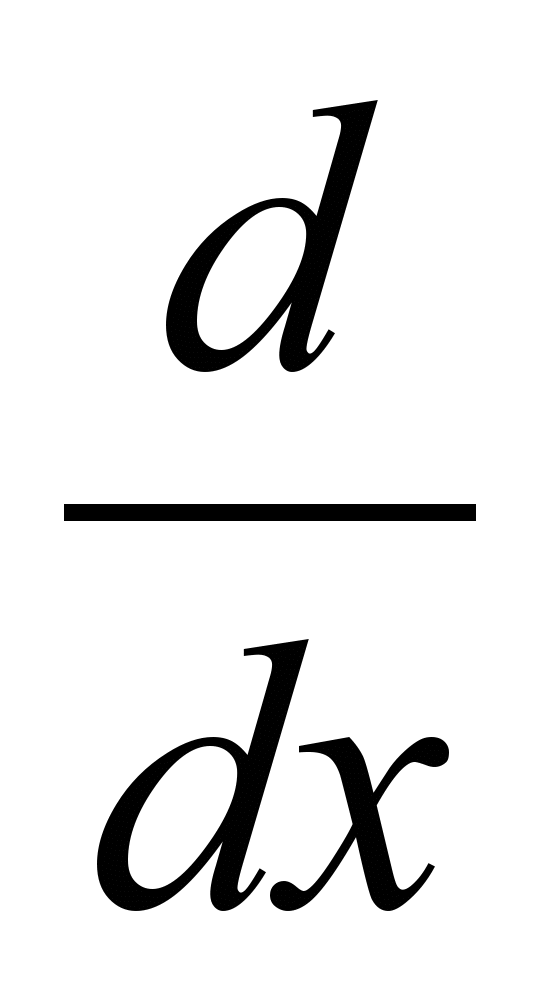заменяется на 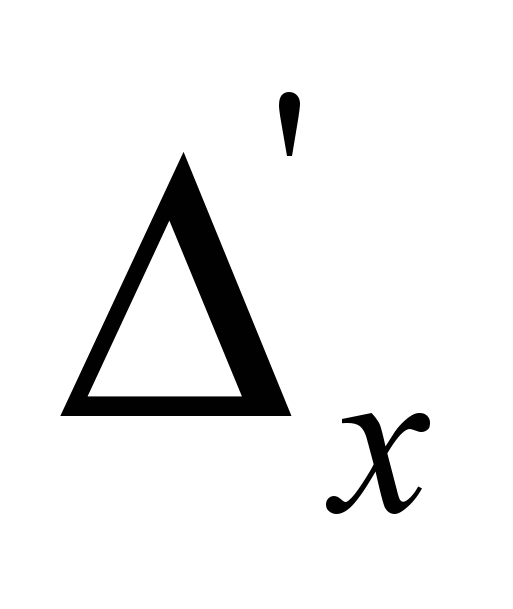. Здесь j – номер узла пространственной сетки. Если выбран шаг сетки 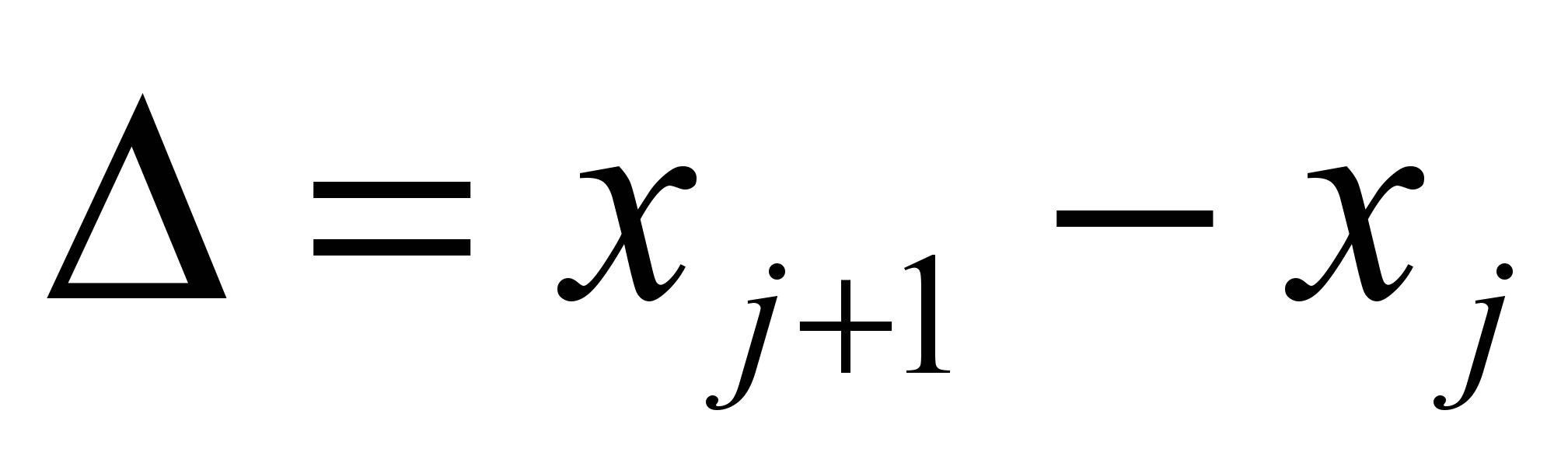, то конечно-разностная производная может быть определена как 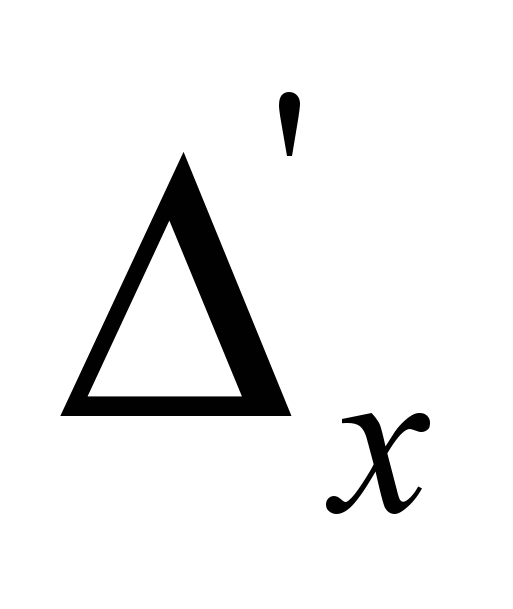=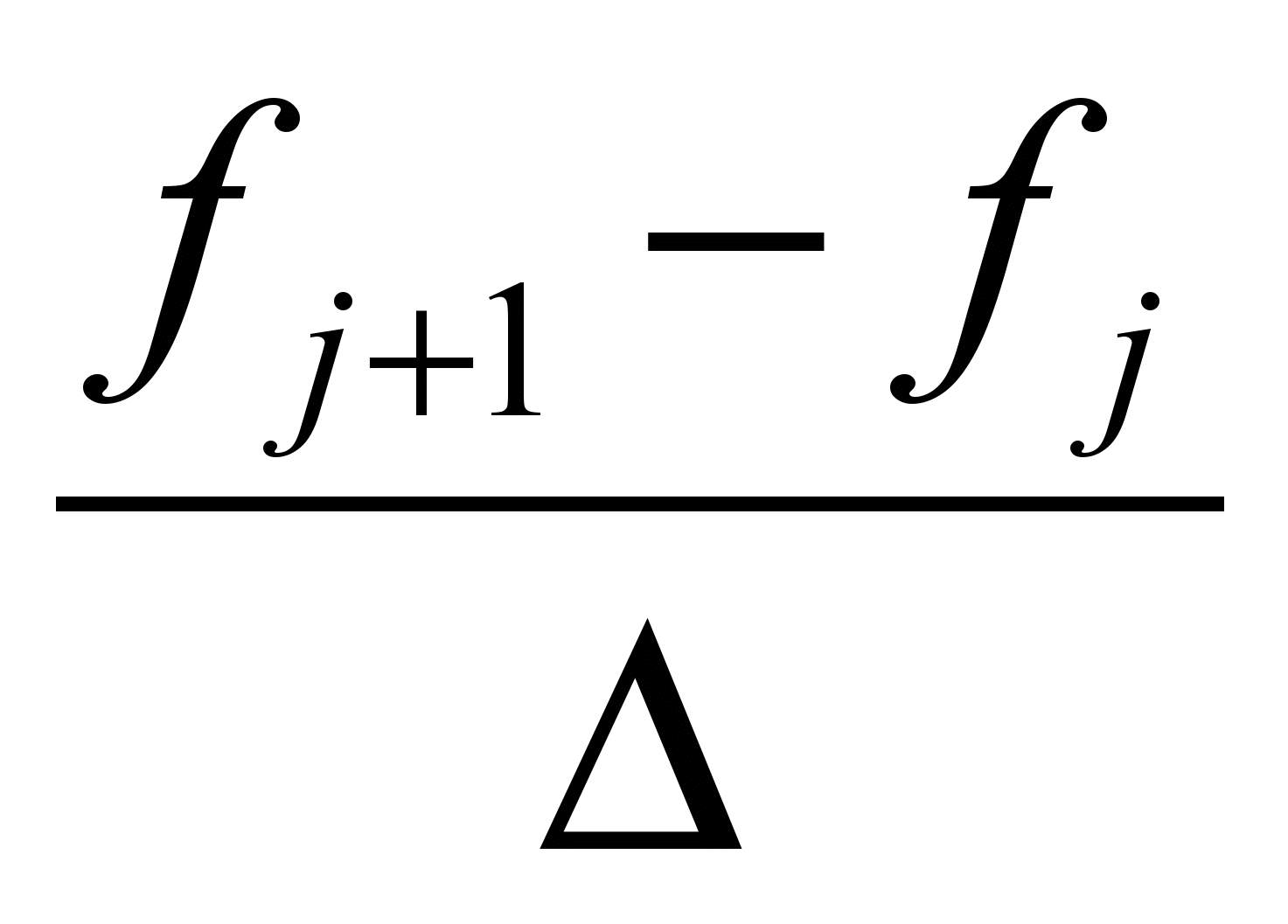. Однако, на практике чаще используется другой вид пространственной производной 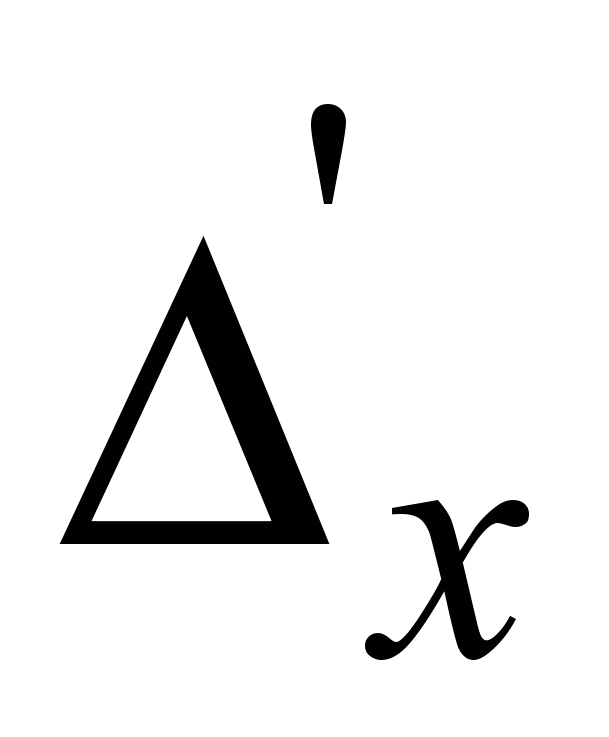= 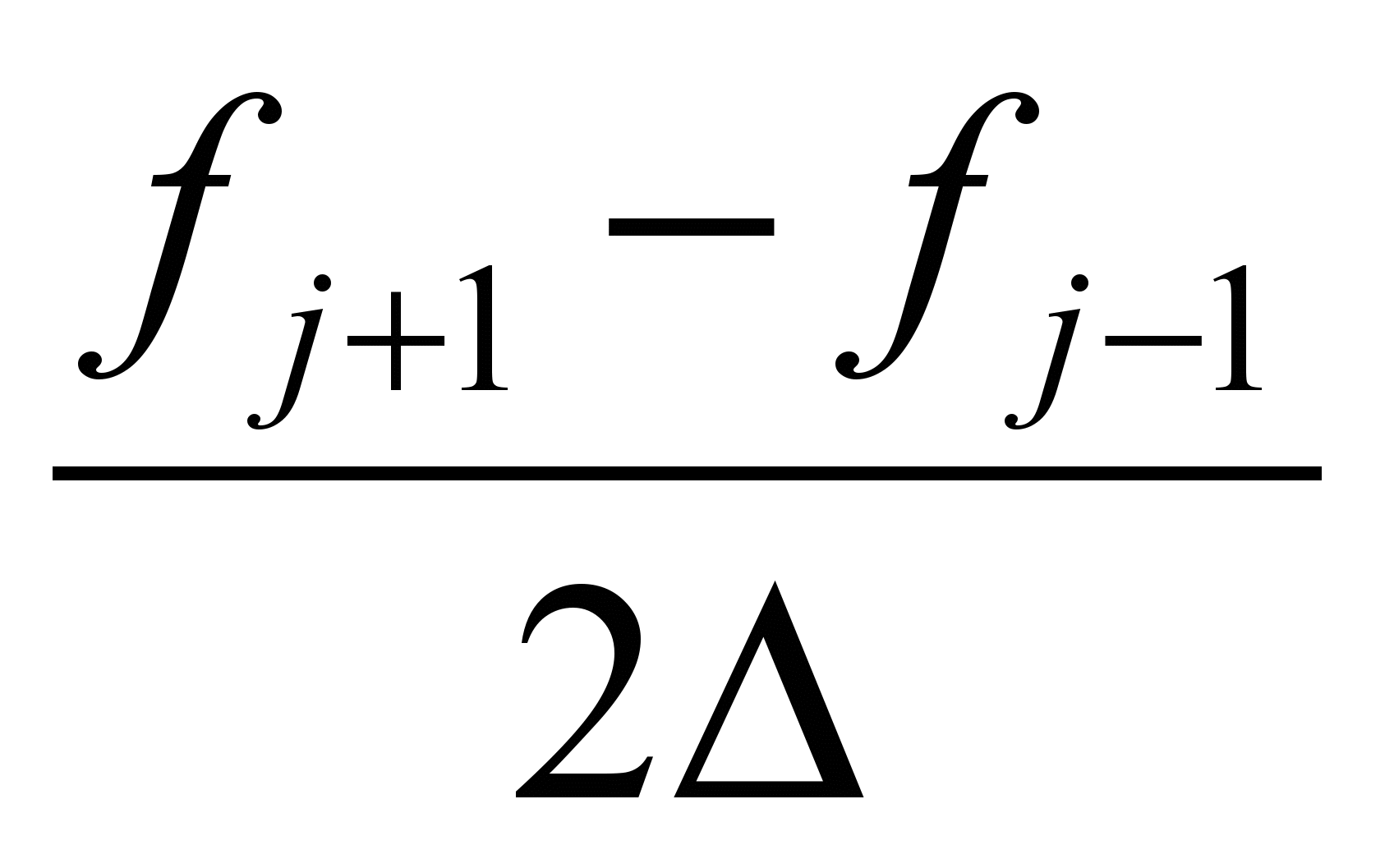Это центрированная производная. Используя этот подход легко записать выражения для пространственных производных старших порядков. Например, =.

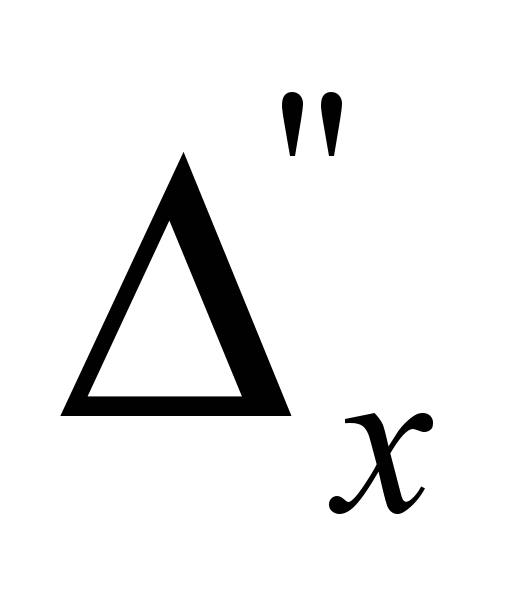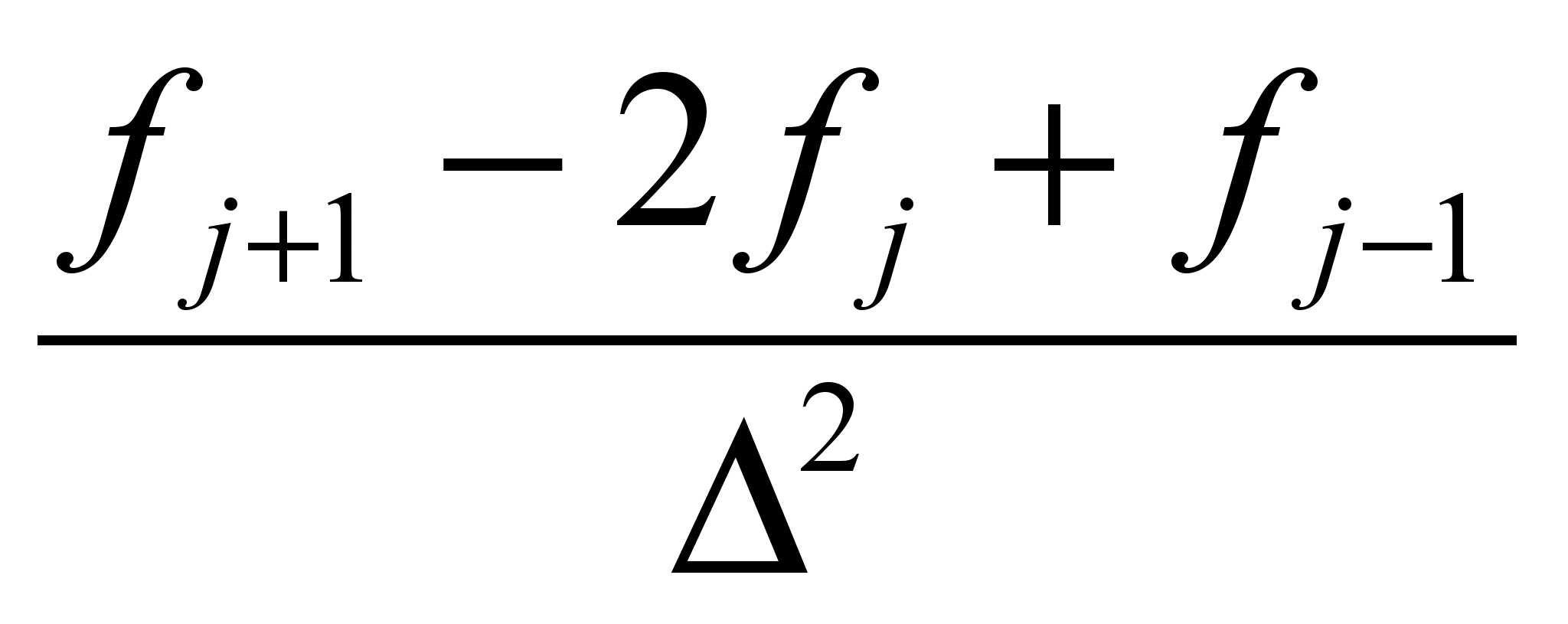Аналогичным образом записываются производные по времени в точке x_j в момент вренмени n. 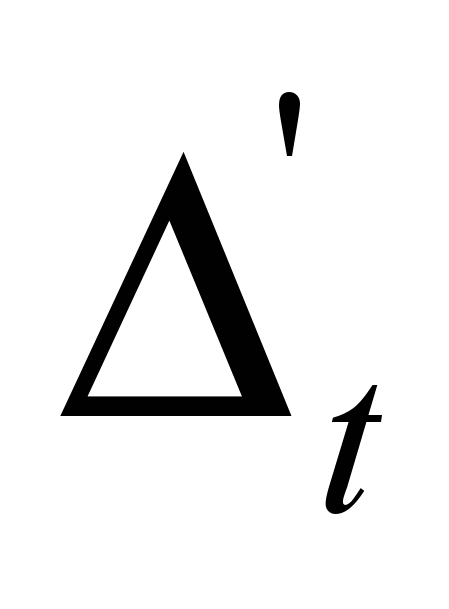= 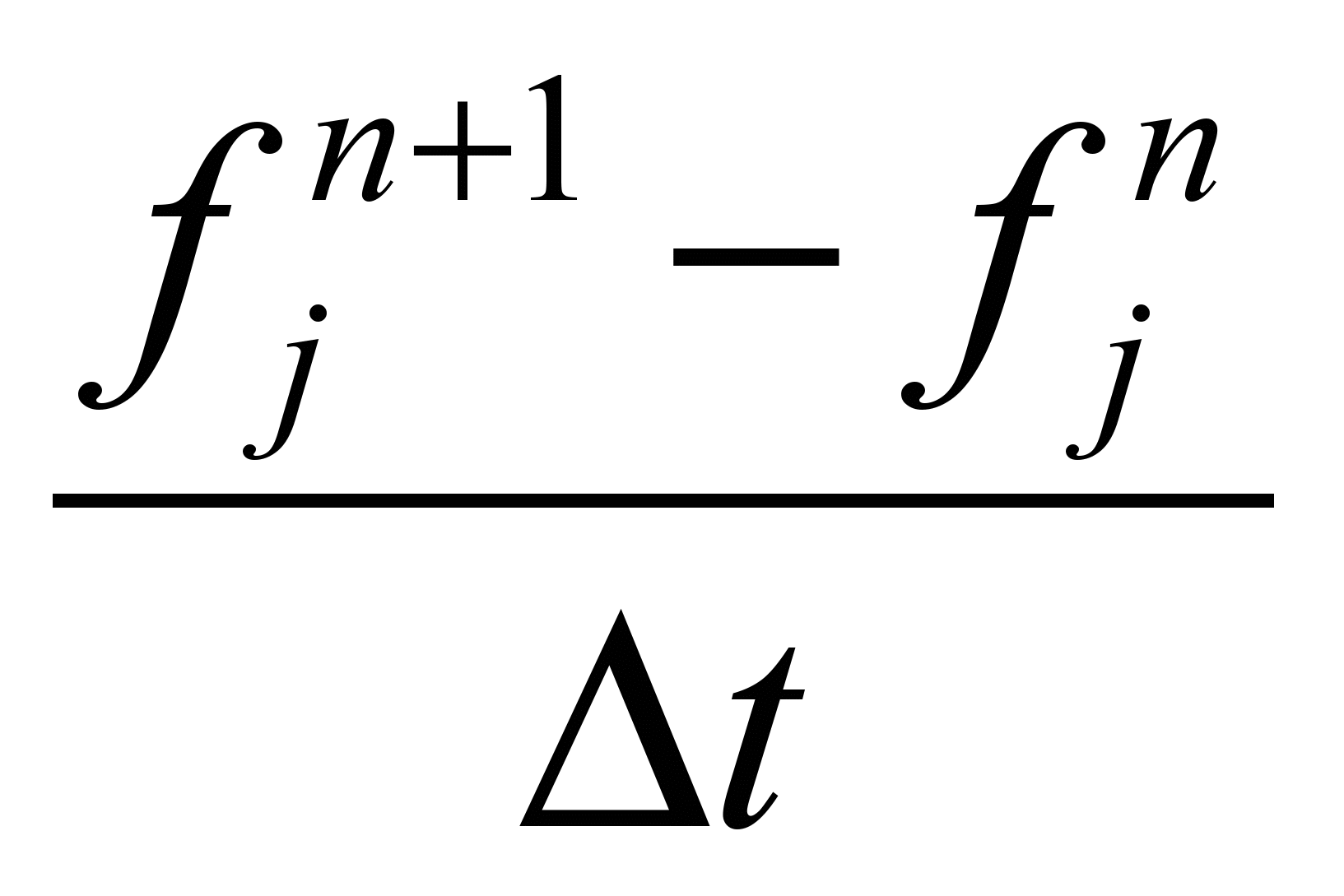или центрированная производная =.

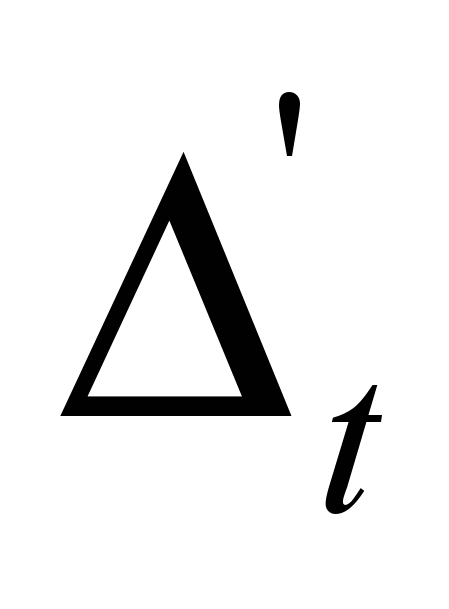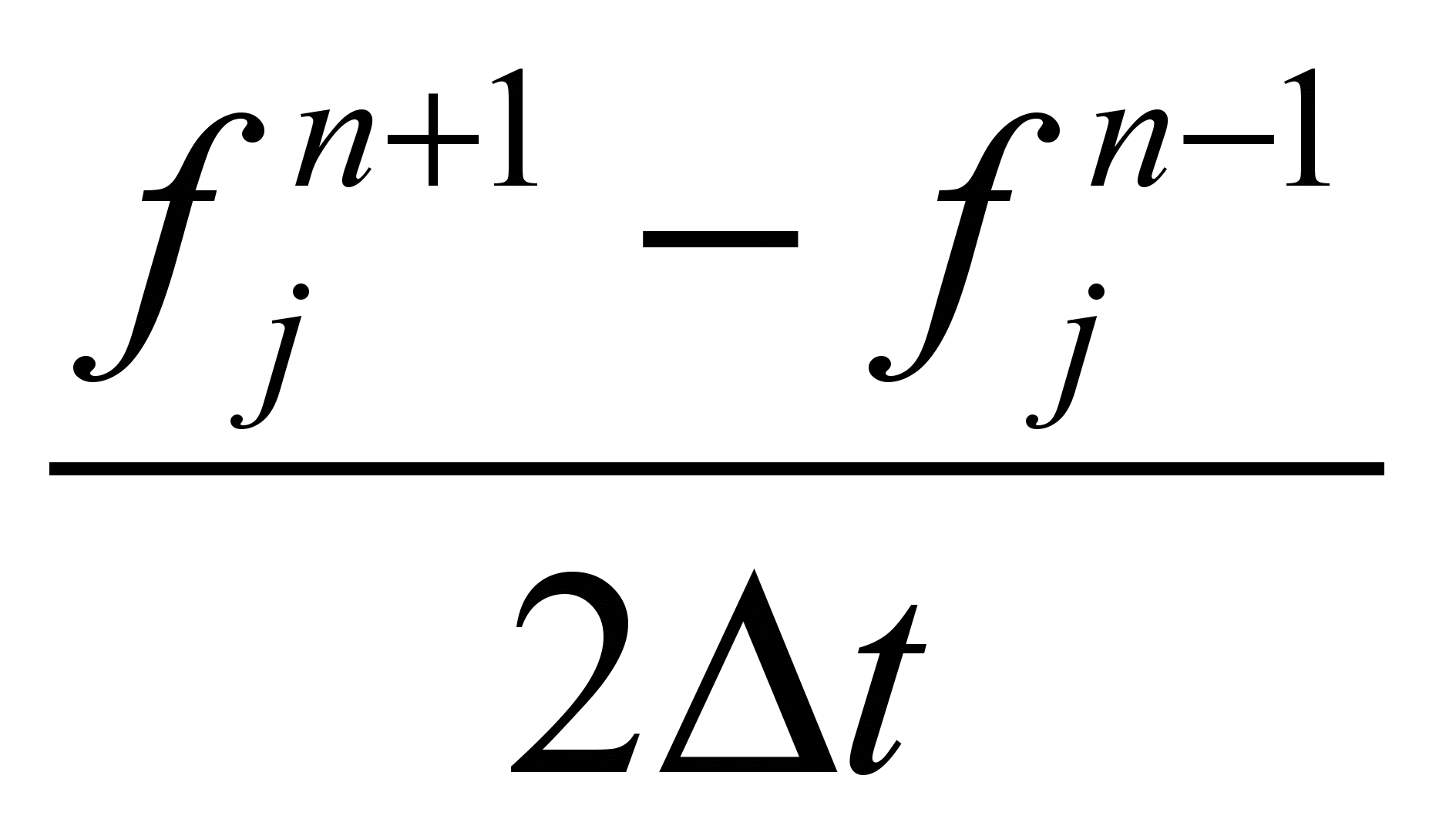При таком определении производной мы, естественно, что-то теряем. Попробуем определить, что именно. Пусть задана периодическая функция с периодом L. Тогда 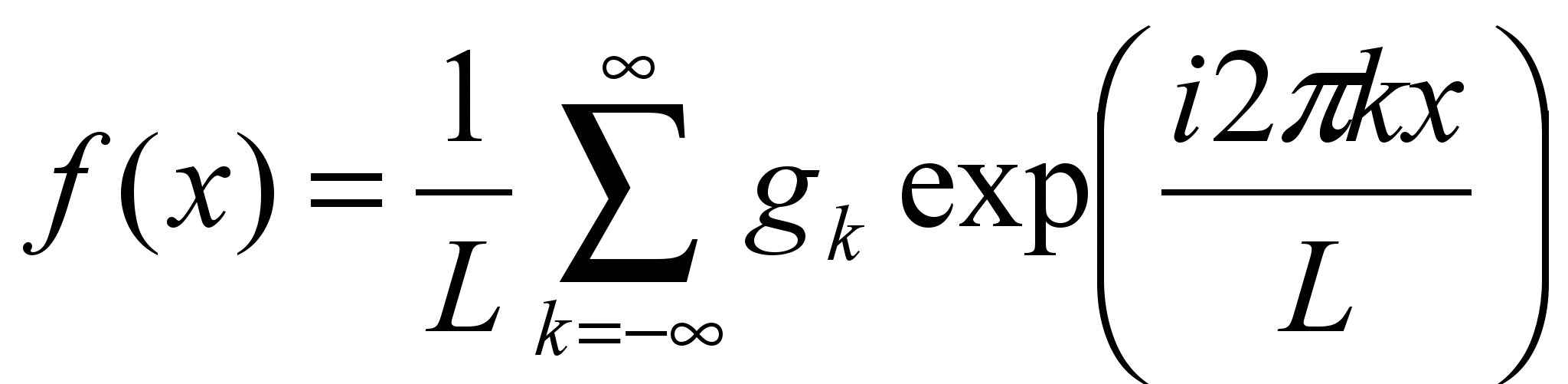, где .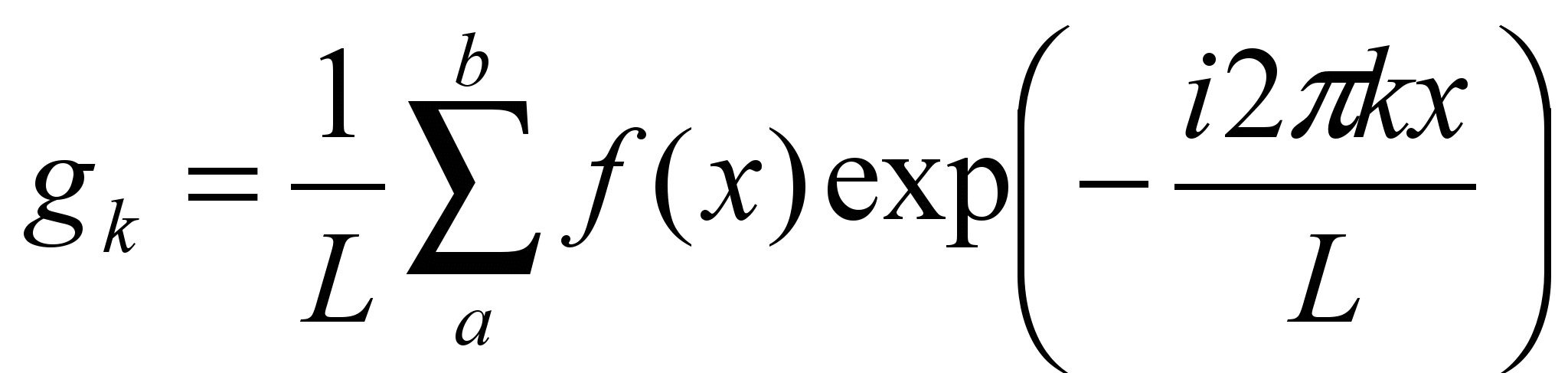


Конечный ряд 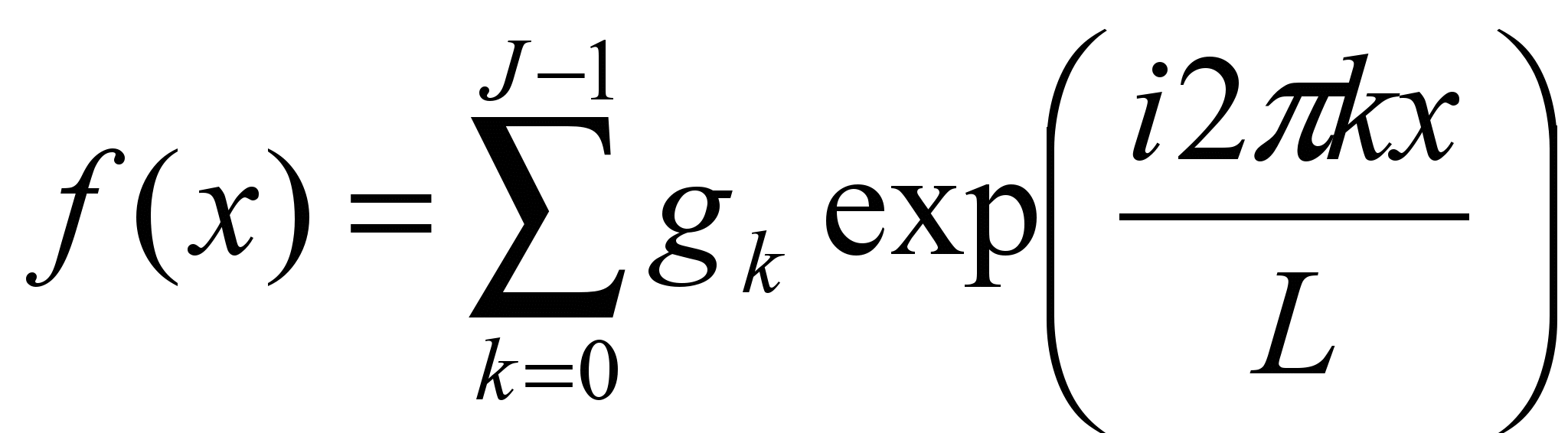, а для дискретно заданной 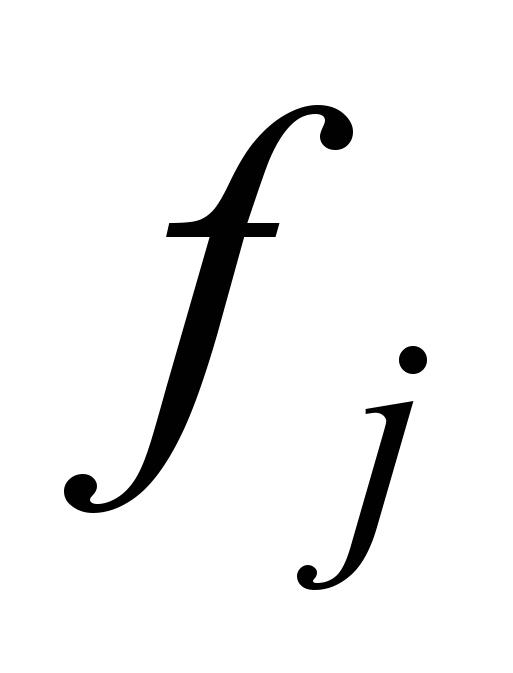можно записать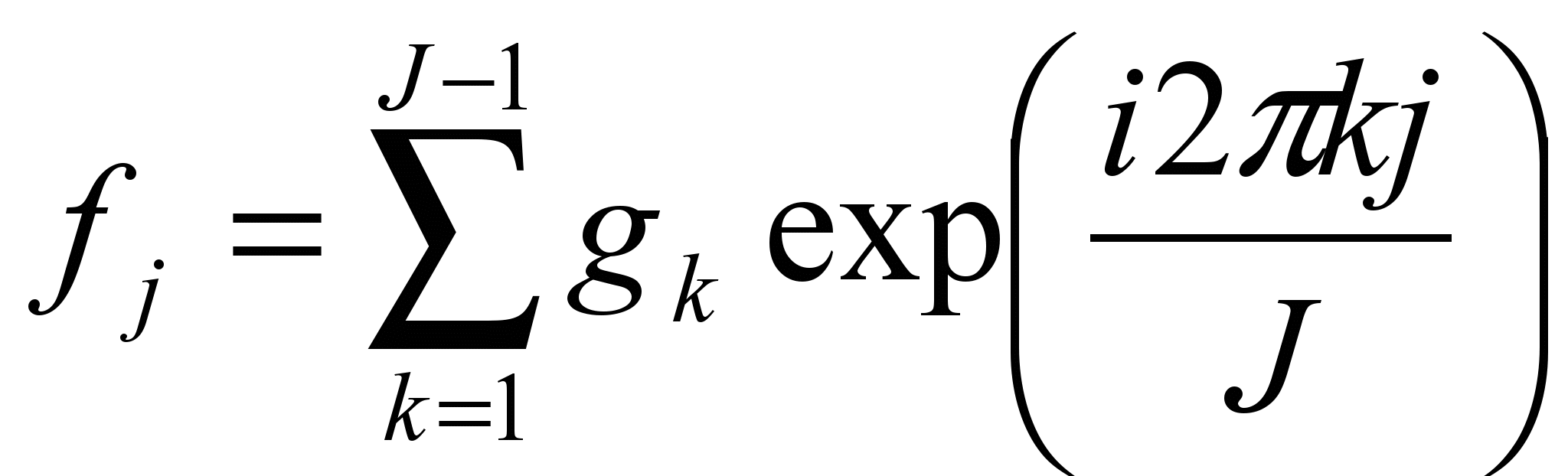



Выберем одну моду (гармонику) из ряда Фурье

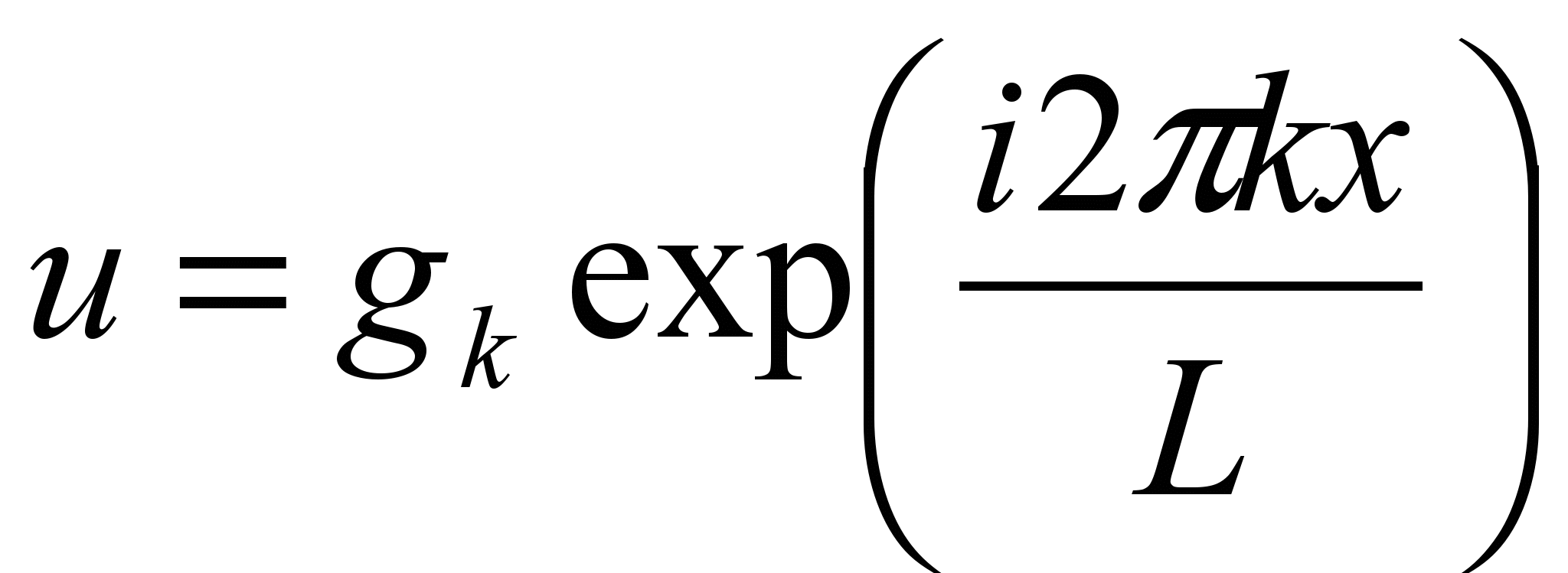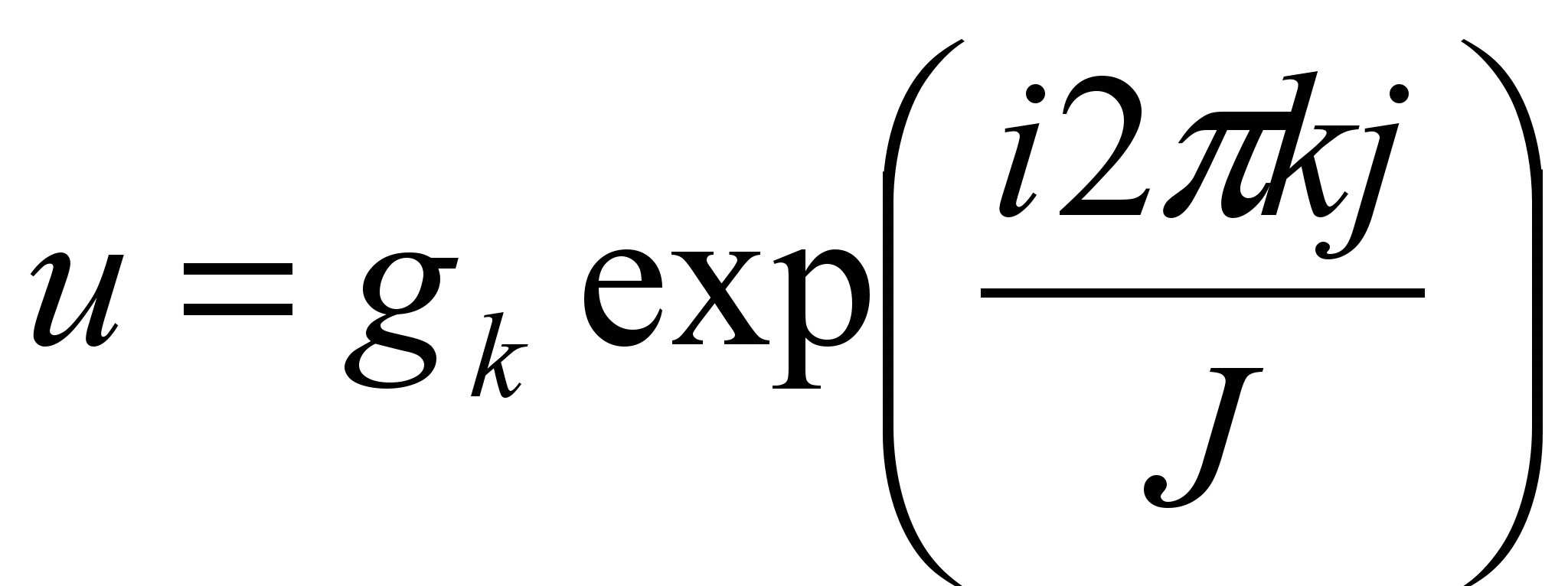и в случае дискретно заданной функции.

Тогда , =.


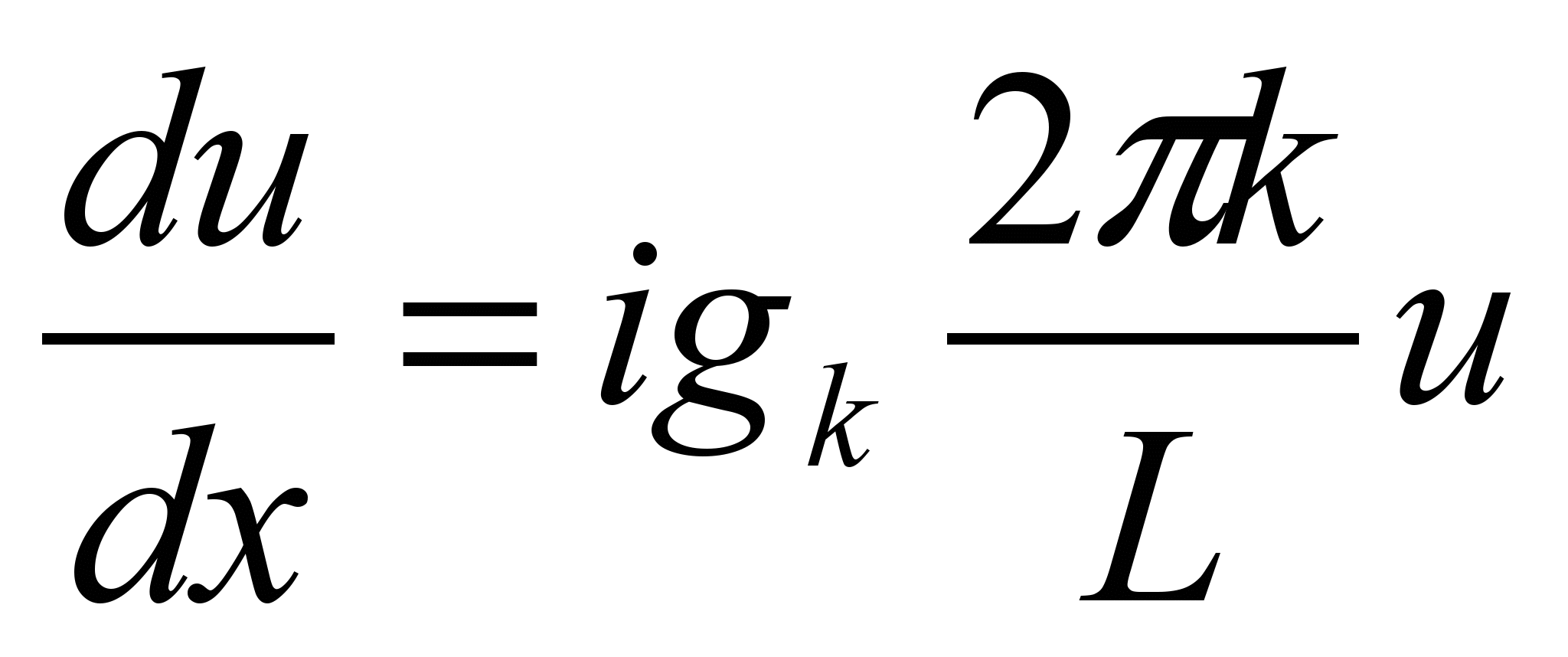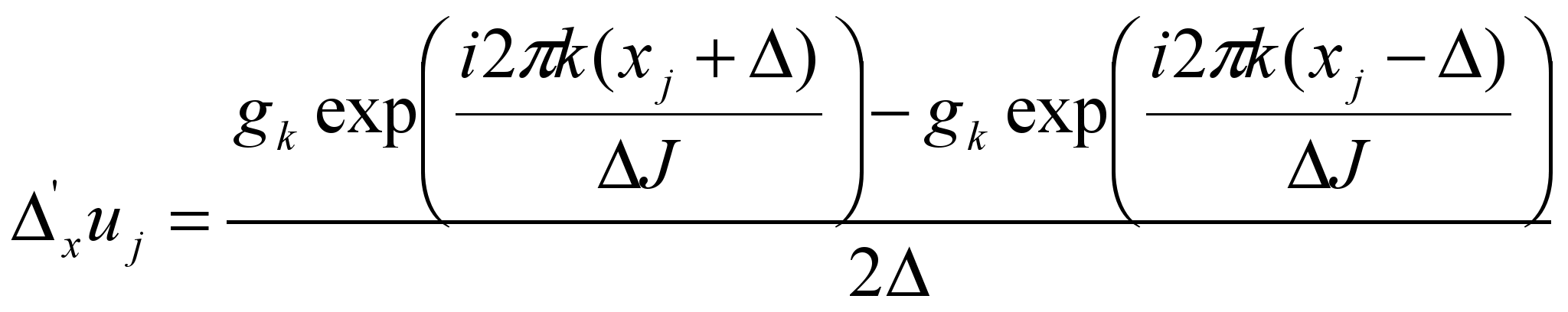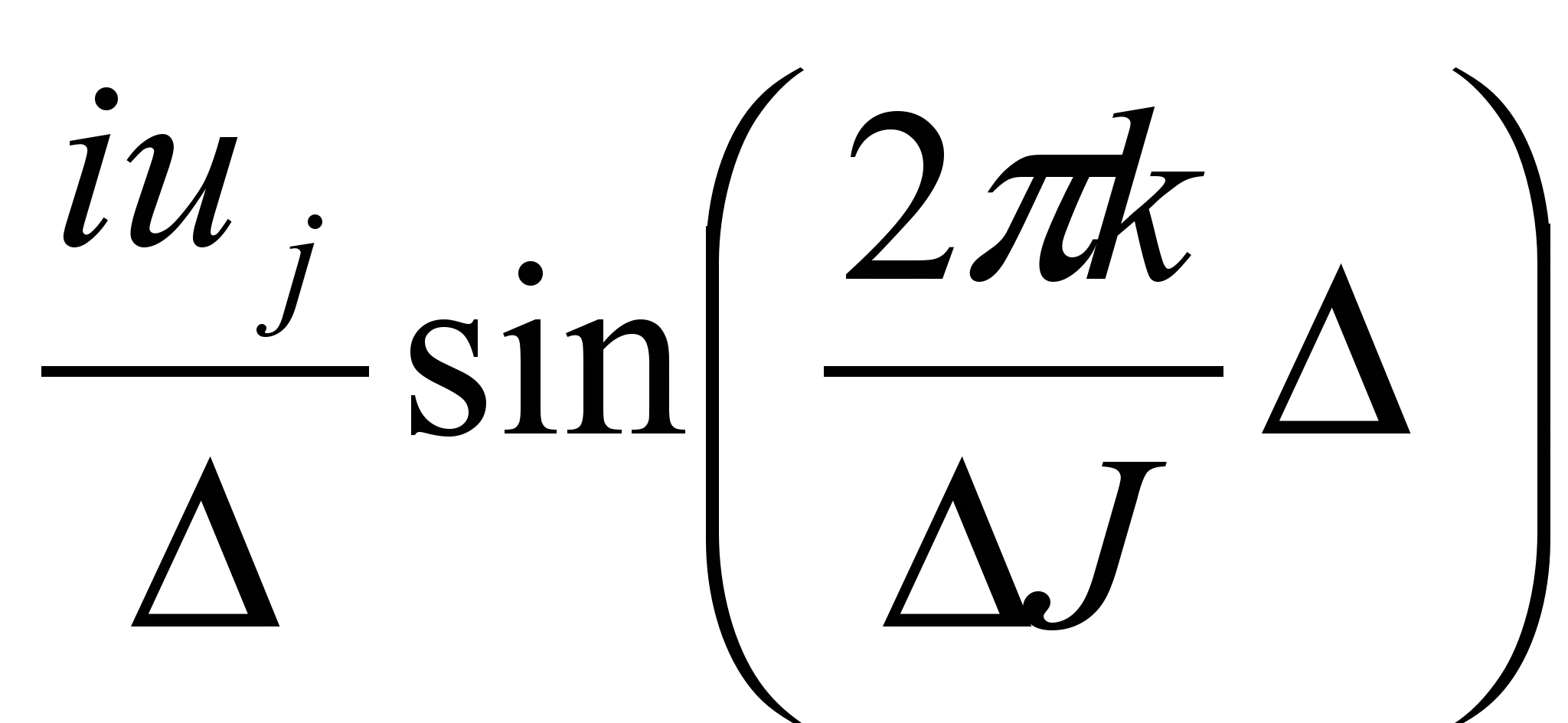Сравнивая полученный результат с аналитическим дифференцированием, приходим к выводу, что конечно-разностные методы, по сути своей, являются длинноволновым приближением.


5.2. Задача с начальными условиями (задача Коши).

На предыдущей лекции мы сформулировали основные идеи метода конечных разностей по пространственным переменным: функции, заданные на континууме 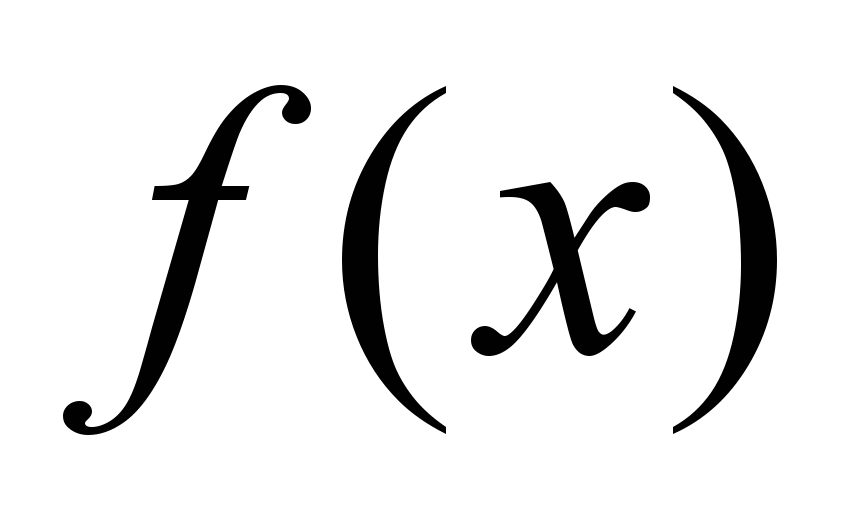заменяются сеточным вектором 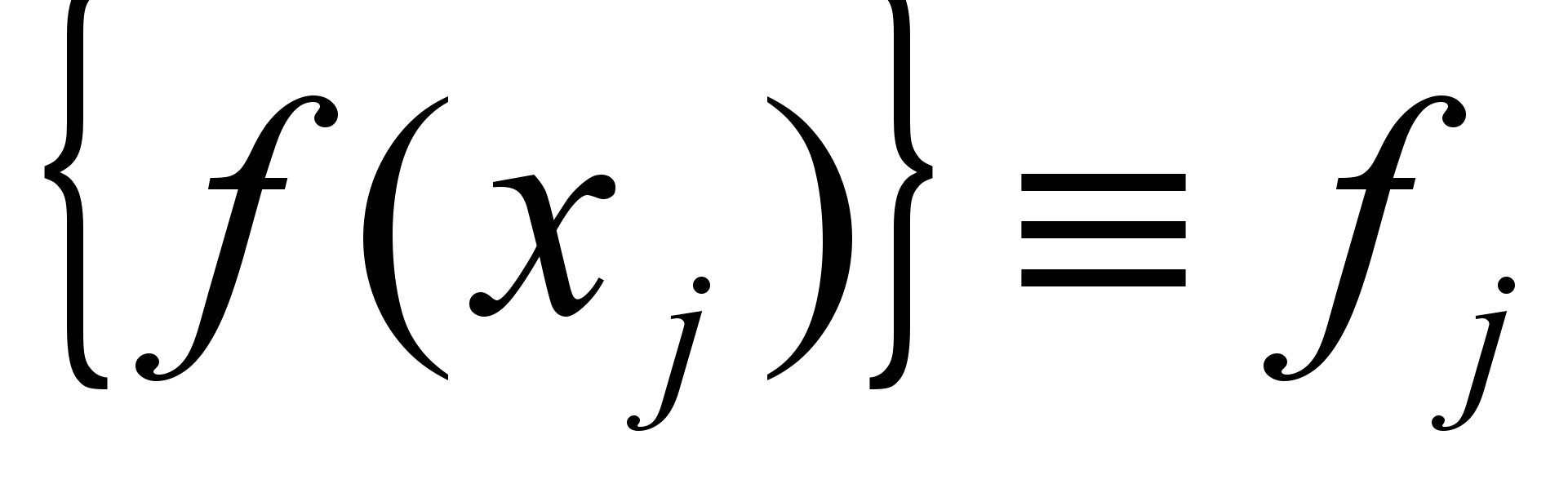, а дифференциальный оператор 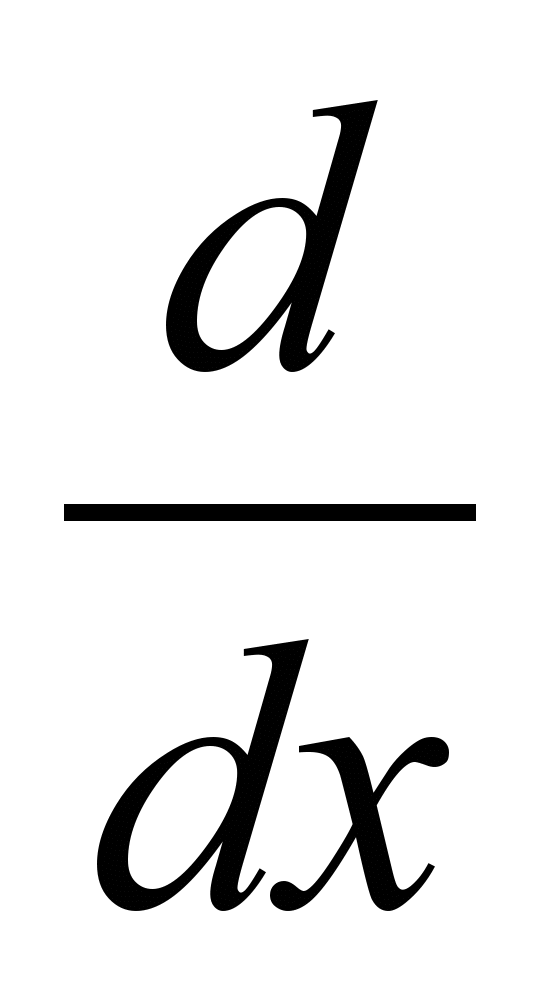заменяется на .

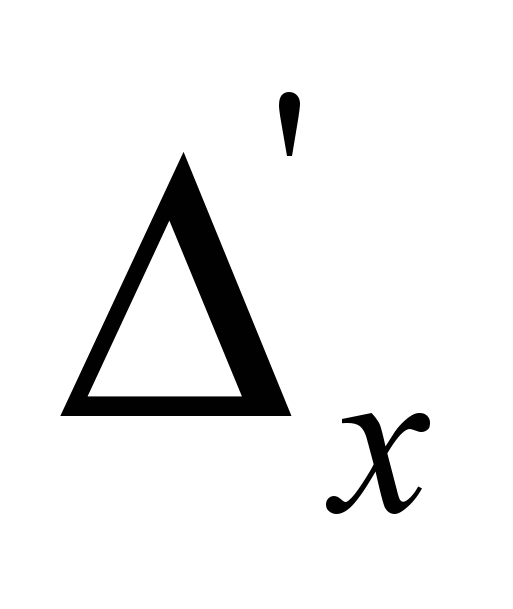В задачах, включающих зависимость от времени операция интегрирования требует специального определения, т.к. мы не знаем решения , соответствующего следующему моменту времени.

Временной задачей будем называть класс задач, в которых заданы начальные условия (Задача Коши).

Пример: решение уравнений движения Ньютона.

Пусть состояние системы определяется вектором. В трехмерном случае это вектор размерности 6 (три координаты и три скорости).

Пусть заданы начальные условия


и граничные условия (для уравнений в частных производных).


Примем, что состояние системы описывается уравнением


где - некоторый оператор (в общем случае нелинейный).

В случае систем линейных обыкновенных дифференциальных уравнений оператор - алгебраический оператор - матрица,

в случае систем уравнений в частных производных - пространственный дифференциальный оператор.

Численные методы решения дифференциальных уравнений


Общий вид дифференциального уравнения F(x, y, y') = 0, где y = y(x) – неизвестная функция от x.

Нормальная форма дифференциального уравнения: y' = f(x, y).

Дифференциальное уравнение вида y' = f(x, y), в котором неизвестная функция y зависит от одного аргумента x называется обыкновенным дифференциальным уравнением, если от нескольких – уравнением в частных производных.

Общим решением дифференциального уравнения y' = f(x, y) является семейство функций y = y(x, C). При решении прикладных задач обычно ищут частное решение. Выделение частного решения из семейства общих осуществляется с помощью начальных условий.

Нахождение частного решения дифференциального уравнения, удовлетворяющего условию y(x₀) = y₀, называется задачей Коши.

Постановка задачи Коши.

Дано: y' = f(x, y)

y(x₀) = y₀

[a; b], h

Решить дифференциальное уравнение.

В численных методах задача Коши ставится следующим образом: найти таб­личную функцию y_i = f(x_i), которая удовлетворяет заданным начальным условиям на участке [a; b] с шагом h.

i	x	y
0
1	x1	y1
2	x2	y2
:	:	:
n	xn	yn

На графике решение задачи Коши численными методами представляется в виде совокупности узловых точек.


Метод Рунге-Кутта

Наиболее эффективными и часто применяемыми методами решения задачи Коши являются методы Рунге-Кутта. Они основаны на аппроксимации искомой функции y в пределах каждого шага h многочленом, который получен при помощи разложения функции y в ряд Тейлора. Разложим функцию y(x) в окрестности шага h каждой i-й точки: 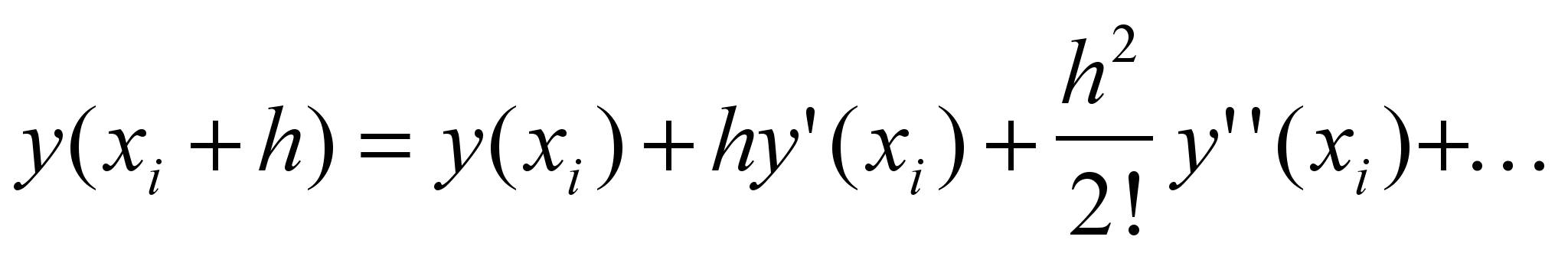(1)

Усекая ряд Тейлора в различных точках Рунге и Кутт обобщили, усовершенствовали и развили методы решения дифференциальных уравнений.


Метод Рунге-Кутта первого порядка (метод Эйлера)

Если шаг h мал, то члены ряда, содержащие h², h³, h⁴ и т.д. являются малыми более высоких порядков. Отбросим в (1) члены ряда, содержащие h², h³ и т.д., тогда получим:



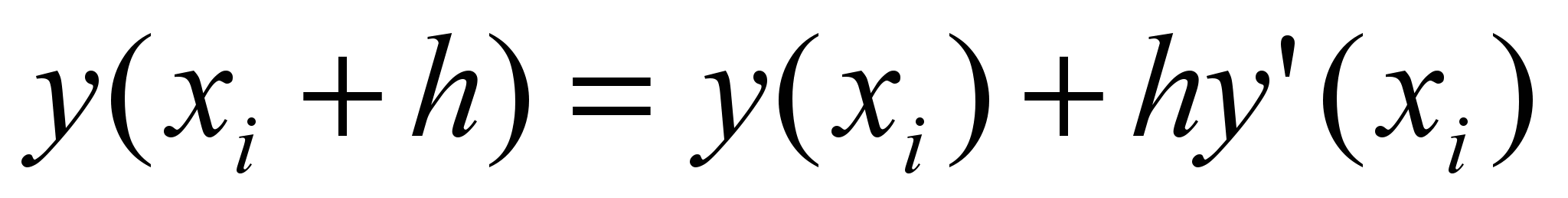
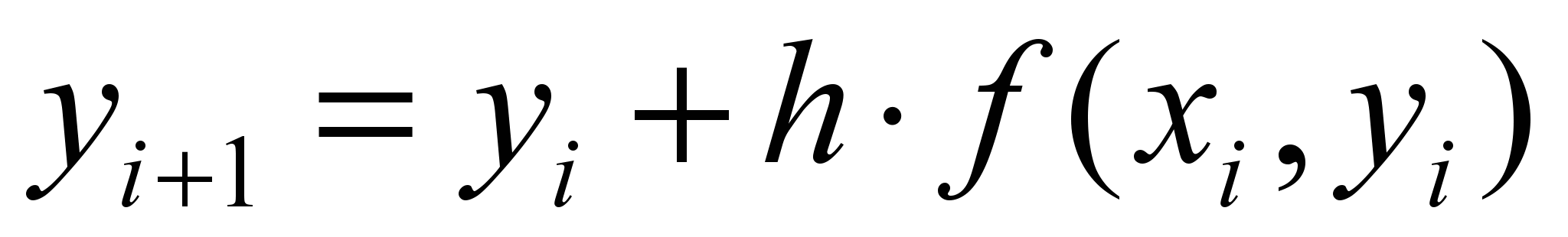– формула Эйлера.

Точность метода Эйлера имеет порядок h².


Блок-схема алгоритма




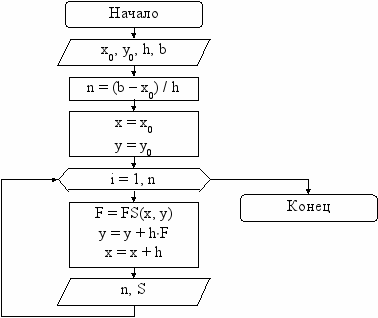
Геометрический смысл метода Эйлера

y_i+1 = y_i + hf(x_i, y_i)

y' = f(x_i, y_i) = tg _i

tg _i – тангенс угла наклона касательной к искомой функции y в точке (x_i; y_i).

y_i+1 = y_i + htg _i.

tg ₀ = f(x₀, y₀)

tg ₁ = f(x₁, y₁)





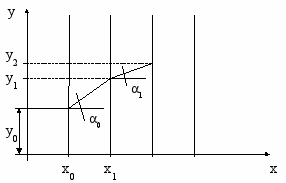
В методе Эйлера на графике искомая функция y(x) заменяется ломаной линией, каждый отрезок которой на шаге h линейно аппроксимирует искомую функцию. Поэтому метод Эйлера получил название метода ломаных. Основной недостаток метода Эйлера – систематическое накопление ошибок.


Модифицированный метод Эйлера (метод Рунге-Кутта второго порядка)

Отбросим в (1) члены ряда, содержащие h³, h⁴ и т.д. Получим ряд

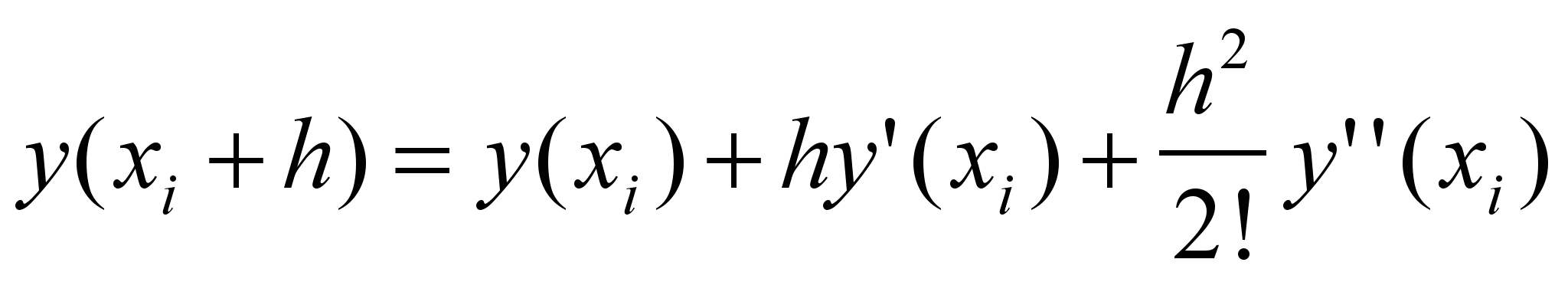(2)

Чтобы сохранить член ряда, содержащий h², нужно определить член ряда, содержащий вторую производную. Будем аппроксимировать вторую производную разделенной разностью 2-го порядка.

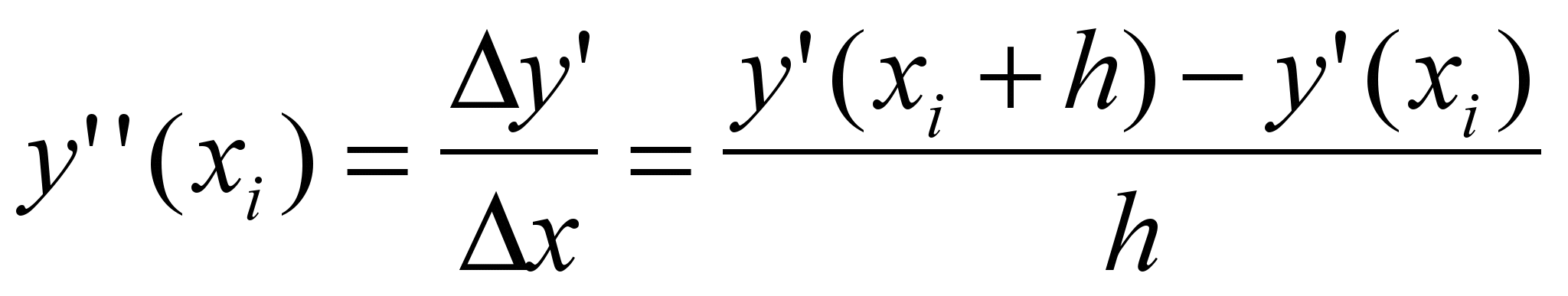(3)

Подставляя (3) в (2), получим:



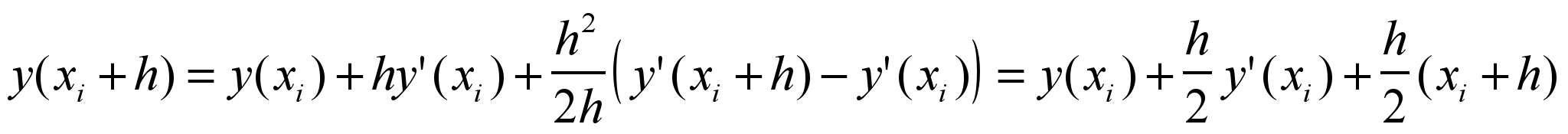
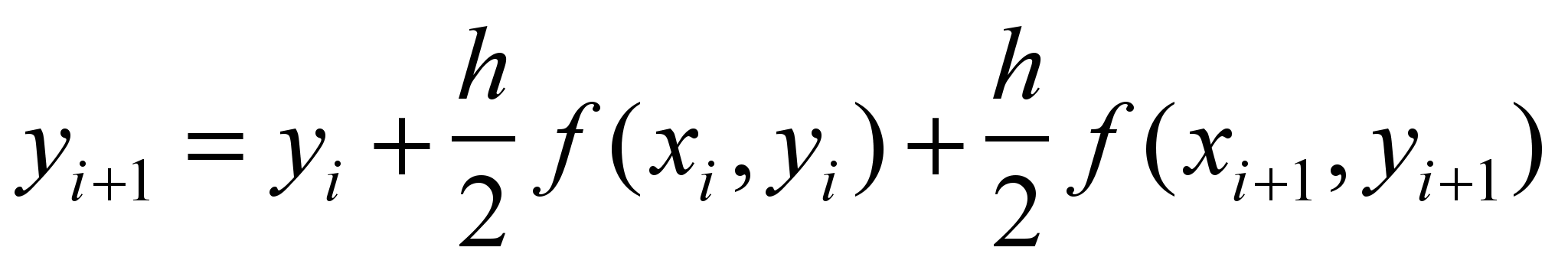– модифицированная (уточненная) формула Эйлера.

Для определения предварительного значения y_i+1 воспользуемся формулой Эйлера, тогда модифицированная формула Эйлера примет вид:

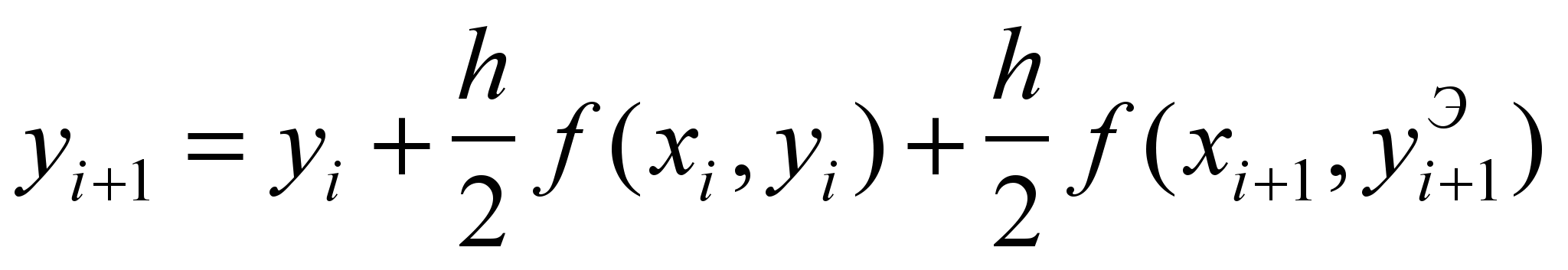, где .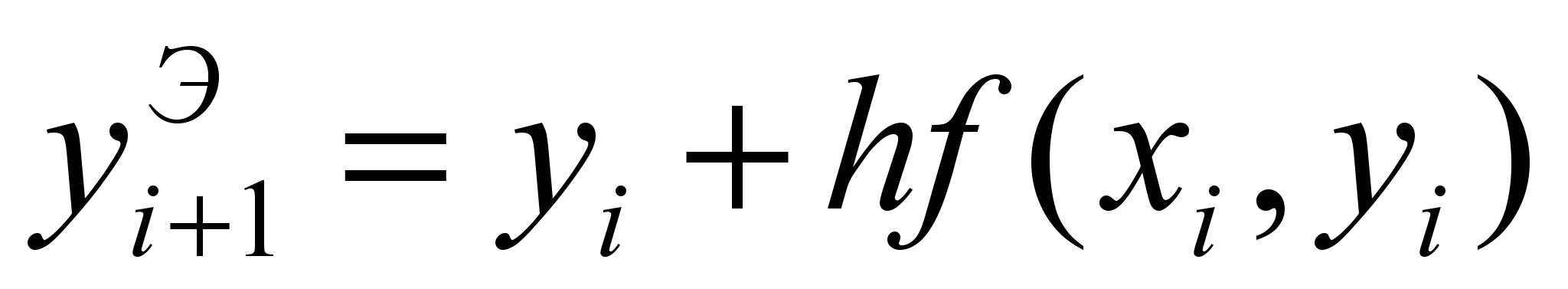

Точность метода имеет порядок h³.

Обозначим




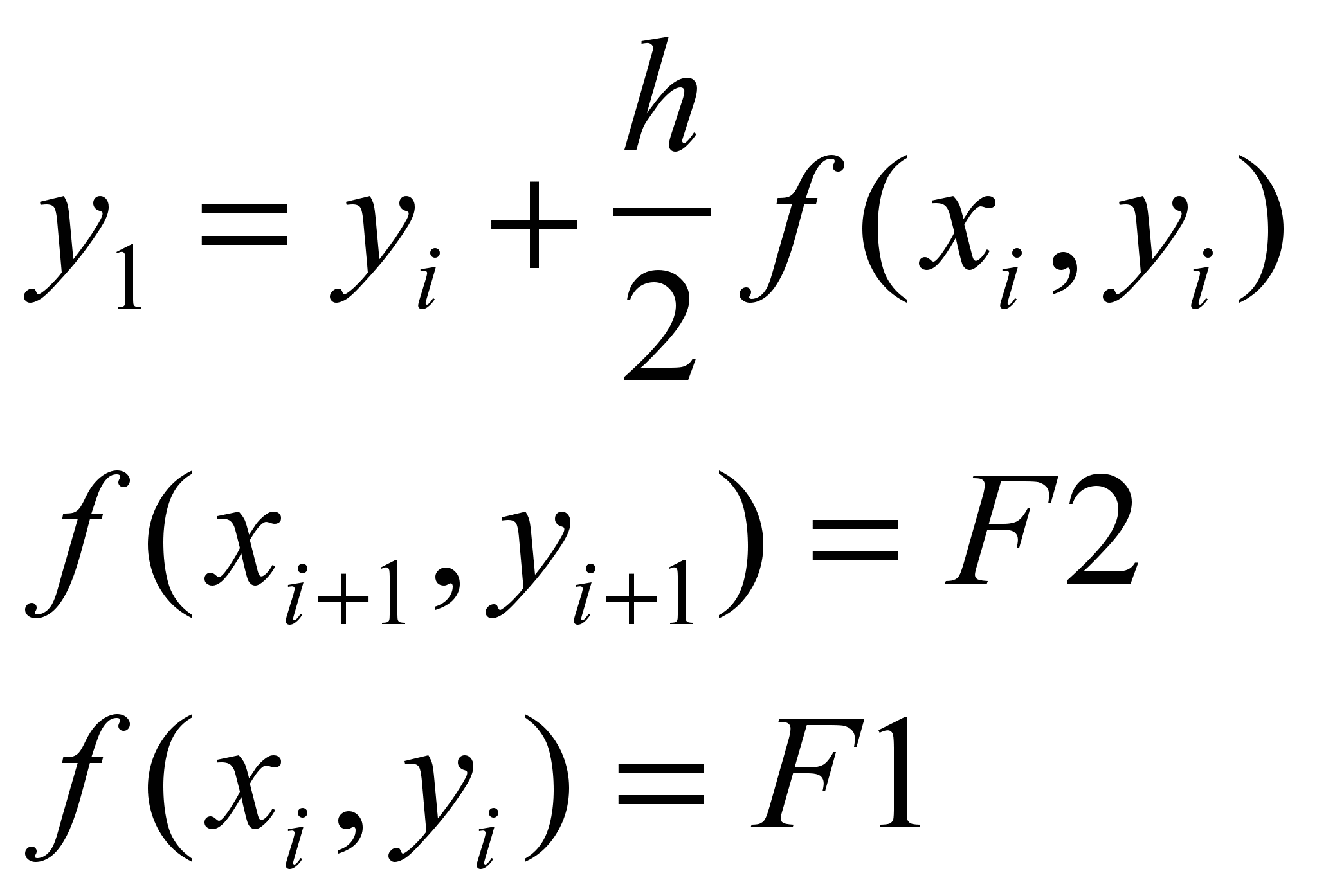
Геометрический смысл модифицированного метода Эйлера

Т.к. f(x_i, y_i) = y'(x_i) = tg _i

f(x_i+1, y_i+1) = y'(x_i+1) = tg _i+1, то модифицированная формула Эйлера примет вид: .





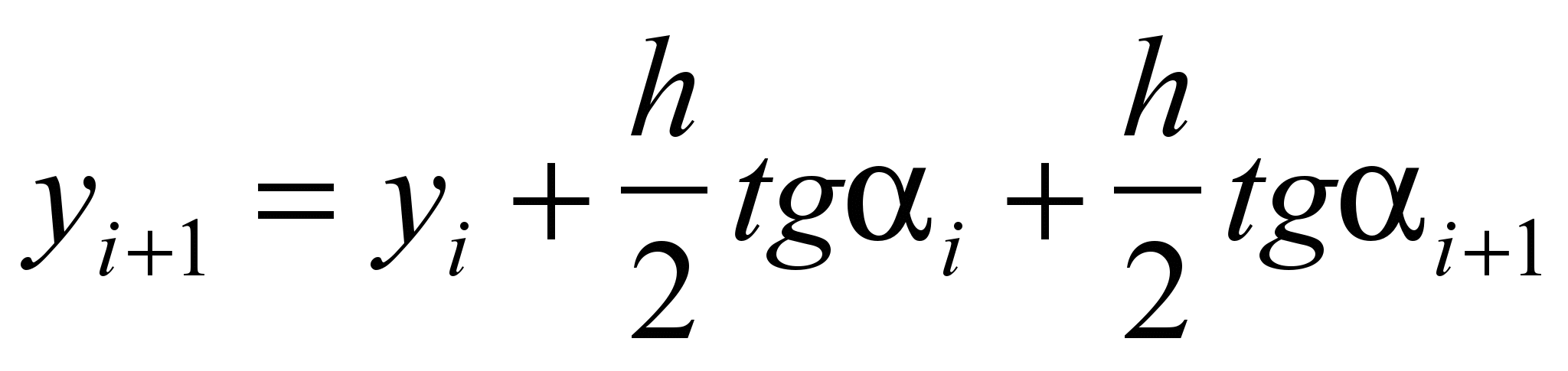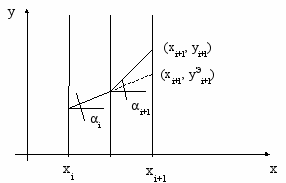
P1 – ошибка по методу Эйлера P2 – ошибка по уточненному методу

В модифицированном методе Эйлера модифицированная функция y(x) на каждом шаге аппроксимируется не одной, а двумя прямыми, каждая из которых аппроксимирует функцию y(x) на полушаге.


Метод Рунге-Кутта 4-го порядка

В методе Эйлера используется член ряда Тейлора (1), содержащий h. Ошибка метода имеет порядок h² .

В модифицированном методе Эйлера используется член ряда (1), содержащий h². Ошибка этого метода составляет h³.

Математики Рунге и Кутт обобщили и развили эти методы. Согласно их классификации, метод Эйлера получил название метода Рунге-Кутта 1-го порядка. Рунге и Кутт предложили методы для решения задачи Коши, в которых более высокая точность решения дифференциальных уравнений может быть достигнута, если в методах сохранять члены ряда Тейлора, содержащие h³, h⁴ и т.д.

Наибольшее распространение получил метод, в котором искомая функция y(x) аппроксимируется рядом Тейлора (1), в котором сохранен член ряда, содержащий h⁴. Метод получил название метода Рунге-Кутта 4-го порядка, но в литературе он известен больше как просто метод Рунге-Кутта. Точность этого метода имеет порядок h⁵

Для получения значения функции y_i+1 по методу Рунге-Кутта необходимо определить y^``` и y^````. Определяем эти производные используя разделенные разности. Окончательно для определения y_i+1 выполняется следующая последовательность вычислительных операций:








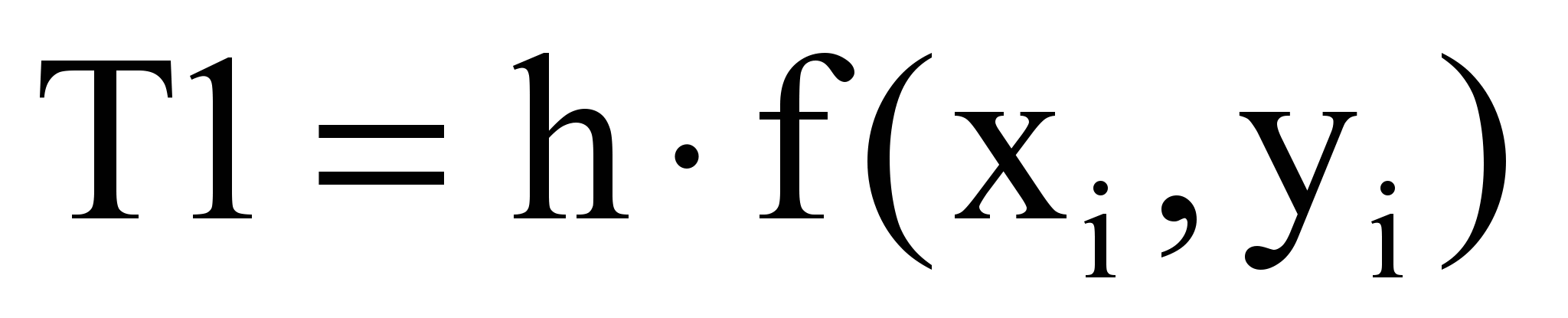
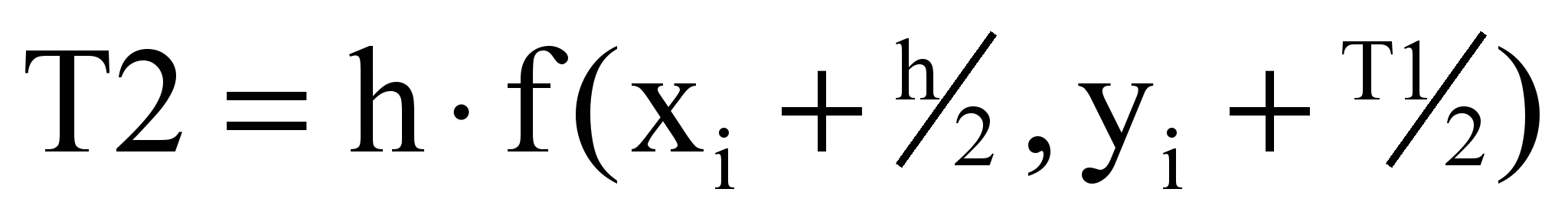
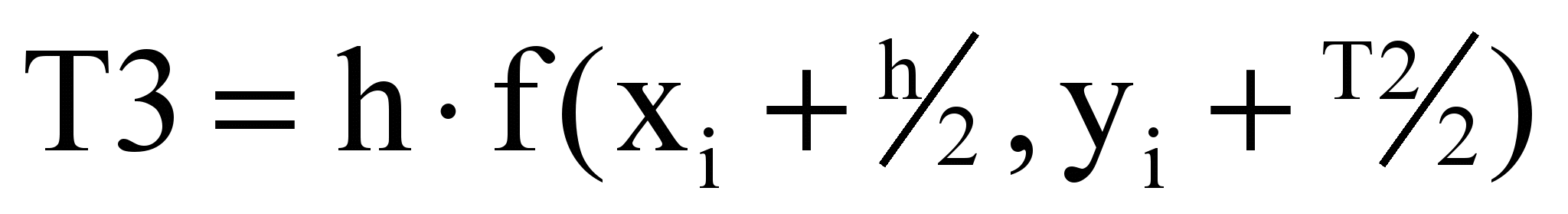
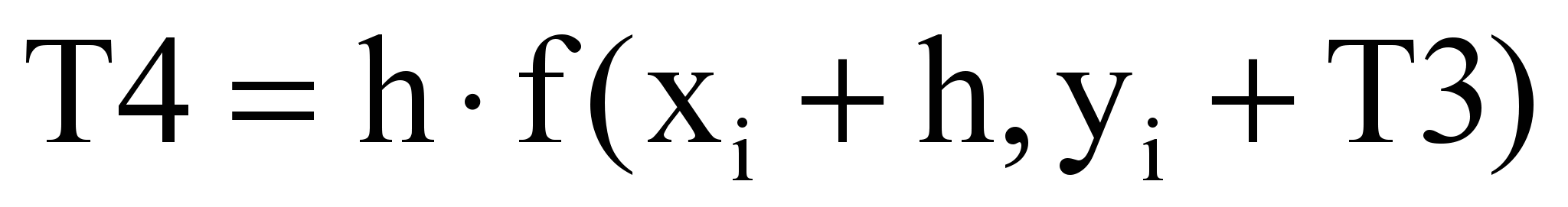
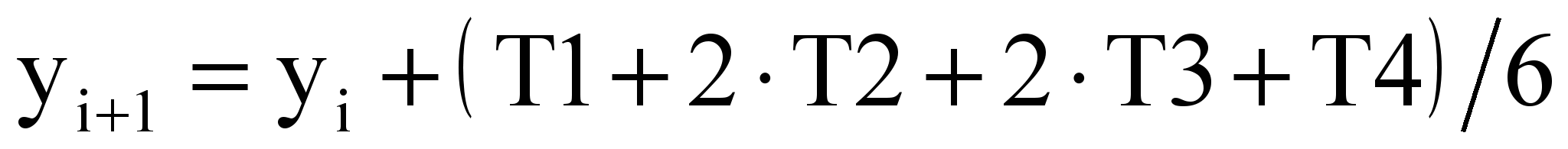
Блок-схема алгоритма


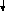
T1 = hFS(x, y)

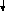
x = x + h/2

y1 = y + T1/2

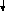
T2 = hFS(x, y1)

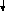
y1 = y + T2/2

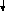
T3 = hFS(x, y1)


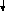
x = x +h/2

y1 = y + T3



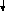
T4 = hFS(x, y1)



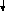
Y = y + (T1 + 2T2 + 2T3 + T4)/6







Пример: Движение одномерного гармонического оператора.


Интегрируя уравнение по времени и переходя к дискретной сетке в пространстве времени


мы стремимся найти решение в точке следуя схеме численного интегрирования:


Это связь между и в общей форме. Но поскольку мы не знаем в интервале мы не можем вычислить интеграл без применения методов численного интегрирования.

То есть надо найти некоторую аппроксимацию для вычисления интеграла.

Для количественной оценки точности такой аппроксимации разложим подинтегральное выражение в ряд Тейлора с конечным числом членов в окрестности точки .


Обычно в численных методах решения дифференциальных уравнений отбрасывают члены выше второго порядка по :


Таким образом, отбрасывая члены порядка и выше, мы сводим проблему вычисления интеграла к проблеме аппроксимации производной по времени , которая безусловно проще. Существуют явные и неявные схемы.


5.3. Основные методы интегрирования обыкновенных дифференциальных уравнений.

Рассмотрим обыкновенное дифференциальное уравнение


с начальным условием


Тогда для двух значений времени мы можем записать решение в точках


Это точно выражение решения. В зависимости от способа аппроксимации этого интеграла различают несколько основных методов интегрирования обыкновенных дифференциальных уравнений.


5.3.1. Метод Эйлера.

Простейший метод аппроксимации интеграла * состоит в замене подинтегральной функции ее значением в момент времени .


Метод Эйлера является явным и имеет первый порядок точности по шагу .


Схематично метод Эйлера можно представить следующим образом


Метод Эйлера имеет первый порядок точности по времени. Решение дифференциального уравнения можно улучшить, взяв последующие члены разложения. В этом случае подинтегральное выражение называется центрированным по времени.


2) Метод "с перешагиванием".

Простейший метод центрирования по времени является метод "с перешагиванием". Интеграл вычисляется как площадь прямоугольника


n+1 шаг


n+2 шаг


Схему с перешагиванием можно изобразить следующим образом.


В методе с перешагиванием первый шаг нужно делать каким-то другим методом, например, методом Эйлера.


3) Метод Рунге-Кутта.

Методы Рунге-Кутта основаны на центрировании по времени интеграла


с помощью некоторой многошаговой процедуры.

Рассмотрим простейший двухшаговый вариант методов Рунге-Кутта.

Значение получается из значения посредством вычисления в промежуточном шаге


Схему метода можно изобразить следующим образом


Можно показать, что условие устойчивости имеет следующий вид:

Для случая


Мы будем работать в основном с методом Рунге-Кутта четвертого порядка точности и с методом "с перешагиванием".

Существует стандартная подпрограмма использующая метод Рунге-Кутта четвертого порядка точности (RKGS).

Описание стандартной подпрограммы RKGS.


6.1. Понятие устойчивости разностных схем.

Выполняемые на ЭВМ арифметические операции являются, как мы уже убедились, неточными. Возникает вопрос о влиянии ошибок на поведения решения. С этой проблемой связано очень важное свойство разностных схем - устойчивость.

Численный метод будем называть устойчивым, если на любой стадии процесса вычислений малая ошибка приводит к еще меньшей ошибке.

В противном случае ошибки могут неограниченно расти (численная неустойчивость). Любой численный метод должен быть устойчивым (по крайней мере при определенных условиях).

Пусть имеется обыкновенное дифференциальное уравнение для некоторой функции .


Обозначим ошибку, появляющуюся на -ом шаге .

Для количественной оценки устойчивости разностной схемы мы должны оценить величину этой ошибки при переходе к шагу . Запишем эту ощибку в виде:


где величина - множитель перехода. Эта величина непосредственно связана с типом разностной схемы, который в общем случае задается оператором перехода .

В соответсвие со сформулированным выше условием устойчивости потребуем выполнения условия


Тогда имеет место численная устойчивость метода.

Примечание. Это условие нужно несколько уточнить для класса задач допускающего растущие решения. В этом случае можно допустить рост при условии, что этот рост отстает от роста самого решения.


Рассмотрим вопрос об устойчивости метода Эйлера.

Из уравнения


получаем


При малом можно разложить в ряд Тейлора в окрестности


Подставляя в уравнение


получим


Отсюда получаем выражение для множителя перехода в методе Эйлера


В случае уравнения с затуханием

из условия получим


Этим выражением определяется верхняя граница допустимого шага по времени, при котором получается устойчивое решение. Подобным же методом можно исследовать и другие случаи.

При получении условия устойчивости мы линеаризировали

разложив ее в ряд Тейлора и взяв первый член.


Исследуем теперь устойчивость метода с перешагиванием.

Здесь уже связаны ошибки в трех узлах.

Та же методика. Разлагаем функцию в ряд Тейлора в окрестности точки получим


Таким образом множитель перехода может быть получен из уравнения


Поскольку для нарастающих и убывающих решений модуль одного из значений больше единицы, эта схема не используется для нарастающих или убывающих решений.

Рассмотрим условие устойчивости метода для осциллятоных решений


Это условие можно сформулировать в виде


7.1. Численные методы решения уравнений в частных производных.

В качестве иллюстрации разностных схем для решения уравнений в частных производных рассмотрим решение уравнение диффузии:


Пусть неизвестная функция определена только в узлах двумерной сетки на плоскости .


Пространственный оператор в этом случае может быть заменен разностным оператором:


Верхний индекс относится к узлу по времени, нижний относится к узлу по пространственной решетке.

Тогда можно использовать простейшую схему:

Существует большое число разностных схем для решения этого уравнения. Все они имеют разные условия устойчивости.

Рассмотрим вопрос об устойчивости разностных схем для уравнений в частных производных.

Как было видно из предыдущего материала устойчивость схем для решения обыкновенных уравнений зависила от соотношения величины шага по времени и характерного времени изучаемых физических процессов.

Характерные времена для уравнений в частных производных могут быть получены из дисперсионных соотношений.

Для этого подставим в уравнение в частных производных Фурье-моду:


После такой подстановки можем получить дисперсионное соотношение


то есть связать частоту (характерный временной масштаб) с определенной длиной волны. Дисперсионное соотношение содержит информацию о зависимости временных масштабов от длины волны.

рассмотрим простейшие примеры дисперсионных соотношений.

Волновое уравнение (например, волны в струне):


Подставляя


Характерный временной масштаб


Уравнение диффузии.


Уравнение диффузии не допускает решений в виде незатухающих волн. Временной масштаб затухания: