«Моделирование систем»
| Вид материала | Курсовая |
- Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
- Рабочая программа По дисциплине «Экономико-математическое моделирование производственных, 373.58kb.
- Календарный план учебных занятий по дисциплине Моделирование информационных процессов, 24.12kb.
- Темы курсовых работ по дисциплине «моделирование систем» Ваш № в списке группы, 19.48kb.
- Программа вступительных испытаний (собеседования) для поступающих в магистратуру, 31.28kb.
- Тематика курсовых работ по курсу «Моделирование систем», 12.64kb.
- Рабочая программа и задание на курсовой проект для студентов Vкурса специальности, 92.59kb.
- Имитационное моделирование инвестиционных рисков, 462kb.
- Моделирование экологических систем, 54.46kb.
- Программы магистерской подготовки 210400. 68. 04 Микроволновая техника и антенны Аннотация, 484.71kb.
Б) Промежуточная информация
Промежуточная информация была приведена в пункте 3.1.3.(Б)
- Результаты решения
Результаты выводятся в виде графиков (траекторий движения) для 5 времен хода и таблиц, в которые сведены:
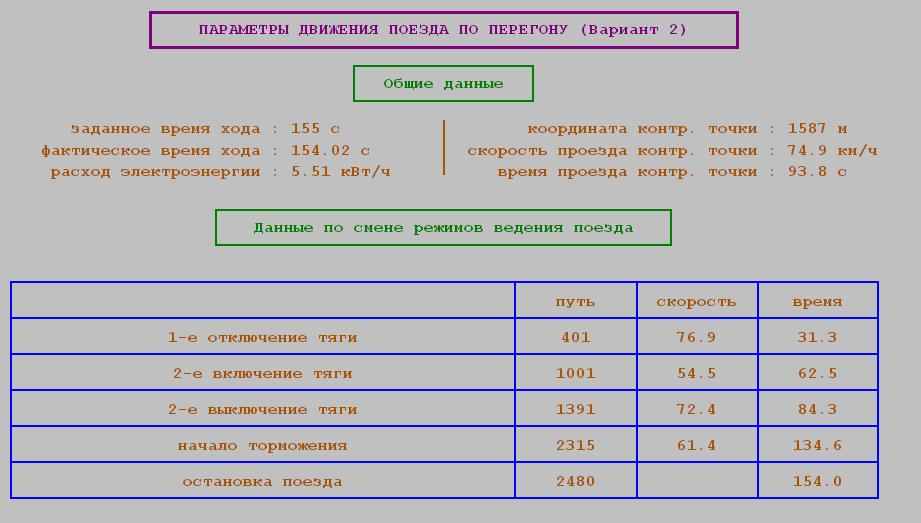
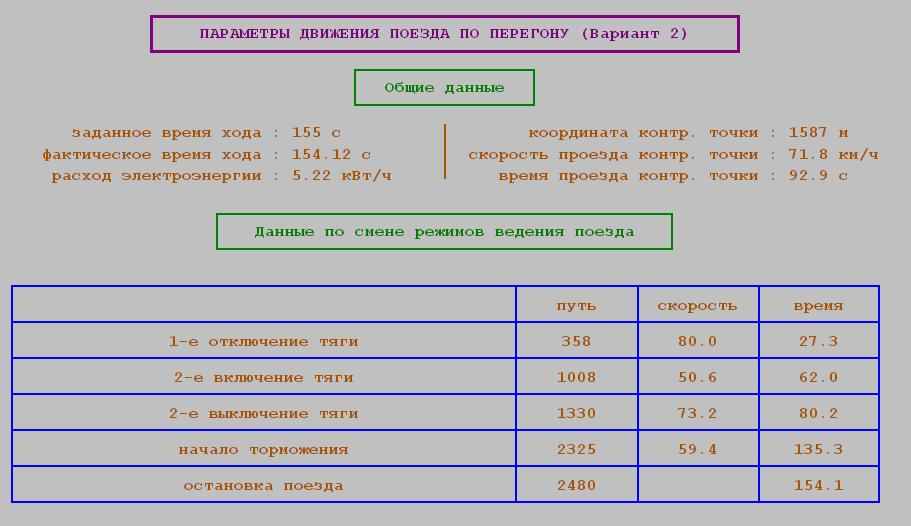
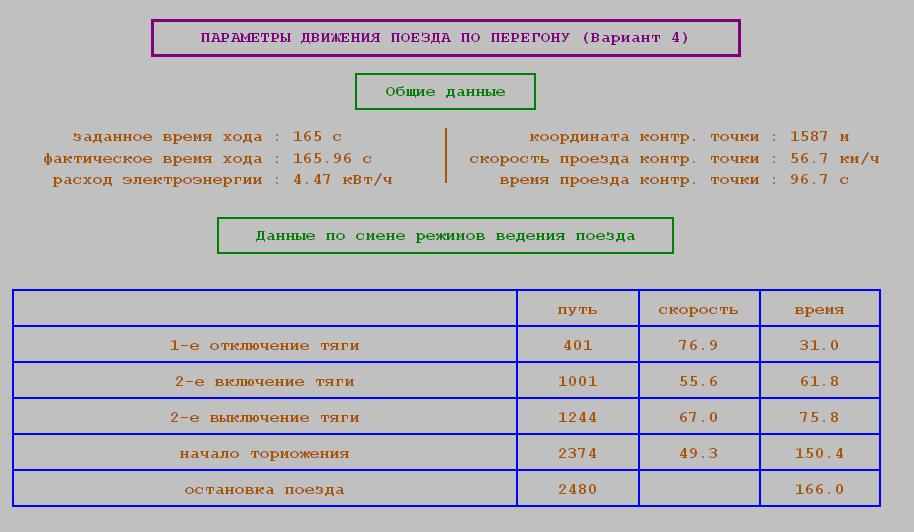
1. Общие данные:
- заданное и фактическое время хода [с]
- расход электроэнергии [кВт/ч]
- координаты контрольной точки [м]
- скорость проезда контрольной точки [м/с]
- время проезда контрольной точки [с]
2. Данные по смене режимов ведения поезда:
- координаты включения и отключения тяг [м]
- координаты начала торможения и остановки поезда [м]
- скорость проезда этих координат [м/с]
- время проезда этих координат [c]
- Математическое описание
Для моделирования движения поезда используется уравнение движения поезда, которое связывает между собой скорость V, путь S и время T в дифференциальной форме. Интегрирование уравнения движения поезда возможно по пути, времени или скорости. В рассматриваемой модели движения поезда при расчете траекторий движения за независимую переменную принимаем путь S.
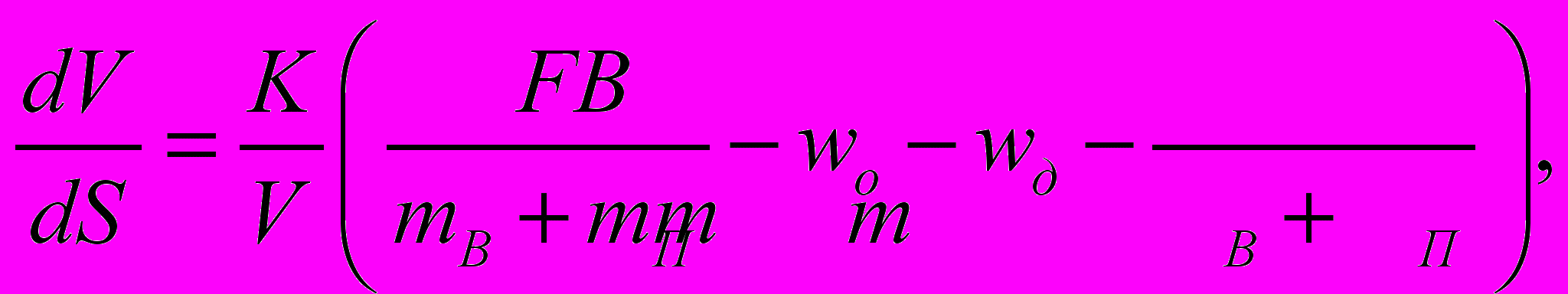 (10)
(10)где F – сила тяги вагона;
mВ - масса вагона;
mП - масса загрузки пассажирами вагона;
В - сила торможения вагона;
К - коэффициент, учитывающий размерность;
w0 – основное сопротивление
wд – дополнительное сопротивление;
V – скорость движения.
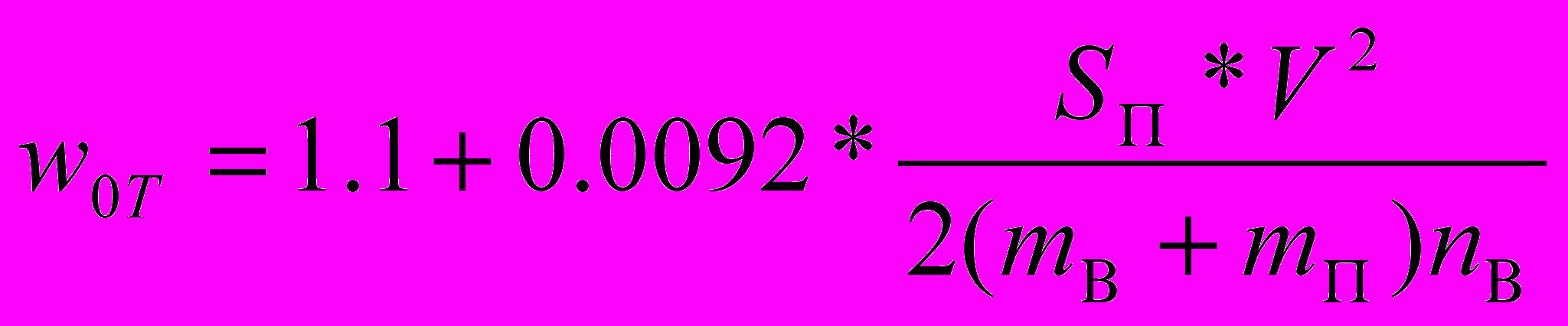 , (11)
, (11)где w0Т - основное сопротивление в режиме тяги;
SП – площадь эквивалентной поверхности.
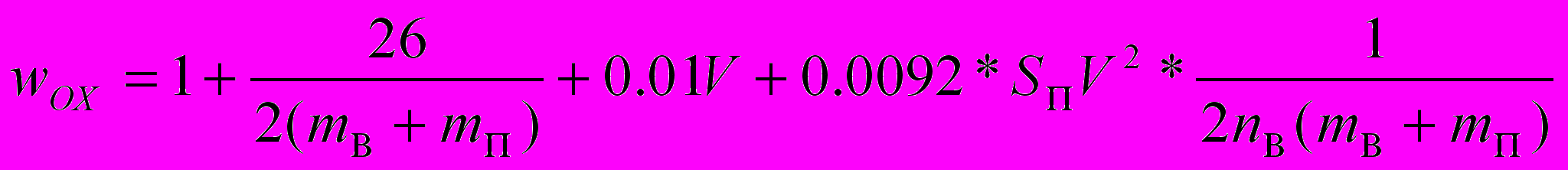 , (12)
, (12)где w0Х – основное сопротивление в режиме холостого хода.
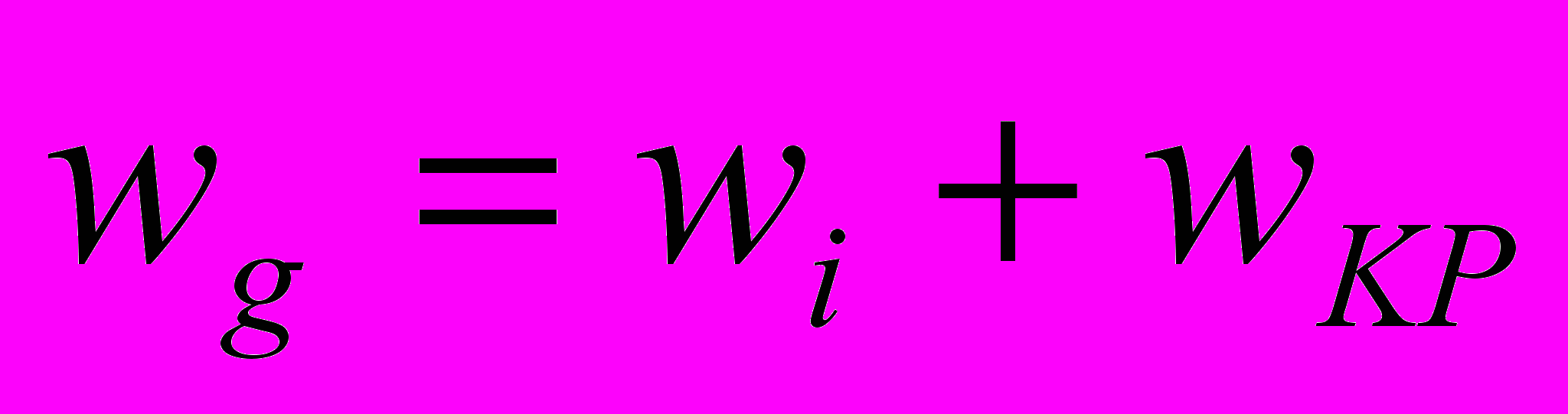 , (13)
, (13)где wi – сопротивление от уклонов, равное уклону;
wКР - сопротивление от кривой.
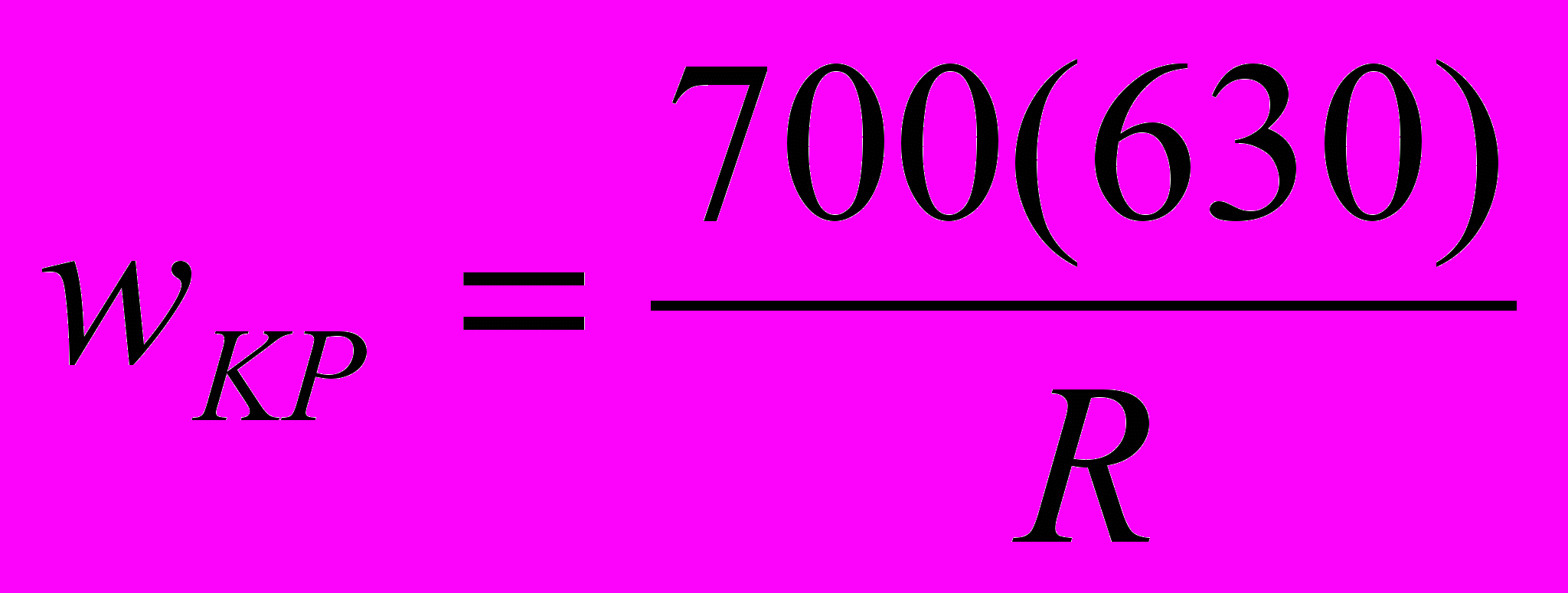 , (14)
, (14)где R – радиус кривой.
Сила тяги двигателя определяется по кусочно-линейно аппроксимированным характеристикам двигателя (6). Перед этим вычисляется ток двигателя Iд (9). Аппроксимация описана в пункте 3.2.3.
Уравнение движения поезда может решаться различными численными методами. В рассматриваемой модели для решения уравнения движения поезда используем метод Эйлера.
Решая уравнение движения поезда (10), скорость поезда на каждом шаге интегрирования определяем по следующей формуле:
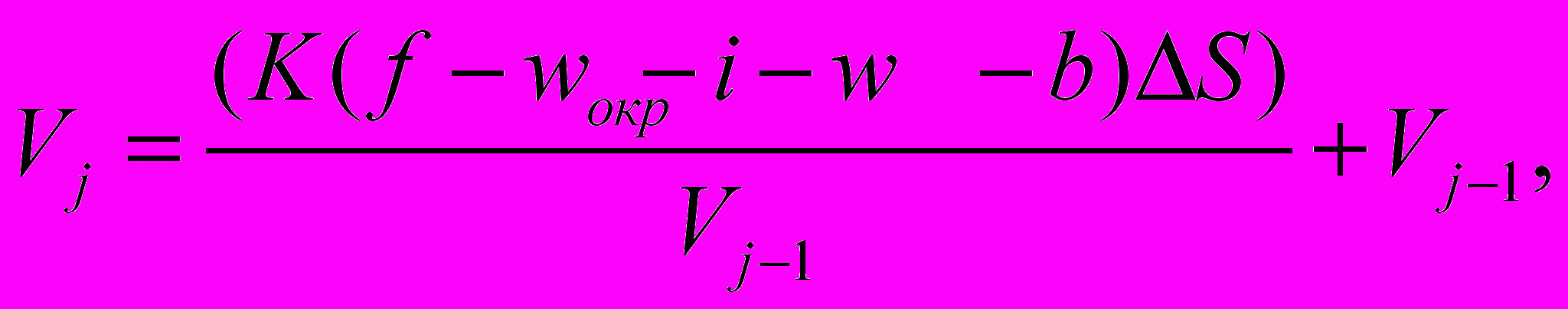 (15)
(15)где Vj - скорость поезда на j-ом шаге интегрирования;
Vj-1 -скорость поезда на (j-1)-ом шаге интегрирования;
ΔS - шаг интегрирования по пути.
От величины шага интегрирования ΔS зависит время счета и точность моделирования. С уменьшением шага интегрирования увеличивается точность и время счета. Шаг интегрирования в режиме выбега можно брать больше, чем в режиме тяги. Шаг интегрирования в режиме тяги следует принимать в диапазоне 1-5 м, в режиме выбега - 1-10м.
Пройденный путь определяется как:
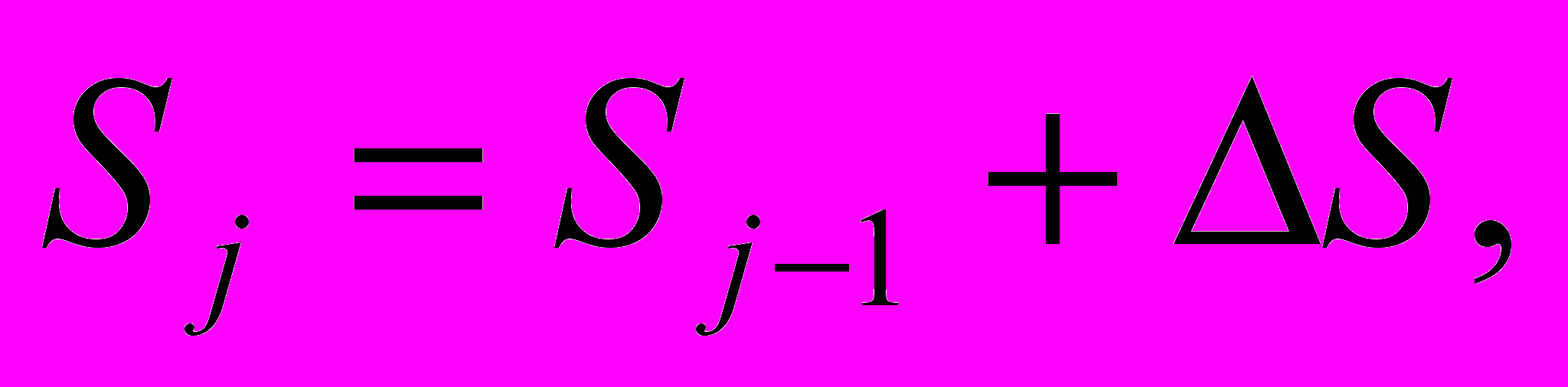 (16)
(16)где Sj, Sj-1 - пройденный поездом путь соответственно к концу j-го и (j-1)-го шагов интегрирования.
При моделировании движения, поезд считается как материальная точка с массой, сосредоточенной в центре поезда.
Время движения поезда вычисляется с учетом средней скорости движения на шаге интегрирования Vср:
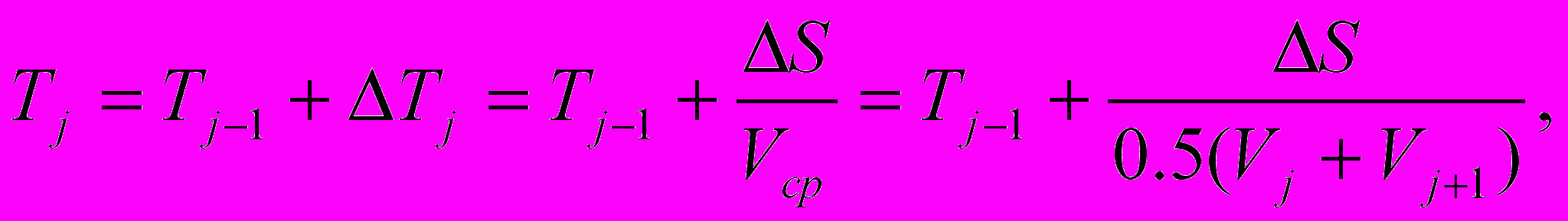 (17)
(17)где Tj, Tj-1 - время хода поезда от начала движения к концу соответственно j-го и (j-1)-го шагов интегрирования;
ΔTj - время хода на j-ом шаге интегрирования.
Расход электроэнергии вагона на тягу поезда вычисляется по формуле:
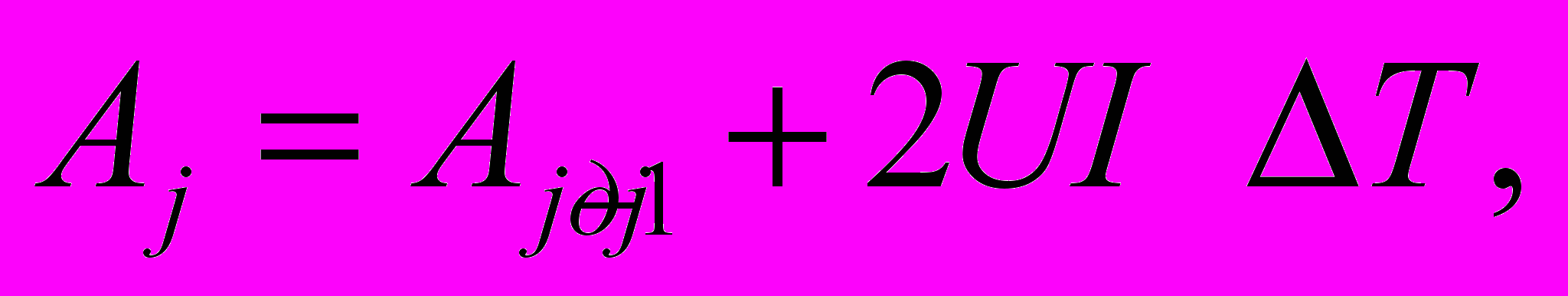 (18)
(18)где Iдj - ток двигателя на j-ом шаге интегрирования.
Моделирование движения поезда в режиме тяги и выбега производится путем решения уравнения движения поезда (10). В режиме тяги F > О, В = 0; в режиме выбега
F = 0, В = 0. В режиме торможения траектория движения поезда рассчитывается, из условия движения поезда по равнозамедленному закону. Начало торможения при остановке поезда на станции определяется из условия:
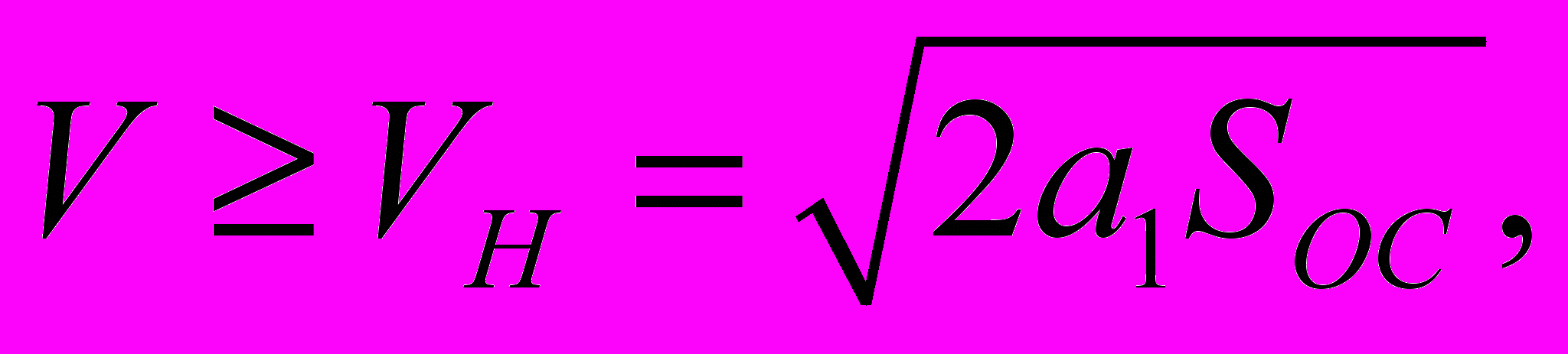 (19)
(19)где a1 - заданное замедление поезда в режиме прицельного торможения при остановке на станции;
VH - скорость поезда в начале торможения;
Sос - оставшийся путь до конца перегона, который равен
Sос = SП – S (20)
где SП -длина перегона;
S- текущая координата поезда.
Время движения в режиме торможения будет равно:
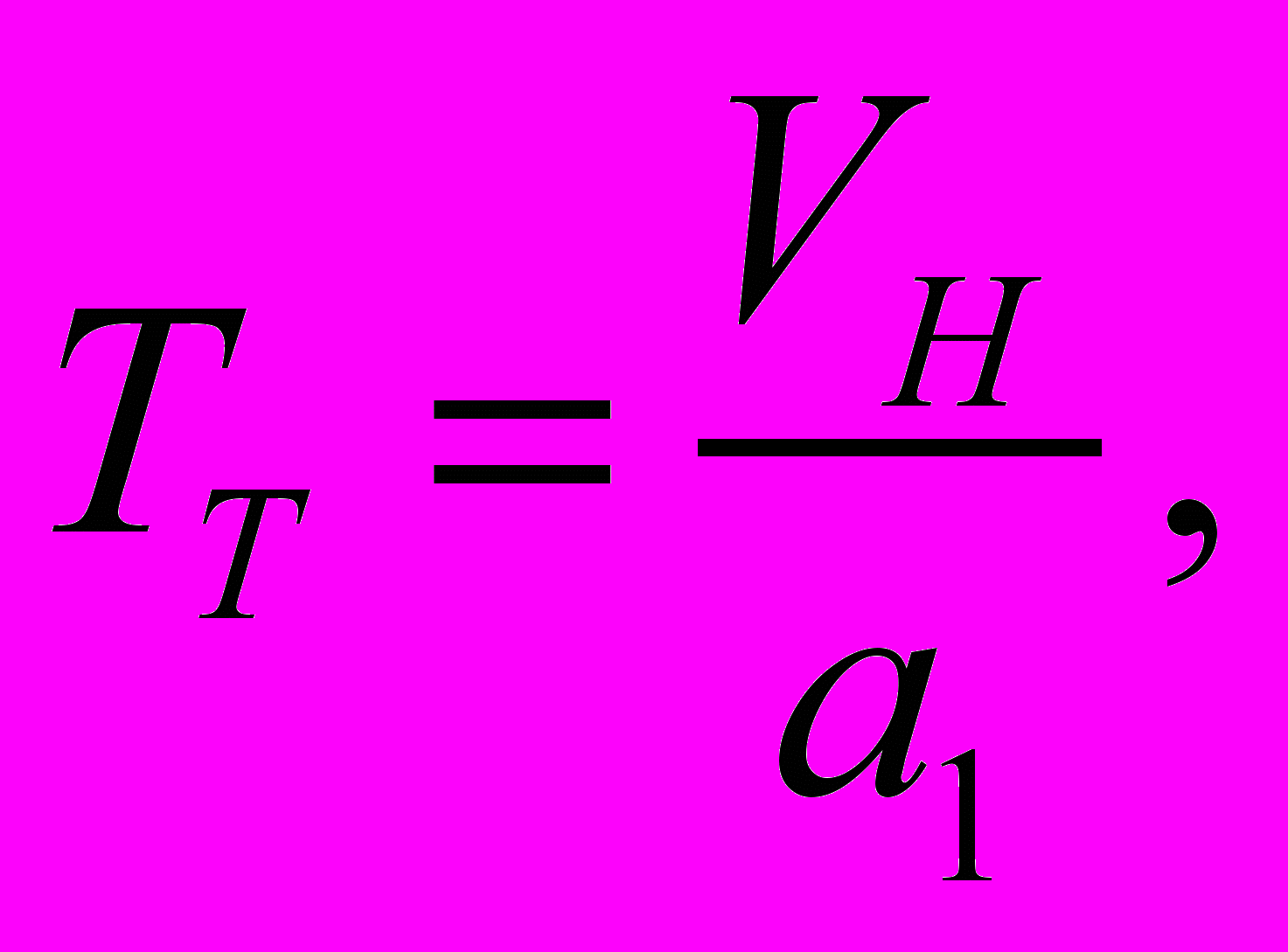 (21)
(21)На перегонах применяется подтормаживание для снижения скорости перед ограничениями скорости. Скорость начала торможения при ограничениях скорости равна:
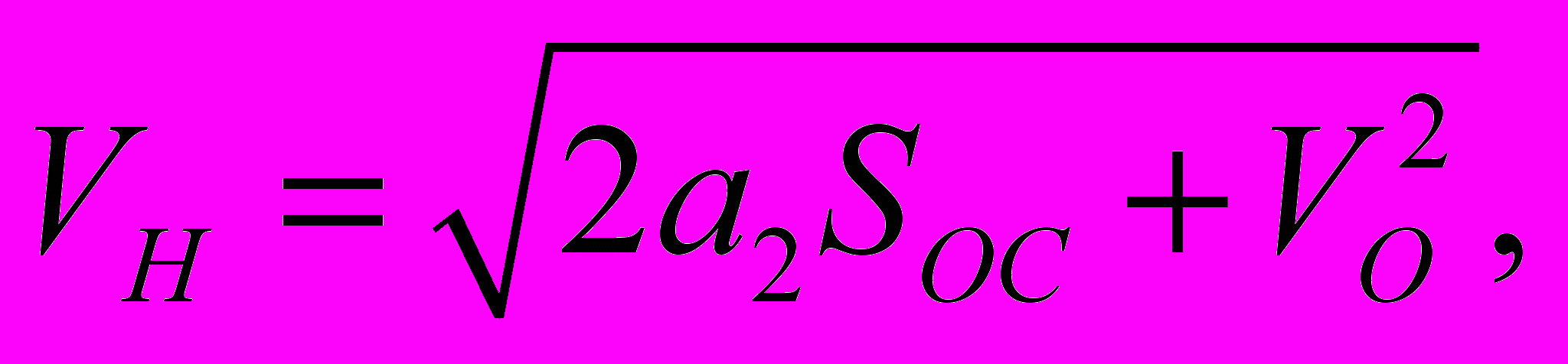 (22)
(22)где a2 - замедление поезда при подтормаживании перед ограничениями скорости;
Sос – оставшийся путь до ограничения скорости;
V0 – скорость ограничения.
Время движения поезда в режиме подтормаживания перед ограничением скорости равно:
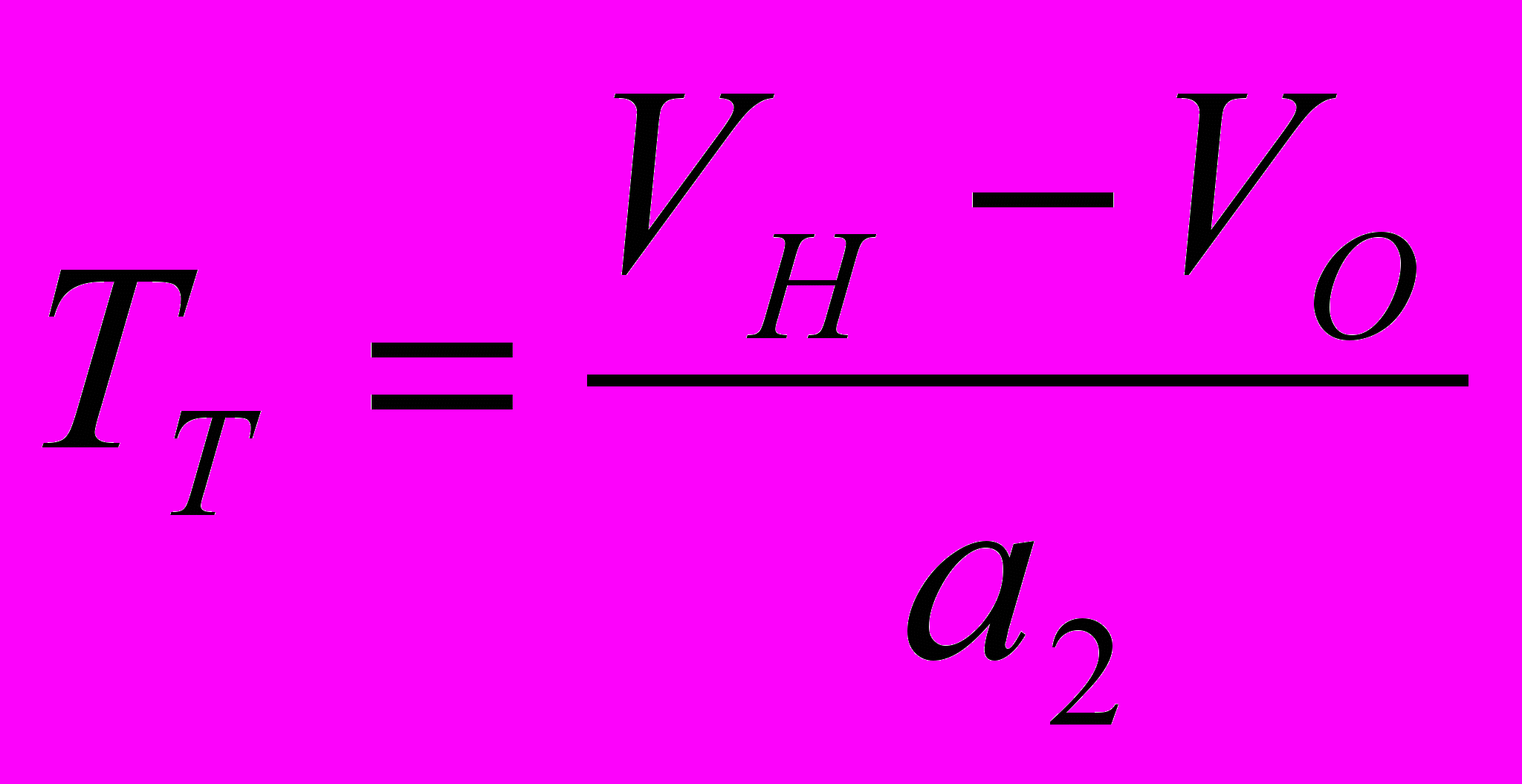 , (23)
, (23)Модель позволяет рассчитывать траектории движения поезда для перегонов с одним и двумя включениями тяговых двигателей. Для перегонов с одним включением тяговых двигателей рассчитываются пять траекторий движения для заданных времен хода по перегону
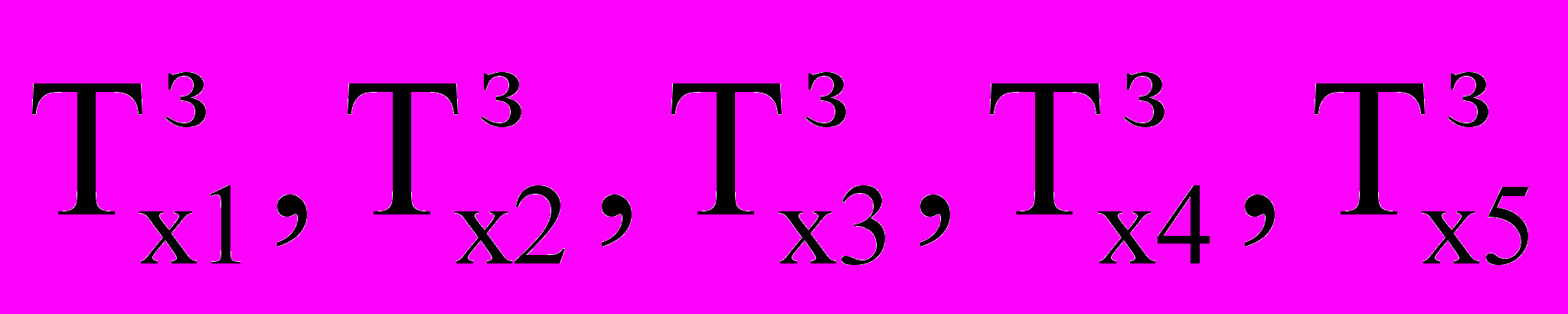 , кратных 5 с. Первая траектория движения поезда рассчитывается для минимального времени хода
, кратных 5 с. Первая траектория движения поезда рассчитывается для минимального времени хода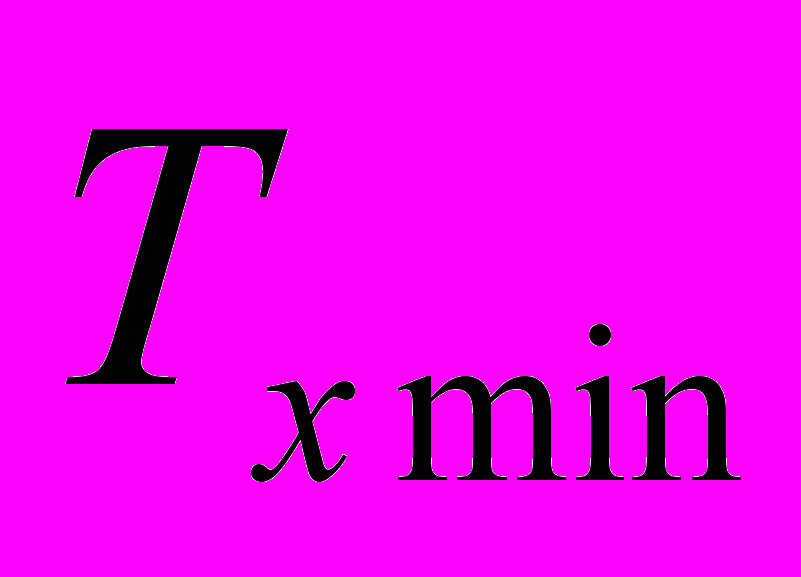 , когда отключение тяговых двигателей производится в момент, когда скорость поезда достигает допустимой скорости
, когда отключение тяговых двигателей производится в момент, когда скорость поезда достигает допустимой скорости 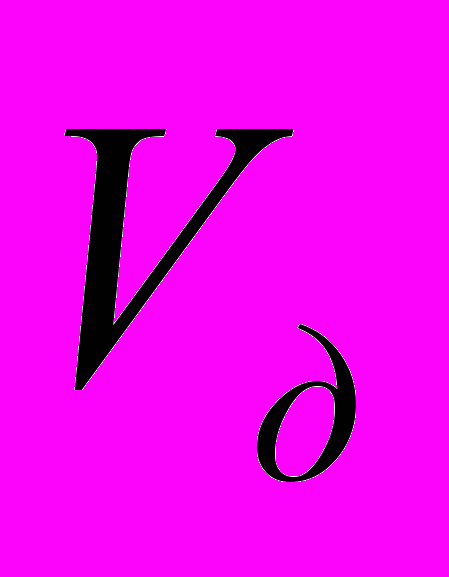 .
.Если
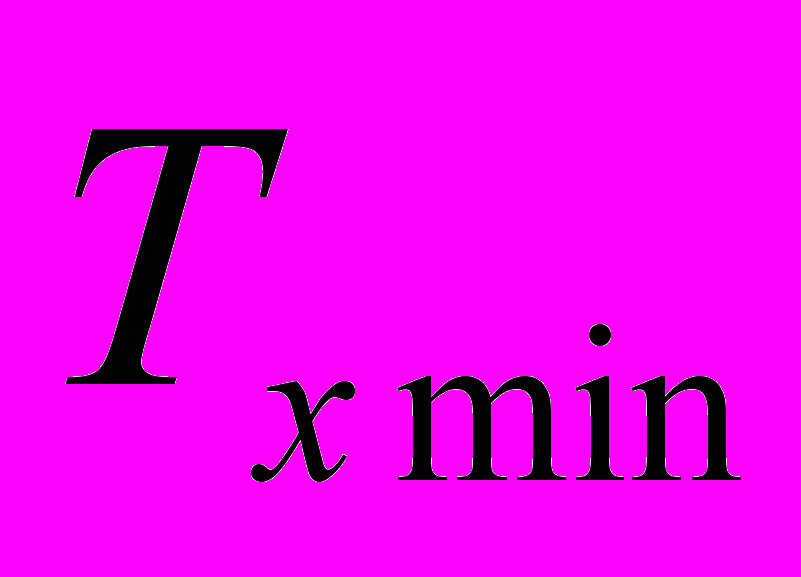 не кратно 5 с, то выбирается первое заданное время-хода, кратное 5 с
не кратно 5 с, то выбирается первое заданное время-хода, кратное 5 с 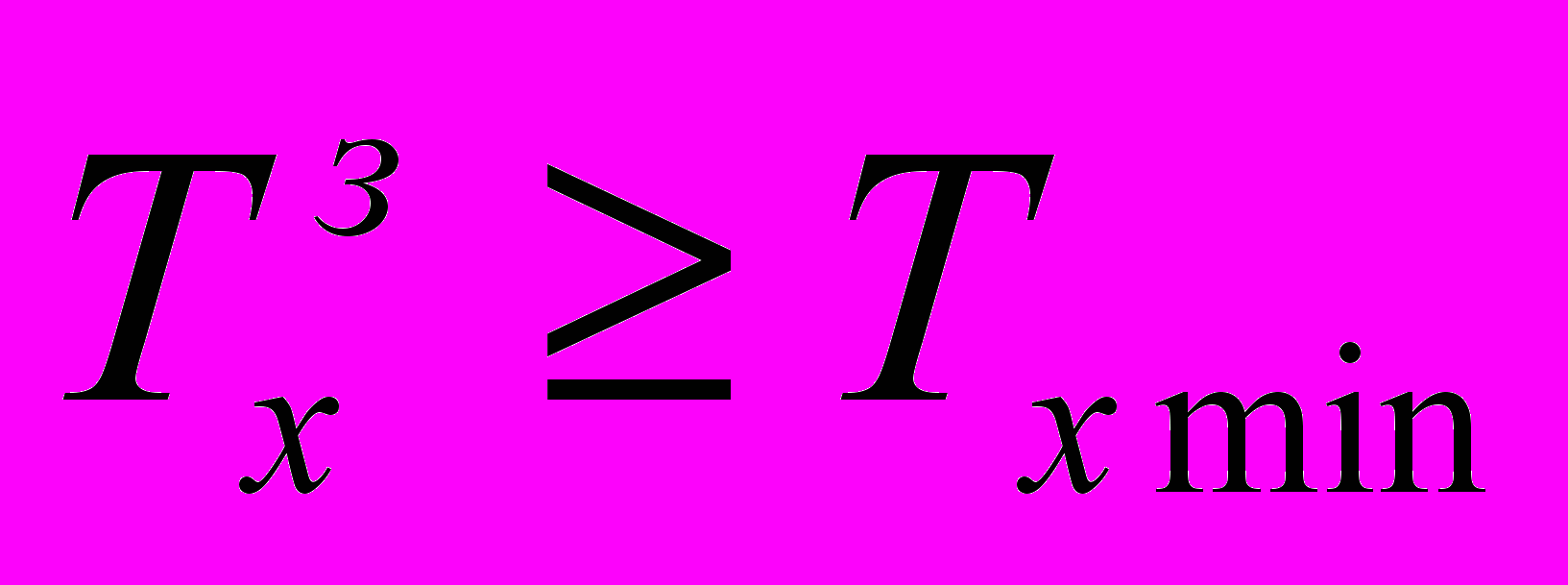 и для этого времени рассчитывается траектория движения. Каждое последующее заданное время хода по перегону увеличивается на 5с, т.е
и для этого времени рассчитывается траектория движения. Каждое последующее заданное время хода по перегону увеличивается на 5с, т.е 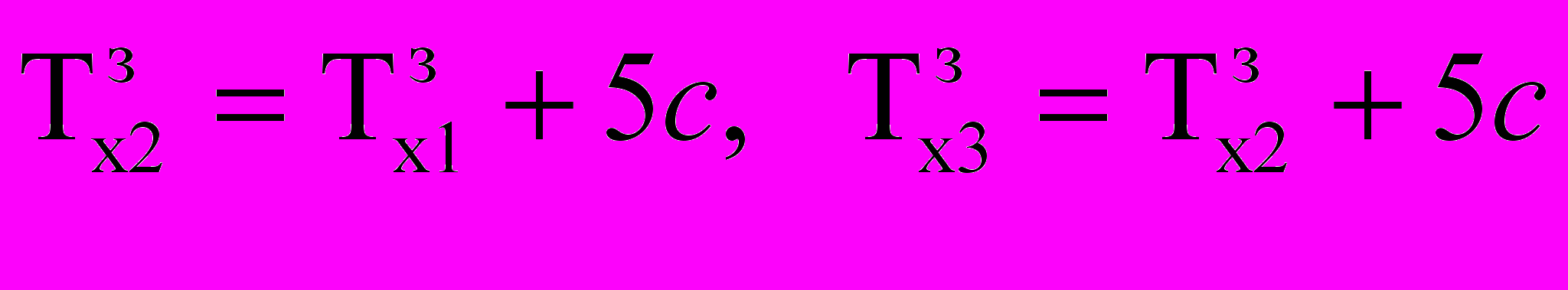 и т.д.
и т.д. Достижение заданного времени хода поезда по перегону достигается выбором координаты выключения тяговых двигателей
 . Если полученное время хода по перегону не равному
. Если полученное время хода по перегону не равному 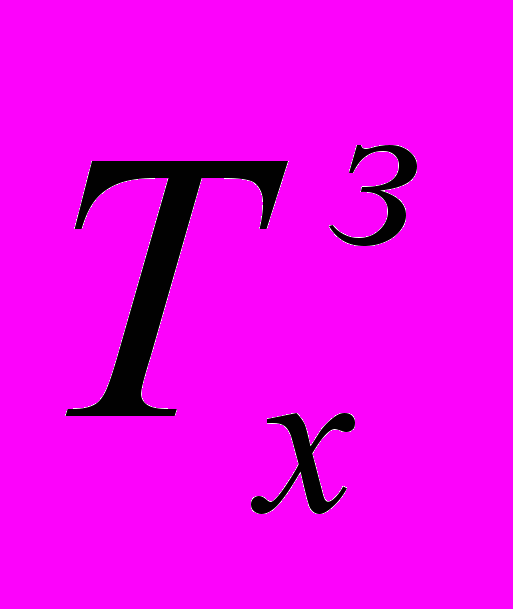 с точностью до 1 с, то изменяется место выключения тяговых двигателей на один шаг интегрирования в ту или иную сторону в зависимости от знака рассогласования времен хода и снова производится моделирование движения поезда до выполнения условия:
с точностью до 1 с, то изменяется место выключения тяговых двигателей на один шаг интегрирования в ту или иную сторону в зависимости от знака рассогласования времен хода и снова производится моделирование движения поезда до выполнения условия: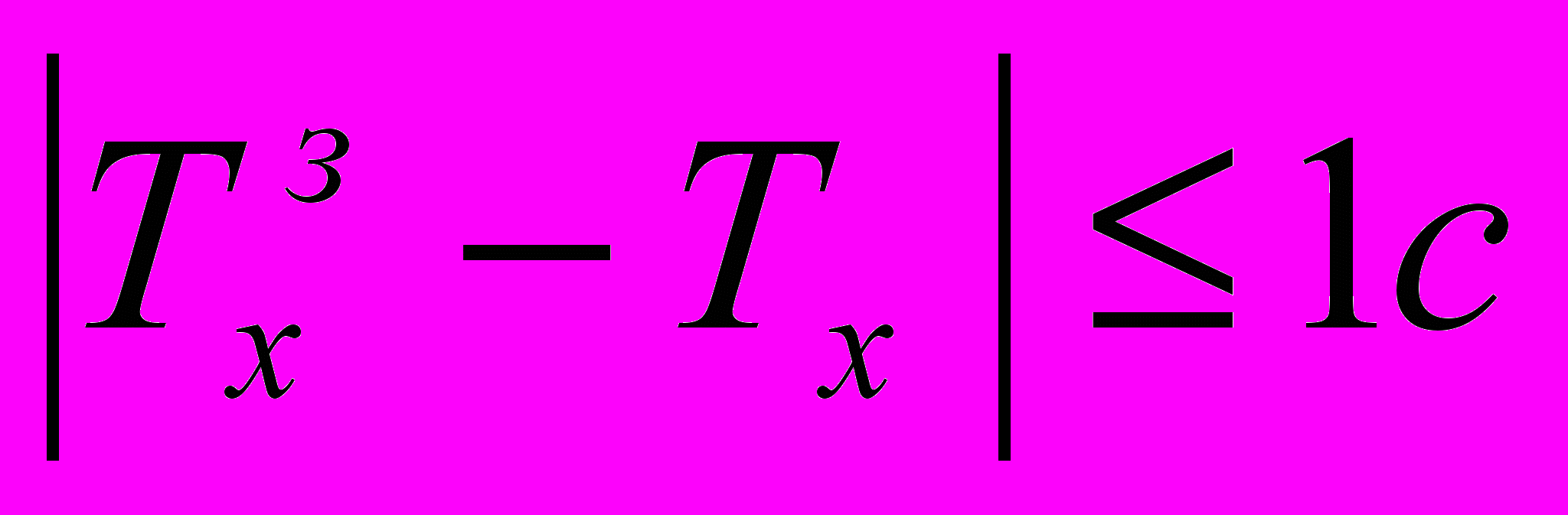 , (24)
, (24)На перегонах с двумя включениями тяговых двигателей первое выключение двигателей производится в фиксированной (заданной) координате SВКЛ1, второе включение производится в заданной координате SВКЛ2, а достижение условия заданного времени хода производится по такому же алгоритму, как и на перегонах с одним включением тяговых двигателей путем подбора координаты SВЫКЛ2.
- Алгоритм решения
А) Блок-схема алгоритма
Укрупненная блок-схема алгоритма представлена на рисунке






Б) Описание логики процесса
1 – обнуление всех значений массива параметров движения поезда;
2 – задание случайных значений массы загрузки вагона, напряжения на токоприемнике и коэффициента учета основного сопротивления;
4-95 – цикл по пяти временам хода по перегону (т.к. должно получиться пять траекторий движения поезда по перегону с разными временами хода; этот цикл организуется, если управление автоматическое);
5 – установка параметров ведения поезда;
7-93 – цикл для поиска заданного времени хода (при автоматическом управлении под заданным временем хода понимается, так называемое программное время хода, которое должно быть кратным пяти и отличаться от реального менее чем на одну секунду);
10-92 – цикл для моделирования одного пробега поезда по перегону;
11 – аппроксимация тяговой характеристики с корректировкой и определение текущих тока и силы тяги (в программе эти пункты алгоритма являются процедурой);
12-14 – определение и корректировка основного сопротивления движению и определение дополнительного сопротивления;
15-25 – выбор шага интегрирования;
27-38 – интегрирование по пути в режиме торможения;
39-45 – интегрирование по пути в режиме тяги или выбега;
47-63 – проверка перехода на уменьшенный шаг интегрирования для поиска точки начала прицельного торможения;
64-77 – проверки движения поезда по перегону;
78-90 – корректировка координаты последнего отключения тяги для выполнения заданного времени хода;
91 – проверка ситуации, когда второе выключение тяги наступает раньше второго включения тяги.
- Изменение параметров в программе движения поезда метрополитена
Модуль модели движения поезда находится в файле LABORANT.pas. В тексте программы именно этого модуля производим изменения. Для того чтобы все внесённые изменения вступили в силу, заново компилируем программу. Для этого запускаем на исполнение файл MSU.pas.
- Случайное изменение загрузки вагона пассажирами в диапазоне от 0 до 20т
Фрагмент программы:
BEGIN
Randomize;
TimeMin:=0.0;
ColTraekt:=0;
for i:=1 to 5 do
with MasParam[i] do
begin
COneOff:=0.0; VOneOff:=0.0; TOneOff:=0.0;
CTwoOff:=0.0; VTwoOff:=0.0; TTwoOff:=0.0;
CTwoOn:=0.0; VTwoOn:=0.0; TTwoOn:=0.0;
CTorm:=0.0; VTorm:=0.0; TTorm:=0.0;
CStop:=0.0; VKT:=0.0; TStop:=0.0;
TKT:=0.0;
end;
Massa:=random(20);
. . . . . . . . . . . . . .
- Случайное изменение напряжения на токоприемнике в диапазоне от 750В до 900В
. . . . . . . . . . . . . .
RealU:=750+random(150);
. . . . . . . . . . . . . .
- Случайное изменение коэффициента учета основного сопротивления движению поезда на ± 20%
. . . . . . . . . . . . . .
KoefWosn:=(8+random(4))/10;
. . . . . . . . . . . . . .
- Одновременное случайное изменение трех параметров
. . . . . . . . . . . . . .
Massa:=random(20);
RealU:=750+random(150);
KoefWosn:=(8+random(4))/10;
. . . . . . . . . . . . . .
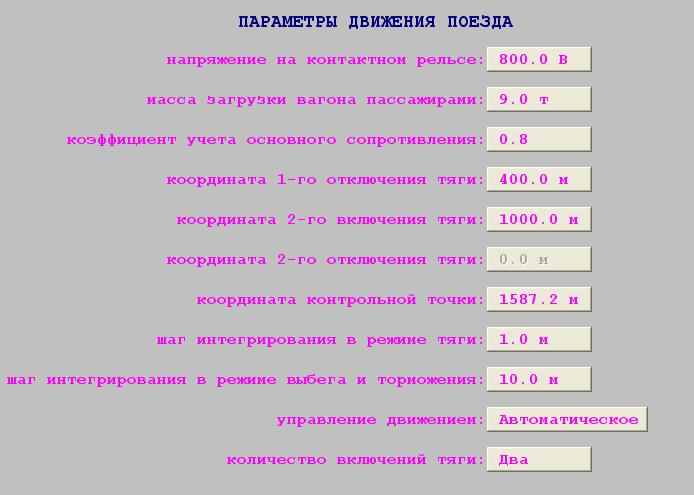
- Траектории и параметры движения поезда для перегона с двумя включениями тяговых двигателей при случайном изменении параметров
1. Случайное значение загрузки вагона пассажирами: 16т

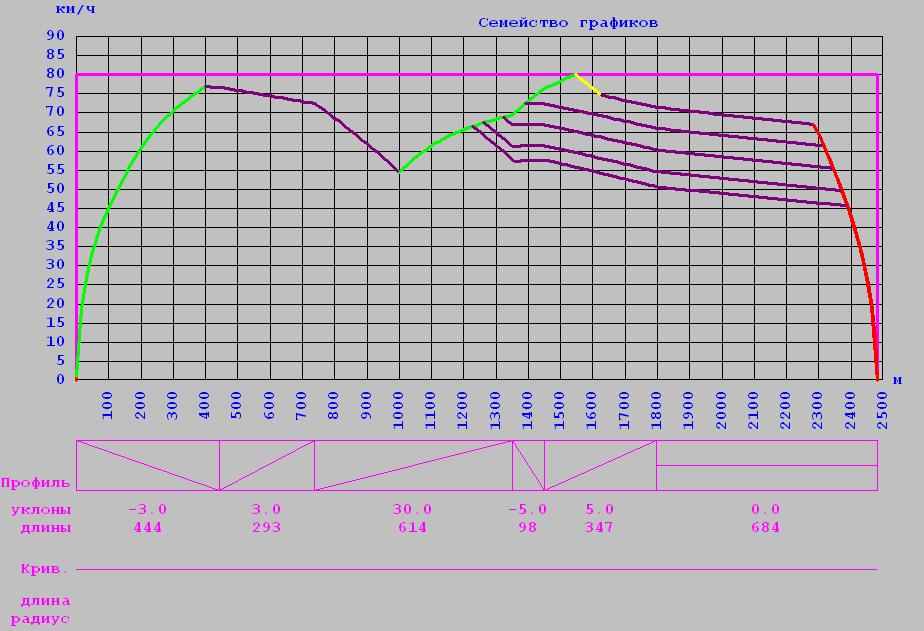

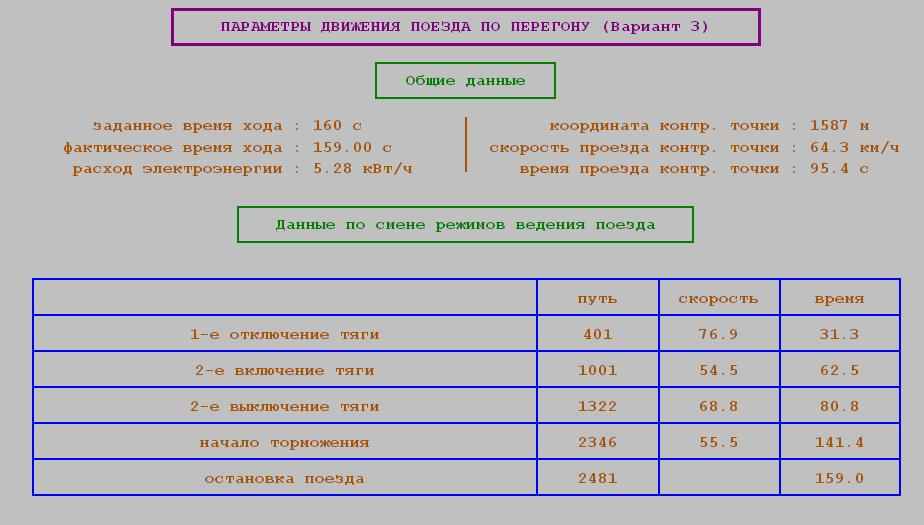


2. Случайное значение напряжения на токоприемнике: 856В
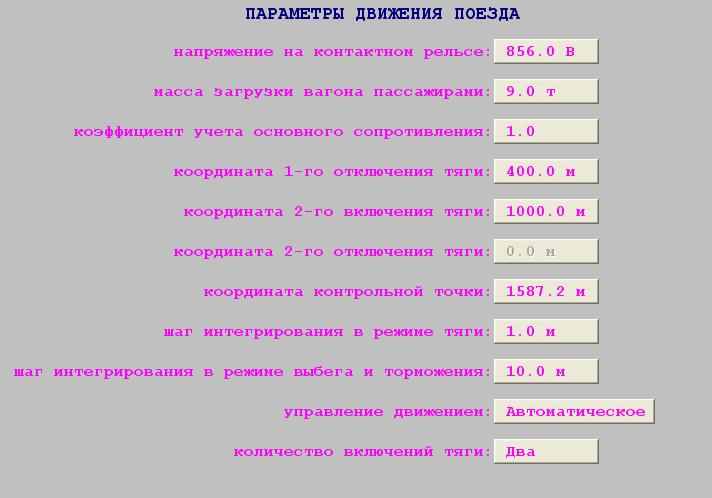
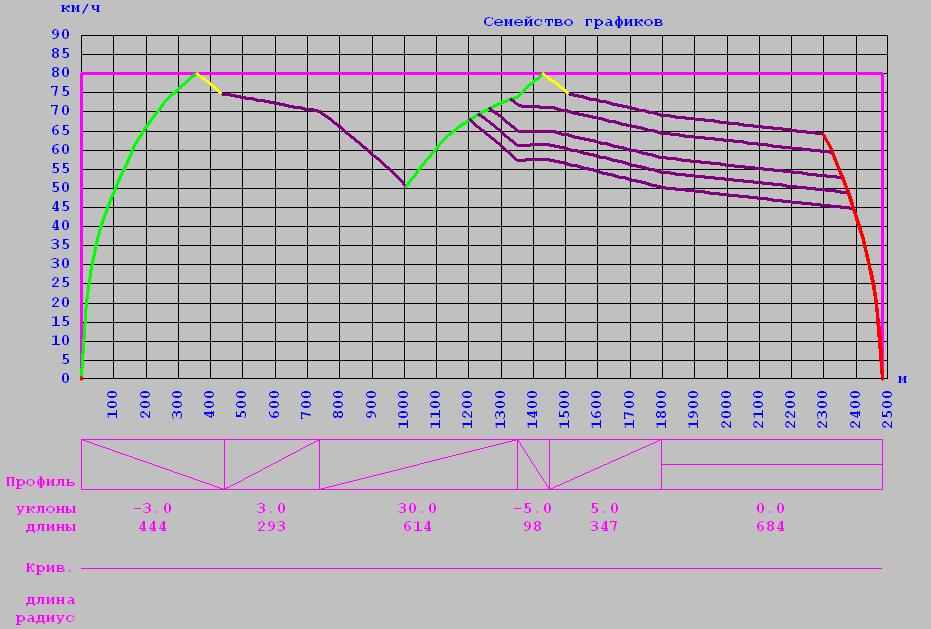




3. Случайное значение коэффициента учета основного сопротивления движению поезда: 0.8
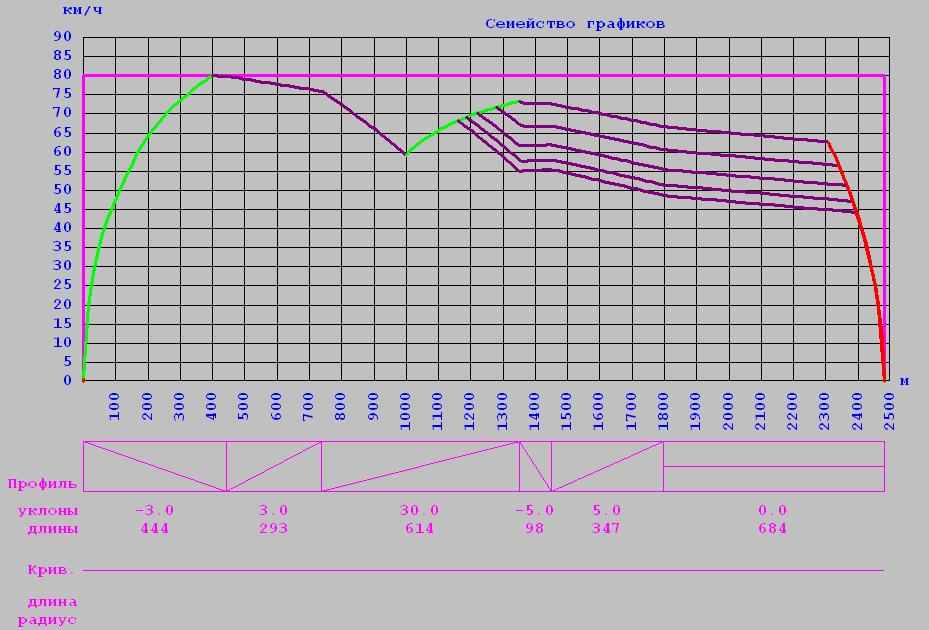





4. Случайные значение всех параметров: масса загрузки = 11т, напряжение на токоприемнике = 758В, коэффициент учета основного сопротивления = 0.8





- Траектории движения поезда для одного времени хода при детерминированной и стохастической моделях при случайном изменении параметров.
1. Параметры движения:
Время хода = 155с;
Напряжение на контактном рельсе = 800В;
Коэффициент учета основного сопротивления движению поезда = 1;
Детерминированная модель: масса загрузки вагона пассажирами = 9т (кривая 1);
Стохастическая модель: масса загрузки вагона пассажирами = 17т (кривая 2);
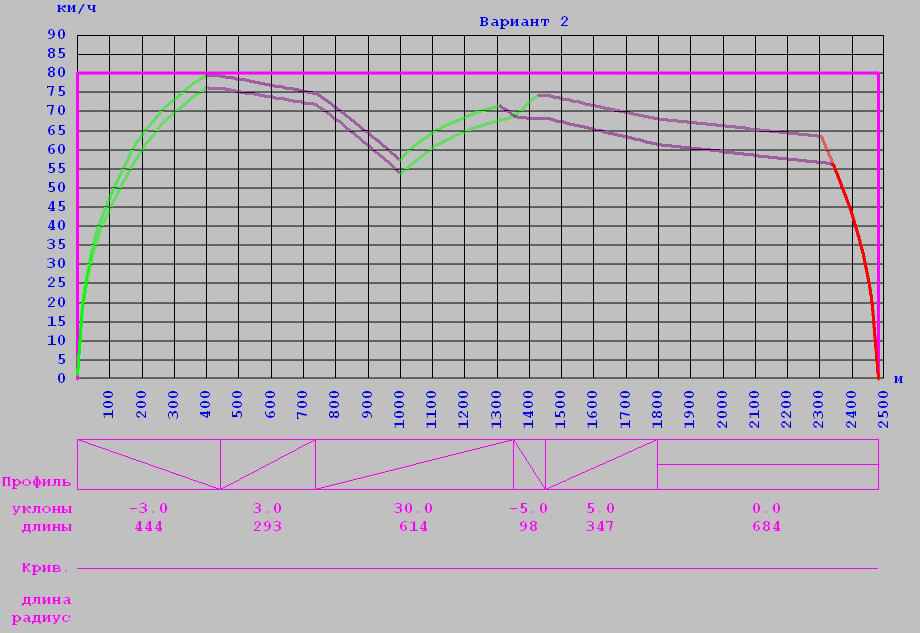
1
2
2. Параметры движения:
Время хода = 155с;
Масса загрузки вагона пассажирами = 9т;
Детерминированная модель: напряжение на контактном рельсе = 800В (кривая 1);
Стохастическая модель: напряжение на контактном рельсе = 835В (кривая 2);
Коэффициент учета основного сопротивления движению поезда = 1;
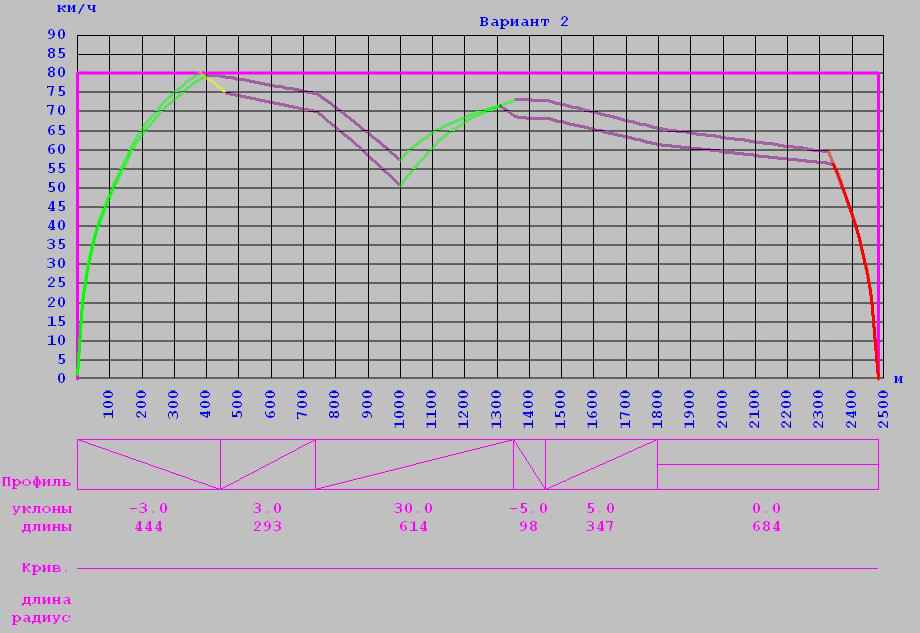
1
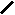
2
3. Параметры движения:
Время хода = 155с;
Масса загрузки вагона пассажирами = 9т;
Напряжение на контактном рельсе = 800В;
Детерминированная модель: коэффициент учета основного сопротивления = 1 (кривая 1);
Стохастическая модель: коэффициент учета основного сопротивления = 1.2 (кривая 2);
1
2
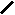
- Испытание имитационной модели
7.1. Проверка адекватности модели
Оценка адекватности модели проводится по следующим параметрам:
- скорость поезда в выбранных точках сравнения;
- время хода поезда в выбранных точках сравнения;
- расход электроэнергии на перегоне.
Проверка производится по средним значениям параметров.
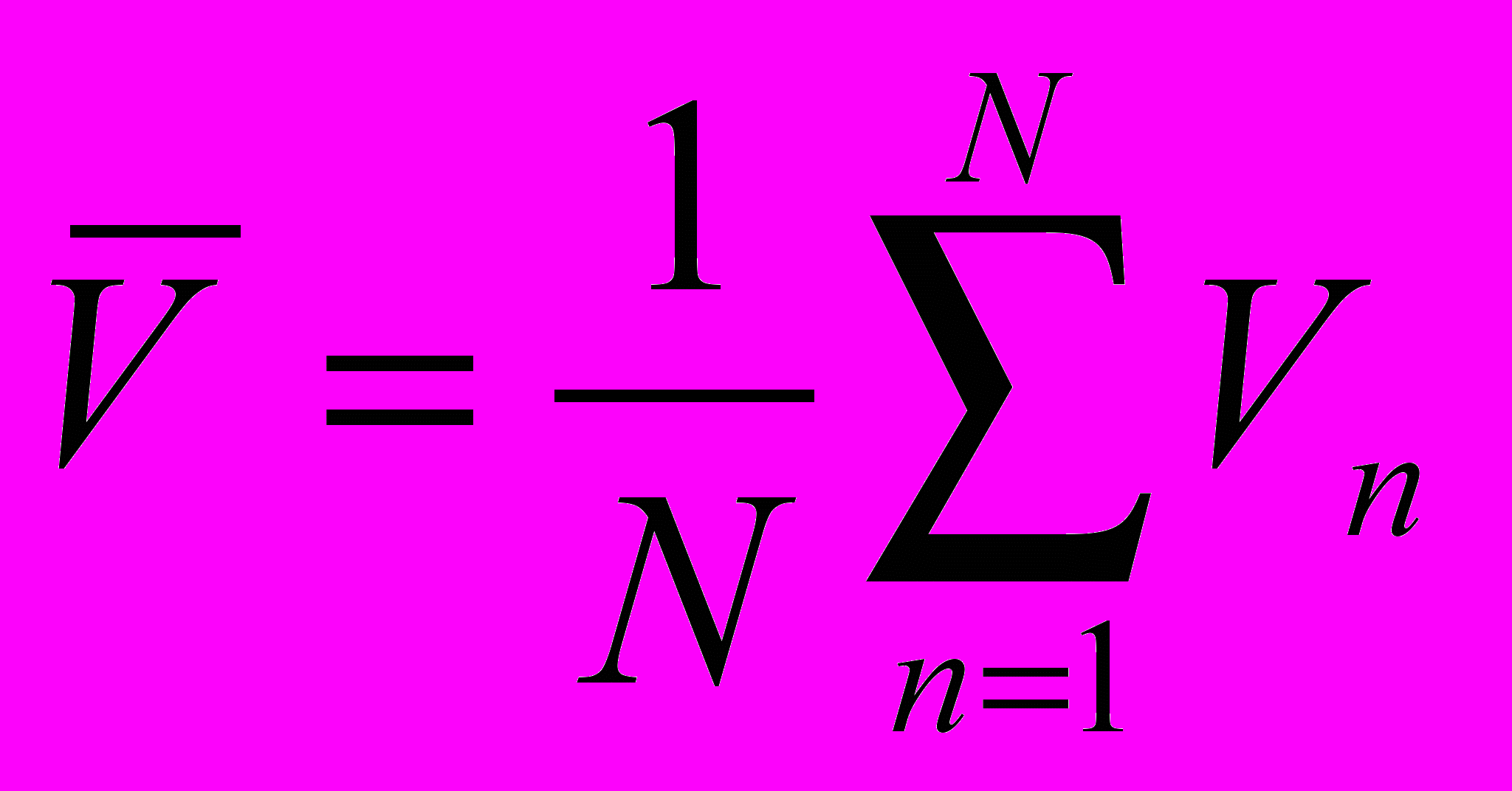 ; (25)
; (25) 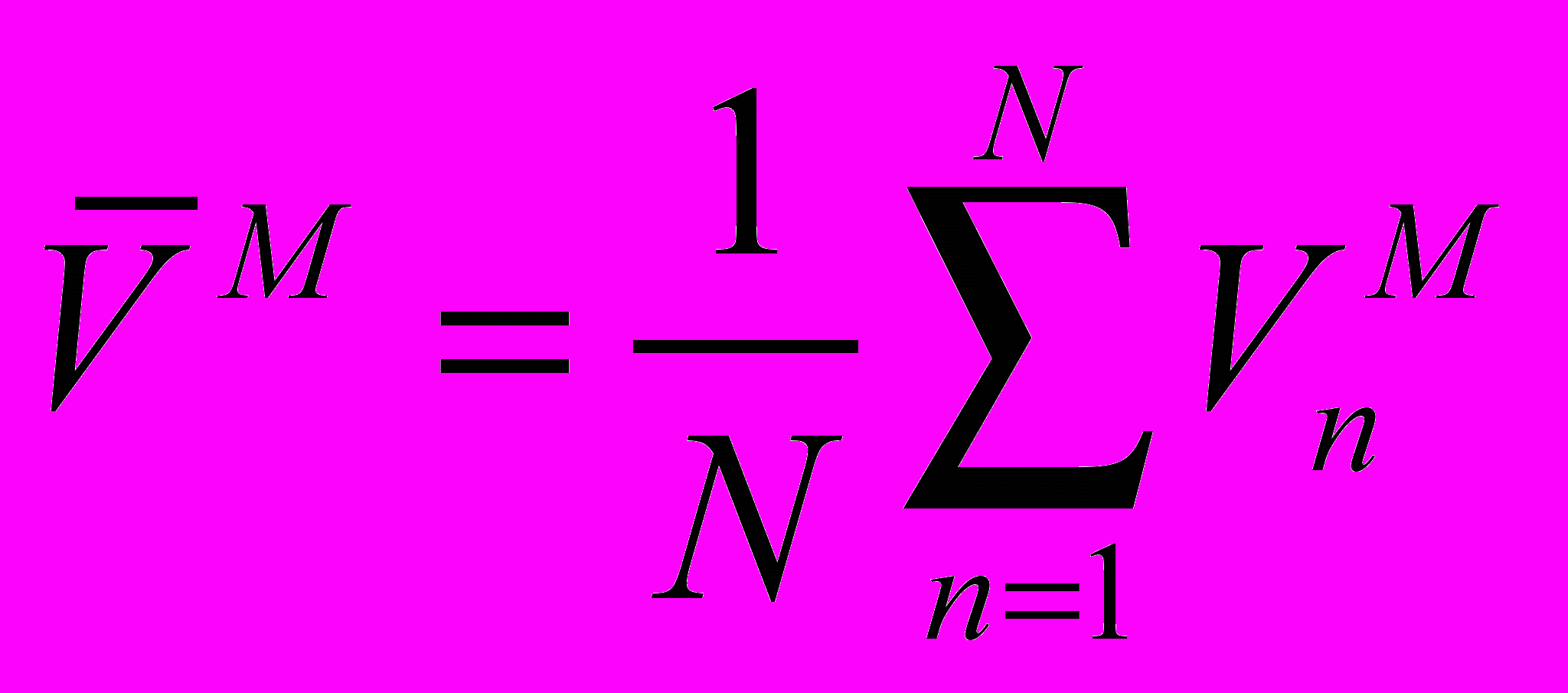 ; (26)
; (26) ; (27)
; (27) 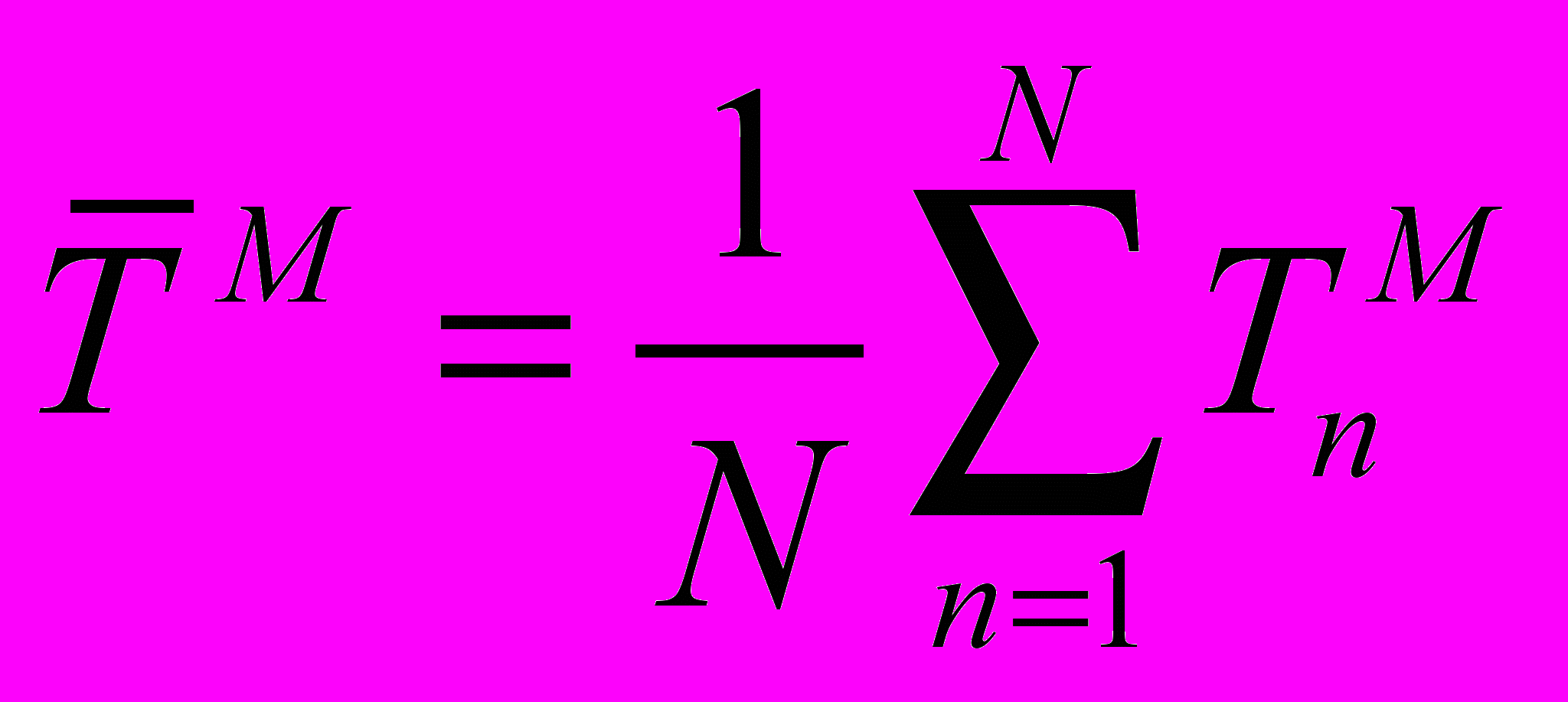 ; (28)
; (28)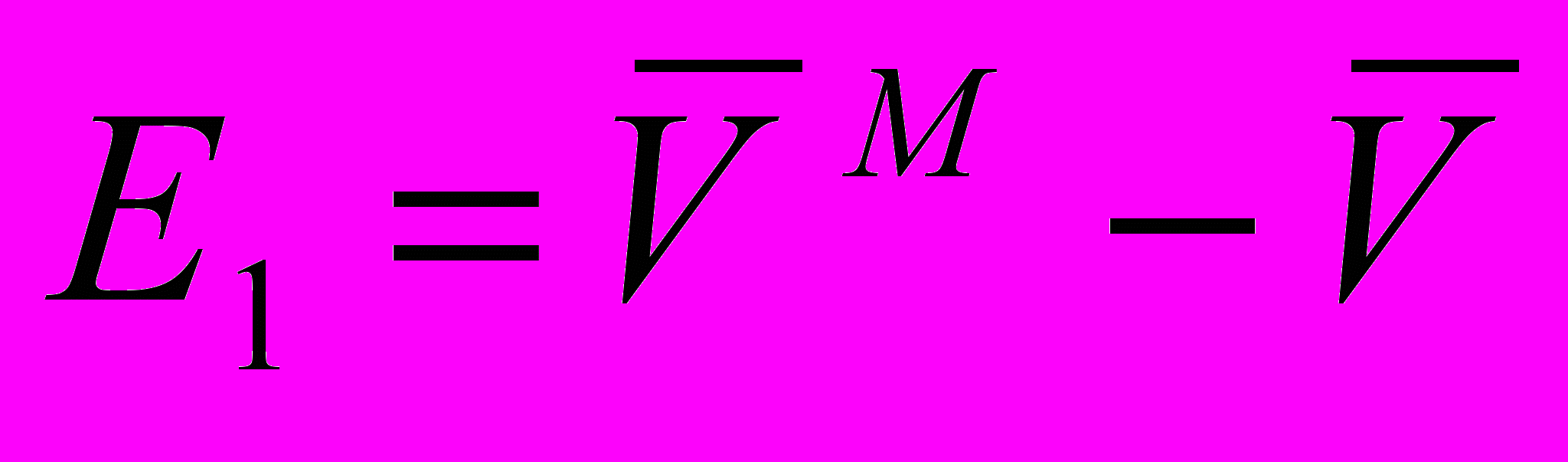 ; (29)
; (29)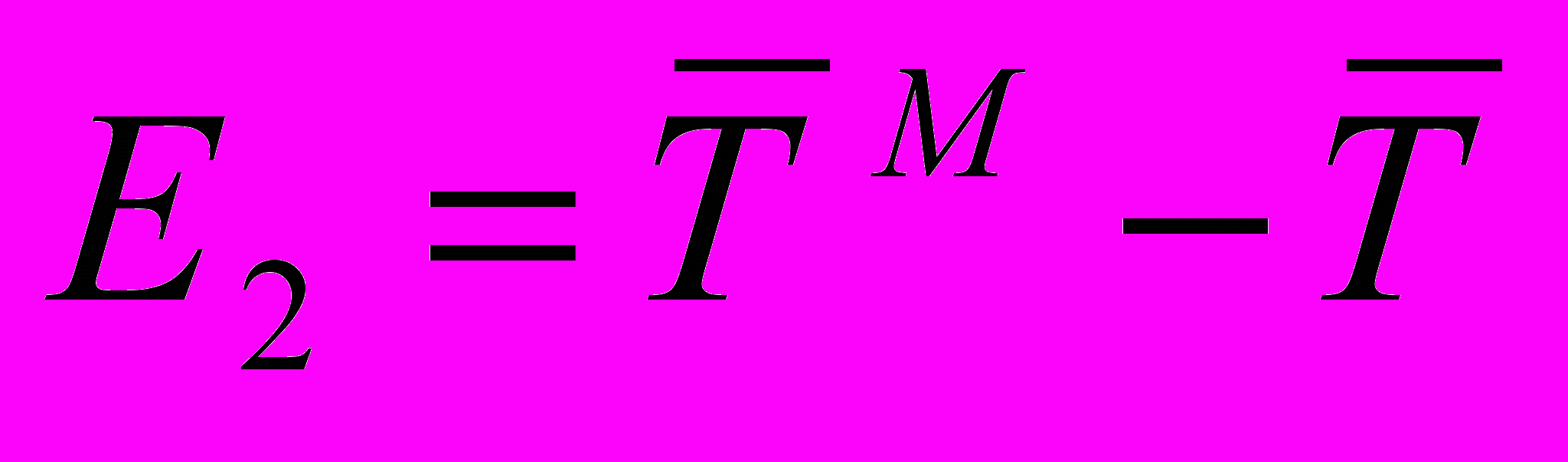 ; (30)
; (30)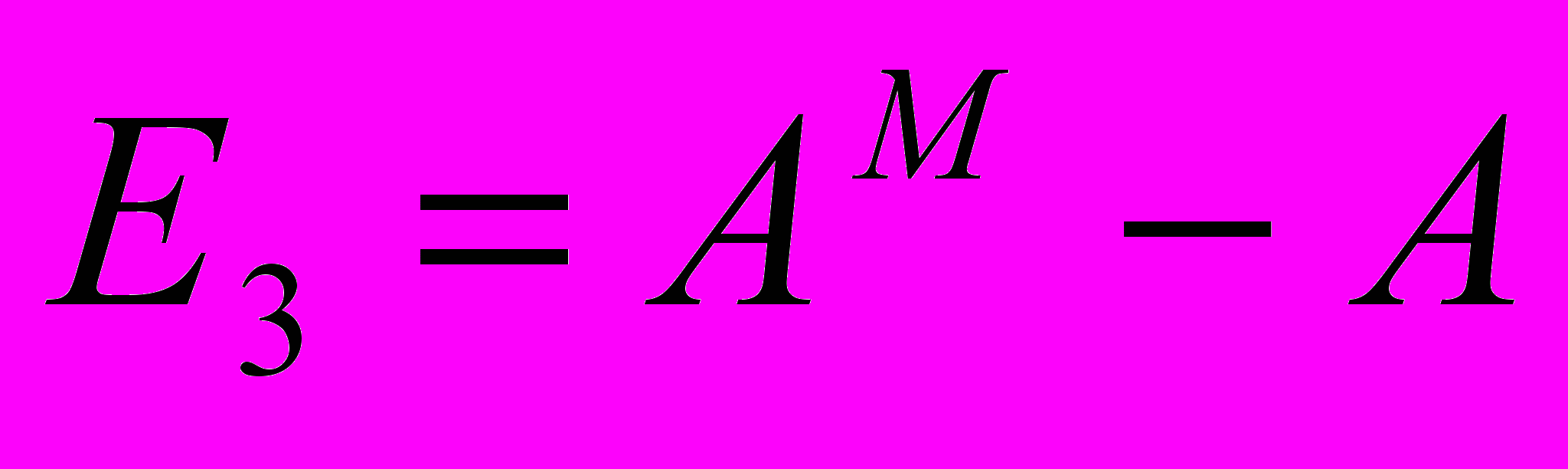 ; (31)
; (31)где
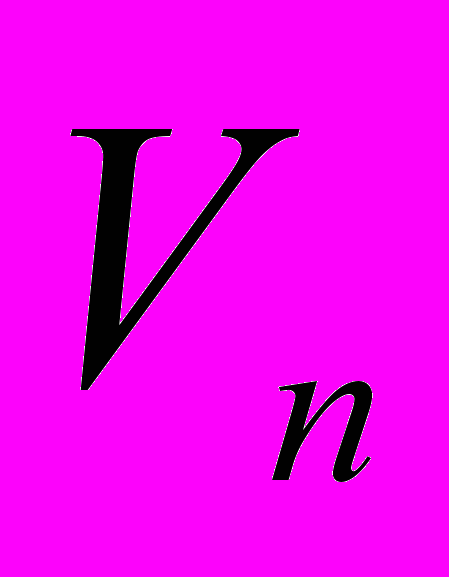 – скорость поезда в n-ой точке траектории; Tn – время поезда в n-ой точке траектории;
– скорость поезда в n-ой точке траектории; Tn – время поезда в n-ой точке траектории; 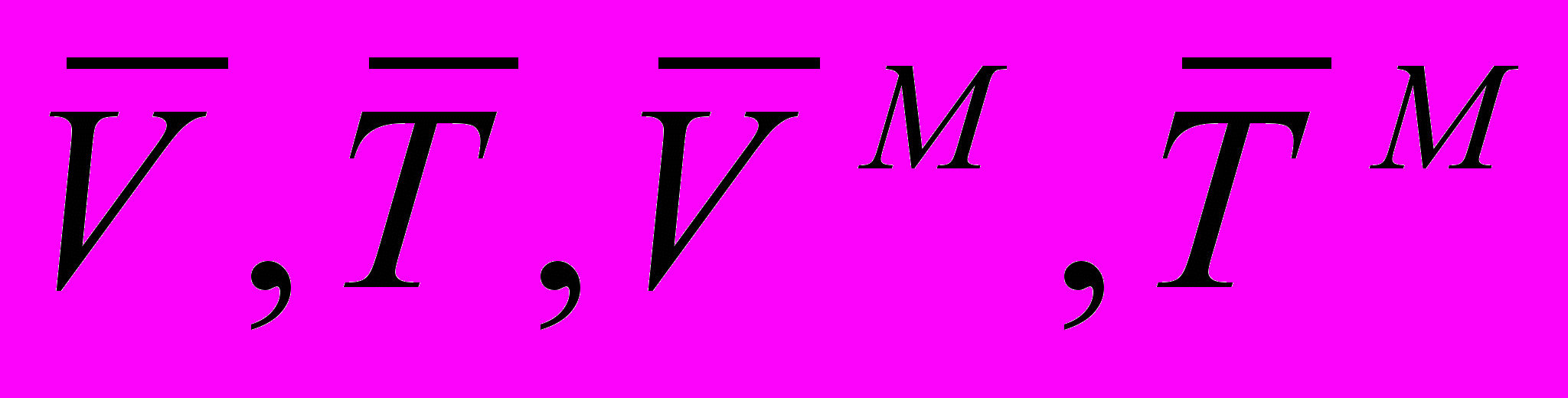 - средние значения скорости и времени в системе и на модели соответственно; E1, E2, E3 – оценки адекватности.
- средние значения скорости и времени в системе и на модели соответственно; E1, E2, E3 – оценки адекватности.Число точек сравнения N = 10.
Расчет проводится при детерминированной модели на перегоне с одним включением тяговых двигателей (U = 800B; m = 9т; k = 1). При шаге интегрирования 1м результаты расчета приняты за фактические значения, а при 5м – за модельные.
Значения параметров в выбранных точках траектории сведены в табл. 5.
Таблица 5
| Координата,м | Система | Модель | ||
| Скорость, км/ч | Время, с | Скорость, км/ч | Время, с | |
| 100 | 48,6 | 14,1 | 47,3 | 12,7 |
| 200 | 63,4 | 19,9 | 64,6 | 19,4 |
| 300 | 73,3 | 25,4 | 74,1 | 24,8 |
| 400 | 79,7 | 30,1 | 80 | 29,3 |
| 500 | 78,6 | 34,6 | 74,3 | 34 |
| 600 | 77 | 39,3 | 72,6 | 39,4 |
| 700 | 75,6 | 43,5 | 71,2 | 43,9 |
| 800 | 71,1 | 48,9 | 66,7 | 49 |
| 900 | 64,5 | 54,2 | 59 | 55,3 |
| 1000 | 57,4 | 60,1 | 52 | 61,2 |
 | 690,2 | 370,1 | 661,8 | 369 |
