Механика и электродинамика пристеночной плазмы

Вид материала

Автореферат

Содержание Общая характеристика работы Цель работы Практическая ценность Апробация работы. Структура диссертации. Объем диссертации. Краткое содержание диссертации. Первая глава 0; 2- ионы,  = /2; 3- ионы,  = ; 4- электроны,  = 0 Во второй главе В третьей главе Четвертая глава В пункте 4.2 В параграфе 4.3 гл. 4 В разделе 4.4 В разделе 4.5 Второй вариант. Рис. 25. Зависимость ne(y) для электрода ленточного типа (r0 = 5;  = 1/3) В параграфе 4.6 Рис. 26. Отклонение потока плазмы поперечным магнитным полем. ... Полное содержание

Подобный материал:

• Программа-минимум кандидатского экзамена по специальности 01. 02. 05 «Механика жидкостей,, 69.43kb.
• Программа учебной дисциплины «Электродинамика плазмы» Специальности 071500, 013900, 74.5kb.
• Программа-минимум кандидатского экзамена по специальности 01. 04. 02 «Теоретическая, 115.8kb.
• Паспорт специальности 01. 02. 05 Механика жидкости, газа и плазмы Шифр специальности:, 20.82kb.
• Физика (греч ta physika, от physis природа), наука о природе, изучающая простейшие, 51.33kb.
• Программа подраздела «История механики», 75.11kb.
• Рабочая программа учебной дисциплины "теоретическая физика", 162.35kb.
• Программа по физике для 10-11 классов общеобразовательных, 75.87kb.
• Диссипативные структуры и нестационарные процессы в межфазной гидродинамике 01. 02., 443.32kb.
• Рабочая программа учебной дисциплины «Физика конденсированного состояния, термодинамика,, 223.9kb.

На правах рукописи


КОТЕЛЬНИКОВ Михаил Вадимович


МЕХАНИКА И ЭЛЕКТРОДИНАМИКА ПРИСТЕНОЧНОЙ ПЛАЗМЫ


Специальность 01.02.05 - механика жидкости, газа и плазмы


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора физико-математических наук


Москва – 2008

Работа выполнена на кафедре «Прикладная физика» в Московском авиационном институте (государственном техническом университете)


Официальные оппоненты:

доктор физико-математических наук,

заслуженный деятель науки РФ,

профессор Алексеев Борис Владимирович,

доктор физико-математических наук,

заслуженный деятель науки и техники РФ,

профессор Киреев Владимир Иванович,

доктор технических наук,

профессор Ким Владимир Павлович


Ведущая организация: Центральный аэрогидродинамический институт

имени Жуковского Н.Е.


Защита диссертации состоится 26 сентября 2008 г. в 10-00 на заседании Диссертационного совета Д 212.125.14 при Московском авиационном институте (государственном техническом университете) по адресу: 125993, Москва, Волоколамское шоссе, д. 4, тел. (499) 158-58-62.


С диссертацией можно ознакомиться в библиотеке МАИ.


Автореферат разослан ____ ____________ 2008 г.


Просим принять участие в работе совета или прислать отзыв в одном экземпляре, заверенный печатью организации.


Ученый секретарь

Диссертационного совета Д 212.125.14 Гидаспов В.Ю.


ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ


Актуальность. Низкотемпературная плазма как четвертое состояние вещества играет всё возрастающую роль в нашей жизни. Она является рабочим телом в самых разнообразных приборах и устройствах. Плазма дугового разряда используется в различного типа технологических плазмотронах, предназначенных для сварки и резки металлов, напыления пленок со специальными свойствами, и, наоборот, распыления вредных пленок, инициирования плазмохимических реакций, изготовления интегральных схем и т.д. Плазма тлеющего разряда применяется в лампах дневного света, в некоторых типах лазеров и электронных приборов, в рекламных целях. Плазма СВЧ-разряда имеет место в различного назначения СВЧ-генераторах. В последние десятилетия для коррекции орбиты спутников применяются высоко эффективные движители малой тяги, рабочим телом для которых является плазма. В обозримом будущем более мощные плазменные движители (ПД) могут быть использованы как маршевые движители для полета на Марс и другие планеты солнечной системы.

С другой стороны низкотемпературная плазма может быть средой обитания для авиационно-космической техники. При движении сверхзвуковых самолетов и ракет в атмосфере Земли в головной ударной волне возникает слабоионизованная плазма, которая обтекает летательный аппарат (ЛА). С ростом скорости летательного аппарата растут концентрация и температура плазмы в пограничном слое. Соответственно возрастают тепловые потоки на поверхность аппарата, для нейтрализации которых применяется специальная тепловая защита. Пристеночная плазма может осложнять радиосвязь ЛА с наземными станциями слежения. Проблема электромагнитной совместимости плазменных струй, истекающих из ПД, и пристеночных плазменных образований с каналами радиосвязи является актуальной до настоящего времени. Искусственные спутники Земли и космические станции движутся в разреженной ионосферной плазме. Выходящие на орбиту ЛА и спускаемые с орбиты аппараты с неизбежностью вынуждены работать в окружении низкотемпературной плазмы. Плазма встречается и в природных условиях. Это искровой и коронный разряд (например, обычная молния), шаровые молнии и т.д. Пламя обычной ацетиленовой горелки, особенно при инжекции в него легко ионизируемых солей щелочных металлов, представляет собой слабоионизованную столкновительную плазму. Плазма возникает при взаимодействии лазерного и других типов излучения с веществом. Она широко используется в научных экспериментах при разработке техники будущего (плазма капиллярного разряда, искусственные образования типа шаровой молнии и др.).

Из приведенного далеко не полного обзора ясно, что исследование плазменного состояния вещества является актуальной задачей. Исследование осуществляется путем проведения физических и вычислительных экспериментов. Наиболее сложной областью для исследования является пристеночная плазма, поскольку в ней возникает возмущенная зона с достаточно сложным распределением потенциала, с отличными от максвеловских функциями распределения заряженных частиц. В пристеночной области возможны многочисленные элементарные процессы (рассеяние, отражение, поглощение, эмиссия, инжекция, сублимация, диссоциация, ионизация, рекомбинация, возбуждение и т.д.), существенно осложняющие физическую, математическую и вычислительную модели задачи. Комплексному исследованию методами вычислительного эксперимента (а иногда и физического эксперимента) пристеночных областей в плазме посвящена настоящая работа. В дополнение к сказанному отметим, что результаты исследований находят еще одну актуальную область применения – это развитие зондовых методов диагностики самой плазмы. В области механики и электродинамики пристеночной плазмы работало и работает огромное число исследователей, обзор работ которых приводится в начале каждой главы диссертации.

Цель работы

• создать надежные методы расчета пристеночных слоев вблизи тел, обтекаемых низкотемпературной плазмой, в широком диапазоне изменения числа Кнудсена (0  Kn < );
  
• исследовать структуру возмущенной зоны вблизи обтекаемых плазмой тел, включая область ближнего следа, в различных режимах течения;
  
• на базе полученных зависимостей тока на тело от его потенциала разработать надежные методы зондовой диагностики плазменных потоков;
  
• разработать теорию нестационарного зонда.
  

Научная новизна и значимость результатов исследования заключается в том, что впервые:

1. С единых позиций сформулированы физические, математические и вычислительные модели механики и электродинамики пристеночной плазмы в достаточно общей постановке;
   
2. С помощью созданного пакета прикладных программ получены функции распределения заряженных частиц вблизи заряженных тел, помещенных в поток бесстолкновительной плазмы как без магнитного поля, так и с магнитным полем. Показано их существенное отличие от аналогичных функций в покоящейся плазме;
   
3. Получены распределения моментов функции распределения и самосогласованного электрического поля в лобовой, боковой и теневой областях заряженного цилиндра, обтекаемого потоком бесстолкновительной плазмы. Обнаружены и исследованы нелинейные эффекты, возникающие при совместном действии направленной скорости, электрических и магнитных полей;
   
4. Дана физическая интерпретация обнаруженных новых нелинейных эффектов в пристеночных слоях плазмы в бесстолкновительном режиме;
   
5. С помощью созданного пакета прикладных программ в режиме сплошной среды найдены области изменения характерных параметров задачи, в которых проявляется аномальная зависимость плотности тока от индукции магнитного поля (типа аномальной диффузии). Обнаружены также области, в которых плотность тока по обводу цилиндра проявляет немонотонность, в частности, ионный ток в теневой области может быть существенным;
   
6. Исследован переходный режим с учетом всех возможных типов столкновений (ион-нейтрал, электрон-нейтрал, ион-ион, ион-электрон, электрон-электрон). Выявлено влияние столкновений на функции распределения заряженных частиц и их моменты;
   
7. Получен достаточный для практики набор вольтамперных характеристик (ВАХ) цилиндрических зондов в поперечном потоке столкновительной и бесстолкновительной плазмы. Предложены новые методы обработки ВАХ;
   
8. Разработана теория нестационарного зонда в столкновительном и бесстолкновительном режимах течения;
   
9. Предложен и разработан метод расчета пристеночного слоя плазменного якоря электромагнитного ускорителя тел;
   
10. Разработаны методы электромагнитного воздействия на параметры пограничного слоя;
    
11. Предложена вычислительная модель расчета электромагнитного управления вектором тяги плазменного движителя.
    

Достоверность основных научных результатов подтверждается применением надежных математических моделей и проверенных вычислительных методов. Полученные в вычислительных экспериментах данные там, где это возможно, сравнивались с результатами других авторов и известными экспериментальными данными. Все сравнения дали положительный результат. Использованные математические и вычислительные модели в области механики и электродинамики пристеночной плазмы разработаны в рамках научной школы МАИ, которая исследует эти проблемы почти 50 лет.

Практическая ценность работы заключается в том, что

1. Полученные функции распределения заряженных частиц в теневой области за спутником (в «следе») позволяют изучать взаимодействие данного спутника с другими телами, попавшими в его возмущенную зону;
   
2. Расчет параметров собственной атмосферы вблизи спутника позволяет учитывать ее при проведении физических экспериментов на спутниках и космических станциях, что повысит точность и надежность таких экспериментов. Появляется также возможность проведения зондовых измерений в следе;
   
3. Предложенные и количественно просчитанные варианты мягкого электромагнитного управления параметрами пограничного слоя позволяют решать ряд проблем, например, проблему создания радиопрозрачного канала;
   
4. Предложенный метод расчета поворота плазменной струи в поперечном магнитном поле может быть полезен при разработке электромагнитных методов управления вектором тяги ПД;
   
5. Разработанные достаточно строгие методы расчета пристеночных слоев в плазме могут быть полезны при расчете различных плазменных систем, в том числе и плазменных движителей;
   
6. Используемый в численных моделях метод крупных частиц представляется весьма эффективным методом для расчета перемешивания и диспергирования многофазных проводящих смесей электромагнитными силами;
   
7. Полученные в работе вольтамперные характеристики оказались важными для уточнения и расширения возможностей методов зондовой диагностики плазменных потоков.
   

Апробация работы. Основные результаты работы докладывались на 2-nd German-Russien conf. on Electric propulsion enqines and theiz technical applications (Moscow, Russia, 1993 г.); 24-th Int. Electric Propulsion conf. (Moscow, Russia, 1995); на международной конференции по вычислительной и прикладной механике (Россия, Москва, 1997 г); на Международной конференции по «Моделированию и исследованию сложных систем № 4, 5, 6, 7, 9, 10. (№ 4 Москва-Кашира, 1996; № 5 Севастополь, 1998; № 6 Севастополь, 1999; № 7 Севастополь, 2000; № 9 Севастополь, 2002; № 10 Севастополь, 2003; на Международной конференции по методам крупных частиц: теория и приложения (№9, 2000 г.; №10 2001 г.; №11, 2002 г.; №12, 2003 г.; №13, 2004 г.; №15, 2006 г.; №16, 2007 г.); на Международном симпозиуме «Динамические и технологические проблемы механики конструкций и сплошных сред» (Москва, 1999 г.), на 4-й и 6-й Международной конференции по Неравновесным процессам в соплах и струях (NPNJ, Санкт-Петербург, 2002 г., 2004 г.); на 12-й Международной конференции по вычислительной механике и современным прикладным программным средствам (Владмир, Россия, 2003); на 8-х Королёвских чтениях (Самара, Россия, 2005); на 33-й и 34-й Международной конференции по Физике плазмы и УТС (Звенигород, 2006, 2007); на XXXIII Гагаринских чтениях (Москва, 2007 г.).

Публикации. Основные результаты, вошедшие в диссертацию, опубликованы в 40 работах, в том числе 3-х научных монографиях, 10 научных статьях, 1 авторском свидетельстве на изобретение и 26 докладах и тезисах докладов на международных конференциях.

Структура диссертации. Изложение материала собственных исследований автора строится по единой схеме для каждого из возможных режимов течения: молекулярного, столкновительного и переходного. Сначала идет обзор работ предшествующих авторов и формулируется физическая модель задачи, затем формулируется математическая модель задачи и далее вычислительная модель. Заканчивается каждая из первых трех глав изложением полученных автором результатов и их обсуждением. В четвертой главе приведены примеры практических приложений результатов, полученных автором с использованием математических и вычислительных моделей, разработанных в первых трех главах.

Объем диссертации. Диссертационная работа состоит из введения, четырех глав, заключения, списка литературы и приложения. Она содержит 275 страниц машинописного текста, 155 иллюстрации, 146 наименований в списке цитируемой литературы.


КРАТКОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ.


Во введении обосновывается актуальность темы, формулируются цели и задачи исследования, раскрывается место данной работы среди других работ по механике и электродинамике пристеночной плазмы, излагается краткое содержание диссертации по главам.

Первая глава диссертации посвящена исследованию механики и электродинамики пристеночной плазмы в молекулярном режиме. В обзоре работ предшествующих авторов особое внимание уделено кинетическому уравнению Больцмана и обобщенной больцмановской кинетике, впервые предложенной Б.В. Алексеевым, а также уравнениям Максвелла.

С целью сокращения необходимых ресурсов ЭВМ и в то же время обеспечения достаточной общности в постановке задачи рассматриваются следующие геометрии тел, обтекаемых разреженной плазмой:

1. Цилиндр радиуса r_p и потенциала _p, расположенный в движущемся со скоростью v_ поперечном потоке плазмы. Внешнее магнитное поле может быть направлено вдоль оси цилиндра. Такое тело можно рассматривать как элемент конструкции спутника, а в зондовой теории как цилиндрический зонд, расположенный поперек потока.
   
2. Удлиненный проводящий прямоугольник шириной 2r_p и потенциала _p, расположенный на большой обтекаемой плазмой со скоростью V_ пластине. Вектор V_ параллелен плоскости пластины и направлен вдоль короткой стороны прямоугольника. Внешнее магнитное поле, если оно существует, параллельно удлиненной стороне прямоугольника. Такое тело можно рассматривать как элемент боковой поверхности спутника, а в зондовой теории как плоский пристеночный зонд ленточного типа.
   

Обе рассмотренные конструкции имеют практические приложения и в вычислительном плане существенно экономят ресурсы ЭВМ, так как оказываются четырехмерными в фазовом пространстве. Для сравнения, тело сферической геометрии в аналогичной постановке должно рассматриваться в пятимерном фазовом пространстве. Система уравнений Власова-Пуассона в случае цилиндрической геометрии тела имеет вид (при указанном выше расположении направленной скорости и магнитного поля)

	(1)
; E = -,	(2)

где f_ - функции распределения ионов и электронов ( = i,e); v_r, v_ - радиальная и азимутальная скорости частиц; E,  - напряженность и потенциал электрического поля; q_, m_ - заряд и масса частиц. Концентрация, плотность тока частиц у поверхности цилиндра и интегральный ток на цилиндр единичной длины запишутся так:

,	(3)
,	(4)
.	(5)

В качестве начальной функции распределения будем рассматривать максвелловскую функцию распределения

f(0,r,,vr,v) = (n/)(m/(2kT))3/2exp[-m{(vr + Vcos)2 + (v - Vsin)2}/(2kT)],

(6)

где n_ - концентрация частиц в невозмущенной плазме, T_ - температура компоненты , V_ - вектор скорости набегающего потока.

Для решения уравнения Пуассона задается значение  при r = r_p и его значение на внешней границе расчетной области, которое, как правило, считается нулевым. Функции распределения на внешней границе совпадают с (6), а на теле ставится условие идеальной каталитичности, т.е. ион, касаясь стенки, получает недостающий электрон, а электрон, коснувшись стенки, поглощается. Система (1)÷(6) составляет систему Власова-Пуассона вблизи заряженного цилиндра, обтекаемого поперечным потоком разреженной плазмы.

Выпишем теперь математическую модель Власова-Пуассона для плоского пристеночного электрода ленточного типа в декартовой системе координат (если B = 0):

,	(7)
, E = -,	(8)
,	(9)
.	(10)

Начальное условие для функции распределения

f(0,x,y,vx,vy) = (n/)(m/(2kT))3/2exp[-m{(vx + V)2 + Vy2}/(2kT)].

(11)

Граничные условия

(xp,yp) = p, |внеш. граница = 0, f|внеш. граница = (n/)(m/(2kT))3/2exp[-m{(vx + V)2 + vy2}/(2kT)].

(12)

Система (7)÷(12) составляет математическую модель для тела ленточной геометрии, расположенного на большой обтекаемой бесстолкновительной плазмой пластине.

Система (1÷6) и (7÷12) приводились к безразмерному виду с помощью следующей системы масштабов:

ML = rd = (okTi/ne2)1/2 - масштаб длины; M = kTi/e - масштаб потенциала; MV = (2kT/m)1/2,  = i,e - масштаб скорости.

(13)

Остальные масштабы получаются по формулам размерностей. Введем безразмерные параметры: r₀ = r_p/M_L; ₀ = _p/M_; V₀ = V_/; B₀ = B/M_B; j₀ = j/M_j; I₀ = I/M_I (r_p, _p – радиус и потенциал тела, V_ - скорость потока плазмы, B – величина индукции внешнего магнитного поля, j – плотность тока на тело, I – интегральный ток, приходящийся на единицу длины тела).

Вычислительная модель задачи основана на методе установления, когда на тело подается импульс потенциала с достаточно крутым фронтом нарастания и моделируется переходный процесс от начального к конечному стационарному состоянию. Для решения уравнения Власова используется алгоритм метода крупных частиц Давыдова или метод характеристик, а уравнение Пуассона решается с использованием спектральных методов. С целью сокращения необходимых ресурсов ЭВМ проводилась оптимизация вычислительного алгоритма. По результатам методических расчетов размер расчетной области не превышал размера возмущенной зоны. Размер шага по времени не превышал t = 0,2. Число узлов расчетной сетки в задаче с цилиндром в большинстве расчетов составляло = 20503030, а в задаче с пристеночной лентой = 100401010.

Программа была составлена на алгоритмических языках Pascal и Cu⁺⁺. В случае обтекания цилиндра использовалась цилиндрическая расчетная сетка, однако отдельные расчеты проводились в однородной декартовой системе координат, что позволило, во-первых, выявить ошибки, связанные с неоднородностью сетки, и, во-вторых, существенно продвинуться в область «следа», возникающего в теневой области за телом вследствие наличия направленной скорости. В процессе отладки вычислительного алгоритма V_ и B вначале полагались равными нулю, что позволяло сравнить результаты расчетов с имеющимися данными для покоящейся плазмы, полученными Лафрамбуазом и В.А. Котельниковым. Затем отдельно вводилось либо магнитное поле, либо направленная скорость и только на третьем этапе задача решалась в общем виде. Такой подход позволил отдельно выявить влияние каждого фактора и дать физическую интерпретацию полученным результатам. Введенный в программу графический блок дал возможность на каждом временном слое следить за ходом решения, выявлять колебательные процессы, немонотонности в ходе кривых, отличия от прогнозируемого хода решения. На экран монитора выводились трехмерные функции распределения, поля скоростей, концентраций и потенциалов, плотности токов, интегральные токи и другая информация. Разработанный и внедренный графический блок позволил существенно упростить физический анализ результатов математического моделирования.

Функции распределения заряженных частиц (ФР) дают исходную информацию для расчета всех процессов переноса в пристеночной плазме. На рис. 1 приведены функции распределения ионов вблизи цилиндра при V_ = 0 и B = 0. Они имеют характерный подковообразный вырез, отмеченный еще в более ранних работах и связанный с отсутствием потока ионов вдоль радиуса от тела. По мере удаления от стенки цилиндра вырез сокращается, так как уменьшается влияние стенки, и у внешней границы расчетной области ФР становятся максвелловскими. По мере приближения к поверхности цилиндра концентрация ионов падает, что выражается в уменьшении объема под куполом ФР. Кроме того ФР смещается в сторону отрицательных радиальных скоростей, так как происходит рост скоростей ионов под действием электрического поля в слое объемного заряда. По направлению азимутальной координаты ФР растягивается, что связано с увеличением скорости ионов, движущихся мимо цилиндра по направлениям, близким к касательной к нему. В случае движущейся плазмы начальные и граничные ФР ионов в лобовой, боковой и теневой областях отличаются одна от другой своим положением центра тяжести, который смещается от начала координат на величину скорости потока V_, а направление смещения зависит от угловой координаты  (рис. 2).

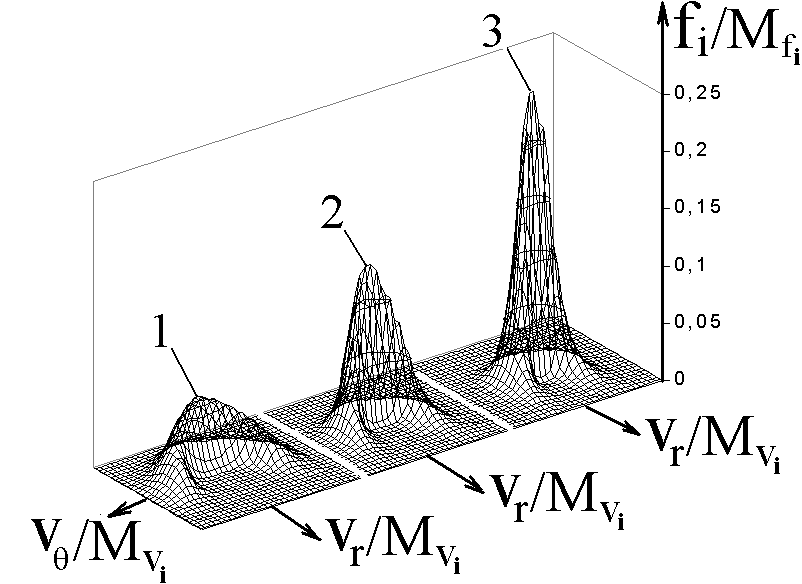Рис. 1. Зависимость функции распределения ионов от расстояния до стенки цилиндра (r0 = 3; 0 = -6; V0 = 0;  = 1; B0 = 0) 1 – r = 0,3; 2 – 1,5; 3 – 3.	Рис.2. Начальная функции распределения ионов (V0 = 5);1 –  = 0; 2 – /2; 3 – ; 4 - 3/2.

На рис. 3. даны профили ФР ионов после установления решения в теневой области за телом (в следе) на различных расстояниях от стенки цилиндра. ФР состоит из двух частей и симметрична относительно плоскости симметрии задачи. Левая часть ФР соответствует частицам, огибающим цилиндр с одной стороны, а правая – частицам, огибающим цилиндр с другой стороны. Провал между отдельными частями ФР связан с отсутствием частиц, движущихся от поверхности цилиндра.

На рис. 4. представлена зависимость ФР ионов от угловой координаты . Если при  =  обе части ФР симметричны, то по мере смещения влево или вправо высота одной части растет, другой – уменьшается. В итоге, выйдя за границу следа, получаем классическую ФР, по форме напоминающую максвелловскую. Это объясняется тем, что пропадает эффект, связанный с появлением двух потоков, идущих с одной и другой стороны от цилиндра.

ФР ионов в боковой и лобовой части, а также ФР электронов существенных отличий от прогнозируемых профилей не показали.

Рис.3. Зависимость функции распределения ионов от расстояния до стенки цилиндра (r0 = 3; 0 = -6; V0 = 5;  = 1; B0 = 0;  = ), 1 – r/ML = 1,8; 2 – 5,4; 3 – 10,8.
Рис.4. Зависимость функции распределения ионов от  (r0 = 3; 0 = -6; V0 = 5;  = 1; B0 = 0; r = 6 rD) 1 –  = 180; 2 – 172; 3 – 164; 4 - 156; 5 - 148.

Включение осевого магнитного поля оказывает существенное влияние на ФР ионов, начиная с величины B₀=(B/M_B)>0,1, когда ионы начинают замагничиваться. В качестве характерного примера на рис. 5,6 приведена ФР ионов и ее изолинии при B₀ = 0,5. Точка геометрического пространства, в которой получена ФР, имеет координаты (r = 6,  = /2). ФР ионов опять оказывается состоящей из двух частей. Часть ФР «а» (см. рис) расположена в отрицательной области азимутальных скоростей, причем, её центр тяжести близок к нулевой координате V_r. Часть ФР «б» оказывается в положительной области по обеим координатам V_r и V_.

Для понимания такого характера ФР на рис. 7 построены траектории фазовых частиц, соответствующих центрам тяжести частей ФР «а» и «б». Из рисунка следует, что часть ФР «а» соответствует потоку ионов, которые под действием силы Лоренца и электрического поля цилиндра двигались по дугообразной траектории вокруг цилиндра. Такие частицы попадают в исследуемую точку с отрицательными V_ и близкими к нулю V_r. Частицы, образовавшие часть ФР «б», под воздействием тех же сил двигались по другую сторону цилиндра и приобрели положительные значения V_r и V_. Ионы, которые двигались по фазовым траекториям между указанными потоками, попали на цилиндр и внесли вклад в интегральный ток. Если продлить траектории этих попавших на тело частиц, то попадем в пространство между частями «а» и «б».

Рис. 5. Функция распределения ионов (r0 = 3; 0 = -6; V0 = 5;  = 1; B0 = 0,5; r = 6 rD;  = /2).	Рис. 6. Изолинии ФР ионов 1 – fi/= 0,005; 2 – 0,01; 3 – 0,015.

Рис. 7. Траектории движения фазовых частиц. 1 – траектория, соответствующая части ФР (a); 2 - траектория, соответствующая части ФР (б).

Полученные достаточно сложные профили ФР заряженных частиц были использованы для получения интегральных характеристик в возмущенной зоне вблизи заряженного цилиндра.

На рис. 8 даны типичные распределения концентраций ионов и электронов вокруг цилиндра радиуса r₀ = 5 при потенциале ₀ = -6 и скорости потока V₀ = 5. Лобовая часть незначительно обеднена ионами за счет их поглощения и в значительно большей степени электронами вследствие их отталкивания. В теневой части формируется «след». Ионный след