Механика и электродинамика пристеночной плазмы

Вид материала

Автореферат

Содержание 0; 2- ионы,  = /2; 3- ионы,  = ; 4- электроны,  = 0 Во второй главе В третьей главе Четвертая глава В пункте 4.2 В параграфе 4.3 гл. 4 В разделе 4.4 В разделе 4.5

Подобный материал:

• Программа-минимум кандидатского экзамена по специальности 01. 02. 05 «Механика жидкостей,, 69.43kb.
• Программа учебной дисциплины «Электродинамика плазмы» Специальности 071500, 013900, 74.5kb.
• Программа-минимум кандидатского экзамена по специальности 01. 04. 02 «Теоретическая, 115.8kb.
• Паспорт специальности 01. 02. 05 Механика жидкости, газа и плазмы Шифр специальности:, 20.82kb.
• Физика (греч ta physika, от physis природа), наука о природе, изучающая простейшие, 51.33kb.
• Программа подраздела «История механики», 75.11kb.
• Рабочая программа учебной дисциплины "теоретическая физика", 162.35kb.
• Программа по физике для 10-11 классов общеобразовательных, 75.87kb.
• Диссипативные структуры и нестационарные процессы в межфазной гидродинамике 01. 02., 443.32kb.
• Рабочая программа учебной дисциплины «Физика конденсированного состояния, термодинамика,, 223.9kb.

уже электронного, так как пролетая мимо цилиндра, ионы притягиваются, а электроны отталкиваются. Для ионов формирование следа является следствием направленной скорости плазмы (направленная скорость сравнима с хаотической скоростью ионов). На электроны фактор направленной скорости оказывает незначительное влияние, поскольку для электронов направленная скорость много меньше хаотической. Причина возникновения электронного следа - самосогласованное электрическое поле. Электроны заполняют ионный след, там возникает объемный отрицательный заряд, в результате чего поле меньше экранируется и глубже проникает в плазму в области следа. Это приводит к падению концентрации электронов в следе.

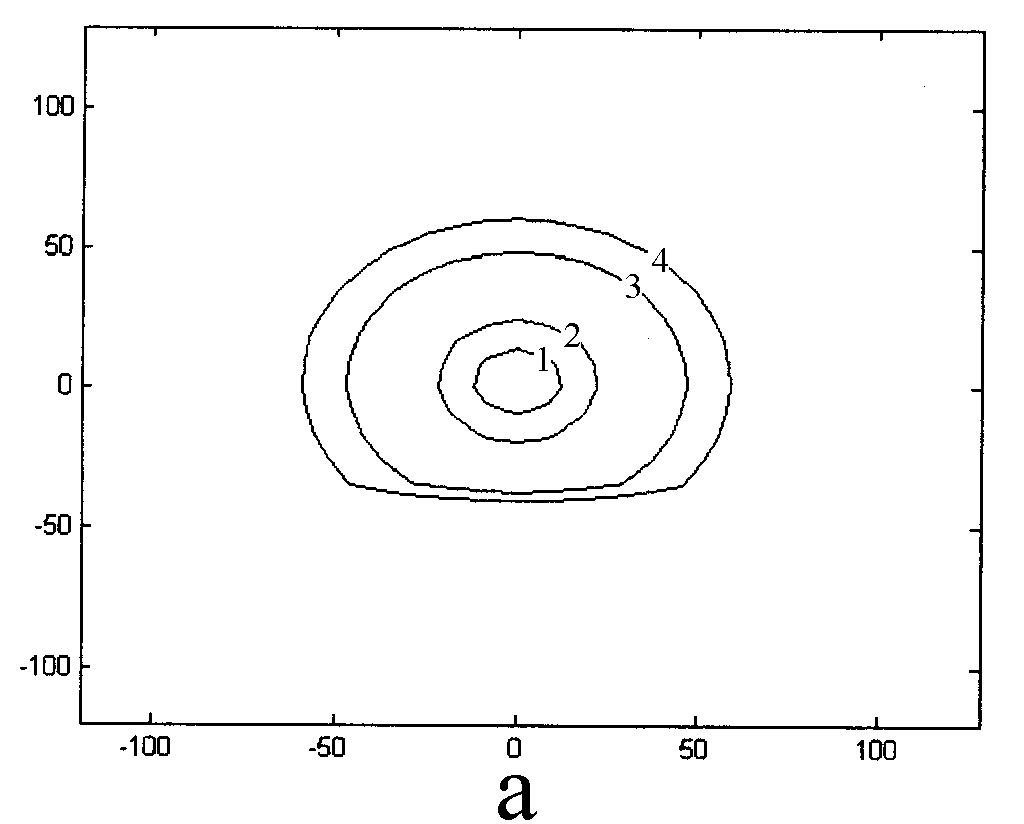
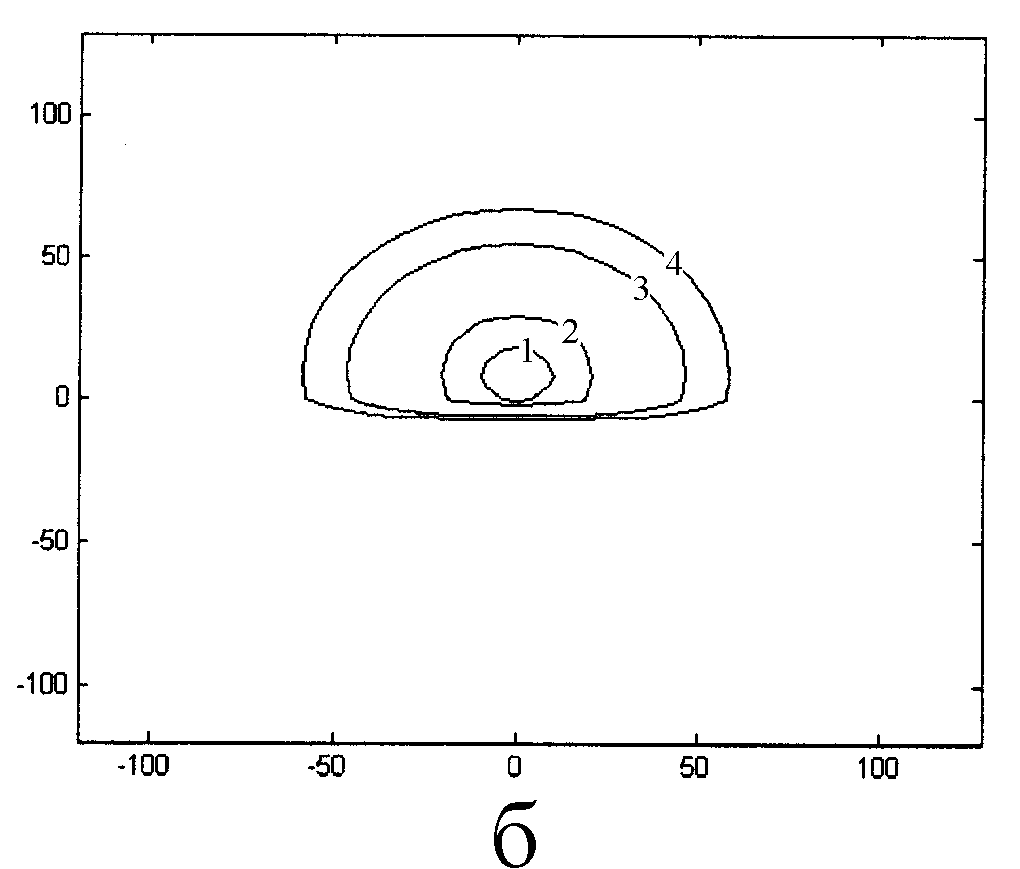
На рис. 9а,б приведены распределения n_i,e(r) и (r) в лобовой, боковой и теневой областях для того же набора параметров. Зависимость n_i,e() приводит к появлению азимутального электрического поля, которое достигает максимума при  ~(3/4) и (5/4).

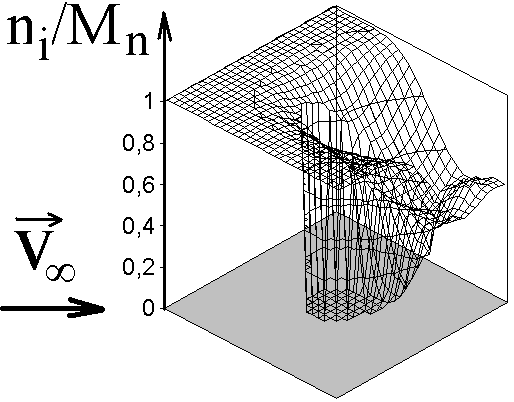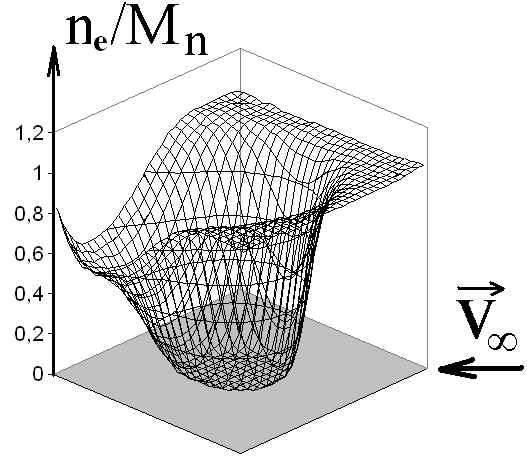Рис. 8. Концентрация ионов и электронов вблизи цилиндра (r0 = 3; V0 = 5; 0 = -6;  = 1; B0 = 0).
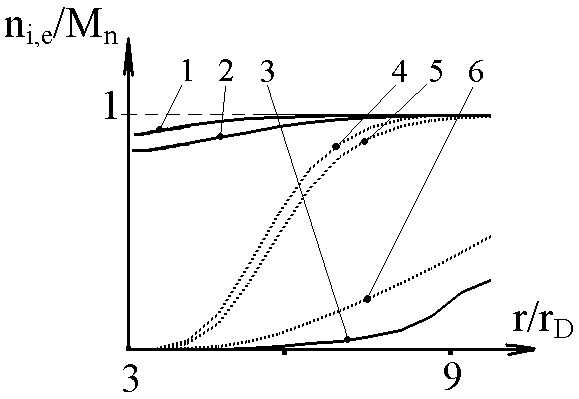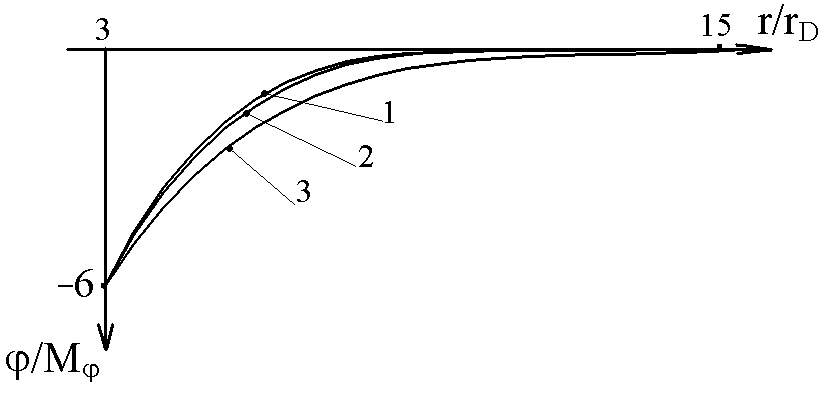Рис. 9а. Распределение концентраций ионов и электронов по радиусу (r0 = 3; V0 = 5; 0 = -6;  = 1; B0 = 0) 1- ионы,  = 0; 2- ионы,  = /2; 3- ионы,  = ; 4- электроны,  = 0; 5- электроны,  = /2; 6- электроны,  = .		Рис. 9б. Распределение потенциала по радиусу (r0 = 3; V0 = 5; 0 = -6;  = 1; B0 = 0) 1-  = 0; 2- /2; 3- ;

На рис. 10 представлены поля скоростей ионов при r₀=3, ₀=-6 и двух значениях направленной скорости V₀=1 и 5. Если при V₀=1 влияние электрического поля цилиндра существенно, то при V₀=5 фактор направленной скорости превалирует над электростатическим притяжением.

v0 = 1	v0 = 5
Рис. 10. Поле скоростей ионов (0 = -6; r0 = 3;  = 1; B0 = 0).
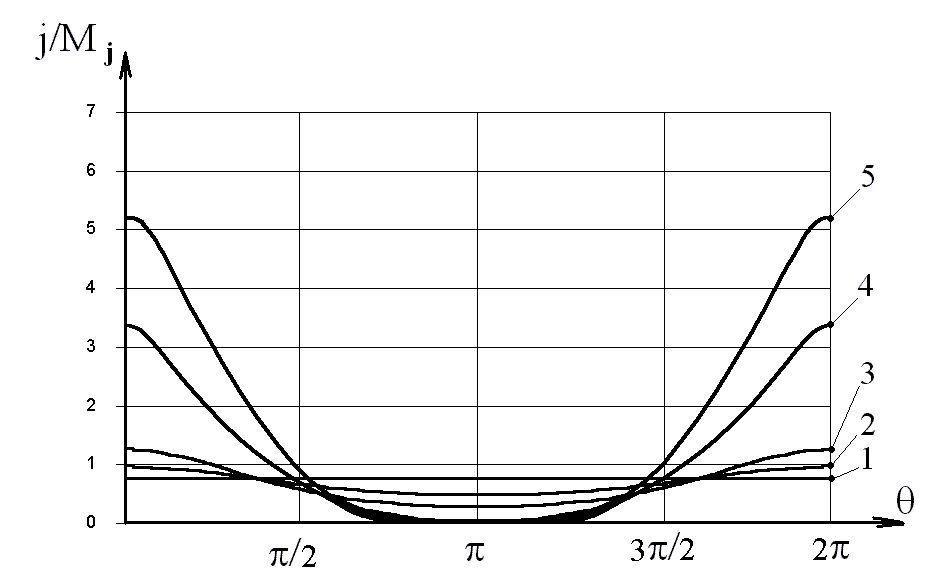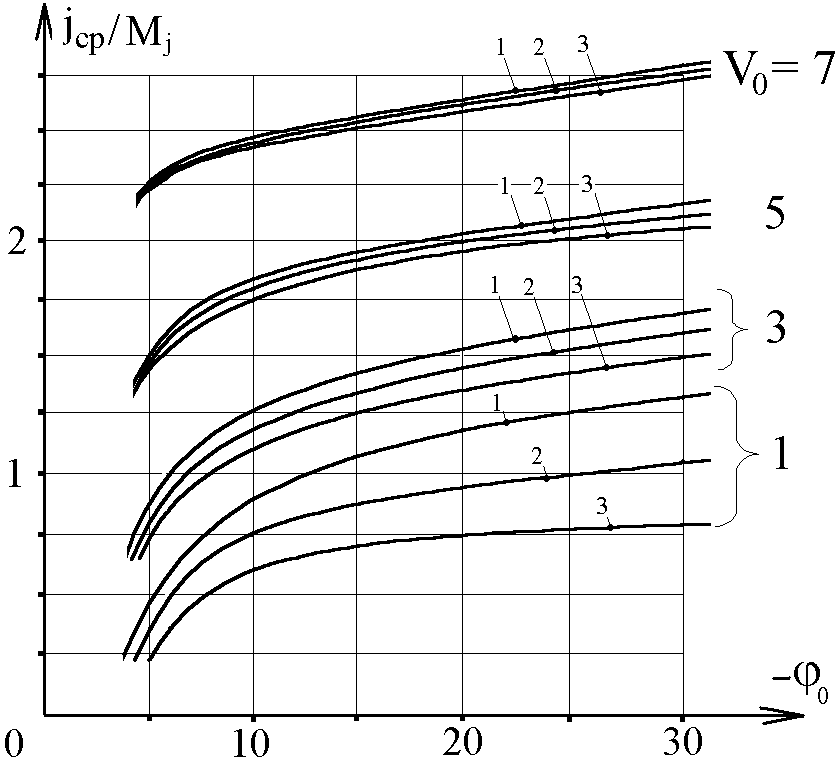Рис. 11а. Распределение плотности ионного тока по обводу цилиндра при различных значениях v0 (r0 = 3; 0 = -6;  = 1; B0 = 0) 1- V0 = 0; 2- 0,5; 3- 1; 4- 3; 5- 5.		Рис. 11б. Зависимость средней плотности тока ионов от его потенциала ( = 1) 1 - r0 = 3; 2 – 10; 3 – 30.

На рис. 11а,б даны распределения плотности ионного тока по обводу цилиндра и зависимость средней плотности тока ионов от его потенциала. Как следует из рисунков 11а,б, при наличии направленной скорости максимальная плотность тока имеет место в лобовой области и она растет с увеличением скорости, а минимальная – в теневой. При V₀3 ток в теневой области становится незначительным и в масштабах рис. 11а совпадает с нулевой линией. Интегральный ток на единицу длины цилиндра с ростом V₀ (при V₀3) растет, что связано с ростом плотности тока на лобовую область.

Последний раздел главы 1 посвящен влиянию осевого магнитного поля на структуру возмущенной зоны и интегральные характеристики. В качестве примера представлены расчеты при следующих параметрах задачи: r₀=3, ₀=-6, V₀=5, =1. Безразмерная величина индукции магнитного поля менялась с пределах 0B₀0,9.

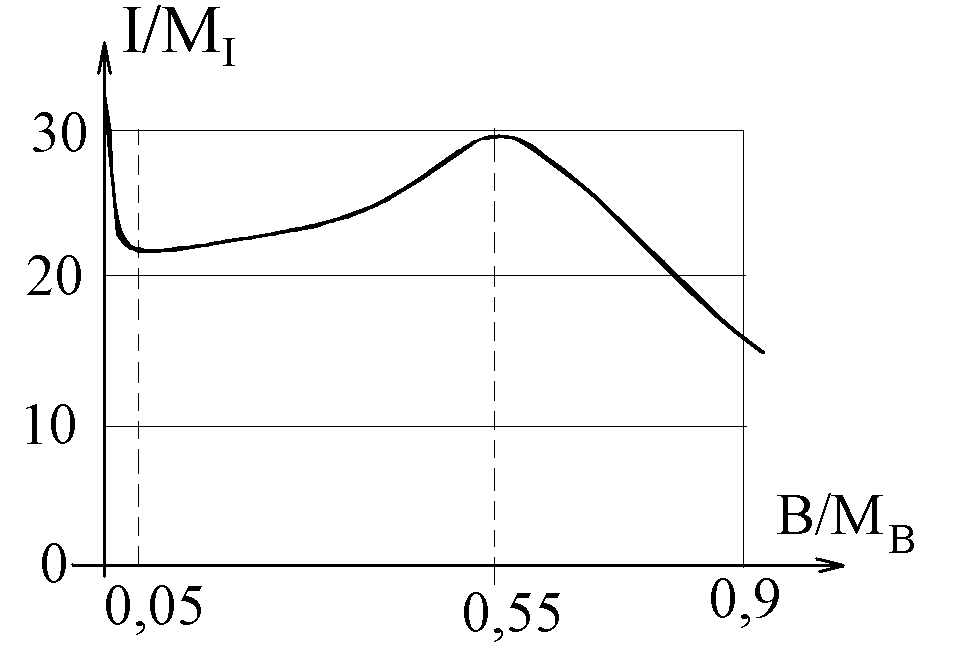Рис.12. Зависимость интегрального тока от величины магнитной индукции (r0 = 3; 0 = -6; V0 = 5).

Зависимость интегрального тока ионов на единицу длины цилиндра I₀ от B₀ существенно нелинейная и имеет области, как с отрицательной, так и с положительной производной (рис. 12). На первом этапе 0B₀0,05 электроны замагничены, а ионы – нет. Электроны, которые раньше участвовали в тепловом хаотическом движении, под действием силы Лоренца поворачивают, начинают попадать на боковую поверхность и поглощаются. Вследствие этого растет положительный объемный заряд в пристеночной зоне, который частично экранирует поток ионов, поэтому ток ионов I₀ уменьшается на 20÷30%. Во второй области 0,05B₀0,5 ионы начинают замагничиваться и поворачивают свой вектор скорости в сторону боковой части цилиндра – их ток растет с ростом B₀. При B₀>0,5 степень замагниченности ионов настолько возрастает, что ионы уже частично не попадают на цилиндр вследствие ларморовского движения и интегральный ток начинает постепенно падать. В численных экспериментах было обнаружено, что ионный след за телом с ростом B₀ поворачивает по угловой координате и при B₀=0,5 угол поворота достигает 90. Плотность ионного тока по обводу тела также проявляет ряд нелинейных особенностей в магнитном поле. Если без поля максимум плотности тока достигается в лобовой области, а максимум – в теневой, то в продольном магнитном поле с ростом B₀ этот максимум уменьшается по величине и смещается по угловой координате от 2 до 3/2 при увеличении B₀ от 0 до 0,9. Площадь под кривой j=j(B₀) дает значение полного тока по обводу, который меняется в соответствии с рис. 12.

Во второй главе рассматриваются вопросы взаимодействия заряженных тел с потоками столкновительной плазмы (число Kn0) при наличии магнитных полей и других осложняющих факторов. Структура второй главы практически полностью повторяет первую главу. В начале сделан обзор работ предшествующих авторов и определены цели и задачи исследования, которые состоят в следующем:

- используя максимально общую математическую модель взаимодействия тел с потоками столкновительной плазмы, разработать надежную и экономичную вычислительную модель и провести обширные вычислительные эксперименты;

- на основе полученных данных усовершенствовать зондовые методы диагностики, методы расчета некоторых типов ускорителей, методы электромагнитного управления параметрами пограничного слоя и др.

В качестве приоритетных геометрических форм вносимых в плазму тел выбраны:

- удлиненное цилиндрическое тело, расположенное поперек потока плазмы. Магнитное поле может направляться вдоль оси цилиндра. Такое тело может быть элементом конструкции гиперзвукового летательного аппарата (ГЛА), а в зондовой теории – цилиндрическим зондом, расположенным поперек потока. Постановка задачи достаточно общая: она учитывает наличие направленной скорости и внешнего магнитного поля, а также возможность различных физических процессов в объеме и на стенке;

- удлиненная прямоугольная пластина, расположенная на большой плоскости, обтекаемой продольным потоком континуальной плазмы. Магнитное поле может быть расположено вдоль удлиненной стороны пластины. Такая пластина может быть элементом боковой поверхности ГЛА, а в зондовой диагностике – плоским пристеночным зондом.

Обе постановки приводят к двумерным нестационарным задачам, что существенно экономит ресурсы ЭВМ. При этом сохраняется достаточная общность задачи.

При формулировке математических моделей задачи особое внимание уделено анализу начальных и граничных условий. Показано, что на границе тела полагать значение концентраций заряженных частиц равными нулю (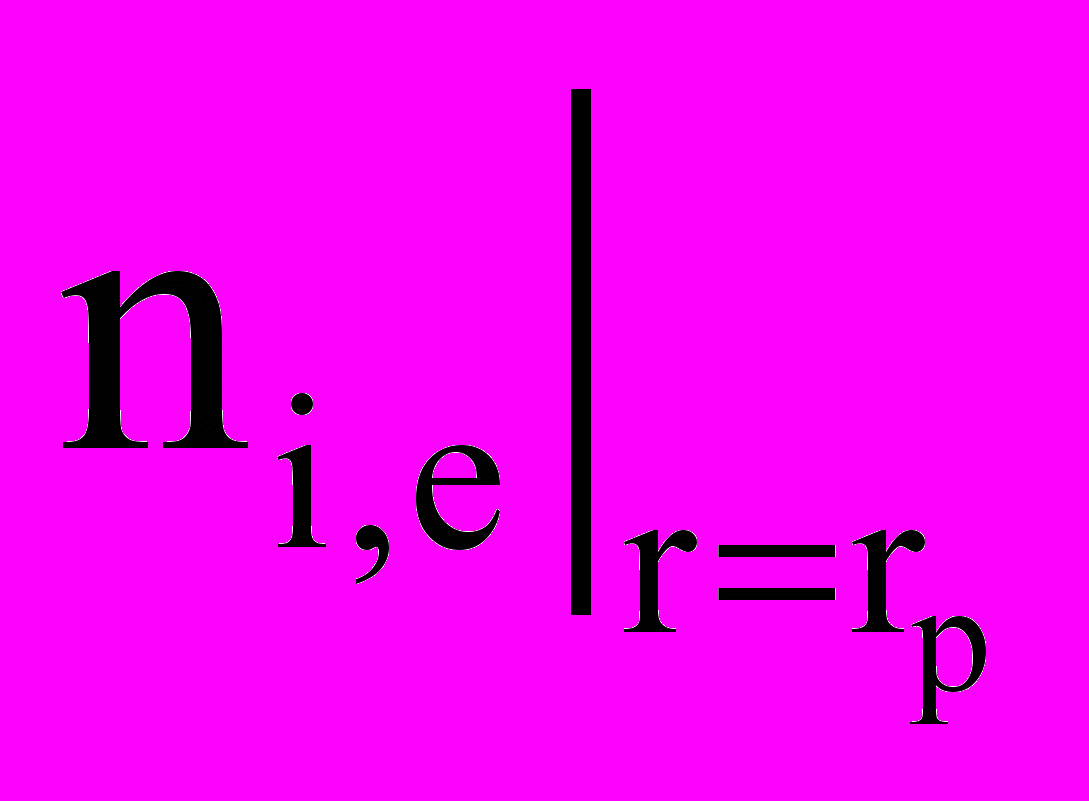= 0) не всегда оправдано. Например, для случая притягивающихся частиц, если выполняется неравенство

r_p >>  >> ,

где r_p – характерный размер тела,  - средний пробег,  - толщина слоя объемного заряда, граничное значение концентрации изменяется в пределах

0,3 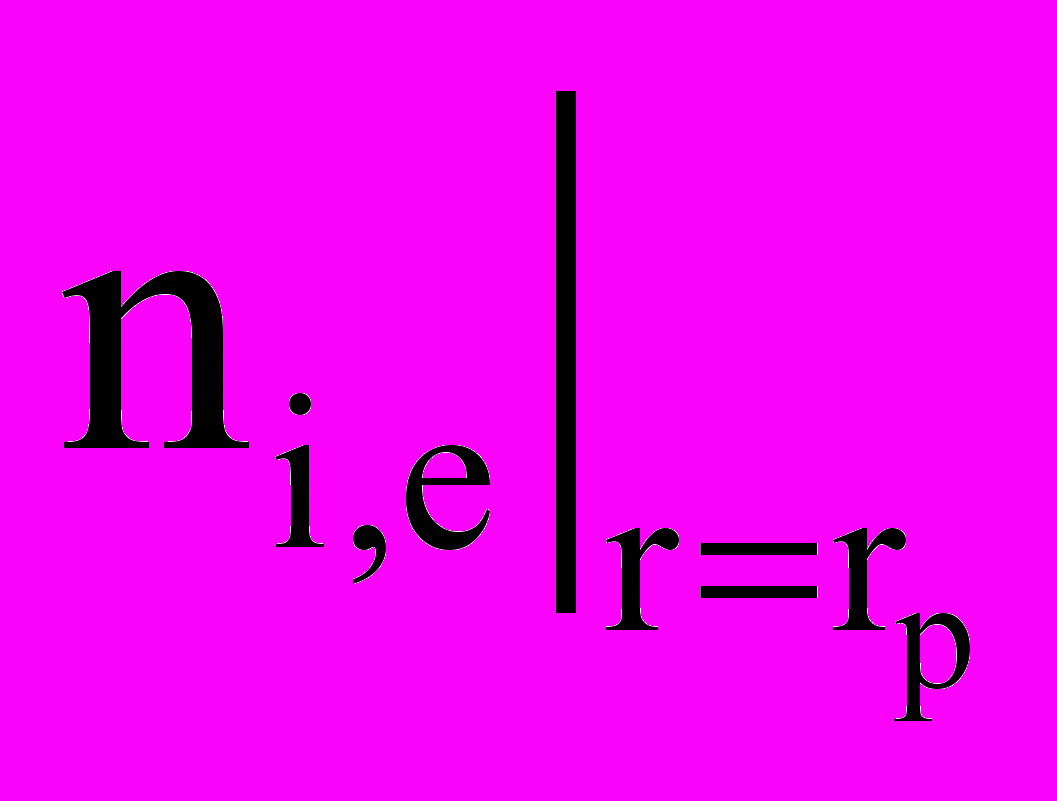  0,75.

Исследование проведено для случая r₀ = r_p/M_r = 10, ₀=_p/M_= -3-9. С уменьшением r₀ и ростом ₀ граничное значение n_i,e может быть еще больше. Проведенный анализ позволяет более корректно ставить граничные условия при решении задач механики и электродинамики пристеночной плотной плазмы.

Система уравнений включала уравнения Эйлера или Навье-Стокса для нейтральной компоненты, уравнения неразрывности и движения для заряженных компонент и уравнение Пуассона для самосогласованного электрического поля. Ниже приводится система уравнений в безразмерном виде:

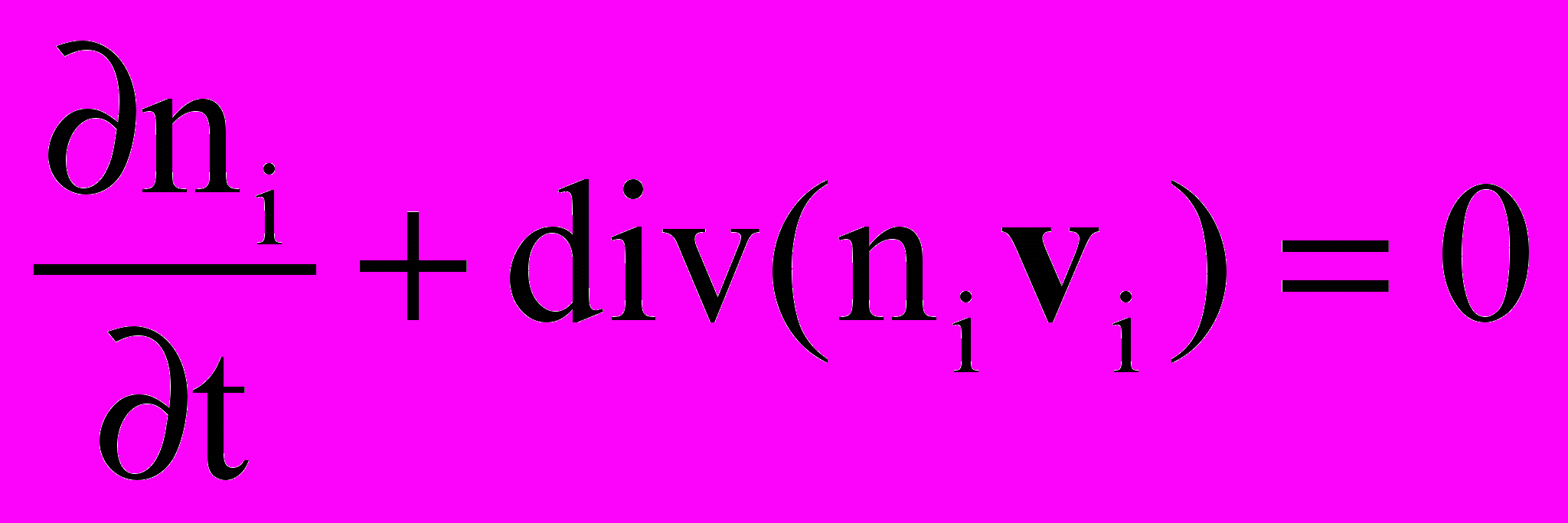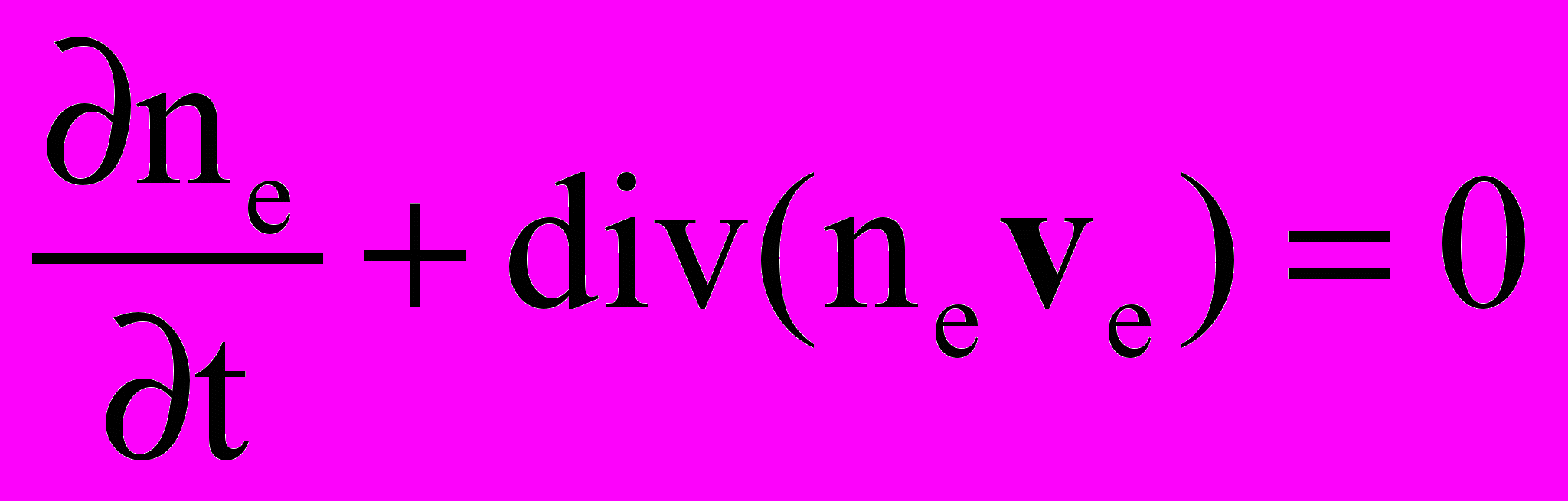;	(14)
,
;

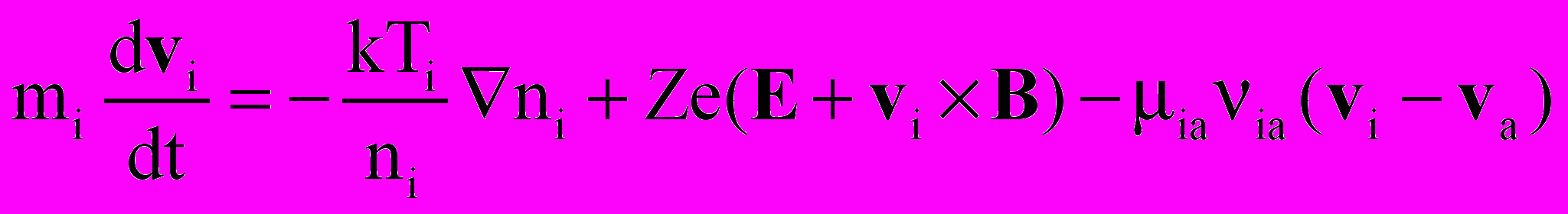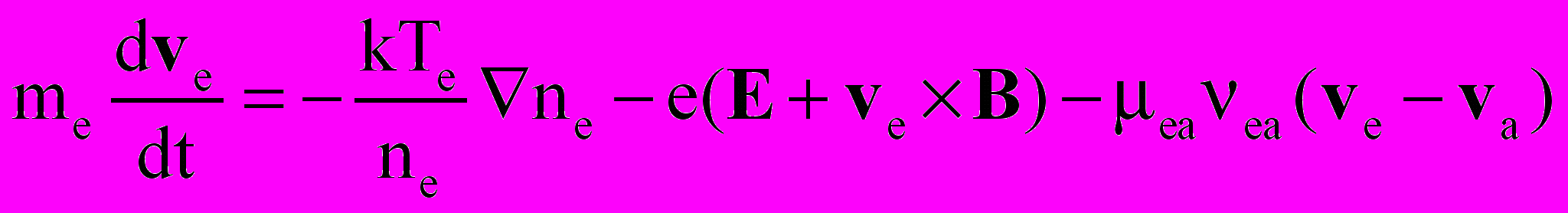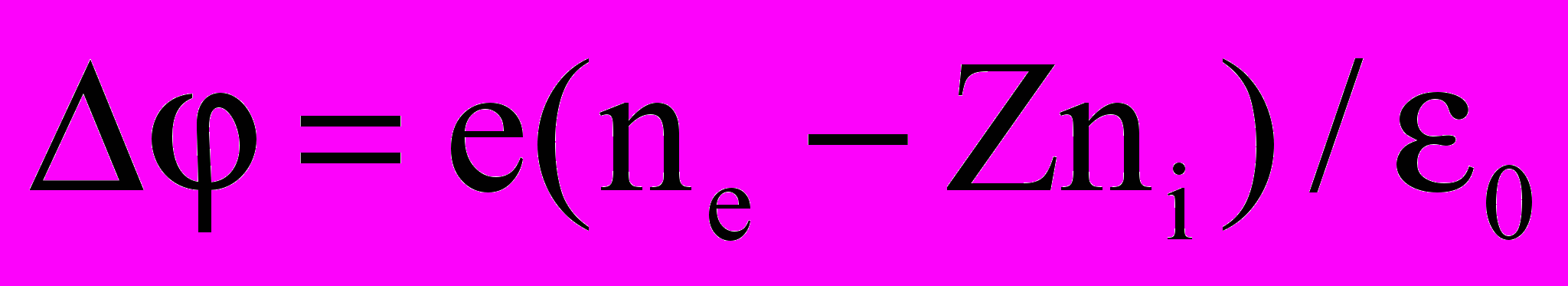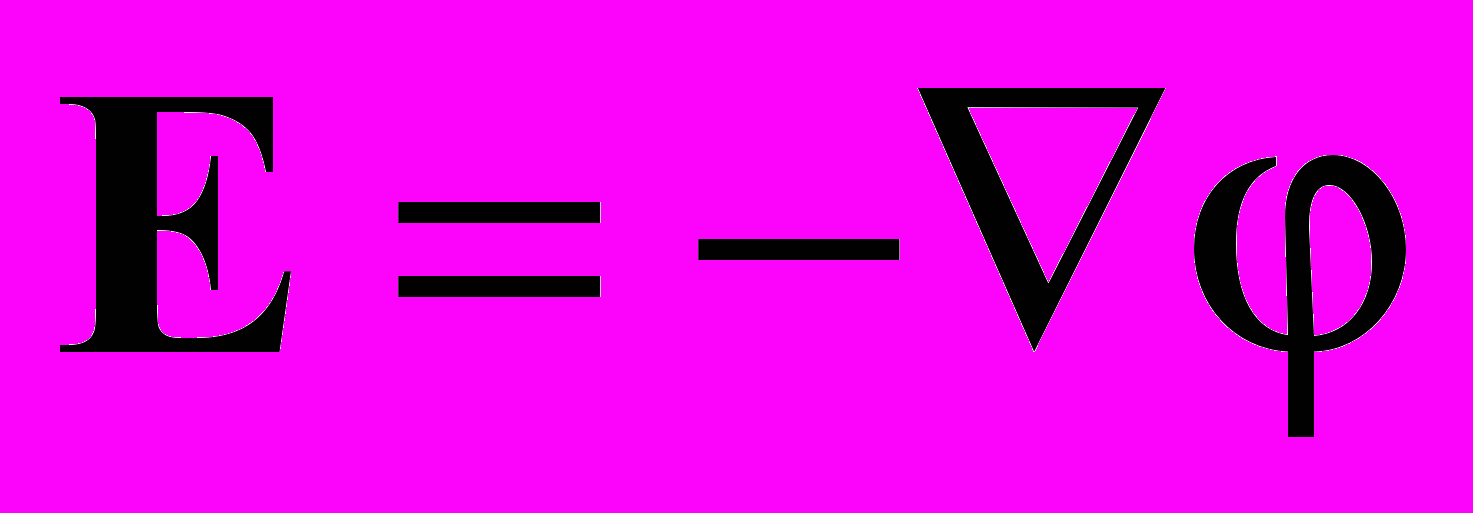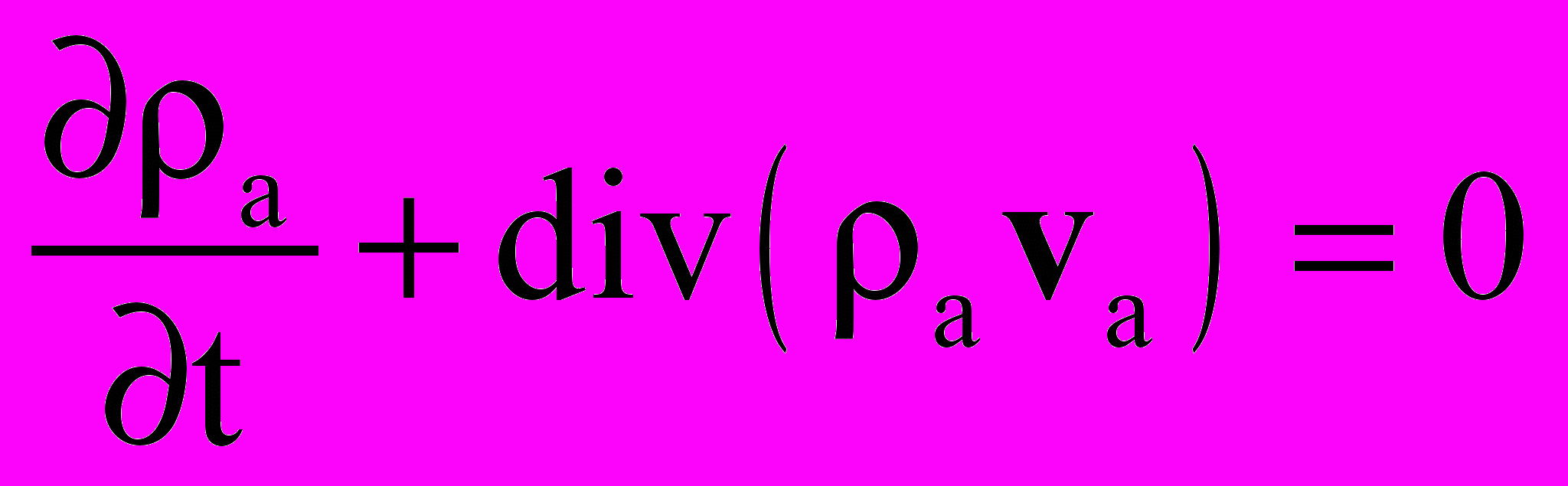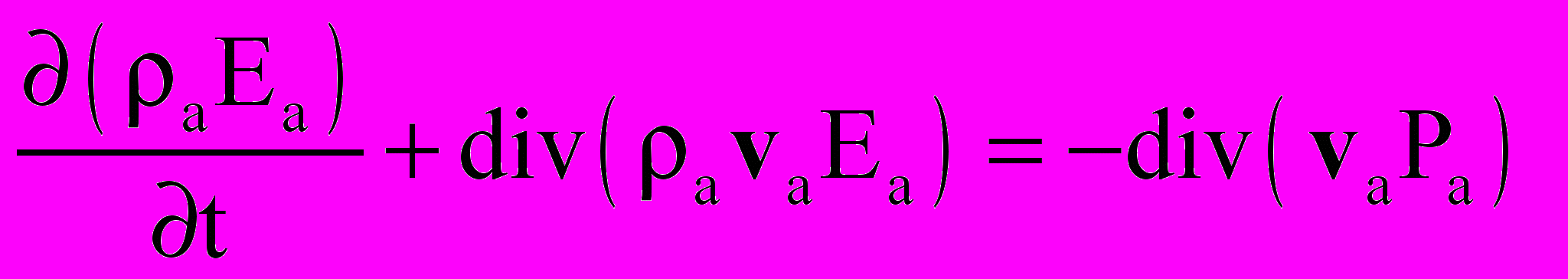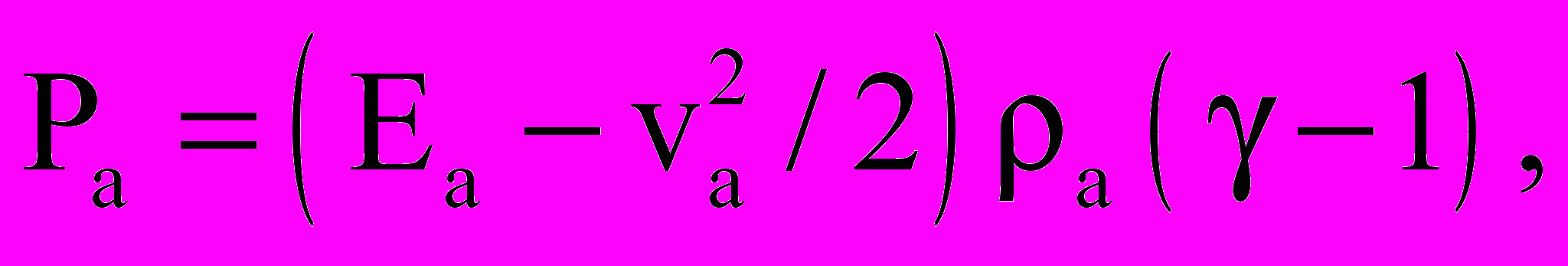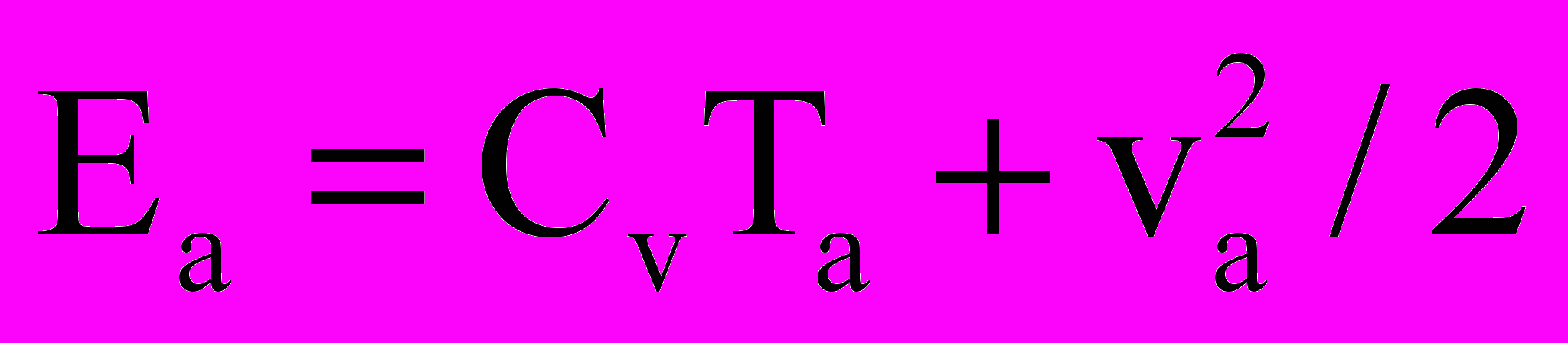При этом использовались следующие масштабы:

Mr = rp - масштаб длины; M = kTi/e - масштаб потенциала; Mn = ni, - масштаб концентрации; Mv = V, - масштаб скорости.

(15)

Система начальных и граничных условий стандартная.

Вычислительная модель задачи, как и в гл. 1, основана на методе установления с использованием алгоритма метода крупных частиц Давыдова для решения уравнений неразрывности и спектральных методов для решения уравнения Пуассона. Из сказанного следует, что удается использовать практически единый вычислительный алгоритм, как в молекулярном, так и в континуальном режимах.

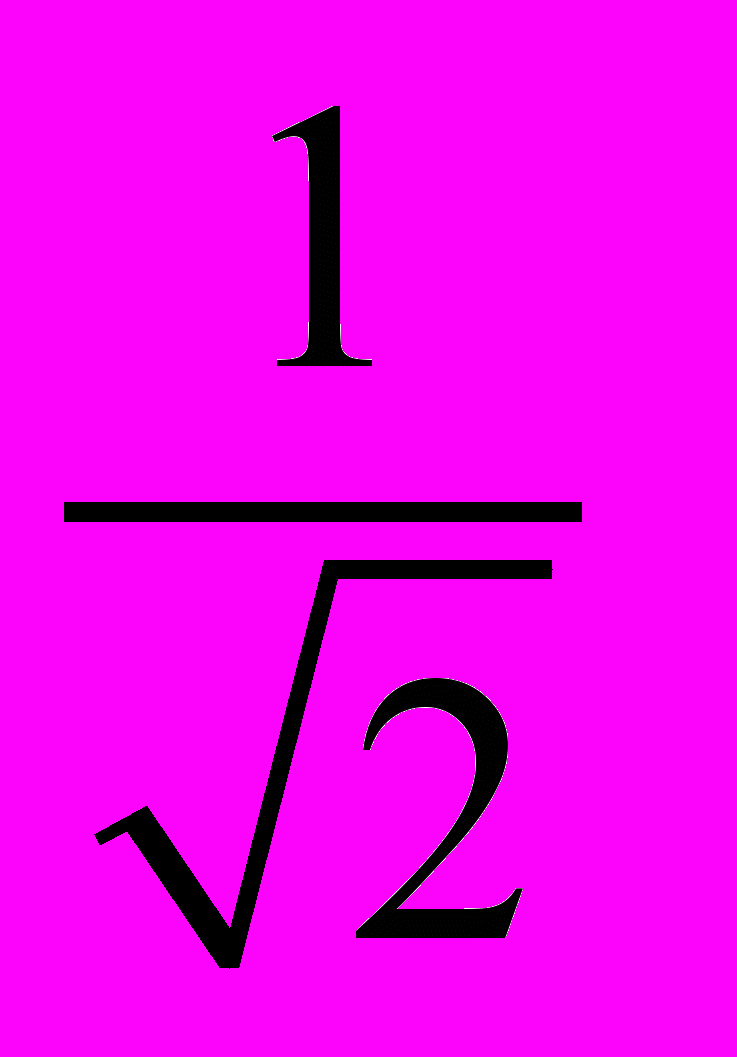
Решение задачи в столкновительном режиме зависит от следующих безразмерных параметров: r₀ = r_p/M_r – безразмерный радиус цилиндра; ₀ = _р/М_ - безразмерный потенциал цилиндра;  = T_i/T_e – отношение температур ионов и электронов; D=D_e/D_i= 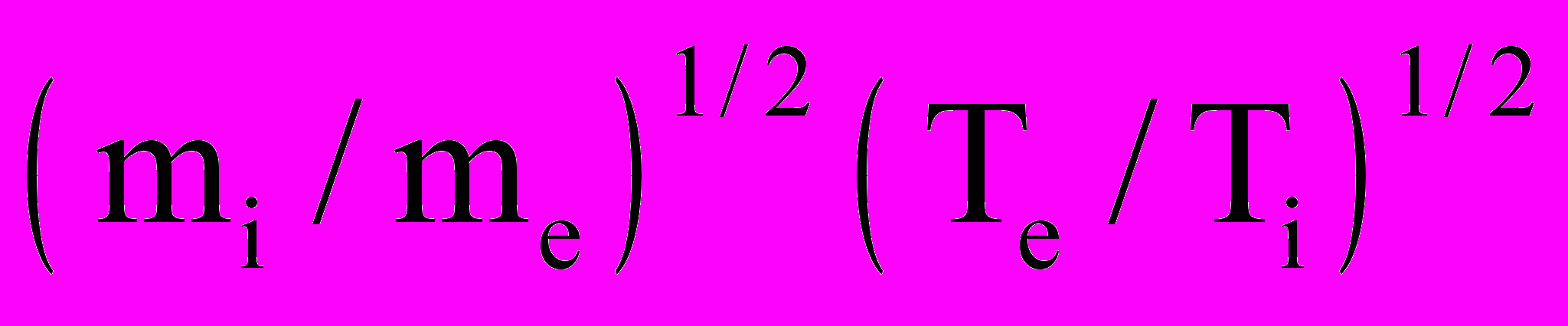- отношение коэффициентов диффузии электронов и ионов; V₀ = V_/M_V – безразмерная направленная скорость; _i,e - параметр Холла для ионов и электронов. Большое количество характерных параметров свидетельствует о необходимости проведения значительного количества вычислительных экспериментов, каждый из которых требует несколько часов.

Разработанный пакет прикладных программ оптимизирован и приспособлен для решения задач механики и электродинамики пристеночной плазмы на ЭВМ средней мощности. В частности, показано, что условие Фридрихса-Куранта-Леви оказывается слишком жестким для задач электродинамики пристеночной плазмы. Шаг по времени в алгоритме метода крупных частиц может быть увеличен в (3÷4) раза по сравнению с его значением, вытекающим из условия Куранта-Фридрихса-Леви без потери устойчивости решения. Показано также, что это утверждение касается не только континуального, но и молекулярного режима.

а)	б)
в)	Рис. 13. Поле скоростей нейтрального газа (а), ионов (б) и электронов (в) ().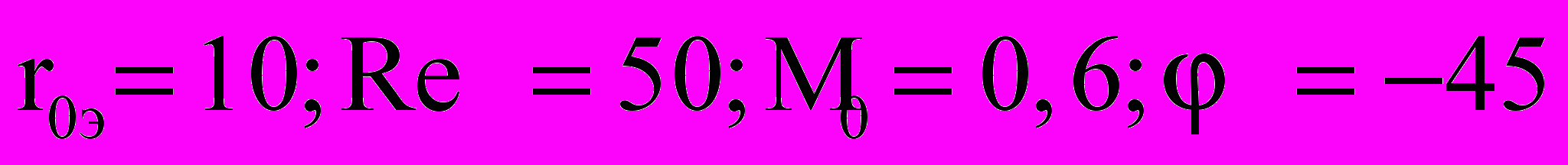

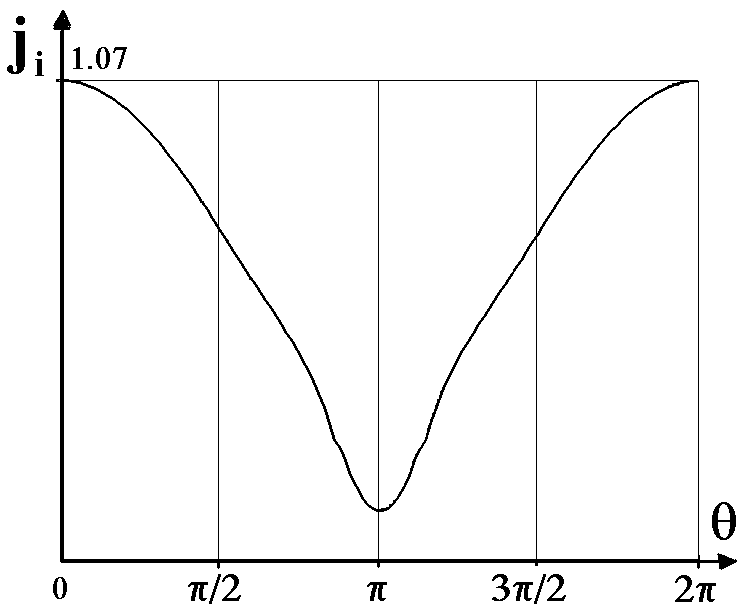
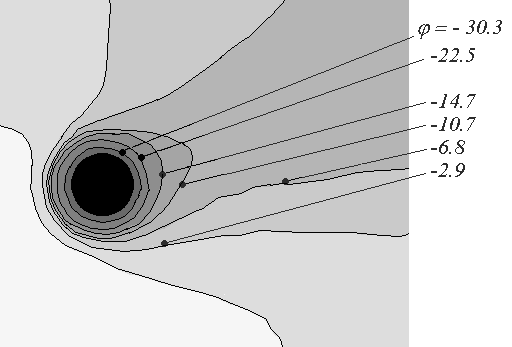
На рис. 13 приведены поля скоростей для нейтральных и заряженных компонент при r₀ = 10; ₀ = -45; M = 0,5; Re_э = 50. Из рис. 13 следует, что линии тока нейтралов и ионов сгущаются в точке, соответствующей угловой координате  ~ 100^ и 260 (на боковой поверхности) и за счет вихревого движения дают всплеск в теневой области. Электроны, как отталкивающиеся частицы, попадают на поверхность цилиндра только за счет конвективного переноса вместе с потоком.

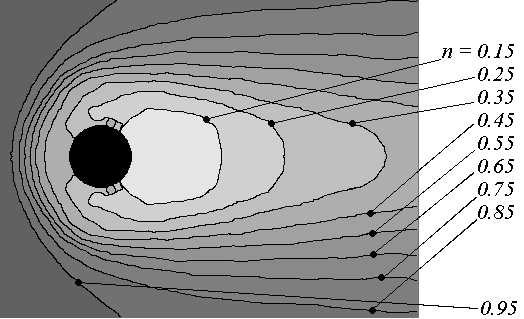
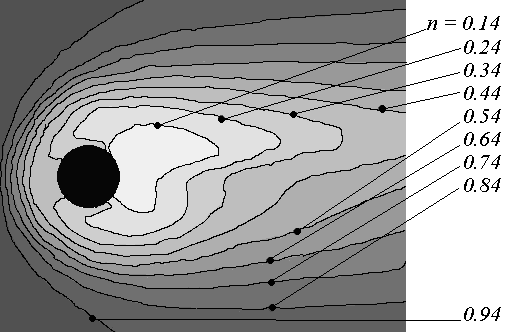
На рис. 14 показаны изолинии поля концентраций ионов и электронов. Из рисунка следует, что имеет место накопление частиц в лобовой части и их разрежение в теневой, где образуется характерный след. Наименьшая концентрация n_i = 0,15n_ образуется вблизи тела в области тени. В боковой области при  ~ 100 и  ~ 260 наблюдается всплеск концентрации ионов. Этот эффект в более ранних работах не наблюдался. Для отталкиваемых частиц (электронов) такого эффекта нет и концентрация вдоль радиуса изменяется монотонно. Концентрация электронов вблизи тела ниже, чем ионов, что связано с отрицательным потенциалом тела.

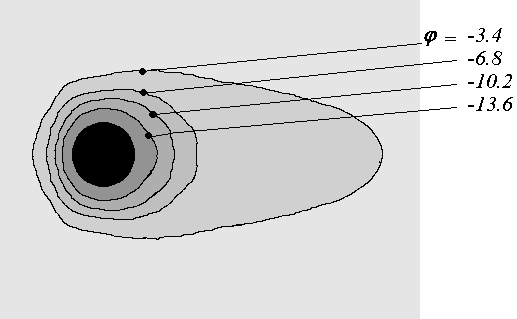
На рис. 15 даны изолинии потенциала и азимутальной составляющей напряженности электрического поля.

а)	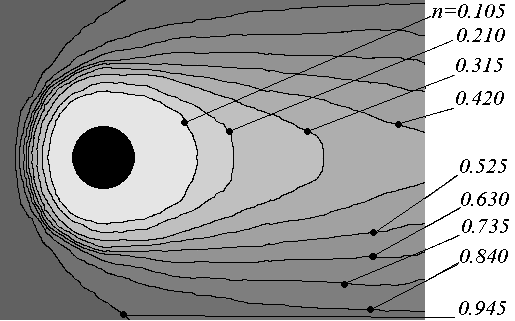б)
Рис. 14. Изолинии концентрации ионов(а) и электронов (б) ().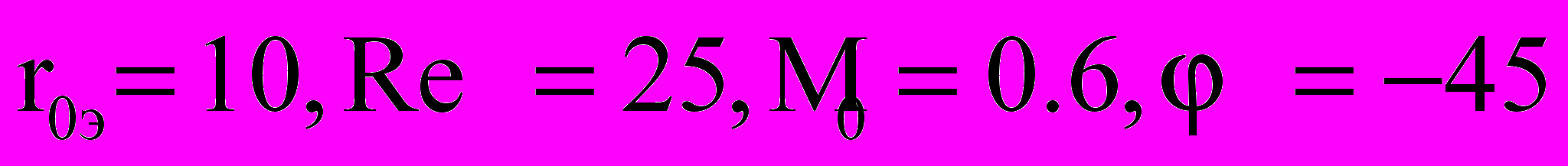
а)		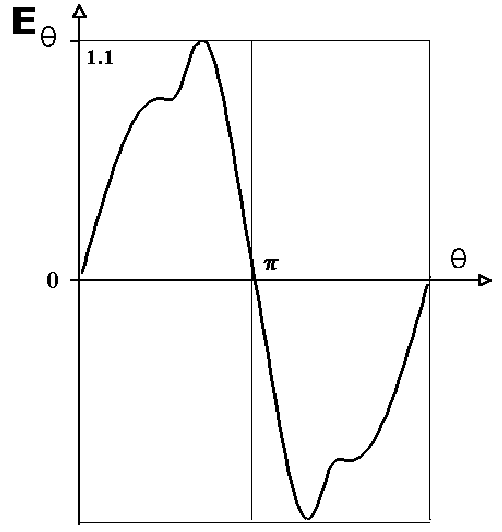б)
Рис. 15. Изолинии потенциала (а) и распределение азимутальной составляющей напряженности электрического поля по обводу цилиндра (б) ().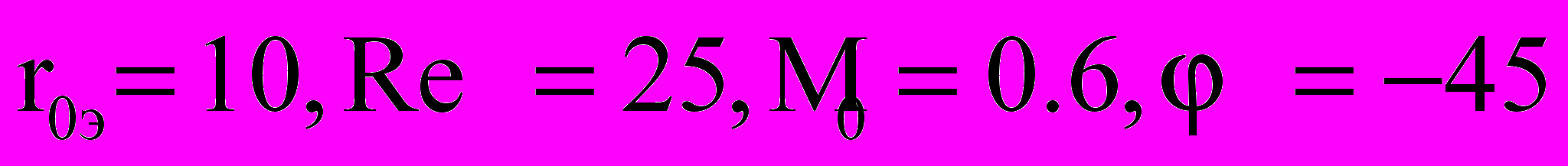

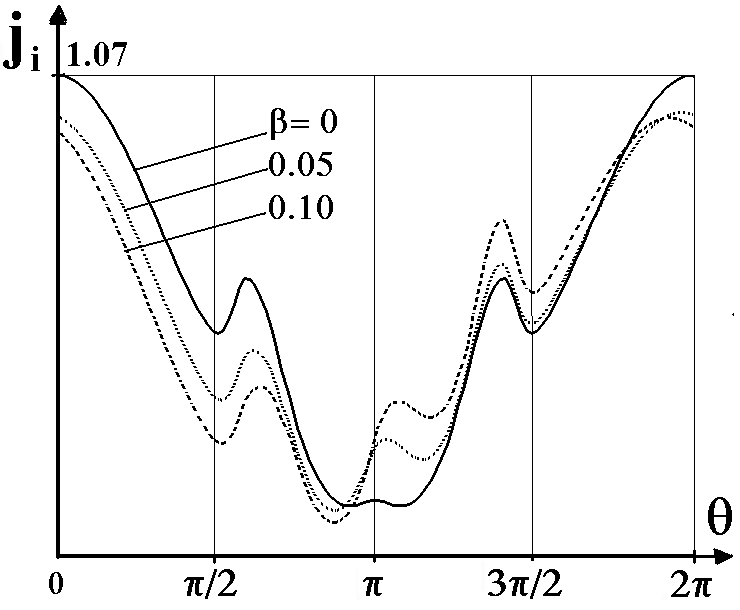
На рис. 16 представлено распределение плотности ионного тока по обводу цилиндра при двух значениях числа Маха: M = 0,05 и М = 0,6. Из рис. 16 следует, что при малых числах Маха распределение имеет монотонный характер, однако с увеличением числа Маха развивается вихревое течение нейтральной компоненты, которая увлекает за собой и заряженные частицы. Вследствие этого в теневой области может появиться всплеск ионного тока (при отрицательном ₀) кроме того, в боковой области могут возникнуть локальные максимумы и минимумы. Физическая причина их возникновения состоит в следующем:

1. Ионы движутся вместе с потоком вдоль боковой поверхности цилиндра и одновременно испытывают электростатические притяжения со стороны тела. В результате их траектории отклоняются в сторону поверхности цилиндра.
   
2. В теневой области ионы вместе с вихрями приближаются к поверхности цилиндра и за счет притяжения также отклоняются в сторону поверхности.
   

Эти два потока ионов, накладываясь друг на друга, дают всплеск концентрации и плотности тока, образуя локальные максимумы и минимумы. Появление этого эффекта возможно лишь в ограниченном интервале изменения характерных параметров задачи. Например, при M = 0,6; Re_ = 25; ₀ = -45 эффект пропадает при r₀30. Влияние параметра  на плотность тока в интервале 0,2 <  < 1 оказалось незначительным.

M = 0,05	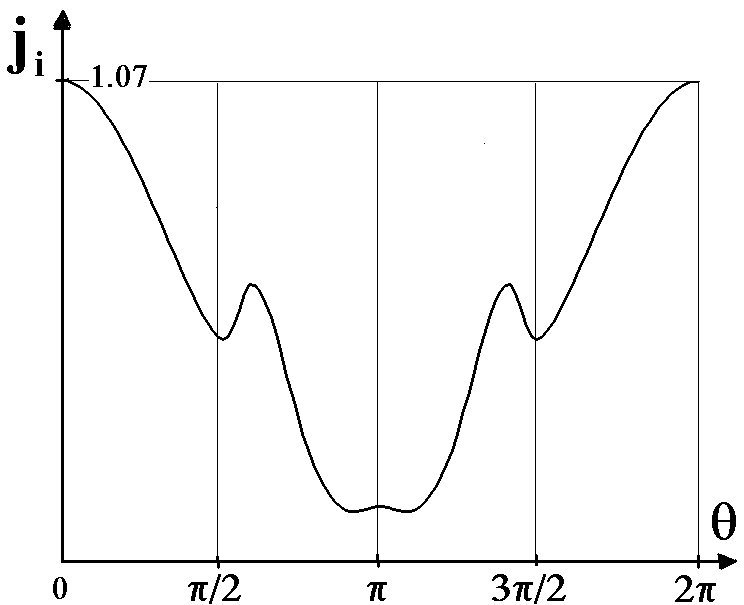M = 0,6
Рис. 16. Безразмерная плотность тока ионов по обводу цилиндра ().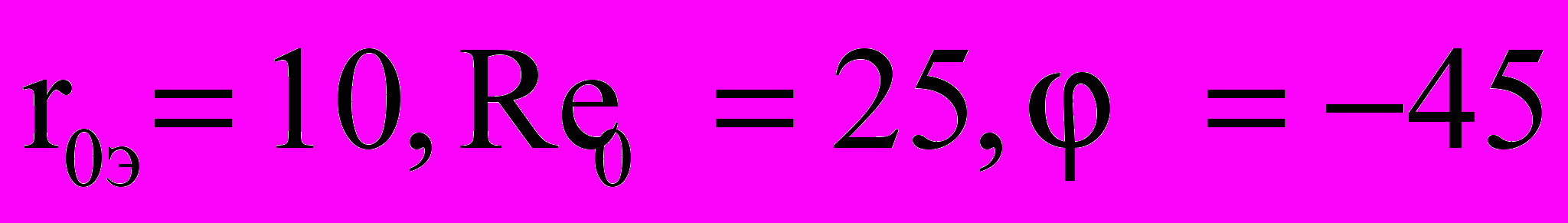

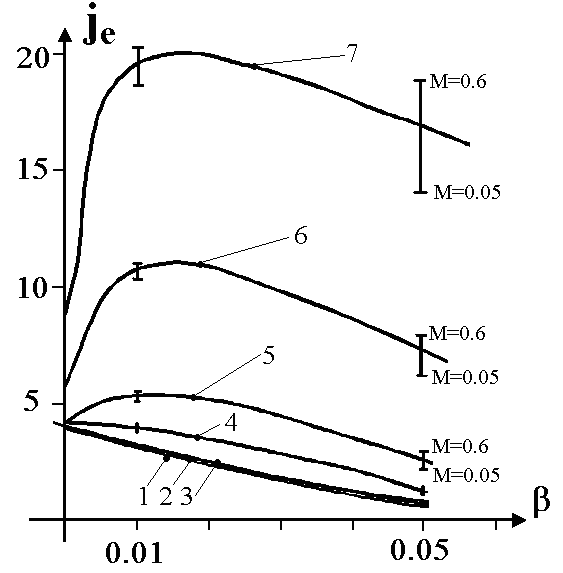
Если включить осевое магнитное поле при сохранении направленной скорости и потенциала цилиндра, пропадает плоскость симметрии, проходящая через вектор скорости и ось цилиндра. На рис. 17 даны изолинии концентраций и потенциала при наличии осевого магнитного поля, а на рис. 18а,б плотность тока по обводу цилиндра и средняя плотность электронного тока как функция параметров Re_ и _i. Из рисунков следует, что локальные боковые максимумы под действием магнитного поля вследствие действия пондеромоторных сил снижаются в области 0 и повышаются в области 2, так как в первой области они действуют по радиусу от центра, а во второй – по радиусу к центру. Второй график рис. 18 получен при положительном потенциале тела, так что ток на тело определяется электронами. Из рис. 18 следует, что при Re_ 100 плотность тока j_e с ростом индукции B уменьшается, что согласуется с известным в литературе эффектом уменьшения поперечной диффузии заряженных частиц в магнитном поле. Однако в области Re_ > 100 на участке _I < 10^-2 плотность тока j_e растет с ростом индукции В, а при _i10^-2 начинает уменьшаться по тому же закону, что и при Re_100. Физическое объяснение обнаруженной аномалии состоит в следующем. При относительно больших Re_ конвекция преобладает над диффузией и подвижностью. Вследствие этого плотность тока электронов на боковую поверхность невелика (заряженные частицы, участвующие в конвективном движении, пролетают мимо цилиндра). Основной поток поступает на лобовую, а также на теневую область за счет вихрей. При включении магнитного поля за счет пондеромоторных сил на один бок цилиндра ток начинает расти, а на другой бок уменьшается, но так как он и без поля был мал, то уменьшение несущественно. При росте индукции (_i10^-2) растет замагниченность электронов, что ведет к уменьшению j_e. Если сравнить рис. 18б j_e = f(B) для режима сплошной среды и рис. 12 для молекулярного режима, то можно заметить много общего. Это касается и физического объяснения обнаруженных аномальных эффектов.

а)	б)
в)	Рис. 17. Изолинии концентраций ионов (а), электронов (б) и потенциала (в)
Рис. 18а. Безразмерная плотность тока ионов по обводу цилиндра (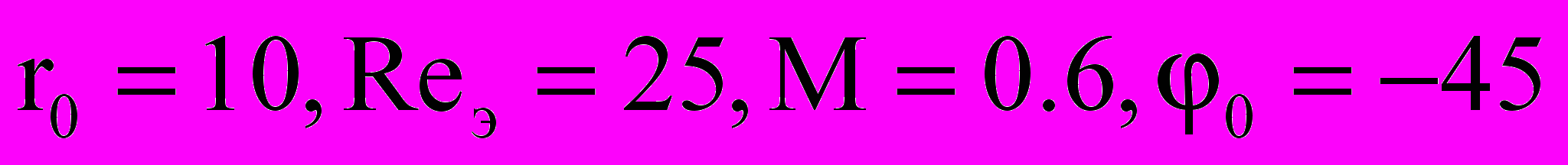)	Рис. 18б. Зависимость средней плотности электронного тока от 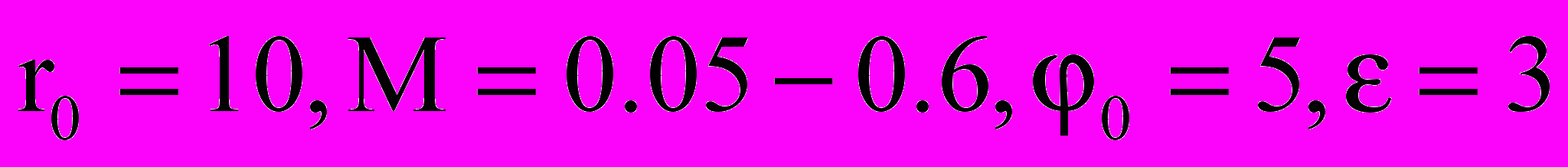 () 1 - Reэ=10; 2 - Reэ=25; 3 - Reэ=50; 4 - Reэ=100; 5 - Reэ=200; 6 - Reэ=500; 7 - Reэ=1000.

Кроме ламинарного режима обтекания цилиндра в работе рассматривается также турбулентный режим обтекания. Из приведенных вычислительных экспериментов следует, что влияние крупномасштабных пульсаций ведет к уменьшению плотности тока заряженных частиц примерно на 10%, что связано с взаимодействием вихрей со слоем объемного заряда. Амплитуда колебаний суммарного тока вследствие турбулентности потока составляет (6÷10)% от его среднего значения, причем токи ионов и электронов колеблются в одной фазе. Если рассмотреть только теневую область цилиндра, где средние значения плотности тока относительно меньше, вклад в плотность тока за счет турбулентности может достигать 100% и более. Влияние осевого магнитного поля на турбулентное обтекание цилиндра аналогично его влиянию на ламинарное обтекание.

В работе рассмотрен также случай ламинарного и турбулентного обтекания плоского электрода ленточного типа, расположенного на большой, обтекаемой плазмой плоскости. Получены поля концентраций, токов и электрических поле вблизи плоского электрода. Обнаруженные особенности полностью соответствуют результатам, полученным при обтекании цилиндра, изложенным выше.

Последний раздел главы 2 диссертации посвящен обтеканию цилиндрического тела потоком столкновительной плазмы при умеренных числах Рейнольдса. Это рассмотрение является весьма актуальным, так как медленно движущаяся плазма встречается в ацетиленовых горелках различного назначения, технологических плазмотронах, в узлах высокотемпературных энергетических установок. Интерес к этому режиму объясняется также тем, что имеется надежный экспериментальный материал по зондовым измерениям цилиндрическим зондом в струях, истекающих из ацетиленовых горелок с добавлением легко ионизуемых солей щелочных металлов, выполненный в ЦАГИ¹. Зондовые измерения дублировались оптическими измерениями, согласно которым концентрация заряженных частиц составляла (1,8÷3,8)10¹⁰см^-3, ионная температура T_i = (237010)K, скорость направленного движения V_{i } = (3÷7) м/с. Сравнение зондовых и оптических измерений показало, что имеет место превышение концентраций, полученных с помощью зондов, над их значениями, полученными оптическими методами, для плазмы с добавками Na в 3,5 раз, с добавками Ka – в 2,4 раза, с добавками рубидия – в 1,5 раз. Анализ автора диссертации, проведенный в работе на основе решения системы уравнений, изложенной в главе 2, методами, изложенными в той же главе, позволил найти систематические неточности в зондовых методах обработки вольтамперных характеристик и полностью согласовать результаты оптических и зондовых измерений.

Обширные вычислительные эксперименты с телами цилиндрической и плоской геометрии, помещенными в потоки столкновительной плазмы, позволили получить достаточный для практического применения набор уточненных ВАХ.

В третьей главе диссертации рассматривается наиболее сложный с точки зрения математического моделирования переходный режим обтекания тел потоками плазмы (Kn ~ 1).

Сформулирована математическая модель механики и электродинамики пристеночной плазмы с учетом столкновений типа ион-нейтрал для упрощенного случая отсутствия направленной скорости потока и внешнего магнитного поля. Она включает кинетическое уравнение Больцмана для ионов, уравнение Власова для электронов и уравнение Пуассона для самосогласованного электрического поля

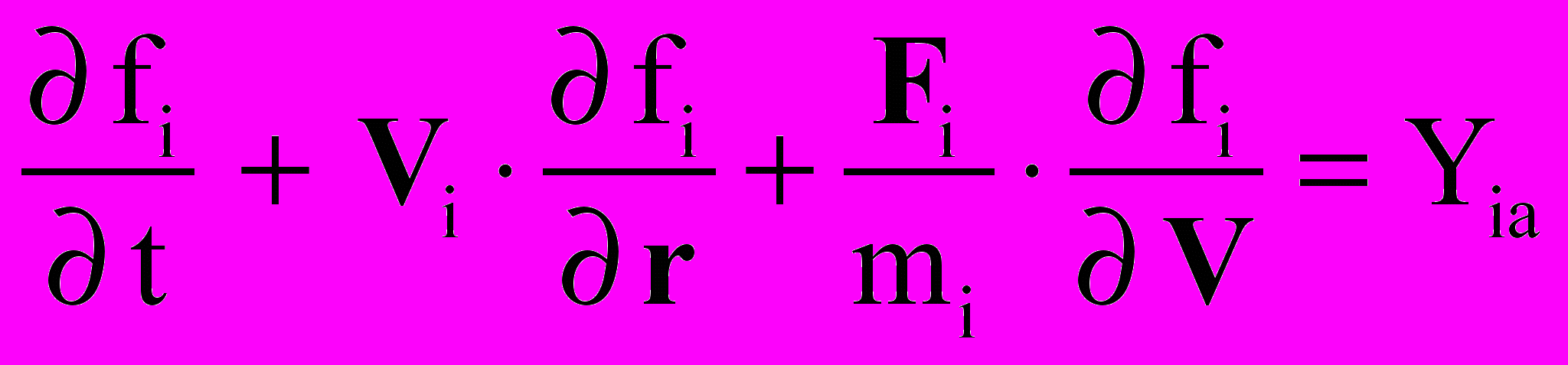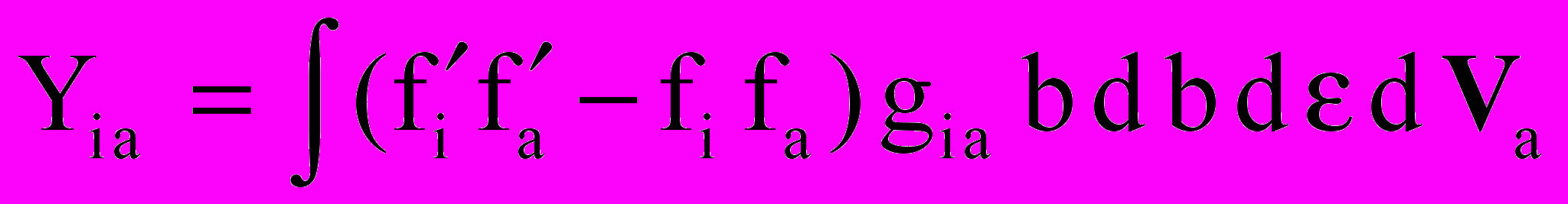, ;	(16)
;
; ;

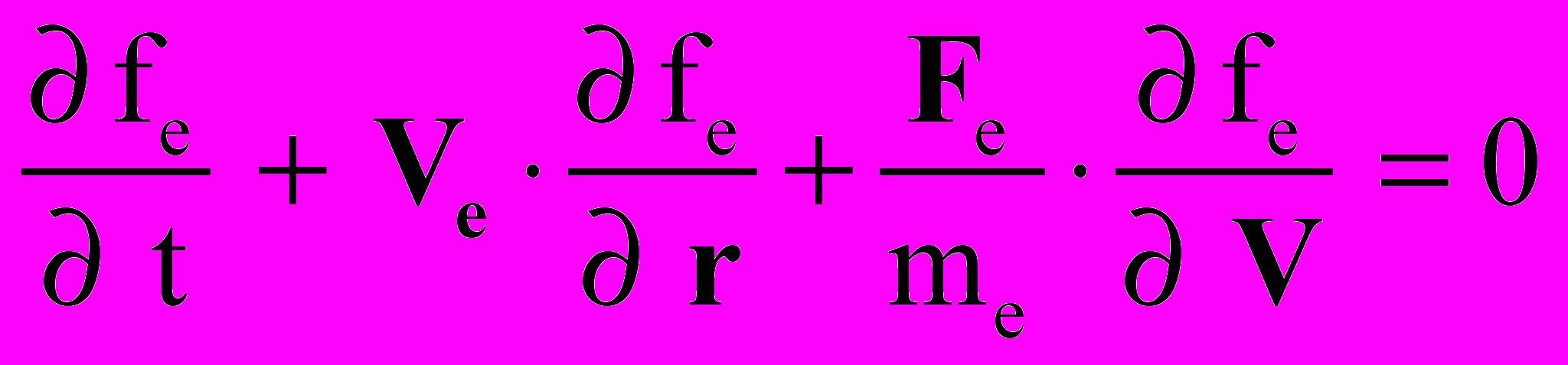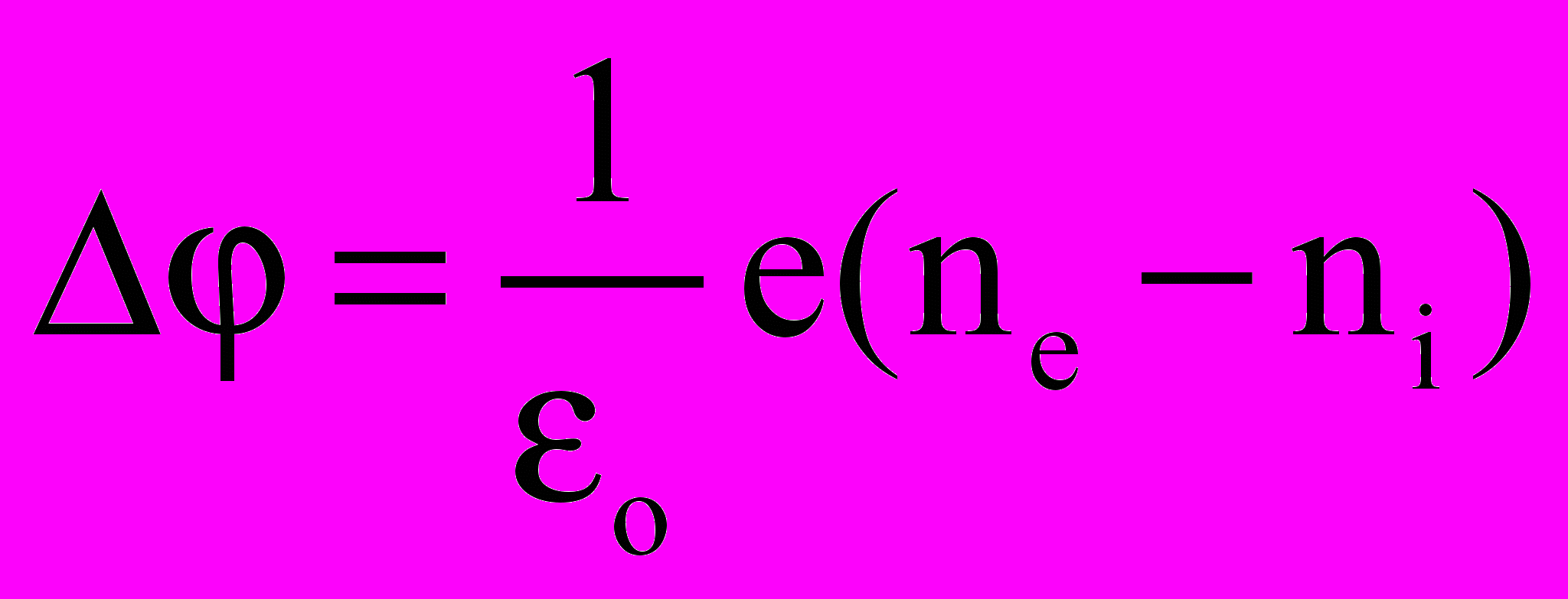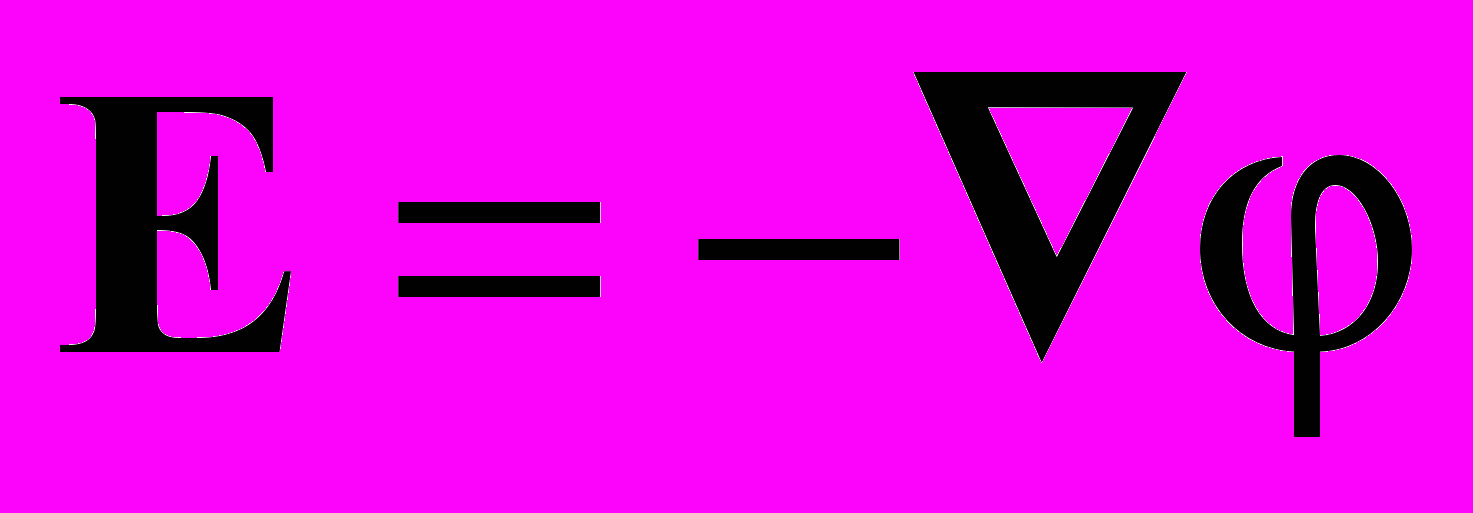где 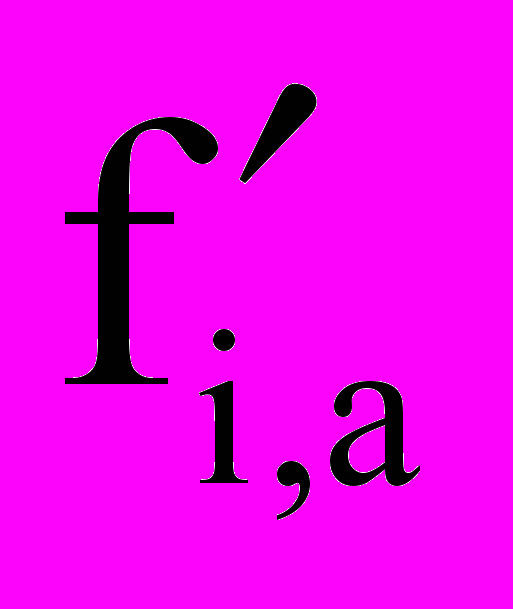-- функции распределения ионов и нейтральных частиц сорта «а» до столкновения; f_i,a -- функции распределения ионов и нейтральных частиц сорта «а» после столкновения ; g – относительная скорость сталкивающихся частиц; b – прицельный параметр; ε -- азимутальный угол; 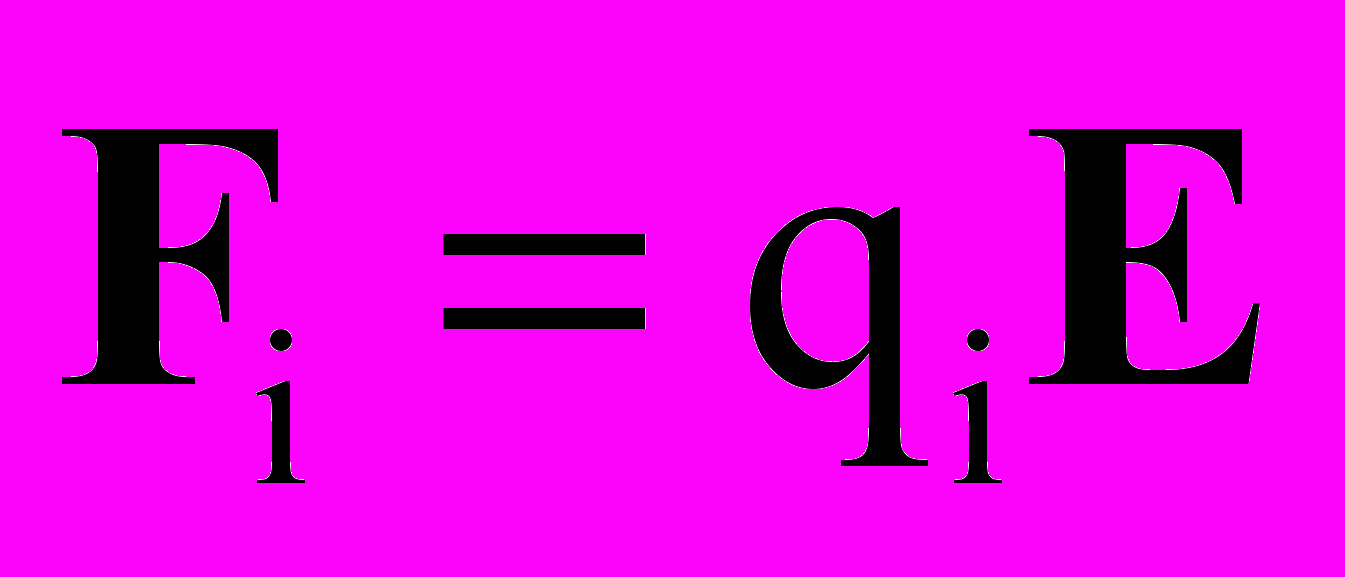- сила, действующая на ионы в электрическом поле, возникающем в пристеночной области.

Система начальных и граничных условий соответствует моделям, изложенным в главе 1 диссертации (см. (1)-(12)).

Математическая модель задачи с учетом столкновений типа «электрон-нейтрал» отличается от приведенной лишь тем, что уравнение Больцмана записывается для электронов, а Власова – для ионов.

Математическая модель задачи с учетом столкновений типа «ион-ион» и «ион-электрон» включает в себя уравнения Фоккера-Планка для ионов и электронов и уравнение Пуассона для самосогласованного электрического поля, а также систему начальных и граничных условий. Учитывая сложность столкновительного оператора Фоккера-Планка, задача рассматривалась в упрощенной постановке, когда в плазме находится бесконечная плоскость, заряженная до потенциала _р. В этом случае функции распределения f_ ( = i,e) будут зависеть только от двух фазовых переменных (y, V_y), и времени t, (ось y направлена по нормали к плоскости). После масштабирования с использованием масштабов (13), система уравнений принимает вид

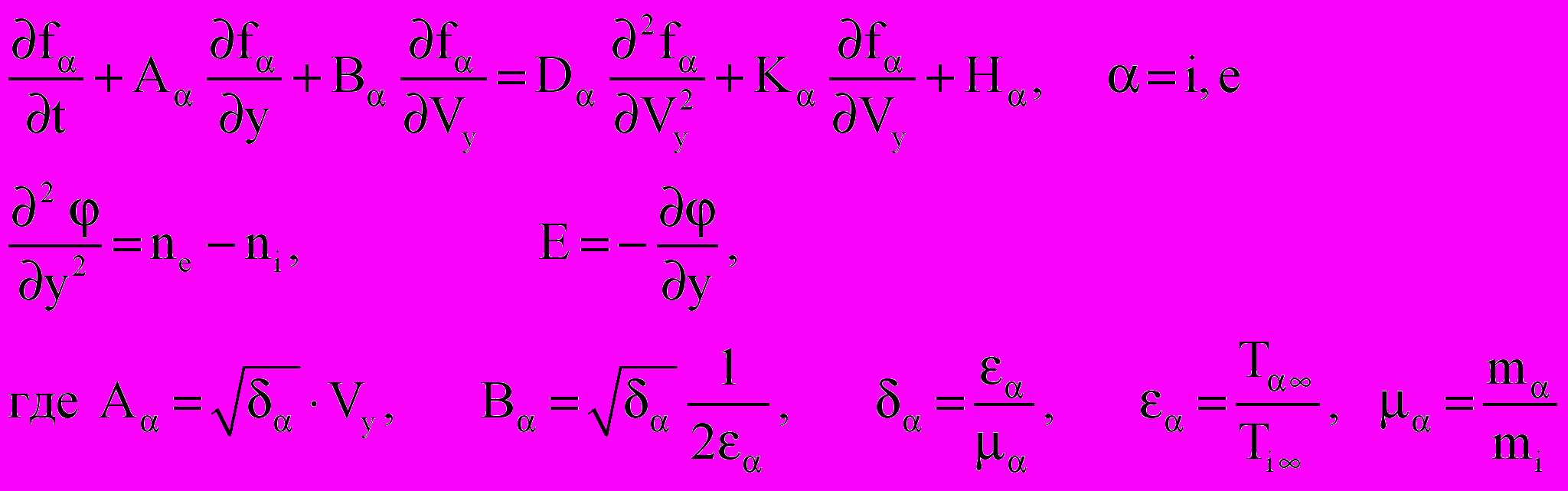	(17)

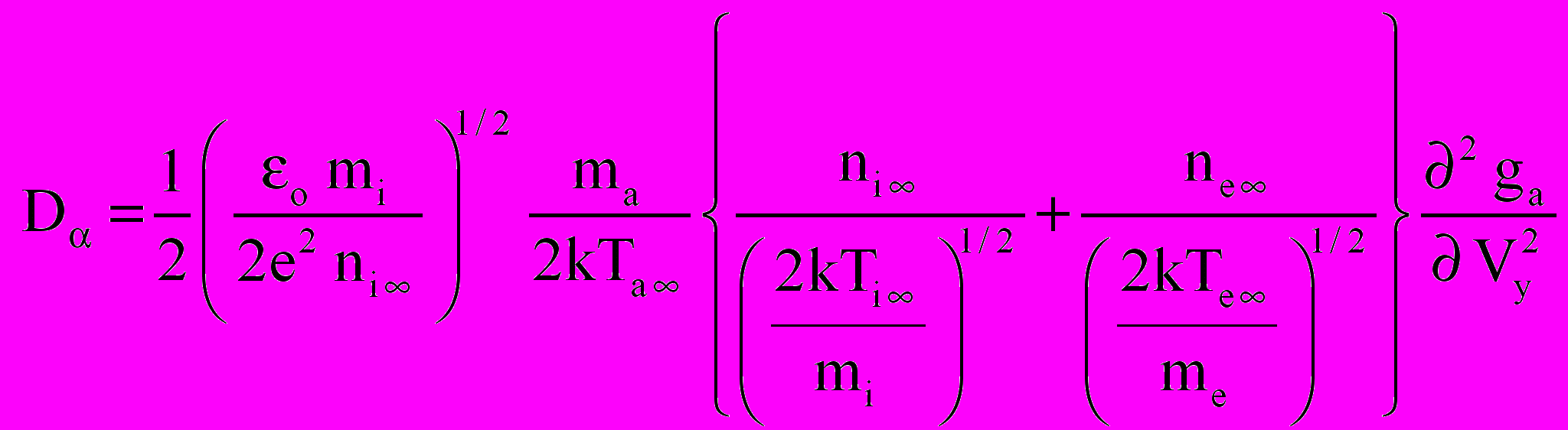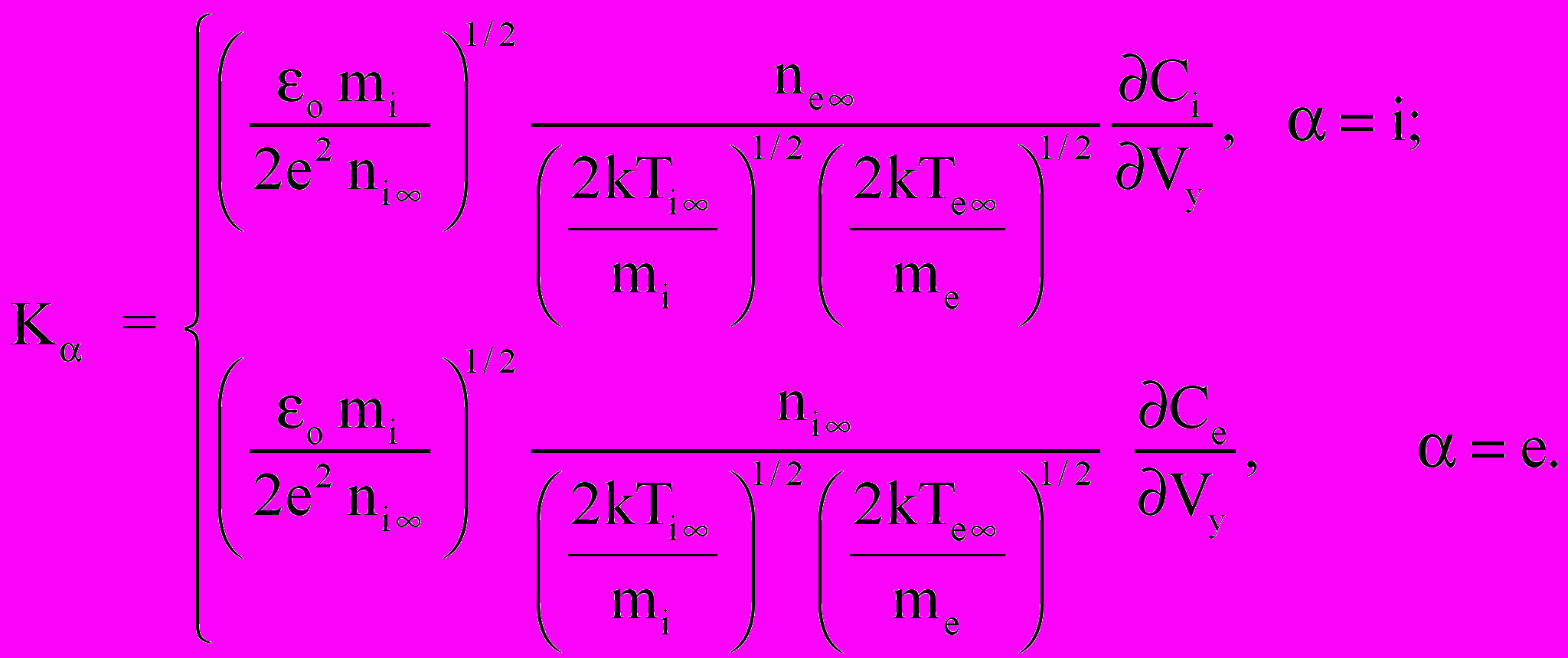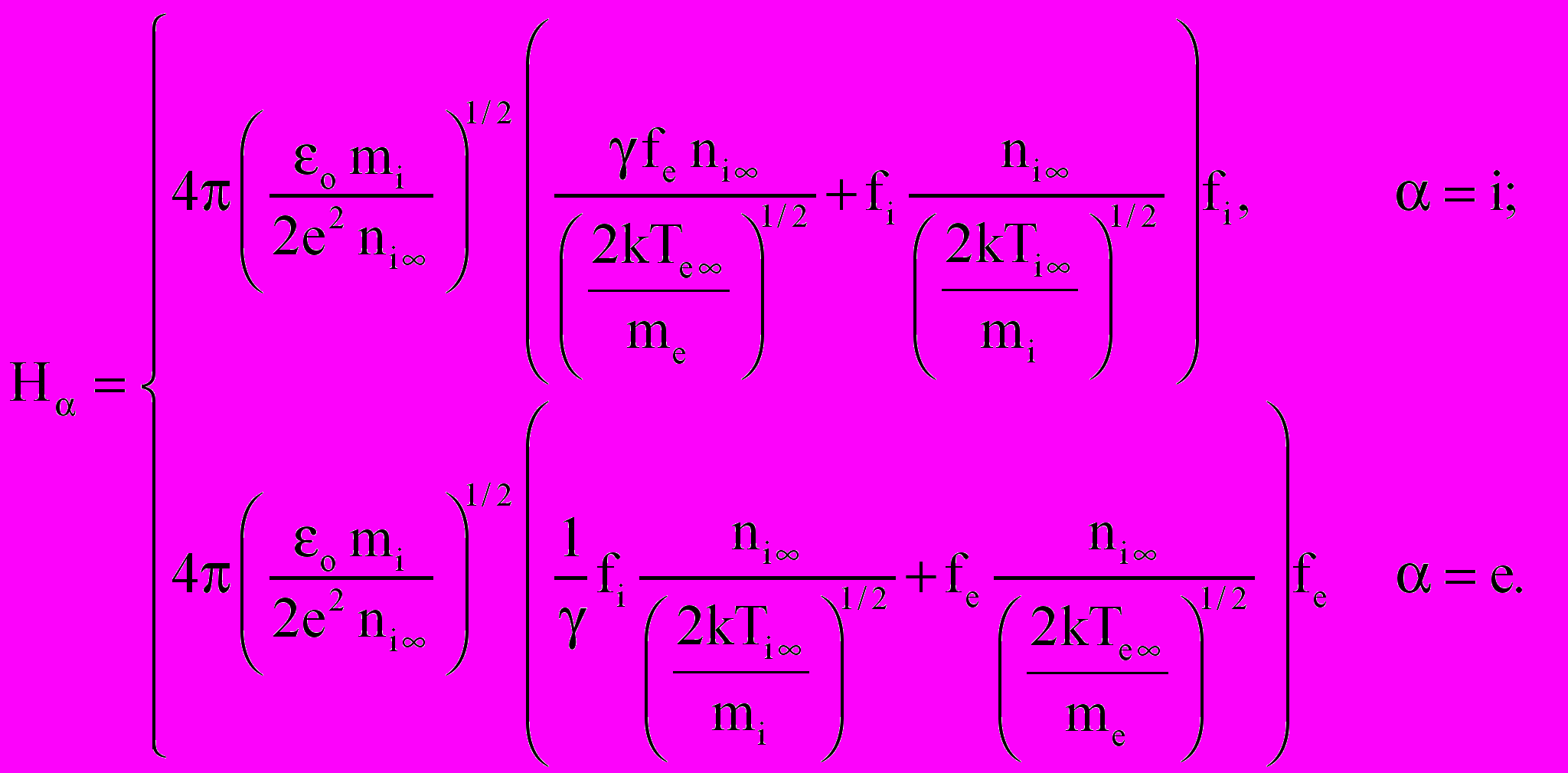Вычислительная модель задачи с учетом столкновений заряженных частиц с нейтральными атомами основана на разбиении траектории движения заряженной частицы на две части: движение между столкновениями на длине пробега и непосредственно само столкновение. На первом участке используется методика, разработанная для свободномолекулярного режима. На втором подшаге вычислительного алгоритма рассматривается процесс столкновения. При этом каждую из сталкивающихся компонент плазмы разбиваем по скорости на S интервалов. Используя модель твердых сфер, получаем скорости частиц после столкновений, зная их скорости до столкновения. Далее рассчитывается число частиц в единице объема, которые покидают ячейку [x, x + x], [y, y + y] за время t вследствие столкновений

∆nстолк = n va ∆t,

(18)

где v_a - частота столкновений частиц сорта  с нейтралами. Эти частицы следует изъять из функций распределения f_ и, придав им новые скорости, перераспределить по другим ячейкам

f_нов = f_стар - f_, f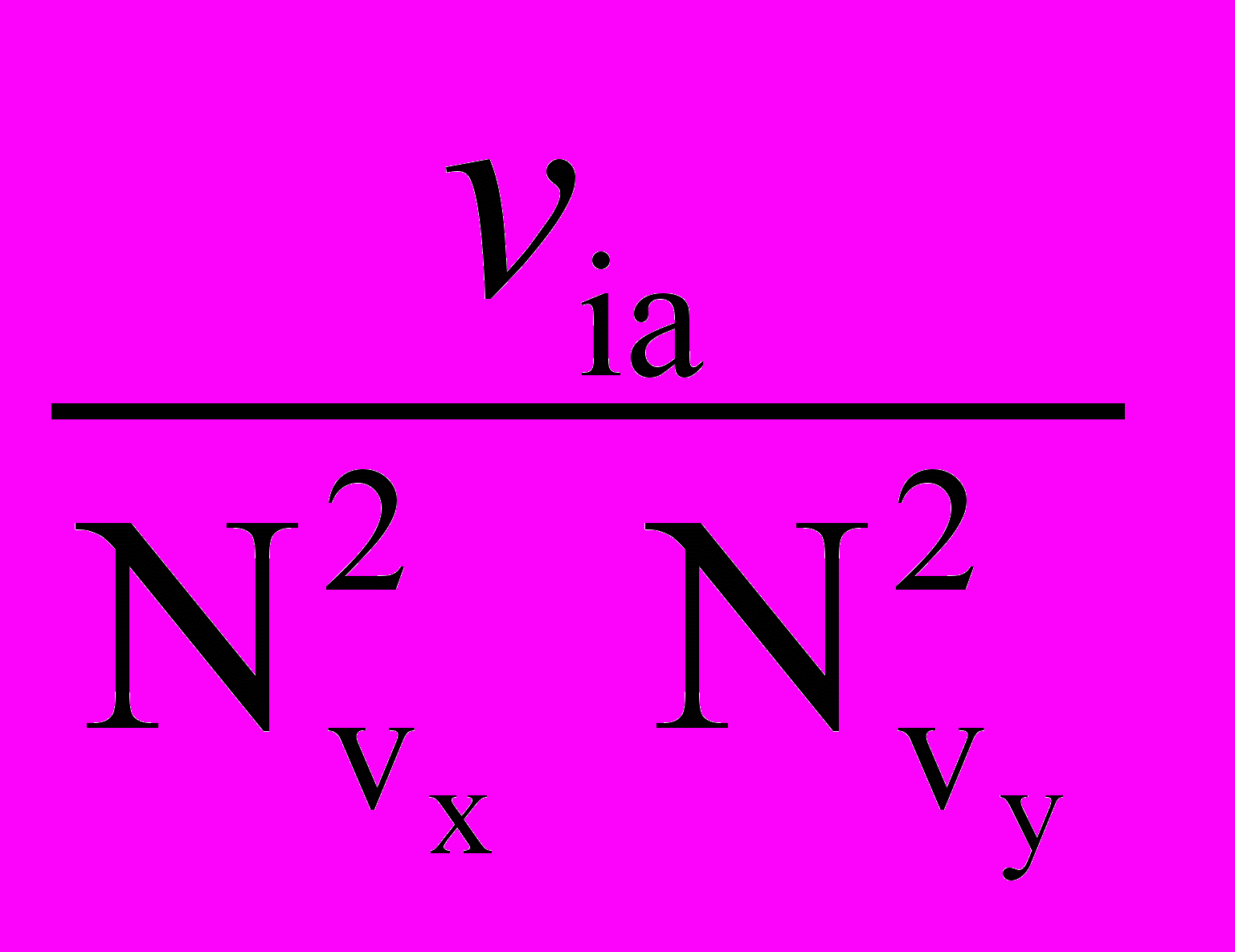_ = ()f_стар,

где 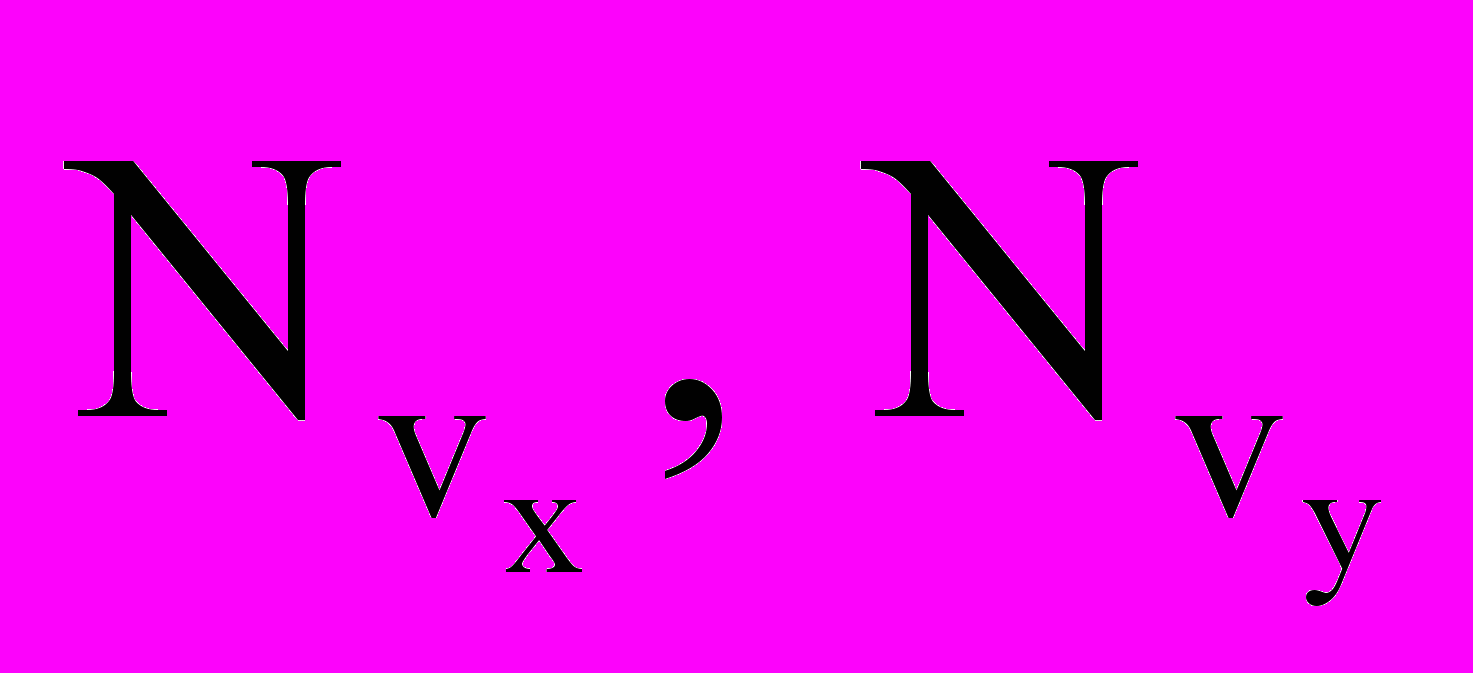- число шагов расчетной сетки по V_x, V_y. Ушедшие из старой ячейки частицы попадают в новую с координатами

x_нов. = x_стар + V_{х нов}t,

y_нов. = y_стар + V_{y нов}t.

В результате прихода частиц в новую ячейку с координатами (х_нов, у_нов) функция распределения в ней изменится:

f_нов = f_стар + ∆f.

Далее происходит переход к новому шагу по времени и так вплоть до установления.

В случае решения уравнений Фоккера-Планка совместно с уравнением Пуассона используется стандартный разностный метод с привлечением алгоритма дробных шагов. Построение вычислительной модели задачи и практические расчеты выполнены аспирантом Кудрявцевой И.В.

В результате расчетов были получены функции распределения ионов и электронов по скоростям, их моменты, потенциал и напряженность самосогласованного электрического поля, а также вольтамперные характеристики пристеночных зондов ленточного типа для различных значений чисел Кнудсена. На рис. 19а,б приведены функции распределения ионов (рис. 19а) и электронов (рис. 19б) с учетом столкновений с нейтральными атомами.

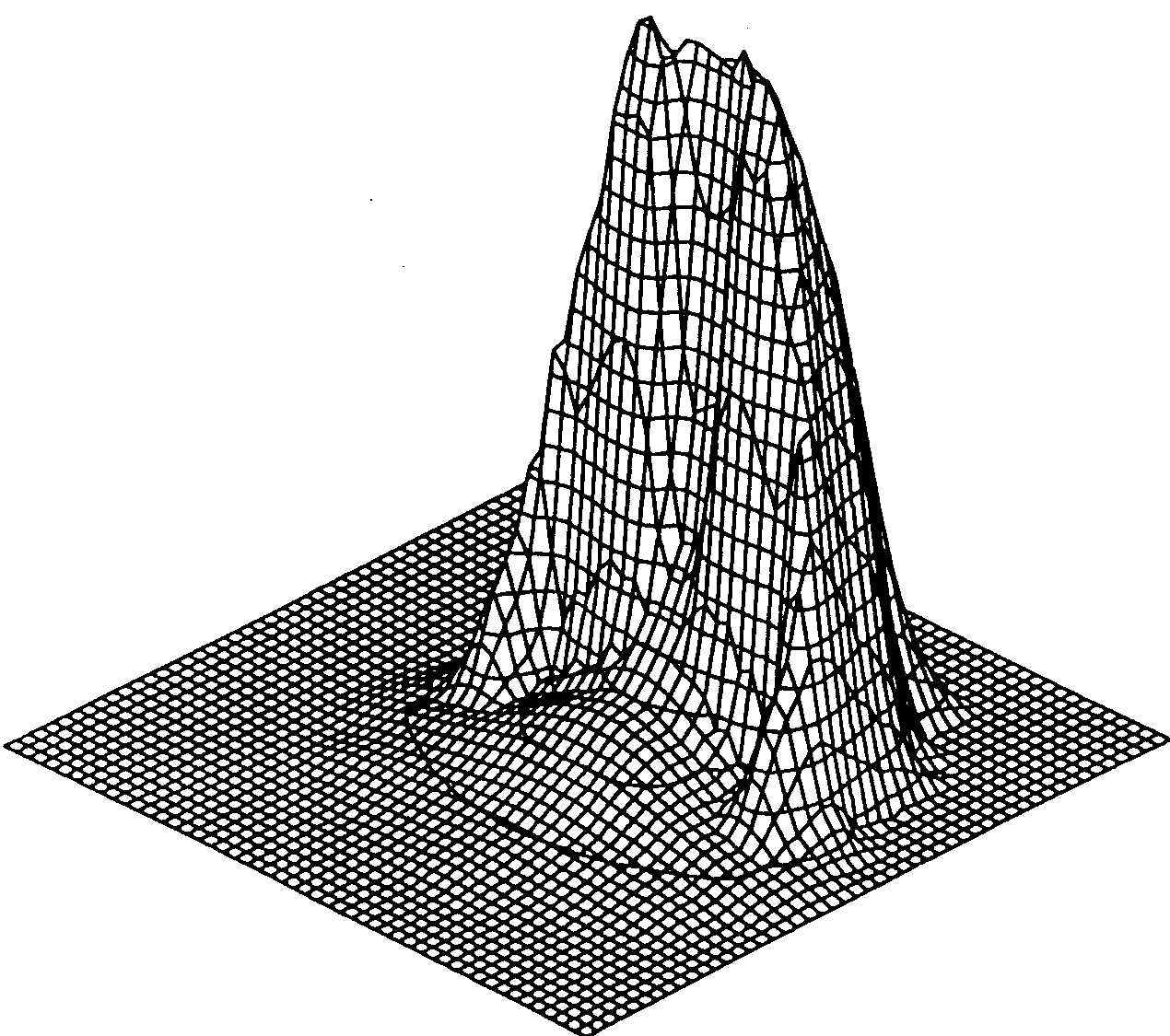а)  = -5	б)  = +5
Рис.19. ФР ионов (а) и электронов (б) с учетом столкновений с нейтральными атомами (r0 = 2, Kn = 2).

В обоих случаях ФР имеет подковообразный вырез, направленный в сторону положительных значений V_y и связанный с отсутствием потока частиц со стороны стенки. Однако, в отличие от молекулярного режима с внутренней стороны подковы наблюдается небольшой подъем, который связан с влиянием столкновений. Часть заряженных частиц в результате столкновений замедляет свои скорости, а часть приобретает скорости в направлении, противоположном действию электрического поля.

Результаты вычислительных экспериментов для тела в виде бесконечной заряженной плоскости с учетом столкновений типа «ион-ион», «ион-электрон» представлены на рис. 20.

Рис. 20. Линии уровня ФР (а – t = 0,1; б – 0,5) 1 – fi = 0,015; 2 – 0,01; 3 – 0,005; 4 – 0,001

Четвертая глава целиком посвящена техническим приложениям в области механики и электродинамики пристеночной плазмы. В параграфе 4.1 рассмотрены некоторые аспекты зондовой диагностики плазменных потоков. Результаты первой главы позволяют уточнить теорию и методику цилиндрического зонда, расположенного поперек потока и плоского пристеночного зонда ленточного типа, как в молекулярном, так и в столкновительном режиме. Среди новых результатов в этой области отметим следующие:

• Получен дополнительный набор уточненных ВАХ, необходимых для обработки зондового эксперимента. Это относится как к цилиндрическому зонду, так и к плоскому пристеночному зонду в молекулярном и столкновительном режимах;
  
• Предложен метод обработки ВАХ цилиндрического зонда в молекулярном потоке плазмы;
  
• Предложен уточненный метод обработки ВАХ цилиндрического зонда в режиме сплошной среды при умеренных значениях электрического числа Рейнольдса. Метод прошел экспериментальную апробацию в плазме ацетиленовой горелки с присадками солей щелочных металлов (эксперимент проведен в ЦАГИ, см. сноску на стр. 20) и показал хорошее совпадение с результатами оптических измерений в тех же условиях;
  
• Предложен метод проведения зондовых измерений в области следа за спутником. Ранее такие измерения были невозможны, так как не было надежной информации о ФР заряженных частиц в этой области;
  
• Рассчитано взаимное влияние плоских пристеночных двойных зондов в молекулярном и столкновительном режимах. Оценено минимальное расстояние между зондами для исключения взаимного влияния, дана оценка систематической погрешности в определении зондового тока в зависимости от расстояния между зондами;
  
• Теоретически получено отношение тока на плоский зонд, расположенный навстречу потоку в молекулярном режиме, и на тот же зонд, ориентированный параллельно потоку. Это отношение позволяет оценить величину направленной скорости плазмы;
  
• Оценено влияние турбулентности на зондовые изменения. Показано, что турбулентный режим в сравнение с ламинарным дает уменьшение зондового тока не более чем на 10%;
  
• Создан автоматизированный блок для обработки характеристик электрических зондов.
  

В пункте 4.2 рассмотрена теория и методика нестационарного электрического зонда. Зонд считается нестационарным, если характерное время изменения его потенциала много меньше характерного времени релаксации в плазме . Под временем релаксации понимается время, за которое осуществляется переход от неравновесного состояния к равновесному, или от одного стационарного состояния к другому в случае импульсного изменения одного из параметров. Чаще всего импульсно меняют потенциал зонда относительно плазмы. В реальных схемах всегда существует конечное время нарастания импульса (t_ф > 0). Для целей построения нестационарной зондовой теории достаточно выполнения неравенства t_ф  0,1. Время релаксации возмущенной зоны  определяется тяжелой компонентой плазмы - ионами. Теоретические исследования показали, что оно зависит от молярной массы ионов, их концентрации и температуры. Если удается измерить  на эксперименте, то появляется еще одна независимая связь между параметрами плазмы, из которой может быть определен еще один параметр плазмы – ионная температура T_i.

В работе приведены результаты вычислительных экспериментов по измерению  в молекулярном, столкновительном и переходном режимах. Получена зависимость  от геометрического фактора, параметров r₀, ₀, , v₀, , числа Кнудсена, наличия термоэмиссии с поверхности тела и т.д.

Нестационарная методика зондового эксперимента должна быть совмещена с классической методикой. Сначала снимается обычная вольтамперная характеристика зонда, из которой классическим методом определяется концентрация заряженных частиц n_i и другие параметры. Затем на зонд подается импульс потенциала с достаточно крутым фронтом нарастания и измеряется время релаксации зондового тока . После этого путем сравнения величин , полученных из физического и вычислительного эксперимента, определяется температура тяжелой компоненты – ионов T_i. В работе приведена подробная методика расчета T_i как в молекулярном, так и в столкновительном режимах.

Предложена электронная измерительная схема для проведения нестационарных зондовых измерений с t_ф ~ 5 нс. Схема испытывалась в плазме тлеющего разряда на неоне и аргоне при давлении порядка 0,5÷3 мм рт. ст. На рис. 21 приведены экспериментально снятые зависимости тока зонда от времени после импульсного изменения его потенциала (фотографии с экрана электронного осциллографа). Отчетливо видно, что ток проходит через максимум, затем плавно спадает и выходит на новое стационарное значение. Экспериментальные кривые на рис. 21 качественно соответствуют теоретическим кривым, полученным в вычислительных экспериментах.

Рис. 21. Осциллограмы тока второго зонда после импульса потенциала на первом зонде.

Разработанная нестационарная зондовая теория и методика обработки зондовых характеристик расширяет возможности зондового метода, позволяет определить еще один параметр плазмы – ионную температуру T_i. Классическая зондовая теория не позволяет получить T_i, для расчета n_i необходимо оценить T_i из дополнительных соображений.

В параграфе 4.3 гл. 4 рассматривается электромагнитный рельсовый ускоритель с якорем, имеющим плазменный контакт. Идея ускорителя состоит в том, что по двум параллельным рельсам пропускается ток I порядка сотен килоампер, который переходит от одного рельса к другому по подвижной перемычке – якорю. В поперечном магнитном поле на контур с током действует сила Ампера, которая приводит к перемещению якоря, а вместе с ним и ускоряемого тела. Якорь может выполняться в виде твердого проводника, или в виде плазменного образования. Используется также гибридный случай, когда основная часть якоря – твердый проводник, а в малом зазоре около рельса образуется плазменная дуга, уменьшающая трение между якорем и рельсом и позволяющая пропускать через якорь ток. При скоростях движения более 3 км/с плазменный или гибридный якорь эффективнее твердотельного.

Проводится математическое моделирование плазменного контакта между рельсом и металлической частью якоря. Задача решается в рамках постановок, сформулированных для столкновительного режима в главе 2 диссертации. В постановке задачи отметим следующие особенности:

1. В систему уравнений входит уравнение энергии для электронов. (В ряде задач гл. 2 это уравнение заменяли условием  = T_i /T_e = const).
   
2. Со стороны рельса в зоне контакта происходит термоэмиссия электронов вследствие сильного разогрева рельса электрическим током. Это означает, что в качестве граничного условия задаются граничная концентрация эмитированных электронов и их концентрация .
   
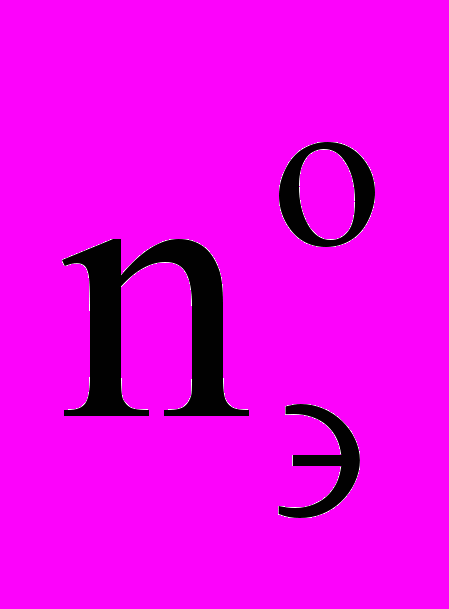3. Релаксация скорости 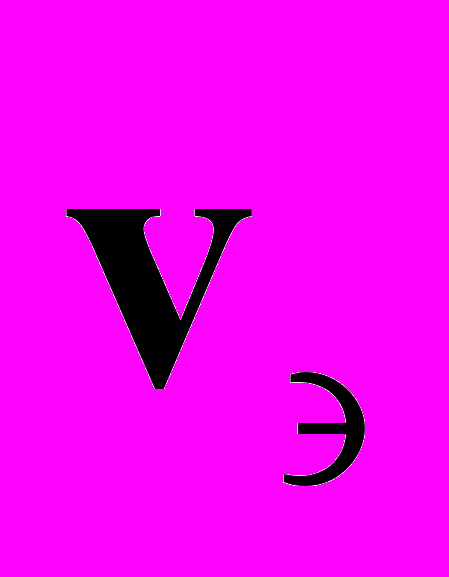со временем удовлетворяет уравнению движения. Входящая в его правую часть сила трения определяется только столкновениями электрона с нейтральными атомами.
   

Таким образом, полная система уравнений включала три уравнения неразрывности (для фоновых и эмитированных электронов и ионов), уравнение энергии для электронов, уравнение движения для эмитированных электронов, уравнения Максвелла для электрических и магнитных полей. Система дополнялась начальными и граничными условиями в стандартной форме.

Вычислительная модель задачи полностью соответствовала главе 2. Использовался метод последовательных итераций по времени с применением на каждом временном шаге метода крупных частиц Давыдова для уравнений неразрывности и схемы среднего арифметического для уравнения движения термоэлектронов и уравнения энергии.

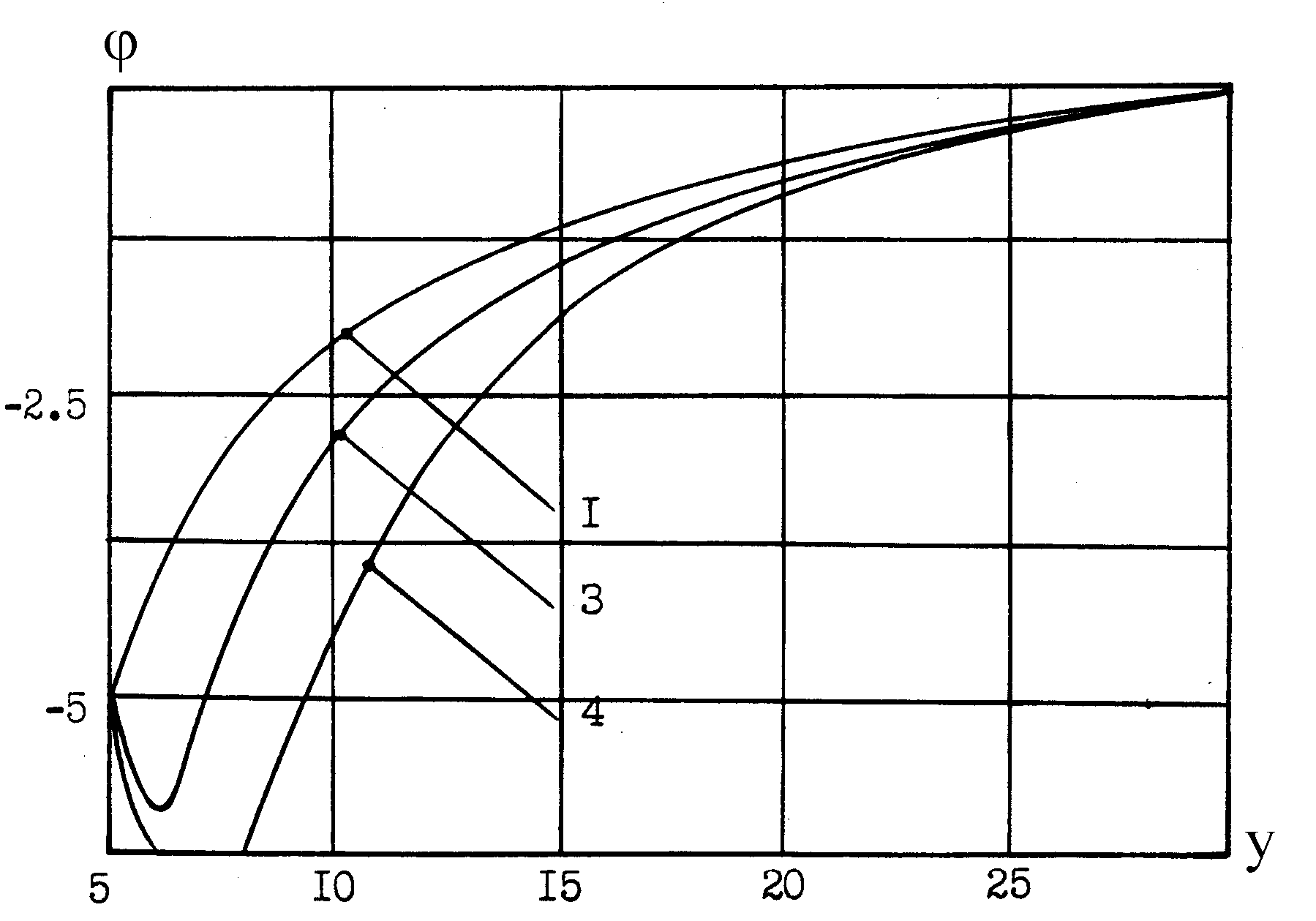
При проведении вычислительных расчетов варьировались плотность тока эмиссии, а также разность потенциалов между рельсом-катодом и невозмущенной областью плазмы. На рис. 22 приведены профили распределения потенциала и концентрации электронов относительно оси у, направленной вдоль якоря.

а)	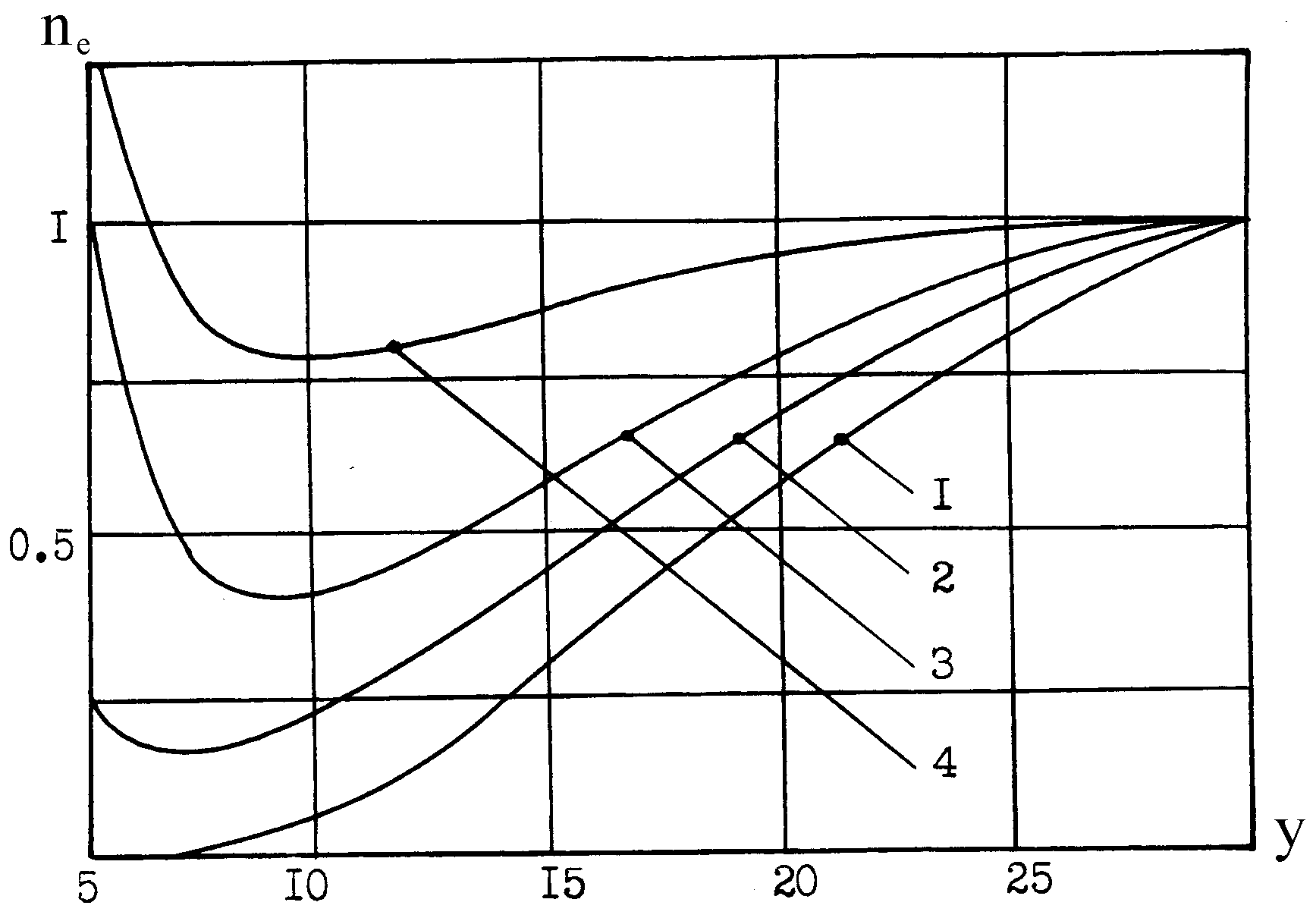б)
Рис. 22. Профили (у) (рис. 22а) и nе(у) (рис. 22б) (r0 = 5; 0 = -5;  = 1) 1 – (jэ = 0); 2 – (1); 3 – (5); 4 – (10).

При возрастании тока эмиссии в пристеночной области образуется избыточный отрицательный заряд, что ведет к образованию потенциальных ям.

В разделе 4.4 анализируется возмущенная зона вблизи космических летательных аппаратов (КЛА) и «собственная атмосфера», образующаяся около них. Все КЛА, запущенные на околоземную орбиту, оказываются в разреженной ионосферной плазме. Если поверхность спутника проводящая, он приобретает «плавающий потенциал», который оказывается ниже потенциала пространства. Вследствие этого около спутника формируется слой объемного заряда и далее квазинейтральная возмущенная зона. Для тел цилиндрической геометрии, которые изучались в гл. 2, возмущенная зона не имеет осевой симметрии. В теневой области она имеет форму удлиненного «следа». Кроме того возмущенная зона может изменяться за счет инжекции в нее различных сортов частиц с поверхности спутника. В этих условиях говорят о собственной атмосфере, формируемой вблизи спутника. Знание параметров возмущенной зоны и собственной атмосферы вблизи спутника необходимо при проведении физических экспериментов на КЛА, при учете взаимодействия спутника с другими телами, при расчете процессов переноса заряда, массы, импульса и энергии из окружающего пространства на поверхность спутника и т.д.

Математическая модель задачи полностью соответствует главе 1 с двумя замечаниями:

1) Характерный размер спутника r₀ должен быть существенно больше размера электрического зонда.

2) Потенциал спутника ₀ должен равняться плавающему потенциалу, если на спутнике не созданы специальные условия, например, инжекция заряженных частиц одного знака с его поверхности.

Вычислительная модель также полностью повторяет модель главы 1. Вычислительные эксперименты проводились с учетом условий полета спутника цилиндрической формы диаметром несколько десятков сантиметров, обладающего плавающим потенциалом, по орбите на расстоянии 500 км от поверхности Земли. Скорость полета – первая космическая, состав плазмы – атомарный кислород. В соответствии с этим безразмерные параметры задачи имели следующие значения: r₀ = 30; ₀ = -6; V₀ = 5,8; T_e/T_i = 1,6; m_i/m_e = 30000. Полученные данные качественно совпали с результатами главы 1(см. рис. 3,4,8-10 реферата).

Следующая серия расчетов относится к исследованию структуры возмущенной зоны спутника при наличии эмиссии электронов и инжекции ионов с его поверхности. Если скорость испускаемых частиц велика по сравнению со скоростью спутника, то последней можно пренебречь и положить v₀ = 0.

Постановка задачи и ее численная реализация находятся в рамках моделей, сформулированных в главе 1. Расчеты показали, что инжекция отрицательно заряженных частиц (например, электронов), приводит к появлению отрицательного пространственного заряда. Начиная с некоторого предельного тока инжекции образуется виртуальный катод. Поступающие с поврехности тела новые порции частиц начинают отражаться от области отрицательного потенциала, что в конечном итоге приводит к осцилляционным процессам. Уменьшая инжектируемый ток, можно перейти от режима осцилляций к режиму с полным прохождением тока. На рис. 23 представлена ФРЭ на оси симметрии системы пучок-плазма, если плотность инжектируемого пучка меньше критической (j_ < j_{ кр}., j_{ кр} – это плотность тока эмиссии, при которой начинает образовываться виртуальный катод). Вычислительный эксперимент позволяет отдельно получить ФРЭ плазмы и инжектируемого пучка. При j_ < j_{ кр} ФРЭ пучка при его полном прохождении меняется слабо, вследствие чего суммарная ФР имеет два максимума: один в низкоэнергетической области (ФРЭ фона), другой при v_z = v_э⁰ (ФРЭ пучка). Следует

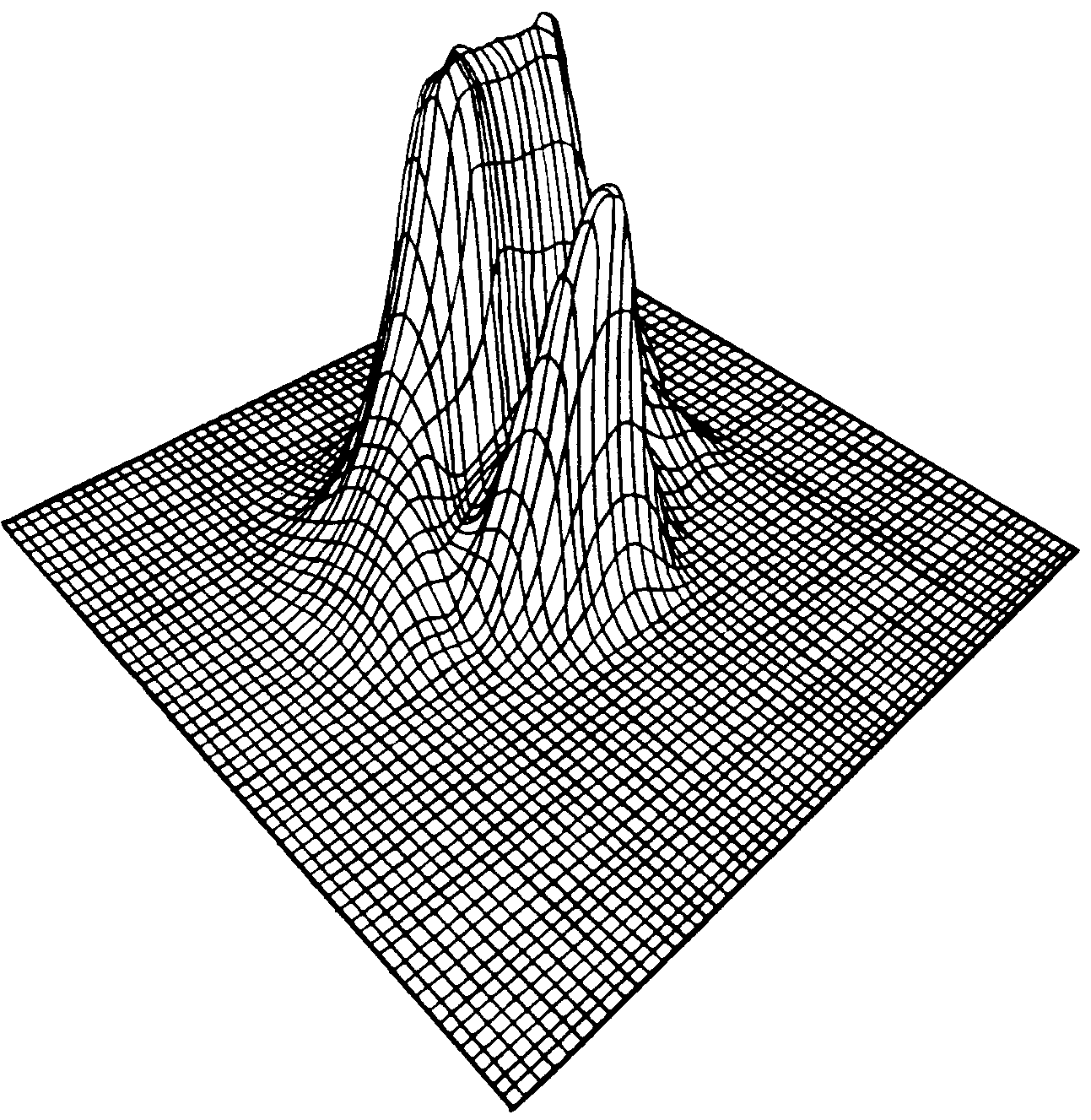Рис. 23. ФРЭ при jэ < jэкр (0= 10; r0= 7;  = 1; jэ = 510-2)

отличать причину появления двух частей ФРЭ в данном случае от причины появления двух частей ФРИ в теневой области цилиндра, обтекаемой разреженной плазмой. На основании полученных ФР рассчитываются все процессы переноса.

В разделе 4.5 рассматриваются электродинамические методы воздействия на ионизованный пограничный слой, возникающий вблизи гиперзвуковых летательных аппаратов (ГЛА). В рамках математических и вычислительных моделей гл. 2 исследуются два способа уменьшения электронной концентрации в некоторой части пограничного слоя. Это необходимо для обеспечения устойчивой радиосвязи между ГЛА и наземными станциями слежения или между двумя ГЛА. Первый вариант: инжектирование в погранслой потока отрицательных ионов; второй вариант: возбуждение в погранслое импульса поперечного магнитного поля. Рассматриваются последовательно оба варианта.

Идея первого варианта состоит в том, что при инжектировании пучка отрицательных ионов внутри него создается отрицательный объемный заряд, создающий сильное отрицательное электрическое поле. Оно в первую очередь вытесняет из канала пучка наиболее легкие частицы – электроны фоновой плазмы. Концентрация электронов снижается, что ведет к созданию радиопрозрачного канала. Ионы, как известно, не вызывают экранирования радиоволн в используемом для связи диапазоне частот. Нестационарный подход, использованный в гл. 2 диссертации, позволяет детально изучить структуру фронта пучка, появление обратных токов, колебательные процессы, развитие неустойчивостей, и, главное, определить необходимые концентрации и скорости инжектируемых отрицательных ионов. Если предположить, что плазма имеет постоянные свойства и замороженные химические реакции, то математическая модель задачи включает уравнения неразрывности для компонент пристеночной плазмы и пучка, уравнение движения для компонент пучка и уравнения Максвелла. Алгоритм решения задачи содержит два этапа. На первом этапе при t  t₀ инжекция пучка еще не началась. Ищется решение задачи для пристеночной плазмы, которое можно рассматривать как начальное для второго этапа. На втором этапе t > t₀ начинается инжекция пучка отрицательных ионов перпендикулярно плоскости инжектора вдоль оси Z. Задается невозмущенная скорость пучка на срезе инжектора 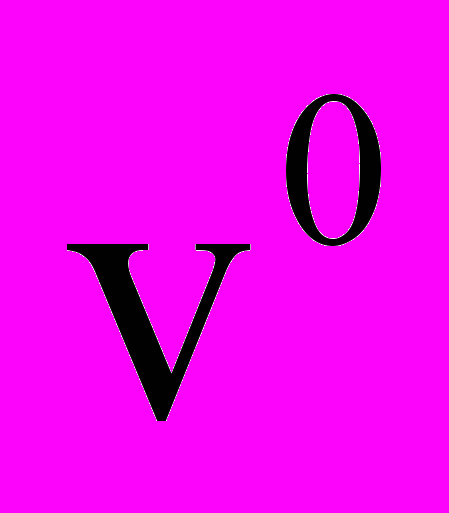и их концентрация 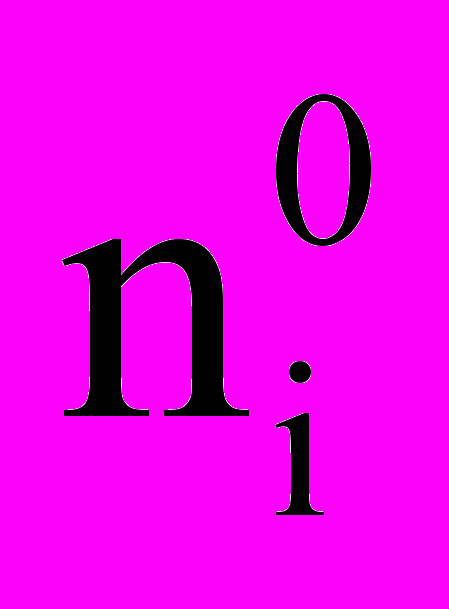. В расчетах используется равномерная сетка с динамической внешней границей. Эволюция плазменно-пучкового образования прослеживается до установления токов на диск, с которого происходит инжекция.

На рис. 24а,б даны профили потенциалов (24а) и концентраций электронов (24 б) как функции координаты Z при различных сочетаниях 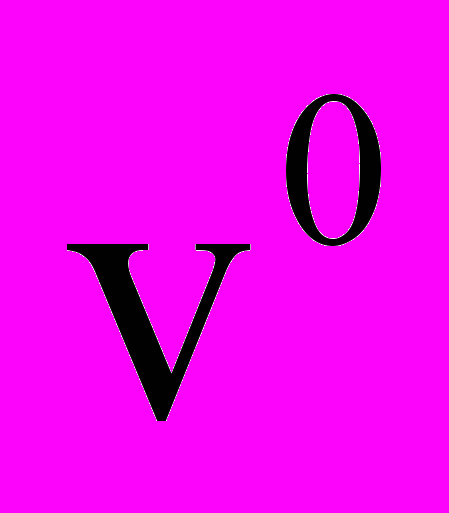и 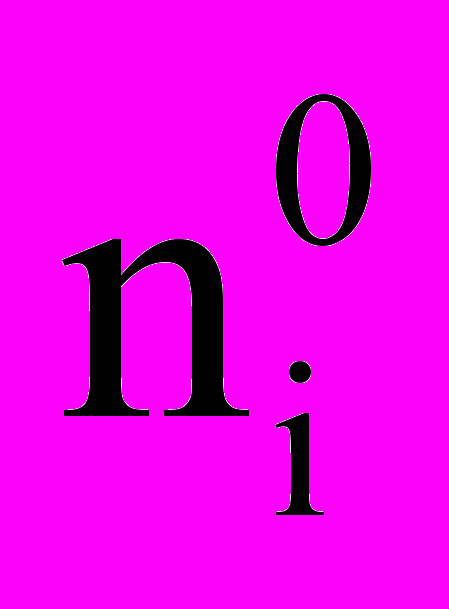. Графики даны в безразмерном виде с учетом масштабов (15). Из кривых рис. 24 следует, что при

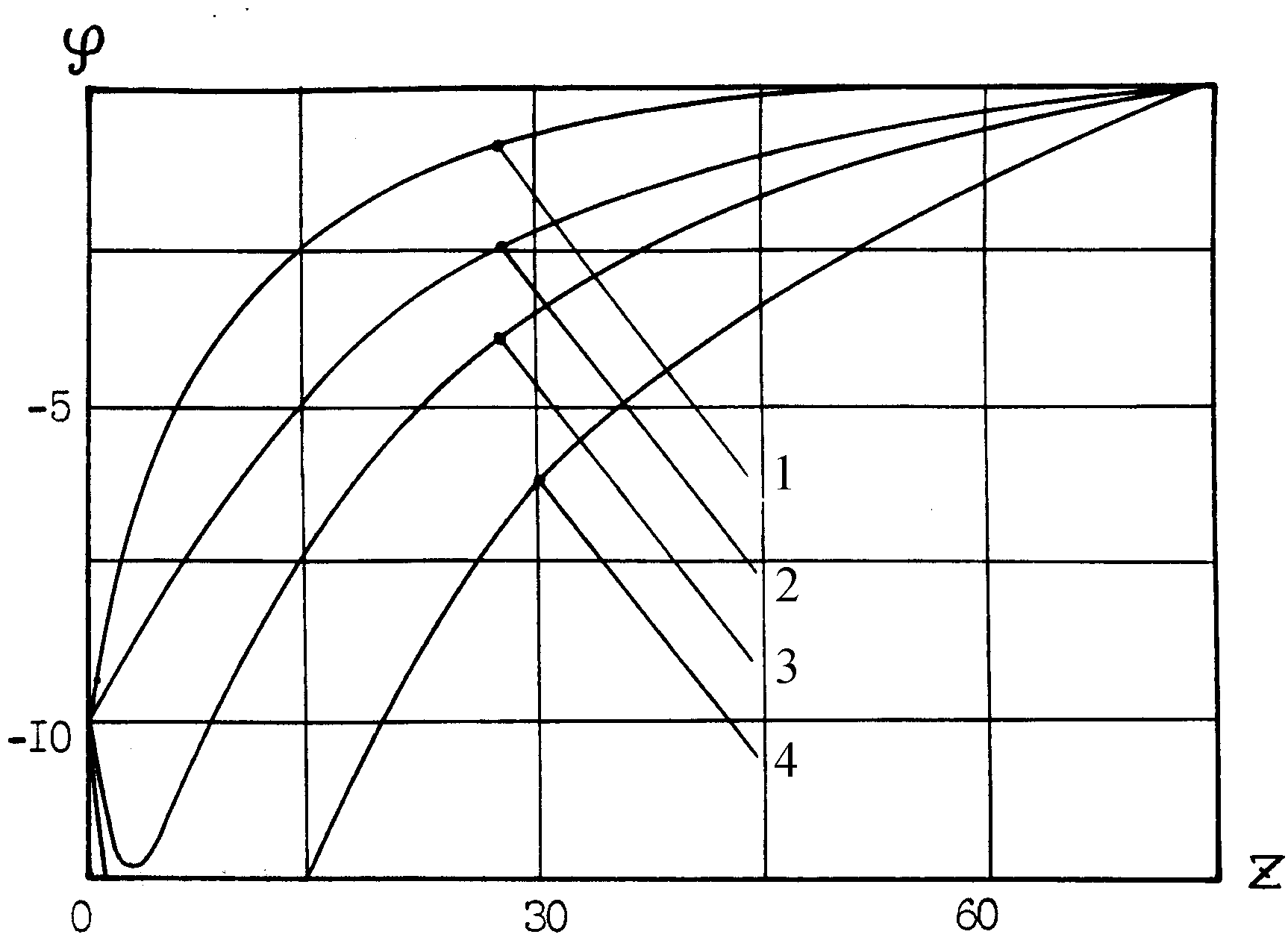а)	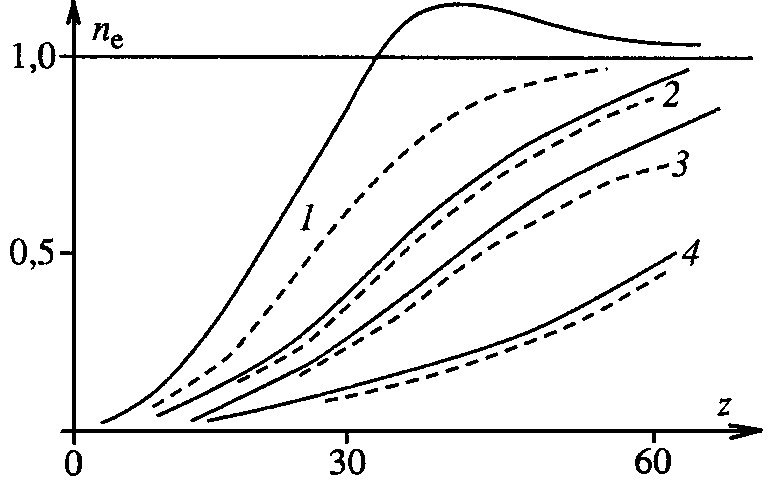б)
Рис. 24а,б. Зависимость (z) (а) и ne (z) (б) (0 = -10; r0 = 5;  = 1) 1 – (n0 = 0; v0 = 0); 2 – (0,5; 1); 3 – (1; 1); 4 – (2; 1). сплошная линия – B0 = 0; штриховая – 0,1.