Математическое моделирование многомерных квазистационарных электромагнитных полей в канале электродинамического ускорителя

Вид материала

Автореферат

Содержание Собственные значения матрицы M для различных способов моделирования испарения материала в двумерном случае Таблица 2. Собственные значения матрицы M для различных способов моделирования испарения материала в трехмерном случае E в диэлектрике, причем поле H В четвертой главе Е значение скалярного потенциала. Показан вид потенциала ( = - (v

Подобный материал:

• Научно-образовательный материал компьютерное моделирование электромагнитных полей, 22.61kb.
• Моделирование электростатических и электромагнитных полей приминительно к процессам, 91.97kb.
• Математическое моделирование управляемого движения космических аппаратов, 213.72kb.
• Программа дисциплины имитационное моделирование в экономике для направления 080100., 228.47kb.
• Правительстве Российской Федерации» (Финансовый университет) Кафедра «Математическое, 246.23kb.
• Математическое моделирование термомеханических процессов в системах армированных стержней, 259.01kb.
• И математическое моделирование, 1392.77kb.
• Вестник Брянского государственного технического университета. 2007. №4(16) математическое, 61.09kb.
• Новые методы защиты населения крупных городов от электромагнитных полей, шума и радоновыделения, 102.38kb.
• Программа вступительного испытания собеседования для магистерской программы «математическое, 67.11kb.

Целью третьей главы является разработка методов моделирования процессов в канале ускорителя в случае изменения границ областей при испарении материала и в случае несвязности границ (см. [22, 23, 25]).

В стандартных ситуациях область, в которой исследуются электромагнитные поля, состоит из проводящих и непроводящих (диэлектрических) подобластей. В общем случае границы проводников и диэлектриков могут изменяться во времени или быть несвязными.

Все исследуемые виды областей встречаются при исследовании импульсных электродинамических ускорителей типа рельсотрон.

Изменение границ диэлектрических и проводящих подобластей при испарении материала проводника связано в рассматриваемом случае с зависимостью электропроводности и других параметров материалов от температуры с учетом фазовых переходов: плавления и кипения.

При описании процессов в рельсотроне со сложной топологией канала появляется также необходимость исследования процессов в многосвязных областях.

При использовании для описания электромагнитных полей квазистационарного приближения возможна потеря единственности решения в диэлектрических подобластях. В однородной модели [1] единственность решения утрачивается при изменении границ проводящих и диэлектрических подобластей (при использовании для решения разностной схемы с неизменной формой шаблонов) и в случае многосвязных границ.

Для моделирования квазистационарноых электромагнитных полей и сопровождающих их распространение процессов в таких областях требуются специальные модели и алгоритмы.

Ранее [1] при моделировании испарения проводника электропроводность в испарившейся части полагалась малой ("фоновой") величиной (на несколько порядков меньшей значения до испарения), что обеспечивало соответствующее перераспределение тока. Но при таком подходе образуются проводящие подобласти с малой электропроводностью, которые должны соответствовать диэлектрическим. Использование для моделирования диэлектрика проводника с малой электропроводностью может серьезно ухудшить устойчивость решения по отношению к возмущениям правой части системы уравнений, что неизбежно приводит к плохой сходимости итераций и резкому уменьшению шага по времени. Если величина "фоновой" электропроводности берется большой, то неверно считается тепловыделение и распределение токов. Однако в идеальном случае она должна стать равной нулю. Для преодоления описанных трудностей в данной главе предложена следующая модель: при превышении температуры кипения в проводящей ячейке такая ячейка заменяется диэлектрической с соответствующей перестройкой логических массивов, используемых для описания расчетной области и разностных схем, соответствующих дифференциальным операторам. Использование такой модели позволяет получить нормальное (обладающее минимальной нормой) решение задачи с нулевой "фоновой" электропроводностью.

Предложенный алгоритм моделирования испарения перестраивает логические массивы, предназначенные для подсчета джоулева тепла, приходящееся на каждое из ребер разностной сетки. Логические массивы учитывают перераспределение тепла от граничных с проводником ребер по ближайшим проводящим ячейкам. Пересчет массивов позволяет избежать эффектов, связанных с отнесением тепла к ячейкам диэлектрика (с "фоновой" электропроводностью). Появление в расчетной области подобластей (состоящих из одной или большего числа ячеек) с "фоновой" электропроводностью приводит к резкому (не соответствующему физике явления, см., например, [14]) возрастанию температуры материала в этих подобластях и, как следствие, ухудшению сходимости итераций, используемых для вычисления температуры (с уменьшением необходимого для сходимости временного шага).

Для сопоставления различных методов моделирования испарения исследованы границы спектра разностного оператора для таких методов.

Рассмотрены задачи в двумерном и трехмерном приближении (двумерное приближение рассматривается для получения качественных картин, основным является трехмерное).

Для иллюстрации на рис. 4 представлена часть двумерной расчетной области и разностной сетки в месте испарения материала проводника. Ось x направлена вертикально, y — горизонтально. С испарением ячеек меняются границы  G₁,  G₂,  G₁₂ и ₁₂.

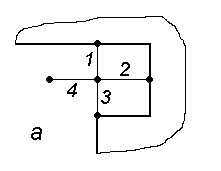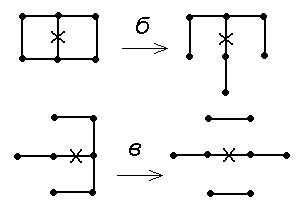Рис. 4. а — расчетная область после испарения материала двух ячеек (испарился материал двух ячеек с общим ребром 2, в задаче нет движения), б — изменение шаблонов разностной схемы для ребер 1 – 3 (преобразование шаблона разностной схемы для оператора (rot rot) c учетом условий div A = 0 на 12), в — изменение шаблона для ребра 4 (к виду шаблона для оператора (rot rot – grad div)). Ребра, для описания которых изменяются шаблоны разностной схемы, обозначены символом Х.

Исследована обусловленность матрицы М системы линейных алгебраических уравнений, получаемых при разностной аппроксимации уравнений Максвелла для различных способов моделирования испарения (см. таб. 1,2).

Расчеты проведены для следующих вариантов: 1 — в области нет кипения; 2 — испаряется материал двух крайних ячеек разностной сетки на границе якоря (в двумерном случае) или на ребре якоря (в трехмерном случае), вводится "фоновая" электропроводность ₀ = 10^-5 (обычно использовалось в расчетах) и ₀ = 10^-10 (вариант 2a), соответственно, при исходной >1; 3 — испаряется материал двух ячеек, и разностные схемы перестраиваются по предложенному алгоритму. Собственные значения приведены для задачи без движения (процессы кипения и испарения проходят в рассматриваемых случаях качественно сходно для различных скоростей движения, в трехмерном случае для моделирования рассматривался U-образный якорь [4 - 6]).


Таблица 1. Собственные значения матрицы M для различных способов моделирования испарения материала в двумерном случае

№ варианта	Наибольшее собственное значение	Наименьшее собственное значение	Число обусловленности
1	52.1784	1.6894·10-2	3.0885·103
2	52.1784	2.5875·10-6	2.0165·107
2a	52.1784	2.5875·10-11	2.0165·1012
3	52.1784	1.6398·10-2	3.1819·103

Таблица 2. Собственные значения матрицы M для различных способов моделирования испарения материала в трехмерном случае

№ варианта	Наибольшее собственное значение	Наименьшее собственное значение	Число обусловленности
1	20.457	5.331·10-5	3.837·105
2	20.457	6.906·10-9	2.963·109
3	20.457	5.326·10-5	3.840·105

Также приведены полученные при численном моделировании изотермы, демонстрирующие картину испарения материала (движения волны кипения) и картины перераспределения магнитного поля при испарении материала в задаче с перестроением разностных схем.

Из приведенных результатов видно, что перестроение разностных схем при испарении материала в двумерном и трехмерном случае позволяет улучшить обусловленность решаемой системы на много порядков. Отметим, что числа обусловленности определяются значением "фоновой" электропроводности. Чем она меньше, тем больше число обусловленности, стремящееся к бесконечности при стремлении "фоновой" величины к нулю. Улучшение обусловленности системы позволяет проводить расчет с большим шагом по времени. Таким образом, при исследовании процессов в ускорителях предпочтительной является модель с перестроением разностных схем и описателей границ при испарении материала в ячейках разностной сетки, относящихся к проводнику.

Преобразование разностной схемы позволяет избежать эффектов отнесения тепла к диэлектрику, выражающемуся в резком возрастании температуры и существенному ухудшению сходимости итераций при вычислении температуры.

Алгоритм обобщается на другие случаи изменения границ.

В [1, 4 - 6] исследовались способы построения единственного решения системы уравнений Максвелла в квазистационарном приближении в неоднородных областях с односвязной диэлектрической подобластью и связной границей ₁₂. Связность ₁₂ в случае многосвязной проводящей подобласти обеспечивает единственность решения (такие случаи исследовались в гл. 2).

Интерес представляет исследование единственности решения системы уравнений Максвелла в трехмерной области, в которой граница ₁₂ несвязна.

Согласно [1] решение системы уравнений Максвелла в квазистационарном приближении в проводнике единственным образом определяется граничными и начальными условиями.

Квазистационарность рассматриваемых полей может привести к неединственности поля E в диэлектрике, причем поле H определяется единственным образом во всей области [1].

Разработаны методы получения единственного квазистационарного решения системы уравнений Максвелла в трехмерной области с многосвязными диэлектрическими и проводящими подобластями. Приведен метод построения системы независимых векторов, представимых в виде градиента скалярной функции для случая m-связной границы ₁₂. Для двусвязной и трехсвязной областей построены векторы, определяющие подпространство, соответствующее ядру оператора квазистационарного приближения уравнений Максвелла. При этом использовалось представление разности решений уравнений Максвелла в виде градиента потенциала.

Показано совпадение в двусвязной области градиента потенциала с собственным вектором, соответствующим минимальному собственному значению матрицы М, полученным численными методами.

Для построения единственного решения системы с вырожденной матрицей целесообразно искать нормальное решение задачи, то есть решение, обладающее минимальной нормой. Это решение принадлежит пространству, ортогональному ядру оператора M.

Представлены алгоритмы получения нормального решения задачи, принадлежащего пространству, ортогональному ядру оператора задачи (в m-связной области), а именно: построены алгоритмы преобразования исходной системы уравнений (разностной схемы) к виду, дающему единственное нормальное решение задачи. Показана положительная определенность матриц преобразованных систем. Для получения одного из решений и последующего нахождения нормального построены простейший вид преобразования системы (с сохранением симметричности матрицы) и оператор, строящий проекцию полученного решения на подпространство, ортогональное ядру разностного оператора M. Предложенные алгоритмы можно применять для нахождения нормального решения и в других случаях вырожденной матрицы M. Алгоритмы решения системы уравнений Максвелла в многосвязной области, позволяющие получить единственное решение, доведены до программной реализации. Получены результаты расчета электромагнитных полей по построенным алгоритмам в областях с несвязными границами в нестационарном случае.

В четвертой главе рассмотрена задача численного моделирования квазистационарных электромагнитных полей в областях с негладкими границами проводящих и диэлектрических подобластей (см. [24]).

Построены алгоритмы позволяющие существенно сократить число шагов по времени и уменьшить число итераций, необходимое для получения решения.

Помимо учета многомерности другой важнейшей задачей в моделировании процессов в ускорителях является необходимость детального исследования полей в некоторых критических местах, где решение задачи имеет сингулярности различного рода. Например, это границы раздела подобластей с различными электрофизическими свойствами, на которых происходит скачок полей. Другой источник сингулярностей - движение проводников друг относительно друга. При этом возникает особенность типа скоростного скин - слоя. Третий источник - углы в рассматриваемой области, где также появляются особенности. При решении многих задач особые точки с различными источниками сингулярностей пространственно совмещены. Детальное описание решений в окрестности особых точек необходимо из - за того, что именно тут происходят различные сопутствующие явления: плавление, деформирование и т.п., определяющие, например, время жизни данного устройства.

Использование для расчета математической модели (2), содержащей уравнения различного типа в различных подобластях и уравнения с разрывными коэффициентами, может привести к появлению особенностей и ухудшению точности решения при численном моделировании. Показано, что для получения численного решения в рассматриваемых областях возможно использование алгоритмов, явным образом выделяющих особенность решения, или преобразование модели с учетом особенности.

В исследуемых в данной главе задачах распределение каждой из декартовых составляющих векторного потенциала в диэлектрических подобластях описывается уравнением Лапласа. Граничные условия для его решения в G₂ определяются значениями тангенциальных составляющих векторного потенциала на границе раздела проводящей и диэлектрической подобластей и условием равенства нулю дивергенции решения на границе (в пределе изнутри G₂).

Исследованию решений уравнений Лапласа и Пуассона в областях с угловыми точками посвящено большое количество работ российских и зарубежных исследователей. В этих работах основное внимание уделяется исследованию дифференциальных свойств решения в областях с угловыми и коническими точками и вблизи ребер области. Но исследуемые в большинстве работ уравнения не меняли свой тип в различных частях расчетной области. Для решения задач в указанных областях предложены различные способы, например, использование разностных схем с переменными коэффициентами вблизи особенности, построение решения в полярных координатах вблизи угловой точки и использование специальных операторов склейки для соединения с остальной областью. Однако такие методы значительно усложняют вид разностных схем, поскольку в рассматриваемых нами задачах граничные функции сами являются неизвестными, что в свою очередь усложняет выполнение каких-либо условий согласования вблизи угловой точки. Поэтому в данном исследовании предпочтение отдано однородным методам моделирования, позволяющим вести расчет во всей области по однотипным разностным уравнениям без специального выделения особенностей.

При решении задачи в двумерном приближении в [1] отмечалось отсутствие гладкости у y-составляющей векторного потенциала в диэлектрике при наличии движения в системе. В данной главе исследованы причины появления экстремумов, обусловленных наличием в модели конвективных слагаемых. Показаны способы их устранения.

При построении модели использовались векторный и скалярный потенциалы

(E= - DA/Dt + (v,)A + [u, rot A] + grad  = - DA/Dt + grad (v, A) +[w, rot A] + grad ).

При выборе кулоновской калибровки векторный потенциал А является решением задачи (2).

Исследовано влияние калибровки в записи математической модели и разностных эффектов (формы разностных операторов) на появление экстремумов, отражающих особенность решения.

Напряженность магнитного поля не изменится, если в (1) вместо нулевого взять любое согласующееся с граничными условиями для Е значение скалярного потенциала.

Показан вид потенциала ( = - (v,A)), при использовании которого (в данной задаче) конвективные слагаемые будут входить только в уравнения для A в рельсе.

Тогда поля описываются уравнениями:

4 (- DA/Dt +[w, rot A]) = rot rot A - () grad div A


или 4 (- DA/Dt ) = rot rot A в якоре; 4 (- DA/Dt - [v, rot A]) = rot rot A в рельсе

(здесь w = u - v, w = 0 в движущейся части).

Модель с измененной калибровкой позволяет увеличить шаг по времени, необходимый для выполнения условий сходимости итераций с учетом конвективных слагаемых в двух- и трехмерном случаях. После проведения преобразований модель остается однородной по пространству.

Показано, что в связи с резким изменением магнитного поля при переходе через границу проводника и диэлектрика разностная схема для модели с преобразованной калибровкой лучше аппроксимирует решение на границе якоря (по сравнению с моделью с кулоновской калибровкой).

При недостижимости заданной точности за определенное число итераций шаг по времени приходится уменьшать [1]. Условия прекращения итераций, как правило, выполняются при малом шаге. Преобразование математической модели делает возможным достижение необходимой точности с большим шагом по времени.

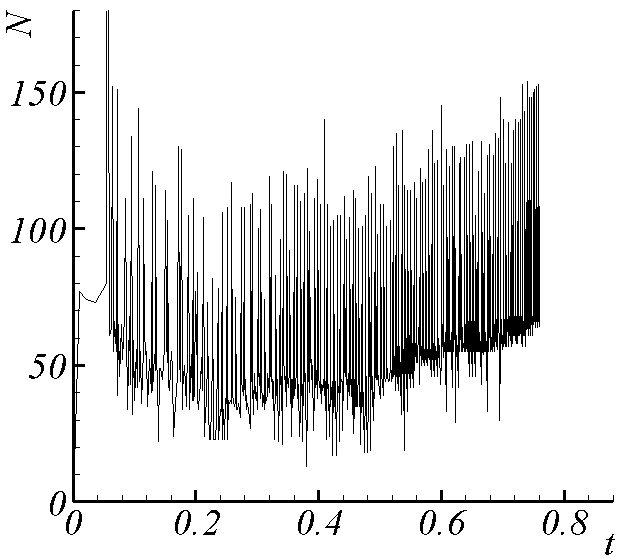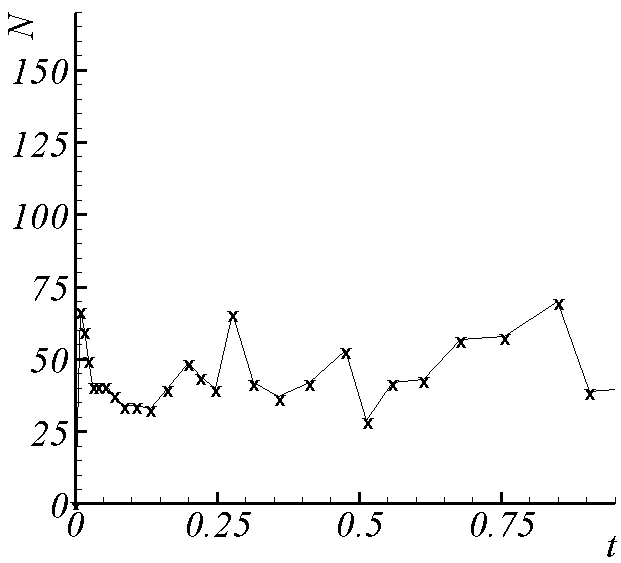Рис. 5.Суммарное количество итераций.
Калибровка  = 0.	Калибровка  = -(v,A).

Проведено сравнение числа итераций для различных способов моделирования в двумерном и трехмерном случае. На рис. 5 приведен пример полученной в расчете зависимости суммарного количества итераций (внешних и внутренних) от времени для двух вариантов калибровки с  = 0 и с  = -(v,A) для двумерного случая.

В трехмерном случае рассмотрены два варианта конфигурации канала ускорителя, и получены качественно сходные с рис. 5 зависимости суммарного количества итераций от времени. В двух- и трехмерном случаях суммарное количество итераций, необходимых для получения решения, существенно сокращается при изменении модели - это позволяет получать разностное решение на данном временном слое за меньшее в несколько раз число шагов по времени.

При явном выделении особенности использована возможность выделения сингулярной части решения в явном виде [15].

Решение представлено в виде суммы негладкой (выделяющей особенность и обозначенной через A₀) и гладкой (A*) частей A= A₀ + A₀*. При таком задании A₀ выполняются требования: div A₀ = 0 и rot A₀ = 0 в диэлектрической подобласти. Получено решение с устраненными экстремумами вблизи угловой точки.

Отметим, что явное выделение особенности решения позволяет стабилизировать число внутренних итераций, но не изменяет способа учета конвективных слагаемых при решении системы линейных алгебраических уравнений и вследствие этого не может существенно увеличить шаг по времени, необходимый для сходимости внешних итераций.

Работы 2003 – 2007 годов поддержаны грантами Российского фонда фундаментальных исследований (проекты РФФИ № 03 – 01 – 00461 и РФФИ № 06 – 01 – 00421) и Фонда содействия отечественной науке, а также грантами в рамках Программы № 3 ОМН РАН (проект № 3.2).

В заключении приведены основные результаты диссертации, а именно:


- разработаны методы математического моделирования квазистационарных электромагнитных полей в неоднородных областях канала ускорителя (в том числе с изменяющимися во времени, несвязными и негладкими границами подобластей);

- построены и программно реализованы вычислительные алгоритмы для моделирования процесса электромагнитного ускорения в указанных областях;

- методами вычислительного эксперимента проведено исследование эрозии металлического контакта, а также качественных особенностей распределений электромагнитных полей в канале ускорителя в процессе разгона.


Цитируемая литература:


1. М. П. Галанин, Ю. П. Попов. Квазистационарные электромагнитные поля в неоднородных средах: Математическое моделирование. М.: Наука, 1995. 320 с.

2. Материалы I Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле (Новосибирск, 10 – 13 апреля 1990 г.). / Под ред. М. Ф. Жукова Новосибирск: Изд. ИТ СО АН СССР, 1990. 350 с.

3. Материалы II Всесоюзного семинара по динамике сильноточного дугового разряда в магнитном поле (Новосибирск, 4 – 6 декабря 1991 г.). / Под ред. В. Е. Накорякова Новосибирск: Изд. ИТ СО РАН. 1992. 367 с.

4. М. П. Галанин, А. П. Лотоцкий, Ю. П. Попов, С. С. Храмцовский. Численное моделирование пространственно трехмерных явлений при электромагнитном ускорении проводящих макротел // Математическое моделирование. 1999. Т. 11, № 8. С.c. 3 – 22.

5. М. П. Галанин. Компьютерное моделирование в задачах конвертирования электромагнитной и кинетической энергии. Задачи и модели. // Информационные технологии и вычислительные системы. 2002. № 4. С.c. 109 - 123.

6. М. П. Галанин. Компьютерное моделирование в задачах конвертирования электромагнитной и кинетической энергии. Решение задач. // Информационные технологии и вычислительные системы. 2003. № 1 – 2. С.c. 112 - 127.

7. А. А. Самарский, В. Ф. Тишкин, А. П. Фаворский, М. Ю. Шашков. Операторные разностные схемы // ДУ. 1981. Т. 17. № 7. С.c. 1317 - 1327.

8. М. В. Дмитриева, А. А. Иванов, В. Ф. Тишкин, А. П. Фаворский. Построение и исследование разностных схем для уравнений Максвелла в цилиндрической геометрии Препр. ИПМ им. М.В. Келдыша АН СССР. 1985. № 27. 22 с.

9. А. А. Самарский, Е. С. Николаев. Методы решения сеточных уравнений. М.: Наука, 1978. 592 с.

10. D. S. Kershaw. The incomplete Cholessky – Conjugate Gradient Method for the iterative solution of system of a linear equations // J. Comput. Phys. 1978. V. 26. P.p. 43 – 65.

11. А. Джордж, Дж. Лю. Численное решение больших разреженных систем уравнений. М.: Мир, 1984. 333 с.

12. Ю. И. Беляков, А. П. Лотоцкий, В. В. Савичев, Ю. А. Халимуллин. Исследование эрозии металлических контактов в рельсотронном ускорителе // Вестник МГТУ им. Н. Э. Баумана. Сер. Естественные науки. 1999. № 2. С.с. 46 – 60.

13. М. П. Галанин, С. С. Храмцовский. Организация расчета трехмерных квазистационарных электромагнитных полей в областях со сложной геометрией проводников и диэлектриков // Препр. ИПМ им. М.В. Келдыша РАН. 1999. № 42. 18 с.

14. А. А. Самарский, Ю. П. Попов. Разностные методы решения задач газовой динамики. М: Едиториал УРСС. 2004. 424 с.

15. Е. А. Волков. О дифференциальных свойствах решений краевых задач для уравнений Лапласа и Пуассона в прямоугольнике // Тр. МИАН СССР.1965. Т. 77. С.c. 89 - 112.


Публикации автора по теме диссертации:


16. М. П. Галанин, А. П. Лотоцкий, С. С. Уразов. Математическое моделирование эрозии металлических контактов в рельсотронном ускорителе // Тезисы докладов Двенадцатой Международной конференции по вычислительной механике и современным прикладным программным системам, Владимир, 30 июня - 5 июля 2003 г. - М.: Изд-во МАИ. 2003. Т. 1. С.c. 184-185.

17. М. П. Галанин, А. П. Лотоцкий, С. С. Уразов, Ю. А. Халимуллин. Математическое моделирование эрозии металлических контактов в рельсотронном ускорителе // Препр. ИПМ им. М.В. Келдыша РАН. 2003. № 79. 28 с.

18. М. П. Галанин, А. П. Лотоцкий, С. С. Уразов. Моделирование эрозии металлического контакта в ускорителе типа рельсотрон // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2004. № 4(15). С.с. 81 – 97.

19. М. П. Галанин, А. П. Лотоцкий, С. С. Уразов. Математическое моделирование в задачах конвертирования электромагнитнойи кинетической энергии // Тезисы докладов Международной конференции "Проблемы численного анализа и прикладной математики" Львов. 2004. С.с. 15-17.

20. М. П. Галанин, С. С. Уразов. Численное моделирование качественных особенностей распределений трехмерных полей в неоднородных подобластях электродинамического ускорителя // Препр. ИПМ им. М.В. Келдыша РАН. 2004. № 27. 30 с.

21. М. П. Галанин, А. П. Лотоцкий, Т. Г. Суфиев, С. С. Уразов. Математическое моделирование процессов в электродинамических импульсных системах // Научная сессия МИФИ – 2005. Сборник научных трудов. ”Физико-технические проблемы нетрадиционной энергетики и мощная импульсная электрофизика”. 2005. Т.8. С.c. 40-41.

22. М. П. Галанин, С. С. Уразов. Математическое моделирование электромагнитных и тепловых полей в многосвязных областях и областях с изменяющимися во времени границами // Препр. ИПМ им. М.В. Келдыша РАН. 2005. № 137. 32 с.

23. М. П. Галанин, Ю. П. Попов, С. С. Уразов. Математическое моделирование многомерных квазистационарных электромагнитных полей в канале электродинамического ускорителя // Тезисы докладов Международной конференции "Тихонов и современная математика", Москва, 19 - 25 июня 2006 г. - М.: Изд-во ВМ и К МГУ им. М.В. Ломоносова. 2006. С. 63.

24. М. П. Галанин, С. С. Уразов. Методы численного моделирования квазистационарных электромагнитных полей в областях с негладкими границами проводящих и диэлектрических подобластей // Препр. ИПМ им. М.В. Келдыша РАН. 2006. №. 83. 27 с.

25. М. П. Галанин, Ю. П. Попов, С. С. Уразов. Математическое моделирование электромагнитных и тепловых полей в многосвязных областях и областях с изменяющимися во времени границами // Мат. моделирование. 2007. Т. 19. № 4. С.с. 3-18.

26. М.П. Галанин, А.П. Лотоцкий, С.С. Уразов. Исследование теплового режима высокоскоростного электрического контакта методами математического моделирования // Инженерно-физический журнал. 2007. Т.80. № 3. С.с. 169 – 176.