Основная образовательная программа высшего профессионального образования Направление подготовки
| Вид материала | Основная образовательная программа |
- Основная образовательная программа высшего профессионального образования Направление, 65.34kb.
- Основная образовательная программа высшего профессионального образования направление, 721.26kb.
- Основная образовательная программа высшего профессионального образования направление, 5151.75kb.
- Основная образовательная программа высшего профессионального образования Направление, 1316.69kb.
- Основная образовательная программа высшего профессионального образования Направление, 3764.91kb.
- Основная образовательная программа высшего профессионального образования Направление, 3396.78kb.
- Основная образовательная программа высшего профессионального образования Направление, 501.83kb.
- Основная образовательная программа высшего профессионального образования Направление, 636.13kb.
- Основная образовательная программа высшего профессионального образования Направление, 506.79kb.
- Основная образовательная программа высшего профессионального образования Направление, 639.3kb.
Раздел 2. Резолюции. Резольвента, метод резолюций. SLD-вывод, опровержение. Теорема о корректности метода резолюций.
Раздел 3. Модели Эрбрана. Интерпретация Эрбрана. Модель Эрбрана. Существование модели Эрбрана для выполнимого множества предложений.
Раздел 4. Наименьшая модель Эрбрана. Теорема Тарского. Оператор непосредственного следствия. Теорема о наименьшей модели Эрбрана.
Раздел 5. Полнота метода резолюций. Лемма о mgu. Лемма о подъеме. Решение программы. Теорема о множестве решений программы. Теорема о полноте резолюций.
Раздел 6. Алгоритмические свойства наименьшей модели Эрбрана. Рекурсивная перечислимость наименьшей модели Эрбрана. Теорема о вычислимости ч.р.ф., ее следствие.
Раздел 7. Проблема отрицания. Различные способы определения правил для вывода негативной информации. Правила CWA и отрицание как неуспех.
Раздел 8. Язык и семантика темпоральной логики программ. Язык и семантика пропозициональной темпоральной логики. Примеры общезначимых формул.
Раздел 9. Исчисление темпоральной логики программ. Исчисление, теорема о корректности. Теоремы о дедукции и слабой полноте. Отсутствие сильной полноты.
Наименование курса:
- ДЕНОТАЦИОННАЯ СЕМАНТИКА
1. Бестиповое λ-исчисление. Синтаксис. λ–Термы. Подтермы. Вхождение подтерма в терм. Множество свободных переменных терма. Свободные и связанные вхождения переменных, а также области действия для λ. α–Эквивалентность λ–термов. Терм свободный для подстановки. Операция подстановки терма в терм вместо всех свободных вхождений переменной. Свойства подстановки. β–Редукции. Редексы. Нормальные формы. Нормализуемые термы. Теорема Чёрча-Россера (доказательство через параллельные редукции и их свойства). Единственность нормальной формы. β–Эквивалентность и ее свойствами.
2. λ-Исчисление как язык программирования. Натуральные числа Чёрча и определение представимых функций. Представимость любых всюду определенных рекурсивных функций. Термы True, False, Cond и их свойства. Свойства терма IsNull. Кодировка пар: термы First, Second, Pair и их свойства. Отнимание 1 в λ–исчислении. Теорема о неподвижной точке. Представимость простейших функций. Представимость композиции. Представимость примитивной рекурсии. Представимость μ–оператора. Неразрешимость проблемы существования нормальной формы для термов.
3. Типизированное λ–исчисление. Простые и составные типы. Правила приписывания типов. Типизируемые термы. Теорема о нормализации типизируемых термов (без доказательства).
4. Семантика Скотта для бестипового λ-исчисления. Направленные множества, Полные частично упорядоченные множества (пчум). Топология Скотта. Критерий непрерывности в топологии Скотта. Монотонность непрерывных отображений. Декартовым произведением семейств пчум. Пчум всех непрерывных отображений полных чум. Теорема о непрерывности функций от двух аргументов. Теорема о непрерывности аппликации. Теорема о непрерывности λ–абстракции. Проекция полных чумов. Ретракты и ретракции. Свойства проекций полных чумов. Перенесение проекций с полных чум на пчумы их непрерывных отображений. Определение пчум D∞. Определение отображений Φmn и их свойства. Определение операции · на D∞, ее непрерывность, связь с операцией применения (аппликации) на Dn+1×Dn. Связь операции · и упорядочения. Теорема о функциональной полноте
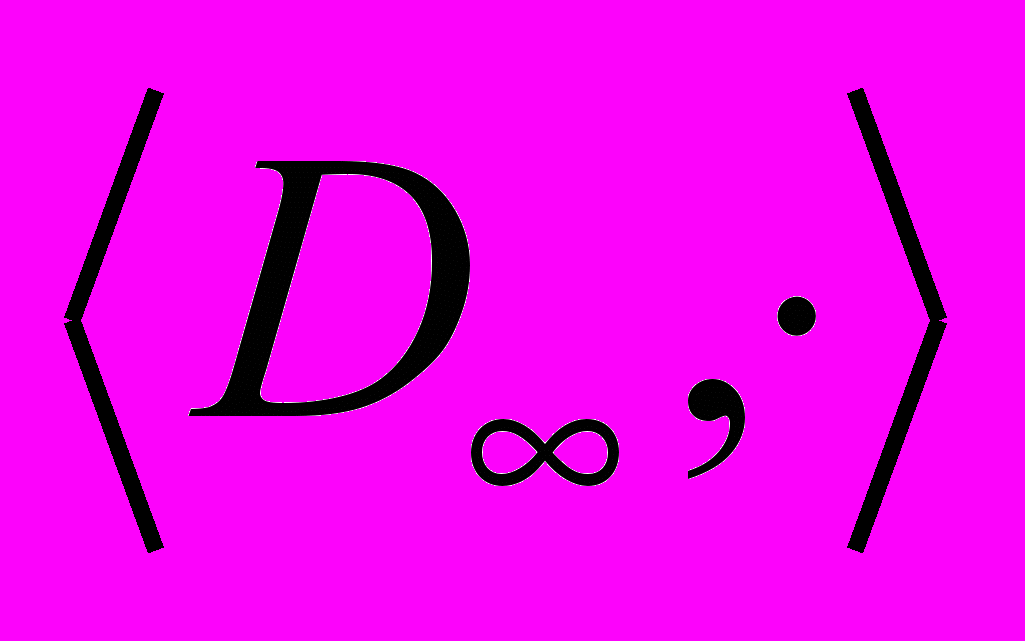. Изоморфизм и гомеоморфизм упорядоченных множеств D∞ и [D∞→ D∞]. Представление непрерывных функций на 
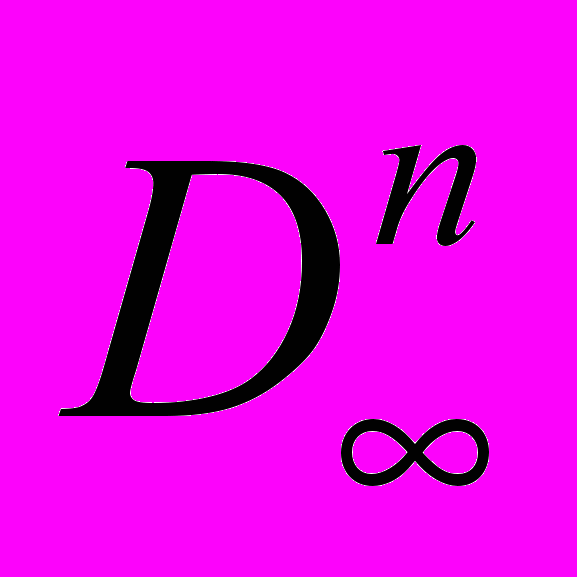с помощью операции ·. Определение семантики Скотта для λ–термов. Теорема о связи β–эквивалентности и семантики Скотта.5. Графиковая модель λ–исчисления. Определение графиковой модели, ее отличие от модели Скотта.
Наименование курса:
- ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1. Введение. Особенности компьютерных вычислений. Обратная устойчивость. Гарантированная оценка точности.
2.1 Системы с квадратной матрицей, число обусловленности, определитель, упрощение с помощью ортогональных преобразований. Решение систем
2.2 Решение систем полного ранга. Метод регуляризации
3.1 Особенности спектра симметричных матриц. Теорема Штурма, последовательности Штурма
3.2 Вычисление собственных значений симметричных матриц. Примеры
3.3 Двусторонние последовательности Штурма и собственные векторы симметричных матриц.
3.4 Примеры: собственные функции оператора Лапласа, полиномы Лежандра и др.
4.1 Теорема Шура. Уравнение Сильвестра
4.2 Эпсилон-спектр, примеры, критерий отсутствия спектра на кривой.
4.3 Обобщенные уравнения Ляпунова
4.4 Задача дихотомии спектра, проекторы на инвариантные подпространства.
4.5 Дихотомия окружностью
4.6 Линейная дихотомия, эллиптическая дихотомия.
4.7 Одномерные спектральные портреты и канонический вид матриц.
4.8 Разложение полинома на множители
Наименование курса:
- ИСТОРИЯ МАТЕМАТИКИ
1. История Российской академии наук.
2. Сибирское отделение Российской АН.
3. Новосибирский государственный университет.
4. Институт гидродинамики СО РАН.
5. Институт математики СО РАН.
6. История алгебры.
7. История геометрии.
8. История математического анализа.
9. История кибернетики.
10. История математической экономики.
11. История дискретной математики.
12. История комбинаторики.
13. История теории вероятностей.
14. История теории чисел
15. История криптографии.
16. История теоремы Ферма.
17. История гипотезы Римана.
18. История гипотезы Пуанкаре.
ПРИЛОЖЕНИЕ 4.2
СОДЕРЖАНИЕ КУРСОВ ПРОФЕССИОНАЛЬНОГО ЦИКЛА ООП
Наименование курса:
- МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Автор: профессор Э.Х. Гимади
1. Основные понятия и модели теории принятия решений.
Введение. Предмет "Исследование операций" (ИО) и основные понятия. Стадии опера-
ционного исследования. Математическое моделирование. Роль исследователя операций.
Типовые модели ИО. Алгоритмы и оценки их качества. Понятие о сложности задач дис-
кретной оптимизации.
2. Многошаговые модели и динамическое программирование (ДП).
Вывод основных рекуррентных соотношений ДП. Принцип оптимальности Беллма-
на. Алгоритм ДП с одним прямым и одним обратным ходом. Релаксационный алгоритм.
Сравнение с полным перебором. Задача о ранце. Связь прямой и обратной задач о ран-
це. Задача альтернатив- ного выбора. Задачи о "ближайшем соседе". Задача Вентцель о
распределении ресурсов между отраслями. Вычислительные трудности для многомерной
задачи.
3. Линейные оптимизационные модели.
Задача об оптимальном рационе. Стандартная задача линейного программирования
(ЗЛП). Двойственность в ЛП: прямая и двойственная задачи ЛП, теоремы двойственно-
сти, экономическая интерпретация. Задачи транспортного типа. Задача об оптимальном
назначении. Многоиндексная задача о назначениях (аксиальная и планарная). Блочные
задачи. Двухэтапная задача линейного стохастического программирования.
4. Элементы теории матричных игр.
Основные понятия теории игр. Матричная игра. Принцип минимакса. Седловая точка.
Смешанные стратегии. Основная теорема матричных игр. Методы решения матричных
игр. Доминирование. Игра 2х2, игры 2хn и mх2. Игры mхn. Итеративный метод Брауна-
Робинсон. Сведение решения матричной игры к задаче ЛП.
5. Сетевое планирование и управление.
Графы. Представление комплекса операций (проекта) в виде сетевой модели (СМ).
Параметры и алгоритмы анализа СМ. Алгоритмы сортировки чисел. Алгоритм обнару-
жения контуров и вычисления рангов вершин СМ. Задача календарного планирования с
ограничениями на ресурсы и директивные сроки. Полиномиальный точный алгоритм в
случае складируемости ограниченных ресурсов. Стохастическая СМ.
6. Задачи теории расписаний.
Задачи с одним рабочим местом. Задача Джонсона с двумя станками. Достаточные
условия сводимости задачи Джонсона с тремя станками к случаю двух станков. Приме-
нение метода компактного суммирования векторов к задаче Джонсона. Задача Акерса-
Фридмена. Задача упаковки в контейнеры и в полосу. Приближенные алгоритмы с гаран-
тированными оценками (NF, FF, BF). Асимптотически точный подход к решению.
7. Модели управления запасами.
Задача об оптимальном объеме партии и периоде поставок в случае детерминированно-
го стационарного спроса. Нестационарный спрос. Вероятностный спрос. Управление мно-
гономенклатурными запасами.
8. Модели замены оборудования.
Аналитические модели при детерминированном спросе. Приведение затрат к текуще-
му моменту. Теорема об оптимальном периоде замены. Применение ДП к задаче замены
оборудования.
9. Метод динамики средних.
Моделирование операций по схеме марковских случайных процессов. Уравнения Кол-
могорова. Метод динамики средних. Модель Хищник-жертва.
10. Экстремальные задачи на графах.
Задача о кратчайших путях. Задача о кратчайшей связывающей сети. Метод ветвей и
границ (МВГ) и применение его к задаче коммивояжера. Условия асимптотической точ-
ности алгоритма "Иди в ближайший непройденный город". Приближенный алгоритм с
использованием решения задачи о назначении.
11. Потоковые модели.
Задачи о потоке максимальной мощности в сети и о потоке минимальной стоимости.
Временная сложность алгоритмов решения потоковых задач. Задача о погашении взаим-
ных долгов между предриятиями. Задача о проведении целесообразных финансовых и
товарообменных операциях с учетом фактора кредитования. Задача о проведении расче-
тов между банками.
12. Задачи размещения и стандартизации.
Постановки задач. Полиномиально разрешимые случаи. Сведение к модели ближай-
шего соседа в случае связных и квазивыпуклых матриц. Приближенные полиномиальные
алгоритмы. Прямо-двойственный жадный алгоритм. Применение МВГ. Асимптотически
точный подход.
Наименование курса:
- ДИСКРЕТНЫЕ ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ
Автор: доцент А.В. Кононов
1.1. Введение. Примеры задач комбинаторной оптимизации. Понятие алгоритма. Алгоритм перебора с возвратом. Время работы алгоритма. Полиномиальный алгоритм. Алгоритм сортировки слиянием.
1.2. Графы и орграфы. Основные понятия. Вершинное покрытие, независимое множество, клика. Цепи и циклы. Критерий связности. Деревья и леса. Характеризация деревьев. Разрезы. Лемма Минти. Сильно связные орграфы. Топологический порядок.
1.3. Алгоритмы сканирования и обхода. Алгоритм сканирования графа. Алгебраические представления графов. Матрица инцидентности. Матрица смежности. Лист смежности. Поиск в глубину. Поиск в ширину. Эйлеров граф. Алгоритм Эйлера. Теорема Кенига.
1.4. Остовные деревья. Задача «Минимальное остовное дерево». Задача «Максимальный взвешенный лес». Эквивалентность задач. Алгоритм Краскала. Алгоритм Прима. Задача «Максимальный взвешенный ориентированный лес». Задача «Минимальное остовное ориентированное дерево». Задача «Минимальное остовное корневое ориентированное дерево». Ориентированный лес и циклы. Алгоритм Эдмондса.
1.5. Решение задач по темам: Графы и орграфы, Алгоритмы сканирования и обхода, Остовные деревья.
1.6. Кратчайшие пути. Задача «Кратчайший путь». Принцип оптимальности Белмана. Алгоритм Дейкстры. Алгоритм Мура-Беллмана-Форда. Допустимый потенциал. Задача «Все Пары Кратчайших путей». Алгоритм Флойда-Уоршелла. Задача «Минимальный усредненный Цикл». Теорема Карпа.
1.7. Потоки в сетях. Задача «Максимальный Поток». Остаточный граф. Увеличивающий путь. Алгоритм Форда-Фалкерсона. Характеризация максимального потока. Теорема о максимальном потоке и минимальном разрезе. Теорема о Декомпозиции Потока.
1.8. Потоки в сетях. Первая Теорема Менгера. Вторая Теорема Менгера. Характеризация k-связных графов. Задача «Ориентированные реберно-непересекающиеся пути». Алгоритм Эдмондса-Карпа. Алгоритм Проталкивания Предпотока. Алгоритм Голдберга-Тарьяна.
1.9. Паросочетания в двудольных графах. Задача «Максимальное Паросочетание». Теорема Холла. Теорема Фробениуса о бракосочетаниях. Паросочетание и увеличивающий путь. Матрица Татта. Вероятностный алгоритм Ловаша.
1.10. Решение задач по темам: Кратчайшие пути, Потоки в сетях, Паросочетания в двудольных графах.
1.11. Паросочетания в произвольных графах. Фактор-критические графы. Условие Татта. Теорема Татта. Формула Бержа-Татта. Нечетная декомпозиция. Характеризация фактор-критических графов.
1.12. M-чередующаяся декомпозиция. Алгоритм построения M-чередующейся декомпозиции. Нечетные циклы. Цветки. Лемма о стягивании цветков. Чередующийся лес.
1.13. Алгоритм построения паросочетания в произвольном графе. Процедура «Прирост». Процедура «Увеличение». Процедура «Стягивание». Цветочный лес. Алгоритм Эдмондса построения паросочетания.
1.14. Матроиды. Независимая система. Циклы, базы, ранг, замыкание. Задача «Максимизация независимой системы». Задача «Минимизация независимой системы». Понятие матроид. Примеры матроидов. Теорема Эдмондса-Радо.
1.15. Решение задач по темам: Паросочетания в произвольных графах, M-чередующаяся декомпозиция, Алгоритм построения паросочетания в произвольном графе, Матроиды.
2.1. NP-полнота. Алфавит. Язык. Машина Тьюринга. Тезис Черча. Задачи распознования. Класс P. Класс NP. Рандомизированный алгоритм. Недетерминированный алгоритм.
2.2. NP-полнота. Полиномиальная сводимость. Задача «Выполнимость». Теорема Кука. Задача «3-Выполнимость».
2.3. NP-полнота. Основные NP-полные задачи. Задача «Независимое множество». Задача «Вершинное покрытие». Задача «Клика». Задача «Гамильтонов цикл». Задача «Разбиение». Задача «3-Разбиение»
2.4. Решение задач по теме NP-полнота.
3.1. Приближенные алгоритмы. Задача оптимизации. NP-трудные задачи. Подходы к решению NP-трудных задач. Приближенный алгоритм. Полиномиальная приближенная схема. Вполне полиномиальная приближенная схема. 2-приближенный алгоритмом для задачи «Вершинное покрытие наименьшей мощности».
3.2. Комбинаторные приближенные алгоритмы. Задача «Покрытие». Алгоритм Хватала. Задача «Вершинное покрытие». Уровневый алгоритм для задачи «Вершинное покрытие». Задача «Кратчайшая суперстрока». Алгоритм Ли.
3.3. Комбинаторные приближенные алгоритмы. Задачи с метрикой. Задача Штейнера. Метрическая задача Штейнера. Алгоритм MST. Задача Коммивояжера. Неаппроксимируемость задачи Коммивояжера. Метрическая задача Коммивояжера. Алгоритм Кристофидиса-Сердюкова. Метрическая задача o k центрах. Алгоритм Хошбаум-Шмойса для задачи o k центрах.
3.4. Комбинаторные приближенные алгоритмы. Метрическая задача o звешенных k центрах. Алгоритм Хошбаум-Шмойса для задачи o взвешенных k центрах. 4-приближенный алгоритм для задачи «Кратчайшая суперстрока».
3.5. Решение задач по теме Комбинаторные приближенные алгоритмы.
3.6. Приближенные схемы. Подходы к построению приближенных схем. Упрощение исходного примера. Разбиение пространства решений. Структурирование работы точного алгоритма. Приближенные схемы для задачи минимизации длины расписания работ на двух параллельных машинах.
3.7. Приближенные схемы. Задача oб упаковке. Алгоритм «Первый подходящий». Неаппроксимируемость задачи об упаковке.
Асимптотическая приближенная схема. Алгоритм Фернандес де ла Вега-Луекера. Задача минимизации длины расписания работ на параллельных машинах. Алгоритм Грэхэма. Приближенные схемы для задачи минимизации длины расписания работ на параллельных машинах.
3.8. Приближенные схемы. Цеховые задачи теории расписаний. Полиномиальная приближенная схема для цеховой задачи открытого типа.
3.9. Приближенные алгоритмы на основе линейного программирования. Задача линейного программирования. Задача минимизации длины расписания работ на параллельных разнородных машинах. Алгоритм Ленстры-Шмойса-Тардаш.
3.10. Приближенные алгоритмы на основе линейного программирования. Алгоритм «Округление ЛП-релаксации» для задачи «Покрытие». Прямая и двойственная задачи. Прямо-двойственный алгоритм для задачи «Покрытие». Задача «Максимальная выполнимость» Вероятностный алгоритм Джонсона. Дерандомизация. Алгоритм Гоеманса-Вильямсона.
3.11. Решение задач по теме. Приближенные схемы. Приближенные алгоритмы на основе линейного программирования.
Наименование курса:
- ДИСКРЕТНЫЙ АНАЛИЗ И КОМБИНАТОРИКА
Автор: профессор А.А. Евдокимов
1. Комбинаторика перечисления и кодирование.
Системы счисления и кодирование натуральных чисел. Задачи о нумерациях подмножеств конечного множества. Коды Грея. Нумерации объектов в порядке минимального изменения.
2. Комбинаторика слов.
Некоторые классические символьные последовательности и способы их задания.
Универсальные слова. Задачи восстановления символьных последовательностей по их фрагментам. Коды без перекрытий. Комбинаторная сложность слов. Псевдослучайные последовательности. Последовательности де Брейна и их число. Графы перекрытия подслов символьных последовательностей. Задачи быстрой сборки слов. Алгоритмы сборки. Аддитивная сложность символьных последовательностей и ее связь с задачами быстрого умножения и вычисления полиномов. Оценки аддитивной сложности индивидуальных последовательностей.
3. Кодирование структурированной информации и вложения дискретных пространств.
Понятия близости, расстояния, метрики. Структуры метрических пространств на множествах подмножеств, словах, символьных последовательностях. Реализация метрик графами.
Гиперкубовая архитектура вычислительных систем. Графы гиперкубов. Кодирования как вложения дискретных объектов в гиперкубы. Изоморфные и изометрические вложения. Вложения с растяжением ребер. Миноры графов. Алгоритмы построения вложений графов в гиперкубы.
Применение методов и алгоритмов вложения. Локально изометрическое кодирование табло. Сеточные графы вычислительных структур. Систолические вычисления. Вложения деревьев. Суффиксные деревья. Префиксные коды.
4. Булевы функции и дискретные модели генных сетей.
Булевы функции, их число, способы задания. Представление формулами. Нормальные формы. Единственность совершенной и сокращённой форм. Представления многочленами Жегалкина. Полнота систем булевых функций. Теорема Поста. K-значные логические функции. Схемы из функциональных элементов. Конечные автоматы.
Ориентированные графы и сети. Достижимость вершин. Алгоритмы нахождения внутренне и внешне устойчивых множеств. Базы и ядра. Алгоритм построения разрезов циклов. Булевы методы в задачах теории графов. Логические производящие функции. Диаметр, радиус и центр в орграфах и алгоритмы их нахождения. Простые дискретные модели генных сетей. Анализ функционирования регуляторного контура генной сети
Наименование курса:
- ТЕОРИЯ ОПТИМАЛЬНЫХ ПРОЦЕССОВ
Авторы: профессор В.М. Александров, доцент А.А. Ломов, к.ф.-м.н. А.А. Коробов
I. Принцип максимума в теории оптимальных процессов
Понятие об управляемых системах. Уравнения движения объекта. Вариационная задача управления. Допустимые управления. Формулировка основной задачи. Видоизменения и обобщения основной вариационной задачи. Принцип максимума как необходимое условие оптимальности. Сопряженная система. Постоянство функции Понтрягина. Необходимое условие (принцип максимума) для задачи быстродействия. Задача синтеза оптимального управления. Синтез оптимального управления в случае комплексно-сопряженных корней. Обсуждение принципа максимума.
II. Другие задачи оптимального управления
Задача с подвижными концами. Условия трансверсальности. Примеры решения задач с подвижными концами. Принцип максимума для неавтономных систем. Неавтономная оптимальная задача с подвижными концами. Задача оптимального быстродействия для неавтономных систем. Задачи с закрепленным временем для автономных и неавтономных систем. Задача терминального управления.
III. Вариационное исчисление и оптимальное управление
Уравнение Эйлера-Лагранжа и другие необходимые условия локального минимума. Сильный и слабый локальный минимум. Обобщенное уравнение Эйлера-Лагранжа. Интегральная форма уравнений Эйлера- Лагранжа. Разрывы и условия скачка. Условия Вейерштрасса-Эрдмана для точек излома. Условия Лежандра-Клебша . Условие Вейерштрасса. Вариация граничных точек (условия трансверсальности). Ограничения в форме равенств и множители Лагранжа. Задачи с ограничениями в форме неравенств (метод функций штрафа, метод Валентайна). Связь вариационного исчисления с принципом максимума Понтрягина.
IV. Линейные оптимальные быстродействия
Формулировка задачи. Принцип максимума — необходимое и достаточное условие оптимальности. Условие общности положения. О системах, не удовлетворяющих условию общности положения. Свойства выпуклых множеств. Теоремы о числе переключений. Теоремы единственности. Теоремы существования оптимального управления. Особые оптимальные управления. Доказательство принципа максимума.
V. Управляемость динамических систем
Управляемость и наблюдаемость динамических систем: условие полной управляемости автономных и неавтономных систем. Связь и различие условия полной управляемости с условием общности положения. Область достижимости. Наблюдаемость. Особые и вырожденные задачи оптимального управления. Количественные оценки управляемости и стабилизируемости.
Наименование курса:
- ТЕОРИЯ ГРАФОВ
Автор: к.ф.-м.н. А.Н. Глебов
- Основные определения и обозначения, связанные с графами, орграфами и мультиграфами.
- Способы задания графов. Матрицы смежности и инцидентности, их свойства. Связь между матрицей смежности и числом маршрутов заданной длины.
- Графы пересечений множеств. Представление произвольного графа в виде графа пересечений.
- Степенные последовательности графов, мультиграфов и псевдографов, их характеризация.
- Двудольные графы. Критерий двудольности графа. Однозначность разбиения связного графа на доли.
- Экстремальные по числу ребер графы. Экстремальные графы без треугольников. Теорема Турана и граф Турана.
- Леса и деревья. Теорема о характеризации деревьев. Корневые и остовные деревья.
- Вершинная и реберная древесность графов. Теорема Нэш-Уильямса о реберной древесности. Понятие линейной древесности.
- Перечисление и кодирование деревьев. Код Прюффера. Теорема Кэли о числе помеченных деревьев.
- Проблема изоморфизма графов. Гипотеза Улама. Полные системы инвариантов для деревьев.
- Вершинная и реберная k-связность графов, числа вершинной и реберной связности, их свойства.
- Точки сочленения, мосты и блоки графа. Теорема о характеризации вершинно двусвязных графов. Взаимное расположение двух блоков в графе. Дерево блоков и точек сочленения.
- Сети и потоки в сетях. Задача о максимальном потоке. Остаточные сети, дополняющие пути и разрезы. Теорема Форда-Фалкерсона о максимальном потоке и минимальном разрезе.
- Наборы непересекающихся цепей, соединяющих два подмножества вершин графа (орграфа). Вершинная и реберная теоремы Менгера. Критерии вершинной и реберной k-связности графа (теоремы Уитни).
- Обходы графов. Гамильтоновы циклы и цепи. Простейшие необходимые условия гамильтоновости графа. Достаточные условия: теоремы Оре и Дирака. Задача коммивояжера.
- Эйлеровы циклы и цепи. Критерий эйлеровости графа. Алгоритм Флери.
- Независимые множества вершин и ребер графа. Вершинные и реберные покрытия, факторы и паросочетания. Числовые параметры, связанные с независимостью и покрытиями, их свойства. Теорема Галлаи.
- Наибольшие паросочетания и чередующиеся цепи. Характеризация наибольших паросочетаний в терминах чередующиеся цепей.
- Паросочетания, покрывающие долю двудольного графа. Связь с системами различных представителей. Теоремы Холла, Кенига-Холла и Кенига-Оре.
- Теоремы Кенига о числе реберной независимости двудольного графа и (0,1)-матрицах. Связь между задачами о наибольшем паросочетании, о наименьшем вершинном покрытии и о максимальном потоке. Задача о назначениях.
- Критерий Татта существования 1-фактора в произвольном графе. Теоремы Петерсена о 2-факторах. Теоремы об 1-факторизуемости и 2-факторизуемости полных графов.
- Плоские и планарные графы. Грани плоского графа. Нормальные карты и эйлеровы многогранники.
- Формула Эйлера и ее следствия. Оценки для числа ребер планарных графов. Максимальные планарные графы, плоские триангуляции и четыреангуляции.
- Понятие k-вырожденного графа. Оценки для числа вырожденности планарных графов.
- Критерий планарности Понтрягина-Куратовского.
- Геометрическая двойственность плоских графов. Двойственность платоновых многогранников.
- Укладки графов на двумерных поверхностях. Эйлерова характеристика поверхности. Род, крупность, толщина и число скрещиваний графа.
- Раскраски вершин графов, k-раскрашиваемые, k-хроматические и критические графы. Хроматическое числа графа, его простейшие оценки. Раскраска k-вырожденных графов. Теорема Брукса.
- Вершинные раскраски графов без треугольников. Графы Мцельского. Хроматическое число графа с большим обхватом.
- Совершенные графы. Теорема о дополнении совершенного графа (малая гипотеза Бержа). Теорема о характеризации совершенных графов (большая гипотеза Бержа). Хордальные графы, их характеризация и совершенство.
- Хроматические полиномы, их свойства. Нерешенные задачи, связанные с хроматическими полиномами.
- Раскраски планарных графов и карт. Теорема о четырех красках, ее эквивалентные формулировки: теорема Тейта и гипотеза Хадвигера.
- Доказательство теоремы о пяти красках. Достаточные условия Грецша и Грюнбаума 3-раскрашиваемости плоских графов.
- Раскраски графов, уложенных на двумерных поверхностях. Хроматическое число поверхности. Теорема Хивуда о раскраске карт.
- Раскраски ребер графов и мультиграфов. Понятие хроматического индекса. Теоремы Визинга и Шэннона, неулучшаемость их оценок. Хроматический индекс двудольного графа.
- Предписанные раскраски вершин и ребер графов. Связь между обычными и предписанными раскрасками. Оценка предписанного хроматического числа через число вырожденности графа.
- Предписанное хроматическое число полного двудольного графа. Критерий предписанной 2-раскрашиваемости.
- Теорема Томассена о предписанной 5-раскрашиваемости плоских графов.
- Предписанный хроматический индекс двудольного графа. Гипотеза о предписанном хроматическом индексе.
- Теорема Рамсея для множеств и графов. Оценки для чисел Рамсея. Обобщения чисел Рамсея.
- Вероятностные методы в теории графов. Моделирование случайных графов. Некоторые свойства "почти всех” графов.
Наименование курса:
- ГРАФЫ И АЛГОРИТМЫ
Автор: к.ф.-м.н. А.Н. Глебов
- История развития теории графов.
Возникновение понятия графа. Графы как модели при решении задач. Задача Эйлера о кенигсбергских мостах. Задача Гамильтона. Исследования деревьев Кирхгофом и Кэли. Мультиграфы, ориентированные графы и сети. Алгоритмы на графах и сетях. Современное состояние развития теории графов.
- Основные понятия. Классификация типов графов.
Основные определения и обозначения, связанные с графами, орграфами и мультиграфами. Способы задания графов. Матрицы смежности и инцидентности, их свойства. Изоморфизм графов. Двудольные графы. Критерий двудольности графа. Леса и деревья. Эквивалентные определения дерева. Корневые и остовные деревья. Бинарные деревья. Хранение и поиск информации в бинарных деревьях. Добавление и удаление элементов. Деревья, сбалансированные по высоте (AVL-деревья) и по весу. Точки сочленения, мосты и блоки графа. Вершинная и реберная связность. Характеризация двусвязных графов. Взаимное расположение двух блоков в графе. Дерево блоков и точек сочленения. Независимые множества вершин и ребер графа. Вершинные и реберные покрытия, факторы и паросочетания. Числовые параметры, связанные с независимостью и покрытиями, их свойства. Теорема Галлаи.
3. Простейшие алгоритмы на графах и сетях.
Поиск по графу в ширину и глубину. Дерево поиска. Связь поиска в ширину с нахождением кратчайших цепей. Модифицированный алгоритм поиска в глубину. Поиск блоков в связном графе. Нахождение минимального остова: алгоритмы Примы и Краскала. Кратчайшие пути во взвешенных орграфах. Алгоритмы Дейкстры и Флойда-Уоршелла. Сети и потоки в сетях. Задача о максимальном потоке. Остаточные сети, дополняющие пути и разрезы. Теорема и обобщенный алгоритм Форда-Фалкерсона. Анализ работы алгоритма в случае целых и рациональных пропускных способностей. Случай иррациональных пропускных способностей. Пример Форда и Фалкерсона. Метод кратчайших путей.
4. Связность и факторизации. Обходы графов.
Наборы непересекающихся цепей, соединяющих два подмножества вершин графа (орграфа). Вершинная и реберная теоремы Менгера. Критерии вершинной и реберной k-связности графов (теорема Уитни). Обходы графов. Эйлеровы и гамильтоновы графы. Теорема Эйлера и алгоритм Флери. Достаточные условия гамильтоновости. Теоремы Дирака и Оре. Гамильтоновы циклы и задача коммивояжера. Наибольшие паросочетания и чередующиеся цепи. Характеризация наибольших паросочетаний в терминах чередующиеся цепей. Паросочетания, покрывающие долю двудольного графа. Связь с системами различных представителей и теоремой Холла. Теоремы Кенига о числе реберной независимости двудольного графа и (0,1)-матрицах. Алгоритм поиска наибольшего паросочетания и наименьшего вершинного покрытия в двудольном графе. Задача о назначениях. Критерий Татта существования 1-фактора в произвольном графе. Теоремы Петерсена о 2-факторах.
5. Планарность и раскраски.
Плоские и планарные графы. Нормальные карты и эйлеровы многогранники. Формула Эйлера и ее следствия. Критерий планарности Понтрягина-Куратовского. Алгоритм укладки графа на плоскости. Понятие геометрически двойственного графа. Раскраски вершин графов. Простейшие оценки хроматического числа. Теорема Брукса. Хроматические полиномы, их свойства. Нерешенные задачи о хроматических полиномах. Раскраски планарных графов и карт. Теорема о четырех красках. Доказательство теоремы о пяти красках. Вопросы 3-раскрашиваемости планарных графов. Теоремы Грецша и Грюнбаума. Реберные раскраски графов и мультиграфов. Теоремы Визинга и Шэннона. Хроматический индекс двудольного графа. Интервальные раскраски. Связь с задачами теории расписаний. Предписанные раскраски. Теорема Томассена о предписанной 5-раскрашиваемости плоских графов.
6. Перечисление и кодирование графов. Вопросы алгоритмической сложности.
Перечисление и кодирование графов. Проблема изоморфизма. Кодирование деревьев. Код Прюфера. Теорема Кэли о числе помеченных деревьев. Классы труднорешаемых задач на графах. Классы P, NP и NPC. Связь между задачами “Клика” и “Выполнимость”. NP-полнота задач “Изоморфный подграф”, “Независимость’’, “Вершинное покрытие’’, “Гамильтонов цикл”, “Гамильтонова цепь”, “3-раскрашиваемость”.
Наименование курса:
- ТЕОРИЯ РАСПИСАНИЙ
Авторы: профессор С.В. Севостьянов, к.ф.-м.н И.Д. Черных
Введение
1. Что изучает теория расписаний?
2. Что значит «решить» оптимизационную задачу?
Глава 1. Модели и задачи теории расписаний
3. Теория расписаний и смежные дисциплины
4. Основные понятия и структурные элементы моделей ТР
5. Классификация задач ТР
Глава 2. Задачи календарного планирования
6. О моделировании сетевых ограничений
7. Унификация ресурсных ограничений
8. Алгоритмы построения «раннего» расписания выполнения работ проекта при разрешении/запрещении контуров в графе предшествований
Глава 3. Задача FLOW SHOP
9. Точное решение двухмашинной задачи Джонсона
10. Задача о «передислокации» и её связь с 2-машинной задачей Джонсона. Новый алгоритм решения задачи Джонсона.
11. NP-трудность 3-машинной задачи Джонсона. Сильная NP-трудность двухстадийной задачи Джонсона для трёх машин.
12. Разрешимые случаи 3-машинных задач Джонсона
12.1. Разрешимый случай Глебова
12.2. Разрешимый случай Серваха
13. Анализ перестановочных расписаний (пример Поттса-Шмойса-Вёгингера)
14. Анализ свойств оптимальных расписаний в задаче Джонсона с прерываниями операций
15. О 2-машинной задаче Джонсона с различными типами ограничений предшествования
Глава 4. Задача JOB SHOP
16. Разрешимые случаи задачи JOB SHOP
16.1. Задача JOB SHOP на двух машинах
16.2. Задача JOB SHOP для двух работ
17. Свойства оптимальных решений в задаче JOB SHOP с прерываниями операций
Глава 5. Задача OPEN SHOP
18. Разрешимые случаи задачи OPEN SHOP
18.1. Задача OPEN SHOP: две машины
18.2. Задача OPEN SHOP с прерываниями операций
19. Труднорешаемость задачи OPEN SHOP
20. Плотные расписания и жадные алгоритмы
21. Задача OPEN SHOP без задержек и простоев и задача об интервальной раскраске рёбер графа
Глава 6. Задача OPEN BLOCK
22. Модель обмена информацией в оптических сетях связи
23. Эффективная разрешимость 4-машинной задачи
24. NP-трудность 6-машинной задачи
25. Приближённый алгоритм с оценкой точности «корень из двух»
Глава 7. Задача на параллельных машинах с прерываниями и миграцией работ
26. Оценка числа миграций в оптимальном расписании
27. Точный (вещественный) барьер между трудными и лёгкими подзадачами
28. Линейный (1 +1/log_2 n)-приближающий алгоритм для случая двух машин
Глава 8. Многопараметрический анализ сложности задач
29. Параметрические семейства подзадач и базисные системы
30. Условия существования, единственности и конечности базисных систем
31. 4-параметрический анализ сложности задачи OPEN SHOP
32. 4-параметрический анализ сложности цеховых задач
Глава 9. Компьютерные доказательства теорем о локализации оптимумов
33. Склейка работ как универсальный приём
34. Метод ветвей и границ в доказательстве теорем
Приложения
35. Некоторые понятия дискретной математики
36. Некоторые понятия из теории сложности дискретных задач
37. Некоторые информационные структуры, используемые в алгоритмах решения дискретных задач
38. Алгоритм отыскания положительного назначения в дважды-стохастической матрице
Наименование курса:
- ДИСКРЕТНЫЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЙ
Авторы: профессор Ю.А. Кочетов, к.ф.-м.н. Е.В. Алексеева
1. Алгоритмы сортировки и их характеристики. Медианы и порядковые статистики, их нахождение за линейное время в среднем и худшем случаях. Сбалансированные деревья, свойства и правила построения.
2. Динамическое программирование на примере распределительной задачи. Обратная
задача и её свойства. Модель размещения капитала, верхняя оценка оптимума, свойство оптимального решения линейной релаксации, алгоритм округления дробного решения.
3. Классическая задача о рюкзаке, теорема об алгоритмах с гарантированной абсолютной
точностью. Жадные алгоритмы для классической задачи о рюкзаке, свойства LP-релаксации. Приближенные алгоритмы с гарантированной относительной точностью.
Аппроксимационные схемы, полиномиальные и полностью полиномиальные схемы для
задачи о рюкзаке. Замена оборудования. Алгоритм динамического программирования для конечного планового периода.
4. Задача упаковки в контейнеры. Алгоритмы NF, FF, BF, FFD и их свойства,
отрицательный результат об аппроксимируемости. Нижние оценки Martello и Toth.
Метод генерации столбцов для задачи упаковки в контейнеры. Задача двумерной упаковки, кодировки решений. Алгоритм имитации отжига.
5. Задача календарного планирования. Критические работы, пути и критическое время
проекта. Постановка задачи календарного планирования с ограниченными ресурсами. Т–поздние расписания. Алгоритм вычисления Т–поздних расписаний. Доказательство оптимальности Т*–позднего расписания. Алгоритм Гимади. Задачи календарного планирования с переменными длительностями работ.
6. Задача коммивояжера. Теорема о погрешности приближенных полиномиальных
алгоритмов и алгоритмов локального спуска. Задача коммивояжера с неравенством треугольника. Алгоритм с гарантированной оценкой точности 2. Доказательство оценки и ее неулучшаемости. Нижние оценки в задаче коммивояжера: примитивная оценка, оценка линейного программирования, оценка задачи о назначениях и минимальные 1-деревья.
Метод ветвей и границ для задачи коммивояжера.
7. Алгоритм решения задачи о назначениях.
8. Вычислительная сложность алгоритмов. Основные классы сложности. Сводимость задач по Карпу, по Тьюрингу.
9. Матроиды, жадный алгоритм для матроидов. Пересечение матроидов.
10. Задачи о покрытии. Жадный алгоритм. Теорема Хватала. Вероятностный жадный алгоритм. Алгоритм муравьиной колонии.
11. Задачи размещения. Математические модели вариантов задач размещения.
Генетический алгоритм.
12. Двухуровневые задачи размещения. Задачи размещения в условиях конкуренции.
Алгоритм локального спуска. «Безнадежный» пример. Задача о (r|p)-центроиде.
13. Рандомизированные алгоритмы. Классификация алгоритмов. Алгоритм Джонсона на
примере задачи MAX SAT. MAX-SAT в виде задачи целочисленного линейного программирования. LP-релаксация. Вероятностный алгоритм Джонсона. Оценка точности.
Алгоритм Гойманса и Уильямсона.
14. Теория игр. Чистые стратегии. Лемма о минимаксе и максимине. Необходимые и
достаточные условия равенства верхней и нижней цен игры в чистых стратегиях. Смешанные стратегии. Теорема Фон-Неймана для смешанных стратегий.
Что показывает «дилемма путешественников»?
Наименование курса:
- ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ
Автор: д.т.н. В.Б. Бериков
| | |
| 1 | Введение. Основные понятия. Стратегия природы. |
| 2 | Вероятность ошибки. Байесовская решающая функция. Разделяющая функция. |
| 3 | Таблица данных. Универсальность класса логических решающих функций. |
| 4 | Построение решающих функций в пространстве бинарных переменных. |
| 5 | Случай многих образов. Произвольные распределения. |
| 6 | Параметрический подход к построению решающих функций. Определение оценки плотности распределения. |
| 7 | Решающая функция при многомерных нормальных распределениях (равные матрицы ковариаций). Случай двух образов. |
| 8 | Решающая функция при многомерных нормальных распределениях (равные матрицы ковариаций). Случай многих образов. |
| 9 | Решающая функция при многомерных нормальных распределениях (неравные матрицы ковариаций). Случай двух образов. |
| 10 | Решающая функция при многомерных нормальных распределениях (неравные матрицы ковариаций). Случай многих образов. |
| 11 | Непараметрический подход к построению решающих функций. |
| 12 | Непараметрическая оценка многомерных плотностей. |
| 13 | Непараметрические методы построения решающих функций. |
| 14 | Метод «парзеновского окна». |
| 15 | Метод «ближайших соседей». |
| 16 | Построение решающих функций в заданном классе. |
| 17 | Дискриминант Фишера. |
| 18 | Алгоритм сокращения размерности пространства переменных. |
| 19 | Класс логических решающих функций от разнотипных переменных. |
| 20 | Оптимальная логическая решающая функция и универсальность класса. |
| 21 | Оптимальная выборочная логическая решающая функция. |
| 22 | Алгоритм LRP. |
| 23 | Алгоритм TEMP. |
| 24 | R-метод. |
| 25 | Проблема статистической устойчивости логических решающих функций. |
| 26 | Задачи упорядочения и группировки объектов. Алгоритм группировки. |
| 27 | Регрессионный анализ в классе логических решающих функций. Постановка задачи. Строгая вложенность и универсальность класса ЛРФ. Выборочная логическая решающая функция. |
| 28 | Алгоритм поиска наилучшей выборочной логической решающей функции в регрессионном анализе. |
| 29 | О статистической устойчивости ЛРФ в регрессионном анализе. |
| 30 | Задача предсказания в общей постановке. Предсказание многомерной переменной. |
| 31 | Принятие решений на основе экспертной информации и выборки. |
| 32 | Методы анализа многомерных разнотипных временных рядов. |
| 33 | Прогнозирование временных рядов при условии неизменности распределений случайного процесса по времени. |
| 34 | Прогнозирование номера образа по текущим характеристикам объекта |
Наименование курса:
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ АНАЛИЗА ДАННЫХ И РАСПОЗНАВАНИЯ ОБРАЗОВ
Автор: д.ф.-м.н. А.В. Кельманов