Математическое моделирование систем массового обслуживания с циклической дисциплиной прохождения заявок

Вид материала

Автореферат

Содержание Общая характеристика работы Цель и задачи исследования. Методы исследования. Достоверность и обоснованность работы. Апробация научных результатов. Структура и объем работы. Краткое содержание диссертации Сбор статистической информации Маршрутизация прохождения диспансеризации Во второй главе Метод рекуррентного переноса нагрузки разрезов вероятностного графа R2 потоки, входящие в вершины типа q Метод матрицы преобразований Лапласа Tнах, случайно покидает заявка, образуя объединенный поток освобождений, функцию распределения которого обозначим через F Интегральный метод для СМО с произвольными типами распределения В третьей главе В четвертой главе Основные результаты работы Публикации по теме диссертации

Подобный материал:

• 2 Имитационное моделирование систем массового обслуживания, 29.08kb.
• Утверждаю, 89.56kb.
• Задачи теории массового обслуживания. Классификация систем массового обслуживания, 38.01kb.
• Исследование характеристик систем массового обслуживания с простейшим входящим потоком, 954.24kb.
• Основные сведения из теории массового обслуживания, 47.41kb.
• Компьютерное моделирование массового обслуживания клиентов на фармацевтическом рынке, 202.1kb.
• Рабочей программы дисциплины «Введение в теорию систем массового обслуживания» по направлению, 20.17kb.
• Задачи теории массового обслуживания (тмо). Типы систем массового обслуживания (смо), 95.6kb.
• Системы массового обслуживания, 754.03kb.
• Задание для выполнения курсовой работы по эммиМ для студентов 2 курса заочного обучения, 277.53kb.

На правах рукописи


ХОЛОДОВ АРТЕМ ЮРЬЕВИЧ


МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ систем

массового обслуживания

с циклической дисциплиной

прохождения ЗАЯВОК


Специальность: 05.13.18 –

Математическое моделирование, численные методы и комплексы программ


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук


Астрахань 2008

Работа выполнена в Астраханском государственном университете

Научный руководитель:	доктор технических наук, профессор Петрова И.Ю.
Официальные оппоненты:	доктор технических наук, профессор Ураксеев М.А.
	доктор технических наук, профессор Голованчиков А.Б.
Ведущая организация	Волгоградский государственный университет

Защита состоится «12» декабря 2008 года в 13.00 на заседании диссертационного совета ДМ 212.009.03 при Астраханском государственном университете по адресу: 414056, Астрахань, ул. Татищева, 20а, конференц-зал.


С диссертацией можно ознакомиться в библиотеке Астраханского государственного университета


Автореферат разослан «11» ноября 2008 года

Ученый секретарь диссертационного совета, к.т.н.

Щербинина О.В.

Общая характеристика работы


Актуальность исследования. В настоящее время в большинство сфер человеческой деятельности успешно интегрируются информационные технологии, сочетающие в себе четкий математический аппарат и стохастическую природу определяемых бизнес-процессов, т.к. исключение вероятностной составляющей, приводит к идеализации систем. Таким образом, становится актуальным создание математических моделей на основе теории вероятностей, теории динамических потоков и, в частности, систем массового обслуживания (СМО). Причем, рассматривая идеализацию систем, через призму теории динамических потоков, получается четкое разделение СМО, описывающих марковские и немарковские процессы. То есть можно абсолютно точно утверждать, что марковский процесс – это определенная идеализация параметров систем, а в целом СМО описывается немарковскими процессами.

Существуют определенные организационные системы, которые можно рассматривать и, соответственно, описывать с позиций СМО с циклической дисциплиной прохождения заявок. Такие системы возникают в бизнес-процессах образования, управления качеством, здравоохранения, в частности, для последнего – бизнес-процессы диспансеризации, профессионального осмотра и дополнительной диспансеризации. Также определенные выше СМО используются для описания вычислительных систем и решения проблем распределения и коллективного доступа к вычислительным ресурсам.

Здравоохранение признано приоритетным направлением развития во всем мире. С начала 2006 года и в Российской Федерации начал реализовываться национальный проект «Здоровье», в рамках которого запланированы многочисленные мероприятия, призванные усовершенствовать и модернизировать сферу здравоохранения.

Решающую роль в снижении стоимости медицинского обслуживания при сохранении его качества и повышении эффективности играют информационные технологии. По оценкам Еврокомиссии, к 2010 году около 5% национальных бюджетов здравоохранения европейских государств будет вложено в системы и услуги электронного здоровья.

Диспансеризация – активное динамическое наблюдение за состоянием здоровья населения, включающее комплекс профилактических, диагностических и лечебно-оздоровительных мероприятий. Целью диспансеризации является формирование, сохранение и укрепление здоровья населения, профилактика заболеваний, снижение заболеваемости, инвалидности, смертности, достижение активного долголетия. Диспансеризация входит в качестве составной части в широкую систему мер по профилактике заболеваний, осуществляемых государством, обществом, здравоохранением. На эти цели в госбюджете предусматривается 6,0 млрд. рублей.

Таким образом, возникает задача качественной и оптимальной организации процесса диспансеризации всего населения, включающая обязательное обследование, как трудового населения, так и неработающего, как одного из эффективных методов улучшения здоровья нации. Качественная характеристика диспансеризации включает в себя не только высокую квалификацию медицинского персонала, но и качество обслуживания: высокую пропускную способность медицинского учреждения, минимальное время ожидания для пациентов, минимальные простои высококвалифицированного медицинского персонала и другие показатели. Количественные характеристики процесса организации диспансеризации определяются интенсивностями потока пациентов, временем осмотра пациентов специалистами лечебного учреждения.

Данная задача принадлежит к классу задач с циклической дисциплиной прохождения и не нашла достаточно полного отражения в существующих подходах к анализу СМО.

Цель и задачи исследования. Целью диссертационной работы является разработка математических моделей СМО с циклической дисциплиной прохождения заявок, соответствующих имитационных моделей, с целью проведения вычислительных экспериментов, их анализа и создания программного комплекса для принятия управленческих решений в соответствующих организационных системах.

Для достижения поставленной цели в диссертационной работе осуществляется решение следующих основных задач:

1. Обзор и анализ существующих математических методов, применяемых для описания немарковских процессов.
   
2. Анализ существующих программных реализаций ИТ-бизнес-процессов для лечебно-профилактических учреждений (ЛПУ).
   
3. Разработка математических моделей СМО с циклической дисциплиной похождения заявок, описывающих различную степень детализации процесса с введением вертикали уровней абстракции.
   
4. Разработка имитационных моделей с целью проверки адекватности предложенных математических моделей и анализа принятия управленческих решений.
   
5. Разработка имитационной модели СМО с циклической дисциплиной похождения заявок.
   
6. Создание программного комплекса определения характеристик и маршрутизации СМО с циклической дисциплиной похождения заявок и, как следствие, для функционирования бизнес-процессов диспансеризации, профессионального осмотра и дополнительной диспансеризации населения, обеспечивающего формирование управленческих решений и рациональное использование ресурсов ЛПУ.
   

Методы исследования. Для решения поставленных задач и достижения намеченной цели использованы методы теории вероятностей и математической статистики, операционного и функционального анализа, объектно-ориентированного программирования и имитационного моделирования в среде «AnyLoqic».

Достоверность и обоснованность работы. Обоснованность результатов обусловлена корректным применением указанных методов. Достоверность подтверждается вычислительными и имитационными экспериментами и практическим применением методов и результатов диссертационной работы, что отображено в актах внедрения.

На защиту выносятся:

1. Математические модели СМО с циклической дисциплиной прохождения трех уровней детализации
   
2. Математический метод «виртуальных очередей».
   
3. Имитационная модель маршрутизации.
   
4. Комплекс программ, обеспечивающий формирование управленческих решений и рациональное использование ресурсов ЛПУ при проведении диспансеризации, профосмотра и дополнительной диспансеризации.
   

Научная новизна:

1. Предложены математические модели с различной степенью абстракций, описывающие этапы процесса и включающие:
   

• метод реккурентного переноса нагрузки разрезов – стратегический уровень абстракции;
  
• метод матриц преобразований Лапласа от плотностей распределений входного и обслуженного потоков – тактический уровень абстракции;
  
• интегральный метод расчета вероятностей отказа СМО – оперативный уровень абстракции.
  

2. Разработана имитационная модель СМО с циклической дисциплиной прохождения заявок в среде «AnyLogic» с целью установления адекватности предложенных математических моделей, и как результат анализа имитационных экспериментов – определен метод «виртуальных очередей», препятствующий вырождению системы в последовательную.
   
3. Разработана диаграмма потоков данных для компьютерной системы, формирующей СМО с циклической дисциплиной прохождения заявок, с целью определения функциональных характеристик системы и маршрутизации заявок.
   

Апробация научных результатов. Основные результаты работы докладывались и обсуждались на X Международной конференции «Региональная информатика – 2006» (Санкт-Петербург, 2006), Международной конференции «АСТИНТЕХ – 2007» (Астрахань, 2007), Международной конференции «ИНФОРМАЦИОННАЯ СРЕДА ВУЗА XXI века – 2008» (Петрозаводск, 2008), Всероссийской школе-конференции «Актуальные вопросы фундаментальной медицины и прикладной фармакологии – 2008» (Москва, 2008). Отдельные результаты работы используются при обучении студентов кафедры «Управление качеством» в Астраханском государственном университете и кафедр «САПР и ПК» и «ЭВМ и сети» Волгоградского государственного технического университета. Предложенные в диссертации методы и модели нашли практическое применение в виде программного комплекса проведения диспансеризации для медицинских учреждений.

Публикации. Основные положения диссертационной работы отражены в 11 опубликованных научных работах.

Структура и объем работы. Диссертационная работа состоит из введения, четырех глав основного текста, заключения, списка литературы из 94 наименований и 4 приложений. Общий объем работы 146 страниц машинописного текста, который включает 41 рисунок, 3 таблицы и 83 формулы.


Краткое содержание диссертации


Во введении обоснована актуальность темы, определены цель и задачи исследования.

В первой главе проводится обзор и анализ существующих математических методов описания немарковских процессов:

• Система физических состояний – система дифференциальных уравнений (динамическое состояние), система алгебраических уравнений (стационарное состояние).
  
• Метод вероятностных графов – описание параллельно-последовательных и простейших мостиковых вероятностных графов.
  
• Использование преобразований Лапласа – правило «свертки» для установления зависимостей между характеристиками процессов.
  
• Использование аппроксимационных приближений – замена различных типов вероятностных распределений показательным распределением.
  

Также проводится обзор, и анализ существующих информационных технологий и программных реализаций для здравоохранения и медицинского страхования, предлагаемых отечественными и иностранными разработчиками.

Для совершенствования и развития лечебно-профилактических учреждений (ЛПУ) в настоящее время используются различные методы и технологии. Применение вычислительной техники и информационных технологий помогает решить проблему эффективного использования мощных концептуальных, математических и технических средств, с целью системной реорганизации материальных, финансовых и информационных потоков, перераспределения и максимального использования различных ресурсов, ориентации на потребности клиентов (для ЛПУ – пациентов), повышения качества их обслуживания. Таким образом, речь идет об использовании совершенно новых подходов, основанных на последних достижениях информационных технологий.

Автором был проведен анализ программного обеспечения для здравоохранения и медицинского страхования, предлагаемого отечественными и иностранными разработчиками: «ЦентрИнвест Софт» (Москва), «МЕДКОР-2000» (Москва), «СоюзМедИнформ» (Москва), «Galen» (Израиль), «Orsis» (Израиль).

Всеми разработчиками предлагаются как различные независимые модули, так и некоторые комплексные решения на их основе. Поскольку существует определенная нормативная документация, описывающая структуру и формат данных, подлежащих хранению, то идет речь о создании единого информационного пространства различных служб территориальных подразделений. Но из-за унификации данных программные реализации различных разработчиков, по сути, эквивалентны и различаются лишь формой реализации и особенностями интерфейса.

По приказу Минздравсоцразвития РФ № 188 от 22.03.2006, каждого диспансерного обследуемого должны осмотреть:

– врач–терапевт (врач общей практики);

– хирург;

– эндокринолог;

– невролог;

– офтальмолог;

– гинеколог (женщин);

– уролог (мужчин).

Кроме того, каждый обследуемый должен сдать анализы (клинический анализ крови и мочи, кровь на уровень холестерина и сахара), пройти ЭКГ и флюорографию. Женщины старше 40 лет – сделать маммограмму или УЗИ молочных желез. Причем, последовательность прохождения хирурга, эндокринолога, невролога, офтальмолога, гинеколога (женщины), уролога (мужчины) не регламентируется. Таким образом, пациент может проходить специалистов в любом порядке.

Таблица 1

Сводная таблица функциональных возможностей программных комплексов, представленных выше разработчиков, применительно к сбору и обработке статистической информации и проведению диспансеризации

Разработчики	Ввод данных о пациенте в формате соответствующего реестра	Сбор статистической информации	Вывод различных отчетов по любым временным интервалам	Обработка статистических данных – построение функций распределения (мониторинг)	Маршрутизация прохождения диспансеризации	Оперативный доступ к динамической информации при проведении диспансеризации
«ЦентрИнвест Софт»	+	+	+	+	–	–
«МЕДКОР-2000»	+	+	+	–	–	–
«СоюзМедИнформ»	+	+	+	+	–	–
«Galen»	+	+	+	–	–	–
«Orsis»	+	+	+	–	–	–

Проведенный обзор и анализ данных (таблица 1) позволяет сделать следующие выводы:

1. В большинстве случаев программные продукты для здравоохранения и медицинского страхования, предлагаемые отечественными и иностранными разработчиками, по своей сути являются реализациями электронного документооборота.
   
2. Предлагаемые информационные технологии построены без учета целенаправленности процессов обслуживания пациентов и не дают возможности для комплексной оценки их эффективности.
   
3. Рассмотренные информационные технологии организации бизнес-процессов системы управления опираются на теорию систем массового обслуживания только с целью прогнозирования.
   

Во второй главе дается описание задач теории массового обслуживания посредством определения трех показателей:

– входящими потоками заявок (функциями плотностей распределения временных интервалов поступления заявок);

– структурой и информацией об обслуживающих устройствах (функциями плотностей распределения времени обслуживания заявок в устройствах и возможными связями между ними);

– дисциплиной обслуживания заявок.

Решение прикладной задачи, принадлежащей к СМО, является получение необходимых характеристик (вероятность занятости–свободности системы, пропускной способности системы, данных о средних величинах времени пребывания в системе и очередях и т.д.), описывающих ее поведение и установление различных закономерностей между ними и структурой системы. Естественно, наиболее полную информацию о системе можно получить из анализа вероятностной функции, описывающей ее поведение, но практически получить ее в аналитическом виде в большинстве случаев невозможно.

Сделан вывод о том, что бизнес-процесс диспансеризации населения является прикладной задачей теории систем массового обслуживания.

Используя обозначения СМО, система, описывающая процесс диспансеризации, в общем случае, может быть представлена как трехфазная система, где вторая фаза есть узел, описываемый как СМО с 10-ю обслуживающими устройствами с циклической дисциплиной прохождения и входным потоком, состоящим из заявок трех типов. Причем можно выделить систему, описываемую как блок с 7-ю обслуживающими устройствами, так же с циклической дисциплиной прохождения, но уже с однородным входным потоком, что представляет прохождение общего модуля. Узел диспансеризации можно представить в виде объединения четырех модулей:

1. – модуль, являющийся общим для всех, включает в себя кабинеты хирурга, эндокринолога, невролога, офтальмолога, параклинических анализов, ЭКГ и флюорографии;
   
2. – модуль, являющийся кабинетом уролога;
   
3. – модуль, являющийся кабинетом гинеколога;
   
4. – модуль, являющийся кабинетом УЗИ.
   

Трехфазная модульная схема процесса диспансеризации представлена на рис. 1.

Профессиональный осмотр и дополнительная диспансеризация так же являются прикладными задачами теории массового обслуживания и являются частными случаями задачи диспансеризации.

Рис. 1. Трехфазное модульное представление процесса диспансеризации

В качестве подходов к построению математических моделей систем с циклической дисциплиной обслуживания объединены методы вариационных принципов и иерархических цепочек, что приводит к введению вертикали абстрактных уровней моделирования:

1. Стратегический уровень – высокий уровень абстракции (минимум деталей, стационарность состояний, высокий уровень обобщений).
   
2. Тактический уровень – средний уровень абстракции (средняя детальность, динамика потоков, очереди, средний уровень обобщений).
   
3. Операционный уровень – низкий уровень абстракции (много деталей, расстояния/маршрутизация, управление очередями, максимальная детализация).
   

Модель стратегического уровня основана на методе рекуррентного переноса нагрузки разрезов вероятностного графа, тактического уровня – на методе матрицы преобразований Лапласа и оперативного уровня основана на интегральном методе представления параллельных соединений с произвольными типами распределения.

Метод рекуррентного переноса нагрузки разрезов вероятностного графа

Рассматривается СМО, состоящая из N обслуживающих устройств с показательными независимыми распределениями интервалов времен обслуживания, простейшим входным потоком и циклической дисциплиной прохождения заявок.

Известный метод вероятностных графов (МВГ) заключается в создании графа, отображающего структуру СМО – в качестве узлов используются обслуживающие устройства, в качестве ребер – доступные переходы между устройствами. В качестве базовой характеристики метода используются вероятности занятости (свободности) дуг (обозначают _k, где k – идентификатор дуги) и, используя структуру графа, находится вероятность занятости (свободности) всей СМО.

Введены шесть (VI) базисных правил, присущих таким системам и описывающих свертки последовательных и параллельных соединений вероятностного графа:

(I) – min(, ) – прохождение потока заявок через обслуживающее устройство;

(II) – – вероятность занятости однолинейной системы;

(III) – 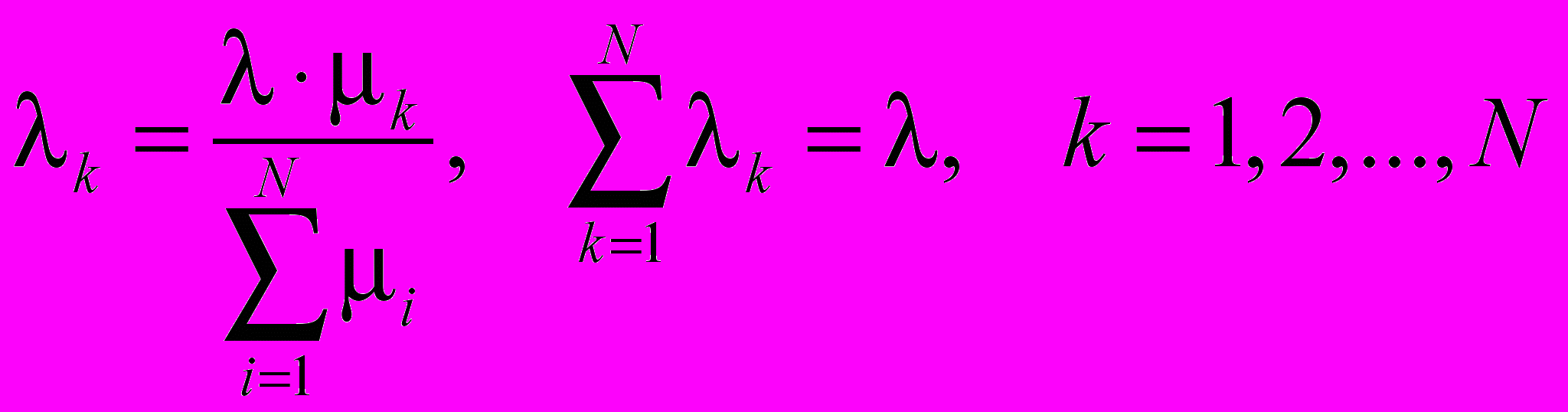– распределение прохождения простейшего потока по параллельно-соединенным обслуживающим устройствам;

(IV) – – сумма простейших входящих потоков (с характеристиками _i) также является простейшим входящим потоком (с характеристикой );

(V) – 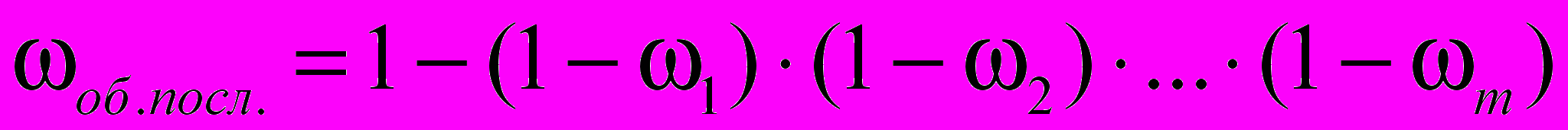– вычисление вероятности занятости для последовательного соединения;

(VI) – 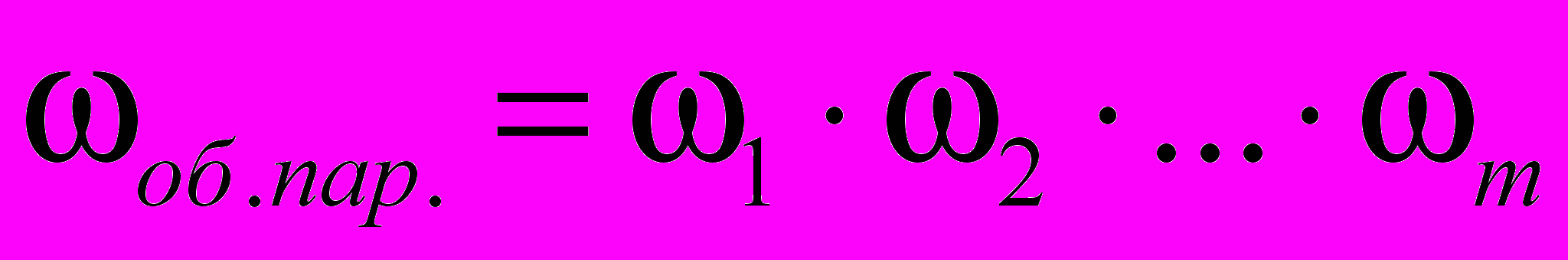– вычисление вероятности занятости для параллельного соединения.

Метод рекуррентного переноса нагрузки разрезов вероятностного графа заключается в преобразовании вероятностного графа со сложной мостиковой структурой в параллельно-последовательный вероятностный граф «всевозможных путей», путем введения разрезов и правил рекуррентного переноса потоков и дальнейшего применения МВГ (рис. 2.).

Рис. 2. Разрезы параллельно-последовательного графа «всевозможных путей»

Введены обозначения вершин графа (двух типов):

• вершины типа «q», где q = 1, 2, …, N.
  
• вершины типа «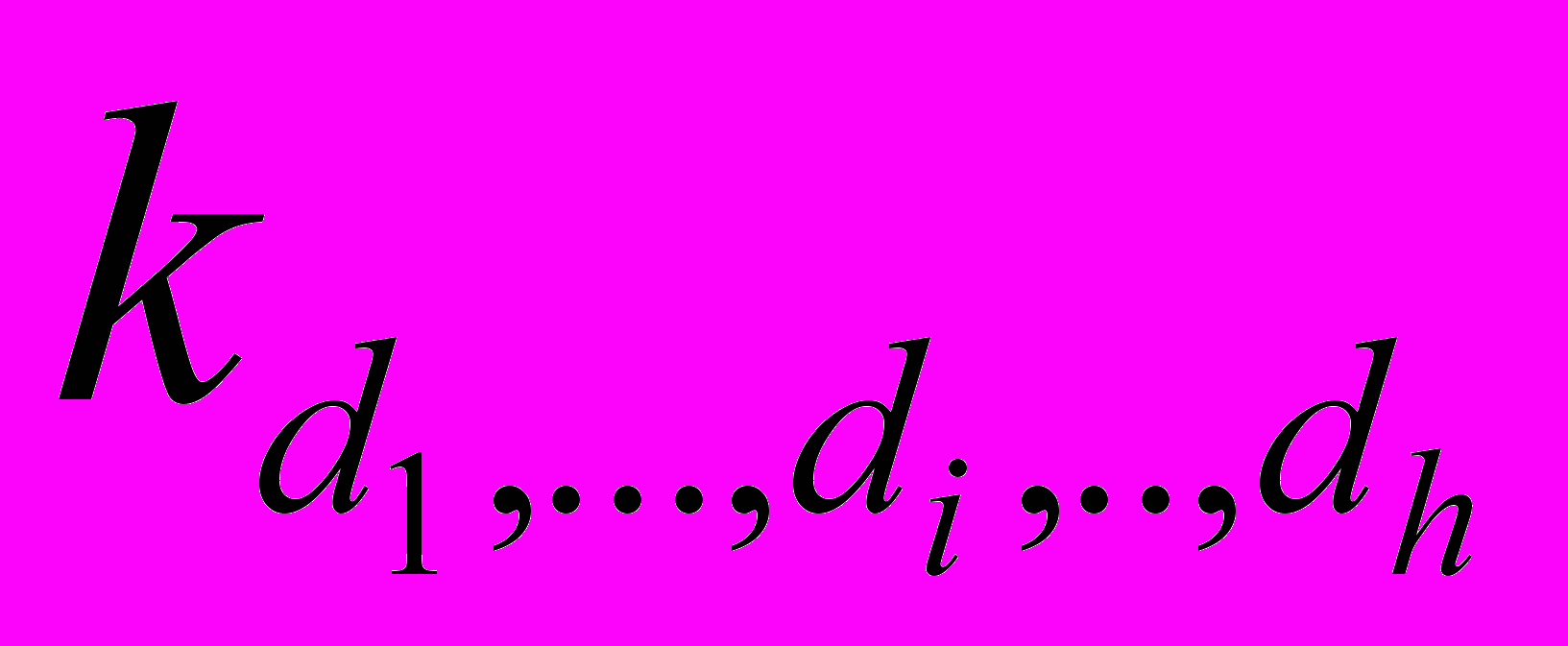», где k = 1, 2, …, N, d_i описаны рекуррентно: d₁ = 1, 2, …, k–1, k+1, …, N, или если  = {1, 2, …, N}, то d_i =   k  [], т.е. k – обслуживающее устройство через которое заявка вошла в систему, индексы d_i содержат информацию о последовательности прохождении заявкой других обслуживающих устройств (повторение исключается).
  

Для определения характеристик входящего потока по дуге к обслуживающему устройству 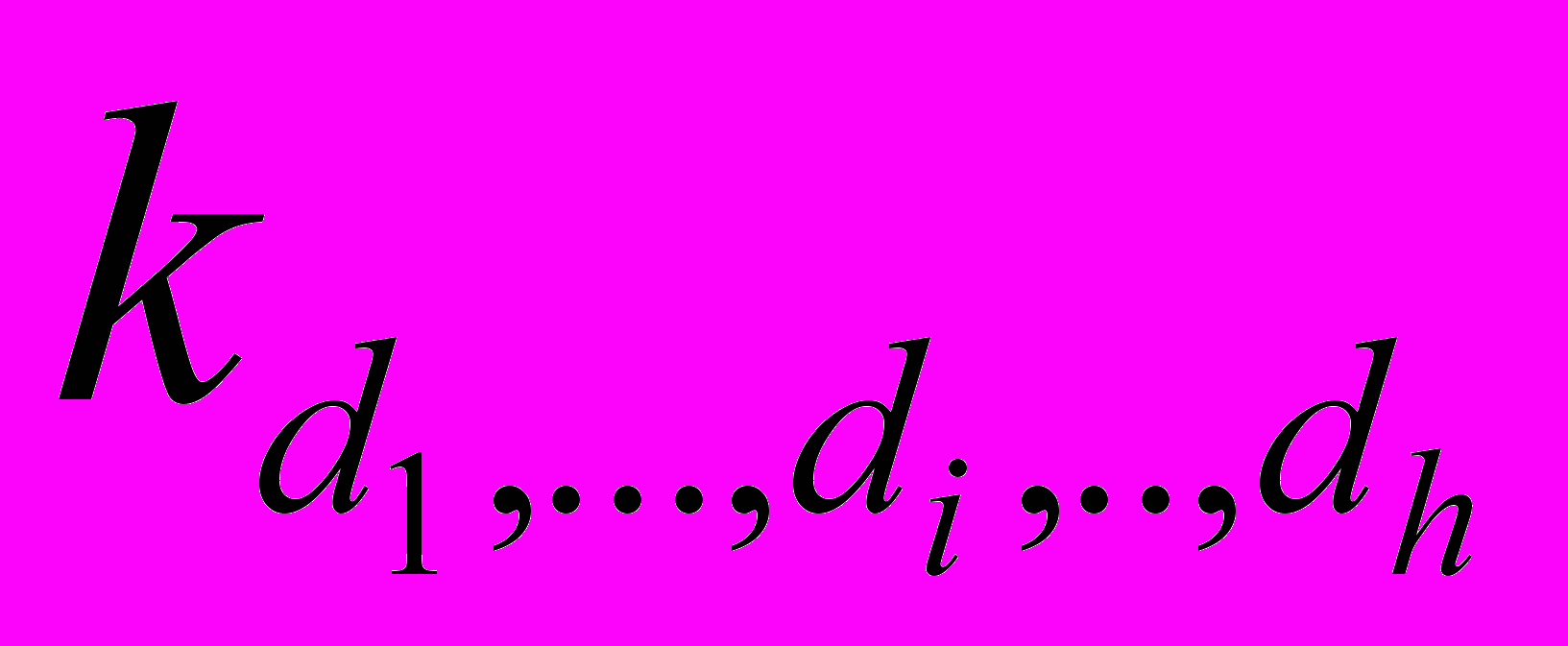в разрезе R_h+1 используются характеристики всех потоков из разрезов R_j (j = 1, …, h) к соответствующим вершинам (устройствам) , т.е. в названии метода вполне оправдано использование слова «рекуррентный».

Начиная с разреза R₂ потоки, входящие в вершины типа q (разрез R₁) переносятся (в данном случае складываются, используя (IV)) с потоками, определенными по «правилу прохождения» (I), входящими в вершины типа 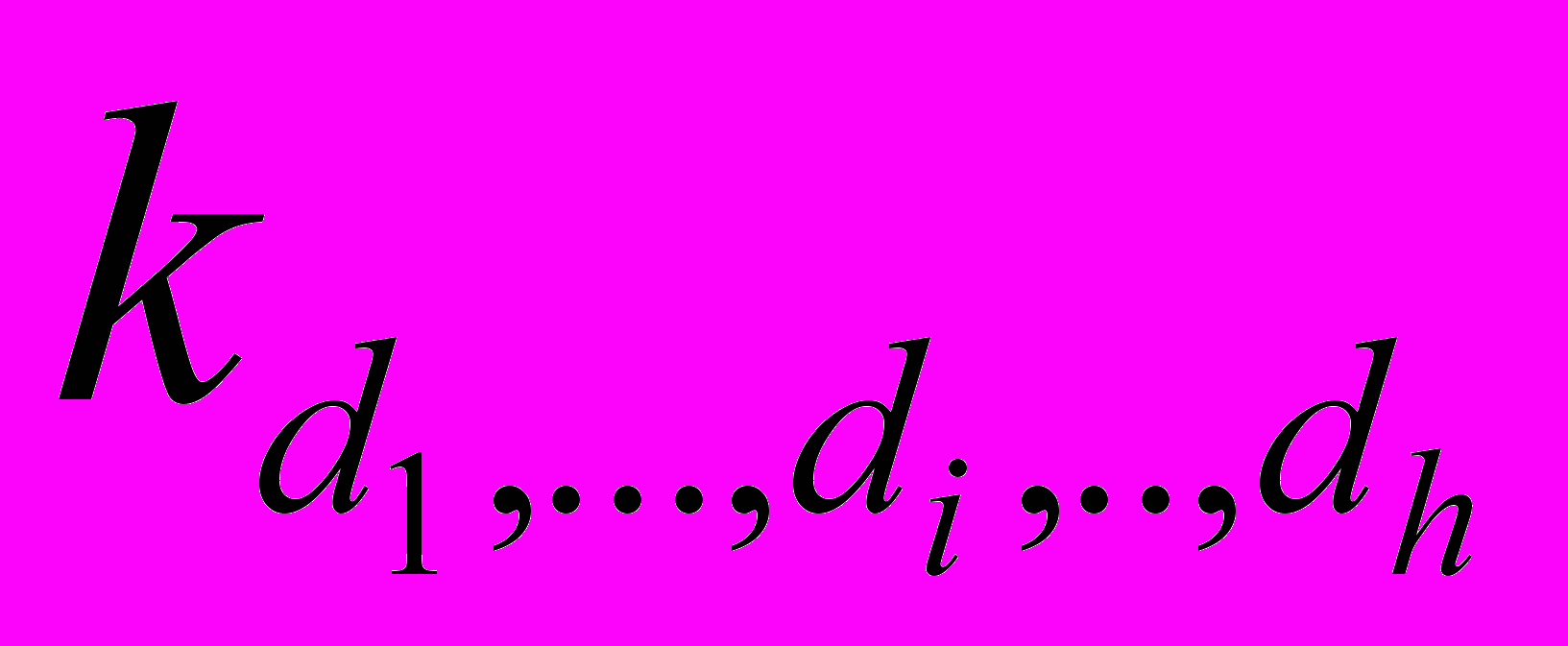при k = q и делятся (используя (III)) на их количество. Дальше процедура продолжается – для разреза R₃ используется информация с разрезов R₁ и R₂ и т.д.

Следующий этап – определение вероятностей занятости дуг (используя (II)) и используя (V) и (VI) – «свертки» вероятностного графа и получения итоговой вероятности занятости системы.

Приведен анализ двухкомпонентных систем и показано теоретически и графически, что вероятность отказов системы с циклической дисциплиной обслуживания всегда меньше, чем для системы с последовательным соединением, таким образом, она более эффективна. Также сформулирована и доказана теорема для произвольного количества обслуживающих устройств (рис. 3.).

Рис. 3. Графическое представление зависимости вероятности отказа от частоты входящего потока для двух, трех, четырех и пятикомпонентных систем с циклической и последовательной дисциплиной прохождения

Сформулирована и доказана теорема.

Вероятность отказа стационарного состояния системы массового обслуживания (СМО) с отказами, определяемая простейшим входящим потоком и показательными независимыми распределениями интервалов времени обслуживания в устройствах, при последовательном соединении всегда больше, чем при циклической дисциплине прохождения для любого количества обслуживающих устройств.

Полученные результаты применения данного метода могут быть использованы для управленческих решений медицинских организаций городского и областного уровня – проводить мониторинг диспансеризации, оценивать загруженность различных районных ЛПУ, а так же функцию распределения интервалов времени, блока обслуживающих устройств.

Метод матрицы преобразований Лапласа

Введено в рассмотрение понятие функционального анализа – преобразование Лапласа и показано его применение в теории вероятностей.

Рассматривается произвольная система с циклической дисциплиной обслуживания. На вход СМО, содержащей n обслуживающих устройств, поступает входной поток заявок, описывающийся функцией распределения интервалов между ними – Q(t). Плотности распределения функций обслуживания каждым обслуживающим устройством соответственно равны f₁(t), f₂(t),…, f_n(t). Заявка, поступающая в систему, проходит n обслуживающих устройств (цикличность дисциплины прохождения), общая плотность распределения функции обслуживания заявки всеми устройствами будет определяться интегралом свертки от плотностей распределений функций обслуживания каждого устройства. В общем случае, когда в системе одновременно находится в среднем k заявок, общая плотность распределения функции обслуживания одной из заявок всеми устройствами, будет равна

, (1)

где ₂(t), ₃(t),…, _n(t) – плотности распределений функций ожидания заявками обслуживания перед соответствующими устройствами. Поскольку интеграл от свертки равен произведению их преобразований Лапласа и в целом в системе существует n! комбинаций прохождения n обслуживающих устройств, последние удобнее представить через квадратную матрицу преобразований Лапласа от плотностей распределения функций обслуживания каждого устройства

, (2)

где F*_i(s) и *_j(s) – преобразования Лапласа от функций f_i(t) и _j(t).

Фиксируя любой элемент матрицы (2) в первом столбце, что характеризует первоначальное поступление заявки в систему через данное обслуживающее устройство и «вычеркивая» первый столбец и соответствующую устройству строку, получаем матрицу размерности [(n – 1)x(n – 1)]. Суммируя элементы главной диагонали, полученной матрицы, с выбранным элементом, получаем преобразование Лапласа общей плотности распределения.

(3)

Из соотношений (3) видно, что преобразования Лапласа для общей плотности распределения функции обслуживания каждой заявки совпадают, поскольку они являются перестановкой одних и тех же сомножителей, и, в общем, полученные соотношения характеризуют среднее время нахождения заявки в системе обслуживания

, (4)

которые, как видно из формул (4) при отсутствии очередей перед обслуживающими устройствами, равны между собой

(4.1)

Этот результат отражает тот факт, что заявки по циклу проходят одни и те же обслуживающие устройства и их времена обслуживания и ожидания суммируются, что и приводит к соотношениям (4). Если на вход системы обслуживания поступает поток заявок, описывающийся функцией распределения интервалов между ними – Q(t), то нетрудно получить величину среднего интервала между ними

, (5)

где плотность функции распределения интервалов поступления между заявками. Тогда в системе обслуживания одновременно в среднем находится k заявок, их количество определяется отношением среднего времени нахождения заявки в системе к величине среднего интервала поступления заявок (формула Литтла)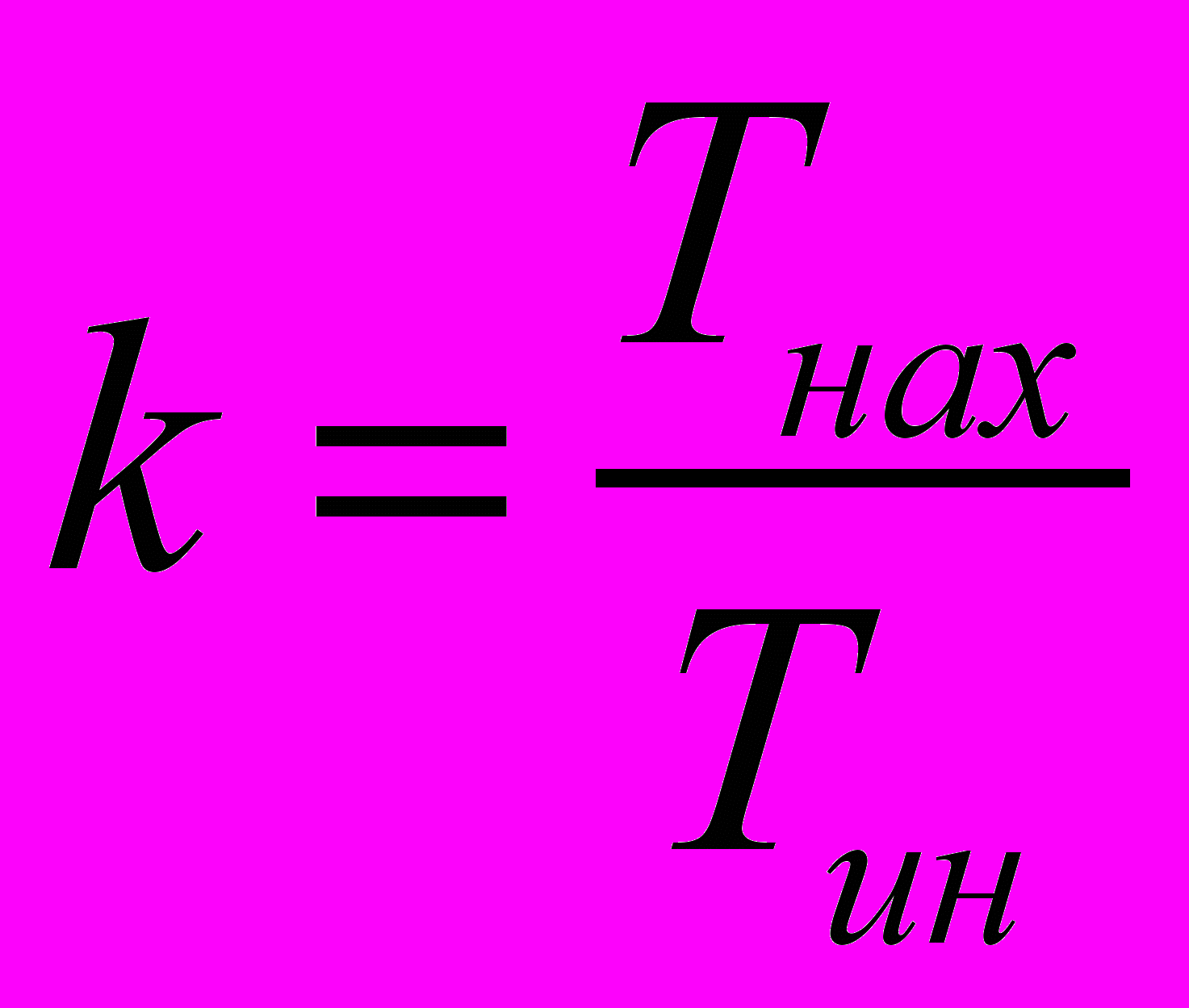

. (6)

Перейдя к рассмотрению частного случая – плотности распределений функций обслуживания устройств подчиняются показательному закону с параметрами обслуживания, т.е. . Вводим зависимость соотношений ₂(t), ₃(t),…, _n(t) – плотностей распределений функций ожидания заявками обслуживания устройствами для потоков заявок от отношения , которое определяет три варианта загрузки системы и получены формулы среднего времени нахождения заявок в системе: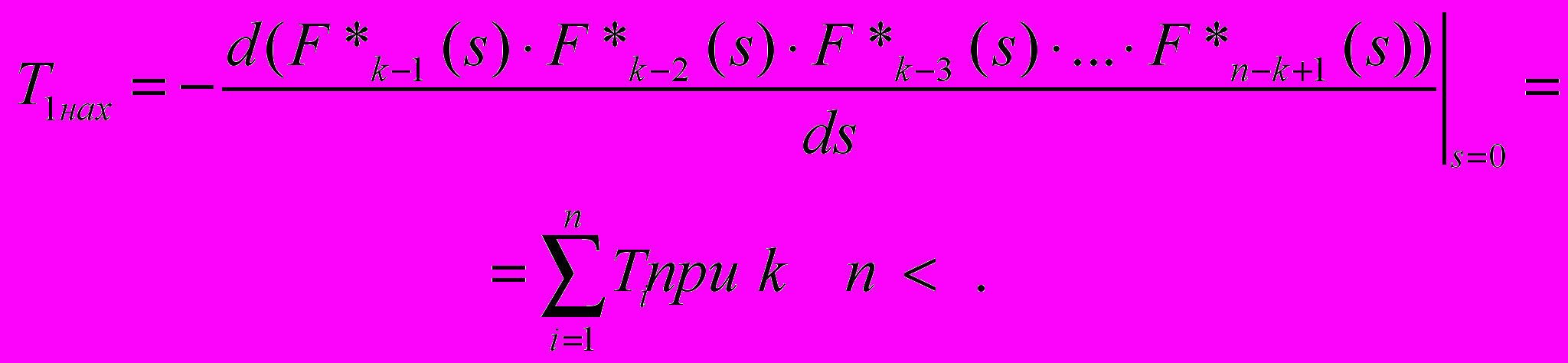

(7)

(8)

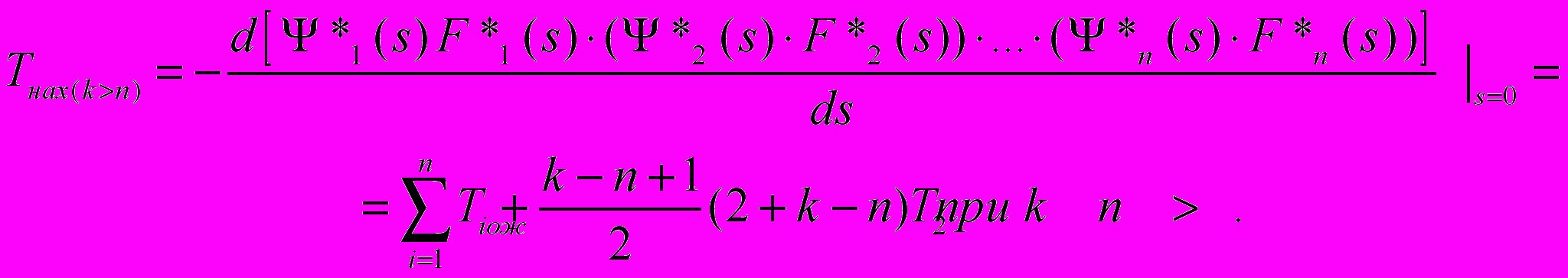(9)

где .

Вводим в рассмотрение F_c,i(t) – распределение длительностей нахождения заявок в системе обслуживания:

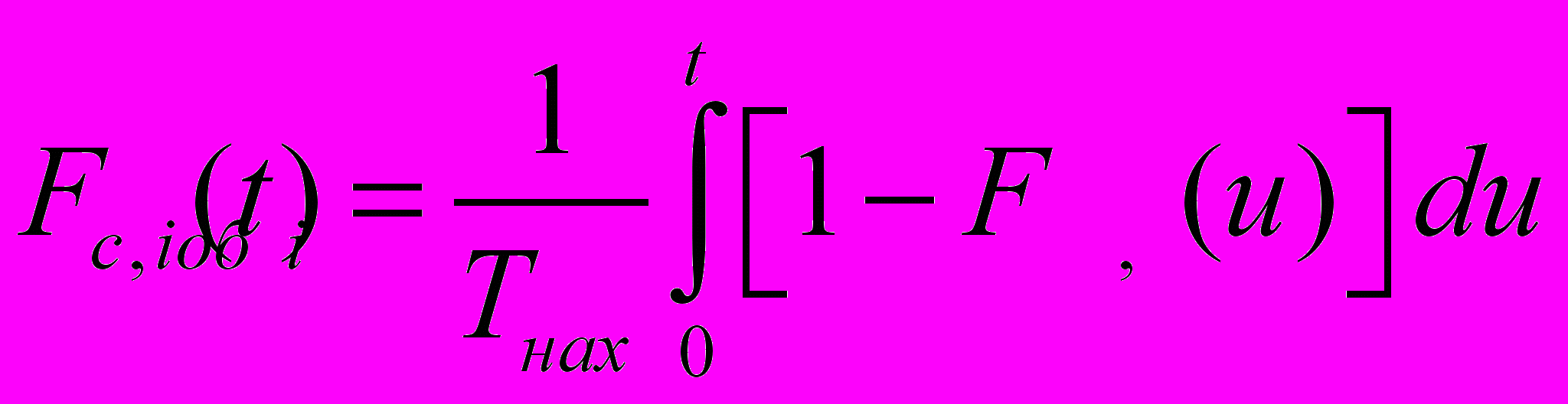, (10)

где i  (1, k).

В системе наблюдается k независимых потоков, каждый из которых, после обслуживания, проведя в нем время T_нах, случайно покидает заявка, образуя объединенный поток освобождений, функцию распределения которого обозначим через F_oc(t). Тогда для объединенного потока имеем

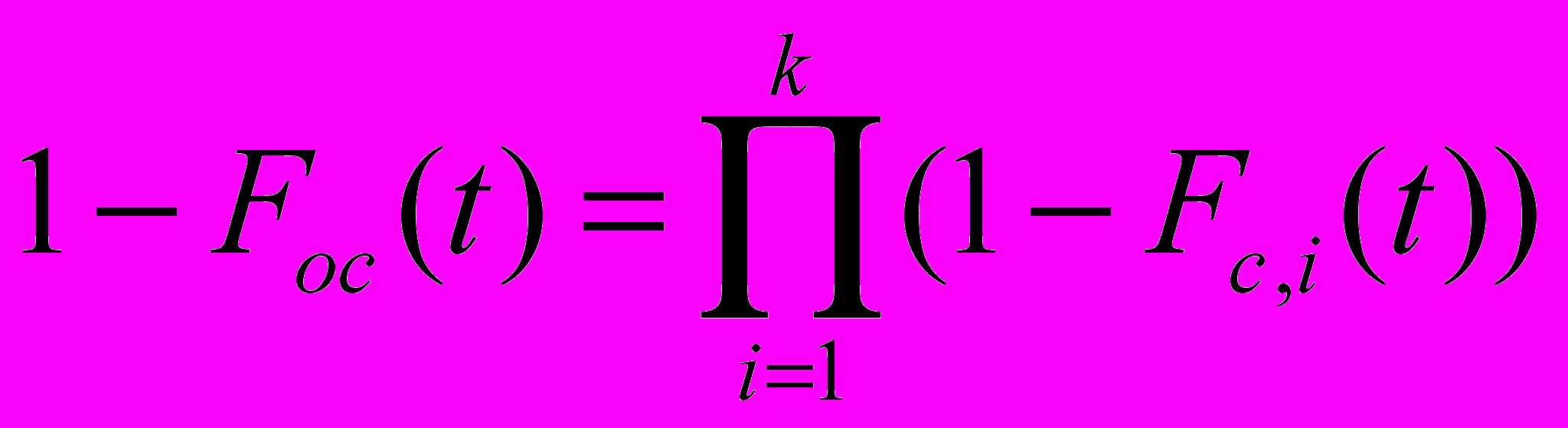, (11)

или

(12)

Используя (3), (4) получаем:

, (13)

то есть средний интервал освобождения системы равен времени нахождения заявки в системе поделенной на среднее число заявок, одновременно находящихся в системе. Причем среднее время нахождения заявки в системе обслуживания в зависимости от загрузки системы определяется по формулам (7), (8) и (9). Необходимо заметить, что данный метод опирается на работы Дж. Джексона, где он рассматривал СМО с произвольной дисциплиной прохождения и покидания системы без очередей, установив тем самым некоторые закономерности между вероятностями состояний при многошаговых переходах.

Резюмируя вышеизложенное, отметим:

1. Предложен матричный метод преобразований Лапласа от плотностей распределений функций ожидания и обслуживания каждого устройства для анализа СМО с циклической дисциплиной обслуживания.
   
2. Разработана математическая модель СМО с циклической дисциплиной прохождения заявок на основе матриц преобразований Лапласа, с помощью которых установлены зависимости между показателями системы обслуживания и потоком обслуженных заявок при различном соотношении количества заявок и количества обслуживающих устройств: формулы (7) – (9), (13) (рис. 4).
   

Количество заявок	Количество заявок
а б
Рис. 4. Графическое представление зависимости времени а – нахождения в системе; б – освобождения из системы, от количества заявок для СМО состоящей из 8-ми обслуживающих устройств, со средними временами обслуживания: T1=3, T2=4, T3=5, T4=6, T5=7, T6=8, T7=9, T8=10 мин.

Интегральный метод для СМО с произвольными типами распределения

Случайный процесс, протекающий в однолинейной системе обслуживания, состоит в том, что в систему в случайные моменты времени приходят заявки, интервалы следования между которыми имеют распределение G(t). Средний интервал следования заявок равен _ср. Пусть распределение времени обслуживания имеет вид F(t) со средним временем обслуживания равным _ср. Естественно предположить, что функции распределения определены в первом квадранте, то есть  и  > 0. При этом, если время обслуживания _i i-ой заявки будет больше, чем _i интервал между приходом i-ой и (i+1)-ой заявками, то (i+1)-ая заявка получит отказ в обслуживание. При этом будет выполняться условие _i – _i < 0. Вероятность указанного события будет определяться распределением процесса

, (14)

Найдем закон распределения величины T, являющийся разностью случайных величин  – интервалов следования заявок и Θ – времени обслуживания однолинейной системы

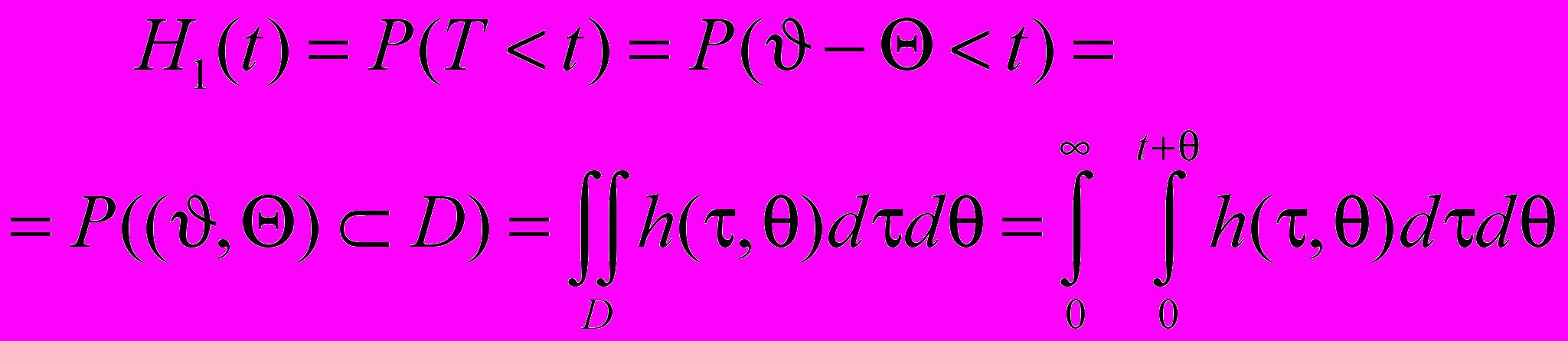, (15)

где h(,) – совместная плотность функции распределения величин  и Θ, область D – проекция сечения плоскости T плоскостью T₁ = t на координатную плоскость О, при чем выбирается та область или то множество точек ,Θ, для которых выполняется условие  – Θ < t.

В силу независимости случайных процессов потока заявок и времени обслуживания их совместная плотность равна произведению плотностей функций распределения каждой величины

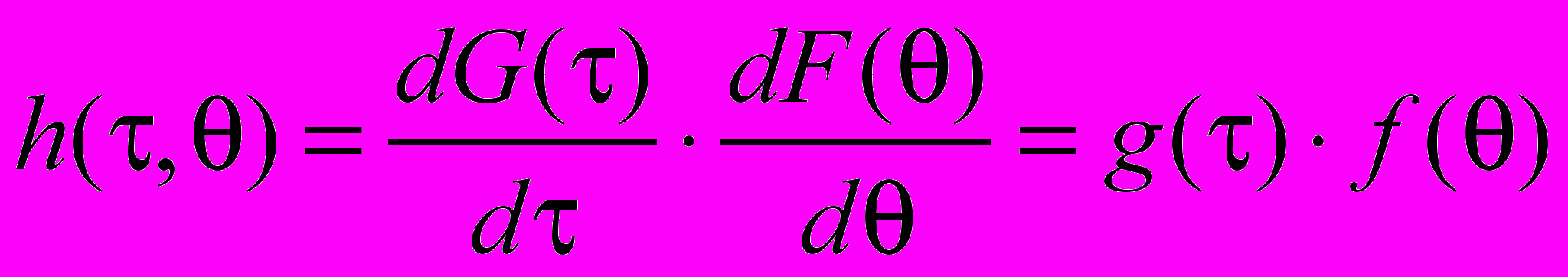. (16)

Подставляя соотношение (16) в формулу (15) получим функцию распределения взаимодействия случайных потоков заявок и обслуживания

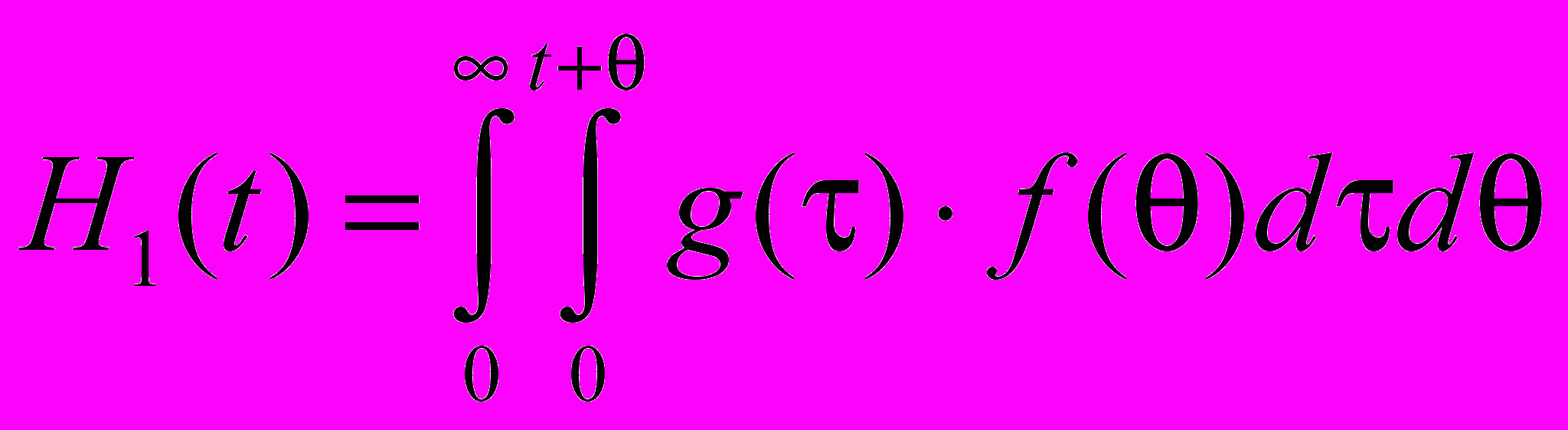. (17)

Из соотношения (17) нетрудно получить вероятность отказа в обслуживания для однолинейной системы через функцию распределения взаимодействия H₁(t) случайных потоков заявок и обслуживания, естественно для этого должно выполняться условие _i – _i < 0, поэтому значение функции распределения в нуле будет определять вероятность отказа

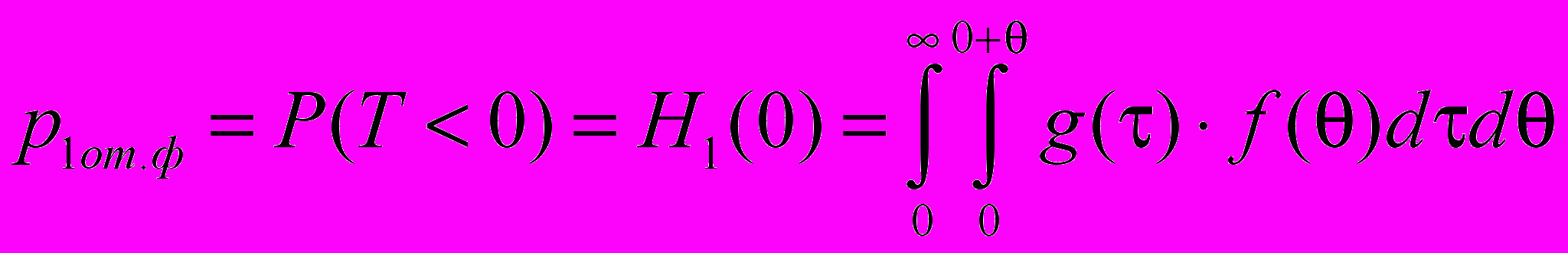. (18)

Нормируем аргументы в функциях распределений

, (19)

тогда функция распределения взаимодействия случайных потоков заявок и обслуживания (17) и вероятность отказа (18) будут иметь следующий вид

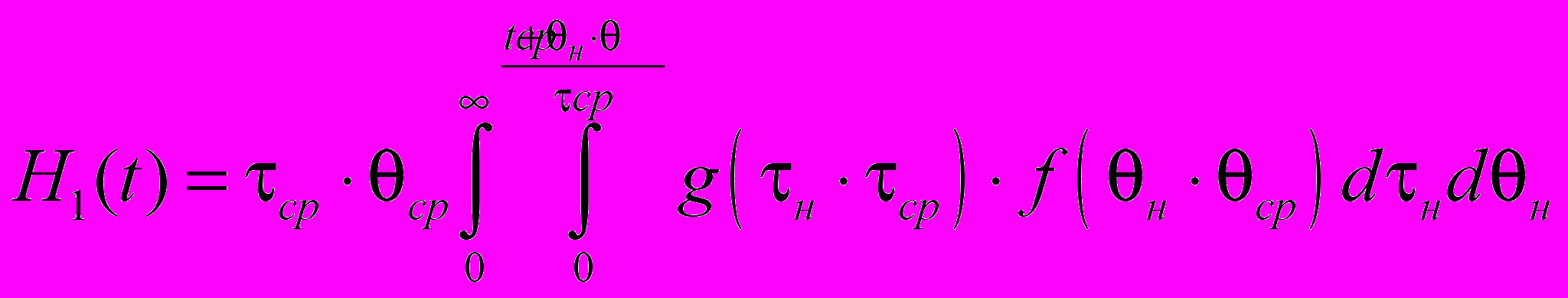(20)

или, переходя к плотностям распределений с нормированными аргументами,

(21)

получим

(22)

и

, (23)

Путем аналогичных рассуждений для двух, трех-линейной систем получены закономерности и определена функция распределения взаимодействия случайных потоков заявок и обслуживания в n-линейной системе обслуживания

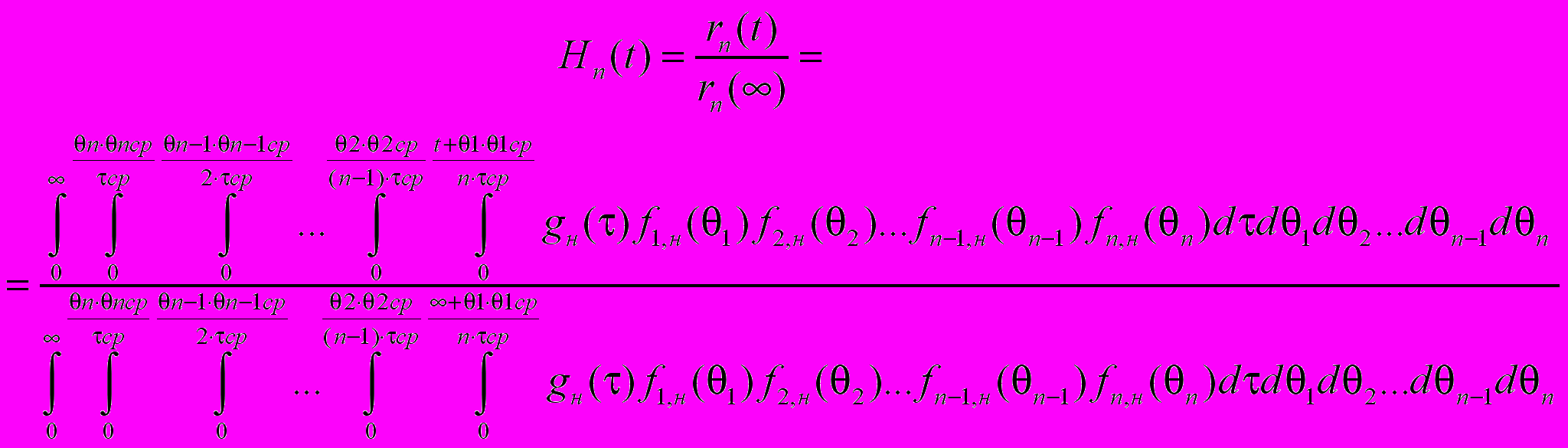(24)

и соответствующая вероятность отказа в n-линейной системе обслуживания

(25)

В качестве проверки предложенного метода использована тождественность вероятностей отказа, рассчитанных с использованием интегрального метода и полученных из формул Эрланга.

Кроме того, интегральный метод позволяет учесть, во-первых, различный порядок дисциплины обслуживания, поскольку перемена мест для внутренних интегралов в соотношение (25) влияет на результат вычислений и, во-вторых, асимметричность, которая возникает при смене порядка прохождения обслуживающих устройств с разным временем обслуживания.

В третьей главе обусловлена важность имитационного моделирования и обоснован выбор пакета AnyLogic.

Приведены данные статистического анализа – использование критерия Пирсона (²) для проверки гипотез о теоретическом распределении на основе экспериментальной генеральной совокупности.

Проведен анализ имитационных моделей двухкомпонентных систем с отказами и установлена адекватность предложенного метода рекуррентного переноса нагрузки разрезов вероятностного графа, для циклической дисциплины прохождения. Так же установлена адекватность интегрального метода и подтвержден основной вывод метода – асимметричность системы (рис. 5).

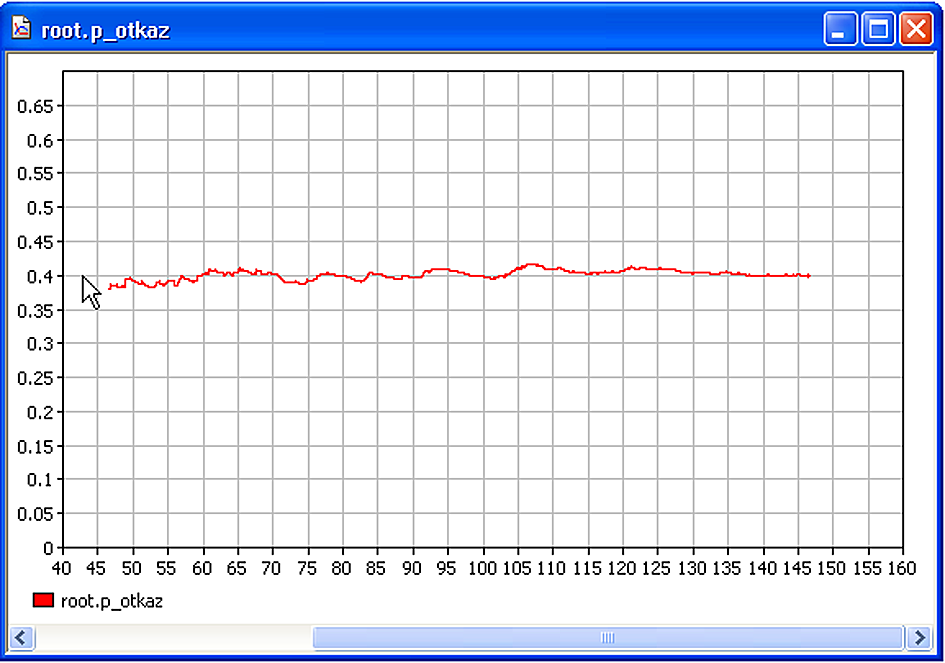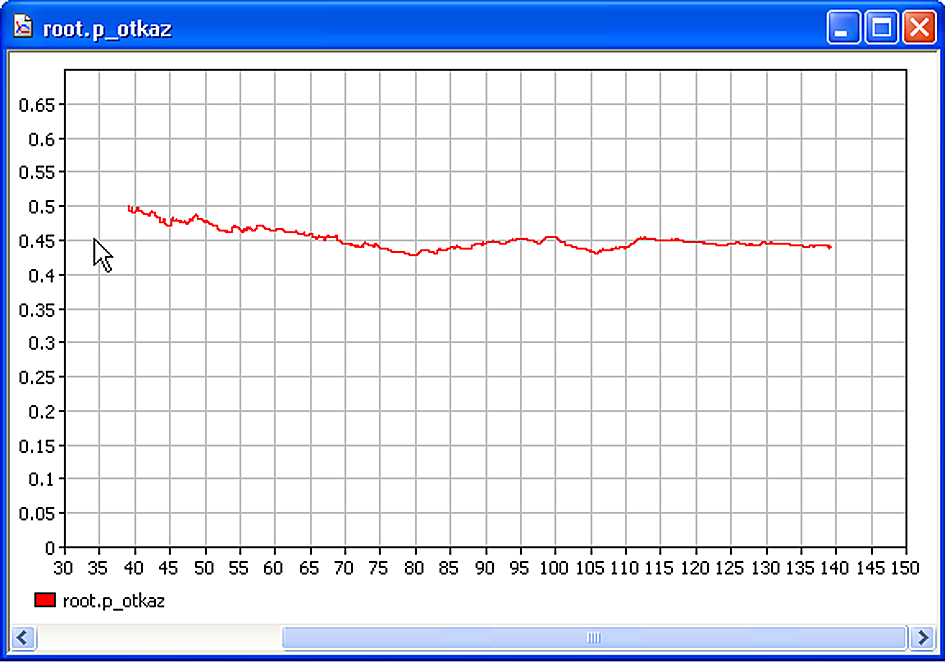а	б
Рис. 5. Графическое представление вероятности отказа от времени для СМО с циклической дисциплиной прохождения заявок, состоящей из 2-х обслуживающих устройств, с частотами обслуживания: 1=3, 2=1 и входящим потоком с частотой =4 при внутренней последовательности доступа: а – устройство с 1, потом 2, p_otkaz  0.4; б – устройство с 2, потом 1 p_otkaz  0.45.

Представлена таблица с описанием активных блоков, используемых в построенных моделях, и создан класс сообщений с полями, фиксирующими прохождение обслуживающих устройств. Реализована пользовательская функция распределения потока заявок.

Построена имитационная модель с семью обслуживающими устройствами и очередями, описывающая поведение общего модуля (1) процесса диспансеризации (рис. 6.).

Рис. 6. Блок-схема имитационной модели с семью обслуживающими устройствами и очередями – реализация общего модуля (1) диспансеризации

Создан активный класс сообщений с девятью полями – семь отвечающих за прохождение обслуживающих устройств и два поля, использующих функцию getTime(), для фиксации модельных времен возникновения заявки в системе и выхода из системы после обслуживания. Использована пользовательская функция управления потоком заявок по принципу минимальной очереди: заявка направляется на обслуживание в то устройство, где она еще не была обслужена и очередь, перед которой минимальна. С помощью данной имитационной модели установлена адекватность метода матриц преобразования Лапласа.

При проведении имитационных экспериментов над данной моделью, с различной градацией средних времен облуживания в устройствах и ограничением количества заявок, была установлена закономерность, приводящая к вырождению циклической дисциплины обслуживания в последовательное прохождение системы, т.е. устройства с меньшим средним временем обслуживания пропускают через себя поток заявок и, останавливаясь, фактически прекращают свое функционирование в системе. В связи с этим, на основании метода матриц преобразований Лапласа предложен метод введения виртуальных очередей, который препятствует вырождению в последовательное прохождение системы, обеспечивая постоянную работу (загрузку) всех обслуживающих устройств. Определяются средние времена обслуживания

, (26)

среди них определяется максимальное T_max с индексом j и 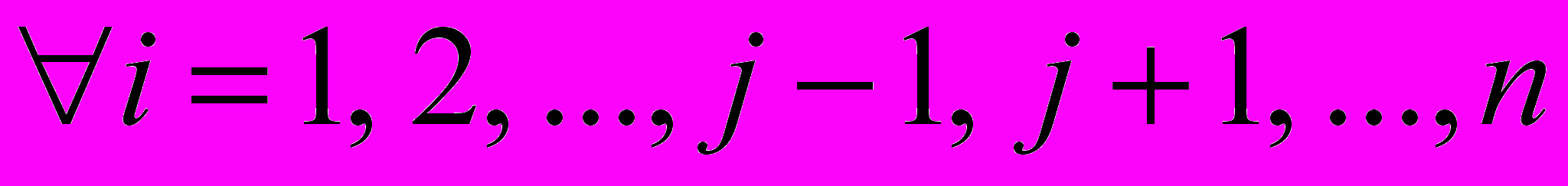вводятся

, (27) где – преобразование Лапласа функции плотности распределения временных интервалов виртуальной очереди, соответствующего i-го обслуживающего устройства. Определяем среднее время нахождения в виртуальной очереди и принимая в качестве количества заявок в виртуальной очереди 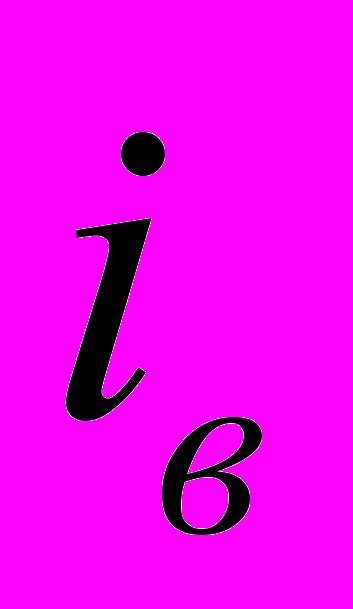округленную величину 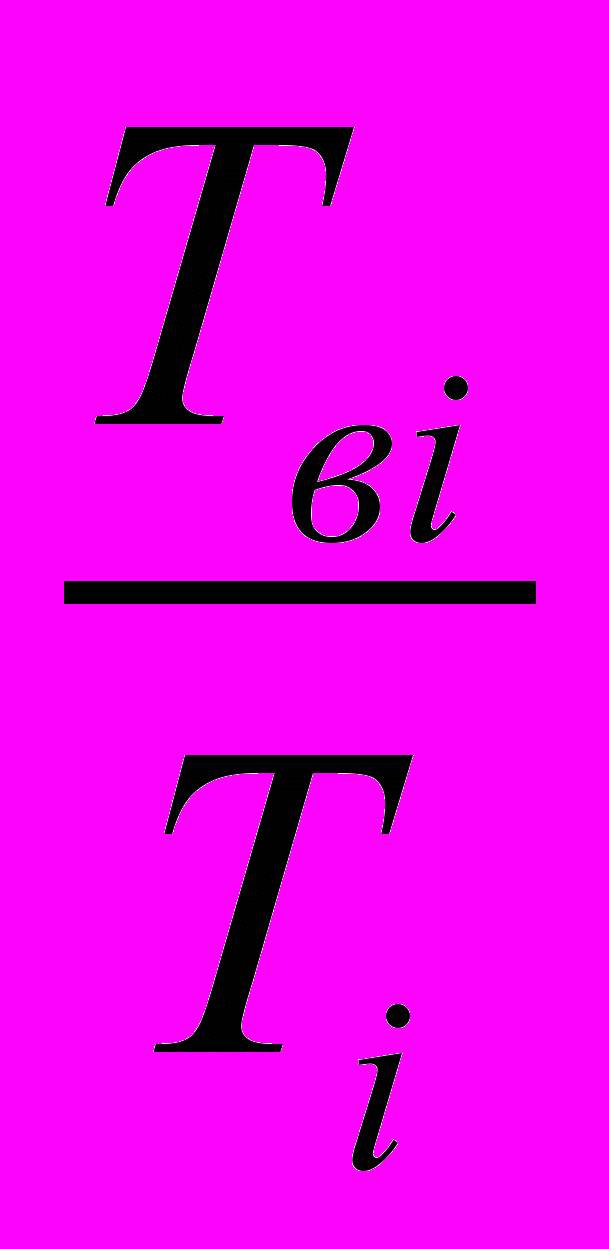, используем ее в пользовательской функции распределения прохождения заявок по принципу минимальной суммы реальной и виртуальной очереди.

Используя средства AnyLogic, реализована имитационная модель процесса диспансеризации с учетом маршрутизации реального плана расположения врачебных и лабораторных кабинетов Областной клинической больницы № 3 г. Астрахани и реальных данных времен обслуживания, на основании схемы на рис. 1., с организацией трех входных потоков. Используя метод введения виртуальных очередей, при обслуживании 150 пациентов (норма медицинского учреждения – прохождение профосмотра и дополнительной диспансеризации 150-тью обследуемыми в течение 6-ти часов) получена экономия времени 18%, что является 65-ю минутами, т.е. чуть больше часа, либо возможностью прохождения дополнительно 27-и пациентов.

В четвертой главе приводится описание программного комплекса определения характеристик и маршрутизации СМО с циклической дисциплиной похождения заявок и, как следствие, разработана система, обеспечивающая формирование управленческих решений и рациональное использование ресурсов ЛПУ для функционирования бизнес-процессов диспансеризации, профессионального осмотра и дополнительной диспансеризации населения. Диаграмма потоков данных представлена на рисунке 7.

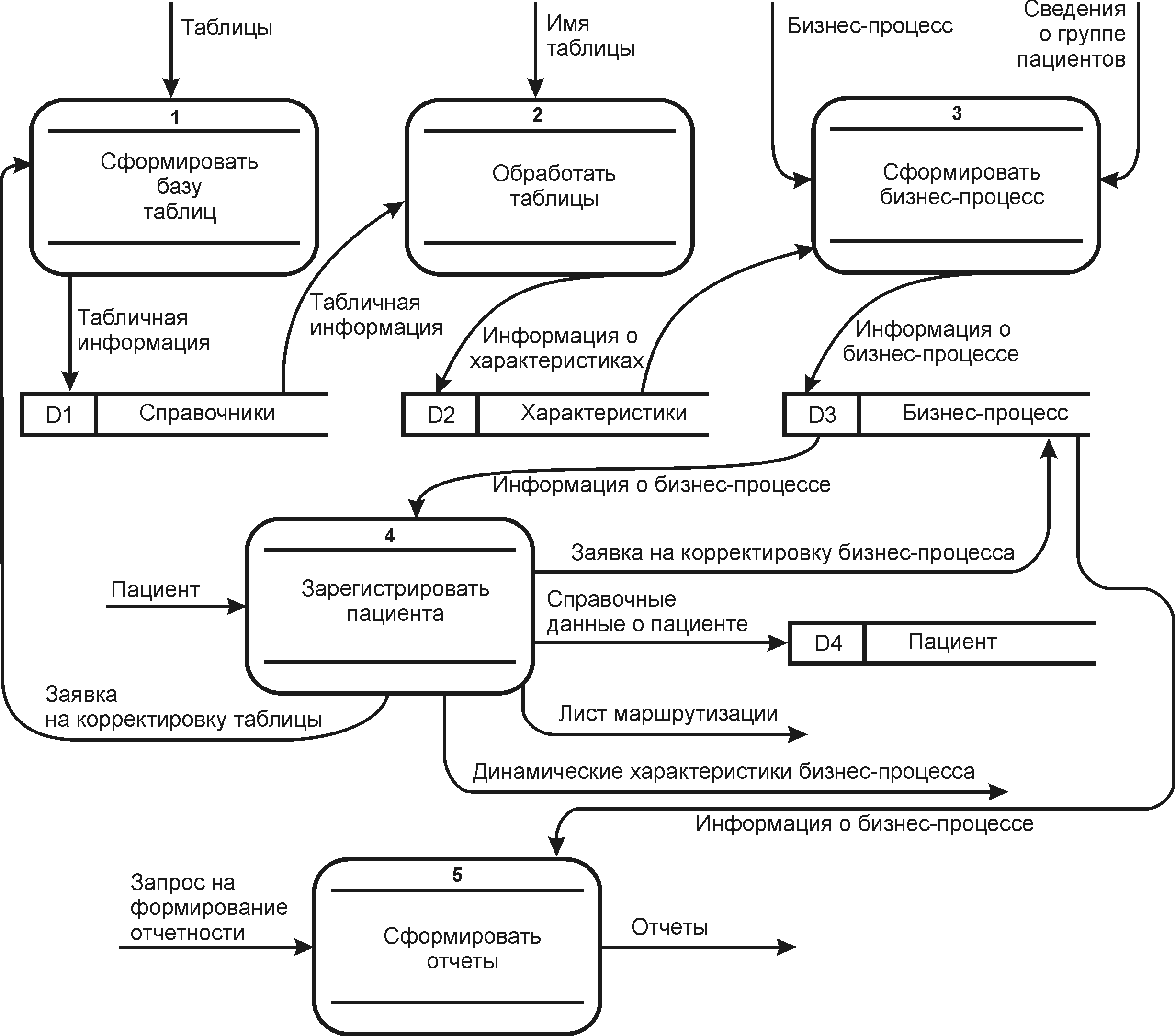Рис. 7. Диаграмма потоков данных

Модуль (1) – реализует сбор статистической информации об интервалах времен обслуживания во врачебных, процедурных и параклинических кабинетах.

Модули (2) – обрабатывает статистическую информацию, определяя типы и характеристики вероятностных распределений, используя аппроксимацию функции плотности нормального закона распределения показательным на временном интервале, используя метод наименьших квадратов и итерационный метод релаксации.

Модуль (3) – фактически создает структуру СМО, описывает входящий поток пациентов (либо путем введения теоретической частоты, либо, используя связь с модулем статистического анализа). Далее вводится количество кабинетов и повторяется процедура введения соответствующих частот, характеризующих показательные распределения, присущие каждому кабинету.

Модуль (4) – реализует регистрацию пациента и формирует листы маршрутизации (рис. 8.).

Модуль (5) – формирует отчеты о количестве пациентов, прошедших диспансеризацию, для заданных интервалов времени.

Рис. 8. Примеры листов маршрутизации для групп диспансеризуемых

В приложениях приведены свидетельства о государственной регистрации программ для ЭВМ, акт о внедрении программного комплекса проведения диспансеризации, профессионального осмотра и дополнительной диспансеризации в Областной клинической больнице №3 г. Астрахани, акты о внедрении программного комплекса определения характеристик и маршрутизации СМО с циклической дисциплиной похождения заявок в учебный процесс Астраханского государственного университета и Волгоградского государственного технического университета.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ

Основные научные и практические результаты диссертационной работы состоят в следующем:

1. Проведен обзор и анализ существующих математических методов описания немарковских процессов, который показал актуальность разработки математических методов, с целью построения моделей СМО с циклической дисциплиной прохождения заявок.

2. Проведен анализ функциональных возможностей программных реализаций ИТ-бизнес-процессов для ЛПУ, который показал необходимость разработки программного комплекса, управляющего маршрутизацией пациентов при проведении диспансеризации, профессионального осмотра и дополнительной диспансеризации.

3. Применен комплексный подход теории моделирования, объединяющий вариационный метод и метод иерархических цепочек, на основании которого введена вертикаль уровней абстракции моделирования, что позволило определить абстракции и математические методы для каждого уровня.

4. Разработан метод рекуррентного переноса нагрузки разрезов вероятностного графа – стратегический уровень абстракции, что позволило определять вероятность отказа стационарного состояния и при определенных допущениях, используя аксиоматическое утверждение Риордана, функцию распределения блока обслуживающих устройств.

5. Разработан метод матрицы преобразований Лапласа – тактический уровень абстракции, что позволило получить временные зависимости от числа находящихся в СМО и обслуженных заявок и, используя формулу Литтла, установить связь с входящим потоком при любых типах распределения времени обслуживания и интервалов поступления заявок.

6. Разработан интегральный метод представления n-линейных СМО – оперативный уровень абстракции, что позволило рассчитать вероятность отказа при любых типах распределения времени обслуживания и интервалов поступления заявок и установить асимметричность системы относительно порядка прохождения устройств.

7. Разработан метод «виртуальных очередей», препятствующий вырождению циклической дисциплины прохождения заявок в последовательную, что позволило разработать алгоритм определения маршрутизации заявок через обслуживающие устройства и реализовать его в программном комплексе.

8. Разработана имитационная модель бизнес-процесса диспансеризации, профессионального осмотра и дополнительной диспансеризации, что позволило путем проведения имитационных экспериментов установить характеристики распределения времени обслуживания во врачебных и лабораторных кабинетах и интервалов поступления пациентов, с целью ограничения времени ожидания и количества пациента в очередях.

9. Разработана и внедрена компьютерная система диспансеризации, профессионального осмотра и дополнительной диспансеризации, что привело, путем организацией управления данными бизнес-процессами, к тому, что время прохождения диспансеризации уменьшилось на 18%.

ПУБЛИКАЦИИ ПО ТЕМЕ ДИССЕРТАЦИИ

Статьи в ведущих рецензируемых научных журналах и изданиях, включенных в список ВАК РФ.

1. Холодов, А.Ю. Математическая модель проведения профессионального осмотра для учреждения здравоохранения / А.Ю. Холодов // Системный анализ и управление в биомедицинских системах. – 2006. – № 4(5). С. 786 – 793.

2. Холодов, А.Ю. Имитационная модель профессионального осмотра для анализа адекватности математической модели систем обслуживания с эйлеровскими циклами / А.Ю. Холодов // Системный анализ и управление в биомедицинских системах. – 2006. – № 4(5). С. 794 – 796.

3. Холодов, А.Ю. Метод вероятностных графов для систем массового обслуживания (СМО) с циклической дисциплиной обслуживания / А.Ю. Холодов // Южно-Российский вестник геологии, географии и глобальной энергии. – 2006. – № 8(21). С. 373 – 378.

4. Холодов, А.Ю. Метод расчета вероятности отказа в однолинейной системе обслуживания на основе функций распределений потока и обслуживающего устройства / А.Ю. Холодов // Вестник Астраханского государственного технического университета. – 2007. – № 1(36). С. 50 – 53.

5. Холодов, А.Ю. Интегральный метод расчета систем массового обслуживания / А.Ю. Холодов // Системы управления и информационные технологии. – 2007. – № 1.1(27). С. 198 – 201.

6. Холодов А.Ю., Зарипов Р.М. Метод рекуррентной нагрузки разрезов вероятностного графа для систем массового обслуживания (СМО) с циклической дисциплиной прохождения / А.Ю. Холодов, Р.М. Зарипов // Известия Волгоградского государственного технического университета: межвуз. сб. науч. ст. – 2007. – № 2(28). С. 20 – 24.

7. Холодов А.Ю. Анализ пропускной способности двухкомпонентных систем путем имитационных экспериментов / А.Ю. Холодов // Известия Волгоградского государственного технического университета: межвуз. сб. науч. ст. – 2008. – № 5. С. 146 – 153.

Другие публикации.

8. Холодов, А.Ю. Описание и создание математической модели класса систем массового обслуживания (СМО) с дисциплиной обслуживания - эйлеровским циклом как подкласса вероятностных потоков / А.Ю. Холодов // «Региональная информатика – 2006»: материалы X Санкт-Петербургской международной конференции 24-26 октября 2006 г. – СПб. – 2006. С. 60.

9. Зарипов, Р.М., Холодов, А.Ю. Математическая модель динамики процесса обучаемости / Р.М. Зарипов, А.Ю. Холодов // Инновационные технологии в управлении, образовании, промышленности «АСТИНТЕХ-2007»: материалы Всероссийской научной конференции 18-20 апреля 2007 г. в 2 ч./ сост. И.Ю. Петрова. – Астрахань: Издательский дом «Астраханский университет» – 2007. – Ч.1. С. 160 – 164.

10. Свидетельство об официальной регистрации программы для ЭВМ № 2007611266. «Автоматизированная система поддержки принятия решений для оптимизации процессов массового обслуживания потребителей в организациях сервиса на базе математического аппарата теории очередей и теории графов». Авторы Холодов А.Ю., Зарипов Р.М. Зарегистрировано в Реестре программ для ЭВМ 23 марта 2007 г.

11. Свидетельство об официальной регистрации программы для ЭВМ № 2007611555. «Имитационная модель систем управления с циклической дисциплиной прохождения обслуживающих блоков». Автор Холодов А.Ю. Зарегистрировано в Реестре программ для ЭВМ 12 апреля 2007 г.