Совершенствование средств управления эксплуатацией систем электроснабжения на основе имитационного моделирования

Вид материала

Автореферат

Содержание Рис.1 Зависимости отношения числа итераций к числу узлов для схем сетей количеством узлов у В третьей главе В четвертой главе

Подобный материал:

• Программа дисциплины Имитационное моделирование экономических процессов Семестры, 11.15kb.
• Алгоритмы и программные средства имитационного моделирования для управления эколого-экономическими, 352.92kb.
• Становление и развитие имитационного моделирования в украине, 227.76kb.
• Коллегия Управления Федерального казначейства по Самарской области (далее Управление), 11.83kb.
• Сравнение качества генерирования случайных чисел в системах имитационного моделирования, 22.53kb.
• Ачи оптимального управления, задачи оптимизации на основе имитационного моделирования, 119.11kb.
• Удк 004. 94 Взаимодействие агентов в распределенной дискретно-событийной системе имитационного, 84.04kb.
• Программно-аппаратные средства функциональной эмуляции микропроцессорных систем управления, 28.14kb.
• Исследования, научную и практическую значимость проводимых исследований; выбирать оптимальные, 147.35kb.
• Задачами дисциплины являются, 22.42kb.

» - скалярное произведение векторов и «_Т» - транспонирование.

На каждой i+1-ой итерации новые значения X_i+1 находятся в виде

X_i+1 = X_i - Т_у grad_X φ^.t (4)

с шагом t по вектору-антиградиенту, вычисленному в X_i, то есть по направлению наискорейшего спуска к абсолютному минимуму , соответствующему положению электрического равновесия по первому закону Кирхгофа для токов в узлах. Это дает значения неизвестных X_i+1, более близкие к решению линейной системы, чем исходное приближение.

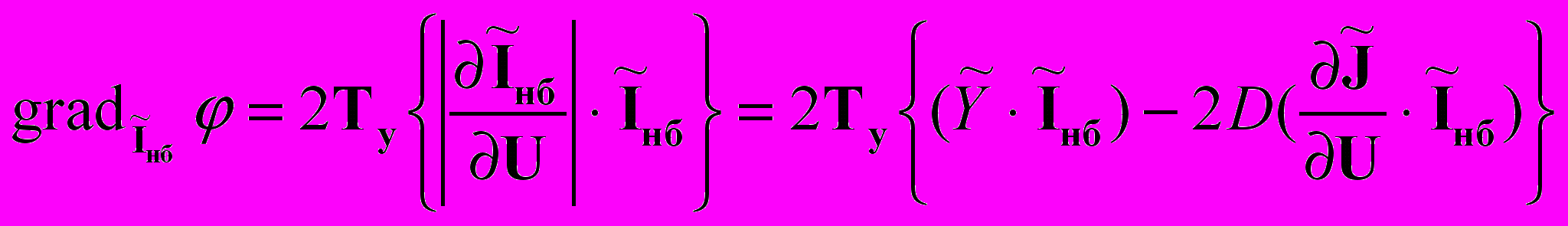; (5)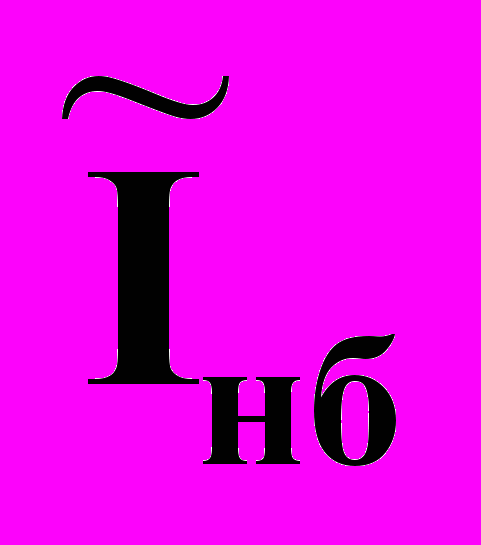

- вектор узловых токов небаланса; - вектор узловых задающих токов.

В работе приведены сравнительный анализ рассмотренных методов, а также принципы построения и основные позиции алгоритмов по выражениям (2) – (5) с помощью табличных операторов Т_ух и Т_у В них по определению вычисления проводятся только по реально существующим связям (ветвям), то есть арифметические операции с нулевыми элементами в отличие от процедур, построенных на основе матричных методов, полностью исключены.

Для расчета режима КЗ в узловой форме в работе предлагается модификация МСГ непосредственно по Т_у. При решении УР в комплексной форме производится их эквивалентное преобразование к вещественному виду и умножение основной матрицы А системы на транспонированную матрицу, чтобы она стала симметричной и положительно определенной. Предлагаемая модификация МСГ в эквивалентной вещественной форме позволяет сократить количество вычислительных операций в 2-4 раза по сравнению с комплексной формой.

Рассмотренные подходы к расчетам режимов КЗ и УР СЭС с использованием табличного способа описания ее топологической структуры реализованы в программном комплексе «ПЕГАС», разработанном в СамГТУ. В частности для фрагмента схемы электроснабжения Новокуйбышевского нефтеперерабатывающего завода выполнялись тестовые расчеты УР и режимов КЗ предложенными модификациями.

В рамках положений ИМ разработан испытательный программный комплекс (ИПК) для анализа режимов КЗ в схемах большого топологического объема на основе табличного подхода. Практическая проверка работоспособности и оценка возможностей модификации МСГ, проведена по результатам серийных расчетов режимов КЗ в сетях, в которых число узлов у > 1000.

Для этого с помощью датчика случайных чисел ИПК строит имитационные топологические модели СЭС в виде таблиц соединений и параметров ветвей. Кроме того, моделируются и формируются следующие основные эксплуатационные признаки, характеристические соотношения и положения построения сетевых структур.

Различные уровни напряжения (≤ 3) сети с произвольными процентными соотношениями состава по ступеням и связям между ними, количеству ветвей с источниками. Произвольное соотношение между числом ветвей в и узлов у (от разомкнутой до сложно замкнутой схемы - 1,0 < в/у < 2,5). Количество трансформаторных и поперечных ветвей, в частности, генераторных с характерными диапазонами сопротивлений для конкретных классов напряжения.

Рис.1 Зависимости отношения числа итераций к числу узлов для схем сетей количеством узлов у до 1000 и при в/у 1,5 < в/у < 2,5

4. Возможность выполнения расчета режима КЗ в вещественной и комплексной форме. В последнем случае – при произвольном соотношении активного и реактивного сопротивлений ветвей.
   

После окончания процесса расчета конкретного режима, когда реккуррентно вычисляемая невязка узловых небалансов по току становилась меньше наперед заданной погрешности, производилась дополнительная независимая от решения по МСГ проверка полученного решения по условиям оценки положения электрического равновесия. Иначе говоря, по рассчитанным напряжениям в узлах определялись токи в ветвях и в последовательном процессе просмотра строк Т_у формировались балансы токов в узлах.

На рис. 1 представлены результаты расчетов режимов КЗ в схемах, имеющих до 1000 узлов при различных показателях замкнутости схемы. Для объективной демонстрации численной устойчивости алгоритма верхняя граница по количеству узлов была выбрана значительно больше, чем это требуется в настоящее время.

По результатам проведенных расчетов можно сделать следующие выводы.

1. Ни в одном из вычислительных экспериментов в диапазоне до 1000 узлов не было зафиксировано случаев численной неустойчивости.
   
2. Отмечена характерная тенденция относительного уменьшения числа шагов в алгоритме МСГ при увеличении числа узлов.
   
3. Слабая зависимость числа шагов вычислительного процесса от диапазона возможных значений сопротивлений ветвей схемы, коэффициента замкнутости схемы, числа генераторных и трансформаторных ветвей.
   

В третьей главе с помощью методов табличного анализа решаются задачи, часто возникающие в процессах тренажирования и управления СЭС. Они связаны с расчетами подрежимов, отличающихся от режима, принятого за основной некоторыми изменениями параметров схемы и режима.

Характерными случаями этих изменений являются отключение существующих и подключение новых ветвей схемы, перемещение точки КЗ по ветви, сети и др. При этом нередко в расчетах возникают численная неустойчивость или полное расхождение результатов с предполагаемыми. Решение задач, связанных с этими изменениями возможно двумя способами: первый из них – изменение топологии сети. В результате перестраивается ВИМ, и по ней любым методом расчета режимов находится новое решение. В качестве второго способа, прежде всего, для режимов КЗ в сложнозамкнутых сетях для анализа подрежимов предлагается использовать метод наложения.

В частности, хорошо известно, что с помощью этого метода действительный режим КЗ можно рассматривать как результат наложения собственно аварийного режима на предшествующий доаварийный.

При решении систем уравнений узловых напряжений и контурных токов, составленных в комплексной форме, с основными матрицами узловых проводимостей Y_у и контурных сопротивлений Z_к для них применяют общепринятое L-U разложение на произведение двух треугольных матриц. С учетом слабого заполнения оно реализуется в так называемой упорядоченной форме (в виде табличных списков) для минимизации появления новых нулевых элементов.

Факт изменения основных матриц систем уравнений узловых напряжений и контурных токов в подрежимах очевиден. Поэтому в работе предлагается методика расчета подрежимов без изменений матриц Y_у и Z_к основного режима, но с их косвенным учетом с помощью метода наложения. При этом становится возможным самую трудоемкую операцию L-U разложение для анализируемой расчетной схемы выполнить только один раз. В работе даны расчетные процедуры учета в правых частях основной системы уравнений физических условий и изменений, связанных с моделированием подрежимов.

В частности, по результатам решения систем уравнений с помощью L-U разложения, можно найти комплексный вектор токов ветвей 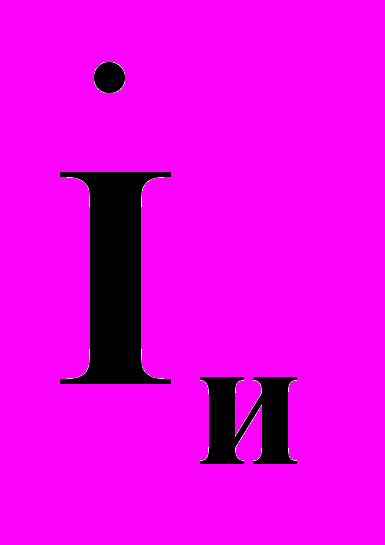исходного режима, а далее - токораспределение 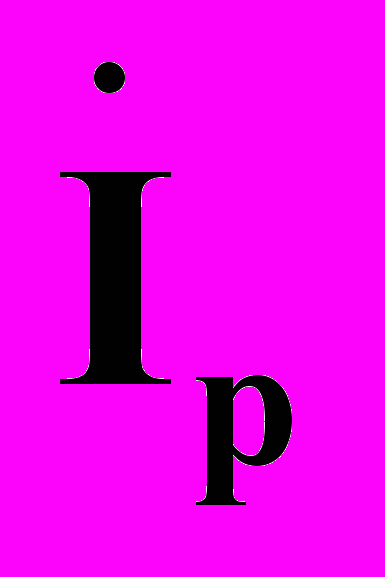для подрежима, отличающегося, например, от исходного режима совместным отключением и подключением ветвей j, k, l, f. Для этого на исходный режим (рис. 2) накладывается искусственный (рис. 3), в котором в отключаемых ветвях включены источники э.д.с. 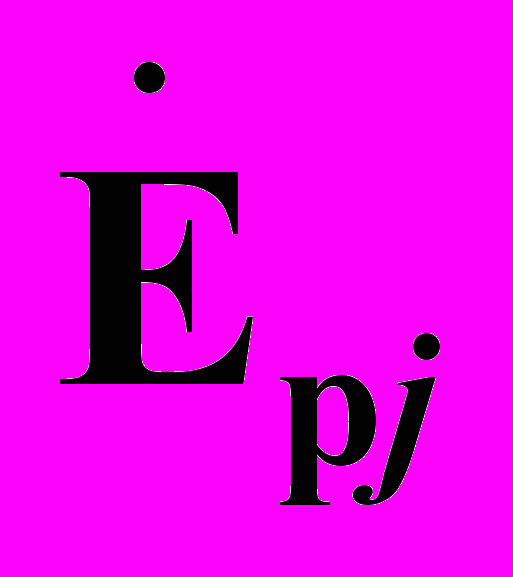, , создающие в этих ветвях совместным действием токи 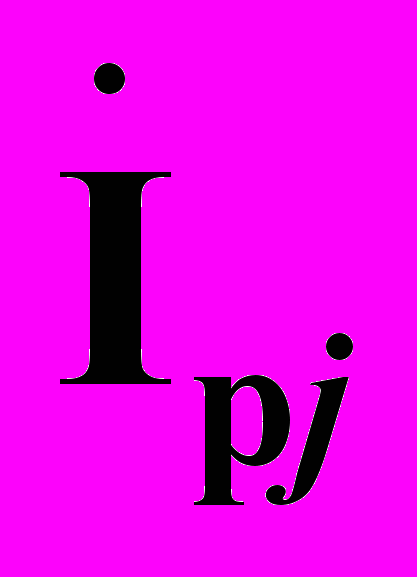, , 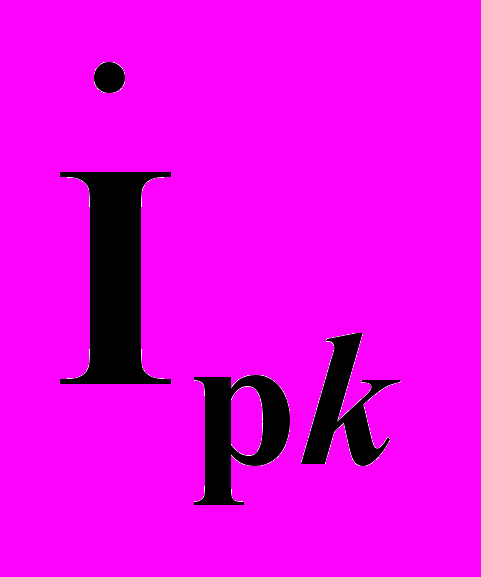равные по величине токам исходного режима 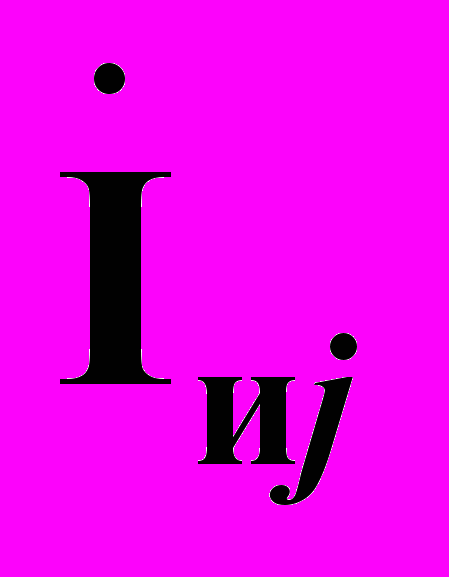, , но противоположные по направлению. В результате наложения искусственного режима на исходный, токи в ветвях j, k будут отсутствовать. В подключаемых ветвях вводятся источники тока 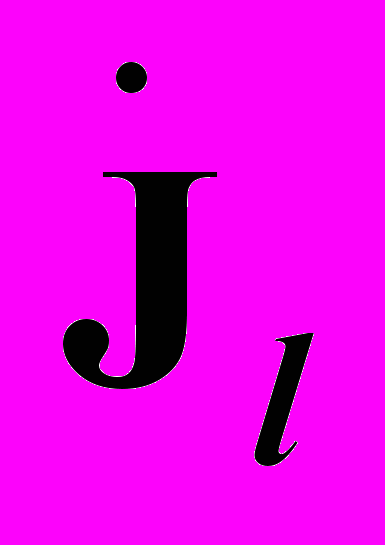, 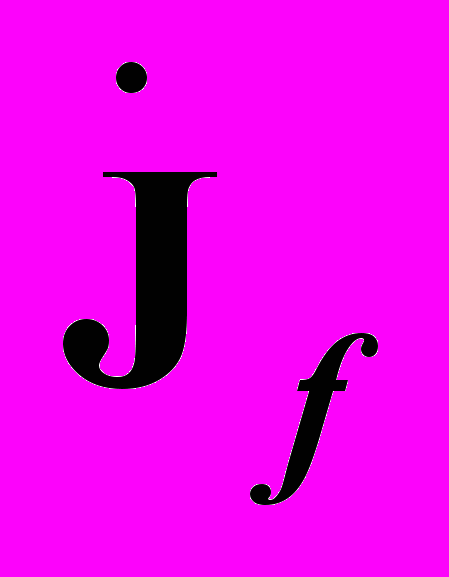суммарное действие которых должно обеспечивать на каждом из них напряжение подключения 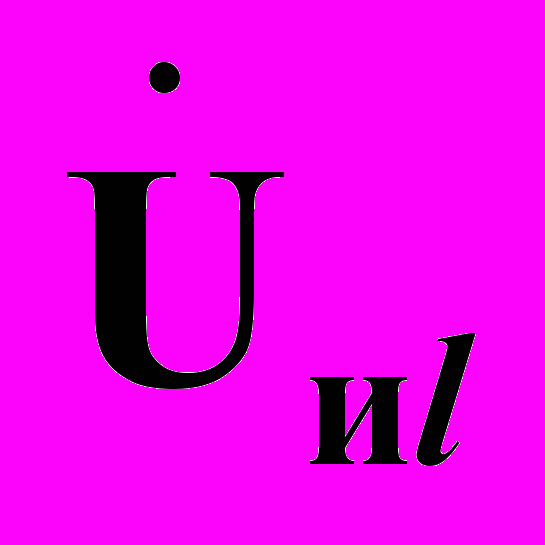, , равное тому, которое было между узлами подключения каждой новой ветви в исходном режиме.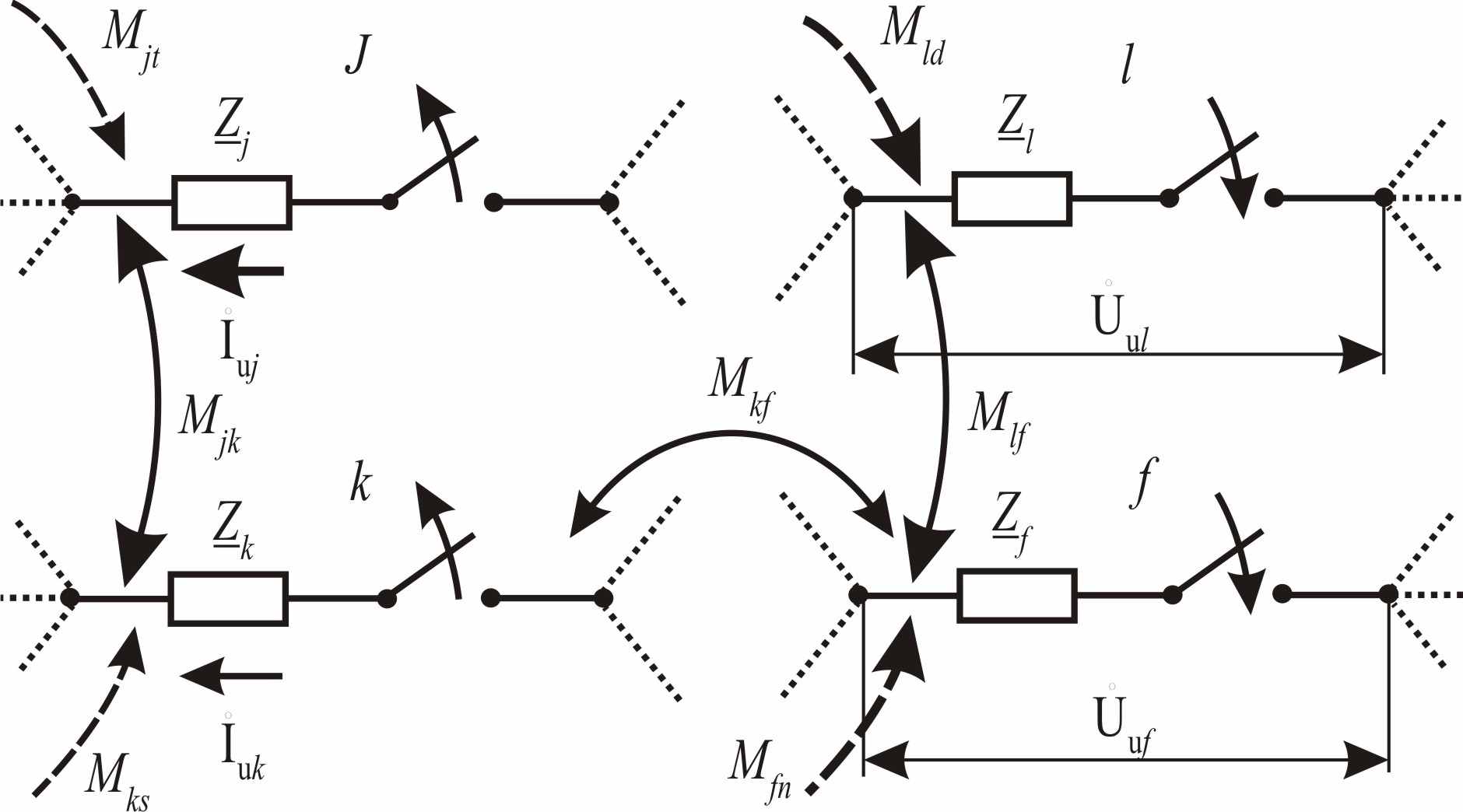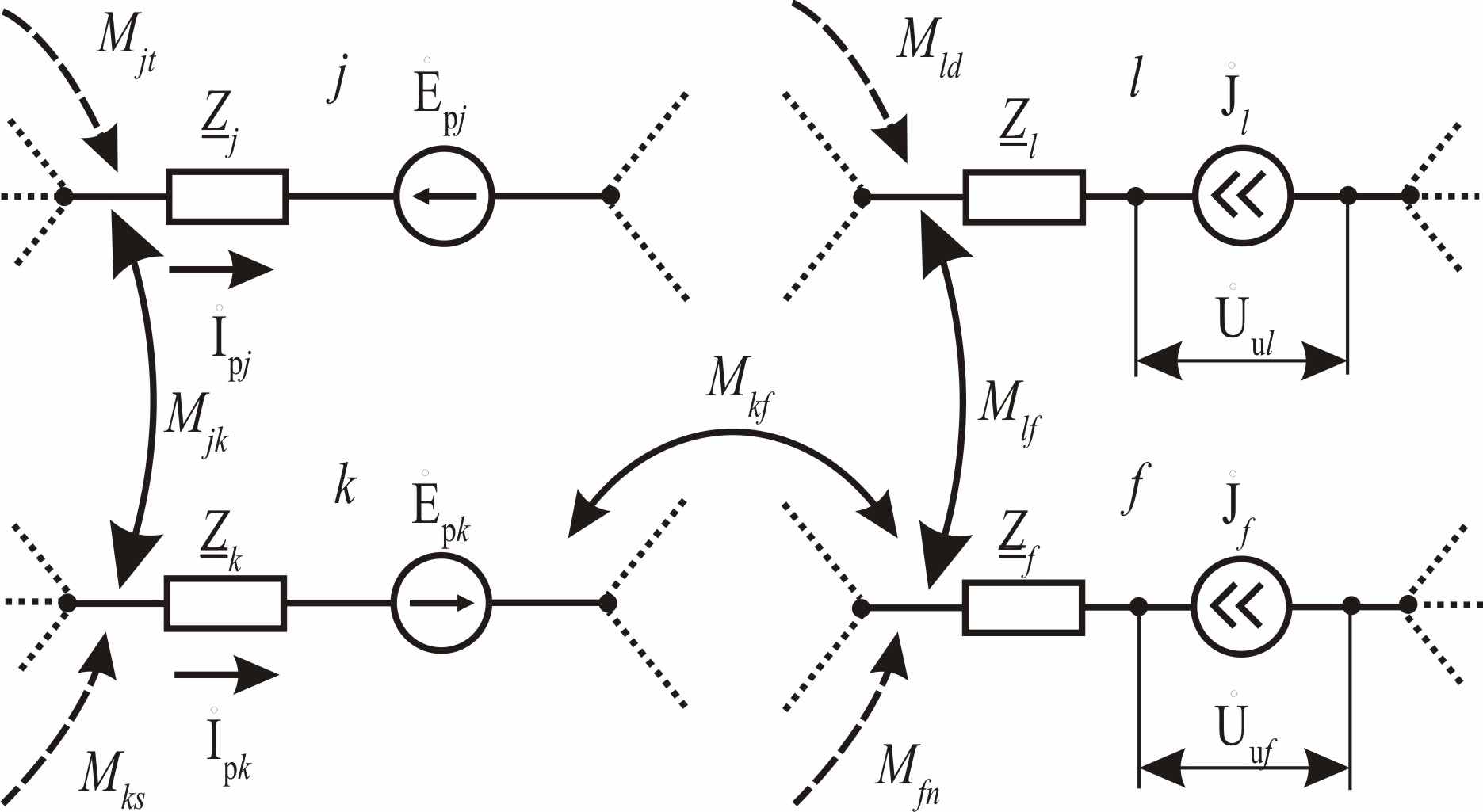

Рис. 2 Исходный режим	Рис. 3 Искусственный режим

При произвольном числе отключаемых n_о и подключаемых n_п ветвей система уравнений для определения значений э.д.с. и токов соответственно источников напряжения и тока может быть записана в матричном виде в комплексной форме

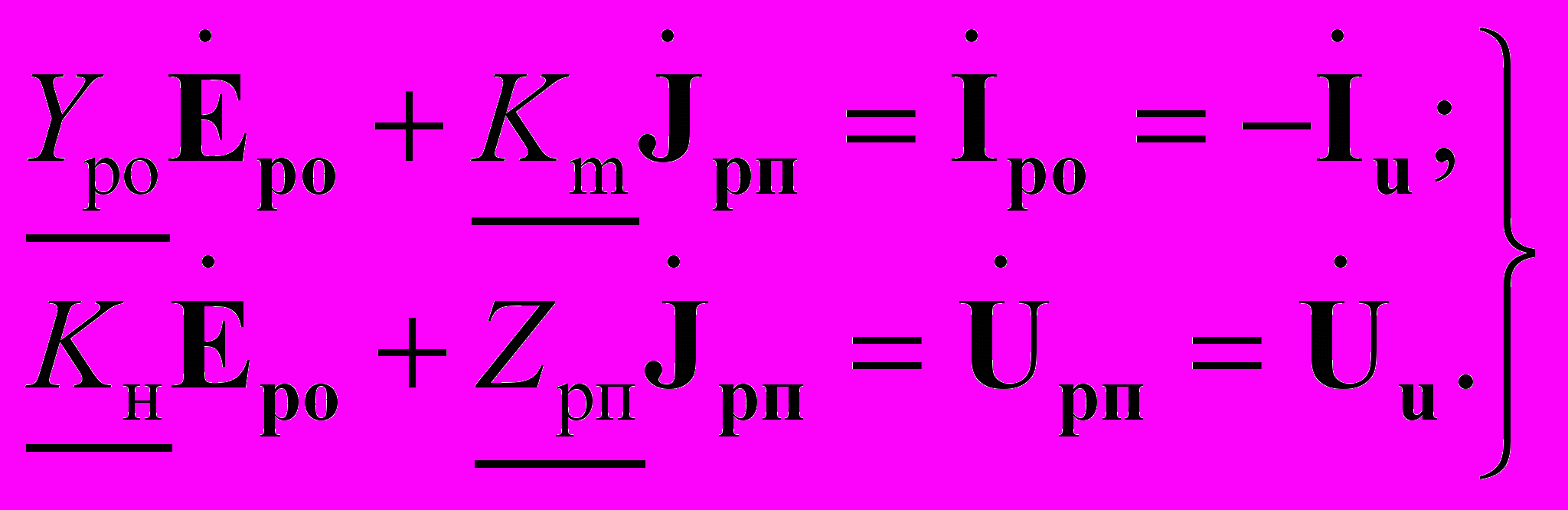(6)

где 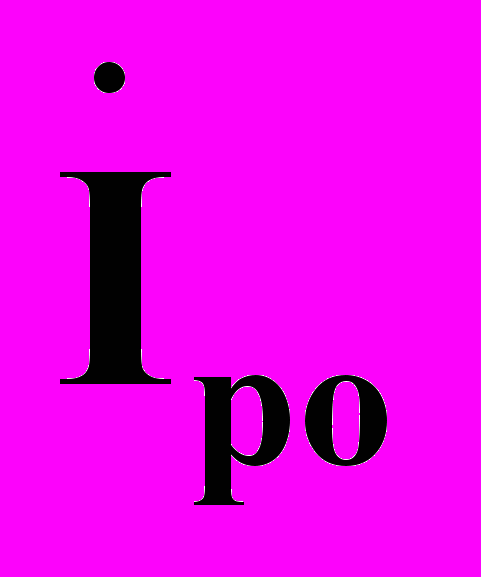- ток, создаваемый источником напряжения в искусственном режиме при отключении линии, равный по величине исходному току 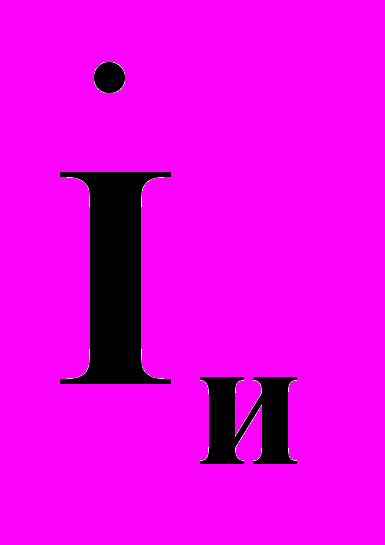, но противоположный ему по направлению; 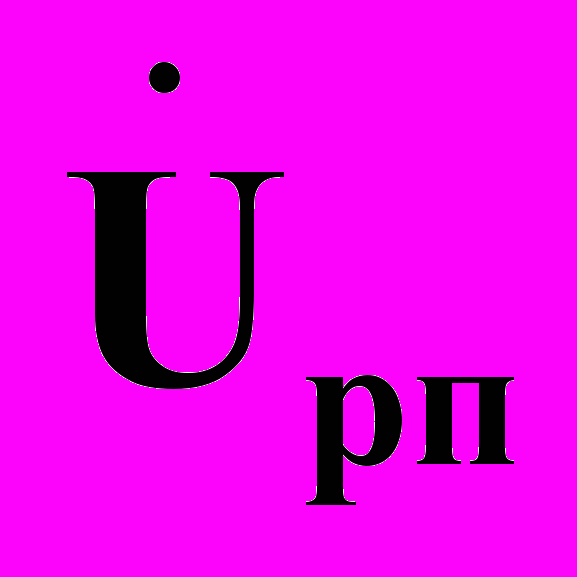- напряжение на зажимах источника тока, вводимого в схему при подключении линии, равное исходному напряжению ; Y_ро и Z_рп - подматрицы узловых проводимостей и контурных сопротивлений при отключении и подключении линий соответственно; и - источники тока и э.д.с при подключении и отключении линии, соответственно.

Число уравнений в системе (6) равно (n_о+ n_п). Размерности векторов , 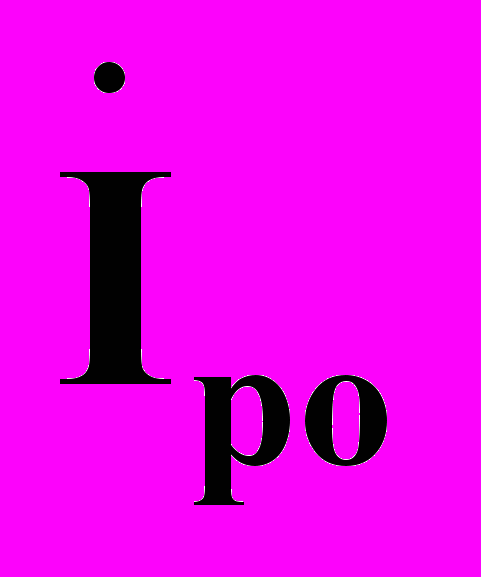и , , 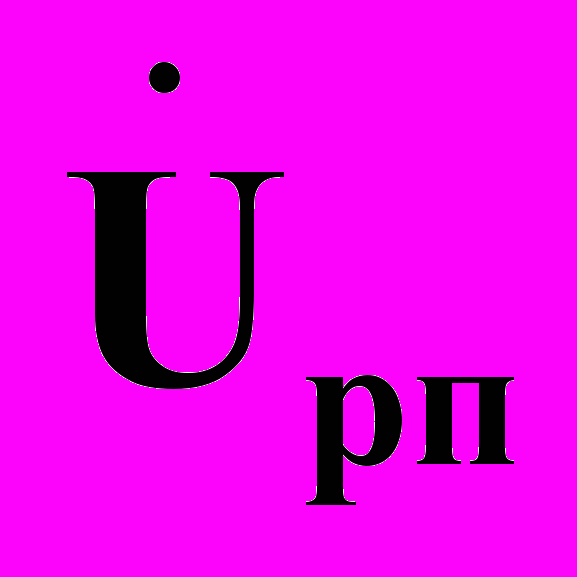a также подматриц Y_ро и Z_рп определяются соответственно числами n_о и n_п. Подматрица К_т, имеющая размерность (n_о, n_п), определяет коэффициенты связей по току ветвей с источниками тока и ветвей с источниками напряжения, или, иначе говоря, между подключаемыми и отключаемыми ветвями. Аналогично подматрица К_н, имеющая размерность (n_п, n_о), определяет коэффициенты связей по напряжению ветвей с источниками напряжения и ветвей с источниками тока, или между отключаемыми и подключаемыми ветвями.

Определение элементов подматриц Y_ро и Z_рп производится по результатам расчетов парциальных режимов (ПР). ПР определяются по тому же треугольному разложению основной матрицы сети. При этом для наиболее простого случая, когда отключается одна ветвь, рассматривается искусственный режим, в котором все источники сети отключены, а в рассматриваемой сети включен единичный источник эдс, направленный против тока предшествующего режима. Этот режим и получил название парциального.

Теперь после решения для него основной системы уравнений, по соотношению предшествующего и парциального тока данной ветви определяется коэффициент пропорциональности, позволяющий получить значение эдс источника из граничного условия по равенству тока отключаемой ветви току предшествующего режима, а также все токи и напряжения от этого одного искусственного источника. Накладывая этот режим на исходный, получаем ноль – отсутствие тока в отключенной ветви и, соответственно, токи и напряжения режима в новом состоянии сети.

Аналогично источники тока определяются в ПР и для подключения ветвей, только в этом случае подключаются единичные источники тока, и определение граничных условий производится по напряжениям.

С использованием предлагаемых принципов в работе решаются и другие задачи: изменение параметров ветвей, в том числе и коэффициентов трансформации, подключение и отключение источников в сети, и изменение их режимного состояния, перемещение точки короткого замыкания по узлам и ветвям сети и т.д.

В результате решения системы (6) определяются значения э.д.с. и токов источников напряжения и тока, являющиеся коэффициентами пропорциональности изменения величин токов парциальных режимов и токораспределение 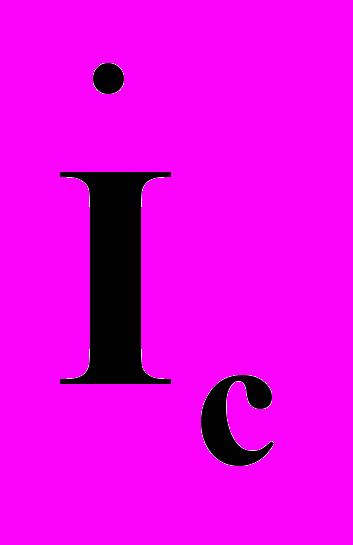подрежима совместного подключения и отключения ветвей:

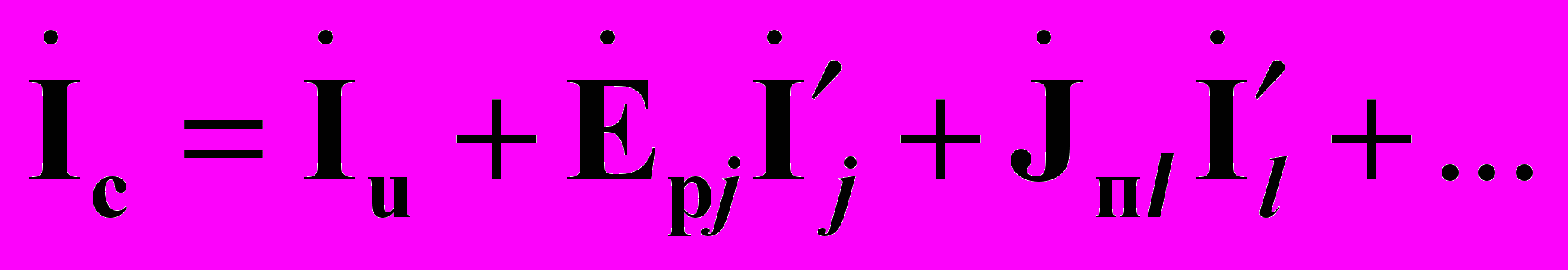(7)

Предлагаемая методика анализа подрежимов КЗ реализована для ряда схем структурных предприятий ОАО «МРСК Волги».

В четвертой главе констатируется, что в настоящее время в СЭС измерительные датчики и преобразователи, устройства сбора телеинформации, средства связи и пр. имеют большой физический износ и морально устарели. Кроме того, на подстанциях, вторичные цепи нередко работают с перегрузкой. Все это приводит к тому, что ОДП довольно часто не имеет всей необходимой информации о текущем режиме СЭС, или она неточна или недостоверна. В результате на ОДП значительно увеличивается аналитическая нагрузка, т.к. необходимо не только анализировать сам режим и, но также оценивать и учитывать возможную неточность имеющейся у него информации. При этом ОДП может принимать неверные решения, приводящие даже к аварийным ситуациям.

Решение проблемы восстановления параметров режима по данным ТИ с оценкой достоверности измеренных и расчетных данных основывается на использовании таблично-топологического узлового метода (ТТУМ), реализованного в ЕИТП.

Из существующих методов оценки режимов СЭС широко распространены матричные методы. Основным моментом в этом случае является построение матриц инциденций и операции с ними. При реализации матричных алгоритмов необходимо применять специальные меры по формированию, упаковке и обработке матриц инциденций, что делает их громоздкими. Кроме этого, эти методы в построении портрета режима используют весь набор приходящих данных, в том числе с ошибками, которые интегрально влияют на конечный результат.

Предлагаемый метод позволяет определить искомые параметры режима в комплексной форме по измеренным модулям напряжения и по составляющим активной (P) и реактивной (Q) мощности на основе одной из заданных форм исходной информации и уравнений четырехполюсника.

1. Модули напряжений КУ (U) и потоки P и Q мощности по ветвям дерева схемы сети, связанных с данным КУ (форма PQU).
   

2. Потоки P и Q и модули токов (I) по ветвям дерева схемы, связанных с данным КУ (форма PQI).

3. Модули U в КУ, потоки Р и модули I в ветвях дерева схемы, связанных с данным КУ (форма PUI).

4. Модули U в КУ, потоки Q и модули I в ветвях дерева схемы, связанных с данным КУ (форма QUI).

Форма PQU

1. КУ на входе четырехполюсника

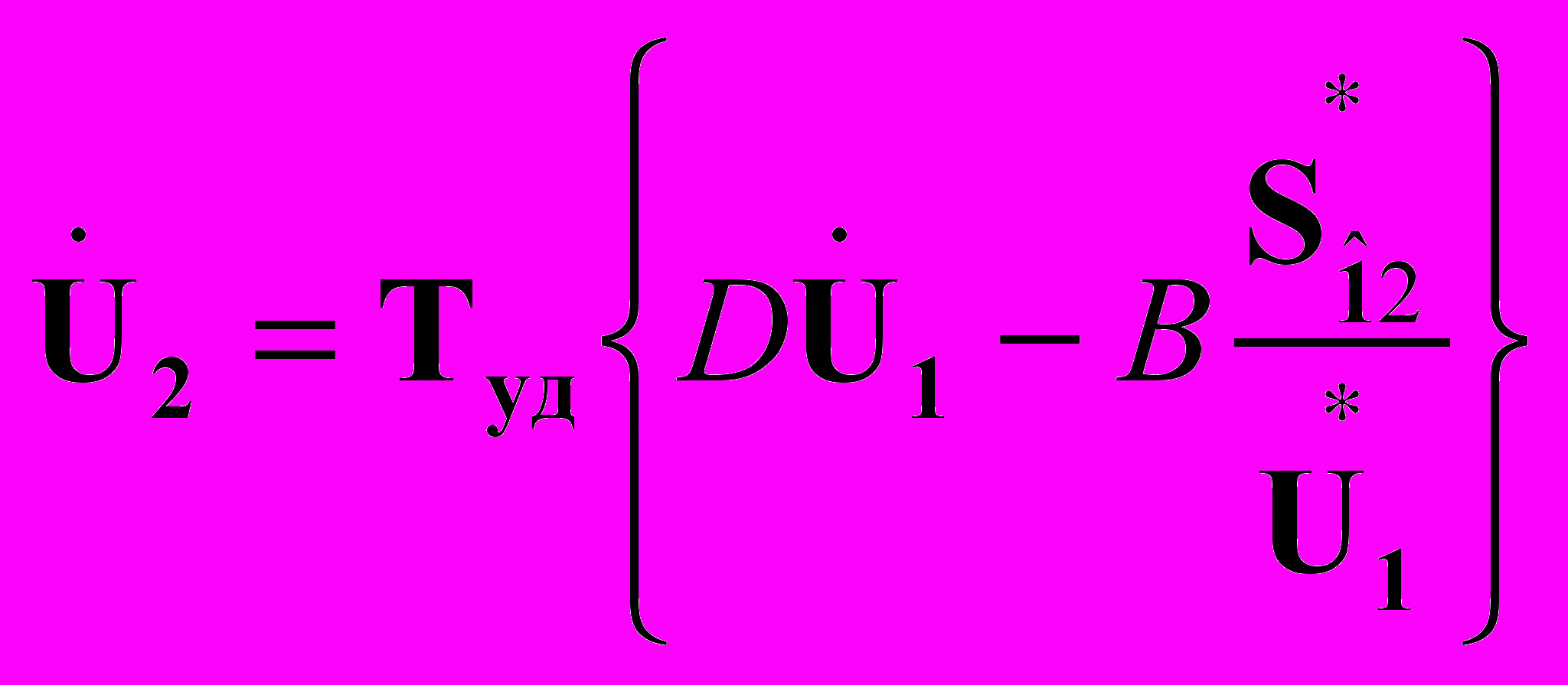(8)

2. КУ на выходе четырехполюсника

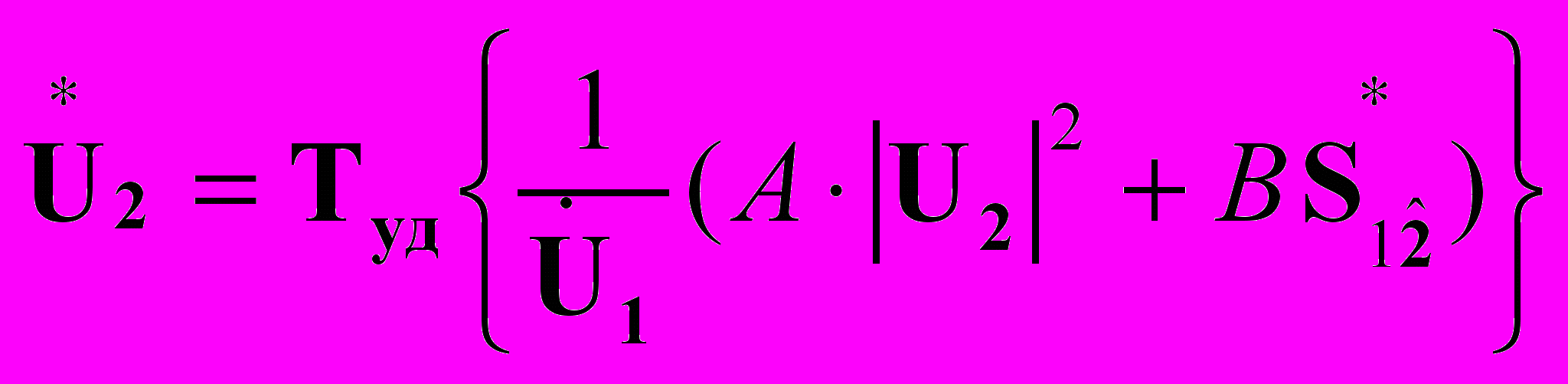(9)

Форма PQI

1. КУ на входе четырехполюсника. Выражение для этого случая совпадает с (8).

2. КУ на выходе четырехполюсника.

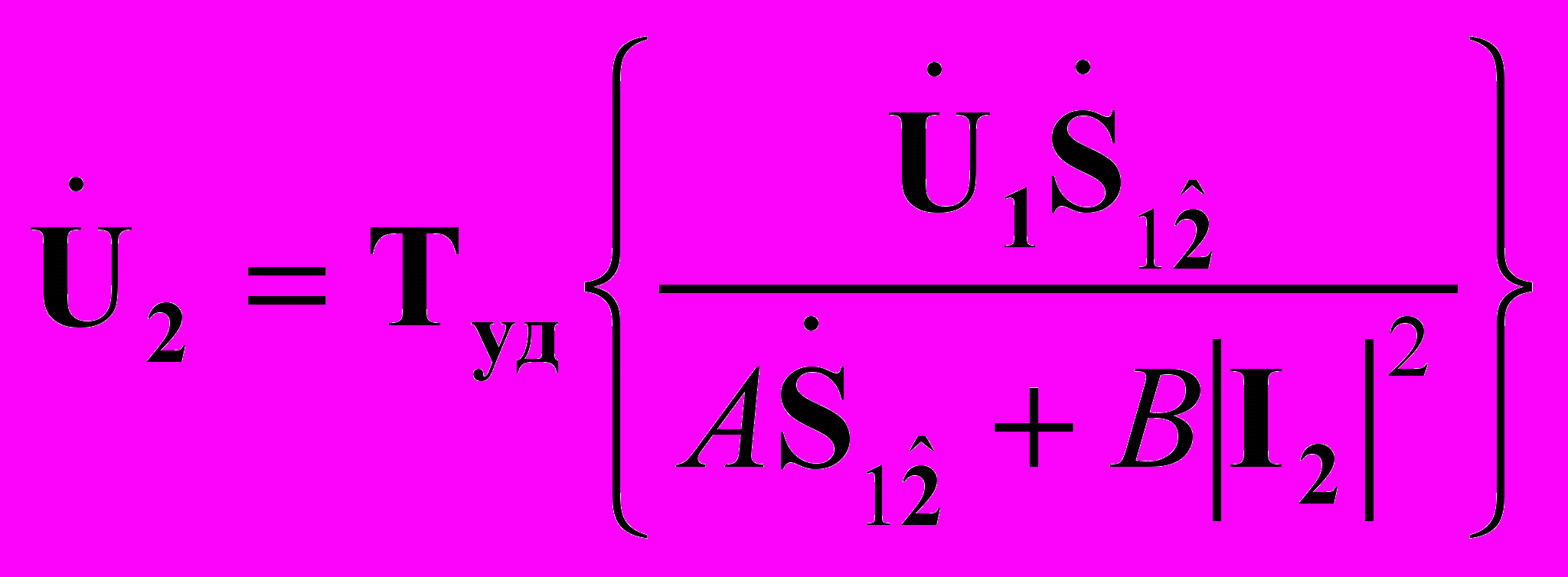(10)

В выражениях (8-10) Т_уд – это оператор табличной реализации расчета узловых напряжений по ветвям дерева схемы. Для форм PUI и QUI определяется по выражениям, записанным для двух предыдущих вариантов задания исходной информации, но только с учетом правильного выбора направления потоков соответствующих мощностей. При этом можно выделить ветви, для которых условные направления потоков Р и Q совпадают. При произвольном направлении потоков Р и Q между двумя соседними узлами эти мощности необходимо определять, выполнив четыре расчета при всех возможных сочетаниях знаков. Расчет с правильным выбором знаков даст совпадение расчетного модуля напряжения узла конца с заданным.

Названные уравнения записаны относительно входа и выхода четырехполюсника, что соответствует условному началу (НВ) и концу (КВ) ветви. При этом для расчета режима текущей ветви дерева возможны только два случая: а) модуль измеренного (ИН) и комплекс рассчитанного напряжения (РН) находятся в узле условного НВ (по ходу дерева); б) модуль ИН находится в конце, а комплекс РН - в узле условного НВ. В обоих случаях необходимо определить комплекс напряжения 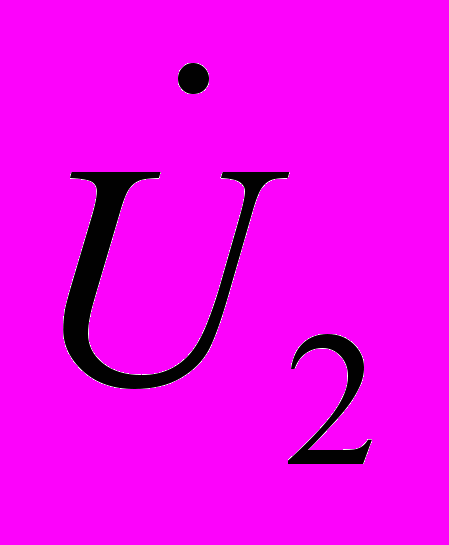в узле, являющемся условным КВ.

В диссертации представлены эффективные алгоритмы выбора состава дерева и расстановка расчетных КУ по одному из деревьев электрической схемы с произвольным выбором одного из них в качестве узла корня дерева.

Полученные расчетные выражения являются универсальными, так как при решении данной задачи с помощью уравнений режима четырехполюсника могут быть представлены схемы замещения любых элементов системы. В работе предложены расчетные выражения для различных схем замещения ветвей.

Предлагаемый метод практически не зависит от полноты исходной информации. В условиях избыточности всей схемы вся информация по узлу, а также о потоках мощности в ветвях используется для контроля результатов и самих измерений. В ненаблюдаемых участках схемы используются псевдоизмерения, которые формируются на основе данных контрольных замеров. Их точность определяется весовыми коэффициентами, которые назначаются по результатам экспертных оценок с использованием статистических методов оценки погрешностей измерений замеров. При задании псевдоизмерений их точность устанавливают в несколько раз меньше точности реального телеизмерения подобного вида в зависимости от качества исходной информации.

В процессе решения задач восстановления режимов СЭС по данным ТИ и учета электроэнергии встает кардинальная проблема определения соответствия портрета – образа расчетного режима измеренным данным. При использовании последних необходимо учитывать их несовершенство, вызванное наличием систематических и спорадических (случайных) ошибок, отклонений и сбоев.

По результатам анализа статистических данных о нарушениях и сбоях в работе ТИ структурных подразделений ОАО МРСК Волги в работе приведены классификация ошибок поступающих ТИ и способы их устранения.

С позиций ТРО основной задачей анализа СЭС является приближение так называемого виртуального портрета режима к реальному режиму сети. Другими словами необходимо установить сходства и различия между ИП и РП сети. Переход от реального режима к его виртуальному портрету осуществляется на основе ИМ, реализуемого с помощью ТМ и установления критериев соответствия между реальной сетью и ее аналогом.

На основе ТРО в работе сформированы формализованные критерии к оценке правдоподобия образа. Далее в таблице 1 приведены критерии правдоподобия образов – портретов режимов СЭС. Эти критерии позволяют проверить достоверность получаемых оценок всей системы в целом и по каждому узлу, параметру в отдельности.


Таблица 1