Geum.ru

Удк 51-72: 574 математическое моделирование загрязнения углеводородами акваторий морей континентального шельфа

Вид материалаДокументы

Содержание


Mathematical modelling of pollution by hydrocarbons of the water areas continental shelf
Key words
Математическое моделирование динамики распространения
Подобный материал:
УДК 51-72:574


МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЗАГРЯЗНЕНИЯ УГЛЕВОДОРОДАМИ АКВАТОРИЙ МОРЕЙ КОНТИНЕНТАЛЬНОГО ШЕЛЬФА


Корнев А.А.

Кубанский государственный университет



Аннотация

В статье предложена модель динамики распространения и деструкции выбросов углеводородов при разведке и освоении нефтегазовых месторождений континентального шельфа. Использование указанной модели в численных экспериментах при различных гидрометеорологических ситуациях позволит вычислять направление, скорость движения нефтяного пятна и место контакта нефти с линией берега, а также определять возможные последствия нефтяного загрязнения побережья после аварийного разлива нефти.


Ключевые слова: математическое моделирование, загрязнение, акватории, нефть, континентальный шельф.


MATHEMATICAL MODELLING OF POLLUTION BY HYDROCARBONS OF THE WATER AREAS CONTINENTAL SHELF


Kornev A.A.


Kuban State University


Annotation: In article the model of distribution and destruction emissions of hydrocarbons at investigation and development of oil and gas deposits of a continental shelf is offered. Use of the specified model in numerical experiments at various hydrometeorological situations will allow to calculate a direction, speed of movement of an oil spillage and a place of contact of oil with a coast line, and also to define possible consequences of oil pollution of coast after emergency flood of oil.


Key words: Mathematical modelling, pollution, water areas, oil, continental shelf.


Введение

За последние 20-30 лет доля нефти и газа в мировом топливно-энергетическом балансе потребления составляет более 70% от всех видов источников энергии. Поисково-разведочные работы на нефть и газ производятся на шельфах более 70 стран [1].

Российская Федерация обладает самым обширным в мире шельфом, площадь которого составляет почти 22% общей площади континентального шельфа Мирового Океана. Перспективными на нефть и газ являются 90% этой площади, основная часть которой приходится на замерзающие моря с тяжелым ледовым режимом, суровыми природно-климатическими условиями и слабо развитой береговой инфраструктурой (арктические и дальневосточные моря) [2], а значит повышенными рисками возникновения аварийных ситуаций.

Степень освоения арктических шельфовых углеводородных ресурсов России чрезвычайно низкая. И хотя в морях российской Арктики аварий на поисковых и разведочных скважинах не было, опыт бурения в Северном море (данные компании STATOIL) показал, что вероятность выброса на скважинах составляет 0,7-0,8%. Очевидна необходимость рассмотрения аварийных ситуаций.

Авария на буровой установке или платформе может сопровождаться поступлением из скважины углеводородов, которые окажут прямое токсичное действие на морских гидробионтов. При этом на поверхность также будут вынесены остатки бурового раствора, шлама и пластовые воды. Поражение биоты будет зависеть от объёма и продолжительности выброса, концентрации конкретных загрязнителей, видовой чувствительности к ним организмов и экологических факторов морской среды (сезон года, температура, освещённость и др.).

Разлив нефти в морской среде подавит на некоторое время первичную продуктивность за счёт снижения численности фитопланктона. Будет заторможен фотосинтез у водорослей. Повысится численность нефтеокисляющих и сапрофитных форм. За счет поражения систем дыхания пострадает зоопланктон. Подвижные беспозвоночные и рыбы уйдут из зоны загрязнения, но если авария произойдет в период нереста, пострадает ихтиопланктон. Если нефтяная пленка дойдет до прибрежных зон, неизбежно воздействие на биоту литорали и эстуариев. При этом в небольшой мере пострадает береговая растительность. Будет нанесен ущерб популяциям птиц за счет загрязнения перьевого покрова и заглатывания нефтеуглеводородов, морским млекопитающим от потери изолирующих свойств кожи, а также от поедания рыб, уже накопивших токсичные вещества [3].

Восстановление биоценозов после такого воздействия может произойти не ранее, чем через 6-7 лет, хотя численность планктона восстановится быстро. Нужно также учитывать, что длительные (1 месяц и более) воздействия нефтепродуктов на морских животных в концентрациях, меньших ПДК, ведут к необратимым структурным изменениям в мозговой ткани, нарушающим поведение.

Чтобы разобраться в последствиях аварийных ситуаций при освоении морских месторождений нефти и газа, целесообразно смоделировать динамику распространения и деструкции углеводородных выбросов. Полученные данные можно использовать для оценки экологического воздействия на окружающую среду деятельности по добыче углеводородов.


Математическое моделирование динамики распространения

нефтяных разливов в условиях геологоразведочных работ

на континентальном шельфе

В настоящее время одним из наиболее экспрессных и информативных методов для исследования динамики углеводородных загрязнений является математическое моделирование (Г.И. Марчук [4] , Л.Н. Тарасенко [5]).

К настоящему моменту разработано не мало математических моделей, описывающих динамику развития нефтяных разливов для различных водных территорий [6]: Принстонская модель (Princeton Ocean Model) разлива нефти компании «ЛУКОЙЛ» для Азербайджанского сектора Каспия; модель пятна на основе исследований, проведенных Государственным Институтом Океанографии РАН для акватории Финского залива (Транзас P1SCES2, 2005г.); математическая модель по ликвидации разливов нефти и спасению людей для Сахалина (ДВНИГМИ, 1997г.). Моделирование аварийных разливов нефти производилось также на моделях участков рек Иртыша, Оби, Волги, Невы, в акватории Обской губы. Разработаны также модели, где особое внимание уделено моделированию физико-химическим свойствам нефтяно­го пятна (ВЦАН СССР, 1987г.). Ряд авторов исследовали процесс движения нефти и имитировали турбулентную диффузию посредством моделирования случайного блуждания частиц нефти (Йохасен, 1995; Элиот, 1998).

Для решения задач, поставленных в рамках гранта РФФИ № 06-05-96624 «Прогнозирование и мониторинг чрезвычайных ситуаций выбросов углеводородов при проведении буровых работ на морском шельфе», автором совместно с Дембицким С.И., А.В. Ларионовым, О.В. Паниной и М.Х. Уртеновым, проводится математическое моделирование динамического взаимодействия разливов нефти с экосистемой моря и морского побережья внутренних морей Азово-Черноморского бассейна. В качестве основных процессов депонирования разливов нефти рассматривается осаждение нефти на берег моря и на дно. Исследуемый процесс загрязнения экосистем описывается краевыми задачами для системы нелинейных уравнений в частных производных, включающих уравнение Невье-Стокса и уравнения физико-химических реакций в водной среде и на суше. При коли­чественном описании разлива нефти на поверхности моря нефтяной разлив описывается как ансамбль нефтяных пятен, каждое объемом до 2 м3 нефти. Для выполнения расчетов необходимо учитывать сведения о вязкости и плотности разлитой нефти, а также скорости вытекания нефти, определяющей размеры элементарного нефтяного пятна. Для описания депонирующей среды, в которую поступает разлитая нефть, в модели должны учитываться: кинематическая характеристика поверхностного течения; сведения о направлении и силе ветра; волнении моря; геоморфологии береговой линии, определяющие экспозицию и «поглощающую способность» береговой линии; координаты источника выброса.

В качестве уравнения, описывающего распространение i-той факторизованной фрак­ции с концентрацией Сi под влиянием турбулентной диффузии, полей ветров и течений с учетом j-той физико-химической реакции или биологического окисления Rj, принято сле­дующее уравнение переноса и диффузии с учетом реакций деструкции нефти [7]:

, (1)

где Ci(x, у, z, t) - концентрация загрязнения, мг/м2; х, у, z - декартовые координаты текущей точки, м; t - время, с; u, v, w - компоненты вектора скорости поверхностного течения, м/с, удовлетворяющего уравнению неразрывности

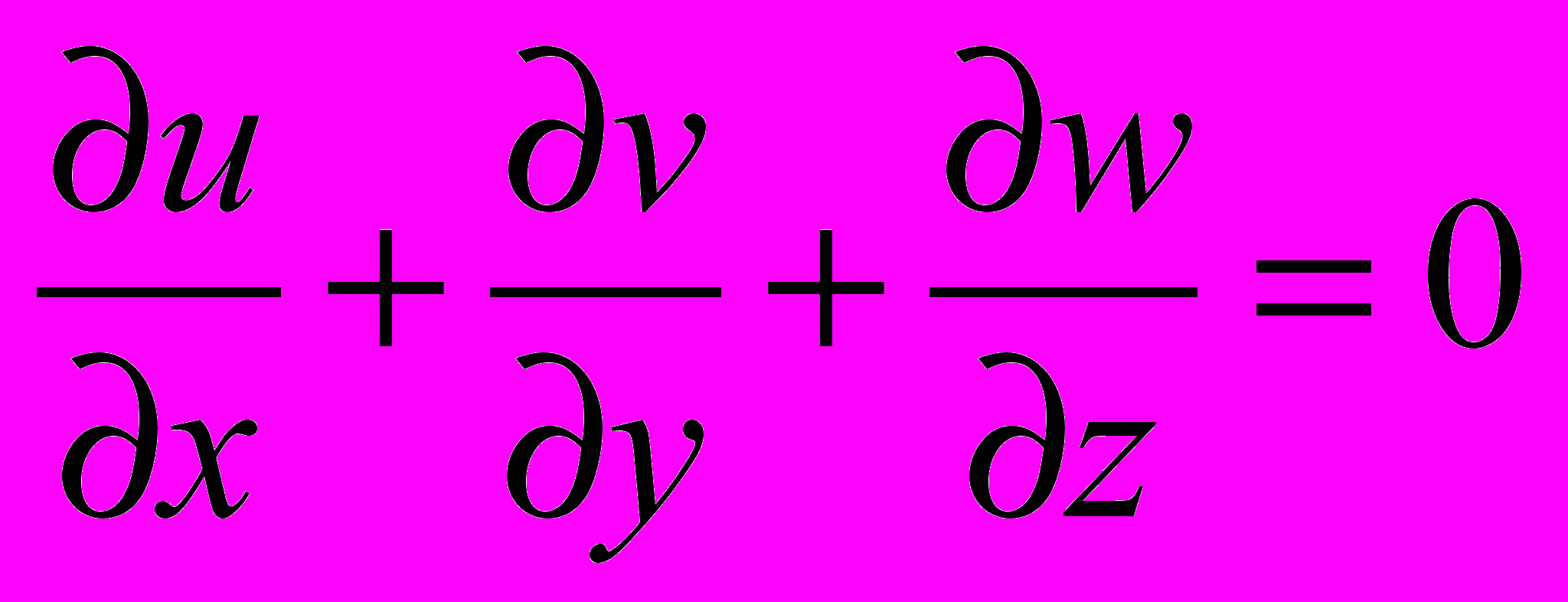, (2)

Kx, Ky, - коэффициенты турбулентной диффузии в плоскости (х,у), м2/с; Kz - коэф­фициенты вертикальной диффузии, м2/с; F(Ci, Rj) - функция, определяющая деструкцию i-той факторизованной фракции в результате j-той реакции Rj (испарение, растворение, био­логическое окисление). Математическая модель динамики нефтяного загрязнения с учётом всех реакций получается при использовании суперпозиции результатов для каждой фракции с учётом каждой реакции.

При достижении границы Г1, в зависимости от физико-химических свойств нефти и морфологической структуры побережья, происходит отражение, частичное или полное при­липание нефти, а соответствующие граничные условия задаются в виде

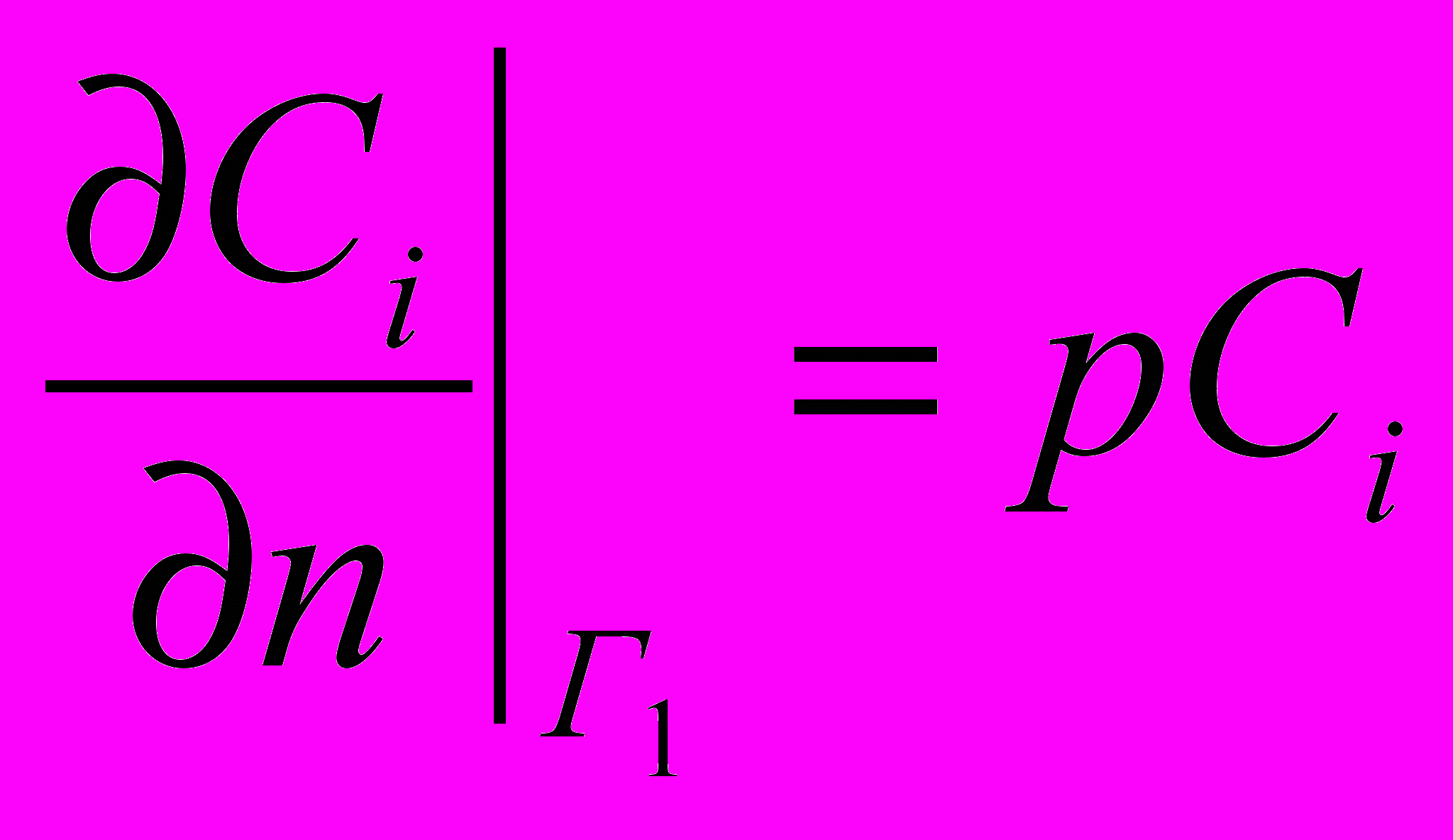, (3)

где n - нормаль к границе Г1; p - коэффициент прилипания нефтепродуктов к берегу, зависящий в общем случае от координат и 0 ≤ Р ≤ 1.

Если p(xδ,yδ)=l, то условие (3) описы­вает полное поглощение нефти берегом в точке (xδ,yδ); если р(xδ,yδ)=0, то условие (3) назы­вают условием непротекания, и оно означает полное отражение нефти в точке (xδ,yδ). Для свободной водной границы рассматриваемого района граничные условия для уравнения (1) записываются в виде

, (4)

Это означает, что за границей области S Сн концентрация загрязнений в расчетах не учитывается.

Рассмотрим значение функции F(Ci, Rj) для фракций, подверженных испарению, растворению и бактериальному разложению [8]. Для процесса испарения:

, (5)

где Mi – количество вещества компонента с номером i, моль; KE – коэффициент массопереноса для углеводорода, м/с; Xi – молярная доля компонента с номером i, равная ; Pi – давление паров компонента с номером i, Па; R – газовая постоянная, 8,314 Дж/моль·К; Т – температура окружающей среды над поверхностью слика, К; А – площадь нефтяного пятна, м2.

Для фракции, подверженной растворению, оператор деструкции F(Ci, Rj) приобретает вид:

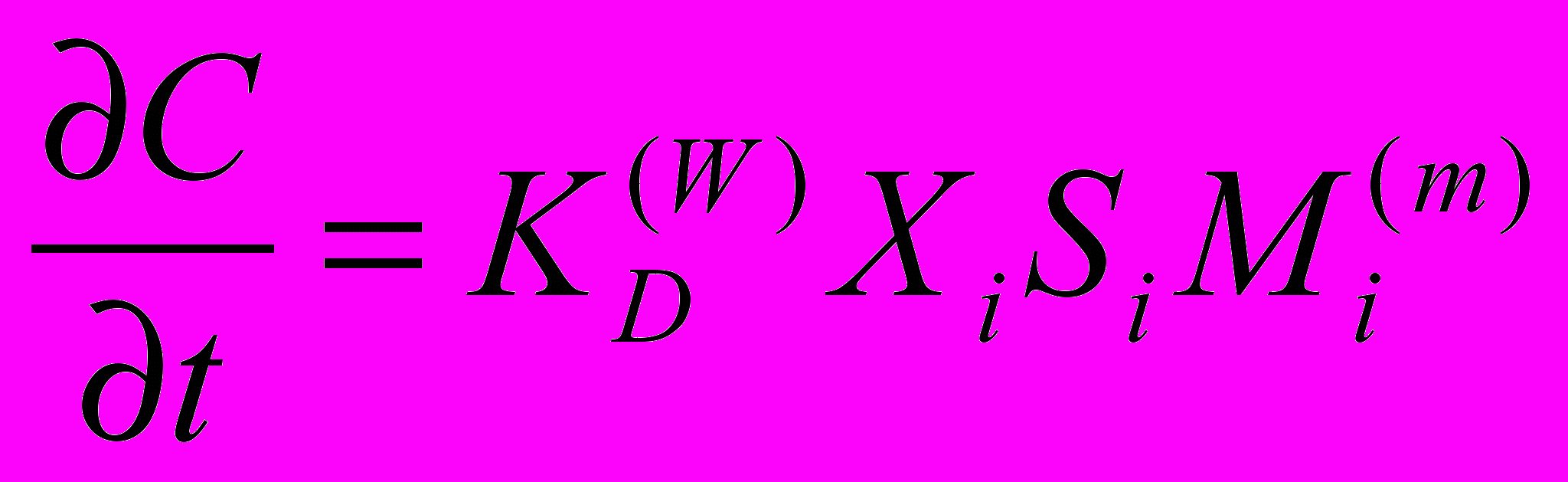, (6)

где Mi – количество вещества компонента с номером i, моль; 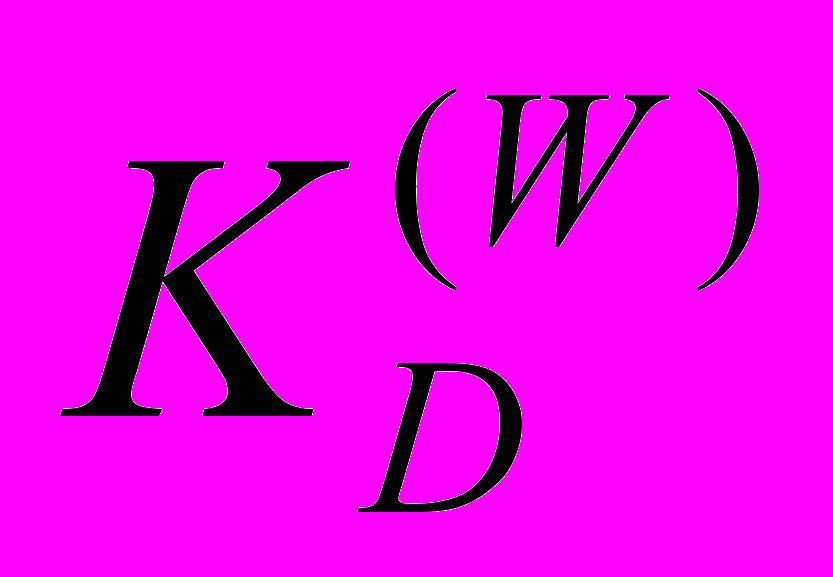– коэффициент массопереноса для углеводорода, м/с; Si – растворимость в воде компоненты с номером i, кг/м3.

Для фракции, подверженной бактериальному разложению, оператор деструкции F(Ci, Rj) приобретает вид:

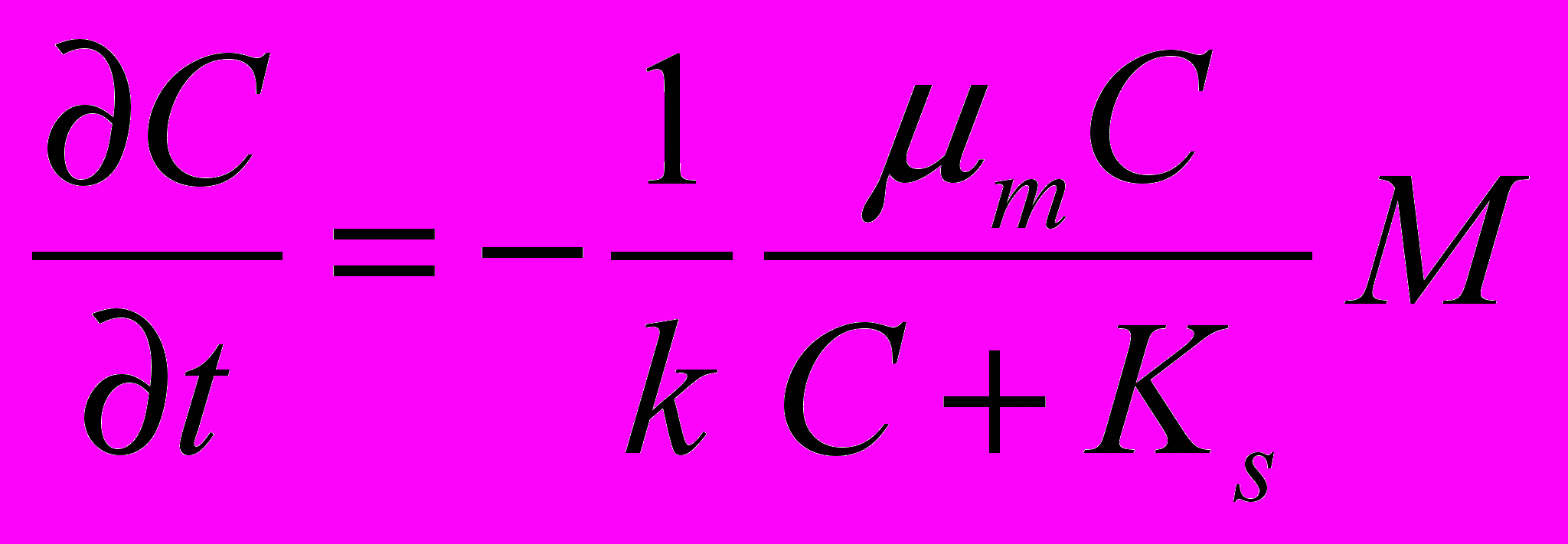, (7)

где k – коэффициент пропорциональности между количеством бактерий и поглощённым субстратом; μm – максимальная скорость роста микроорганизмов; Ks– коэффициент насыщения; M – численность популяции бактерий.

В дальнейшем автором планируется применение вышеописанной модели в численных экспериментах на ЭВМ при различных гидрометеорологических ситуациях для вычисления направления, скорости движения нефтяного пятна и места контакта нефти с линией берега, а также для определения возможных последствий нефтяного загрязнения побережья после аварийного разлива нефти на территории внутренних морей Азово-Черноморского бассейна. Полученные в ходе экспериментов данные можно будет использовать для оценки экологического воздействия на окружающую среду деятельности по добычи углеводородов в акватории Азово-Черноморского бассейна, в том числе для работ МЧС России. В условиях бурения на континентальном шельфе математическое моделирование может применяться для расчётов параметров загрязнения от:

• системы приготовления и циркуляции бурового раствора;

• загрязнения при испытании эксплуатационной колонны на герметичность;

• оборудования устья скважины после завершения бурения и при демонтаже оборудования.


Заключение

Описанные математические модели в сочетании с компьютерными технологиями геоинформационных систем предоставляют возможность отследить траекторию перемещения пятна и изменение его пространственных характеристик, изучить влияние процессов деструкции на концентрацию загрязнения, сравнить комплексное воздействие всех моделируемых процессов с воздействием какого-либо отдельно взятого процесса деструкции, а также при заданных параметрах выброса и окружающей среды определить район возможного контакта пятна нефти с линией берега.

На фоне возрастающего интереса нефтегазовых компаний к практически не освоенным шельфам Российской Федерации, детальное прорабатывание всевозможных ситуаций позволит минимизировать возможные негативные последствия.

Работа выполнена в рамках гранта РФФИ № 06-05-96624 «Прогнозирование и мониторинг чрезвычайных ситуаций выбросов углеводородов при проведении буровых работ на морском шельфе».


Литература


1. Мирзоев Ф.Д. Методы выбора рационального варианта нефтегазопромысловых платформ для освоения шельфа // Дис.канд.техн.наук – М., 2003. - РГБ. – 112 с.

2. Вяхирев Р.И., Никитин Б.А., Гриценко А.И., Захаров Е.В., Никитин П.Б. Актуальность выявления и освоения месторождений газа и нефти на шельфе России. – М.: Газойлпресс, 2000 – 112 с.

3. Сочнева И.О. Научно-методические основы обеспечения экологической безопасности работ по освоению месторождений Арктического шельфа // Дис.канд.техн.наук – М., 2005. - РГБ. – 162 с.

4. Марчук Г.И. Математическое моделирование в проблеме окружающей среды. М.: Наука, 1982.

5. Тарасенко Л.Н. Об оценке нефтяного загрязнения в шельфовой зоне. М.: ВЦ АН СССР, 1989.

6. Панина О.В. Обоснование разработки математических моделей ликвидации нефтяных разливов с использованием биосорбентов // Современные методы эколого-геохимической оценки состояния и изменений окружающей среды. Докл. Междунар. Школы 15-18 сент. 2003 г. – г.Новороссийск, 2003, С.53-59.

7. Дембицкий С.И., Дунаев И.М., Лаврентьев А.В., Ларионов А.В., Уртенов М.Х. Математические модели динамики и деструкции нефтяного слика на акватории моря. - Краснодар, 2003 – КубГУ – 71 с.

8. Дембицкий С.И., Лаврентьев А.В., Ларионов А.В., Уртенов М.Х. Динамика нефтяного пятна в море с учётом процессов деструкции. Математические оценки. Изв. Вузов Северо-Кавказского региона. Естественные науки, 2004, вып. 1.