Математическое и компьютерное моделирование длительной эволюции пучков частиц

Вид материала

Документы

Содержание 2.1.2. Символьное представление матриц 2.1.3. Численное представление матриц 2.2. Реализация матричного формализма. 2.2.1. Парадигма динамического моделирования 2.2.2. Декомпозиция задачи на вычислительные потоки. 3. Вычислительный эксперимент Второй уровень

Подобный материал:

• Компьютерное моделирование фоновых условий в эксперименте gerda и радиационной обстановки, 318kb.
• Математическое и компьютерное моделирование динамического состояния систем передачи, 388.39kb.
• Аннатационная программа дисциплины интегральные преобразования и операционное исчисление, 30.41kb.
• Аннатационная программа дисциплины стохастический анализ направление подготовки 010200., 38.6kb.
• Е. Е. Гетманова компьютерное моделирование нелинейных колебаний, 81.56kb.
• Календарный план учебных занятий по дисциплине «Компьютерное моделирование оптических, 38.78kb.
• Вестник ргу им. Иммануила, вып. 10, 2007г., с. 8-14, 89.44kb.
• Математическое компьютерное моделирование технических и социально-экономических систем, 72.14kb.
• Уважаемые коллеги!, 46.85kb.
• Учебно-методический комплекс по дисциплине "компьютерное моделирование" (факультет, 384.08kb.

Математическое и компьютерное

моделирование длительной

эволюции пучков частиц

Андрианов С.Н. Санкт-Петербургский государственный университет

Введение


В данной работе обсуждаются некоторые проблемы обучения студентов старших курсов и магистрантов методам и технологиям моделирования длительной эволюции пучков части с использованием высокопроизводительных вычислительных систем. Сложность системы управления и многовариативность различных моделей представления динамики пучка частиц позволяет реализовать процесс обучения студентов старших курсов использованию современных математических методов и информационных технологий с целью повышения эффективности процесса исследования и дизайна сложных систем управления. Обсуждается проблема выбора математического аппарата, адекватного как предметной области исследований, так и используемым вычислительным системам.

Хорошо известно, что решение современных задач физики пучков приводит к необходимости использования высокопроизводительной вычислительной техники для получения в достаточной мере адекватных результатов, допускающих их экспериментальную (прямую или косвенную) проверку. С другой стороны сложность динамики пучка и самой системы управления приводит, с одной стороны, к необходимости аккуратного выбора как аналитических, так и численных математических методов, реализующих физическую (аппроксимирующую) модель подобных объектов, а с другой – эффективного вычислительного инструментария с учетом современного состояния вычислительных технологий (в их аппаратной и программной реализации). Особое внимание при моделировании именно длительной эволюции приобретает проблема выбора методов численного интегрирования соответствующих динамических уравнений, обеспечивающих сохранение известных интегралов движения [1]. Кроме того, необходимо заметить, что традиционные численные методы, используемые например, при интегрировании дифференциальных уравнений, описывающих динамику частиц, приходится «приспосабливать» к технологиям параллельных и распределенных вычислений, поскольку изначально они строились как последовательные методы. Таким образом, математический аппарат, используемый в физике пучков, должен обеспечивать возможность проведения качественного анализа нелинейной динамики, синтеза оптимальных систем управления на основе эффективных вычислительных экспериментов с использованием технологии параллельных и распределенных вычислительных систем [2].

В качестве базового математического аппарата в данной работе рассматриваются алгебраические методы Ли, на основе которых строиться так называемый матричный формализм для этих методов [3], позволяющая, не только эффективно «загружать» вычислительные ресурсы, но и использовать методы и технологии компьютерной алгебры как на этапе предварительной подготовки задачи, так и на этапе проведения вычислительного эксперимента.


2. Постановка задачи


2.1. Основные определения и понятия. В качестве начальной модели динамики пучка частиц рассматривается задача Коши для системы обыкновенных дифференциальных уравнений следующего вида

(1)

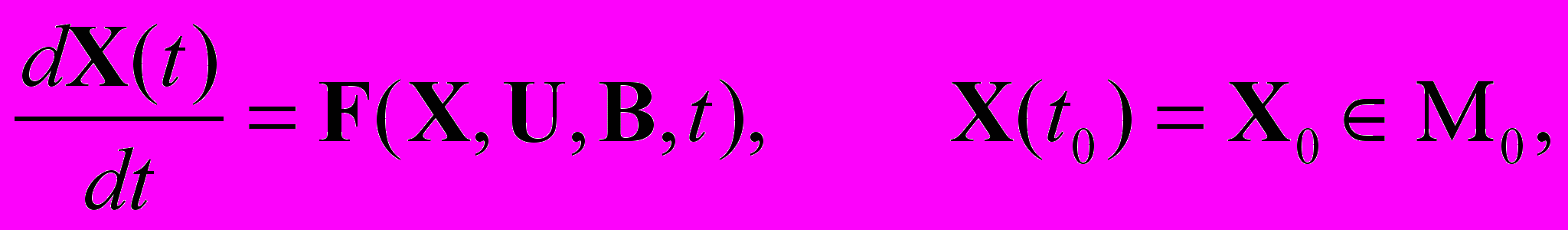
где 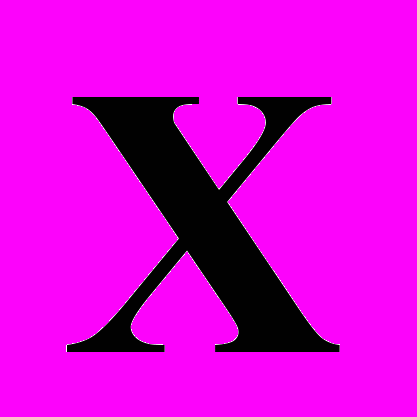– 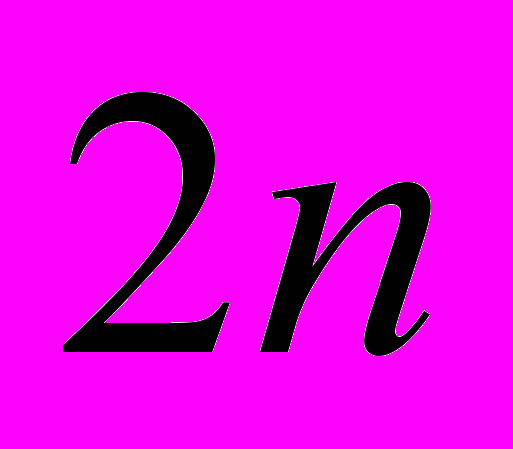-мерный фазовый вектор, описывающий состояние частиц пучка, 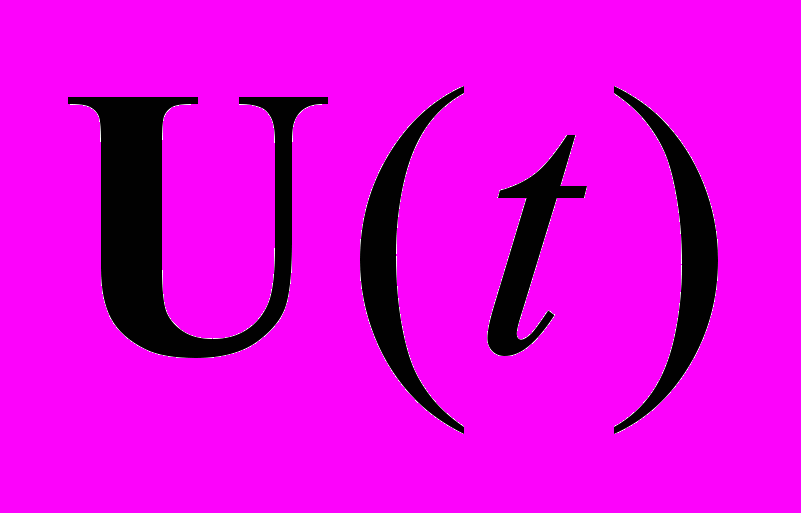– 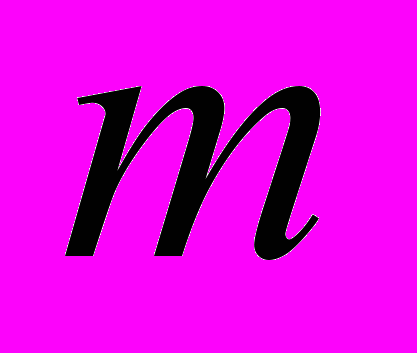-мерная вектор-функция, описывающая управляющие (внешние) электромагнитные поля и – 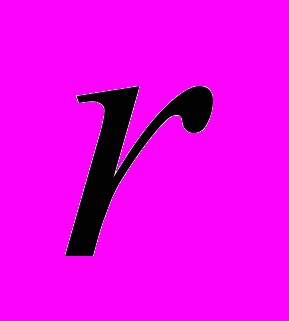-мерный вектор управляющих (установочных) параметров, определяющих функционирование системы, – независимая переменная, в качестве которой часто выбирается длина, измеряемая вдоль некоторой (опорной) кривой. Заметим, что размерность данной системы определяется математической моделью пучка частиц как ансамбля частиц. В случае динамики отдельной частицы 2n суть число фазовых координат (например, координат и импульсов частицы). Однако пучок представляет собой ансамбль частиц, состоящий из громадного числа частиц , значение которого чрезвычайно велико для реальных установок: (10¹²–10¹⁶) частиц, проходящих через «площадку» 1 см². Специфика динамики пучка (частицы «движутся» в окрестности так называемой равновесной траектории) позволяет перейти к так называемой натуральной системе координат, которая «движется» с некоторой скоростью вдоль равновесной траектории. Пусть 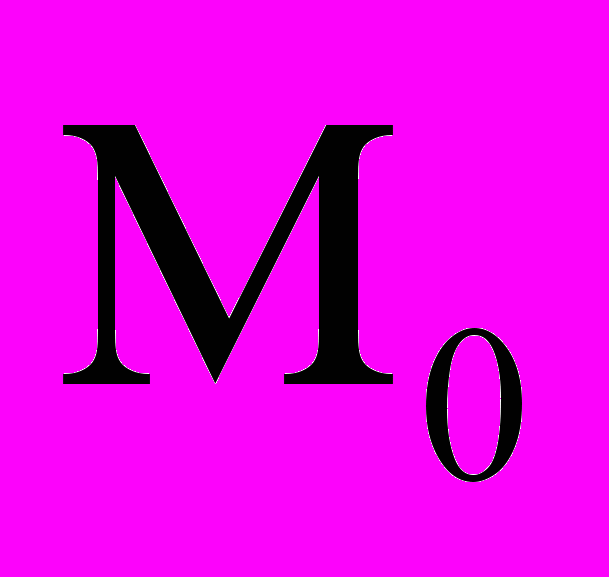– множество начальных данных, описывающее начальное состояние пучка как совокупности частиц, и функция допускает разложение в ряд в окрестности точки .

Очевидно, что непосредственное интегрирование системы (1) для столь большого набора начальных данных не является возможным даже при использовании суперкомпьютеров. В качестве примера можно привести работы группы R. Ryne, в которых в качестве перспективы рассматривается моделирование динамики 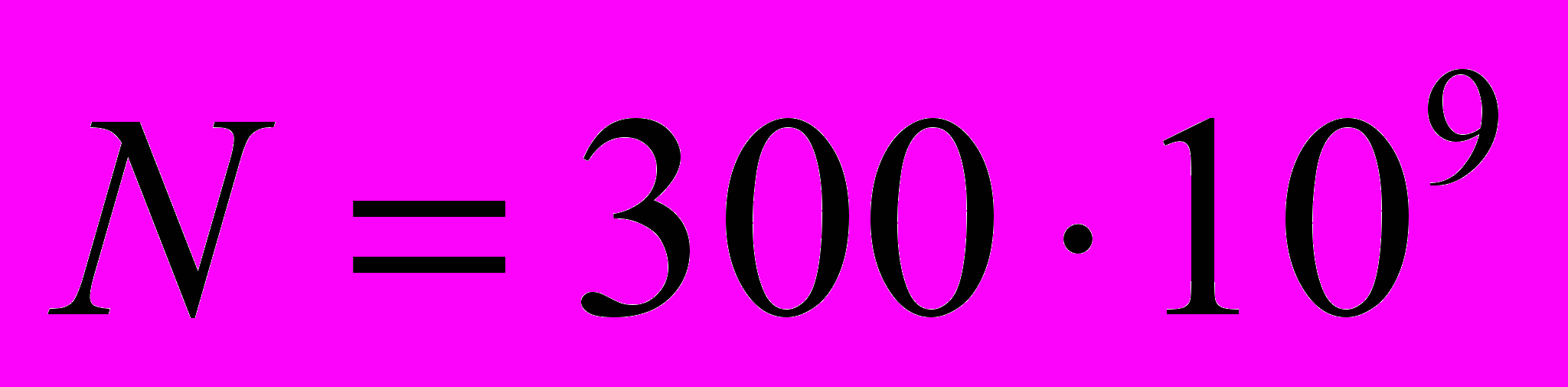частиц с использованием специально спроектированного суперкомьютера. Уравнению (1) сопоставляется операторное уравнение вида



где – тождественный оператор и – Ли оператор. Оператор будем называть оператором эволюции (пропагатором), так как имеет место равенство



Для построения пропагатора будем использовать так называемый базис Пуанкаре-Витта 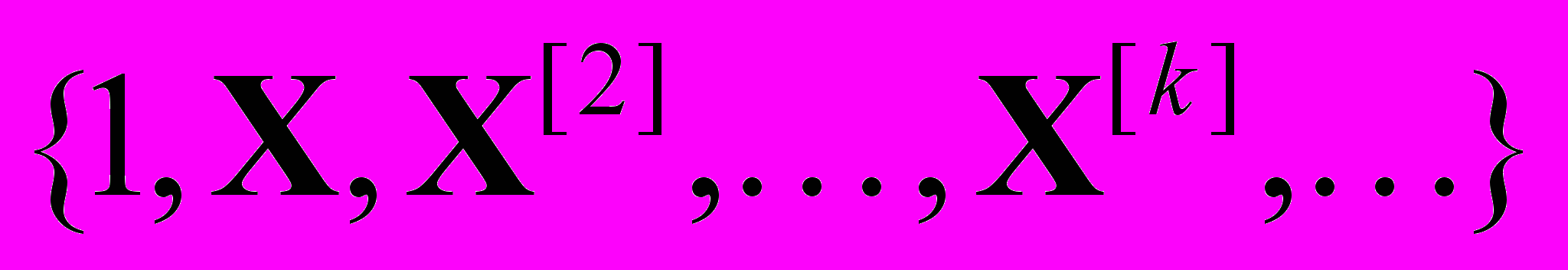, где 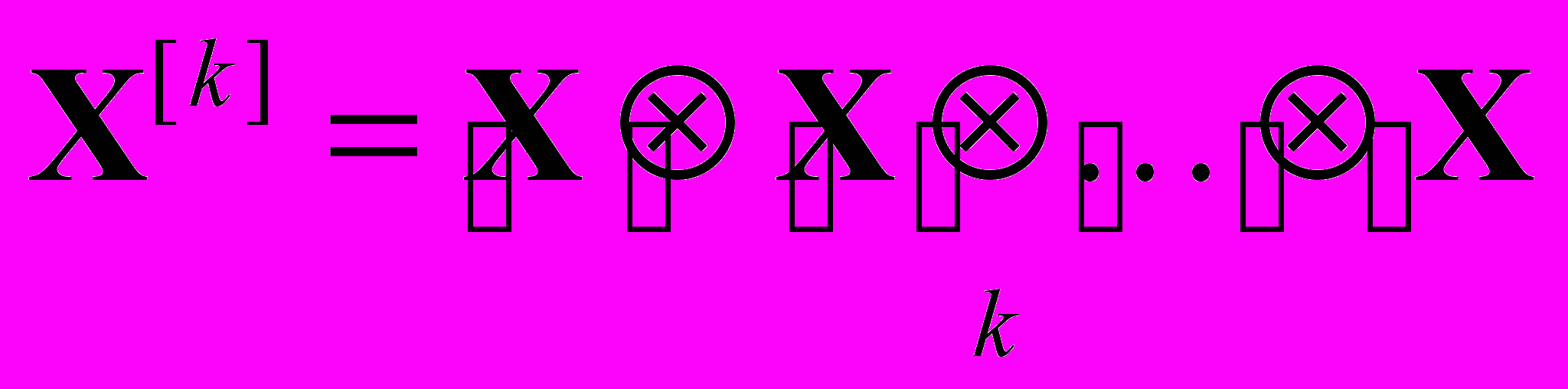- кронекерова степень вектора 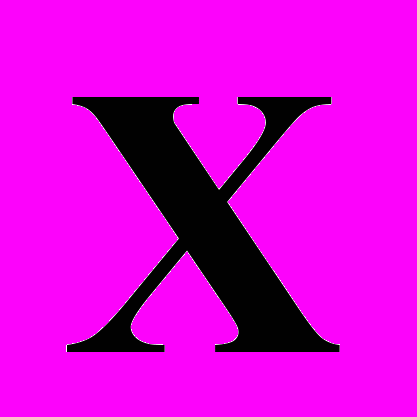, содержащая все мономы -порядка относительно компонент вектора 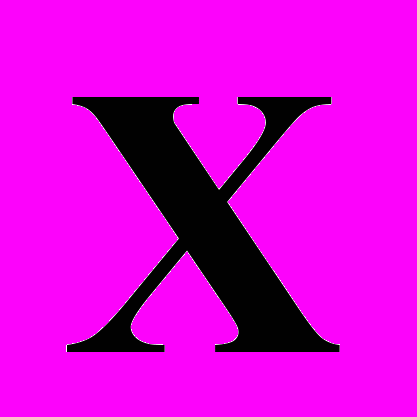, имеющие следующий общий вид , где 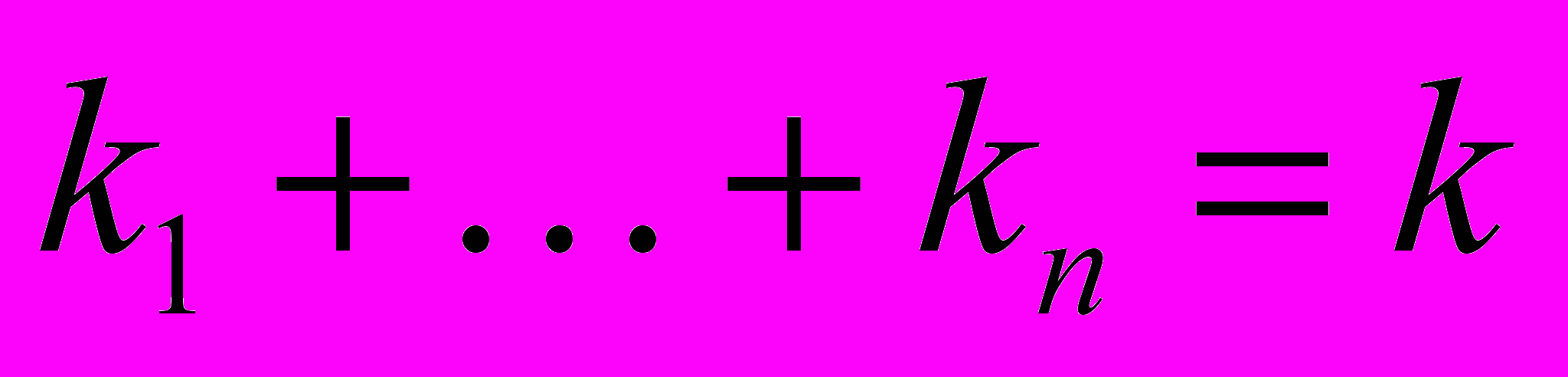. Заметим, что в случае Кронекерово произведение совпадает с обычным тензорным произведением. В случае одинаковых векторов, т.е. для , можно понизить размерность получаемого вектора, “вычеркивая” одинаковые компоненты. Таким образом, имеет место равенство 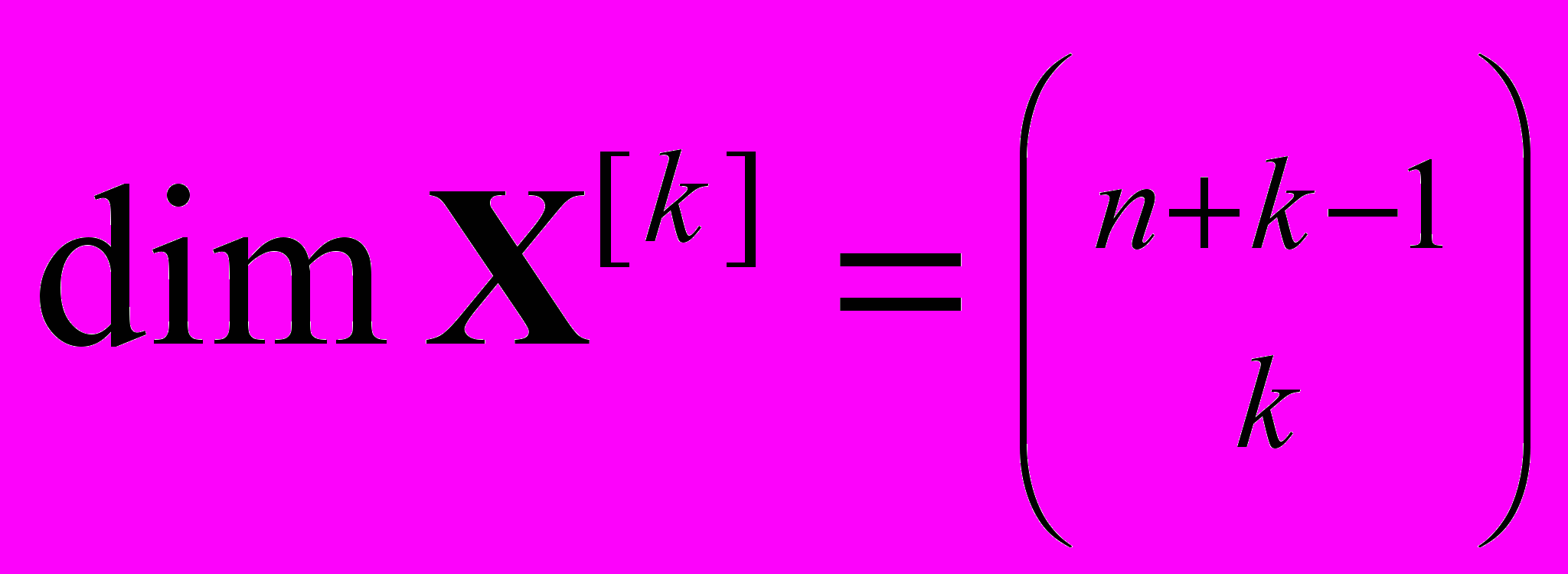вместо 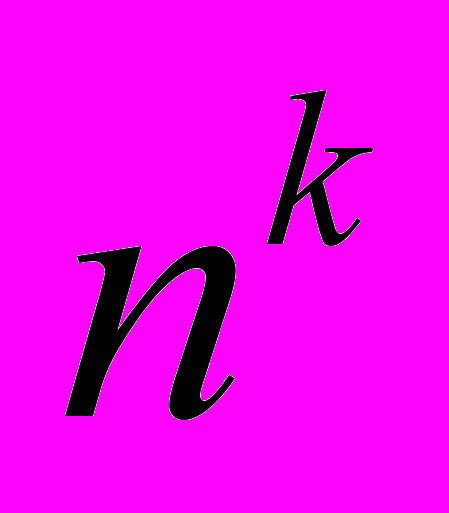, что особенно существенно для высоких порядков нелинейностей. Используя введенные обозначения и свойства гладкости функции уравнение (1) можно переписать в следующем виде

(2) ,

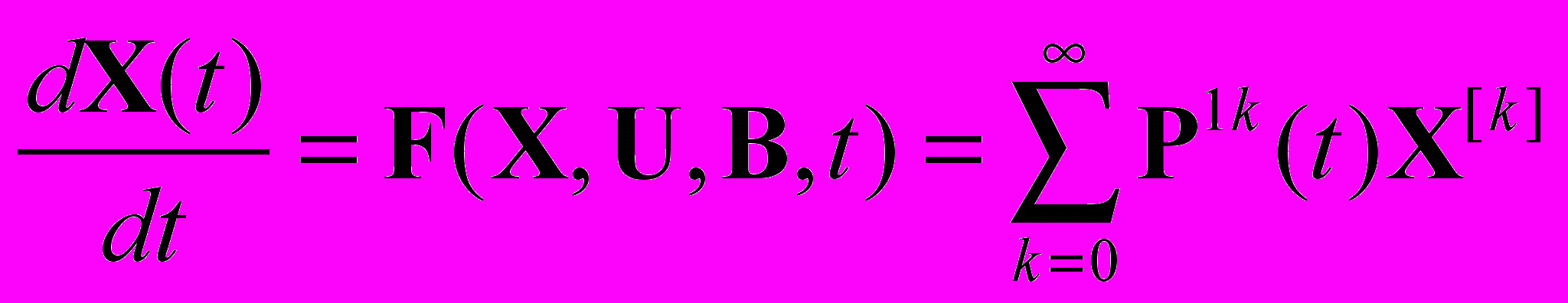где матрицы 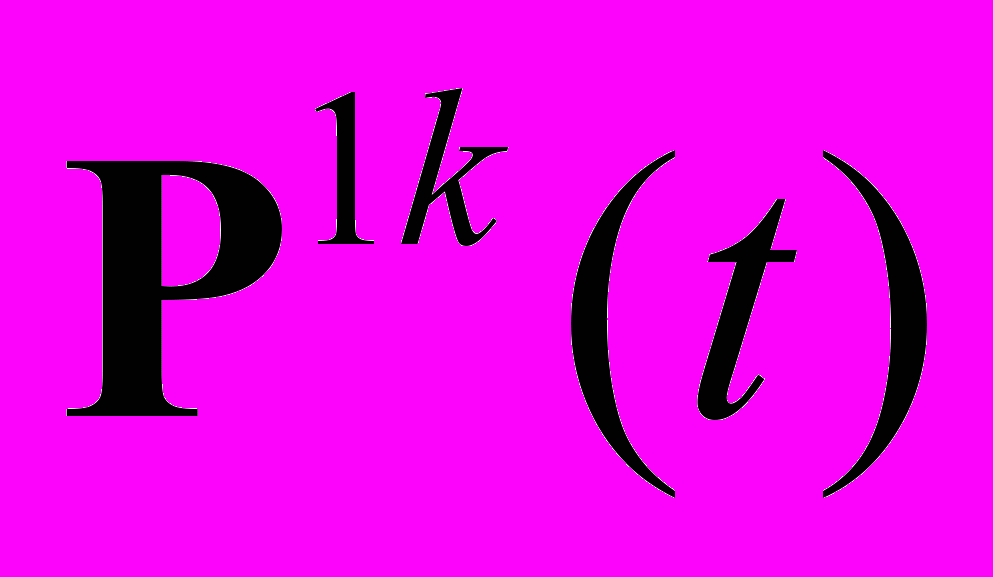описывают нелинейные эффекты -го порядка и легко могут быть вычислены в символьном виде (при известной функции ) с помощью, например, кодов Maple. Следуя [3] решение уравнения (2) будем искать в виде

(3) .

Тем самым мы получаем матричное представление оператора эволюции в базисе Пуанкаре-Витта. Матрицы описывают аберрации соответствующих порядков, и поэтому будем их называть аберрационными матрицами. Заметим, что вычисление этих матриц возможно как в аналитическом (символьном) так и в численном виде. Заметим, что именно разделение динамической компоненты (в нашем случае матрицы) и фазовой – в форме вектора 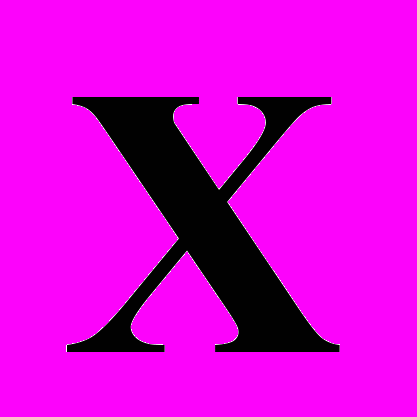, позволяет существенно уменьшить вычислительные затраты на «отслеживание» динамики пучка. Действительно, нам достаточно представить пучок в виде совокупности частиц и мы вместо уравнения (4) прейдем к уравнению для матрицы 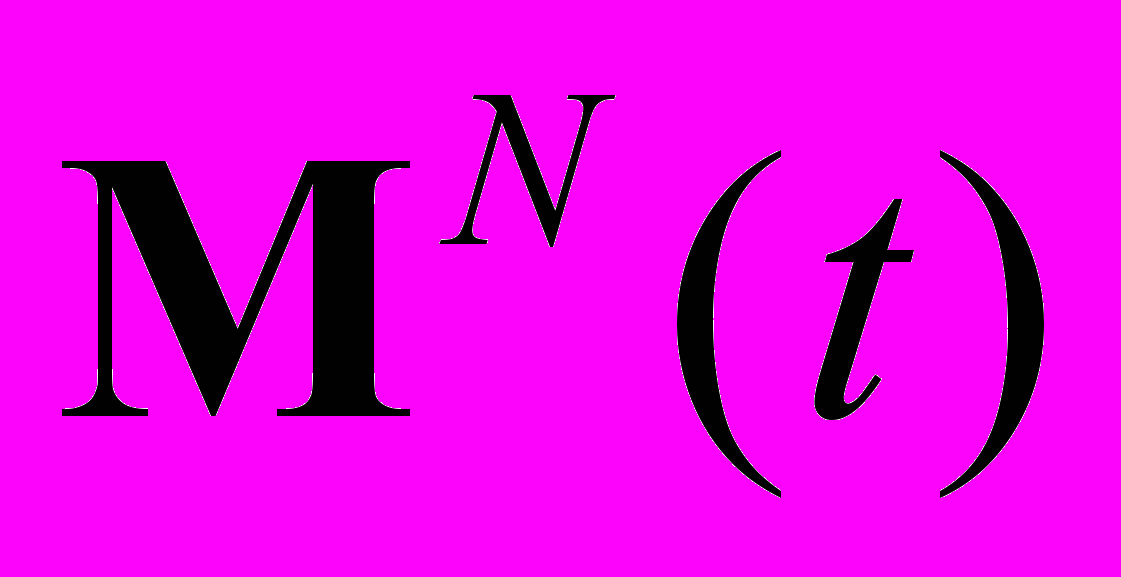, состоящей из столбцов – фазовых координат частиц.

2.1.2. Символьное представление матриц . Согласно идеологии матричного формализма [3] процесс вычислений аберрационных матриц начинается с решения линеаризованной системы уравнений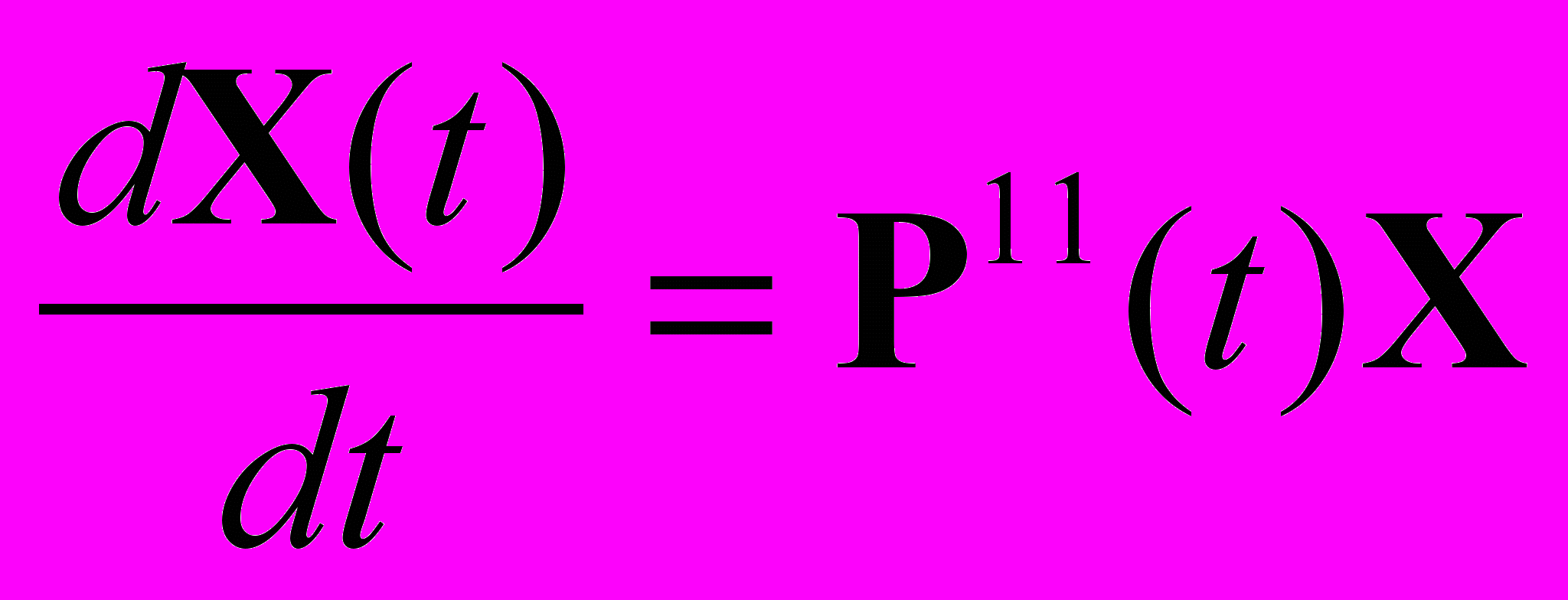

,

решение которого записывается с помощью матрицанта 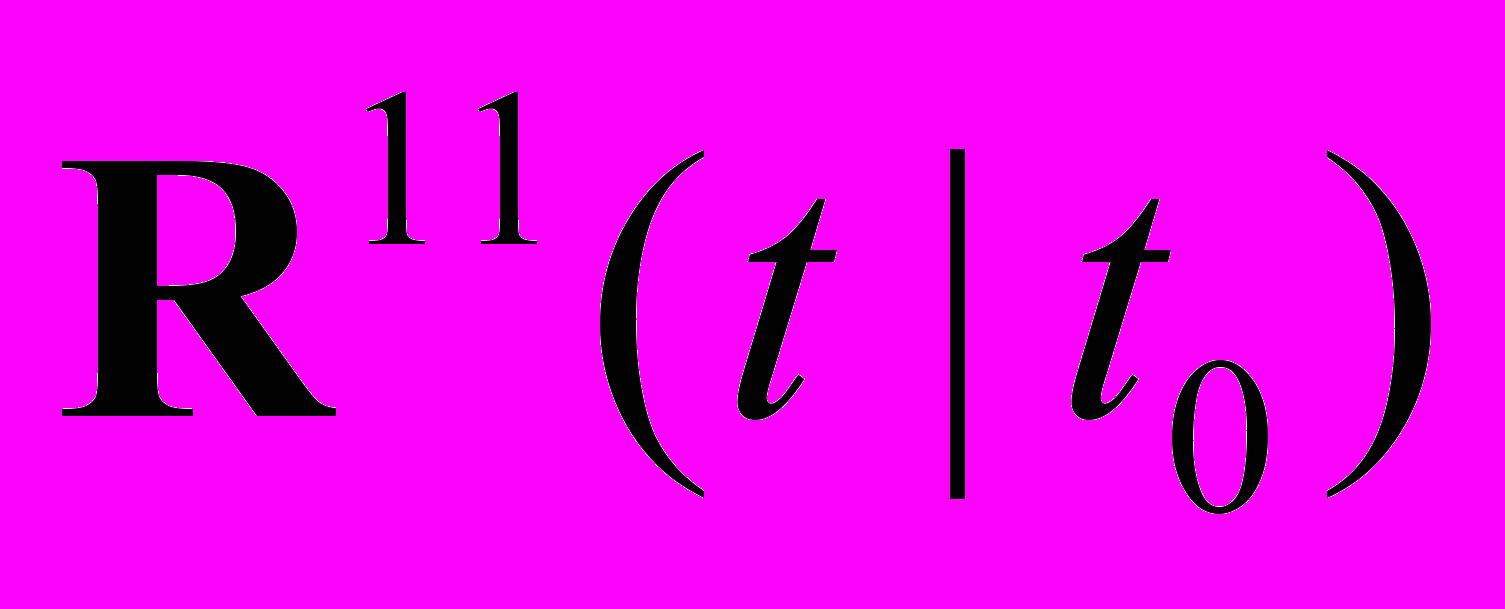: , или .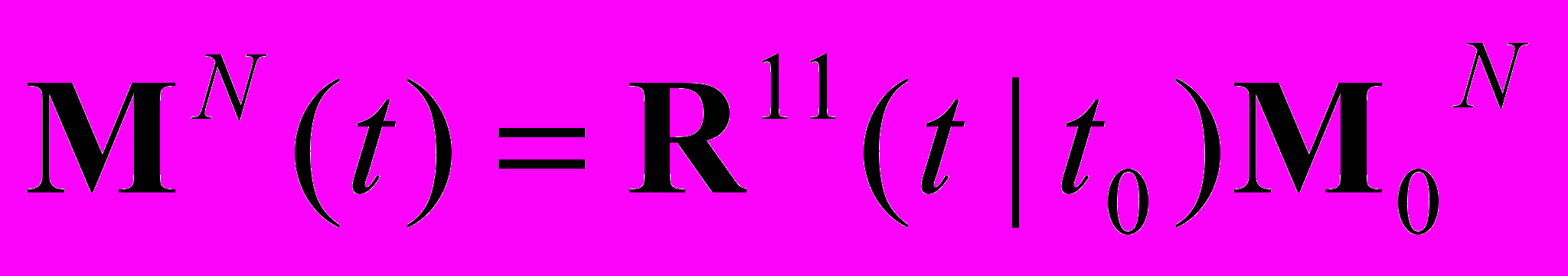

Хорошо известно, что символьное вычисление для матрицанта возможно для ограниченного набора матричных функций . В частности, в случае кусочно-постоянной аппроксимации функциональной зависимости от независимой переменной такое построение возможно. Существуют также и другие, интересные с практической точки зрения, функциональные зависимости, для которых подобное представление возможно.

2.1.3. Численное представление матриц . В случае необходимости (например, сложной зависимости матриц 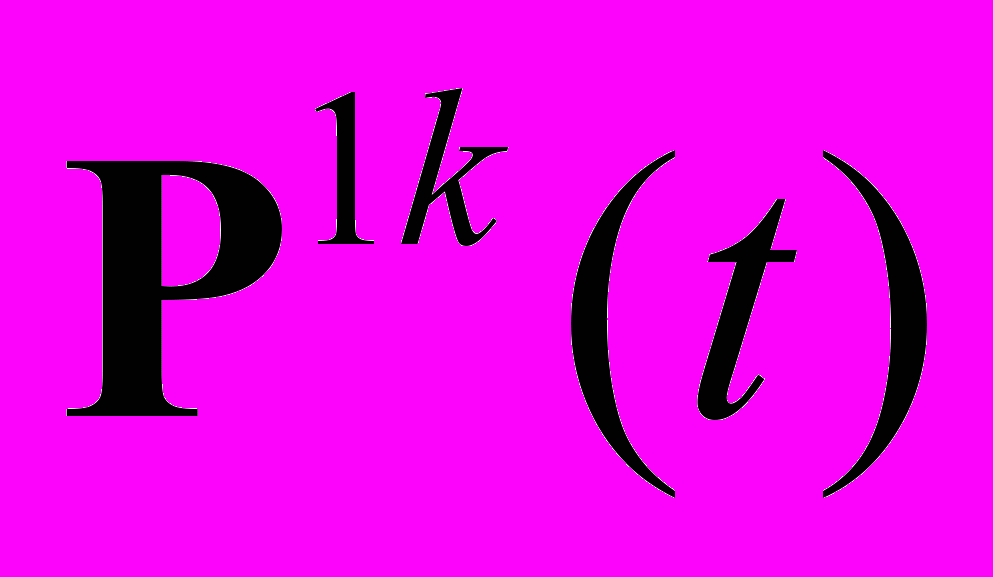) аберрационные матрицы могут быть вычислены с использованием следующих дифференциальных уравнений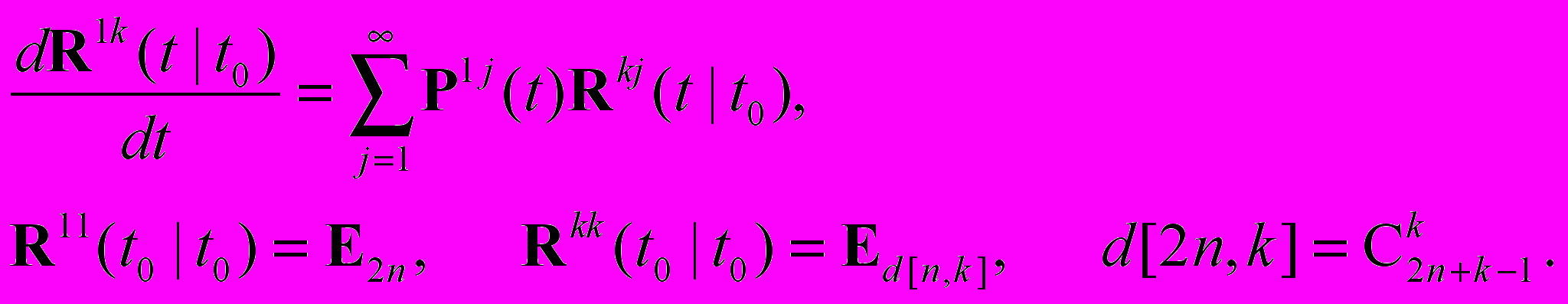



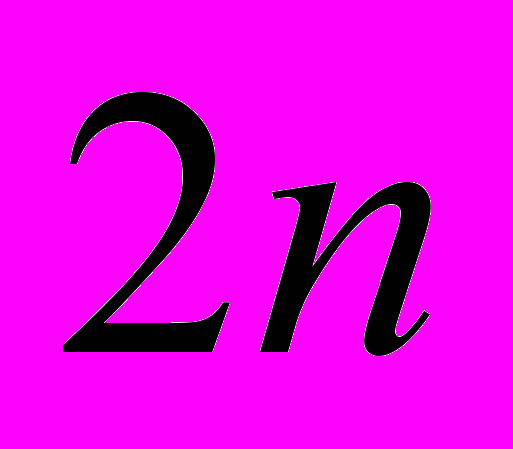Здесь – единичная матрица -порядка. Естественно, что решение этих уравнений, как и в случае символьных вычислений, осуществляется вплоть до некоторого порядка аппроксимации . В отличие от решения уравнений (1), мы получаем матричное представление искомого (приближенного) решения не используя начальные условия для фазового вектора. Заметим, что матричное представление пропагатора пучка, иными словами матриц может быть реализовано аналитически и/или численно не зависимо от числа представляющих пучок частиц только в случае пренебрежения эффектом самодействия пучка, т.е. при пренебрежении эффекта пространственного заряда пучка (слаботочное приближение).

2.2. Реализация матричного формализма. Описанный выше метод позволяет реализовать процесс исследования динамики частиц существенно более эффективно. Опишем последовательность выполняемых процедур на подготовительном этапе.

1. Вычисление (в символьном виде) матриц для некоторых классов дифференциальных уравнений движения, используемых в физике пучков.
   
2. Вычисление (в символьном виде) аберрационных матриц для некоторых классов функциональных зависимостей, представляющих практический интерес для физики пучков.
   
3. Построение баз данных из этих матриц и соответствующих систем управления ими.
   
4. Построение баз данных, содержащих дополнительные операции над операторами и матрицами, позволяющие существенно повысить эффективность численного моделирования (в частности, длительной эволюции динамических систем).
   
5. Используя знания экспертов, строятся базы знаний (основанные, например, на системах ориентированных графов), позволяющие сопоставлять тем или иным «физическим» эффектам соответствующие матрицы, как в уравнениях движения, так и в решении.
   
6. Строятся базы данных, содержащие необходимые символьные выражения для построения аппроксимантов для инвариантов и симметрий.
   
7. Строится пользовательский интерфейс (с использованием естественного языка для данной предметной области), обеспечивающий гибкое и эффективное «изъятие» необходимых данных, построение алгоритмов уже численного характера.
   

Естественно, что перечисленная информация не покрывает полностью потребности физики пучков (здесь, например, не перечислены объекты, необходимые для моделирования влияния сил пространственного заряда). Однако основные объекты указаны. Следует также указать на следующую возможность, предоставляемую матричным формализмом. Дело в том, что при описании математических моделей физических объектов (соответствующих управляющим элементам, например, таким, как мультипольные линзы, дипольные магниты, соленоиды и т.п.) удобно вводить декомпозицию соответствующих описаний на виртуальные подобъекты, каждый из которых самостоятельного (с физической точки зрения) не имеет. Однако, такое представление позволяет более гибко вводить в процесс исследования те или иные модели и исследовать их влияние на динамику пучка в системе. Подобный формализм получил название технологии LEGO-объектов (см. [4]). Следует заметить, что в случае численного представления аберрационных матриц, мы теряем в определенной степени гибкость в манипулировании объектами. Однако многое из указанного остается (в том числе и возможность работы с LEGO-объектами) в силе.

2.2.1. Парадигма динамического моделирования. Весь естественный ход развития математики, компьютерной архитектуры, системного и математического обеспечения с одной стороны подготовили базу, а указанные выше и другие причины "заставили" исследователей разрабатывать и реализовывать новые идеи. Развитие математики привело к чрезвычайно глубокому взаимному проникновению и взаимовлиянию практически всех ее разделов. Развитие же процесса осмысления реальных процессов и явления в самых различных областях человеческого знания привело к глубокому пониманию процессов описания (формализации, моделирования) с целью анализа и синтеза динамических (в широком смысле этого слова) систем. Сформулируем определение понятия динамического моделирования, объединяющего в себе современные идеи моделирования сложных систем.

О п р е д е л е н и е 1. Под динамическим моделированием будем понимать процесс моделирования того или иного процесса, объекта, при котором сами модели, или их составные части, рассматриваются как объекты, снабженные как всеми атрибутами экспертных систем, так и средствами «склейки» этих объектов в суперобъекты.

Огромную помощь при формировании объектов, обеспечении их оптимального функционирования играют методы и средства компьютерной алгебры (КА). Формирование баз данных и знаний, генерируемых средствами человеческого интерфейса и компьютерной алгебры, позволяет построить те базовые кирпичики, из которых строятся соответствующие модели. Очевидно, что используемые математические модели должны допускать, с одной стороны, возможность построения баз данных и знаний средствами КА, а с другой стороны, обеспечить гибкость и адекватность процесса моделирования.

2.2.2. Декомпозиция задачи на вычислительные потоки. Как уже ранее указывалось, на практике полная задача моделирования динамики пучков частиц может быть представлена виде совокупности (вообще говоря, взаимодействующих) потоков, которые в процессе вычислений обмениваются информацией. Укажем типы потоков, возникающих в физике пучков, и опишем характер их взаимодействия.

1. Поток динамики – является основным.
   
2. Поток фазового портрета пучка – предназначен для вычислений характеристик текущего фазового портрета.
   
3. Поток визуализации динамики пучка – предназначен для графического отображения текущей информации.
   
4. Поток сил пространственного заряда – предназначен для вычисления необходимых для расчета динамики компонент электромагнитного поля, порождаемого текущим распределением заряженных частиц, составляющих пучок.
   
5. Поток оптимизации – предназначен для решения задач оптимизации.
   

3. Вычислительный эксперимент


Хорошо известно, что при параллельном программировании существенное место занимает проблема выявления взаимосвязей между структурой математического алгоритма и архитектурой многопроцессорной вычислительной системы. Ранее уже указывались два типа реализации различных видов взаимосвязей на основе многоуровневой декомпозиции исходной задачи.

Напомним, что первый уровень основан на выделении вычислительных потоков, синхронизация между которыми не столь затратна по времени, как синхронизация между процессами внутри каждого потока.

Второй уровень - разбиение каждого потока на множество одновременно выполняемых при различных исходных данных однородных (или почти однородных) процедур. Такой тип параллелизма обычно называют параллелизмом данных.

На третьем уровне осуществляется распараллеливание отдельных процедур. На втором и третьем уровнях существенным образом сказывается выбор методов численного моделирования (например, метода интегрирования уравнений движения частиц).

И, наконец, четвертый уровень распараллеливания основан на разбиении арифметических процессов на число процессоров.

В данной работе основное внимание при написании прикладного программного обеспечения уделяется первым трем уровням. С точки зрения автора алгебраические методы Ли и его реализация на основе матричного формализма в достаточной мере являются адекватными современным кластерным вычислительным системам.


4. Заключение


Итак, сформулируем основные выводы. Во-первых, алгебраический аппарат Ли позволяет проводить глубокую декомпозицию задачи моделирования эволюции пучка заряженных частиц. Во-вторых, использование матричного формализма позволяет сократить временные затраты за счет сведения задачи интегрирования уравнений движения к манипуляции матричными объектами, что, как хорошо известно, хорошо распараллеливается с использованием существующих средств программирования для многопроцессорных вычислительных систем. Использование традиционных для физики пучков представлений фазового портрета пучка в рамках матричного формализма демонстрирует несомненную эффективность при увеличении числа процессоров, включаемых для решения задачи. И хотя в данной работе не рассматривались вопросы учета сил пространственного заряда, существующие предварительные эксперименты также демонстрируют большую эффективность матричного формализма по сравнению с традиционными методами интегрирования дифференциальных уравнений. Описанный в работе подход хорошо «ложится» на методику обучения решения сложных (прежде всего ресурсоемких) задач с привлечением высокопроизводительной техники, что позволило внедрить его составляющие в учебный процесс на факультете ПМ-ПУ СПбГУ.


Список литературы

1. Andrianov S.N. Symplectification of Truncated Maps for Hamiltonian Systems. Mathematics and Computers in Simulation. Vol. 57, issue 3-5 (2001), P. 139-146.
   
2. Andrianov S.N. Role of Parallel and Distributed Computing in Beam Physics. Nuclear Instruments and Methods A. Vol. 519 (2004), P. 37-41.
   
3. Andrianov S.N. A Matrix Representation of the Lie Algebraic Methods for Design of Nonlinear Beam Lines // AIP Conf. Proc. 1997. No 391. N.-Y., P. 355-360.
   
4. Andrianov S.N. LEGO-Technology Approach for Beam Line Design. Proc. of the Eighth European Particle Accelerator Conference. Paris. France, Austria, 3-7 June 2002, P. 1607-1609.