Инвариантность законов физики канарёв Ф. М. Анонс
| Вид материала | Закон |
- Инвариантность законов физики в коллайдерах канарёв Ф. М. Анонс, 194.26kb.
- Введение в механодинамику канарёв Ф. М. kanphil@mail ru Анонс, 203.52kb.
- Элементы теории научного познания канарёв Ф. М. Анонс, 198.49kb.
- Просвещаем механиков-теоретиков канарёв Ф. М. Анонс, 91.8kb.
- Закон эволюции фундаментальных знаний канарёв Ф. М. Двенадцатая лекция аксиомы Единства, 87.02kb.
- Ответы на вопросы системного анализа канарёв Ф. М. Анонс, 173.5kb.
- Первая вводная лекция о микромире канарёв Ф. М. Анонс, 155.47kb.
- Комментарии читателей к дискуссии плазара с канарёвым канарёв, 471.26kb.
- Ф. М. Канарёв вводная лекция аксиомы единства искателям научных истин анонс. «Триумфальное», 111.72kb.
- Анализ фокусов квантовой теории канарёв, 982.47kb.
ИНВАРИАНТНОСТЬ ЗАКОНОВ ФИЗИКИ
Канарёв Ф.М.
Анонс. Физики ХХ века, пленённые завораживающей таинственностью математических символов, свято верили математикам в достоверности отражения ими физической реальности, забыв о том, что математическое описание физических процессов и явлений должно привлекаться только тогда, когда понята их физическая сущность, следующая из экспериментов [1].
ВВЕДЕНИЕ
В 1987 г. исполнилось 300 лет с момента публикации фундаментальных теоретических идей И. Ньютона «Математические начала натуральной философии». Ученые тех времён критически относились к его трудам, но когда они начали давать практические результаты, итогом которых является вся современная техника, то критика сама собой и достаточно быстро угасла [2]. Ушли в небытие и критики. Однако время показало, что Ньютон допустил ряд фундаментальных ошибок, которые оказались так глубоко замаскированными, что их удалось обнаружить лишь спустя 322 года [3].
В 2005 году исполнилось 100 лет с момента выхода статьи А. Эйнштейна «К электродинамике движущихся тел», которая, как считают релятивисты, явилась началом новой теоретической физики [4]. Но ста лет оказалось мало, чтобы получить с помощью этой теории какой – либо ощутимый практический результат, если не считать глобальный раскол ученых на сторонников и противников А. Эйнштейна. Количество последних растёт так быстро, и результаты их исследований приобретают такую основательность, что у эйнштейновских идей относительности остаётся одна дорога - на полку истории науки. Правда, осталась ещё одна идея, которая держит релятивистов на плаву – математическая инвариантность уравнений Максвелла преобразованиям Лоренца. Однако, детальный анализ этой инвариантности показывает, что она – тоже миф. Аналогичный вывод следует и из глубокого анализа математических проблем электродинамики [1], [5].
1. Инварианты в математике
Инвариант – это величина, не изменяющаяся при каких-либо математических действиях или преобразованиях. Например, если мы имеем окружность радиуса
с центром в точке 0 в декартовой системе координат 
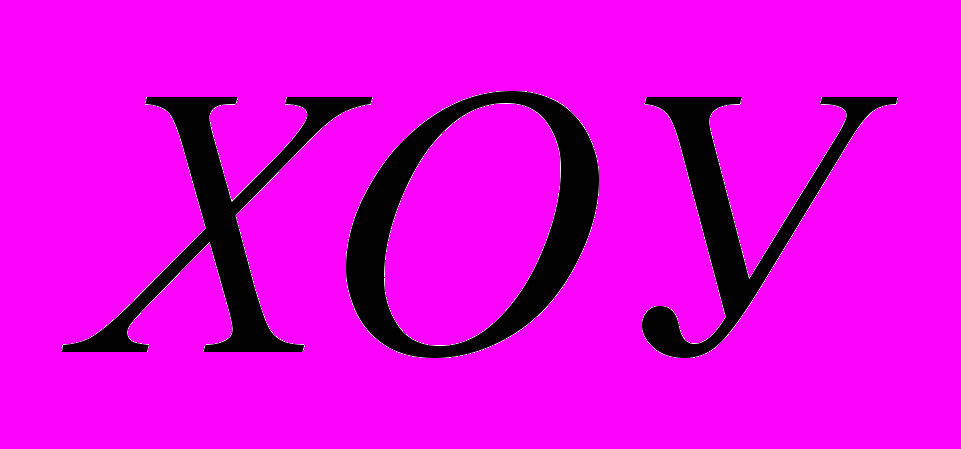, то её уравнение имеет вид (рис. 1) [1]
. (1)
Рис. 1. Схема преобразования координат центра окружности
Если начало новой системы координат
сместить вправо на расстояние 
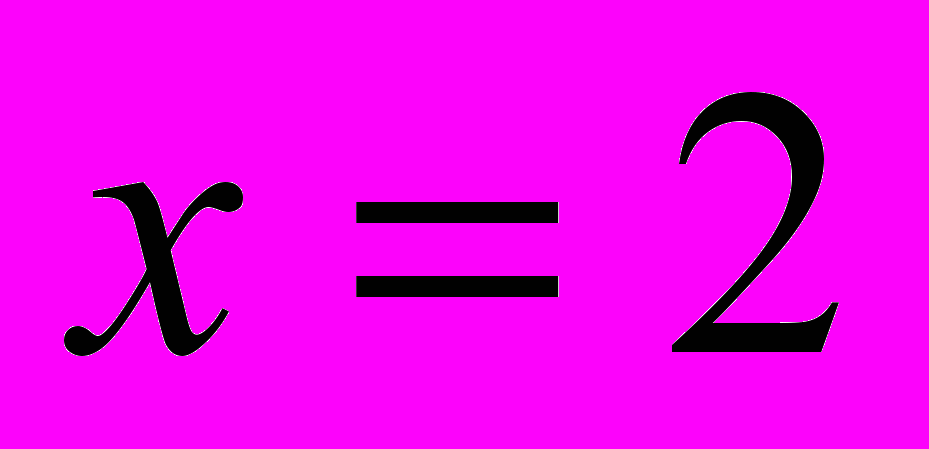, то 
, 
, а в новой системе координат уравнение этой же окружности запишется так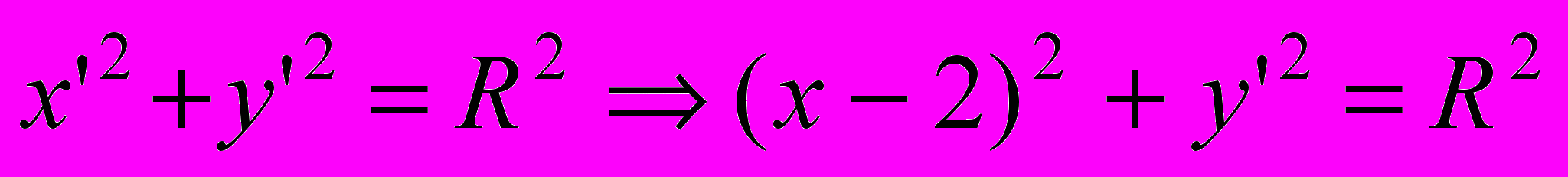
. (2)Итак, форма окружности, её радиус и длина инвариантны преобразованию координат (рис. 1), а формулы (1-2), описывающие эту окружность, - разные, то есть неинвариантные. С учётом этого сохранение вида математической модели, описывающей какой-либо объект при преобразованиях координат, считается математической инвариантностью, а сохранение физических параметров объекта – физической инвариантностью.
Если в математических уравнениях появляется время, то они начинают отражать не только статическую форму геометрических фигур, но и их движение и движение систем координат. Когда силы, действующие на эти фигуры, не заданы, то такое движение рассматривается, как кинематическое, а если заданы, то - как динамическое, то есть появление времени в математических уравнениях значительно усложняет процесс оценки одновременной физической и математической инвариантности.
2.Физическая инвариантность
Под физической инвариантностью будем понимать инвариантность самой физической величины, а не её математического символа или их совокупности. Самой простой физической инвариантностью является инвариантность законов кинематики при переходе из неподвижной системы координат в подвижную и наоборот. Основными законами кинематики являются законы, описывающие траектории движения точек и тел, и законы, описывающие изменение их скоростей и ускорений [2].
Поскольку релятивисты рассматривают только прямолинейное и равномерное движение подвижной системы координат относительно неподвижной, то и мы остановимся на анализе лишь этого случая. Напомним, что если система отсчёта покоится или движется прямолинейно с постоянной скоростью, то она называется инерциальной.
- Реализация кинематической инвариантности в преобразованиях Галилея
Если точка движется относительно подвижной системы координат Х’О’У’ (рис. 2) по закону
, то в соответствии с преобразованиями Галилея: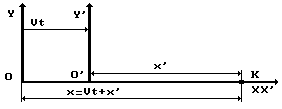
Рис. 2. Схема к анализу преобразований Галилея
(3)
, (4)закон движения этой точки относительно неподвижной системы координат запишется так
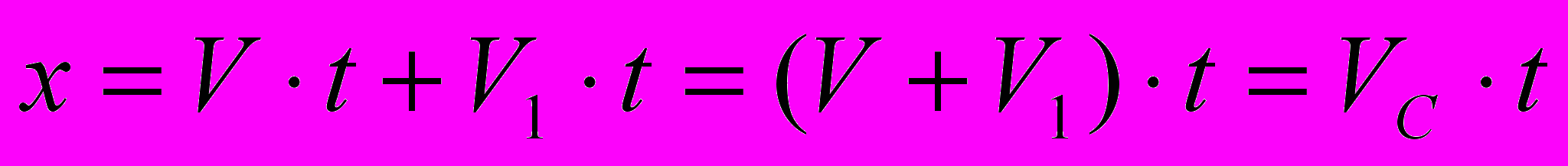. (5)То есть математическая запись этого закона (
), а значит и его физическая суть, инвариантны преобразованиям Галилея (рис. 2) [1].2.2. Кинематическая инвариантность в преобразованиях Лоренца
Основываясь на постулате о постоянстве скорости света
, Лоренц нашел, что указанный переход связан со скоростью света зависимостями (рис. 3) [6]: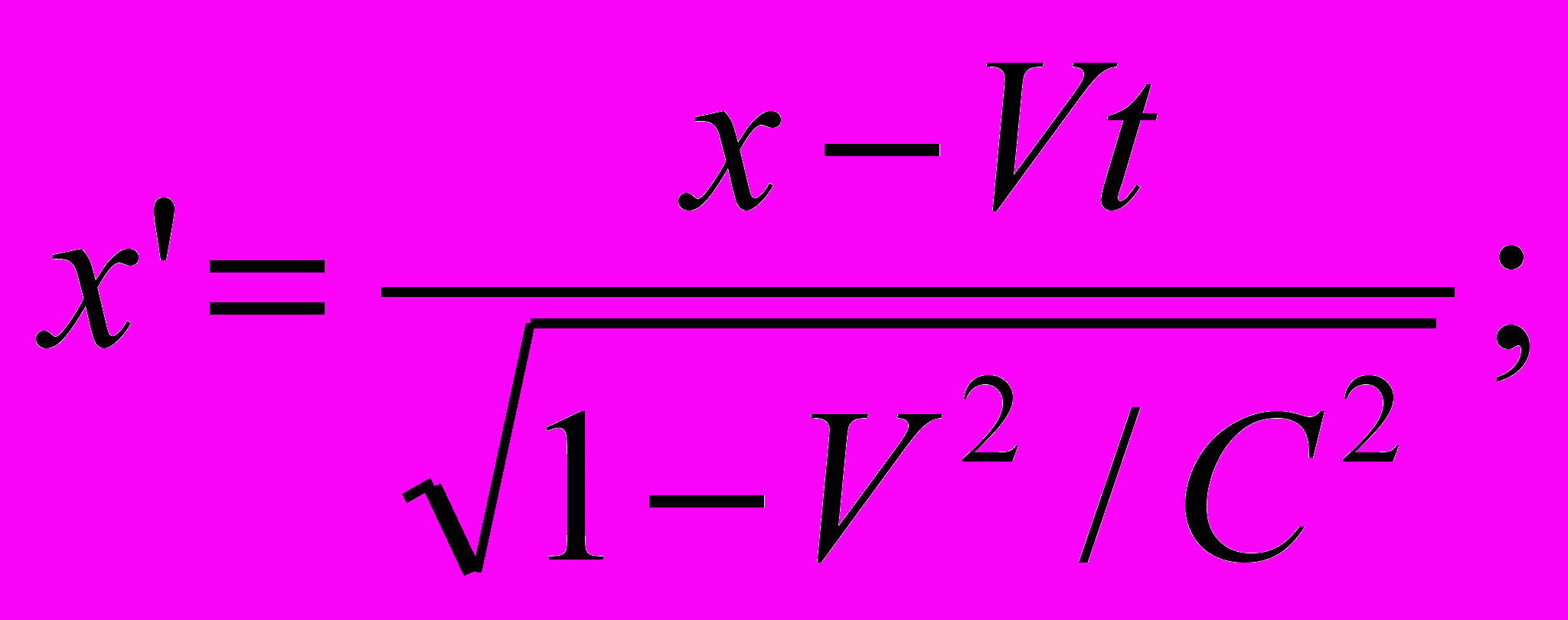
(6)
(7)Из соотношения (6) неявно следует, что с увеличением скорости
величина пространственного интервала 
уменьшается, что соответствует относительности пространства. Аналогичное следствие вытекает и из соотношения (7). При величина 
также уменьшается, что соответствует уменьшению темпа течения времени (рис. 3) или - относительности времени. 
Рис. 3. Схема к анализу преобразований Лоренца
У нас есть все основания задать кинематический закон прямолинейного движения точки в подвижной системе координат (рис. 3) в таком виде
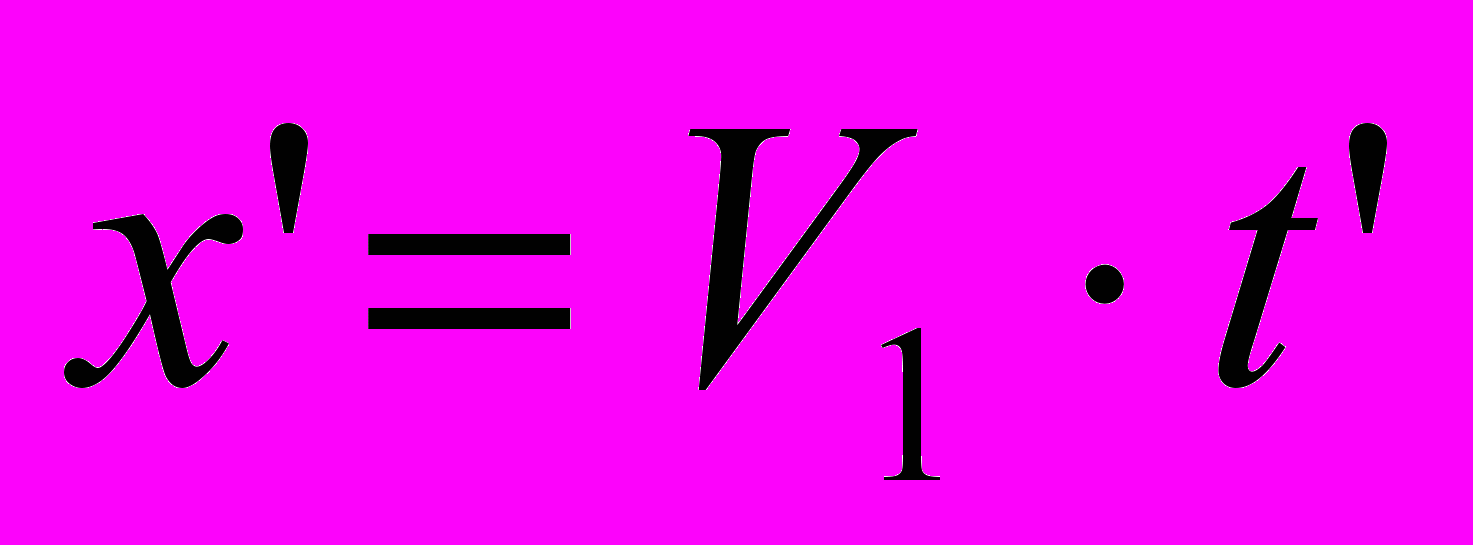. Тогда формула (6) Лоренца становится такой [1]
(8)Подставляя значение
(7) и преобразовывая, найдём
(9)Таким становится закон прямолинейного и равномерного движения точки относительно неподвижной системы отсчёта. Здравомыслящему человеку трудно комментировать такой результат, поэтому мы формулируем сразу вывод, который следует из этого результата. Закон самого простого прямолинейного и равномерного движения точки (9) не инвариантен преобразованиям Лоренца (6) и (7). Что это значит? Ответ один: преобразования Лоренца генерируют мистическую информацию, не имеющую никакого отношения к реальности.
2.3. Динамическая инвариантность в преобразованиях Галилея
Пусть тело движется прямолинейно под действием силы
относительно подвижной инерциальной системы координат X’O’Y’, которая движется относительно неподвижной системы XOY с постоянной скоростью 
(рис. 2). Уравнение (закон) движения тела относительно подвижной системы координат запишется так [1]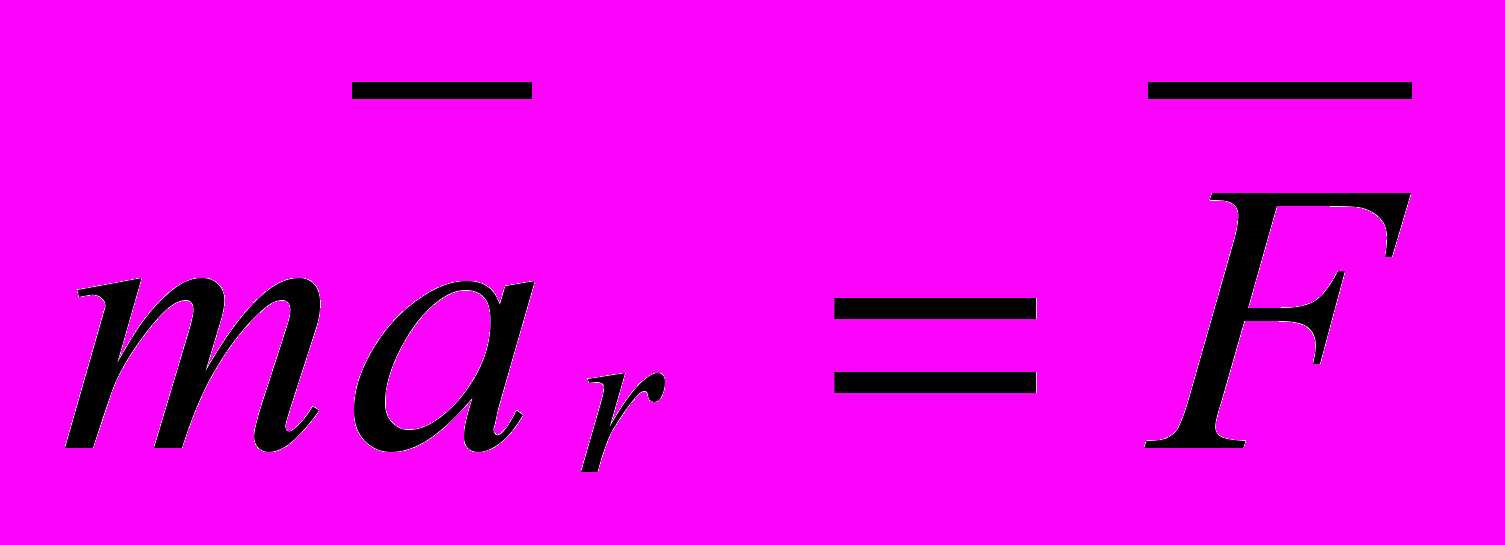
, (10)здесь
- относительное ускорение тела. Если тело движется прямолинейно относительно неподвижной системы координат под действием аналогичной силы
, то закон его движения будет иметь вид
, (11)здесь
- абсолютное ускорение тела. Поскольку подвижная система отсчёта движется равномерно, то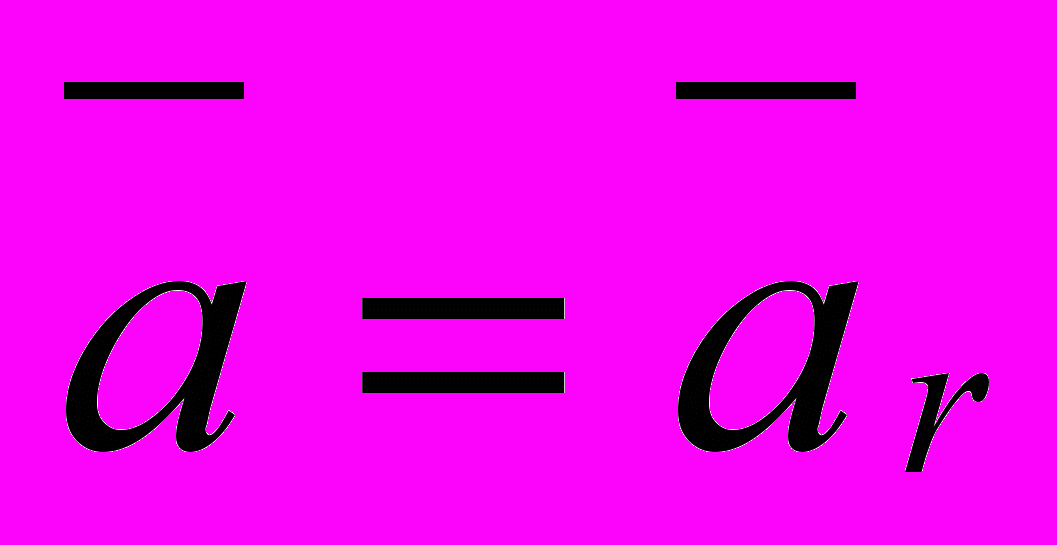 
.Таким образом, из изложенного следует, если подвижная система отсчета движется параллельно неподвижной системе отсчета с постоянной скоростью
, то динамическое уравнение прямолинейного ускоренного движения тела в этой системе отсчёта инвариантно динамическому уравнению ускоренного движения этого же тела относительно неподвижной системы отсчета. Это доказывает физическую и математическую инвариантность второго закона Ньютона преобразованиям Галилея. Главным является то, что описанные явления и их закономерности не зависят от скорости движения подвижной системы координат. Важно и то, что и кинематические (5), и динамические законы (10) инвариантны преобразованиям Галилея.2.4. Динамическая инвариантность в преобразованиях Лоренца
Пусть точка или тело движутся относительно подвижной системы отсчёта (рис. 3) по закону
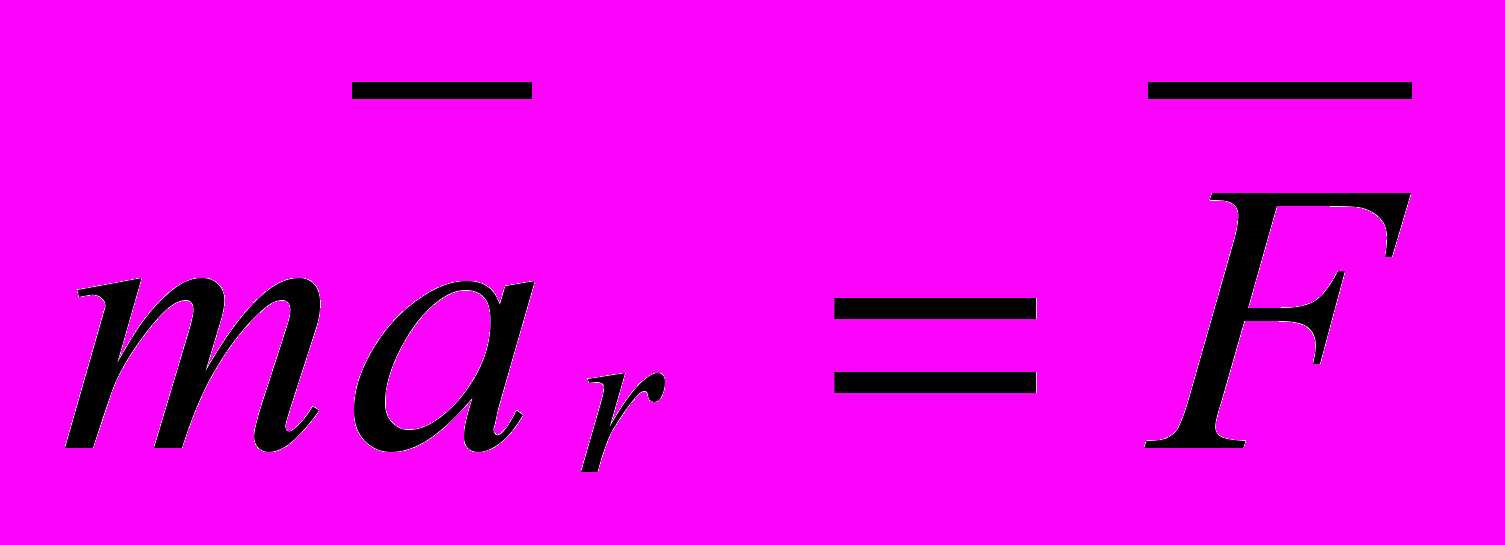. Сразу возникает вопрос: каким образом ввести этот закон в преобразования Лоренца (6) и (7), чтобы увидеть процесс реализации его инвариантности в этих преобразованиях? Поскольку преобразования Лоренца сокращают любой пространственный интервал вдоль оси , то вполне естественно, что они будут сокращать и траекторию тела, движущегося вдоль оси по закону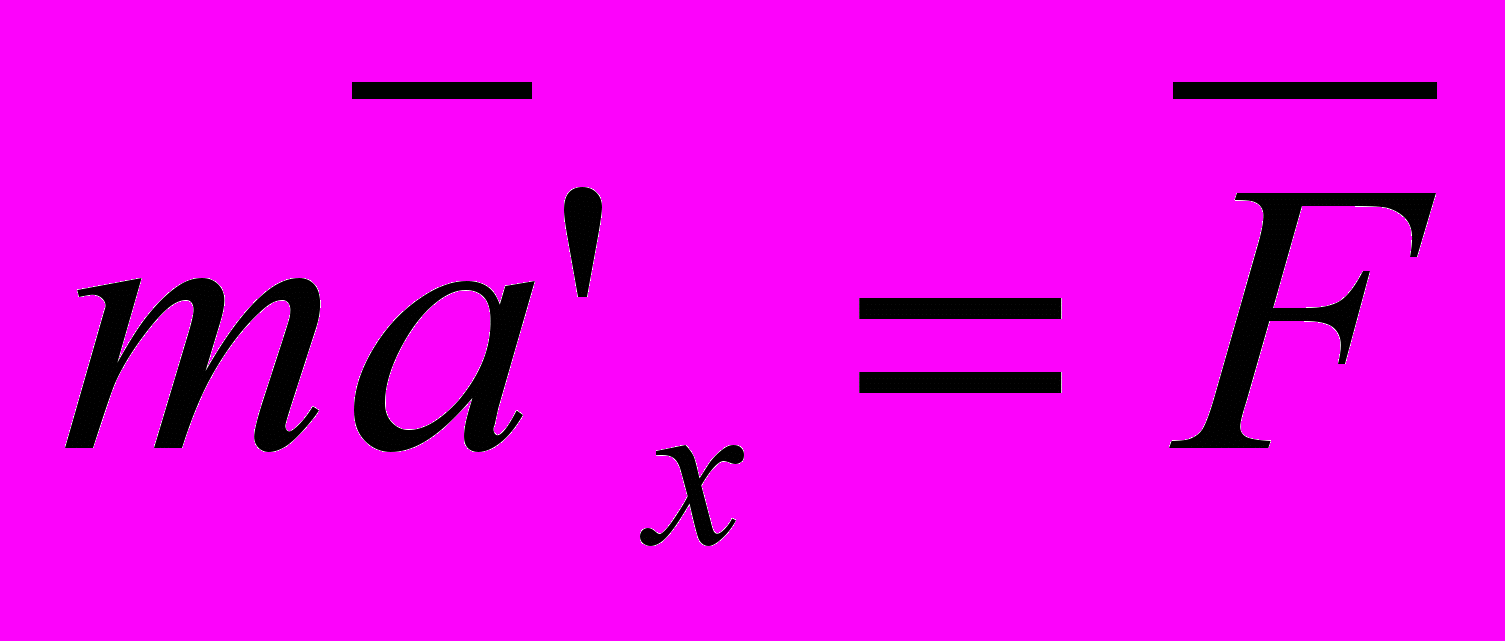 
. Чтобы убедиться в возможности реализации указанного закона движения тела относительно подвижной лоренцевской системы отсчёта (рис. 3), необходимо найти ускорение 
. Для этого надо продифференцировать дважды закономерность изменения координаты по времени . Из уравнений (6) и (7) имеем [1]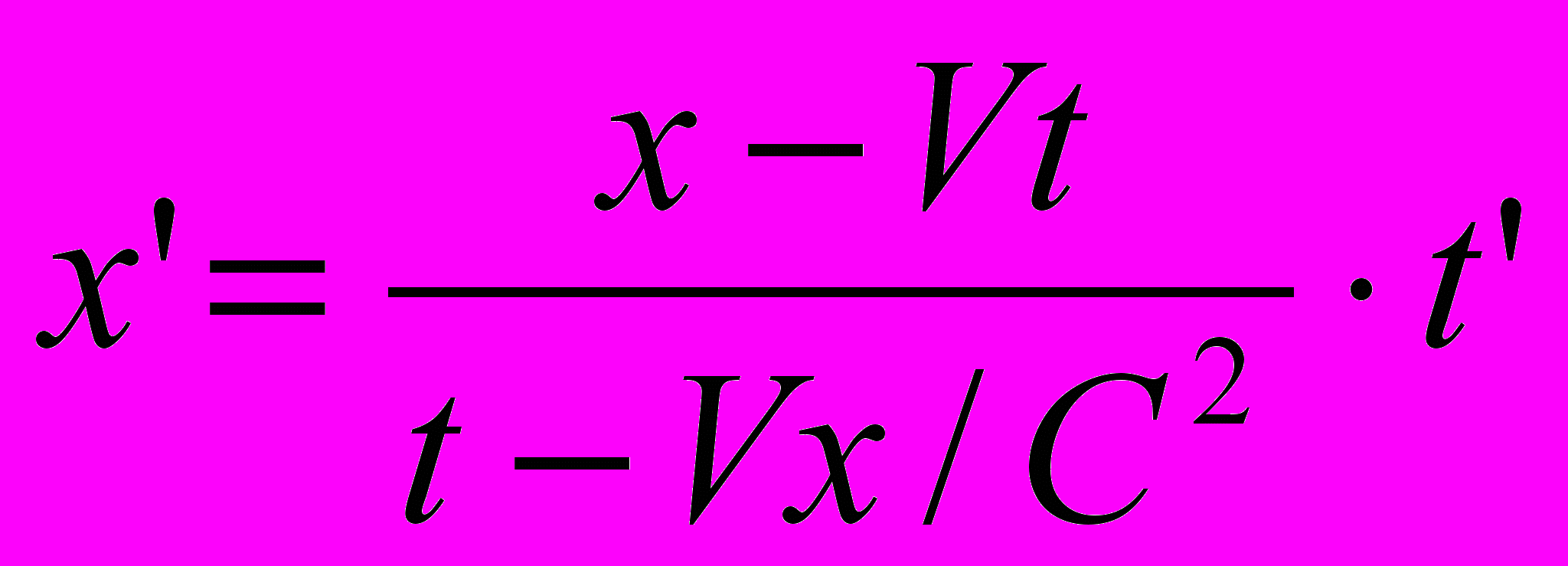
(12)и сразу попадаем в затруднительное положение. В формуле (12) два времен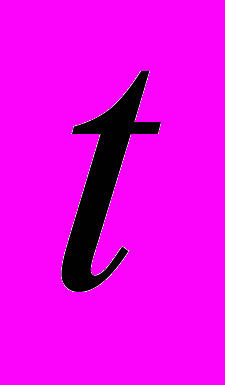и:
и . Одно течет в подвижной, другое - в неподвижной системах отсчёта. Как быть? Брать частные производные по двум временам, то есть останавливать поочерёдно времена 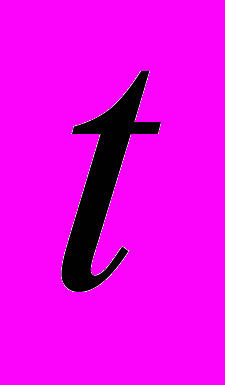и ? При этом надо учесть, что 
в уравнении (12) - тоже величина переменная и её также надо дифференцировать. Читатель представляет сложность получаемого при этом результата. Он будет отличаться значительно от математической модели 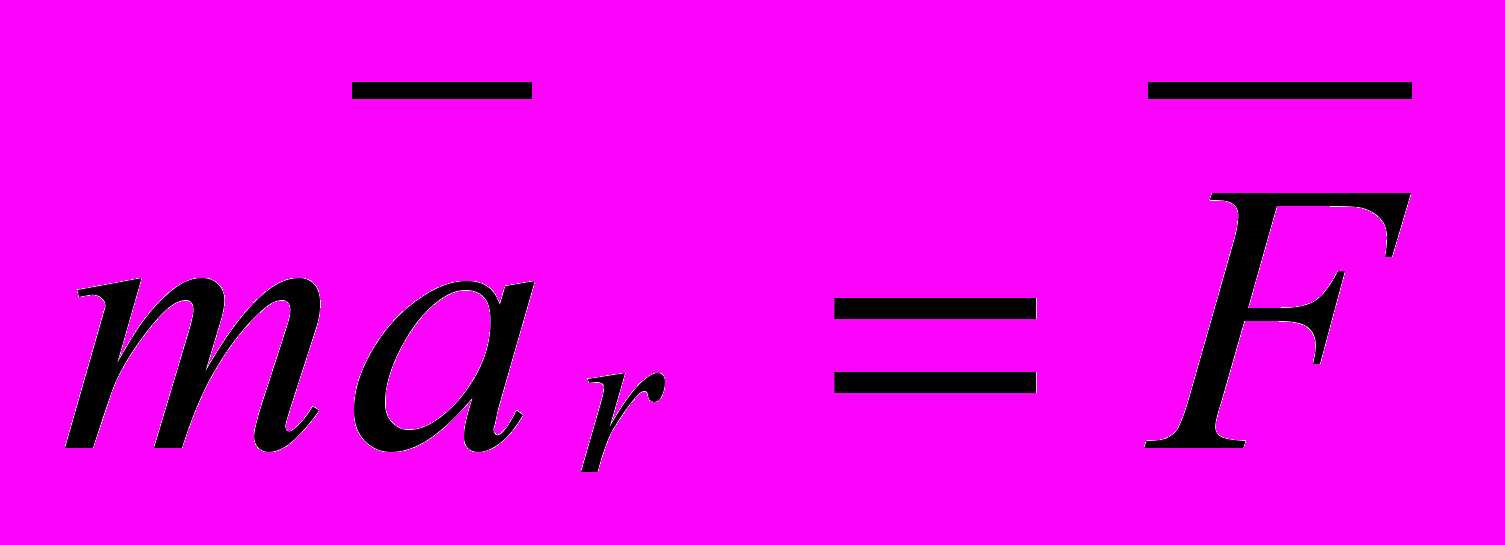движения этого тела в галилеевской подвижной системе координат, что даёт нам право утверждать, что закон движения точки или тела инвариантен галилеевским преобразованиям координат (3) и (4), и не инвариантен преобразованиям Лоренца (6), (7). 2.5. Инвариантность закона Кулона
Закон Кулона описывает взаимодействие между электрическими зарядами, находящимися в покое. Два неподвижных электрических заряда отталкивают или притягивают друг друга с силой
, пропорциональной произведению величин зарядов 
, 
и обратно пропорциональной квадрату расстояния 
между ними.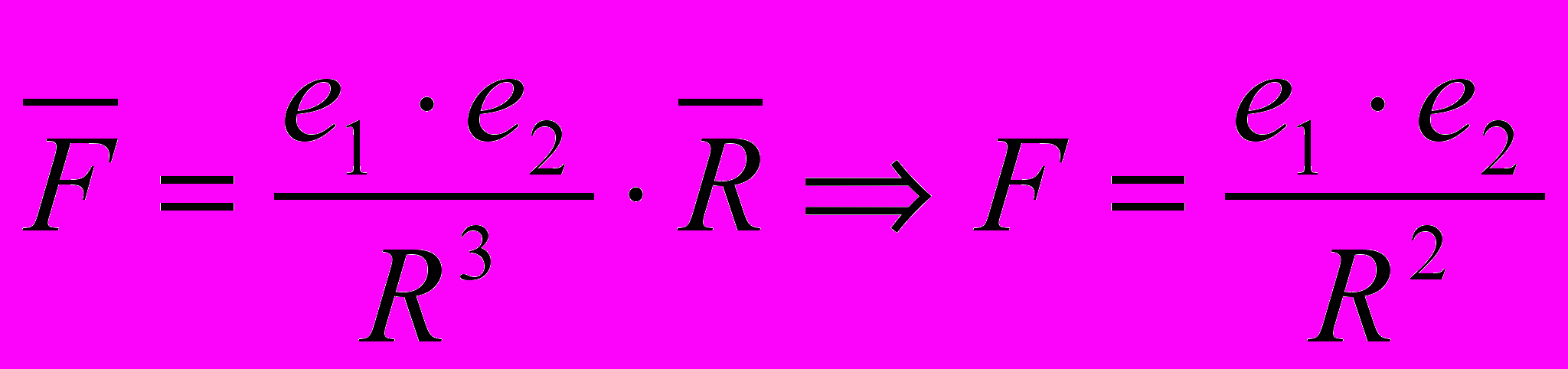
. (13)Из определения закона Кулона однозначно следует, что он инвариантен преобразованиям Галилея (3, 4). Ни один параметр, входящий в этот закон (13), не изменяется при переходе из неподвижной в подвижную систему координат (рис. 2).
Преобразования Лоренца отрицают эту инвариантность, так как в математическую модель закона Кулона входит пространственный интервал
- расстояние между зарядами, величина которого изменяется при 
. Если заряды будут расположены в подвижной системе отсчета (рис. 3), движущейся со скоростью
, близкой к скорости света, вдоль оси , то с увеличением скорости движения подвижной системы отсчёта расстояние между зарядами начнёт уменьшаться. В результате сила (13) начнет увеличиваться. Если заряды будут расположены так, что линия, соединяющая их, будет перпендикулярна оси , то параметр , а значит, и сила останутся неизменными. На примере анализа инвариантности закона Кулона преобразованиям Лоренца покажем антинаучные действия релятивистов при доказательстве инвариантности уравнений Максвелла преобразованиям Лоренца.
Если надо доказать инвариантность закона Кулона преобразованиям Лоренца, то релятивисты берут вариант расположения зарядов перпендикулярно подвижной оси
(в этом случае величина не изменяется) и отбрасывают вариант расположения зарядов вдоль этой оси (в этом случае величина изменяется). В первом случае закон Кулона физически инвариантен преобразованиям Лоренца, а во втором нет, но они отбрасывают его. Какие могут быть тут комментарии!?Описанная процедура установления инвариантности физических законов и их математических моделей преобразованиям Лоренца оказывается единственно возможной. Она и используется для установления инвариантности уравнений Максвелла преобразованиям Лоренца. Релятивисты считают эту процедуру непререкаемой и не подлежащей сомнению, так как она необходима им для связи между уравнениями Максвелла и теориями относительности А. Эйнштейна. Они идут на любые искажения ради спасения указанной связи.
Релятивисты много пишут о том, что уравнения Максвелла не инвариантны преобразованиям Галилея, а значит и его принципу относительности, но инвариантны преобразованиям Лоренца, и, следовательно, - принципу относительности А. Эйнштейна. Однако при этом не отмечается, что это - математическая инвариантность. О физической, более ценной инвариантности уравнений Максвелла преобразованиям Лоренца, информации меньше, но она есть [6].
2.6. Физическая инвариантность уравнений Максвелла
Д. Максвелл постулировал свои уравнения в 1865г. Они считаются основой электродинамики. Главная область их применения – анализ электромагнитных процессов и излучений. Запишем их в дифференциальной форме [6].
(14)
, (15)
, (16)
. (17)Здесь:
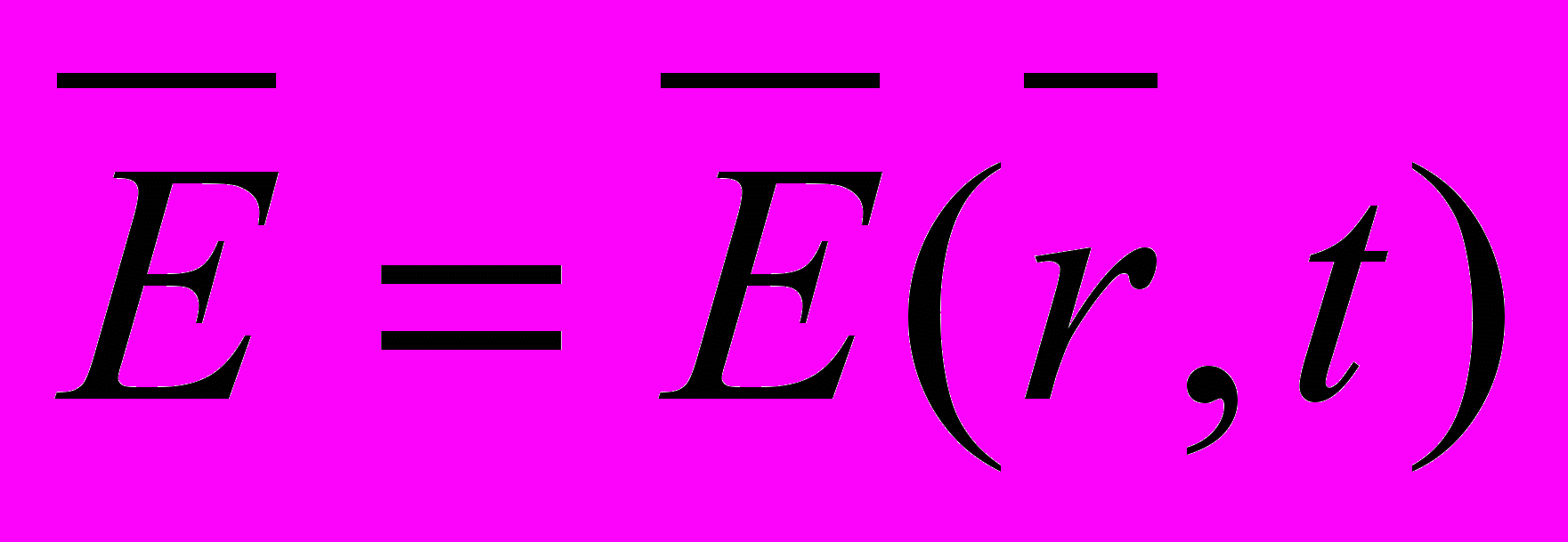- напряженность электрического поля;
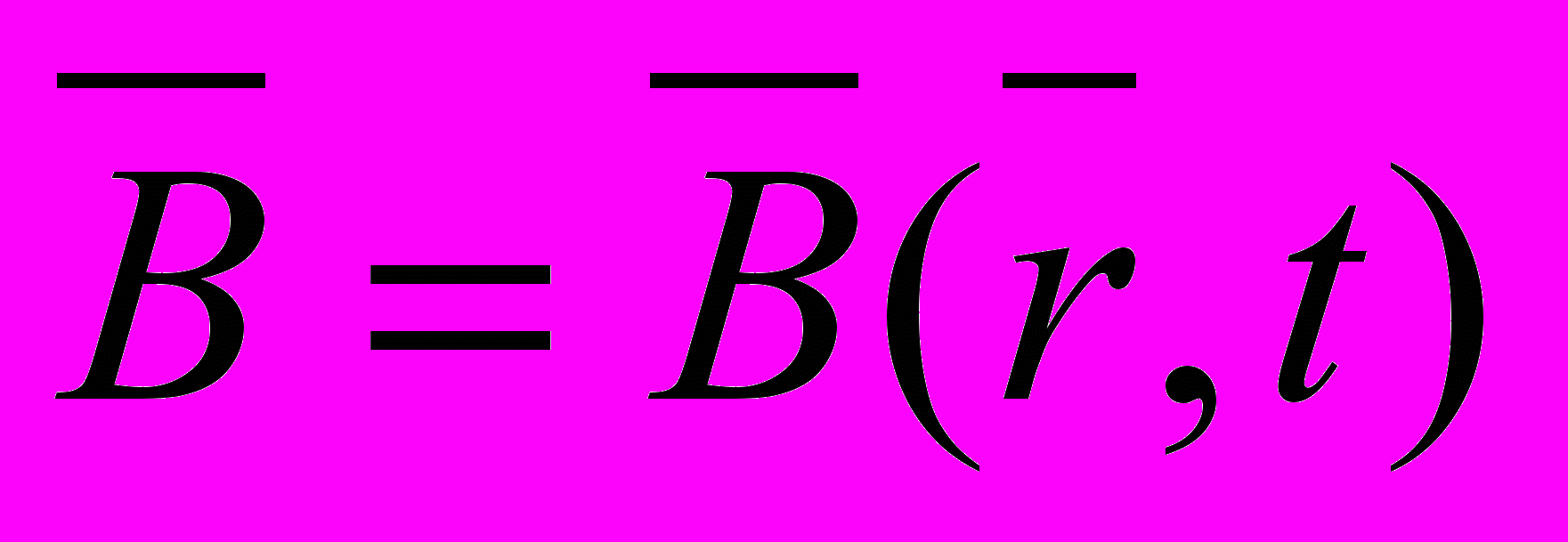- напряженность магнитного поля;
- ток смещения;
- ток проводимости.Как видно (14-17), это - уравнения в частных производных, поэтому они автоматически противоречат аксиоме Единства. Это противоречие усиливается независимостью
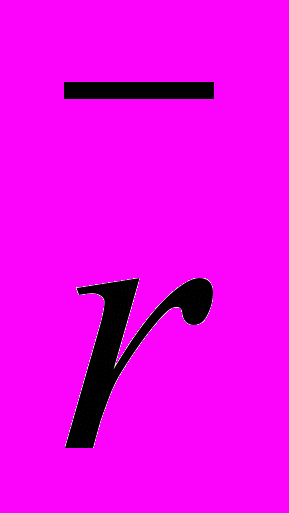и 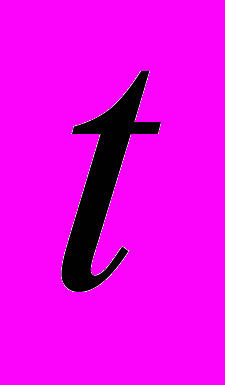. В результате они не могут описывать корректно движение в пространстве каких-либо объектов. Поэтому у нас есть основание поставить под сомнение, соответствие реальности математического доказательства инвариантности уравнений Максвелла преобразованиям Лоренца.Дальше мы покажем, что уравнения Максвелла описывают несуществующие в Природе электромагнитные волны, а сейчас убедимся в том, что отсутствует более важная – физическая инвариантность уравнений Максвелла преобразованиям Лоренца.
Мы не будем рассматривать математическую инвариантность уравнений Максвелла преобразованиям Галилея или Лоренца. Для нас важнее физическая инвариантность этих уравнений в указанных преобразованиях. Суть физической инвариантности заключается в неизменности физических законов, входящих в уравнения Максвелла при любых преобразованиях координат. Главными из них являются законы, описывающие изменение напряженностей электрических и магнитных полей, так как их величины зависят от пространственных координат и времени. Можно к этому добавить ещё ток проводимости. Ток смещения трогать не будем, так как его физический смысл до сих пор остаётся таинственным и мы посвятим анализу этой таинственности специальный параграф [1].
Опишем кратко суть «доказательства» инвариантности напряженности электрического поля преобразованиям Лоренца, изложенного в Берклеевском курсе физики (учебнике) [7]. Представим ситуацию, когда неподвижные пластины конденсатора ориентированы перпендикулярно к оси
в подвижной системе отсчёта. По данным неподвижного наблюдателя в направлении оси величина 
. Автор [7] утверждает, что в этом случае поверхностная плотность заряда, наблюдаемая в подвижной системе отсчёта, такая же, как и в неподвижной. По его мнению происходит это потому, что размеры слоёв электрического поля конденсатора не сокращаются; сокращается только расстояние между ними, но оно не входит в определение поля. Поэтому, как пишет автор, 
[7]. А как же быть с эффектом пробоя конденсатора с уменьшением расстояния между его пластинами? Автор скромно обходит этот неприятный для него вопрос. Но он не единственный. А если расположить пластины конденсатора в подвижной системе отсчёта вдоль оси
? Их размеры уменьшатся. Автоматически изменится и удельная напряженность электрического поля конденсатора. О какой физической инвариантности напряженности электрического поля преобразованиям Лоренца можно говорить? Нет тут физической инвариантности и быть не может.Аналогичным образом доказывается инвариантность напряженности магнитного поля преобразованиям Лоренца. Опишем кратко и это «доказательство». Автор рассматривает компоненту
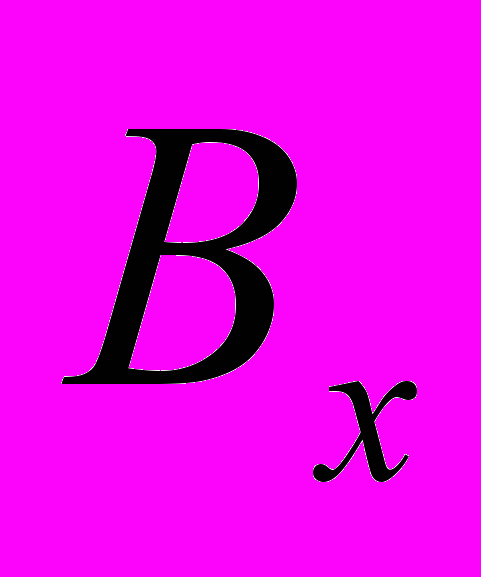магнитного поля, которая создаётся соленоидом, намотанным вдоль оси в неподвижной системе координат и правильно считает, что 
.Далее, автор считает, что в подвижной системе координат такой соленоид будет претерпевать лоренцевское сокращение и число витков в этой системе координат на единице длины вдоль оси
будет больше, но сила тока в подвижной системе координат будет меньше, так как подвижный наблюдатель будет измерять силу тока по числу электронов, проходящих через данную точку провода за единицу времени, используя медленно идущие часы. В результате, как считает автор, растяжение времени компенсирует сокращение длины и таким образом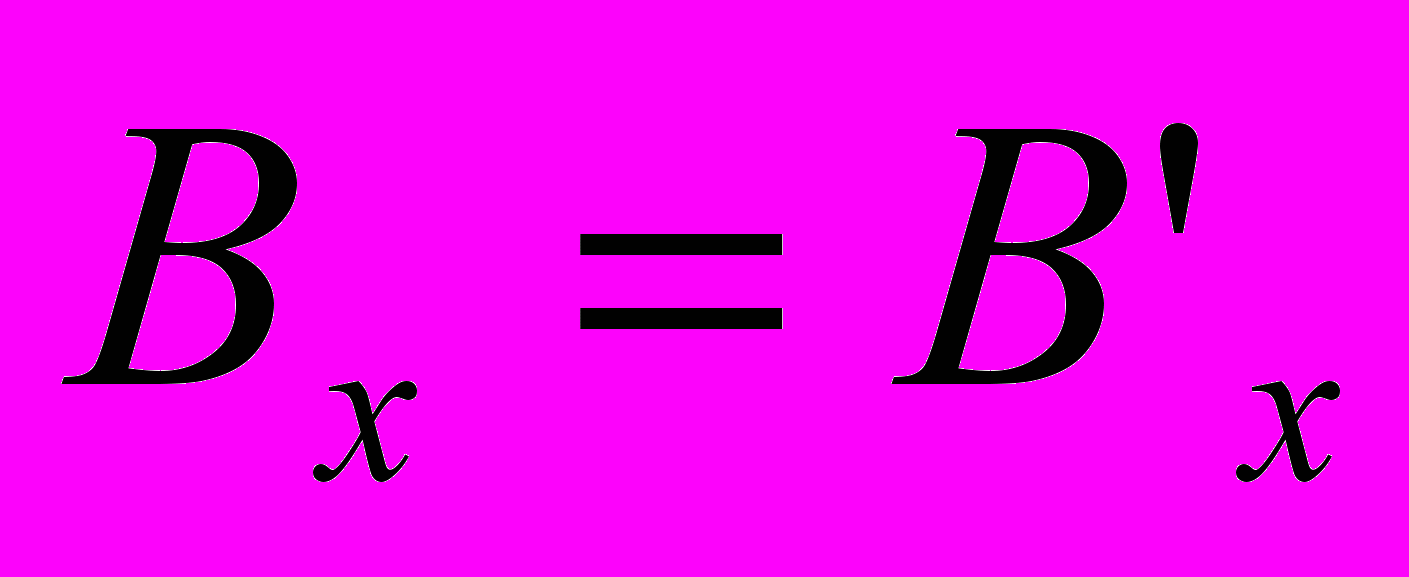 
.Уважаемый релятивист, зачем Вы опускаете анализ варианта, когда ось соленоида будет перпендикулярна оси
? Никакого изменения числа витков на единицу длины в направлении, перпендикулярном оси не будет, а замедленный темп течения времени в подвижной системе отсчёта сохранится, в результате изменится сила тока, и, как следствие, - напряженность магнитного поля, генерируемого таким соленоидом. А вот в галилеевской подвижной системе отсчета все параметры конденсатора и соленоида остаются действительно неизменными - инвариантными преобразованиям Галилея при любом их положении в этой системе. Причина этой инвариантности одна - неизменный темп течения времени.Из изложенного следует, что главные физические параметры: напряжённости электрических и магнитных полей, входящие в уравнения Максвелла, инвариантны преобразованиям Галилея и не инвариантны преобразованиям Лоренца.
Заключение
Усиленная пропаганда релятивистами инвариантности законов Природы преобразованиям Лоренца - миф, призванный спасти идею связи этих законов с теориями относительности А. Эйнштейна. Нет таких законов в Природе, которые бы были инвариантны преобразованиям Лоренца. Не имеют этой инвариантности физические параметры, входящие в уравнения Максвелла.
Доказательство математической инвариантности уравнений Максвелла преобразованиям Лоренца при отсутствии физической инвариантности – яркая демонстрация негативной роли математики в познании реальности. Если нет физической инвариантности, то кому нужна математическая инвариантность? Отсутствие физической инвариантности автоматически закрывает дорогу математикам гипнотизировать научную общественность таинственностью математических символов. Но они этого до сих пор не понимают и плетут кружева бесплодных математических доказательств.
Литература
1. Канарёв Ф.М. «Начала физхимии микромира». Монография доступна для копирования по адресу: ссылка скрыта
2. Канарёв Ф.М., Зеленский С.А. Курс лекций по теоретической механике. Краснодар, 2007. 360 с.
3. Канарёв Ф.М. ВВЕДЕНИЕ В МЕХАНОДИНАМИКУ
ссылка скрыта ссылка скрыта
4. Эйнштейн А. К электродинамике движущихся тел. Сборник работ по специальной теории относительности. М.: Атомиздат, 1973.
5. Кулигин В.А. Электродинамика отвергает теорию относительности.
ссылка скрыта
6. Матвееев А.Н. Механика и теория относительности. М.: Высшая школа, 1976.
7. Парселл Э. Электричество и магнетизм. Берклеевский курс физики. Том II. М. «Наука». 1983. 415с.