Рабочая программа учебной дисциплины
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины ф тпу 1 -21/01, 102.93kb.
- Рабочая программа учебной дисциплины судебная фотография и видеозапись Специальность, 90.44kb.
- Рабочая программа учебной дисциплины судебная этика Направление подготовки 030500., 197.85kb.
- Рабочая программа учебной дисциплины судебная психиатрия Специальность 030501. 65 «Юриспруденция», 141.66kb.
- Рабочая программа учебной дисциплины судебная адвокатура Специальность 030501. 65 «Юриспруденция», 148.98kb.
- Рабочая программа учебной дисциплины современные способы фиксации следственных действий, 170.54kb.
- Учебно-методического комплекса (умк) Учебной дисциплины «Финансы и кредит» Проектирование, 424.52kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 утверждаю, 360.66kb.
- Рабочая программа учебной дисциплины (место, цели и задачи учебной дисциплины в общей, 498.45kb.
- Рабочая программа учебной дисциплины математика и информатика, 188.66kb.
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве
Российской Федерации»
Кафедра «Теория вероятностей и математическая статистика»
И.Е. Денежкина, С.А. Зададаев
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Рабочая программа учебной дисциплины
Для бакалавров направления 080500 «Менеджмент» и направления 080500 «Менеджмент» по профилю «Финансовый менеджмент
М
 осква 2010
осква 2010 Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве
Российской Федерации»
Кафедра «Финансовый менеджмент»
утверждаю
Ректор
__________ М.А. Эскиндаров
_______ ___________ 2010 г.
И.Е. Денежкина, С.А. Зададаев
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Рабочая программа учебной дисциплины
Для бакалавров направления 080500 «Менеджмент» и направления 080500 «Менеджмент» по профилю «Финансовый менеджмент
Рекомендовано Ученым советом факультета «Математические
методы и анализ рисков», протокол № ___ от ___ ___________ 2010 г.
Одобрено кафедрой «Теория вероятностей и математическая статистика», протокол № ___ от ___ ___________ 2010 г.
М
 осква 2010
осква 2010 УДК ?
ББК ?
Рецензент: Т.Л. Мелехина, доцент кафедры «Теория вероятностей и математическая статистика»
?? И.Е. Денежкина, С.А. Зададаев
«Теория вероятностей и математическая статистика». Программа дисциплины для студентов, обучающихся для бакалавров направления 080500 «Менеджмент» и направления 080500 «Менеджмент» по профилю «Финансовый менеджмент (программа подготовки бакалавров) – очная форма обучения.– М.: ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», кафедра «Теория вероятностей и математическая статистика», 2010. - 23 с.
Дисциплина «Теория вероятностей и математическая статистика» является компонентой базовой части математического цикла дисциплин ФГОС ВПО по направлению 080500 «Менеджмент». Программа содержит: программу дисциплины; рабочий план изучения дисциплины; тематику и планы лекций, тематику практических и самостоятельных занятий с указанием технологии их проведения; формы контроля за их выполнением.
УДК ?
ББК ?
Учебное издание
Ирина Евгеньевна Денежкина
Сергей Алексеевич Зададаев
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Рабочая программа учебной дисциплины
Компьютерный набор, верстка: Зададаев С.А.
Формат 60х90/16. Гарнитура Times New Roman
Усл.п.л.1,1. Изд. № 13.18-2010. Тираж ___ экз.
Отпечатано в ФГОУ ВПО «Финансовый университет при
Правительстве Российской Федерации»
И.Е. Денежкина, 2010
С.А. Зададаев, 2010
 ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», 2010
ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», 2010Содержание
- Цели и задачи дисциплины…………………………………………4
- Место дисциплины в структуре ООП……………………………...4
- Требования к результатам освоения дисциплины………………...5
- Объем дисциплины и виды учебной работы……………………...7
- Содержание дисциплины:
5.1 Содержание разделов дисциплины……………………………...7
5.2 Разделы дисциплины и междисциплинарные
связи с обеспечиваемыми дисциплинами……………………..11
5.3 Разделы дисциплины и виды занятий………………………….12
- Практические (семинарские) занятия…………………………….12
- Самостоятельная работа…………………………………………...14
- Оценочные средства для текущего контроля успеваемости
и промежуточной аттестации по итогам освоения дисциплины..15
- Учебно-методическое и информационное обеспечение
дисциплины………………………………………………………….16
- Приложение. Учебно-методическая карта дисциплины…………19
1. Цели и задачи дисциплины
Цель дисциплины –
1. Получение базовых знаний и формирование основных навыков по теории вероятностей и математической статистике, необходимых для решения задач, возникающих в практической экономической деятельности.
2. Развитие понятийной теоретико-вероятностной базы и формирование уровня алгебраической подготовки, необходимых для понимания основ экономической статистики и её применения.
Задача дисциплины –
В результате изучения дисциплины «Теория вероятностей и математическая статистика» студенты должны владеть основными математическими понятиями курса; уметь использовать теоретико-вероятностный и статистический аппарат для решения теоретических и прикладных задач экономики уметь решать типовые задачи, иметь навыки работы со специальной математической литературой.
2. Место дисциплины в структуре ООП
Дисциплина «Теория вероятностей и математическая статистика» является компонентой базовой части математического цикла Федеральных государственных образовательных стандартов высшего профессионального образования (ФГОС ВПО) по направлению по направлению 080500 «Менеджмент» (бакалавриат).
Изучение дисциплины «Теория вероятностей и математическая статистика» основывается на базе знаний, полученных студентами на первом курсе в ходе освоения дисциплин «Линейная алгебра» и «Математический анализ» того же блока.
Дисциплина «Теория вероятностей и математическая статистика» изучается на втором году обучения, закладывает фундамент для понимания экономической статистики и является базовым теоретическим и практическим основанием для всех последующих математических и финансово-экономических дисциплин подготовки бакалавра экономики, использующих теоретико-вероятностные и статистические методы анализа.
3. Требования к результатам освоения дисциплины
В совокупности с другими дисциплинами базовой части математического цикла ФГОС ВПО дисциплина «Теория вероятностей и математическая статистика» обеспечивает инструментарий формирования следующих профессиональных компетенций бакалавра менеджмента:
- владеет культурой мышления, способен к восприятию, обобщению и анализу информации, постановке цели и выбору путей её достижения (ОК–5);
- умеет логически верно, аргументировано и ясно строить устную и письменную речь (ОК-6);
- владеет методами количественного анализа и моделирования, теоретического и экспериментального исследования (ОК-15);
- способен использовать основные методы финансового менеджмента для стоимостной оценки активов, управления оборотным капиталом, принятия решений по финансированию, формированию дивидендной политики и структуре капитала (ПК-11);
- умеет применять количественные и качественные методы анализа при принятии управленческих решений и строить экономические, финансовые и организационно-управленческие модели (ПК-31);
- способен выбирать математические модели организационных систем, анализировать их адекватность, проводить адаптацию моделей к конкретным задачам управления (ПК-32);
В результате освоения содержания дисциплины «Теория вероятностей и математическая статистика» студент должен:
знать
- основы теории вероятностей и математической статистики, необходимые для понимания финансовых и экономических задач;
уметь
- применять теоретико-вероятностные и статистические методы для решения задач менеджмента;
владеть
- навыками применения современного математического инструментария для решения экономических задач и задач менеджмента;
- методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений с позиций управленческих процессов (в части компетенций, соответствующих методам теории вероятностей и математической статистики).
4. Объём дисциплины и виды учебной работы
Общая трудоёмкость дисциплины составляет 4 зачётных единиц.
Вид промежуточной аттестации – 1 экзамен.
| Вид учебной работы | Часы | Семестры (II курса) |
| 3 | ||
| Общая трудоёмкость дисциплины | 144 | 144 |
| Аудиторные занятия | 68 | 68 |
| Лекции (Л) | 34 | 34 |
| Практические занятия (ПЗ) | 34 | 34 |
| Самостоятельная работа | 76 | 76 |
| В семестрах | 40 | 40 |
| В сессию / форма | 36 | 36 |
| | экзамен |
5. Содержание дисциплины
5.1. Содержание разделов дисциплины
Часть I. Теория вероятностей
Раздел 1. Вероятности событий
1.1. Основные понятия комбинаторики: комбинаторное правило умножения, перестановки, сочетания из
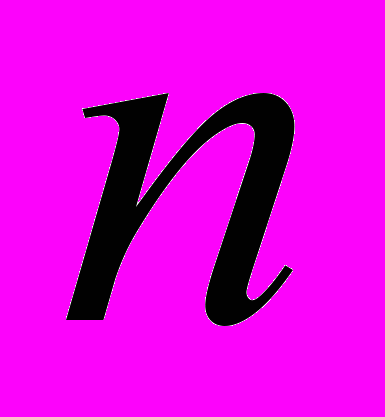 по
по  , размещения из
, размещения из 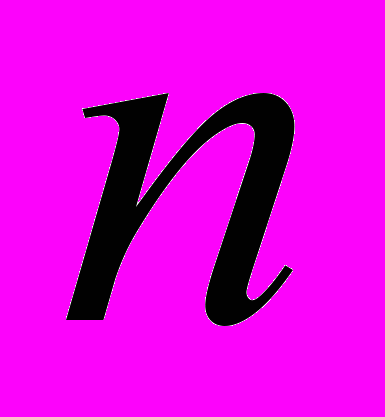 по
по  , сочетания с повторениями. Бином Ньютона и свойства биномиальных коэффициентов.
, сочетания с повторениями. Бином Ньютона и свойства биномиальных коэффициентов.1.2. Случайные события, частота и вероятность. Классический способ подсчета вероятностей. Геометрические вероятности. Пространство элементарных событий. Случайное событие как подмножество в пространстве элементарных событий. Алгебра событий. Аксиомы вероятности и вероятностное пространство. Следствия из аксиом. Статистическое определение вероятности.
1.3. Основные формулы для вычисления вероятностей. Условные вероятности. Теорема умножения вероятностей. Формула полной вероятности и формулы Байеса вероятностей гипотез. Независимые события.
1.4. Схема повторных независимых испытаний (схема Бернулли). Формула Бернулли. Наиболее вероятное число успехов в схеме Бернулли. Приближенные формулы Лапласа. Функции Гаусса и Лапласа. Предельная теорема и приближенная формула Пуассона.
Раздел 2. Случайные величины
2.1. Случайная величина как функция на пространстве элементарных событий. Функция распределения случайной величины. Свойства функции распределения. Независимость случайных величин. Функции от одной или нескольких случайных величин. Арифметические операции над случайными величинами.
2.2. Дискретная случайная величина (ДСВ) и ее закон распределения. Основные числовые характеристики ДСВ: математическое ожидание, дисперсия, стандартное отклонение, ковариация и коэффициент корреляции. Математическое ожидание функции от ДСВ.
2.3. Свойства математического ожидания, дисперсии, ковариации и коэффициента корреляции.
2.4. Примеры классических дискретных распределений (биномиальное, пуассоновское, геометрическое) и вычисление их числовых характеристик. Производящие функции*.
2.5. Непрерывные и абсолютно непрерывные случайные величины. Свойства функции плотности. Математическое ожидание и дисперсия абсолютно непрерывной случайной величины. Математическое ожидание функции от абсолютно непрерывной случайной величины.
2.6. Равномерное распределение на отрезке, показательное (экспоненциальное) распределение и нормальное распределения, их числовые характеристики. Нормальность суммы независимых нормальных случайных величин.
2.7. Начальные и центральные моменты случайной величины. Асимметрия и эксцесс.
Раздел 3. Предельные теоремы теории вероятностей
3.1. Неравенство Чебышева. Правило «трех сигм» в общем случае. Теоремы Чебышева и Бернулли. Последовательности случайных величин. Сходимость по вероятности и закон больших чисел.
3.2. Понятие характеристической функции*. Центральная предельная теорема (ЦПТ) в форме Ляпунова для одинаково распределенных слагаемых и в общем случае. Применение ЦПТ.
Раздел 4. Случайные векторы
4.1. Совместное распределение случайных величин. Случайный вектор. Зависимые и независимые случайные векторы. Функция распределения случайного вектора и ее свойства. Одинаково распределенные случайные векторы. Связь функции распределения случайного вектора с функциями распределения его компонент.
4.2. Дискретные случайные векторы. Вероятность попадания дискретного случайного вектора в заданное множество. Закон распределения двумерного дискретного случайного вектора и его связь с распределениями компонент.
4.3. Абсолютно непрерывные случайные векторы. Вероятность попадания абсолютно непрерывного случайного вектора в заданное множество. Связь функции плотности распределения случайного вектора с функциями плотности его компонент. Функция плотности и независимость компонент случайного вектора. Равномерное распределение в ограниченной области в Rn.
4.4. Числовые характеристики дискретных и абсолютно непрерывных случайных векторов. Математическое ожидание функции от компонент случайного вектора. Ковариационная матрица случайного вектора. Неотрицательная определенность ковариационной матрицы.
4.5. Условные распределения и условные плотности. Условное математическое ожидание и его свойства. Формула полного математического ожидания. Условная дисперсия. Формула полной дисперсии.
Часть II. Математическая статистика
Раздел 5. Эмпирические характеристики и выборки
5.1. Статистические методы обработки экспериментальных данных. Генеральная совокупность. Эмпирическая функция распределения и вариационный ряд. Гистограмма. Мода и медиана.
5.2. Генеральные среднее, дисперсия, моменты высших порядков (асимметрия, эксцесс). Эмпирическая ковариация.
5.3. Повторные и бесповторные выборки. Математическое ожидание и дисперсия выборочного среднего для повторной и бесповторной выборки.
Раздел 6. Точечные и интервальные оценки
6.1. Статистические оценки параметров распределения. Несмещенность, состоятельность и эффективность точечных оценок. Оценка неизвестной вероятности по частоте. Точечные оценки для математического ожидания и дисперсии. Метод моментов.
6.2. Доверительные вероятности и интервалы. Приближенный доверительный интервал для оценки генеральной доли признака. Приближенный доверительный интервал для оценки генерального среднего.
5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми дисциплинами
| № п/п | Наименование обеспечиваемых дисциплин базовой части | Часть I Теория вероятностей | Часть II Математическая статистика |
| 1 | Статистика | * | * |
| 2 | Бизнес-планирование | | * |
| 3 | Основы финансовых вычислений | * | * |
| 4 | Маркетинг | | * |
| 5 | Финансовый учёт | | * |
| 6 | Экономика фирмы | * | * |
| 7 | Финансовый менеджмент | * | * |
5.3. Разделы дисциплины и виды занятий
| № п/п | Наименование раздела (темы) дисциплины | Трудоёмкость в часах | ||||
| Всего часов | Аудиторная работа | Внеауди-торная (самостоя-тельная) работа | ||||
| Общая | Лекции | Семинары | Общая | |||
| 1 | Вероятности событий | 22 | 14 | 6 | 8 | 8 |
| 2 | Случайные величины | 30 | 20 | 10 | 10 | 10 |
| 3 | Предельные теоремы теории вероятностей | 8 | 6 | 4 | 2 | 2 |
| 4 | Случайные векторы | 18 | 12 | 6 | 6 | 6 |
| 5 | Эмпирические характеристики и выборки | 7.5 | 4 | 2 | 2 | 3.5 |
| 6 | Точечные и интервальные оценки | 22.5 | 12 | 6 | 6 | 10.5 |
| | Экзамен | 36 | - | - | - | 36 |
| | Итого: | 144 | 68 | 34 | 34 | 76 |
6. Практические (семинарские) занятия
Рабочая учебная программа дисциплины предусматривает 17 аудиторных практических занятий (семинаров), каждое из которых рассчитано на 2 аудиторных часа.
Подробная тематика семинаров (с указанием соответствующей самостоятельной работы, форм контроля и связи с тематикой лекций) представлена в пункте 10. Приложение.
По структуре семинары следует разделить на учебные, контрольные и учебно-контрольные:
- Учебные семинары (№№: 1, 2, 3, 4, 6, 7, 9, 10, 11, 12, 13, 15 и 16) структурно состоят из
1) Проверка наличия выполненного задания самостоятельной работы
каждого студента;
2) Выборочная проверка корректности выполнения домашнего задания;
3) Разбор типичных ошибок, возникших в самостоятельной работе;
4) Рассмотрение теоретических оснований для практики текущей темы;
5) Разбор практических методов и решение соответствующих задач;
6) Корректировка заданий для самостоятельной работы студентов.
- Контрольные семинары (№№: 8 и 17) структурно состоят из
1) Проверка наличия домашней контрольной работы каждого студента;
2) Разбор типичных ошибок, возникших при решении домашней
контрольной работы;
3) Проведение аудиторной контрольной работы.
- Учебно-контрольные семинары (№№: 5 и 14) структурно состоят из
1) Проверка наличия выполненного задания самостоятельной работы
и/или домашней контрольной работы каждого студента;
2) Разбор типичных ошибок, возникших в самостоятельной работе или
решении домашней контрольной работы;;
3) Рассмотрение теоретических оснований для практики текущей темы;
4) Разбор практических методов и решение соответствующих задач;
6) Проведение аудиторной контрольной работы.
7. Самостоятельная работа
Внеаудиторными формами и инструментами самостоятельной работы студентов по дисциплине являются:
- выполнение 13-ти домашних заданий;
- выполнение 4-х домашних контрольных работ (как средство подготовки
к аудиторным контрольным работам);
- подготовка к практическим занятиям с использованием тестов
cамоконтроля;
- подготовка к одному экзамену.
Самостоятельная работа студентов по дисциплине состоит из 17 еженедельных заданий, каждое из которых рассчитано на 2 часа внеаудиторной нагрузки для части I дисциплины и по 3.5 часа для части II. Подробный перечень заданий для самостоятельной работы (с тематической связью аудиторных занятий, формами контроля и рекомендуемой учебно-методической литературой) приведен в пункте 10. Приложение.
Формы самостоятельной работы и нормы нагрузки
| №№ | Домашние задания ед./час. | Домашние контрольные работы ед./час. | Всего | Экзамен ед./час. |
| Часть I | 10/20 | 3/6 | 13/26 | 1 / 36 |
| Часть II | 3/10.5 | 1/3.5 | 4/14 | - |
| Итог | 13/30.5 | 4/9.5 | 17/40 | 1 / 36 |
Всего 76 часов самостоятельной работы, из них:
- работа в семестре - 40 часов,
- экзамен (часть I) - 36 часов.
8. Оценочные средства для текущего контроля
успеваемости и промежуточной аттестации по итогам освоения дисциплины
В качестве оценочных средств программой дисциплины предусматривается:
- текущий контроль (аудиторные контрольные работы, домашние контрольные работы, домашние задания, коллоквиум).
- промежуточный контроль – экзамен.
Итоговая оценка дисциплины проставляется по 100-бальной системе:
- неудовлетворительно – менее 51 балла;
- удовлетворительно – от 51 до 69 баллов;
- хорошо – от 70 до 85 баллов;
- отлично – свыше 85 баллов;
и формируется:
- аттестационными баллами семестра (20)
- экзаменационным баллом (80)
Аттестационный балл семестра (триместра) складывается из баллов текущей «аттестации» в середине семестра (триместра) (10) и баллами второй половины семестра (триместра) «работа в году» (10), каждый из которых учитывает успешность работы студента (выполнение 13-ти домашних заданий, 4-х аудиторных и домашних контрольных работ, выступления у доски).
Экзаменационные требования (теоретические вопросы и практические задания) изложены в [7].
9. Учебно-методическое
и информационное обеспечение дисциплины
Рекомендуемая литература
а) основная:
1. Браилов А.В., Солодовников А.С. Сборник задач по курсу «Математика в экономике». Часть 3. Теория вероятностей. М.:Финансы и статистика, 2010.
2. Денежкина И.Е., Орлова М.Г., Швецов Ю.Н. Основы математической статистики. Учебно-методическое пособие для самостоятельной работы бакалавров. М.: Финансовая академия при правительстве РФ, 2010.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. Учебник в 3 ч. Ч.3. Теория вероятностей и математическая статистика. М:. Финансы и статистика, 2008.
4. Браилов А.В., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Части 1,2. Учебное издание для студентов экономических специальностей. М.: Финансовая академия при правительстве РФ, 2007.
5. Браилов А.В., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 3. Учебное издание для студентов экономических специальностей. М.: Финансовая академия при правительстве РФ, 2006.
6. Браилов А.В., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 4. Учебное издание для студентов экономических специальностей. М.: Финансовая академия при правительстве РФ, 2008.
7. Браилов А.В., Гончаренко В.М., Конов В.В. Вопросы и задачи по теории вероятностей. Учебное издание для студентов общеэкономических специальностей. М.: Финансовая академия при правительстве РФ, 2006.
б) дополнительная:
8. Мелехина Т.Л. Коллоквиум по теории вероятностей. М.: Электронный фонд кафедры, 2010.
9. Пыркина О.Е. Тесты самоконтроля по теории вероятностей. М.: Электронный фонд кафедры, 2010.
3. Браилов А.В., Зададаев С.А., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 1. Учебное издание для студентов бакалавриата по направлению «Экономика». М.: Финансовая академия при правительстве РФ, 2010.
4. Браилов А.В., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 2. Учебное издание для студентов бакалавриата по направлению «Экономика». М.: Финансовая академия при правительстве РФ, 2010.
5. Браилов А.В., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 3. Учебное издание для студентов бакалавриата по направлению «Экономика». М.: Финансовая академия при правительстве РФ, 2010.
6. Браилов А.В., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 4. Учебное издание для студентов бакалавриата по направлению «Экономика». М.: Финансовая академия при правительстве РФ, 2010.
7. Браилов А.В., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 5. Учебное издание для студентов бакалавриата по направлению «Экономика». М.: Финансовая академия при правительстве РФ, 2010.
8. Браилов А.В., Горяинов В. Б., Рябов П.Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 6. Учебное издание для студентов бакалавриата по направлению «Экономика». М.: Финансовая академия при правительстве РФ, 2010.
10. Приложение
Учебно-методическая карта дисциплины
"Теория вероятностей и математическая статистика"
| Наименование раздела | № | Содержание лекций | Содержание семинаров | Самостоятельная работа | Вид контроля |
| Часть I: Теория вероятностей | |||||
| Вероятности событий: 6 ч. лекций, 8 ч. практические занятия 8 ч. самостоятельной работы. | 1 | Классический способ подсчета вероятностей. Геометрические вероятности. Пространство элементарных событий. Случайные события, частота и вероятность. Случайное событие как подмножество в пространстве элементарных событий. Алгебра событий. Аксиомы вероятности и вероятностное пространство. Следствия из аксиом. | Основные понятия комбинаторики: комбинаторное правило умножения, сочетание из n по k, размещения из n по k. Бином Ньютона. [1] § 1.1. | Решение задач из [1] § 1.1. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. |
| 2 | Основные формулы для вычисления вероятностей. Условная вероятность. Теорема умножения вероятностей. Независимость событий. Формула полной вероятности. Формула вероятностей гипотез (формулы Байеса). | Практическое занятие по теме лекции №1. [1] § 1.2 и § 1.3. | Решение задач из [1] § 1.2 и § 1.3. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| 3 | Схема повторных независимых испытаний (схема Бернулли). Формула Бернулли. Наиболее вероятное число успехов. Приближенные формулы Лапласа и Пуассона. | Практическое занятие по теме лекции №2. [1] § 1.4 и § 1.5. | Решение задач из [1] § 1.4 и § 1.5. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| Случайные величины: 10 ч. лекций, 10 ч. практические занятия, 10 ч. самостоятельной работы. | 4 | Случайные величины. Случайная величина как функция на пространстве элементарных событий. Функция распределения случайной величины. Независимость случайных величин. Дискретная случайная величина (ДСВ) и ее закон распределения. Функция от ДСВ и арифметические операции над ДСВ. | Практическое занятие по теме лекции №3. [1] § 1.6. | Указания к самостоятельной работе [4] Домашняя контрольная работа №1. | Контроль наличия и выборочная проверка домашнего задания. Проверка домашней контрольной работы |
| 5 | Числовые характеристики дискретных случайных величин: математическое ожидание, дисперсия, стандартное отклонение, ковариация и коэффициент корреляции. Свойства математического ожидания, дисперсии, ковариации и коэффициента корреляции. | Аудиторная контрольная работа №1. Практическое занятие по теме лекции №4. [1] § 2.1 и § 2.2. | Указания к самостоятельной работе [4] Решение задач из [1] § 2.1 и § 2.2. | Самотестирование [9] Контроль наличия и выборочная проверка домашнего задания. | |
| 6 | Типичные дискретные распределения (биномиальное, пуассоновское, геометрическое), их производящие функции и числовые характеристики. | Практическое занятие по теме лекции №5. [1] § 2.3, § 2.4 и § 2.5. | Решение задач из [1] § 2.3, § 2.4 и § 2.5. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| 7 | Непрерывные и абсолютно непрерывные случайные величины. Свойства функции плотности. Математическое ожидание и дисперсия абсолютно непрерывной случайной величины. Математическое ожидание функции от абсолютно непрерывной случайной величины. | Практическое занятие по теме лекции № 6. [1] § 2.7. | Решение задач из [1] § 2.7. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| 8 | Равномерное распределение на отрезке, показательное (экспоненциальное) распределение, нормальный закон распределения, числовые характеристики непрерывных случайных величин. | Аудиторная контрольная работа №2. | Указания к самостоятельной работе [4] Домашняя контрольная работа №2 | Самотестирование [9] Проверка домашней контрольной работы | |
| Предельные теоремы теории вероятностей 4 ч. лекций, 2 ч. практические занятия, 2 ч. самостоятельной работы. | 9 | Неравенство Чебышева. Закон больших чисел. Теорема Чебышева. Теорема Бернулли. | Практическое занятие по теме лекции №7. Общие характеристики НСВ [1] § 2.8. | Решение задач из [1] § 2.8. Указания к самостоятельной работе [5] | Контроль наличия и выборочная проверка домашнего задания. |
| 10 | Характеристическая функция и производящая функция моментов. Центральная предельная теорема Ляпунова. Центральная предельная теорема для одинаково распределенных слагаемых. Роль нормального закона в приложениях теории вероятностей. | Практическое занятие по теме лекции №7, 8, 10 Специальные распределения НСВ [1] § 2.9. | Решение задач из [1] § 2.8 - § 2.9. Указания к самостоятельной работе [5] | Контроль наличия и выборочная проверка домашнего задания. | |
| Случайные векторы: 6 ч. лекций, 6 ч. практические занятия, 6 ч. самостоятельной работы. | 11 | Векторные случайные величины. Функции распределения и плотности случайного вектора и его компонент. Числовые характеристики случайного вектора. Ковариационная и корреляционная матрицы. | Практическое занятие по теме лекции №11. [1] § 3.1. | Решение задач из [1] § 3.1. Указания к самостоятельной работе [5] | Контроль наличия и выборочная проверка домашнего задания. |
| 12 | Функция от случайных величин (общий случай). Математическое ожидание функции от случайных величин. Функции распределения и плотности суммы независимых случайных величин. | Практическое занятие по теме лекции №12. [1] § 3.2 | Решение задач из [1] § 3.2. Указания к самостоятельной работе [5] | Контроль наличия и выборочная проверка домашнего задания. | |
| 13 | Понятие условного математического ожидания и дисперсии, их свойства. | Практическое занятие по теме лекций №13 [1] § 3.3 | Указания к самостоятельной работе [5] Домашняя контрольная работа №3. | Контроль наличия и выборочная проверка домашнего задания. Проверка домашней контрольной работы | |
| Часть II: Математическая статистика | |||||
| Эмпирические характеристики и выборки 2 ч. лекций, 2 ч. практических занятий, 3.5 ч. самостоятельной работы. | 14 | Генеральная совокупность и выборка. Эмпирическая функция распределения и вариационный ряд. Гистограмма. Выборочное среднее и выборочная дисперсия. Выборочные моменты, асимметрия, эксцесс. | Аудиторная контрольная работа №3. Практическое занятие по теме лекции №14 [2] § 1.1 - §1.4 | Указания к самостоятельной работе [5] Решение задач из [2] § 1.1 - § 1.4 Указания к самостоятельной работе [6] | Самотестирование [9] Контроль наличия и выборочная проверка домашнего задания. |
| Точечные и интервальные оценки 4 ч. лекций, 4 ч. практических занятий, 10.5 ч. самостоятельной работы. | 15 | Статистические оценки параметров распределения. Несмещенность, состоятельность, эффективность. Точечные оценки для математического ожидания и дисперсии. Метод максимального правдоподобия. Метод моментов. | Практическое занятие по теме лекции № 15. Точечные оценки. [2] § 1.5 - §1.7 | Решение задач из [2] § 1.5 - §1.7 Указания к самостоятельной работе [6] | Контроль наличия и выборочная проверка домашнего задания. |
| 16 | Интервальные оценки. Приближенный доверительный интервал для оценки генеральной доли и генерального среднего. | Практическое занятие по теме лекции №16. Интервальные оценки. Решение задач из [2] § 1.1 - § 1.4 | Решение задач из [2] § 1.5 - §1.7 Указания к самостоятельной работе [6] | Контроль наличия и выборочная проверка домашнего задания. | |
| 17 | Обзорная лекция | Аудиторная контрольная работа №4. | Указания к самостоятельной работе [6] Домашняя контрольная работа №4. | Самотестирование [9] Проверка домашней контрольной работы | |
