«Конструирование радиоэлектронной аппаратуры»

Вид материала

Автореферат

Содержание Содержание работы В первой главе Вторая глава Третья глава В четвертой главе Оператор создания начальной популяции Оператор селекции Оператор кроссинговера Оператор мутации Оператор отбора Пятая глава M  количество областей по длине RC-ЭРП, К L  наличие материала соответствующего слоя, Null В шестой главе В седьмой главе

Подобный материал:

• Конструирование радиоэлектронной геофизической аппаратуры, 395.03kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 376.83kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 346.73kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 299.74kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 446.09kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 385.32kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 402.82kb.
• Синтез аналоговых активных фильтров на двумерных rc-элементах с распределенными параметрами, 255.97kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 487.83kb.
• Конструирование радиоэлектронной геофизической аппаратуры, 301.73kb.

СОДЕРЖАНИЕ РАБОТЫ


Введение содержит обоснование актуальности проблемы, описываются объект и предметы исследования, формулируются цель и задачи диссертационной работы, определены методы исследования, дается краткое содержание диссертации по главам, приведены основные положения диссертационной работы, выносимые на защиту.

В первой главе дается краткая характеристика объекта исследования и его основных параметров и особенностей, проводится системный анализ существующих конструктивных вариантов RC-ЭРП и устройств на их основе, а также объектов и процессов распределенной и фрактальной природы и определяется необходимость разработки нового класса RC-ЭРП, который обеспечит повышение эффективности функционирования устройств обработки информации, точности моделирования объектов и процессов распределенной и фрактальной природы.

RC-ЭРП представляет собой конструктивно законченный элемент (подобно элементам с сосредоточенными параметрами), но характеризующийся не номиналом, а функциями электрической цепи (подобно RC-цепям на элементах с сосредоточенными параметрами), обеспечивая при меньших габаритах лучшие частотно избирательные свойства и наличие участка постоянства фазы (90 < _с < 0) ФЧХ входного импеданса, отражающего наличие у него дробностепенной зависимости частоты.

Предложены принципы и разработана классификации RC-ЭРП. В качестве классификационных предложены признаки, характерные для обычных элементов цепей (количество внешних выводов, зависимость характеристик и параметров от токов и напряжений), и признаки, характеризующие RC-ЭРП с конструктивно-технологической точки зрения (количество слоев материалов, характер неоднородности среды, возможность и способ изменения характеристик и параметров элемента).

Проведен анализ возможностей применения RC-ЭРП в устройствах обработки сигналов (в том числе фрактальных устройствах), в качестве моделей элементов интегральных микросхем, процессов и объектов распределенной и фрактальной природы, в устройствах управления динамическими системами дробного порядка.

Анализ показал, что использование RC-ЭРП в устройствах и электрических моделях позволяет: улучшить качественные и количественные характеристики существующих устройств генерирования и обработки сигналов, создавать устройства обработки сигналов в пространстве дробной меры, повысить точность моделирования процессов распространения сигналов в межсоединениях СБИС и точность оценки параметров биполярных и МОП-структур нанометровых размеров, создавать модели электронных компонентов, сложных физико-химических и биологических объектов для идентификации их структуры, параметров, и прогнозирования надежности, повысить точность и быстродействие систем автоматического управления процессами и объектами, которые характеризуются динамикой дробного порядка, уменьшить стоимость систем.

На основе проведенного анализа предложена классификация областей применения RC-ЭРП и их математических моделей в науке и технике.

Однако существующие в настоящее время конструкции RC-ЭРП и их математические модели не позволяют реализовать те потенциальные возможности, которые предоставляются резистивно-емкостными структурами с распределенными параметрами для улучшения показателей систем обработки информации, идентификации параметров и управления процессами и объектами фрактальной и распределенной природы.

Поэтому предложена новая универсальная конструктивная основа для реализации RC-ЭРП и их моделей в виде двумерного n-слойного RLCG-ЭРП с распределенными L-, R-, C- и G-параметрами, которая позволит существенно расширить количество конструктивных вариантов RC-ЭРП и их математических моделей для решения отмеченных выше задач.

Для практической реализации предложенного подхода, учитывая технологические возможности изготовления многослойных RLCG-ЭРП, выявленные структуры объектов моделирования и диапазон рабочих частот, решено ограничиться конструктивной основой в виде RC-ЭРП со структурой слоев R1-G1-C1-R-C2-G2-R2 (обобщенный RCG-ЭРП), вид которой изображен на рис. 1.

Обоснован выбор технологических вариантов реализации RC-ЭРП на основе обобщенного RCG-ЭРП, в виде многослойных толсто- и тонкопленочных структур, который при существующих материалах и технологиях изготовления позволяет создавать RC-ЭРП с удельными постоянными времени от 2·10^11 сек/мм (для планарных RC-ЭРП) до 1 сек/см², способных работать в диапазоне частот от долей герц до единиц гигагерц.





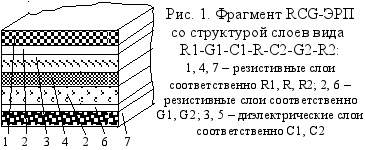
Показана возможность создания параметрических RC-ЭРП за счет использования материалов, электрофизические свойства которых зависят от величин воздействующих на них полей различной природы. Приведена классификация физических эффектов в материалах слоев, которые можно использовать для расширения функциональных возможностей RC-ЭРП.

Проведена оценка состояния вопросов анализа и синтеза RC-ЭРП, которая показывает, что разработанные к настоящему времени методы и программное обеспечение позволяют выполнять анализ одномерных однородных и неоднородных по ширине RC-ЭРП со структурами слоев вида R-C-0, R-C-NR, C-R-NC, R-C-G-0, синтез неоднородных по ширине RC-ЭРП со структурой слоев вида R-C-0, а также анализ и синтез двумерных однородных RC-ЭРП со структурой слоев вида R-C-0.

Получена математическая модель обобщенного RCG-ЭРП в виде системы трех дифференциальных уравнений в частных производных, описывающих распределение потенциалов в резистивных слоях R1, R, R2 (см. рис. 1) и отражающая многообразие конструктивно-технологических вариантов RC-ЭРП, которые можно формировать на основе модели обобщенного RCG -ЭРП.

Проведенный анализ состояния проблемы показывает, что в силу отмеченных ранее причин лишь небольшое число из громадного многообразия конструктивно-технологических вариантов RC–ЭРП нашло применение для улучшения электрических и эксплуатационных характеристик функциональных устройств. Из этого вытекают цели и задачи настоящей работы.

Вторая глава посвящена разработке метода анализа RC-ЭРП с использованием обобщенных RCG-ЭРП, позволяющего получать решение системы дифференциальных уравнений в частных производных, описывающих процессы в многослойной неоднородной резистивно-емкостной среде.

С этой целью предложен метод, являющийся дальнейшим теоретическим развитием методов конечных элементов (МКЭ) и конечных распределенных элементов (МКРЭ), который сочетает в себе разбиение области определения потенциалов в резистивных слоях обобщенного RCG-ЭРП на конечные элементы (КЭ) с аналоговым моделированием распределения потенциалов в выделенных областях и в пределах всего анализируемого RC-ЭРП. Схематичное изображение алгоритма метода показано на рис. 2.

Обобщенный RCG-ЭРП как и в МКЭ, разбивается на множество КЭ (рис. 2, а), в данном случае, объемных с одинаковой формой сечения (треугольной, прямоугольной, трапециевидной и т.п.) (рис. 2, б). Но, в отличие от МКЭ, в котором распределение потенциалов в резистивных слоях в пределах каждого КЭ аппроксимируют полиномиальной финитной функцией, в предлагаемом методе распределение потенциалов задается электрической моделью распределенной физической структуры, выделяемой в процессе разбиения RC-ЭРП (подобно тому, как это делается в МКРЭ) (рис. 2, в). Основным условием, которому должна удовлетворять модель, является наличие аналитического решения для потенциалов в пределах каждого КЭ.



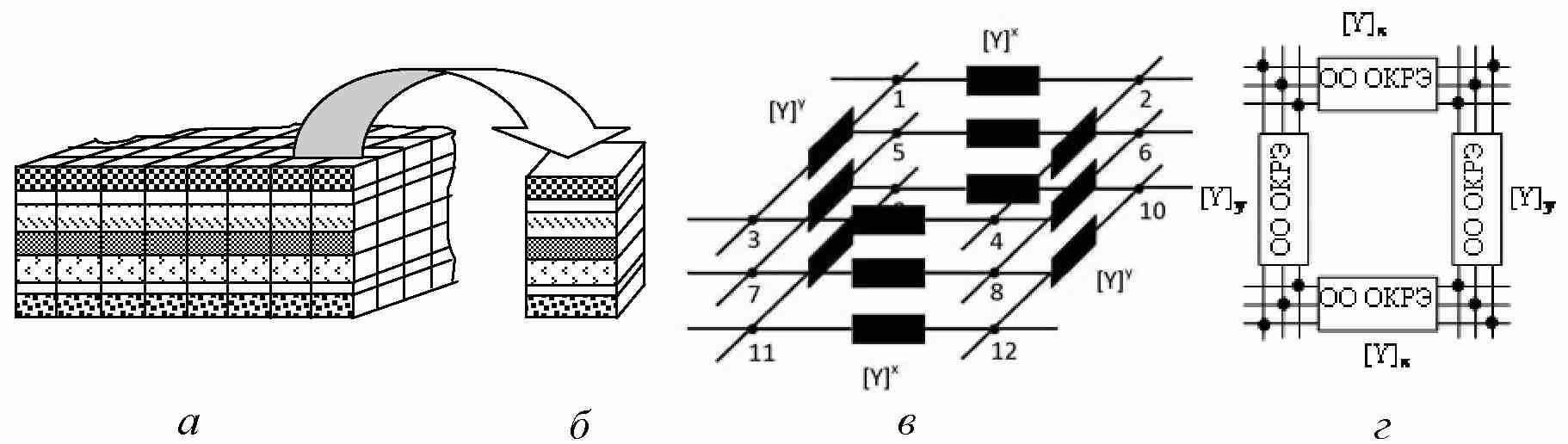
Рис. 2. Иллюстрация алгоритма предлагаемого метода анализа: а – разбиение обобщенного RCG-ЭРП на КЭ; б – отдельный КЭ, в – схема замещения КЭ; г – упрощенное изображение модели КЭ

В отличие от принятой классификации КЭ, модель, изображенная на рис. 2, б, была названа обобщенным конечным распределенным элементом (ОКРЭ). Поэтому предлагаемый метод решения определен как метод обобщенных конечных распределенных элементов (МОКРЭ).

Разработан алгоритм МОКРЭ, в котором матрицы формы имеют смысл матриц проводимости ОКРЭ, а глобальная матрица формируется как матрица проводимости некоторой цепи по заданной структуре цепи и известным матрицам проводимостей отдельных элементов этой цепи (в данном случае, ОКРЭ). Очевидно, что для анализа характеристик RC-ЭРП, формируемого на основе обобщенного RCG-ЭРП, нет необходимости находить узловые потенциалы во всей области их определения. Достаточно получить решение относительно внешних узлов, связанных с выводами RC-ЭРП, т.е. получить матрицу проводимости RC-ЭРП как многополюсного элемента.

Учитывая, что для большинства RC-ЭРП, полученных на основе обобщенного RCG-ЭРП, нет аналитических решений, необходимое количество КЭ, обеспечивающих заданную точность решения, целесообразно определять путем оценки скорости сходимости решения при увеличении количества КЭ.

Для уменьшения погрешностей, возникающих за счет граничных КЭ, на которых задаются граничные условия первого рода, вводится приграничная область с комбинированием КЭ прямоугольной и треугольной форм уменьшенных размеров, а также используются модели граничных ОКРЭ, учитывающие иную структуру их слоев по сравнению со структурой слоев остальных ОКРЭ.

Для получения аналитических выражений у-параметров ОКРЭ сделан переход от электродинамической модели системы с распределенными параметрами к равноценной ей модели в виде бесконечнозвенной лестничной цепи, переменными состояния в которой являются токи и напряжения. Достоинством такого подхода является то, что эквивалентная схема может содержать как линейные, так и нелинейные R-, L- и C-компоненты, источники токов и напряжений. Поэтому рассмотренный подход можно распространить на случаи параметрических и нелинейных ОКРЭ.

На основании полученного в работе общего решения системы дифференциальных уравнений, описывающих состояние эквивалентной электрической цепи, найдены аналитические выражения у-параметров ОКРЭ.

Для проверки корректности полученных аналитических выражений использовано сравнение частотных характеристик у-параметров ОКРЭ и его электрического эквивалента, созданного в программе схемотехнического моделирования на RC-ЭСП (Spice-модель).

Предварительно была проведена оценка необходимого количества звеньев Spice-модели, которое обеспечивает требуемую точность моделирования элемента с распределенными параметрами его схемой замещения на RC-ЭСП (на примерах RC-ЭРП со структурами слоев вида R-C-0 и R-C-NR). Получено выражение, связывающее количество звеньев, необходимых для обеспечения погрешности у-параметров модели не более 1%, и максимальную нормированную частоту рабочего диапазона.

Проведенные оценки показали, что для достоверной оценки корректности параметров модели ОКРЭ необходимо использовать Spice-модель с числом звеньев от 256 до 512 при допустимой погрешности моделирования RC-ЭРП не более 1% вплоть до нормированной частоты RC = 500.

Сходимость частотных характеристик у-параметров разработанной Spice-модели к частотным характеристикам у-параметров, вычисленным на основе аналитических выражений для ОКРЭ с ростом числа звеньев Spice-модели, доказывает, что полученные аналитические выражения точно описывают поведение идеализированного ОКРЭ.

Одним из принципиальных положений МОКРЭ является возможность на основе ОКРЭ формировать конечные распределенные элементы (КРЭ), совокупность которых вместе с граничными условиями определяет характеристики анализируемого RC-ЭРП. Разработанная классификация КРЭ, которые можно сформировать на основе ОКРЭ, включает 18 не повторяющихся вариантов структур слоев.

Большинство из этих КРЭ рассматриваются впервые, и для них в доступной литературе нет соответствующих математических моделей. Поэтому в работе предложен способ преобразования математической модели ОКРЭ в математические модели любого из указанных КРЭ. Было замечено, что структура слоев может быть задана присвоением удельным поперечным проводимостям материалов слоев G1, G2, и удельным сопротивлениям материалов слоев R1, R2, входящим в выражения у-параметров ОКРЭ, значений 0,  или определенных значений, не равных нулю или бесконечности. Тогда любому КРЭ можно сопоставить четырехпозиционный троичный код х₁х₂х₃х₄, где x_i = {0, 1, +}. Здесь цифра 0 соответствует нулевому значению параметра, 1 – бесконечно большому значению, а знак "+" – значению, отличному от 0 и 1.

В этом случае конструкцию RC-ЭРП, которая формируется из обобщенного RCG-ЭРП путем модификации его ОКРЭ, можно представить в виде множества кодовых комбинаций, отражающих структуру каждого КРЭ, моделирующего один из конечных элементов. При сборке глобальной матрицы проводимости RC-ЭРП модель ОКРЭ модифицируется в соответствии с кодовой комбинацией, присвоенной данному КЭ. Иллюстрация способа приведена на рис. 3.




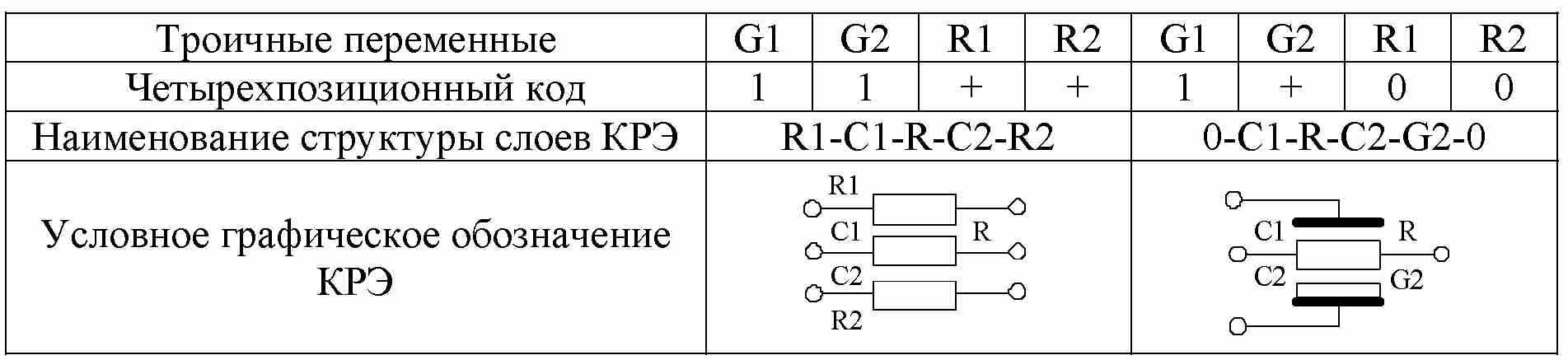
Рис. 3. Иллюстрация метода преобразования ОКРЭ в варианты КРЭ


Справедливость такого подхода доказана сравнением частотных характеристик известных RC-ЭРП, полученных расчетами с использованием преобразованной модели ОКРЭ и с использованием аналитических выражений у-параметров для этих RC-ЭРП, найденных другими авторами.

Получены аналитические выражения у-параметров для одномерных неоднородных ОКРЭ при условии, что r(x)c₁(x) = const, для ограниченного числа законов изменения ширины. Такие ОКРЭ можно использовать для уменьшения числа КЭ при сложной геометрии RC-ЭРП. Проведена проверка справедливости полученных выражений для экспоненциального и гиперболического законов изменения ширины с помощью схемотехнического моделирования, используя Spice-модели.

Третья глава посвящена разработке математического, алгоритмического и программного обеспечения для анализа и исследования реализационных возможностей различных конструкций RC-ЭРП, получаемых на основе обобщенных RCG-ЭРП.

На основе обобщенного RCG-ЭРП предложен новый класс одномерных неоднородных RC-ЭРП, который представляет собой единую конструкцию, на отдельных участках которой структуры слоев могут быть неодинаковыми (одномерный структурно-неоднородный (ОСН) RC-ЭРП).

Для исследования возможностей нового класса RC-ЭРП исходная среда моделирования, имеющая структуру слоев вида NR-C-R-MC-KR, где коэффициенты N, M, и K – множители, задающие удельные параметры слоев по отношению к удельным параметрам слоев R и С, была условно разбита на четыре КЭ, как показано на рис. 4, а. Каждый из КЭ замещается одномерным однородным (ОО) ОКРЭ (рис. 4, б). На этой основе можно провести анализ характеристик как известных конструкции ОСН RC-ЭРП, так и новых, которые будут сформированы с целью исследования реализационных возможностей нового класса RC-ЭРП.

Разработана программа анализа, в которой описание конструктивных, структурных и параметрических неоднородностей задается двумя векторами: вектором электрофизических параметров слоев 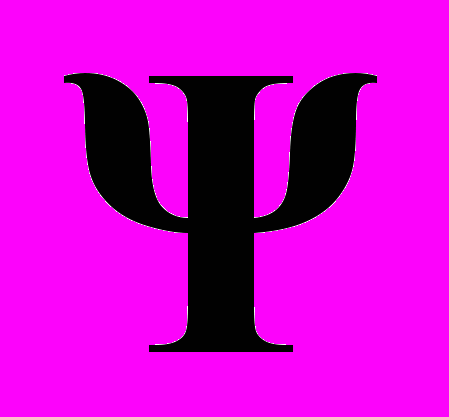и вектором конструктивных и структурных параметров RC-ЭРП D. Вектор в данном случае определяется как = {С_уд1, r_‰, N, M, K}, где N = {N_i}, M = {M_i}и K = {K_i}, 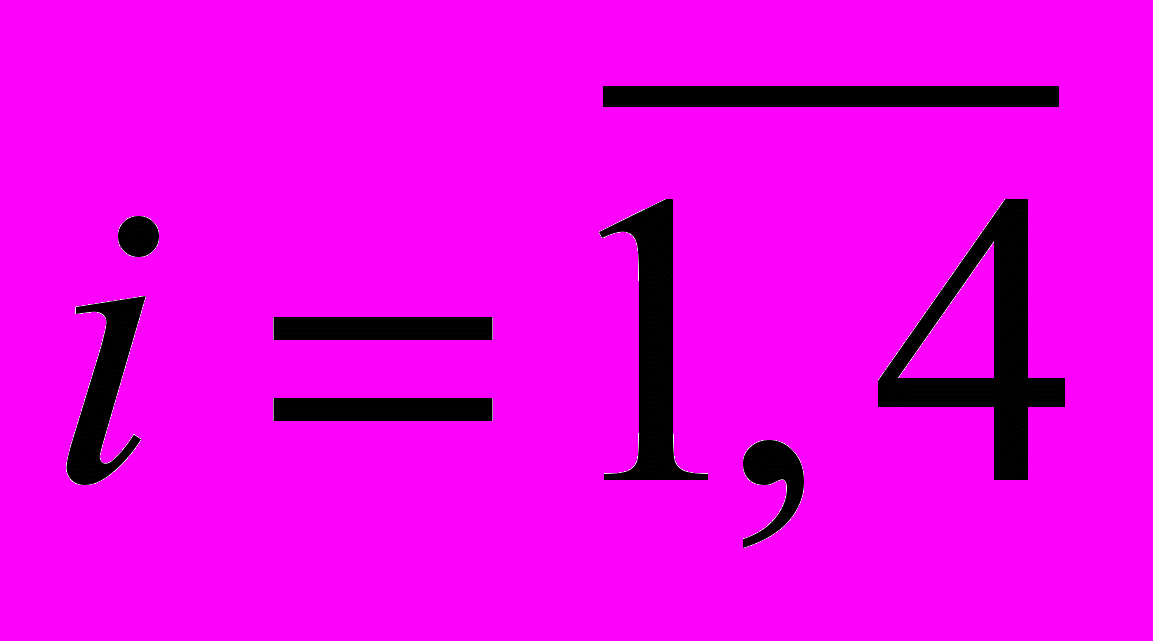. Вектор D определим как D = {L, S}, где L = {L_i}, 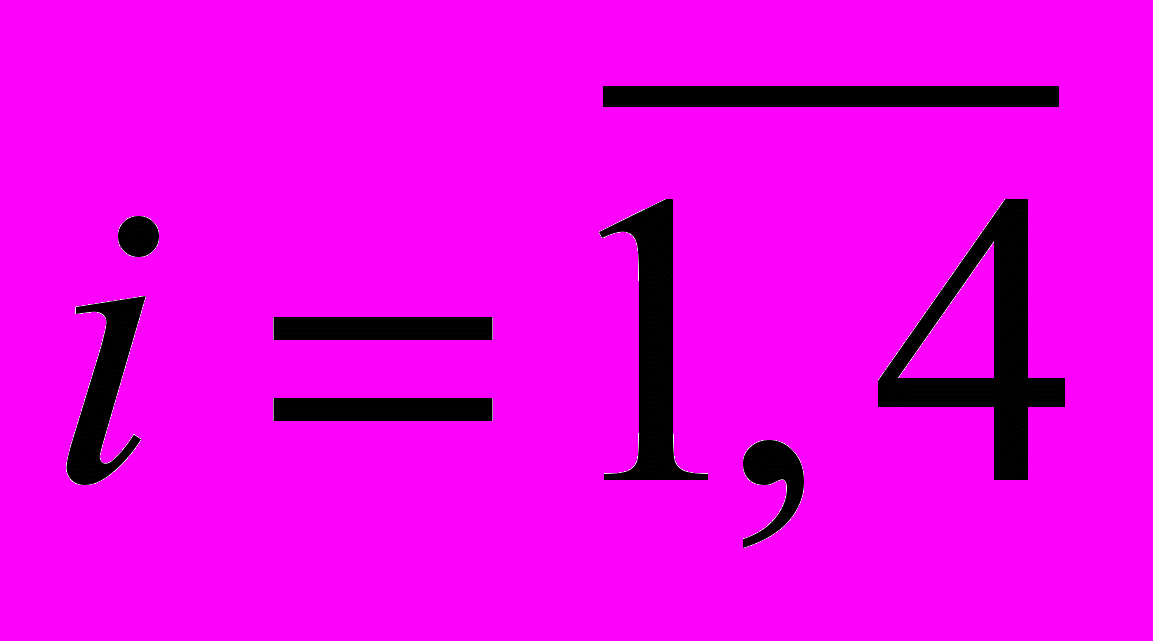 вектор длин КЭ, S = {S_ij}, 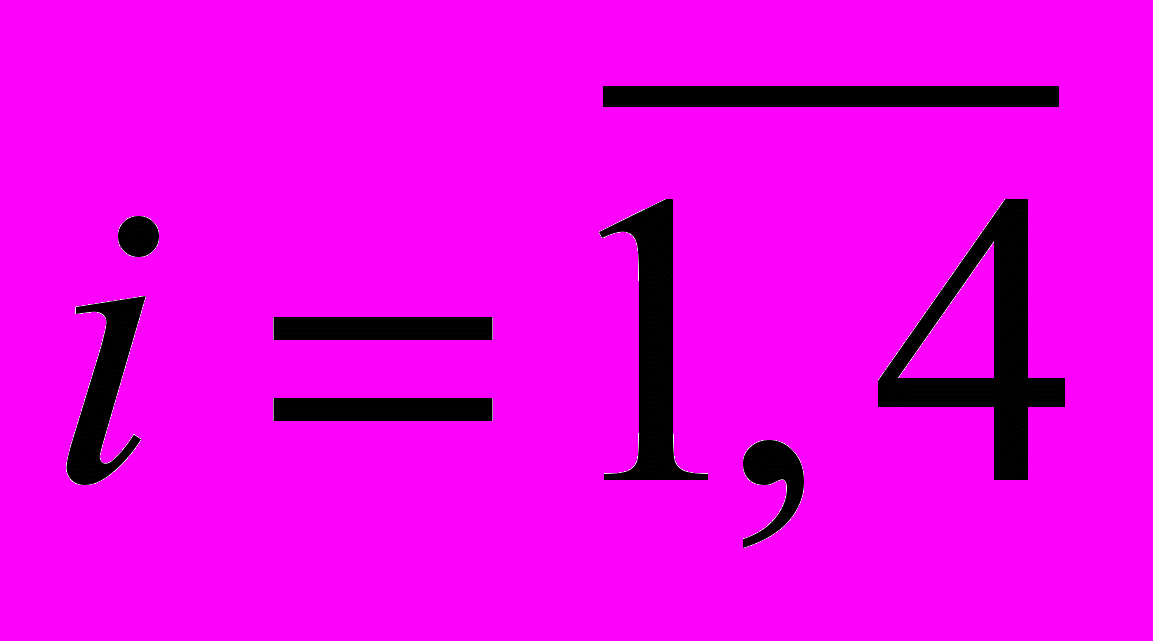, 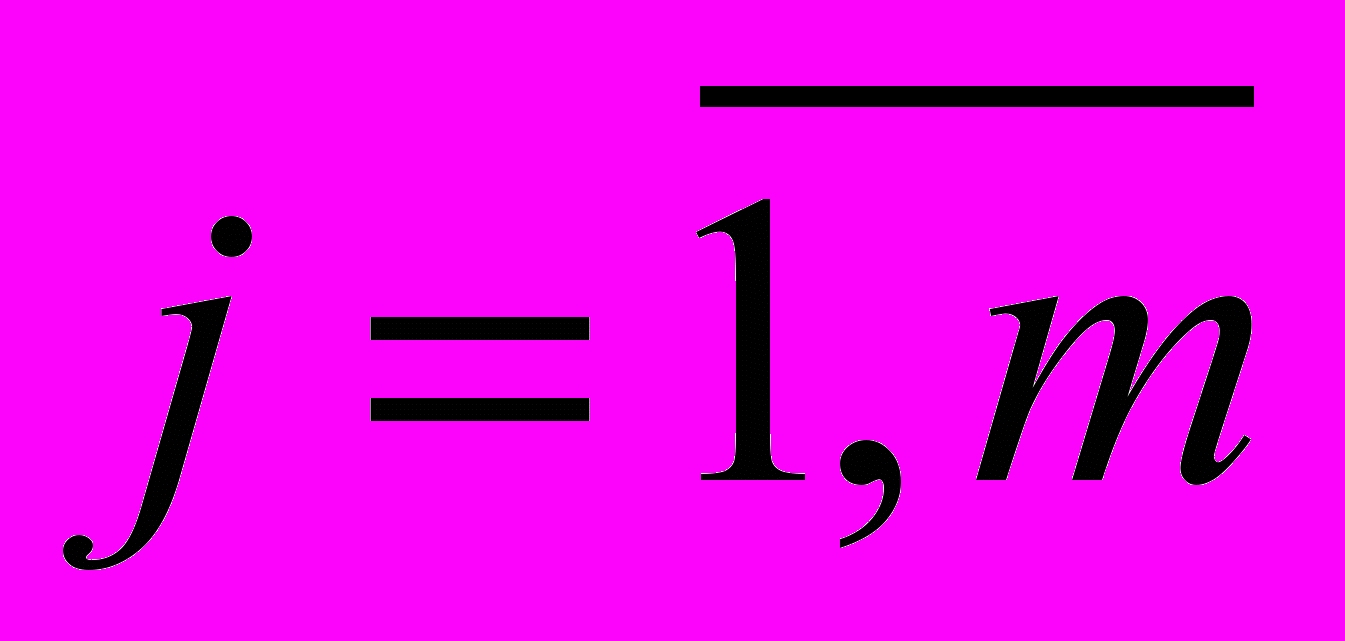 вектор, определяющий все физически реализуемые сочетания вариантов структур в ОСН RC-ЭРП, которые можно сформировать на основе обобщенного RCG-ЭРП, m – число вариантов.

К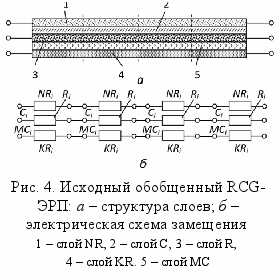роме отмеченных параметров существует еще один путь изменения характеристик ОСН RC-ЭРП – изменение схемы включения отдельных КРЭ между собой, соблюдая при этом условия физической реализуемости вариантов соединения.

Как следует из рис. 4, б, каждый ОКРЭ представляет собой многополюсник, аналитические выражения у-параметров которого найдены в гл. 2. Алгоритм сборки глобальной матрицы основан на методе многополюсных подсхем, а исключение внутренних узлов схемы осуществляется методом блочных матриц. Изменение структуры ОКРЭ в соответствии с имеющейся конструкцией или в соответствии с заданием осуществляется с помощью коэффициентов N_i и K_i, которые определяют номиналы сопротивлений слоев соответственно R1 и R2 (для простоты параметрам G1 и G2 присвоены значения «1»).

Корректность работы программы подтверждена совпадением передаточных характеристик известных RC-ЭРП со структурами слоев R-C-NR и 0-C-R-NC-0, вычисленных по точным аналитическим выражениям, и передаточных характеристик ОСН RC-ЭРП, вычисленных в разработанной программе при соответствующем выборе составляющих векторов , и D и S. Достоверность результатов анализа, полученных с помощью программы для тех вариантов ОСН RC-ЭРП, для которых нет аналитических выражений, проверена с помощью Spice-моделей в программе схемотехнического моделирования.

С помощью разработанной программы анализа ОСН RC-ЭРП найдены новые конструкции RC-ЭРП и варианты схем их включения, позволяющие при меньшей занимаемой площади получать такие АЧХ коэффициента передачи (в частности, с двумя частотами режекции, с затуханием за полосой пропускания 88,5 дБ при расстройке на две декады), которые при реализации их с помощью RC-ЭСП потребуют на порядок большего количества элементов. Это подтверждает перспективность применения конструктивной основы в виде обобщенного RCG-ЭРП для создания новых функциональных элементов с улучшенными характеристиками.

Разработана математическая основа, алгоритмы и программы для анализа нового класса одномерных неоднородных RC-ЭРП, в котором одновременно сочетается структура слоев вида R-C-G-0 с неоднородностью по ширине и с неоднородностью погонных параметров слоев. В известной нам литературе такое сочетание неоднородностей в RC-ЭРП не рассматривалось ни с одной из структур слоев.

Разработан алгоритм вычисления у-параметров ОО КРЭ, алгоритм сборки и вычисления частотных характеристик ОН R-C-G-0 ЭРП при различных схемах включения. В программе предусмотрен анализ и одномерных комплементарных R-C-G-0 ЭРП, которые состоят из двух ОН RC-ЭРП, законы изменения ширины которых связаны соотношением b₀ = b₁(x) + b₂(x). Здесь b₀  постоянная величина, обычно соответствующая ширине исходного ОО RC-ЭРП, b₁(x) и b₂(x)  законы изменения ширины двух частей, составляющих ОК RC-ЭРП, х – координата по длине RC-ЭРП.

Разработан интерфейс программы, позволяющий задавать законы неоднородностей, параметры RC-ЭРП, выбирать схему его включения, вид анализируемой частотной характеристики, диапазон рабочих частот, количество отсчетов в этом диапазоне и количество ОО КРЭ, на которые разбивается RC-ЭРП.

Проведена оценка погрешности вычисления частотных характеристик ОН
R-C-G-0 ЭРП в зависимости от числа КРЭ для экспоненциального закона изменения ширины RC-ЭРП. В качестве сравнения использовалась АЧХ, вычисленная по известному аналитическому выражению коэффициента передачи экспоненциальной RC-линии. Сравнение характеристик показало, что при числе конечных элементов равном 50 максимальная погрешность на частоте RC = 100 не превышает 0,04%, а на RC = 500 не превышает 0,1%. Поэтому увеличение числа конечных элементов целесообразно лишь с увеличением максимальной частоты для обеспечения необходимой точности вычислений.

Если в качестве метода анализа ОН RC-ЭРП взять МКЭ или соответствующий ему по сути метод схем замещения многозвенными цепями на RC-ЭСП, то количество элементов, необходимое для получения той же точности будет на порядок больше.

В развитие концепции обобщенного RCG-ЭРП и МОКРЭ впервые разработаны математическая основа, алгоритм и программы анализа двумерных однородных и неоднородных RC-ЭРП, со структурами слоев вида R-C-G-0 и R-C-NR.

Интерфейс программы анализа двумерных R-C-NR ЭРП позволяет в удобной графической форме задавать пять типов двумерных КРЭ, которые могут составлять конструкцию двумерного RC-ЭРП, топологию контактных площадок, выбирать схему включения, визуализировать результаты расчетов.

Исследована зависимость точности анализа с помощью МОКРЭ от числа конечных распределенных элементов путем сравнения частоты режекции АЧХ коэффициента передачи однородного двумерного R-C-NR ЭРП с известной частотой режекции одномерного однородного R-C-NR ЭРП. Показано, что при сетке КРЭ 612 погрешность вычисления частоты режекции составляет не более 1 %. Также показано, что применение МОКРЭ уменьшает необходимое количество конечных элементов и сокращает время вычисления при одинаковой точности более чем на два порядка по сравнению с МКЭ.

Достоверность результатов анализа двумерного R-C-NR ЭРП со структурными неоднородностями подтверждена анализом с помощью Spice-модели в стандартных программах схемотехнического моделирования.

Получены зависимости частотных характеристик коэффициента передачи двумерного R-C-NR ЭРП от конструктивных параметров RC-ЭРП, которые, в частности, показывают возможность применения разработанной программы анализа для пополнения базы данных RC-ЭРП новыми базовыми конструкциями, определения стратегии подгонки характеристик RC-ЭРП после изготовления.

Для подтверждения адекватности математических моделей и корректности работы программ анализа были изготовлены экспериментальные образцы толстопленочные RC-ЭРП (фотография тестовой подложки с RC-ЭРП изображена на рис. 5). Сравнение частотных характеристик изготовленных образцов R-C-NR ЭРП с расчетными говорит об адекватности используемых моделей RC-ЭРП и результатов анализа с помощью метода обобщенных конечных распределенных элементов. Однако на отдельных участках частотного диапазона наблюдаемые отклонения характеристик на 10%  20% превышают погрешности измерений. Это связано с тем, что разработанные математические модели RC-ЭРП учитывают далеко не все возможные неидеальности проводящих, диэлектрических и резистивных материалов, а также краевые эффекты, локальные неоднородности геометрии и свойств материалов слоев.

В четвертой главе предложена общая концепция синтеза, дана постановка задачи синтеза RC-ЭРП, разработаны теоретические положения, алгоритмы и программы синтеза одномерных неоднородных RC-ЭРП с использованием генетических алгоритмов.

Классические методы синтеза входных и передаточных функций цепей, содержащих RC-ЭСП, используемые в теории цепей, не нашли применения для синтеза RC-ЭРП. Это связано в первую очередь с отсутствием завершенных исследований о потенциальных возможностях той или иной базовой конструкции RC-ЭРП, а также методов декомпозиции синтезируемой функции на такие, которые можно было бы реализовать с помощью этих базовых конструкций.

Поэтому предлагается концепция синтеза RC-ЭРП, которая предусматривает два последовательных этапа. Сначала производится поиск подходящей базовой конструкции, на основе которой можно реализовать заданные требования ТЗ. Сведения о базовых конструкциях и их реализационных возможностях аккумулируются в специализированной базе данных, в том числе с помощью разработанных программ анализа RC-ЭРП. Если необходимая конструкция в базе данных отсутствует, то реализуется второй этап – структурный синтез RC-ЭРП на основе обобщенного конструктивного базиса, которым, с определенными ограничениями, является обобщенный RCG-ЭРП.

Проведенные ориентировочные оценки количества различных конструктивных вариантов RC-ЭРП, которые можно получить на основе обобщенного RCG-ЭРП, используя различные типы неоднородностей конструктивного, технологического и схемотехнического характера, а также варианты их сочетаний в одном RC-ЭРП, показывают, что число таких вариантов составляет десятки тысяч. Поэтому для синтеза RC-ЭРП на базе обобщенного RCG-ЭРП необходима реализация некоторой оптимизационной задачи, позволяющей резко уменьшить число одновременно варьируемых переменных, не ограничивая потенциальные возможности RC-ЭРП.

Проведенный анализ методов, используемых для решения задач оптимизации сложных технических объектов по различным критериям, показал, что одним из наиболее эффективных является, так называемое эволюционное проектирование, бурно развивающееся в последнее время и основанное на псевдослучайном поиске решения, на основе генетических алгоритмов.

Прежде чем построить поисковый алгоритм, нужно определиться с моделью задачи, которая включает в себя пространство потенциальных решений O, пространство представлений S, функции кодирования f и декодирования f^1, функцию цели F. Тогда задачу поиска наилучшего объекта o* из множества O можно сформулировать следующим образом

o* = argmax F(f^1(s)), где s  S. (1)

Ее решение осуществляется манипулированием параметрами объектов в пространстве представлений S.

Однако, универсальных генетических алгоритмов, эффективно решающих любые оптимизационные задачи не существует. Поэтому в работе предложена и реализована методика разработки генетических алгоритмов синтеза RC-ЭРП, включающая следующие основные этапы:

1. Разработка способа кодирования информации о конструктивных параметрах RC-ЭРП (переход из О в S).
   
2. Выбор типов генетических операций и математическое описание характера манипуляций, выполняемых с параметрами при реализации этих операций.
   
3. Разработка общей структуры генетического алгоритма.
   
4. Разработка программы, реализующей последовательность манипуляций с параметрами в области S в соответствии с выбранной структурой алгоритма.
   
5. Определение оптимальных параметров генетического алгоритма, обеспечивающих заданную скорость и вероятность получения решений.
   
6. Разработка способов декодирования (переход от s* к о*).
   
7. Уточнение полученного решения с учетом способа реализации и возможностей технологического оборудования.
   

Следуя этой методике, был разработан алгоритм и программа синтеза одномерных неоднородных (ОН) R-C-G-0 ЭРП.

На основе сравнительного анализа конструктивных особенностей возможных вариантов R-C-G-0 ЭРП обоснован способ кодирования топологии ОН R-C-G-0 ЭРП в виде вектор-функции неоднородности F(x), задаваемой при шести значениях аргумента x, соответствующего шести координатам по длине элемента (х = 0, 0.2, 0.4, 0.6, 0.8, 1). Значения вектора F(x) = {F(x₁) … F(x₆)} представляют собой значения либо ширины, либо погонного сопротивления (емкости) RC-ЭРП в указанных точках.

Обоснованы структура и способы реализации операторов генетического алгоритма.

Оператор создания начальной популяции осуществляет генерацию случайного множества решений, достаточно большого, но не исчерпывающего все возможные варианты.

Оператор селекции осуществляет предпочтительный выбор пар по лучшим значениям функции фитнесса (полезности), которая характеризует близость полученного решения к заданному.

Оператор кроссинговера реализован по одноточечной схеме, поскольку применение многоточечного оператора нецелесообразно ввиду малой размерности вектора, задающего неоднородность RC-ЭРП.

Оператор мутации действует так, что после каждой итерации генетического алгоритма компоненты вектора F(x), соответствующего наихудшему значению функции фитнесса, полностью изменяются случайным образом в пределах конструктивных ограничений, задаваемых в программе.

Оператор отбора реализован по селекционной схеме, в которой на основе упорядоченного по убыванию функций фитнесса набора реализаций происходит формирование следующей популяции, куда включают только первые r⁰ особей из общего количества полученных реализаций. Достоинством такой схемы является фиксированный объем памяти, требуемой для хранения реализаций R-C-G-0 ЭРП, и фиксированное время вычислений на каждой итерации генетического алгоритма, поскольку численность популяции ограничена.

Разработана программа синтеза ОН R-C-G-0 ЭРП, позволяющая проводить синтез законов изменения ширины и законов изменения удельного сопротивления по длине RC-ЭРП. В качестве критериев синтеза выбраны постоянство фазы ФЧХ входного сопротивления и крутизна АЧХ передаточной функции при различных вариантах включения RC-ЭРП в заданном частотном диапазоне. В программе использована гибридная схема генетического алгоритма, заключающийся в том, что после каждой итерации осуществляется движение в сторону антиградиента функции фитнесса. Такая схема поисковой оптимизации позволила увеличить скорость сходимости в среднем в 4 раза.

Исследовано влияние вероятностей выполнения операций кроссинговера и мутации на скорость сходимости алгоритма. В результате исследований были найдены оптимальные по скорости сходимости вероятности кроссинговера с = 0,6 и мутации  = 0,2 при синтезе по заданной крутизне АЧХ, и с = 0,2,  = 0,8 при синтезе по заданному значению постоянства фазы входного импеданса. Результаты тестового синтеза по обоим критериям, проведенного при найденных оптимальных вероятностях, показали, что скорость сходимости увеличилась в среднем в 2,5 раза.

Проведена статистическая оценка величины уровней постоянства фазы ФЧХ входного импеданса при различных диапазонах рабочих частот, которые могут быть реализованы на базе R-C-G-0 ЭРП. С вероятностью 0,25 можно реализовать постоянство фазы в диапазоне от 23 до 63 в пределах одной декады, от 31 до 55 в пределах двух декад и от 47 до 51 в пределах трех декад.

Разработаны теоретические положения синтеза на основе генетических алгоритмов и программа синтеза ОСН RC-ЭРП. Конструкция ОСН RC-ЭРП полно и однозначно представляется множеством

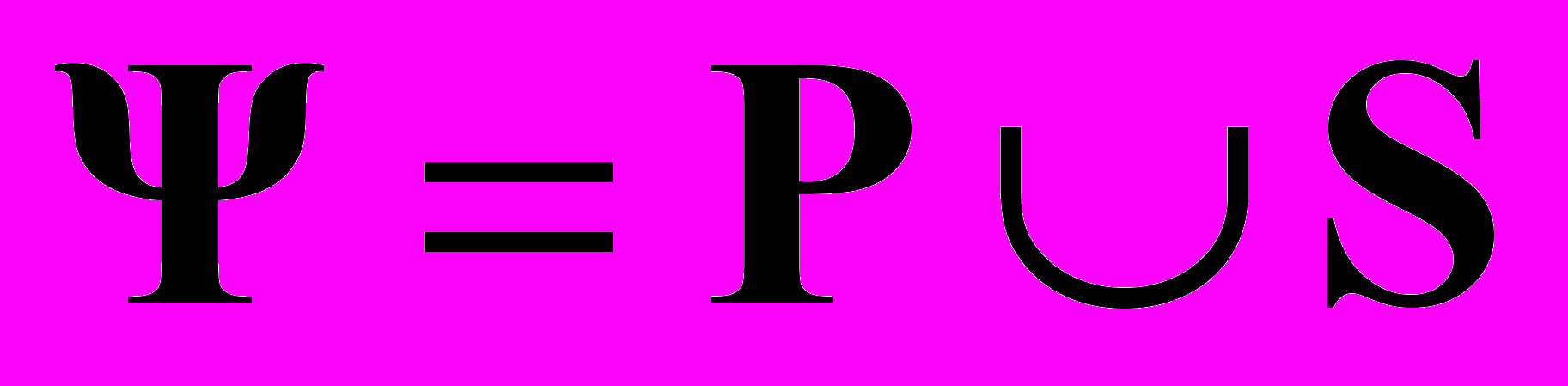, (2)

где Р  конструктивно-параметрическая составляющая, задаваемая выражением

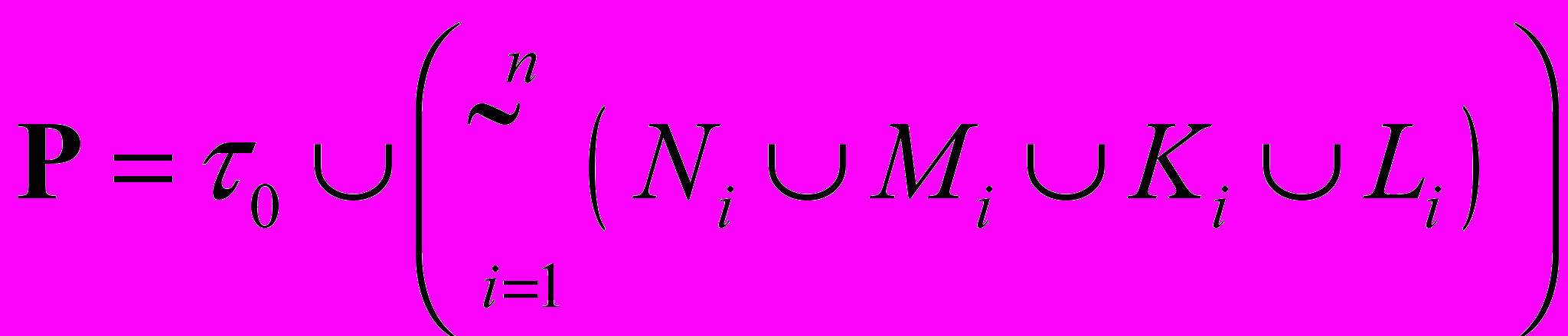, (3)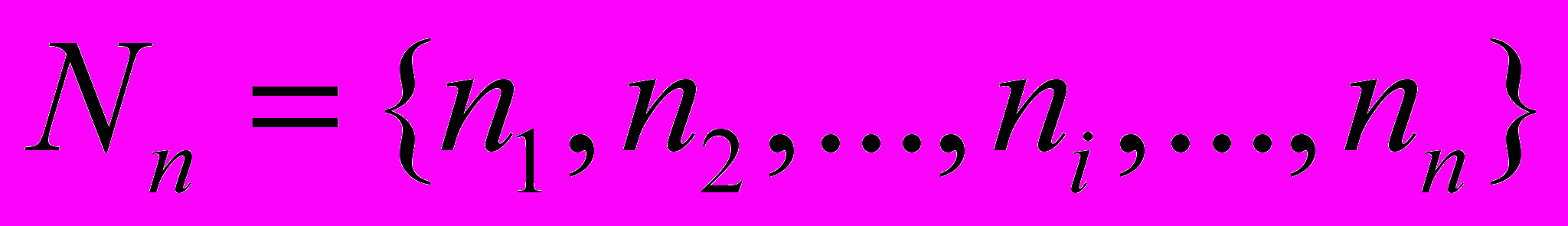

, ,

, ,

, ,

,

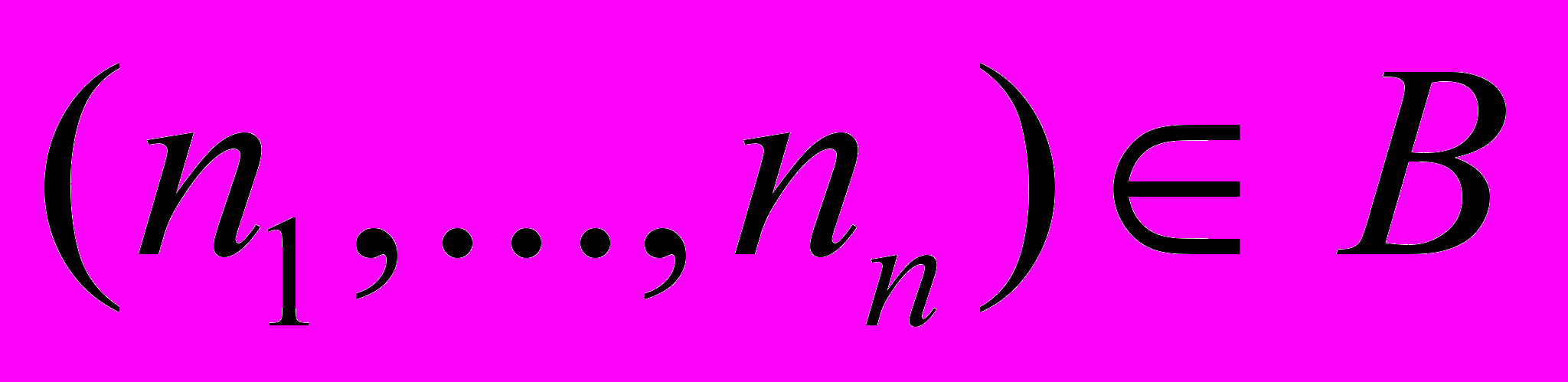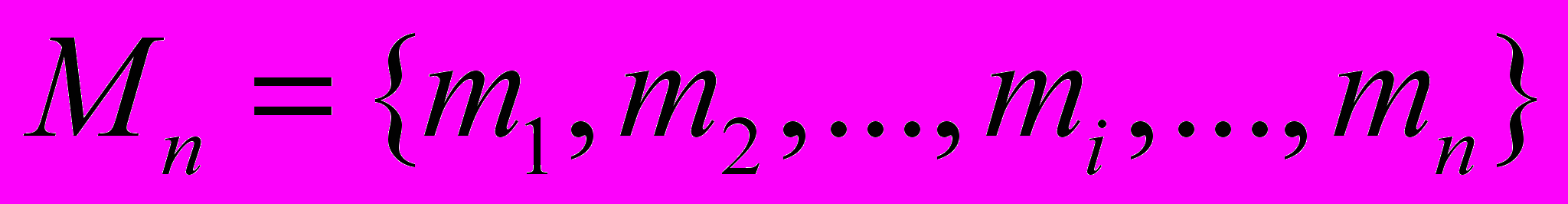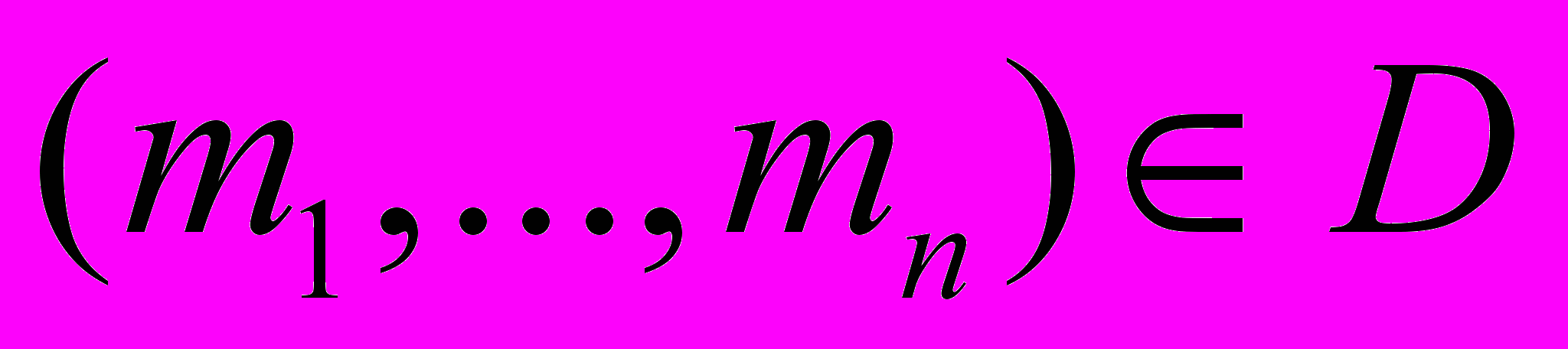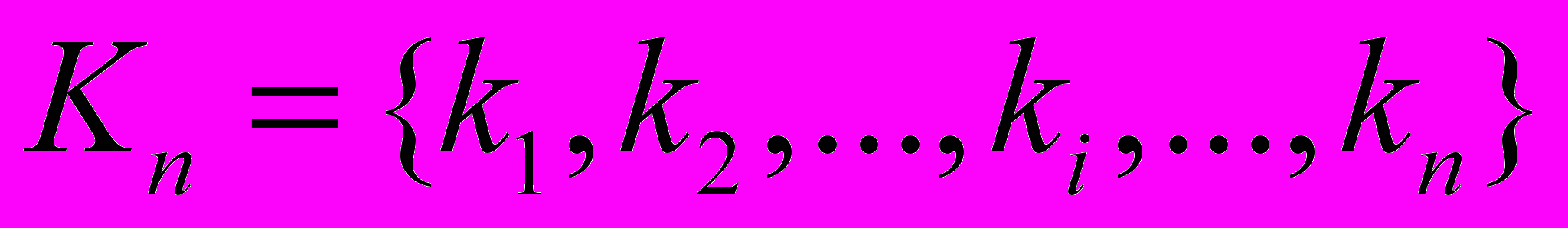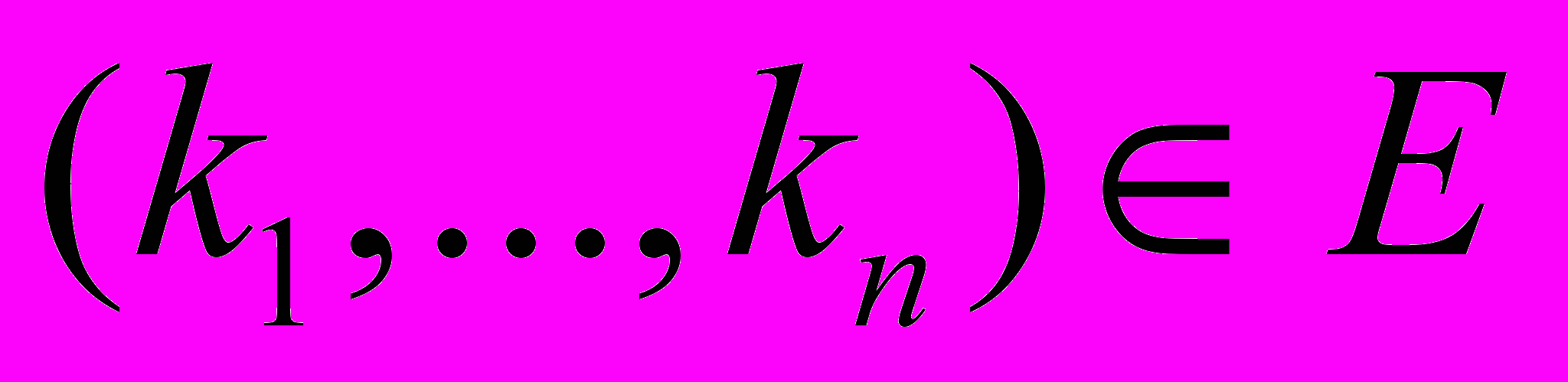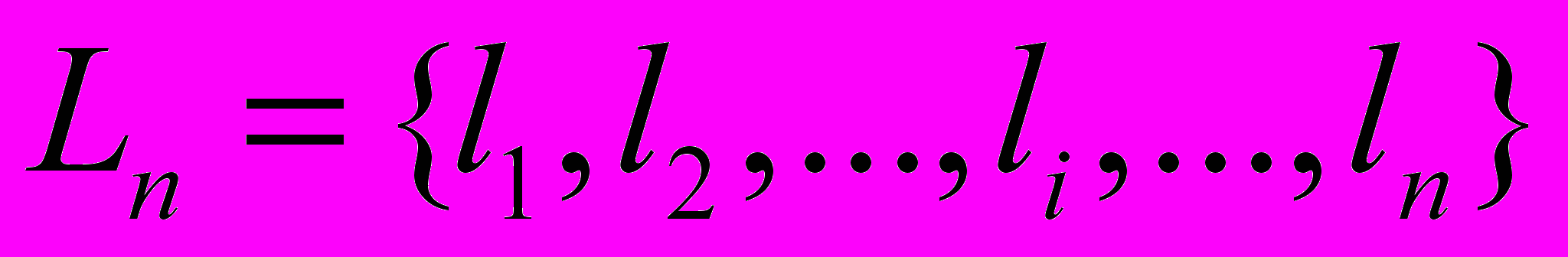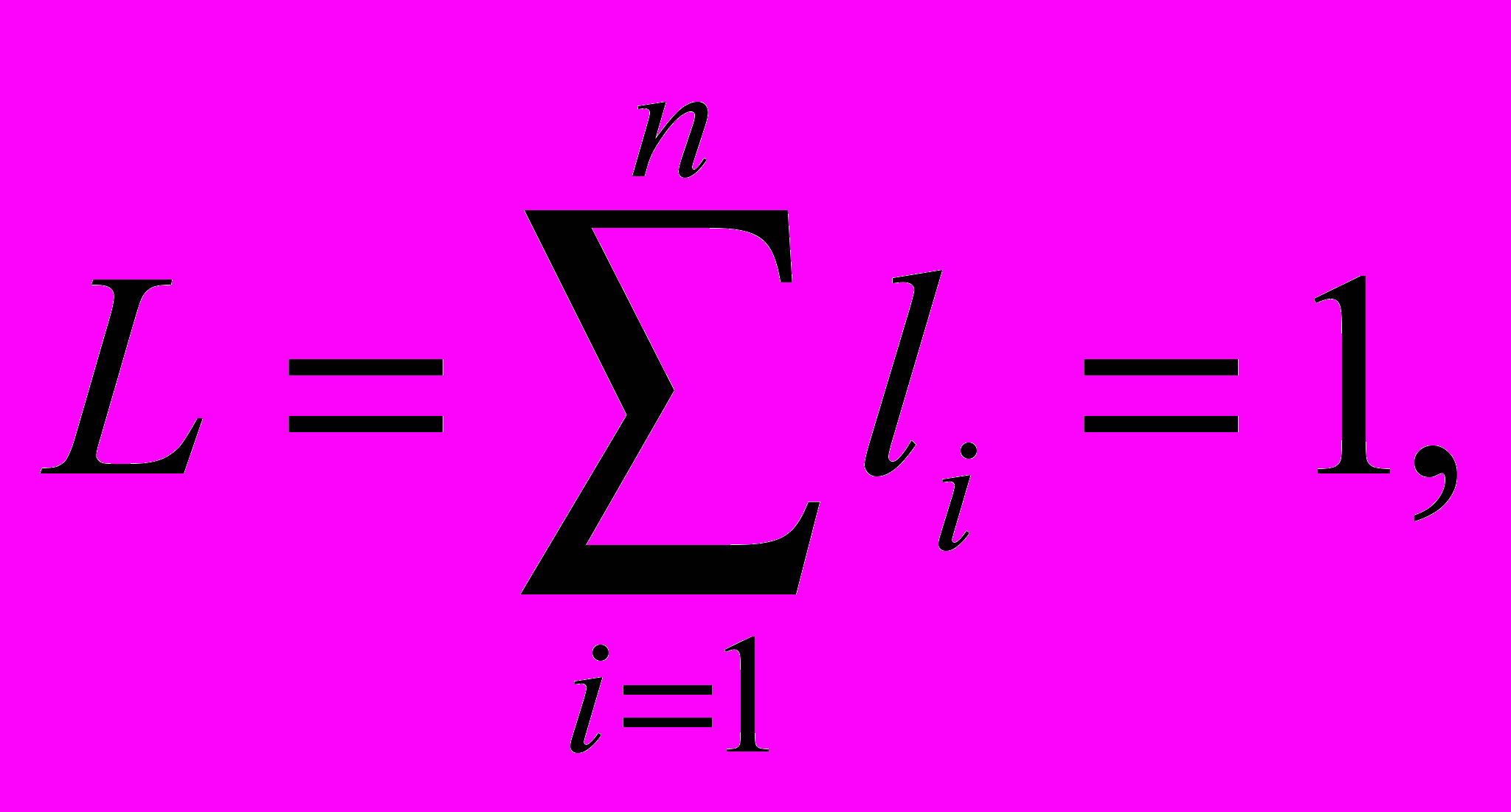
B, D, E, J  области допустимых значений соответствующих параметров.

S  схемотехническая составляющая, определяемая как

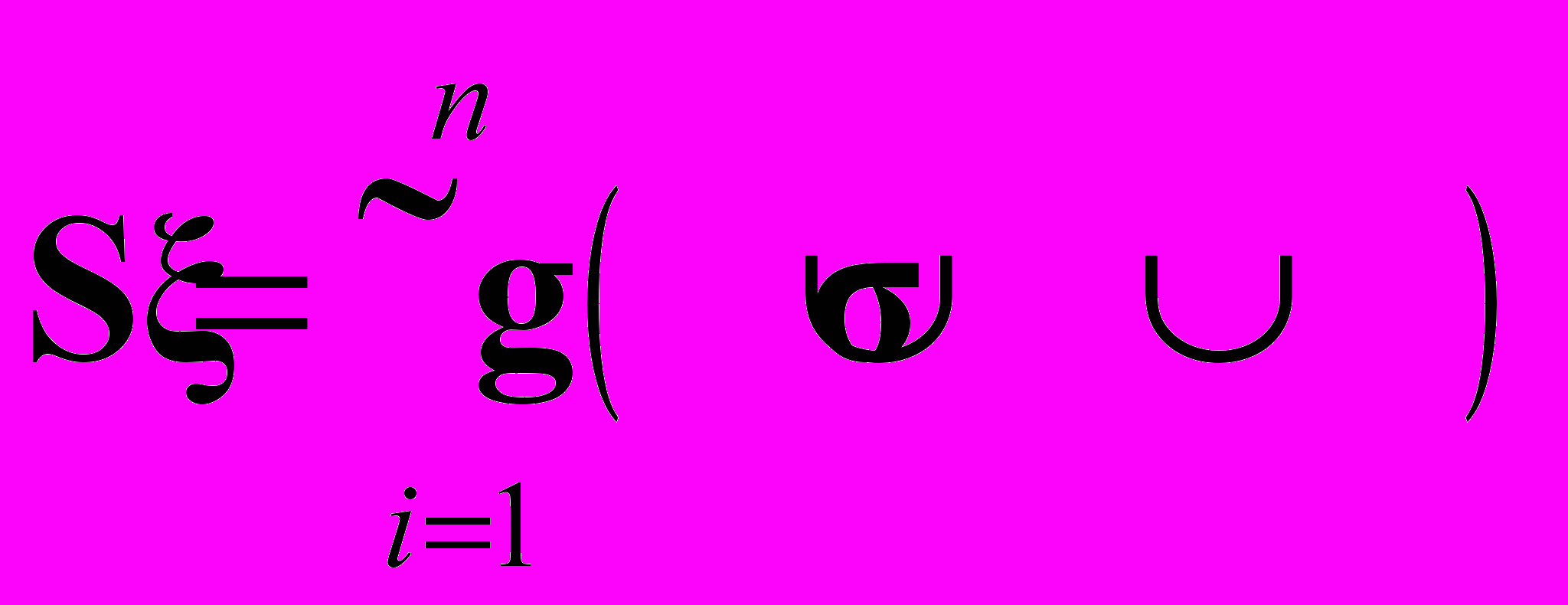. (4)

Здесь, кроме определенных раньше параметров N_i, M_i, К_i, L_i, введены переменная τ₀ – удельная постоянная времени RC-ЭРП, ξ – множество схем соединений смежных отрезков, g – множество заземленных узлов в схемах соединений смежных отрезков, σ – множество схем включений RC-ЭРП во внешнюю цепь; n – количество отрезков, на которые условно разделяется основа синтеза ОСН RC-ЭРП.

Разработан способ кодирования схем внутренних соединений, основанный на табличном задании физически реализуемых вариантов соединений. При этом каждой схеме соединения сопоставляется матрица инциденций. В дальнейшем формируется общая матрица инциденций, определяющая алгоритм сборки глобальной матрицы проводимостей.

Разработан способ кодирования схемы внешних соединений, основанный на формировании квадратной матрицы соответствия шестого порядка, в которой положение ненулевых элементов задает тип вывода (вход, выход и т.д.) и номер вывода, которому этот тип присвоен. Алгоритм предусматривает выполнение некоторых правил, обеспечивающих физическую реализуемость RC-ЭРП.

Разработаны алгоритмы выполнения генетических операторов, учитывающие способ кодирования параметров и их физический смысл. В виду того, что кодируемые параметры имеют различную физическую природу, реализован двухступенчатый генетический алгоритм: отдельно для конструктивно-параметрической составляющей (3) и отдельно для схемотехнической составляющей (4).

Разработаны общая структура алгоритма синтеза ОСН RC-ЭРП, программа вычисления целевой функции и интерфейс пользователя. Проведено исследование и оптимизация параметров алгоритма: количества итераций и величины порога значения функции фитнесса, при достижении которого программа переходит от одной ступени генетического алгоритма к другой.

Проверка корректности работы программы синтеза осуществлена в программе схемотехнического моделирования с помощью Spice-моделей. ФЧХ входного импеданса, синтезированного ОСН RC-ЭРП и полученного с помощью модели, содержащей 2048 звеньев на RC-ЭСП, совпадают во всем диапазоне рабочих частот с погрешностью не превышающей 0,5%.

Проведена статистическая оценка величины уровней постоянства фазы ФЧХ входного импеданса при различных диапазонах рабочих частот, которые могут быть реализованы на базе ОСН RC-ЭРП. С вероятностью 0,25 можно реализовать постоянство фазы в диапазоне от 5 до 75 в пределах одной декады, от 5 до 67 в пределах двух декад, от 11 до 63 в пределах трех декад, от 31 до 51 в пределах четырех декад и от 39 до 47 в пределах пяти декад.

Таким образом, использование в качестве основы для синтеза обобщенного RCG-ЭРП позволило значительно расширить границы реализуемых уровней постоянства фазы ФЧХ входного импеданса и границы рабочего диапазона частот.

Пятая глава посвящена разработке теоретических положений, генетических алгоритмов и программ синтеза двумерных RC-ЭРП со структурами слоев вида
R-C-G-0 и R-C-NR, как частных случаев обобщенного RCG-ЭРП.

Поскольку в основе МОКРЭ лежит идея разбиения RC-ЭРП на КЭ, следовательно, конструкция RC-ЭРП полностью определяется параметрами этих элементов, являющихся в определенном смысле, самоподобными структурами одинаковой формы, количеством параметров, размерностью и т.п. Поэтому, кодированием информации в виде совокупности множеств однотипных параметров ОКРЭ, обеспечивается возможность выполнения основных генетических операторов мутации и скрещивания без потери физического смысла результатов этих операций.

На этом основан предложенный в данной работе теоретико-множественный подход к преобразованию варьируемых переменных из пространства объектов в пространство состояний. Суть подхода состоит в следующем.

Пусть S_х = {a_1, a_2, … a_i,… a_n} – множество прямоугольных областей разбиения слоя 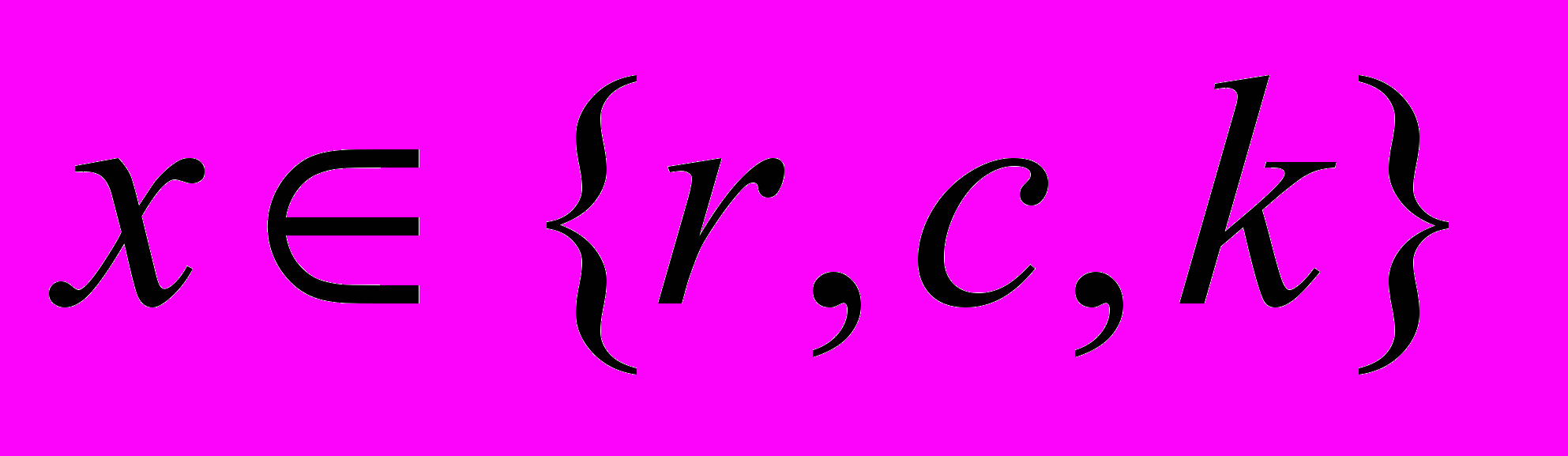, где r  резистивный слой, с  проводящий слой, k – слой контактных площадок,

,

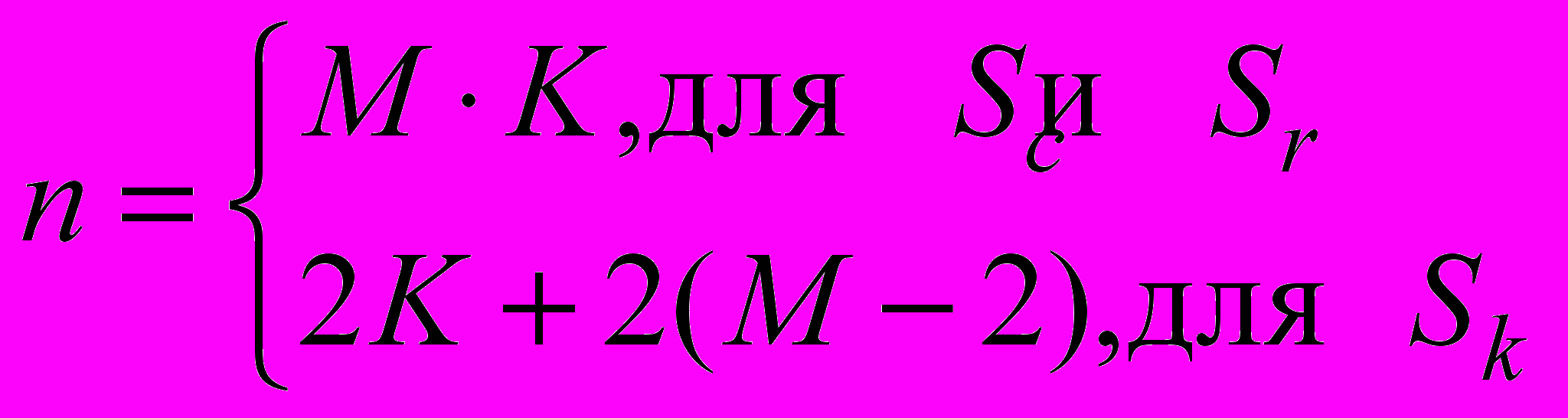M  количество областей по длине RC-ЭРП, К  количество областей по ширине RC-ЭРП.

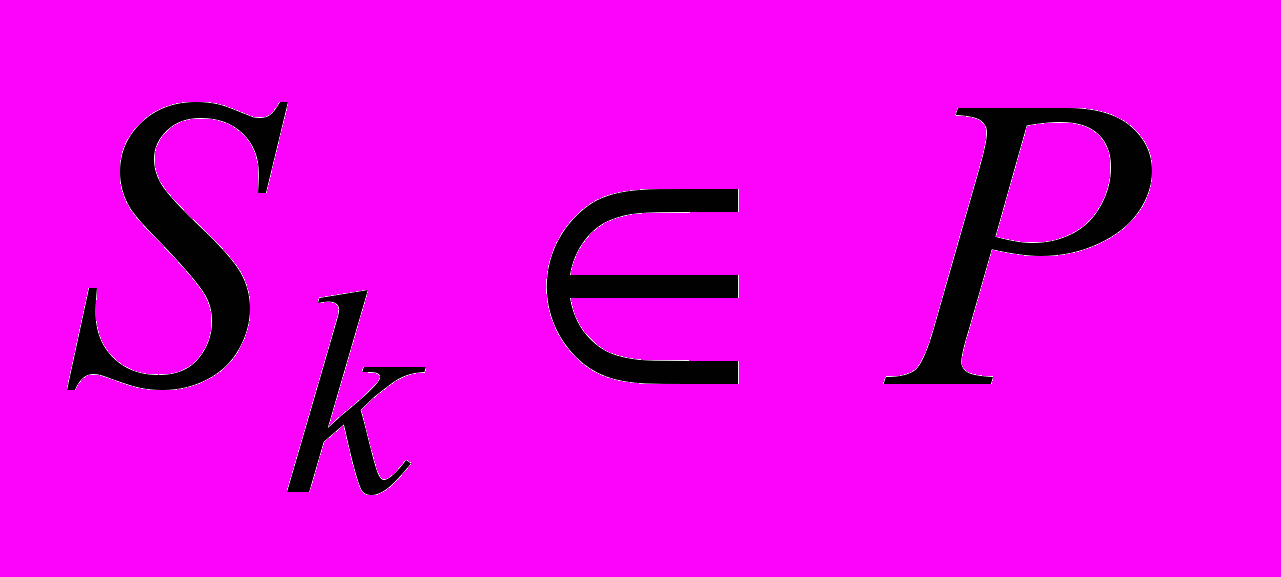, где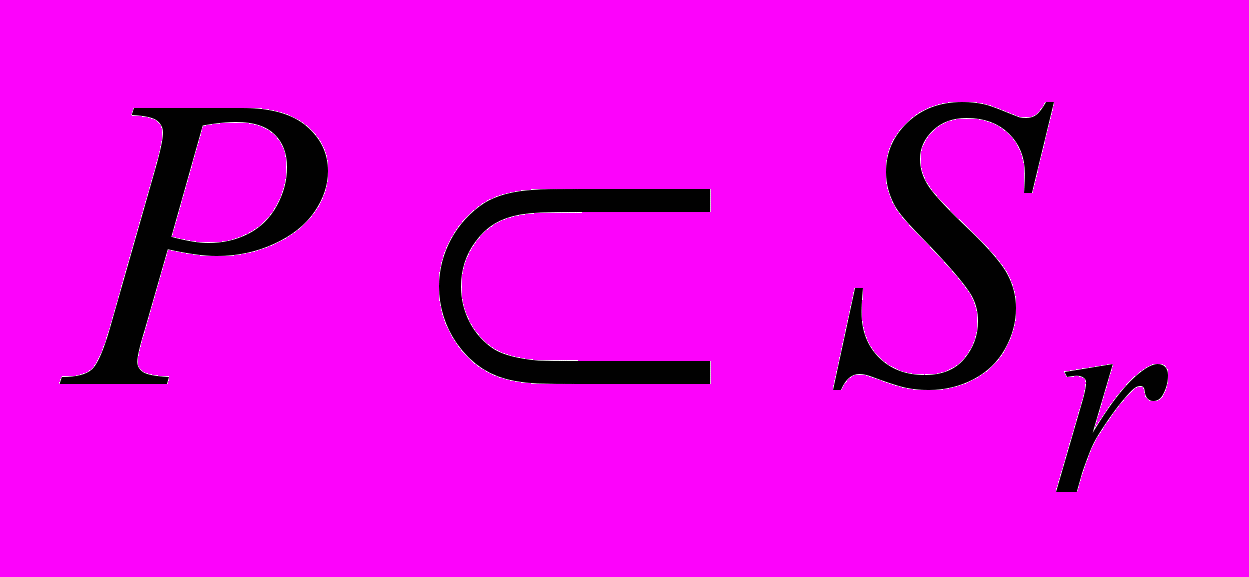 подмножество областей r, расположенных по периметру ДО RC-ЭРП.

Тогда информацию о топологии слоя можно представить в виде множества E_x = {b₁b₂…b_i…b_n}, b₁…b_n  B, где B = {0, 1}.

При этом функция отображения множества S_х на множество E_х запишется в виде:

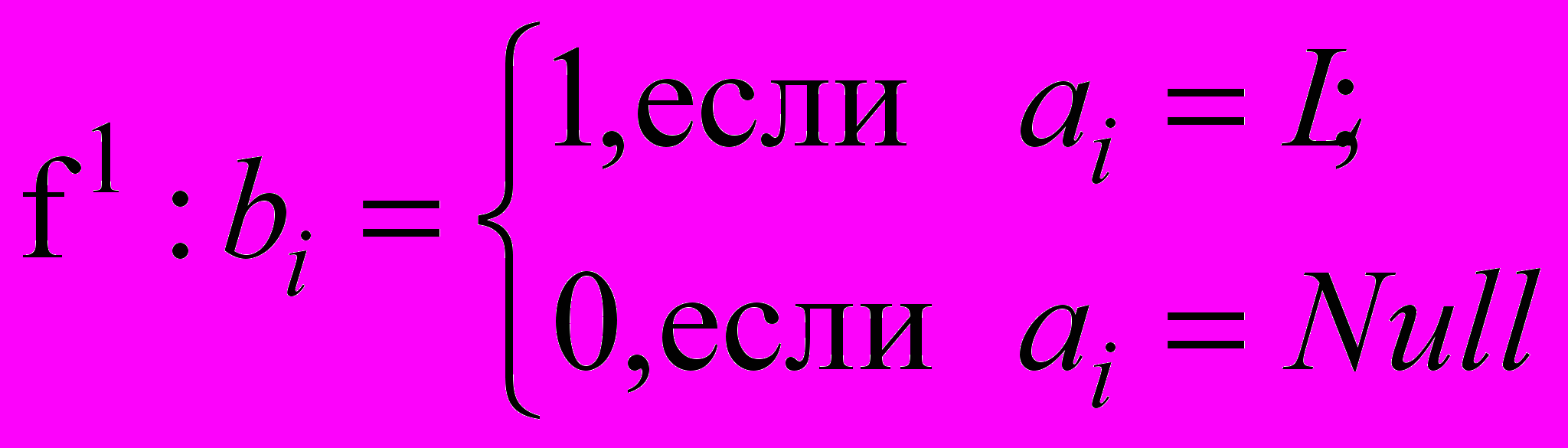, (5)

где L  наличие материала соответствующего слоя, Null  отсутствие материала соответствующего слоя.

Функция обратного отображения в этом случае будет

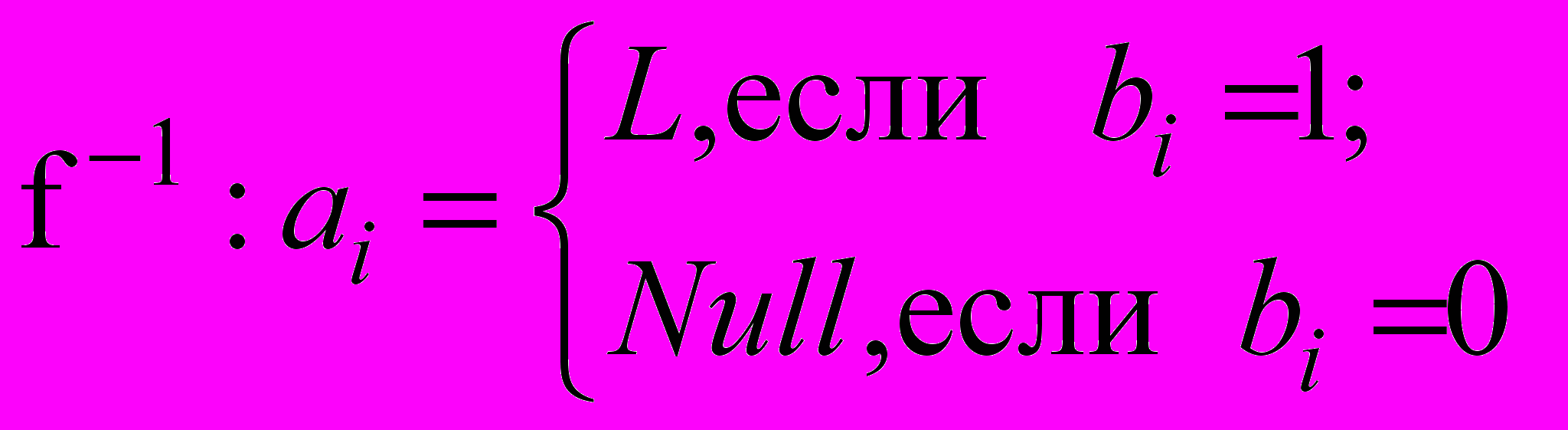. (6)

Таким образом, множество E = {E_kE_rE_c} содержит информацию о параметрах всей конструкции двумерного RC-ЭРП. Параметры слоя G задаются коэффициентом  = RG в матрицах проводимости КРЭ.

При использовании предложенного способа кодирования топологии пространство изменения неоднородностей ограничивается лишь числом конечных элементов RC-ЭРП. Поэтому требуемый объем памяти для хранения информации о конструкции RC-ЭРП зависит от числа конечных элементов и не зависит от сложности синтезируемой топологии.

Предложены алгоритмы выполнения основных генетических операций, учитывающие двумерный характер распределения потенциалов в резистивных слоях: двухточечный оператор для слоя контактных площадок, обмен (при скрещивании) и инвертирование (при мутации) нескольких групп элементов множеств E_r и E_s, образующих прямоугольные области на поверхности синтезируемого объекта.

На основе разработанного генетического алгоритма создана программа синтеза двумерного R-C-G-0 ЭРП, имеющая удобный графический интерфейс, позволяющий задавать критерии синтеза, в интерактивном режиме создавать одну из реализаций топологии R-C-G-0 ЭРП начальной популяции, задавать и корректировать вероятности действия генетических операторов, границы частотного диапазона и т.п.

Разработана методика оптимизации параметров генетического алгоритма, основанная на формировании и исследовании поверхностей скорости сходимости алгоритма от вероятностей выполнения генетических операторов. Применение оптимальных вероятностей позволило увеличить скорость сходимости почти в 4 раза по сравнению с первоначальной.

В результате исследований были найдены оптимальные вероятности выполнения операторов скрещивания и мутации: с = 0,8 и  = 0,6 при синтезе по критерию крутизны АЧХ, и с = 0,6 и  = 0,4 при синтезе по критерию постоянства фазы входного импеданса. Результаты тестового синтеза, проведенного при найденных оптимальных вероятностях показали, что скорость сходимости увеличилась в среднем в 1,9 раза. Использование оптимальных вероятностей изменения ширины контактных площадок w и изменения положения контактных площадок p увеличило скорость сходимости еще в 1,8 раза.

Исследована динамика действия генетического алгоритма, которая выявила следующие особенности:

• скорость сходимости алгоритма снижается по мере уменьшения разницы между текущей и заданной частотной характеристиками;
  
• выбор места действия генетических операторов никак не связан с частотной зависимостью отклонения текущей частотной характеристик от заданной;
  
• вероятности выполнения операторов, заданные как оптимальные, остаются неизменными, несмотря на то, что условия, при которых они действуют, постоянно меняются;
  
• положение и размер контактных площадок меняются только в начале синтеза, несмотря на то, что вероятности изменения их размеров и положения постоянны в течение всего времени синтеза.
  

Поэтому проведены дополнительные исследования и разработаны соответствующе механизмы адаптации ГА к изменяющимся условиям в процессе синтеза.

В частности, проведено исследование влияния места действия (на топологии RC-ЭРП) основных генетических операторов на степень изменения синтезируемых частотных характеристик в различных участках рабочего диапазона частот. На основании результатов этого исследования разработан алгоритм вычисления вероятности выбора места действия генетических операторов в зависимости от диапазона частот, в котором текущее значение критерия синтеза максимально отклоняется от заданного.

Для сокращения времени работы генетического алгоритма при неизменных размерах и положении контактных площадок была введена функциональная зависимость между вероятностью изменения топологии слоя контактных площадок и достигнутым значением целевой функции.

Применение алгоритма динамической подстройки вероятности выбора места действия генетических операторов и указанной функциональной зависимости позволило повысить скорость сходимости вычислений на завершающих стадиях решения почти в 2 раза.

Разработаны генетический алгоритм и программа синтеза двумерного
R-C-N-R ЭРП, которые отражают основные принципы синтеза RC-ЭРП на основе обобщенного RCG-ЭРП. Создан более экономичный и физически оправданный способ кодирования информации, в котором информация о параметрах КЭ не распределяется по слоям, а полностью характеризует структуру КЭ в одной локальной области хромосомы. В связи с этим упрощены алгоритмы выполнения операторов скрещивания и мутации. Переработан графический интерфейс программы, позволяющий вводить информацию о топологии дополнительного резистивного слоя.

Исследованы потенциальные возможности программы по реализации диапазона постоянства фазы ФЧХ входного импеданса в рабочем диапазоне частот от одной до трех декад. Показано, что при вероятности успешных решений 0,8 на основе R-C-N-R ЭРП можно реализовать уровни постоянства фазы от 10 до 80 в диапазоне двух декад и от 36 до 56 в диапазоне трех декад.

Важное теоретическое и практическое значение имеет разработанный способ и алгоритм упорядочения топологии резистивного слоя двумерного RC-ЭРП после синтеза с целью повышения технологичности конструкций синтезированных RC-ЭРП. Алгоритм основан на применении прямого и обратного дискретного косинусного преобразований к элементам изображения синтезированной топологии. При этом фрагменты малых размеров, которые не существенно влияют на частотную характеристику исчезают и конфигурация элементов упрощается до пределов, определяемых допустимой степенью отклонения синтезированной частотной характеристики от заданной.

Показана возможность использования разработанных программ для синтеза электрических моделей объектов и процессов распределенной и фрактальной природы. Предложена методика оценки адекватности синтезированной структуры RC-ЭРП фрактальной размерности моделируемого объекта, гарантирующая с определенной точностью достоверность результатов идентификации.

В шестой главе определены критерии синтеза активных RC-фильтров
(АRC-Ф) на основе двумерных RC-ЭРП, разработаны алгоритмы, инструментальные средства и методики проектирования АRC-Ф, а также проведено исследование реализационных возможностей программы синтеза для проектирования стабильных и экономичных АRC-Ф высокого порядка.

Необходимость в разработке аналоговых фильтров, совместимых с технологией интегральных схем, является актуальной и в настоящее время, о чем свидетельствуют многочисленные публикации и появление такого класса активных RC-фильтров, как аналоговые адаптивные фильтры (CT-фильтры) и фильтры на основе транскондуктивных усилителей и конденсаторов (G_m-C-фильтры).

Однако при реализации фильтров высокого порядка (п = 10-12) на интеграторах габаритные размеры фильтров и трудоемкость настройки возрастают, а точность формирования частотной характеристики падает. Поэтому, на наш взгляд, применение в СТ-фильтрах звеньев АRC-Ф на RC-ЭРП, в которых элемент перестройки один, а порядок одного звена фильтра по сравнению с интегратором может быть 2-3 раза увеличен за счет неоднородностей RC-ЭРП, является предпочтительным.

Вопросы проектирования АRC-Ф на основе RC-ЭРП рассмотрены, в частности, в работах Гильмутдинова А.Х. с участием автора. Но полученные результаты ограничены АRC-Ф на основе одномерных однородных RC-ЭРП, передаточная характеристика которых аппроксимируется полиномиальной функцией второго порядка, т.е. учитывается влияние только «доминирующей» или «эквивалентной» пары полюсов. Разработка программ синтеза двумерных RC-ЭРП со структурой слоев, определяемой обобщенным RCG-ЭРП, позволяет расширить рамки этих работ и создать на этой основе АRC-Ф с лучшими электрическими и эксплуатационными характеристиками.

Проведено сравнение различных методов анализа АRC-Ф, содержащих RC-ЭРП, в результате чего предложено в процессе анализа и синтеза АRC-Ф, содержащих двумерные RC-ЭРП, учитывать не только «доминирующую пару полюсов» передаточной функции фильтра, но и полюсы более высоких порядков. С этой целью разработан метод вычисления коэффициентов полиномов дробно-рациональной передаточной функции, которая с заданной погрешностью аппроксимирует трансцендентную передаточную функцию АRC-Ф, определенную значениями ее АЧХ и ФЧХ на дискретном наборе частот.

Предложен критерий синтеза АRC-Ф по требованиям к характеристике затухания, которая реализуется не за счет каскадного (или иного) соединения отдельных звеньев первого или второго порядка, а за счет увеличения порядка звена путем синтеза неоднородностей в двумерном RC-ЭРП по этому критерию.

Разработаны дополнительные к программе синтеза двумерных RC-ЭРП инструментальные средства, позволяющие задавать требования к характеристике затухания фильтра и в интерактивном режиме влиять на процесс сходимости алгоритма синтеза. Наглядное представление о характере неоднородностей двумерного RC-ЭРП со структурой слоев вида R-C-NR, которые были получены в результате работы программы для получения заданной АЧХ фильтра, дано на рис. 6.




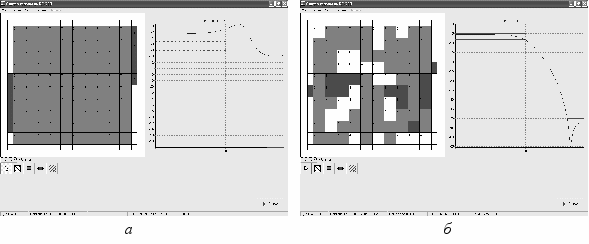
Рис. 6. Топология и АЧХ АRC-Ф: а – исходное состояние;
б - результаты синтеза по требованиям к характеристике затухания


Проведено исследование возможностей программы синтеза по реализации различных требований к характеристике затухания для выбранной конфигурации АRC-Ф. Показано, что звено, содержащее один активный элемент и двумерный RC-ЭРП, может реализовать требования к характеристике затухания эллиптического фильтра 4-го порядка, фильтра Чебышева 5-го порядка или фильтра Баттерворта 7-го порядка, подтверждая предположение о том, что использование двумерных RC-ЭРП в АRC-Ф позволяет уменьшить занимаемую площадь фильтра не менее чем в два раза и энергопотребление от двух до четырех раз по сравнению с его аналогами на RC-ЭСП.

Для оценки других параметров синтезированного АRC-Ф предусмотрен инструмент «Анализ», с помощью которого можно просмотреть АЧХ и ФЧХ в более широком диапазоне частот, оценить крутизну ската АЧХ и величину фазового сдвига, вручную изменить параметры активных и пассивных элементов схемы и проверить их влияние на частотные характеристики фильтра.

Реализована методика синтеза АRC-Ф по заданной форме полюсного годографа, основанная на синтезе пассивного четырехполюсника цепи обратной связи фильтра, содержащего двумерный RC-ЭРП, по критерию формы ФЧХ коэффициента передачи цепи.

Важным практическим результатом является возможность построения карты нулей и полюсов трансцендентной передаточной функции фильтра и построения годографов всех ее особых точек. Это позволяет автоматизировать синтез АRC-Ф по заданной форме полюсного годографа первой пары полюсов, оценивать устойчивость фильтра и использовать метод корневых годографов для синтеза стабильных и регулируемых АRC-Ф на новой элементной базе.

С помощью разработанной программы проведено исследование влияния неидеальности проводящей обкладки двумерного R-C-0 ЭРП на характеристики синтезируемого АRC-Ф. Показано, что АЧХ фильтра сильно зависит от величины сопротивления обкладки, от размеров и места подключения к ней контактной площадки. Рассмотрен пример синтеза АRC-Ф по требованиям к характеристике затухания с ненулевым сопротивлением обкладки, который показывает, что программа синтезирует двумерный RC-ЭРП с такими параметрами, которые полностью компенсируют влияние этой неидеальности на характеристики фильтра.

Предложен новый принцип управления параметрами АЧХ активного RC-фильтра, основанный на формировании закона изменения удельного сопротивления (емкости) RC-ЭРП за счет изменения электрофизических характеристик соответствующих слоев RC-ЭРП под действием управляющего поля.

Найдены аналитические зависимости частоты и добротности доминирующего полюса передаточной характеристики фильтра от параметров закона изменения погонной емкости RC-ЭРП, позволяющие формировать необходимый закон изменения погонного параметра в режиме, близком к режиму реального времени.

Результаты компьютерного моделирования показывают, что заданием определенного закона изменения погонной емкости по длине RC-ЭРП можно осуществить независимую настройку частоты и добротности доминирующей пары полюсов передаточной функции фильтра с добротностями от 5 до 150 в диапазоне нормированных частот RC от 25 до 40.

Предложенный принцип управления можно применить в аналоговых адаптивных фильтрах, необходимость создания которых определяется, в частности, интенсивным развитием беспроводных технологий передачи данных от интеллектуальных датчиков.

В седьмой главе рассмотрены теоретические положения синтеза интеграторов и дифференциаторов дробного порядка и разработана методика проектирования системы управления, использующей ПИД-регулятор дробного порядка на основе предложенных RC-ЭРП.

В многочисленных научных публикациях различных авторов показано, что большинство реальных объектов и процессов являются динамическими системами дробного порядка, поведение которых описывается дифференциальными уравнениями дробного порядка или передаточными функциями с дробными показателями степени комплексной частоты. Поэтому существует потребность в создании устройств дробного интегрирования и дифференцирования (ДИД), которые можно использовать, в частности, для управления динамическими системами дробного порядка, для создания аналоговых или гибридных вычислительных машин.

Проведен анализ вариантов схемотехнической реализации операций ДИД с наибольшей точностью в широком интервале частот и с минимальным влиянием источника сигнала на результат операции. Оптимальными по данным критериям являются схемы классического интегратора и дифференциатора на операционном усилителе, в которых вместо конденсатора включается двухполюсник Z_F, выражение для импеданса которого в общем виде можно записать как

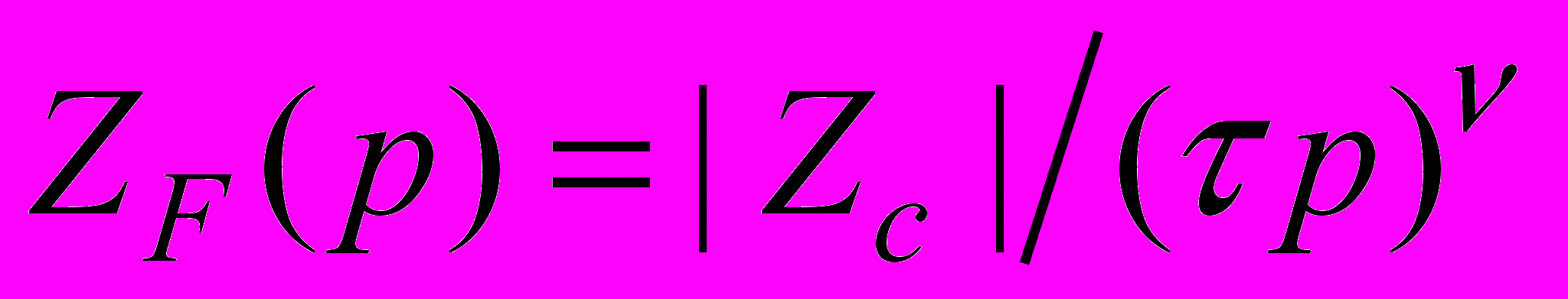, (7)

где Z_c – величина импеданса двухполюсника на частоте _с,  = 1/_с, р – комплексная частота,   в общем случае комплексное число с дробной действительной и/или мнимой частями.

Тогда выражение для передаточной функции дробного дифференциатора, построенного на Z_F, будет иметь вид:

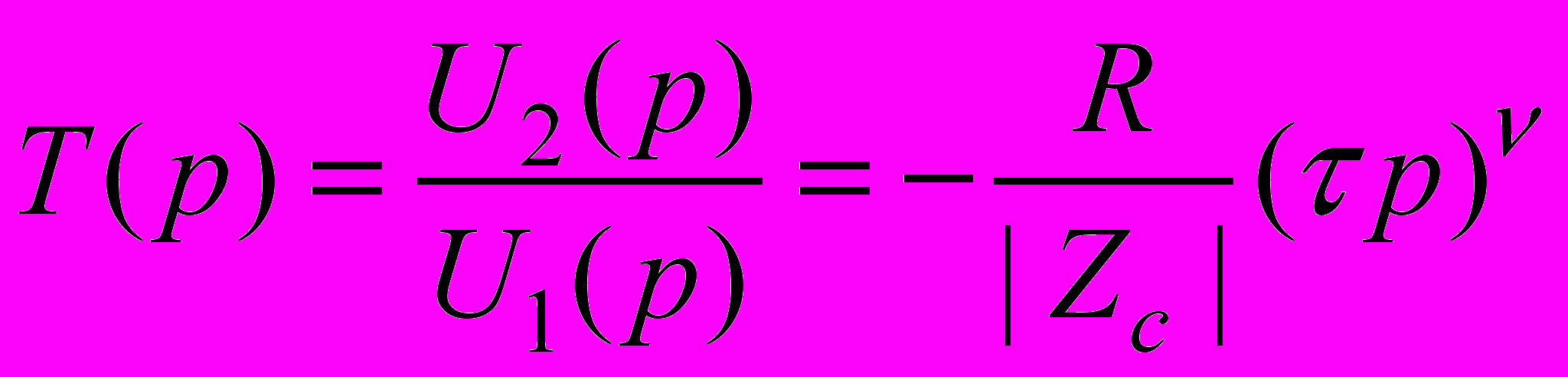. (8)

Во временной области выражению (8) будет соответствовать уравнение

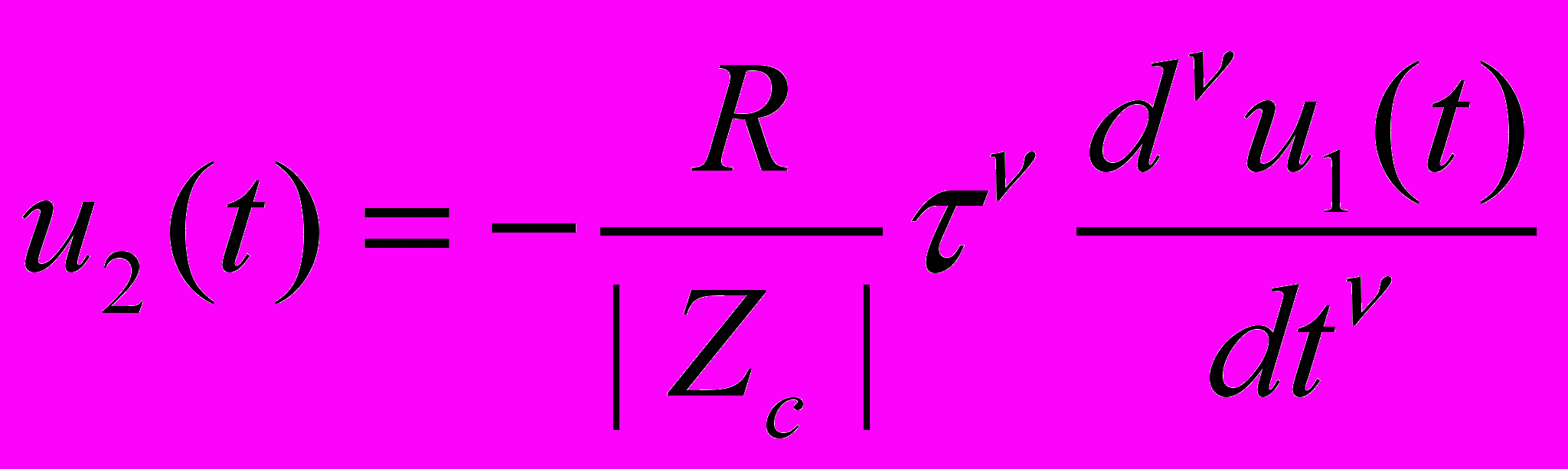, (9)

показывающее, что мгновенные значения выходного напряжения пропорциональны производной порядка  от входного напряжения.

В частотной области выражение для нормированной передаточной характеристики устройства ДИД при  =  + j можно записать как

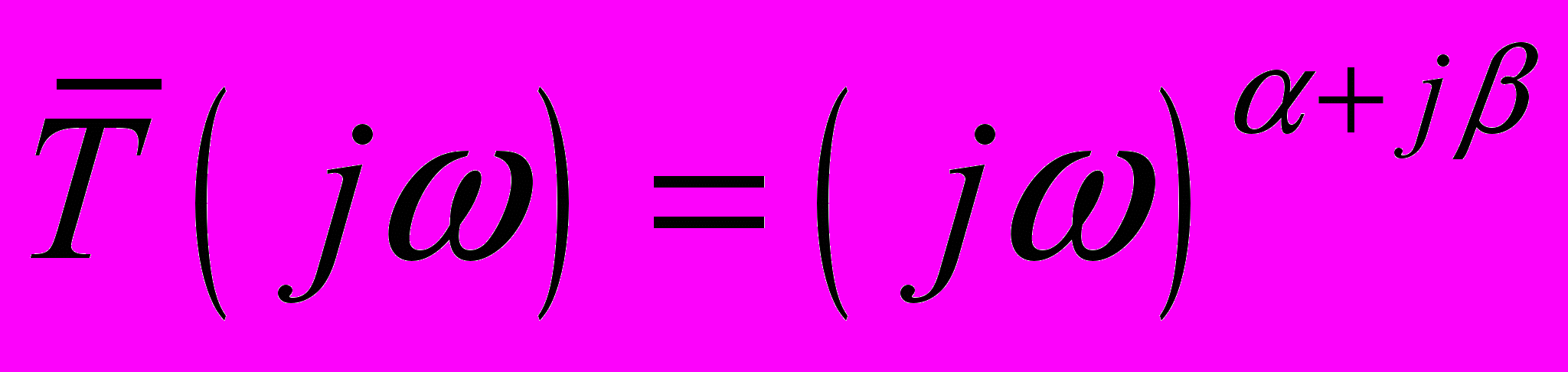. (10)

При этом выражения для ЛАЧХ и ФЧХ нормированной передаточной характеристики будут иметь вид

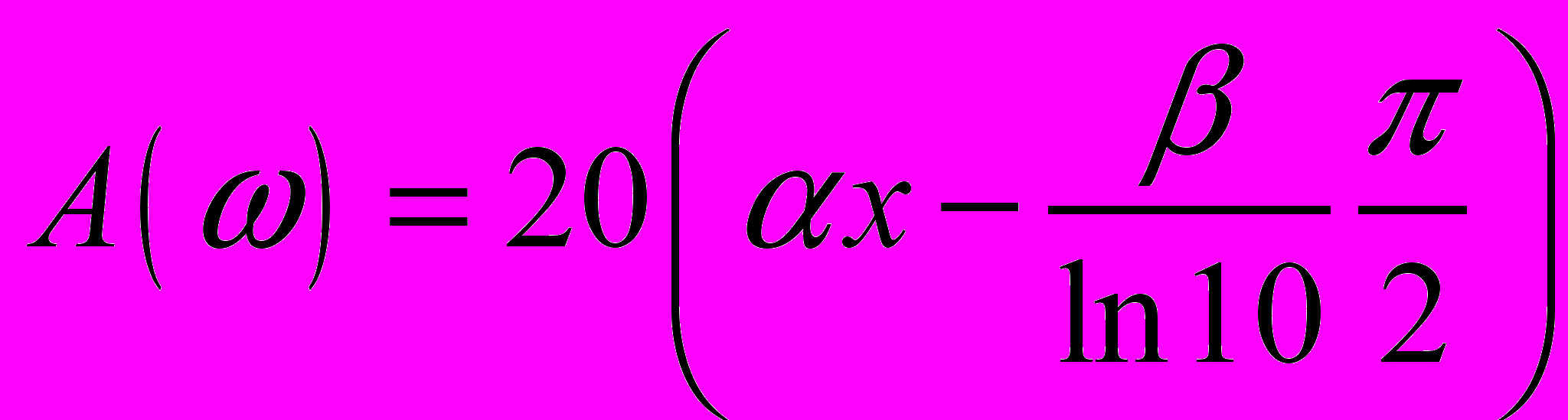, (11)

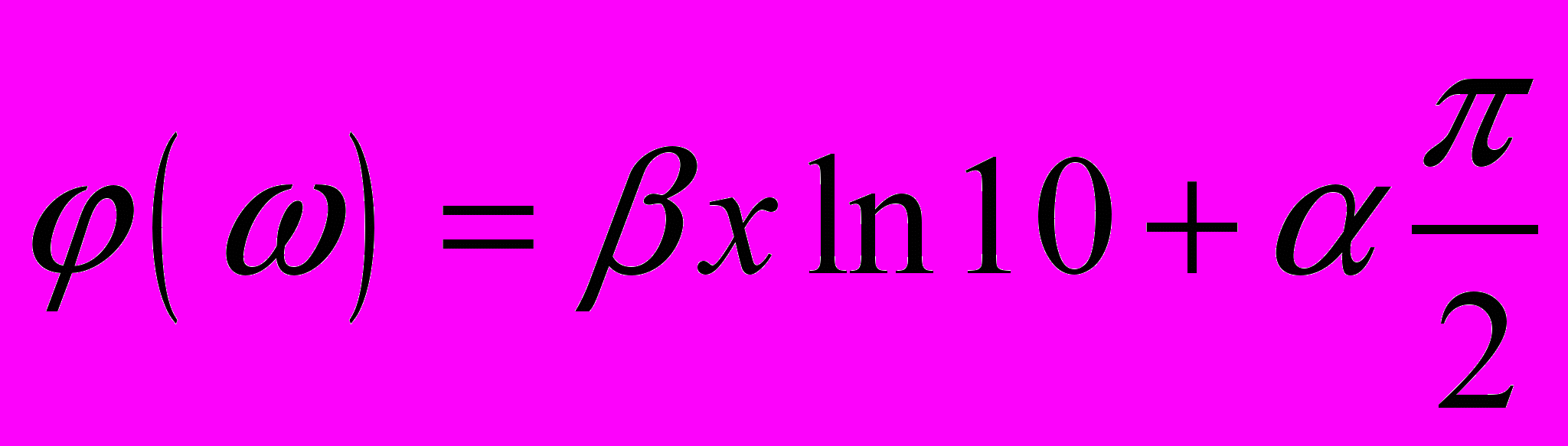, (12)

где x = lg.

Сравнение выражений (7) и (8) показывает, что задачу синтеза оператора ДИД можно свести к синтезу двухполюсника Z_F с АЧХ или ФЧХ, определяемыми соответственно выражениями (11) и (12), которые являются обобщенными критериями синтеза устройств ДИД. Обычно синтез ведут по критерию, определяемому выражением (12).

В частном случае, когда  = 0, () = /2 (0 < || < 1) и двухполюсник Z_F называют элементом с постоянной фазой (ЭПФ), с помощью которого можно реализовать оператор вещественного ДИД (ОВДИД).

Оператор комплексного ДИД (ОКДИД) предложено реализовать с помощью двухполюсника с линейной фазой, который сокращенно будем называть ДЛФ. Однако реализовать двухполюсник Z_F с ФЧХ, удовлетворяющей (12) во всем диапазоне частот, практически невозможно. Поэтому предлагается заменить задачу синтеза ДЛФ на синтез двухполюсника, ФЧХ которого определяется выражением

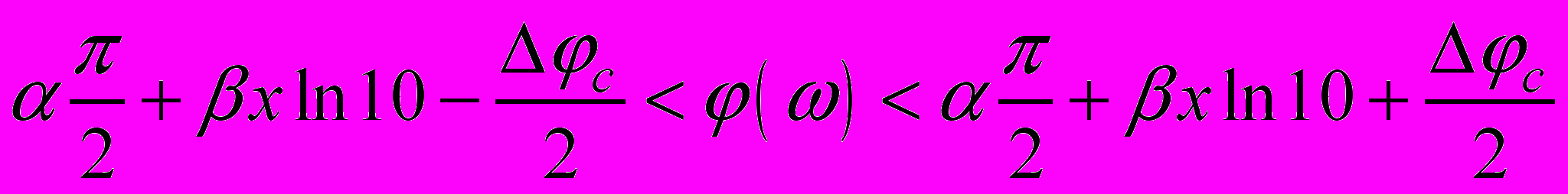, для 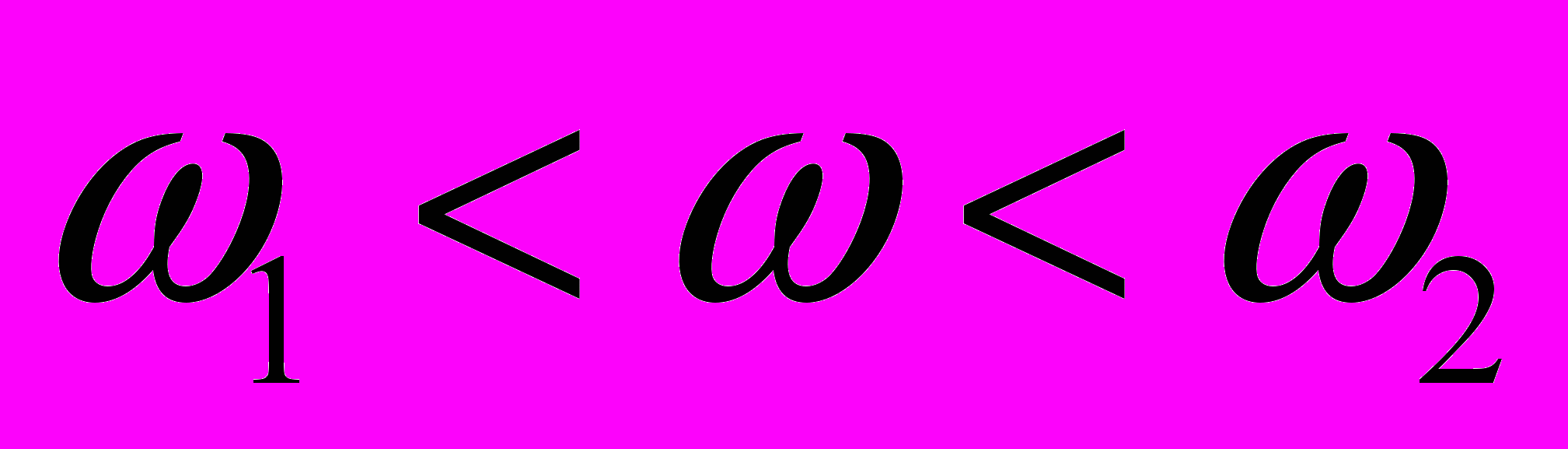, (13)

где _с – допустимая неравномерность ФЧХ в рабочем диапазоне частот.

При этом фазовый сдвиг в пределах границ, определяемых величиной , может принимать любые значения в указанном диапазоне частот.

Для задания обоснованных значений и 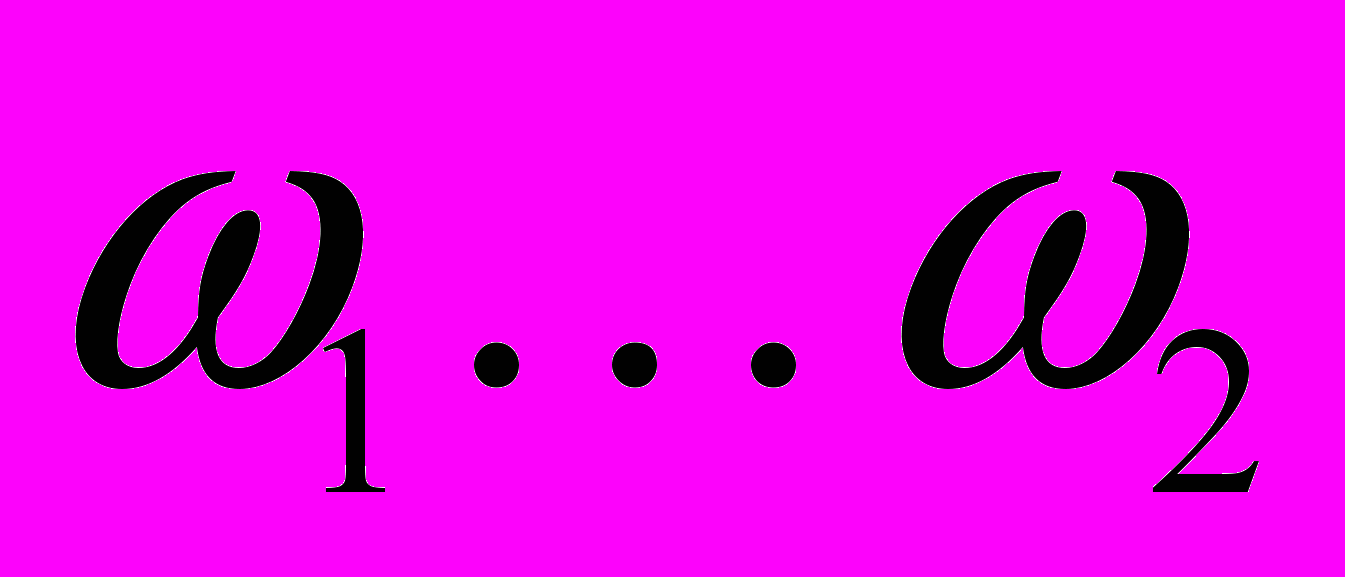было проведено исследование влияния этих параметров на точность выполнения операций ДИД, определяемую по величине среднеквадратического отклонения формы сигнала в виде прямоугольной импульсной последовательности, прошедшего через неидеальный интегратор (дифференциатор), от формы этого же сигнала на выходе идеального интегратора (дифференциатора).

Результаты исследования показали, что с увеличением ширины рабочего диапазона частот точность выполнения операций ДИД быстро возрастает независимо от порядка ДИД и формы сигнала. Неравномерность ФЧХ оказывает на точность выполнения операций ДИД большее влияние, чем ширина рабочего диапазона частот. В целом сделаны следующие выводы: для выполнения операций ДИД с допустимым значением СКО формы сигнала не более 5% достаточной является ширина диапазона рабочих частот 3 декады при неравномерности ФЧХ не более 2,5% от среднего уровня постоянства фазы.

В настоящее время в большинстве случаев в качестве двухполюсника Z_F используют многозвенные RC-цепи. Кроме больших габаритов, эти цепи имеют и другие существенные недостатки: зависимость количества элементов цепи от точности выполнения операций ДИД и ширины рабочего диапазона частот, сложность перестройки величины .

Для того чтобы показать, что двухполюсники Z_F на основе RC-ЭРП не имеют этих недостатков, в работе приведены примеры физически реализуемых двухполюсников в виде одномерных параметрических, одномерных структурно-неоднородных и двумерных RC-ЭРП при различных порядках интегрирования и дифференцирования, обеспечивающих ОВДИД в диапазоне рабочих частот не менее 4 декад и ОКДИД  в диапазоне до 2 декад.

Проведено сравнение конструктивно-технологических параметров двухполюсников Z_F на основе ОСН RC-ЭРП и на основе RC-ЭСП, которое показало, что при реализации ОВДИД порядка 0,167 двухполюсники Z_F на основе толстопленочных ОСН RC-ЭРП занимают площадь примерно в 20 раз меньше, чем двухполюсники Z_F на основе толстопленочных RC-ЭСП при одинаковых электрических характеристиках. При реализации ОКДИД порядка (0,5 + j0,5) устройства на основе ОСН RC-ЭРП имеют почти десятикратный выигрыш по занимаемой площади и четырехкратный выигрыш по энергопотреблению перед аналогичными устройствами на RC-ЭСП.

Разработана методика и приведен пример проектирования ПИД-регулятора дробного вещественного порядка для системы управления двигателем постоянного тока с независимым возбуждением. Модель управляемого объекта была задана передаточной функцией дробного порядка

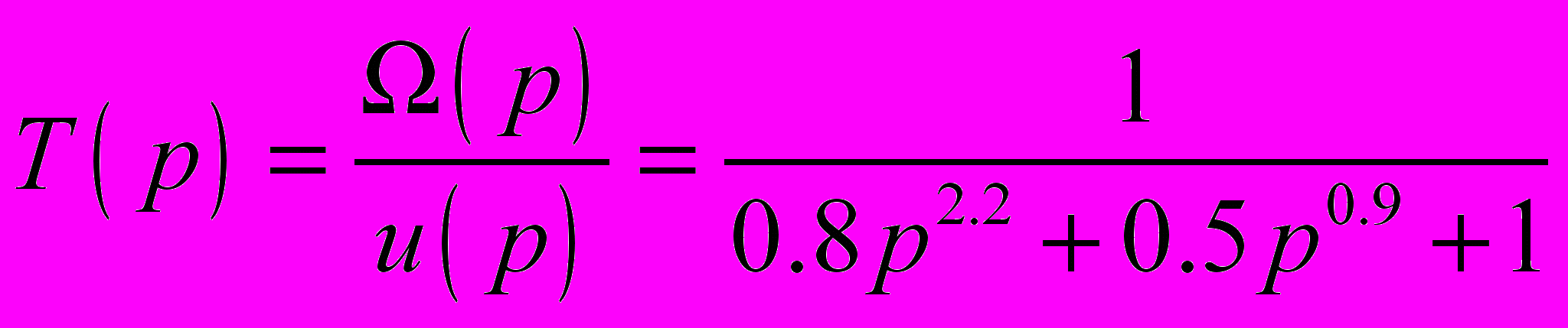, (14)

где (р)  угловая скорость вращения ротора, u(p)  напряжение на якорной цепи.

При требуемых параметрах регулировочной характеристики: статическая ошибка 5%; перерегулирование 0,4; коэффициент затухания 5 в соответствии с разработанной методикой определена передаточная функция ПИД контроллера дробного порядка

C(p) = 20,5 + 31,6226p^0,2 + 6,647p^1,15. (15)

Для проверки адекватности полученной математической модели ПИД-регулятора система управления динамическим объектом дробного порядка была промоделирована в программе Simulink. Измеренные характеристики регулирования с точностью 0,1% совпали с заданными. Кроме того показано, что эта система по таким параметрам, как величина перерегулирования, время установления и статическая ошибка вдвое превосходит систему управления с обычным ПИД-регулятором при управлении тем же объектом.

Система управления дробного порядка была также промоделирована в виде электрической схемы в программе схемотехнического моделирования SWCAD. При этом дробные порядки интегратора и дифференциатора, соответствующие передаточной функции (15) определялись двухполюсниками Z_F на основе ОСН RC-ЭРП, синтезированными по частотным критериям (13). Результаты моделирования системы управления в виде электрической схемы с точностью 0,5% совпали с результатами, полученными в программе Simulink. Таким образом, доказана корректность разработанных нами критериев синтеза устройств ДИД, корректность разработанных программ синтеза RC-ЭРП, практическая реализуемость и высокая эффективность систем управления дробного порядка.

Предложена концепция САПР RC-ЭРП и устройств на их основе, в которой будут сочетаться возможности конструктивной основы обобщенного RCG-ЭРП, метод обобщенных конечных распределенных элементов и поисковая оптимизация, основанная на генетических алгоритмах. Дано обоснование функций основных модулей системы, предложена общая структурная схема программного комплекса анализа и синтеза устройств на основе RC-ЭРП, которая составит ядро будущей специализированной САПР.