Рабочая программа учебной дисциплины
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины ф тпу 1 -21/01, 102.93kb.
- Рабочая программа учебной дисциплины судебная фотография и видеозапись Специальность, 90.44kb.
- Рабочая программа учебной дисциплины судебная этика Направление подготовки 030500., 197.85kb.
- Рабочая программа учебной дисциплины судебная психиатрия Специальность 030501. 65 «Юриспруденция», 141.66kb.
- Рабочая программа учебной дисциплины судебная адвокатура Специальность 030501. 65 «Юриспруденция», 148.98kb.
- Рабочая программа учебной дисциплины современные способы фиксации следственных действий, 170.54kb.
- Учебно-методического комплекса (умк) Учебной дисциплины «Финансы и кредит» Проектирование, 424.52kb.
- Рабочая программа учебной дисциплины ф тпу 1-21/01 утверждаю, 360.66kb.
- Рабочая программа учебной дисциплины (место, цели и задачи учебной дисциплины в общей, 498.45kb.
- Рабочая программа учебной дисциплины математика и информатика, 188.66kb.
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве
Российской Федерации»
Кафедра «Теория вероятностей и математическая статистика»
А.В. Браилов, С.А.Зададаев
ТЕОРИЯ ВЕРОЯТНОСТЕЙ и
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 2
Рабочая программа учебной дисциплины
Для подготовки бакалавров направления 010400.62 «Прикладная
математика и информатика» по профилю «Математическое и
информационное обеспечение экономической деятельности»
Москва 2010
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве
Российской Федерации»
Кафедра «Теория вероятностей и математическая статистика»
утверждаю
Ректор
__________ М.А. Эскиндаров
_______ ___________ 2010 г.
А.В. Браилов, С.А.Зададаев
ТЕОРИЯ ВЕРОЯТНОСТЕЙ и
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 2
Рабочая программа учебной дисциплины
Для подготовки бакалавров направления 010400.62 «Прикладная
математика и информатика» по профилю «Математическое и
информационное обеспечение экономической деятельности»
Рекомендовано Ученым советом факультета «Математические
методы и анализ рисков», протокол № ___ от ___ ___________ 2010 г.
Одобрено кафедрой «Прикладная математика», протокол № ___ от ___ ___________ 2010 г.
М
 осква 2010
осква 2010 УДК ?
ББК ?
Рецензент: И.Е. Денежкина, заведующая кафедры «Теория вероятностей и математическая статистика»
?? А.В. Браилов, С.А. Зададаев
«Теория вероятностей и математическая статистика 2». Программа дисциплины для студентов, обучающихся по направлению «Прикладная математика и информатика» по профилю «Математическое и информационное обеспечение экономической деятельности» (программа подготовки бакалавров) – очная форма обучения.– М.: ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», кафедра «Теория вероятностей и математическая статистика», 2010. - с.
Дисциплина «Теория вероятностей и математическая статистика 2» является дисциплиной базовой компоненты математического цикла дисциплин ФГОС ВПО по направлению 010400.62 «Прикладная математика и информатика» по профилю «Математическое и информационное обеспечение экономической деятельности». Рабочая программа содержит: программу дисциплины; рабочий план изучения дисциплины; тематику и планы лекций, тематику практических и самостоятельных занятий с указанием технологии их проведения; формы контроля за их выполнением.
УДК ?
ББК ?
Учебное издание
Браилов Андрей Владимирович
Сергей Алексеевич Зададаев
ТЕОРИЯ ВЕРОЯТНОСТЕЙ и
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 2
Рабочая программа учебной дисциплины
Компьютерный набор, верстка: С.А.Зададаев.
Формат 60х90/16. Гарнитура Times New Roman
Усл.п.л.1,1. Изд. № -2010. Тираж ___ экз.
Отпечатано в ФГОУ ВПО «Финансовый университет при
Правительстве Российской Федерации»
А.В. Браилов, 2010
С.А. Зададаев, 2010
 ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», 2010
ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», 2010Содержание
- Цели и задачи дисциплины………………………………………...4
- Место дисциплины в структуре ООП……………………………..4
- Требования к результатам освоения дисциплины………………..5
- Объем дисциплины и виды учебной работы……………………..8
- Содержание дисциплины:
5.1 Содержание разделов дисциплины……………………………..8
5.2 Разделы дисциплины и междисциплинарные
связи с обеспечиваемыми дисциплинами…………………….12
5.3 Разделы дисциплины и виды занятий…………………………13
- Практические (семинарские) занятия……………………………13
- Самостоятельная работа…………………………………………..14
- Контрольные вопросы и система оценивания…………………..15
- Учебно-методическое и информационное обеспечение
дисциплины…………………………………………………………16
- Приложение. Учебно-методическая карта дисциплины………...19
1. Цели и задачи дисциплины
Цель дисциплины –
1. Получение базовых знаний и формирование основных навыков по теории вероятностей, необходимых для решения задач, возникающих в математическом обеспечении прикладной экономической деятельности.
2. Развитие понятийной теоретико-вероятностной базы и формирование уровня алгебраической подготовки, необходимых для понимания основ математической и экономической статистики и её применения.
Задача дисциплины –
В результате изучения дисциплины «Теория вероятностей и математическая статистика 2» студенты должны владеть основными математическими понятиями курса; уметь использовать аппарат математической статистики для решения теоретических и прикладных задач экономики и финансов; уметь решать типовые задачи, иметь навыки работы со специальной математической литературой.
2. Место дисциплины в структуре ООП
Дисциплина «Теория вероятностей и математическая статистика 2» является дисциплиной базовой компоненты математического цикла дисциплин ФГОС ВПО по направлению 010400.62 «Прикладная математика и информатика» по профилю «Математическое и информационное обеспечение экономической деятельности».
Изучение дисциплины «Теория вероятностей и математическая статистика 2» основывается на базе знаний, полученных студентами в ходе освоения на первом году обучения дисциплин «Алгебра и геометрия», «Математический анализ» и «Дискретная математика» того же цикла. А также в ходе освоения дисциплины «Теория вероятностей и математическая статистика 1» второго курса.
Дисциплина «Теория вероятностей и математическая статистика 2» изучается на втором году обучения, закладывает фундамент для понимания основных статистических методов решения задач профессиональной деятельности и является базовым теоретическим и практическим основанием для многих последующих математических и финансово-экономических дисциплин подготовки бакалавра «Прикладная математика и информатика» для профиля «Математическое и информационное обеспечение экономической деятельности».
3. Требования к результатам освоения дисциплины
В совокупности с другими дисциплинами базовой и вариативной части математического цикла ФГОС ВПО дисциплина «Теория вероятностей и математическая статистика 2» обеспечивает инструментарий формирования следующих общих и профессиональных компетенций подготовки бакалавра «Прикладная математика и информатика» по профилю «Математическое и информационное обеспечение экономической деятельности»:
- владение культурой мышления, умение аргументировано и ясно строить устную и письменную речь (ОК-1);
- способность к интеллектуальному, культурному и профессиональному саморазвитию, стремление к повышению свей квалификации и мастерства (ОК-2);
- способность осознавать социальную значимость своей профессии, обладание высокой мотивацией к выполнению профессиональной деятельности (ОК-9);
- демонстрация общенаучных базовых знаний естественных наук, математики и информатики, понимание основных научных фактов, концепций, принципов теорий, связанных с прикладной математикой (ОК-10);
- умение использовать навыки поиска и работы с информацией из различных источников, включая сетевые ресурсы сети Интернет, для решения профессиональных и социальных задач (ОК-15);
- умение приобретать новые научные и профессиональные знания, используя современные и информационные технологии (ОК-16);
- способность собирать, обрабатывать и интерпретировать данные современных научных исследований, необходимые для формирования выводов по соответствующим научным, профессиональным, социальным и этическим проблемам (ПК-1);
- способность понимать и применять в исследовательской и прикладной деятельности современный математический аппарат (ПК-2);
- способность в составе научно-исследовательского и производственного коллектива решать задачи профессиональной деятельности (в соответствии с профилем подготовки) (ПК-4);
- способность критически переосмысливать накопленный опыт, изменять при необходимости вид и характер своей профессиональной деятельности (ПК-5);
- способность осуществлять целенаправленный поиск информации о новейших научных и технологических достижениях в сети Интернет и из других источников (ПК-6);
- знание и следование в жизни кодексу профессиональной этики (ПК-7);
- способность формировать суждения о значении и последствиях своей профессиональной деятельности с учетом социальных, профессиональных и этических позиций (ПК-8);
- понимание сущности и значения информации в развитии современного общества; владение основными методами, способами и средствами получения, хранения, переработки информации (ПК-9);
- способность решать задачи производственной и технологической деятельности на профессиональном уровне (ПК-10);
- способность составлять и контролировать план выполняемой работы, планировать необходимые для выполнения работы ресурсы, оценивать результаты собственной работы (ПК-12);
В результате освоения содержания дисциплины «Исследование операций» студент должен:
знать
- основы теории вероятностей, необходимые для решения математических и финансово-экономических задач;
уметь
- применять теоретико-вероятностные методы для решения задач экономики и финансов;
владеть
- навыками применения современного математического инструментария для решения экономических задач;
- методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов (в части компетенций, соответствующих понятиям и методам математической статистики).
4. Объём дисциплины и виды учебной работы
Общая трудоёмкость дисциплины составляет 4 зачётных единиц.
Вид промежуточной аттестации – 1 экзамен.
| Вид учебной работы | Часы | Семестр 4 (II курс) |
| 3 | ||
| Общая трудоёмкость дисциплины | 216 | 216 |
| Аудиторные занятия | 85 | 85 |
| Лекции (Л) | 34 | 34 |
| Семинарские занятия (СЗ) | 34 | 34 |
| Практические занятия (ПЗ) | 17 | 17 |
| Самостоятельная работа | 131 | 131 |
| В семестрах | 95 | 95 |
| В сессию / форма | 36 | 36 |
| | экзамен |
5. Содержание дисциплины
5.1. Содержание разделов дисциплины
Раздел 1. Случайные процессы.
Случайные процессы. Основные типы случайных процессов. Геометрическое броуновское движение. Случайное блуждание.
Раздел 2. Статистика конечной совокупности.
Эмпирические характеристики признака: среднее, дисперсия, СКО, асимметрия, эксцесс, функция распределения. Эмпирическая ковариация двух признаков. Вариационный ряд, размах и эмпирическая медиана. Среднее арифметическое и дисперсия совокупности, разбитой на группы. Среднее арифметическое и дисперсия интервального распределения. Связь с характеристиками исходной совокупности. Поправка Шеппарда.
Генеральная совокупность, выборка и основные способы организации выборки. Основные выборочные характеристики и их свойства. Повторные и бесповторные выборки. Математическое ожидание и дисперсия выборочного среднего. Ковариация выборочных средних двух признаков. Математическое ожидание и дисперсия выборочной доли.
Раздел 3. Точечные оценки параметров распределений.
Вариационный ряд и порядковые статистики. Распределение порядковых статистик. Статистическое оценивание параметров. Точечные оценки и их свойства (несмещенность, состоятельность и эффективность). Состоятельность и сходимость по вероятности. Несмещенная оценка начального момента произвольного порядка. Выборочное среднее как эффективная оценка математического ожидания. Достаточные условия состоятельности статистической оценки. Состоятельные оценки начальных моментов. Несмещенная оценка
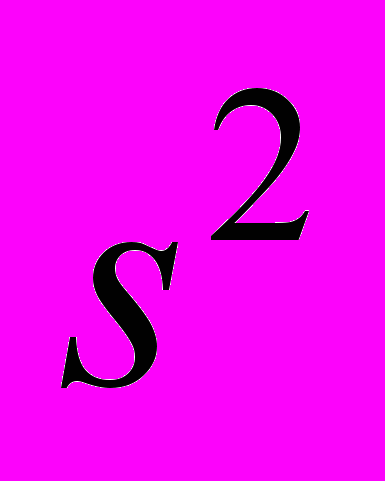 генеральной дисперсии и ее состоятельность.
генеральной дисперсии и ее состоятельность.Неравенство информации, метод максимального правдоподобия и метод моментов. Оценки параметров распределения методом моментов и их состоятельность. Метод максимального правдоподобия. Неравенство Рао – Крамера и информация Фишера. Выборочное среднее как эффективная оценка математического ожидания нормального распределения в классе всех несмещенных оценок.
Раздел 4. Интервальные статистические оценки.
Интервальные оценки и доверительные области. Байесовское статистическое оценивание. Медиана и другие квантили непрерывных распределений. Интервальные оценки параметров распределения, доверительная вероятность и точность оценки. Построения интервальных оценок методом центральной статистики. Законы распределения выборочных характеристик в нормальной генеральной совокупности. Распределения
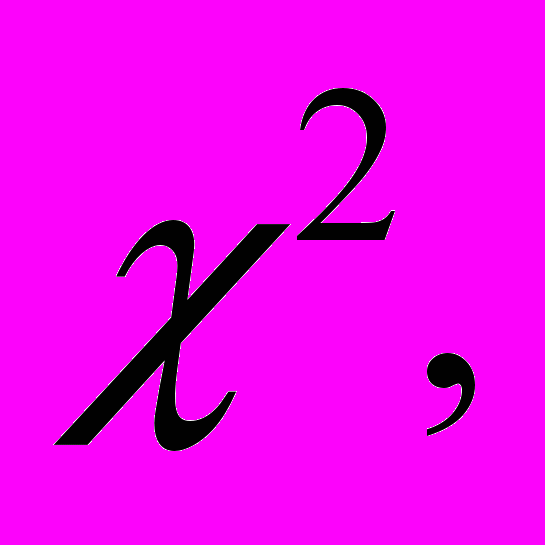 Стьюдента и Фишера. Определения и простейшие свойства. Доверительный интервал для математического ожидания при известной дисперсии. Доверительные интервалы для математического ожидания и вероятности события в случае выборки большого объема. Доверительный интервал для математического ожидания при неизвестной дисперсии. Доверительный интервал (симметричный по вероятности) для дисперсии при известном математическом ожидании. Доверительный интервал (симметричный по вероятности) для дисперсии при неизвестном математическом ожидании. Интервал предсказания.
Стьюдента и Фишера. Определения и простейшие свойства. Доверительный интервал для математического ожидания при известной дисперсии. Доверительные интервалы для математического ожидания и вероятности события в случае выборки большого объема. Доверительный интервал для математического ожидания при неизвестной дисперсии. Доверительный интервал (симметричный по вероятности) для дисперсии при известном математическом ожидании. Доверительный интервал (симметричный по вероятности) для дисперсии при неизвестном математическом ожидании. Интервал предсказания.Раздел 5. Статистическая проверка гипотез
Статистическая проверка гипотез: основные типы гипотез и общая логическая схема статистического критерия; характеристики качества критерия. Проверка статистических гипотез. Критическая область. Мощность критерия. Отношение правдоподобия и лемма Неймана-Пирсона. Пример построения наиболее мощного критерия. Проверка гипотез об определенных значениях параметров нормальных распределений. Проверка гипотезы о равенстве средних при известной дисперсии. Проверка гипотезы о равенстве средних при неизвестной дисперсии. P-значение критерия. Определение и способ его вычисления. Проверка гипотезы о равенстве дисперсий. Критерии согласия и однородности, проверка гипотезы о числовых значениях параметров. Проверка гипотезы о соответствии эмпирических данных теоретическому закону с данной функцией распределения по критерию Пирсона. Проверка гипотезы об однородности нескольких выборок по критериям Пирсона и Колмогорова – Смирнова. Сравнение нескольких средних методом дисперсионного анализа.
Раздел 6. Основы статистического исследования зависимостей.
Решение СЛУ методом наименьших квадратов. Общая дисперсия как сумма факторной и остаточной дисперсии. Коэффициент детерминации R2 и его связь с коэффициентом корреляции. Линейная модель парной регрессии и теорема Гаусса – Маркова. Несмещенность МНК-оценок коэффициентов парной регрессии. Дисперсия МНК-оценок коэффициентов парной регрессии.
5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми дисциплинами
| № п/п | Наименование обеспечиваемых дисциплин | Разделы 1 и 6 | Раздел 2 | Раздел 3 и 4 | Раздел 5 |
| 1 | Общая теория статистики | * | * | * | * |
| 2 | Введение в теорию случайных процессов | * | | | |
| 4 | Основы финансовых вычислений | * | * | * | |
| 5 | Вероятностные модели актуарной математики | * | | | |
| 6 | Дискретные модели финансовых рынков и процессов управления активами | * | | | |
| 7 | Вероятностные основы управления рисками | * | * | * | * |
| 8 | Вычислительные аспекты математической статистики | * | * | * | * |
5.3. Разделы дисциплины и виды занятий
| № п/п | Наименование раздела (темы) дисциплины | Трудоёмкость в часах | ||||
| Всего часов | Аудиторная работа | Внеауди-торная (самостоя-тельная) работа | ||||
| Общая | Лекции | СЗ / ПЗ | Общая | |||
| 1 | Случайные процессы | | | | | |
| 2 | Статистика конечной совокупности | | | | | |
| 3 | Точечные оценки параметров распределений | | | | | |
| 4 | Интервальные статистические оценки | | | | | |
| 5 | Статистическая проверка гипотез | | | | | |
| 6 | Основы статистического исследования зависимостей | | | | | |
| | Экзамен | 36 | | | | |
| | Итого: | 216 | 85 | 34 | 34 / 17 | 131 |
6. Практические и семинарские занятия
Рабочая учебная программа дисциплины предусматривает 17 аудиторных семинарских занятий (по 2 часа каждое) и 8 аудиторных практических занятий (по 2 часа каждое, за исключением последнего – 3 часа).
Семинары
Структурно каждый семинар содержит следующие ниже решаемые учебно-методические задачи:
1) Проверка наличия выполненного задания самостоятельной работы
каждого студента;
2) Выборочная проверка корректности выполнения домашнего задания;
3) Разбор типичных ошибок, возникших в самостоятельной работе;
4) Рассмотрение теоретических оснований для решения задач текущей
темы;
5) Разбор практических методов и решение соответствующих задач;
6) Корректировка заданий для самостоятельной работы студентов.
План семинаров
Занятие 1. Освоение Матричного калькулятора. Решение задач на точное вычисление вероятности событий и моментов распределения с использованием компьютера. Компьютерное построение графиков плотностей и функций распределения.
Занятие 2. Метод Монте-Карло. Решение задач на приближенное вычисление вероятности событий и моментов распределения с использованием компьютера.
Занятие 3. Компьютерное моделирование случайных процессов. Разыгрывание процесса цены актива. Решение методом Монте-Карло задач на приближенное вычисление вероятности достижения случайным процессом заданного значения.
Занятие 4. Основные характеристики статистической совокупности и их свойства. Эмпирическая функция распределения. Числовые характеристики двумерной совокупности.
Занятие 5. Полигон и гистограмма. Расчет числовых характеристик статистической совокупности по таблице интервальных частот. Поправка Шеппарда. Среднее и дисперсия совокупности, разбитой на группы.
Занятие 6. Повторные и бесповторные выборки. Выборки, основанные на предварительном разбиении генеральной совокупности. Математическое ожидание и дисперсия выборочного среднего простой бесповторной выборки.
Занятие 7. Точечные оценки параметров распределения. Смещенные и несмещенные статистические оценки. Эффективные и состоятельные оценки. Достаточное условие состоятельности. Оценки математического ожидания и дисперсии.
Занятие 8. Методы построения точечных оценок параметров генерального распределения. Метод моментов.
Занятие 9. Метод максимального правдоподобия. Информация Фишера и неравенство Рао – Крамера.
Занятие 10. Распределения
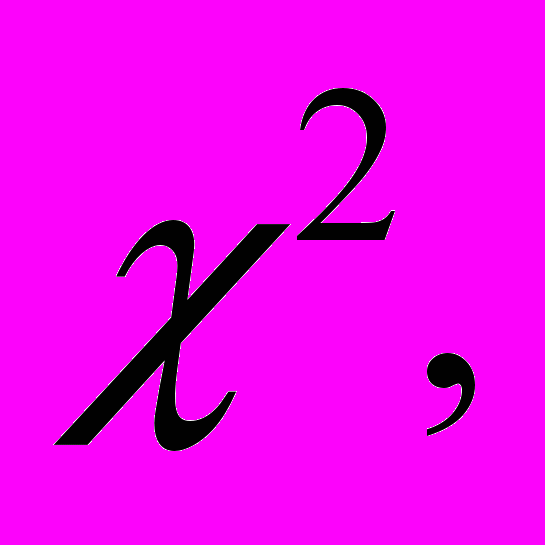 Стьюдента и Фишера. Построения интервальных оценок методом центральной статистики.
Стьюдента и Фишера. Построения интервальных оценок методом центральной статистики. Занятие 11. Интервальные оценки математического ожидания нормального распределения при известной и неизвестной дисперсии. Оценка неизвестной вероятности по частоте.
Занятие 12. Односторонние и двусторонние симметричные по вероятности оценки дисперсии нормальной генеральной совокупности при известном и неизвестном генеральном среднем. Оценки прогноза.
Занятие 13. Статистическая проверка гипотез: основные типы гипотез и общая логическая схема статистического критерия; характеристики качества критерия. Уровень значимости и мощность критерия. Проверка гипотезы о числовых значениях параметров.
Занятие 14. Проверка гипотез о равенстве средних и дисперсий двух нормально распределенных генеральных совокупностей.
Занятие 15. Критерий согласия Пирсона. Проверка гипотезы о соответствии наблюдаемых значений предполагаемому распределению вероятностей. Проверка гипотез: о заданном конечном распределении, о распределении Пуассона, о нормальном распределении.
Занятие 16. Проверка гипотезы об однородности нескольких выборок по критериям Пирсона и Колмогорова – Смирнова. Критерий Колмогорова.
Занятие 17. Метод наименьших квадратов.
Практические занятия
Структурно каждое практическое занятие содержит следующие ниже решаемые учебно-методические задачи:
1) Проверка наличия выполненного задания самостоятельной работы
каждого студента;
2) Выборочная проверка корректности выполнения домашнего задания;
3) Разбор типичных ошибок, возникших в самостоятельной работе;
4) Рассмотрение теоретических и практических оснований для
компьютерной практики текущей темы;
5) Разбор программных методов и программирование решения
соответствующих задач;
6) Корректировка заданий для самостоятельной работы студентов.
План практических занятий
Занятие 1. Освоение Матричного калькулятора. Решение задач на точное вычисление вероятности событий и моментов распределения с использованием компьютера. Компьютерное построение графиков плотностей и функций распределения.
Занятие 2. Метод Монте-Карло. Решение задач на приближенное вычисление вероятности событий и моментов распределения с использованием компьютера.
Занятие 3. Компьютерное моделирование случайных процессов. Разыгрывание процесса цены актива. Решение методом Монте-Карло задач на приближенное вычисление вероятности достижения случайным процессом заданного значения.
Занятие 4. Основные характеристики статистической совокупности и их свойства. Эмпирическая функция распределения. Числовые характеристики двумерной совокупности.
Занятие 5. Полигон и гистограмма. Расчет числовых характеристик статистической совокупности по таблице интервальных частот. Поправка Шеппарда. Среднее и дисперсия совокупности, разбитой на группы.
Занятие 6. Повторные и бесповторные выборки. Выборки, основанные на предварительном разбиении генеральной совокупности. Математическое ожидание и дисперсия выборочного среднего простой бесповторной выборки.
Занятие 7. Точечные оценки параметров распределения. Смещенные и несмещенные статистические оценки. Эффективные и состоятельные оценки. Достаточное условие состоятельности. Оценки математического ожидания и дисперсии.
Занятие 8. Методы построения точечных оценок параметров генерального распределения. Метод моментов.
7. Самостоятельная работа
Внеаудиторными формами и инструментами самостоятельной работы студентов по дисциплине являются:
- выполнение 25-ти домашних заданий;
- выполнение 4-х домашних контрольных работ (как средство подготовки
к устной защите контрольных тем);
- написание курсовой работы
- подготовка к одному экзамену.
Самостоятельная работа студентов по дисциплине состоит из 25 домашних заданий (соответственно 13 к семинарам, 8 к каждой практике и 4 - домашние контрольные работы), рассчитанных на 3 часа внеаудиторной нагрузки.
Тематика домашних контрольных работ
1) Эмпирические характеристики и метод Монте-Карло.
2) Повторные и бесповторные выборки.
3) Точечные и интервальные статистические оценки.
4) Статистическая проверка гипотез.
При этом первая контрольная выполняется студентами на домашних компьютерах и может быть приравнена к лабораторной работе.
Тематика курсовых работ
Большинство предлагаемых тем курсовых работ (20 часов внеаудиторной нагрузки) связано с исследованием статистических свойств логарифмической доходности наиболее ликвидных акций. При выполнении курсовой работы студенты могут использовать в качестве исходных статистических данных как данные, встроенные в программу «Матричный калькулятор», так и данные, полученные ими самостоятельно из Интернета. Набор исследуемых акций должен характеризоваться каким-либо общим признаком, например, определенной отраслевой принадлежностью, уровнем капитализации или вхождением в определенный фондовый индекс.
После получения соответствующих временных рядов (рекомендуется использовать цену закрытия) их следует проверить на наличие необычно резких скачков цен, возможно вызванных дроблением акций. Исследование всех отобранных акций следует проводить на одинаковом интервале времени (5–15 лет), включающем достаточно новые данные.
Методику проверки статистической гипотезы для реальных финансовых данных рекомендуется предварительно проверить на искусственно созданных временных рядах. Все статистические расчеты проводятся с применением программ «Матричный калькулятор» или MATLAB. Примерная тематика курсовых работ:
- Проверка гипотезы о биномиальном распределении числа положительных изменений курса акции.
- Проверка гипотезы о независимости логарифмической доходности за различные интервалы времени при большом, среднем и малом объеме торгов.
- Проверка гипотезы о совпадении генеральных средних логарифмической доходности для всех дней недели.
- Проверка гипотезы о совпадении генеральных дисперсий логарифмической доходности для всех дней недели.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Пирсона при оценке параметров методом максимального правдоподобия.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Пирсона при оценке параметров квантильным методом.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Дарбина.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Филлибена.
- Проверка гипотезы о нормальном распределении логарифмической доходности по модифицированному критерию Колмогорова–Смирнова.
- Проверка гипотезы о нормальном распределении логарифмической доходности по модифицированному критерию Пирсона.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Шапиро–Уилки.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Шапиро–Франчиа.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Харке–Бера.
- Проверка гипотезы о нормальном распределении логарифмической доходности по критерию Саркади.
- Проверка гипотезы о нормальном распределении линейных комбинаций дневной логарифмической доходности за ближайшие три рабочих дня.
- Проверка гипотезы о распределении дневной логарифмической доходности по закону Стьюдента.
- Проверка гипотезы о совпадении дисперсии праздничной логарифмической доходности на коротком промежутке времени с эмпирической дисперсией дневной логарифмической доходности за период с 2000 по 2007 годы.
- Проверка гипотезы о равенстве 0 коэффициента корреляции дневной логарифмической доходности.
- Проверка гипотезы о равенстве математического ожидания дневной логарифмической доходности на коротком промежутке времени средней дневной логарифмической доходности за период с 2000 по 2007 годы.
- Проверка гипотезы о нормальном распределении логарифмической доходности при условии определенного изменения фондового индекса накануне.
- Проверка гипотезы о нормальном распределении логарифмической доходности при условии определенного уровня объема торгов накануне.
- Сравнительный анализ распределений дневной логарифмической доходности за периоды "открытие–закрытие" и "закрытие–открытие".
- Сравнительный анализ распределений дневной логарифмической доходности при большом, среднем и малом объеме торгов.
- Сравнительный анализ распределений дневной логарифмической доходности при росте и падении цены накануне.
- Статистический анализ торговых стратегий на основе коэффициента Модильяни–Модильяни.
- Проверка гипотезы о нормальном распределении логарифмической доходности при условии, что накануне значение индикатора MACD находилось в определенном диапазоне.
- Проверка гипотезы о нормальном распределении логарифмической доходности при условии, что накануне значение индикатора RSI находилось в определенном диапазоне
- Проверка гипотез о виде распределения остатков модели GARCH(1,1).
Формы самостоятельной работы и нормы нагрузки
| №№ | Практические домашние задания ед./час. | Домашние контрольные работы ед./час. | Курсовая работа | Всего | Экзамен ед./час. |
| Семестр | 21 / 63 | 4 / 12 | 1 / 20 | 26 / 95 | 1 / 36 |
| Итог | 21 / 63 | 4 / 12 | 1 / 20 | 26 / 95 | 1 / 36 |
Всего 131 час самостоятельной работы, из них:
- работа в семестре - 95 часов,
- экзамен - 36 часов.
8. Контрольные вопросы и система оценивания
В качестве оценочных средств программой дисциплины предусматривается:
- текущий контроль (контроль наличия вместе с выборочной проверкой
домашних заданий и устная защита домашних контрольных работ)
- защита курсовой работы
- промежуточный контроль – экзамен.
Итоговая оценка данной части дисциплины проставляется по 100-бальной системе:
- неудовлетворительно – менее 51 балла;
- удовлетворительно – от 51 до 69 баллов;
- хорошо – от 70 до 85 баллов;
- отлично – свыше 85 баллов;
и формируется:
- аттестационными баллами семестра (20)
- экзаменационным баллом (80)
Аттестационный балл семестра складывается из баллов текущей «аттестации» в середине семестра (10) и баллами второй половины семестра «работа в году» (10), каждый из которых учитывает успешность работы студента (выполнение 21-ого домашнего задания, 4-х домашних контрольных работ, защиты курсовой, выступления у доски).
Перечень контрольных вопросов к экзамену
- Основные типы случайных процессов.
- Геометрическое броуновское движение.
- Выборочный метод. Генеральная и выборочная совокупности. Повторные и бесповторные выборки.
- Эмпирические характеристики признака: среднее, дисперсия, СКО, асимметрия, эксцесс, функция распределения. Эмпирическая ковариация двух признаков.
- Вариационный ряд, размах и эмпирическая медиана.
- Генеральные и выборочные характеристики признака. Математическое ожидание и дисперсия выборочного среднего.
- Ковариация выборочных средних двух признаков.
- Математическое ожидание и дисперсия выборочной доли.
- Среднее арифметическое и дисперсия совокупности, разбитой на группы.
- Среднее арифметическое и дисперсия интервального распределения. Связь с характеристиками исходной совокупности. Поправка Шеппарда.
- Разложение в ряд по центральным моментам среднего арифметического функции от эмпирических значений.
- Распределение порядковых статистик.
- Точечная статистическая оценка. Несмещенность, эффективность, состоятельность.
- Состоятельность и сходимость по вероятности.
- Несмещенная оценка начального момента произвольного порядка.
- Выборочное среднее как эффективная оценка математического ожидания.
- Достаточные условия состоятельности статистической оценки.
- Состоятельные оценки начальных моментов.
- Несмещенная оценка
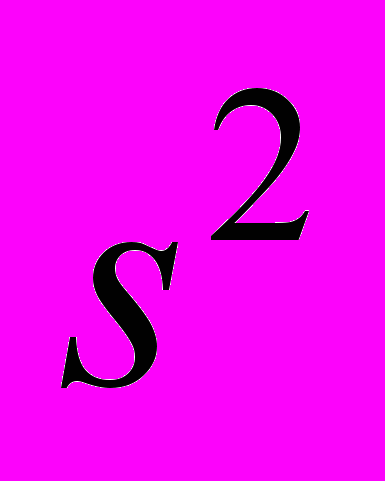 генеральной дисперсии и ее состоятельность.
генеральной дисперсии и ее состоятельность.
- Оценки параметров распределения методом моментов и их состоятельность.
- Метод максимального правдоподобия.
- Многомерная центральная предельная теорема.
- Неравенство Рао – Крамера и информация Фишера.
- Выборочное среднее как эффективная оценка математического ожидания нормального распределения в классе всех несмещенных оценок.
- Распределения
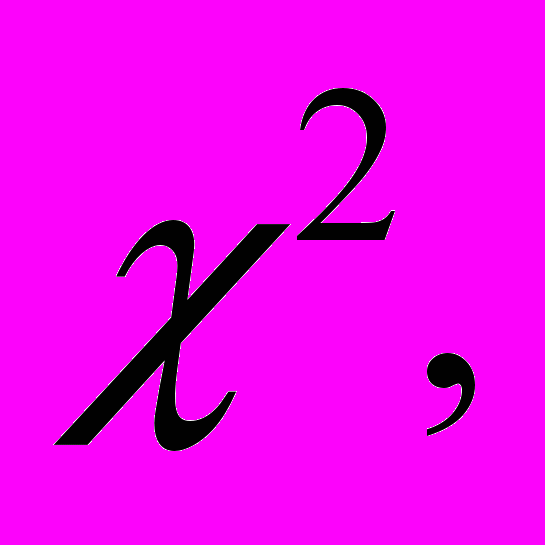 Стьюдента и Фишера. Определения и простейшие свойства.
Стьюдента и Фишера. Определения и простейшие свойства.
- Медиана и другие квантили непрерывных распределений.
- Интервальные оценки параметров распределения, доверительная вероятность и точность оценки. Общая схема построения интервальных оценок.
- Доверительный интервал для математического ожидания при известной дисперсии.
- Доверительные интервалы для математического ожидания и вероятности события в случае выборки большого объема.
- Доверительный интервал для математического ожидания при неизвестной дисперсии.
- Доверительный интервал (симметричный по вероятности) для дисперсии при известном математическом ожидании.
- Доверительный интервал (симметричный по вероятности) для дисперсии при неизвестном математическом ожидании.
- Интервал предсказания.
- Проверка статистических гипотез. Критическая область. Мощность критерия.
- Отношение правдоподобия и лемма Неймана-Пирсона.
- Пример построения наиболее мощного критерия.
- Проверка гипотез об определенных значениях параметров нормальных распределений.
- Проверка гипотезы о равенстве средних при известной дисперсии.
- Проверка гипотезы о равенстве средних при неизвестной дисперсии.
- P-значение критерия. Определение и способ его вычисления.
- Проверка гипотезы о равенстве дисперсий.
- Проверка гипотезы о соответствии эмпирических данных теоретическому закону с данной функцией распределения по критерию Пирсона.
- Проверка гипотезы об однородности нескольких выборок по критериям Пирсона и Колмогорова – Смирнова.
- Сравнение нескольких средних методом дисперсионного анализа.
- Решение СЛУ методом наименьших квадратов.
- Общая дисперсия как сумма факторной и остаточной дисперсии.
- Коэффициент детерминации R2 и его связь с коэффициентом корреляции.
- Линейна модель парной регрессии и теорема Гаусса – Маркова.
- Несмещенность МНК-оценок коэффициентов парной регрессии.
9. Учебно-методическое
и информационное обеспечение дисциплины
Рекомендуемая литература
а) основная:
- Браилов А.В. Лекции по математической статистике. — М.: Финансовая академия, 2007. — 172 с.
- Браилов А.В. Математическая статистика. Контрольные работы (для ММЭк) — М.: Финансовая академия, 2004. — 39 с.
- Сборник задач по курсу математики / Под ред. А.С. Солодовникова, А.В. Браилова. — М.: Финансовая академия, 2001. — 508 с.
- Семаков С.Л., Солодовников А.С. Лекции по курсу «Введение в теорию случайных процессов». — М.: Финансовая академия, 2001. — 75 с.
б) дополнительная:
- Беляев Ю.К., Носко В.П. Основные понятия и задачи математической статистики. — М.: Изд-во МГУ, ЧеРо,1998. — 192 с.
- Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. — М.: Наука, 1983. — 416 с.
- Горяинов В.Б., Павлов И.В., Цветкова Г.М., Тескин И.О. Математическая статистика. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. — 424 с.
- Дж. Халл. Опционы, фьючерсы и другие производные финансовые инструменты, 6-е издание. — M.: ООО "И.Д. Вильямс, 2007. — 1056 с.
- Кобзарь А.И. Прикладная математическая статистика. — М.: ФИЗМАТЛИТ, 2006. — 816 с.
- Колемаев В.А., Калинина В.Н. Теория вероятностей и математическая статистика. — М.: ИНФРА-М, 1999. — 302 с.
- Крамер Г. Математические методы статистики. — Москва–Ижевск: НИЦ «Регулярная и хаотическая динамика», 2003. — 648 с.
- Кремер Н.Ш. Теория вероятностей и математическая статистика. — М.: ЮНИТИ-ДАНА, 2000. — 543 с.
- Лагутин М.Б. Наглядная математическая статистика. — М.: БИНОМ. Лаборатория знаний, 2007. — 472 с.
- Люу Ю.-Д. Методы и алгоритмы финансовой математики. — М.: БИНОМ. Лаборатория знаний, 2007. — 751 с.
- Пугачев В.С. Теория вероятностей и математическая статистика. — М.: ФИЗМАТЛИТ, 2002. — 496 с.
- Соколов Г.А., Гладких И.М. Математическая статистика. — М.: Изд-во «Экзамен», 2004. — 432 с.
- Фельмер Г., Шид А. Введение в стохастические финансы. Дискретное время. . — M.: МЦНМО, 2008. — 496 с.
- Ширяев А.Н. Основы стохастической финансовой математики. — М.: Фазис, 1998. Т.1,Т.2. — 1017 с.
10. Приложение Учебно-методическая карта дисциплины
"Теория вероятностей и математическая статистика 2"
| Наименование раздела | № | Содержание лекций | Содержание практических/семинарских занятий | Самостоятельная работа | Вид контроля |
| Вероятности событий: 8 ч. лекций, 10 ч. семинаров, 15 ч. самостоятельной работы. | 1 | Операции над случайными событиями, связанными с опытом. Геометрические вероятности. Статистическое «определение» вероятности и аксиоматика А.Н. Колмогорова. Вероятностное пространство как модель случайного эксперимента. | Практическое занятие по теме Комбинаторика [2] § 1.1. | Решение задач из [2] § 1.1. Указания к самостоятельной работе [3] | Контроль наличия и выборочная проверка домашнего задания. |
| 2 | Условные вероятности. Независимые события и правило умножения вероятностей. Формула полной вероятности. Формула Байеса вероятностей гипотез. | Практическое занятие по теме лекции №1 [2] § 1.2. | Решение задач из [2] § 1.2. Указания к самостоятельной работе [3] | Контроль наличия и выборочная проверка домашнего задания. | |
| 3 | Независимые испытания. Схема Бернулли. Вероятность заданного числа успехов и наиболее вероятное число успехов в схеме Бернулли. | Практическое занятие по теме лекции №2 [2] § 1.3-1.4. | Решение задач из [2] § 1.3-1.4. Указания к самостоятельной работе [3] | Контроль наличия и выборочная проверка домашнего задания. | |
| 4 | Локальная и интегральная приближенные формулы Лапласа. Вероятность отклонения относительной частоты от вероятности. Приближенные формулы Пуассона. | Практическое занятие по теме лекции №2 [2] § 1.5. | Решение задач из [2] § 1.5. Указания к самостоятельной работе [3] | Контроль наличия и выборочная проверка домашнего задания. | |
| Случайные величины: 12 ч. лекций, 14 ч. семинаров, 20 ч. самостоятельной работы. | 5 | Дискретная случайная величина и ее закон распределения. Примеры дискретных законов распределения: биномиальный, геометрический, пуассоновский. | Практическое занятие по теме лекции №3-4. [2] § 1.6. | Решение задач из [2] § 1.6. Контрольная работа №1. Указания к самостоятельной работе [3] | Самотестирование. [9] Контроль наличия и выборочная проверка домашнего задания. Зачет по контрольной работе №1 |
| 6 | Математическое ожидание и дисперсия дискретной случайной величины. Свойства математического ожидания и дисперсии произвольной случайной величины. Неравенство Йенсена. Стандартное и среднее линейное отклонения. | Практическое занятие по теме лекции №5. [2] § 2.1-2.2. | Решение задач из [2] § 2.1 и § 2.2. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| 7 | Ковариация и коэффициент корреляции. Производящая функция целочисленной случайной величины и числовые характеристики типичных дискретных законов. | Практическое занятие по теме лекции №6. Математическое ожидание дискретной случайной величины. [2] § 2.3. | Решение задач из [2] § 2.3. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| 8 | Абсолютно непрерывные случайные величины. Плотность вероятности и ее свойства. Математическое ожидание и дисперсия абсолютно непрерывной случайной величины. Равномерное распределение на отрезке и показательное распределение на полупрямой. Медиана и квантили непрерывного распределения. | Практическое занятие по теме лекции №6. Дисперсия дискретной случайной величины. [2] § 2.4. | Решение задач из [2] § 2.4. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| 9 | Центральные и начальные моменты вероятностного распределения. Асимметрия и эксцесс. Производящая функция моментов и ее свойства. | Практическое занятие по теме Числовые характеристики основных дискретных законов. [2] § 2.7. | Решение задач из [2] § 2.7. Указания к самостоятельной работе [4] | Контроль наличия и выборочная проверка домашнего задания. | |
| 10 | Нормальное распределение на прямой. Свойства нормальных случайных величин. Логарифмически нормальное распределение. | Практическое занятие по теме лекции №7. Ковариация и коэффициент корреляции. [2] § 2.5. | Решение задач из [2] § 2.5. Контрольная работа №2. Указания к самостоятельной работе [4] | Самотестирование. [9] Контроль наличия и выборочная проверка домашнего задания. Зачет по контрольной работе №2 | |
| Случайные векторы: 8 ч. лекций, 8 ч. семинаров, 12 ч. самостоятельной работы. | 11 | Зависимые и независимые случайные векторы. Функция распределения случайного вектора и ее свойства. Одинаково распределенные случайные векторы. Дискретные случайные векторы. | Практическое занятие по теме лекции №8. [2] § 2.8. | Решение задач из [2] § 2.8. Указания к самостоятельной работе [5] | Контроль наличия и выборочная проверка домашнего задания. |
| 12 | Абсолютно непрерывные случайные векторы. Связь функции плотности распределения случайного вектора с функциями плотности его компонент. Равномерное распределение в ограниченной области. | Практическое занятие по темам лекций №9 и №10 [2] § 2.6, § 2.9. | Решение задач из [2] § 2.6, § 2.9. Контрольная работа №3. Указания к самостоятельной работе [5] | Самотестирование. [9] Контроль наличия и выборочная проверка домашнего задания. Зачет по контрольной работе №3 | |
| 13 | Условные распределения и условные плотности. Условное математическое ожидание и его свойства. Формула полного математического ожидания. Условная дисперсия. Формула полной дисперсии. | Практическое занятие по теме лекции №11. [2] § 3.1 | Решение задач из [2] § 3.1. Указания к самостоятельной работе [6] | Контроль наличия и выборочная проверка домашнего задания. | |
| 14 | Многомерное нормальное распределение. Приведение к каноническому виду. Нормальные случайные векторы и их свойства. | Практическое занятие по теме лекции №12. [2] § 3.2 | Решение задач из [2] § 3.2. Указания к самостоятельной работе [6] | Контроль наличия и выборочная проверка домашнего задания. | |
| Предельные теоремы теории вероятностей: 6 ч. лекций, 2 ч. семинаров, 2 ч. самостоятельной работы. | 15 | Неравенство Чебышева. Закон больших чисел. Теорема Чебышева. Теорема Бернулли. | Практическое занятие по теме лекции №13. Условные распределения [2] § 3.3. | Решение задач из [2] § 3.3. Указания к самостоятельной работе [6] | Контроль наличия и выборочная проверка домашнего задания. |
| 16 | Характеристические функции и их свойства. Центральная предельная теорема для одинаково распределенных слагаемых. | Практическое занятие по теме лекции №14. Двумерное нормальное распределение [2] § 3.3. | Решение задач из [2] § 3.3. Указания к самостоятельной работе [6] Теоретический разбор темы лекции №15-16 [1] | Контроль наличия и выборочная проверка домашнего задания. | |
| Цепи Маркова: 6 ч. лекций, 2 ч. семинаров, 2 ч. самостоятельной работы. | 17 | Определение и способы задания цепей Маркова. Вероятности и матрица переходов. Многошаговые вероятности переходов и теорема о матрице многошаговых переходов. Предельные вероятности. Теорема Маркова о предельных вероятностях. | Практическое занятие по теме Решение экзаменационных задач. [7] | Теоретический разбор темы лекции №17 [1] Решение задач из [7] Контрольная работа №4. Указания к самостоятельной работе [6] | Самотестирование. [9] Контроль наличия и выборочная проверка домашнего задания. Зачет по контрольной работе №4 |
