Экзамен проводится в письменной форме. Время на испытание 4 часа
| Вид материала | Документы |
СодержаниеТеоретические вопросы |
- Программа для подготовки к экзамену по истории вступительное испытание по курсу «История, 22.62kb.
- Экзамен осуществляется письменно на русском языке. Время на испытание 4 часа. На экзамен, 265.24kb.
- Экзаменационные материалы по английскому языку 8 класс 2010 переводной экзамен по английскому, 105.15kb.
- Рекомендации абитуриентам Экзамен по физике проводится в письменной форме. На выполнение, 87.67kb.
- Программа вступительного экзамена в магистратуру по спец предмету специальности 6М071200, 156.59kb.
- Программа вступительного экзамена в магистратуру по спец предмету специальности 6М071700, 116.52kb.
- Программа вступительного экзамена в докторантуру по спец предмету специальности 6D070900, 109.99kb.
- Программа по литературе Экзамен по литературе проводится в форме сочинения, 28.4kb.
- Программа итогового междисциплинарного экзамена по специальности " экономика и менеджмент, 203.14kb.
- Программа итогового междисциплинарного экзамена "Управление проектами" (для слушателей, 63.98kb.
Дисциплина «Математический анализ»
Общие положения
Перечень вопросов для подготовки абитуриентов к вступительному экзамену по дисциплине «Математический анализ» в магистратуру высшего профессионального образования по направлению 231300 «Прикладная математика» предназначен для оказания помощи при подготовке к сдаче экзамена.
В ходе подготовки к экзамену следует руководствоваться Программой экзамена.
Предложенные вопросы позволяют выяснить базовые знания по дисциплине «Математический анализ» в соответствии с требованиями Государственного образовательного стандарта по направлению подготовки «Прикладная математика» (квалификация магистр).
Прием вступительного экзамена осуществляет экзаменационная комиссия из научно-педагогического состава Академии. На прием экзамена выделяется один день.
Экзамен проводится в письменной форме.
Время на испытание – 4 часа.
На экзамен выносится 2 (два) теоретических вопроса и 1 (одна) задача.
Оценка за ответы по каждому вопросу, определяется по следующим критериям:
«Отлично» – при наличии у абитуриента фундаментальных знаний по заданному вопросу, аргументированном и логически стройном построении ответа по существу вопроса. В ответе должны быть представлены определения, соответствующие рассматриваемому вопросу. Правильно решённая задача.
«Хорошо» – при наличии твердых и достаточно полных знаний по заданным вопросам, логически стройном построении ответа, понимании сущности вопроса, но при этом допущенных неточностях, ошибки в определениях, незначительные ошибки в детализации теоретических основ рассматриваемого вопроса. Правильно решенная задача.
«Удовлетворительно» – при наличии твердых знаний по сущности заданного вопроса, изложении ответа с ошибками либо существенные ошибки в представлении их содержания. Правильно решенная задача.
«Неудовлетворительно» – выставляется оценка за вопрос в случаях:
слабого знания материала,
непонимания сущности излагаемого вопроса,
наличия грубых ошибок в ответе, неточности ответов, требующих дополнительных вопросов,
представление ответа, не соответствующего рассматриваемому вопросу и неправильно или нерешенная задача.
По результатам экзамена оценка:
«отлично» выставляется, если за ответы на вопросы билета получены отличные оценки при правильно решенной задачи и не более одной хорошей на дополнительно заданные вопросы;
«хорошо» – за ответы на вопросы билета получены отличные и хорошие оценки при правильно решенной задачи и не более одной удовлетворительной на дополнительные вопросы причем;
«удовлетворительно» – за ответы на вопросы билета получены положительные оценки и не более одной неудовлетворительной при правильно решенной задачи и не более одной не удовлетворительной на дополнительные вопросы;
«неудовлетворительно» – не выполнены условия на оценку «удовлетворительно».
Теоретические вопросы
к вступительному экзамену по дисциплине
«Математический анализ»
в магистратуру Академии Гражданской защиты МЧС России
по направлению 231300 «Прикладная математика»
(квалификация магистр)
1. Функция. Четные и нечетные, ограниченные и неограниченные, монотонные, периодические функции. Обратная функция. Сложная функция. Элементарные функции и их графики.
2. Числовые последовательности. Предел последовательности. Вычисление пределов последовательностей.
3. Предел функции. Свойства пределов функций.
4. Вычисление пределов функций. Неопределенности при вычислении пределов (
; 
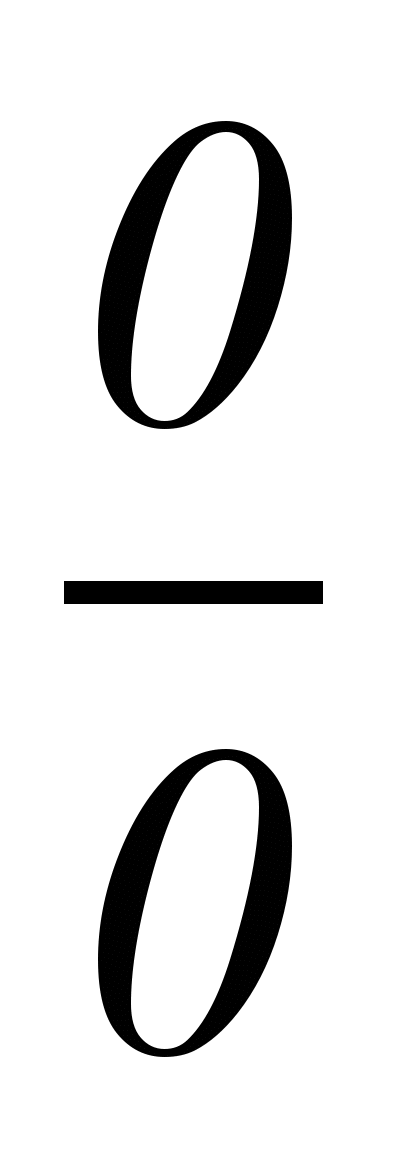; 0 ; – ; 1 ; 0 ; ; 0 0 ; 0 ) и методы их устранения. Правило Лопиталя.5. Первый замечательный предел.
6. Второй замечательный предел.
7. Бесконечно малые и их свойства. Эквивалентные функции. Сравнение бесконечно малых. Бесконечно большие, их связь с бесконечно малыми.
8. Непрерывность функции в точке. Точки разрыва и их классификация.
9. Равномерная непрерывность функции. Теорема Кантора.
10. Производная функции в точке. Геометрический смысл производной. Механический смысл производной.
11. Правила дифференцирования суммы, произведения и частного функций. Производная обратной функции. Производная сложной функции.
12. Дифференциал функции.
13. Логарифмическая производная. Производная функции, заданной неявно. Производная функции, заданной параметрически.
14. Формула Тейлора. Разложение элементарных функций по формуле Тейлора.
15. Экстремумы функции. Необходимые и достаточное условия существования экстремума функции.
16. Исследование функций и построение графиков.
17. Первообразная функции. Неопределенный интеграл. Свойства неопределенного интеграла.
18. Методы интегрирования неопределенного интеграла: замена переменной; интегрирование по частям.
19. Интегрирование рациональных функций.
20. Интегрирование тригонометрических функций.
21. Интегрирование иррациональных функций.
22. Определенный интеграл. Свойства определенного интеграла.
23. Формула Ньютона-Лейбница.
24. Геометрические приложения определенного интеграла: вычисление длин дуг кривых в прямоугольных и полярных координатах, объема тел вращения, площади поверхности вращения.
25. Несобственные интегралы и их сходимость.
26. Вычисление несобственных интегралов 1-го и 2-го рода.
27. Функции нескольких переменных. Дифференцируемость функций многих переменных. Частные производные.
28. Формула Тейлора для функций нескольких переменных.
29. Экстремумы функций нескольких переменных. Необходимое и достаточные условия локального экстремума дифференцируемой функции нескольких переменных.
30. Условный экстремум функций нескольких переменных.
31. Числовые ряды. Сходящиеся и расходящиеся числовые ряды. Свойства сходящихся числовых рядов.
32. Необходимое условие сходимости числовых рядов.
33. Признаки сравнения для числовых рядов с положительными членами.
34. Признак Даламбера сходимости числовых рядов.
35. Радикальный признак Коши сходимости числовых рядов.
36. Интегральный признак Коши сходимости числовых рядов.
37. Знакочередующиеся ряды. Абсолютная и условная сходимость числовых рядов. Признак Лейбница.
38. Степенные ряды. Теорема Абеля.
39. Тригонометрические ряды Фурье. Дифференцирование и интегрирование ряда Фурье.
40. Двойной интеграл. Свойства двойного интеграла.
41. Вычисление двойного интеграла. Сведение двойного интеграла к повторному по элементарной области. Изменение порядка интегрирования в двойном интеграле.
42. Замена переменных в двойном интеграле. Вычисление двойного интеграла путем перехода от декартовых координат к полярным.
43. Тройной интеграл. Замена переменных в тройном интеграле.
44. Вычисление тройного интеграла путем перехода от декартовых координат к цилиндрическим и сферическим.
45. Преобразование Фурье. Обратное преобразование Фурье.
46. Криволинейные интегралы первого рода и их свойства. Геометрический и механический смысл криволинейных интегралов первого рода.
47. Криволинейные интегралы второго рода и их свойства. Механический смысл криволинейных интегралов второго рода.
48. Формула Грина. Ориентация границы плоской области. Применение формулы Грина для вычисления площадей.
49. Поверхностные интегралы первого рода.
50. Поверхностные интегралы второго рода. Поток вектора через ориентируемую поверхность.
51. Скалярные и векторные поля. Потенциал векторного поля. Оператор Гамильтона.
52. Дивергенция и вихрь векторного поля.
53. Теорема Остроградского-Гаусса.
54. Формула Стокса. Потенциальные векторные поля. Оператор Лапласа.
Литература
- Г.М. Фихтенгольц, Курс дифференциального и интегрального исчисления, том 1. Физматгиз,
- Г.М. Фихтенгольц, Курс дифференциального и интегрального исчисления, том 2. М.: Физматгиз,
- Г.М. Фихтенгольц, Курс дифференциального и интегрального исчисления, том 3. М.: Физматгиз,
- Демидович Б.П. Сборник задач и упражнений по математическому анализу.
- Запорожец Г.И. «Руководство к решению задач по математическому анализу»,