Тема : Оптимизация потокового процесса встроенными средствами вычислительного пакета Mathcad (реализация сбалансированной транспортной задачи с использованием компьютерных технологий)
| Вид материала | Документы |
СодержаниеПример постановки задачи Пример решения транспортной задами средствами Mathcad Постановка задачи Ввод первичных данных Таб. 2. Цена транспортировки |
- Контроль функционального состояния человека с использованием компьютерных технологий., 166.24kb.
- Реферат Транспортные задачи в Excel, 285.79kb.
- Название диссертации, 449.82kb.
- Оптимизация спортивной подготовленности квалифицированных каратистов средствами восточных, 484.58kb.
- Тематический план введение, 469.57kb.
- Стратегическое адаптивное планирование 26 Реализация маи в Excel 32 Реализация маи, 808.16kb.
- Курсовой проект по дисциплине «Теория информационных процессов и систем» тема: Задачи, 258.87kb.
- Использование Mathcad и Excel при изучении школьного курса физики, 67.71kb.
- Моделирование и оптимизация систем с распределенными параметрами, 14.61kb.
- Лекция №1 Тема: Создание тестов с использованием Microsoft Excel, 22.51kb.
Задание по курсу «Datortehnoloģijas transportā»
Тема : Оптимизация потокового процесса встроенными средствами вычислительного пакета Mathcad (реализация сбалансированной транспортной задачи с использованием компьютерных технологий)
Задание: найти оптимальный с точки зрения экономии транспортных расходов план перевозки однородного груза потребителям Задачу решить, используя метод линейного программирования. Вариант задания получить у преподавателя
Краткие сведения из теории
При организации потоковых процессов часто возникают задачи, которые требуют принятия обоснованного управленческого решения для уменьшения расходов по доставке ресурса от поставщика к потребителю. Простейший пример такой задачи: менеджер фирмы-перевозчика разрабатывает оптимальный план доставки однородного продукта (нефти, бензина, электроэнергии, молока и пр.), который в определенных количествах предлагается различными производителями различным потребителям (базам, заправкам, грузовым станциям, магазинам и пр.) так, чтобы минимизировать суммарные расходы на транспортировку. Другой пример: фирма-посредник организует снабжение территориально распределенных заказчиков некоторым оборудованием; поставщики этого оборудования расположены в различных городах и связаны с заказчиками различными путями сообщения и различными тарифами; требуется разместить заказы на оборудование таким образом, чтобы были удовлетворены запросы заказчиков, а при этом затраты на перевозки фирмы-посредника были бы минимальными. Задачи такого типа носят название транспортных задач.
Несмотря на различные области приложения задачи линейного программирования имеют единую постановку. Формально общая задача линейного программирования понимается как задача поиска экстремума скалярной линейной целевой функции F(X) - вектора управляемых (искомых) переменных X=(x1,..., xn) и сводится к определению значений переменных X=(x1,x2, , xn), приводящих к экстремуму линейную целевую функцию
F(X) = C1*X1 + ... + Cj*Xj + ... + Cn*Xn -> extr;
при линейных функциональных ограничениях:
Ai1*X1 + ... + Aij*Xj + ... + Ain*Xn (Ri) = Bi, i = 1,.2., , m
и прямых ограничениях по управляемым параметрам:
Xj 0, j = 1,...,n,
где Ri - любые из отношений < ; > ; = или их комбинации.
Классическая транспортная задача в общем виде формулируются следующим образом:
имеется несколько территориально удаленных пунктов поставки однородного продукта; известно, какой объем продукта нужно поставить потребителям, также находящимся в территориально удаленных пунктах; требуется определить, от каких поставщиков и в каких объемах выгоднее доставлять продукцию потребителям; поставки должны осуществляться таким образом, чтобы совокупные издержки на транспортировку продукта были наименьшими. . Предполагается, что известны :
- ресурс от любого производителя может быть доставлен к любому потребителю;
- размеры отправлений и размеры приема по каждому из пунктов, выражаемые в тоннах, киловаттах или других единицах
- стоимость доставки продукта от каждого пункта производства в каждый пункт приема .
Требуется найти оптимальный план доставки продукта (т.е. план, который обеспечит минимальные расходы на с транспортировку). При заданной стоимости доставки продукта между каждой парой пунктов поставки и потребления оптимальный план должен удовлетворять следующим условиям :
- минимизировать транспортные расходы,
- обеспечить вывоз всего продукта от каждого пункта производства ,
- полностью покрыть установленные размеры потребления подукта в каждом пункте приема.
Исходные данные транспортной задачи удобно задавать таблицей вида:
| A  j jBi | A1 | A2 | A3 |
| B1 | с1,1 | с1,2 | с1,3 |
| B2 | с2,1 | с2,2 | с2,3 |
где
Bi – возможности производителей или поставщиков ( установленные объемы продукта, которые требуется вывезти c пунктов поставки )
Aj – возможности потребителей ( установленные размеры потребления в пунктах приема продукта Aj
Сij – стоимость доставки единицы груза доставки продукта от i-того пункта производства в j-тый пункт приема
Пример постановки задачи:
Дано: n=2 - число пунктов отправления однородного продукта (дизельного топливо, бензина, каменного угля, электрической энергии и др)
m=3 -число пунктов приема ресурса (дизельного топлива, бензина каменного угля, потребителей электроэнергии и др);
Известны возможности поставщиков (Bi). – объемы отправляемого продукта (число цистерн , число бензовозов, число вагонов и др
Известны возможности потребителя (Aj); (например мощности станций по по приему и обработке вагонов на пунктах приема (Aj);
Заданы потребности (например, число вагонов, которое могут обработать принимающие станции )
Задача сбалансирована, т. е. общий объем произведенной продукции в точности покрывает суммарные потребности пунктов приема. В нашем случае
B1 + B2 = A1 + A2 + A3)
Известна стоимость доставки единицы груза Ci,j из каждого пункта отправления в каждый пункт приема в виде таблицы
| Пункты отправления | Пункты приема | ||
| | A1 | A2 | A3 |
| B1 | С 1,1 | С1,2 | С1,3 |
| B2 | С 21 | С2,2 | С2,3 |
Требуется получить план траспортировки с целью минимизации суммарных транспортных расходов. Найти значение минимальных расходов
Обозначим через xij искомый объем перевозки -
В случае сбалансированного производства и потребления, когда выполняется условие
B1+ B2 = A1 + A2 + A3 ,
оптимальный план доставки соответствует минимуму линейной целевой функции:

при n=2 линейных ограничениях по отправлениям
x11+x12+x13 = B1
x21+x22+x23 = B2
и m=3 линейных ограничениях пo потреблению
x11+x21+x31 =A1
x12+x22+x32 = A2
x13+x23+x33 = A3
и при очевидном условии неотрицательности управляемых переменных:
x i,j 0, i = 1,2, и j = 1,.2,3
задача может быть решенв с помощью инструментов, предлагаемых любой современной вычмслительной системой, а также в программа Excel. Ниже приведен пример решения транспортной задачи средствам вычислительной системы Mathcad и средствами Excel
Пример решения транспортной задами средствами Mathcad
Задача: принять решение по проблеме оптимальной организации доставки электроэнергии потребителям с точки зрения экономии транспортных расходов.
Имеется n электростанций и m потребителей электроэнергии. Пусть Xi,j – искомый объем передачи энергии от i-той электростанции (i=1,..., N) к j-тому потребителю (j =1,..., M). Управляемые (искомые) параметры Xi,j характеризуют объем передачи энергии между каждой электростанцией i=1,..., N и каждым потребителем j=1,..., M
Для каждой электростанции i=1,..., n задан объем выработанной энергии Bi, для каждого потребителя j= 1,..., m задан объем потребления Aj ;
Известна также стоимость потерь энергии при передаче каждого киловатта энергии Ci,j от i-той электростанции в j.-ый пункт потребления.
В случае сбалансированного производства и потребления, когда выполняется условие
B1 + ... + BN = A1 + ... + AM ,
оптимальный план доставки соответствует минимизации линейной целевой функции:

при n линейных ограничениях по отправлениям:
Xi,1 + ... + Xi,j + ... + Xi,n = Ai, где i = 1,..., N
и m линейных ограничениях пo потреблению:
X1,j + ... + Xi,j + ... + Xm,j = Bj, j = 1,..., M,
а также при очевидном условии неотрицательности управляемых переменных:
Xi,j 0, i = 1,...,N и j = 1,..., M
Известна также стоимость потерь энергии Ci,j при передаче ее от каждой станции в каждый пункт приема в виде следующей таблицы:
| Электростанции | Потребители | ||
| | A1=145 | A2=210 | A3=160 |
| B1=237 | с1,1=11,5 | с1,2=7 | с1,3=12 |
| B2=278 | с2,1=6,2 | с2,2=10 | с2,3=9 |
Найти оптимальный план доставки энергии потребителям
Л
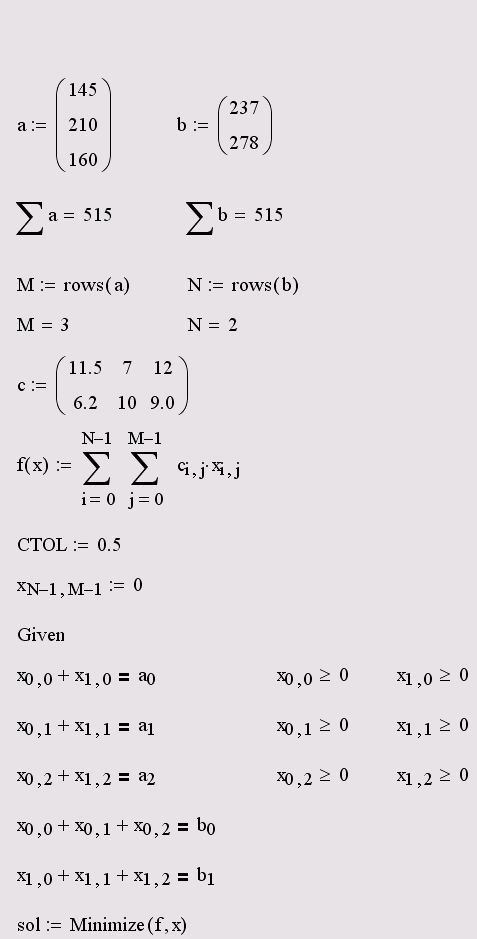
истинг решения задачи
 ,
, 
Пример реализация транспортной задачи в Excel (программа Solver)
Solver это отдельная программа, которую необходимо предварительно загрузить, выбрав команду Tools Add Insв спискеAdd-Ins Available выбрать Solver Add-InsOK Excel добавит Solver в меню Tools. Чтобы принимать оптимальное решение с использованием Solver, достаточно иметь математическую модель, на основе которой это решение принимается. Алгоритм определения решения в программе Solver таков: в окне программы в целевую ячейку заносится формула, определяющая желаемый результат, искомые переменные заносятся в изменяемые ячейки, сообщается программе требуемый конечный результат и указываются переменные, которыми нужно управлять. Выполняя последовательность итераций, Solver находит оптимальное решение. При этом значения параметров в изменяемых ячейках варьируются так, чтобы значение в целевой ячейке стало равно заданному (желаемому) значению.
Постановка задачи: составить оптимальный план перевозок для фирмы-перевозчика, получившей долгосрочный заказ от фирмы-поставщика на транспортировку бензина из трех портов (m=3) в пять (n=5) заправочных станций.. При этом должен быть обеспечен минимум общих затрат фирмы-перевозчика на транспортировку и удовлетворены поставленные ограничения:
- с каждого порта должен быть вывезен весь бензин
- нельзя превысить возможности емкостей каждой заправочной станци
Бензин может быть перевезен из любого порта на любую заправочную станцию, но тарифы, а следовательно и стоимость перевозок, различны. Определить количество бензина, перевозимого из каждого порта на каждую заправку при обеспечении минимума общих затрат на транспортировку и удовлетворения поставленных ограничений (не превышать предложения каждого порта и максимально используя возможности каждой заправочной станции.
Накладывая условие линейности, будем считать, что при перевозке Xij единиц продукта из пункта Si в пунктQj транспортные расходы будут равны Сij * Xij.
Чтобы найти решение поставленной задачи с помощью программы Solver, необходимо выполнить следующие процедуры:
Ввести данные так, как это показано на вкладке, размещенной на столе преподавателя:
После ввода данных необходимо выполнить следующие процедуры:
a. задание цели: выбрать команду Tools-Solver,откроется окно Solver Parameters;
- в поле Set Target ввести ссылку на целевую ячейку-ту, в которой находится формула для оптимизации;
- в разделе Equal To включить соответствующую кнопку-max, min, value;
b. задание переменных:
- в поле By Changing Cells ввести адреса ячеек, значения которых Solver будет изменяться в процессе поиска решения;
c. задание ограничений на условия:
- в разделе Subject to the Constraints окнаSolver выбрать команду Add-
- в окне Add Constraint в поле Cell Referens ввести адрес ячейки, для которой будет введено ограничение-;
- в ниспадающем списке выбрать подходящий оператор для ограничения;
- в поле Constraint ввести предельное значение ограничения;
- выбрать Add-чтобы ввести новое ограничениу; ввести OK -для возврата в окно Solver Parameter;
- нажать Solve. Откроется окно Solve Result с результатом;
- если решение удовлетворяет- включить Keep solver Solution-OK,если нет -включить Cancel
| | B | C | D | E | F | G | H | |
| Ввод первичных данных | ||||||||
| | Количество товара, перевозимое из каждого порта в каждую заправочную станцию | | | |||||
| Порт | Заправочная станция 1 | Заправочная станция 2 | Заправочная станция 3 | Заправочная станция 4 | Заправочная станция 5 | Общее количество бензина из одного порта на все заправочные станции | Предложение порта | |
| | primarie dati iteracijai | | | |||||
| Порт1 | 1 | 1 | 1 | 1 | 1 | =SUM(B6:F6) | 310 | |
| Порт 2 | 1 | 1 | 1 | 1 | 1 | =SUM(B7:F7) | 260 | |
| Порт 3 | 1 | 1 | 1 | 1 |
| =SUM(B8:F8) | 280 | |
| Общее количество бензина из всех портов на конкретную заправочную станцию не должно превышать возможности станции | =SUM(B6:B8) | =SUM(C6:C8) | =SUM(D6:D8) | =SUM(E6:E8) | =SUM(F6:F8) | | =SUM(H6:H8) | |
| Возможности станций | 140 | 100 | 200 | 160 | 220 | Ограничения | | |
| Таб. 2. Цена транспортировки | ||||||||
| Порт | станция 1 | станция 2 | станция 3 | станция 4 | станция 5 | | | |
| Порт1 | 10 | 8 | 6 | 5 | 4 | | | |
| Порт1 | 6 | 5 | 4 | 3 | 6 | | | |
| Порт1 | 3 | 4 | 5 | 5 | 9 | =B6:F8 | | |
| Транспортные расходы | =B13*B6+B14*B7+B15*B8 | =C13*C6+C14*C7+C15*C8 | =D13*D6+D14*D7+D15*D8 | =E13*E6+E14*E7+E15*E8 | =F13*F6+F14*F7+F15*F8 |
| Целевая функция | |
| |
| =G6:G8<=H6:H8 | | |||||
| Ограничения |
| =B9:F9>=B10:F10 | | |||||
| |
| =B6:F8>=0 | | |||||


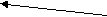 SUM(B16:F16)
SUM(B16:F16) бщее количество бензина, перевозимое из одного порта на все заправочные станции должно быть меньше или равным предложению порта
бщее количество бензина, перевозимое из одного порта на все заправочные станции должно быть меньше или равным предложению порта