Geum.ru

Российской Федерации " мати"

Вид материалаРабочая учебная программа

Содержание


Уравнения математической физики
1. Цели и задачи дисциплины. ее
2. Содержание дисциплины
3. Практические занятия
4. Курсовые работы
Подобный материал:
Министерство образования Российской Федерации



“МАТИ” - РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ им. К. Э. ЦИОЛКОВСКОГО

    "УТВЕРЖДАЮ"




    Проректор по учебной работе




    ___________ В. Ф. Мануйлов




    "____" _____________ 2001 г.






    Кафедра “Высшая математика”


    Рабочая учебная программа по дисциплине

    УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ


    Направление: 5533 “Прикладная механика”

    Факультет: № 5

Выпускающие кафедры: МОПК, ПД, ММК

    Форма обучения: очная

    Часов всего по дисциплине: 238

    Цикл дисциплин: ЕНД

    Распределение времени студента по видам учебных занятий

    (часы аудиторных занятий / самостоятельная работа)



      Семестр

      4

    По уч. плану (АР / СР )

      96/142

    Лекции

      48/48

    Практические занятия

      48/48

    Лабораторные занятия



      Курсовая работа

      0/46

      Форма контроля

      экзамен



    Москва 2001 год



Рабочая учебная программа по дисциплине “Уравнения математической физики” составлена в соответствии с требованиями Государственного образовательного стандарта и учебному плану по направлению 5533 “Прикладная механика”.



Программа составлена: доц. Селиванов Ю. В.

    ст. преп. Выск Н. Д.



Рабочая учебная программа рассмотрена кафедрой “Высшая математика” и одобрена 8 февраля 2001 г.



    Зав. кафедрой “Высшая математика”

    ____________ К. Ю. Осипенко



Рабочая учебная программа по дисциплине “Уравнения математической физики” рассмотрена и признана соответствующей требованиям ГОС и учебному плану по направлению 5533 “Прикладная механика”.




    Декан факультета № 5

    ____________ Л. В. Агамиров


    Программа согласована с НМО

    Учебного управления МАТИ

    ____________ В. М. Морозов


    1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ. ЕЕ

    МЕСТО В УЧЕБНОМ ПРОЦЕССЕ



Предметом изучения дисциплины являются основные понятия и методы теории уравнений математической физики. Целью преподавания дисциплины является обеспечение базовой математической подготовки специалистов в соответствии с требованиями Государственного образовательного стандарта РФ и учебному плану по направлению 5533 “Прикладная механика”. Основные задачи изучения дисциплины состоят, во-первых, в обучении студентов фундаментальным разделам высшей математики, формировании математического мировоззрения, развитии научного, логического мышления, необходимого в дальнейшей работе по специальности; во-вторых, в овладении студентами достаточным количеством математических методов, выработке твердых навыков построения математических моделей и умения провести вычислительный расчет.



    В результате изучения курса студент должен:
  • освоить основные теоретические методы дисциплины, используемые в инженерной практике или служащие для обоснования используемых на практике алгоритмов;
  • приобрести твердые навыки решения задач теории уравнений математической физики с доведением решения до практически приемлемого результата;
  • выработать начальные навыки математического исследования прикладных вопросов;
  • выработать умение самостоятельно разбираться в математическом аппарате, содержащемся в литературе, связанной со специальностью студента;
  • уметь при решении задач выбирать и использовать необходимые вычислительные методы и средства, а также таблицы и справочники.



    Учебные дисциплины, владение которыми необходимо для изучения данной дисциплины: курсы математики и физики средней школы, курсы математики и физики в МАТИ.

    2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

    4 СЕМЕСТР

    Лекции - 48 часов, практические занятия - 48 часов.

    ЛЕКЦИЯ 1. Скалярное произведение функций, ортогональные системы функций, норма функции. Разложение функции по ортогональной системе. Тригонометрическая система функций на отрезке 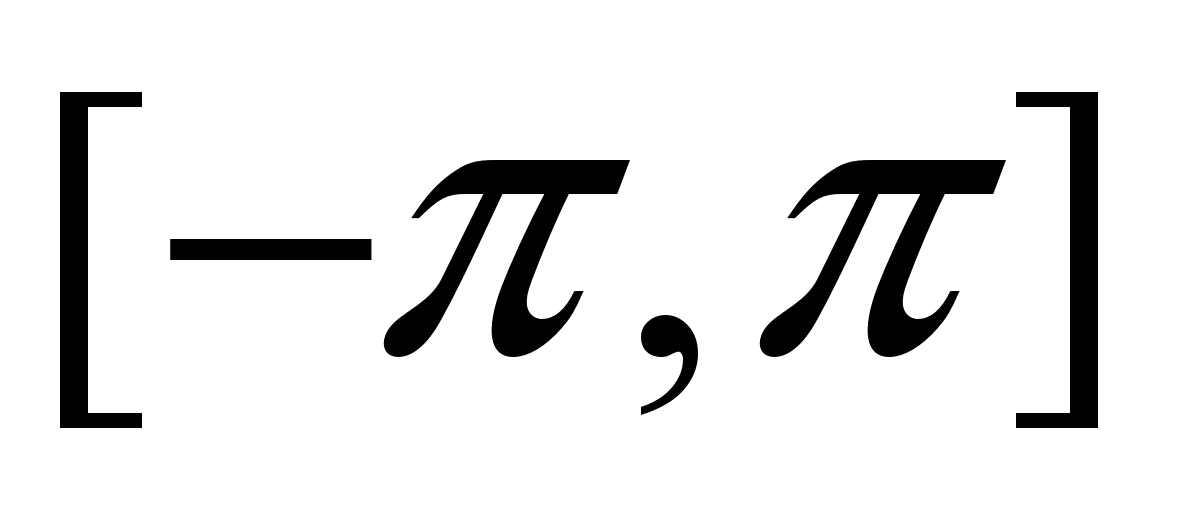, ее ортогональность. Тригонометрический ряд. Коэффициенты Фурье. Ряд Фурье. Теорема Дирихле.

    ЛЕКЦИЯ 2. Ряд Фурье на отрезке 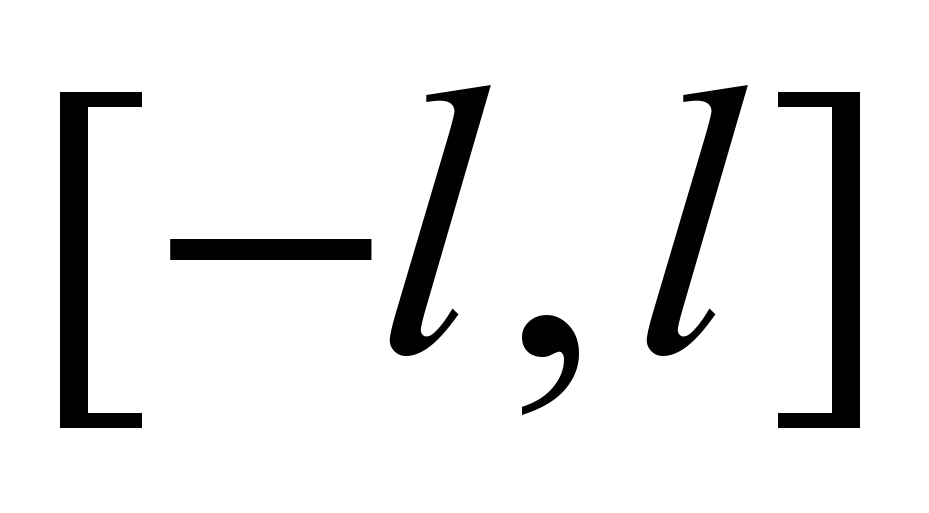. Разложение четных и нечетных функций. Ортогональные системы и ряды Фурье на отрезках 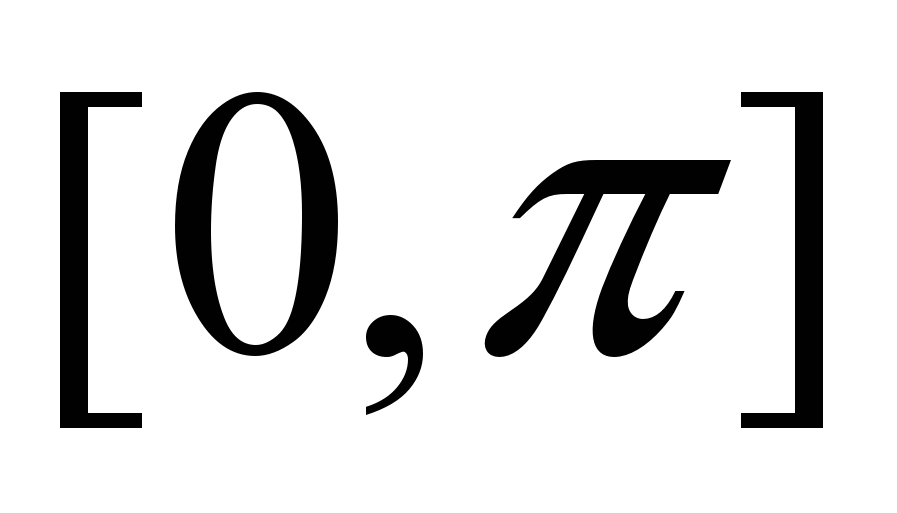и .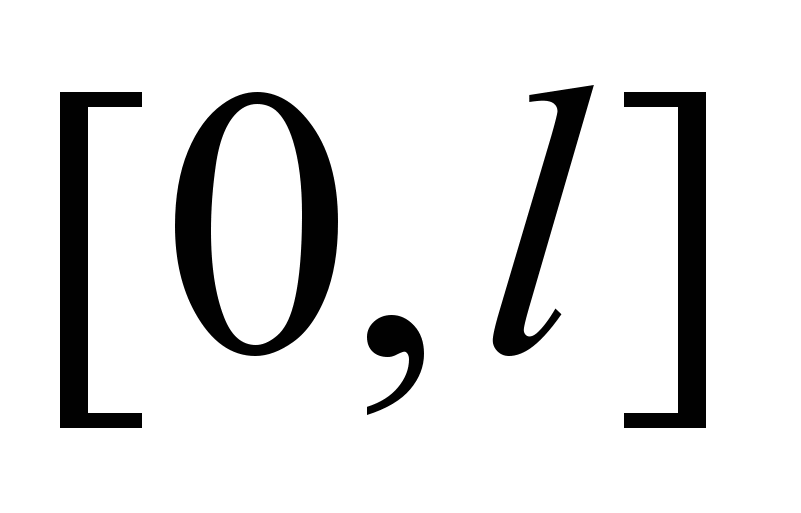

    ЛЕКЦИЯ 3. Комплексная форма ряда Фурье. Понятие об интеграле Фурье.



ЛЕКЦИЯ 4. Дифференциальные уравнениях в частных производных. Общие понятия. Задача Коши для уравнения первого порядка. Интегральные поверхности. Линейные уравнения, их свойства. Линейные однородные уравнения в частных производных первого порядка. Характеристическая система; первый интеграл системы. Общее решение линейного однородного уравнения в частных производных первого порядка.


ЛЕКЦИЯ 5. Квазилинейные уравнения в частных производных первого порядка. Их решение. Геометрическая интерпретация. Задача Коши для квазилинейных уравнений.


ЛЕКЦИЯ 6. Линейные уравнения в частных производных второго порядка, их преобразование и классификация.


ЛЕКЦИЯ 7. Приведение линейного уравнения в частных производных второго порядка к каноническому виду. Уравнение характеристик. Канонические формы линейных уравнений с постоянными коэффициентами.


ЛЕКЦИЯ 8. Уравнения гиперболического типа. Задачи, приводящие к уравнениям гиперболического типа (уравнение поперечных колебаний струны, поперечные колебания мембраны, волновое уравнение в пространстве). Начальные и граничные условия. Краевые задачи.


ЛЕКЦИЯ 9. Неограниченная струна и формула Даламбера. Метод распространяющихся волн. Полуограниченная струна. Метод продолжений.


ЛЕКЦИЯ 10. Ограниченная струна. Метод Фурье для свободных колебаний струны, закрепленной на обоих концах. Гармоники и стоячие волны.


ЛЕКЦИЯ 11. Метод Фурье для вынужденных колебаний струны с закрепленными концами. Общая первая краевая задача для уравнения колебаний струны.


ЛЕКЦИЯ 12. Метод Фурье решения двумерного волнового уравнения для прямоугольной мембраны.


ЛЕКЦИЯ 13. Уравнение Бесселя и отыскание его решений с помощью рядов. Функции Бесселя, их свойства.


ЛЕКЦИЯ 14. Колебания круглой мембраны с закрепленной границей.


ЛЕКЦИЯ 15. Уравнения параболического типа. Задачи, приводящие к уравнениям параболического типа. Постановка задачи о распространении тепла в стержне. Вывод уравнения теплопроводности.


ЛЕКЦИЯ 16. Начальные и граничные условия для уравнения теплопроводности. Виды краевых задач. Трехмерное уравнение теплопроводности. Уравнение диффузии. Метод математического моделирования.


ЛЕКЦИЯ 17. Одномерное однородное уравнение теплопроводности. Метод Фурье.


ЛЕКЦИЯ 18. Решение первой краевой задачи для неоднородного уравнения теплопроводности.


ЛЕКЦИЯ 19. Вторая и третья краевые задачи для однородного уравнения теплопроводности.


ЛЕКЦИЯ 20. Решение уравнения теплопроводности для бесконечного стержня.


ЛЕКЦИЯ 21. Двумерное уравнение теплопроводности. Решение для случаев прямоугольной и круговой области.


ЛЕКЦИЯ 22. Уравнения эллиптического типа. Задачи, приводящие к уравнениям Лапласа и Пуассона. Постановка краевых задач Дирихле и Неймана. Выражение оператора Лапласа в полярных, цилиндрических и сферических координатах. Некоторые частные решения уравнения Лапласа.


ЛЕКЦИЯ 23. Решение задачи Дирихле для уравнения Лапласа для простейших областей: прямоугольника, полуплоскости и круга. Формула Пуассона.


    ЛЕКЦИЯ 24. Приближенные (сеточные) методы решения уравнений в частных производных.




    3. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

    4 СЕМЕСТР

    ЗАНЯТИЯ 1-2. Разложение функций в ряды Фурье.



ЗАНЯТИЕ 3. Интеграл Фурье.


ЗАНЯТИЕ 4. Линейные однородные уравнения в частных производных первого порядка.


ЗАНЯТИЕ 5. Линейные и квазилинейные уравнения в частных производных первого порядка.


ЗАНЯТИЕ 6. Приведение линейных уравнений в частных производных второго порядка к каноническому виду.


ЗАНЯТИЕ 7. Канонические формы линейных уравнений в частных производных второго порядка с постоянными коэффициентами.


ЗАНЯТИЕ 8. Вывод уравнений и постановка задач математической физики. Выдача КР 1.


ЗАНЯТИЕ 9. Решение уравнений колебаний струны методом Даламбера (неограниченная струна).


ЗАНЯТИЕ 10. Решение уравнений колебаний струны методом Даламбера (полуограниченная струна).


    ЗАНЯТИЕ 11. Решение уравнений гиперболического типа методом Фурье (однородное волновое уравнение с однородными граничными условиями).

    ЗАНЯТИЕ 12. Решение уравнений гиперболического типа методом Фурье (первая краевая задача для неоднородного волнового уравнения).


ЗАНЯТИЕ 13. Колебания прямоугольной мембраны.


ЗАНЯТИЕ 14. Функции Бесселя и колебания круглой мембраны.


    ЗАНЯТИЕ 15. Решение уравнений параболического типа методом Фурье (одномерное однородное уравнение теплопроводности).

    ЗАНЯТИЕ 16. Решение уравнений параболического типа методом Фурье (первая краевая задача для неоднородного уравнения теплопроводности).



ЗАНЯТИЕ 17. Решение второй краевой задачи для уравнений гиперболического и параболического типа.


ЗАНЯТИЕ 18. Решение третьей краевой задачи для уравнений гиперболического и параболического типа.


ЗАНЯТИЕ 19. Решение уравнения теплопроводности для бесконечного стержня.


ЗАНЯТИЕ 20. Двумерное уравнение теплопроводности. Решение для случая прямоугольной области.


ЗАНЯТИЕ 21. Двумерное уравнение теплопроводности. Решение для случая круговой области.



ЗАНЯТИЕ 22. Задача Дирихле для прямоугольника.


ЗАНЯТИЕ 23. Задача Дирихле для круга.


ЗАНЯТИЕ 24. Задача Дирихле для полуплоскости. Прием КР 1.


    4. КУРСОВЫЕ РАБОТЫ

    Помимо времени, предусмотренного студенту для подготовки к лекционным и практическим занятиям, предполагается выполнение курсовой работы. Она должна способствовать овладению студентами навыками самостоятельной работы и реализации индивидуального творческого мышления по основным темам курса ”Уравнения математической физики”. Курсовая работа содержит теоретические упражнения и расчетную часть - задачи. Теоретические упражнения являются общими для всех студентов, задачи - для каждого студента группы индивидуальные.

    Контроль за выполнением курсовой работы проводится в два этапа.

    1). Предварительная проверка правильности письменного решения теоретических упражнений и задач;

    2). Защита курсовой работы (возможна в двух вариантах, устном или письменном).

    4 СЕМЕСТР

    КР 1. Уравнения математической физики. [5], гл. XI, задачи 1-7, 9-15.



Цель задания - освоение студентами методики применения дифференциальных уравнений с частными производными к решению физических, механических, инженерных и др. прикладных задач.



    ЛИТЕРАТУРА

    1. Асеев В.М., Горбацевич В.В., Осипенко К.Ю. Методическое пособие по курсу “Уравнения с частными производными”. Части 1-5. М., МАТИ, 1983-1984.

    2. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М., Наука, 1985.

3. Вергасов В.А., Гусев Е.В., Макаров Г.Д. Уравнения математической физики. Методические указания к практическим занятиям по курсу “Высшая математика”. М., МАТИ, 1987.

    4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. М.., Высшая школа, 1996.

    5. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). М., Высшая школа, 1994.

6. Сборник задач по математике для втузов. Специальные курсы. Под ред. А.В. Ефимова. М., Наука, 1984.

7. Сборник задач по математике для втузов. Ч. 4. Методы оптимизации. Уравнения в частных производных. Интегральные уравнения. Под ред. А.В. Ефимова. М., Наука, 1990.

    8. Сборник задач по уравнениям математической физики. Под ред. В.С. Владимирова. М., Наука, 1982.

    9. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., Наука, 1993.

    10. Фарлоу С. Уравнения с частными производными для научных работников и инженеров. М., Мир, 1985.

    11. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. М., Наука, 1969.