Системный анализ и обработка результатов гидродинамических исследований нефтегазодобывающих предприятий
| Вид материала | Автореферат |
- Устройство для проведения гидродинамических исследований в скважинах, 34.11kb.
- Повышение эффективности функционирования транспортно-погрузочного комплекса предприятий, 243.9kb.
- Системный анализ параметров сердечно-сосудистой системы учащихся югры 05. 13. 01 системный, 641.8kb.
- Планирование маркетингового исследования спроса на продукцию компании 35 Обработка, 9.15kb.
- Системный анализ параметров вектора состояния организма человека, проживающего в условиях, 694.75kb.
- Системный анализ параметров вектора состояния организма женщин репродуктивного возраста, 689.14kb.
- Эволюционный метод синтеза непрерывно дискретных систем управления, 288.26kb.
- Цех по добыче нефти и газа, 33.17kb.
- Высокоточное нейросетевое распознавание в системах технического зрения, 248.39kb.
- Разработка нелинейных динамических систем для формирования хаотических колебаний, 219.26kb.
На правах рукописи
НЕБОЖЕНКО Виктор Александрович
СИСТЕМНЫЙ АНАЛИЗ И ОБРАБОТКА РЕЗУЛЬТАТОВ ГИДРОДИНАМИЧЕСКИХ ИССЛЕДОВАНИЙ НЕФТЕГАЗОДОБЫВАЮЩИХ ПРЕДПРИЯТИЙ
Специальность 05.13.01 – Системный анализ, управление и обработка
информации (промышленность)
АВТОРЕФЕРАТ
диссертации на соискание ученой степени
кандидата технических наук
Самара - 2007
Работа выполнена на кафедре «Вычислительная техника» Государственного образовательного учреждения высшего профессионального образования «Самарский государственный технический университет»
| Научный руководитель: | Заслуженный деятель науки РФ, доктор технических наук, профессор Семенов Владимир Семенович |
| | |
| Официальные оппоненты: | доктор технических наук, профессор Кузнецов Павел Константинович, ГОУВПО «Самарский государственный технический университет», г. Самара |
| | кандидат технических наук Минаков Игорь Александрович, Институт проблем управления сложными системами РАН, г. Самара |
| | |
| Ведущая организация: | ОАО «Гипровостокнефть», г. Самара |
Защита состоится «13» ноября 2007 г. в 9 часов на заседании диссертационного совета Д 212.217.03 ГОУВПО «Самарский государственный технический университет» по адресу:
г. Самара, ул. Галактионовская, 141, корпус 6, аудитория 28.
С диссертацией можно ознакомиться в библиотеке ГОУВПО «Самарский государственный технический университет» по адресу:
г. Самара, ул. Первомайская 18.
Отзывы на автореферат (в двух экземплярах, заверенные печатью) просим направлять по адресу: 443100, г. Самара, ул. Молодогвардейская, 244, СамГТУ, главный корпус, на имя ученого секретаря диссертационного совета Д 212.217.03.
Автореферат разослан «11» октября 2007 г.
| Ученый секретарь диссертационного совета Д 212.217.03 | Губанов Н.Г. |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность работы. Проектирование и осуществление контроля над процессом разработки нефтяных месторождений неотъемлемо связаны с определением свойств и изучением фильтрационных параметров продуктивных коллекторов.
Сведения о пласте при всем их разнообразии всегда ограничены. Они складываются из геологической и геофизической информации: данных исследования образцов породы и гидродинамических исследований скважин; результатов анализа отобранных из скважин проб нефти, газа и пластовой воды; из истории разработки, т.е. совокупности данных по динамике изменения давлений, отбора нефти и закачки воды по отдельным скважинам и в целом по объекту. Даже если имеется весь перечисленный объем информации, что бывает далеко не всегда, ее недостаточно для построения адекватной модели пласта. Модель пласта строится на основе данных измерений параметров скважин и предполагает применение интерполяции по этим данным. Количество скважин ограничено, поэтому имеет место ограниченность информации о процессах, протекающих внутри пласта. Поэтому, нет веских оснований считать такую модель адекватным представлением того, что на самом деле происходит в пласте.
Существует множество аналитических моделей определения параметров пласта (Д.М. Ахметзянова, В.Я. Булыгин, Д.В. Булыгин, Я.М. Вайнберг, Г.А. Вирновский, Р.Н. Дияшев, А.В. Костерин, М.П. Швидлер). Часто проблема формулируется либо как задача Коши, либо как обратная коэффициентная задача. Почти всегда задача определения параметров пластовой системы некорректна в силу неединственности ее решения. Поэтому широкое распространение получила задача идентификации параметров пластовой системы с привлечением многофазных математических моделей фильтрации. Под идентификацией модели понимается физически обоснованное изменение отдельных параметров (которые не поддаются прямому измерению) и строения геологической и фильтрационной моделей, при которых обеспечивается возможно максимальная сходимость в динамике фактических и модельных показателей разработки как по отдельным скважинам, так и в среднем по эксплуатационному объекту (забойные и пластовые давления, дебиты скважин по нефти, воде и газу, накопленные технологические показатели разработки). Процесс идентификации является неотъемлемым этапом проектирования разработки нефтяных месторождений. Руководящие документы, «Правила проектирования разработки нефтяных и газовых месторождений», обязывают создавать постоянно-действующие геолого-математические модели нефтяных месторождений (ПДГМ), параметры которых должны подвергаться регулярному уточнению. Вместе с тем, в документе отмечено, что формализованная методика идентификации параметров пласта по истории разработки в настоящее время отсутствует.
В связи с вышеизложенным, проблема разработки методов и алгоритмов интерпретации результатов промысловых гидродинамических исследований скважин с целью идентификации параметров пласта является актуальной задачей нефтегазодобывающей промышленности. В данной работе рассмотрена возможность применения методов теории оптимального управления к задаче интерпретации результатов промысловых гидродинамических исследовании скважин.
Целью работы является системный анализ и обработка результатов промысловых гидродинамических исследований скважин и пластов на основе модификации классических методик с учетом априорной информации об исследуемом объекте (скважине, пласте) методами теории оптимального управления, а также усовершенствование методики интерпретации и технологии проведения промысловых гидродинамических исследований скважин и пластов.
Достижение поставленной цели базируется на решении следующих задач.
- Системного анализа существующих методов интерпретации результатов промысловых гидродинамических исследований скважин. История методов и тенденции развития.
- Формирования требований, предъявляемых к алгоритму решения задачи идентификации параметров математической модели пласта.
- Разработки методики интерпретации результатов промысловых гидродинамических исследований скважин, основанной на применении методов теории оптимального управления.
- Разработки и реализации алгоритма интерпретации результатов промысловых гидродинамических исследований скважин и пластов, и его апробации.
- Исследования результатов численных расчетов, проведенных по предложенной методике. Определения степени соответствия полученных результатов фактическим показателям.
- Исследования разработанного алгоритма на устойчивость. Исследования результатов интерпретации на достоверность.
Объект исследования. Объектом исследования являются данные промысловых гидродинамических исследований скважин и пластов и задачи, связанные с интерпретацией этих данных.
Предмет исследования. Методика и алгоритмы идентификации параметров математической модели нефтяного месторождения по данным истории разработки. Достоверность результатов идентификации. Повышение эффективности методов идентификации.
Методы исследования. В работе использовались методы системного анализа, теории оптимального управления, математического моделирования, теории фильтрации, методы решения некорректных задач и др. Использовались программные средства Borland Delphi 7.0, Schlumberger 2005a_1, Golden Software Surfer 8.0, Golden Software Grapher 4.0.
Научной новизной обладают следующие результаты.
- Разработан метод автоматизированной идентификации параметров модели нефтяного месторождения по результатам гидродинамических исследований скважин с использованием методов теории оптимального управления. Метод позволяет устранить субъективизм в решении, а также позволяет решать задачи идентификации в трехмерной трехфазной постановке.
- Разработан и реализован алгоритм решения задачи идентификации параметров нефтяного месторождения по результатам гидродинамических исследований скважин, основанный на применении градиентной процедуры поиска минимума целевой функции. Применение этого алгоритма позволило повысить устойчивость и достоверность решения, одновременно снизив требования к вычислительным ресурсам.
- Предложена методика комплексной оценки методов идентификации параметров модели нефтяного месторождения по результатам гидродинамических исследований скважин. В отличие от существующих методик, комплексная методика включает в себя исследование на реальных месторождениях, исследование на достоверность и устойчивость решения на модельном месторождении.
- На основе разработанной методики построены соответствующие алгоритмы и создана информационно-аналитическая система обработки и интерпретации промысловых гидродинамических исследований скважин и пластов (Свидетельство № 50200701344 об официальной регистрации программы для ЭВМ “Адаптация математической модели нефтяного месторождения по данным истории разработки”).
Практической полезностью обладают.
- Полученные в диссертационной работе результаты математического моделирования гидродинамических процессов могут быть основой для развития новых методических рекомендаций и обоснованием практических изменений, направленных на повышение соответствия математических моделей реальным процессам.
- Разработанная программа интерпретации промысловых гидродинамических исследований скважин использовалась при составлении проектов доразработки Солоцкого и Красноярского месторождений Самарской области.
Реализация результатов работы. В настоящее время материалы исследования внедрены в процесс анализа разработки месторождений в ООО «Технологический центр Б.Ф. Сазонова» г. Самара.
Апробация работы. Основные результаты работы докладывались и обсуждались на следующих конференциях:
- Всероссийской научно-практической конференции «Компьютерные технологии в науке, практике и образовании» (Самара, СамГТУ, 2004, 2005, 2006);
- Всероссийской научно-практической конференции «Нефтегазовые и химические технологии» (Самара, СамГТУ, 2005);
- 63, 64 Всероссийских научно-практических конференциях по итогам НИР за 2005, 2006 год (Самара, СГАСУ, 2006, 2007);
- Международной научно-практической конференции «Ашировские чтения» (Самара, СамГТУ, 2006).
Публикации. По теме диссертации опубликовано 13 печатных работ, в том числе из перечня, рекомендованного ВАК России - 1.
Основные положения, выносимые на защиту:
- Системный анализ проблемы интерпретации промысловых гидродинамических исследований скважин, а также решений этой задачи.
- Применение методов теории оптимального управления для задачи интерпретации промысловых гидродинамических исследований скважин.
- Алгоритм процедуры решения задачи идентификации с использованием градиентного метода.
- Апробация предложенного алгоритма на действующих месторождениях.
- Оценка результатов работы предложенного метода.
Структура и объем диссертации. Работа состоит из введения, четырех глав, заключения, библиографического списка и 3 приложений, содержащих акт внедрения. Общий объем работы 147 страниц машинописного текста, включая 5 таблиц, 11 рисунков и перечень использованной литературы из 142 наименований.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обоснована актуальность проблемы, научная и практическая значимость работы, сформулирована цель работы и ее научная новизна, изложены основные выносимые на защиту положения.
В первой главе приведены основные понятия из теории разработки месторождений углеводородов, которые используются в последующих главах. Рассмотрены стадии разработки нефтяных месторождений и особенности динамики характеристик разработки. Понимание этих вопросов очень важно для дальнейшего анализа полученных результатов решения обратной задачи теории прогнозирования показателей разработки нефтяных месторождений. Рассмотрены существующие модели нефтяных месторождений и сделан вывод, что на данном этапе развития средств вычислительной техники наиболее эффективным является использование трехфазных математических моделей трехмерного объекта. Дана краткая характеристика прямых задач прогнозирования показателей разработки месторождений. Проведен детальный обзор литературы, посвященной решению обратных задач теории фильтрации, а также обзор современных технологий компьютерного моделирования залежей углеводородов.
Во второй главе дана развернутая характеристика обратных задач теории разработки месторождений углеводородов. Высокая степень неопределенности исходной информации при построении модели пласта делает необходимым этапом моделирования уточнение параметров модели по данным наблюдений. На этом этапе путем решения обратной задачи осуществляется идентификация основных фильтрационно-емкостных параметров пласта, заложенных в модель. Этот процесс называется воспроизведением истории разработки. При воспроизведении истории разработки известны фактические поля давлений, добыча и закачка каждого компонента по скважинам. Обратная задача решается итерационно до тех пор, пока модель фильтрации не воспроизведет распределение давлений и насыщенностей, которые возникают в результате приложенного воздействия – заданной добычи и закачки скважин. Процедура идентификации параметров пласта может быть автоматизированной или осуществляться вручную. Несмотря на высокую трудоемкость, наиболее часто используемым, в настоящее время, является способ ручной подгонки истории. Ручной способ вносит субъективизм в решение и его качество зависит от опыта инженера-разработчика. Автоматизированный способ позволяет повысить объективность решения задачи.
Алгоритмы автоматизированной идентификации параметров модели основаны на поиске минимума функционала:
 .
.Здесь wi – весовые коэффициенты, Xi и X0i – наблюдаемые и расчетные значения показателей, по которым ведется подгонка. Это могут быть значения пластового давления, обводненности и газового фактора по отдельным скважинам или по их группам на заданные моменты времени и т.д. Весовые коэффициенты обычно равны единице, но в зависимости от целей подгонки могут изменяться для того, чтобы обеспечить различное влияние отдельных факторов на результирующее решение.
Как известно, обратная задача для системы нелинейных дифференциальных уравнений может иметь не единственное решение, поэтому нельзя принимать найденные в результате идентификации значения параметров пласта в качестве истинных. Особенности строения пласта, выявленные в ходе воспроизведения истории разработки, должны быть непосредственно подтверждены или опровергнуты непосредственными исследованиями.
Даже при хорошей подгонке истории по имеющимся данным нет никакой гарантии, что новые фактические данные будут воспроизведены моделью без ее дополнительной корректировки. Поэтому при решении задачи идентификации модели необходимо использовать всю имеющуюся информацию в наиболее полном объеме.
Приведена процедура воспроизведения истории разработки. Сформулированы требования к методу и алгоритму решения задачи идентификации, такие как: процесс идентификации должен сходиться к оптимуму даже при возможном использовании неблагоприятного начального приближения; алгоритм идентификации должен обладать высокой скоростью сходимости при минимальных вычислительных затратах; минимизирующая процедура должна быть такой, чтобы ослабить некорректную природу задачи идентификации.
Наиболее часто задача идентификации ставится как обратная коэффициентная задача. Поэтому детально рассмотрена эта задача и способы ее решения. Несмотря на наличие множества аналитических методов решения задачи, в настоящее время для автоматизированного решения задачи применяются решения, основанные на методах теории чувствительности и методах теории оптимального управления. Решения, основанные на методах теории чувствительности, исторически возникли первыми и достаточно эффективно решали задачи на математических моделях одно- и двумерных объектов. Но для использования моделей трехмерных объектов более эффективными оказываются решения, основанные на методах теории оптимального управления.
В третьей главе задается функционал качества. Этот функционал отвечает за степень адекватности модели, то есть соответствия модели реальным данным, измеренным на месторождении. Так как в работе используется трехфазная модель фильтрации трехмерного объекта, то функционал качества принимает вид:

(1)
Здесь P, O, ГНФ, ВГФ, S – значения соответственно давления, обводненности продукции, газонефтяного фактора, водогазового фактора, насыщенности какой-то определенной фазой; α, β, γ, δ – весовые множители; индексы ф, р – означают фактические и расчетные параметры соответственно; индекс i характеризует скважину, j – интервал (по разрезу) замера, n – момент времени замера, L, M, N – число скважин, интервалов замера и моментов времени соответственно.
Известными являются фактические замеры перечисленных показателей эксплуатации добывающих и нагнетательных скважин, а также значения давлений и насыщенностей в наблюдательных и пьезометрических скважинах.
Предложено рассматривать математическую модель месторождения в виде преобразователя входной информации (рисунок 1), где входные данные - это исходные параметры математической модели (геометрические размеры пласта, начальное пластовое давление, физические и химические свойства нефти, коэффициенты проницаемости и пористости в каждой ячейке модели и т.д.), а выходные данные – это выходные данные модели (параметры разработки: динамика добычи нефти, воды; динамика пластовых и забойных давлений; динамика обводненности продукции и т.д.).

Рисунок 1 - Представление математической модели
нефтяного месторождения в виде преобразователя информации
Обозначим через
 вектор управляющих параметров, за счет вариации которых мы хотим получить совпадение между фактическими и расчетными показателями разработки. Под управляющими параметрами, для упрощения задачи, мы будем понимать пористость и проницаемость.
вектор управляющих параметров, за счет вариации которых мы хотим получить совпадение между фактическими и расчетными показателями разработки. Под управляющими параметрами, для упрощения задачи, мы будем понимать пористость и проницаемость.В случае полного и точного соответствия модели реальному пласту значение функционала равнялось бы нулю. Однако, полное совпадение уточняемой модели и реального пласта недостижимо с практической точки зрения, например, вследствие погрешностей в промысловых замерах. Поэтому ставится и решается задача идентификации лишь на основе минимизации функционала (1). После выбора и нахождения набора управляющих параметров, минимум функционала соответствует их наиболее близкому к истинному распределению управляющих параметров.
Представим функционал в ином виде, удобном для дальнейших рассуждений:
 . (2)
. (2)Здесь
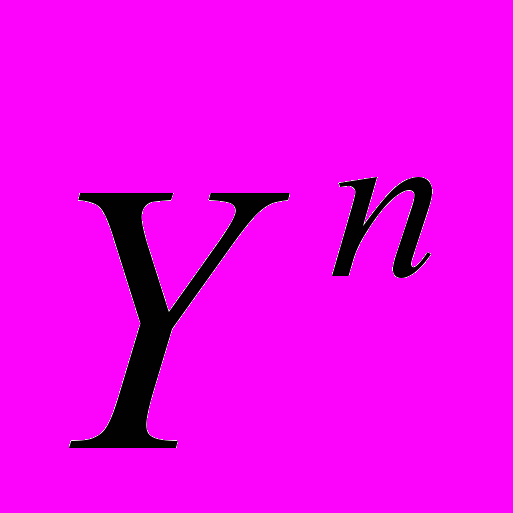 - замеренные значения (любая комбинация из давлений, обводненности продукции, газонефтяного или водогазового фактора, насыщенности в исследуемых скважинах);
- замеренные значения (любая комбинация из давлений, обводненности продукции, газонефтяного или водогазового фактора, насыщенности в исследуемых скважинах); 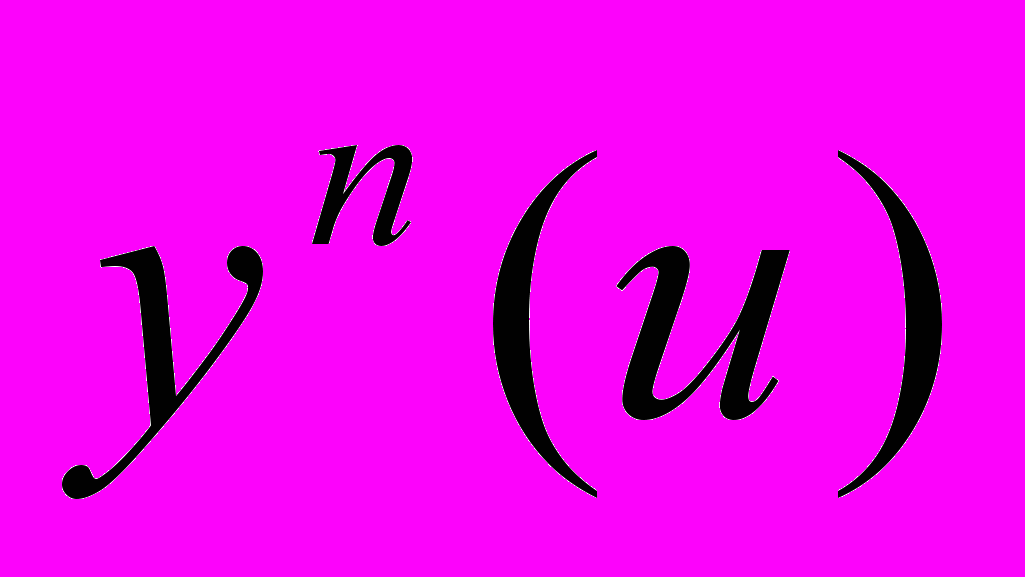 - расчетные параметры, соответствующие замеренным данным; N – число временных интервалов замеров; верхние индексы n и T относятся к номеру замера и матричной операции транспонирования соответственно;
- расчетные параметры, соответствующие замеренным данным; N – число временных интервалов замеров; верхние индексы n и T относятся к номеру замера и матричной операции транспонирования соответственно;  обозначает матрицу весовых коэффициентов. Физический смысл указанной матрицы состоит в возможности задания различных весов замерам в целевой функции (2) в соответствии со степенью их достоверности. Чем больше весовой коэффициент, тем значительнее вклад и влияние оказывает соответствующий замер на величину функционала.
обозначает матрицу весовых коэффициентов. Физический смысл указанной матрицы состоит в возможности задания различных весов замерам в целевой функции (2) в соответствии со степенью их достоверности. Чем больше весовой коэффициент, тем значительнее вклад и влияние оказывает соответствующий замер на величину функционала.Заметим, что на область изменения вектора управляющих параметров обычно налагаются некоторые ограничения как физического, так и смыслового характера:
 . (3)
. (3)Так, например, пористость не может находиться вне интервала (0,1), а для проницаемости задается определенный диапазон величин, без нарушения представлений о геологическом строении месторождения.
Прямое определение вектора управляющих параметров, доставляющее минимум функционалу (2) при наличии ограничений (3) в случае модели реального пласта, не представляется возможным. Поэтому рассматриваются только итерационные методы, а именно в данном подходе для минимизации целевой функции (2) используется метод сопряженных градиентов (метод Флетчера-Ривса). Итерационный процесс строится следующим образом. Уточняемая оценка управляющего вектора
 на (v + 1)-ой итерации вычисляется через значение управляющего вектора
на (v + 1)-ой итерации вычисляется через значение управляющего вектора  на (v)-ой итерации на основании направления поиска, предопределяемом градиентом целевой функции:
на (v)-ой итерации на основании направления поиска, предопределяемом градиентом целевой функции: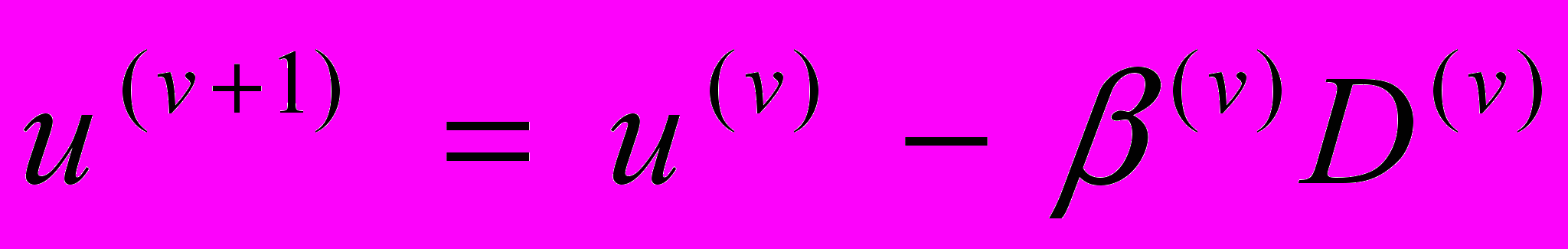 , (4)
, (4) , (5)
, (5) . (6)
. (6)где
 - градиент целевой функции относительно управляющих параметров;
- градиент целевой функции относительно управляющих параметров;  - направление поиска экстремума функционала; а
- направление поиска экстремума функционала; а  - величина шага смещения вдоль направления поиска.
- величина шага смещения вдоль направления поиска.Для достижения наилучшей скорости сходимости процедуры (4)-(6), величина шага
 должна находиться из решения следующей одномерной экстремальной задачи:
должна находиться из решения следующей одномерной экстремальной задачи: , (7)
, (7)т.е.
 - это значение шага смещения
- это значение шага смещения  , на котором достигается минимум выражения
, на котором достигается минимум выражения 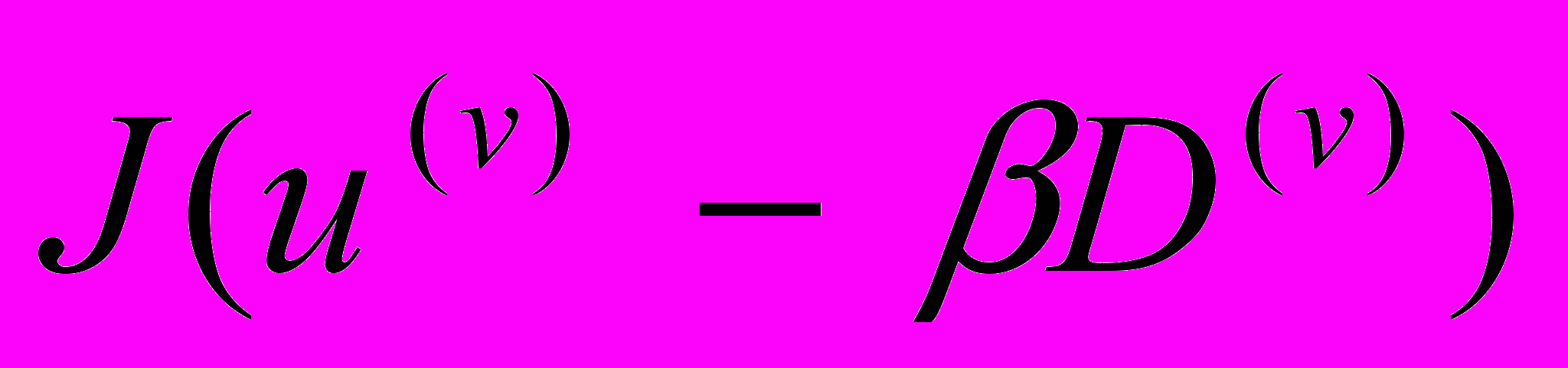 .
.Таким образом, для осуществления одной итерации методом сопряженных градиентов требуется знать градиент целевой функции для вычисления направления поиска (формулы (5)-(6)) и величину шага смещения вдоль направления поиска.
Таким образом, под решением задачи идентификации понимается такой вектор управляющих параметров
 , который удовлетворяет ограничением (3) и доставляет минимум целевой функции (2):
, который удовлетворяет ограничением (3) и доставляет минимум целевой функции (2):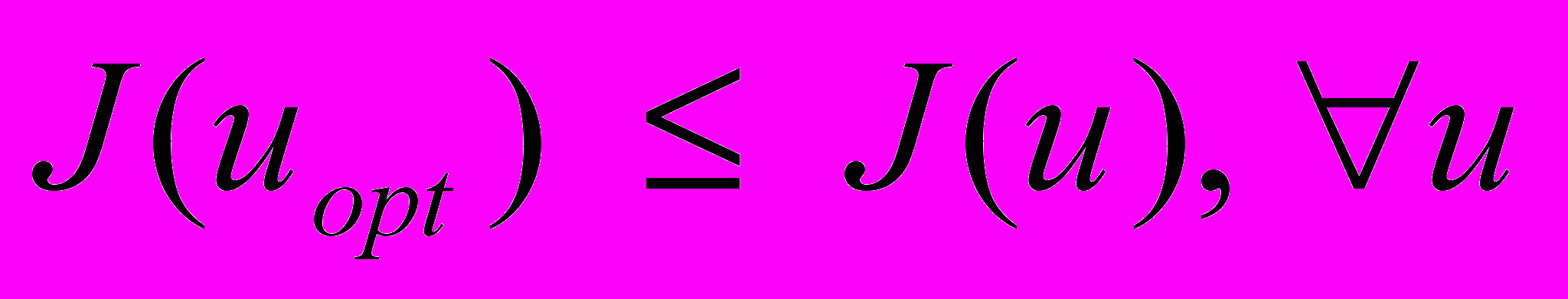 . (8)
. (8)Т.е. при решении обратной задачи по уточнению коллекторских свойств необходимо найти такое допустимое управление, чтобы вычисленные значения (на основе этого набора управляющих параметров) показателей разработки в функционале (2), максимально приближались в среднеквадратичном смысле к замеренным значениям.
Опишем алгоритм решения задачи идентификации с использованием методов теории оптимального управления.
- До начала решения задачи идентификации должно быть предложено, задано исходное распределение управляющих параметров. С учетом допущений, подходящим объектом для начального приближения выступает геологическая модель месторождения с соответствующими параметрами.
- Решается задача прогноза (прямая задача) при текущем распределении управляющих параметров и задании по скважинам фактических отборов, например, нефти. Значения фазовых переменных и дебитов компонентов на каждом временном шаге сохраняются для дальнейшего использования в сопряженной задаче и задаче для вариаций.
- Отыскивается решение сопряженной краевой задачи. Для этой цели используются как расчетные, так и замеренные данные плюс сохраненные на этапе 2 распределения фазовых переменных задачи, благодаря которым становится возможным подготовить матрицу сопряженной системы для каждого временного шага. На основе полученного решения сопряженной задачи, т.е. значения сопряженной функции, удается вычислить градиент целевой функции.
- По формулам (5)- (6) отыскивается направление поиска.
- Решается задача для вариации фазовых переменных. На основе полученного решения вычисляется оптимальная величина шага смещения вдоль направления поиска.
- На основе процедуры (4) осуществляется пересчет вектора управляющих параметров.
- Если критерий сходимости итерационного процесса удовлетворяется, то решение задачи идентификации найдено. Если нет, то для нахождения нового множества управляющих параметров повторяются шаги 2-7 до достижения критерия сходимости или критерия остановки вычислительного алгоритма.
В качестве критерия сходимости могут выступать различные условия. Например, в качестве такого может использоваться условие обязательного снижения функционала не менее, чем на определенную долю от предыдущего значения функционала. Другой подход предусматривает наблюдение за итерационным процессом в реальных обратных задачах. Особенностью применения метода сопряженных градиентов является то, что величина функционала быстро снижается на первых итерациях, затем функционал стабилизируется, и темпы его снижения уменьшаются. Критерием сходимости может выступать требование снижения функционала, т.е. если при новом распределении параметров функционал возрос, то критерий считается нарушенным, и вычислительный алгоритм останавливается.
Применение в качестве алгоритма минимизации метода сопряженных градиентов (метода Флетчера-Ривса) позволяет устранить недостатки Ньютоновских методов. Данный метод не требователен к первоначальному приближению параметров, он всегда сходится, метод относится к методам первого порядка – не требует вычисления вторых производных. Кроме того, этот метод обладает сверхлинейной скоростью сходимости, что в купе с отсутствием необходимости вычислять вторые производные делает сравнимыми времена решения задачи этими методами.
В четвертой главе предложенный метод и алгоритм идентификации был использован применительно к Солоцкому и Красноярскому месторождениям Самарской области. Результаты идентификации изображены на рисунках 2-5.
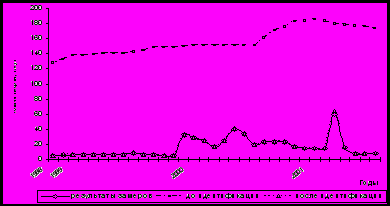
Рисунок 2 - Динамика добычи нефти для скважины 32
Солоцкого месторождения

Рисунок 3 - Динамика добычи воды для скважины 32
Солоцкого месторождения
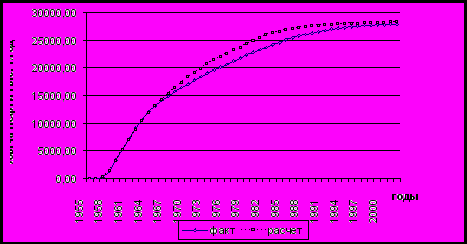
Рисунок 4 - Динамика добычи нефти для пласта Б2+ Б3
Красноярского месторождения

Рисунок 5 - Динамика добычи воды для пласта Б2+ Б3
Красноярского месторождения
Приведенные результаты позволяют делать вывод о возможности применения разработанного метода и алгоритма для идентификации параметров математической модели нефтяного месторождения по истории его разработки. Вместе с тем следует обратить внимание на некоторые рекомендации при воспроизведении истории разработки.
Наиболее хорошие результаты удается получить на месторождениях, которые введены в разработку в последние годы. Это объясняется тем, что при обустройстве нефтяного месторождения, устанавливаются наиболее современные приборы измерения, с достаточно малой погрешностью. Кроме того, вся собранная информация хранится в базе данных. Достоверность такой информации и ее доступность высока. На месторождениях, которые введены в разработку более 30-40 лет назад таких точных приборов не было, а данные, особенно по начальному этапу разработки, как правило, не сохранились.
Также из результатов идентификации видно, что при увеличении истории разработки в 10 раз, погрешность счета может увеличиться на несколько порядков. Таким образом, рекомендуется проводить уточнение параметров каждые 3-5 лет. А за начальное приближение в первой итерации брать предыдущую уточненную модель. Такой подход позволить минимизировать погрешность счета и повысить качество идентификации параметров модели. Но здесь следует отметить, что уточнение параметров пласта по истории разработки – это не дешевый процесс. Поэтому добывающие компании стараются делать его как можно реже, только когда проектные данные и факт расходятся очень серьезно.
Произведен анализ степени достоверности решения обратной задачи. Здесь выражение «степень достоверности» используется по следующей причине. В многомерных обратных задачах речь не идет об определении (уточнении) одного, двух, трех параметров пласта. При решении таких задач подлежат уточнению коллекторские свойства пласта в большом количестве элементарных ячеек. Естественно, что в каких-то ячейках будет иметь место наиболее близкое соответствие уточненных параметров к реальным значениям, а в других – довольно отдаленное. Поэтому указанное словосочетание будет характеризовать степень приближения массива уточняемых параметров к реальным значениям.
Исследование достоверности проводилось на тестовой модели. В качестве тестовой модели была выбрана модель неоднородно-анизотропного по коллекторским свойствам пласта, который в плане имеет вид квадрата размерами 3 км х 3 км. Продуктивный пласт аппроксимируется равномерной сеткой с числом ячеек 30х30х1 вдоль трех пространственных координатных осей. Для упрощения анализа получаемых результатов, задача решалась в двумерной постановке. Размеры элементарных ячеек вдоль осей x и y равняется 100 м, а вдоль оси z – 3.33 м. Следовательно, общее число сеточных ячеек равняется 900.
Из опыта решения обратных задач мы имеем, что емкостной параметр (коэффициент пористости) идентифицируется с большой точностью. С коэффициентом проницаемости дело обстоит хуже. Поэтому в исследованных вариантах уточнению подвергались наборы проницаемостей (вдоль осей x и y – kx и ky) в каждой элементарной ячейке. Следовательно, число определяемых (уточняемых) параметров для 900 ячеек равнялось 1800.
Коэффициенты проницаемости вдоль каждого направления были сгенерированы с использованием датчика случайных чисел. На рисунке 6 приводится распределение коэффициента проницаемости по площади продуктивности.

Рисунок 6 - Истинное распределение проницаемости
в модельной задаче
При проведении тестирования предлагается размещение эксплуатационных скважин в каждой элементарной ячейке. Это позволит получить «фактические» данные о добыче, пластовых и забойных давлениях и их зависимость от времени по 900 скважино-ячейкам. Именно в такой постановке можно вести речь об оценке степени достоверности решения обратной задачи во всех элементарных ячейках.
На указанной модели пласта, исходных данных и допущениях были просчитаны различные варианты решения прямых и соответственно обратных задач. Обратная задача решалась двумя способами: методом Ньютона-Раффсона (предлагает пакет MORE) и разработанным методом.
Варианты I и II решения обратных задач основывались на исходной информации по скважинам, эксплуатировавшихся при одинаковых дебитах. В вариантах III и IV суммарный отбор нефти из скважины был постоянным в течение 5 суток и равнялся отбору согласно вариантам I – II.
Таблица 1 - Сопоставление степени достоверности решения обратных задач в исследованных вариантах
| №№ варианта | Использованный метод | Погрешность определения kx и ky | |||||
| 1% | 10% | 20% | 30% | 40% | ≥50% | ||
| I | Разработанный метод | 71 | 493 | 478 | 364 | 242 | 152 |
| II | Ньютона-Рафсона | 53 | 453 | 448 | 374 | 272 | 200 |
| III | Разработанный метод | 110 | 671 | 488 | 342 | 168 | 21 |
| IV | Ньютона-Рафсона | 65 | 528 | 459 | 359 | 276 | 113 |
Результаты решения обратных задач для указанных вариантов приведены в таблице 1, и они означают следующее. Например, первая колонка отражает количество ячеек, в которых коэффициенты проницаемости определены с погрешностью не более 1%, во второй колонке – с погрешностью не более 10% и т.д.
Анализ представленных результатов позволяет отметить следующее: предложенный алгоритм осуществления итераций оказывается более эффективным по сравнению с методом Ньютона-Рафсона. Здесь под эффективностью понимается более высокая степень достоверности решения обратной задачи. Это проявляется, например, в том, что разработанный метод обеспечивают наибольшее число элементарных ячеек, где параметры kx и ky определены с погрешностью не более 1%. С другой стороны, данный метод дает наименьшее число элементарных ячеек, в которых коэффициенты находятся с погрешностью 50% и более.
Приводятся способы повышения устойчивости решения задачи идентификации, а также проблемы, возникающие при автоматизированной идентификации параметров модели месторождения.
В заключении приведены основные научные результаты и выводы работы.
Основные результаты работы
- На основе проведенного системного анализа проблем решения задачи интерпретации промысловых гидродинамических исследований скважин и пластов сформулированы основные требования к методу и алгоритму решения, такие как процесс решения должен сходиться к оптимуму даже при неблагоприятном начальном приближении, процедура должна обладать высокой скоростью сходимости при минимальных затратах вычислительных ресурсов, процедура должна быть такой, чтобы ослабить некорректную природу задачи.
- Показано, что в настоящее время наиболее часто используемым методом решения задачи интерпретации промысловых данных является “ручной”. Этот факт вносит большую долю субъективизма в решение.
- Показано, что обратная задача прогнозирования показателей разработки нефтяного месторождения является типичной некорректной задачей, поэтому интерпретация промысловых данных не должна ограничиваться простым расчетом фильтрационных параметров по готовым формулам. Обязательным этапом обработки промысловых данных является проверка полученных данных на устойчивость.
- Предложено рассматривать математическую модель продуктивного пласта в виде объекта управления, управляющими воздействиями которого являются геологические данные о пласте, а ответом на управляющие воздействия – динамики показателей разработки. Такой подход позволяет использовать методы теории оптимального управления для решения задачи идентификации параметров математической модели по истории разработки.
- Разработан метод интерпретации результатов промысловых гидродинамических исследований скважин, основанный на применении методов теории оптимального управления, который позволяет решать поставленную задачу в трехмерной трехфазной постановке.
- Проведено комплексное исследование предложенного метода интерпретации результатов промысловых гидродинамических исследований скважин, которое показало, что для более точного решения задачи необходимо усовершенствовать технологию проведения промысловых гидродинамических исследований.
- Разработано информационное и программное обеспечение для обработки и интерпретации результатов промысловых гидродинамических исследований скважин и пластов, которое может быть рекомендовано к использованию проектными организациями, работающими в сфере нефтегазового комплекса.
Основные положения и результаты диссертации опубликованы в следующих работах:
- Семенов В.С., Небоженко В.А. Повышение эффективности процесса адаптации гидродинамической модели нефтяного месторождения // Вестник СамГТУ выпуск №1(19), Серия Технические науки, Самара, 2007. С.95-100.
- Семенов В.С., Небоженко В.А. О некоторых методах решения обратных задач теории прогнозирования показателей разработки месторождений нефти и газа // Научно-технический журнал «ИНТЕРВАЛ. Передовые нефтегазовые технологии» выпуск №4(99), 2007. С. 42-46.
- Семенов В.С., Небоженко В.А. Адаптация математической модели нефтяного месторождения по данным истории разработки // Инновации в науке и образовании. – 2007, №6(29). С. 21.
- Семенов В.С., Небоженко В.А. Некоторые аспекты исследования временных рядов // Ашировские чтения: Материалы 3-й Международной научно-практической конференции, Самара, 2006. С. 184-186.
- Семенов В.С., Небоженко В.А. О задаче идентификации математических моделей нефтяных залежей // Ашировские чтения: Материалы 3-й Международной научно-практической конференции, Самара, 2006. С. 189.
- Небоженко В.А. Применение компьютерного моделирования при проектировании разработки нефтяных и газовых месторождений // Компьютерные технологии в науке, практике и образовании: Труды Всероссийской научно-практической конференции, Самара, 2004. С. 158-162.
- Небоженко В.А. Обзор современных технологий компьютерного моделирования залежей // Нефтегазовые и химические технологии: Тезисы докладов третьей Всероссийской научно-практической конференции, Самара, 2005. С. 93.
- Небоженко В.А. Повышение точности прогноза динамики показателей разработки нефтяных месторождений // Нефтегазовые и химические технологии: Тезисы докладов третьей Всероссийской научно-практической конференции, Самара, 2005. С. 94.
- Небоженко В.А. Построение математических моделей при решении задач оптимизации // Компьютерные технологии в науке, практике и образовании: Труды Всероссийской научно-практической конференции, Самара, 2005. С. 42-44.
- Небоженко В.А. Сравнительный анализ моделей, используемых при оценке процесса разработки нефтяных месторождений // Компьютерные технологии в науке, практике и образовании: Труды Всероссийской научно-практической конференции, Самара, 2005. С. 44-46.
- Небоженко В.А. Уточнение модели пласта по фактическим данным разработки месторождения // Компьютерные технологии в науке, практике и образовании: Труды Всероссийской научно-практической конференции, Самара, 2006. С. 47-50.
- Семенов В.С., Небоженко В.А. Исследование возможности применения элементов теории оптимального управления для решения задачи адаптации гидродинамической модели нефтяного месторождения // 63-я Всероссийская научно-техническая конференция СГАСУ по итогам НИР университета за 2005 год, Самара, 2006. С. 407-408.
- Небоженко В.А. Оптимизация решения задачи идентификации параметров математической модели нефтяной залежи // 64-я Всероссийская научно-техническая конференция СГАСУ по итогам НИР университета за 2006 год, Самара, 2007. С. 553-554.
Автореферат отпечатан с разрешения диссертационного совета
Д 212.217.03 ГОУВПО «Самарский государственный технический университет» (протокол № 12 от «5» октября 2007 г.)
Формат 60х84 1/16. Усл. печ. л. 1. Тираж 100 экз. Заказ № 704.
ГОУ ВПО “Самарский государственный технический университет”
Типография СамГТУ
443100, г. Самара, ул. Молодогвардейская, 244.
