Математическая логика, основанная на теории типов
| Вид материала | Реферат |
- Рабочей программы учебной дисциплины дв2 Математическая логика и теория алгоритмов, 50.1kb.
- Математическая логика, 1012.22kb.
- Рабочая программа по дисциплине в 2-Математическая логика и теория алгоритмов шифр, 316.78kb.
- Программы кандидатского экзамена по специальности 01. 01. 06 "Математическая логика,, 50.44kb.
- Рабочая учебная программа по дисциплине математическая логика, 72.41kb.
- Рабочая учебная программа по дисциплине «Математическая логика и теория алгоритмов», 69.99kb.
- Н. В. Папуловская Математическая логика Методическое пособие, 786.38kb.
- Уакиев Валериан Савирович рекомендуемая литература, 334.04kb.
- Аннотация программы учебной дисциплины «Дискретная математика и математическая логика, 55.65kb.
- Рабочей программы дисциплины математическая логика по направлению подготовки 220400, 21.67kb.
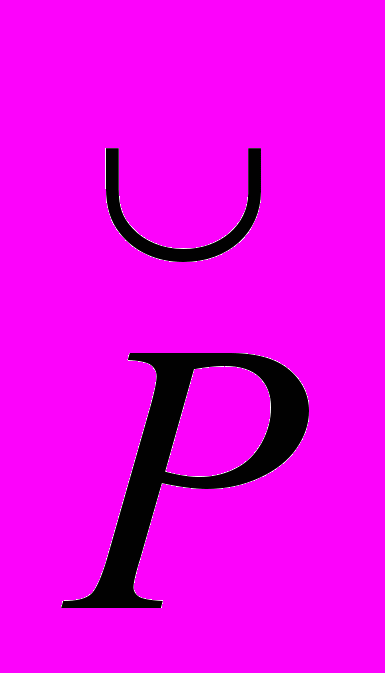 ‘‘)} Df.;
‘‘)} Df.;т.е. P порождает вполне упорядоченные ряды, если Р есть отношение ряда, и любой класс , содержащийся в поле Р и не являющийся нулевым, имеет первый член. (Отметим, что
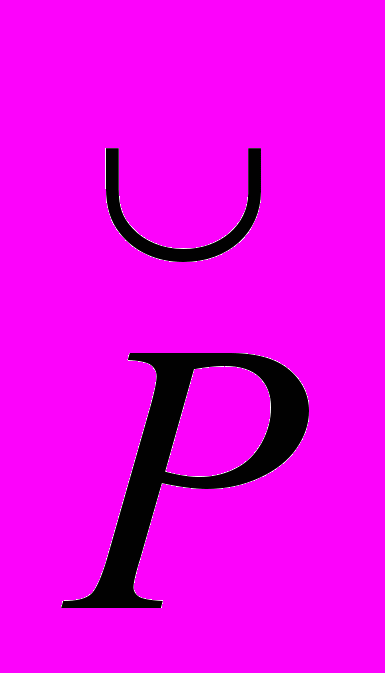 ‘‘ суть члены, входящие после некоторого члена ).
‘‘ суть члены, входящие после некоторого члена ).Если как No‘P обозначить ординальное число вполне упорядоченного отношения Р, а как NO класс ординальных чисел, то мы получим:
No =
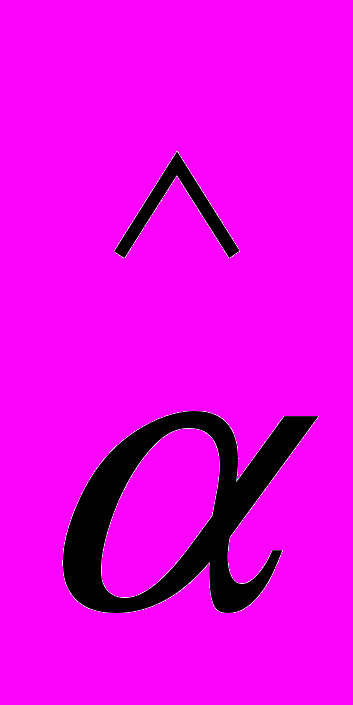
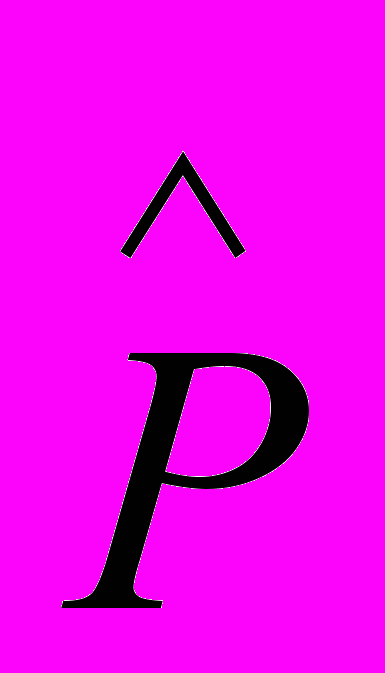 {P . =
{P . = 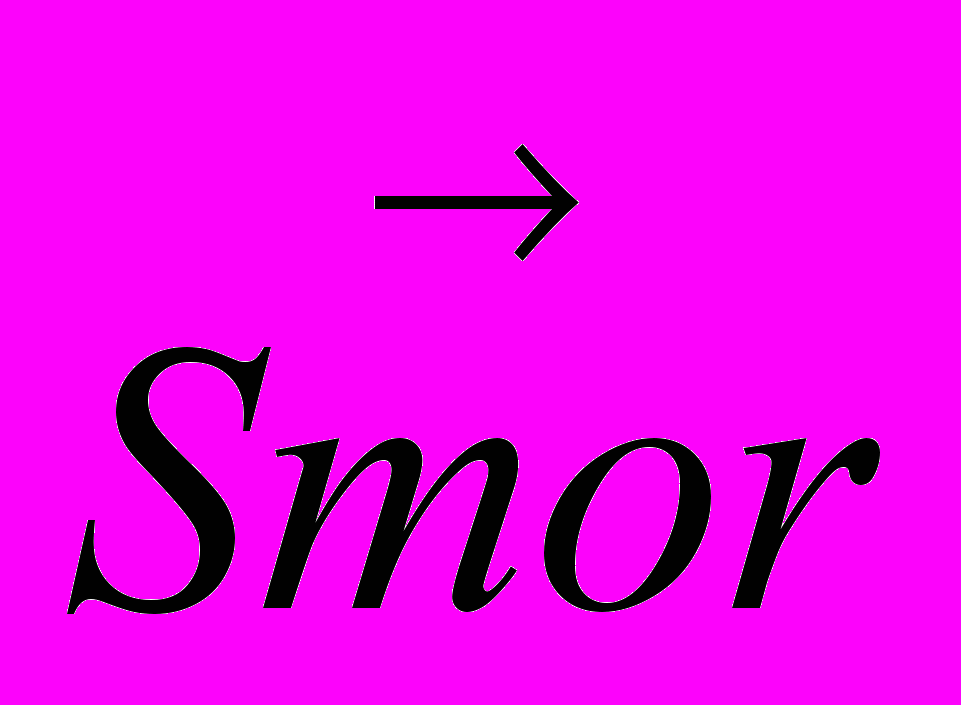 ‘P} Df.,
‘P} Df.,NO = No‘‘.
Из определения No мы получаем:
├ : P . . No‘P =
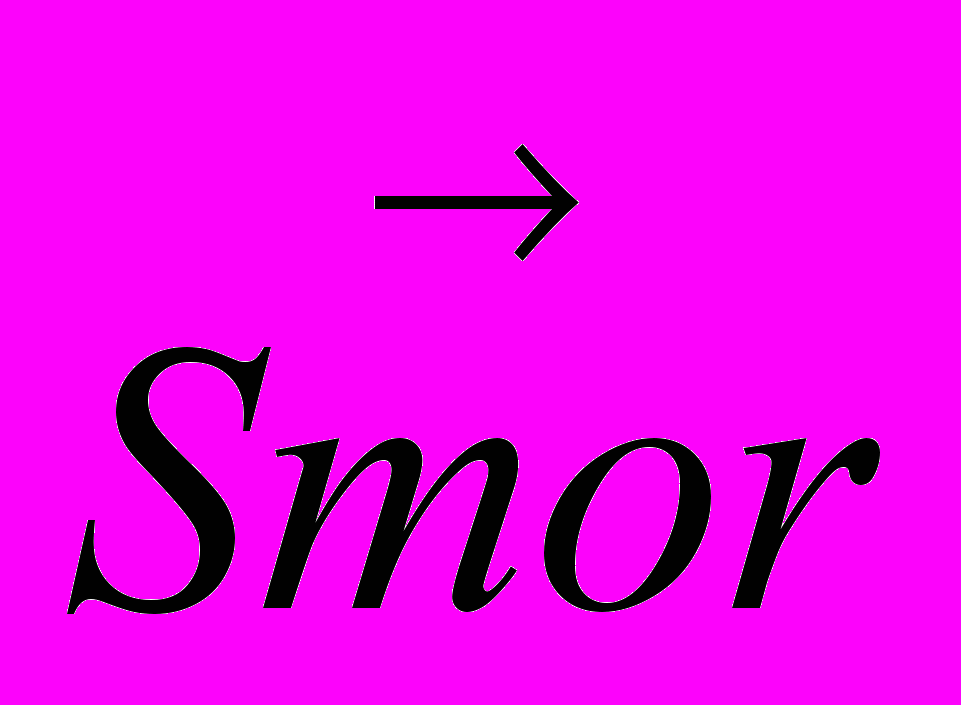 ‘P ,
‘P ,├ : (P ) . . E!No‘P.
Если теперь мы проверим наши определения с точки зрения их связи с теорией типов, мы увидим, прежде всего, что определения ‘Ser’ и включают поля отношений ряда. Поле же значимо только тогда, когда отношение является однородным; следовательно, отношения, которые не являются однородными, не порождают ряд. Например, можно подумать, что отношение порождает ряд ординального числа , типа
x, ‘x, ‘‘x, … n‘x, …,
и этим способом мы можем попытаться доказать существование и א0. Но х и ‘x относятся к различным типам и, следовательно, согласно нашему определению, такого ряда нет. Ординальное число ряда индивидов, согласно приведённому выше определению No, есть класс отношений индивидов. Следовательно, он по типу отличается от любого индивида, и не может образовывать часть какого-то ряда, в котором встречаются индивиды. Опять же, предположим, что все конечные ординалы имеют место как ординальные числа индивидов; т.е. как ординалы рядов индивидов. Тогда, конечные ординалы сами образуют ряд, чьё ординальное число есть ; таким образом, существует как ординальное число ординалов, т.е. как ординал ряда ординалов. Но тип ординального числа ординалов – это тип классов отношений классов отношений индивидов. Таким образом, существование доказывалось в рамках более высокого типа, чем тип конечных ординалов. Опять таки, кардинальное число ординальных чисел вполне упорядоченного ряда, который может быть создан из конечных ординалов, есть א1; следовательно, א1 имеет место в типе классов классов классов отношений классов отношений индивидов. К тому же, ординальные числа вполне упорядоченных рядов, составленных из конечных ординалов, могут быть упорядочены в порядке величины, и результатом будет вполне упорядоченный ряд, чьё ординальное число есть 1. Следовательно, 1 имеет место как ординальное число ординалов ординалов. Этот процесс можно повторить любое конечное число раз и, таким образом, мы можем в соответствующих типах установить существование אn и n для любого конечного значения n.
Но вышеуказанный процесс порождения более не ведёт к какой-то целостности всех ординалов, поскольку, если мы возьмём все ординалы какого-то заданного типа, всегда существуют более высокие ординалы в более высоких типах; и мы не можем объединить множество ординалов, тип которого превышает любую конечную границу. Таким образом, ординалы в каком-то типе могут быть упорядочены в порядке величины во вполне упорядоченный ряд, который имеет ординальное число более высокого типа, чем тип ординалов, составляющих ряд. В новом типе этот новый ординал не является наибольшим. Фактически, не существует наибольшего ординала в каком-то типе, но в каждом типе все ординалы меньше, чем некоторый ординал более высокого типа. Невозможно завершить ряд ординалов, поскольку это приводило бы к типам, превышающим каждую приписываемую конечную границу; таким образом, хотя каждый сегмент ряда ординалов вполне упорядочен, мы не можем сказать, что вполне упорядочен весь ряд, поскольку ‘весь ряд’ является фикцией. Следовательно, парадокс Бурали-Форти исчезает.
Из двух последних разделов обнаруживается, что если принять, что число индивидов не является конечным, то можно доказать существование всех канторовских кардинальных и ординальных чисел, за исключением א и . (Хотя вполне возможно, чтобы их существование было доказуемым.) Существование всех конечных кардинальных и ординальных чисел можно доказать без предпосылки о существовании чего бы то ни было. Ибо, если кардинальное число членов в каком-то типе есть n, число членов в следующем типе есть 2n. Таким образом, если бы индивидов не существовало, то был бы один класс (а именно, нуль-класс), два класса классов (а именно, тот, что не содержит классов, и тот, что содержит нуль-класс), четыре класса классов классов, и в общем 2n–1 классов n-го порядка. Но мы не можем объединить члены различных типов и, поэтому, не можем этим способом доказать существование какого-то бесконечного класса.
Теперь мы можем подвести итог всему рассмотрению. После установления некоторых парадоксов логики, мы нашли, что все они вырастают из того факта, что выражение, указывающее на всё из некоторой совокупности, по-видимому, обозначает само себя как одно из этой совокупности; как, например, ‘все пропозиции являются либо истинными, либо ложными’ само, по видимости, является пропозицией. Мы решили, что там, где это, судя по всему, встречается, мы имеем дело с ложной целостностью, и что, фактически, ничего вообще нельзя значимо сказать обо всём из предполагаемой совокупности. Чтобы дать ход этому решению, мы объяснили доктрину типов переменных, придерживающуюся принципа, что любое выражение, которое указывает на всё из некоторого типа, должно, если оно что-либо обозначает, обозначать нечто более высокого типа, чем всё то, на что оно указывает. Там, где указывается на всё из некоторого типа, есть мнимая переменная, принадлежащая этому типу. Таким образом, любое выражение, содержащее мнимую переменную, относится к более высокому типу, чем эта переменная. Это – фундаментальный принцип доктрины типов. Изменение в способе, которым конструируются типы, (это следует доказать с необходимостью) оставило бы решение противоречий незатронутым до тех пор, пока соблюдается этот фундаментальный принцип. Метод конструирования типов, объяснённый выше, продемонстрировал нам, как возможно установить все фундаментальные определения математики и в то же время избежать всех известных противоречий. И оказалось, что на практике доктрина типов уместна лишь там, где затрагиваются теоремы о существовании, или там, где необходимо перейти к некоторому частному случаю.
Теория типов ставит ряд трудных философских вопросов, касающихся её интерпретации. Однако эти вопросы в сущности отделимы от математического развития этой теории и, подобно всем философским вопросам, вводят элемент неопределённости, который не относятся к самой теории. Следовательно, по-видимому, лучше формулировать эту теорию без ссылки на философские вопросы, оставляя их для независимого исследования.
1 См. ниже.
2 Две пропозиции называются эквивалентными, когда обе они истины или обе ложны.
1 Этот парадокс принадлежит м-ру Дж. Берри из Бодлианской библиотеки.
2 Ср.: König, ‘Über die Grundlagen der Mengenlehre und das Kontinuum-problem’, Math. Annalen, Vol. LXI (1905); A.C. Dixon, ‘On “well-ordered” aggregates’, Proc. London Math. Soc., Series 2, Vol. IV, Part I (1906); E.W. Hobson, ‘On the Arithmetic Continuum’, ibid. Решение, предложенное в последней из этих статей, не кажется мне адекватным.
3 Ср.: Poincaré, ‘Les mathématiques et la logique’, Revue de Métaphysique et de Morale (May, 1906), особенно разделы VII и IX; см., также, Peano, Revista de Mathematica, Vol. VIII, No.5 (1906), С. 149 и далее.
4 ‘Una questione sui numeri transfiniti’, Rendiconti del circolo matematico di Palermo, Vol. XI (1897).
1 Ср. мою статью: ‘Les paradoxes de la logique’, Revue de Métaphysique et de Morale (May, 1906), С. 645.
2 Говоря, что совокупность не обладает целостностью, я подразумеваю, что высказывания о всех её членах являются бессмысленными. Кроме того, обнаружится, что использование этого принципа требует различия между все и какие-то, рассмотренное в Разделе 2.
1 Этими двумя терминами мы обязаны Пеано, который использует их приблизительно в указанном выше смысле. Ср.: например, Formulaire Mathématique (Turin, 1903), Vol. IV, C. 5.
2 М-р МакКолл говорит, что ‘пропозиции’ делятся на три класса: достоверные, переменные и невозможные. Мы можем принять это деление в применении к пропозициональным функциям. Функция, которую можно утверждать, является достоверной, функция, которую можно отрицать, является невозможной, все другие функции являются (в смысле м-ра МакКолла) переменными.
1 См. его Grundgesetze der Arithmetik (Jena, 1893), том I, § 17, C. 31.
1 Это выражение не отличается от ‘все свойства’.
2 Область действительной переменной – эта вся функция, относительно которой рассматривается ‘какое-то значение’. Так в ‘х влечёт р’ область х – это не х, но ‘х влечёт р’.
1 Logic, часть I, раздел II.
2 ‘On Denoting’, Mind (October, 1905). [Русский перевод см.: Рассел Б. Об обозначении // Язык, истина, существование. – Томск: изд-во Томского госуниверситета, 2002.]
1 Функция называется значимой для аргумента х, если она имеет значение для этого аргумента. Таким образом, мы можем кратко сказать ‘х является значимой’, подразумевая ‘функция имеет значение для аргумента х’. Область значимости функции состоит из всех аргументов, для которых функция является истинной, в совокупности со всеми теми аргументами, для которых она является ложной.
1 Лингвистически удобное выражение для этой идеи следующее: ‘х – истинно для всех возможных значений х’, возможное значение понимается как значение, для которого х является значимой.
1 Например, Пуанкаре. См.: Revue de Métaphysique et de Morale (May, 1906).
1 См.: Principles of Mathematics, § 48.
1 В предыдущей статье для этого журнала в качестве неопределяемой вместо дизъюнкции я брал импликацию. Выбор между ними – это предмет вкуса; Теперь я выбираю дизъюнкцию, поскольку она позволяет нам минимизировать число исходных пропозиций. [См.: ‘The Theory of Implication’, American Journal of Mathematics, Vol. XXVIII, 1906, P. 159-202.]
2 При использовании точек мы следуем Пеано. Это использование полностью объяснено м-ром Уайтхедом; см.: ‘On Cardinal Numbers’, American Journal of Mathematics, Vol, XXIV, и ‘On Mathematical Concepts of Material World’, Phil. Trans. A., Vol. CCV, P. 472.
3 Этим знаком, как и введением идеи, которую он выражает, мы обязаны Фреге. См. его Begriffsschrift (Halle, 1879), C.1 [Русский перевод см.: Исчисление понятий // Фреге Г. Логика и логическая семантика. – М.: Аспект Пресс, 2000.] и Grundgesetze der Arithmetik (Jena, 1983), Vol. I, C. 9.
1 Удобно использовать запись х, чтобы обозначить саму функцию в противоположность тому или иному значению этой функции.
1 Это отождествление подлежит модификации, которая вскоре будет объяснена.
1 См. упомянутую выше статью ‘On Denoting’, где причины этого представлены более пространно.
1 Таким образом,
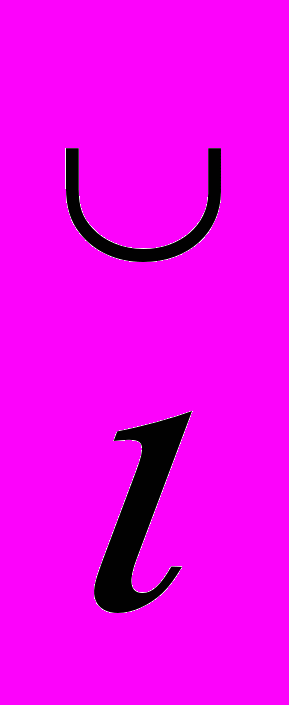 ‘ есть то, что Пеано называет .
‘ есть то, что Пеано называет .1 Ср.: часть III моей статьи ‘On some Difficulties in the Theory of Transfinite Numbers and Order Types’, Proc. London Math. Soc. Ser. II, Vol. IV, Part I.
2 Об аксиоме Цермело и о доказательстве того, что эта аксиома влечёт мультипликативную аксиому см. предыдущую сноску. Обратный вывод выглядит так: Обозначим как Prod‘k мультипликативный класс k, рассмотрим
Z‘ =
 {(x) . x . D‘R = ‘ . [D]‘R = ‘x} Df.,
{(x) . x . D‘R = ‘ . [D]‘R = ‘x} Df.,и предположим, что
Prod‘Z‘‘cl‘a . R =

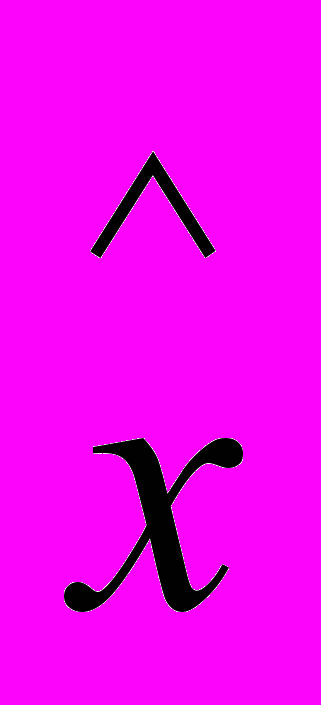 {(S) . S . Sx}.
{(S) . S . Sx}.Тогда R – это соответствие Цермело. Следовательно, если Prod‘Z‘‘cl‘a не является нулевым, то для а существует по крайней мере одно соответствие Цермело.
3 См.: Zermelo, ‘Beweis, dass jede Menge wohlgeordnet werden kann’. Math. Annalen, Vol. LIX, C.514-16.
