Урок-лекция по теме «понятие математической логики»
| Вид материала | Урок |
СодержаниеОсновные законы алгебры логики |
- Элементы математической логики, 189.46kb.
- Лекции по математической логике и теории алгоритмов для студентов 2 курса специальности, 769.24kb.
- Отличия человеческой логики от математической логики, 139.86kb.
- Контрольная работа по теме «Элементы математической логики», 36.88kb.
- Урок по теме «Основы логики и логические основы компьютера», 276.49kb.
- 1. Введение в алгебру логики Прямое произведение множеств. Соответствия и функции., 38.38kb.
- «Искусственный интеллект.», 86.69kb.
- Логика и плешь б. Рассела, 204.41kb.
- Внеклассное мероприятие по математике на тему: "В мире логики Льюиса Кэрролла", 72.43kb.
- Научная программа молодежной школы-конференции «Современные проблемы алгебры и математической, 48.63kb.
Seminar_ID_046
Урок-лекция по теме
«ПОНЯТИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ».
Логика — наука о законах и правилах мышления.
Формальная логика — наука о законах и формах мышления.
Математическая логика изучает логические связи и отношения, лежащие в основе дедуктивного вывода.
В 4 века до н.э. древнегреческий ученый Аристотель заложил основы формальной логики. Он исследовал терминологию логики, разобрал теорию умозаключений и доказательств, вывел понятие силлогизма.
В 16 веке в алгебре была создана буквенная символика. Она получила название алгебры логики, или математической логики. Основы математической логики заложил в 17 веке немецкий математик Лейбниц. Он сделал попытку построить первые логические исчисления. Лейбниц только развил идею, а окончательно развил и сформулировал ее ученый Джон Буль (1815-1864). В работах Буля логика приобрела свой алфавит, грамматику, орфографию. Поэтому иногда математическую логику называют Булевой алгеброй.
Алгебра логики — это математический аппарат, с помощью которого записывается, вычисляется, упрощается и преобразуется логическое высказывание.
Основным понятием математической логики является высказывание.
Высказывание — это повествовательное предложение, про которое всегда можно сказать истинное оно или ложное.
Истинные высказывания обозначаются — 1, а ложные — 0
Высказывания бывают просты и сложные. Сложные состоят из простых, соединенных знаками логических операций.
Высказывания обозначаются заглавными буквами латинского алфавита (простые): A,B,C,D…
Рассмотрим логические операции.
- Инверсия
- соответствует частице НЕ
- обозначается ¬А
- называется: отрицание
- Конъюнкция
- соответствует союзу И
- обозначается &, ●
- называется: логическое умножение
- Дизъюнкция
- соответствует союзу ИЛИ
- обозначается v
- называется: логическое сложение
Примеры:
1. Два больше трех А=0
Пять на пять равно пятнадцать В=0
конъюнкция: А & В=0
2. Погода безоблачная А=1
Не идет дождь В=1
конъюнкция: А & В=1
- Лев Толстой — великий русский писатель А=1
Исмагил Гаспринский — знакомый Льва Толстого В=1
дизъюнкция: А v В=1
- Дуб — хвойное дерево А=0
Щука — рыба В=1
дизъюнкция: А v В=1
ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений.
ЗАКОН | Для ИЛИ | Для И |
| Переместительный | x v y = y v x | x & y = y& x |
| Сочетательный | x v (y v z) = (x v y)v z | x& (y & z) = (x & y) & z |
| Распределительный | x (y v z ) = x y v x z | x v y& z = x v y& x v z |
| Правило де Моргана | 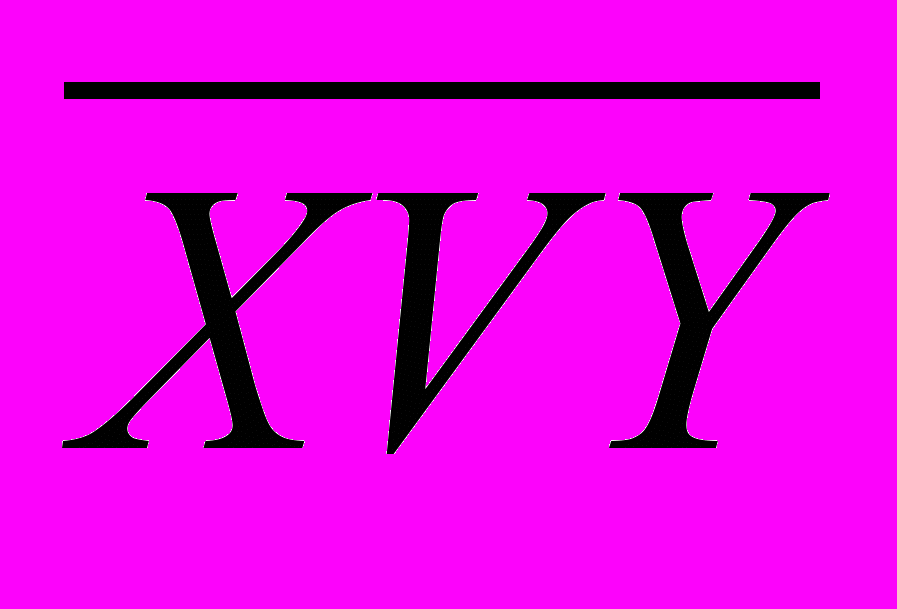 = = 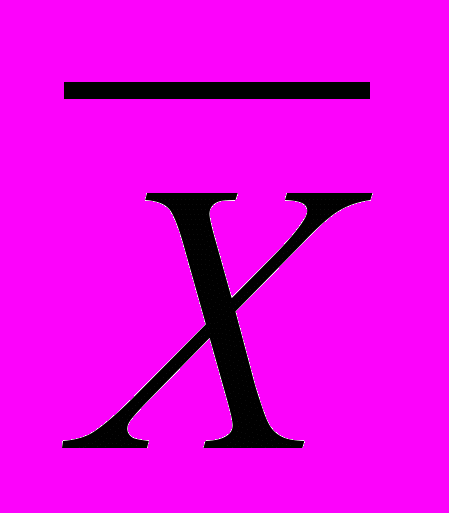 & & 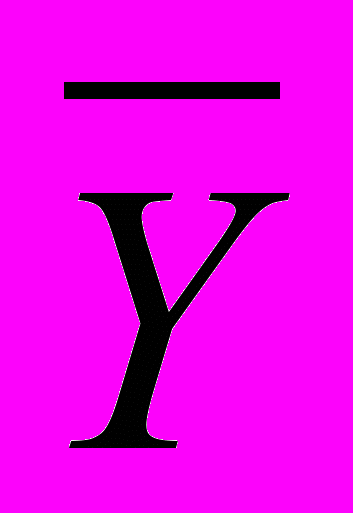 | 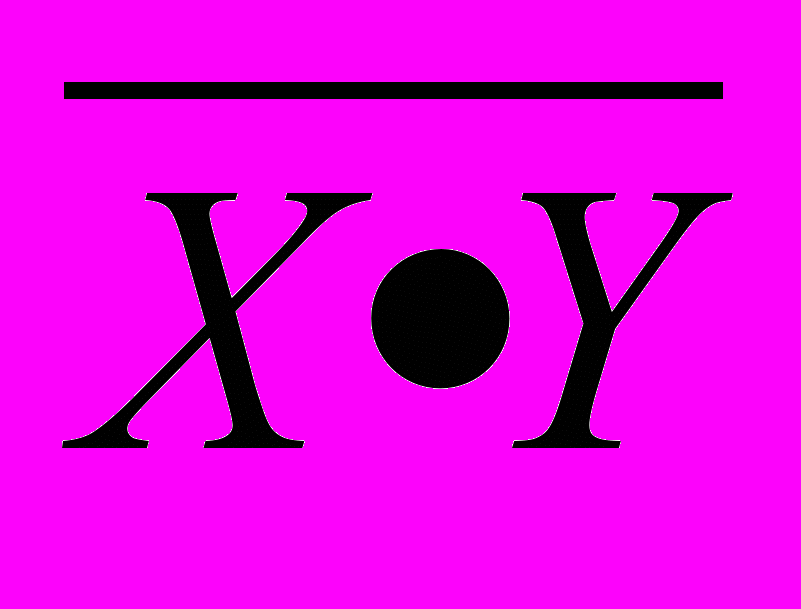 = = 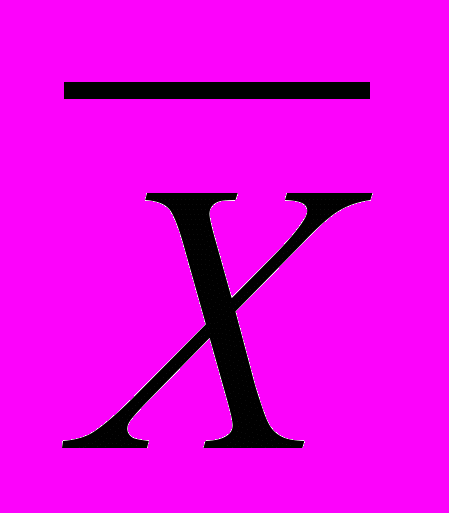 v v 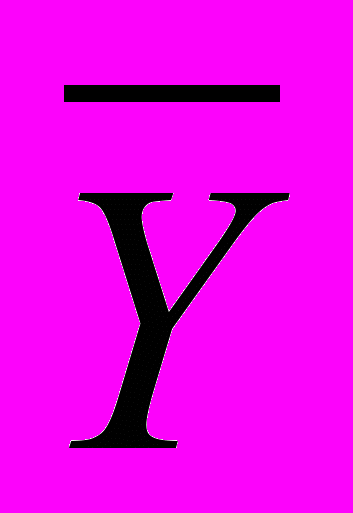 |
| Идемпотенции | x v x = x | x & x = x |
| Поглощения | x v x & y = x | x& (x v y) = x |
| Склеивания | (x& y) v ( 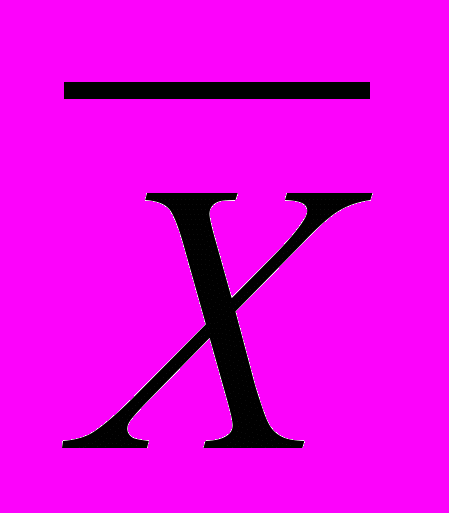 & y) = y & y) = y | (x v y) & ( 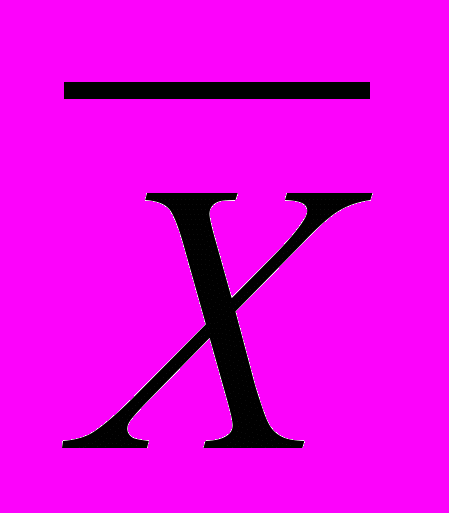 v y) = y v y) = y |
| Операции переменной с ее инверсией | x v x = 1 | х & x = 0 |
| Операции с константами | x v 0 = x; x v 1 = 1 | x& 0 = 0; x& 1 = x |
| Двойное отрицание | 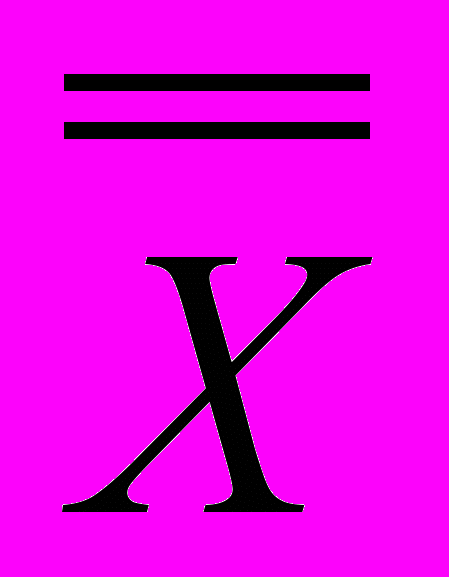 = x = x | |
Равносильные преобразования логических формул имеют то же назначение что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики.
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного, сочетательного законов и т.д.), но есть и другие преобразования (использование распределительного закона для конъюнкции, законы поглощения, склеивания, де Моргана и др.)
Законы алгебры логики применяются в такой последовательности:
- правило де Моргана
- сочетательный закон
- операции переменной с ее инверсией
- операции с константами
Примеры:
-
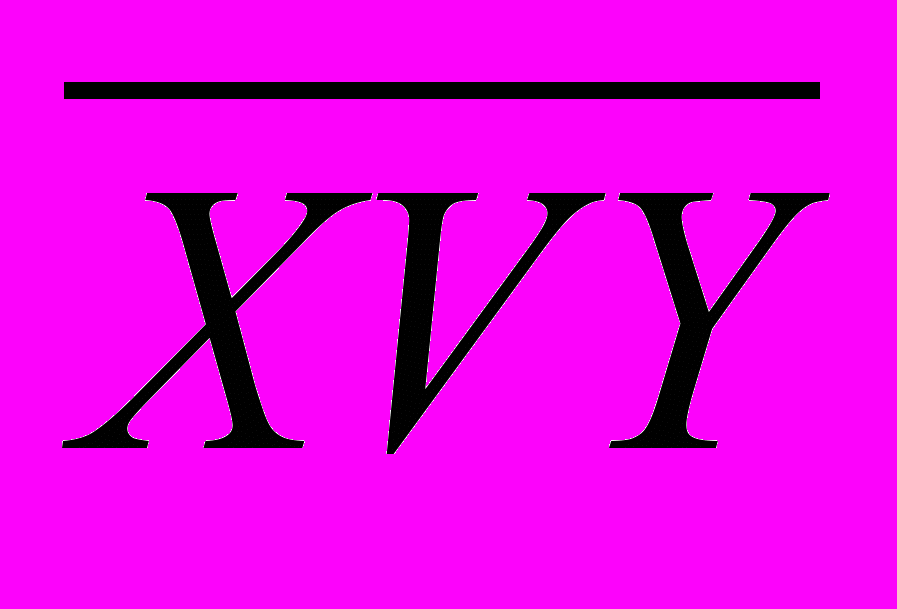 & (x&
& (x& 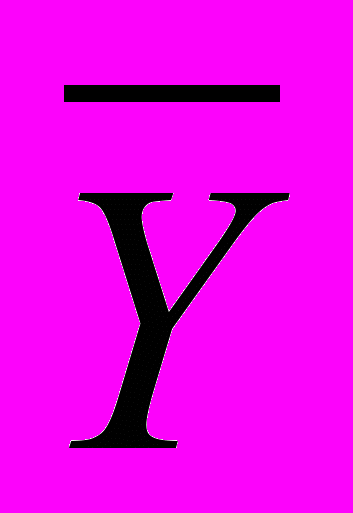 )=
)= 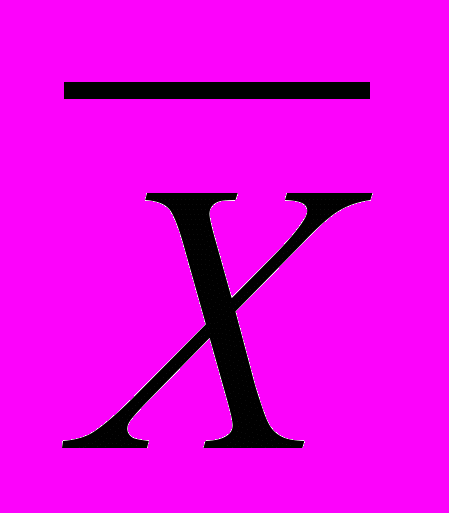 &
& 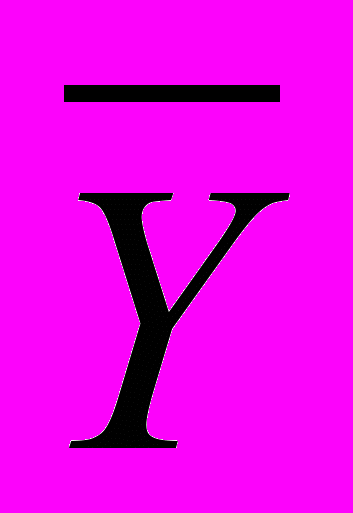 & (x&
& (x& 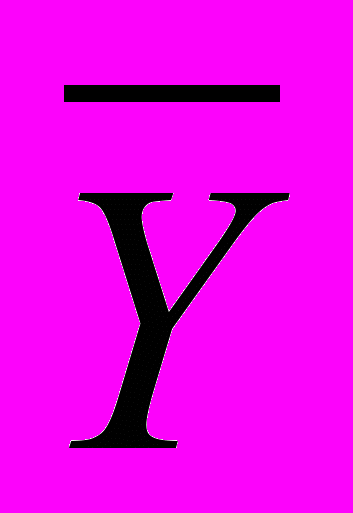 )=
)=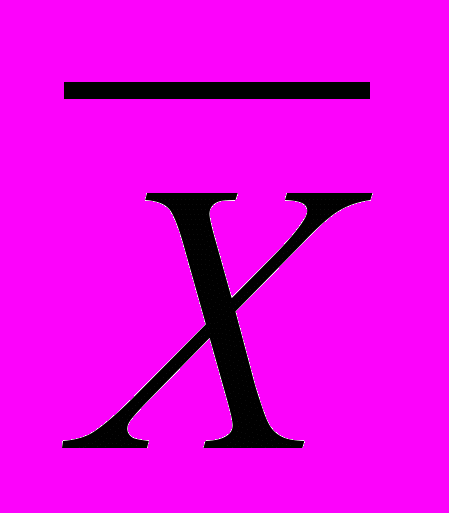 &
& 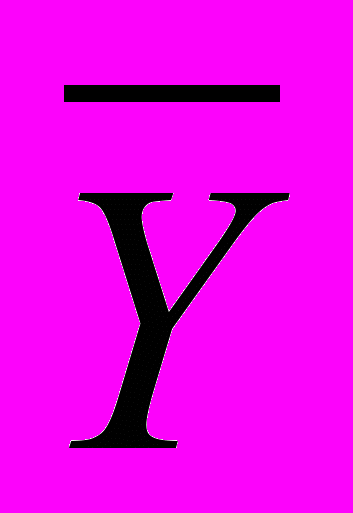 & x&
& x& 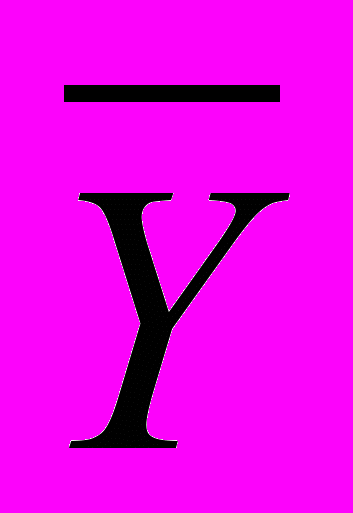 =
= 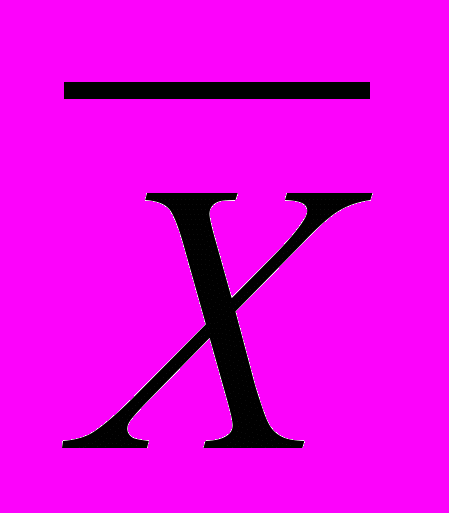 & x &
& x & 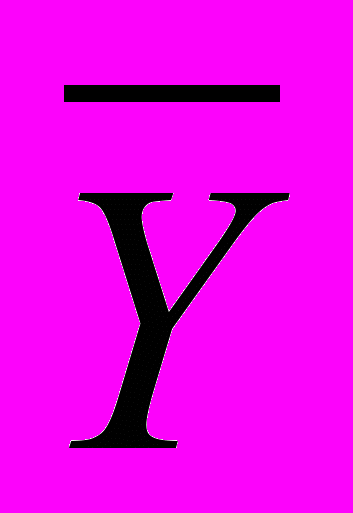 &
& 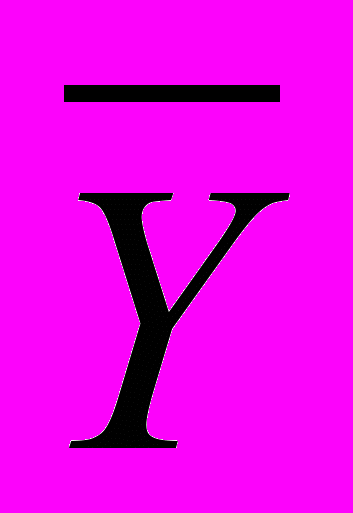 =0
=0
-
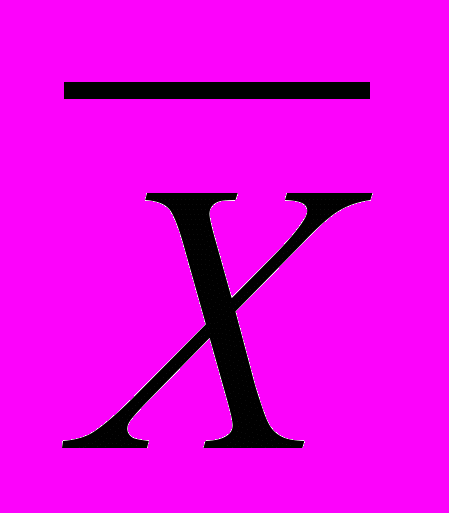 & y v
& y v 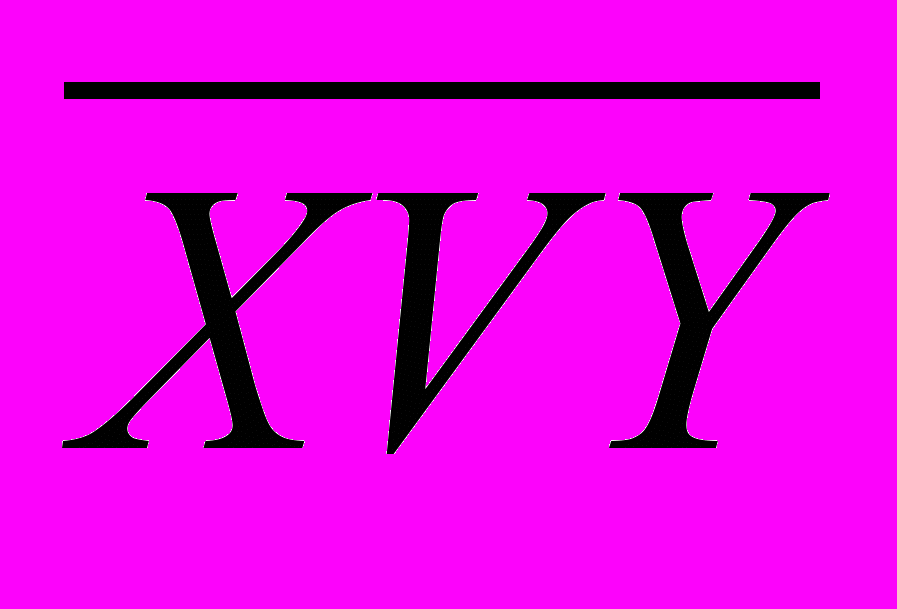 v x=
v x=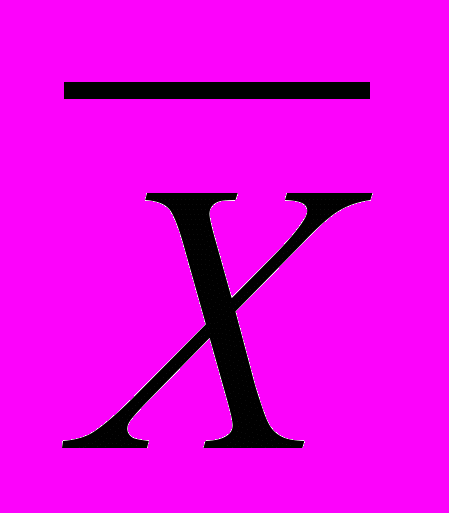 & y v
& y v 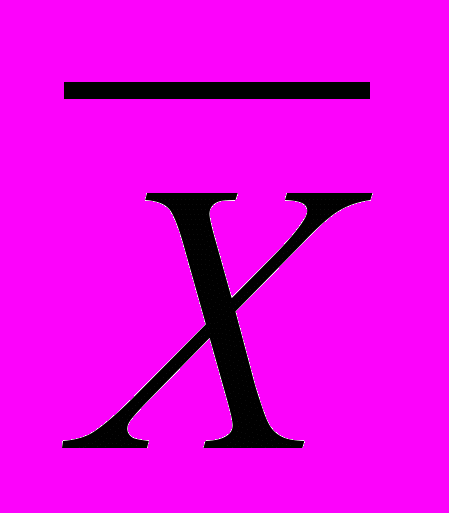 &
&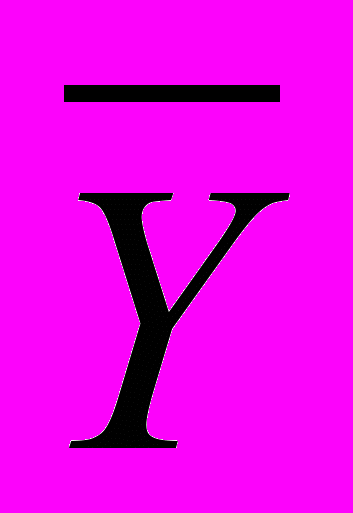 v x=
v x=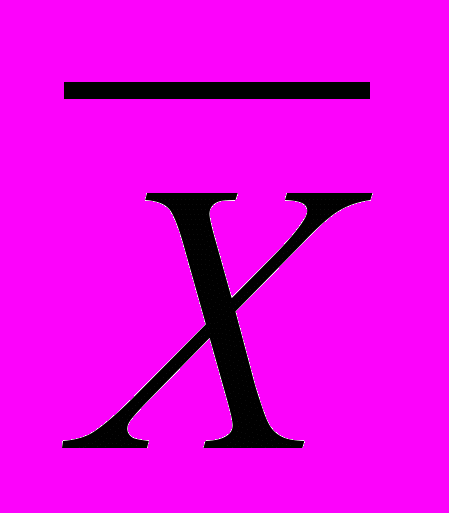 & (y v
& (y v 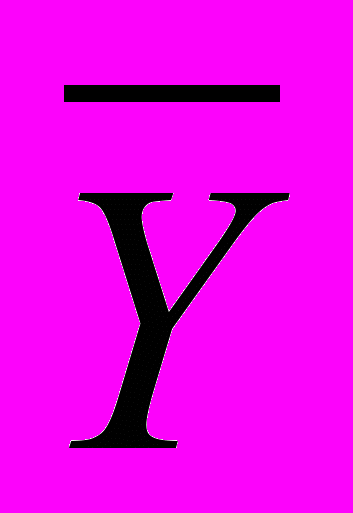 ) v x=
) v x= 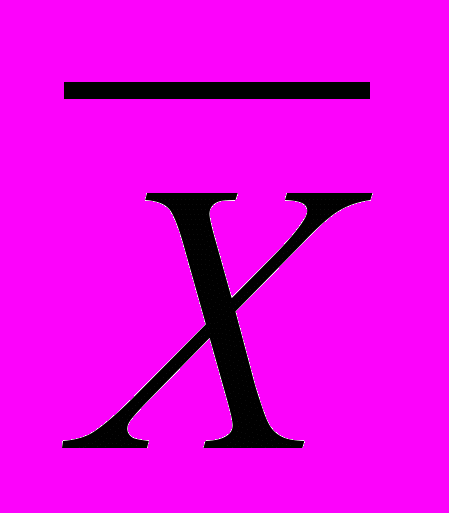 & 1 v x=
& 1 v x=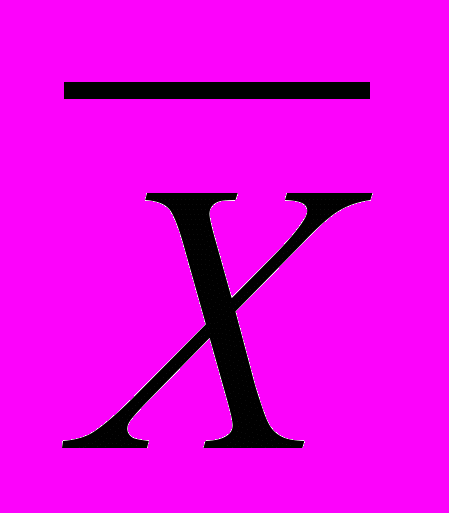 v x=1
v x=1
- (x v y) & (
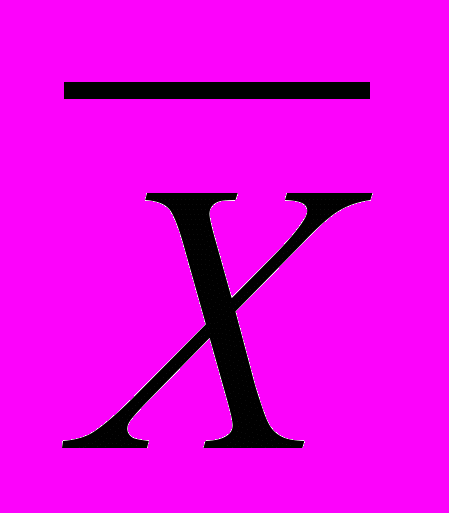 v y) & (
v y) & ( 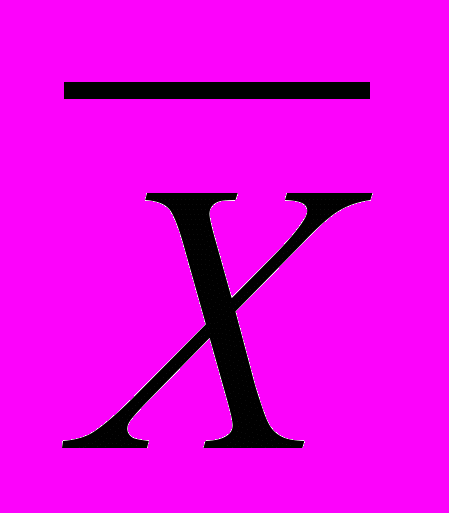 v
v 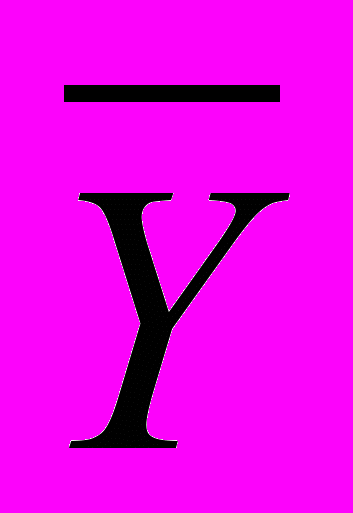 )=(x v y) & (
)=(x v y) & (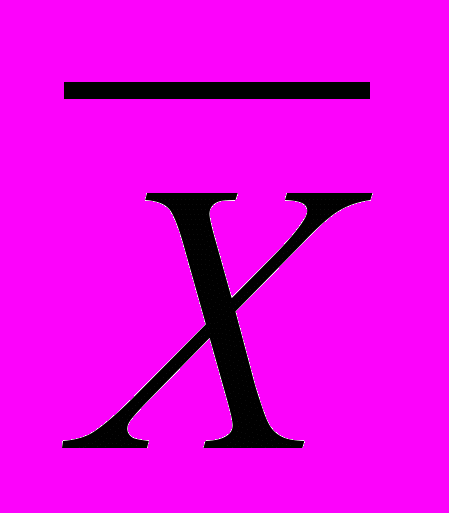 v y) & (
v y) & (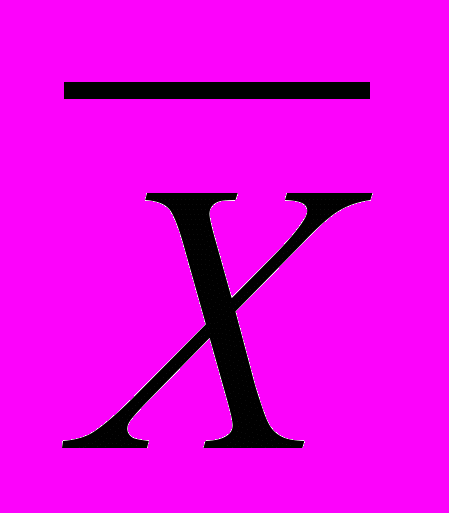 v y) & (
v y) & (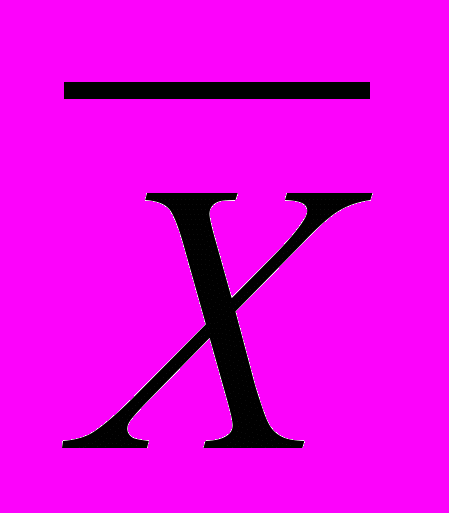 v
v 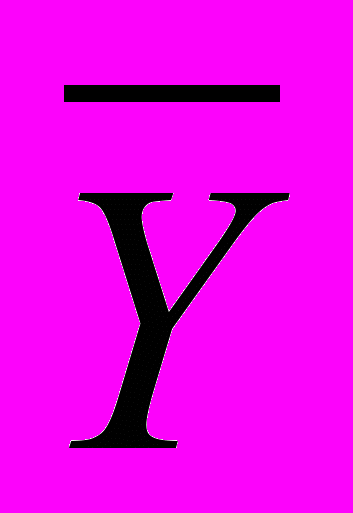 )=y&
)=y& 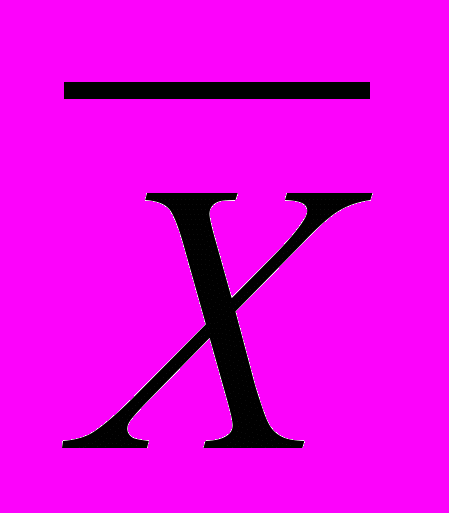
-
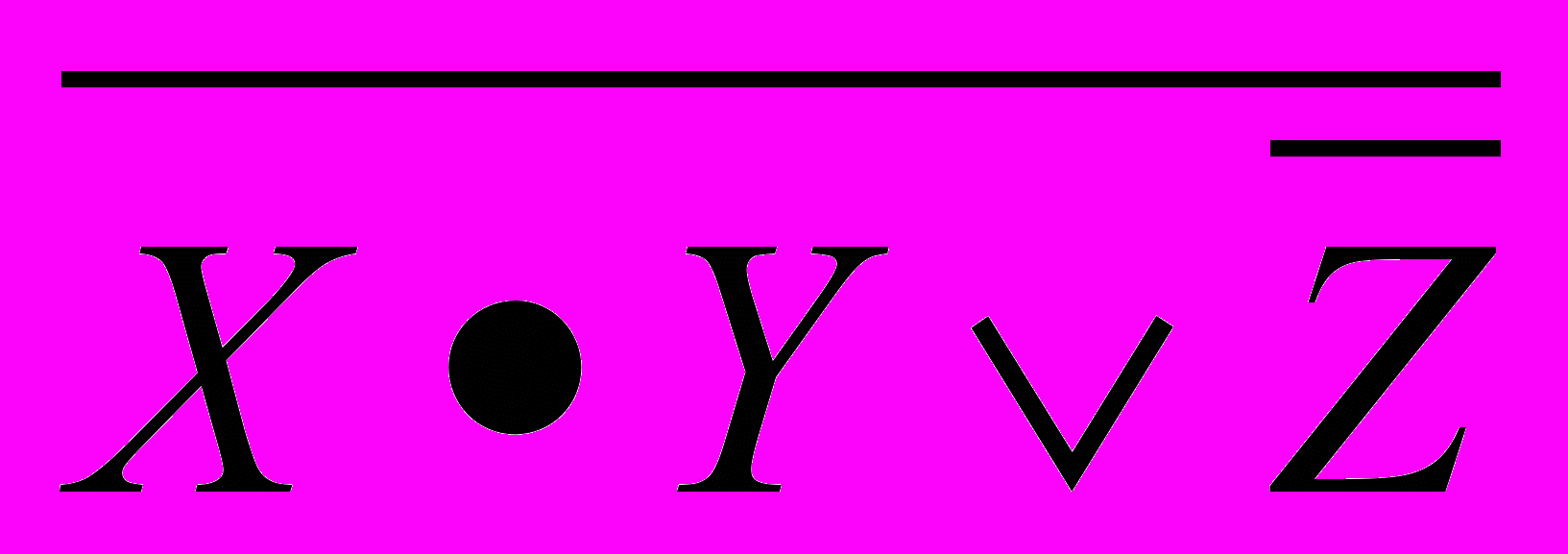 =
= 
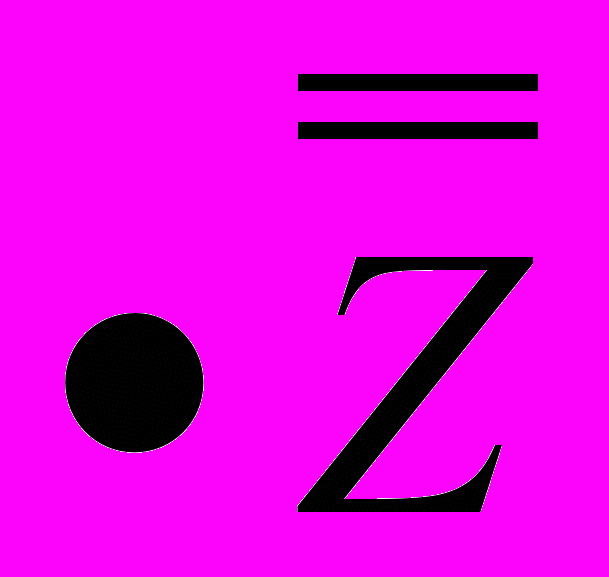 =(
=(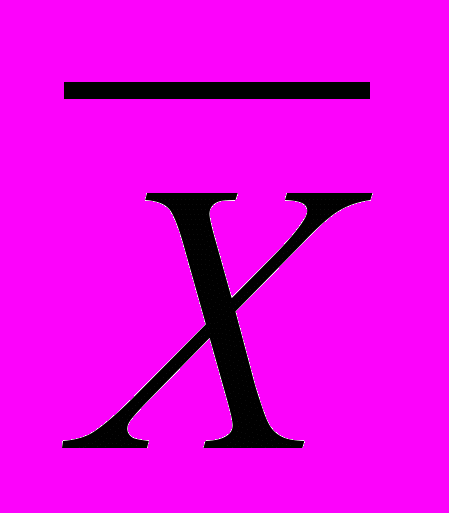 v
v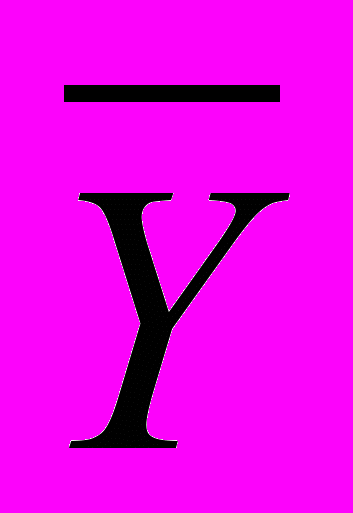 )
)  z
z
Егорчева Светлана Валентиновна, учитель информатики и математики школы №113, г. Казань
