Материя и мышление
| Вид материала | Документы |
- Жан-пьер шанжё, ален конн материя и мышление, 6789.87kb.
- Пространство и материя, 398.24kb.
- Мышление и его патология Мышление, 686.03kb.
- Понятие «критическое мышление» и его характеристики, 304.37kb.
- План: Понятие мышления в психологии. Виды мышления, 126.54kb.
- Триглав Природы Материя, 120.3kb.
- Заключение. Живая материя, 669.86kb.
- Материя. Сотворение. Этика и религия. Мокша. Общая оценка}, 934.61kb.
- Центр "синтез" Н. И. Сиянов. Триумф Виджл-воина. (Конспект), 693.84kb.
- I. Мышление как высший психологический процесс, 10.28kb.
5. Квантовая механика: первичный осмотр
Ж.-П. HL: Я хотел бы вернуться к квантовой механике и к тем выводам, которые можно получить посредством грубого, примитивного, но все же достаточно уместного приложения математики к биологии. Время от времени мы сами превращаемся в математиков, или же сотрудничаем с математиками, стремясь отыскать, скажем так, математическую рамку, которая по возможности наилучшим образом подошла бы к интересующим нас биологическим феноменам. Причем речь идет вовсе не об идентификации биологических реалий с математическими объектами. Мы всего лишь пытаемся сконструировать математические объекты, которые со-
ι
5. КВАНТОВАЯ МЕХАНИКА: ПЕРВИЧНЫЙ ОСМОТР 75
ответствовали бы объектам природным. Мы размышляем, находим решение, разрабатываем модель за моделью, обращаемся к литературе и находим там множественные свидетельства предшествующих нашим попыток и ошибок. И что же мы делаем в результате? Мы выбираем модель, которая лучше всего «сидит». Иначе говоря, наш подход к математике является крайне прагматичным и конкретным. Мы берем от нее только то, что наиболее полно соответствует природной реальности. Математика для нас есть набор мысленных объектов. Ни больше, ни меньше.
В связи с чем мне хотелось бы снова вместе с тобой обратиться к квантовой механике — области физики, которая мало мне знакома. У меня такое чувство, что физики работают в области, в рамках которой им весьма сложно представить то, что происходит в масштабе, очень отличном от того, в котором функционирует наш мозг и органы чувств (см. рис. 14). И когда физик говорит нам, что законы квантовой физики предполагают фундаментальную неопределенность (я умышленно употребляю термины, которыми они пользуются в своих трудах), возникает вопрос, а не совершают ли физики серьезную эпистемологическую ошибку...
А. К.: Ты хочешь сказать «ошибку на языковом уровне»?
Ж.-П. Ш.: Ошибку, которая заключается в идентификации природы и модели, созданной ими для описания этой природы. Учитывают ли они всерьез не только инструмент измерения и взгляд наблюдателя, но и особенности функционирования собственного мозга, равно как и его способность воспринимать явления в том масштабе, в котором повседневный опыт и здравый смысл оказываются неприменимы. Что ты думаешь об этом?
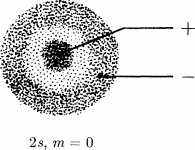
А. К.: Я и сам уже сталкивался с вопросом о фундаментальной неопределенности. Поэтому я смогу тебе ответить. В первую очередь, возникает проблема языка — впрочем, она не является самой важной. Известно, что нельзя представлять частицу как материальную точку с определенными местоположением и скоростью. Если мы хотим, например, построить мысленный образ электрона, вращающегося вокруг ядра атома водорода, то правильнее будет вообразить некую волновую функцию, определяемую уравнением Шредингера и уровнем энергии, нежели планетарную систему. В случае же более сложного атома — например, атома гелия, в котором ядро окружают два электрона, — мысленный образ окажется гораздо более сложным, поскольку волновая функция, пространственную форму которой в случае с одним электроном
76
ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ

Рис. 14. Гравюра из «Трактата о равновесии жидкостей» Блеза Паскаля (1664, 2-е издание, С. Desprez, Париж). Исследуется проблема меры в физике и связи этой меры с экспериментатором. Любопытно, что последний изображен ниже уровня воды.
(см. рис. 15) еще можно хотя бы визуализировать, представляет теперь собой функцию с двумя пространственными переменными, т.е. функцию в шестимерном пространстве. Следующим шагом мы должны понять, что хотя язык частиц и нельзя назвать самым удобным для восприятия, он тем не менее позволяет формулировать вопросы, на которые природа дает ответы. В качестве конкретного примера рассмотрим некий дискретный источник частиц — скажем, электронов, — который время от времени испускает их в направлении очень узкой прорези, создавая эффект дифракции. Можно описать эту систему, отталкиваясь от волновых функций, и предсказать вид дифракционной картины на экране, расположенном за прорезью, в любой точке траектории электрона. Если бы язык частиц никуда не годился, мы сразу получили бы тому доказательство: вследствие дифракции электрон должен был бы трансформироваться в облако. Однако этого не происходит. Проводя опыт, мы каждый раз будем получать попадание в ту или иную точку на экране. Иначе говоря, электрон остается частицей. Именно в подобных опытах и проявляется особенно ярко упомя-
5. КВАНТОВАЯ МЕХАНИКА: ПЕРВИЧНЫЙ ОСМОТР
77

т — О

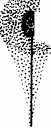
т -
2р, т = О Рис. 15. Пример волновой функции электрона в атоме водорода.
I
78 ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
нутая тобой фундаментальная неопределенность. Всякий раз, как источник испускает электрон, этот электрон действительно ударяется в некоторую точку χ на регистрирующем экране (см. рис. 16). Все дело, однако, в том, что результат такого эксперимента («источник испускает электрон, который затем достигает некоторой точки χ на экране») невоспроизводим в принципе. И это нисколько не зависит от точности задания величины х. Равно невоспроизводим и результат эксперимента «источник испускает электрон, который затем достигает верхней половины экрана». Нам никогда не удастся воспроизвести исходные данные с точностью, достаточной для того, чтобы наверняка получить тот же самый конечный результат. При проведении второго опыта у нас будет не более одного шанса из двух, что результат будет тем же. Какова бы ни была точность испускающего электроны аппарата, мы не сможем повторить опыт с тем же результатом. Воспроизводима лишь частота, вероятность появления электрона в той или иной точке экрана. Единственная воспроизводимая величина — нечто вроде плотности, иначе говоря, кривая частоты попадания электронов в различные точки регистрирующего экрана. Она имеет форму кривой дифракции и позволяет предположить, что электрон прибудет в ту или иную точку с такой-то вероятностью.
Ж.-П.Ш.: Существование фундаментальной неопределенности, тем не менее, не доказано. Аналогичные вещи могут происходить и в гораздо более макроскопических ситуациях, например, при броуновском движении...
А. К.: Если бы так. Необходимо уяснить, что сам факт удара электрона в ту или иную точку экрана ни в коем случае не следует принимать за воспроизведение результата эксперимента. Этот результат не в состоянии предусмотреть ни одна теория, поскольку он невоспроизводим. Если мы намерены заниматься физикой, то нужно четко определить, что такое физическое явление. Как только мы дадим этому понятию связное определение, в квантовой механике больше не возникнет никакой путаницы и никаких парадоксов. Теория замечательно согласуется с соответствующей математической моделью. Какое же определение можно дать понятию «физическое явление»? О физическом явлении можно говорить, только располагая воспроизводимыми экспериментальными результатами. Таким образом, физическое явление есть результат опыта, который, если точно оговорить исходные данные, сможет с идентичным результатом воспроизвести далее экспериментатор
5. КВАНТОВАЯ МЕХАНИКА: ПЕРВИЧНЫЙ ОСМОТР
79
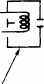
Источник электронов

Прорезь в перегородке
Фотографическая пластинка
Рис. 16. Явление дифракции.
в другой лаборатории. Если же, напротив, мы не можем передать исходные данные настолько точно, чтобы получить при повторении эксперимента тот же результат, то рассматриваемое нами явление не является физическим явлением. Поэтому оно и не может быть предусмотрено теорией.
Ж.-П.Ш.: То есть фундаментальной неопределенности не существует. Тому факту, что электрон в один момент времени попадает в одну точку, а в другой момент — в другую, может, в конце концов, кто-нибудь не сегодня завтра даст детерминистское объяснение.
А. К.: Не даст. Известно, что это явление необъяснимо даже с помощью так называемых «скрытых переменными».
Ж.-П.Ш.: Это потому, что гипотеза скрытых переменных выводится из частной модели. Но, возможно, существует какая-либо другая модель, о которой физики еще не задумывались.
А. К.: Нет. Гипотезу скрытых переменных невозможно совместить с существующей моделью квантовой механики, моделью, единственным оправданием которой служит ее невероятная по-
80 ПРИРОДАг ОДЕТАЯ ПО МЕРКЕ
пулярность. Можно представить последовательность опытов, подтверждающих неравенства Белля, согласно которым интерпретация посредством скрытых переменных совместима с существующей моделью. Моя точка зрения очень проста. Существуют результаты, которые можно назвать физическими, поскольку они воспроизводимы. И есть другие результаты, физическими не являющиеся, поскольку воспроизвести их нельзя.
Ж.-П. Ш.: Я все думаю об употреблении термина «невоспроизводимость». Когда при стимуляции глаза записывают реакцию нейрона, то получают целый пакет импульсов. Однако из опыта в опыт мы вовсе не обязательно записываем при этом одинаковое количество импульсов...
А. К.: Естественно. Зато опираясь на эти результаты, можно вывести некий закон, который будет воспроизводим, и именно это обстоятельство и решает дело в данном случае.
Ж.-П. Ш.: Так и есть. После некоторого количества опытов обнаруживается некий усредненный и вполне воспроизводимый отклик. И многие биологи скажут, что формирование этого отклика можно считать «детерминистским» — от сенсорного рецептора к нейрону, независимо от всевозможных «колебаний», вносящих в процесс свой вклад. Я использую термин «колебания», поскольку речь идет о изменчивости, вызванной более тонкими модальностями передачи сигнала на уровне синапсов, геометрии контактов между нервными клетками и т. д., которые исследователь в опытах такого рода не контролирует. На деле при переносе информации внутри нервной системы существует несколько уровней изменчивости. В них нет ничего загадочного [5J. Если применить такое рассуждение к процессам, которые изучают физики, то возникает вопрос, не в том ли все дело, что те просто пока не нашли модель, которая дала бы более глубокое объяснение. Модель скрытых переменных не работает. Разве не следует, столкнувшись с отрицательным результатом или неудачной интерпретацией, остановиться и задуматься? Возможно, когда-нибудь мы сможем прийти к более рациональному объяснению.
А. К.: В случае с глазом известно, что при повторении опыта с одними и теми же исходными данными каждый раз получается один и тот же пакет импульсов.
Ж.-П. Ш.: Да, теоретически. На практике же это невозможно.
А. К.: В то время как в квантовой механике мы имеем дело именно с теоретической невозможностью; в этом-то и разница.
5. КВАНТОВАЯ МЕХАНИКА: ПЕРВИЧНЫЙ ОСМОТР 81
Ж.-П.Ш.: Боюсь, я не совсем понимаю твое рассуждение. Нечто представляется теоретически невозможным — может быть лишь потому, что до сих пор не была обнаружена адекватная теория?
А. К.: Нет. К сожалению, это очень сложный момент. Моя позиция в этом вопросе вполне однозначна. Некоторые экспериментальные результаты можно счесть физическими явлениями. Однако они таковыми не являются, поскольку невоспроизводимы. Никакая теория не может предсказать явление, если его нельзя воспроизвести.
Ж.-П.Ш.: Но это вовсе не исключает того, что экспериментальный результат может стать физическим явлением. Создается впечатление, что физики оказались во власти теории, которая объясняет природные явления слишком хорошо, и им теперь ни к чему искать — и найти наконец — другую теорию. Разве что они, заинтересовавшись какой-нибудь поставленной задачей, рискнут-таки углубиться в суть вопроса.
А. К.: Согласно теории в ее современном состоянии, фундаментальная неопределенность проявляется непосредственно при измерении двух последовательно наблюдаемых (некоммутируемых) величин; количественно эту неопределенность выражает принцип неопределенности Гейзенберга. Этот принцип имеет не только теоретическую, но и практическую значимость. На экспериментальном уровне квантовая механика ставит проблему проведения опытов и невоспроизводимости их результатов. Если в опыте с электроном я закрываю щель и измеряю отдачу экрана, вызванную попаданием электрона, то это явление можно замечательно воспроизвести и отлично объяснить с помощью физики. Здесь действует закон сохранения импульса. Когда я говорю «При значительном количестве испущенных электронов вероятность попадания в определенную точку на экране имеет такое-то значение», я описываю явление совершенно воспроизводимое и вполне объяснимое с точки зрения теории. Если же я скажу «Электрон прибыл в такую-то точку на экране», то я опишу лишь результат, который экспериментально воспроизвести невозможно.
Ж.-П.Ш.: Под физическим явлением ты понимаешь явление воспроизводимое. Это значит, что нужно определить экспериментальные условия таким образом, чтобы эксперимент впоследствии можно было бы воспроизвести. Если бы мы знали о фактах, опре-
82 ПРИРОДА, ОДЕТАЯ по МЕРКЕ
делающих передвижение электрона вверх или вниз, то мы смогли бы воспроизвести это явление.
А. К.: Того, о чем ты говоришь, нельзя достичь, не изменив результата, даже на статистическом уровне.
Ж.-П. ILL: В таком случае, теория никуда не годится.
А. К.: Возможно, однако она точно объясняет воспроизводимые экспериментальные явления. И, как я уже упоминал, с помощью этой теории (правда, в несколько более уточненном виде) стало возможным предсказать, например, так называемый аномальный магнитный момент электрона, с погрешностью измерения, соответствующей погрешности в толщину волоса при измерении расстоянии от Парижа до Нью-Йорка.
Ж.-П. ILL: Необъясненным остается наиболее фундаментальный уровень, к которому математики еще не получили «мысленного» доступа. Модель Ходжкина и Хаксли отлично подходит для объяснения электрических феноменов в нервном импульсе в понятиях ионного переноса. Тем не менее, в ее рамках невозможно непосредственно идентифицировать соответствующие ионные каналы, что удалось, однако, осуществить молекулярному биолоху, использовавшему методы, радикально отличающиеся от тех, что использовали в своих опытах Ходжкин и Хаксли.
А. К.: Я все же приведу иллюстрацию, чтобы показать, как можно избавиться от дискомфорта, возникающего вследствие явной неопределенности квантовой механики. Если ограничить поле исследований физика воспроизводимыми явлениями, то мы получим совершенно связное единое целое, а невозможность предсказать, в какую точку угодит электрон, — это своего рода отступление, вызывающее сильную фрустрацию у теоретика. Возьмем пример, хорошо знакомый физикам: параллельные вселенные Эверет-та [32]. Все выглядит так, будто могут происходить все возможные события, что электрон может ударить в любую точку на экране. Однако каждый из этих возможных вариантов означает бифуркацию вселенной на две параллельных вселенных. Простоты ради предположим, например, что мы производим измерение с двумя возможными результатами. Это измерение, таким образом, создает бифуркацию на две параллельных вселенных. Мы окажемся в одной из них или в другой, в зависимости от той или иной реализованной возможности. Взаимосвязанность этих двух параллельных вселенных достаточна для того, чтобы в статистике средний результат был одинаковым. Каждый результат опыта
5. КВАНТОВАЯ МЕХАНИКА: ПЕРВИЧНЫЙ ОСМОТР 83
зависит от той конкретной параллельной вселенной, по отношению к которой происходит бифуркация. Сам по себе результат не воспроизводим.
Ж.-П. Ш.: Идея мне кажется интересной. Но умело поддерживаемая путаница между невоспроизводимостью и неопределенностью наводит на мысль, что большинство теоретиков бессознательно просто отказываются признать, что они потерпели здесь неудачу.
А. К.: Нельзя даже надеяться на возможность предсказания невоспроизводимого результата. Главным свойством физического эксперимента — думается, в этом вопросе все со мной согласятся — является его воспроизводимость. Если эксперимент невозможно воспроизвести, значит, он не обладает физическим содержанием. Неудача здесь не в теории, а в эксперименте. Настраивая экспериментальную установку, мы не приходим к знанию того, как уточнить исходные данные так, чтобы заранее знать точку попадания электрона. Принцип неопределенности Гейзенберга показывает, что достичь этого абсолютно невозможно; та же неопределенность проявляется и тогда, когда мы последовательно измеряем две наблюдаемые величины, которые не коммутируют между собой (как, например, в опыте Штерна - Герлаха).
Ж.-П. Ш.: Может быть, ты смог бы найти способ управлять каким-либо физическим параметром, на который раньше никто не обращал внимания. Это способ может быть как теоретическим, так и экспериментальным. Было бы пикантно, если бы провести эксперимент физикам предложил математик!
А. К.: И все-таки важно понять, что эта неудача есть неудача эксперимента. Поэтому мне и нравится приводить именно этот пример. Как правило, значение придают только теории, хотя эксперимент в данном случае играет роль едва ли не большую: в конце концов, наблюдаем мы именно экспериментальный результат, и именно этот результат не поддается воспроизведению.
Ж.-П.Ш.: Хороший эксперимент поставить гораздо сложнее, чем выдумать посредственную теорию. И наша беседа со всей очевидностью показывает, что в этой загадочной неопределенности, о которой говорят некоторые физики, особого смысла нет. Скорее всего, следует смириться с тем, что состояние наших знаний не позволяет нам пока оперировать этими понятиями, как в экспериментальном плане, так и в плане теории. Мне как-то сложно принять в качестве закона природы собственное невежество...
84
ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
А. К.: Действительно, в рамках существующей вполне связной системы воззрений мы научились объяснять воспроизводимые экспериментальные результаты. Я просто не представляю себе, как можно достичь понимания результатов невоспроизводимых. Весьма сложно принять, что на микроскопическом уровне, на квантовом уровне, существуют явления, которые мы не в состоянии воспроизвести. Впрочем, неприятие факта не отменяет самого факта. Сложно оценить и его последствия в философском смысле. Непостижимо, что на атомном уровне природные феномены абсолютно непредсказуемы. Даже физико-химическая «реальность» оказывается гораздо неуловимее, чем кажется на первый взгляд.
Нейронный математик
1. Озарение
ЖАН-ПЬЕР ШАНЖЁ: В наши дни немногие математики занимаются исследованием мозга. Читая книгу Дьедонне «Во славу человеческого разума» [28] — название которой немного напоминает Ad majorem dei gloriam1 Игнатия Лойолы, — я заметил, что слово «мозг» употребляется на ее страницах очень редко. Во всяком случае, не с объясняющей целью. Как раз совсем наоборот. Например, он пишет: «Рациональная активность творящего мозга никогда еще не получала равно рационального объяснения. Причем в математике меньше, чем где бы то ни было» [28, с. 38]. В этой книге, которая мне очень нравится, и которую я прочел с большим интересом, Дьедонне рассматривает развитие математики совершенно независимо от мозга — примерно так же историк искусства увлеченно исследует развитие живописи и скульптуры, не желая отдавать себе отчет в том, что и видим-то мы, по большей части, мозгом, а не глазами! Хорошо бы напомнить, что математик занимается математикой, все же используя свой мозг, иначе и быть не может!
АЛЕН Конн: Полностью с этим согласен. Мозг — материальный инструмент математика; понимание принципов функционирования мозга в применении к работе математика крайне важно.
Ж.-П. Ш.: Сходные соображения мы находим и у некоторых математиков прошлого — например, у Пуанкаре и Адамара. В своем замечательном «Эссе о психологии изобретения в математике» [49] Адамар размышляет о бессознательном и его последовательных слоях, участвующих в процессе математического творения. Он приводит выдержки из книги «Об уме и познании» Ипполита Тэна, философа, который еще удостаивал своим вниманием научные данные (в особенности это касается наук о нервной
*«К вящей славе Господней» (лат.) — Прим. перев.
86 НЕЙРОННЫЙ МАТЕМАТИК
системе), интерес к которым со времен Сартра, Фуко и их последователей постепенно сместился у многих современных философов в сторону психоанализа, хотя в последнее время начинают появляться исключения из этого правила, и весьма притом заметные [63].
Адамар описывает свою работу математика в очень интересной, на мой взгляд, манере. В первую очередь, он выделяет подготовительную работу, которая неизбежно включает в себя — причем здесь я с ним полностью согласен — провалы и ошибки, даже если математик скромно умалчивает об этом, представляя свои результаты в «хорошо переработанном», как правило, виде. Как и Пуанкаре, Адамар пытается свести вместе эти попытки «управления бессознательным» и различает в «математическом творчестве» несколько этапов, которые он называет «подготовка», «созревание» и «озарение». Он также подчеркивает важность использования знаков, равно как и методов мысленной визуализации, и ссылается на современного ему психолога Бине, который, как и Тэн, очень интересовался экспериментами по визуализации, начатыми английскими ассоциационистами. Замечательно, что совсем недавно этот интерес к мысленной визуализации снова проявился в экспериментальной психологии — через посредство таких авторов, как Косслин, Шепард и наш соотечественник Дени [22]. Здесь мы встречаемся с совместной заинтересованностью психологов и нейробиологов. Мысленный образ не следует рассматривать как нечто эфемерное и нематериальное, напротив, это результат весьма конкретной и вполне определенной активности мозга. Адамар указывает на то, что во время подготовительной работы, когда в мозге математика начинают возникать образы, иногда случается так, что его собственный мозг и чувства внезапно охватывает некое озарение. Оно составляет очень важный этап в творческой работе математика. Необходимо, впрочем, чтобы за озарением последовал третий этап, более осознанный, нежели предыдущий. Он состоит из проверок и определений, позволяющих более точно сформулировать рассуждение, теорему или доказательство. На этом последнем этапе вводятся такие понятия, как суждение и рассуждение.
Способ рассуждения Адамара относится к интроспективному типу. Он всегда подвергается критике психологов, философов и, естественно, нейробиологов, поскольку он субъективен. Тем не менее, это рассуждение весьма интересно, так как вы-
ι
1. ОЗАРЕНИЕ 87
ражено в форме повествования, обладающего некоей объективностью — его могут воспроизвести и другие математики. Что ты думаешь об этом описании математического творчества, предложенного Пуанкаре и Адамаром?
А. К.: Я сам пережил — по крайней мере, мне так кажется — такого рода опыт. Первая фаза, созревание, представляет собой подход, основанный на уже приобретенных знаниях: мы постепенно концентрируемся на каком-то определенном мысленном объекте. Мы пытаемся сфокусировать свою мысль, подготавливаем рабочее пространство, окружаем себя знакомыми вещами. Третья фаза, верификация, начинается тогда, когда озарение уже произошло. Процесс верификации очень мучителен, так как всегда опасаешься, что где-то ошибся. Это самая болезненная фаза, поскольку невозможно узнать наверняка, права ли твоя интуиция... это почти как во сне, интуиция часто обманывает. Я помню, как однажды проверял полученный результат целый месяц: возвращался к малейшим деталям доказательства, это было вроде наваждения, хотя эту задачу можно было, в крайнем случае, доверить и компьютеру, который проверил бы логику рассуждения. А с другой стороны, когда озарение уже произошло, оно привносит значительную долю аффективности, так что ты уже не можешь остаться пассивным и безразличным. В тех редких случаях, когда со мной действительно происходило такое, я каждый раз не мог сдержать слезы. Я часто сталкивался со следующей ситуацией: в определенный момент, когда первый, подготовительный, этап уже завершен, натыкаешься на стену. Здесь ни в коем случае не следует совершать распространенной ошибки и переходить сразу к самому сложному. Нужно продвигаться неявно, где-то вблизи задачи. Если думать непосредственно о задаче, то накопленные в первой фазе средства очень быстро исчерпываются, и приходится отступать. Необходимо освободить мысль для того, чтобы в мозге могла совершаться подсознательная работа. Например, когда производишь алгебраические исчисления, относительно простые, но довольно длинные, мысль в течение этого времени не полностью сфокусирована на задаче, что благоприятствует подключению к работе подсознания. Естественно, математик должен быть при этом достаточно спокоен. Так можно достичь своего рода созерцательного состояния, которое не имеет ничего общего с состоянием концентрации студента, сдающего экзамен по математике. Воспользовавшийся этой техникой на экзамене студент, выйдя из
88 НЕЙРОННЫЙ МАТЕМАТИК
аудитории, скажет: «Я провалил экзамен, но мне пришла в голову идея, над которой я хочу еще поработать». Меня каждый раз поражает (я все еще о неявном подходе к задачам) величина видимой удаленности исходной задачи от того, чем я в данный момент занимаюсь.
Ж.-П. III.: Конечно. В течение всего этого периода полным ходом идет развитие твоего мозга. Ты строишь гипотезы, создаешь заготовки...
А. К.: Но задача-то стоит на месте.
Ж.-П. Ш.: Как же тогда неожиданно возникает решение задачи, если ты ходишь вокруг да около?
А. К.: Это достаточно трудно описать. Опыт показывает, что, если приступать к решению самой задачи непосредственно, то ресурсы такого «прямого», рационального, мышления очень быстро исчерпываются. Зависит, конечно, от сложности задачи, но если не достичь полного освобождения, то решение, как правило, не приходит. И все происходит с точностью до наоборот, когда речь идет о решении задачи, скажем, на экзамене, когда необходимо просто автоматически выполнить некие действия. Эта стадия примерно соответствует фазе концентрации всех знаний о данной задаче, которыми располагают математики. При этом мы легко уточняем задачу, точно определяем степень ее сложности, но дальше прямая мысль уже не помогает. Продвинуться можно только в том случае, если в наличии есть стратегия, пусть и неявная, состоящая в том, чтобы рассмотреть все дополнительные вопросы, не имеющие a priori отношения к самой задаче.
Ж.-П. Ш.: Совершенно посторонние вопросы или все же связанные с поставленной задачей?
А. К.: Бывает, совсем посторонние.
Ж.-П. Ш.: Идет ли речь в данном случае лишь о том, чтобы занять рабочую память и позволить происходить на более глубоком уровне работе бессознательной, предполагающей более значительный вклад долговременной памяти? Или это, напротив, своеобразная ассоциативная процедура, которая занимает много времени, т.к. соединяющиеся элементы относятся к очень разным контекстам? Я так понимаю, «хождение вокруг задачи» позволяет задействовать математические объекты, которые не имеют к ней непосредственного отношения. По совокупности они приводят к решению или вызывают каким-то окольным путем, обращаясь к долговременной памяти, наиболее соответствующее по-
1. ОЗАРЕНИЕ 89
ставленному вопросу представление. Идет ли речь о процессе сокрытия рациональной мысли, ослабления работы сознания, который дает проявиться внутренним «посторонним» представлениям и позволяет математическим объектам сочетаться «против природы»? Не находишь ли ты, что конечное решение включает в себя, в некоей «химерической» форме, все эти элементы параллельного размышления? Причины своего вопроса я объясню позже.
А. К.: Я могу говорить только о собственном опыте. Хотя мои размышления и касались одного вопроса, они a priori не пересекались. Они вели к решению самой задачи, хотя ни на минуту не были направляемы этой задачей.
Ж.-П. Ш.: Но задача все же присутствовала где-то внутри твоего мозга.
А. К.: Возможно. Однако я совершенно этого не сознавал. Я задавал себе другой вопрос, отвечал на него, и это как-то вело меня к решению первой задачи.
Ж.-П.Ш.: Я снова спрошу: когда ты используешь для решения задачи связанное или не связанное с этой задачей знание, присутствует ли использованный математический материал в конечном решении в сколько-нибудь «рекомбинируемой» форме?
А. К.: Сложно сказать. Задача заключалась в следующем: доказать, что некий объект, вполне определяемый и, как нам было заранее известно, реализуемый, допускает одну и только одну реализацию. Техническая задача, весьма сложная, к ней очень трудно было подступиться напрямик, поскольку все средства, имеющиеся в нашем распоряжении, очень быстро себя исчерпали. Благодаря тому, что я переключился на соседнее, никак не связанное с прежним, поле исследования, располагавшее большим количеством более доступных объектов для изучения, я получил некоторые навыки и интуитивные представления, которые и применил затем к решению первой задачи. Иначе говоря, для успеха необходимо было сменить окружение, выбрать какое-нибудь не связанное явно с решаемой задачей поле исследования.
Ж.-П. Ш.: То есть ты использовал скорее окружение, чем мысленные объекты.
А. К.: Именно так. Окружение, в рамках которого моя мысль могла перемещаться и развиваться, тогда как в узко определенном контексте задачи мысль, будучи загнанной в угол, застывает, блокируется сложностью.
90 НЕЙРОННЫЙ МАТЕМАТИК
Ж.-П.Ш.: Ты в некотором роде расширил контекст с тем, чтобы ввести изменчивость. Здесь твои действия полностью согласуются с дарвиновской эволюцией. Ты определяешь период, в течение которого сознательно или бессознательно порождаются вариации, сочетаются мысленные объекты и формируются окружения внутри плана более общего, нежели план поставленной задачи.
А. К.: Для простоты скажем так: математики, которым не удается решить задачу, имеют привычку обобщать ее и отыскивать затем частное с помощью общего. Такое начало и в самом деле позволяет обнаружить недостающий кусочек мозаики. При этом мы, разумеется, надеемся, что решение частного случая обобщенной задачи, которая имеет мало общего с задачей исходной, позволит получить некую идею, которая, в свою очередь, окажется применимой к решению этой самой исходной задачи. Таким образом, мы пытаемся обобщить для того, чтобы раскрыть какие-то ранее неизвестные аспекты поставленной задачи. Мы продвигаемся постепенно, относительно медленно и подбираемся, в конце концов, к рассматриваемому объекту.
Ж.-П.Ш.: Иначе говоря, пытаемся сочетать элементы, помещая их в более широкий контекст, несмотря на то, что до этого они были разделены.
А. К.: Не следует смешивать подсознательный процесс второго этапа и упомянутую мною только что программу, по которой он осуществляется и которая принадлежит к культурному достоянию человечества. Это — просто стратегия, в ней нет ничего бессознательного, поскольку она известна всем специалистам. Однако у меня часто возникало впечатление, что церебральный механизм располагает некоей системой, которая, как бы это сказать, не открыта, — ее нельзя воспринимать непосредственно, но она основана на очень похожих механизмах.
Ж.-П.Ш.: Вполне возможно, что в памяти присутствует ряд объектов, едва достигающих уровня того, что можно назвать сознанием. Происходит некая мысленная работа, причем не все производимые операции оказываются подконтрольны воле. Это применимо как к математике, так и к мышлению вообще. Мышление без помощи языка возможно [102]. Твой опыт математика подтверждает для меня случайность фазы созревания и заставляет предположить, что в течение этой фазы рекомбинируемые во времени дарвиновские вариации производятся посредством переходов. В определенный момент одна из них оказывается адекватной по-
1. ОЗАРЕНИЕ 91
тавленной задаче и в этом расширенном контексте обеспечивает решение: это и есть озарение!
Можешь ли ты уточнить, поскольку это очень важно, каковы условия этой адекватности? Вызывается множество преходящих математических объектов, сознательных или бессознательных, а затем вдруг все увязывается, ключ входит в замочную скважину, и дверь открывается. По схеме «мысленного дарвинизма» [14] за этапом вариаций «генератора разнообразия» следует «процесс отбора».
А. К.: Вряд ли можно быть уверенным в том, что в ходе второй фазы эту роль исполняет именно генератор разнообразия. Твоя модель подошла бы для компьютеров, играющих в шахматы. Они демонстрируют относительно дарвиновское поведение: производится большое число попыток, которые ни к чему не привели бы, если б не было функции отбора, которая одновременно измеряет выгоду от нескольких ходов и силу позиции, к которой они приведут. Нам остается ввести величину, которая выражала бы эту выгоду и силу позиции и которую компьютер мог бы оптимизировать. Чтобы отыскать в функционировании мозга математика, решающего задачу, дарвиновский механизм, следует начать с поиска аналогов этой функции отбора.
Математикам хорошо известно, что понимание теоремы не означает понимания каждого шага доказательства, расшифровка которого может длиться несколько часов. Здесь, напротив, речь идет о целостном видении всего доказательства за чрезвычайно краткий промежуток времени. Мозг должен быть способен «проверять» — не знаю, каким образом — все доказательство за одну или две секунды. Уверенность в том, что ты понял теорию, возникает только при условии возникновения вот этого самого чувства. А вовсе не в результате того, что ты можешь провести все доказательство от начала до конца без единой ошибки — это всего лишь локальное понимание. Момент озарения «производится» механизмом, который я не в состоянии определить, обеспечивающим, что ключ откроет замок. Для того, чтобы убедиться в наличии в мозге дарвиновского механизма, необходимо понять, какой тип функции оценки используется в фазе созревания для выбора решения задачи. В самых общих чертах мы могли бы тогда сказать, что в течение первой фазы происходит построение, причем вполне сознательное, функции оценки, обусловленное аффективностью, которая выражается приблизитель-
92 НЕЙРОННЫЙ МАТЕМАТИК
но следующим образом: «я хочу решить эту задачу». Дарвиновский механизм соответствовал бы в этом случае фазе созревания, так как озарение происходит только тогда, когда значение функции оценки достаточно велико для того, чтобы вызвать аффективную реакцию.
Ж.-П.Ш.: И тогда мы слышим не тревожный звон, а звонок удовольствия...
А. К.: ...который дает нам понять, что все, что мы нашли, работает, что все это связно и, можно даже сказать, эстетично. Это удовольствие, я уверен, схоже с удовольствием, которое испытывают художники, находя свое решение, придающее картине совершенно целостный и гармоничный вид. Работа мозга должна быть при этом в точности такой же. Впрочем, слово «дарвиновский», как мне кажется, указывает на нечто таинственное, что ставит проблему функции отбора и величины, подвергаемой оптимизации.
Ж.-П. III: Разумеется. Однако ничего таинственного здесь нет. Механизм мышления основан на отборе. Мы прибегли к дарвиновскому рассуждению, главным образом, для того, чтобы определить фазы, которые иначе остались бы неразличимыми или неясными. Модель становится интересной, если с ее помощью мы можем продвигаться вперед — если и не в понимании, то, как минимум, в анализе.
