Материя и мышление
| Вид материала | Документы |
- Жан-пьер шанжё, ален конн материя и мышление, 6789.87kb.
- Пространство и материя, 398.24kb.
- Мышление и его патология Мышление, 686.03kb.
- Понятие «критическое мышление» и его характеристики, 304.37kb.
- План: Понятие мышления в психологии. Виды мышления, 126.54kb.
- Триглав Природы Материя, 120.3kb.
- Заключение. Живая материя, 669.86kb.
- Материя. Сотворение. Этика и религия. Мокша. Общая оценка}, 934.61kb.
- Центр "синтез" Н. И. Сиянов. Триумф Виджл-воина. (Конспект), 693.84kb.
- I. Мышление как высший психологический процесс, 10.28kb.
2. Поразительная эффективность математики
А. К.: Я далек от мысли, что математическая реальность располагается в физическом мире. И я совсем не пытаюсь отождествлять природные объекты с объектами математическими. Проведя границу между математической реальностью и реальностью физической, мы сталкиваемся с проблемой их отношений между собой. Приведу для начала пример того, что Юджин Вигнер называет «непостижимой эффективностью математики», которая, в общем случае, не сводится только лишь к попыткам адекватно «оформить» природные закономерности. Я говорю о теории узлов [3] (см. рис. 9 и 10). Когда берешь веревку и завязываешь сложный узел, то всегда встает вопрос о том, сможешь ли ты потом его распутать, не прибегая к методу гордиева узла. Так вот, существует одна замечательная теория, которая позволяет в большинстве случаев эту проблему разрешить: называется она теорией узлов. Эта теория не так давно весьма серьезно продвинулась вперед, хотя изначальные устремления ответственного за этот прогресс математика не имели к узлам никакого отношения. Мы с новозеландцем В. Джонсом начинали работу над совсем другой проблемой.
2. ПОРАЗИТЕЛЬНАЯ ЭФФЕКТИВНОСТЬ МАТЕМАТИКИ
57
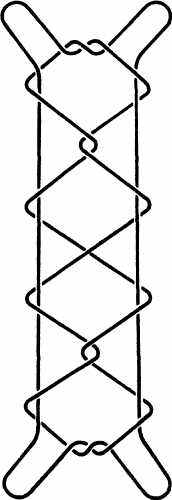
Рис. 9. Лестница Иакова. Этот узел знаком многим детям, его завязывают, пропуская между четырех пальцев веревочную петлю и продевая затем свободные концы между другими пальцами. Эта лестница Иакова, очевидно, эквивалентна самому обычному узлу на петле. Эскимосы и североамериканские индейцы обожают такие игры с веревкой, демонстрирующие бесконечные возможности реализации геометрических мотивов при помощи петли, простейшего из узлов. (Теория узлов)
58
ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
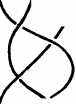
Коса
Соответствующий узел


Узел "клеверный лист" Его отображение
Рис. 10
2. ПОРАЗИТЕЛЬНАЯ ЭФФЕКТИВНОСТЬ МАТЕМАТИКИ 59
Потом он заинтересовался одной деликатной проблемой анализа в бесконечномерном пространстве. Речь шла о том, чтобы классифицировать подмножители одного данного множителя — куда уж, казалось бы, дальше от теории узлов. Долгое время он работал один, и никто не верил, что то, над чем он работает, может представлять какой бы то ни было интерес. Все полагали, что он лишь зря теряет время. Спустя несколько лет ему удалось доказать, что индекс подмножителя принимает дискретные значения или имеет непрерывный спектр. Джонс обнаружил, что в процессе доказательства возникала группа, известная как «группа кос», о которой у нас имеется вполне конкретное представление, в основе которого лежат самые обычные косы, получаемые переплетением нескольких нитей. Сначала это была всего лишь простая картинка. Выступая на конференциях, он иллюстрировал свое представление об этой группе, рисуя косы. Наконец, в Нью-Йорке он встретился с топологом по фамилии Бирман и, беседуя с ней, заметил, что его построение, след на алгебре группы кос, дает, по сути, новый инвариант для узлов. Он вычислил этот инвариант на узлах самого простого типа, названных им «клеверными листами», и обратил внимание на тот факт, что если отразить такой узел в зеркале, то его инвариант уже не будет тем же, что прежде. Джонса это удивило, поскольку классические инварианты являются инвариантами и при отражении. Впоследствии на примере большого количества узлов он испробовал всевозможные новые способы вычисления своего инварианта, который, вообще говоря, вычисляется весьма просто, а вот о чисто геометрической его интерпретации нам до сих пор ничего не известно. Этот инвариант чрезвычайно мощен и позволяет различить узлы, которые мы прежде не различали. Он позволяет, например, определять так называемое гордиево число — смысл этого термина думаю, вполне, прозрачен. Развязывая узел, мы обычно вытягиваем концы нити из-под других ее участков до тех пор, пока узел не развяжется; количество нитей, которые необходимо миновать для того, чтобы развязать узел и называется гордиевым числом. С помощью упомянутого инварианта можно определить гордиево число, не развязывая узла! И это очень необычно, так как Джонс начинал работу с чисто математической задачи — с территории, затерянной в одном из самых отдаленных уголков математической географической карты, в одной из самых пустынных ее областей. Однако решение этой задачи привело его прямо к узлам, которые, как тебе известно,
60 ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
находят применение и в биологии, поскольку они участвуют во всякого рода задачах по кодировке очень сложных молекул — таких, например, как полимеры. Теперь, впрочем, он активно исследует возможности практического применения своих результатов к вполне конкретным задачам. Вот отличная иллюстрация труднопостижимой мощи математики ради математики, если подходить к этой самой математике без предвзятых идей о возможных дальнейших применениях тех или иных открытий.
Ж.-П. Ш.: Рассказанная тобой история все же подразумевает некое познание на основе опыта.
А. К.: Опыт здесь ни при чем. Здесь, скорее, совпадение.
Ж.-П.Ш.: Да, в конечном счете, .. . когда он встретил ту то-пологиню и в результате этой встречи пришел к тому, чтобы соотнести некоторые виды математических инструментов с вполне конкретной задачей. Узлы могут существовать в природе, а также являются результатом (по большей части) творческой деятельности человека. Однако я так и не могу представить себе, что теория узлов существовала в природе до того, как у нас скопился целый набор всевозможных видов узлов. Этому замечательному математику просто удалось создать мысленный инструмент, который ты называешь инвариантом, и им воспользоваться... Он разработал инструмент, как и человек, который придумал колесо для того, чтобы быстрее передвигаться по земле. Вместо того, чтобы переходить от одного рассуждения к другому, Джонс создал «уплотнение мысли», позволившее ему мгновенно решить задачу.
А. К.: Что меня больше всего поражает, так это то, что его исследование и его открытие не были изначально мотивированы проблемой узлов. Очень интересный пример открытия, мотивированного глубинными проблемами чистой математики. Исследование множителей привело Джонса к открытию центральной функции на группе кос. Поскольку эта функция была нужна ему только для решения задачи по классификации подмножеств, он не усмотрел в ней никаких очевидных связей с узлами. Что называется, грех по неведению. После встречи с Бирман, Джонс выяснил, что в теории узлов тоже используются группы кос и что там требуется, по теореме Маркова, некая функция на группе кос с такими-то и такими-то свойствами. И он воскликнул: «Но у меня есть такая функция, она у меня в кармане».
Ж.-П.Ш.: Я понимаю, что ты хочешь сказать. Два изначально совершенно независимых друг от друга подхода, сошлись в одной
3. ЭЙНШТЕЙН И МАТЕМАТИКА
61
точке. Математический объект, созданный одним, открыл замок, не поддававшийся всем усилиям других. Это, впрочем, не означает, что ключ и замок, открываемый этим ключом, существовали и раньше!
А. К.: Не знаю.
Ж.-П. Ш.: Мы затрагиваем здесь глубинную проблему познания — отыскание причин того, что отдельные математические инструменты, созданные независимо от каких бы то ни было исследований всевозможных частиц, узлов, и прочих природных объектов, оказываются настолько адекватными...
А. К.: Совершенно верно. Это и называется непостижимой эффективностью математики.
Ж.-П. Ш.: Я все же хотел бы, чтобы ты разъяснил мне, до каких пределов простирается эта самая эффективность и какова степень ее универсальности? Я отмечаю среди физиков и некоторых математиков определенную тенденцию к увлечению различными модными математическими моделями. Предполагается, что эти модели применимы к чему угодно, и с их помощью можно с равным успехом описывать поведение совокупностей атомов, нейронов, муравьев, людей. Ты не понаслышке знаком с отношениями между математикой и физикой. Что ты обо всем этом думаешь?
3. Эйнштейн и математика
А. К.: В первую очередь, как в физике, так и в любой другой дисциплине, всякая модель поддается пересмотру и зависит от времени. Мы хорошо усвоили урок — не приходится сомневаться в том, что существующая модель физической реальности рано или поздно будет вытеснена другой моделью. Это та сторона восприятия нами мира, которая поддается пересмотру. Можно пойти еще дальше и спросить себя, в какой степени физическая истина зависит от вопросов, которые мы задаем природе посредством проводимых нами опытов. Однако я глубоко убежден в том, что как только физическая модель разработана достаточно полно, в игру вступает генеративность математики: может даже создаться такое впечатление, что мы, изучая модель с точки зрения строго математической, становимся, тем не менее, немного физиками. Показательна, в этом смысле, эволюция убеждений Эйнштейна. Сложности математического происхождения, с которыми он столкнулся,
62 ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
пытаясь сформулировать общий принцип относительности, изменили его позицию: он перестал быть чистым физиком, каковым, несомненно, являлся в 1905 году, и стал математиком. Большую часть своей жизни в науке Эйнштейн провел в попытках разработать теорию, которая объединила бы в себе электромагнетизм и гравитацию. Успех математической модели общей теории относительности был настолько велик, что Эйнштейн пришел к мысли, что решение его проблемы лежит в области математики. В 1921 году он писал о теории относительности: «Я хотел бы, чтобы вы поняли — эта теория изначально не была спекулятивной, она целиком и полностью обязана своим появлением желанию выработать физическую теорию, способную как можно лучше объяснить наблюдаемые факты. Это не революционный акт: отказ от некоторых типов понятий должен рассматриваться не как произвол, а как прямое следствие наблюдения за фактами». Но в 1933 году он пишет обратное: «Если правда то, что аксиоматическая база теоретической физики не может происходить из опыта, а должна быть выдумана, то можем ли мы тогда рассчитывать на то, что найдем однажды правильный метод? Я убежден, что если подходить к делу со стороны чистых математических конструкций, то возможно отыскать концепции и законы, объединяющие одни такие конструкции с другими, — концепции и законы, которые должны дать нам ключ к пониманию природных явлений... Созидательный принцип следует искать в математике.» [90].
В настоящее время мы являемся свидетелями очень похожего явления в теоретической физике: исчерпав все возможности, физик-теоретик приходит, за неимением лучшего выбора, к необходимости переквалифицироваться в математики. Я говорю о теории струн. В конце шестидесятых годов физики пытались отыскать непосредственно, без исследования локальных механизмов сильных взаимодействий, математическую форму так называемой 5-матрицы, которая определяет вероятность того, что в результате сильного взаимодействия двух произвольных частиц с импульсами pi и р2 образуются две частицы рз и р4- Речь идет о том, чтобы найти функцию четырех переменных pi, p2, рз и р. Относительная инвариантность позволяет свести ее к функции двух переменных. Выдвигая упрощающую гипотезу, мы приходим к тому, чтобы решить ее и указать решение в форме интеграла даже для процессов, включающих более четырех частиц. Эта гипотеза называется моделью Венециано. Далее физики-теоретики доказали — отсю-
3. ЭЙНШТЕЙН И МАТЕМАТИКА 63
да и берет начало большая часть расхождений во мнениях, — что в действительности эта модель описывает взаимодействие не точечных частиц, но малых струн (см. рис. 11α).
Интерес к этой теории сильных взаимодействий был, однако, недолговечен — после доказательства т'Хоофтом возможности перенормировки теорий калибровочных функций, открытия асимптотической свободы и т.д. ее вытеснила хромодинамика. Наконец, к 1980 году, теория струн пережила свое второе рождение, но уже не в качестве модели сильных взаимодействий, а как модель квантовой гравитации.
Ж.-П. Ш.: Речь идет все о том "же математическом формализме?
А. К.: О том же самом математическом формализме. Дело лишь в изменении масштаба: при сильном взаимодействии стандартный масштаб длины составляет 10~13 сантиметров, в то время как в случае гравитации он будет равен 10~33 сантиметров. Следовательно, необходима энергия, намного превосходящая все то, что мы можем получить, иначе говоря, очевидно, что ни один доступный нам экспериментальный феномен из этой теории не следует. На данный момент теория струн имеет значение лишь в плане, не скажу, что чисто философском, поскольку это не так, но, скорее, формальном. Известно, что описание расходимостей в теории поля можно уточнить посредством введения этих самых «струн». Заменим точки струнами, а частицы малыми струнами, способными перемещаться. Смысл такой замены объясняется очень просто. Когда две частицы сталкиваются, образуя новую частицу, или когда одна частица делится на две, мы наблюдаем сингулярный процесс, т. е. возникает особого рода точка, из которой выходят три ветви (рис. 11). Это и есть сингулярность, которая является источником упомянутых мною только что расходимостей и возникает при обмене одной или нескольких виртуальных частиц. Однако если заменить линию, символизирующую частицу, цилиндром малого диаметра, по которому перемещается струна, то хорошо видно, что три цилиндра, подобно самым обыкновенным водопроводным трубам, могут соединяться и без сингулярности, оставаясь при этом везде круглыми (рис. 11α). Чего можно ожидать от этой теории? Заменив траектории цилиндрами, мы избавляемся от сингулярности, она становится конечной, вместо того, чтобы быть бесконечной, как предполагает классическая теория.
64
ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
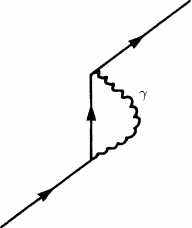
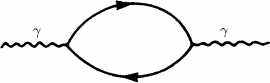
Рис. 11. Пример расходящихся диаграмм в квантовой электродинамике.

Рис. 11α. Диаграмма без сингулярности, согласно теории струн.
3. ЭЙНШТЕЙН И МАТЕМАТИКА 65
Я хотел бы повторить, что мое личное отношение к физике совсем не является отношением физика, хотя я восхищаюсь всеми открытиями, сделанными физиками — как, например, открытие Гейзенберга — в их весьма прагматичной манере, т. е. происходящими из опыта. Физикам принадлежит и честь такого необычайно важного открытия, как теория поля, однако на данном этапе развития науки эта теория не укладывается пока так просто в рамки уже известной нам области математической реальности. Собран огромный объем необработанного материала, о добыче новых экспериментальных результатов речь уже не идет. Математика в этом смысле отстает; переварить то, что поступает от физиков, мы пока не в состоянии. Таким образом, нам, очевидно, следует сосредоточить наши усилия на этих физических открытиях, причем работать нужно, скорее, в рамках чистой математики, не пытаясь искусственно втиснуть в рамки те вещи, которые естественным образом туда не помещаются.
Ж.-П. Ш.: У меня создается впечатление, что работа физика — равно, как и работа математика — очень похожа на изготовление «интеллектуальных самоделок1», если воспользоваться термином, который так нравится Клоду Леви-Строссу [71] и Франсуа Жако-бу [62]. Берем модель в одном месте и применяем ее к экспериментальному наблюдению в другом. Теория струн не годится для того, чтобы объяснить диффузию частиц. Отказаться от такой теории! Но вдруг она совершенно неожиданно оказывается пригодной для уточнения теории квантовой гравитации. Здесь мы имеем дело, скорее, с этаким теоретическим «прет-а-порте», нежели с «шитьем по мерке». Это в какой-то степени делает более привлекательными и те дисциплины, которые несколько легкомысленно принято называть «точными науками», снимает с них завесу таинственности!
С другой стороны, я отчетливо помню, что, говоря об отношении математических объектов к объектам физическим, ты употребил выражение «втиснуть в рамки», вместо «отождествить». И этими самыми рамками ты определяешь весьма специфичный способ описания физической реальности. Мне же, напротив, кажется, что если бы математика присутствовала изначально в природе, если бы материя организовывалась посредством математических законов, то мы имели бы тогда полное отождествление между математиче-
*В оригинале bricolage, что приблизительно означает «поделки», «всевозможные вещи, которые мастерят своими руками из подручных материалов». — Прим. перев.
66 ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
скими и природными объектами. Ничего подобного, однако, мы не наблюдаем. Это означает, если следовать твоей логике, что математических объектов в природе нет. Они где-то в другом месте, но где? В каком-то ином состоянии, в какой-то иной форме, которые ты пока еще не определил. У тебя получается своего рода дуализм между материей и математикой, этакий раскол между телом и духом, которого я, естественно, принять не могу.
А. К.: Дуализм тела и духа располагается в иной плоскости. Окружающий нас физический мир, не являясь вместилищем математической реальности, обладает, в то же время, некоторой труднообъяснимой взаимосвязанностью с этой математической реальностью. Как сказал, если не ошибаюсь, Эйнштейн: самая непостижимая черта физики в том, что она постижима. Сложно представить, что именно математика ответственна за организацию природных феноменов.
Ж.-П.Ш.: Согласен с «организацией феноменов», добавлю лишь «в нашем мозге».
А. К.: Не знаю. Я не совсем уверен, что можно говорить «в нашем мозге». Так можно договориться и до того, что внутри нашего мозга сосредоточено все восприятие внешнего мира.
Ж.-П.Ш.: Так оно и есть.
А. К.: Да, но мы же только что сошлись на том, что внешний мир существует независимо от нас.
Ж.-П.Ш.: Верно, а воспринимаем мы его исключительно посредством нашего мозга и наших органов чувств.
А. К.: Точно такое же отношение к нам имеет и математический мир. Он существует независимо от нас, коль скоро все математики согласны друг другом относительно независимой структуры индивидуального восприятия. С другой стороны, очевидно, что это вполне может побудить кого-нибудь высказаться в том духе, что математический мир реализуется исключительно в его мозге, точно так же, как внешний физический мир воспринимается человеком только через мозг.
Ж.-П.Ш.: Разумеется. Понимаю. Но не согласен. В частности, с твоим «точно так лее». Я уже подчеркивал опасность употребления метафор в таких ситуациях. Аналогия не является доказательством. В конце концов, отношения математики с биологией более просты, чем с физикой, и гораздо менее двусмысленны. Построение моделей требует использования математического аппарата, иногда даже происходит смешение биологии с математикой,
4. ПОЛЬЗА ОТ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ В БИОЛОГИИ 67
как ты только что отметил. Наша точка зрения менее амбициозна, но обеспечивает более значительную дистанцию. Таким образом, мне кажется, что наша позиция является более определенной, чем позиция некоторых физиков.
А. К.: Естественно, дистанция здесь больше. Переплетение математики и физики объясняет то, что физикам удается удерживать дистанцию, лишь прилагая большие усилия. Да, я согласен.
4. Польза от математических моделей в биологии
Ж.-П.Ш.: Вера в объясняющую способность математической модели встречается у биологов реже. Применительно к биологии математика служит, главным образом, двум целям. Первая — это анализ экспериментальных данных...
А. К.: Это ты о статистике.
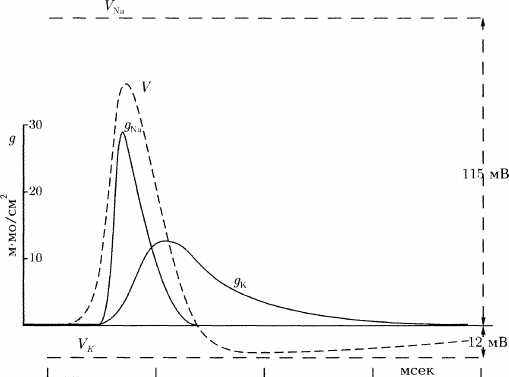
Ж.-П.Ш.: Да, о получении и обработке данных. Это можно делать и при помощи компьютера, автоматически, не привлекая интеллектуальные способности экспериментатора. Кроме того, математика помогает нам при построении теоретических моделей. Эти модели разрабатываются на основе экспериментальных данных, как и в физике. Мы учитываем соответствующие посылки — например, для исследования распространения нервного импульса нам необходимо учесть величину изменения потенциала в определенной точке нерва и силу тока, создаваемого ионами натрия или калия в зависимости от потенциала. Ходжкин и Хаксли предложили уравнение [55], которое на основании этих посылок дает представление об ионной природе нервного импульса. Это уравнение позволяет описать явление, реконструировать его, опираясь на элементарные данные (см. рис. 12 и 12α).
А. К.: Такой способ кодировать информацию...
Ж.-П.Ш.: И, по большей части, воссоздавать ее заново.
А. К.: То есть это почти как в языке, поскольку язык служит как раз для воспроизводства...
Ж.-П.Ш.: Да. Язык позволяет воспроизводить информацию, но он, кроме того, обладает предсказательным характером. Во всяком случае, ни один знакомый мне биолог не скажет, что уравнение Ходжкина и Хаксли можно идентифицировать с нервным импульсом, ни даже то, что оно управляет его распространением. Распространение нервного импульса диктуется вовсе не тем или
68
ПРИРОДА, ОДЕТАЯ ПО МЕРКЕ
01234
Рис. 12. Модель нервного импульса, предложенная Ходжкином и Хаксли. Волна распространяющегося потенциала показана прерывистой чертой (V). Ее можно разложить на две составляющих: транспорт ионов Na"1" внутрь клетки и ионов К"1" за пределы клетки, представленные здесь в виде проводимостей #Na и #к. (Воспроизводится по [56].}
Рис. 12α. Первичная структура канала, селективного в отношении ионов натрия, которые задействованы в распространении нервного импульса. С помощью методов молекулярной генетики был идентифицирован генетический материал, содержащий код протеина, ответственного за транспорт ионов Na"1" сквозь мембрану нейрона в процессе распространения нервного импульса. Этот протеин состоит из одной цепочки длиной в 1820 аминокислот. В нижней строке цепочки — участок молекулы ДНК, представленный в виде последовательности триплетов из четырех оснований (А, Т, G и С); в верхней строке — участок молекулы протеина, образуемый соединением существующих в природе аминокислот (21 аминокислота), обозначенных здесь трехбуквенным кодом. (Воспроизводится по [85])
4. ПОЛЬЗА ОТ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ В БИОЛОГИИ
69
zs
** * ____ и » «»
