Программа курса двойные интегралы в пространстве и векторный анализ
| Вид материала | Программа курса |
СодержаниеЭлементы теории функций комплексной переменной 4. Экзаменационные вопросы |
- Программа дисциплины «математический анализ», 432.47kb.
- Программа дисциплины «Математический анализ», 500.52kb.
- Отсчета. Модели объектов и процессов, 26.46kb.
- Программа обсуждена на заседании кафедры Математики фнти, 28.33kb.
- Гранта: «Внешняя политика России на постсоветском пространстве: проблемы и тенденции, 68.45kb.
- Программа курса элективных занятий по физике для 9-го класса «Решение задач по механике», 36.39kb.
- Учебная программа Дисциплины 08 «Численное моделирование в акустике и гидродинамике», 97.4kb.
- Карцев Евгений Александрович Аннотация: программа курса, 233.93kb.
- Программа курса «Оператор арм «Анализ очагов потерь» Цели и задачи курса, 67.94kb.
- Программа элективного курса по географии для 9 класса «География российского порубежья:, 187.36kb.
МАТЕРИАЛЫ
для СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ СПбГЭТУ (ЛЭТИ)
Курс «Математический анализ»
Кафедра ВМ-2
Курс 2
Семестр 4
Санкт-Петербург
2009 г
1. ВВЕДЕНИЕ
В программе перечислены изучаемые темы, литература, экзаменационные вопросы и варианты контрольных работ.
2. ПРОГРАММА КУРСА
ДВОЙНЫЕ ИНТЕГРАЛЫ В ПРОСТРАНСТВЕ И ВЕКТОРНЫЙ АНАЛИЗ
- Двойные интегралы. Условия интегрируемости функций.[см [1]- п 588 - 590; [3]- п 7.1, 7.2], Основные свойства интегралов: нормировка, монотонность, аддитивность;[ см [1]- п 592, п 593; [3]- п 7.3]. Сведение двойных интегралов к повторным.[ см [1]- п 594; [3]- п 7.4] Формулы замены переменных в двойном интеграле. Полярные координаты.[ см [1]- п 603; [3]- п 7.5] Приложения двойных интегралов. [ см [1]- п 598; [3]- п 7.6].
- Тройные интегралы: определения и свойства. .[ см [1]- п 642 - 644; [3]- п 8.1]. Вычисление тройного интеграла. .[ см [1]- п 645; [3]- п 8.2]. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты. .[ см [1]- п 655, п 656; [3]- п 8.3]. Приложения тройного интеграла. .[ см [1]- п 649; [3]- п 8.6]
- Криволинейные интегралы первого рода. .[ см [1]- п 543; [3]- п 9.1] Свойства и методы их вычисления. .[ см [1]- п 544; [3]- п 9.2] Приложения криволинейных интегралов первого рода .[ см [1]- п 545, п 554; [3]- п 9.3]. Криволинейные интегралы второго рода. .[ см [1]- п 546; [3]- п 10.1]. Свойства и методы их вычисления. .[ см [1]- п 547; [3]- п 10.2]. Условия независимости криволинейного интеграла второго рода от пути интегрирования. Формула Грина. .[ см [1]- п 555 - 558; п 601; [3]- п 10.3, 10.4]. Приложения криволинейных интегралов второго рода .[ см [1]- п 554; [3]- п 10.5].
- Поверхностные интегралы первого типа. .[ см [1]- п 630; [3]- п 11.1] Методы их вычисления. .[ см [1]- п 631; [3]- п 11.2] Приложения поверхностных интегралов первого типа. .[ см [1]- п 632; [3]- п 11.3]. Поверхностные интегралы второго типа. .[ см [1]- п 634; [3]- п 12.1]. Методы их вычисления. .[ см [1]- п 635; [3]- п 12.2]. Приложения поверхностных интегралов второго типа. .[ см [1]- п 638; [3]- п 12.5]. Формула Остроградского – Гаусса. Формула Стокса. .[ см [1]- п 639, п 651; [3]- п 12.3, 12.4].
- Основные понятия и формулы векторного анализа. Скалярные и векторные поля. .[ см [1]- п 664, п 665; [3]- п24.1, 25.1]. Градиент функции нескольких переменных, поток вектора через поверхность, дивергенция векторного поля, циркуляция векторного поля,. потенциал векторного поля, ротор векторного поля. .[ см [1]- п 666 - 669; [3]- п 24.3, 25.2 – 25.5]. Основные классы векторных полей. .[ см [1]- п 670; [3]- п27.1, 27.2]
ЭЛЕМЕНТЫ ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- Функции комплексной переменной (ФКП): предел, непрерывность, производная, ее геометрический смысл. .[ см [6]- §3,5,; [3]- п 28.1, 28.2,] Условия Коши- Римана существования производной ФКП .[ см [6]- §6,8,; [3]- п 28.4, 28.5,] . Интеграл от ФКП. Теорема Коши. Неопределенный интеграл. Формула Ньютона – Лейбница. Интегральная формула Коши. .[ см [6]- §15 - 18, [3]- п 29.1 - 29.3,] Ряды с комплексными членами. Разложение аналитической ФКП в ряд Тейлора. Ряд Лорана. .[ см [6]- §22, §25, [3]- п 30.2 -30.5,] Классификация особых точек. Вычеты: определение, методы вычисления. .[ см [6]- §26,27, [3]- п 30.6, п 31.1, 31.2] Вычисление интегралов при помощи вычетов. .[ см [6]- §28; [3]- п 31.2]
3. ЛИТЕРАТУРА
Основная литература
- Г.М Фихтенгольц. Курс дифференциального и интегрального исчисления. Т.3 М
- Я.С.Бугров, С.М.Никольский. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. Ч.3 М.: Дрофа, 2003.
- Д.Т.Письменный. Конспект лекций по высшей математике. Ч.2 И 3. М.: Айрис-пресс, 2004.
- Сборник задач по математике для втузов. Специальные разделы математического анализа. Под редакцией А.В.Ефимова, Б.П.Демидовича. М.,"Наука", 1986.
- Н.С.Пискунов. Дифференциальное и интегральное исчисления для втузов. Тома 1, 2
- .В. Я. Эйдерман. Основы теории функций комплексного переменного и операционного исчисления. М., Физматлит , 2002
4. ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
- Двойные интегралы. Определение двойного интеграла, как предела интегральных сумм.
- Геометрический и физический смысл двойного интеграла..
- Основные свойства двойного интеграла: нормировка, монотонность, аддитивность.
- Сведение двойного интеграла к повторному.
- Формула замены переменной в двойном интеграле.
- Двойной интеграл в полярных координатах.
- Приложения двойного интеграла.
- Тройной интеграл и его свойства: нормировка, монотонность, аддитивность.
- Вычисление тройного интеграла в декартовых координатах.
- Тройной интеграл в цилиндрических и сферических координатах.
- Приложения тройных интегралов.
- Криволинейные интегралы первого рода. Методы их вычисления. Приложения криволинейных интегралов первого рода.
- Криволинейные интегралы второго рода. Методы их вычисления. Приложения криволинейных интегралов второго рода.
- Условия независимости криволинейного интеграла второго рода от пути интегрирования. Формула Грина.
- Поверхностные интегралы первого типа. Методы их вычисления. Приложения поверхностных интегралов первого типа.
- Поверхностные интегралы второго типа. Методы их вычисления. Приложения поверхностных интегралов второго типа
- Формула Остроградского – Гаусса. Формула Стокса.
- Скалярное и векторное поля. Градиент скалярного поля.
- Поток вектора через поверхность. Дивергенция. векторного поля.
- Циркуляция векторного поля. Ротор векторного поля.
- Основные классы векторных полей.
- Функции комплексной переменной: предел, непрерывность.
- Основные элементарные функции комплексного переменного.
- Производная и дифференциал функции комплексной переменной. Условия Коши- Римана.
- Интеграл от функции комплексной переменной.
- Теорема Коши.
- Неопределенный интеграл. Формула Ньютона – Лейбница.
- Интегральная формула Коши.
- Разложение аналитической функции в ряд Тейлора.
- Ряд Лорана.
- Классификация особых точек.
- Определение вычета. Методы вычисления вычетов (в простых и кратных полюсах).
- Теорема о вычетах.
- Вычисление интегралов при помощи вычетов.
Контрольная работа. Вариант №1
Часть №1
- Вычислить, перейдя к полярным координатам,
 , где область D ограничена линиями:
, где область D ограничена линиями: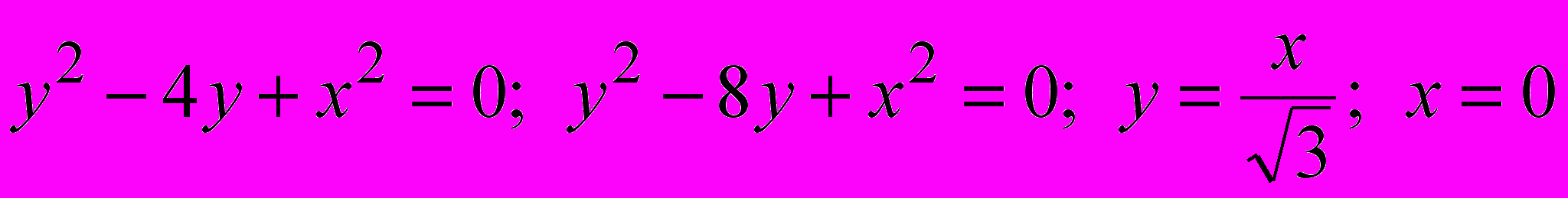 . Сделайте рисунок.
. Сделайте рисунок.
- Найти площадь фигуры, ограниченной заданными линиями:
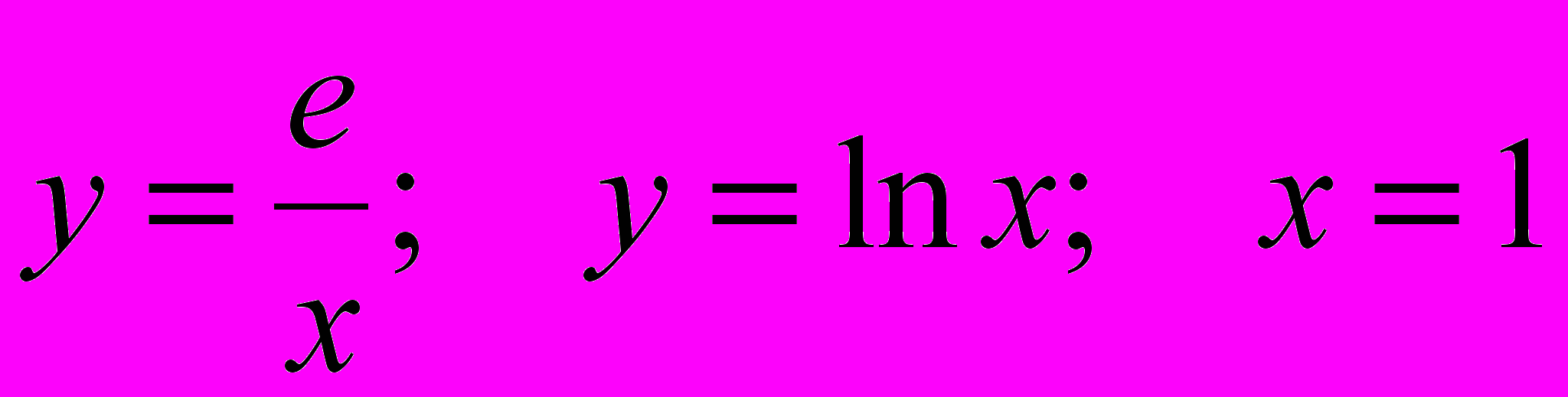 . Сделайте рисунок.
. Сделайте рисунок.
- Вычислить, перейдя к цилиндрическим координатам
 , где область
, где область  ограничена линиями:
ограничена линиями:  .
.
- Вычислить криволинейный интеграл
 , где L – отрезок прямой от точки
, где L – отрезок прямой от точки
А(0;-2) до точки В(4;0).
- Вычислить криволинейный интеграл
 , где L первый виток винтовой линии x=cost; y=sint; z=t.
, где L первый виток винтовой линии x=cost; y=sint; z=t.
Часть №2
- Найдите геометрическое место точек, изображающих числа z, удовлетворяющих системе неравенств
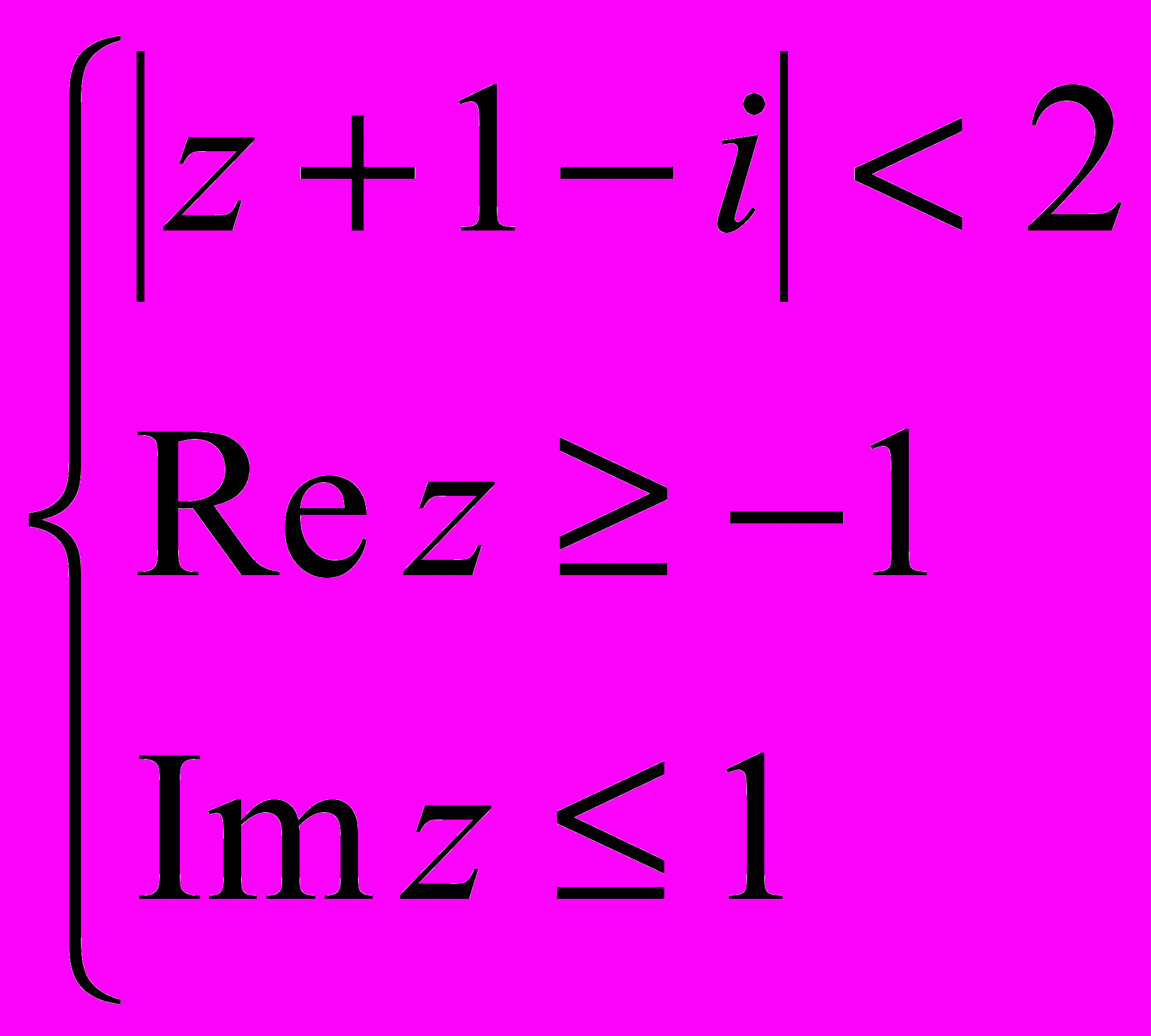 .
.
- Найти аналитическую функцию f(z), если задана ее действительная часть
 и
и 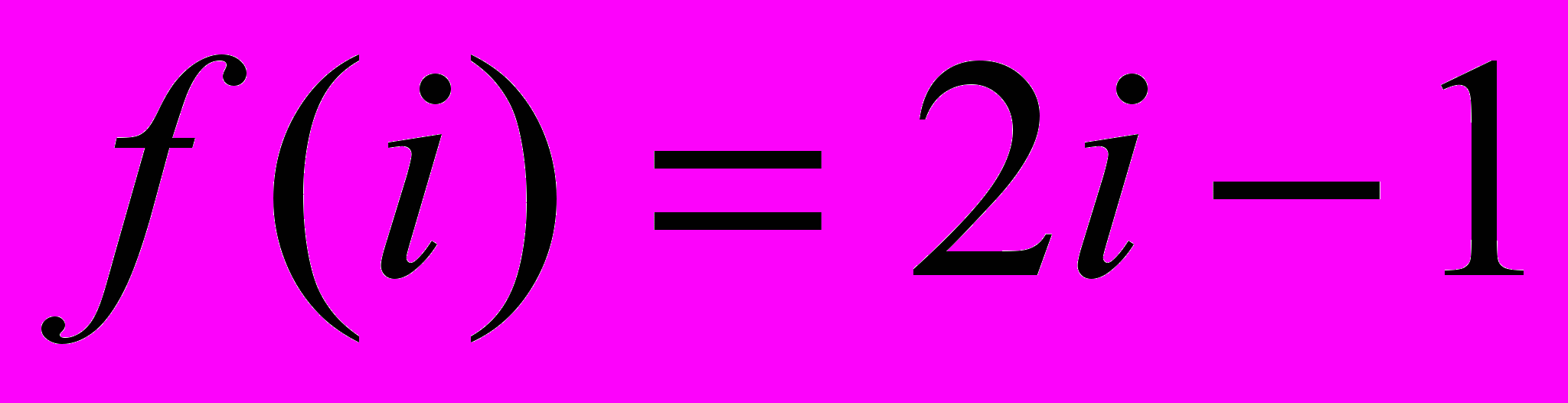 .
.
- Вычислить

- Вычислить
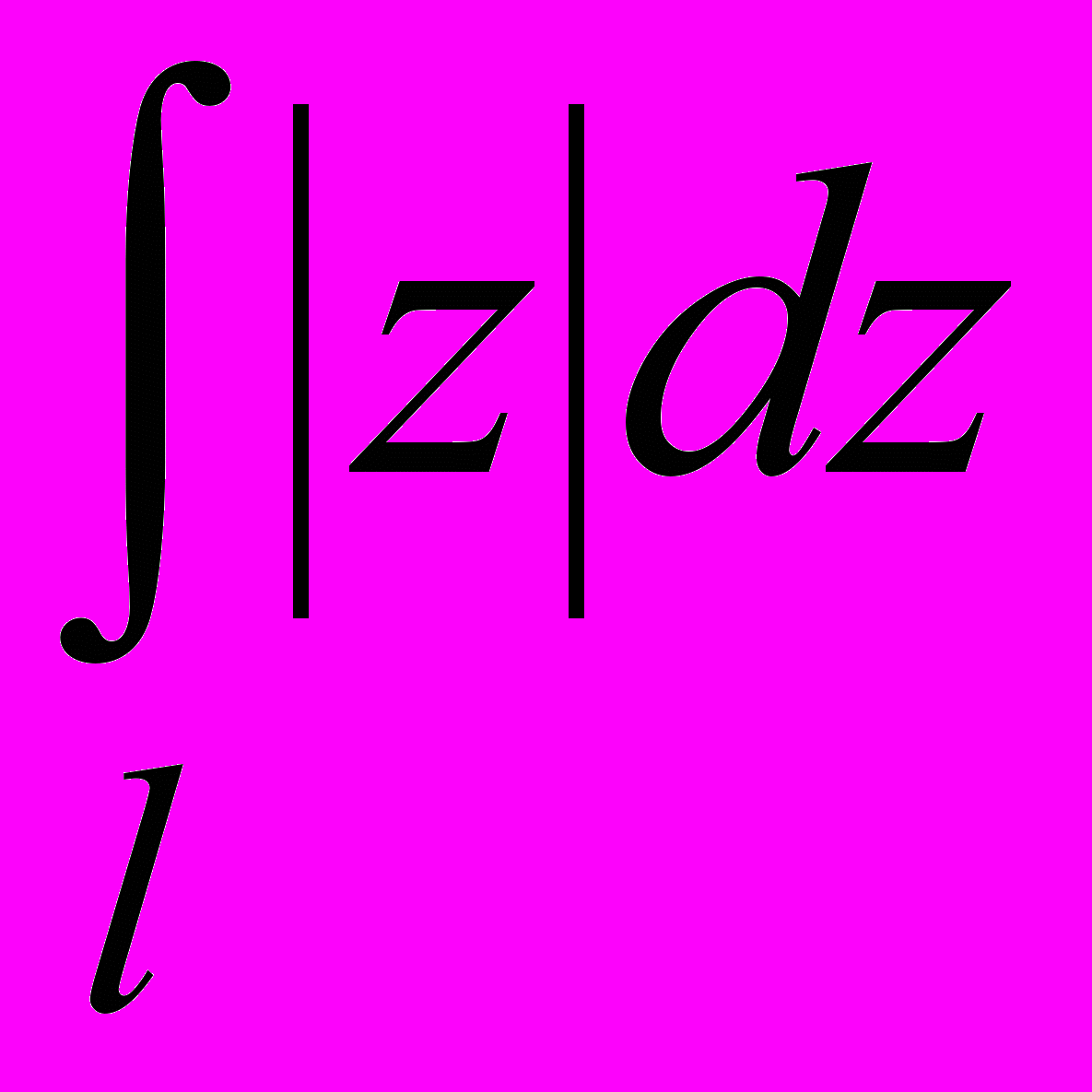 , где l – прямолинейный отрезок, соединяющий точки
, где l – прямолинейный отрезок, соединяющий точки  и
и  .
.
- Вычислить
 , где АВ – часть параболы
, где АВ – часть параболы  от точки
от точки  до точки
до точки  .
.
- Вычислить
 .
.
- Вычислить
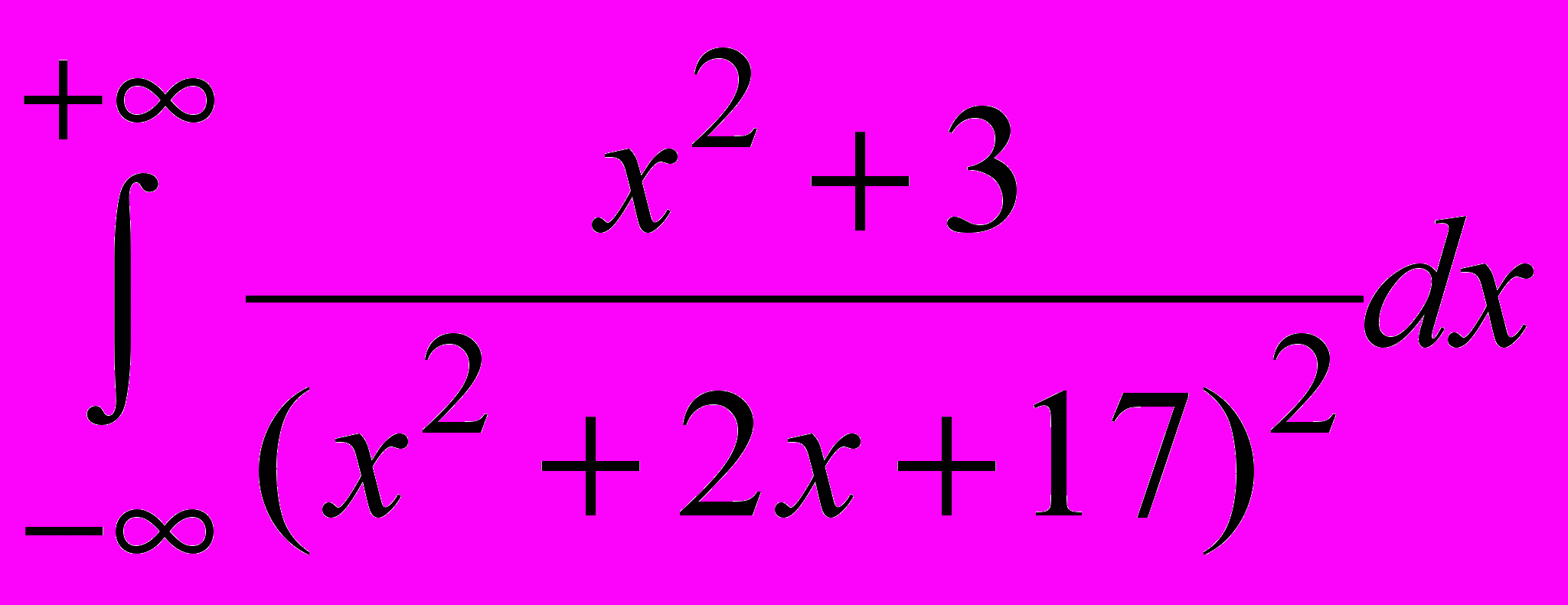 .
.
Контрольная работа. Вариант №2
Часть №1
- Вычислить, перейдя к полярным координатам,
 , где область D ограничена линиями:
, где область D ограничена линиями: . Сделайте рисунок.
. Сделайте рисунок.
- Найти площадь фигуры, ограниченной заданными линиями:
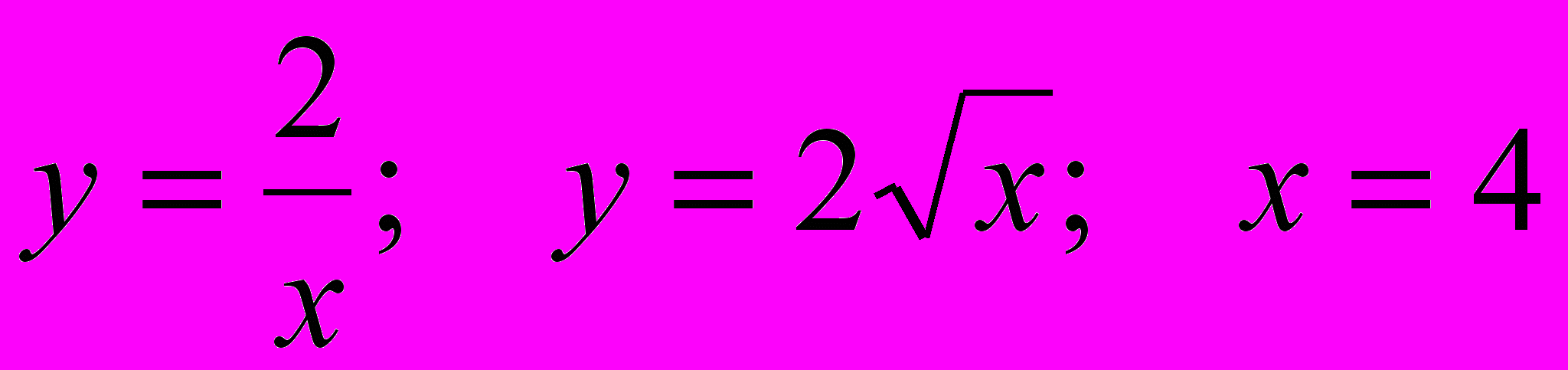 . Сделайте рисунок.
. Сделайте рисунок.
- Вычислить, перейдя к цилиндрическим координатам
 , где область
, где область  ограничена линиями:
ограничена линиями: 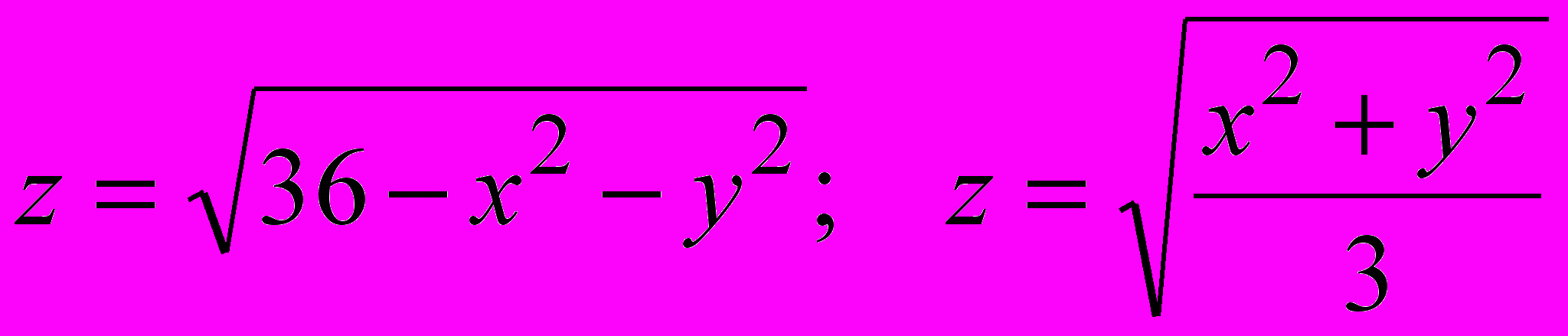 .
.
- Вычислить криволинейный интеграл
 , где L –часть параболы от точки А(0;0) до точки В(2;4).
, где L –часть параболы от точки А(0;0) до точки В(2;4).
- Вычислить криволинейный интеграл
 , где L – часть кривой
, где L – часть кривой  от точки А(0;0;0) до точки В(1;1;1).
от точки А(0;0;0) до точки В(1;1;1).
Часть №2
- Найдите геометрическое место точек, изображающих числа z, удовлетворяющих системе неравенств
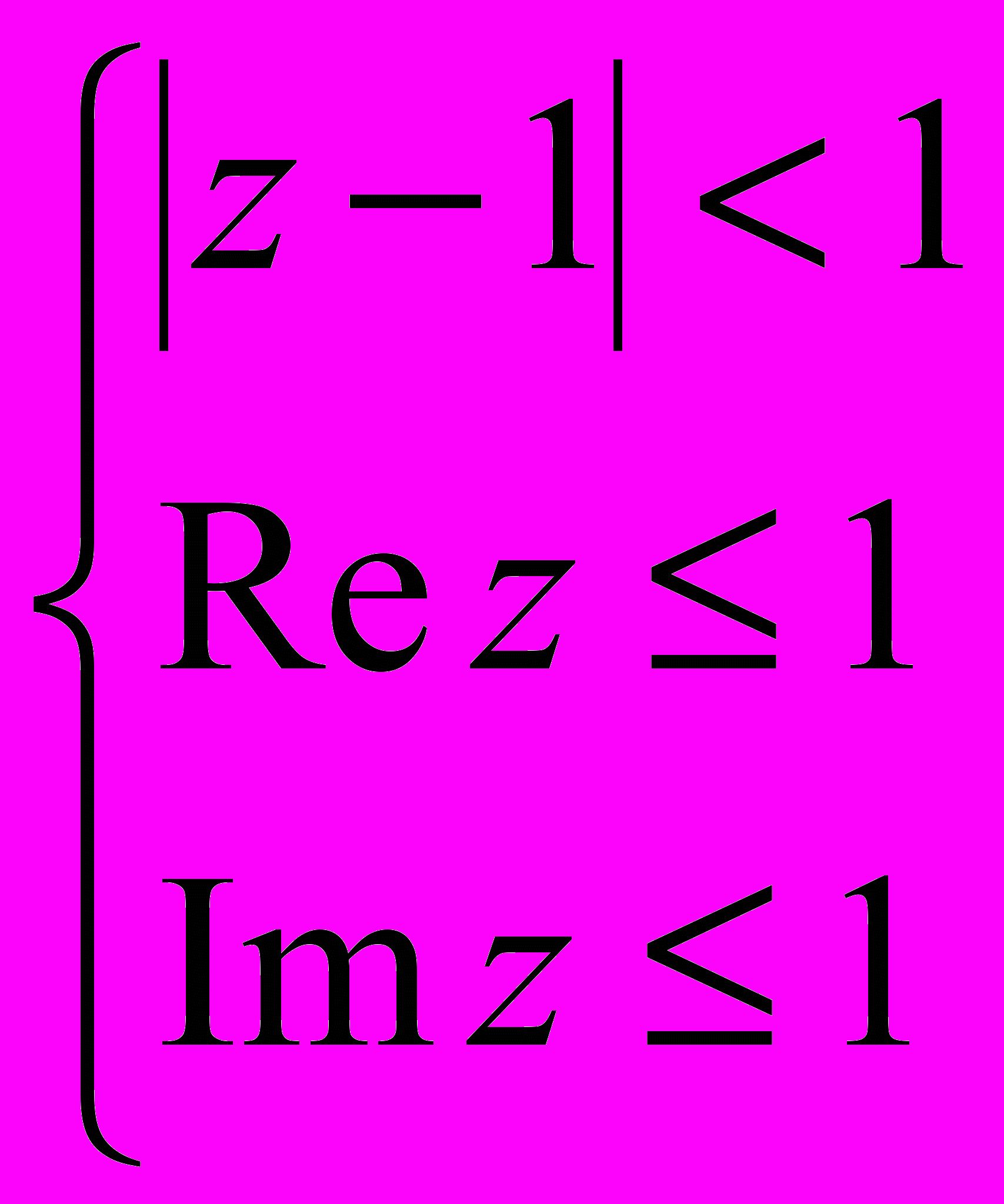 .
.
- Найти аналитическую функцию f(z), если задана ее мнимая часть
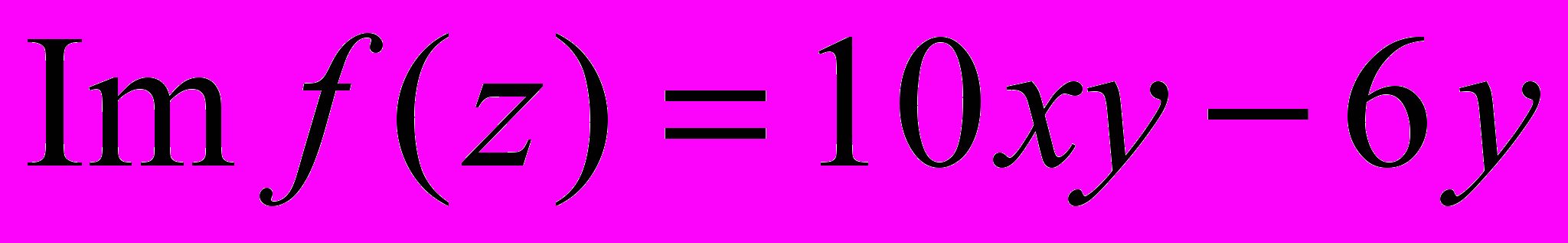 и
и 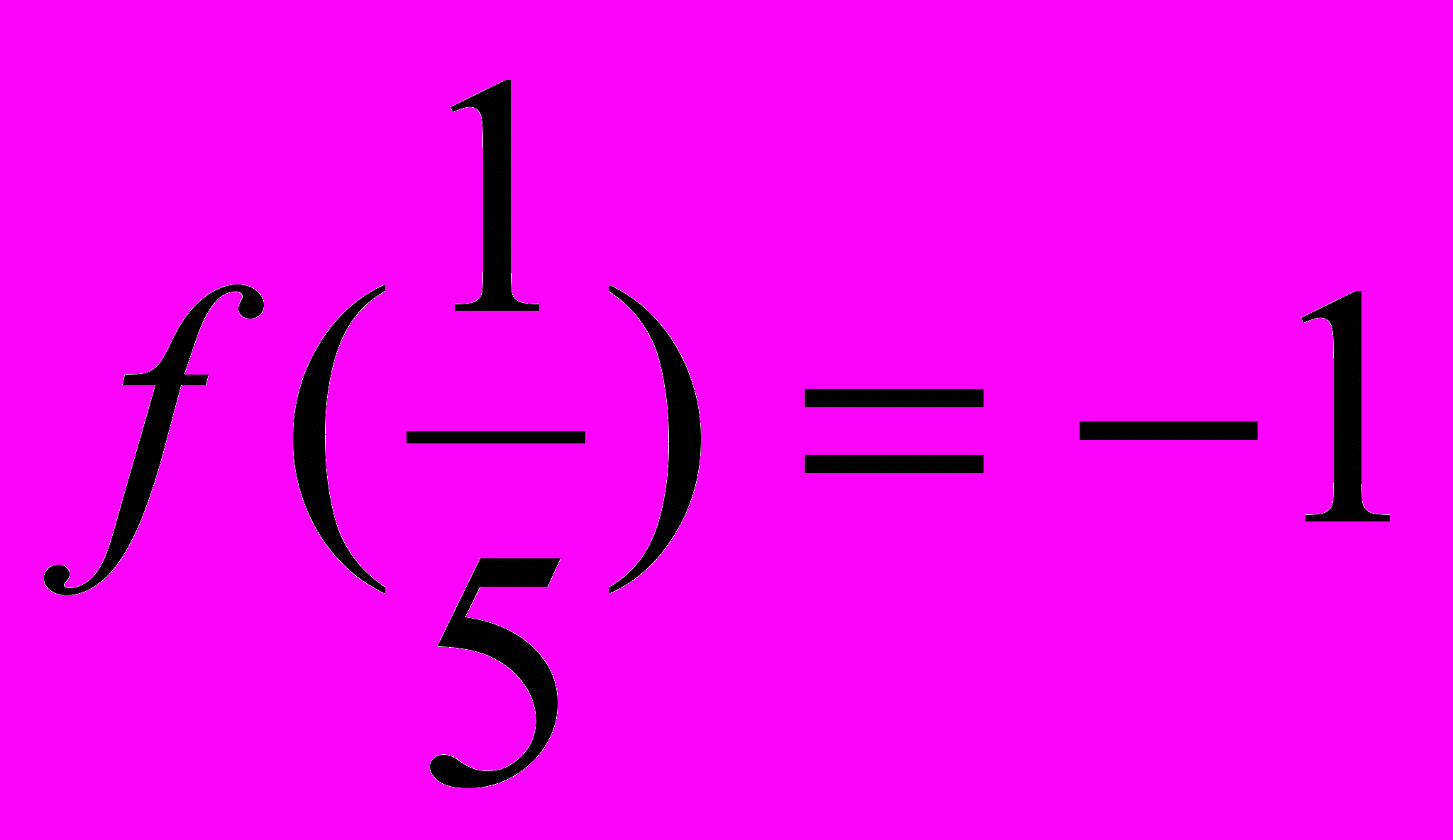 .
.
- Вычислить

- Вычислить
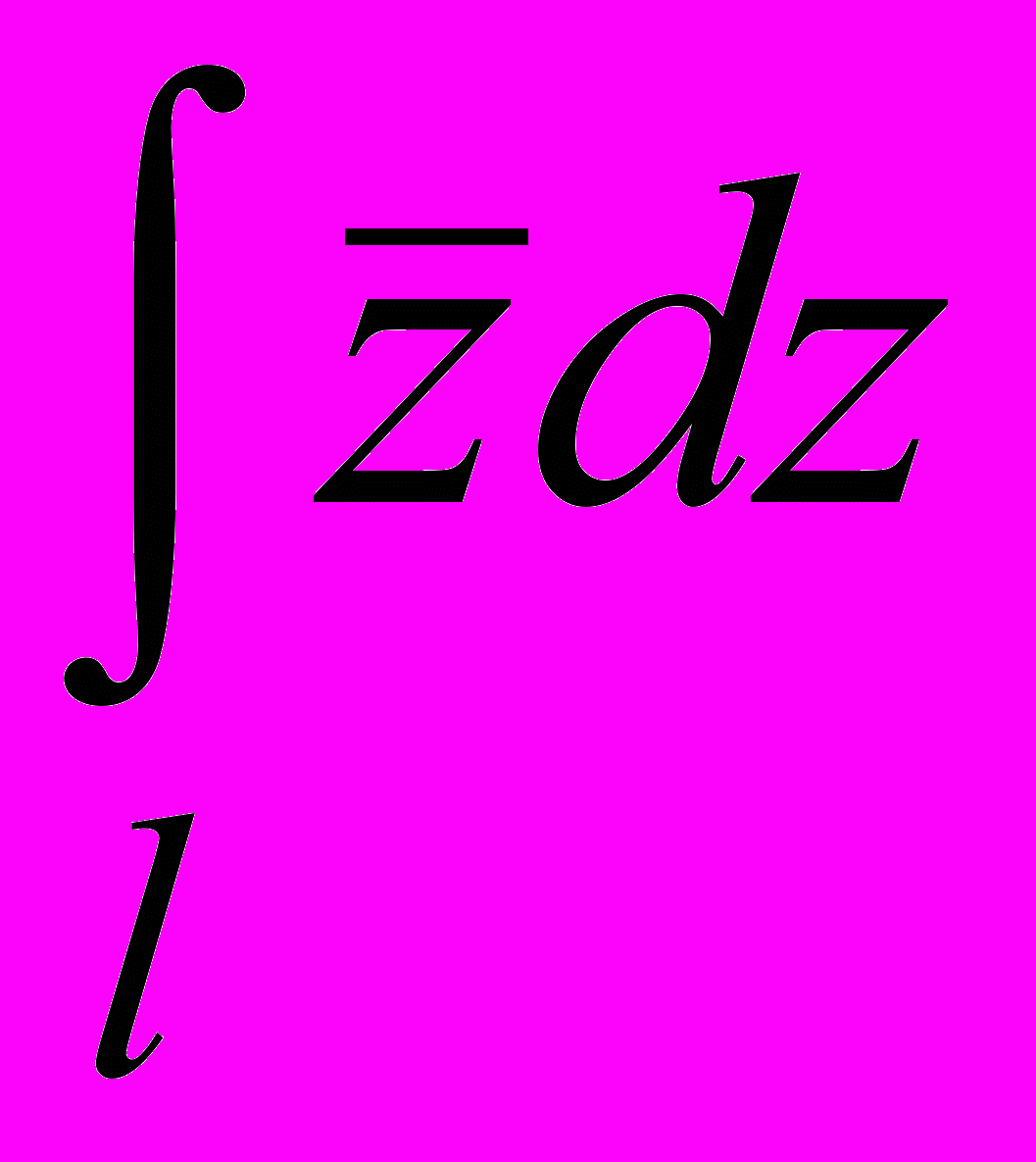 , где l – прямолинейный отрезок, соединяющий точки
, где l – прямолинейный отрезок, соединяющий точки  и
и 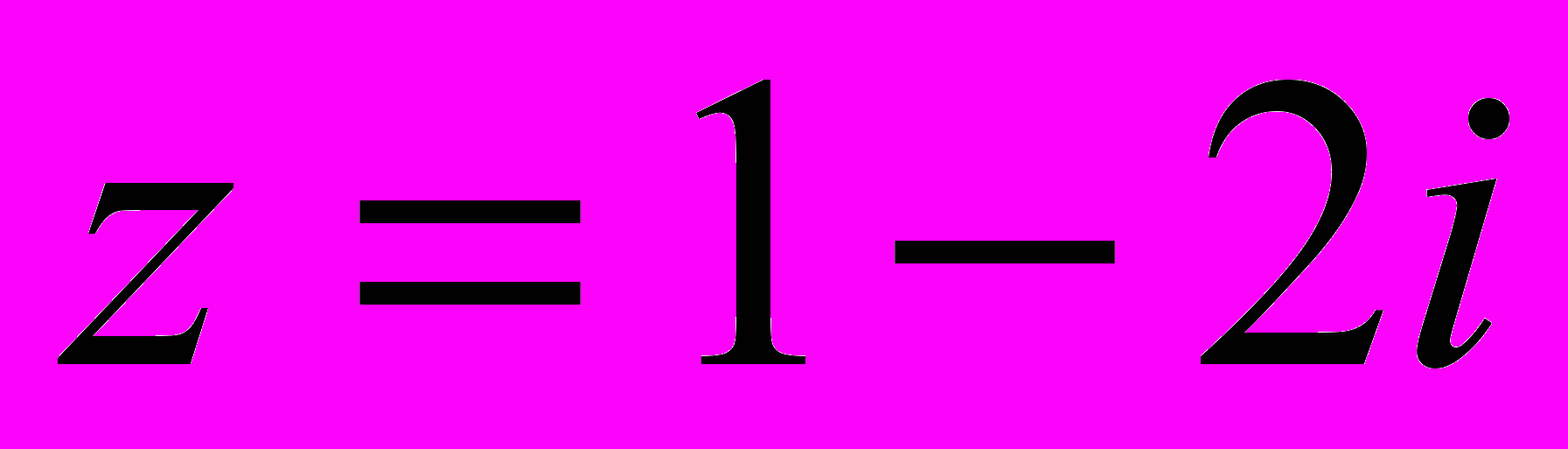 .
.
- Вычислить
 , где АВ –отрезок прямой от точки
, где АВ –отрезок прямой от точки  до точки
до точки  .
.
- Вычислить
 .
.
- Вычислить
 .
.
