«Книга абака», иначе «Книга счета»
| Вид материала | Книга |
СодержаниеХVIII век Изучение свойств периодических дробей |
- Реферат на тему, 149.58kb.
- Исследовательская деятельность, 243.02kb.
- Книга Иова, Книга Экклесиаста, Книга Ионы, 38.38kb.
- Академическая книга, 294.07kb.
- Армянская Патриархия Иерусалима, Монастырь Святых Иаковых редактор: Виталий Кабаков, 2449.03kb.
- Тема Дата, 281.03kb.
- Красная книга, 61.68kb.
- С. Н. Воробьева Абу-л Фазл и «Акбар-наме» Книга, 562.48kb.
- С. В. Воронин Настольная книга предпринимателя Москва «Копиринг» 2009 удк 339. 138, 4209.96kb.
- В. В. Полуэктов полевые и манипуляционные технологии настольная книга, 6716.55kb.
| | Европа  | |
| XII век | Понятия [2] В руководствах по арифметике дробь определяли как часть числа (когда деление одного числа на другое не заканчивается без остатка). Действия с обыкновенными дробями описали европейские переводчики ал-Хорезми на латинский язык: [2] Леонардо Пизанским (Фибоначчи) в работе «Книга абака», иначе - «Книга счета», (1200 г.) рассказывает о действиях над дробями, о тройном правиле и многом другом. – становится тем сочинением, по которому училось не одно поколение купцов и ремесленников в средние века Введение десятичных дробей. [2] Иоанн Севильский – испанский епископ – проделал значительную работу, переведя на латынь математический труд Ибн Мусы и некоторые работы арабских ученых, опиравшиеся на произведения Аристотеля: основанием систематических дробей при употреблении десятичной системы счисления для натуральных чисел должно быть взято число 10. | |
| XIII век | Терминология [11] [2] Максим Плануд (Μάξιμος Πλανούδης; 1260-1305 гг) – византийский грамматик, математик и теолог, единственный крупный математик за всю византийскую историю после гибели античной культуры в VI веке – написал трактат о системе счисления индусов (то есть десятичной позиционной системе), способствовал её внедрению, открыл для византийцев некоторые новые математические операции, например, извлечение квадратного корня, а также написал комментарии к первым двум книгам «Арифметики» Диофанта – использовал в своих трудах термины «числитель» [11] и «знаменатель» дроби [2]. [2] Действия с единичными и обыкновенными дробями, с пропорциями: [7] Иордан Неморарий – математик, о личности которого точных сведений не имеется. Возможно, что это был не кто иной, как Иордан Саксонский, генерал монашеского ордена доминиканцев, одно время живший в Париже и умерший в 1237 году. Трактат Иордана Неморария «Об элементах арифметического искусства» (De elementis arismetice artis) сделался одним из самых распространенных в Западной Европе учебников и после введения книгопечатания выдержал несколько печатных изданий. Замечательной особенностью этого сочинения является постоянное употребление в нём букв для обозначения чисел. В трактате «Объяснение алгоритма» (Algorismus demonstratus) рассматривается счёт в разных системах: словесное счисление по десятичной системе с разделением чисел на пальцевые от 1 до 9 и на суставные различных порядков (десятки, сотни, тысячи и т. д.); индийский письменный счёт; действия над целыми числами; дроби обыкновенные и шестидесятеричные и действия над ними (дробь определялась как часть числа [2]); наконец, действия с пропорциями. | |
| XV век | Запись десятичных дробей: [2] Региомонта́н (Йоганн Мюллер, 1436-1476) – выдающийся немецкий астроном и математик отделял дробную часть числа от целой части чёрточкой. [8] Франческо Pellos (Pellizzati) в своей «Арифметике» (Турин, 1492 г.) описывает основные операции с целыми числами, применение пропорций, извлечение квадратного корня и кубического корня, тройное правило, правила ложного положения и др. Главный интерес книге придает тот факт, что Pellos «находится» в непосредственной близости от изобретения десятичных дробей, использует десятичную точку, чтобы указать, деление на некоторую степень десяти: чтобы разделить 425 на 70, Pellos бы разделил 42,5 на 7 и записал результат 65/70. [2] Действия с десятичными дробями. Систематическое развитие идеи десятичных дробей принадлежит Бонфис Иммануэлю бен Якобу (1470-1530 гг.) из Тараскона. | |
| ХVI век | Терминология [2] Ж. Траншан в своей «Арифметике» (1558 г.) вводит термин «обыкновенная»/ «вульгарная» для обозначения дробей вида p/q, отличая их от астрономических/шестидесятеричных дробей. [2] Действия с обыкновенными (народными) дробями Действия с шестидесятеричными (физическими, астрономическими) дробями. [2] Действие деления на 10, 100, 1000: Джерола́мо Кардано (1501-1576 гг.) – итальянский математик, инженер, философ, медик и астролог – находит частное от деления на 10, 100, 1000 отбрасыванием последних цифр делимого, называя это «правилом Региомонтана». [2] Петер Апиан (Петер Биневиц или Бенневиц, 1495-1552 гг.) – немецкий механик и астроном приводит простейшие случаи обращения обыкновенной дроби в десятичную (1527 г.): 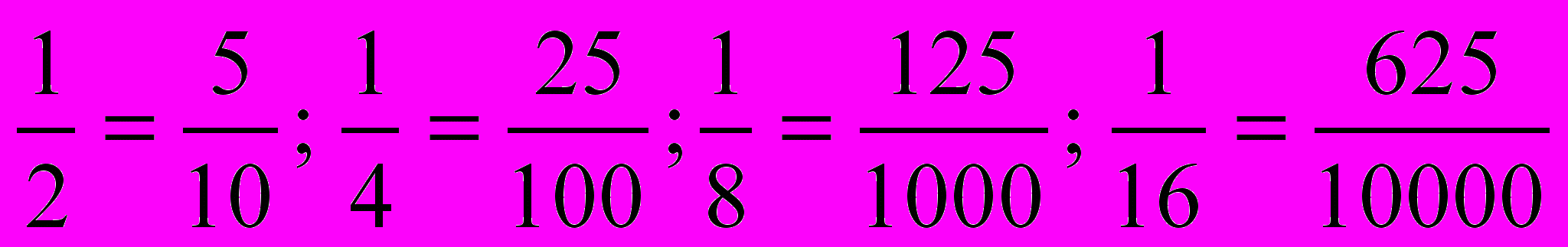 с той же целью, с которой современный учитель подчёркивает эти равенства на первых уроках, посвящённых десятичным дробям.Теория обыкновенных дробей: [3] Си́мон Сте́вин (1548-1620 гг.) – фламандский математик-универсал, инженер – в своём трактате «Арифметика» он определяет число как «меру количества некоей вещи» и провозглашает: «единица делима», и что «нет никаких неправильных чисел». Запись десятичных дробей: [2] [3] Стевин для ясности указывал над каждой цифрой (или после неё) заключённый в кружок её номер разряда, положительный для целой части, отрицательный для дробной части: 3  752 (0, 3752) или 54 (0,54) и 8937 (8,937).Запись сложения/вычитания при этом выглядит так: 8 9 3 7 – 3 7 5 2 8 5 6 1 8 Запись умножения: 3 7 8 5 4 1 5 1 2 1 8 9 0 2 0 4 1 2 [2] Франсуа́ Вие́т (1540-1603 гг.) – французский математик, основоположник символической алгебры: длину отрезка в 5 радиусов и 73652 стотысячных его изображает так 5 736 52, позднее 5/736 52 (равносильно нашему 5,73652), понимает и подчёркивает преимущество десятичных дробей при десятичной системе счисления. [2] Клавий (Christophorus Clavius; 1537-1612) – германский математик и астроном, автор григорианского календаря – использует точку для отделения целой части дроби от её дробной части (1593 г.). [2] Иост Бюрги (1552-1632 гг.) – швейцарский высококвалифицированный механик и часовых дел мастер – самостоятельно пришел к идее десятичных дробей. [2] Ио́ганн Ке́плер (1571-1630 гг.) – немецкий математик, астроном, оптик и астролог – в астрономических и логарифмических таблицах изображал десятичные дроби в виде 0/567 (0,567). Действия с десятичными дробями. [3] Трактат Стевина «Децималь» (De Thiende, La Disme) – десятичное счисление, изданный на фламандском и французском языках в 1585 г. содержал практическое описание арифметики десятичных дробей, а также пылкую и хорошо аргументированную пропаганду полезности их применения, в частности, в системах мер и монетном деле. С книги «De Thiende» в Европе началось широкое использование десятичных дробей. Изложение дробей в учебниках. [10] Пьер де ла Раме (Prierre de la Ramée, Петр Рамус, Petrus Ramus, 1515-1572 гг.) – профессор Наваррского колледжа Парижа, наиболее яркий ученый Франции XVI века – философ, математик, педагог, страстный борец за реформу системы образования. Его «Арифметика» – наиболее популярный учебник конца XVI века. В разделе его сочинения, озаглавленном «О простой арифметике», подробно разъясняются правила вычислений с целыми и дробными числами, причем особое внимание уделяется различным методам, облегчающим операции. В разделе сочинения, носящем название «О сравнительной арифметике», Рамус подробно анализирует виды числовых пропорций, рассматривая теорию отношений Евклида как основу всех правил практической арифметики. Обращает на себя внимание трактовка понятия числа у Рамуса, которая показывает, что он был одним из тех ученых XVI в., которые оценили важность пересмотра этого основного понятия математики с новых позиций и расширения его содержания по сравнению с общепринятым до тех пор. С точки зрения истории учения о числе представляет интерес третья часть «Арифметики» Рамуса, которая была им опущена в поздних изданиях и восстановлена Шонером в издании 1592 г. Здесь можно видеть одну из сделанных в XVI в. попыток объединить различные разделы арифметики и алгебры, и построить на некоторой строгой основе единое учение о рациональном и иррациональном числе. | |
| ХVII век | [2] В начале века с появлением логарифмов получили широкое распространение десятичные дроби, без которых невозможны логарифмические вычисления. Трактаты по арифметике содержат главы о десятичных дробях. Запись десятичных дробей [2] Джон Не́пер (1550-1617) – шотландский математик, один из изобретателей логарифмов, первый публикатор логарифмических таблиц – ввёл запятую/точку для отделения целой части от дробной. Действия с обыкновенными и десятичными дробями. [2] Меций Адриен (Mеtius Adriaan, 1571-1635 гг.), – голландский астроном, математик и врач, профессор математики и медицины университета им. Франекере (с 1598 г). Известны его некоторые математические работы, относящиеся к арифметике и геометрии. В работе «Arithmetica et Geometria nova» (1625 г.) имеется раздел, посвященный десятичным дробям. [5] Уингейт Эдмунд (ок. 1586-1656 гг.) – английский юрист и математик. Опубликовал работу «Арифметика» (ок.1629 г.), состоявшую из двух книг: «Естественная арифметика» и «Искусственная арифметика». [2] Бонавенту́ра Франче́ско Кавалье́ри (Bonaventura Francesco Cavalieri, 1598-1647) – итальянский математик, предтеча математического анализа, наиболее яркий и влиятельный представитель «геометрии неделимых» излагает теорию вопроса перевода обыкновенной дроби в десятичную и обратно, на рассматривая периодичности (1643 г.). [2] Такэ (André Tacquet, 1612 -1660 гг.) – фламандский математик в «Теории и практике арифметики» (Arithmetical theoria et praxis, 1656 г.) указывает, что десятичные дроби делают действия над обыкновенными дробями лишними. Возникновение периодических дробей. [2] В научных трактатах появляются периодические десятичные дроби. [9] Джон Ва́ллис/Уо́ллис (John Wallis, 1616 -1703 гг.) – английский математик, один из предшественников математического анализа – традиционно определил число как собрание единиц, но в действительности трактовал это понятие шире: «Дробные числа – не суть числа в собственном смысле (proprie dicti), они отвечают не на вопрос: сколько? (например, сколько часов (quot horae), но на вопрос: какое количество? (quantum horae) и относятся скорее к категории непрерывных величин». [2] Большой трактат Валлиса по алгебре (1676 г.) содержит ряд предложений о периодических дробях: от обращения каких обыкновенных получается периодическая чистая или смешанная дробь; сколько цифр содержит период; как превратить периодическую дробь в обыкновенную; при извлечении корня квадратного из неполного квадрата или корня кубического из неполного куба никогда не получается периодическая дробь. Валлис не касается вопроса о природе непериодической бесконечной дроби. [2] Готфрид Вильгельм фон Лейбниц (Gottfried Wilhelm von Leibniz; 1646-1716 гг.) – немецкий философ, математик, юрист, дипломат – изучает свойства периодических дробей. Изложение дробей в учебниках. [2] Уи́льям О́тред (William Oughtred, 1575-1660 гг.) – английский математик, изобретатель логарифмической линейки (1622 г.) и один из создателей современной математической символики – в учебнике арифметики «Clavis Mathematicae» (Ключ к математике, 1631 г.) посвятил главу десятичным дробям. | |
| ХVIII век | Терминология. [2] Сегнер Янош Андрош (Segner, 1704-1777 гг.) – венгерский математик и физик, иностранный член Петербургской АН (1754 г.) – ввёл термины «правильная дробь», «неправильная дробь». Изучение свойств периодических дробей: [2] Иоганн Генрих Ламберт (Johann Heinrich Lambert; 1728-1777 гг.) – физик, философ, математик – изучает свойства периодических дробей, устанавливая связь этих свойств с теорией чисел; впервые доказывает иррациональность чисел π и e (1766 г.). [2] Леона́рд Э́йлер (Leonhard Euler; 1707- 1783 гг.) – швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук – изучает свойства периодических дробей, устанавливая связь этих свойств с теорией чисел; исследует константы е и γ (названа в его честь), создал полную теорию непрерывных/цепных дробей. [2] Джон Робертсон, преподаватель Королевской математической школы в Портсмуте, а затем библиотекарь лондонского Королевского общества в 1768 г. впервые отмечает, что 0,999…=1. Изложение дробей в учебниках. [  2] В предисловии к 16 изданию «Арифметики» Уингейта (1735 г.) читаем: «изложении арифметики целых чисел, необходимой для денежных расчётов, для торговли и других приложений, даётся раньше, чем открывается доступ к крутым, трудным путям дробей, при одном виде которых учащиеся приходят в такое уныние, что останавливаются и восклицают: ради бога, не дальше». [6] Христиан фон Вольф (1679-1754 гг.) - знаменитый немецкий ученый-энциклопедист, философ, юрист и математик опубликовал несколько руководств по математике, оказавших сильное влияние на организацию преподавания этой дисциплины в Германии и России: «Математический лексикон» (Mathematisches Lexikon) и «Курс математика» (Course de Matématique), – требовал (впервые), чтобы свойства действий, установленные для целых чисел, обосновывались и для дробей [2]. Действия с систематическими дробями: [2] Жозе́ф Луи́ Лагра́нж (фр. Joseph Louis Lagrange, итал. Giuseppe Lodovico Lagrangia; 1736 –1813) – французский математик, астроном и механик итальянского происхождения; | |
| XIX век | Изучение свойств периодических дробей: [2] Иоганн Карл Фри́дрих Га́усс (Johann Carl Friedrich Gauß; 1777-1855 гг.) – немецкий математик, астроном и физик, считается одним из величайших математиков всех времён, «королём математиков» – устанавливает связь периодических дробей с учением о степенных вычтах и первообразных корнях; приводит периоды для дробей 1/р для многих простых чисел р. Главная закономерность, которую он обнаружил: длина наименьшего периода такой дроби, является делителем числа (р – 1), иногда совпадая с ним (для чисел 7, 17, 23, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181,193 и др. ) Изложение периодических десятичных дробей в учебниках. [2] Правило (современное школьное) обращения чистых и смешанных периодических дробей в обыкновенные излагается впервые в руководстве Августа (1822 г.) | |
[3] ссылка скрыта /Википедия – (ссылка скрыта)
[5] Уингейт Эдмунд /Личности – (ссылка скрыта)
[6] Христиан фон Вольф. Курс математики, том 1 / Коллекция старинных математических книг // Каталог математических Интернет-ресурсов MATHTREE.RU. – (htree.ru/wolf/volume1/index_r.php">).
[7] ссылка скрыта/ Википедия – (ссылка скрыта)
[8] Plimpton G.A. The history of elementary mathematics in the plimpton library / Jeremy Norman`s HistoryofScience.com History of Science, Medicine, and Technology. – (ссылка скрыта).
[9] Всеобщая арифметика – часть 57/Энциклопедия знаний Рandia.ru. – (ссылка скрыта).
[10] Матвиевская Г. П. Рамус (1515-1572). – М.: Наука,1981. – 150 с., ил. – С.100-101.
[11] ссылка скрыта /Википедия – (ссылка скрыта)