Задачи курса: Обеспечить углубленное изучение отдельных предметов программы полного общего образования
| Вид материала | Пояснительная записка |
- Задачи специализированного класса Обеспечить углубленное изучение предметов физика,, 98.2kb.
- Учебная программа дисциплины дс. Ф. 00. Нестандартные задачи по программированию Специальность:, 68.72kb.
- Тезисы Автор: Лобанова Татьяна Николаевна учитель математики моу сош с. Филиппово Кирово-Чепецкого, 31.6kb.
- «Активизация познавательного интереса учащихся на уроках математики», 491.27kb.
- Перечень актуальных тем авторских разработок, 69.39kb.
- Программа курса изучение математики, 368.25kb.
- Стандарт среднего (полного) общего образования по русскому языку, 57.63kb.
- Стандарт среднего (полного) общего образования по русскому языку, 137.77kb.
- Стандарт среднего (полного) общего образования по русскому языку, 82kb.
- Стандарт среднего (полного) общего образования по русскому языку, 59.74kb.
Раздел 5. МАТЕМАТИКА
«Математика в современном мире»
Панаринва И.В., учитель математики высшей квалификационной категории Красногвардейской СОШ №2
Пояснительная записка
В настоящее время в соответствии с распоряжением Правительства Российской Федерации от 29.12.2001 № 175-р "Об одобрении концепции модернизации российского образования на период до 2010 г" на старшей ступени образовательной школы предусматривается введение профильного обучения, а в 9-м классе – введение предпрофильной подготовки и усиление профессиональной ориентации.
Курс "Математика в современном мире" знакомит учащихся с развитием математики в настоящее время и связывает предмет с выбором профессии. Современный мир неожиданно обнаружил, что математика уверенно расположилась в самых разных его частях и уголках. Сейчас уже все привыкли к словосочетаниям "математическая биология", "математическая психология", "математическая лингвистика", "математическая экономика". Распространение математики вширь сопровождается её проникновением вглубь: математика теперь занимает видное положение в жизни общества. Так что же дает людям математика как практическая наука?
Ответ на этот вопрос предлагает данный элективный курс.
Цель курса - знакомство с профессиями и специальностями, требующими математической подготовки; выбор профиля для обучения на старшей ступени общеобразовательной школы.
Задачи курса:
- Обеспечить углубленное изучение отдельных предметов программы полного общего образования,
- Создать условия для существенной дифференциации содержания обучения старшеклассников с широкими и гибкими возможностями построения школьниками индивидуальных образовательных программ;
- Расширить возможности социализации учащихся;
- Обеспечить преемственность между общим и профессиональным образованием;
- Более эффективно подготовить выпускников школы к освоению программ высшего профессионального образования.
Данный элективный курс является попыткой эффективно разрешить поставленные задачи на базе общеобразовательной области - математика. Он интересен тем, что привлекается обширный материал о различных специальностях и профессиях требующих математической подготовки разного уровня, тесно увязывается с направленностью ВУЗов Оренбургской области, дает представление о предмете «Высшая математика», который изучается на первых курсах высших учебных заведений. Курс должен сориентировать девятиклассников на выбор предметов для дальнейшего профильного обучения. Вместе с тем познавательный, также развлекательный материал активизирует познавательные процессы, расширяет мировоззрение.
Известно, что новый учебный материал усваивается школьниками (особенно имеющими проблемы в общеобразовательной подготовке), если он сопровождается достаточно большим числом иллюстрирующих его примеров. Поэтому программа совершенствования полученных знаний включает различные формы организации учебной деятельности: практикумы, круглые столы, деловые игры, тестирования.
В курсе имеется инвариантная и вариативная части. К сравнительно четко структурированному и подобранному обязательному материалу (инвариантная часть) можно подключать в процессе занятий большой объем произвольно выбранной, актуальной для темы информации, черпаемой из средств массовой информации, книг.
Объем различных форм учебной работы. Всего уроков - 16 часов, в том числе: практические занятия, деловые игры, тесты.
Критерии оценивания работы учащегося в рамках данного элективного курса
- Оценка за результат участия в эксперименте "Скорость обучаемости".
- Оценка за решение расчётных задач. Техника вычислений.
- Уровень усвоения учебного материала. Квадратный трёхчлен.
- Результаты тестирования.
Оценивание проводится карточками трёх цветов: зелёного, желтого, красного. Зелёный цвет - лучший результат, жёлтый - удовлетворительный результат, красный - неудовлетворительный. По результатам портфолио пишутся рекомендации.
Учебно-тематическое планирование
| Основное содержание | Всего уроков | В том числе | |||
| лекции | практикумы | деловые игры | тестирование и др. | ||
| 1. Что такое профессия, специальность. | 2 | 1 | | 1 | |
| 2.Математика - профилирующий предмет. | 2 | 1 | | | 1 |
| 3. Математика в инженерных специальностях. | 2 | 1 | 1 | | |
| 4. Математика для экономистов. | 2 | 1 | 1 | | |
| 5. Математика в биологии, медицине, сельском хозяйстве. | 2 | 1 | | | 1 |
| 6. Математика в общественных науках. | 2 | 1 | 1 | | |
| 7.Математическое моделирование. | 2 | 1 | 1 | | |
| 8. Основные ошибки и затруднения при выборе профессии. | 2 | 1 | | | 1 |
Содержание курса
Занятие 1.
Введение. Цели и задачи курса "Математика в современном мире". Что такое профессия, специальность? Пост, должность, рабочее место. О системе народного хозяйства России: классификация отраслей. Поиск адресов, где можно получить заинтересовавшую профессию и специальность.
Деловая игра "Я выбираю профессию". Работа со справочниками для поступающих в ВУЗы, ССУЗы России, Оренбургской области.
Занятие 2.
Математика - профилирующий предмет, что это означает? Различные уровни овладения учебным материалом на примере темы "Квадратный трёхчлен и квадратное уравнение": решение квадратных уравнений; вывод формулы корней квадратного уравнения; исследование взаимного расположения корней квадратного уравнения.
Способности общие и специальные.
Групповой эксперимент "Скорость обучаемости".
Занятие 3.
Математика в инженерных специальностях. Разделы математики, необходимые для освоения техники: функциональный анализ, начертательная геометрия и др.
Практикум по решению расчётных задач.
Занятие 4.
Математика для экономистов. Прикладная экономическая направленность: балансовые модели, предельный анализ, закон убывающей доходности, условия оптимального выпуска продукции.
Практикум по решению задач линейного программирования. Метод Гаусса.
Занятие 5.
Математика в биологии и медицине. Математика и сельскохозяйственное производство. Модель Леонтьева многоотраслевой экономики ( балансовый анализ).
Развлекательное мероприятие "Хочу всё знать!" - турнир остросюжетных задач из живой и неживой природы.
Занятие 6.
Математика в общественных науках. Статистические характеристики: размах, мода, частота, среднее арифметическое и среднее геометрическое.
Деловая игра: Опрос общественного мнения. Составление таблиц и диаграмм.
Занятие 7.
Математическое моделирование как основа решения задач. Плохо и хорошо поставленные задачи, этапы решения задачи. Составление алгоритма. Интерпретация ответа.
Практикум, экспериментальные задачи.
Занятие 8.
Основные ошибки и затруднения учащихся при решении вопроса о выборе профессии. Профессиональная пригодность и индивидуальный стиль работы. Содержание работы и абсолютные противопоказания.
Тест. Желания и возможности при выборе будущей профессии.
Методические рекомендации (фрагмент)
Рекомендации разработаны в соответствии с концепцией построения программы и позволяют учителям сориентироваться как в методических особенностях изложения учебного материала, так и в требованиях, предъявляемых к работе учащихся.
Основное назначение рекомендаций - помочь учителям в организации учебной деятельности школьников. В нём даются по каждому занятию:
- общая характеристика содержания;
- методические рекомендации к изучению материала с разбивкой по вопросам;
- указания к решению задач;
- рекомендации по форме проведения занятий;
- содержание используемых методик;
- указатель используемой литературы;
- описываются критерии оценивания деятельности учащихся.
Использование в учебном процессе данной программы и методического пособия к нему позволит учителю помочь каждому школьнику в осознанном выборе профиля обучения, связанного с математикой, а возможно, и отказаться от него; сформировать у школьников объективную оценку своих возможностей и желаний обучения по тому или иному профилю; расширит мировоззренческие представления учащихся о мире профессий.
Основными особенностями авторского подхода к изложению материала являются:
- Опора на наглядность;
- Снижение уровня строгости логических рассуждений при изложении теоретического материала, очевидного с точки зрения учащегося.
Такой подход и определяет главный метод работы учителя с классом - продуктивное обучение в группах в сочетании с индивидуальной деятельностью каждого учащегося. Отсюда следует, что большую часть времени каждого занятия необходимо использовать для выполнения практических заданий, проведения мини-экспериментов; организации деловых игр; семинаров-практикумов.
В систему вопросов, которые расширяют содержание базового курса основной школы, входят: «Решение систем линейных уравнений», «Квадратный трёхчлен с параметрами», «Текстовые задачи на оптимальное решение», «задачи на проценты». Эти темы, как правило вызывают затруднения у основной массы школьников, но широко используются в итоговой аттестации, а главное в углублённом курсе математики старшей школы.
Все методические рекомендации должны адаптироваться к конкретной группе учащихся, объективному уровню их подготовки, сформированности познавательных интересов и общеучебных навыков. Такая адаптация может привести к увеличению или уменьшению рассматриваемого материала.
В большинстве случаев нецелесообразно конспектировать теоретический материал о профессиях, т.к. он носит иллюстративный характер и содержится в печатных источниках (статьях, книгах).
Письменно учащиеся выполняют только практические групповые или индивидуальные задания.
Значительную помощь учителю может оказать школьная библиотека и проведение занятий в её читальном зале, особенно в том случае, если там есть видеоматериалы о различных профессиях.
Занятие 1. Что такое профессия? Что такое специальность?
Вопросы для обсуждения.
1.Что такое профессия?
2. Что такое специальность?
3. Что такое пост? Рабочее место?
4. Как можно получить профессию?
Средства обучения.
- Справочники для поступающих в вузы России, начиная с 2000 года.
- Справочник учебных заведений Оренбургской области.
- Учебные заведения Башкирии.
- Контурные административные карты России (для каждого ученика).
Формы и методы проведения занятия и организации учебной деятельности учащихся.
- Проблемная лекция на основе информационных материалов.
Постановка проблемных вопросов.
-Запишите в два столбика сначала известные вам профессии и специальности (5 примеров), а потом неизвестные вам профессии и специальности.
Но так как лекция в чистом виде довольно утомительна для школьников, то лучше всего проводить лекцию-беседу. На таких лекциях старшеклассники работают более активно, спорят, приводят примеры, деятельны, рассказывают о прочитанном, делают выводы. Насыщая беседу новым фактическим материалом, предлагая ребятам наводящие вопросы, мы приучаем их самостоятельно делать выводы, правила, закономерности. Известно, что изложенное учителем не всегда переходит в знания ученика, но те знания, к которым он подошёл самостоятельно, сохраняются практически на всю жизнь. Лекция-беседа кажется нам эффективной ещё и потому, что она позволяет учителю установить тесный контакт с учениками.
-Почему выбору профессии и специальности придают такое большое значение, как сам человек, так и государство?
-Какие профессии, по вашему мнению, будут востребованы через 5-8 лет, т. е. тогда, когда вы начнёте свою трудовую деятельность?
Информационный материал содержится в книге Климова Е. А. «Как выбрать профессию?»
2.Деловая игра «Образовательная карта региона».
Учащиеся разбиваются на группы по 4-5 человек. Каждая группа получает задание для работы со справочниками. Например, какие учебные заведения расположены в областном центре? Представьте одно из них.
Далее во время отчёта группы все остальные учащиеся наносят месторасположение учебных заведений на контурную карту. Так складывается карта «желаний», прогнозов получения образования.
Время для отчёта группы 10-12 минут.
Учащимся рекомендуется ещё и дома обсудить образовательную карту региона с родителями, нанести на неё учебные заведения, рекомендуемые родителями.
3.Дифференциально- диагностический опросник (ДДО).
Методика предназначена для отбора на различные типы профессий в соответствии с классификацией типов профессий Е. А. Климова. Используется при профориентации подростков.
Занятие 4. Математика для экономистов.
Вопросы для обсуждения.
- Профессия экономист.
- Профессия бухгалтер.
- Профессия маркетолог.
- Есть ли различие между этими профессиями? В чём оно?
- Решение систем линейных уравнений. Формулы Крамера. Метод Гаусса.
Средства обучения.
- БСЭ.
- Кремер Н. Ш. , Путко Б. А. , Тришин И. М. Высшая математика для экономистов.
- Климов Е. А. Как выбрать профессию?
Формы и методы проведения занятия и организации учебной деятельности.
- Круглый стол. Заслушивание сообщений, ответы на вопросы, дискуссии. Методику см. в предыдущем занятии.
- Лекционно-практическое занятие.
Учитель излагает материал темы в виде лекции, учащиеся конспектируют записи и начинают отработку навыков в парах, выполняя практическую работу.
Сведения, сообщаемые в данной лекции расширяют тему основного курса математики, т.к. вооружают учащихся двумя новыми способами решения систем линейных уравнений.
Вначале на простых примерах повторяются алгоритмы решения систем способом подстановки и сложения.
Дидактический материал.
1. Решить методом сложения системы уравнений:
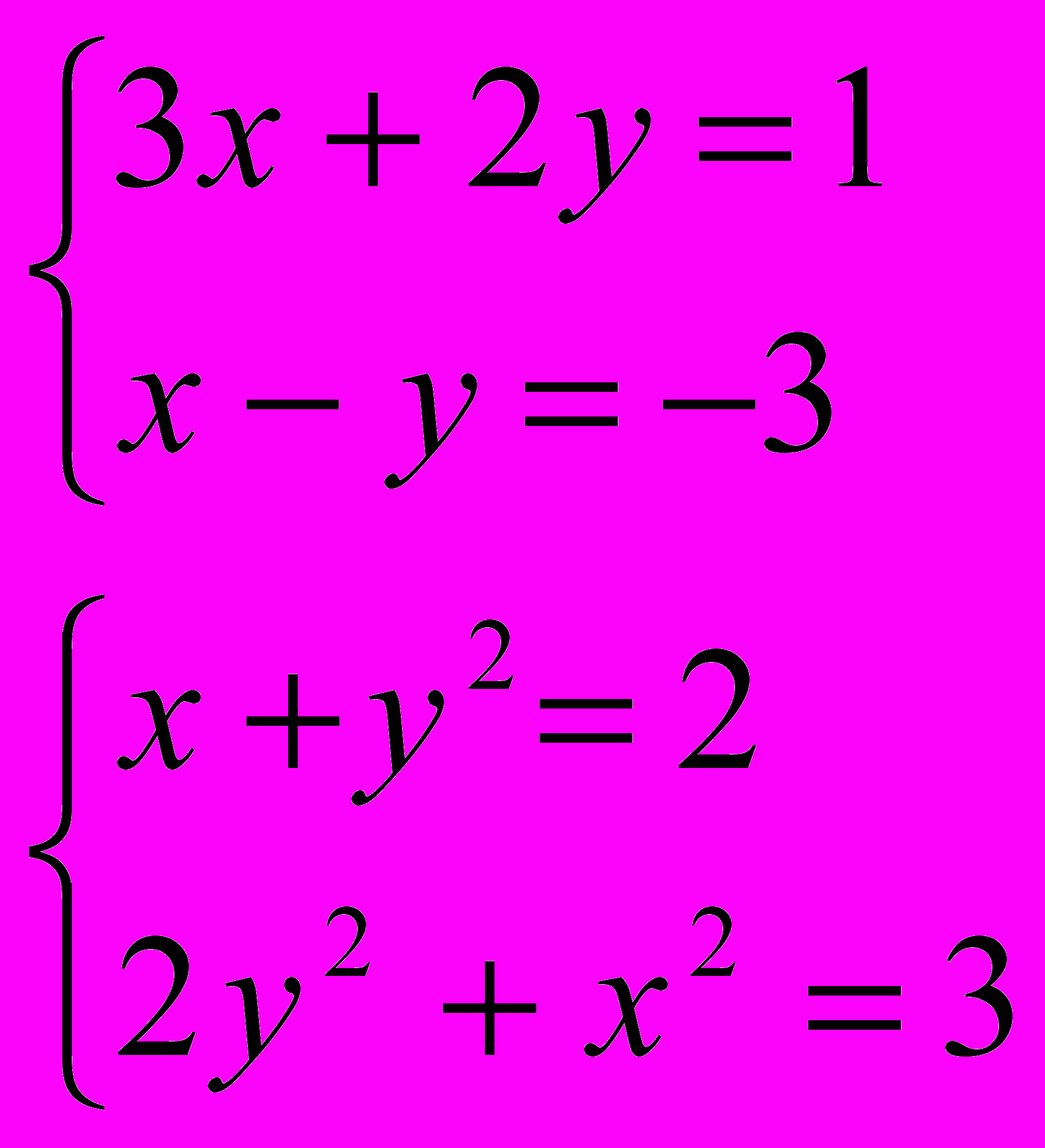
2. Решить методом подстановки систему уравнений

3. Метод Гаусса – метод последовательного исключения переменных - заключается в том, что с помощью элементарных преобразований система приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находят все остальные переменные.
Обучаем школьников на примере системы:

Задания для самостоятельной работы
Решите методом Гаусса системы:

4. Метод Крамера.
Рассматриваем на примере решения системы двух уравнений с двумя переменными:

В конце решения системы (любым способом) рекомендуем сделать проверку, подставляя найденные значения переменных в уравнения системы, и убедится в том, что они обращаются в верные равенства.
Изложенный материал имеет большой объём, является совершенно новым для учащихся и вызывает определённые вычислительные трудности. Поэтому рекомендуем его закрепить, организовав работу в парах: два ученика одновременно решают одну и туже систему, выполняя пошаговую взаимопроверку.
Перечень рекомендуемой литературы
- Высшая математика для экономистов: учебник для вузов/ Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман; Под ред. проф. Н.Ш.Кремера. - 2-е изд., перераб. и доп.-М: ЮНИТИ, 2001.
- Колмогоров А.Н. О профессии математика. - М.,1954.
- Лурье А.А. Методы линейного программирования и их применение в экономике. - М., 1964.
- Лютикас B.C. Школьнику о теории вероятностей. Учебное пособие по факультативному курсу для учащихся 8-9 классов. - М., 1986.
- Пекелис В.Д. Кибернетика от А до Я: маленькая энциклопедия. - М.: Дет. лит, 1990
«Элементы теории вероятностей»
разработала группа учителей математики (слушателей проблемных курсов ООИПКРО):
Морозова Н. Д., Воякина Н.В., Морозова Н.М., Черникова Е.В., Рябчевских Т.И., Сафонова Г.А., Иванникова Н.Е., Туюшева О.В.
Пояснительная записка
В содержание среднего образования России вносятся существенные изменения, в частности, в программу по математике основной школы включена теория вероятностей и элементы статистики.
Теория вероятностей – это математическая наука о случайном и закономерностях случайного. В школьном курсе математики и других естественных науках господствовала только одна идея – о существовании жестких связей между явлениями и событиями. Эти связи представлены в форме законов физики, химии, математики, даже в курсе истории нет места случайности. он построен так, что складывается впечатление, что все события предопределены и закономерны .
Но окружающий нас мир полон случайностей. Это землетрясения, ураганы, подъемы и спады экономического развития, войны, болезни, случайные встречи и т.д.
Впрочем, мысль о том, что в окружающем мире много случайного, останется очевидной, но бесплодной, если не научится измерять случайность числом, вычислять шансы различных событий.
Теория вероятностей в средней школе - это признание обществом необходимости формирования своевременного мировоззрения, для которых одинаково важны представления и о жестких связях, и о случайном. Без знания понятий и методов тории вероятности и статистики невозможна организация эффективного конкурентоспособного производства, внедрение новых лекарств и методов лечения в медицине, обеспечения страховой защиты граждан от непосредственных обстоятельств, проведения обоснованной социальной политики.
Уже несколько лет в различных регионах России учащееся основной школы занимаются по учебным комплектам “Математика 5-6” по редакцией Г.В. Дорофеева и И.Ф. Шарыгина, “Математика 7-9” под редакцией Г. В. Дорофеева. Это первые российские учебники в которых последовательно с 5 по 9 классы проводится вероятностно-статистическая линия, органично связанная с другими темами курса. В учебных комплектах “Алгебра 7-9” А.Г. Мордковича выпущены дополнительные параграфы для ознакомления учащихся с элементами теории вероятностей и математической статистики. В других учебных комплектах эта линия не просматривается.
Предлагаемая программа “Элементы теории вероятностей” разработана в рамках предпрофильной подготовки в связи с задачами модернизации образования. Программа направлена на повышение общей культуры мышления учащихся, развитие и систематизацию навыков логического мышления .
Курс предполагает изложение теоретического материала в комплексе с практическими заданиями.
“Элементы теории вероятностей” - это предметно-ориентированный курс по выбору, который расширяет базовые знания учащихся и рассчитан на 14 часов.
Основная цель:
- предоставление учащимся возможности самоопределения с выбором профиля;
- формирование вероятностно-статистических представлений учащихся, навыков творческой деятельности.
Задачи:
- Формирование умения творчески мыслить, решать нестандартные задачи.
- Реализовать гуманитарную составляющую курса через знакомство с историческими сведениями.
- Подчеркнуть эстетические аспекты изучаемых вопросов
Учебно-тематическое планирование
| № п/п | Название темы | Количество часов | Форма занятия |
| I. Основные понятия комбинаторики (4 часа) | |||
| 1 | Понятие факториала | 1 | лекция |
| 2 | Перестановки | 1 | практикум |
| 3 | Сочетания | 1 | практикум |
| 4 | Размещения | 1 | практикум |
| II. Основные понятия теории вероятностей (6 часов) | |||
| 5 | Предмет теории вероятностей | 1 | круглый стол |
| 6 | Основные понятия и определения | 1 | лекция |
| 7 | Относительная частота событий | 1 | практикум |
| 8 | Определения вероятности события | 1 | практикум |
| 9 | Вероятность и графы | 1 | семинар |
| 10 | Вероятность и числовые ряды | 1 | лекция |
| III. Операции над событиями (4 часа) | |||
| 11 | Теорема сложения вероятностей | 1 | лекция |
| 12 | Условная вероятность | 1 | практикум |
| 13 | Независимость событий | 1 | практикум |
| 14 | Формула полной вероятности | 1 | круглый стол |
| | Итого | 14 | |
Содержание курса
- Основные понятия комбинаторики
Факториал; вычисление значений выражений, содержащих факториал; перестановки; формула нахождений перестановок; размещения; формула для нахождения размещений; сочетания, формула для нахождения сочетаний.
- Основные понятия теории вероятностей.
Знакомство с предметом теории вероятностей; испытания; случайное событие; равновозможные события; несовместные и совместные события; достоверные и невозможные события; полная система событий; противоположные события; свойства вероятностей; решение задач на нахождение вероятности события; составление графов; полная и условная вероятность; формула Байеса; суммирование числовых рядов вероятностными методами.
- Операции над событиями.
Сумма событий; теорема сложения вероятностей, ее доказательство и следствия из неё; произведение событий; частный случай события; вероятность суммы двух совместных событий; условная вероятность; независимые события; теорема умножения вероятностей; формула полной вероятности; гипотеза; решение задач с применением операций над событиями.
Методические рекомендации
- Основные понятия комбинаторики.
При изучении комбинаторики необходимо демонстрировать комбинаторные методы на большом количестве простых и конкретных примерах.
При усвоении курса рекомендуется решать задачи самостоятельно в классе, а часть заданий выполнять дома с последующим обсуждением в классе на занятиях семинаров и практикумов.
Прежде всего нужно обозначить круг задач, которые будут предложены ученикам. Это задачи, содержащие вопросы типа: “Сколькими способами?”, “Сколько всего существует вариантов?”. Например, сколько существует способов распределения золотой, серебряной и бронзовой медалей между командами в чемпионате по футболу? Сколькими способами можно добраться из одного города в другой? Сколько абонентов может обслужить телефонная станция, если телефонные номера четырехзначные и должны начинаться с цифры 9? Подобные задачи и называются комбинаторными.
II. Основные понятия теории вероятностей.
При изучении данного раздела заложить основу логического мышления, которая заучиванием аксиом и формул заменяет развитием вероятности интуиции, формальный вывод статистических оценок и критериев – их практическим применением. Предложить учащимся задачи на классическую вероятность (описание множества исходов – обоснование равновозможности – подсчет общего количества исходов – подсчет количества благоприятных исходов – вычисление вероятности). Обратить внимание на практическую значимость данных тем. На семинарах предложить вероятностные ситуации из повседневной жизни, где есть проблема выбора, оценка степени риска и шансов на успех. Целесообразно для проведения “круглого стола” пригласить представителей профессий, где используется изучаемая теория. При усвоении раздела рекомендуется решать задачи самостоятельно в классе, а часть заданий выполнить дома с последующим обсуждением на занятиях практикумах. Также для домашнего задания предложить подобрать примеры о связи изучаемой темы с реальной действительностью. Предложить эксперимент, выполнение проектов и исследовательских заданий.
III. Операции над событиями.
При изучении этого раздела необходимо ознакомить учащихся с процессом построения модели, учить их анализировать, проверять адекватность построенной модели реальными ситуациями, развивать вероятностную интуицию. Проиллюстрировать применение формулы полной вероятности на практике, показать связь с другими областями знаний. Использовать прием “привлекательная цель”. Большую часть времени отводить на практические работы. Рекомендуется выполнять творческие задания (рефераты, сообщения, эссе). В конце изучения всего курса целесообразно изучить мнение учащихся о проделанной работе.
Перечень рекомендуемой литературы
- Афанасьев В.В. Теория вероятностей в примерах и задачах: Учебное пособие.-Ярославль,1994
- Афанасьев В.В. Введение в теорию вероятностей с помощью графов //Приложение к газете “Первое сентября” “Математика”.– 1999. - №35. - с.8-12
- Бунимович Е.А. , Булычев В.А. Вероятность и статистика 5-9 кл.- М.: Дрофа, 2002
- Глеман М., Варга Т. Вероятность в играх и вычислениях. - М.:Просвещение, 1979
- Матюхин В. Задания по теории вероятностей //Приложение к газете “Первое сентября” “Математика”. – 1999. - №3.- с.23-24
- Оре Т.Теория графов: перевод с английского.-М.: Наука,1980
- Плоцки А Вероятность в задачах для школьников: Книга для учащихся. – М.: Просвещение, 1996
- Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. Теория вероятностей и статистика. – М.: Изд-во МЦ НМО АО “Московские учебники”, 2004
- Элементы теории вероятностей //Приложение к газете “Первое сентября” “Математика”. - 1999- №41-42.
«Этот удивительный симметричный мир»
разработала группа учителей математики (слушателей проблемных курсов ООИПКРО): Забарова Е.А., Иванова В.И., Ильина С.Ю., Полоненко А.В., Солодовникова С.Ф., Тарасова Н.Н., Тимина Н.Н., Ягофарова Г.М.
Пояснительная записка
В гармонии, соперник мой,
Был шум лесов иль вихрь буйный,
Иль иволги напев живой,
Иль ночью моря гул глухой,
Иль шепот речки тихоструйной.
А.С.Пушкин
Курс по выбору для предпрофильной подготовки учащихся 9-х классов посвящен одной из интереснейших тем математики - симметрии.
Геометрические преобразования – тема школьного курса геометрии, которая застывшие формы геометрических фигур позволяет сделать динамичными.
Одним из недостатков упражнений школьного курса математики является их однофункциональность. Часто они направлены на достижение одной цели, выполняют одну функцию (освоение введенных понятий, закрепление способов действий). Между тем необходимо учитывать интересы школьников, их предпочтения и вводить в процесс обучения упражнения, которые включают учеников в осмысленную, продуктивную деятельность.
В каждом классе есть много учеников – «гуманитариев», которым интересны приложения математики, применение ее элементов в искусстве, архитектуре, дизайне и т.д. Их привлекает конкретная деятельность с интересными для них объектами. Им доставляет огромное удовольствие занятия геометрическими играми, упражнениями, т.е. буквально все, что связано с геометрией (рисование, конструирование, лепка и т.д.).
Материал данного курса отобран в соответствии с общими целями образования и помогает учащимся овладеть системой знаний и умений для дальнейшего формирования ценностных ориентаций, а также помогает осознанно выбрать дальнейший профиль обучения.
Темы курса предусматривают организацию творческой деятельности, результаты которой могут войти в «портфель» достижений учащихся.
Динамика интереса к курсу фиксируется с помощью диагностирования.
Цель курса: способствовать самоопределению школьников относительно направления дальнейшего профилирования, включить математику в сферу познавательных интересов учащихся.
Задачи курса:
- показать красоту математики как безусловную и несомненную реальность;
- дать ученику возможность реализовать свой интерес к предмету;
- уточнить готовность и способность ученика осваивать выбранный предмет (математику) на повышенном уровне;
- создать условия для подготовки к экзаменам по выбору, т.е. по наиболее вероятным предметам будущего профиля;
- расширить представления учащихся о сферах применения математики(не только в естественных науках, но и в такой области гуманитарной сферы деятельности, как искусство);
- расширить общекультурный кругозор учащихся посредством знакомства их с лучшими образцами произведений искусства.
В программе предусмотрена вариативность в преподавании курса.
К подобранному обязательному материалу можно подключить в процессе занятий большой объем информации, черпаемой из различных информационных ресурсов (в том числе Интернет).
Курс рассчитан на 8 часов.
Основные принципы курса:
- систематичность;
- воспитывающий и обучающий характер;
- доступность;
- индивидуальность;
- дифференциация;
- учет уровня развития интересов учащихся.
Методы реализации принципов:
- тестирование;
- беседа;
- наблюдение;
- моделирование;
- работа в творческой мастерской;
- работа со справочной литературой.
Механизм реализации программы:
I. Подготовительный этап:
- утверждение курса;
- «рождение коллектива»;
- родительское собрание по знакомству с программой;
- входная диагностика.
II. Основной этап:
- изучение основ курса по плану;
- изучение справочной литературы;
- выполнение практических и творческих работ.
III. Заключительный этап:
Разработка проекта творческих мастерских с защитой каждого проекта. Выдвижение лучших работ на районные или областные конференции.
Ожидаемый результат
В ходе изучения курса учащиеся должны:
- получить представление о сферах применения математики не только в естественных науках, но и в такой области гуманитарной сферы деятельности, как искусство;
- сформировать познавательные интересы и общеучебные умения учащихся.
Инструментарий для оценивания результатов:
- тестирование;
- беседа;
- наблюдение.
Учебно-тематическое планирование
| глава | тема | количество часов | ||
| всего | в том числе | |||
| теоретич. | практич. | |||
| Часть I. Введение | ||||
| 1 | Математические основы законов красоты в окружающем нас мире | 1 | 1 | |
| Часть II. Симметрия и ее виды | ||||
| 1 | Симметрия в природе живой и неживой | 1 | | 1 |
| 2 | Симметрия и стили | 1 | | 1 |
| 3 | Зеркальная симметрия | 1 | | 1 |
| 4 | Другие виды симметрии | 1 | | 1 |
| 5 | Орнаменты, бордюры, их построение | 1 | | 1 |
| Часть III. Творческая мастерская | ||||
| 1 | Творческая мастерская | 2 | | 2 |
| Итого: | 8 | 1 | 7 | |
Содержание курса
1. Введение. Математические основы законов красоты в окружающем нас мире.
Эстетическое содержание математики: абстрактность, единство частей, совершенство языка.
Математика в технической эстетике, стандартизации и квалиметрии:
- Техническая эстетика. Математика художника-конструктора.
- Стандартизация.
- Квалиметрия. Математика в квалиметрии.
2. Симметрия и ее виды.
Симметрия в природе живой и неживой. Симметрия в мире растений; в мире животных, насекомых, птиц. Асимметрия. Симметрия в кристаллах, технике, архитектуре.
Симметрия и стили. Русский классический стиль. Стили: готический, Возрождения, барокко и др.
Зеркальная симметрия. Объект и его зазеркальный двойник. Зеркальная симметрия (левая и правая).
Поворотная симметрия. Зеркально-поворотная симметрия. Переносная симметрия (трансляционная). Виды симметрий (косая, квадратная, прямоугольная, ромбическая). Орнаменты и бордюры. Построение орнаментов и бордюров. 7 типов бордюров.
3. Творческая мастерская.
Творческие отчеты в виде проекта (фотоальбом, выставка).
Методические рекомендации
1 занятие. Учащимся сообщается цель и значение курса. На лекционном занятии рекомендуется остановиться на определении эстетики как науки о прекрасном и показать эстетический элемент в математике – реальная вещь.
2 и 3 занятия рекомендуется провести в форме семинаров по группам. Цель занятий: активизация познавательных интересов учащихся посредством сотрудничества ученика и учителя. Группам даются примерные задания: симметрия растений, симметрия кристаллов, симметрия в архитектуре. На семинарских занятиях дети защищают свои работы в виде проекта, реферата и т.д.
4, 5 и 6 занятия предлагается провести как практические по группам, для выработки навыков исследовательской и практической деятельности по математике.
7 и 8 занятия – практические работы: рефераты, модели, рисунки, лепки, фотоальбомы.
Примерные задания для исследовательской работы
Нарисуйте какие-нибудь бордюры, используя в качестве трафарета буквы русского или латинского алфавита.
Гуляя по улицам, найдите и зарисуйте различные бордюры на зданиях, в переходах, в оформлении изгородей и т.д.
По предложенному образцу (см. приложение) провести исследование и определить, где применяется симметрия, какого вида в готическом стиле.
Нарисуйте орнамент в круге, нарисуйте свою «готическую» розу.
Перечень рекомендуемой литературы
- Болтянский В.П. Геометрия 7 – 9. –М.: Институт учебника, 1998.
- Болтянский В.П. Поворот и центральная симметрия //Математика в школе. – 1989. - № 6
- Жданова Н.С. Основы архитектуры.: Альбом на печатной основе. – Магнитогорск, 1999
- Зенкевич И.Т. Эстетика урока математики: Пособие для учителя. – М.: Просвещение, 1981
- Методическое пособие по декоративной композиции для абитуриентов ХГФ, составитель Лагвиненко Г.М. – Магнитогорск, 1997
- Сонин А.С. Постижение совершенства. – М.: Знание, 1987
- Тарасов Л. Этот удивительно симметричный мир. – М.: Просвещение, 1982
- Шарыгин И.Ф. Наглядная геометрия: Учебное пособие для учащихся. М.: МИФОС, 1995
Научно-методическая консультация осуществлялась О.Н.Скрынниковой, зав. УМК математики ООИПКРО
